Bidirectional heterostructures consisting of graphene and lateral MoS₂/WS₂ composites: a first-principles study

Abstract

First-principles calculations have been performed to explore the structural and electronic properties of bidirectional heterostructures composed of graphene and (MoS₂)_X/(WS₂)_4−X (X = 1, 2, 3) lateral composites and compare them with those of heterobilayers formed by graphene and pristine MS₂ (M = Mo, W). The band gaps of the lateral heterostructures lie between those of pristine MoS₂ and WS₂. The weak coupling between the two layers can induce a tiny band-gap opening of graphene and formation of an n-type Schottky contact at the G-(MoS₂)_X/(WS₂)_4−X interface. Moreover, the combination ratio of MoS₂/WS₂ can control the electronic properties of G-(MoS₂)_X/(WS₂)_4−X. By applying external electric fields, the band gaps of (MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) monolayers undergo a direct–indirect transition, and semiconductor–metal transitions can be found in WS₂. External electric fields can also be used effectively to tune the binding energies, charge transfers, and band structures (the types of Schottky and Ohmic contacts) of G-(MoS₂)_X/(WS₂)_4−X heterostructures. These findings suggest that G-(MoS₂)_X/(WS₂)_4−X heterostructures can serve as high-performance nano-electronic devices.

---

1. Introduction

Graphene has been used widely in various fields owing to its electronic, mechanical, and optical properties since it was discovered in 2004.^1,2 However, the zero gap of graphene limits its development and applications.³ A vertical heterostructure formed by graphene and other two-dimensional matter, e.g., hexagonal boron nitride or transition-metal dichalcogenides (TMDs), via van der Waals forces is a promising method of solving this problem because it could lead to a band-gap opening while preserving the mechanical and electronic structures of graphene.^2–19 Most TMDs, of which the general chemical formula is MX₂ (M = Mo, W, V, Co etc., X = S, Se, or Te, etc.), are promising candidates for electronic devices because they have a direct band gap, high carrier mobility, high on/off current ratios, and unique exaction properties.^{2,6,12,16–24} Vertical heterostructures composed of a pristine TMDs monolayer and graphene have been the subject of extensive investigation.^{2,10,12–16,19,25–28}

Lateral heterostructures have been fabricated within TMD monolayers (MoS₂/WS₂, WS₂/WSe₂, MoSe₂/WSe₂, etc.) and have opened up unprecedented opportunities to improve the performance of electronic devices with tunable electronic properties.^2,29–34 However, due to limitations of the experimental techniques, the electrochemical properties of such in-plane heterostructures have not been fully explored. Although theoretical studies have reported the electronic properties of some lateral heterostructures,^24,35–39 the effects of the component ratio and external electric fields on the properties of such hybrid systems remain unclear. We are left with an interesting question: would any peculiar properties appear in the vertical and lateral combined bidirectional heterostructures formed by graphene and in-plane TMDs composites in comparison with the heterobilayer from graphene and pristine TMDs?

Although extraordinary bidirectional heterostructures of γ-graphyne-MoSe₂/WSe₂ were investigated by Sun et al.,³⁵ the G-MoS₂/WS₂ system has not been studied. Inspired by the above factors, bidirectional heterostructures formed by graphene and lateral MoS₂/WS₂ composite are explored here on the basis of first-principles calculations. For comparison purposes, the heterobilayers from graphene and pristine MoS₂ or WS₂ are also considered. Because previous research has demonstrated that external electric fields can be used to tune the band gaps or other electronic structures of vertical heterostructures,^{9,10,15,17–19,27,28,40–45} the structural and electronic properties of a (MoS₂)_X/(WS₂)_4−X, (X = 0, 1, 2, 3, 4) monolayer with different proportions and vertical heterobilayers with graphene under external electric fields are systematically investigated by density functional theory (DFT) calculations. The results indicate that external electric fields can induce consequential changes in the properties of a (MoS₂)_X/(WS₂)_4−X monolayer and G-(MoS₂)_X/(WS₂)_4−X heterostructures.

2. Computational methods

The DMol³ code was used for geometric optimization and electronic properties calculations.^46,47 The generalized gradient approximation (GGA) with a Perdew–Burke–Ernzerhof (PBE) functional and the DFT semi-core pseudo-potentials (DSPP) double numerical atomic basis set plus polarization (DNP) were employed.⁴⁸ To show the expected differences with the different function, the on-site Coulomb interaction (GGA + U approach) was adopted to study the electric properties using Vienna ab initio simulation package program (VASP) package.^49,50 Due to the poor description of the weak van der Waals interactions of the popular PBE functional,⁵⁶ an empirical dispersion-corrected density functional theory approach proposed by Grimme was used.⁵¹ The optimal geometric convergence criteria of energy, force, and displacement were 1.0 × 10⁻⁵ Ha, 0.002 Ha Å⁻¹, and 0.005 Å, respectively. The K-point was set to 9 × 9 × 1 for structural optimization and to 15 × 15 × 1 to calculate electronic properties. The vacuum thickness was set to more than 20 Å to avoid interactions between the neighboring layers. A vertical external electric field in the range of 0 to 1.0 V Å⁻¹ was applied to (MoS₂)_X/(WS₂)_4−X lateral heterostructures and −1.0 to 1.0 V Å⁻¹ to the G-(MoS₂)_X/(WS₂)_4−X heterobilayer, with a positive electric field pointing from (MoS₂)_X/(WS₂)_4−X to graphene and a negative field pointing in the reverse d direction.^39,41 Electron density differences were computed by CASTEP code.⁵²

The optimized lattice constants of graphene, MoS₂, and WS₂ were 2.472 Å, 3.214 Å, and 3.206 Å, respectively. In line with the modeling methods of graphene-MoS₂,^16,45 silicene-MoS₂,⁴⁴ and germanene-MoS₂ heterostructures,^43,53 a 4 × 4 substrate layer of (MoS₂)_X/(WS₂)_4−X was chosen to match the 5 × 5 graphene monolayer, producing a tolerable lattice mismatch for this system (∼4.0%). To quantitatively describe the interaction strength between the graphene sheet and the (MoS₂)_X/(WS₂)_4−X monolayer, the binding energies were defined as

E_b=(E_total − E_{(MoS2)X/(WS2)4−X} − E_graphene)/N

where E_total, E_{(MoS2)X/(WS2)4−X}, and E_graphene are the energies of the G-(MoS₂)_X/(WS₂)_4−X heterostructures, isolated (MoS₂)_X/(WS₂)_4−X, and graphene monolayers, respectively, and N is the number of carbon atoms in the supercell.

3. Results and discussion

3.1. (MoS₂)_X/(WS₂)_4−X monolayer

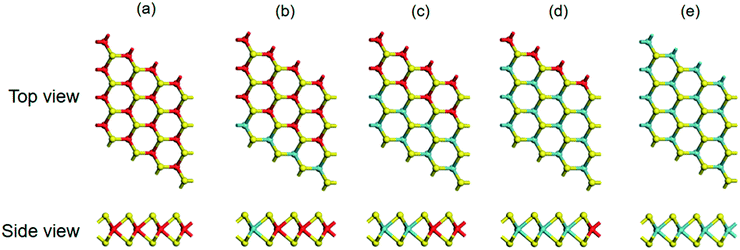
The electronic properties of pristine MoS₂ or WS₂ and the (MoS₂)_X/(WS₂)_4−X lateral heterostructures systems illustrated in Fig. 1, i.e., (MoS₂)₁/(WS₂)₃, (MoS₂)₂/(WS₂)₂, and (MoS₂)₃/(WS₂)₁, were examined first. Fig. 2 presents the calculated electronic band structures of G-(MoS₂)_X/(WS₂)_4−X heterostructures. As shown in Fig. 2, pristine MoS₂ and WS₂ (x = 0 and 4) have respective direct band gaps at the K point of 1.59 eV and 1.81 eV, which are almost identical to previously reported values.^22,36,37,45 The band gaps of the hybrid lateral heterostructures with different combination MoS₂/WS₂ ratios lie between those of pristine MoS₂ and WS₂, and they all maintain the direct band gaps of a pristine TMDs monolayer.

Fig. 1 Top and side views of stable configurations of WS₂ (a), (MoS₂)₁/(WS₂)₃ (b), (MoS₂)₂/(WS₂)₂ (c), (MoS₂)₃/(WS₂)₁ (d), MoS₂ (e), respectively. The yellow, green, and red balls denote S, Mo and W atoms, respectively.

Fig. 2 Band structures of WS₂ (a), (MoS₂)₁/(WS₂)₃ (b), (MoS₂)₂/(WS₂)₂ (c), (MoS₂)₃/(WS₂)₁ (d), and MoS₂ (e), respectively. The horizontal red lines represent the Fermi level. (f) Calculated band gap of (MoS₂)_X/(WS₂)_4−X monolayer as a function of electric field intensity.

Although some theoretical studies of MoS₂/WS₂ lateral heterostructures have been reported in recent years,^24,35–38 the effects of external electric fields on the electronic properties of this lateral hybrid monolayer have been ignored. As the external electric field varies from 0 to 0.6 V Å⁻¹, the bond distance of WS₂ monolayer increases with the electric field strength. And the bond distance decreases when the electric field strength more than 0.7 V Å⁻¹. The bond distance of MoS₂ was also increases with the electric field strength, but the change is weak (<0.1 Å). The change of bond distance of the lateral hybrid (MoS₂)_X/(WS₂)_4−X (X = 1, 2, 3) heterostructures are not obvious. As shown in Fig. 2, the applied electric fields are associated with a decreasing trend in band gaps for the above systems because field-induced repulsion among the electronic levels results in a shift in conduction band minimum (CBM) toward the Fermi level (E_F), consequently, a reduction in band gaps (Fig. S1† and 2).

Furthermore, a direct–indirect band gap transition of (MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) under vertical electric fields has also been observed. The pristine MoS₂ and (MoS₂)_X/(WS₂)_4−X lateral heterostructures maintain semiconductor characteristics under an external electric field (F ≤ 1.0 V Å⁻¹). While for WS₂, the conduction band overlaps the valence band across the Fermi level at 0.6 V Å⁻¹ to 0.7 V Å⁻¹ (Fig. S1†), and the band gap of WS₂ shows a semiconductor–metal transition, which is consistent with a report by Affandi.⁵⁴ As shown in Fig. S1,† the band structures of MoS₂ are more stable than that of WS₂ under the external electronic fields with different intensity. We suspect that the 5d electrons of W may cross the Fermi level under the strong electric field, which would cause the materials to be metallic. This is in good agreement with previous studies.^20,25,54 As a result, the electric properties of (MoS₂)_X/(WS₂)_4−X monolayer with high W concentration become not stable under the electric field and present different trend.

3.2. G-(MoS₂)_X/(WS₂)_4−X heterostructures

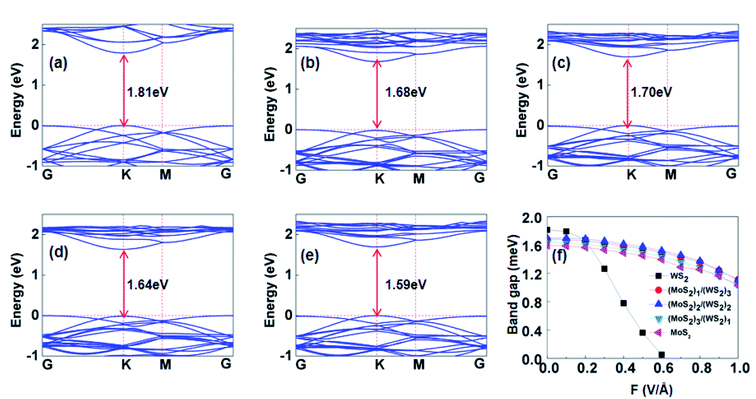
Vertical hybrid structures of graphene stacked on a (MoS₂)_X/(WS₂)_4−X monolayer were constructed and calculated. A supercell is formed by alternate stacking of graphene sheets on a (MoS₂)_X/(WS₂)_4−X monolayer, with 16 metal (Mo or W) atoms, 32 S atoms, and 50 C atoms. To analyze the optimal stacking patterns, two representative approaching modes were considered. The C atom was placed on top of the metal atoms (W or Mo) or was located above the top of the S atoms (Fig. S2†). The binding energies for different stacking patterns differ by less than 0.1 meV per C atom. This indicates that interlayer bonding takes place irrespective of stacking pattern, which is in agreement with G-MoS₂ and Si-MoS₂.^16,44 Only the most stable configuration shown in Fig. 3 is considered in the following discussions. The interlayer distances between a (MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) monolayer and graphene are ∼3.2 Å, which suggests that the coupling between them is dominated by van der Waals forces. Graphene exhibits a small wrinkle (∼0.1 Å) in its planar atomic framework for all G-(MoS₂)_X/(WS₂)_4−X heterostructures, similar to the previous calculation.^16,26,55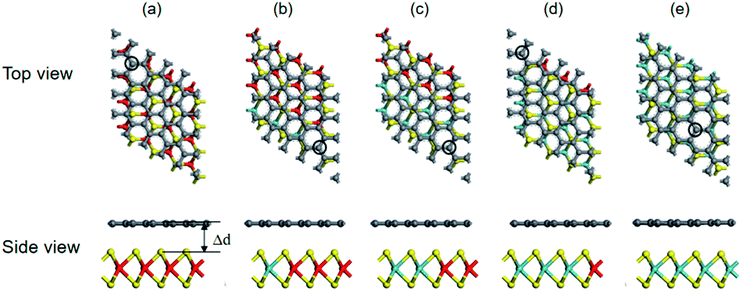

Fig. 3 Top and side views of stable configurations of G-WS₂ (a), G-(MoS₂)₁/(WS₂)₃ (b), G-(MoS₂)₂/(WS₂)₂ (c), G-(MoS₂)₃/(WS₂)₁ (d), G-MoS₂ (e), respectively. The gray balls denote C atom.

Fig. 4 shows the calculated E_b values of G-(MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) heterobilayers. The calculated E_b of G-WS₂ is −26.9 meV per C atom, which is nearly identical to previously reported values based on the GGA-PBE function (−26.8 meV and −29 meV).^15,55 The E_b of G-MoS₂ is −10.2 meV per C atom, which is smaller than the value (−23 meV) reported by Ma et al. based on local density approximation (LDA) calculations,¹⁶ which is not surprising given that the LDA method overestimates the calculated results. The binding energies of graphene with (MoS₂)₁/(WS₂)₃, (MoS₂)₂/(WS₂)₂, and (MoS₂)₃/(WS₂)₁ lateral heterostructures were −24.1, −18.9, and −14.4 meV, respectively. This clearly shows that the E_b between graphene and the lateral hybrid MoS₂/WS₂ with different mixing proportions lies between those of graphene with pristine MoS₂ or WS₂. As expected, binding strength increases with proportion of WS₂ units in (MoS₂)_X/(WS₂)_4−X, in the order of G-WS₂ > G-(MoS₂)₁/(WS₂)₃ > G-(MoS₂)₂/(WS₂)₂ > G-(MoS₂)₃/(WS₂)₁ > G-MoS₂. These E_b values confirm weak van der Waals interactions between the graphene sheet and the (MoS₂)_X/(WS₂)_4−X monolayer, including pristine MX₂ and hybrid lateral heterostructures. As shown in the Fig. S3,† the d band of MoS₂ has much sharper peak than WS₂ around the Fermi level, indicating that the 4d electrons of Mo atoms are more localized than the 5d electrons of W atoms. The more delocalized 5d orbitals leads to the enhancement of interlayer coupling with the concentration of W increases, and consequently results in the strengthen of binding energy.

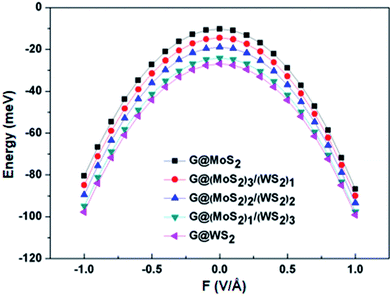Fig. 4 Binding energies (E_b) as a function of the electric field intensity for graphene-(MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) heterobilayers.

To probe the effect of external electric fields on the interaction strength of G-(MoS₂)_X/(WS₂)_4−X heterostructures, vertical electric fields in the range of −1.0 V Å⁻¹ to 1.0 V Å⁻¹ were applied to the heterobilayer. The computed E_b as a function of electric fields for G-(MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) is plotted in Fig. 4. The stability order of the heterostructures was maintained regardless of electric field intensity. An applied positive or negative electric field can result in a more negative E_b for the above systems, which suggests that the external electric field can intensify the interaction between the layers and enhance heterobilayer stability. Moreover, the direction of the electric field has a weak influence on E_b, with the effect of the positive field being slightly more pronounced. For G-(MoS₂)_X/(WS₂)_4−X heterobilayers, the change of bond length and the interlayer distance are both less than 0.1 Å under the external electric field. So, there is no obvious structural changes in the heterobilayers under the external electric field. Enhancement of interlayer binding in the heterostructures can be attributed to built-in electric fields that are asymmetrical in the sense that graphene and the (MoS₂)_X/(WS₂)_4−X monolayer have different electron affinities. Field-driven charge transfer among the component layers then enhances the electrostatic interaction between heterobilayers.

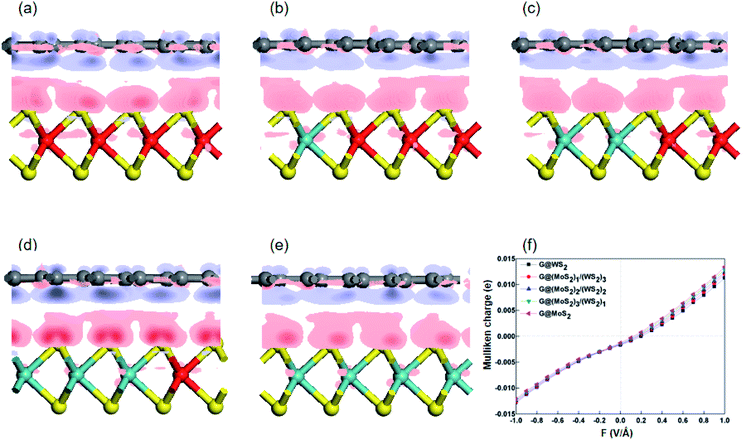
To further explore the bonding nature of graphene and the (MoS₂)_X/(WS₂)_4−X monolayer, the charge density difference of the G-(MoS₂)_X/(WS₂)_4−X hybrid systems, indicated in Fig. 5(a–e), was used to visualize electron transfer upon formation of the interlayer. This can be defined as

Δρ = ρ_total − ρ_{(MoS2)X/(WS2)4−X} − ρ_graphene

where ρ_total, ρ_{(MoS2)X/(WS2)4−X}, and ρ_graphene are the charge densities for G-(MoS₂)_X/(WS₂)_4−X heterostructures, the isolated (MoS₂)_X/(WS₂)_4−X monolayer, and graphene, respectively. The pink and blue areas denote electron accumulation and depletion, respectively, which clearly demonstrate the charge transfer direction between graphene and (MoS₂)_X/(WS₂)_4−X in the heterobilayers. In these heterostructures, electrons are lost on the graphene side, while they accumulate mainly on the (MoS₂)_X/(WS₂)_4−X side, and a small amount of electrons accumulate on the graphene sheet. The electrons spontaneously transfer from (MoS₂)_X/(WS₂)_4−X monolayer to the graphene sheet. An interface dipole is defined by the potential step, forming in ther interface, is due to the difference in the work function of the MoS₂/WS₂ and graphene. Although such a value of charge transfer is quite small, it leads to an interface dipoles that cannot be ignored. This is consistent with experimental phenomena.^27,28 As supported by Mulliken population analysis (Fig. 5f), the charge accumulated on the graphene sheet increases with proportion of WS₂ units in (MoS₂)_X/(WS₂)_4−X, although the change is small. This small charge transfer suggests a weak van der Waals force between the interlayers, which is consistent with the E_b results.

Fig. 5 Differential electron density of G-WS₂ (a), G-(MoS₂)₁/(WS₂)₃ (b), G-(MoS₂)₂/(WS₂)₂ (c), G-(MoS₂)₃/(WS₂)₁ (d), and G-MoS₂ (e), respectively. Pink and blue areas correspond to the accumulation and depletion of electronic densities. (f) Mulliken populations of per C atom in graphene for (MoS₂)_X/(WS₂)_4−X as a function of the electric field strength.

The effect of the external electric field on charge redistribution among the G-(MoS₂)_X/(WS₂)_4−X interlayers was further examined. Fig. 5f displays the average Mulliken population per C atom in graphene as a function of electric field strength. The extent of charge transfer is in the order of G-WS₂ < G-(MoS₂)₁/(WS₂)₃ < G-(MoS₂)₂/(WS₂)₂ < G-(MoS₂)₃/(WS₂)₁ < G-MoS₂ regardless of field strength and direction. The negative electric fields cause more electrons to flow from (MoS₂)_X/(WS₂)_4−X to graphene; thus, the graphene monolayer is more negatively charged with increasing field intensity. When the electric field reaches −1.0 V Å⁻¹, the graphene in G-WS₂, G-(MoS₂)₁/(WS₂)₃, G-(MoS₂)₂/(WS₂)₂, G-(MoS₂)₃/(WS₂)₁, and G-MoS₂ gains 0.0128 e, 0.0127 e, 0.0124 e, 0.0123 e, and 0.0121 e per C atom, respectively. When the external electric field is applied in the positive direction, the heterostructures exhibit the opposite response: the transferred electrons of G-WS₂ gradually decrease to zero at 0.2–0.3 V Å⁻¹, while other G-(MoS₂)_X/(WS₂)_4−X hybrid systems reach zero at 0.1–0.2 V Å⁻¹. A further increase in the strength of the electric field alters the transferred direction of electrons from graphene to the (MoS₂)_X/(WS₂)_4−X monolayer, with graphene being more positively charged. In brief, graphene sheets lose electrons as the electric field changes from negative to positive, reaching 0.0113 e, 0.0120 e, 0.0124 e, 0.0129 e, and 0.0134 e per C atom at F = 1.0 V Å⁻¹ for G-WS₂, G-(MoS₂)₁/(WS₂)₃, G-(MoS₂)₂/(WS₂)₂, G-(MoS₂)₃/(WS₂)₁, and G-MoS₂, respectively.

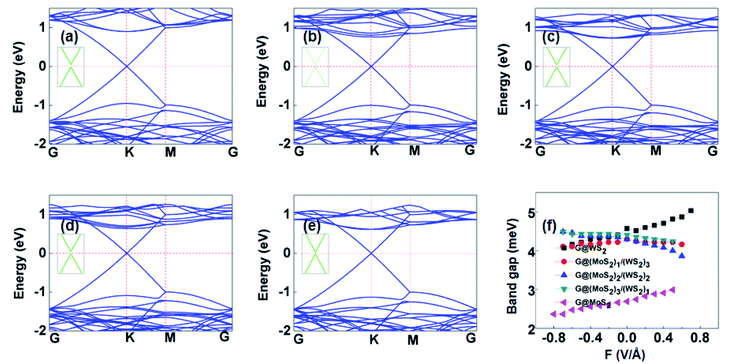
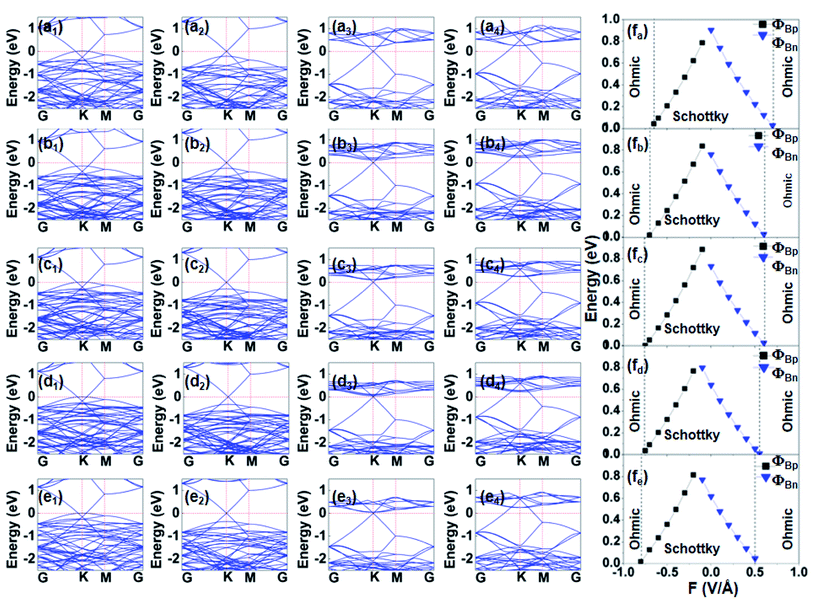
The degree of charge transfer between heterobilayers can reflect variation in the interface dipole and the magnitude of the band gap opening. To analyze the impact of the weak van der Waals forces between the interlayer on the band gaps of the hybrid G-(MoS₂)_X/(WS₂)_4−X heterostructures, the calculated gaps are presented in Fig. 6(a–e). Small band gap openings of 4.6, 4.3, 4.3, 4.4, and 2.7 meV for respective stable heterostructures of G-WS₂, G-(MoS₂)₁/(WS₂)₃, G-(MoS₂)₂/(WS₂)₂, G-(MoS₂)₃/(WS₂)₁, and G-MoS₂ were observed. The derived gaps of G-WS₂ and G-MoS₂ are consistent with previously reported results (3.9 meV for WS₂, 2 meV for MoS₂),^16,26 indicating the plausibility of our calculated results. As shown in Fig. S4,† the band structure which used the on-site Coulomb interaction (GGA + U approach) is same to our result in current research. And the difference of band gap is small (2 meV). So, our results are credible. Fig. 6(a–e) shows that the Dirac point of graphene around the Fermi level is well preserved in the band structure of all G-(MoS₂)_X/(WS₂)_4−X heterostructures, which suggests a high carrier mobility of the hybrid systems. As shown in Fig. 6f, when an external electric field is applied, the band gaps at the Dirac point of graphene change only slightly (<0.5 meV) in those heterobilayers, regardless of the field direction.

Fig. 6 Band structures of G-WS₂ (a), G-(MoS₂)₁/(WS₂)₃ (b), G-(MoS₂)₂/(WS₂)₂ (c), G-(MoS₂)₃/(WS₂)₁ (d), and G-MoS₂ (e), respectively. The insets in figure are a magnification of the area near the linear dispersion band at the K point. The horizontal red lines represent the Fermi level. (f) Band gaps of G-(MoS₂)_X/(WS₂)_4−X heterostructures as a function of the electric field intensity.

External electric fields have a large effect on the Schottky barrier of the G-(MoS₂)_X/(WS₂)_4−X heterostructures in our calculations. When the Fermi level is close to the CBM, known as the n-type Schottky barrier (Φ_Bn), it is defined as Φ_Bn = E_C − E_F. Similarly, the p-type Schottky contact corresponds to the Fermi level close to the valence band maximum (VBM), and the Schottky barrier (Φ_Bp) is defined as Φ_Bp = E_F − E_V, where E_V and E_F are the CBM and VBM, respectively. The Fermi level was referenced at 0 eV. To quantitatively characterize regulation of the external electric field on the Schottky barrier of the above heterobilayers, the evolutions of Schottky contact type and Schottky barrier height of G-(MoS₂)_X/(WS₂)_4−X heterostructures as a function of electric field intensity are supplied in Fig. 7(f_a–e). The corresponding band structures of G-(MoS₂)_X/(WS₂)_4−X heterostructures under external electric fields at 1.0, −0.5, 0.5 and 1.0 V Å⁻¹ are also shown.

Fig. 7 Band structures of G-WS₂ (a₁₋₄), G-(MoS₂)₁/(WS₂)₃ (b₁₋₄), G-(MoS₂)₂/(WS₂)₂ (c₁₋₄), G-(MoS₂)₃/(WS₂)₁ (d₁₋₄) and G-MoS₂ (e₁₋₄) under electric fields at F = −1.0, −0.5, 0.5 and 1.0 V Å⁻¹ (1–4). The horizontal red lines represent the Fermi level. (f_a–f_e) Schottky barrier in the G-(MoS₂)_X/(WS₂)_4−X heterostructures as a function of the electric field intensity.

Combining Fig. 6(a–e) with Fig. 7(f_a–e), it becomes clear that, without the external electric field, coupling of graphene with the (MoS₂)_X/(WS₂)_4−X monolayer causes the heterostructures to form an n-type Schottky contact. In addition, as the X value increases in G-(MoS₂)_X/(WS₂)_4−X heterostructures, the position of the Fermi level shifts toward the CBM of the (MoS₂)_X/(WS₂)_4−X monolayer and, consequently, the n-type Schottky barrier height decreases. Thus, different ratios of Mo and W in lateral composites can effectively control the Schottky barrier of G-(MoS₂)_X/(WS₂)_4−X heterostructures.

When positive electric fields are applied, the CBM of the (MoS₂)_X/(WS₂)_4−X monolayer shifts down to the Fermi level to reduce the n-type Schottky barrier height gradually as the intensity increases. The Φ_Bn of the G-(MoS₂)_X/(WS₂)_4−X heterostructures disappears, along with a transition to Ohmic contact to present metallic characteristics, when the electric field intensity increases to 0.7, 0.6, 0.6, 0.5, and 0.5 V Å⁻¹ for G-(MoS₂)_X/(WS₂)_4−X heterostructures (X = 0, 1, 2, 3, 4), respectively. Moreover, the Fermi level falls to below the Dirac point of graphene, leading to p-type (hole) doping in graphene. The trend in variation of the Schottky barrier height of G-MoS₂ under positive electric fields is consistent with results reported by Hu et al.⁴¹ As the electric field varies from 0 to −0.1 V Å⁻¹, the n-type Schottky contact transforms to p-type Schottky contact for the G-WS₂, G-(MoS₂)₁/(WS₂)₃, and G-(MoS₂)₂/(WS₂)₂ interfaces. While the applied negative electric field strength is more than −0.1 V Å⁻¹, the VBM of WS₂, (MoS₂)₁/(WS₂)₃, and (MoS₂)₂/(WS₂)₂ above the Fermi level declines, and the Φ_Bp decreases gradually. Finally, the corresponding heterostructures change into the Ohmic contact when the respective field strength approaches −0.6, −0.7, and −0.7 V Å⁻¹. The Dirac point of graphene decreases to below the Fermi level, resulting in n-type (hole) doping in graphene. For the G-(MoS₂)₃/(WS₂)₁ and G-MoS₂ interfaces, at a strength less than −0.1 V Å⁻¹, they retain an n-type Schottky contact. Variation of the electric field from −0.1 to −0.2 V Å⁻¹ can induce a transition from n-type to p-type Schottky contacts. Under applied negative electric fields strength greater than −0.2 V Å⁻¹, the VBM of (MoS₂)₃/(WS₂)₁ and MoS₂ below the Fermi level decreases gradually to reduce Φ_Bp. When the strength increases to −0.7 and −0.8 V Å⁻¹, conversion from the p-type Schottky contact to the Ohmic contact occurs at the G-(MoS₂)₃/(WS₂)₁ and G-MoS₂ interface. The graphene's Dirac point crosses the Fermi level and moves into the valence band of (MoS₂)₃/(WS₂)₁ and MoS₂, which is below the Fermi level, resulting in n-type (hole) doping in graphene. In summary, electric fields can induce an electrostatic potential difference at the G-(MoS₂)_X/(WS₂)_4−X interface and affect the charge transfer process between graphene and the (MoS₂)_X/(WS₂)_4−X monolayer. Applied external electric fields can therefore control contact formation (Schottky and Ohmic contacts) in G-(MoS₂)_X/(WS₂)_4−X heterostructures and tune the type of doping in graphene.

4. Summary and conclusions

We performed density functional theory calculations to systematically study the structural and electronic properties of (MoS₂)_X/(WS₂)_4−X monolayers and G-(MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) heterobilayers. The impact of external electric fields was also explored. We found that the band gaps of lateral hybrid (MoS₂)_X/(WS₂)_4−X (X = 1, 2, 3) heterostructures lie between those of the pristine MoS₂ and WS₂. Applied external vertical electric fields can gradually decrease the band gaps and produce a direct–indirect transition. External electric fields can also induce a semiconductor–metal transition in the WS₂ monolayer when the field strength is more than 0.6 V Å⁻¹. Interlayer coupling in graphene and the (MoS₂)_X/(WS₂)_4−X (X = 0, 1, 2, 3, 4) monolayer is dominated by weak van der Waals interactions. A tiny band gap opening (<5 meV) at the Dirac point of graphene suggests such hybrid materials have a high carrier mobility. The E_b, charge transfers, and Φ_Bn of G-(MoS₂)_X/(WS₂)_4−X bidirectional heterostructures increase with proportion of WS₂ units in (MoS₂)_X/(WS₂)_4−X, while they all lie between those of G-WS₂ and G-MoS₂. Furthermore, external electric fields can greatly enhance coupling strength, efficiently tuning the amount and direction of charge transfer between the interlayer. External electric fields can therefore not only control the Schottky barrier height, but also the type of Schottky barrier (n-type and p-type) and contact formation type (Schottky and Ohmic contacts) at the G-(MoS₂)_X/(WS₂)_4−X interface. External electric fields can tune the position of the Dirac point relative to the Fermi level to achieve effective doping (p-type and n-type) in graphene. Due to their electronic properties, G-(MoS₂)_X/(WS₂)_4−X heterostructures provide a significant opportunity to design high-performance nano-electronic devices, such as tunable G-(MoS₂)_X/(WS₂)_4−X-based Schottky barrier diodes and field-effect transistors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 21103096), the Natural Science Foundation of Shandong Province (ZR2014AM025). We also thank the Taishan Scholar Program of Shandong Province (ts201511027).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306(5696), 666.
2. C. Tan, X. Cao, X.-J. Wu, Q. He, J. Yang, X. Zhang, J. Chen, W. Zhao, S. Han, G.-H. Nam, M. Sindoro and H. Zhang, Recent Advances in Ultrathin Two-Dimensional Nanomaterials, Chem. Rev., 2017, 117(9), 6225–6331.
3. Y. Wu, Y.-M. Lin, A. A. Bol, K. A. Jenkins, F. Xia, D. B. Farmer, Y. Zhu and P. Avouris, High-frequency, scaled graphene transistors on diamond-like carbon, Nature, 2011, 472, 74.
4. A. Ebnonnasir, B. Narayanan, S. Kodambaka and C. V. Ciobanu, Tunable MoS₂ bandgap in MoS₂-graphene heterostructures, Appl. Phys. Lett., 2014, 105(3), 031603.
5. X. Chen, R. Meng, J. Jiang, Q. Liang, Q. Yang, C. Tan, X. Sun, S. Zhang and T. Ren, Electronic structure and optical properties of graphene/stanene heterobilayer, Phys. Chem. Chem. Phys., 2016, 18(24), 16302–16309.
6. K. D. Pham and C. V. Nguyen, First principles calculations of the geometric structures and electronic properties of van der Waals heterostructure based on graphene, hexagonal boron nitride and molybdenum diselenide, Diamond Relat. Mater., 2018, 88, 151–157.
7. H. V. Phuc, V. V. Ilyasov, N. N. Hieu, B. Amin and C. V. Nguyen, Van der Waals graphene/g-GaSe heterostructure: tuning the electronic properties and Schottky barrier by interlayer coupling, biaxial strain, and electric gating, J. Alloys Compd., 2018, 750, 765–773.
8. K. D. Pham, N. N. Hieu, H. V. Phuc, I. Fedorov, C. Duque, B. Amin and C. V. Nguyen, Layered graphene/GaS van der Waals heterostructure: controlling the electronic properties and Schottky barrier by vertical strain, Appl. Phys. Lett., 2018, 113(17), 171605.
9. P. Le, N. N. Hieu, L. M. Bui, H. V. Phuc, B. D. Hoi, B. Amin and C. V. Nguyen, Structural and electronic properties of a van der Waals heterostructure based on silicene and gallium selenide: effect of strain and electric field, Phys. Chem. Chem. Phys., 2018, 20(44), 27856–27864.
10. T. Georgiou, R. Jalil, B. D. Belle, L. Britnell, R. V. Gorbachev, S. V. Morozov, Y.-J. Kim, A. Gholinia, S. J. Haigh, O. Makarovsky, L. Eaves, L. A. Ponomarenko, A. K. Geim, K. S. Novoselov and A. Mishchenko, Vertical field-effect transistor based on graphene–WS₂ heterostructures for flexible and transparent electronics, Nat. Nanotechnol., 2012, 8, 100.
11. C. R. Dean, A. F. Young, I. Meric, C. Lee, L. Wang, S. Sorgenfrei, K. Watanabe, T. Taniguchi, P. Kim, K. L. Shepard and J. Hone, Boron nitride substrates for high-quality graphene electronics, Nat. Nanotechnol., 2010, 5, 722.
12. C. Li, Q. Cao, F. Wang, Y. Xiao, Y. Li, J.-J. Delaunay and H. Zhu, Engineering graphene and TMDs based van der Waals heterostructures for photovoltaic and photoelectrochemical solar energy conversion, Chem. Soc. Rev., 2018, 47(13), 4981–5037.
13. L. Britnell, R. V. Gorbachev, R. Jalil, B. D. Belle, F. Schedin, A. Mishchenko, T. Georgiou, M. I. Katsnelson, L. Eaves, S. V. Morozov, N. M. R. Peres, J. Leist, A. K. Geim, K. S. Novoselov and L. A. Ponomarenko, Field-Effect Tunneling Transistor Based on Vertical Graphene Heterostructures, Science, 2012, 335(6071), 947.
14. A. K. Geim and I. V. Grigorieva, Van der Waals heterostructures, Nature, 2013, 499, 419.
15. F. Zhang, W. Li, Y. Ma, Y. Tang and X. Dai, Tuning the Schottky contacts at the graphene/WS₂ interface by electric field, RSC Adv., 2017, 7(47), 29350–29356.
16. Y. Ma, Y. Dai, M. Guo, C. Niu and B. Huang, Graphene adhesion on MoS₂ monolayer: an ab initio study, Nanoscale, 2011, 3(9), 3883–3887.
17. W. Zan, W. Geng, H. Liu and X. Yao, Electric-field and strain-tunable electronic properties of MoS₂/h-BN/graphene vertical heterostructures, Phys. Chem. Chem. Phys., 2016, 18(4), 3159–3164.
18. Y. Li, C. Y. Xu, J. K. Qin, W. Feng, J. Y. Wang, S. Zhang, L. P. Ma, J. Cao, P. A. Hu and W. Ren, Tuning the excitonic states in MoS₂/graphene van der Waals heterostructures via electrochemical gating, Adv. Funct. Mater., 2016, 26(2), 293–302.
19. H. Tian, Z. Tan, C. Wu, X. Wang, M. A. Mohammad, D. Xie, Y. Yang, J. Wang, L.-J. Li and J. Xu, Novel field-effect Schottky barrier transistors based on graphene-MoS₂ heterojunctions, Sci. Rep., 2014, 4, 5951.
20. D. J. Trainer, A. V. Putilov, C. Di Giorgio, T. Saari, B. Wang, M. Wolak, R. U. Chandrasena, C. Lane, T.-R. Chang and H.-T. Jeng, Inter-layer coupling induced valence band edge shift in mono-to few-layer MoS₂, Sci. Rep., 2017, 7, 40559.
21. H. He, P. Lu, L. Wu, C. Zhang, Y. Song, P. Guan and S. Wang, Structural Properties and Phase Transition of Na Adsorption on Monolayer MoS₂, Nanoscale Res. Lett., 2016, 11(1), 330.
22. I.-G. Buda, C. Lane, B. Barbiellini, A. Ruzsinszky, J. Sun and A. Bansil, Characterization of thin film materials using SCAN Meta-GGA, an accurate nonempirical density functional, Sci. Rep., 2017, 7, 44766.
23. C. Lane, D. Cao, H. Li, Y. Jiao, B. Barbiellini, A. Bansil and H. Zhu, Understanding Phase Stability of Metallic 1T-MoS₂ Anodes for Sodium-Ion Batteries, Condens. Matter, 2019, 4(2), 53.
24. J. Lee, J. Huang, B. G. Sumpter and M. Yoon, Strain-engineered optoelectronic properties of 2D transition metal dichalcogenide lateral heterostructures, 2D. Mater, 2017, 4(2), 021016.
25. C. Zhang, A. Johnson, C.-L. Hsu, L.-J. Li and C.-K. Shih, Direct imaging of band profile in single layer MoS₂ on graphite: quasiparticle energy gap, metallic edge states, and edge band bending, Nano Lett., 2014, 14(5), 2443–2447.
26. Z. Wang, Q. Chen and J. Wang, Electronic Structure of Twisted Bilayers of Graphene/MoS₂ and MoS₂/MoS₂, J. Phys. Chem. C, 2015, 119(9), 4752–4758.
27. C.-J. Shih, Q. H. Wang, Y. Son, Z. Jin, D. Blankschtein and M. S. Strano, Tuning On–Off Current Ratio and Field-Effect Mobility in a MoS₂–Graphene Heterostructure via Schottky Barrier Modulation, ACS Nano, 2014, 8(6), 5790–5798.
28. W. Zhang, C.-P. Chuu, J.-K. Huang, C.-H. Chen, M.-L. Tsai, Y.-H. Chang, C.-T. Liang, Y.-Z. Chen, Y.-L. Chueh, J.-H. He, M.-Y. Chou and L.-J. Li, Ultrahigh-Gain Photodetectors Based on Atomically Thin Graphene-MoS₂ Heterostructures, Sci. Rep., 2014, 4, 3826.
29. Y. Gong, J. Lin, X. Wang, G. Shi, S. Lei, Z. Lin, X. Zou, G. Ye, R. Vajtai, B. I. Yakobson, H. Terrones, M. Terrones, B. K. Tay, J. Lou, S. T. Pantelides, Z. Liu, W. Zhou and P. M. Ajayan, Vertical and in-plane heterostructures from WS₂/MoS₂ monolayers, Nat. Mater., 2014, 13, 1135.
30. X. Duan, C. Wang, J. C. Shaw, R. Cheng, Y. Chen, H. Li, X. Wu, Y. Tang, Q. Zhang, A. Pan, J. Jiang, R. Yu, Y. Huang and X. Duan, Lateral epitaxial growth of two-dimensional layered semiconductor heterojunctions, Nat. Nanotechnol., 2014, 9, 1024.
31. Z. Zhang, P. Chen, X. Duan, K. Zang, J. Luo and X. Duan, Robust epitaxial growth of two-dimensional heterostructures, multiheterostructures, and superlattices, Science, 2017, 357(6353), 788.
32. X.-Q. Zhang, C.-H. Lin, Y.-W. Tseng, K.-H. Huang and Y.-H. Lee, Synthesis of Lateral Heterostructures of Semiconducting Atomic Layers, Nano Lett., 2015, 15(1), 410–415.
33. K. Bogaert, S. Liu, J. Chesin, D. Titow, S. Gradečak and S. Garaj, Diffusion-Mediated Synthesis of MoS₂/WS₂ Lateral Heterostructures, Nano Lett., 2016, 16(8), 5129–5134.
34. P. K. Sahoo, S. Memaran, Y. Xin, L. Balicas and H. R. Gutiérrez, One-pot growth of two-dimensional lateral heterostructures via sequential edge-epitaxy, Nature, 2018, 553, 63.
35. Q. Sun, Y. Dai, Y. Ma, W. Wei and B. Huang, Vertical and Bidirectional Heterostructures from Graphyne and MSe₂ (M = Mo, W), J. Phys. Chem. C, 2015, 6(14), 2694–2701.
36. W. Wei, Y. Dai and B. Huang, In-plane interfacing effects of two-dimensional transition-metal dichalcogenide heterostructures, Phys. Chem. Chem. Phys., 2016, 18(23), 15632–15638.
37. J. Sun, N. Lin, H. Ren, C. Tang, L. Yang and X. Zhao, Gas adsorption on MoS₂/WS₂ in-plane heterojunctions and the I–V response: a first principles study, RSC Adv., 2016, 6(21), 17494–17503.
38. J. Kang, H. Sahin and F. M. Peeters, Tuning Carrier Confinement in the MoS₂/WS₂ Lateral Heterostructure, J. Phys. Chem. C, 2015, 119(17), 9580–9586.
39. K. Kośmider and J. Fernández-Rossier, Electronic properties of the MoS₂-WS₂ heterojunction, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(7), 075451.
40. S. Nigam, S. K. Gupta, C. Majumder and R. Pandey, Modulation of band gap by an applied electric field in silicene-based hetero-bilayers, Phys. Chem. Chem. Phys., 2015, 17(17), 11324–11328.
41. W. Hu, T. Wang, R. Zhang and J. Yang, Effects of interlayer coupling and electric fields on the electronic structures of graphene and MoS₂ heterobilayers, J. Mater. Chem. C, 2016, 4(9), 1776–1781.
42. P. Zhang, X. Yang, W. Wu, L. Tian, H. Cui, K. Zheng, J. Jiang, X. Chen and H. Ye, Tunable electronic properties of silicene/GaP heterobilayer: effects of electric field or biaxial tensile strain, Chem. Phys. Lett., 2018, 700, 114–121.
43. H. Li, Y. Yu, X. Xue, J. Xie, H. Si, J. Y. Lee and A. Fu, Electroic and optical properties of germanene/MoS₂ heterobilayers: first principles study, J. Mol. Model., 2018, 24(12), 333.
44. N. Gao, J. Li and Q. Jiang, Tunable band gaps in silicene–MoS₂ heterobilayers, Phys. Chem. Chem. Phys., 2014, 16(23), 11673–11678.
45. X. Liu and Z. Li, Electric Field and Strain Effect on Graphene-MoS₂ Hybrid Structure: Ab Initio Calculations, J. Phys. Chem. C, 2015, 6(16), 3269–3275.
46. B. Delley, An all-electron numerical method for solving the local density functional for polyatomic molecules, J. Chem. Phys., 1990, 92(1), 508–517.
47. B. Delley, From molecules to solids with the DMol³ approach, J. Chem. Phys., 2000, 113(18), 7756–7764.
48. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
49. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
50. G. Kresse and J. Hafner, Ab initio molecular dynamics for open-shell transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(17), 13115.
51. S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124(3), 034108.
52. M. Segall, P. J. Lindan, M. a. Probert, C. J. Pickard, P. J. Hasnip, S. Clark and M. Payne, First-principles simulation: ideas, illustrations and the CASTEP code, J. Phys.: Condens. Matter, 2002, 14(11), 2717.
53. S. Zhou and J. Zhao, Electronic structures of germanene on MoS₂: effect of substrate and molecular adsorption, J. Phys. Chem. C, 2016, 120(38), 21691–21698.
54. Y. Affandi, M. Absor and K. Abraha, Effect of external electric field on spin-orbit splitting of the two-dimensional tungsten dichalcogenides WX₂ (X= S, Se), J. Phys.: Conf. Ser., 2018, 012070.
55. S.-S. Li and C.-W. Zhang, First-principles study of graphene adsorbed on WS₂ monolayer, J. Appl. Phys., 2013, 114(18), 183709.
56. J. Sun, R. C. Remsing, Y. Zhang, Z. Sun, A. Ruzsinszky, H. Peng, Z. Yang, A. Paul, U. Waghmare, X. Wu, M. L. Klein and J. P. Perdw, Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional, Nat. Chem., 2016, 8(9), 831.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra05692k

‡ These authors contributed equally to this work.

---