Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coexistence of normal and inverse deuterium isotope effects in a phase-transition sequence of organic ferroelectrics†
Sachio Horiuchi *a,
Shoji Ishibashi
*a,
Shoji Ishibashi b,
Kensuke Kobayashic and
Reiji Kumai
b,
Kensuke Kobayashic and
Reiji Kumai c
c
aElectronics and Photonics Research Institute (ESPRIT), National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki 305-8565, Japan
bResearch Center for Computational Design of Advanced Functional Materials (CD-FMat), National Institute of Advanced Industrial Science and Technology (AIST), Tsukuba, Ibaraki 305-8568, Japan
cCondensed Matter Research Center (CMRC) and Photon Factory, Institute of Materials Structure Science, High Energy Accelerator Research Organization (KEK), Tsukuba, Ibaraki 305-0801, Japan
First published on 2nd December 2019
Abstract
Supramolecular cocrystals of anilic acids with 2,2′-bipyridines exhibit successive phase transitions as well as unusual isotope effects. Ferroelectricity driven by a cooperative proton transfer along the supramolecular chains is accompanied by huge permittivity (a maximum of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) at the Curie point, as well as a large spontaneous polarization (maximum 5 μC cm−2) and a low coercive field ranging from 0.5 to 10 kV cm−1. Deuterium substitutions over the hydrogen bonds smoothly raise the Curie point and simultaneously reduce other phase-transition temperatures by a few tens of degrees. The coexistence of opposite isotope effects reduces the temperature interval of the intermediate paraelectric phase from 84 to 10 K for the 5,5′-dimethyl-2,2′-bipyridinium bromanilate salt. The bipyridine molecules exhibit interplanar twisting, which represents the order parameter relevant to the high-temperature phase transitions. The normal and inverse temperature shifts are ascribed to the direct and indirect effects, respectively, of the lengthened hydrogen bonds, which adjusts the molecular conformation of the flexible bipyridine unit so as to minimally modify their adjacent intermolecular interactions.
000) at the Curie point, as well as a large spontaneous polarization (maximum 5 μC cm−2) and a low coercive field ranging from 0.5 to 10 kV cm−1. Deuterium substitutions over the hydrogen bonds smoothly raise the Curie point and simultaneously reduce other phase-transition temperatures by a few tens of degrees. The coexistence of opposite isotope effects reduces the temperature interval of the intermediate paraelectric phase from 84 to 10 K for the 5,5′-dimethyl-2,2′-bipyridinium bromanilate salt. The bipyridine molecules exhibit interplanar twisting, which represents the order parameter relevant to the high-temperature phase transitions. The normal and inverse temperature shifts are ascribed to the direct and indirect effects, respectively, of the lengthened hydrogen bonds, which adjusts the molecular conformation of the flexible bipyridine unit so as to minimally modify their adjacent intermolecular interactions.
Introduction
The mobility of protons over hydrogen bonds often triggers various types of structural transformation in the solid state. The most fascinating examples include ferroelectrics and antiferroelectrics, in which crystal structures and the associated electric polarization are transformed in response to such external stimuli as changes in temperature, pressure, stress, or electric fields.1,2 These strong couplings among electric, mechanical, and thermal inputs and outputs have been utilized in capacitors, sensors, memories, actuators, and optoelectronics devices, among others.3,4Other intriguing issues pertaining to hydrogen-bonded compounds are related to the replacement of hydrogen by deuterium, because the distinct quantum–mechanical properties of deuterium often change the potential-energy curves of hydrogen bonds and alter proton dynamics sufficiently to have marked effects on the relative stability of phases and on electric, elastic, and optical properties, as well as on hydrogen-bond geometries.5–11 These effects have been observed in many inorganic and organic compounds, including the KH2PO4 (KDP) family, squaric acid, and 9-hydroxyphenalen-1-one, in which proton dynamics play crucial roles in polarization- and phase-switching, as evidenced by the huge isotope effects observed upon deuteration of the hydrogen bonds.12–17
Over the last decade, similar microscopic principles have been increasingly applied in the design of high-performance ferroelectric organic solids for use in environmentally benign electronic devices.18–26 One successful approach has been to accommodate mobile protons between proton-donating (D) and proton-accepting (A) moieties or molecules, as exemplified by the discovery of ferroelectric cocrystals of phenazine (Phz) with the haloanilic acids (2,5-dihalo-3,6-dihydroxy-p-benzoquinones) chloranilic acid (H2ca) or bromanilic acid (H2ba).27 These haloanilic acids, designated as H2xa, are strong dibasic acids suitable for realizing ferroelectricity. As shown in Chart 1, two-step deprotonation of the hydroxy groups transforms the π-conjugated molecular symmetry as well as the charge state from neutral H2xa through the Hxa− monoanion to the xa2− dianion. Whereas H2xa and xa2− are nonpolar, Hxa− monoanions display bistable polarities, as they can be polarized in either of two opposing directions, depending on the location of the proton. Their counterparts are nitrogen-containing aromatic compounds such as Phz, various 2,2′-bipyridine derivatives, 2,3-di-2-pyridinylpyrazine (dppz), or 1,5-naphthyridine (npd), which have moderate basicities. The presence of two more nitrogen atoms in each molecule of the base permits the acid and base molecules to self-assemble alternately to form linear supramolecular chains.28–30 The resulting series of acid–base cocrystals provide a suitable platform for achieving a deeper understanding of how hydrogen-bonded structures show changes in their microscopic ferroelectric properties and related macroscopic properties through the ordering or dynamics of protons. Earlier studies on some ionic crystals found some analogous behaviors with the KDP family; deuterium substitution elongated their hydrogen-bond length, and increased the potential-energy barriers for proton dynamics.28,31–33 The relative stabilization of the proton-ordered ferro/antiferroelectric state raises the Curie point as well as the ferroelectric polarizations.
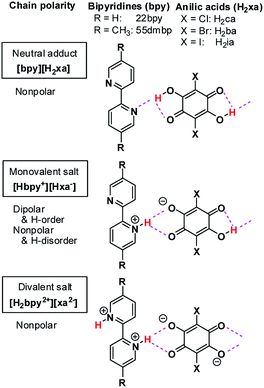 | ||
| Chart 1 Haloanilic acids, 2,2′-bipyridines, and their supramolecular chains of different valence states. | ||
Here we report some exotic isotope effects and successive phase transitions in new supramolecular ferroelectrics consisting of anilic acids and 2,2′-bipyridine derivatives (Chart 1). Deuterium substitution over the hydrogen bonds smoothly raises the Curie point and simultaneously lowers other phase-transition temperatures by a few tens of degrees. The coexistence of opposing isotope effects reduces the temperature separation of the two phase transitions from 84 K to 10 K. The bipyridines exhibit molecular flexibility through interplanar twisting, which turns out to be relevant to the high-temperature phase transitions. The inverse temperature shift originates from an indirect effect of the hydrogen-bond geometry, which adjusts the molecular conformation of the bipyridine unit upon deuteration so as to minimize the changes in adjacent intermolecular interactions.
Results and discussion
General properties of materials
First, let us review the basic properties of the ferroelectric cocrystals as an introduction to the physical and structural assessments reported below.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 cocrystal of 2,2′-bipyridine (22bpy) and iodanilic acid (H2ia) is a new compound that crystallizes as a proton-transferred monovalent salt. As reference compounds for our study we chose two compounds with similar crystal structures; these were cocrystals of 5,5′-dimethyl-2,2′-bipyridine (H55dmbp) with Hia28 and with Hba,34 the ferroelectricity of which has been reported independently. All these single crystals can be satisfactorily grown through slow evaporation of solutions in methanol, and they comprise linear supramolecular chains of alternating acid and base molecules, as demonstrated below. The use of CH3OD (99.5% D) solutions gave the corresponding deuterium-bonded D55dmbp-Dba (degree of deuteration: 94%), D55dmbp-Dia (93%), and D22bpy-Dia (85%) crystals (Fig. S1†). We also studied the thermal properties of the iodanilate salt of fully deuterated 2,2′-bipyridine (22bpy-d8), prepared as a reference material.
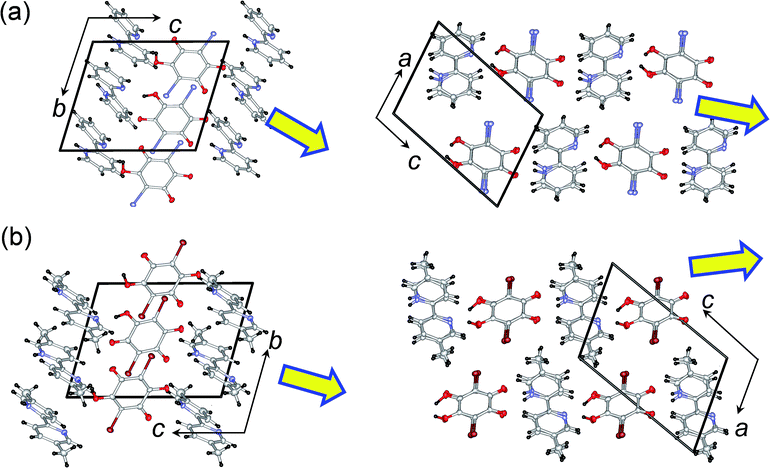
1 cocrystal of 2,2′-bipyridine (22bpy) and iodanilic acid (H2ia) is a new compound that crystallizes as a proton-transferred monovalent salt. As reference compounds for our study we chose two compounds with similar crystal structures; these were cocrystals of 5,5′-dimethyl-2,2′-bipyridine (H55dmbp) with Hia28 and with Hba,34 the ferroelectricity of which has been reported independently. All these single crystals can be satisfactorily grown through slow evaporation of solutions in methanol, and they comprise linear supramolecular chains of alternating acid and base molecules, as demonstrated below. The use of CH3OD (99.5% D) solutions gave the corresponding deuterium-bonded D55dmbp-Dba (degree of deuteration: 94%), D55dmbp-Dia (93%), and D22bpy-Dia (85%) crystals (Fig. S1†). We also studied the thermal properties of the iodanilate salt of fully deuterated 2,2′-bipyridine (22bpy-d8), prepared as a reference material.These two crystal structures appear to have very similar molecular arrangements when viewed along the crystal a or b axis, as well as similar unit-cell parameters. Whereas the H55dmbp-Hba is isomorphous with ferroelectric H55dmbp-Hia, H22bpy-Hia shows a trivial difference in the orientation of the base molecules in the b-axis projection (Fig. 1b). The intermolecular hydrogen-bonds form a straight chain of alternating acid and base molecules, each of which form a separate π–π stack. In the H22bpy-Hia and H55dmbp-Hxa crystals, the chains are oriented parallel to the [212] direction. Note that the molecules are stacked with a doubled periodicity along the b-direction.
Dielectric properties
The dielectric permittivity and polarization hysteresis were examined for the H22bpy-Hia and H55dmbp-Hba crystals as well as for their deuterated analogues. Below, we describe the anisotropic and thermal behaviors of the former two crystals, as well as the effects of deuteration, before discussing theoretical simulations of electric polarizations in comparison with the experimental ones.| Compounda | Space Gr. of FE (PE) structure | Tc (K) {ΔTc (K)} | Permittivity | Ferroelectric polarization (μC cm−2) | Ref. | ||
|---|---|---|---|---|---|---|---|
| C (K) | θ (K) | Experimental Pr (or Ps) | Theoreticalb |P| (Px, Py, Pz) | ||||
| a dppz = 2,3-di-2-pyridinylpyrazine; tppz = 2,3,5,6-tetra-2′-pyridinylpyrazine; 66dmbp = 6,6′-dimethyl-2,2′-bipyridine; H2fa = fluoranilic acid; see Chart 1 for abbreviations of other chemicals.b The Cartesian coordinate system (x, y, z) was chosen to be parallel to (a, b′, c*) and (a, b, c*) for the triclinic and monoclinic crystallographic axes, respectively, where the b′-direction is taken as perpendicular to the a and c* axes.c This work.d Depolarization temperature.e Spontaneous polarization values obtained from measuring the pyroelectric current.f The ferroelectric phase appears only at high pressures. | |||||||
| Ionic supramolecules | |||||||
| 1h H22bpy-Hia | P1 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
158 | 4.49 × 104 | 111.1 | 3.6⊥(101) | — | —c |
| 1d D22bpy-Dia | P1 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
190 {+32} | 5.88 × 104 | 92.9 | 4.7⊥(101) | 8.21 (1.77, 1.72, 7.83) | —c |
| 2h H55dmbp-Hia | P1 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
268 | 1.39 × 104 | 251 | 4.2⊥(101) | 6.56 (0.76, 2.77, 5.90) | 20 and 28 |
| 2d D55dmbp-Dia | P1 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
335 {+67} | 2.26 × 104 | 319 | 4.0⊥(101) | — | 20 and 28 |
| 3h H55dmbp-Hba | P1 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
259 | 2.43 × 104 | 258.4 | 3.6⊥(101) | 7.22 (3.73, 0.37, 6.17) | —c |
| 3d D55dmbp-Dba | P1 (P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) ) |
303 {+44} | 1.9 × 104 | 299 | 4.2⊥(101) | — | —c |
| 4 H66dmbp-Hca | P21 (P21/c) | 378d | — | — | 8∥[010] | 9.94 (0, 9.94, 0) | 30 |
| 5 Hdppz-Hca | Cc (C2/c) | 402 | — | — | 5.2∥[001] | 7.51 (0.08, 0, −7.51) | 29 |
| 6 Hdppz-Hba | Cc | >420 | — | — | 5.8∥[001] | — | 29 |
| 7h H2tppz-(Hca)2 | Cc (C2/c) | 172 | — | — | 0.062∥[110]e | — | 32 |
| 7d D2tppz-(Dca)2 | Cc (C2/c) | 240 {+68} | — | — | — | — | 32 |
| 8h H2tppz-(Hba)2 | Cc (C2/c) | 334 | 39.5 | 333.3 | 0.12∥[110]e | — | 32 |
| 8d D2tppz-(Dba)2 | Cc (C2/c) | 365 {+31} | 51.9 | 363.4 | ∥[110] | — | 32 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| Neutral supramolecules | |||||||
| 9h Phz-H2ca | P21 (P21/n) | 253 | 4.96 × 103 | 253 | 1.7∥[010]e | (0, 0.55, 0) | 27 |
| 9d Phz-D2ca | P21 (P21/n) | 303.5 {+50} | 5.02 × 103 | 301.2 | 1.7∥[010]e | — | 31 |
| 10h Phz-H2ba | P21 (P21/n) | 138 | 3.97 × 103 | 137.4 | 0.9∥[010]e | — | 27 |
| 10d Phz-D2ba | P21 (P21/n) | 204 {+66} | 4.60 × 103 | 201.6 | 1.2∥[010]e | — | 31 |
| 11 Phz-H2fa | P21 (P21/n) | >0.6 GPaf | 4.68 × 103 | 190.7 | — | — | 33 |
| 12 dppz-H2fa | (C2/c) | >0.3 GPaf | — | — | — | — | 29 |
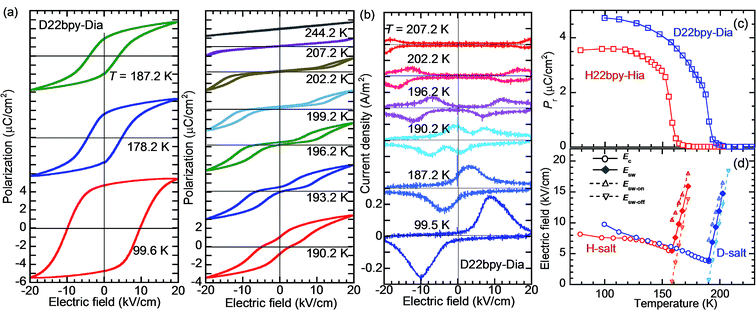
The polarization–electric field (P–E) hysteresis curve appears as a parallelogram loop, providing evidence of ferroelectricity in Phase I (Fig. 3a and S4†). The P–E curve changes abruptly to double hysteresis loops in a narrow temperature range just above Tc. The corresponding current density (J) versus E curve (Fig. 3b) changes so that each pair of peaks is further split into doublets. The coercive field, which decreases with temperature in ferroelectric Phase I, is continuously converted at Tc into the switching field of the double loops (Fig. 3c). Such behavior can be explained by a reversible field-induced paraelectric-to-ferroelectric phase transitions as a characteristic near the strong first-order ferroelectric transition, as previously observed in BaTiO3.35
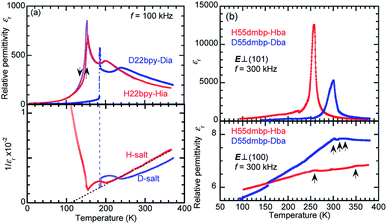
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. H55dmbp-Hba, as well as H55dmbp-Hia and H22bpy-Hia, exhibited a huge Curie–Weiss constant (Table 1), which is about two orders of magnitude larger than Tc. The Curie point (Tc = 259 K) of H55dmbp-Hba was 9 K lower than that of H55dmbp-Hia (268 K). The phase transition is first order for H55dmbp-Hia and nearly second order for the H55dmbp-Hba crystal, considering the differences between θ and Tc (17 K and <1 K, respectively). This explains why the permittivity showed more-pronounced divergent behavior (a peak value of 13
000. H55dmbp-Hba, as well as H55dmbp-Hia and H22bpy-Hia, exhibited a huge Curie–Weiss constant (Table 1), which is about two orders of magnitude larger than Tc. The Curie point (Tc = 259 K) of H55dmbp-Hba was 9 K lower than that of H55dmbp-Hia (268 K). The phase transition is first order for H55dmbp-Hia and nearly second order for the H55dmbp-Hba crystal, considering the differences between θ and Tc (17 K and <1 K, respectively). This explains why the permittivity showed more-pronounced divergent behavior (a peak value of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) in the latter crystal.
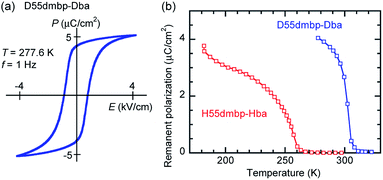
000) in the latter crystal.The presence of ferroelectricity was confirmed by the change in the P–E hysteresis curve from a straight line, through an S-shaped line, to a parallelogram-like loop in Phase I (Fig. S5†). The magnitude of the remanent polarization tended to depend on the specimen, due to differences in crystal quality. By careful selection of regularly shaped crystals, the best performance that we achieved in our reexamination (3.6 μC cm−2; Fig. 4) was about three times that in the original report.
A similar simulation of H55dmbp-Hba gave a spontaneous polarization of 6.73 μC cm−2 with direction components of (Pa, Pb′, Pc*) = (−3.49, −0.11, −5.75) μC cm−2. The direction component of 6.39 μC cm−2 along the electric-field direction [E⊥ (101) plane] also explains the observed value.
Phase-transition sequences
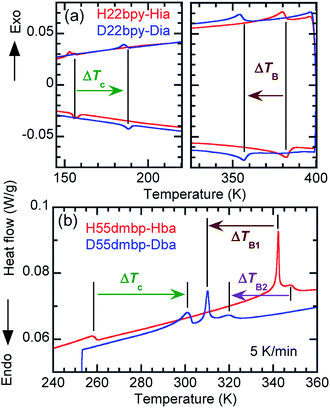
An alternative method for identifying phase transitions is by means of the heat-flow profiles determined by high-sensitivity differential scanning calorimetry (DSC). H22bpy-Hia and deuterated D22bpy-Dia showed pairs of exothermal and endothermal peaks at Tc, and their isotope shift was in agreement with the dielectric measurements (Fig. 5a and S7†). These faint peaks due to the small entropy changes suggested that the phase transitions are not the order-disorder type. In contrast, there were no detectable anomalies at TA between phases IC and II, probably because the entropy change is too small, and this leaves the possibility of some crossover phenomenon. H55dmbp-Hba, H55dmbp-Hia, and their deuterated salts also exhibited tiny peaks or kink-like anomalies at their Curie points (Fig. 5b and S7f†).The emergence of Phase III at temperatures far above room temperature is identified by an additional pair of exothermal and endothermal peaks for the H22bpy-Hia and deuterated D22bpy-Dia salts. The reversible phase transition at TB = 357 K is also related to a faint kink in the intrastack permittivity (shown by an arrow in Fig. S2†) for the latter crystal. An exotic feature is its downward shift of as much as 25 K upon deuterium substitution of the hydrogen bonds. In sharp contrast, full deuteration of the base (22bpy-d8) except for the hydrogen-bonding acidic protons has little effect on the phase-transition temperatures (Fig. S7c†). These observations show that hydrogen bonds play crucial roles on both the low- and high-temperature phase transitions.
A transition to Phase III likewise appears for the H55dmbp-Hba and deuterated D55dmbp-Dba (Fig. 5b), but is absent in the isomorphous compounds H55dmbp-Hia and D55dmbp-Dia below the thermal-stability limit (Fig. S7e†). Note that the anomaly consists of two phase transitions for H55dmbp-Hba. The sharp peak at TB1 = 343 K is accompanied by the small and blunt anomaly at TB2 = 348 K, suggesting that an additional intermediate phase (denoted as IIC) is present between Phases II and III. Deuterium substitution significantly decreases TB1 and TB2 by 31 and 28 K, respectively. This inverse isotope effect, together with the normal isotope effect on Tc, dramatically collapses the temperature window of Phase II from 84 to 10 K. On the basis of the electrical and thermal properties, the phase-transition sequences are summarized in Fig. 6.
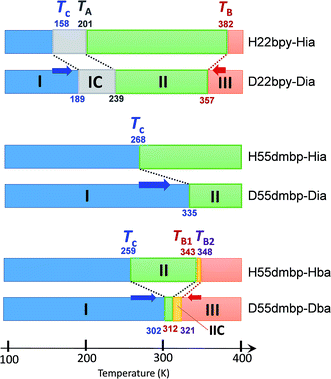 | ||
| Fig. 6 Phase-transition sequences of H22bpy-Hia, H55dmbp-Hba, H55dmbp-Hia, and their deuterated salts. The numbers represent the phase-transition temperatures in Kelvin. | ||
Thermal structural changes
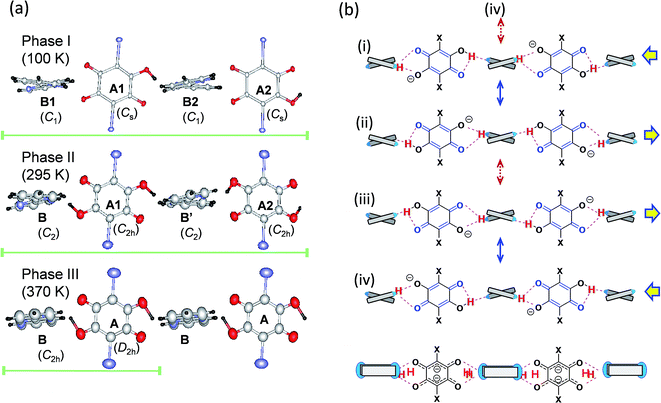
The thermal structural changes of the D22bpy-Dia and H55dmbp-Hba salts were examined. Under ambient conditions, both crystals adopt the Phase II form, which consists of two formula units in a triclinic unit cell. The transition from Phase I to Phase II adds inversion symmetry to each Hxa− molecule, and can thus be of a true ferroelectric type. Note that the D22bpy and H55dmbp molecules remain twisted in these phases. For both compounds, the high-temperature Phase III form retains a triclinic P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) symmetry, but it consists of only one formula unit in a halved unit-cell volume. Halving of the unit-cell parameter b in Phase III is demonstrated by the disappearance of k = odd reflections (Fig. 8). The D22bpy and H55dmbp molecules also acquire an inversion symmetry that necessitates that they have exactly coplanar conformations. Fig. 7a illustrates the structural changes in the supramolecular chain from Phase I to Phase III.
symmetry, but it consists of only one formula unit in a halved unit-cell volume. Halving of the unit-cell parameter b in Phase III is demonstrated by the disappearance of k = odd reflections (Fig. 8). The D22bpy and H55dmbp molecules also acquire an inversion symmetry that necessitates that they have exactly coplanar conformations. Fig. 7a illustrates the structural changes in the supramolecular chain from Phase I to Phase III.
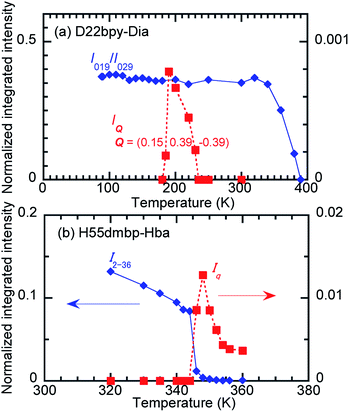
In the temperature range for Phase IC, the D22bpy-Dia crystal shows X-ray satellite reflections around each Bragg reflection, suggesting the formation of a superlattice with noninteger periodicity, as shown by Fig. 8a, and S8a.† Therefore, Phase IC just above Tc is as an ‘incommensurately’ modulated structure. Some modulated structures exist in the very narrow temperature range of Phase IIC (Fig. 8b, and S8b†), although a confirmation of this fact is beyond the scope of this paper.
Unfortunately, accurate locations of hydrogen atoms are difficult to determine by X-ray analysis, especially for the disordered case (form C), because the crystals contain heavy bromine or iodine atoms with large scattering factors. A clue to their locations can be obtained from local molecular geometries, which are closely interrelated to the local degrees of proton transfer between the neutral N⋯H–O and ionic N–H+⋯O− forms. This analysis has been previously applied to evaluate the ferroelectric phase transition in the H55dmbp-Hia crystal.28
The molecular structures of neutral H2xa adopt a planar and typical para-quinoid form that corresponds to the point-group symmetry C2h. Their symmetry is lowered to a point-group symmetry of Cs upon deprotonation to the monovalent Hxa− anions; the C–O− bond with length of 1.25–1.26 Å is substantially shorter than that of the corresponding C–OH bond (bond length 1.32–1.33 Å) with a corresponding lengthening of the adjacent C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. The change in the geometry of the base molecules upon protonation is most obvious in the pyridine ring C
C bond. The change in the geometry of the base molecules upon protonation is most obvious in the pyridine ring C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C angle, which is 116–117° for the neutral ring and widens to 121–123° for the protonated ring. Therefore, the degrees of proton transfer can be evaluated by plotting the change in the C
N–C angle, which is 116–117° for the neutral ring and widens to 121–123° for the protonated ring. Therefore, the degrees of proton transfer can be evaluated by plotting the change in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–C angle (δ) against the C–O bond length (dC–O) (Fig. 6b) relative to the shaded boxes N and I, which denote the standard geometries of the neutral N⋯H–O and ionic N–H+⋯O− forms, respectively.
N–C angle (δ) against the C–O bond length (dC–O) (Fig. 6b) relative to the shaded boxes N and I, which denote the standard geometries of the neutral N⋯H–O and ionic N–H+⋯O− forms, respectively.
In each supramolecular chain of the ordered Phase I structures, four crystallographically independent hydrogen bonds form a repeating unit, as exemplified by the chemical structure (i) and the corresponding drawings in Fig. 7. Actually, the diagnostic diagram (Fig. S9†) distinguishes two neutral N⋯H–O and two ionic N–H+⋯O− bonds as the ordered monovalent state of the protons. The phase transition to a paraelectric form (Phase II) halves the asymmetric unit, and then reduces the number of independent hydrogen bonds to two. Each local bond geometry is dynamically averaged between the N⋯H–O and N–H+⋯O− forms, indicating a disorder of the protons in Phase II. Fig. 7b shows the resonance scheme for this disordered structure: the solid double-headed arrows represent intermixes of two contributing structures so that the resonance hybrids (i) ↔ (ii) and (iii) ↔ (iv) preserve the same para-quinoid geometry with a point-group symmetry of C2h. Note that the molecules A1 and A2 are symmetric but crystallographically independent of each other, whereas molecules B and B′ are related to one another by inversion symmetry. This phase transition picture is very similar to the hydrogen dynamics found by the 2H magic-angle spinning NMR and 14N nuclear quadrupole resonance studies made on the chlorine-substituted H55dmbp-Hca,39,40 which is comparable to H55dmbp-Hba salt in both the O⋯N bond lengths and the phase transition temperatures.
In the highest-temperature Phase III, the volumes of the unit cell and asymmetric unit are further halved and contain only one crystallographically independent hydrogen bond. Addition of an inversion symmetry to the base increases the degree of configurational disorder. The additional intermixing process indicated by the dotted double-headed arrows in Fig. 7b involves an orientational switching of the para-quinoid structure. The bottom scheme represents the resonance hybrid for the Phase III structures formed from all four contributing structures. The anilate ion in the hybrid resonance approximately exhibits a molecular structure of point-group symmetry D2h, and its divalent character is consistent with the local hydrogen-bond geometry, shown as increasing ionicity in the diagram (Fig. S9†).
Besides the hydrogen-bond geometry, the molecular flexibility of the base is a key characteristic of the high-temperature phase transition, above which temperature the twisted conformation becomes coplanar with the emergence of an inversion symmetry. A fundamental concern regarding neutral and protonated 22bpy molecules is the relative geometric stability of the cis and trans forms and of the coplanar and twisted forms. For the monoprotonated H-22bpy+ cation, the cis form is relatively stable due to presence of the intramolecular N–H+⋯N bond, and the cis–trans interconversion energy has been estimated to be 14 kJ mol−1.41 Actually, both cis and trans forms exist in the three polymorphs of the H66dmbp-Hca salt. The ferroelectric D22bpy-Dia and H55dmbp-Hba salts were shown to exist in a twisted trans form at both phases I and II. At room temperature, the corresponding NCCN torsion angles are 16.7° and 12.6°, respectively, which are less than that of the H55dmbp-Hia salt (16.9°). The torsion angles increase on lowering the temperature below Tc; 17.6 and 17.9° at 100 K for D22bpy-Dia and 13.5 and 14.8° at 173 K for H55dmbp-Hba. Therefore, the presence of a smaller twisting angle might explain the easier transformation into coplanar conformation with the emergence of Phase III. To summarize the structural transformations discussed above, the phase sequence I → II → III successively involves symmetry elements on both molecules as described in terms of point-group symmetry as C1 → C2 → C2h for Hbpy+ and Cs → C2h → D2h for Hxa−.
Hydrogen-bond geometry and deuteration effects
KH2PO4 (KDP)-type ferroelectrics exhibit strong correlations between some of their macroscopic properties and their hydrogen-bond lengths. For instance, the application of a hydrostatic pressure shrinks the separation of the two equilibrium proton positions and weakens the potential-energy barrier between the two minima. The Curie point is decreased toward zero temperature during destabilization of the ferroelectric state until the protons occupy a single minimum at the midpoint of the bond.42 On the other hand, the substitution of protons for deuterons significantly diminishes quantum-mechanical tunneling and favors off-center locations due to a distinct zero-point motion. This is also accompanied by a feedback effect of hydrogen-bond elongation known as the Ubbelohde effect,43 and the combined effects create a huge isotope effect manifested as significant increases in both the Curie point and hydrogen-bond length. For the series of supramolecular ferroelectrics, both the Tc and Ps increase monotonously with increasing hydrogen-bond length.30 Actually, deuteration of the hydrogen bonds elongates the nearest O⋯N bond length dO⋯N(1) by 0.03–0.05 Å (Table S1†); the observed positive Tc can then be understood by analogy with that of KDP. Note that full deuteration of pyridine C–H sites does not produce this geometric effect, in agreement with the unchanged Tc. On the other hand, other structural mechanisms should be considered for the negative shift in the transition point at higher temperatures.Among hydrogen-bonded ferroelectrics, Rochelle salt (potassium sodium tartrate tetrahydrate) exhibits an exceptional isotope effect, which has been long known since Valasek's findings regarding the reentrant phase transition44 and the inverse isotope effect,45 following his initial discovery of ferroelectricity in 1920.46 A novel feature of Rochelle salt is its intermediate ferroelectric phase that penetrates through a chiral paraelectric ground state in a narrow temperature range (255–297 K). Deuterium substitution raises the upper Curie point by 11 K, whereas an inverse effect with a shift of only 5 K emerges for the lower (i.e., reentrant) Curie point. These behaviors are consistent with a model of the KDP family in which deuteration energetically stabilizes the ferroelectric phase relative to the paraelectric one. Compared with the observations for Rochelle salt, deuterium substitution of our two supramolecular ferroelectrics has an opposite but much stronger influence on the thermal stability of the intermediate phase. The other distinct feature is that the present ferroelectrics do not show a reentrant phase.
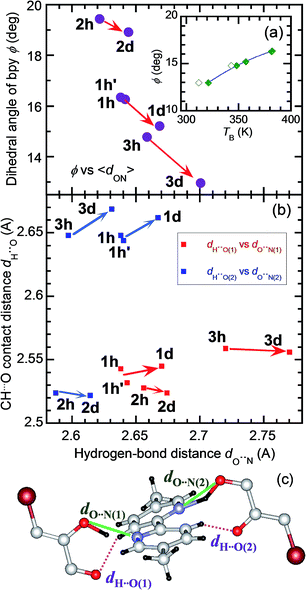
The strong temperature shifts suggest that hydrogen bonds play crucial roles in the microscopic mechanisms of the high-temperature phase transition and the low-temperature ferroelectric transition. These phase transitions are commonly accompanied by increased degrees of disorder; the number of configurations involved in the resonance hybrid increases with temperature from one in Phase I through two in Phase II to four in Phase III. On the other hand, the microscopic features that are exclusively present in the high-temperature phase-transition (coupling between the hydrogen-bond geometry and the twisting deformation of the bipyridine) should provide a clue for identifying the origins of the exotic isotope effect. The inset to Fig. 9a shows the systematic increase in the phase-transition temperature TB (or TB1 and TB2) with an increase in the twisting angle φ, defined as the dihedral angle between the two pyridyl rings at room temperature. The extrapolation of this curve also explains the nominally high TB concealed beyond the onset temperature of decomposition (∼418 K) for H55dmbp-Hia and D55dmbp-Dia with larger values of φ (19.5° and 18.9°, respectively). These behaviors suggest that φ can be used as the corresponding order parameter, so that a smaller value of φ permits easier transformation to the coplanar conformation in Phase III near to or above room temperature.
The origin of the inverse isotope effect is relevant to how the geometry of the hydrogen bonds is interrelated to the twisting deformation. Fig. 9c depicts the crystallographically independent unit in the Phase II structure to highlight the intermolecular contacts between the hydrogen-bonded molecules. Each pyridyl ring is involved in hydrogen bonding of a bifurcated type with two oxygen atoms; the hydroxyl oxygen atom with the shortest distance dO⋯N(1) (or dO⋯N(2)) and the carboxyl oxygen atom in the next-nearest neighbor. Besides such moderately strong hydrogen bonding, this molecular pair exhibits weak CH⋯O hydrogen bonding, which appears as the only intermolecular contact with a shorter distance than the sum of the corresponding van der Waals radii. The H⋯O distance dH⋯O(1) [or dH⋯O(2); Fig. 9c] between the carbonyl oxygen atom and the remainder of the pyridyl ring ranges from 2.52 to 2.67 Å. Because both pyridyl rings interact with each Hxa− ion in the neighborhood, their dihedral angle is determined by these bond geometries. For all three compounds examined, deuteration similarly decreases the twisting angles φ and increases the average hydrogen bond length 〈dO⋯N〉, calculated by averaging over all the crystallographically independent sites at room temperature [e.g., dO⋯N(1) and dO⋯N(2) in Fig. 9a]. On the other hand, deuteration has little effect on dH⋯O(1) and dH⋯O(2) (Fig. 9b). These observations show that the geometric isotope effects adjust the molecular conformation of the flexible bipyridine units to minimize the change in adjacent CH⋯O interactions.
Few other deuterium-bonded crystals exhibit a relatively large downward shift in the phase-transition temperature. Note that these inverse isotope effects are similarly explained by geometric isotope effects on molecular dynamics, although the details of the induced structural changes vary with the material. For example, K3H(SO4)2 crystals exhibit a shift of −9 K for the phase transition from the ferroelastic to superionic state.47 A larger shift of −33 K has recently been reported for the antiferroelectric crystal of imidazolium hydrogen terephthalate.11 This observation was explained in terms of the host–guest framework, in which a deuteration-induced geometric change suppresses freezing of the libration of the guest molecules in the loosened packing space.
Experimental
Commercially available H2ba, 22bpy, and 22bpy-d8 were repeatedly purified by vacuum sublimation. H2ia, prepared from p-iodanil by the reported method,48 was purified twice by gradient sublimation in vacuum until its purity became satisfactory, as assessed by elementary analysis and mass spectrometry. Reddish brown plates of the H55dmbp-Hba and H55dmbp-Hia salts, as well as dark-brown plates of the H22bpy-Hia salt, were grown by slow evaporation of methanolic solutions at room temperature. Crystal growth of H55dmbp-Hba was performed by seeding with crystals to avoid the preferential formation of a fibrous polymorph of unknown crystal structure.Deuterium substitution of the hydrogen bonds was achieved by the slow evaporation of a mixed solution in 99.5%-deuterated CH3OD (Aldrich). The degrees of deuteration of D55dmbp-Dba (94%), D55dmbp-Dia (93%), and D22bpy-Dia (85%) were determined by infrared vibrational spectroscopy in KBr disks. The amount of residual nondeuterated species was estimated from the reduction in the band intensity for the nondeuterated acid at 970 cm−1 (H2ba) or 958 cm−1 (H2ia) by using the band at 1040 cm−1 (55dmbp) or 1001 cm−1 (22bpy) as an internal relative standard.
The permittivity was measured with an LCR meter (4284A Precision; Agilent Technologies, Santa Clara, CA) by using single crystals with painted silver or carbon-paste electrodes. The P–E hysteresis curves were measured on a ferroelectrics evaluation system (FCE-1; Toyo Corp., Kariya) consisting of a current/charge–voltage converter (Model 6252), an arbitrary waveform generator (Biomation 2414B), an analogue-to-digital converter (WaveBook 516), and a voltage amplifier (HVA4321; NF Corp.). The measurements at room temperature were performed with a high-voltage triangular wave field and various alternating frequencies.
The high-sensitivity thermal analysis was performed by using a differential scanning calorimeter (DSC7000X; Hitachi High-Technologies Corp., Tokyo). The crystals (10–20 mg) were crushed and encapsulated in an aluminum pan and cooled (or heated) at a rate of 5 K min−1 under nitrogen flowing at 60 mL min−1. The temperature was calibrated by using the melting point of indium (429.8 K).
Collection of the X-ray diffraction data at room temperature and the assignment of the crystallographic axes of the bulk single crystals were performed by using graphite-monochromated MoKα radiation (λ = 0.71073 Å) and a four-circle diffractometer equipped with a hybrid pixel detector (Rigaku AFC10 with PILATUS200K). The intensity data were analyzed by means of the Crystal Structure crystallographic software packages (Molecular Structure Corp. and Rigaku Corp.). The final refinements of the nonhydrogen atoms were performed with anisotropic thermal factors. The hydrogen-bonded hydrogen atoms were found by means of differential Fourier synthesis and refined isotropically, and the other hydrogen atoms were calculated in their ideal geometrical positions. The same setup was employed for the analysis of the H55dmbp-Hba crystal at 173 K in a stream of cooled nitrogen gas.
The temperature-variable diffraction data were collected by using synchrotron X-rays, except for the H55dmbp-Hba crystal at 173 K. The diffraction experiments were conducted on Rigaku DSC diffractometers equipped with an imaging plate detector installed in beamlines BL-8A and BL-8B of the Photon Factory of the High Energy Accelerator Research Organization (KEK). The X-ray (λ = 0.689 or 1.00 Å) beam, monochromatized by using a Si(111) double crystal, was collimated to 0.3 × 0.3 mm by a collimator set immediately upstream of the sample. The reflection intensity data were collected by using the Rapid-AUTO software package (Rigaku Corp.). All the calculations were performed by using the Crystal Structure crystallographic software package.
Electronic polarizations were evaluated by means of the Berry phase approach49,50 with the QMAS code51 based on the projector augmented-wave method52 and the plane–wave basis set. To describe the electronic exchange–correlation energy, the Perdew–Burke–Ernzerhof (PBE) version of the generalized gradient approximation (GGA)53 was used. The total polarization was obtained as the sum of the electronic polarization and the ionic polarization; further details are described elsewhere.54,55 The target ferroelectric structures (degree of polar distortion λ = 1) were constructed from the atomic coordinates of all the nonhydrogen atoms as determined by the experiments. The locations of the hydrogen atoms were computationally relaxed so as to minimize the total energy. The reference paraelectric structures (λ = 0) were constructed from averaged molecular structures for λ = ±1.
Conclusions
Supramolecular ferroelectric H22bpy-Hia and H55dmbp-Hba salts show a large relative permittivity (maximum 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), a large spontaneous polarization (maximum 5 μC cm−2), and a low coercive field ranging from 0.5 to 10 kV cm−1. The ferroelectric phase transition at low temperatures is followed by successive phase transitions and exotic isotope effects at higher temperatures. Deuterium substitution over the hydrogen bonds smoothly raises the Curie point in a similar manner to that of KDP, but unexpectedly lowers another phase-transition temperature by a few tens of degrees Kelvin. The cooccurrence of opposite isotope effects reduces the temperature interval of the intermediate paraelectric Phase II of H55dmbp-Hba from 84 to 10 K. This observation is in contrast to effect of deuteration of Rochelle salt, which expands the temperature range for the intermediate ferroelectric phase.
000), a large spontaneous polarization (maximum 5 μC cm−2), and a low coercive field ranging from 0.5 to 10 kV cm−1. The ferroelectric phase transition at low temperatures is followed by successive phase transitions and exotic isotope effects at higher temperatures. Deuterium substitution over the hydrogen bonds smoothly raises the Curie point in a similar manner to that of KDP, but unexpectedly lowers another phase-transition temperature by a few tens of degrees Kelvin. The cooccurrence of opposite isotope effects reduces the temperature interval of the intermediate paraelectric Phase II of H55dmbp-Hba from 84 to 10 K. This observation is in contrast to effect of deuteration of Rochelle salt, which expands the temperature range for the intermediate ferroelectric phase.
According to temperature-variable X-ray diffraction studies, both phase transitions modify the molecular and hydrogen-bonded geometries, as expected from their significant isotope effects. Both events are usually accompanied by increased degrees of disorder with temperature, as in the case of the KDP family. Nevertheless, the conventional picture for KDP cannot explain the microscopic origins of the exotic isotope effect on the high-temperature phase transitions. The bipyridine molecules exhibit an interplanar twisting, which represents an order parameter relevant to the high-temperature phase transitions. The inverse temperature shift originates from the indirect effect of the hydrogen-bond geometry, which adjusts the molecular conformation of the flexible bipyridine unit so as to minimize the change in adjacent intermolecular CH⋯O interactions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by JSPS KAKENHI Grant Number JP16H02301 and JST CREST Grant Number JPMJCR18J2, Japan. The synchrotron X-ray study was performed with approval from the Photon Factory Program Advisory Committee (No. 2014S2-001 and 2017S2-001).Notes and references
- M. E. Lines, and A. M. Glass, Principles and Applications of Ferroelectrics and Related Materials, Oxford University Press, New York, 1977 Search PubMed.
- Ferro- and Antiferroelectricity: Order/Disorder Versus Displacive, ed. N. S. Dalal and A. Bussmann-Holder, Springer, Berlin, 2007 Search PubMed.
- K. Uchino, Ferroelectric Devices, Marcel Dekker, New York, 2000 Search PubMed.
- M. Dawber, K. M. Rabe and J. F. Scott, Rev. Mod. Phys., 2005, 77, 1083 CrossRef CAS.
- G. A. Jeffery, An Introduction to Hydrogen Bonding, Oxford University Press, Oxford, 1997 Search PubMed.
- Hydrogen Bonding: New Insights, ed. S. J. Grabowski, Springer, Dordrecht, 2006 Search PubMed.
- T. Mitani and T. Inabe, in Spectroscopy in New Materials, ed. R. J. H. Clark and R. E. Hester, Wiley, New York, 1993, p. 291 Search PubMed.
- T. Sugawara and I. Takasu, Adv. Phys. Org. Chem., 1999, 32, 219 CrossRef CAS.
- T. Matsuo, A. Inaba, O. Yamamoto and N. Onoda-Yamamuro, J. Phys.: Condens. Matter, 2000, 12, 8595 CrossRef CAS.
- A. Ueda, S. Yamada, T. Isono, H. Kamo, A. Nakao, R. Kumai, H. Nakao, Y. Murakami, K. Yamamoto, Y. Nishio and H. Mori, J. Am. Chem. Soc., 2014, 136, 12184 CrossRef CAS PubMed.
- C. Shi, X. Zhang, C.-H. Yu, Y.-F. Yao and W. Zhang, Nat. Commun., 2018, 9, 481 CrossRef PubMed.
- R. Blinc, J. Phys. Chem. Solids, 1960, 13, 204 CrossRef CAS.
- M. Ichikawa, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 2074 CrossRef.
- E. Matsushita and T. Matsubara, Prog. Theor. Phys., 1982, 67, 1 CrossRef CAS.
- M. I. McMahon, R. J. Nelmes, W. F. Kuhst, R. Dorwarth, R. O. Piltz and Z. Tun, Nature, 1990, 348, 317 CrossRef CAS.
- A. Bussmann-Holder and K. H. Michel, Phys. Rev. Lett., 1998, 80, 2173 CrossRef CAS.
- S. Koval, J. Kohanoff, R. L. Migoni and E. Tosatti, Phys. Rev. Lett., 2002, 89, 187602 CrossRef CAS PubMed.
- T. Furukawa, Phase Transitions, 1989, 18, 143 CrossRef CAS.
- Ferroelectric Polymers: Chemistry, Physics, and Applications, ed. H. S. Nalwa, Marcel Dekker, New York, 1995 Search PubMed.
- S. Horiuchi and Y. Tokura, Nat. Mater., 2008, 7, 357 CrossRef CAS PubMed.
- T. Hang, W. Zhang, H.-Y. Ye and R.-G. Xiong, Chem. Soc. Rev., 2011, 40, 3577 RSC.
- D.-W. Fu, H.-L. Cai, Y. M. Liu, Q. Ye, W. Zhang, Y. Zhang, X.-Y. Chen, G. Giovannetti, M. Capone, J. Y. Li and R.-G. Xiong, Science, 2013, 339, 425 CrossRef CAS PubMed.
- A. S. Tayi, A. Kaeser, M. Matsumoto, T. Aida and S. I. Stupp, Nat. Chem., 2015, 7, 281 CrossRef CAS PubMed.
- J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata and T. Inabe, Nat. Chem., 2016, 8, 946 CrossRef CAS PubMed.
- S. Horiuchi, K. Kobayashi, R. Kumai and S. Ishibashi, Nat. Commun., 2017, 8, 14426 CrossRef CAS PubMed.
- H.-Y. Ye, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, J.-X. Gao, X.-N. Hua, H. Cai, P.-P. Shi, Y.-M. You and R.-G. Xiong, Science, 2018, 361, 151 CrossRef CAS PubMed.
- S. Horiuchi, F. Ishii, R. Kumai, Y. Okimoto, H. Tachibana, N. Nagaosa and Y. Tokura, Nat. Mater., 2005, 4, 163 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and Y. Tokura, Angew. Chem., Int. Ed., 2007, 46, 3497 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and Y. Tokura, J. Am. Chem. Soc., 2013, 135, 4492 CrossRef CAS PubMed.
- K. Kobayashi, S. Horiuchi, S. Ishibashi, F. Kagawa, Y. Murakami and R. Kumai, Chem.–Eur. J., 2014, 20, 17515 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai and Y. Tokura, J. Am. Chem. Soc., 2005, 5010 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai, Y. Tokunaga and Y. Tokura, J. Am. Chem. Soc., 2008, 130, 13382 CrossRef CAS PubMed.
- S. Horiuchi, R. Kumai, J. Fujioka and Y. Tokura, J. Am. Chem. Soc., 2012, 134, 1036 CrossRef PubMed.
- Y. Yamamura, F. Saito, H. Saitoh, N. Hoshino and K. Saito, Chem. Lett., 2012, 41, 119 CrossRef CAS.
- W. J. Merz, Phys. Rev., 1953, 91, 513 CrossRef CAS.
- F. Ishii, N. Nagaosa, Y. Tokura and K. Terakura, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 212105 CrossRef.
- S. Horiuchi, R. Kumai and S. Ishibashi, Chem. Sci., 2018, 9, 425 RSC.
- S. Ishibashi, S. Horiuchi and R. Kumai, Phys. Rev. B, 2018, 97, 184102 CrossRef CAS.
- T. Asaji, M. Hara, H. Fujimori and S. Hasegawa, Hyperfine Interact., 2016, 237, 101 CrossRef.
- J. Seliger, V. Žagar, T. Asaji, K. Gotoh and H. Ishida, Phys. Chem. Chem. Phys., 2011, 13, 9165 RSC.
- S. T. Howard, J. Am. Chem. Soc., 1996, 118, 10269 CrossRef CAS.
- Y. Moritomo, Y. Tokura, H. Takahashi and N. Mōri, Phys. Rev. Lett., 1991, 67, 2041 CrossRef CAS PubMed.
- A. R. Ubbelohde and K. J. Gallagher, Acta Crystallogr., 1955, 8, 71 CrossRef CAS.
- J. Valasek, Phys. Rev., 1924, 24, 560 CrossRef CAS.
- A. N. Holden and W. P. Mason, Phys. Rev., 1940, 57, 54 CrossRef CAS.
- J. Valasek, Phys. Rev., 1920, 15, 537 Search PubMed.
- Y. Matsumoto, K. Shimada and K. Tsuru, J. Phys. Soc. Jpn., 2013, 82, 104601 CrossRef.
- H. A. Torrey and W. H. Hunter, J. Am. Chem. Soc., 1912, 34, 702 CrossRef CAS.
- R. D. King-Smith and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1651 CrossRef CAS PubMed.
- R. Resta, Rev. Mod. Phys., 1994, 66, 899 CrossRef CAS.
- S. Ishibashi, T. Tamura, S. Tanaka, M. Kohyama and K. Terakura, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 153310 CrossRef.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Ishibashi, K. Terakura and S. Horiuchi, J. Phys. Soc. Jpn., 2010, 79, 043703 CrossRef.
- S. Ishibashi and K. Terakura, Phys. B, 2010, 405(suppl. 1), S338 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details and characterization data. CCDC 1944394–1944403. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra06489c |
| This journal is © The Royal Society of Chemistry 2019 |