Open Access Article
Open Access ArticleValence electronic structure of [EMIM][B(CN)4]: ion-pair vs. bulk description †
I. Kuusik a,
M. Berholtsac,
J. Kruusmab,
A. Tõnisooa,
E. Lustb,
E. Nõmmiste‡
a and
V. Kisanda
a,
M. Berholtsac,
J. Kruusmab,
A. Tõnisooa,
E. Lustb,
E. Nõmmiste‡
a and
V. Kisanda
aInstitute of Physics, University of Tartu, W. Ostwaldi 1, 50411 Tartu, Estonia
bInstitute of Chemistry, University of Tartu, Ravila 14a, 50411 Tartu, Estonia
cDept. of Physics and Astronomy, University of Turku, FIN-20014 Turku, Finland
First published on 16th October 2019
Abstract
The ultraviolet photoelectron spectrum of the [EMIM][B(CN)4] ionic liquid was recorded and analyzed. Together with different ab initio calculation methods, detailed insight into the electronic structure of this simple room temperature ionic liquid is possible. The ion-pair approximation to the liquid electronic structure was not sufficient. Therefore bulk ab initio calculations were performed on a proposed crystal structure. The modelling of bulk electronic spectra is able to explain the experimental electronic structure of the ionic liquid. Most notably, the dispersion corrected PBE calculation (PBE-D3BJ) showed good agreement with the experimental UPS spectrum. The spectra simulated by the B97-D and the BLYP-D3(BJ) functionals were also in agreement with the experimental data. The LDA approximation only provided qualitative agreement while the optB88-vdW and CX-vdW functionals were not good. However, it will be shown that many requirements have to be met in order to accurately describe the electronic structure of this ionic liquid.
1. Introduction
Ionic liquids (ILs) have recently gained much attention due to their many useful properties, like low melting temperatures and vapor pressure, excellent solvation ability, low chemical volatility, high thermal stability and ionic conductivity. They have possible applications in diverse fields, such as catalysis, biocatalysis, chemical synthesis, analytical chemistry, nanotechnology, fuel cells, solar cells, electrochemistry, etc.1 Using the large number of available anions and cations, it is possible to synthesize a vast number of different ionic liquids leading to a wide variety of electrolytes.The high viscosity of commonly used ionic liquids such as [EMIM][BF4], [BMIM][BF4] and [EMIM][TFSI] limits their performance when used as electrolytes in electrochemical devices.2 Cyano-functionalized anions produce some of the most fluid and conductive ionic liquids with low melting temperatures and low viscosities.3 However, there are relatively few studies of the electronic structure of the cyano-anion based ionic liquids compared to fluorinated anions.3–5
Therefore the simple cyano-anion based ionic liquid 1-ethyl-3-methylimidazolium tetracyanoborate was studied. [EMIM][B(CN)4] consists of the EMIM cation and the B(CN)4 anion. The notation [CATION][ANION] for the cations and anions has been used in this study. The EMIM cation is well studied and also tends to form low viscosity liquids with a large number of anions.6
Nishi et al.7 pointed out that the understanding the electronic structure of the ionic liquids is important and an essential question is how the electronic structures of the cations and the anions are combined to form the overall ionic liquid electronic structure. Yoshimura et al. noted, that the understanding of the electronic structure of room-temperature ionic liquids, especially the top of the valence band, is very important in the study of ionic liquids.8 It is also important to know, whether the top of the valence band is connected with the anion, cation or both. Cremer et al. pointed out that photoelectron spectroscopy (PES) is a very powerful experimental method, which provides direct access to the electronic structure of ionic liquids.9 The valence band of ionic liquids is accessible with ultraviolet photoelectron spectroscopy (UPS).
Weingarth et al. recorded the valence band photoemission spectra of [EMIM][B(CN)4] using Al Kα radiation.5 However, the resolution of the measurements was relatively low and the inelastic scattering background was high due to the use of high photon energy. Unfortunately, there is also about a 3.5 eV binding energy shift compared to our spectra.
The interpretation of the experimental valence band photoemission spectra calls for the support from theoretical modelling and electronic structure calculations. We have shown previously, that a good qualitative description of the ionic liquid electronic structure can be obtained when dispersion-corrected DFT (density functional theory) calculations of the bulk are performed.10
We focus mainly on the shape and features of the experimental UPS spectrum and the comparison with ab initio calculated density of states (DOS) in order to better understand the electronic structure of the [EMIM][B(CN)4] room temperature ionic liquid.
2. Experimental and computational details
The [EMIM][B(CN)4] IL with a stated purity of >99% was purchased from Sigma-Aldrich and was kept under high vacuum before measurement. The IL film was deposited on an amorphous carbon surface (Mo2C derived micro-mesoporous) and the film was thick enough to avoid any signal from the substrate. The measurements were performed at room temperature.The experiment was performed at an undulator source beamline I-411 of the MAX-II synchrotron radiation facility (Lund, Sweden).11 The beamline was equipped with a modified SX-700 monochromator with 1220 lines per mm plane grating and an elliptical focusing mirror. The incidence photon energy during the photoemission measurements was 100 eV and the photon beam size incident on the sample was about 0.5 × 1 mm. The incidence angle of the photon beam and the electron spectrometer were at 45° with respect to the surface normal. The electron spectrometer was oriented at 90° to the photon beam. No change in the spectra in time or after refreshing the sample were observed during the experiment. Therefore, beam damage is expected to be negligible. No charging related issues were observed.
The kinetic energies of the photoelectrons were measured with a hemispherical electron analyzer Scienta SES-200. The energy scale was calibrated by Au 3d photolines. Pass energy of 50 eV was chosen for the measurements. These operation conditions lead to a total binding energy resolution around 0.1 eV fwhm (full width at half maximum).
Electron spectroscopy is highly surface sensitive and the bands which originate from the atoms, which are closer to the surface, should be more intense. However, due to the excellent quantitative agreement between the experimental and the modelled spectrum (see Fig. 3), the surface sensitivity of UPS is not a major issue in this case. Due to the high isotropy of the ionic liquid and the high purity of the sample, the recorded UPS spectrum is not expected to be influenced by the experimental conditions used.
Ab initio DFT calculations were performed with the Abinit (version 8) code.12,13 The exchange–correlation functionals used were the Perdew–Wang version of the local density approximation (LDA)14 and the Perdew–Burke–Ernzerhof (PBE).15 van der Waals (vdW) effects were studied using the optB88 (ref. 16) and CX17 exchange functionals or the Grimme D2, D3 and D3(BJ) dispersion correction terms.18–20 Pseudopotentials optimized for the PBE functional were used throughout, except for the LDA calculation, where pseudopotentials optimized for LDA were used.
Ab initio Møller–Plesset perturbation theory (MP2) calculations on ion-pairs were performed using Spartan 14 (ref. 21) software. The hybrid B3LYP and M06 functionals were also used. The Gaussian basis set 6-311++G** (d,p-polarized basis set) was used in the ion-pair calculations.
To the best of our knowledge, the experimental crystal structure of [EMIM][B(CN)4] is unpublished at this point. The crystal structures of [PMIM][B(CN)4]4 and [EMIM][BF4]22 were taken as a starting point. The space group of those IL crystals is P21/c. La(NO3)2 mixed with [EMIM][B(CN)4] also crystallizes in the P21/c space group.23 The unit cell is therefore monoclinic and symmetry is taken to be P21/c (space group number 14). The Broyden–Fletcher–Goldfarb–Shanno algorithm was used for geometry optimization. The unit cell structure (atomic positions and cell shape) was optimized with all studied functionals: PBE, LDA, PBE-D3(BJ), BLYP-D3(BJ), B97-D, optB88-vdW, CX-vdW. The geometry optimization was converged at least to 4 × 10−4 eV Å−1 rms forces. The cut-off energy for the plane waves was chosen to be 1200 eV. The PBE-D3(BJ) optimized structure is shown in Fig. 1. A 3 × 3 × 3 Monkhorst–Pack k-point grid was found to be sufficient for the convergence of the DOS. For added accuracy the DOS was calculated using the tetrahedron method. The local density of states (LDOS) was obtained by calculating the DOS inside a sphere centered on the atoms. Zero point energy and vibronic effects are not taken into account in the calculations.
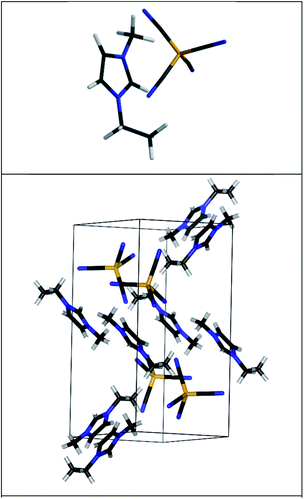 | ||
| Fig. 1 The MP2 predicted ion-pair structure of [EMIM][B(CN)4] (upper panel). The predicted unit cell of [EMIM][B(CN)4] (lower panel). The structure has been optimized using the PBE-D3(BJ) functional and the corresponding electronic structure is shown in Fig. 3. The different bonds are shown using different colors: gray (hydrogen), orange (boron), black (carbon), blue (nitrogen). The cations and anions are unbroken so that some atoms from adjacent cells are also shown. | ||
The energy scale of the calculated DOS was shifted for a better fit to the observed spectrum. Accurate calculation of absolute binding energies is difficult24 and it is well-known that DFT has many issues in predicting band-gap values. The shifts used were between 7.3 eV and 8.4 eV. The calculated bulk DOS has been Gaussian broadened by 0.7 eV fwhm. No stretching (or compressing) of the energy scale of the simulated bulk DOS was performed.
To account for the photoemission cross sections, the data of Yeh and Lindau was used.25,26
Mostly these large shifts are due to the difference of the zero energy of the calculation (vacuum energy) and experiment (Fermi energy).27,28 The former is roughly at the top of the valence band and the latter is at the bottom of the conduction band. Therefore a shift at least of the order of the experimental bandgap is easily explained.
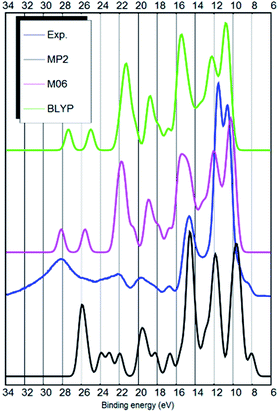
The DOS of the ion-pair was obtained by assuming all molecular orbitals contribute a Gaussian peak with 0.8 eV fwhm. The energy scale was compressed to 80% and shifted by 0.5 eV (MP2), 4.2 eV (M06) or 6.3 eV (BLYP) to obtain a better fit to the experiment. The hybrid functionals (M06 and B3LYP) needed smaller shifts than the standard DFT functional (BLYP). The MP2 optimized ion-pair structure is depicted in Fig. 1 (upper panel).
3. Results and discussion
As mentioned by Ikari et al. the DOS of the ion-pair is not fully adequate to describe liquid phase DOS, but seemingly provides good peak positions.29 Indeed, most ab initio ground state calculations have primarily considered isolated ion-pairs.30 In case of the [EMIM][BF4] IL, the gas and liquid phase spectra are indeed similar and the ion-pair DOS calculation provides a reasonable approximation to the liquid phase UPS spectrum.10,31However, in case of the [EMIM][B(CN)4] IL, the ion-pair approximation is insufficient. The ion-pair calculation of Weingarth et al. does not qualitatively explain the actual liquid phase spectrum.5 For example, some peaks, including the top of the valence band, are missing.
Our ion-pair calculation confirms this result: the DFT ion-pair calculations are quantitatively inadequate to describe the liquid phase UPS spectrum. Most notably, the energy scale of the ion-pair calculations needs to be compressed to adequately match the liquid phase spectrum. The hybrid B3LYP (not shown, similar to M06) or M06 functionals are also not sufficient. Indeed, most DFT functionals produce similar results (see M06 or BLYP results in Fig. 2). Secondly, there are numerous quantitative differences in the peak positions and intensities between the DFT ion-pair calculations and the experiment.
The MP2 calculation is qualitatively somewhat better. For example, it has the HOMO state as a shoulder to the strong peak at 10 eV binding energy, similar to the experimental spectrum. Also, there is less predicted intensity around 22 eV binding energy similar to the experimental UPS spectrum and in contrast to the results of the DFT functionals. The MP2 calculation only needed a 0.5 eV shift after the energy scale was compressed. The main deficiency of the MP2 calculation is the too large separation between anion related peaks at around 9.8 and 11.9 eV. See Fig. 2 for the results from the ion-pair calculations.
However, Reinmöller et al. pointed out that the ion-pair approximation to the bulk is better in the case of larger anions (like Tf2N)27 while in the case of relatively small anions, bulk calculations may be necessary. Ulbrich et al. also understood that ion-pair calculations were not adequate to describe the condensed phase.32
Dhungana et al. estimated the bulk structure of [EMIM][B(CN)4] from MD (molecular dynamics) calculations and performed DOS and dynamic structure factor calculations.3 However, their calculation did not account for dispersion effects, which are very important for the description of ILs.
Most assessments of DFT functionals concentrate on the prediction of structure and energies, not on spectroscopic properties.33 The agreement between calculated and experimental spectral features is an indication of correct structure.33 This principle was used to predict the crystal structure of [EMIM][B(CN)4].
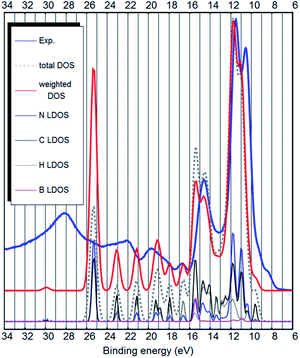
Our predicted bulk (crystal) structure of [EMIM][B(CN)4] is shown in Fig. 1. The experimental UPS spectrum of [EMIM][B(CN)4] along with the PBE-D3(BJ) calculated DOS is shown in Fig. 3.
It has been shown, that the spectral intensities can be described better if the photoemission cross sections are taken into account.27,32 This is also confirmed by our calculation (see Fig. 3 and ESI S1–S4†) where we see an improvement in the similarity with the experimental UPS spectrum from the total DOS calculation to the DOS calculation, where the intensities are weighted to account for the different photoemission cross sections of different atoms and orbitals. It is also evident, that in contrast to the ion-pair calculation, the energy scale of the bulk calculation would benefit from about 10% stretching.
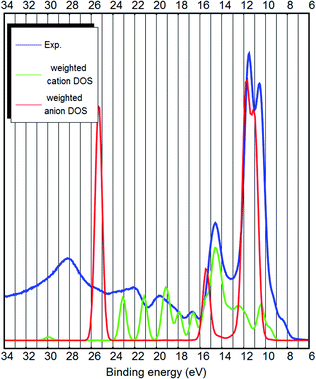
The strongest peak of the UPS spectrum at around 9–13 eV is due to the nitrogen- and carbon-related states. These are the C–N triple bonds of the anion. Interestingly, both the calculation and the experiment show that they are further split into two. The peak at 14.5 eV binding energy is partly due to B–C bonds of the anion, but also the cation related states lie around that energy. Most other bands are cation-related. See Fig. 4 for the decomposition of the DOS into cation–anion contributions. Hydrogen LDOS contribution in the UPS spectrum is expected to be insignificant due to the low photoemission cross section of hydrogen.27
Overall, there is a good quantitative agreement between the weighted DOS and the experimental UPS spectrum. Only the experimental wide peak at around 28 eV binding energy is at too low energy in the calculation (around 25.5 eV). However, this state is due to deep carbon and nitrogen 2s orbitals and may not be correctly described by the pseudopotential calculation. The corresponding state is also very broad in the experimental UPS spectrum. The vibronic effects, which were not considered in this study, could also influence the width of the peaks in the DOS.
Both from a practical and from a theoretical point of view the outer valence band and the states near the bandgap are the most interesting.7 The top of the valence band shows up as a double shoulder to the main anion-related peak (see Fig. 3 and 4). The first shoulder is around 9 eV binding energy and the second shoulder representing the top of the valence band is around 8 eV binding energy.
Only the MP2 ion-pair calculation predicts a similar configuration where the HOMO is situated next to the strong main peak (see Fig. 2). Also, only the MP2 calculation has the imidazolium-related π-state as the HOMO state. The standard and hybrid DFT functionals do not describe this shoulder. This inability of DFT to predict HOMO of the ion-pair is very similar to the case of [EMIM][BF4].10,31 This could be the reason why Weingarth et al. misinterpreted the HOMO state of [EMIM][B(CN)4] as due to the anion.
However, in the case of bulk calculations, DFT is able to describe the top of the valence band qualitatively correctly (see Fig. 3 and 4 and ESI S1–S4†). Dhungana et al. used bulk (periodic) calculations and also correctly assigned the top of the valence band to the cation.
The bulk calculations confirm that the top of the valence band is imidazolium-related, because the carbon-related LDOS at the top of the valence band is from the carbon atoms of the imidazolium (see Fig. 3 and 4). This is opposite to the claim by Weingarth et al., who thought that the HOMO state of [EMIM][B(CN)4] arises from the C–N triple bonds5 (of the anion). Therefore, with the results of the ab initio calculations and the UPS measurements, it is possible to solve the question5 whether the oxidative stability of [EMIM][B(CN)4] is dependent on the anion or the cation – it is the cation which limits the oxidative potential. Dhungana et al. also concluded that the HOMO state of [EMIM][B(CN)4] is mostly due to the cation.3
As shown by Mardirossian et al.,34 BLYP is also a good functional for the description of noncovalent interactions. Indeed, the resulting electronic structure of [EMIM][B(CN)4] calculated by the BLYP-D3(BJ) functional (ESI S1†) is similar to the PBE-D3(BJ) functional. The B97 functional is also recommended. Indeed the B97-D35 functional also produces a electronic structure, which is in agreement with the experimental UPS spectrum (ESI S2†).
When the comparison between the different DFT functionals is made, it is evident that PBE-D3(BJ) seems to perform best in terms of the electronic structure. The B97-D and the BLYP-D3(BJ) functionals follow closely. The LDA calculation is also surprisingly good, but lacks quantitative accuracy (ESI S3†). For example, it pushes the two strong anion related bands too close together and predicts a too strong signal at 21 eV binding energy. The non-local vdW-DF functionals optB88 and CX (not shown), which performed very well in the case of [EMIM][BF4], did not describe the electronic structure of [EMIM][B(CN)4] sufficiently accurately. The modelled spectra are different from the experimental spectrum in many respects and are therefore not shown.
The experimental liquid phase density (at room temperature) is 1036 kg m−3.3,36,37 If the bulk density is assumed to be the same, then the unit cell volume should be 1447 Å3. However, in the case of the [EMIM][B(CN)4] crystalline phase at 0 K, the density is definitely higher, which implies a unit cell volume of smaller than 1447 Å3.
PBE-D3 predicts a unit cell volume of 1300 Å3 and a resulting density of 1154 kg m−3. The corresponding figures for the LDA functional are 1146 Å3 and 1309 kg m−3. It is well-known that LDA tends to overbind and therefore compress the crystal structure. BLYP-D3(BJ) predicts a density in-between these values: 1223 kg m−3. B97-D predicts a density of 1106 kg m−3. The vdW-DF functionals optB88 and CX expand the cell too much and do not offer the best description of the electronic structure, as mentioned above.
We believe that in ILs the energy gaps are very similar in solid, liquid and vapor phase. Indeed, the calculated HOMO–LUMO gap of the [EMIM][B(CN)4] ion-pair and the bandgap of the solid are almost equal at about 4.8 eV (4.76 eV). LDA predicts a somewhat smaller bandgap value of 4.56 eV. There is little variation in the band gap estimates of the DFT functionals. However, it is well-known that DFT underestimates bandgaps substantially.
In the first approximation, the anodic and cathodic limits and the electrochemical window can be related to the HOMO and LUMO levels of the ion-pairs of the liquid.3,38,39 The electrochemical window of [EMIM][B(CN)4] was estimated to be about 4.5 eV,40 4.6 eV![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 or 4.65 eV.39 Dhungana et al. calculated the electrochemical window to be 4.37 eV. However, [EMIM][B(CN)4] showed high oxidation resistance on a Pt electrode, as no significant current attributable to oxidative decomposition was observed even at potentials beyond 5.0 V vs. Ag/Ag(I).42 This would seem to imply an electrochemical window of more than 7.5 eV.
41 or 4.65 eV.39 Dhungana et al. calculated the electrochemical window to be 4.37 eV. However, [EMIM][B(CN)4] showed high oxidation resistance on a Pt electrode, as no significant current attributable to oxidative decomposition was observed even at potentials beyond 5.0 V vs. Ag/Ag(I).42 This would seem to imply an electrochemical window of more than 7.5 eV.
Although there is good agreement between the bandgaps calculated by DFT and the experimental electrochemical windows, the actual bandgap of [EMIM][B(CN)4] is probably higher than 4.8 eV. This is because DFT underestimates the bandgap substantially and the experimental range of the electrochemical stability is also probably not limited by the bandgap of the IL.43 Our previous similar calculations on [EMIM][BF4] also yielded a bandgap estimate of 4.8 eV, but the experimental bandgap of that IL is about 7.4 eV.10 The MP2 calculation predicts a HOMO–LUMO gap of about 10 eV for the [EMIM][B(CN)4] ion-pair. Since all ion-pair calculations needed to be contracted to 80% to match the liquid phase experiment, the predicted bandgap is about 8 eV. The low binding energy tail in the UPS spectrum is at about 7.5 eV binding energy.
4. Conclusions and outlook
The experimental UPS spectrum of [EMIM][B(CN)4] was compared to ion-pair DOS simulations and bulk electronic structure calculations. The ion-pair approximation to the liquid phase electronic structure is not sufficient. Only the MP2 ion-pair calculation provided a qualitatively good overview of the electronic structure of the liquid.However, there is a good agreement between the experimental UPS spectrum and the ab initio reconstructed (DOS weighted by photoemission cross sections) bulk spectra, when the PBE-D3(BJ) functional is used. This agreement validates the predicted bulk structure of [EMIM][B(CN)4] (see Fig. 1).
The low binding energy part of the [EMIM][B(CN)4] UPS spectrum is dominated by the anion-related states and the higher binding energies are mostly due to the cation. However, the top of the valence band is due to the π-bonds of the imidazolium. The positioning of the cation and anion-related bands is similar to [EMIM][BF4], which also has a tetrahedral anion and the cation-related π-states also reside at the top of the valence band.
The nonlocal vdW-DF based functionals optB88 and CX, which worked excellently in the case of [EMIM][BF4], were not as useful in the description of [EMIM][B(CN)4]. Interestingly, the LDA approximation produces surprisingly good qualitative results, but again overestimates the density.
The [EMIM][B(CN)4] ionic liquid provides a good challenge for the ab initio calculation methods. The convergence of the electronic structure requires a large cutoff energy of about 1000 eV, which is much larger than typically used. Accounting for dispersion forces is also essential, as the pure PBE calculation (ESI S4†) does not produce an electronic structure that is in agreement with the experimental UPS spectrum. This means, that the van der Waals forces are relatively strong and highly important in [EMIM][B(CN)4]. Unfortunately, many studies on ionic liquids still do not account for van der Waals forces.
In the case of [EMIM][B(CN)4], the electron structure is very sensitive on the underlying physical structure. It requires good (realistic) estimation of bulk structure. MD (equilibrium) derived structures are probably insufficient, although they may have many correct bulk properties (density, conductivity etc.).
These findings have many implications for ab initio ionic liquid studies. Most notably many estimations of the electrochemical window(s), both for the isolated electrolyte and for ILs on different surfaces, need to be reevaluated. Also surface absorption and charge transfer studies need to use correct electronic structure to make accurate predictions.
Although the DFT calculation was able to explain the electronic structure of the [EMIM][B(CN)4] ionic liquid, no general recipe can be recommended in the selection of a suitable functional. Therefore, further experimental and theoretical investigation of various ionic liquids is necessary in order to understand the performance of different DFT functionals. This would enable the selection of the best computational method for a specific ionic liquid.
Conflicts of interest
There are no conflicts of interests to declare.Acknowledgements
Financial support by the Estonian Ministry of Education and Research (target-financed themes IUT2-25 and IUT20-13) and Estonian Centre of Excellence TK141 “Advanced Materials and High-Technology Devices for Sustainable Energetics, Sensorics and Nanoelectronics” (1.01.2016–1.03.2023) are gratefully acknowledged. The ab initio computations were carried out at the High Performance Computing Center of the University of Tartu, with support provided by I. Koppel.References
- P. Wasserscheid and T. Welton, Ionic liquids in synthesis, WILEY-VCH Verlag GmbH & Co., Weinheim, 2008 Search PubMed.
- G. P. Pandey and S. A. Hashmi, Studies on electrical double layer capacitor with a low-viscosity ionic liquid 1-ethyl-3-methylimidazolium tetracyanoborate as electrolyte, Bull. Mater. Sci., 2013, 36(4), 729–733 CrossRef CAS.
- K. B. Dhungana, L. F. O. Faria, B. Wu, M. Liang, M. C. C. Ribeiro, C. J. Margulis and E. W. Castner, Structure of cyano-anion ionic liquids: X-ray scattering and simulations, J. Chem. Phys., 2016, 145, 024503 CrossRef.
- M. Marszalek, Z. Fei, D.-R. Zhu, R. Scopelliti, P. J. Dyson, S. M. Zakeeruddin and M. Grätzel, Application of Ionic liquids containing Tricyanomethanide [C(CN)3]− or tetracyanoborate [B(CN)4]− anions in Dye-Sensitized Solar Cells, Inorg. Chem., 2011, 50, 11561–11567 CrossRef CAS.
- D. Weingarth, I. Czekaj, Z. Fei, A. Foelske-Schmitz, P. J. Dyson, A. Wokaun and R. Kötza, Electrochemical Stability of Imidazolium Based Ionic Liquids Containing Cyano Groups in the Anion: A Cyclic Voltammetry, XPS and DFT Study, J. Electrochem. Soc., 2012, 159(7), H611–H615 CrossRef CAS.
- M. Galinski, A. Lewandowski and I. Stepniak, Ionic liquids as electrolytes, Electrochim. Acta, 2006, 51(26), 5567–5580 CrossRef CAS.
- T. Nishi, T. Iwahashi, H. Yamane, Y. Ouchi and K. K. Kanai, Electronic structures of ionic liquids Cnmim BF4 studied by ultraviolet photoemission, inverse photoemission, and near-edge X-ray absorption fine structure spectroscopies, Chem. Phys. Lett., 2008, 455, 213–217 CrossRef CAS.
- D. Yoshimura, T. Yokoyama, T. Nishi, H. Ishii, R. Ozawa, H. Hamaguchi and K. Seki, Electronic structure of ionic liquids at the surface studied by UV photoemission, J. Electron Spectrosc. Relat. Phenom., 2005, 144–147, 319–322 CrossRef CAS.
- T. Cremer, C. Kolbeck, K. R. Lovelock, N. Paape, R. Wölfel, P. S. Schulz, P. Wasserscheid, H. Weber, J. Thar, B. Kirchner, F. Maier and H.-P. Steinrück, Towards a Molecular Understanding of Cation–Anion Interactions—Probing the Electronic Structure of Imidazolium Ionic Liquids by NMR Spectroscopy, X-ray Photoelectron Spectroscopy and Theoretical Calculations, Chem.–Eur. J., 2010, 30, 8929 CrossRef.
- I. Kuusik, M. Berholts, J. Kruusma, V. Kisand, A. Tõnisoo, E. Lust and E. Nõmmiste, Valence electronic structure of [EMIM][BF4] ionic liquid: photoemission and DFT+D study, RSC Adv., 2018, 8(53), 30298–30304 RSC.
- M. Bässler, J.-O. Forsell, O. Björneholm, R. Feifel, M. Jurvansuu, S. Aksela, S. Sundin, S. L. Sorensen, R. Nyholm, A. Ausmees and S. Svensson, Soft X-ray undulator beam line I411 at MAX-II for gases, liquids and solid samples, J. Electron Spectrosc. Relat. Phenom., 1999, 953, 101–103 Search PubMed.
- X. Gonze, F. Jollet, F. A. Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J.-M. Beuken and J. Bieder, Recent developments in the ABINIT software package, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- M. Torrent, F. Jollet, F. Bottin, G. Zerah and X. Gonze, Implementation of the Projector Augmented-Wave Method in the ABINIT code. Application to the study of iron under pressure, Comput. Mater. Sci., 2008, 42, 337 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Rev. B, 1992, 45, 13244 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS.
- J. Klimes, D. R. Bowler and A. Michaelides, Chemical accuracy for the van der Waals density functional, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef.
- K. Berland and P. Hyldgaard, Exchange functional that tests the robustness of the plasmon description of the van der Waals density functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 035412 CrossRef.
- S. Grimme, Semiempirical hybrid density functional with perturbative second-order correlation, J. Chem. Phys., 2006, 124, 034108 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction DFT-D for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- Y. Shao, L. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. Brown, A. Gilbert, L. Slipchenko, S. Levchenko, D. O'Neill, R. D. Jr, R. Lochan, G. B. T. Wang, N. Besley, J. Herbert, C. Lin, T. V. Voorhis and S. Chien, Advances in methods and algorithms in a modern quantum chemistry program package, Phys. Chem. Chem. Phys., 2006, 8, 3172 RSC.
- A. R. Choudhury, N. Winterton, A. Steiner, A. I. Cooper and K. A. Johnson, In situ Crystallization of Low-Melting Ionic Liquids, J. Am. Chem. Soc., 2005, 127, 16792–16793 CrossRef CAS.
- S. H. Zottnick, M. Finze and K. Müller-Buschbaum, Transformation of the ionic liquid [EMIM][B(CN)4] into anionic and neutral lanthanum tetracyanoborate coordination polymers by ionothermal reactions, Chem. Commun., 2017, 53, 5193–5195 RSC.
- T. Ozaki and C.-C. Lee, Absolute Binding Energies of Core Levels in Solids from First Principles, Phys. Rev. Lett., 2017, 118, 026401 CrossRef.
- J. J. Yeh, Atomic Calculation of Photoionization Cross-Sections and Asymmetry Parameters, Gordon and Breach Science Publishers, Langhorne, PE (USA), 1993 Search PubMed.
- J. J. Yeh and I. Lindau, Atomic subshell photoionization cross sections and asymmetry parameters, At. Data Nucl. Data Tables, 1985, 32, 1–155 CrossRef CAS.
- M. Reinmöller, A. Ulbrich, T. Ikari, J. Preis, O. Höfft, F. Endres, S. Krischok and W. J. D. Beenken, Theoretical reconstruction and elementwise analysis of photoelectron, Phys. Chem. Chem. Phys., 2011, 13, 19526–19533 RSC.
- J. Cornil, S. Vanderdonckt, R. Lazzaroni, D. A. Santos, G. Thys, H. J. Geise, L. M. Yu and M. Szablewski, Valence Electronic Structure of δ-Conjugated Materials: Simulation of the Ultraviolet Photoelectron Spectra with Semiempirical Hartree-Fock Approaches, Chem. Mater., 1999, 11, 2436–2443 CrossRef CAS.
- T. Ikari, A. Keppler, M. Reinmöller, W. J. D. Beenken, S. Krischok, M. Marschewski, W. Maus-Friedrichs, O. Höfft and F. Endres, Surface Electronic Structure of Imidazolium-Based Ionic Liquids Studied by Electron Spectroscopy, e-J. Surf. Sci. Nanotechnol., 2010, 8, 241–245 CrossRef CAS.
- R. M. Fogarty, R. P. Matthews, M. T. Clough, C. R. Ashworth, A. Brandt-Talbot, P. J. Corbett, R. G. Palgrave, R. A. Bourne, T. W. Chamberlain, T. Vander Hoogerstraete, P. B. J. Thompson, P. A. Hunt, N. A. Besley and K. R. J. Lovelock, NEXAFS spectroscopy of ionic liquids: experiments versus calculations, Phys. Chem. Chem. Phys., 2017, 19, 31156–31167 RSC.
- I. Kuusik, M. Tarkanovskaja, J. Kruusma, V. Kisand, A. Tõnisoo, E. Lust and E. Nõmmiste, Valence band photoelectron spectra of [EMIM][BF4] ionic liquid vapor: Evidences of electronic relaxation, J. Mol. Liq., 2016, 223, 939–942 CrossRef CAS.
- A. Ulbrich, M. Reinmöller, W. J. D. Beenken and S. Krischok, Photoelectron spectroscopy on ionic liquid surfaces - Theory and experiment, J. Mol. Liq., 2014, 192, 77–86 CrossRef CAS.
- G. Saielli, Computational Spectroscopy of Ionic Liquids for Bulk Structure Elucidation, Adv. Theory Simul., 2018, 1800084 CrossRef.
- N. Mardirossian and M. Head-Gordon, Thirty years of density functional theory in computational chemistry: an overview and extensive assessment of 200 density functionals, Mol. Phys., 2017, 115(19), 2315–2372 CrossRef CAS.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- T. Koller, J. Ramos, N. M. Garrido, A. P. Fröba and I. G. Economou, Development of a united-atom force field for 1-ethyl-3-methylimidazolium tetracyanoborate ionic liquid, Mol. Phys., 2012, 110(11–12), 1115–1126 CrossRef CAS.
- T. M. Koller, M. H. Rausch, J. Ramos, P. S. Schulz, P. Wasserscheid, I. G. Economou and A. P. Fröba, Thermophysical Properties of the Ionic Liquids [EMIM][B(CN)4] and [HMIM][B(CN)4], J. Phys. Chem. B, 2013, 117(28), 8512–8523 CrossRef CAS.
- S. P. Ong, O. Andreussi, Y. Wu, N. Marzari and G. Ceder, Electrochemical Windows of Room-Temperature Ionic Liquids from Molecular Dynamics and Density Functional Theory Calculations, Chem. Mater., 2011, 23(11), 2979–2986 CrossRef CAS.
- Y. Zhang, C. Shi, J. F. Brennecke and E. J. Maginn, Refined Method for Predicting Electrochemical Windows of Ionic Liquids and Experimental Validation Studies, J. Phys. Chem. B, 2014, 118, 6250–6255 CrossRef CAS.
- J. Kruusma, A. Tõnisoo, R. Pärna, E. Nõmmiste, I. Kuusik, M. Vahtrus, I. Tallo, T. Romann and E. Lust, The electrochemical behavior of 1-ethyl-3-methyl imidazolium tetracyanoborate visualized by in situ X-ray photoelectron spectroscopy at the negatively and positively polarized micro-mesoporous carbon electrode, J. Electrochem. Soc., 2017, 164(13), A3393–A3402 CrossRef CAS.
- S. Thiemann, S. Sachnov, S. Porscha, P. Wasserscheid and J. Zaumseil, Ionic Liquids for Electrolyte-Gating of ZnO Field-Effect Transistors, J. Phys. Chem. C, 2012, 116(25), 13536–13544 CrossRef CAS.
- S. Seki, N. Serizawa, K. Hayamizu, S. Tsuzuki, Y. Umebayashi, K. Takei and H. Miyashiroa, Physicochemical and Electrochemical Properties of 1-Ethyl-3-Methylimidazolium Tris(pentafluoroethyl)trifluorophosphate and 1-Ethyl-3-Methylimidazolium Tetracyanoborate, J. Electrochem. Soc., 2012, 159(7), A967–A971 CrossRef CAS.
- P. Peljo and H. H. Girault, Electrochemical potential window of battery electrolytes: the HOMO–LUMO misconception, Energy Environ. Sci., 2018, 11, 2306 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra06762k |
| ‡ We wish to commemorate our early-deceased author, colleague and friend Prof. Ergo Nõmmiste, who was the initiator and leader of the study of the electronic structure of ionic liquids and a member of the Estonian Academy of Sciences. |
| This journal is © The Royal Society of Chemistry 2019 |