Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Study of half metallicity, structural and mechanical properties in inverse Heusler alloy Mn2ZnSi(1−x)Gex and a superlattice
M. Ramab,
A. Saxenaa,
Abeer E. Aly *c and
A. Shankarb
*c and
A. Shankarb
aDepartment of Physics, North-Eastern Hill University, Shillong, India-793022. E-mail: atulnehu@yahoo.co.in
bCondensed Matter Theory Research Lab, Department of Physics, Kurseong College, Darjeeling, Kurseong, India-734203. E-mail: amitshan2009@gmail.com
cBasic Science Department, El Salam Institute for Engineering and Technology, Cairo, Egypt. E-mail: abeerresmat782000@yahoo.com
First published on 11th November 2019
Abstract
The electronic and magnetic properties of Mn2ZnSi(1−x)Gex (x = 0.0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, and 1.0) inverse Heusler alloys and Mn2ZnSi/Mn2ZnGe superlattice have been investigated using first-principles calculations. All these alloys are stable in the fcc magnetic phase and satisfies the mechanical and thermal stability conditions as determined from the elastic constants and negative formation energy. The spin-polarized electronic band structures and the density of states indicate half-metallicity with 100% spin polarization at the Fermi energy level for x = 0.0, 0.125, 0.25, 0.50, and 1.0, with the integral values of the total magnetic moments per formula unit at their equilibrium lattice constants, following the Slater–Pauling rule. The electronic properties and the magnetic moments are mostly contributed by two Mn atoms and are coupled anti-parallel to each other, making them ferrimagnetic in nature. The presence of the half-metallic bandgap with an antiparallel alignment of Mn atoms makes these Heusler alloys a potential candidate for spintronic applications.
1. Introduction
Half-metals (HMs) are a type of materials where we observe a metallic nature for one kind of electron spin and a semiconducting gap at the Fermi energy level (EF) for the other electron spin, thus having 100% spin-polarized electrons at EF. Such materials are a good source of spin-polarized electrons for applications in the trending field of spintronics, which manipulates the spin degrees of freedom of electrons in addition to their charges, and are finding large applications in new phenomena such as giant magnetoresistance,1,2 tunnelling magnetoresistance, and magnetic tunnel junctions.3 Although the half-metallic properties have been observed in systems like oxides, manganites, double perovskites, and pyrites,4–8 it is the half-metallic Heusler alloys that are getting more preference over others due to the similarity in the crystal structure with the primarily used binary semiconductors (GaAs) and comparatively high Curie temperature (Tc) (Co2FeSi, Tc = 1100 K).9,10 The half-metal (HM) nature has been predicted by several authors in a variety of Heusler alloys,11–14 including full Heusler alloys with a general formula of X2YZ (where X and Y are transition metals and Z is an sp block element), from their theoretical and experimental studies, with Co2MnSi(Ge) being the first member.15,16The Mn-based Heusler alloys in cubic and tetragonal phases have gained much interest among the Heusler alloys in the field of shape memory,17 giant topological Hall effect,18 spin-transfer torque,19 and large exchange bias20,21 owing to their stable half-metallicity with 100% polarization at EF and high Tc with ferri/ferro-magnetism.22–26 A compensating ferrimagnetic order of Mn also results in low saturation magnetization in these alloys,27 which results in the reduction of power loss due to the absence of stray fields; also, the absence of inversion symmetry evolves interesting phenomena such as non-collinear magnetism, topological Hall effect, and skyrmions that are absent in the centrosymmetric Heusler structures like Mn2YGa (Y = Ti, V, Cr).27 A significant amount of theoretical and experimental investigations are in progress to explore the physical properties of Mn-based candidates28 as observed from literature, but new Mn-based Heusler alloys are waiting to be discovered with better and untapped properties. Although detailed studies on Mn2ZnSi(Ge) have been reported by previous authors,29–32 there exist some discrepancies in their reports. In this context, Wei et al.31 have estimated a smaller lattice constant of 5.75 Å for Mn2ZnGe as compared to that of Mn2ZnSi (5.80 Å),29,30 which could be due to the larger atomic size of Ge than that of Si. A similar anomaly was also communicated in their electronic properties.29,31 Lie et al.32 suggested the occurrence of an energy band gap of 0.52 eV at the majority spin, inconsistent with the energy gap of 0.48 eV at the minority spin channel, as reported by Bhat et al.30 Similarly, the asymmetric electronic structure has been reported for isoelectronic Mn2ZnSi and Mn2ZnGe31 in contrast to the symmetric profile of analogous systems like Mn2FeZ (Z = Al, Ga, Si, Ge, and Sb),33 Mn2VZ (Z = Al, Ge),34 and Mn2CoZ (Z = Al, Ga, Si, and Ge).35
To remove the above anomaly observed in the physical properties of Mn2ZnSi(Ge), we performed a detailed investigation of the structural and electronic properties using the well-known density functional theory (DFT). Since there are no experimental reports available for the title compounds, the results obtained for Mn2ZnSi(Ge) were validated by systematically doping the Mn2ZnSi system with Ge and subsequently comparing with the available theoretical data. A similar study of the substitution of Si by Ge in Fe2MnSi(1−x)Gex was studied by Hamad et al.,36 where the valence bands and the conduction bands shift to higher energies for 0.75 concentration of Ge, causing the bands to cross EF and resulting in the loss of half-metallicity. A similar behaviour for 0.75 concentration of Ge could also be expected and it motivated us to do similar studies on more finer concentrations of Ge, i.e., Mn2ZnSi(1−x)Gex (x = 0.0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, and 1.0) to understand and verify whether such similar properties, due to the symmetry in the concentration of Si and Ge, exist.
It is also intended to construct a superlattice of Mn2ZnSi/Mn2ZnGe along the [001] direction of the parent (Mn2ZnSi) fcc lattice. The half-metallicity and the Slater–Pauling rule in the superlattice of two Heusler alloys remained unaffected by the crystal directions, as shown by Azadani et al. along [001], [110], and [111] direction with various thickness.37 Moreover, they have reported the presence of induced uniaxial magnetocrystalline anisotropy in the superlattice, which is prohibited in L21 and C1b structure of Heusler alloys due to their symmetry. These superlattices are also reported to be efficient in reducing the thermal conductivity (κ) in the thermoelectric materials by reducing the phonon contribution to κ, which is achieved by the additional photon scattering at the interface of the superlattice.38
2. Computational details
The DFT based plane-wave pseudopotential (PW-PP)39 and full potential-linearized augmented plane-wave (FP-LAPW) methods40 were employed to investigate the results presented in this manuscript. The basis set was expanded in terms of plane waves in PW-PP, whereas in the FP-LAPW method, space was divided into non-overlapping muffin-tin (MT) spheres centred on the atomic sites and in an interstitial region (IR). The basis set inside the MT sphere consists of a linear combination of radial functions times spherical harmonics, whereas it consists of plane waves in the IR. The Kohn–Sham orbitals were described by expanding the kinetic energy with the cut-off value of 50 Ry in PW-PP and charge-density cut-off value of 500 Ry. The electron–ion interactions were described by the Vanderbilt ultrasoft potentials. The fermionic occupations were described by the Marzari–Vanderbilt41 scheme of smearing, with a value of 7.4 × 10−3 Ry. The energy convergence was achieved in the FP-LAPW method by expanding the plane wave functions in IR, with a cut off RMT × Kmax = 8, where RMT denotes the smallest muffin-tin sphere radius and Kmax gives the maximum value of the wave vector (K) in wave expansion. Different MT sphere radii (RMT) were used with the value of 2.44 a.u., 2.40 a.u., 2.30 a.u., and 2.40 a.u. for Mn, Zn, Si, and Ge, respectively. For the non-spherical contributions, charge density and the potential inside the MT spheres were expanded up to lmax = 14, while the charge density and the potential were expanded as a Fourier series with the wave vectors up to Gmax = 14. Integration over the Brillouin zone was carried out on a grid of 16 × 16 × 16 with automatically generated k-points following the convention of Monkhorst and Pack42 centred at Γ-point. The effect of exchange-correlation functional was treated with the Perdew–Burke–Ernzerhof scheme of generalised gradient approximation (PBE-GGA).433. Results and discussions
3.1 Crystal structure and structural properties
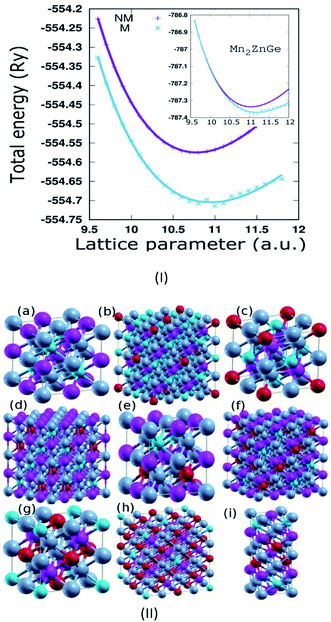
Mn2ZnSi(Ge) crystallizes in the fcc structure of prototype Hg2CuTi-type (space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m),11 as shown in Fig. 1, where Mn occupies the position (0, 0, 0) and (1/4, 1/4, 1/4) labelled as MnI and MnII, respectively, while Zn occupies (1/2, 1/2, 1/2) and Si(Ge) occupies (3/4, 3/4, 3/4) of a unit cell, with the atomic sequence being Mn–Mn–Zn–Si(Ge).31 The non-magnetic (NM) and magnetic (M) phases of the sample materials were optimized to verify the most stable configuration. The lattice constant (a) versus the total energy fitted into empirical Murnaghan's equation of state is shown in Fig. 1(I). We can conclude that the sample materials crystallize in the magnetic phase ground state. The optimized a for Mn2ZnSi (5.79 Å) is in qualitative agreement with the previous report (5.80 Å); however, there exist discrepancy in the results for Mn2ZnGe. We obtained an optimized a = 5.93 Å for Mn2ZnGe, but Wei et al.31 have mentioned that Mn2ZnGe reflects HM behaviour, with the value of a ranging from 5.69 to 5.80 Å and an equilibrium lattice constant of 5.75 Å. It can also be mentioned here that slightly higher a is expected for Mn2ZnGe as compared to Mn2ZnSi, due to the addition of Ge having a bigger atom radius, as observed in analogous Fe2MnZ (Z = Si, Ge, and Sn) reported by Jain et al.,44 where the crystal size increases with the replacement of Z from Si to Sn.
3m),11 as shown in Fig. 1, where Mn occupies the position (0, 0, 0) and (1/4, 1/4, 1/4) labelled as MnI and MnII, respectively, while Zn occupies (1/2, 1/2, 1/2) and Si(Ge) occupies (3/4, 3/4, 3/4) of a unit cell, with the atomic sequence being Mn–Mn–Zn–Si(Ge).31 The non-magnetic (NM) and magnetic (M) phases of the sample materials were optimized to verify the most stable configuration. The lattice constant (a) versus the total energy fitted into empirical Murnaghan's equation of state is shown in Fig. 1(I). We can conclude that the sample materials crystallize in the magnetic phase ground state. The optimized a for Mn2ZnSi (5.79 Å) is in qualitative agreement with the previous report (5.80 Å); however, there exist discrepancy in the results for Mn2ZnGe. We obtained an optimized a = 5.93 Å for Mn2ZnGe, but Wei et al.31 have mentioned that Mn2ZnGe reflects HM behaviour, with the value of a ranging from 5.69 to 5.80 Å and an equilibrium lattice constant of 5.75 Å. It can also be mentioned here that slightly higher a is expected for Mn2ZnGe as compared to Mn2ZnSi, due to the addition of Ge having a bigger atom radius, as observed in analogous Fe2MnZ (Z = Si, Ge, and Sn) reported by Jain et al.,44 where the crystal size increases with the replacement of Z from Si to Sn.
For doping with the Ge concentration of x = 0.25, 0.5, and 0.75, a 1 × 1 × 1 unit cell of Mn2ZnSi, with 16 basis was used, giving 4 atomic positions to Si. All these 4 positions were equivalent due to symmetry, and any Si atom(s) can be replaced by Ge to give 0.25, 0.5, and 0.75 concentrations (Fig. 1(II)). However, the doping by 0.125, 0.375, 0.625, and 0.875 concentration of Ge needs a 2 × 2 × 2 supercell with 32 atom basis, giving 8 atomic positions to Si. Now, for the Ge concentration of 0.125, any 1 Si atoms can be replaced, since all the positions are equivalent due to symmetry. However, for Ge concentration of 0.375, 3 Si atoms have to be replaced, which can be achieved in 56 ways. However, symmetry reduces the number of structures, giving a total of 5 types of different structures. For the Ge concentrations of 0.625 and 0.875, the different types of structures were obtained by exchanging the atomic positions between Si and Ge for 0.375 and 0.125, respectively. Subsequently, we computed the ground state energies of all the possible structures for each doping, and the structure with minimum energy was considered for further studies. The ground state optimized a of the 1 × 1 × 1 unit cell for all doping concentrations along with the calculated av from the Vegards law (eqn. (1)) are given in Table 1. The optimized values were found to be in qualitative agreement with that obtained from the Vegards law, which is given as:
| ax = 5.793(1 − x) + 5.926(x) | (1) |
| Ge concentration (x) | Optimized a (Å) | Vegards av (Å) | Difference between a and av | Eform (eV) |
|---|---|---|---|---|
| 0.0 | 5.793 | — | — | −2.866 |
| 0.125 | 5.798 | 5.809 | −0.001 | −2.830 |
| 0.25 | 5.814 | 5.826 | −0.012 | −2.738 |
| 0.375 | 5.837 | 5.843 | −0.006 | −2.639 |
| 0.5 | 5.861 | 5.86 | 0.001 | −2.625 |
| 0.625 | 5.883 | 5.876 | 0.007 | −2.532 |
| 0.75 | 5.895 | 5.893 | 0.002 | −2.471 |
| 0.875 | 5.913 | 5.909 | 0.004 | −2.417 |
| 1.0 | 5.926 | — | — | −2.374 |
| Superlattice | 4.091, 11.57 | — | — | −2.106 |
For the construction of the superlattice of [Mn2ZnSi]n/[Mn2ZnGe]n (for notation, refer 45), we used the technique used by Culbert et al.46 and Tirpanci et al.45 As described earlier in section 3.1, the structure of X2YZ inverse Heusler alloys with space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m is generally described as fcc with four atom basis. However, it can also be considered as a bcc layered structure along the [001] direction with two atoms in a layer (Fig. 1 of ref. 46). The lattice constant (as/bs, subscript s for superlattice) of the layered superlattice and the lattice constant (a) of the parent fcc are related as as = bs = a/√2, while cs depends on the n value. In the present case with n = 1, the sequence of the atomic layer in the periodic superlattice is MnZn–MnSi–ZnMn–GeMn–MnZn–MnGe–ZnMn–SiMn. For example, for the superlattices of lattices A and B, Tirapanci et al.45 took the lattice constant of the superlattice as the average of the lattice constants of A and B, whereas in the present study, we performed the volume optimization of the superlattice, which gives us as = bs = a/√2 = 4.091 Å, and a = 5.786 Å for the parent fcc lattice. The c value (Table 1) is exactly double of a, and this exactly corresponds to a bcc structure for n = 1. However, an intermediate a value between that of Mn2ZnSi and Mn2ZnGe was expected.
3m is generally described as fcc with four atom basis. However, it can also be considered as a bcc layered structure along the [001] direction with two atoms in a layer (Fig. 1 of ref. 46). The lattice constant (as/bs, subscript s for superlattice) of the layered superlattice and the lattice constant (a) of the parent fcc are related as as = bs = a/√2, while cs depends on the n value. In the present case with n = 1, the sequence of the atomic layer in the periodic superlattice is MnZn–MnSi–ZnMn–GeMn–MnZn–MnGe–ZnMn–SiMn. For example, for the superlattices of lattices A and B, Tirapanci et al.45 took the lattice constant of the superlattice as the average of the lattice constants of A and B, whereas in the present study, we performed the volume optimization of the superlattice, which gives us as = bs = a/√2 = 4.091 Å, and a = 5.786 Å for the parent fcc lattice. The c value (Table 1) is exactly double of a, and this exactly corresponds to a bcc structure for n = 1. However, an intermediate a value between that of Mn2ZnSi and Mn2ZnGe was expected.
In the present study, all the structures obtained were optimized by using the force minimization method, and their stability was verified by calculating their formation energy (Eform) per atom. The formula Eform per atom of full Heusler alloys as given in ref. 47 and 48 was modified in our case Mn2ZnSi(1−x)Gex as
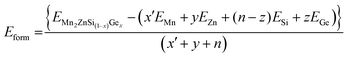 | (2) |
3.2 Mechanical properties
It is also very important to determine the elastic constants of a material to understand their significant properties in the solid-state, such as interatomic potential, mechanical deformation and stress, specific heat, and Debye temperature. The nature of the structural transitions can also be understood by observing the behaviour of parent phases near transitions. Hence, we calculated independent elastic constants (Cij) using the volume conservation technique,49 in which the strain was chosen in such a way that the total volume of the system remains constant. The cubic symmetry of the crystal reduces the total number of independent elastic constants from 21 to 3, namely, C11, C12, and C44. The mechanical stability of the structure, after the deformation of a cubic crystal with the F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3m space group, were verified by the expression C11 > 0, C11 − C12 > 0, and C11 + 2C12 > 0.44 The calculated values of Cij are given in Table 2, and the values are found to fulfil the above stability conditions.
3m space group, were verified by the expression C11 > 0, C11 − C12 > 0, and C11 + 2C12 > 0.44 The calculated values of Cij are given in Table 2, and the values are found to fulfil the above stability conditions.
| Ge doping (x) | C11 | C12 | C44 | B | G | Y | ΘD | ν | A |
|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 252.06 | 102.45 | 168.89 | 152.32 | 121.81 | 288.53 | 594.75 | 0.18 | 2.26 |
| 0.125 | 205.35 | 153.3 | 76.75 | 170.65 | 49.79 | 136.14 | 385.64 | 0.37 | 2.95 |
| 0.25 | 148.79 | 101.09 | 112.82 | 116.99 | 61.25 | 156.44 | 415.99 | 0.28 | 4.73 |
| 0.375 | 212.38 | 185.22 | 97.14 | 194.68 | 45.57 | 126.82 | 359.41 | 0.39 | 7.32 |
| 0.50 | 202.24 | 182.44 | 104.28 | 189.11 | 44.04 | 122.59 | 349.76 | 0.38 | 10.59 |
| 0.625 | 132.97 | 102.97 | 105.69 | 112.97 | 50.16 | 131.09 | 364.55 | 0.31 | 7.05 |
| 0.75 | 95.58 | 48.06 | 67.92 | 63.89 | 44.61 | 108.56 | 339.30 | 0.22 | 2.86 |
| 0.875 | 185.19 | 148.6 | 108.46 | 160.79 | 54.45 | 146.78 | 379.38 | 0.35 | 5.93 |
| 1.0 | 241.35 | 119.81 | 195.33 | 160.33 | 122.54 | 292.98 | 548.33 | 0.19 | 3.21 |
We also computed other parameters, as described in Table 2, from independent elastic constants. The isotropic B and G values for the samples were estimated from the Voigt–Reuss–Hill (VRH) approximation,50–54 where the B value defines the hardness of a material, and for pure compounds (x = 0.0 and 1.0), it is comparable to that of Mn2ZrSi (B = 187.015 GPa)55 and Mn2ZrGe (B = 175.478 GPa)55 and was found to be highest for 0.375 concentration of Ge among the studied alloys. Similarly, the analysis of Table 2 for resistant to plastic deformation, i.e., the value of G also suggest that Mn2ZnSi has more resistance as compared to analogous Mn2ZrSi (G = 80.249 GPa),55 Mn2ZrGe (G = 71.088 GPa),55 Fe2MnSi (G = 73 GPa),44 and Fe2MnGe (G = 86 GPa),44 as the resistance becomes lower with the further addition of Ge and again becomes higher for x = 1.0. The Young's modulus (Y) is a measure of the stiffness of a material, and the higher the Young's modulus value, the stiffer is the material. Typically, pure elements are stiffer than the doped ones, and on comparing with analogous Mn2ZrSi (Y = 210.622 GPa),55 Mn2ZrGe (Y = 187.189 GPa),55 Fe2MnSi(Y = 198 GPa),44 and Fe2MnGe (Y = 202 GPa),44 it was observed that both of our sample materials are the stiffest of all.
It is known that Pugh's ratio (B/G) determines the brittleness or ductility56,57 of a material with its critical value of 1.75, and the nature of atomic bonding present in the material can be verified from its critical value of 0.26 for the Poisson's ratio (ν).58 We can note from Table 2 that both Mn2ZnSi and Mn2ZnGe are brittle in nature with the directional covalent type of bonding, but the partial doping of Ge somehow make these alloys ductile in nature. The probability of developing microcracks or defects during the growth process of the crystal was expected for these materials, as observed from their Zener anisotropy factor (A),59 which is much greater than unity. The thermodynamic property can also be studied from the elastic parameters at Debye temperature (ΘD) and low temperature, with the crystal vibration being the acoustic type, where ΘD, estimated from the elastic constant, was expected to describe their real value. It is evident from their values that ΘD decreases with the replacement of Si by Ge with a bigger atomic radius, and a similar feature was also observed for isotropic Fe2MnZ (Z = Si, Ge, and Sn).44
3.3 Electronic properties and magnetic moments
A semi relativistic calculation of the energy bands of Mn2ZnSi along the high symmetric directions of the Brillouin zone (BZ) was performed to understand the ground state electronic properties using the FP-LAPW and PW methods (Fig. 2a and b). The energy bands obtained from the two methods had a similar profile and were consistent with the previous reports.29,30 Further, from Fig. 2, one can note that the majority spin channel had dense bands crossing EF, which was set to 0.0 eV, giving a metallic nature for majority spin, whereas minority spin had a discontinuity with a distinct energy gap (Eg) at EF, showing a semiconducting behaviour. The valence band maximum and conduction band minimum was found to be at the L symmetry point of the BZ, producing a direct band Eg at this point. The Eg so obtained by the PW and FP-LAPW methods were 0.61 eV and 0.57 eV, respectively, with the values being in qualitatively good agreement. Kervan et al. have reported a direct Eg of 0.48 eV at the L symmetry point of the BZ in minority spin,29 which is consistent with the present report. In addition, the present FP-LAPW-estimated Eg at a = 5.79 Å is in close agreement with the previous reports.32 The energy bands and Eg values so obtained are also comparable to the values reported by Bhat et al.30 In the case of Mn2ZnGe, the obtained Eg in the present study at a = 5.93 Å is 0.39 eV, which is inconsistent with that of 0.21 eV reported by Wei et al. at an optimized lattice constant of 5.75 Å.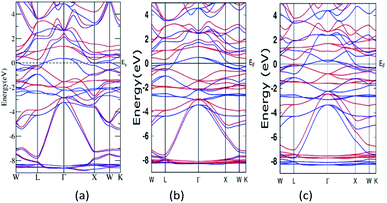 | ||
| Fig. 2 Band structure for Mn2ZnSi as calculated from (a) FP-LAPW and (b) PW-PP and for (c) Mn2ZnGe. (Colour scheme: blue colour for majority states and red colour for minority states). | ||
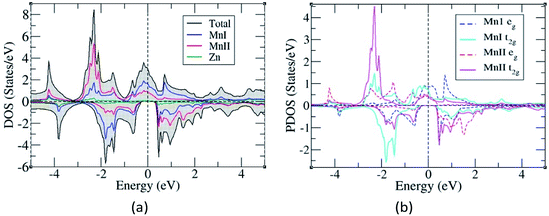
The total and partial density of states were also studied to understand their energy bands (Fig. 3), and since the electronic structures of Mn2ZnSi and Mn2ZnGe have a similar profile, we plotted only for one material. From the analysis of the density of states (DOS) for Mn2ZnSi(Ge), it is clear that the asymmetry in the DOS of majority and minority spins was due to the asymmetry in the partial density of states (PDOS) of Mn atoms (Fig. 3b). For majority spin, the DOS across the EF was arising because of deg and dt2g states of the MnI atom, whereas −3 eV below EF was arising from dt2g states of the MnII atom. Likewise, in the minority spin, the DOS above EF was because of the d electrons of MnII atoms, whereas below EF, it was arising from dt2g states of MnI atoms. There exists a weaker hybridization between Mn and Zn atoms as their peaks are at different positions. Moreover, similar to EF, the DOS is mainly because of the Mn atoms, which are responsible for the formation of Eg and dominates the overall electronic properties of the material. The contribution of Si or Ge around EF is insignificant and mainly in the region of −5 eV to −3 eV, which is not visible in the DOS plot (Fig. 3).
The occurrence of a bandgap in the cubic inverse full Heusler compounds has been discussed by Skaftouros et al.11 The Zn atom has completely filled d orbitals that contribute to the core region (−9 eV to −8 eV). The p states of Si(Ge) contribute to the lower valence region, i.e., from −5 eV to −3 eV. The region close to EF arises from the Mn atoms due to the interaction of MnI and MnII atoms. Mn atoms have tetrahedral symmetry; therefore, the 3 dt2g orbitals of MnI hybridize with the 3 dt2g orbitals of MnII atoms, giving 3 dt2g bonding and 3 dt2g anti-bonding orbitals. In the same fashion, the 2 deg orbitals of MnI atoms hybridize with the 2 deg orbitals of the MnII atoms, again giving 2 deg bonding and 2 deg anti-bonding orbitals. Thus, we have five bonding and five anti-bonding d orbitals with EF just falling in between the two bands formed by these orbitals.
Furthermore, the sample material was doped with a slightly bigger Ge atom in the varying concentration. The presence of Ge in the 0.125, 0.25, 0.375, and 0.5 leads to similar results with a continuous band across EF, thus showing metallic nature for majority spin, while a direct bandgap of 0.47 eV, 0.56 eV, 0.43 eV, and 0.40 eV was observed for x = 0.125, 0.25, 0.375, and 0.5, respectively, in the minority spin. At the Ge concentration of 0.625, 0.75, and 0.875, the band profile reflects their metallic nature (Fig. 4). Moreover, the Eg value decreases linearly with the increase in the Ge concentration, and shows the metallic character for highest concentration, which is consistent with the previous report published by Hamad et al.36 describing Fe2MnSi(1−x)Gex, where the doping at x = 0.75 Ge results in the loss of HM, which is otherwise present for x = 0.25 and 0.50. The partial substitution of Ge in Si creates a discrete energy level below the conduction band edge and broadens the energy levels and hence, the EF shifts towards the conduction band edge, which results in the n-type semiconducting nature of the alloys. However, for the sufficiently high doping of Ge, the conduction and valence band overlap with each other, and Eg vanishes.
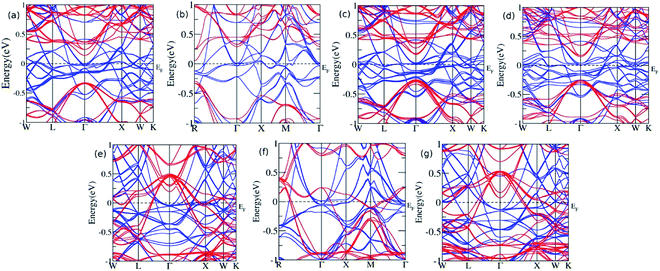 | ||
| Fig. 4 The band structure for Ge doping at varying concentration (a) x = 0.125 (b) x = 0.25 (c) x = 0.375 (d) x = 0.5 (e) x = 0.625 (f) x = 0.75, and (g) x = 0.875. | ||
To further analyse the electronic structure and to understand the cause for the loss of HM for higher Ge concentration, we plotted the total DOS in Fig. 5a for x = 0.5 and 0.75. The DOS reflects the features observed in bands, namely, HM for 0.5 Ge and metallic for 0.75 Ge. The two DOS almost appear the same in nature with a shift along the energy axis, except for the appearance of a flat valley between two peaks at −1 eV and 0 eV for x = 0.75, which is absent between the two peaks at −1.75 and −0.65 for x = 0.5. The flat valley for x = 0.75 appears to originate from the slightly lower adjacent peak at −1 eV for x = 0.5, which is absent for x = 0.75, thus pushing the peak towards EF and eventually crossing EF. This can be understood from the comparison of DOS of MnI and MnII for x = 0.5 and 0.75 (Fig. 5b). The solid lines for MnI and MnII for x = 0.5 show the asymmetry in their DOS and peaks at different positions. However, in the case of x = 0.75, the MnI and MnII peaks appear almost in the same place but with different strengths.
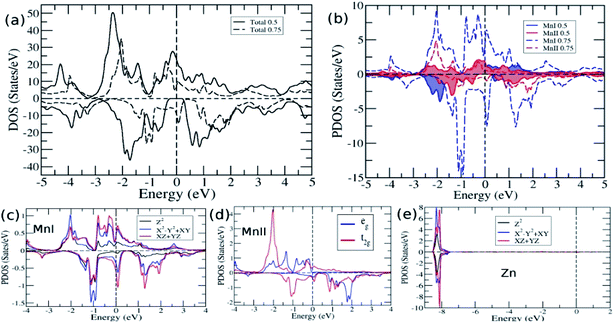 | ||
| Fig. 5 (a) Total DOS for x = 0.5 and 0.75 (b) DOS of MnI and MnII for x = 0.5 and 0.75 and PDOS for x = 0.75 of (c) MnI (d) MnII and (e) Zn. | ||
As explained earlier, the Eg in the minority spin was due to the hybridization between the d bands of MnI and MnII with tetrahedral symmetry (Td) that leads to the splitting of d bands into doubly degenerate eg and triply degenerate t2g bands (Fig. 3b). However, on higher doping of Ge, the symmetry of d orbitals was further lowered, and both MnI and Zn exhibited the D3h symmetry (Fig. 5c and e), while MnII maintained the Td symmetry (Fig. 5d). The D3h symmetry splits the d orbitals into three bands, namely, singlet Z2 and two doubly degenerate X2-Y2, XY, and XZ, YZ bands. Moreover, due to the difference in the symmetry of MnI and MnII atoms, there is a weaker hybridization between these atoms, resulting in the loss of Eg in minority spin.
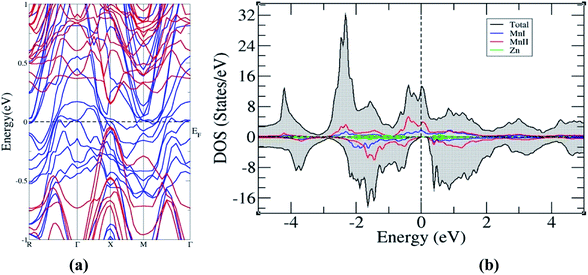
The electronic structure of the superlattice, presented in Fig. 6, shows the preservation of the HM character of the bulk Mn2ZnSi(Ge), and on comparative analysis with the band structures of Mn2ZnSi and Mn2ZnGe, we found that the bandgap reduces to 0.22 eV with the shift in the bandgap from L to X. The reduction in the bandgap can be understood by comparing the minority band edge below and above EF of the bulk (Fig. 3a and b) and superlattice (Fig. 6b), as suggested by Ghaderi et al.60 There is a contribution from both MnI and MnII in the minority valence band edge below EF in the case of bulk Mn2ZnSi(Ge). However, in the case of a superlattice of Mn2ZnSi/Mn2ZnGe, the contribution comes only from MnII atoms. This is due to the lowering of the coordination number of atoms at the interface of a superlattice with respect to the atoms of the bulk, which enhances the exchange and thus increases the splitting of majority and minority DOS, as observed by the number of finer peaks in Fig. 6b.
The calculated individual and total magnetic moments for pure and Ge-doped compounds are presented in Table 3, which depicts that the magnetic behaviour mainly arises from the Mn atoms as the magnetic moment of Zn and Si (Ge) are comparatively minuscule. The total magnetic moments of Mn2ZnSi(Ge) per unit formula is 2.00 μB, in accordance with the Slater–Pauling (SP) rule11 of MT = ZT – 28, where MT is the total magnetic moment and ZT is the number of valence electron of the material. This rule is in accordance with the hybridization mechanism explained above for the formation of Eg. The individual magnetic moments of MnI and MnII are aligned antiparallel to each other, which can be explained from their asymmetric spin-polarized DOS and PDOS of Mn2ZnSi (Fig. 3a and b).29,30 As a result of unoccupied 3d spin-up states of MnI and 3d spin-down states of MnII, the magnetic moments of the two Mn atoms are aligned anti-parallel to each other.
| Magnetic moment in (μB) | MnI | MnII | Zn | Si | Ge | Total | |
|---|---|---|---|---|---|---|---|
| Mn2ZnSi | Present work | −1.279 | 3.213 | 0.009 | 0.059 | — | 2.00 |
| Others | −0.778 (ref. 29) | 2.664 | 0.268 | 0.032 | — | 2.00 | |
| −0.741 (ref. 30) | 2.596 | 0.020 | 0.032 | — | 2.00 | ||
| Ge concentration (x) | 0.125 | −0.823 | 2.703 | 0.028 | 0.035 | 0.032 | 15.969 |
| 0.25 | −0.654 | 2.573 | 0.026 | 0.026 | 0.031 | 7.993 | |
| 0.375 | −0.064 | 2.583 | 0.025 | 0.025 | 0.03 | 16.177 | |
| 0.5 | −0.542 | 2.49 | 0.023 | 0.026 | 0.03 | 16.054 | |
| 0.625 | 1.248 | 2.185 | −0.009 | −0.001 | −0.03 | 27.8 | |
| 0.75 | 0.73 | 2.543 | −0.012 | −0.099 | 0.007 | 13.282 | |
| 0.875 | 1.012 | 2.753 | −0.015 | −0.005 | 0.003 | 30.079 | |
| Mn2ZnGe | Present work | −1.181 | 2.629 | −0.021 | — | 0.059 | 1.98 |
| Others | 0.43 (ref. 31) | −2.4 | −0.02 | — | −0.01 | −2.00 | |
As shown in Fig. 7, we plotted the variation of individual magnetic moments of MnI, MnII, and total magnetic moment per formula unit of partially Ge doped compounds as a function of Ge concentration. The total magnetic moment per formula unit remains almost 2.0 μB up to 0.5 Ge, in accordance with the SP rule of MT = ZT − 28, confirming the HM for these dopings. The magnetic moment of MnII remains positive throughout the concentration of Ge, whereas it remains negative up to 0.5 Ge and thereafter, it becomes positive in the case of MnI. This can be explained in terms of Mn–Mn interaction, which depends upon the Mn–Mn distance. Mn magnetic moments couple anti-parallel to each other for small Mn–Mn distances and couple parallel to each other for large Mn–Mn distances, which is consistent with the report by Bethe and Slater.61 Hence, increasing the Ge concentration expands the crystal size, which in turn increases the Mn–Mn distances and favours the parallel alignment of the Mn moment, as reported by Galanakis et al. for Ni2MnAl.62
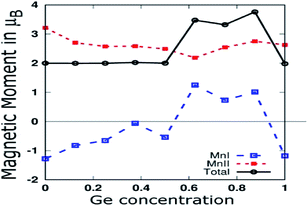 | ||
| Fig. 7 MnI and MnII Magnetic moments, and total magnetic moment per formula unit of partial Ge doped compounds. | ||
4. Conclusions
We have investigated the ground state electronic and magnetic properties of Mn2ZnSi(1−x)Gex (x = 0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875, and 1.0) Heusler alloys and Mn2ZnSi/Mn2ZnGe superlattice using DFT-based PW-PP and FP-LAPW methods. The stable ground state structures for these alloys were found to energetically favour the magnetic phase over the non-magnetic phases. The results so obtained using PW-PP and FP-LAPW were in good agreement with the previous studies. The elastic constants predicted the mechanical stability of these alloys at ambient conditions. The spin-polarized electronic band structures and DOS were also studied for pure, doped, and superlattice compounds. The analysis of the electronic band structures predicted half-metallicity with 100% spin-polarized electrons at EF for the pure Heusler alloys. However, the partial doping of Ge resulted in HM for x = 0.125 to 0.5 and a higher concentration leads to a metallic state. A deeper analysis of DOS and PDOS for HM and metallic phases revealed the change in the symmetry of MnI and Zn from Td to D3h as the cause of the transition from HM to metallic nature. The PDOS also revealed the antiparallel coupling of Mn atoms and the interaction of the neighbouring Mn atoms, which is the cause of Eg. The electronic structure for the superlattice of Mn2ZnSi/Mn2ZnGe also conserves the HM of bulk Mn2ZnSi(Ge). The total magnetic moments per formula unit for these alloys were close to the integral value and were in good agreement with the Slater–Pauling rule of MT = ZT − 28. Thus, the presence of a half-metallic bandgap with 100% spin-polarized electrons at EF and the ferrimagnetic ordering of Mn atoms resulting in low saturation magnetic moments make these Mn2ZnSi(1−x)Gex Heusler alloys suitable materials in spintronic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
M. Ram acknowledges SULEKOR, NEHU, Shillong and A. Shankar acknowledges SERB-New Delhi.Notes and references
- M. N. Baibich, J. M. Broto, A. Fert, F. N. Van Dau, F. Petroff, P. Etienne and J. Chazelas, Giant magnetoresistance of (001) Fe/(001) Cr magnetic superlattices, Phys. Rev. Lett., 1988, 61(21), 2472 CrossRef CAS.
- G. Binasch, P. Grünberg, F. Saurenbach and W. Zinn, Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39(7), 4828 CrossRef CAS.
- S. Tsunegi, Y. Sakuraba, M. Oogane, K. Takanashi and Y. Ando, Large tunnel magnetoresistance in magnetic tunnel junctions using a Co2MnSi Heusler alloy electrode and aMgO barrier, Appl. Phys. Lett., 2008, 93(11), 112506 CrossRef.
- J. M. D. Coey and C. L. &Chien, Half-metallic ferromagnetic oxides, MRS Bull., 2003, 28(10), 720–724 CrossRef CAS.
- J. M. Pruneda, V. Ferrari, R. Rurali, P. B. Littlewood, N. A. Spaldin and E. Artacho, Ferrodistortive instability at the (001) surface of half-metallic manganites, Phys. Rev. Lett., 2007, 99(22), 226101 CrossRef CAS.
- J. H. Park, S. K. Kwon and B. I. Min, Half-metallic antiferromagnetic double perovskites: LaAVRuO 6 (A= Ca, Sr, and Ba), Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(17), 174401 CrossRef.
- K. Ramesha, R. Seshadri, C. Ederer, T. He and M. A. Subramanian, Experimental and computational investigation of structure and magnetism in pyrite Co1−xFexS2: Chemical bonding and half-metallicity, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(21), 214409 CrossRef.
- J. Zhang, G. Shan, Z. Zheng and C. H. Shek, Structure and magnetic behaviors of Gd6FeBi2 compound, Intermetallics, 2016, 68, 51–56 CrossRef CAS.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser, H. J. Lin and J. Morais, Geometric, electronic, and magnetic structure of Co2FeSi: Curie temperature and magnetic moment measurements and calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72(18), 184434 CrossRef.
- S. Wurmehl, G. H. Fecher, H. C. Kandpal, V. Ksenofontov, C. Felser and H. J. Lin, Investigation of Co2FeSi: The Heusler compound with highest Curie temperature and magnetic moment, Appl. Phys. Lett., 2006, 88(3), 032503 CrossRef.
- S. Skaftouros, K. Özdoğan, E. Şaşıoğlu and I. Galanakis, Generalized Slater-Pauling rule for the inverse Heusler compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(2), 024420 CrossRef.
- I. Galanakis, P. H. Dederichs and N. Papanikolaou, Slater-Pauling behavior and origin of the half-metallicity of the full-Heusler alloys, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(17), 174429 CrossRef.
- Y. Sakuraba, J. Nakata, M. Oogane, H. Kubota, Y. Ando, A. Sakuma and T. Miyazaki, Huge spin-polarization of L21-ordered Co2MnSi epitaxial Heusler alloy film, Jpn. J. Appl. Phys., 2005, 44(8L), L1100 CrossRef CAS.
- M. Jourdan, J. Minár, J. Braun, A. Kronenberg, S. Chadov, B. Balke and H. Ebert, Direct observation of half-metallicity in the Heusler compound Co2MnSi, Nat. Commun., 2014, 5, 3974 CrossRef CAS.
- S. Ishida, S. Fujii, S. Kashiwagi and S. Asano, Search for half-metallic compounds in Co2MnZ (Z= IIIb, IVb, Vb element), J. Phys. Soc. Jpn., 1995, 64(6), 2152–2157 CrossRef CAS.
- K. R. A. Ziebeck and P. J. Webster, A neutron diffraction and magnetization study of Heusler alloys containing Co and Zr, Hf, V or Nb, J. Phys. Chem. Solids, 1974, 35(1), 1–7 CrossRef CAS.
- P. J. Brown, T. Kanomata, K. Neumann, K. U. Neumann, B. Ouladdiaf, A. Sheikh and K. R. A. Ziebeck, Atomic and magnetic order in the shape memory alloy Mn2NiGa, J. Phys.: Condens. Matter, 2010, 22(50), 506001 CrossRef CAS.
- Z. H. Liu, A. Burigu, Y. J. Zhang, H. M. Jafri, X. Q. Ma, E. K. Liu and G. H. Wu, Giant topological Hall effect in tetragonal Heusler alloy Mn2PtSn, Scr. Mater., 2018, 143, 122–125 CrossRef CAS.
- T. Gasi, A. K. Nayak, J. Winterlik, V. Ksenofontov, P. Adler, M. Nicklas and C. Felser, Exchange-spring like magnetic behavior of the tetragonal Heusler compound Mn2FeGa as a candidate for spin-transfer torque, Appl. Phys. Lett., 2013, 102(20), 202402 CrossRef.
- A. K. Nayak, C. Shekhar, J. Winterlik, A. Gupta and C. Felser, Mn2PtIn: A tetragonal Heusler compound with exchange bias behavior, Appl. Phys. Lett., 2012, 100(15), 152404 CrossRef.
- A. K. Nayak, M. Nicklas, S. Chadov, C. Shekhar, Y. Skourski, J. Winterlik and C. Felser, Large zero-field cooled exchange-bias in bulk Mn2PtGa, Phys. Rev. Lett., 2013, 110(12), 127204 CrossRef CAS.
- K. Özdogan, I. Galanakis, E. Şaşioglu and B. Aktaş, Search for half-metallic ferrimagnetism in V-based Heusler alloys Mn2VZ (Z= Al, Ga, In, Si, Ge, Sn), J. Phys.: Condens. Matter, 2006, 18(10), 2905 CrossRef.
- H. Luo, G. Liu, F. Meng, L. Wang, E. Liu, G. Wu and C. Jiang, Slater–Pauling behavior and half-metallicity in Heusler alloys Mn2CuZ (Z= Ge and Sb), Comput. Mater. Sci., 2011, 50(11), 3119–3122 CrossRef CAS.
- A. Abada, K. Amara, S. Hiadsi and B. Amrani, First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe, J. Magn. Magn. Mater., 2015, 388, 59–67 CrossRef CAS.
- G. D. Liu, X. F. Dai, H. Y. Liu, J. L. Chen, Y. X. Li, G. Xiao and G. H. Wu, Mn2CoZ(Z= Al, Ga, In, Si, Ge, Sn, Sb) compounds: Structural, electronic, and magnetic properties, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77(1), 014424 CrossRef.
- J. Zhang and S. Bobev, Correlations between Chemical Bonding and Magnetic Exchange Interactions: Synthesis, Crystal Structures, and Magnetic Properties of the New Family RE2AlGe2 (RE= Tb–Tm, Lu), Inorg. Chem., 2013, 52(9), 5307–5315 CrossRef CAS.
- L. Wollmann, S. Chadov, J. Kübler and C. Felser, Magnetism in tetragonal manganese-rich Heusler compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(6), 064417 CrossRef.
- G. Kreiner, A. Kalache, S. Hausdorf, V. Alijani, J. F. Qian, G. Shan and C. Felser, New Mn2-based Heusler Compounds, Z. Anorg. Allg. Chem., 2014, 640(5), 738–752 CrossRef CAS.
- S. Kervan and N. Kervan, Half-metallic properties of the CuHg2Ti-type Mn2ZnSi full-Heusler compound, Curr. Appl. Phys., 2013, 13(1), 80–83 CrossRef.
- I. H. Bhat, S. Yousuf, T. M. Bhat and D. C. Gupta, Investigation of electronic structure, magnetic and transport properties of half-metallic Mn2CuSi and Mn2ZnSi Heusler alloys, J. Magn. Magn. Mater., 2015, 395, 81–88 CrossRef CAS.
- X. P. Wei, X. R. Hu, B. Liu, Y. Lei, H. Deng, M. K. Yang and J. B. Deng, Electronic structure and magnetism in full-Heusler compound Mn2ZnGe, J. Magn. Magn. Mater., 2011, 323(12), 1606–1610 CrossRef CAS.
- Y. Lei, H. Deng, T. Lei, M. Yang and J. Deng, First-Principles Study on Half-Metallic Full-Heusler Compound Mn2ZnSi, J. Supercond. Novel Magn., 2013, 26(2), 389–395 CrossRef CAS.
- H. Z. Luo, H. W. Zhang, Z. Y. Zhu, L. Ma, S. F. Xu, G. H. Wu and H. B. Xu, Half-metallic properties for the Mn2FeZ (Z= Al, Ga, Si, Ge, Sb) Heusler alloys: A first-principles study, J. Appl. Phys., 2008, 103(8), 083908 CrossRef.
- E. Şaşioglu, L. M. Sandratskii and P. Bruno, First-principles study of exchange interactions and Curie temperatures of half-metallic ferrimagnetic full Heusler alloys Mn2VZ (Z= Al, Ge), J. Phys.: Condens. Matter, 2005, 17(6), 995 CrossRef.
- N. Xing, H. Li, J. Dong, R. Long and C. Zhang, First-principle prediction of half-metallic ferrimagnetism of the Heusler alloys Mn2CoZ (Z= Al, Ga, Si, Ge) with a high-ordered structure, Comput. Mater. Sci., 2008, 42(4), 600–605 CrossRef CAS.
- B. Hamad, Z. Charifi, H. Baaziz and F. Soyalp, A DFT study of the electronic and magnetic properties of Fe2MnSi1− xGexalloys, J. Magn. Magn. Mater., 2012, 324(20), 3345–3350 CrossRef CAS.
- J. G. Azadani, K. Munira, J. Romero, J. Ma, C. Sivakumar, A. W. Ghosh and W. H. Butler, Anisotropy in layered half-metallic Heusler alloy superlattices, J. Appl. Phys., 2016, 119(4), 043904 CrossRef.
- P. Hołuj, C. Euler, B. Balke, U. Kolb, G. Fiedler, M. M. Müller and G. Jakob, Reduced thermal conductivity of TiNiSn/HfNiSn superlattices, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(12), 125436 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni and A. Dal Corso, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef.
- P. Blaha, K. Schwarz, G. K. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An augmented plane wave+ local orbitals program for calculating crystal properties ( 2014) Search PubMed.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892 CrossRef.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13(12), 5188 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865 CrossRef CAS.
- V. K. Jain, N. Lakshmi, R. Jain and A. R. Chandra, Electronic Structure, Elastic, Magnetic, and Optical Properties of Fe2MnZ (Z = Si, Ge, and Sn) Full Heusler Alloys: First-Principle Calculations, J. Supercond. Novel Magn., 2019, 32(3), 739–749 CrossRef CAS.
- Ş. Tırpancı, E. Şaşıoğlu and I. Galanakis, Design of half-metallic Heusler-based superlattices with vanishing net magnetization, J. Appl. Phys., 2013, 113(4), 043912 CrossRef.
- C. A. Culbert, M. Williams, M. Chshiev and W. H. Butler, Half-metallic L21 structures with (001) planar insertions, J. Appl. Phys., 2008, 103(7), 07D707 CrossRef.
- H. Joshi, D. P. Rai, A. Laref and R. K. Thapa, Electronic and thermoelectric properties of half-heusler compounds MCoSb (M= Ti, Zr, Hf): a first principles study, Mater. Res. Express, 2019, 066307 CrossRef.
- A. Amirabadizadeh, S. A. A. Emami, Z. Nourbakhsh, S. M. A. Sadr and S. M. Baizaee, The effect of substitution of As for Ga on the topological phase and structural, electronic and magnetic properties of Mn2ZrGa Heusler alloy, J. Supercond. Novel Magn., 2017, 30(4), 1035–1049 CrossRef CAS.
- A. H. Reshak and M. Jamal, DFT calculation for elastic constants of orthorhombic structure within WIEN2K code: A new package (ortho-elastic), J. Alloys Compd., 2012, 543, 147–151 CrossRef CAS.
- W. Voigt, Lehrbuch der Kristallphysik, Aufl. Teubner, Berlin/Leipzig, 1928, Vol. 1 Search PubMed.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349 CrossRef.
- R. S. Crosson and J. W. Lin, Voigt and Reuss prediction of anisotropic elasticity of dunite, J. Geophys. Res., 1971, 76(2), 570–578 CrossRef.
- W. Voigt, Lehrbuch der Kristallphysik:BG Terbner, Leipzig, 1910, p. 964p Search PubMed.
- A. Reuss, Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingungfüreinkristalle, J. Appl. Math. Mech., 1929, 9(1), 49–58 CAS.
- A. Abada, K. Amara, S. Hiadsi and B. Amrani, First principles study of a new half-metallic ferrimagnets Mn2-based full Heusler compounds: Mn2ZrSi and Mn2ZrGe, J. Magn. Magn. Mater., 2015, 388, 59–67 CrossRef CAS.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, Philos. Mag., 1954, 45(367), 823–843 CAS.
- D. G. Pettifor, Theoretical predictions of structure and related properties of intermetallics, Mater. Sci. Technol., 1992, 8(4), 345–349 CrossRef CAS.
- I. N. Frantsevich, F. F. Voronov and S. A. Bakuta, Elastic Constants and Elastic Moduli of Metals and Nonmetals, Naukova Dnmka, Kiev, 1982 Search PubMed.
- V. Tvergaard and J. W. Hutchinson, Microcracking in ceramics induced by thermal expansion or elastic anisotropy, J. Am. Ceram. Soc., 1988, 71(3), 157–166 CrossRef CAS.
- N. Ghaderi, S. J. Hashemifar, H. Akbarzadeh and M. Peressi, First principle study of Co2MnSi/GaAs (001) heterostructures, J. Appl. Phys., 2007, 102(7), 074306 CrossRef.
- Y. Mokrousov, G. Bihlmayer, S. Blügel and S. Heinze, Magnetic order and exchange interactions in monoatomic 3d transition-metal chains, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(10), 104413 CrossRef.
- I. Galanakis and E. Şaşıoğlu, Structural-induced antiferromagnetism in Mn-based full Heusler alloys: The case of Ni2MnAl, Appl. Phys. Lett., 2011, 98(10), 102514 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |