Open Access Article
Open Access ArticleImpact of metallic trace elements on relaxivities of iron-oxide contrast agents
Ji
Ma
and
Kezheng
Chen
 *
*
Lab of Functional and Biomedical Nanomaterials, College of Materials Science and Engineering, Qingdao University of Science and Technology, Qingdao 266042, China. E-mail: kchen@qust.edu.cn; Fax: +86-532-84022509; Tel: +86-532-84022509
First published on 30th September 2019
Abstract
In this work, well-defined 3 nm-sized Ca2+, Fe3+, Na+, Mg2+, Zn2+, Ni2+, Co2+, and Cd2+ cation-adsorbed Fe3O4/γ-Fe2O3 nanoparticles were used as prototype systems to investigate the influence of metallic trace elements in body fluids on the relaxivities of iron-oxide contrast agents. It was found that surface-adsorbed cations formed a deterioration layer to induce pronounced relaxivity loss. Theoretical study showed that such relaxivity loss can be well described by a modified GCAS function, taking into account the harmonic cation oscillations around Fe3O4/γ-Fe2O3 nanoparticles. Quantum mechanics analyses revealed that even-parity and odd-parity states of harmonic oscillations are dominant in r1 and r2 relaxivities, respectively. Moreover, the harmonic oscillations of Na+ and Mg2+ cations around Fe3O4/γ-Fe2O3 nanoparticles are found to be classical forbidden, which are quite different from their counterparts located in the classical permissive area.
Introduction
During the last decade or so, magnetic resonance imaging (MRI) has become a vital non-invasive technique that aims to obtain high-resolution anatomical images for diagnosing various kinds of diseases.1–6 In this scenario, contrast agents are widely employed based on the fact that they can enhance the image contrast in designated regions with brighter or darker signals,7,8 and hence greatly boosting imaging sensitivity in MRI. Despite strenuous and unremitting efforts towards exploring new contrast agents, two tough issues have still been lingering around and plaguing academia. The first one is MRI artifacts, which are always undesirable but unavoidable due to signals yielding from calcification, haemorrhage, blood clot, fat, air, and so forth.9,10 These artifacts are sometimes indistinguishable from the MRI signals of the applied contrast agents, and probably result in the inaccurate interpretation for the diagnosis. Although various techniques have been developed to suppress artifacts by means of resonant radio frequency tuning,11,12 successful applications of these techniques are very limited.13–16 The second pressing issue is mainly related to in vivo surroundings, in which the adsorption of macroelements and trace elements onto the contrast agents in body fluids may greatly alter their MRI properties determined from in vitro tests. This means that the well-defined MRI performance of as-prepared contrast agents may not be realized or even real in clinical application due to the presence and adsorption of elements in complex fluid environments. This is an important but poorly understood matter open to discussion.Given that these two tough issues are mainly related to the complicated in vivo environments, therefore, in this work, we study the influence of metallic trace elements in fluids on relaxivities of iron-oxide contrast agents. Basically, trace elements in human body can be divided into three types: (i) essential trace elements, including iodine, zinc, selenium, copper, molybdenum, chromium, cobalt, and iron elements; (ii) possibly essential trace elements, including manganese, silicon, boron, vanadium, and nickel elements; (iii) potentially toxic elements but essential in their low dose, including fluorine, lead, cadmium, mercury, arsenic, aluminium, and tin elements. In this study, Fe3+, Zn2+, Co2+ (type i), Mg2+, Ni2+ (type ii), Cd2+ (type iii) cations together with two macroelements (Ca2+ and Na+ cations) were chosen as typical elements to separately adsorb onto negatively charged 3 nm-sized Fe3O4/γ-Fe2O3 contrast agents. Relaxivity measurements were then performed to demonstrate relaxivity loss and its variation rule after adsorption of various metallic cations.
Results and discussion
The XRD pattern of the as-synthesized pristine product in Fig. 1(a) shows the presence of Fe3O4 (JCPDS no. 85-1436) phase or γ-Fe2O3 (JCPDS no. 39-1346) phase, or both. Further, XPS spectrum in Fig. 1(b) gives two distinct peaks at ∼711 and ∼724 eV corresponding to Fe2p3/2 and Fe2p1/2 levels, respectively.17 Two satellite peaks around 718 and 732 eV demonstrate the existence of γ-Fe2O3 phase,18 indicating that the pristine product is a hybrid of both Fe3O4 phase and γ-Fe2O3 phase. The TEM study shows that pristine Fe3O4@γ-Fe2O3 particles are near spherical [inset of Fig. 1(a)], with an average diameter around 3 nm. These 3 nm-sized Fe3O4@γ-Fe2O3 particles possess negatively charged surfaces with a zeta potential value of −27.6 mV, which is of benefit to cation adsorption in aqueous solutions. Prior to the impregnation of these bare nanoparticles into various cation stock solutions, control experiments on relaxivities were carried out for these pristine Fe3O4/γ-Fe2O3 nanoparticles. Fig. 1(c) shows r1 and r2 relaxivities are determined (from slopes) to be 3.86 and 17.41 s−1 mmol−1 L, respectively, with an r2/r1 ratio of 4.51. Although these values are barely comparable to Magnevist (a commercial gadolinium complex, r1 = 4.6 s−1 mmol−1 L, r2 = 4.5 s−1 mmol−1 L, r2/r1 ∼ 1)19,20 and much inferior to commercial Feridex (r2 = 109.4 s−1 mmol−1 L),1 the optimization of relaxivities and development of new contrast agents are outside the scope of this work.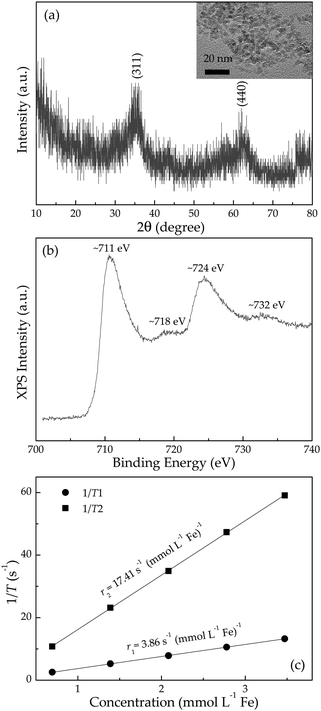 | ||
| Fig. 1 (a) XRD pattern, TEM image (inset), (b) XPS spectrum and (c) proton longitudinal r1 and transverse r2 relaxivities (measured at 1.41 T and 37 °C) of pristine Fe3O4/γ-Fe2O3 nanoparticles. | ||
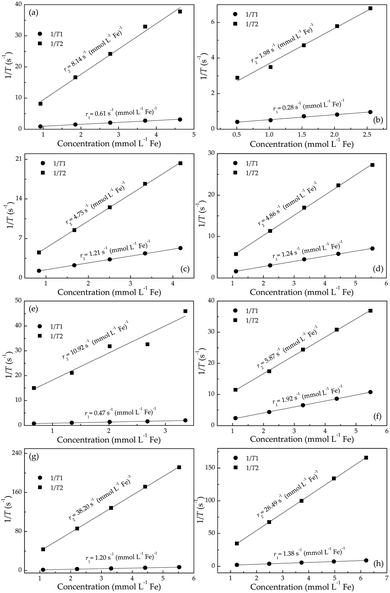
After various cation adsorptions, all r1 relaxivities and most r2 relaxivities drastically fall into decline (Fig. 2), indicating the degradation of MRI performance of Fe3O4/γ-Fe2O3 nanoparticles. That is to say, the inevitable adsorption of ions in body fluids in clinical application may well deteriorate the as-designed MRI properties from in vitro tests. In this scenario, the quantitative research on the variation of r1 and r2 relaxivities after adsorption of various metallic cations is of fundamental importance to predicting MRI performance for in vivo applications.
Based on observations in Fig. 2, the surface-adsorbed metallic cations form a deterioration layer on relaxivities of Fe3O4/γ-Fe2O3 nanoparticles. Therefore, simplifications like independency between adsorbed cationic shell and interior iron-oxide core will not yield the accurate results and are full of fallacies. Along this line, it is essential to consider synergetic interactions between adsorbed cations and particle surfaces from a microscopic standpoint, and even to consider stochastic dependence between electrons and ions at a more microcosmic level. We can describe this idea more precisely in the following way: consider an electrostatically adsorbed cation vibrating at an iron-oxide particle surface. It becomes common sense that any three-dimensional vibration can always be decomposed into numerous one-dimensional harmonic vibrations. In this sense, we draw lessons from conclusions in quantum mechanics and use Hermite polynomials, which belong to a classical orthogonal polynomial sequence, to make the association between final relaxivities and a defined parameter Xr/Z of adsorbed cations. Here, X, r and Z denote electronegativity, radius and atomic number of the cation under discussed (Table 1), respectively. The constructed function of Xr/Z-dependent relaxivity distribution is based on the probability density function utilized in Gram–Charlier A series (GCAS) with some modifications. As known, GCAS function can also be expressed by using Hermite polynomials but it is not guaranteed to be positive, and is therefore not a valid probability distribution. It does not converge in many cases of interest, making it not a true asymptotic expansion, because it is not possible to estimate the error of the expansion. Based on the preceding analyses, the relaxivities rk (k = 1 or 2) can be given by
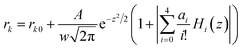 | (1) |
| Parameters | Ca2+ | Fe3+ | Na+ | Mg2+ | Zn2+ | Ni2+ | Co2+ | Cd2+ |
|---|---|---|---|---|---|---|---|---|
| Atomic number | 20 | 26 | 11 | 12 | 30 | 28 | 27 | 48 |
| Electronegativity | 11.30 | 15.38 | 9.44 | 17.13 | 10.38 | 9.60 | 9.10 | 9.79 |
| Radius (Å) | 0.99 | 0.64 | 0.95 | 0.65 | 0.74 | 0.72 | 0.74 | 0.97 |
By applying eqn (1), the experimental data of both r1 and r2 relaxivities for various adsorbed cations can be separately connected with smooth curves, as shown in Fig. 3(a) and (b), respectively. The correlation coefficient R2 values of the fitting plots are beyond 0.95, indicating the applicability of eqn (1) to make an association between relaxivities and the characteristic parameter Xr/Z of adsorbed cations. Most strikingly, the cumulants ai are close to zero at i = 1, 3 in longitudinal case and at i = 0, 2, 4 in transverse case (Table 2). This intriguing finding reminds us of the parity of Hermite polynomials, that is, Hi(−z) = (−1)iHi(z). Along this line, we boldly propose a general formula of cumulants ai according to the harmonic oscillator theory in quantum mechanics:
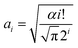 | (2) |
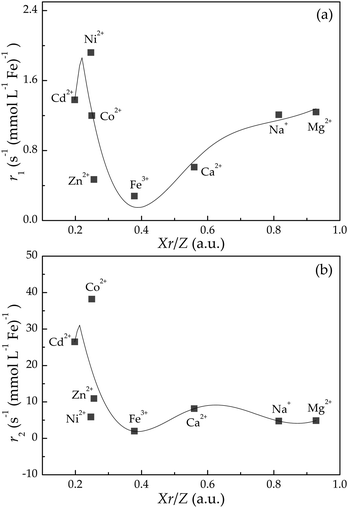 | ||
| Fig. 3 Dependence of (a) r1 and (b) r2 values on Xr/Z with regard to various cation-adsorbed Fe3O4/γ-Fe2O3 nanoparticles. The experimental data are plotted as solid squares, and the solid lines are fitting results according to eqn (1). | ||
| Relaxivity | r k0 | A | w | x c | a 0 | a 1 | a 2 | a 3 | a 4 |
|---|---|---|---|---|---|---|---|---|---|
| Longitudinal | 3.95 | −1.6 × 10−3 | 0.37 | 0.26 | 0.73 | 4.5 × 10−5 | 0.53 | 2.5 × 10−6 | 0.89 |
| Transverse | 17.86 | −19.33 | 0.38 | 0.29 | 1.2 × 10−3 | 0.58 | 1.7 × 10−6 | 0.66 | 8.9 × 10−8 |
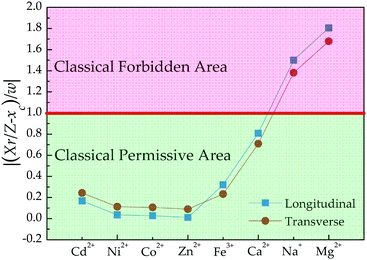
In addition, the quantum mechanics gives the characteristic length (i.e., 1/α) dividing classical forbidden area (|z| > 1/α) and classical permissive area (|z| ≤ 1/α) for harmonic oscillators. In this work, z values can be calculated based on the fitting values of xc and w according to the equation of z = (Xr/Z − xc)/w. Fig. 4 shows that z values of Na+ and Mg2+ cations are beyond 1/α = 1, indicating that the harmonic oscillations of Na+ and Mg2+ cations around Fe3O4/γ-Fe2O3 nanoparticles are classical forbidden. By contrast, Ca2+, Fe3+, Zn2+, Ni2+, Co2+, and Cd2+ cations can oscillate around Fe3O4/γ-Fe2O3 nanoparticles within classical permissive area.
Experimental
Synthesis and characterization
The pristine Fe3O4/γ-Fe2O3 nanoparticles were synthesized according to the method reported elsewhere21,22 with little modification. Typically, 10 mL of Na2CO3 aqueous solution (0.6 mol L−1) was added into 50 mL of FeCl3·6H2O aqueous solution (0.04 mol L−1) and vigorously stirred for five minutes. After that, ascorbic acid (0.5 g) was added into the above solution and stirred for another ten minutes. Finally, the mixture was transferred into a Teflon-lined stainless-steel autoclave with a capacity of 100 mL for hydrothermal treatment at 160 °C for 3 h. After the autoclave had cooled down to room temperature naturally, the Fe3O4/γ-Fe2O3 precipitate was separated by centrifugation, washed successively with distilled water and absolute ethanol, and dried in the air at 60 °C for 4 h.To mimic the actual element concentration in human body, the concentration of Ca2+, Fe3+, Na+, Mg2+, Zn2+, Ni2+, Co2+, and Cd2+ cations was uniformly set to be 2 mmol L−1. In a typical adsorption experiment, eight sets of 50 mg of the as-prepared Fe3O4/γ-Fe2O3 nanoparticles were separately soaked into 100 mL of CaCl2, FeCl3, NaCl, MgCl2, ZnCl2, NiCl2, CoCl2, and CdCl2 aqueous solutions for 1 h. After the above adsorption, all precipitates were separated by centrifugation, washed successively with distilled water and absolute ethanol, and dried in the air at 60 °C for 4 h.
The X-ray diffraction (XRD) pattern of the sample was recorded with a Rigaku D/max-γB diffractometer equipped with a rotating anode and a Cu Kα source (λ = 0.154056 nm) at 40 kV and 150 mA between 10° and 80° (2θ) with a step size of 0.02°. The phase composition was further confirmed by X-ray photoelectron spectroscopy (XPS), which was performed on VG ESCALAB 220i-XL system. The morphology and structure of the sample was characterized by transmission-electron microscope (TEM) with an operating voltage of 200 kV (JEM-2100). The zeta potential values of the samples were determined by dynamic light scattering (DLS, Zetasizer Nano, Malvern Instrument). Iron concentrations in relaxivity experiments were determined by inductively coupled plasma-optic emission spectrometry (ICP-OES, PerkinElmer Optima 8000).
Relaxivity measurement
A mq-60 NMR analyzer (Bruker Minispec) was applied to measure proton transverse (r2) and longitudinal (r1) relaxivities of the samples. Specifically, a certain amount of sample was dissolved in deionized water at 37 °C and laid in a magnetic field of 1.41 T with a frequency of 60 MHz. Then a Carr–Purcell–Meiboom–Gill spin-echo pulse sequence was adopted and the interecho time and repetition time were set to be 1 ms and 6 s, respectively. The as-measured signal data was fitted by a monoexponential decay curve to yield the T2 relaxation time. On the other hand, an inversion recovery (IR) pulse sequence was adopted by using 10 inversion times between 0.05 and 10 s. Then a monoexponential recovery curve was utilized to fit the signal data to finally obtain T1 relaxation time. All data were presented as arithmetic means of 3 replicates. After the measurements of T1 and T2, the relaxivities r1 and r2 could be obtained by fitting respective relaxation rate (s−1) versus iron concentration (mmol L−1 Fe).Conclusions
In summary, Ca2+, Fe3+, Na+, Mg2+, Zn2+, Ni2+, Co2+, and Cd2+ cation-adsorbed Fe3O4/γ-Fe2O3 nanoparticles are synthesized by a facile soaking method to mimic actual element adsorption in human body. The r1 and r2 relaxivities of bare Fe3O4/γ-Fe2O3 nanoparticles are 3.86 and 17.41 s−1 mmol−1 L, respectively. However, after cation adsorption, nearly all relaxivity values show a great decrease, manifesting surface-adsorbed cations greatly degenerate the MRI capability of iron-oxide contrast agents. Such relaxivity loss can be described by a modified GCAS function, taking into account of numerous harmonic oscillations of various cations around Fe3O4/γ-Fe2O3 nanoparticles. The quantum mechanics analyses show that even-parity and odd-parity states of harmonic oscillators are dominant in r1 and r2 relaxivities of cation-adsorbed Fe3O4/γ-Fe2O3 nanoparticles, respectively. Moreover, the harmonic oscillations of Na+ and Mg2+ cations around Fe3O4/γ-Fe2O3 nanoparticles are found to be classical forbidden, which are quite different from their counterparts located in the classical permissive area.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the financial aid from the National Natural Science Foundation of China (NSFC No. 51472133).Notes and references
- T. Shin, J. Choi, S. Yun, I. Kim, H. Song, Y. Kim, K. I. Park and J. Cheon, ACS Nano, 2014, 8, 3393 CrossRef CAS.
- J. Y. Park, M. J. Baek, E. S. Choi, S. Woo, J. H. Kim, T. J. Kim, J. C. Jung, K. S. Chae, Y. Chang and G. H. Lee, ACS Nano, 2009, 3, 3663 CrossRef CAS.
- Q. Wang, A. Xiao, Y. Liu, Q. Zou, Q. Zhou, H. Wang, X. Yang, C. Zheng, Y. Yang and Y. Zhu, Nanomedicine, 2018, 14, 2551 CrossRef CAS.
- Y. Li, Y. Chang, R. Yuan and Y. Chai, ACS Appl. Mater. Interfaces, 2018, 10, 25213 CrossRef CAS.
- I. Monaco, P. Armanetti, E. Locatelli, A. Flori, M. Maturi, S. Del Turco, L. Menichetti and M. C. Franchini, J. Mater. Chem. B, 2018, 6, 2993 RSC.
- Z. Zhao, C. Sun, J. Bao, L. Yang, R. Wei, J. Cheng, H. Lina and J. Gao, J. Mater. Chem. B, 2018, 6, 401 RSC.
- H. B. Na, I. C. Song and T. Hyeon, Adv. Mater., 2009, 21, 2133 CrossRef CAS.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167 CrossRef CAS.
- H. U. Ahmed, A. Kirkham, M. Arya, R. Illing, A. Freeman, C. Allen and M. Emberton, Nat. Rev. Clin. Oncol., 2009, 6, 197 CrossRef.
- J. W. M. Bulte and D. L. Kraitchman, NMR Biomed., 2004, 17, 484 CrossRef CAS PubMed.
- W. Liu, H. Dahnke, E. K. Jordan, T. Schaeffter and J. A. Frank, NMR Biomed., 2008, 21, 242 CrossRef.
- C. A. Helms, Am. J. Roentgenol., 1999, 173, 234 CrossRef CAS PubMed.
- W. S. Seo, J. H. Lee, X. Sun, Y. Suzuki, D. Mann, Z. Liu, M. Terashima, P. C. Yang, M. V. McConnell and D. G. Nishimura, Nat. Mater., 2006, 5, 971 CrossRef CAS.
- C. Richard, B. T. Doan, J. C. Beloeil, M. Bessodes, E. Tóth and D. Scherman, Nano Lett., 2008, 8, 232 CrossRef CAS.
- J. Shin, R. M. Anisur, M. K. Ko, G. H. Im, J. H. Lee and I. S. Lee, Angew. Chem., Int. Ed., 2009, 48, 321 CrossRef CAS.
- J. S. Choi, J. H. Lee, T. H. Shin, H. T. Song, E. Y. Kim and J. Cheon, J. Am. Chem. Soc., 2010, 132, 11015 CrossRef CAS.
- Z. Li, J. F. Godsell, J. P. O'Byrne, N. Petkov, M. A. Morris, S. Roy and J. D. Holmes, J. Am. Chem. Soc., 2010, 132, 12540 CrossRef CAS.
- T. Yamashita and P. Hayes, Appl. Surf. Sci., 2008, 254, 2441 CrossRef CAS.
- T. Kim, E. Momin, J. Choi, K. Yuan, H. Zaidi, J. Kim, M. Park, N. Lee, M. T. McMahon, A. Quinones-Hinojosa, J. W. M. Bulte, T. Hyeon and A. A. Gilad, J. Am. Chem. Soc., 2011, 133, 2955 CrossRef CAS.
- W. A. Seo, J. H. Lee, X. Sun, Y. Suzuki, D. Mann, Z. Liu, M. Terashima, P. C. Yang, M. V. McConnell, D. G. Nishimura and H. Dai, Nat. Mater., 2006, 5, 971 CrossRef CAS.
- J. Ma, L. Cheng and K. Chen, J. Appl. Phys., 2015, 117, 154701 CrossRef.
- J. Ma and K. Chen, Sci. Rep., 2017, 7, 42312 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |