Tailoring intermolecular interactions to develop a low-temperature electrolyte system consisting of 1-butyl-3-methylimidazolium iodide and organic solvents

Abstract

Ionic liquids (ILs) exhibit remarkable properties and great tunability, which make them an attractive class of electrolyte materials for a variety of electrochemical applications. However, despite the promising progress for operating conditions at high temperatures, the development of their low-temperature viability as electrolytes is still limited due to the constrains from thermal and ion transport issues with a drastic decrease in temperature. In this study, we present a liquid electrolyte system based on a mixture of 1-butyl-3-methylimidazolium iodide ([BMIM][I]), γ-butyrolactone (GBL), propylene carbonate (PC), and lithium iodide (LiI) and utilize its molecular interactions to tailor its properties for extremely low-temperature sensing applications. In particular, the carbonyl group on both PC and GBL can form hydrogen bonds with the imidazolium cation, as indicated by Fourier transform infrared spectroscopy (FTIR), and the extent of these interactions between ions and molecules was also characterized and quantified via proton nuclear magnetic resonance (¹H NMR) spectroscopy. More importantly, at the optimal ratio, the organic solvents do not have excess content to form aggregates, which may cause undesired crystallization before the glass transition. The microscopic evolutions of the systems are correlated with their bulk behaviors, leading to improvements in their thermal and transport properties. The optimized formulation of [BMIM][I]/PC/GBL/LiI showed a low glass transition temperature (T_g) of −120 °C and an effectively reduced viscosity of 0.31 Pa s at −75 °C. The electrochemical stability of the electrolyte was also validated to support the targeted iodide/triiodide redox reactions without interference.

---

Introduction

Ionic liquids (ILs), which are materials that consist of ions and remain a liquid at room temperature, are known as “designer solvents” due to their great versatility in properties via the selection of cation and anion, and have been utilized in a variety of applications, such as facilitators for synthesis and catalysis,^1,2 media for separation processes,^3,4 and thermal fluids for heat storage and transfer.^5,6 In particular, the unique characteristics of ILs, including negligible volatility, good electrochemical stability, wide liquidus range, and considerable ionic conductivity, have made them popular candidates as electrolytes for electrochemical devices including dye-sensitized solar cells,^7,8 batteries,^9–11 supercapacitors,^10,12 and sensors.^13–15 ILs-based electrolytes can enhance device stability and broaden the operating temperature window,^16,17 which are common bottlenecks for electrolyte development when using conventional molecular liquids (MLs) as media.^18,19 However, although ILs-based electrolytes possess these excellent traits, their ionic conductivities are yet comparable with that of MLs-based electrolytes due to their high viscosities and insufficient ion-disassociation, which both originate from the electrostatic attractions between the cations and anions of ILs.²⁰ When operating at relatively high temperatures, the transport properties of ILs-based electrolytes are not a major concern since both conductivity and fluidity improve with elevated temperatures. But, at low temperatures, ILs-based electrolytes often exhibit a significant decrease in ionic conductivity, rendering unsatisfying functionalities even if they remain liquids. With the increasing need of applying energy devices and sensors under extreme environmental conditions, this restrains the potential use of ILs-based electrolytes for low-temperature applications.

To resolve the poor ionic conductivity of ILs-based electrolytes for low-temperature applications, incorporating MLs as co-solvents has become a broadly applied strategy. The introduction of MLs, such as water or organic solvents, can provide an electrostatic screening effect due to the molecular interactions between MLs and ILs, where the cohesive energy from the coulombic attractions of the ions in ILs can be reduced to drastically change both the macroscopic and microscopic properties of the mixture.²¹ Moreover, the specific intermolecular interactions between the ions of ILs and molecular solvents further improve the mobilities of particular ions with altered coordination.²² Owing to the solvation effect, reduced viscosity and boosted ionic conductivity are widely observed in binary mixtures of water and ILs. However, the approach of adding water to ILs to improve the electrolyte properties is rigorously restricted by their relatively narrow electrochemical window.^23,24 More importantly, the very limited liquidus temperature range of water above 0 °C makes mixtures of water and ILs unfavorable candidates for low-temperature applications. On the other hand, organic solvents are a strong complement to water when employing ILs as electrolytes. Binary mixtures of ILs and organic solvents have been investigated to support various electrochemical devices because of their significantly advanced transport properties.^25,26 Moreover, these electrolyte systems have shown improved thermal stability and safety without a great compromise in ionic conductivity compared to conventional organic electrolytes.¹⁹ For example, Ruiz et al. reported that electrolytes composed of pyrrolidinium-based ILs with nitrile and carbonate-based organic solvents at optimized concentrations showed satisfactory thermal stability, increased conductivity, and a wide electrochemical window, which are suitable for supercapacitors operating over a broad temperature range from −20 °C to 80 °C.²⁷

Since there is a large selection of organic solvents, their mixtures with ILs provide the flexibility to develop tailored properties for task-specific functionalities. Among the various organic solvents, carbonate- and lactone-based liquids are attractive candidates for designing electrolytes operating over a broad temperature range due to their low melting points and high boiling points. When targeting low temperatures, the conductivity of the electrolyte is directly affected by the working temperature and has a major impact on the overall performance of the device. Aguilera et al. investigated the effects of composition on the coordination of solvated lithium ions and observed an enhancement in ionic conductivity at a temperature as low as −90 °C from mixtures of two carbonate solvents (ethylene carbonate and dimethyl carbonate), 1-butyl-1-methylpyrrolidinium bis(trifluoromethanesulfonyl)imide and lithium salt.²⁸ Tian et al. formulated electrolytes based on mixtures of 1-ethyl-3-methylimidazolium tetrafluoroborate ([EMIM][BF₄]) with γ-butyrolactone (GBL) and propylene carbonate (PC), respectively, for supercapacitor operating at −70 °C, which exhibited superior device performances, and experimentally validated their liquidus range down to −80 °C.²⁹ Although both of the abovementioned studies have demonstrated considerable progress on electrolyte properties at low temperatures, efforts have not been invested in fully exploring the lower temperature limit of liquid-state electrolytes. Therefore, designing strategies to develop low-temperature electrolytes is desirable to accommodate potential operations under extreme conditions. Furthermore, with supercapacitors and batteries as the mainstreams for low-temperature electrochemical applications, most research groups focus on ILs with favorable anions such as tetrafluoroborate ([BF₄]⁻) and bis(trifluoromethane)sulfonimide ([TFSI]⁻).^29–31 However, the development of low-temperature electrolytes needs to be extended to a broader range of ILs, especially for electrochemical devices that require specific types of ions according to their working principles.

We have been investigating the molecular interactions between ILs and cosolvents to modify and improve their properties, starting from the discovery of hydrogen bonding in 1-butyl-3-methylimidazolium iodide ([BMIM][I])/water mixtures and the resulting improvement in transport properties at room temperature.³² Recently, we designed an aqueous-based electrolyte of [BMIM][I], ethylammonium nitrate ([EA][N]), water, and lithium iodide (LiI) with the aim to optimize the intermolecular forces between the four components.³³ This electrolyte formulation possessed a glass transition temperature (T_g) of −108 °C and showed remarkable enhancements in fluidity, ionic conductivity, and ionicity. These iodide-containing electrolytes were specifically formulated for molecular electronic transducer (MET) sensors that rely on the electrochemical reactions between iodide (I⁻) and the triiodide (I₃⁻) redox couple.³⁴ To aim for extremely low-temperature environments in space missions, we utilized intermolecular interactions to design electrolytes for a wider operating temperature range, specially focusing on the extension of their liquidus limit to the lower end. Herein, we report an electrolyte system consisting of [BMIM][I], PC, GBL, and LiI and the investigation of its thermal, transport, and electrochemical properties. The carefully formulated composition resulted in optimized molecular interactions and achieved tailored properties for iodide-containing low-temperature liquid electrolytes. The results of this work present a viable liquid electrolyte system to support MET-based sensing technology for planetary explorations. Moreover, we anticipate the proposed strategy via modifying molecular interactions will continue to extend the limit of liquid-state electrolytes for low-temperature electrochemical applications.

Experimental

Materials

The organic solvents, γ-butyrolactone (≥99%) and propylene carbonate (99.7%), were both purchased from Sigma-Aldrich, the ionic liquid, 1-butyl-3-methylimidazolium iodide ([BMIM][I]) (>98%), was purchased from IoLiTec, and anhydrous lithium iodide (≥98%) was purchased from VWR International. All chemicals were used as received without further purification.

Sample preparation

The electrolytes of the IL/organic solvent mixtures were manually mixed and ultrasonically agitated in an ice-water bath for 90 s using a Sonics VibraCell at 500 W. Lithium iodide salt (5 mol%) as the default component was added and dissolved in all the mixtures to boost the concentration of iodide ions in the electrolytes. After sonication, all the sample solutions were homogeneous and fully miscible by visual inspection. The formulations of the sample electrolytes studied in this work are named based on their composition in mol%, for example, a sample electrolyte that consists of 5 mol% [BMIM][I], 90 mol% GBL, and 5 mol% LiI is referred to as [BMIM][I]/GBL/LiI – 5/90/5. If the solution contains only a single component that was used as received, it is referred to as “neat”.

Differential scanning calorimetry

A TA Instruments Q-20 differential scanning calorimeter (DSC) was employed to characterize the low-temperature thermal behaviors of the prepared electrolyte formulations. Each sample solution was quench-cooled using liquid nitrogen from 40 °C to −160 °C and then heated at a controlled heating rate of 5 °C min⁻¹ from −160 to 40 °C.

Fourier transform infrared spectroscopy (FTIR)

FTIR spectra of the sample solutions were measured under vacuum using a Bruker IFS 66V/S FTIR, with a deuterated lanthanum α-alanine doped triglycine sulphate (DLATGS) detector, KBr mid-IR beam-splitter, and Pike diamond-ATR module.

Nuclear magnetic resonance spectroscopy

A Bruker 400 MHz nuclear magnetic resonance (NMR) spectrometer was utilized to detect and confirm the intermolecular interactions among the ions in the ionic liquids and the solvent molecules in the organic carbonates, and ¹H NMR spectroscopy was performed 2 h after preparing 20 mg sample solutions in 1 mL deuterium oxide (D₂O).

Rheology

A TA Instruments DHR-2 rheometer was used to measure the viscosities of the sample solutions by performing a temperature sweep at 1 rad s⁻¹, and the temperature control was realized inside a TA Instruments Environmental Test Chamber built into the rheometer.

Electrochemical impedance spectroscopy

All presented electrochemical experiment results were collected using a Bio-Logic VMP3 multichannel potentiostat. Electrochemical impedance spectroscopy (EIS) was performed with a customized conductivity cell using two fixed platinum wires as the electrodes. The cell constant of the customized conductivity cell was calibrated with 0.1 and 0.01 m potassium chloride solutions prior to measurement. The impedance of each sample solution was measured using a sinusoidal voltage with an amplitude of 10 mV over the frequency range of 900 kHz to 1 Hz. During the low temperature measurements, the temperature of the sample solution was controlled using a methanol/water/dry ice cooling bath and monitored by an Omega OMEGAETTE HH303A thermometer/data logger. Measurements were performed after the open circuit voltage was stabilized for at least 1 min under each equilibrated temperature point. Ionic conductivity was calculated based on the real impedance at high frequency, which represents the resistance of the electrolyte formulations.

Electrochemical window

Cyclic voltammetry (CV) was performed with a Dr Bob's electrochemical cell purchased from Gamry, a platinum disk (3 mm diameter) working electrode, platinum wire as the counter electrode, and silver wire as the reference electrode. The counter electrode and the reference electrode were separated from the sample solution to minimize contamination during the experiments using a glass frit and bridge tube, respectively. The electrochemical windows (EWs) for respective electrolyte formulations at room temperature were determined at a scan rate of 100 mV s⁻¹. The obtained profiles were reproducible for at least 10 cycles. Additional CV scans were conducted at 25, 50, 200, and 400 mV s⁻¹ within the determined EWs for the investigation of the I₃⁻ reduction kinetics in different organic solvents.

Results and discussion

Effects of incorporating organic solvents on the thermal properties of the electrolytes

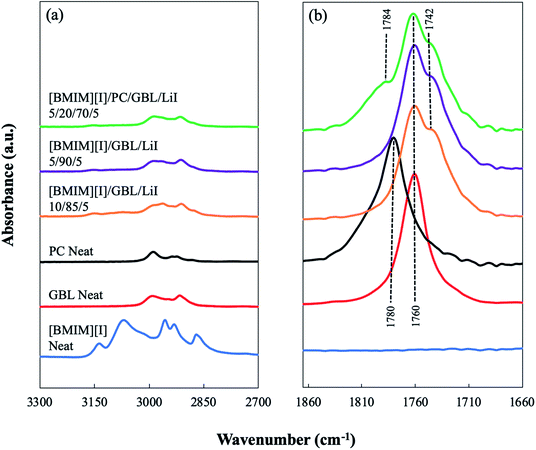
When designing an electrolyte system for low-temperature operations, the phase behaviors of the materials, such as freezing and glass transition, set the physical limit of the liquid electrolyte for its applications. Thus, differential scanning calorimetry (DSC) was used to characterize the thermal transitions of the prepared electrolyte formulations, revealing the interplay between IL and organic solvents in their mixture solution at various formulations over the temperature range of 40 °C to −160 °C. As shown in Fig. 1(a), the effect of GBL can be clearly seen by DSC analysis. Neat [BMIM][I] demonstrated a T_g at −67.4 °C and did not appear to have any additional thermal transitions. GBL was employed as the primary organic solvent to host IL for formulating the mixture-based electrolyte due to its potential in designing molecular interactions. When GBL was added to [BMIM][I], the T_g of the mixture system was effectively reduced. Furthermore, as the concentration of GBL increased, a decrease in the T_g of the mixture solution was observed. When the concentration of GBL was at 90 mol%, the formulation [BMIM][I]/GBL/LiI – 5/90/5 showed the most reduced T_g at −124.6 °C. Vraneš et al. also observed a similar effect of the suppressing phase transition temperatures of IL when mixing 1-butyl-3-methylimidazolium bis(trifluoromethylsulfonyl)imide ([BMIM][NTf₂]) with a variety of lactone solvents, including GBL.³⁵ This strong effect of shifting T_g towards a lower temperature by introducing GBL into the electrolyte can be interpreted by the interactions in the mixture solution at the molecular level. The ionic liquids and molecular liquids are able to establish notable intermolecular interactions through multiple routes. For example, [BMIM][I] has been shown to form hydrogen bonding via its iodide anions with surrounding water molecules in their binary mixtures.^32,33 On the other hand, the cations of imidazolium-based ILs have been observed both computationally and experimentally to interact with various organic molecular solvents via the formation of hydrogen bonding between the most acidic hydrogen on the imidazolium ring and the lone electron pair of the solvent molecules.^36–39 Papović et al. studied binary systems of GBL and various imidazolium-based ionic liquids and discovered that longer alkyl side chains on the imidazolium cation leads to stronger interactions between GBL and ILs.^39,40 In our developed mixture system consisting of [BMIM][I] and GBL, we hypothesized that a similar intermolecular interaction between the imidazolium moiety of the [BMIM]⁺ cations and the carbonyl group of the solvent molecules through hydrogen bonding disrupts the ion-pair formation between the [BMIM]⁺ cations and iodide anions within the [BMIM][I] network. Consequently, the cohesive energy of the system is significantly reduced, as reflected by the lower T_g of the resulting mixture solution. The existence of these intermolecular interactions will be further revealed experimentally in later sections.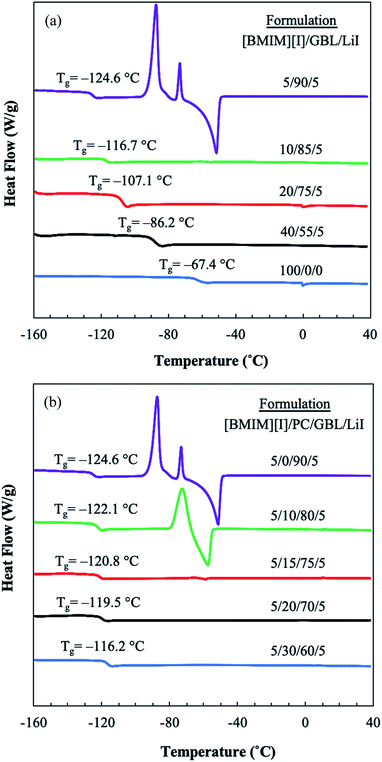

Fig. 1 DSC thermograms (exothermic up) from −160 to 40 °C for the various formulations of (a) [BMIM][I]/GBL/LiI mixture solutions and (b) [BMIM][I]/PC/GBL/LiI mixture solutions.

Although the addition of GBL shifted the T_g of the mixtures towards a favorable lower temperature, it had a negative impact by introducing undesirable thermal transitions to the electrolyte. Although the [BMIM][I]/GBL/LiI – 5/90/5 formulation displayed the lowest T_g among all solutions, it showed the critical drawback of a series of undesirable thermal transitions above the T_g. The predominating exothermic peaks at approximately −87 °C and −73 °C indicate the occurrence of crystallization, which will not only fail the function of liquid electrolyte owing to the insufficient motion of flow, but also cause high risks of structural damage to the device by volume change in the solution and accumulation of mechanical stress. Although the low T_g promises a wider liquidus window for low-temperature sensing operations in MET sensors, the phase transitions associated with this formulation were not suitable for our targeting liquid electrolyte systems. Thus, another cosolvent component, PC, was introduced into the mixture to further optimize the properties of the electrolyte. Fig. 1(b) demonstrates the effects of incorporating PC on the thermal behaviors of the multicomponent system. When PC was used to replace a varying fraction of GBL in the solution, the tendency of the mixture to crystalize in this composition changed. With an increase in the concentration of PC, the corresponding exothermic heat flow of crystallization decreased. When the concentration of PC was 15 mol%, the phase transition of the [BMIM][I]/PC/GBL/LiI – 5/15/75/5 formulation was significantly mitigated. After increasing the PC concentration to 20 mol% or higher, we no longer observed any phase transitions other than the glass transition from these formulations. In contrast to the [BMIM][I]/GBL/LiI – 5/90/5 formulation, very smooth DSC curves were presented by the [BMIM][I]/PC/GBL/LiI – 5/20/70/5 and 5/30/60/5 formulations. Meanwhile, their T_g values, despite a slight increase, were still retained at a very low temperature. The [BMIM][I]/PC/GBL/LiI – 5/20/70/5 formulation showed a T_g at approximately −120 °C. To the best of our knowledge, this is the lowest T_g reported to date for a liquid electrolyte system. The effects of incorporating PC on retaining the T_g at low temperatures and tuning the thermal behaviors of the electrolyte can also be interpreted by the modified intermolecular interactions. It can be viewed that the similar carbonyl functional groups shared by both PC and GBL can interact with the [BMIM]⁺ cation to keep the glass transition from occurring at higher temperatures, while the existence of PC in the mixture also interferes with GBL to prevent its crystallization. Thus, this low T_g, free-crystallization, IL-dual organic solvent mixture system exhibits great potential as a liquid electrolyte for low-temperature applications. Since we attributed the desired thermal behaviors to the effects of the optimized molecular interactions, further studies were performed to investigate the interactions between the IL and the organic solvents.

Probing the molecular interactions between [BMIM][I] and organic solvents

To reveal the hypothesized molecular interactions, FTIR was first employed to investigate the modification of the bonding structures in the developed IL–organic solvents electrolytes. As shown in Fig. 2(a), the FTIR spectra confirmed the signature peaks from the functional groups of each main chemical in the multicomponent system. For example, neat [BMIM][I] displayed the C–H stretching vibrations from both the alkenyl group and the carbon–hydrogen bond in between two adjacent nitrogen atoms on the imidazolium ring at 3136 cm⁻¹ and 3070 cm⁻¹, respectively.⁴¹ The former peaks from the alkenyl group were still observed in the electrolyte formulations, [BMIM][I]/GBL/LiI – 10/85/5 and 5/90/5, and [BMIM][I]/PC/GBL/LiI – 5/20/70/5, but at a much smaller magnitude (with shifts of 9–18 cm⁻¹). However, the latter peak was no longer significant in these formulations, indicating the disruption of the bonding configuration due to the interaction between cations and organic solvent molecules. This emerged interaction was further disclosed by the IR response of the carbonyl group, which is the same functional group shared by both solvent molecules. Both neat GBL and PC each showed a peak of C=O stretching at 1760 and 1780 cm⁻¹, respectively. It is known that the carbonyl stretching is sensitive to the formation of hydrogen bonding.^42,43 When the total number of present carbonyl groups is excessive to that of the available donor groups in the system, a partial number of the carbonyl groups will exhibit a peak shift in the spectrum because their intrinsic vibrations are altered as they accept protons from the most acidic hydrogen of the [BMIM]⁺ cations, while the other carbonyl groups that are not hydrogen-bonded remain uninfluenced.^43,44 When GBL was incorporated with [BMIM][I], the hydrogen bonding formation between a fraction of the carbonyl groups from GBL as acceptors and [BMIM]⁺ cations as donors was clearly demonstrated by the appearance of a “shoulder” off the original carbonyl peak at approximately 1742 cm⁻¹ in the spectra of the [BMIM][I]/GBL/LiI – 10/85/5 and 5/90/5 formulations, as shown in Fig. 2(b). This indicates the emergence of a new peak from the carbonyl groups that strongly interact with [BMIM][I] via hydrogen bonding. This observation serves as a direct manifestation of the hypothesized GBL–[BMIM]⁺ interaction in the electrolyte solutions. When the mixture was incorporated with both GBL and PC, a similar effect from the interaction between GBL and [BMIM]⁺ was also seen in the spectrum of the [BMIM][I]/PC/GBL/LiI – 5/20/70/5 formulation; however, it was much less significant for PC. Instead of “splitting” into two peaks, the carbonyl stretching of PC only displayed a minor shift from 1780 cm⁻¹ to 1784 cm⁻¹ without showing any “shoulder” peak from the original peak, suggesting that its ability to form hydrogen bonding with [BMIM]⁺ cations is weaker when competing against GBL for a limited number of donors, and therefore the interaction was not as predominant. This trend is consistent with the mixture system reported by Tian et al., where [EMIM]⁺ cations showed stronger interactions with GBL than PC, and this difference was also reflected in the bulk properties of the studied formulations.²⁹ We also noticed that the minor shift from PC was a blue shift. Although blue shifts for hydrogen bonds can exist in various cases, red shifts are generally expected.⁴⁵ In comparison to GBL, which can be viewed as the primary source to form hydrogen bonding with the imidazolium cation in our developed system, the hydrogen bonding associated with PC was much weaker and more subtle since PC is known to demonstrate strong dipole–dipole interactions via its carbonyl group and form local structures among itself.^46,47 When PC was incorporated in the mixture, we hypothesized that the overall electronegative environment of its carbonyl groups was altered by more than a single factor of hydrogen bonding, and therefore caused a minor blue shift. Thus, the FTIR results validated the modified molecular interactions in the mixture system and further details of the targeted ion–solvent interactions were subsequently unveiled by NMR spectroscopy.

Fig. 2 FTIR spectra of the electrolyte formulations, [BMIM][I]/GBL/LiI – 10/85/5, 5/90/5, and [BMIM][I]/PC/GBL/LiI – 5/20/70/5, and their neat components as controls in the range of (a) 2700–3300 cm⁻¹ and (b) 1660–1885 cm⁻¹.

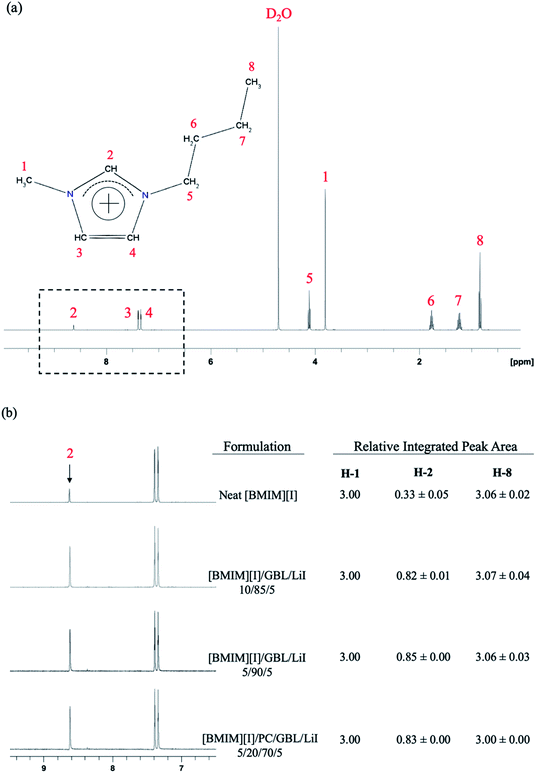
The ¹H NMR spectrum of neat [BMIM][I] is shown in Fig. 3(a), and the chemical shifts for all the protons at each position of its molecular structure are in agreement with the literature values.^48–50 In addition, an effect from hydrogen–deuterium exchange was also detected. The numbering of each carbon on the imidazolium cation is schematically depicted in the inset of Fig. 3(a), where it can be noticed that the peak of the proton at H-2 position is significantly weaker than its corresponding stoichiometric ratio among the protons at other positions. This feature can be explained by the dynamic process of equilibrium, where the labile protons on the [BMIM]⁺ cations are replaced by the deuterons in the solvent when they are dilute in D₂O.⁵¹ The hydrogen at the H-2 position is known to be more acidic, and thus its lower surrounding electron density makes the proton tend to exchange with deuterons from the solution, while the rest of the protons from other positions of the cation remain stable.^52–54 This phenomenon has also been observed in other chemical systems that contain imidazole groups such as histidine.^55,56 When [BMIM][I] was incorporated with organic solvents to form a mixture solution, more interestingly, the evolution of the hydrogen–deuterium exchange was observed in the ¹H NMR spectrum. All the electrolyte formulations shown in Fig. 3(b) demonstrate a significantly larger integrated peak area for the hydrogen at the H-2 position than the neat [BMIM][I], which indicates a reduced extent of hydrogen–deuterium exchange with the presence of carbonyl groups in the solution. The integrated peak area for the hydrogen at H-1 position was set as a baseline value of 3.00 considering the alkyl group possesses three hydrogens at this position. Accordingly, the hydrogen at the H-8 position demonstrated a matching integrated peak area of approximately 3.06, validating the quantitative results from ¹H NMR based on the stoichiometric ratio between H-1 and H-8. In comparison, at the H-2 position, the neat [BMIM][I] and mixture solutions showed integrated peak areas of 0.33 and an approximate range between 0.82 and 0.85, respectively, which again confirmed the additional molecular interactions between the [BMIM]⁺ cations and the solvent molecules. In the mixture solution, the carbonyl groups from the organic solvents become acceptors to form hydrogen bonding with the hydrogens at H-2 position of [BMIM]⁺ cation as donors and modify the surrounding electron density accordingly. Thus, the hydrogen at this position is more stabilized and its exchange with the deuterium from the solution is significantly reduced, as reflected by the higher integrated peak area of the H-2 protons than that of neat [BMIM][I] in the ¹H NMR spectrum.

Fig. 3 ¹H NMR spectra of (a) neat [BMIM][I] with the inset showing the numbered chemical structure of the [BMIM]⁺ cation and (b) neat [BMIM][I], [BMIM][I]/GBL/LiI – 10/85/5, 5/90/5, and [BMIM][I]/PC/GBL/LiI – 5/20/70/5 focusing on the peaks of H-2 with a comparison of the relative integrated peak areas also provided.

Transport properties of designed electrolytes

Besides thermal properties, the interactions between ILs and organic solvents also affect the transport properties of electrolytes, which are critical for their electrochemical applications. ILs typically possess high viscosities due to various intermolecular forces such as the prominent coulombic attractions, van der Waals forces, and hydrogen bonding.^20,57 The neat [BMIM][I] solution, as shown in Fig. 4(a), displayed high viscosities with a strong temperature dependence, increasing by approximately six orders of magnitude from 25 °C to −75 °C. However, although temperature dependence was observed for all the formulations, the ones that were incorporated with molecular solvents demonstrated not only a much less drastic viscosity increase as temperature decreased but also significantly lower viscosities over the entire temperature range of testing. At room temperature, two selected electrolyte formulations from this study, [BMIM][I]/GBL/LiI – 10/85/5 and [BMIM][I]/PC/GBL/LiI – 5/20/70/5 with low T_g and free of crystallization, exhibited a similar magnitude of viscosity between 0.002 and 0.005 Pa s with minor differences. As the temperature decreased to −75 °C, [BMIM][I]/GBL/LiI – 10/85/5 evolved to a significantly higher viscosity of 1.29 Pa s, presumably due to its higher concentration of [BMIM][I]. In contrast, [BMIM][I]/GBL/PC/LiI – 5/20/70/5 yielded a much lower viscosity of 0.31 Pa s at −75 °C, indicating that the addition of PC did not compromise the fluidity of the solution and effectively prevented the undesirable phase transition of the electrolyte system. Compared to the aqueous-based IL electrolyte formulation previously developed by our group,³³ [BMIM][I]/[EA][N]/water/LiI – 5/35/55/5 showed a comparable viscosity to [BMIM][I]/PC/GBL/LiI – 5/20/70/5 at room temperature but a significantly higher viscosity by more than 30 times at −75 °C owing to the stronger temperature dependence of the employed solvents. The effectiveness of reducing viscosity by incorporating organic solvents into the system can be attributed to the intrinsic superior fluidity of GBL and PC at low temperatures, which is consistent with the observations for other IL-based electrolyte systems.^29,58,59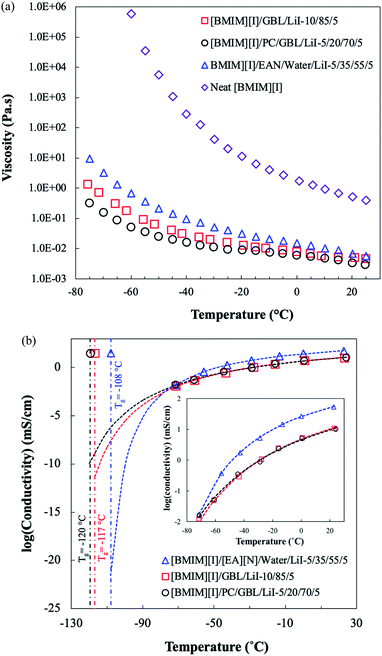

Fig. 4 Temperature dependence of (a) viscosity and (b) ionic conductivity for the neat [BMIM][I], selected organic solvent-based electrolyte formulations from this study, and aqueous-based formulation from the previous study.³³ In (b), the dashed lines and the dot-dashed lines represent the VFT fitting result for each formulation and their experimentally measured T_g, respectively, showing the predicted conductivities when approaching the glass transition, and the inset provides a magnified view of the measured conductivities between 25 °C and −75 °C.

Although viscosity depicts the overall fluidity of liquid-state electrolytes, ionic conductivity is another key transport property that directly reflects the mobility of charge carriers in a system. As shown in Fig. 4(b), the ionic conductivity of all the electrolyte formulations decreased significantly as the temperature decreased. The behavior of this exponential correlation between ionic conductivity and temperature can be well described by the Vogel–Fulcher–Tammann (VFT) equation.⁶⁰ For each formulation, the dashed line was plotted based on the VFT fitting results, showing the ionic conductivity evolution over the testing temperature range and prediction extended down to the respective experimental T_g as marked by the dot-dashed line. The inset in Fig. 4(b) presents the ionic conductivity data collected via EIS in the temperature range of 25 to −75 °C. Starting from 25 °C, [BMIM][I]/GBL/LiI – 10/85/5 and [BMIM][I]/PC/GBL/LiI – 5/20/70/5 showed comparable ionic conductivities, which were approximately 5 times lower than that of [BMIM][I]/[EA][N]/water/LiI – 5/35/55/5. Although the aqueous-based electrolyte had a higher ionic conductivity initially, the gap was narrowed gradually with a decrease in temperature. At around −70 °C, [BMIM][I]/PC/GBL/LiI – 5/20/70/5 reached a similar ionic conductivity as the aqueous-based electrolyte. Moreover, following the trajectory of the VFT fitting curves in Fig. 4(b), the two organic solvent-based electrolytes will eventually possess higher ionic conductivities than that of the aqueous-based electrolyte at around −80 °C. The [BMIM][I]/GBL/LiI – 10/85/5 and [BMIM][I]/PC/GBL/LiI – 5/20/70/5 formulations are expected to retain better ionic conductivities until their ideal glass transition temperatures, where the VFT model no longer provides adequate predictions for supercooled liquids.

The ionic conductivities of IL-based mixtures can be determined by several factors simultaneously. In general, we often focus on two tunable properties from the electrolyte design standpoint, namely viscosity and ionicity (the degree of ion disassociation). The former affects the mobility of existing species, while the latter corresponds to the number of charge carriers available for the conduction mechanism, both contributing to the overall bulk ionic conductivity.⁶⁰ The experimental results showcase that over the tested temperature range, the aqueous-based electrolyte provided the highest ionic conductivity despite it having the highest viscosity, indicating the impact from available charge carriers. The aqueous-based electrolyte was incorporated with [EA][N], another ionic liquid, as an approach to inhibit predominant crystallization. Consequently, [BMIM][I]/[EA][N]/water/LiI – 5/35/55/5 possessed the highest theoretical ion concentration among the three electrolyte formulations. However, in reality the actual number of ions available for conduction also depends on the extent of ion disassociation. For pure ILs, where the sole medium is formed by ions with strong coulombic attractions, considerable ions exist in the form of pairs or aggregates, which are not accountable for charge transport.²⁰ It is known that the selection of molecular solvents and ionic liquids has a great impact on optimizing the ionicity of electrolytes, which is attributed to the structures and properties of existing species that result in different degrees of interactions.^61,62 For instance, Li et al. performed a comprehensive discussion on the transport properties of binary mixtures by incorporating imidazolium ionic liquids with water and several organic solvents.⁶³ Particularly, water appeared to be the most effective in weakening the coulombic attractions between ions due to both its high dielectric constant and ability to form hydrogen bonds with the anions. Therefore, we hypothesize that the higher ionic conductivity of the aqueous-based electrolyte at higher temperatures can be explained by the highest number of available ions owing to the potentially higher extent of ion disassociation. However, when temperature decreases to −70 °C or below, the ionic conductivities of both organic solvent-based electrolytes are predicted to be comparable and even exceeding that of the aqueous-based electrolyte according to the trends based on the VFT fitting. This result suggests potential changes in viscosity and ionicity, which are both known to be temperature dependent and can also be correlated to intermolecular interactions. Our comparison showed that the differences in viscosity between the aqueous-based electrolyte and the organic solvent-based electrolytes become more prominent as the temperature decreases. Although the viscosity difference at higher temperatures may be insignificant compared to the ionicity, we speculate it to be more influential on the ionic conductivity at low temperatures since the differences evolved to over an order of magnitude. Papović et al. also discussed the combined impact of viscosity and ionicity on the conductivity of [BMIM][NTf₂]/GBL binary mixtures, concluding that improvements in electrochemical properties are more likely due to the significant reduction of viscosity when increasing the GBL fraction in the system.⁴⁰ Therefore, despite the lower effectiveness in solvation, the incorporation of GBL and PC successfully reduced the viscosity, which indicates it is a more viable strategy for designing electrolytes for the promotion of low-temperature applications than the aqueous-based approach from the perspective of optimizing transport properties.

Electrochemical stability

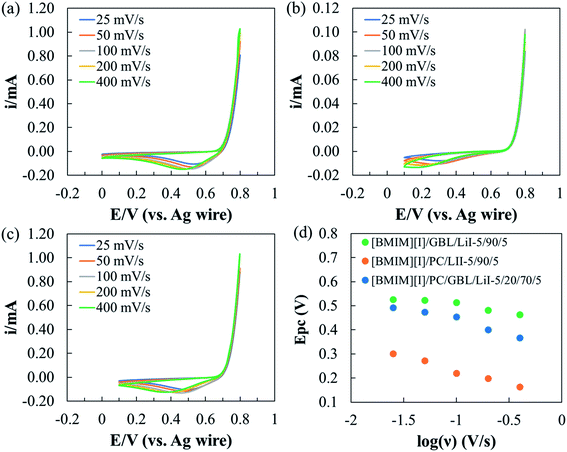
To develop an electrolyte system that provides functionality via electrochemical reactions, it is important to understand its electrochemical stability with the working mechanism of the device as the premise. In MET sensors, I₃⁻ reduction and I⁻ oxidation take place at the cathode and anode, respectively, leading to current outputs as a function of the detected seismic activities.³⁴ Therefore, for these electrolytes, we define their electrochemical windows (EWs) as the potential range where I⁻/I₃⁻ redox reactions can be steadily activated without additional faradaic processes originated from other species. Moreover, we are particularly interested in the effects of the intermolecular interactions between organic solvents and IL on the electrochemistry of I⁻/I₃⁻ redox couples. Cyclic voltammetry (CV) was performed on the optimized formulation [BMIM][I]/PC/GBL/LiI – 5/20/70/5, which presented desirable thermal and transport properties. To further explore the effects of the respective organic solvents, two additional formulations, [BMIM][I]/PC/LiI – 5/90/5 and [BMIM][I]/GBL/LiI – 5/90/5, were also characterized for comparison.

Fig. 5 shows the CV scans of the above three selected formulations at a scan rate (ν) of 100 mV s⁻¹, where we observed the successful oxidization of I⁻ during positive polarization, followed by I₃⁻ reduction during the reverse scan within the properly controlled potential range. Although the three electrolytes demonstrated some similarities in response to the potential sweep, there were also different electrochemical behaviors corresponding to the redox kinetics. First, the identified EWs for [BMIM][I]/GBL/LiI – 5/90/5, [BMIM][I]/PC/LiI – 5/90/5, and [BMIM][I]/PC/GBL/LiI – 5/20/70/5 were 0.8 V, 0.7 V, and 0.7 V, respectively. Numerous organic solvents, such as acetonitrile and PC, are known for their wide EWs, and hence have been broadly explored for the development of supercapacitor electrolytes.^19,64 However, since the sensing mechanism of MET sensors particularly relies on electrochemical reactions, we primarily focused on the reproducibility of the I⁻/I₃⁻ redox instead of the stability of the incorporated solvents. Therefore, a relatively narrow EW was defined for our I⁻/I₃⁻-containing electrolytes specifically designed for MET sensors, despite the generally extraordinary electrochemical stability of organic solvents. At a cathodic potential more negative than 0 V, the generated currents varied and decreased gradually with time. However, no additional current generation was observed for all the electrolytes until lithium reduction, indicating the interference was unlikely due to other faradaic processes. Hanson and Tobias investigated the electrochemistry of iodide in PC with studies on various anodic switching potentials during CV scans.⁶⁵ Consequently, they observed shifts in the cathodic current peak potential of I₃⁻ reduction and concluded that I₃⁻ reduction was sensitive to the state of the electrode surface. Thus, we hypothesize the unsteady profile could have originated from other non-faradaic processes at the electrode surface, which requires follow-up analytical investigation for clarification. For anodic polarization, before reaching 0.8 V, the measured anodic currents corresponded to the desired oxidation of I⁻ conversion to I₃⁻. However, beyond 0.8 V, the generation of iodine (I₂) as a side product was observed by visual inspection, which could have resulted from both the oxidation of I₃⁻ and equilibrium between I⁻, I₂, and I₃⁻ in the solution.^66,67 When I₂ is generated, it may occupy the effective surface of the electrode and change the concentration profiles in the proximity, interfering with I⁻ oxidation. Swathirajan and Bruckenstein reported that the I⁻ oxidation at the electrode surface is significantly slower when I⁻ diffuses through the I₂ film than via convection in solution.^68,69 More importantly, if I₂ is produced from I₃⁻ oxidation, the additional anodic current contribution introduces complications in detection. Therefore, we set the anodic limit of the three electrolytes at 0.8 V. Secondly, significant differences in the starting potential and the magnitude of the currents from both oxidation and reduction processes were observed, depending on the organic solvent composition. During anodic polarization, the oxidation currents started to increase at around 0.7 V for both [BMIM][I]/GBL/LiI – 5/90/5 and [BMIM][I]/PC/GBL/LiI – 5/20/70/5, but [BMIM][I]/PC/LiI – 5/90/5 did not show significant anodic current generation until around 0.77 V. At the cutoff anodic potential of 0.8 V, the anodic current of [BMIM][I]/GBL/LiI – 5/90/5 and [BMIM][I]/PC/GBL/LiI – 5/20/70/5 were comparable, while that of [BMIM][I]/PC/LiI – 5/90/5 ended at a current one order of magnitude lower. Similarly, during I₃⁻ reduction, [BMIM][I]/GBL/LiI – 5/90/5 showed the highest cathodic peak current (i_pc), followed by [BMIM][I]/PC/GBL/LiI – 5/20/70/5, and [BMIM][I]/PC/LiI – 5/90/5 had the lowest. Furthermore, a trend was also observed in the shift of the cathodic peak current potential (E_pc), with [BMIM][I]/GBL/LiI – 5/90/5 possessing the least shift towards a more negative potential and [BMIM][I]/PC/LiI – 5/90/5 showing the greatest. Both trends in magnitude of i_pc and shift in E_pc indicate differences in the kinetics of I⁻/I₃⁻ when incorporated with respective organic solvents and their mixtures.

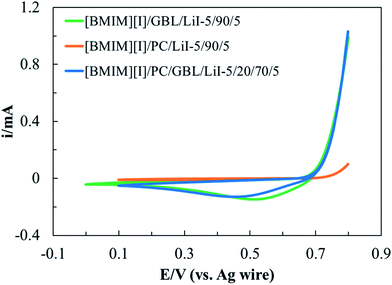Fig. 5 Identified EWs for selected electrolyte formulations of ILs/organic solvents/LiI electrolytes at 100 mV s⁻¹ scan rate.

Thus, to reveal the effects of the selected organic solvents on the I⁻/I₃⁻ redox kinetics, multiple CV scans were performed on the three electrolyte formulations at various scan rates ranging from 25 to 400 mV s⁻¹. When the scan rate increased, as shown in Fig. 6(a–c), the E_pc of all three electrolyte formulations shifted towards a more negative potential but to different extents. Fig. 6(d) depicts the relationship between E_pc and log(ν) for each electrolyte formulation. Similar to the previous discussion on E_pc at 100 mV s⁻¹ scan rate, [BMIM][I]/PC/LiI – 5/90/5 started with the most negative E_pc (−0.3 V) at 25 mV s⁻¹ scan rate and displayed the most significant potential shift of −0.139 V at 400 mV s⁻¹ scan rate. Both features serve as evidence of the relatively irreversible nature of I₃⁻ reduction in PC. The effect of solvents on the kinetics of the I⁻/I₃⁻ redox couple has been a longstanding interest, and has been studied by several groups.^70–74 Bentley et al. conducted a comprehensive study on the electrochemical behaviors of I⁻/I₃⁻ in conventional solvents and ILs.⁷⁵ Among the four conventional solvents, water, ethanol, acetonitrile, and PC, they reported that I₃⁻ had the highest stability constant in PC and attributed it to the interactions between the ions and solvents, which led to varying kinetics for respective species. We hypothesize that the electrochemical stability of I₃⁻ was higher in PC than in GBL or the PC/GBL mixture, and thus a more negative potential was required to drive I₃⁻ reduction in PC. On the other hand, I₃⁻ reduction was activated at a relatively high potential in [BMIM][I]/GBL/LiI – 5/90/5, and a considerable shift in E_pc was only observed starting at a scan rate of 200 mV s⁻¹. The [BMIM][I]/PC/GBL/LiI – 5/20/70/5 formulation exhibited electrochemical behaviors in between the other two, demonstrating negligible effects on the reduction kinetics at scan rates of up to 50 mV s⁻¹. Thus, it can be concluded that the results show that the optimized formulation [BMIM][I]/PC/GBL/LiI – 5/20/70/5 can provide steady I⁻/I₃⁻ redox reactions for MET sensors within the identified EW at room temperature.

Fig. 6 CV scans at different scan rates for the electrolyte formulations (a) [BMIM][I]/GBL/LiI – 5/90/5, (b) [BMIM][I]/PC/LiI – 5/90/5, and (c) [BMIM][I]/PC/GBL/LiI – 5/20/70/5. (d) Relationship between E_pc and log(ν) for the three selected formulations.

In addition to kinetics and transport that govern the electrochemical behaviors, for the I⁻/I₃⁻ redox couple, the unique Grotthuss mechanism was also reported to provide an alternative way for charge conduction when doping electrolytes with I₂.⁷⁶ However, the significance of the Grotthuss mechanism is mostly highlighted in viscous iodide-based ILs doped with a considerably high concentration of I₂ ^77,78 and ionic crystals,^79,80 which contradicted with our primary goals of optimizing the thermal properties and fluidity of liquid-state electrolytes. Furthermore, in the working principle of MET sensors, the generated current should be an accurate reflection of mass transport induced by detected seismic waves, and therefore the non-Stokesian behaviors of the Grotthuss mechanism may introduce unaccounted noise components. Therefore, instead of delving into other charge conduction mechanisms of I⁻/I₃⁻, herein we mainly focus on effects of the introduced organic solvents on the transport and electrochemical kinetics of the I⁻/I₃⁻ couple. The Grotthuss mechanism will be further investigated in our future work on low-temperature electrochemical experiments, where the electrochemical properties of I⁻/I₃⁻ may depend on both Stokesian and non-Stokesian behaviors.

Conclusions

In this work, we demonstrated the development of a low-temperature liquid electrolyte system by tailoring intermolecular interactions, and investigated their effects on thermal, transport, and electrochemical behaviors. By incorporating PC and GBL with [BMIM][I] at an optimal ratio, the designed intermolecular interactions via hydrogen bonding between the carbonyl groups of the organic solvents and the imidazolium cations of the IL, which were confirmed via FTIR and ¹H NMR, successfully modified and optimized the properties of the electrolytes. Consequently, the [BMIM][I]/PC/GBL/LiI – 5/20/70/5 formulation showcased remarkable improvement in thermal property with an extended liquidus range down to −120 °C. Furthermore, it also possessed the highest fluidity over a wide temperature range from 25 to −75 °C among the tested formulations, leading to the highest ionic conductivity at temperatures lower than −70 °C based on the predictions from the VFT fitting. The electrochemical stability was confirmed at room temperature, where I⁻/I₃⁻ reduction can be steadily activated within the identified potential window to support the sensing mechanism of the MET sensor. We anticipate the presented results will not only support the potential seismic investigations of MET sensors for planetary explorations, but also inspire low-temperature electrolyte development from a greater selection of materials by employing the design of intermolecular interactions.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

We gratefully acknowledge the financial support from NASA NNX17AF70G and the Fulton Undergraduate Research Initiative at Arizona State University. We also acknowledge Professor Matthew Green, Professor Candace Chan, LeRoy Eyring Center for Solid State Science, and Magnetic Resonance Research Center (MRRC) at Arizona State University for the equipment access.

References

1. J. P. Hallett and T. Welton, Chem. Rev., 2011, 111, 3508–3576.
2. H. Olivier-Bourbigou, L. Magna and D. Morvan, Appl. Catal., A, 2010, 373, 1–56.
3. J. G. Huddleston, H. D. Willauer, R. P. Swatloski, A. E. Visser and R. D. Rogers, Chem. Commun., 1998, 1765–1766.
4. E. D. Bates, R. D. Mayton, I. Ntai and J. H. Davis Jr, J. Am. Chem. Soc., 2002, 124, 926–927.
5. M. E. V. Valkenburg, R. L. Vaughn, M. Williams and J. S. Wilkes, Thermochim. Acta, 2005, 425, 181–188.
6. J. Liu, F. Wang, L. Zhang, X. Fang and Z. Zhang, Renewable Energy, 2014, 63, 519–523.
7. Y. Cao, J. Zhang, Y. Bai, R. Li, S. M. Zakeeruddin, M. Grätzel and P. Wang, J. Phys. Chem. C, 2008, 112, 13775–13781.
8. J. Wu, Z. Lan, J. Lin, M. Huang, Y. Huang, L. Fan and G. Luo, Chem. Rev., 2015, 115, 2136–2173.
9. A. Lewandowski and A. Świderska-Mocek, J. Power Sources, 2009, 194, 601–609.
10. M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239.
11. A. M. Haregewoin, A. S. Wotango and B. J. Hwang, Energy Environ. Sci., 2016, 9, 1955–1988.
12. A. Eftekhari, Energy Storage Materials, 2017, 9, 47–69.
13. D. Wei and A. Ivaska, Anal. Chim. Acta, 2008, 607, 126–135.
14. D. S. Silvester, Analyst, 2011, 136, 4871–4882.
15. A. Rehman and X. Zeng, Acc. Chem. Res., 2012, 45, 1667–1677.
16. C. Arbizzani, M. Biso, D. Cericola, M. Lazzari, F. Soavi and M. Mastragostino, J. Power Sources, 2008, 185, 1575–1579.
17. W. Y. Tsai, R. Lin, S. Murali, L. L. Zhang, J. K. McDonough, R. S. Ruoff, P. L. Taberna, Y. Gogotsi and P. Simon, Nano Energy, 2013, 2, 403–411.
18. Q. Li, J. Chen, L. Fan, X. Kong and Y. Lu, Green Energy Environ., 2016, 1, 18–42.
19. C. Zhong, Y. Deng, W. Hu, J. Qiao, L. Zhang and J. Zhang, Chem. Soc. Rev., 2015, 44, 7484–7539.
20. H. Ohno, Electrochemical Aspects of Ionic Liquids, John Wiley & Sons, Inc., Hoboken, New Jersey, 2nd edn, 2011.
21. C. Hardacre, J. D. Holbrey, M. Nieuwenhuyzen and T. G. A. Youngs, Acc. Chem. Res., 2007, 40, 1146–1155.
22. S. Menne, T. Vogl and A. Balducci, Phys. Chem. Chem. Phys., 2014, 16, 5485–5489.
23. C. E. S. Bernardes, M. E. Minas da Piedade and J. N. Canongia Lopes, J. Phys. Chem. B, 2011, 115, 2067–2074.
24. A. M. O'Mahony, D. S. Silvester, L. Aldous, C. Hardacre and R. G. Compton, J. Chem. Eng. Data, 2008, 53, 2884–2891.
25. D. R. MacFarlane, A. L. Chong, M. Forsyth, M. Kar, R. Vijayaraghavan, A. Somers and J. M. Pringle, Faraday Discuss., 2018, 206, 9–28.
26. D. R. MacFarlane, N. Tachikawa, M. Forsyth, J. M. Pringle, P. C. Howlett, G. D. Elliott, J. H. Davis Jr, M. Watanabe, P. Simon and C. A. Angell, Energy Environ. Sci., 2014, 7, 232–250.
27. V. Ruiz, T. Huynh, S. R. Sivakkumar and A. G. Pandolfo, RSC Adv., 2012, 2, 5591–5598.
28. L. Aguilera, J. Scheers and A. Matic, Phys. Chem. Chem. Phys., 2016, 18, 25458–25464.
29. J. Tian, C. Cui, Q. Xie, W. Qian, C. Xue, Y. Miao, Y. Jin, G. Zhang and B. Guo, J. Mater. Chem. A, 2018, 6, 3593–3601.
30. G. Zhu, K. Wen, W. Lv, X. Zhou, Y. Liang, F. Yang, Z. Chen, M. Zou, J. Li, Y. Zhang and W. He, J. Power Sources, 2015, 300, 29–40.
31. M. Kunze, S. Jeong, G. B. Appetecchi, M. Schönhoff, M. Winter and S. Passerini, Electrochim. Acta, 2012, 82, 69–74.
32. S. D. Nickerson, E. M. Nofen, H. Chen, M. Ngan, B. Shindel, H. Yu and L. L. Dai, J. Phys. Chem. B, 2015, 119, 8764–8772.
33. Y. Xu, W. J. Lin, M. Gliege, R. Gunckel, Z. Zhao, H. Yu and L. L. Dai, J. Phys. Chem. B, 2018, 122, 12077–12086.
34. H. Huang, V. Agafonov and H. Yu, Sensors, 2013, 13, 4581–4597.
35. M. Vraneš, N. Cvjetićanin, S. Papović, B. Šarac, I. Prislan, P. Megušar, S. Gadžurić and M. Bešter-Rogač, J. Mol. Liq., 2017, 243, 52–60.
36. N. Zec, A. Idrissi, M. Bešter-Rogač, M. Vraneš and S. Gadžurić, J. Mol. Liq., 2018, 268, 481–489.
37. A. Ali, M. Ali, N. A. Malik, S. Uzair and A. B. Khan, J. Chem. Eng. Data, 2014, 59, 1755–1765.
38. B. R. Mellein, S. N. V. K. Aki, R. L. Ladewski and J. F. Brennecke, J. Phys. Chem. B, 2007, 111, 131–138.
39. S. Papović, N. Cvjetićanin, S. Gadžurić, M. Bešter-Rogač and M. Vraneš, Phys. Chem. Chem. Phys., 2017, 19, 28139–28152.
40. S. Papović, S. Gadžurić, M. Bešter-Rogač, B. Jović and M. Vraneš, J. Chem. Thermodyn., 2018, 116, 330–340.
41. Q. G. Zhang, N. N. Wang and Z. W. Yu, J. Phys. Chem. B, 2010, 114, 4747–4754.
42. A. M. Modro and T. A. Modro, Can. J. Chem., 1999, 77, 890–894.
43. I. S. Ryu, X. Liu, Y. Jin, J. Sun and Y. J. Lee, RSC Adv., 2018, 8, 23481–23488.
44. S. W. Kuo, C. F. Huang and F. C. Chang, J. Polym. Sci., Part B: Polym. Phys., 2001, 39, 1348–1359.
45. K. Hermansson, J. Phys. Chem. A, 2002, 106, 4695–4702.
46. A. Tagawa, T. Numata and T. Shikata, AIP Adv., 2017, 7, 095103.
47. V. A. Koverga, I. V. Voroshylova, Y. Smortsova, F. A. Miannay, M. N. D. S. Cordeiro, A. Idrissi and O. N. Kalugin, J. Mol. Liq., 2019, 287, 110912.
48. P. F. Salazar, K. J. Chan, S. T. Stephens and B. A. Cola, J. Electrochem. Soc., 2014, 161, H481–H486.
49. Q. Li, D. Liu, L. Song, X. Hou, C. Wu and Z. Yan, Ind. Crops Prod., 2018, 113, 157–166.
50. K. Saihara, Y. Yoshimura, S. Ohta and A. Shimizu, Sci. Rep., 2015, 5, 10619.
51. A. G. Avent, P. A. Chaloner, M. P. Day, K. R. Seddon and T. Welton, J. Chem. Soc., Dalton Trans., 1994, 3405–3413.
52. S. Cha, M. Ao, W. Sung, B. Moon, B. Ahlström, P. Johansson, Y. Ouchi and D. Kim, Phys. Chem. Chem. Phys., 2014, 16, 9591–9601.
53. S. T. Handy and M. Okello, J. Org. Chem., 2005, 70, 1915–1918.
54. S. Ohta, A. Shimizu, Y. Imai, H. Abe, N. Hatano and Y. Yoshimura, Open J. Phys. Chem., 2011, 1, 70–76.
55. N. Hayashi, H. Kuyama, C. Nakajima, K. Kawahara, M. Miyagi, O. Nishimura, H. Matsuo and T. Nakazawa, Biochemistry, 2014, 53, 1818–1826.
56. M. Cebo, M. Kielmas, J. Adamczyk, M. Cebrat, Z. Szewczuk and P. Stefanowicz, Anal. Bioanal. Chem., 2014, 406, 8013–8020.
57. S. Zhang, J. Wang, X. Lu and Q. Zhou, Structures and Interactions of Ionic Liquids, Springer-Verlag, Berlin, Heidelberg, 2014.
58. M. Anouti and L. Timperman, Phys. Chem. Chem. Phys., 2013, 15, 6539–6548.
59. M. Wang, Z. Shan, J. Tian, K. Yang, X. Liu, H. Liu and K. Zhu, Electrochim. Acta, 2013, 95, 301–307.
60. M. Galiński, A. Lewandowski and I. Stepniak, Electrochim. Acta, 2006, 51, 5567–5580.
61. K. Ueno, H. Tokuda and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 1649–1658.
62. Y. S. Ye, J. Rick and B. J. Hwang, J. Mater. Chem. A, 2013, 1, 2719–2743.
63. W. Li, Z. Zhang, B. Han, S. Hu, Y. Xie and G. Yang, J. Phys. Chem. B, 2007, 111, 6452–6456.
64. A. González, E. Goikolea, J. A. Barrena and R. Mysyk, Renewable Sustainable Energy Rev., 2016, 58, 1189–1206.
65. K. J. Hanson and C. W. Tobias, J. Electrochem. Soc., 1987, 134, 2204–2210.
66. A. J. Bard, Encyclopedia of Electrochemistry of the Elements, Marcel Dekker, Inc., New York, 1973.
67. Y. A. Yaraliev, Russ. Chem. Rev., 1982, 51, 990–1016.
68. S. Swathirajan and S. Bruckenstein, J. Electroanal. Chem., 1981, 125, 63–71.
69. S. Swathirajan and S. Bruckenstein, J. Electroanal. Chem., 1983, 143, 167–178.
70. R. T. Iwamoto, Anal. Chem., 1959, 31, 955.
71. I. V. Nelson and R. T. Iwamoto, J. Electroanal. Chem., 1964, 7, 218–221.
72. L. Cantrel, J.-M. Fulconis and J. Chopin-Dumas, J. Solution Chem., 1998, 27, 373–393.
73. L. M. Dané, L. J. J. Janssen and J. G. Hoogland, Electrochim. Acta, 1968, 13, 507–518.
74. R. Zarrougui, M. Dhahbi and D. Lemordan, J. Electroanal. Chem., 2014, 717–718, 189–195.
75. C. L. Bentley, A. M. Bond, A. F. Hollenkamp, P. J. Mahon and J. Zhang, J. Phys. Chem. C, 2015, 119, 22392–22403.
76. G. Boschloo and A. Hagfeldt, Acc. Chem. Res., 2009, 42, 1819–1826.
77. V. K. Thorsmølle, G. Rothenberger, D. Topgaard, J. C. Brauer, D.-B. Kuang, S. M. Zakeeruddin, B. Lindman, M. Grätzel and J.-E. Moser, ChemPhysChem, 2011, 12, 145–149.
78. V. K. Thorsmølle, D. Topgaard, J. C. Brauer, S. M. Zakeeruddin, B. Lindman, M. Grätzel and J.-E. Moser, Adv. Mater., 2012, 24, 781–784.
79. J. Grossi, J. J. Kohanoff, N. J. English, E. M. Bringa and M. G. Del Popolo, J. Phys. Chem. B, 2017, 121, 6436–6441.
80. J. G. Mcdaniel and A. Yethiraj, J. Phys. Chem. B, 2018, 122, 250–257.

---

Footnote

† Equal contribution to this manuscript.

---