DOI:
10.1039/C9RA07338H
(Paper)
RSC Adv., 2019,
9, 37526-37536
Theoretical investigation of various aspects of two dimensional holey boroxine, B3O3†
Received
12th September 2019
, Accepted 10th November 2019
First published on 18th November 2019
Abstract
By means of first-principles calculations, we study the structural, electronic and mechanical properties of the newly synthesized boron–oxygen holey framework (Chem. Comm. 2018, 54, 3971). It has a planar structure formed by B3O3 hexagons, which are joined via strong covalent boron–boron bonds. The six B3O3 units are connected with six-fold symmetry exhibiting a large hole with a surface area of 23 Å2, which is ideal for the adsorption of alkalis. For neutral alkalis, we found that the adsorption energy of potassium is 14 and 12 kcal mol−1 larger than those determined for sodium and lithium, respectively. In contrast, for alkali cations, there is a clear preference for lithium over sodium and potassium. With regard to its electronic properties, it is an insulator with an electronic band gap of 5.3 eV, at the HSE level of theory. We further investigate the effect of strain on the band gap and find it a less efficient technique to tune the electronic properties. The wide optical gap of B3O3 can be utilized in ultraviolet (UV) applications, such as UV photodetectors, etc. Additionally, the 2D elastic modulus of B3O3 (53.9 N m−1) is larger than that of Be3N2, silicene, and germanene. Besides, we also report bilayer and graphite-like bulk B3O3 and furthermore, find that the optoelectronic properties of the bilayer can be tuned with an external electric field. The great tunability of optical properties from UV to the visible range offers a vast range of applications in optoelectronics.
1. Introduction
The preparation of graphene in 2004 opened new research directions in all branches of science.1 It is difficult to make a full list of the two dimensional (2D) materials available. Without trying to be exhaustive, we can mention the transition metal chalcogenides2,3 MoS2, WS2, MoSe2, WSe2, MoTe2, the MXenes,4 which are layered compounds formed by transition metal nitrides or carbides, the p-block based 2D materials like silicene,5,6 germanene,7 antimonene,8 bismuthene,9 black10 and blue phosphorene11 as well as graphdyne12 and the isoelectronic analog of graphene, boron nitride13,14 among many others. Upon reading the latter list it is possible to postulate that 2D materials can only exist when their bulk materials are layered. However, it has been shown that it is possible to synthesize an atomic single layer material when the bulk is not layered, being silicene a clear example. Recently, Stredansky et al.15 reported the synthesis of a novel 2D material based on the boronic acid condensation. Using three tetrahydroxyboron (H2B2O4) molecules, a six-membered boroxine ring molecule was formed along with three molecules of water. Although the boroxine layers could readily be identified in the STM studies, the authors suggested that further improvements in the synthetic procedure should be made in order to reduce the occurrence of non-six-fold symmetry motifs. Concomitantly, Lin et al.16 proposed a porous boron oxide monolayer with a robust band gap, which is similar to the one synthesized by Stredansky et al.15 They showed that boroxine is perfectly planar with uniform pores with a 6.27 Å diameter and exhibit an indirect wide band gap with the possible applications in optoelectronics This work is the extension to the previous predicted (theoretical) and synthesized (experimentally) boroxine by exploring the microscopic science and including new interesting capabilities such as the high affinity for alkalis and the study of bilayer boroxine as well as the bulk layered material. As by-product, we have found a minor discrepancy in the electronic structure of boroxine. In effect, our HSEH1PBE calculations indicated that the gap is direct, in contrast with the results reported by Lin et al.16 In the text, the only “B3O3” will refer to the monolayer B3O3 unless it is followed by “ring” or “hexagon”.
2. Methods
We study boroxine (B3O3) by means of spin-polarized vdW-DF,17 M06-L,18 and HSEH1PBE19 density functional theory (DFT) calculation. We use SIESTA20,21 code to perform vdW-DF calculations. We select the double-zeta basis set with polarization functions and fixed the orbital confining cut-off to 0.01 Ry with the default value (0.15) of split-norm. The interaction between ionic cores and valence electrons is described by the Troullier–Martins norm-conserving (NC) pseudopotentials.22 Geometry optimizations were carried out using the conjugate gradient algorithm until all the residual forces were smaller than 0.01 eV Å−1. The unit cells were optimized and they were sampled using a 50 × 50 × 1 (about 900 k-points gamma centered) Monkhorst–Pack sampling, the periodic M06-L and HSEH1PBE calculations were carried out with Gaussian 09.23 The basis set selected were Pople's 6-31G* and 6-311G*.24 In general, we did not observe significant differences in the results obtained using both basis sets. 1000 k-points were used to sample the unit cell and the ultrafine grid was employed. For comparative calculations, we also investigate the adsorption of alkalis employing a boroxine (B3O3) cluster formed by six B3O3 units and terminated with hydrogen atoms. In general, the results indicate the same trend as that obtained employing infinite models.
We also perform PBE-D2 (ref. 25) and PBE-D3 (ref. 26) calculations with the help of VASP code.27 We use generalized gradient approximation (GGA) with the flavor proposed by Perdew, Burke, and Ernzerhof (PBE)28,29 assisted with the projector augmented wave (PAW).30
Finally, we also use a hybrid functional (not in a true sense) which is a mixture of LDA-GGA28,29,31 as implemented in SIESTA, especially for the calculation of in-plane elastic modulus to compare our results with our previous work on graphene and Be3N2.32 The details are in ref. 31. Throughout the manuscript, the hybrid is referring to the aforementioned method. Finally, we also report ab initio molecular dynamics (AIMD) simulations at 300–600 K with the aid of SIESTA code. Further details regarding the computational methods can be seen in the ESI.†
3. Results and discussion
3.1 Structural properties of 2D boroxine
As suggested by the experimental study15 and the theoretical study by Lin et al.,16 we find that 2D boroxine can adopt six-fold symmetry. The unit cell employed in our calculations is shown in Fig. 1.
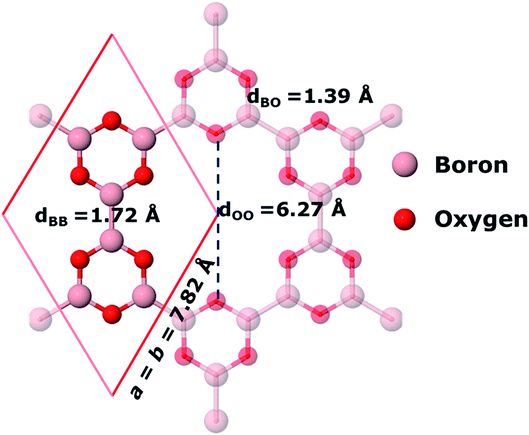 |
| | Fig. 1 The unit cell and bond lengths of 2D boroxine (B3O3) at PBE-D3 level of theory. Periodically repeated atoms are made translucent. | |
The six-fold symmetry structure is obtained by joining the B3O3 hexagons obtained after the condensation of three tetrahydrodiboron molecules. The B–B bonds are 1.71–1.72 Å long, a value which is bracketed by the B1–B1 and B1–B2 bond distances found in Pmmn borophene, namely, 1.613 and 1.879 Å, respectively, which are in excellent agreement with the PBE results previously reported.16 The B–O bond length 1.38–1.39 Å is among the highest values of which B–O can adopt in molecular forms. As suggested by Coulson,32 this may indicate a moderate to weak participation of the π orbitals of boron and oxygen. A fact that seems to be corroborated by the partial density of states presented in Fig. 2. When the six B3O3 molecules are joined, they leave a hole in which the distance between the opposite O atoms is 6.21–6.28 Å (depending on the level of theory) and the surface is close to 23 Å2, ideal for the adsorption of large atoms or molecules, as observed for crown ethers. For example, the 18-crown-6 ether has a high affinity for the hydronium ion H3O+. In addition to this, it allows the dissolution of KMnO4 in benzene thanks to the complexation of the potassium ion. We show in Section 3.8 that 2D boroxine has also a strong affinity towards alkalis, especially to potassium.
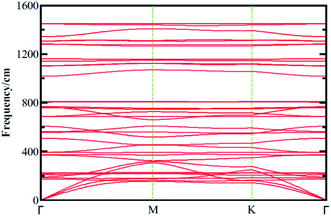 |
| | Fig. 2 Phonon dispersion curves calculated for boroxine (B3O3) calculated at vdW-DF/DZP level of theory with SIESTA code. | |
To report the structural stability, we calculate the formation energy and since we use the atomic form of B and O as the chemical potential, the formation energy here is equal to the cohesive energy. We make use of the following expression: 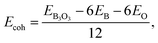 where EB3O3 is the total energy of the unit cell containing 6B and 6O atoms. EB and EO are taken as the gas-phase energies of B and O, respectively. The cohesive energy of B3O3 PBE-D3 level is −6.72 eV per atom, just 0.04 lower than the value reported by Lin et al.16 For the comparison, the cohesive energy of graphene at the same level of theory is −8.07 eV per atom. This means that B3O3 has a comparable strength to that of graphene. At the M06-L level, the cohesive energy of B3O3 −6.3 eV per atom which is twice the value calculated for phosphorene (−3.1 eV per atom) at the same level. Further information is given in ESI.† The data regarding structural properties and stability at various levels of theory is shown in Table S1.†
where EB3O3 is the total energy of the unit cell containing 6B and 6O atoms. EB and EO are taken as the gas-phase energies of B and O, respectively. The cohesive energy of B3O3 PBE-D3 level is −6.72 eV per atom, just 0.04 lower than the value reported by Lin et al.16 For the comparison, the cohesive energy of graphene at the same level of theory is −8.07 eV per atom. This means that B3O3 has a comparable strength to that of graphene. At the M06-L level, the cohesive energy of B3O3 −6.3 eV per atom which is twice the value calculated for phosphorene (−3.1 eV per atom) at the same level. Further information is given in ESI.† The data regarding structural properties and stability at various levels of theory is shown in Table S1.†
3.2 Dynamical stability
In the experiment, 2D boroxine (B3O3) was grown on Au (111) surface and, therefore, it is necessary to check the dynamical stability of free-standing boroxine (B3O3). To that end, we calculate phonon spectrum by supercell approach as implemented in SIESTA code along the G–M–K–G high symmetry points. We use a 2 × 2 × 1 supercell to calculate the phonon band spectrum, whereas, a 1 × 1 × 1 cell also give converged result, keeping in mind that the unit cell size is already large enough. The phonon spectrum graph is shown in Fig. 2 where it is clear that 2D boroxine is certainly a local minimum in the potential energy surface due to the absence of any negative frequency. The highest frequency of B3O3 is ∼1450 cm−1.
3.3 Electronic properties
The electronic properties of 2D boroxine are predicted by calculating the electronic band structure and for additional comprehension, the orbital projected density of states (PDOS) is also computed. With SIESTA (both the levels employed), 2D boroxine (B3O3) is a wide and indirect band gap material with conduction band minima (CBM) lie at M point, while valence band maxima (VBM) at gamma point. However, the energy difference between gamma and M points is quite low (55 meV). This indirect gap nature is also confirmed by VASP code with a slight disagreement as the CBM appears at the K point which is in line with the previous findings by Lin et al.16 The calculated value of band gap, at vdW-DF level is 3.80 eV. However, the M06-L level of theory revealed a direct gap with a value of 3.9 eV. As expected, the band gap was significantly underestimated by the vdW-DF method and also by the M06-L functional. In effect, HSEH1PBE calculations indicated that the band gap of boroxine is direct, namely 5.30 eV which is a bit higher than the previously reported value of 5.23 eV. The latter value is smaller than the gap computed for boron nitride at the HSEH1PBE level, namely, 6.1 eV. Moreover, B3O3 bears the same direct-indirect band gap controversy as that of boron nitride.
From the PDOS, the CBM has a π character and mostly composed of B-pz with a slight involvement from O-pz. However, the O-p(x+y) strongly hybridized with B-p(x+y) to form the VBM and, therefore, has a σ-like character. Furthermore, the valence and conduction bands are mostly governed by O and B, respectively. Additionally, this outcome also reflects in LDOS plots shown in Fig. 3 where the density around O atoms can be seen in VB case, whereas, for CB, the density can be spotted around B and O with a larger LDOS amplitude on B in comparison with O. Besides, we also check the effect of strain on the electronic structure of B3O3 and find that it is a less efficient technique to alter the electronic properties. The band structures are given in Fig. S1 in ESI.†
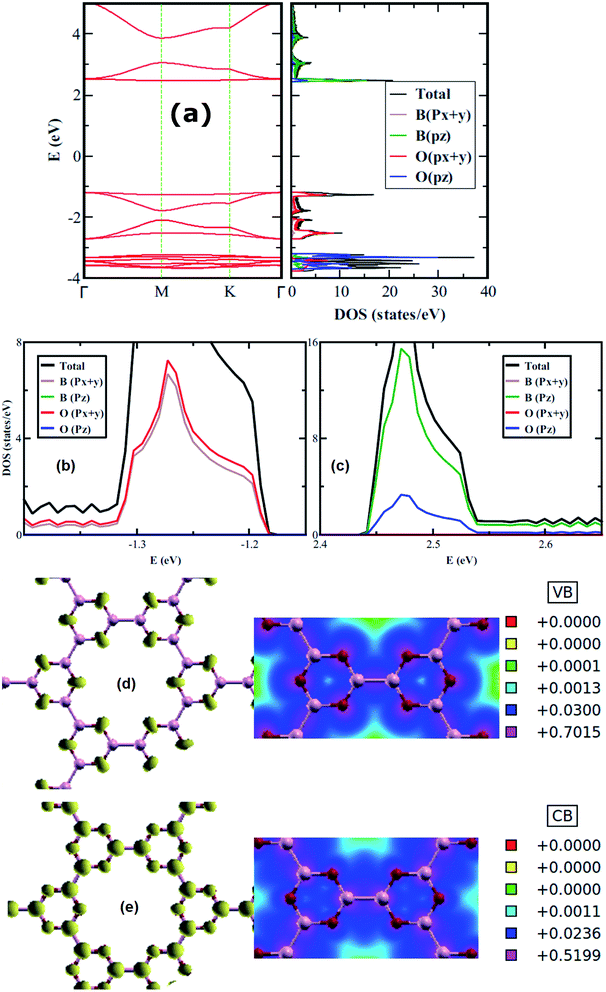 |
| | Fig. 3 Electronic band structure along with (total and projected) density of states (a); projected density of states near the (b) valence band maximum and (c) the conduction band minimum; 3D plots along with their 2D cuts of LDOS of filled (d) and empty states (e) of boroxine calculated at the hybrid level of theory. | |
3.4 Chemical analysis and bonding character
We calculate the charge transfer with the help of various charge transfer mechanisms namely Hirshfeld and Voronoi as in SIESTA, Mulliken as in Gaussian, and Bader as in VASP. Each of these methods reveals qualitatively the same results of charge transfer from B to O as in the spirit of their electronegativity values. The total charge density calculated at PBE-D3 level is plotted in Fig. 4(a), where charge accumulation on O atoms can be seen quite vividly. The quantitative results are given in Table S1.† Furthermore, to picture the electron localization in B3O3, we calculate electron localization function (ELF) which is quite useful in predicting the bonding character, as well as the stability mechanism. The details regarding the interpretation of ELF plots can be seen in ref. 31 and 33. In B3O3 rings, we see electron localization on O atoms broadens towards B atoms and a complete charge delocalization in the vicinity of B atoms. This is in perfect agreement with the previous experimental + DFT study on B3O3 rings held together by phenyl molecules where the authors reported the ultra-fast charge delocalization with the charge localization on O atoms34 Such an analysis, however, is absent for phenyl-free B3O3 rings which are bonded via B atoms. Consequently, the ELF becomes crucial and much more meaningful. Interestingly, we find a strong charge localization between B–B atoms, the region between two B3O3 rings. This indicates that the B3O3 rings are held together by strong covalent bonds with the ionic bonds (by virtue of charge transfer) present between B–O. This strong covalent bond might be responsible for the stability of B3O3 monolayer consisting of B3O3 rings. Moreover, we also calculate simulated scanning tunneling microscopy (STM) image (based on Tersoff–Hamann approximations)35 of B3O3 monolayer which is given in (c) and is in agreement with the experimental result. O atoms in the unit cell are shown for the sake of brevity. In addition, we also calculate STM images of the filled and empty states which are in agreement with the PDOS (and LDOS) calculations.
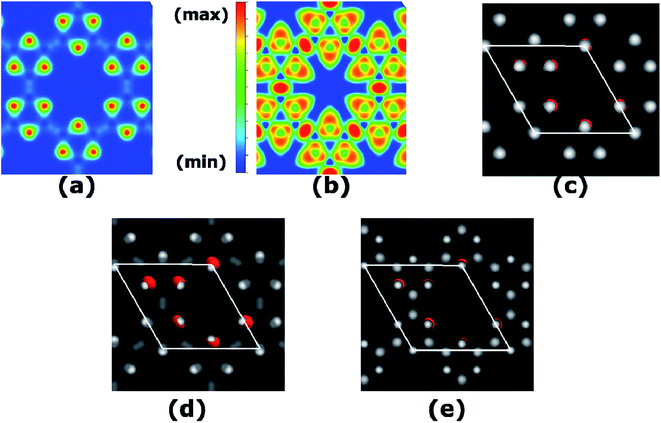 |
| | Fig. 4 (a) Total charge density, (b) ELF, where red means strong electron localization and blue means the opposite, whereas, the green represents a region with a homogenous electron density, (c) STM image of B3O3, (d) STM image of filled and (e) empty states. | |
3.5 Kinetic stability
We also test boroxine with high temperatures (300 and 600 K) to see the response. The initial and final structures treated at 600 K are shown in Fig. 5. The negligible structural modifications suggest that B3O3 is quite stable at high temperatures. This point has already been proved experimentally. In addition, we also calculate the average change appeared in the B–O and B–B bond lengths at a temperature of 600 K. We find a slight variation of 0.986% and 0.602% in B–O and B–B bonds, respectively. That being said, boroxine can be used in high temperatures environment, such as space, aircraft, oil, and gas research applications.36 Nevertheless, it will be interesting to see the highest temperature range that B3O3 can withstand and, therefore, propose a separate investigation to find the melting point of B3O3.
 |
| | Fig. 5 Snapshots of the results of AIMD of boroxine at (a) 0 K, and (b) 600 K. The negligible distortion in the structure reflects its robustness. | |
3.6 Mechanical properties
In Fig. 6, we present the stress curve employed to calculate the in-plane elastic modulus (Y2D) of 2D boroxine. We vary the lattice constant in small steps and observe the energy change as a function of lattice parameter. The second derivative from the plot gives the Y2D and is given by: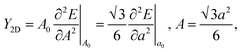 represents the 2D area of B3O3 and a is the lattice constant. At the hybrid level, the 2D bulk modulus of B3O3 is 53.9 N m−1, about 17.93 N m−1 smaller than the values reported by Lin et al.16 The latter values are significantly smaller than the one determined for graphene (206 N m−1) in our earlier study at the same level of theory.31The earlier reported value of Y2D of graphene (206.6 N m−1), hBN (177 N m−1), SiC (116.5 N m−1), and GeC (101 N m−1) are higher than that of B3O3. However, this value is slightly higher than that of Be3N2 (46.5 N m−1),31 silicene (44.5 N m−1), and germanene (29.6 N m−1).37
represents the 2D area of B3O3 and a is the lattice constant. At the hybrid level, the 2D bulk modulus of B3O3 is 53.9 N m−1, about 17.93 N m−1 smaller than the values reported by Lin et al.16 The latter values are significantly smaller than the one determined for graphene (206 N m−1) in our earlier study at the same level of theory.31The earlier reported value of Y2D of graphene (206.6 N m−1), hBN (177 N m−1), SiC (116.5 N m−1), and GeC (101 N m−1) are higher than that of B3O3. However, this value is slightly higher than that of Be3N2 (46.5 N m−1),31 silicene (44.5 N m−1), and germanene (29.6 N m−1).37
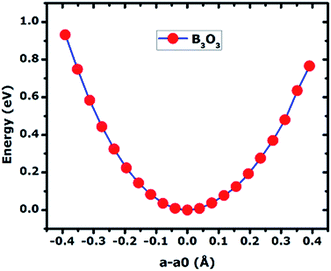 |
| | Fig. 6 The curve of total energy (in eV) vs. change in lattice constant (in Å) calculated of 2D B3O3 at the hybrid level of theory. The in-plane stiffness is calculated by taking the second derivative at the minimum. | |
3.7 Optical properties
Optical absorption spectra are also calculated for parallel polarization without taking into account the excitonic effect. The onset of optical absorption, which is the optical gap, appears around 5.7 eV as can be seen in Fig. 7. This value is sufficiently larger than the electronic band gap of 3.66 eV, meaning that the optical transition from first valence to first conduction band is forbidden as per dipole selection rules. This can be understood by looking at the orbital character shown in PDOS plot. The first transition occurs from the blue peak to the green peak (pz–pz). Moreover, the separation between these two pi bands is around 5.7 eV, thus agreeing well the optical gap. Additionally, the optical gap is in the deep UV range.
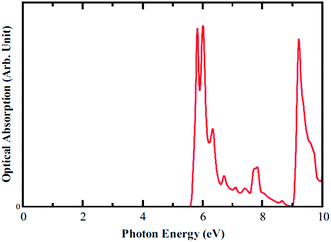 |
| | Fig. 7 Optical Absorption spectra calculated for B3O3, at the hybrid level of theory. | |
3.8 Adsorption of alkalis
As expressed in the first section, based on the chemistry displayed by the 18-crown-6 ether, we expect a strong affinity of 2D boroxine towards potassium. In Table 1, we list the adsorption energies computed for lithium, sodium, and potassium using finite and infinite models. The calculations were performed at the M06-L/6-31G* level of theory and we used a larger unit cell composed by six B3O3 rings so that the unit cell contains a complete hole (as shown in Fig. 1, but including the translucent atoms). The adsorption energies of lithium, sodium, and potassium on the hexagonal hole of boroxine are −52.0, −50.6 and −64.1 kcal mol−1, respectively. Large differences, which may indicate that it is possible to separate selectively adsorb the latter alkali. However, for the adsorption of cations, the situation is reversed and lithium becomes clearly favored. In addition to this, it will also be interesting to integrate a metal atom in the hole of B3O3 and utilize it as a B3O3-supported metal single-atom catalyst, just like C2N.38,39 With regard to the electronic properties, in Fig. 8 we present the band structure and total and projected density of states for boroxine with a potassium atom adsorbed in the hole. The band gap determined for boroxine with a Li, Na and K atoms adsorbed in the hole are: 0.16/3.86, 0.03/3.79 and 0.08/3.93 eV, respectively, at the M06-L/6-31G* level of theory (spin-up/spin-down notation). Thus, alkali atom adsorption dramatically changes the gap for one spin channel while the other is minimally affected. Therefore, it may be possible to attain selective pins polarized transport using these elements.
Table 1 Adsorption energies for lithium, sodium, and potassium at the M06-L/6-31G* level of theory
| |
Infinite boroxine |
(B3O3)6H6 flake |
| Li |
−52.0 |
−55.2 |
| Na |
−50.6 |
−54.2 |
| K |
−64.1 |
−67.8 |
| Li+ |
|
−60.7 |
| Na+ |
|
−51.63 |
| K+ |
|
−47.3 |
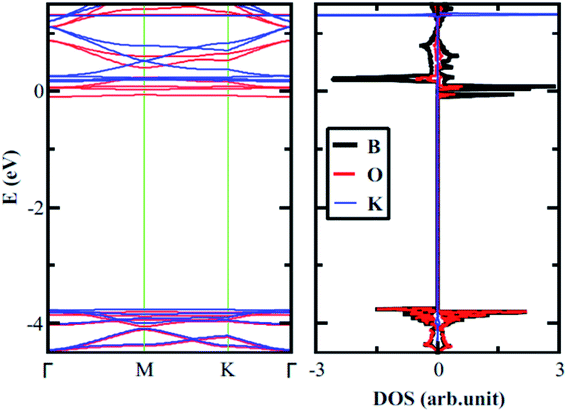 |
| | Fig. 8 Band structure and density of states determined for boroxine with a potassium atom adsorbed in the central hole, at the VDW-DF/DZP level of theory. | |
3.9 Bilayer boroxine
We also calculate B3O3 bilayers in AA, AB, and AB2 stacking as shown in Fig. 9. In AA stacking, the interlayer distance is about 3.57 Å. In AB stacking, the second layer is translated about 1.39 Å (the B–O bond length) along the x-axis, whereas, in AB2 stacking, this translation is about 2.78 Å (the next neighboring B–O bond length) at PBE-D3 level. The interlayer separation in AB (h1 = 3.18, h2 = 3.3 Å) is larger than that of AB2 (h1 = 3.02, h2 = 3.28 Å). Here, h1 is the interlayer separation between B–O (or O–B), whereas, h2 refers to the separation between B–B (O–O) in AB (AB2) bilayer. We show the periodic structures of these bilayers in Fig. S2 bilayer in ESI.† For comparison, the interlayer distance in bilayer graphene at PBE-D3 level is 3.33 Å, which is larger than that of AB2 stacking. Furthermore, the interlayer separation has a direct impact on the stability of the bilayers, AB2 being the most favorable, whereas, AA is the least. We also calculate the interlayer interaction energy (IIE) as: 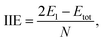 where E1 and Etot are the energies of monolayer and bilayer, respectively. In addition, we compare the outcome with bilayer graphene. Interestingly, we find that IIE in AB2 stacking is comparable to that of bilayer graphene. Table 2 is decorated with relevant data at the PBE-D3 level. The results obtained using other methods are gathered in Table S2.† The electronic band structures are given in Fig. 10. Furthermore, the bilayer gaps are found to be lower than that of the single layer.
where E1 and Etot are the energies of monolayer and bilayer, respectively. In addition, we compare the outcome with bilayer graphene. Interestingly, we find that IIE in AB2 stacking is comparable to that of bilayer graphene. Table 2 is decorated with relevant data at the PBE-D3 level. The results obtained using other methods are gathered in Table S2.† The electronic band structures are given in Fig. 10. Furthermore, the bilayer gaps are found to be lower than that of the single layer.
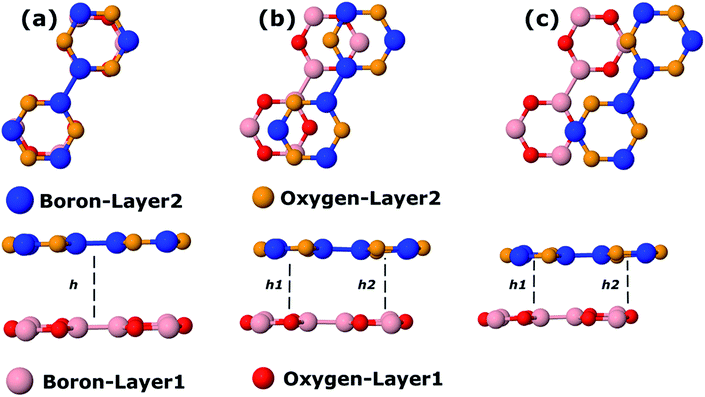 |
| | Fig. 9 Top and side view bilayer B3O3 with (a) AA, (b) AB, and (c) AB2 stacking. In the AA pattern, h represents the interlayer distance. In the other two stackings, h1 and h2 correspond to the separation between B–O (O–B) and B–B (O–B), respectively. | |
Table 2 Relative energy (in meV), interlayer interaction energy (IIE) (in meV per atom), exfoliation energy (Eexf) (in meV A−2), and interlayer separation at PBE-D3 level in B3O3 patterns. The h represents interlayer distance in the AA pattern, whereas, h1/h2 represents B–O/B–B (or O–O) separation in different layers of other patterns
| |
Relative energy (meV) |
IIE (meV per atom) |
Eexf (meV A−2) |
Interlayer separation, h, h1/h2 (Å) |
| B3O3 |
743.71 |
|
|
|
| AA-bilayer |
589 |
6.45 |
|
3.57 |
| AB-bilayer |
443 |
12.5 |
|
3.18/3.3 |
| AB2-bilayer |
358 |
16.05 |
|
3.02/3.28 |
| AA-bulk |
447 |
12.4 |
2.8 |
3.48 |
| AB-bulk |
150 |
24.7 |
5.6 |
3.15/3.15 |
| AB2-bulk |
0 |
31 |
7 |
3.09/3.11 |
| Graphene-bilayer |
|
24 |
|
3.33 |
| Graphite |
|
52.7 |
20 |
3.34 |
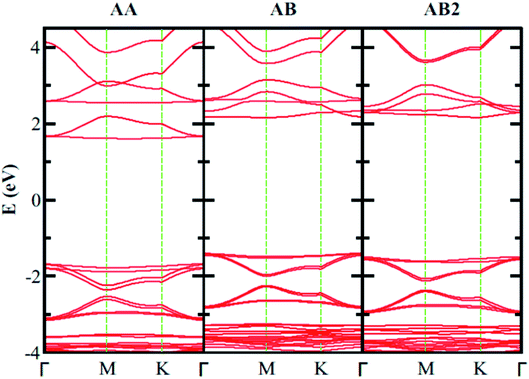 |
| | Fig. 10 Electronic band structure of bilayer B3O3 with different stacking at vdW-DF level. The band gaps in AA, AB, and AB2 stacking are 3.28 eV, 3.56, and 3.65 eV, respectively, at the vdW-DF level. | |
We also consider the effect of an external electric field on the electronic structure of AB2 stacked bilayer B3O3. We keep on increasing the field until we reach a limit where the gap becomes zero. The band structure plots are shown in Fig. S3 in ESI† and the band gap values as a function of the increasing field are shown in Fig. 11. We divide the plot into three parts where green, orange, and red colors represent reasonably-high, very-high, and extremely-high external electric field range. It is not known how much external electric field can be applied to B3O3 until it reaches its breakdown region. However, this study can motivate both theoreticians and experimentalists to initiate such an investigation. Moreover, it can be noted that the external electric field can significantly alter the electronic properties. The gap reaches a value of 1.7 eV at a field of 1.2 V Å−1 from 3.47 eV (at 0 V Å−1). In addition to this, we also calculate the optical properties of AB2 bilayer with and without the external electric field. Here, we consider the structure at 0, 0.6, and 1.2 V Å−1 external electric field. The layer-resolved PDOS along with the optical absorption spectra is given in Fig. 12. Unlike the monolayer, it seems that the σ to π transition becomes allowed by the dipole selection rule in bilayer. Furthermore, there induce some extra peaks which seem to be coming from the transition between the broad B–O-σ band and the narrow B–O-π band. Most interestingly, these peaks correspond to interlayer transition and, furthermore, can be tuned right in the visible range. Nevertheless, those intense peaks in the deep UV range also look like the result of an interlayer transition. In photovoltaics, such transitions have an edge over the intralayer ones.40–44 However, we propose that more accurate calculations, such as GW/BSE are required to confirm these outcomes.
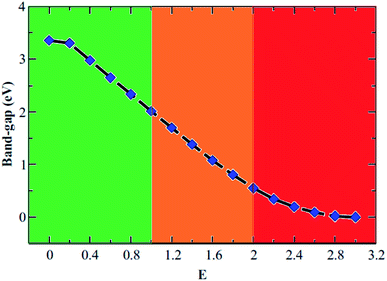 |
| | Fig. 11 Band gap (in eV) variation as a function of external electric field (in V Å−1) for AB2 stacked bilayer boroxine. | |
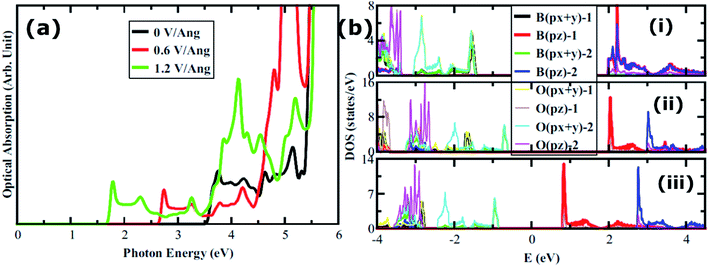 |
| | Fig. 12 (a) Optical absorption spectra of AB2 bilayer at various values of the external electric field. (b) Layer-resolved PDOS of AB2 bilayer (i) at 0, (ii) 0.6, and (iii) 1.2 V Å−1. | |
3.10 Graphite-like bulk B3O3
Finally, we consider graphite-like B3O3 in bulk form which is a new phase of B3O3 at PBE-D3 level. We consider the same patterns as that of the bilayers. From the total energy calculations, it is evident that these patterns are local minima in the total energy surface, again AB2 pattern being the most favorable. The same outcome is confirmed by all the employed levels of theory. In bulk form, they exhibit the same band gaps like that in the bilayer-form and as a comparison, the bilayer and bulk band structures of AB2 stacking are given in Fig. 13. We also calculate the exfoliation energy as reported elsewhere using the following equation:31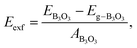 where the energy difference between monolayer B3O3 and graphite-like bulk B3O3 is divided by the monolayer area. From Table 2, it is evident that B3O3 in bulk form is not only comparably robust to that of graphite but the monolayer can be exfoliated with a lot ease as well. The geometries are given in Fig. 14.
where the energy difference between monolayer B3O3 and graphite-like bulk B3O3 is divided by the monolayer area. From Table 2, it is evident that B3O3 in bulk form is not only comparably robust to that of graphite but the monolayer can be exfoliated with a lot ease as well. The geometries are given in Fig. 14.
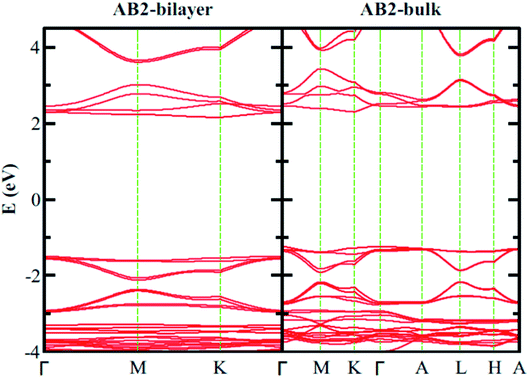 |
| | Fig. 13 Comparison of the electronic band structure of AB2 stacking of B3O3 in bilayer and bulk form at vdW-DF level. | |
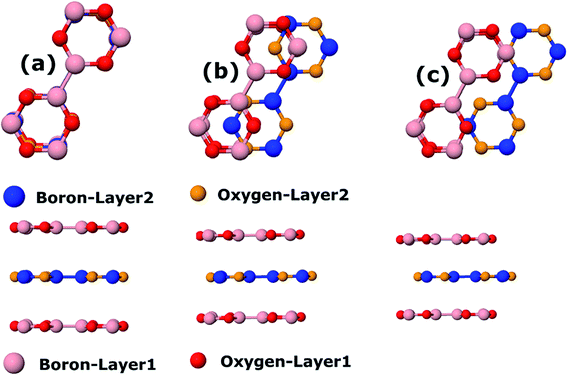 |
| | Fig. 14 Top and side view of (a) AA, (b) AB, and (c) AB2 patterns of B3O3 in bulk form at PBE-D3 level. | |
4. Conclusions
We employed first-principles calculations to perform a thorough theoretical characterization of the various aspects of the recently synthesized boroxine B3O3 monolayer. In agreement with previous theoretical investigations by Lin et al.,16 we found that the structure is perfectly planar formed by B3O3 hexagons with hexagonal symmetry, joined by a strong covalent bond between BB as reveal by ELF. The six B3O3 units joined with six-fold symmetry exhibiting a large hole with a surface of 23 Å2, which is ideal for the adsorption of potassium and the hydronium ion. In effect, we found that boroxine preferentially binds potassium over sodium. In contrast with previous works, we found that the band gap is direct. In effect, HSE calculations indicate that it is an insulator with a direct electronic band gap equal to 5.3 eV. Based on the cohesive energy calculations, B3O3 monolayer is comparably strong as that of graphene and remains negligibly distorted even at 600 K as from AIMD simulations. The elastic modulus is higher than that of Be3N2, silicene, and germanene. Besides, we also explore the bilayer and bulk form of B3O3 and find that those phases are equally robust in comparison to bilayer graphene and graphite. Furthermore, the exfoliation energy calculations suggest that the exfoliation of monolayer B3O3 from the bulk phase is quite easier than that of graphene-graphite. In addition, we find a great tenability of the optoelectronic properties in the presence of external electric field. That being said, the optical properties can be tuned from deep UV to the visible range thus offering a vast range of applications in optoelectronics.
Conflicts of interest
The authors declare no conflicts of interest.
References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- Z. Zeng, Z. Yin, X. Huang, H. Li, Q. He, G. Lu, F. Boey and H. Zhang, Angew. Chem., Int. Ed., 2011, 50, 11093–11097 CrossRef CAS PubMed.
- G. Ye, Y. Gong, J. Lin, B. Li, Y. He, S. T. Pantelides, W. Zhou, R. Vajtai and P. M. Ajayan, Nano Lett., 2016, 16, 1097–1103 CrossRef CAS.
- Y. Gogosti and B. Anasori, ACS Nano, 2019, 13, 8491–8494 CrossRef.
- P. Vogt, P. De Padova, C. Quaresima, J. Avila, E. Frantzeskakis, M. C. Asensio, A. Resta, B. Ealet and G. Le Lay, Phys. Rev. Lett., 2012, 108, 155501 CrossRef PubMed.
- P. A. Denis, Phys. Chem. Chem. Phys., 2015, 17, 5393–5402 RSC.
- M. E. Davila, L. Xian, S. Cahangirov, A. Rubio and G. Le Lay, New J. Phys., 2014, 16, 095002 CrossRef.
- J. Ji, X. Song, J. Liu, Z. Yan, C. Huo, S. Zhang, M. Su, L. Liao, W. Wang, Z. Ni, Y. Hao and H. Zeng, Nat. Commun., 2016, 7, 13352 CrossRef CAS PubMed.
- F. Reis, G. Li, L. Dudy, M. Bauernfeind, S. Glass, W. Hanke, R. Thomale, J. Schäfer and R. Claessen, Science, 2017, 357, 287–290 CrossRef CAS PubMed.
- H. Liu, A. T. Neal, Z. Zhu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033 CrossRef CAS PubMed.
- Z. Zhu and D. Tomanek, Phys. Rev. Lett., 2012, 112, 176802 CrossRef PubMed.
- M. Zhang, H. Sun, X. Wang, H. Du, J. He, Y. Long, Y. Zhang and C. Huang, J. Phys. Chem. C, 2019, 123, 5010–5016 CrossRef CAS.
- J. Wang, F. Ma and M. Sun, RSC Adv., 2017, 7, 16801–16822 RSC.
- P. A. Denis and F. Iribarne, J. Phys. Chem. C, 2018, 122, 18583–18587 CrossRef CAS.
- M. Stredansky, A. Sala, T. Fontanot, R. Costantini, C. Africh, G. Comelli, L. Floreano, A. Morgante and A. Cossaro, Chem. Commun., 2018, 54, 3971 RSC.
- S. Lin, J. Gu, H. Zhang, Y. Wang and Z. Chen, FlatChem, 2018, 9, 27–32 CrossRef CAS.
- M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- J. Heyd and G. E. Scuseria, J. Chem. Phys., 2004, 120, 7274–7280 CrossRef CAS PubMed.
- J. M. Soler, E. Aratacho, J. D. Gale, A. Garcia, J. Junquera, P. Ordejon and S.-D. Portal, The SIESTA Method for Ab Initio Order-N Materials Simulation, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- P. Ordejon, E. Artacho and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, R10441–R10444 CrossRef CAS PubMed.
- N. Troullier and J. L. Martins, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 1993–2006 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- W. Hehre, L. Radom, P. v. R. Schleyer, and J. A. Pople, Ab initio Molecular Orbital Theory, Wiley, New Work, 1986 Search PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmuller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- S. Ullah, P. A. Denis, R. B. Capaz and F. Sato, New J. Chem., 2019, 43, 2933–2941 RSC.
- C. A. Coulson and T. W. Dingle, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1968, 24, 153 CrossRef CAS.
- A. Savin, R. Nesper, S. Wengert and T. F. Fässler, Angew. Chem., Int. Ed., 1997, 36, 1808–1832 CrossRef CAS.
- D. Toffoli, M. Stredansky, Z. Feng, G. Balducci, S. Furlan, M. Stener, H. Ustunel, D. Cvetko, G. Kladnik, A. Morgante, A. Verdini, C. Dri, G. Comelli, G. Fronzoni and A. Cossaro, Chem. Sci., 2017, 8, 3789–3798 RSC.
- J. Tersoff and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805–813 CrossRef CAS PubMed.
- C. Buttay, D. Planson, B. Allard, D. Bergogne, P. Bevilacqua, C. Joubert, M. Lazar, C. Martin, H. Morel, D. Tournier and C. Raynaud, J. Mater. Sci. Eng. B, 2011, 176, 283–288 CrossRef CAS.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- L. Liu and A. Corma, Chem. Rev., 2018, 118, 4981–5079 CrossRef CAS PubMed.
- J. Mahmood, F. Li, C. Kim, H.-J. Choi, O. Gwon, S.-M. Jung, J.-M. Seo, S.-J. Cho, Y.-W. Ju, H. Y. Jeong, G. Kim and J.-B. Baek, Nano Energy, 2018, 44, 304–310 CrossRef CAS.
- S. Ullah, P. A. Denis, M. G. Menezes and F. Sato, Appl. Surf. Sci., 2019, 493, 308–319 CrossRef CAS.
- S. Gélinas, O. Paré-Labrosse, C.-N. Brosseau, S. Albert-Seifried, C. R. McNeill, K. R. Kirov, I. A. Howard, R. Leonelli, R. H. Friend and C. Silva, J. Phys. Chem. C, 2011, 115, 7114–7119 CrossRef.
- S. Gélinas, A. Rao, A. Kumar, S. L. Smith, A. W. Chin, J. Clark, T. S. van der Poll, G. C. Bazan and R. H. Friend, Science, 2014, 343, 512 CrossRef PubMed.
- M. M. Furchi, A. Pospischil, F. Libisch, J. Burgdörfer and T. Mueller, Nano Lett., 2014, 14, 4785–4791 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07338h |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *b,
Pablo A. Denis
*b,
Pablo A. Denis *a and
Fernando Satob
*a and
Fernando Satob


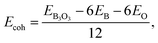 where EB3O3 is the total energy of the unit cell containing 6B and 6O atoms. EB and EO are taken as the gas-phase energies of B and O, respectively. The cohesive energy of B3O3 PBE-D3 level is −6.72 eV per atom, just 0.04 lower than the value reported by Lin et al.16 For the comparison, the cohesive energy of graphene at the same level of theory is −8.07 eV per atom. This means that B3O3 has a comparable strength to that of graphene. At the M06-L level, the cohesive energy of B3O3 −6.3 eV per atom which is twice the value calculated for phosphorene (−3.1 eV per atom) at the same level. Further information is given in ESI.† The data regarding structural properties and stability at various levels of theory is shown in Table S1.†
where EB3O3 is the total energy of the unit cell containing 6B and 6O atoms. EB and EO are taken as the gas-phase energies of B and O, respectively. The cohesive energy of B3O3 PBE-D3 level is −6.72 eV per atom, just 0.04 lower than the value reported by Lin et al.16 For the comparison, the cohesive energy of graphene at the same level of theory is −8.07 eV per atom. This means that B3O3 has a comparable strength to that of graphene. At the M06-L level, the cohesive energy of B3O3 −6.3 eV per atom which is twice the value calculated for phosphorene (−3.1 eV per atom) at the same level. Further information is given in ESI.† The data regarding structural properties and stability at various levels of theory is shown in Table S1.†
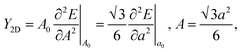 represents the 2D area of B3O3 and a is the lattice constant. At the hybrid level, the 2D bulk modulus of B3O3 is 53.9 N m−1, about 17.93 N m−1 smaller than the values reported by Lin et al.16 The latter values are significantly smaller than the one determined for graphene (206 N m−1) in our earlier study at the same level of theory.31The earlier reported value of Y2D of graphene (206.6 N m−1), hBN (177 N m−1), SiC (116.5 N m−1), and GeC (101 N m−1) are higher than that of B3O3. However, this value is slightly higher than that of Be3N2 (46.5 N m−1),31 silicene (44.5 N m−1), and germanene (29.6 N m−1).37
represents the 2D area of B3O3 and a is the lattice constant. At the hybrid level, the 2D bulk modulus of B3O3 is 53.9 N m−1, about 17.93 N m−1 smaller than the values reported by Lin et al.16 The latter values are significantly smaller than the one determined for graphene (206 N m−1) in our earlier study at the same level of theory.31The earlier reported value of Y2D of graphene (206.6 N m−1), hBN (177 N m−1), SiC (116.5 N m−1), and GeC (101 N m−1) are higher than that of B3O3. However, this value is slightly higher than that of Be3N2 (46.5 N m−1),31 silicene (44.5 N m−1), and germanene (29.6 N m−1).37

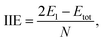 where E1 and Etot are the energies of monolayer and bilayer, respectively. In addition, we compare the outcome with bilayer graphene. Interestingly, we find that IIE in AB2 stacking is comparable to that of bilayer graphene. Table 2 is decorated with relevant data at the PBE-D3 level. The results obtained using other methods are gathered in Table S2.† The electronic band structures are given in Fig. 10. Furthermore, the bilayer gaps are found to be lower than that of the single layer.
where E1 and Etot are the energies of monolayer and bilayer, respectively. In addition, we compare the outcome with bilayer graphene. Interestingly, we find that IIE in AB2 stacking is comparable to that of bilayer graphene. Table 2 is decorated with relevant data at the PBE-D3 level. The results obtained using other methods are gathered in Table S2.† The electronic band structures are given in Fig. 10. Furthermore, the bilayer gaps are found to be lower than that of the single layer.



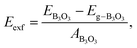 where the energy difference between monolayer B3O3 and graphite-like bulk B3O3 is divided by the monolayer area. From Table 2, it is evident that B3O3 in bulk form is not only comparably robust to that of graphite but the monolayer can be exfoliated with a lot ease as well. The geometries are given in Fig. 14.
where the energy difference between monolayer B3O3 and graphite-like bulk B3O3 is divided by the monolayer area. From Table 2, it is evident that B3O3 in bulk form is not only comparably robust to that of graphite but the monolayer can be exfoliated with a lot ease as well. The geometries are given in Fig. 14.







