Open Access Article
Open Access ArticleA molecular understanding of the interaction of typical aromatic acids with common aerosol nucleation precursors and their atmospheric implications†
Hetong Wangab,
Xianwei Zhaob,
Chenpeng Zuob,
Xiaohui Mab,
Fei Xu *ab,
Yanhui Sun
*ab,
Yanhui Sun c and
Qingzhu Zhang
c and
Qingzhu Zhang b
b
aShenzhen Research Institute of Shandong University, Shenzhen 518057, P. R. China. E-mail: xufei@sdu.edu.cn; Fax: +86-532-5863198
bEnvironment Research Institute, Shandong University, Qingdao 266237, P. R. China
cCollege of Environment and Safety Engineering, Qingdao University of Science & Technology, Qingdao 266042, P. R. China
First published on 6th November 2019
Abstract
Aromatic acids, which are generated from numerous anthropogenic emissions and secondary transformations, have been considered to play a crucial role in new particle formation. In this study, we performed theoretical calculations at the PW91PW91/6-311++G(3df,3pd) level to investigate the interaction between typical aromatic acids namely benzoic acid (BA), phenylacetic acid (PAA), phthalic acid (PA), isophthalic acid (mPA), and terephthalic acid (PTA) and common atmospheric nucleation precursors namely sulfuric acid (SA), water (H2O), ammonia (NH3), methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA). The geometric analysis, Gibbs free energy analysis, OH/NH-stretching vibrational frequency calculation, and atoms in molecules (AIM) analysis were conducted to determine the interactions in the complexes. The heterodimers formed a six to eight membered ring through four types of hydrogen bond, and the bond strength could be ranked in descending order: SO–H⋯O > O–H⋯O/N > N–H⋯O. The BA/PAA/mPA/PTA–SA complexes had the lowest Gibbs free energy values. PA was more likely to interact with NH3 or amines rather than SA due to an intra-molecular hydrogen bond. Additionally, the aromatic acids have similar ability to interact with SA and NH3 as monocarboxylic/dicarboxylic acid. The formation potential of the heterodimers from aromatic acids with common nucleation precursors in ambient atmosphere was investigated.
1. Introduction
Atmospheric aerosols can substantially increase the concentration of cloud condensation nuclei (CCN) and may affect the Earth's climate.1–4 Gas-phase nucleation is a key research area, and new particle formation (NPF) through nucleation is a vital source of atmospheric aerosols.5 However, the NPF process in the atmosphere, which includes multiple components, is highly complex. Although several investigations have been conducted on this process, the precise mechanisms and substances involved at the molecular level are still not adequately understand.To explain the nucleation mechanisms, binary sulfuric acid (SA)–water (H2O), ternary SA–H2O–ammonia (NH3),6 and ion-induced nucleation,7,8 and nucleation enhanced by organic compounds have been proposed.9 The importance of SA in new particle formation has been widely investigated, and numerous studies have proven that SA is a crucial atmospheric nucleating species.1,10 However, a gaseous SA concentration of more than 105 molecules per cm3 is required to observe NPF in the atmosphere.11,12 Therefore, the vital role of organic species in NPF has attracted considerable attention. On the basis on the experimental methods, research has been proven that atmospheric aerosol particles indeed contain a large amount of organic compounds.13–15 Experimental results obtained from such research have shown that organic acids play a key role in the initial growth stage of newly nucleated embryos, and this process is crucial for the subsequent step of particle growth through adsorption or heterogeneous reactions of other organic vapors. Additionally, quantum chemical calculations have demonstrated that an aromatic acid–SA cluster can reduce the nucleation barrier and that a binary SA–H2O nucleation system can be enhanced by sub-ppb levels of organic acids simultaneously.9
Aromatic acids belong to a group of organic acids, which include monocarboxylic acids and dicarboxylic acids. Benzoic acid (BA) is a typical aromatic monocarboxylic acid, that is generated from numerous anthropogenic emissions, such as motor vehicles and fuel burning.16 BA is also a secondary product of the photochemical degradation of aromatic hydrocarbons.17 Phthalic acid (PA), isophthalic acid (mPA), and terephthalic acid (PTA) are aromatic dicarboxylic acids, that have been extensively discovered in the ambient atmosphere. PA can be emitted from the oxidation of polycyclic aromatic hydrocarbons (PAHs), including benz[a]anthracene and naphthalene.18–21 It can also be generated from the burning of biomass, combustion of coal, and exhaust of diesel engines.22 Furthermore, mPA and PTA are primarily produced from the direct emission of automobile exhaust and biomass burning; mPA can also be derived from secondary aerosols.23 Liu and Zeng demonstrated that aromatic acids may be transformed by interacting with common atmospheric oxidants (O3, Cl, NO3, and OH radicals) through heterogeneous or homogeneous reactions.24 Zhang et al. detected five types of aromatic acids in PM2.5 in the northern suburb of Nanjing during winter; the average total concentration of the detected aromatic acids was (50.01 ± 16.05) ng m−3, and the average concentrations of PA, mPA and PTA were (8.14 ± 3.34), (1.08 ± 0.43), and (34.54 ± 12.79) ng m−3, respectively.23 In addition, a study reported the detection of aromatic dicarboxylic acids in the Los Angeles ambient atmosphere.25 Zhang et al. verified that the nucleation rates of SA–H2O systems can be extensively reinforced by the presence of a small quantity of aromatic organic acids.9 Xu and Zhang verified that PA can interact with sulfuric acid and ammonia to playing a key role in aerosol nucleation.26 Therefore, further investigation regarding the role of aromatic acids in nucleation is worthwhile.
In the present study, we investigated the interaction of five aromatic acids namely BA, PAA, PA, mPA, and PTA with common atmospheric aerosol nucleation precursors (SA, H2O, NH3, methylamine (MA), dimethylamine (DMA), and trimethylamine (TMA)) at the molecular level. By using density functional theory (DFT) methods, we conducted theoretical calculations of these complexes to determine geometric parameters, binding energies and Gibbs free energies. Subsequently, we used atoms in molecules analysis (AIM) to determine the electronic densities and hydrogen bonding interactions in the complexes.27,28
2. Computational methods
The chemical geometries for the investigated compounds were determined by an artificial bee colony algorithm software called ABCluster (artificial bee colony algorithm for cluster), which is used for the global optimization of atomic and molecular clusters.29,30 ABCluster is a useful tool for determining the geometry of a cluster with the lowest energy. Density functional theory (DFT) calculations were performed using the Gaussian 09 package.31 First, up to 1000 initially guessed structures were auto-generated and pre-optimized by the semiempirical PM6 method using ABCluster. Second, up to 100 conformations with relatively low energies were selected from the 1000 structures and subsequently optimized at the B3LYP/6-31g(d,p) level; their corresponding vibrational frequencies were calculated at the same level. Finally, the PW91PW91 density functional method with a 6-311++G(3df,3pd) basis set was employed to further reoptimize the 10 most stable of the 100 optimized structures in order to derive the global minimum structure. Their corresponding thermal free energies (ΔG), thermal enthalpies (ΔH), zero-point vibrational energy (ZPVE), and binding energy (BE) were also obtained at the PW91PW91/6-311++G(3df,3pd) level. The BEs of the complexes were corrected with ZPVEs. Several basic clusters formation has been investigated at the M06-2X/6-311++G(3df,3pd) level of theory and recommended to be a more reliable method for predicting the formation of binary and ternary clusters.32–34 The comparison of Gibbs free energy calculated by two different DFT theories in this study was shown in Table 2. The differences between the Gibbs free energies calculated at PW91PW91/6-311++G(3df,3pd) and M06-2X/6-311++G(3df,3pd) were within 2.0 kcal mol−1, which proves the consistency of the two methods. In this study, the analysis of configurations and energies was carried out at PW91PW91/6-311++G(3df,3pd) level of theory.To describe the strength and various classes of the hydrogen bonds, we performed a topological analysis of the charge density by using the AIM2000 program package through atoms in molecules (AIM) theory. AIM theory has been recognized as a powerful method for obtaining a relatively clear understanding of hydrogen bonding interactions.27,28 Additionally, electron density properties at the bond critical point (BCP), bond critical point charge density ρ(r), and Laplacian of charge density ∇2ρ(r) serve as an indicator to describe hydrogen bonding.35
3. Results and discussion
3.1 Geometric analysis
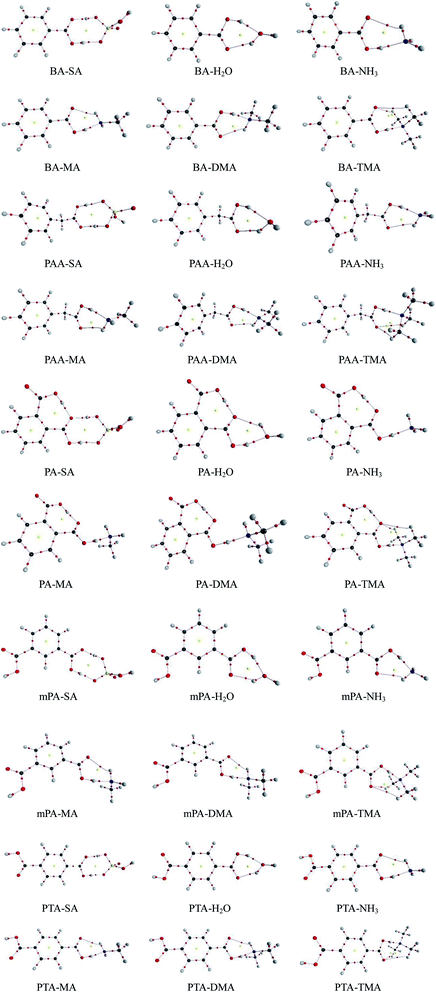
The geometries of SA, H2O, NH3, MA, DMA, and TMA as well as those of BA, PAA, PA, mPA, and PTA were optimized at the PW91PW91/6-311++G(3df,3pd) level using the Gaussian 09 package. Several possible configurations of the complexes were found, but only the most stable structures of the clusters are discussed in this paper. The minimum energy configurations of monomer are displayed in Fig. S1.† The optimized structures of the heterodimers are shown in Fig. 1, and the geometric parameters of the clusters are presented in Table 1. The intra-molecular O–H⋯O hydrogen bonds of PA-containing complexes are displayed in Table S1.† Cartesian coordinates of the minimum energy configurations are shown in Table S4.†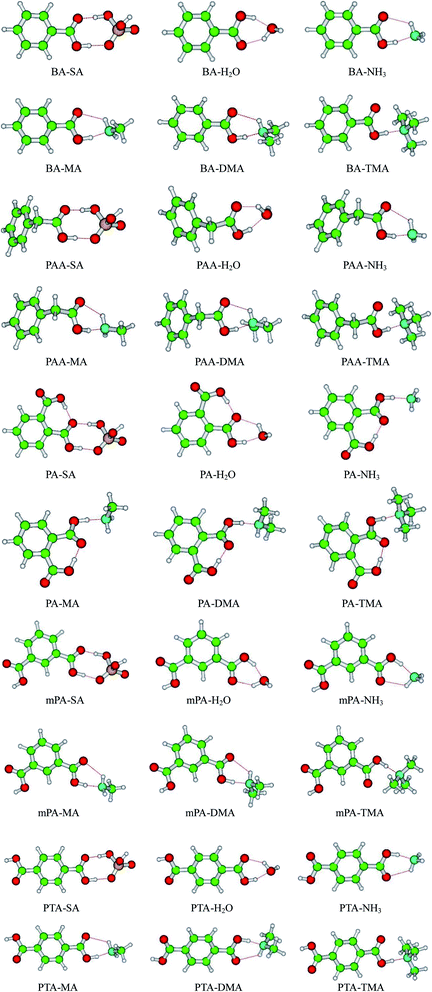 | ||
| Fig. 1 Geometries of aromatic acid-containing complexes calculated at the PW91PW91/6-311++G(3df,3pd) level. Green, yellow, blue, white, and red balls denote C, S, N, H, and O atoms, respectively. | ||
| Conformer | SO–H⋯O | O–H⋯O/N | N–H⋯O | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Δr(OH)a | r(HB)b | θ(HB)c | d(O⋯O)d | Δr(OH)a | r(HB)b | θ(HB)c | d(O⋯O)d | Δr(NH)e | r(HB)b | θ(HB)c | |
| a Δr(OH) = rdimer − rmonomer, is the OH bond length change in the complexation.b The distance of inter-molecular hydrogen bond.c The angle of inter-molecular hydrogen bond.d The two oxygen atoms contact distance in the hydrogen bond.e Δr(NH) = rdimer − rmonomer, is the NH bond length change in the complexation. | |||||||||||
| BA–SA | 0.0863 | 1.4431 | 175.5 | 2.5036 | 0.0321 | 1.6380 | 178.4 | 2.6457 | |||
| BA–H2O | 0.0297/0.0222 | 1.7147/1.8450 | 157.8/143.7 | 2.6728/2.7073 | |||||||
| BA–NH3 | 0.0499 | 1.6789 | 168.1 | 0.0042 | 2.2890 | 123.6 | |||||
| BA–MA | 0.0630 | 1.6329 | 169.3 | 0.0052 | 2.3061 | 122.7 | |||||
| BA–DMA | 0.0721 | 1.6072 | 169.8 | 0.0063 | 2.2809 | 123.9 | |||||
| BA–TMA | 0.0727 | 1.6096 | 179.3 | ||||||||
| PAA–SA | 0.0818 | 1.4577 | 175.8 | 2.5139 | 0.0321 | 1.6415 | 178.9 | 2.6504 | |||
| PAA–H2O | 0.0293/0.0215 | 1.7198/1.8582 | 157.2/143.3 | 2.6758/2.7168 | |||||||
| PAA–NH3 | 0.0499 | 1.6792 | 167.8 | 0.0040 | 2.3140 | 122.9 | |||||
| PAA–MA | 0.0634 | 1.6314 | 169.1 | 0.0051 | 2.3257 | 122.3 | |||||
| PAA–DMA | 0.0724 | 1.6054 | 169.8 | 0.0060 | 2.3136 | 122.8 | |||||
| PAA–TMA | 0.0729 | 1.6071 | 179.2 | ||||||||
| PA–SA | 0.0493 | 1.5675 | 177.3 | 2.5921 | 0.0333 | 1.6269 | 170.0 | 2.6360 | |||
| PA–H2O | 0.0348/0.0122 | 1.6610/2.0343 | 163.4/131.2 | 2.6460/2.7797 | |||||||
| PA–NH3 | 0.0667 | 1.6082 | 174.5 | 2.5221 | |||||||
| PA–MA | 0.0911 | 1.5434 | 175.2 | 2.5175 | |||||||
| PA–DMA | 0.1158 | 1.4880 | 175.5 | 2.5155 | |||||||
| PA–TMA | 0.1264 | 1.4699 | 177.2 | 2.5150 | |||||||
| mPA–SA | 0.0786 | 1.4621 | 175.9 | 2.5159 | 0.0330 | 1.6333 | 178.7 | 2.6420 | |||
| mPA–H2O | 0.0310/0.0210 | 1.7038/1.8633 | 160.0/142.2 | 2.6641/2.7135 | |||||||
| mPA–NH3 | 0.0537 | 1.6626 | 168.7 | 0.0038 | 2.3267 | 121.6 | |||||
| mPA–MA | 0.0684 | 1.6129 | 170.2 | 0.0047 | 2.3529 | 120.4 | |||||
| mPA–DMA | 0.0794 | 1.5824 | 170.9 | 0.0059 | 2.3326 | 121.5 | |||||
| mPA–TMA | 0.0804 | 1.5837 | 178.7 | ||||||||
| PTA–SA | 0.0775 | 1.4661 | 175.9 | 2.5186 | 0.0330 | 1.6320 | 178.7 | 2.6408 | |||
| PTA–H2O | 0.0311/0.0204 | 1.7021/1.8723 | 158.1/141.8 | 2.6634/2.7191 | |||||||
| PTA–NH3 | 0.0541 | 1.6604 | 169.1 | 0.0035 | 2.3457 | 120.9 | |||||
| PTA–MA | 0.0691 | 1.6110 | 170.2 | 0.0048 | 2.3538 | 120.4 | |||||
| PTA–DMA | 0.0803 | 1.5804 | 170.7 | 0.0059 | 2.3267 | 121.6 | |||||
| PTA–TMA | 0.0818 | 1.5792 | 178.8 | ||||||||
Aromatic acids and SA formed an eight-membered ring through a SO–H⋯O and a CO–H⋯O hydrogen bonds. For the PA–SA complex, the carboxyl group formed an intra-molecular CO–H⋯O hydrogen bond with a second carboxyl group of PA apart from the eight-membered ring. For the aromatic acid–NH3/MA/DMA complexes, the carboxyl group in the aromatic acids and the nitrogen atom in NH3/MA/DMA formed a CO–H⋯N hydrogen bond, and the N–H⋯O hydrogen bond was formed between the hydrogen atom in NH3/MA/DMA and the oxygen atom in the carboxyl of the aromatic acid. All of these heterodimers formed a six-membered ring. For the aromatic acid–TMA cluster, a seven-membered ring was produced through a CO–H⋯N hydrogen bond and a C–H⋯O hydrogen bond. PA contained one more intra-molecular hydrogen bond compared with the other aromatic acids. The aromatic acids formed a six-membered ring with H2O through a CO–H⋯O hydrogen bond and an O–H⋯O hydrogen bond. The bond length r(H⋯B) in hydrogen bonds has been employed as an indicator of the hydrogen bond strength. Clearly, the hydrogen bond distances of all the complexes could be ranked as follows in ascending order: SO–H⋯O < CO–H⋯O/N < NH⋯O. This indicates that the SO–H⋯O hydrogen bond was the strongest in the complexes. Gilli et al. identified the contact distance d(O⋯O) between two oxygen atoms in a hydrogen bond as an indicator of hydrogen bond strength.36 In the same complexes in this study, the contact distance d(O⋯O) of the SO–H⋯O hydrogen bond was shorter than that of the CO–H⋯O hydrogen bond. These results confirm that the SO–H⋯O hydrogen bond was the strongest in the complexes. The CO–H⋯O/N hydrogen bond was stronger than the N–H⋯O hydrogen bonds.
3.2 Interaction energy
The calculated binding energy (BE), zero-point vibrational energy (ZPVE), enthalpy of formation (ΔHθ298 K) and Gibbs free energy of formation (ΔGθ298 K) for the complexes are summarized in Table 2. The calculated ΔGθ298 K values were −7.99, −7.39, −4.47, −7.48, and −7.35 kcal mol−1 for BA–SA, PAA–SA, PA–SA, mPA–SA, and PTA–SA, respectively. This result indicates that the aromatic acids had the similar reactivity to interact with sulfuric acid except for PA. Apart from those observed for PA, the ΔGθ298 K values calculated for aromatic acid–SA complexes were more negative than those calculated for the aromatic acid–NH3/amine complexes, indicating that the aromatic acids were more likely to interact with SA. This may have been due to the presence of intra-molecular hydrogen bonds, so PA is different from the other aromatic acids. The interaction of PA with NH3/amine produced a lower Gibbs free energy compared with that produced by the PA–SA cluster. The ΔGθ298 K values of the aromatic acid–NH3/amine complexes were obviously quite similar. Among all aromatic acid–NH3/amine clusters, apart from PAA-containing clusters, the aromatic acid–DMA clusters had the lowest Gibbs free energy and the aromatic acid–TMA complexes had the highest Gibbs free energy in most clusters. This result proves that the interaction of aromatic acids with DMA was much stronger than those with NH3, MA, and TMA. All aromatic acid–H2O complexes, except for PAA, had the similar ΔGθ298 K value; the ΔGθ298 K value of PAA–H2O was slightly higher than those of the other aromatic acid–H2O clusters. The negative value of BEs indicates that the cluster was stable. Therefore, based on the BE, we can conclude that the aromatic acid–SA complexes were the easiest to form, followed by the aromatic acid–DMA complexes. The enthalpy ΔHθ298 K of hydrogen bond formation is directly related to the stabilization energy of a complex.37 When we considered enthalpy, we could observe that the calculated values were consistent with the Gibbs free energy values of the complexes.| Conformer | BEa | ZPVE | ΔHθ298 K | ΔGθ298 K (PW91PW91) | ΔGθ298 K (M06-2X) |
|---|---|---|---|---|---|
| a BE corrected with ZPVE. | |||||
| BA–SA | −19.78 | −19.26 | −19.29 | −7.99 | −8.25 |
| BA–H2O | −11.84 | −9.50 | −10.27 | −0.57 | −0.30 |
| BA–NH3 | −12.46 | −10.70 | −11.09 | −2.12 | −1.78 |
| BA–MA | −13.47 | −12.27 | −12.24 | −2.59 | −2.05 |
| BA–DMA | −13.82 | −12.85 | −12.63 | −2.79 | −0.98 |
| BA–TMA | −13.23 | −12.41 | −12.09 | −1.89 | −3.51 |
| PAA–SA | −19.43 | −18.81 | −18.89 | −7.39 | −7.41 |
| PAA–H2O | −11.76 | −9.47 | −10.80 | 0.77 | −0.62 |
| PAA–NH3 | −12.49 | −10.69 | −11.12 | −2.03 | −0.12 |
| PAA–MA | −13.47 | −12.28 | −12.26 | −2.72 | −1.65 |
| PAA–DMA | −13.87 | −12.85 | −12.68 | −2.51 | −1.45 |
| PAA–TMA | −13.40 | −12.40 | −12.19 | −1.31 | −2.22 |
| PA–SA | −16.46 | −15.67 | −15.57 | −4.47 | −5.26 |
| PA–H2O | −11.84 | −9.73 | −10.36 | −0.84 | −1.41 |
| PA–NH3 | −14.81 | −13.36 | −13.70 | −4.95 | −4.06 |
| PA–MA | −16.18 | −15.36 | −15.32 | −5.86 | −4.14 |
| PA–DMA | −16.71 | −16.34 | −16.09 | −6.41 | −4.97 |
| PA–TMA | −16.46 | −16.34 | −16.03 | −5.64 | −5.34 |
| mPA–SA | −19.31 | −18.75 | −18.76 | −7.48 | −7.94 |
| mPA–H2O | −11.94 | −9.63 | −10.38 | −0.64 | −0.46 |
| mPA–NH3 | −13.01 | −11.29 | −11.66 | −2.73 | −2.42 |
| mPA–MA | −14.16 | −13.02 | −12.96 | −3.40 | −2.37 |
| mPA–DMA | −14.52 | −13.65 | −13.39 | −3.77 | −3.07 |
| mPA–TMA | −13.96 | −13.18 | −12.87 | −2.38 | −3.44 |
| PTA–SA | −19.24 | −18.67 | −18.67 | −7.35 | −7.67 |
| PTA–H2O | −11.88 | −9.58 | −10.33 | −0.64 | −0.37 |
| PTA–NH3 | −13.05 | −11.34 | −11.70 | −2.80 | −2.18 |
| PTA–MA | −14.14 | −13.00 | −12.85 | −3.25 | −2.51 |
| PTA–DMA | −14.51 | −13.62 | −13.39 | −3.50 | −1.41 |
| PTA–TMA | −14.02 | −13.36 | −12.99 | −3.09 | −3.66 |
We compared the Gibbs free energy values of the aromatic monocarboxylic acids (BA, PAA)–SA complexes with those of the aromatic dicarboxylic acid (mPA, PTA)–SA complexes; we observed that the presence of the two carboxyls had little effect on the complexation process. However, increasing the number of carboxyl groups influenced the interaction of aromatic acids with NH3 or amines. For example, the ΔGθ298 K value of the mPA–TMA cluster was lower than that of the PAA–TMA cluster by up to 4.33 kcal mol−1. The value of the Gibbs free energy value of the BA-containing complexes was slightly lower than that of the PAA-containing complexes, signifying that methyl had an inhibitory role in the complexation process. Considering the different positions of the two carboxyl groups, the ΔGθ298 K value of the PA–SA complex (−4.47 kcal mol−1) was quite different from those of the mPA–SA (−7.48 kcal mol−1) and PTA–SA (−7.35 kcal mol−1) complexes. The reason is that the two carboxyl groups in the ortho-position could form an intra-molecular hydrogen bond. Therefore, the presence of the intra-molecular hydrogen bond had a negative effect on the interaction of the aromatic acids and SA. This is consistent with the investigation of Jonas et al., no or weak presence of intramolecular hydrogen bond can stabilize the sulfuric acid cluster.38 However, the Gibbs free energy values derived for mPA–SA and PTA–SA were nearly the same. A possible reason is that, when the two carboxyl groups were in the meta-position and para-position, they were not sufficiently far apart to form an intra-molecular hydrogen bond. Therefore, only one carboxyl was involved in the hydrogen bond formation in both. For the PA–NH3/amines complexes, the complexation process was different from the complexation of the aromatic acids and SA. The presence of intra-molecular hydrogen bonds had a positive effect on the interaction of the aromatic acids and NH3/amine. The Gibbs free energy value of PA–DMA was 6.41 kcal mol−1, whereas mPA–DMA was −3.77 kcal mol−1.
According to the investigation by Nadykto and Yu at the PW91PW91/6-311++G(3df,3pd) level,39 the ΔGθ298 K values obtained for formic acid (HCOOH)–SA and acetic acid (CH3COOH)–SA were −6.44 and −7.46 kcal mol−1, respectively. Xu et al. discussed the Gibbs free energy of a pyruvic acid (CH3COCOOH)–SA cluster at the PW91PW91/6-311++G(3df,3pd) level,40 the value which was −4.17 kcal mol−1. According to the calculation, the interaction between CH3COCOOH and SA was weaker than that between BA and SA. Although CH3COCOOH has a lower pKa value, the fact indicated that the acidity of monocarboxylic acid was not directly related to its cluster formation ability with SA. Comparing the Gibbs free energy values of BA–SA and PAA–SA clearly revealed that, aromatic monocarboxylic acids were basically similar or more likely to interact with SA compared with linear monocarboxylic acids. Xu et al. also reported that the Gibbs free energy values of malic acid (HOOCCHOHCH2COOH)–SA and tartaric acid (HOOCCHOHCHOHCOOH)–SA were −7.46 and −7.82 kcal mol−1, respectively, at the PW91PW91/6-311++G(3df,3pd) level.40 Miao et al. observed that the ΔGθ298 K values derived for oxalic acid (HOOCCOOH)–SA was −5.38 kcal mol−1 at the PW91PW91/6-311++G(3df,3pd) level.41 PA has a lower pKa value compared with mPA and PTA, however, the Gibbs free energies of PA–SA are about 3 kcal mol−1 lower than mPA–SA and PTA–SA complexes. The pKa value of HOOCCOOH is lower than mPA and PTA, the formation of mPA–SA and PTA–SA heterodimers are easier than that of HOOCCOOH–SA. These all suggests that the acid strength does not directly correlate with its ability to form clusters with SA. We can conclude that the aromatic dicarboxylic acids had similar abilities to interact with SA than did the linear dicarboxylic acid. These results indicate that the affinities of aromatic acids to the SA were similar than those of linear monocarboxylic/dicarboxylic acid into SA. Moreover, the Gibbs free energy values of HCOOH–NH3, CH3COOH–NH3, and CH3COCOOH–NH3 were calculated to be −2.82, −2.35, and −0.96 kcal mol−1, respectively.39,40 For the dicarboxylic acids–NH3 clusters, the ΔGθ298 K value of HOOCCHOHCH2COOH–NH3, HOOCCHOHCHOHCOOH–NH3 and HOOCCOOH–NH3 were −3.62, −5.41, and −5.14 kcal mol−1, respectively.40,42 Hence, aromatic acids have similar ability to interact with NH3 compared with that of monocarboxylic/dicarboxylic acids which is consistent with that of atomatic acid–SA and monocarboxylic/dicarboxylic acid–SA. According to Xu et al. and Nadykto et al.,43,44 the Gibbs free energy value for SA–H2O, SA–NH3, SA–MA, SA–DMA, and SA–TMA were −0.28, −7.77, −11.03, −11.38, and −10.56 kcal mol−1, respectively. Aromatic acids–SA and SA–NH3 clusters have a similar magnitude of Gibbs free energies. However, the interactions between aromatic acid and SA are weaker than those between SA and MA/DMA/TMA.
3.3 Calculated OH/NH-stretching vibrational frequencies
To clarify the variety classes and the strength of the different hydrogen bonds in the aromatic acid containing heterodimers, we used the red shift (Δṽ), which is the wavenumber difference between free and hydrogen bonded OH-/NH-stretching vibrational transitions (Δṽ = ṽmonomer − ṽdimer), to determine the interaction of different types of hydrogen bonds.45,46 The calculated OH- and NH-stretching fundamental transition wavenumbers and the red shifts with respect to the heterodimers are summarized in Table 3. The red shifts and the changes in the intra-molecular OH bond lengths in the PA complexes are presented in Table S2.†| Conformer | SO–H⋯O | O–H⋯O/N | N–H⋯O | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ṽ | Δṽa | fD/fMb | ṽ | Δṽa | fD/fMb | ṽ | Δṽa | fD/fMb | |
| a Δṽ = ṽmonomer − ṽdimer.b fD/fM stands for the increase of intensity during the complexation. | |||||||||
| BA–SA | 2222 | 1443 | 84.1 | 3044 | 609 | 37.6 | |||
| BA–H2O | 3077/3372 | 576/451 | 12.9/18.5 | ||||||
| BA–NH3 | 2725 | 928 | 7.3 | 3492 | 213 | 14.8 | |||
| BA–MA | 2513 | 1140 | 43.8 | 3483 | 19 | 16.2 | |||
| BA–DMA | 2369 | 1284 | 52.4 | 3378 | 76 | 194 | |||
| BA–TMA | 2349 | 1303 | 57.3 | ||||||
| PAA–SA | 2284 | 1381 | 69.8 | 3035 | 599 | 47.5 | |||
| PAA–H2O | 3070/3383 | 564/440 | 11.3/14.5 | ||||||
| PAA–NH3 | 2716 | 918 | 43.6 | 3493 | 21 | 13.2 | |||
| PAA–MA | 2498 | 1136 | 58.3 | 3482 | 19 | 14.8 | |||
| PAA–DMA | 2358 | 1276 | 68.3 | 3383 | 71 | 151 | |||
| PAA–TMA | 2341 | 1294 | 75.4 | ||||||
| PA–SA | 2741 | 924 | 49.8 | 3018 | 626 | 34.5 | |||
| PA–H2O | 2982/3042 | 662/21 | 18.2/0.8 | ||||||
| PA–NH3 | 2443 | 1201 | 34.4 | ||||||
| PA–MA | 2114 | 1530 | 41.2 | ||||||
| PA–DMA | 1828 | 1816 | 40.5 | ||||||
| PA–TMA | 1745 | 1899 | 28.8 | ||||||
| mPA–SA | 2313 | 1352 | 83.1 | 3029 | 624 | 29.8 | |||
| mPA–H2O | 3055/3394 | 597/429 | 11.5/17.0 | ||||||
| mPA–NH3 | 2665 | 987 | 28.9 | 3494 | 20 | 14.9 | |||
| mPA–MA | 2432 | 1212 | 37.1 | 3483 | 18 | 16.0 | |||
| mPA–DMA | 2269 | 1383 | 44.5 | 3386 | 68 | 145 | |||
| mPA–TMA | 2241 | 1411 | 48.4 | ||||||
| PTA–SA | 2329 | 1336 | 85.6 | 3027 | 624 | 18.2 | |||
| PTA–H2O | 3052/3404 | 599/419 | 6.9/16.6 | ||||||
| PTA–NH3 | 2658 | 994 | 17.0 | 3495 | 19 | 14.7 | |||
| PTA–MA | 2422 | 1230 | 21.7 | 3483 | 19 | 16.9 | |||
| PTA–DMA | 2253 | 1399 | 25.8 | 3386 | 68 | 156 | |||
| PTA–TMA | 2220 | 1431 | 28.1 | ||||||
The red shifts of the OH-stretching transitions of the SO–H⋯O hydrogen bonds of BA/PAA/mPA/PTA–SA were calculated to be within the range of 1336–1443 cm−1, and their corresponding intensities were increased by 70–84 times compared with those of the monomers. For the PA–SA complex, the red shift of the OH-stretching transition was calculated to be 924 cm−1, and the intensity was calculated to be 50 times stronger than those of the monomers. This result is consistent with the Gibbs free energy value. Regarding the CO–H⋯O/N hydrogen bonds, formed between BA/PAA/mPA/PTA and NH3 or amines, the red shift of the OH-stretching transition was within 918–1431 cm−1, and the intensity was increased by more than 7 times relative to those of the monomers. Thus, we could rank the hydrogen bonds according to their strength as follows: SO–H⋯O > CO–H⋯O/N > N–H⋯O. Additionally, the red shifts of the OH-stretching transition of the intra-molecular hydrogen bond in the PA-containing complexes were considerably smaller than those of the inter-molecular hydrogen bond, indicating that the inter-molecular O–H⋯O hydrogen bond was stronger than the intra-molecular O–H⋯O hydrogen bond.
3.4 Topological analysis
The AIM analysis serves as a tool to gain deep insights into the nature of hydrogen bond interactions. The AIM calculations were performed at the PW91PW91/6-311++G(3df,3pd) level according to the wavefunctions of the monomers and heterodimers. The AIM plots of all the heterodimers with bond critical points (BCPs), ring critical points (RCPs), and electron density paths are depicted in Fig. 2. The topological parameters, including electron density ρ(r), Laplacian of electron density ∇2ρ(r) at the BCPs, and changes in atomic charge Δq(H) at the H atom determined using the PW91PW91 method, are listed in Table 4. The AIM parameters for the intra-molecular hydrogen bonds of the PA complexes are presented in Table S3.†| Conformer | SO–H⋯O | O–H⋯O/N | N–H⋯O | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Δq(H)a | ρb | ∇2ρc | Δq(H)a | ρb | ∇2ρc | Δq(H)a | ρb | ∇2ρc | |
| a The change in atomic charge at the H atom.b The electron density at the BCPs.c The Laplacian electron density at the BCPs. | |||||||||
| BA–SA | 0.0396 | 0.0903 | 0.0704 | 0.0580 | 0.0524 | 0.1066 | |||
| BA–H2O | 0.0371/0.0551 | 0.2656/0.2037 | 0.1059/0.1010 | ||||||
| BA–NH3 | 0.0198 | 0.0597 | 0.0169 | 0.0654 | 0.0147 | 0.0490 | |||
| BA–MA | 0.0116 | 0.0684 | 0.0481 | 0.0621 | 0.0145 | 0.0478 | |||
| BA–DMA | 0.0049 | 0.0740 | 0.0373 | 0.0596 | 0.0153 | 0.0503 | |||
| BA–TMA | 0.0045 | 0.0747 | 0.0319 | ||||||
| PAA–SA | 0.0396 | 0.0871 | 0.0745 | 0.0604 | 0.0519 | 0.1065 | |||
| PAA–H2O | 0.0395/0.0554 | 0.2630/0.1976 | 0.1056/0.0993 | ||||||
| PAA–NH3 | 0.0225 | 0.0598 | 0.0617 | 0.0636 | 0.0141 | 0.0464 | |||
| PAA–MA | 0.0137 | 0.0688 | 0.0477 | 0.0612 | 0.0140 | 0.0458 | |||
| PAA–DMA | 0.0078 | 0.0745 | 0.0365 | 0.0578 | 0.0144 | 0.0470 | |||
| PAA–TMA | 0.0072 | 0.0752 | 0.0313 | ||||||
| PA–SA | 0.0414 | 0.0646 | 0.0971 | 0.0493 | 0.0536 | 0.1066 | |||
| PA–H2O | 0.0756/0.0531 | 0.0531/0.0227 | 0.1039/0.0790 | ||||||
| PA–NH3 | 0.0076 | 0.0714 | 0.0430 | ||||||
| PA–MA | −0.0045 | 0.0856 | 0.0144 | ||||||
| PA–DMA | −0.0164 | 0.0996 | −0.0218 | ||||||
| PA–TMA | −0.0214 | 0.1053 | −0.0412 | ||||||
| mPA–SA | 0.0395 | 0.0858 | 0.0779 | 0.0560 | 0.0529 | 0.1066 | |||
| mPA–H2O | 0.0359/0.0567 | 0.2721/0.1958 | 0.1059/0.0995 | ||||||
| mPA–NH3 | 0.0173 | 0.0622 | 0.0584 | 0.0641 | 0.0138 | 0.0459 | |||
| mPA–MA | 0.0076 | 0.0719 | 0.0423 | 0.0606 | 0.0134 | 0.0443 | |||
| mPA–DMA | 0.0011 | 0.0787 | 0.0286 | 0.0574 | 0.0140 | 0.0460 | |||
| mPA–TMA | 0.0004 | 0.0796 | 0.0230 | ||||||
| PTA–SA | 0.0401 | 0.0849 | 0.0791 | 0.0551 | 0.0531 | 0.1067 | |||
| PTA–H2O | 0.0358/0.0558 | 0.2732/0.1918 | 0.1059/0.0984 | ||||||
| PTA–NH3 | 0.0179 | 0.0626 | 0.0578 | 0.0657 | 0.0134 | 0.0444 | |||
| PTA–MA | 0.0086 | 0.0723 | 0.0416 | 0.0607 | 0.0134 | 0.0442 | |||
| PTA–DMA | 0 | 0.0791 | 0.0277 | 0.0583 | 0.0141 | 0.0466 | |||
| PTA–TMA | −0.0007 | 0.0804 | 0.0214 | ||||||
For the aromatic acid–SA complexes, the electron densities ρ(r) at the BCPs for SO–H⋯O and CO–H⋯O were within 0.0646–0.0903 and 0.0519–0.0536 a.u., respectively. The electron densities ρ(r) at the BCPs for the CO–H⋯O and N–H⋯O hydrogen bonds were within the limits of 0.0597–0.0804 and 0.0134–0.1053 a.u., respectively, in the aromatic acid–NH3/MA/DMA/TMA complexes. On the basis of the standard proposed by Koch and Popelier,47 for a hydrogen bond, the electron density ρ(r) is usually within 0.002–0.040 a.u.47,48 Clearly, the aforementioned ρ(r) of the hydrogen bonds considerably exceed the upper limit of electron density values. The reason may be that the aromatic acids and SA/H2O/NH3/MA/DMA/TMA had strong hydrogen bond interactions. The values derived for the ∇2ρ(r) for SO–H⋯O and CO–H⋯O hydrogen bonds in the aromatic acid–SA complexes, were within the ranges of 0.0704–0.0971 and 0.1065–0.1067 a.u., respectively. For the aromatic acid–NH3/MA/DMA/TMA clusters, the ∇2ρ(r) values obtained for the CO–H⋯O and N–H⋯O hydrogen bonds were in the range of from −0.0412 to 0.0617 and from 0.0442 to 0.0503 a.u., respectively. These values were almost within the range of Laplacian criteria (0.014–0.139 a.u.).47,48
3.5 Atmospheric implication
To explain the role of aromatic acids in the formation of heterodimers from aromatic acids with common nucleation precursors in the atmosphere, the mass-balance equation was used to evaluate the atmospheric implication. Take BA–SA cluster as an example, the [BA–SA] concentration can be expressed as follows:
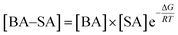 | (1) |
Eqn (1) reveals that the concentration of the BA–SA complex is related to the concentrations of BA and SA and the value of the Gibbs free energy for cluster formation. The concentrations of SA, H2O, NH3, MA, DMA and TMA in ambient atmosphere were approximately 1 × 107, 2.46 × 1014, 1 × 1011, 1 × 109, 1 × 109, and 1 × 109, respectively. The concentrations of BA, PAA, PA, mPA, and PTA were 1.05 × 103, 7.50 × 108, 4.16 × 101, 5.47 × 100, and 1.71 × 102 molecule per cm3, respectively.49–51 The concentrations of the complexes from dimerization of aromatic acid and common nucleation precursor calculated by the mass-balance equation are listed in Table 5. For a given aromatic acid, the aromatic acid–H2O complexes had the highest concentrations in the ambient atmosphere, followed by the aromatic acid–SA, and aromatic acid–NH3/DMA. When compared the concentration of aromatic acid–NH3 and aromatic acid–DMA clusters, for a given aromatic acid, the concentration of aromatic acid–NH3 heterodimer is higher than that of aromatic acid–DMA heterodimer. Thus, we can conclude that aromatic acid–H2O complexes are abundant heterodimers due to the high concentration of water in the atmosphere. Owing to the lower Gibbs free energies of aromatic acid–SA/NH3/DMA compared with that of aromatic acid–H2O, they have a great possibility to form. Although the aromatic acid–SA/NH3/DMA has a lower concentration compared with that of aromatic acid–H2O complexes, the role of SA, NH3 and DMA in the dimerization cannot be ignored.
| Complexes | Concentrations | Complexes | Concentrations |
|---|---|---|---|
| BA–SA | 2.98 × 10−4 | BA–MA | 8.47 × 10−6 |
| BA–H2O | 1.59 × 10−2 | BA–DMA | 1.19 × 10−5 |
| BA–NH3 | 3.64 × 10−4 | BA–TMA | 2.60 × 10−6 |
| PAA–SA | 2.37 × 102 | PAA–MA | 7.41 × 100 |
| PAA–H2O | 1.44 × 103 | PAA–DMA | 5.20 × 102 |
| PAA–NH3 | 2.31 × 102 | PAA–TMA | 6.85 × 10−1 |
| PA–SA | 9.96 × 10−8 | PA–MA | 8.84 × 10−5 |
| PA–H2O | 6.71 × 10−4 | PA–DMA | 2.06 × 10−4 |
| PA–NH3 | 1.93 × 10−3 | PA–TMA | 5.32 × 10−5 |
| mPA–SA | 2.08 × 10−6 | mPA–MA | 1.70 × 10−7 |
| mPA–H2O | 6.50 × 10−5 | mPA–DMA | 3.35 × 10−7 |
| mPA–NH3 | 5.23 × 10−6 | mPA–TMA | 3.15 × 10−8 |
| PTA–SA | 5.50 × 10−5 | PTA–MA | 4.51 × 10−6 |
| PTA–H2O | 2.16 × 10−3 | PTA–DMA | 6.33 × 10−6 |
| PTA–NH3 | 1.94 × 10−4 | PTA–TMA | 3.17 × 10−6 |
4. Conclusions
In summary, we theoretically investigated the molecular interaction between five aromatic acids (BA, PAA, PA, mPA, PTA) and some common atmospheric aerosol nucleation precursors. The following conclusions were drawn from the present study:(1) The strength of the hydrogen bonds in aromatic acid-containing complexes could be ranked as follows in descending order: SO–H⋯O/N > CO–H⋯O/N > N–H⋯O hydrogen bonds.
(2) The BA/PAA/mPA/PTA–SA complexes had the lowest Gibbs free energy, followed by the BA/PAA/mPA/PTA-DMA complexes. For the PA-containing cluster, PA was more likely to interact with NH3 or amines rather than SA.
(3) For the aromatic monocarboxylic acids, the presence of methyl impeded the complexation process. For the aromatic dicarboxylic acids, the two carboxyl groups in the ortho-position that formed an intra-molecular hydrogen bond promoted the interaction of NH3 and amines, but hindered the interaction of SA. When the two carboxyl groups were in the meta-position and para-position, the extra carboxyl had little influence on the complexation.
(4) The aromatic monocarboxylic/dicarboxylic acids had similar abilities to interact with SA than did the linear monocarboxylic/dicarboxylic acids, apart from PA. The affinities of the linear monocarboxylic/dicarboxylic acids to NH3 are similar compared with those of the aromatic acid–NH3 complexes.
(5) The atomatic acid–H2O clusters have the highest concentrations in the formation of heterodimers. Simultaneously, although the concentrations of aromatic acid–SA/NH3/amine clusters are relatively a little low, they also have the potential to form during the formation of heterodimers owing to the relative low Gibbs free energies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by NSFC (National Natural Science Foundation of China, project no. 91644214, 21677089, 21876102), Shenzhen Science and Technology Research and Development Funds (project no. JCYJ20160510165106371), FRFSDU (the Fundamental Research Funds of Shandong University, project no. 2016WLJH51, 2017JC033), the China Postdoctoral Science Foundation funded project (project no. 2017M612277, 2017T100493), SKLECRA (the open foundation of State Key Laboratory of Environmental Criteria and Risk Assessment, Chinese research academy of environmental sciences no. 2016OFP09).References
- R. Y. Zhang, Science, 2010, 328, 1366–1367 CrossRef CAS.
- F. Q. Yu and G. Luo, Atmos. Chem. Phys., 2009, 9, 7691–7710 CrossRef CAS.
- P. Paasonen, A. Asmi, T. Petäjä, M. K. Kajos, M. Äijälä, H. Junninen, T. Holst, J. P. Abbatt, A. Arneth and W. Birmili, Nat. Geosci., 2013, 6, 438–442 CrossRef CAS.
- F. Q. Yu and A. G. Hallar, J. Geophys. Res.: Atmos., 2014, 119(12), 246–255 Search PubMed.
- R. Y. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2011, 112, 1957–2011 CrossRef.
- S. Ball, D. Hanson, F. Eisele and P. McMurry, J. Geophys. Res.: Atmos., 1999, 104, 23709–23718 CrossRef CAS.
- F. Q. Yu and R. P. Turco, J. Geophys. Res.: Atmos., 2001, 106, 4797–4814 CrossRef CAS.
- S.-H. Lee, J. Reeves, J. Wilson, D. Hunton, A. Viggiano, T. Miller, J. Ballenthin and L. Lait, Science, 2003, 301, 1886–1889 CrossRef CAS.
- R. Y. Zhang, I. Suh, J. Zhao, D. Zhang, E. C. Fortner, X. X. Tie, L. T. Molina and M. J. Molina, Science, 2004, 304, 1487–1490 CrossRef CAS.
- J. Zheng, A. Khalizov, L. Wang and R. Y. Zhang, Anal. Chem., 2010, 82, 7302–7308 CrossRef CAS.
- T. Nieminen, H. E. Manninen, S.-L. Sihto, T. Yli-Juuti, R. L. Mauldin, T. Petaja, I. Riipinen, V.-M. Kerminen and M. Kulmala, Environ. Sci. Technol., 2009, 43, 4715–4721 CrossRef CAS.
- R. Weber, P. H. McMurry, R. Mauldin, D. Tanner, F. Eisele, A. Clarke and V. Kapustin, Geophys. Res. Lett., 1999, 26, 307–310 CrossRef CAS.
- A. Chebbi and P. Carlier, Atmos. Environ., 1996, 30, 4233–4249 CrossRef CAS.
- J. Duplissy, P. F. DeCarlo, J. Dommen, M. R. Alfarra, A. Metzger, I. Barmpadimos, A. S. Prevot, E. Weingartner, T. Tritscher and M. Gysel, Atmos. Chem. Phys., 2011, 11, 1155–1165 CrossRef CAS.
- I. G. Kavouras, N. Mihalopoulos and E. G. Stephanou, Nature, 1998, 395, 683 CrossRef CAS.
- W. F. Rogge, L. M. Hildemann, M. A. Mazurek, G. R. Cass and B. R. Simoneit, Environ. Sci. Technol., 1993, 27, 636–651 CrossRef CAS.
- I. Suh, R. Y. Zhang, L. T. Molina and M. J. Molina, J. Am. Chem. Soc., 2003, 125, 12655–12665 CrossRef CAS.
- M. Jang and S. R. McDow, Environ. Sci. Technol., 1997, 31, 1046–1053 CrossRef CAS.
- K. Kawamura and K. Ikushima, Environ. Sci. Technol., 1993, 27, 2227–2235 CrossRef CAS.
- T. Kleindienst, M. Jaoui, M. Lewandowski, J. Offenberg and K. Docherty, Atmos. Chem. Phys., 2012, 12, 8711–8726 CrossRef CAS.
- M. Fraser, G. Cass and B. Simoneit, Environ. Sci. Technol., 2003, 37, 446–453 CrossRef CAS.
- J. J. Schauer, M. J. Kleeman, G. R. Cass and B. R. Simoneit, Environ. Sci. Technol., 1999, 33, 1578–1587 CrossRef CAS.
- Y. F. Zhang, Y. Ma, L. Qi, Z. Wang, L. P. Wang and L. Zhu, Environ. Sci., 2016, 37, 2436–2442 Search PubMed.
- C. G. Liu and C. H. Zeng, Chemosphere, 2018, 209, 560–567 CrossRef CAS.
- K. Kawamura and I. R. Kaplan, Environ. Sci. Technol., 1987, 21, 105–110 CrossRef CAS.
- W. Xu and R. Y. Zhang, J. Phys. Chem. A, 2012, 116, 4539–4550 CrossRef CAS.
- J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266 CrossRef CAS.
- R. Parthasarathi, V. Subramanian and N. Sathyamurthy, J. Phys. Chem. A, 2006, 110, 3349–3351 CrossRef CAS.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010 RSC.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, revision A.02, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- J. Elm, M. Bilde and K. V. Mikkelsen, J. Chem. Theory Comput., 2012, 8, 2071–2077 CrossRef CAS.
- H. R. Leverentz, J. I. Siepmann, D. G. Truhlar, V. Loukonen and H. Vehkamaki, J. Phys. Chem. A, 2013, 117, 3819–3825 CrossRef CAS PubMed.
- H. J. Zhang, O. Kupiainen-Määttä, X. H. Zhang, V. Molinero, Y. H. Zhang and Z. S. Li, J. Chem. Phys., 2017, 146, 184308 CrossRef.
- R. F. Bader, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1994, 116, 909–915 CrossRef CAS.
- L. Curtiss and M. Blander, Chem. Rev., 1988, 88, 827–841 CrossRef CAS.
- J. Elm, N. Myllys and T. Kurtén, J. Phys. Chem. A, 2017, 121, 4578–4587 CrossRef CAS.
- A. B. Nadykto and F. Q. Yu, Chem. Phys. Lett., 2007, 435, 14–18 CrossRef CAS.
- Y. S. Xu, A. B. Nadykto, F. Q. Yu, J. Herb and W. Wang, J. Phys. Chem. A, 2009, 114, 387–396 CrossRef.
- S.-K. Miao, S. Jiang, J. Chen, Y. Ma, Y.-P. Zhu, Y. Wen, M.-M. Zhang and W. Huang, RSC Adv., 2015, 5, 48638–48646 RSC.
- X.-Q. Peng, Y.-R. Liu, T. Huang, S. Jiang and W. Huang, Phys. Chem. Chem. Phys., 2015, 17, 9552–9563 RSC.
- W. Xu and R. Y. Zhang, J. Chem. Phys., 2013, 139, 064312 CrossRef.
- A. B. Nadykto, F. Q. Yu, M. Jakovleva, J. Herb and Y. S. Xu, Entropy, 2011, 13, 554–569 CrossRef CAS.
- Q. Zhang and L. Du, Comput. Theor. Chem., 2016, 1078, 123–128 CrossRef CAS.
- L. Du and H. G. Kjaergaard, J. Phys. Chem. A, 2011, 115, 12097–12104 CrossRef CAS.
- U. Koch and P. L. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- S. J. Grabowski, J. Phys. Org. Chem., 2004, 17, 18–31 CrossRef CAS.
- R. Y. Zhang, A. Khalizov, L. Wang, M. Hu and W. Xu, Chem. Rev., 2011, 112, 1957–2011 CrossRef.
- F. Riccobono, S. Schobesberger, C. E. Scott, J. Dommen, I. K. Ortega, L. Rondo, J. Almeida, A. Amorim, F. Bianchi and M. Breitenlechner, Science, 2014, 344, 717–721 CrossRef CAS.
- X. Ge, A. S. Wexler and S. L. Clegg, Atmos. Environ., 2011, 45, 524–546 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The minimum energy configurations of monomer. Geometric parameters of the O–H⋯O intra-molecular hydrogen bonds in the PA-containing complexes. Intra-molecular bonded OH-stretching wavenumbers and red shifts of PA-containing complexes. Atoms in molecules (AIM) parameter analysis for the intra-molecular hydrogen bonds of PA-containing complexes. Cartesian coordinates of the minimum energy configurations. See DOI: 10.1039/c9ra07398a |
| This journal is © The Royal Society of Chemistry 2019 |