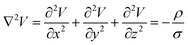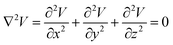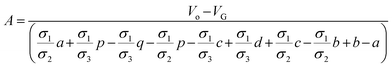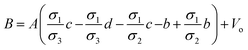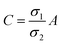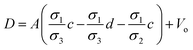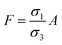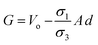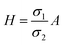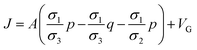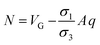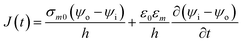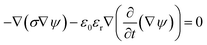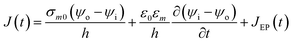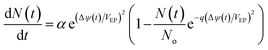DOI:
10.1039/C9RA07428G
(Paper)
RSC Adv., 2019,
9, 41518-41530
Hybrid analytical-numerical approach for investigation of differential effects in normal and cancer cells under electroporation†
Received
15th September 2019
, Accepted 5th December 2019
First published on 16th December 2019
Abstract
Electroporation has offered important biomedical applications in electrochemotherapy, tissue ablation and gene editing recently. Time and computation efficient analytical and numerical models should be developed to understand the differential effects of electroporation on normal and cancer cells. In this work, we present a hybrid analytical–numerical approach to investigate the behavior of normal and cancer cells under electroporation. We have compared the human breast cancer cell (MCF-7) and non-tumorigenic human breast cell (MCF-10A) under electroporation in terms of change in transmembrane voltage and pore formation on cell surface. The effects of electric pulse time, amplitude and membrane conductivity variation are analyzed in a systematic manner. To accelerate the calculation of transmembrane voltage, we have introduced a simple Multilayer Electric Potential Model (MEPM) which calculates the potential distribution across the cell analytically. The MEPM calculates electric potential distribution across a biological cell sandwiched between two semi-circular electrodes held at fixed potential, by solving the Laplace's equation over an equivalent planar, multilayer geometry. The MEPM model is then used in a Finite Element Method (FEM) based numerical model of electroporation. Transmembrane voltage and pore density for electroporated MCF-10A are estimated to be 1.31 V and 2.98 × 1013 m−2 respectively, and for MCF-7 the estimated values are 0.53 V and 1.93 × 1014 m−2, respectively. Our results suggest that under electroporation, the cancer cell's membrane get much more permeabilized than its counterpart normal cell even at small values of transmembrane voltage. This work provides a theoretical basis for further experimental exploration of electroporation process in cancer therapy, and serves as a design tool for performance optimization.
1. Introduction
Electroporation (EP) is a biophysical technique which induces and expands the nano-meter sized pores (nano-pores) on cell membrane when the cell is exposed to an external electric field.1,2 The nano-pores get resealed after the removal of external electric field, this process is known as reversible electroporation (REP)3–5 as shown in Fig. 1(b). However, if the electric field parameters are well above REP; the nano-pores will not be resealed after the removal of electric field, this process is known as irreversible electroporation (IRE)6,7 which deforms the cell permanently leads to cell lysis/death.8,9 The external electric field induces change in voltage/potential across the cell membrane which is termed as induced transmembrane voltage/potential (ITV).10,11
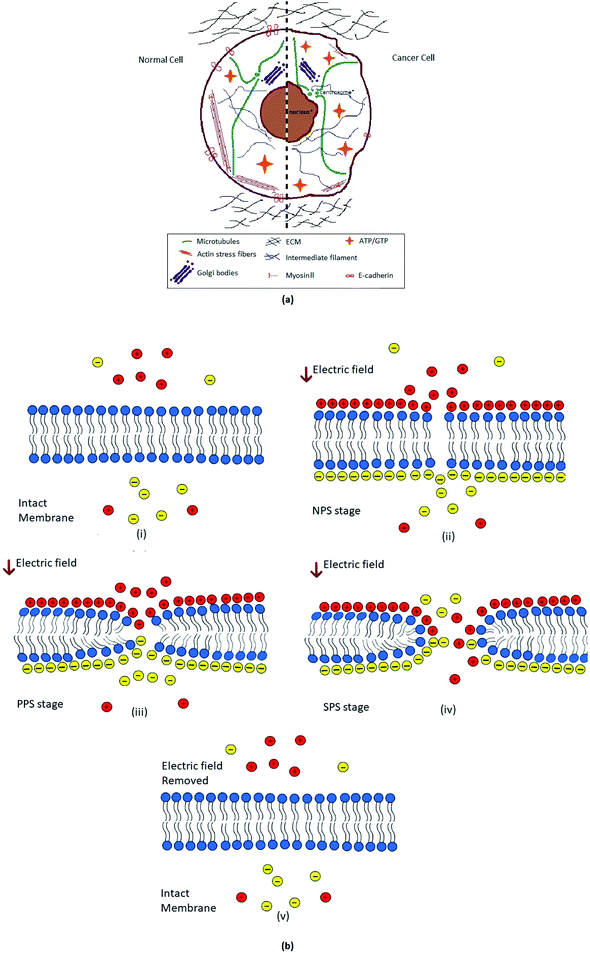 |
| | Fig. 1 (a). Schematic illustration of contrast between cancer and normal cell constituents.42 Where the comparison of normal cell and cancer cell organelles i.e. nucleus, Golgi bodies, microtubules, actin stress fibers, myosin II, and IF (intermediate filaments) etc. has been shown. Besides the ECM (extra cellular matrix), energy sources ATP/GTP and membrane protein E-cadherin, effect in both normal and tumorigenic cell has been portrayed. (b). Schematic representation of different stages of reversible electroporation; (i) when no external electric field (E-field) is experienced by biological cell's plasma membrane. Charges inside and outside the cell are freely moving. (ii) Non-permeable stage (NPS), very after applying external electric field (E-field) charges on both sides of membrane are aligned now; hydrophobic tails start tilting and deforming. (iii) Primary permeable stage (PPS), Lipid head groups of membrane started moving inside forming hydrophobic pores. (iv) Secondary permeable stage (SPS), hydrophilic pore formation and movement of charges across the cell through cell membrane. (v) After removal of electric field membrane retrieve its original intact form in few moments. | |
The electroporation effect becomes prominent and detectable only when the ITV exceeds the critical or threshold value.12,13 Cell membrane is an excellent barrier to extracellular molecules in normal physiological conditions although there is very low resting transmembrane potential and few nano-pores due to thermal fluctuations exists on the membrane surface.14 After the induction of transmembrane voltage above critical or threshold value, the nano-pores increase exponentially in number and size making cell membrane permeable to extracellular content.12 It is important to accurately determine the electric potential, ITV and pore density across the cell membrane for understanding, optimization and efficient electroporation process for different applications and cell types.
The size and pore density induced on cell membrane determines the degree and efficiency of electroporation. The size and pore density depends on many parameters but most important are electric parameters such as the field strength and duration.15 Electroporation can be effected by other parameters such as cell type and different cell properties, temperature, EP media properties, molecules to be transferred etc.,.1 Higher values of electric field strength and duration can be used for higher permeability, hence higher efficiency but cell viabilities will decrease as the strength of electric parameters increases.16 There is a tradeoff between electroporation efficiency and cell viability, however, selection of electric parameters are related to cell type and application of interest.17–19 There are EP applications where higher efficiencies and cell viabilities are required such as gene therapy,20 DNA vaccination, vascular and intraocular therapy,18 transdermal therapy,21 electro-insertion,22 electro-encapsulation,23 wound healing,24 stem cell therapy25 etc. In such applications electric field strength and duration complement each other during electroporation process5 and optimization of electric parameters are required.26,27 There are also irreversible EP applications6,7,28,29 where cell viabilities of targets are of no concern or cell death is targeted such as electrochemotherapy,30,31 cell/tissue ablation,32 electric cell lysis,9 intracellular content extraction,33 non-thermal food and liquid preservation and sterilization,34,35 electrical inactivation of microorganisms36 etc. In such applications, cell selectivity of electroporation is very important for target cells/tissues and spare as many healthy or non-target cells/tissues as possible.37,38
Normal and cancer cells have different electrical, physical, mechanical, biological and chemical properties.39 In cancer cells, the deficiency of lipoproteins in plasma membrane40 and lack of fatty acids in phospholipid make membrane more diluted, deformed and alleviated.41 This is why membrane of cancer cells is much softer, irregular, loose as compare to normal ones.39 Cancer cells showed low adhesion and less sticky surfaces than normal cells due to lack of lipoproteins on membrane surface.41 Cancer cells are found to be much softer than normal ones due to low surface tension and Young's modulus; this is why they are more vulnerable to deformation.41–43 As the membrane of cancer cell become more soft and loose, the cell loses its minerals like calcium, potassium, magnesium etc., and water become an excessive constituent.44 Cancer cells demonstrated low capacitance and higher membrane conductance as compare to normal cells.39,45,46 Cancer cells demonstrated greater permittivity, low transmembrane potential (ITV) and low impedance than normal cells.39,47–49
Schwan and Grosse50,51 developed the classical analytical model of electroporation for singular spherical cell. The model considered the constant electric field and derived the Schwan equation for transmembrane potential. This model was further extended to general analytical model to analyze temporal transmembrane potential against time varying electric fields.10,52 The initial approach treated biological cell as a single layer, which was further extended to multilayer cell model53 including different layers for inner membrane, cytoplasm, cell membrane, extracellular medium etc. for more accurate calculations.
The transmembrane potential can be determined experimentally,54 analytically10,50–53 or numerically.11,15,16,37,55,56 These analytical models are based on solution of electrostatic equations in spherical coordinates combined with multiple boundary conditions.10,50–52 Some analytical models also solved Laplace equation in other coordinates to determine solutions for regular cylinders, spheroids, and ellipsoids cell shapes.57–59 Irregular shaped cells were also analyzed deploying spherical shaped schwan model50 but discrepancies were found in achieving transmembrane potential results and waveshape.60 The calculation of potential distribution across the cell surface through these models appeared to be relatively complicated as the problem was solved in spherical and other complex coordinates. Few studies have been carried to investigate the differential effects of electroporation on normal and cancer cells.38,55,61,62 These studies suggested that electroporation is selective between normal and cancer cells in term of applied electric parameters. These studies concluded that transmembrane potential and pore density are dependent on applied electric parameters like field strength, duration and number of pulses.38,55,61,62 The time and computation efficient analytical and numerical models should be developed to understand the differential effects of electroporation on normal and cancer cells.
In this work, we present a hybrid analytical-numerical approach where we calculate induced-transmembrane-voltage analytically and use this information in a finite-element-method (FEM) based numerical scheme to calculate the pore density formation. The analytical ITV calculation is based on a simple Multilayer Electric Potential Model (MEPM) which calculates electric potential distribution across a biological cell sandwiched between two semi-circular electrodes held at fixed potential, by solving the Laplace's equation over an equivalent planar, multilayer geometry. The electric potential distribution by MEPM is in good agreement with FEM simulation results on a spherical cell. The calculated ITV from analytical MEMP is then utilized in FEM based numerical solver for pore-density estimation in normal and cancer cell. The differential effects of electroporation process on normal and cancer cell of same particular organ (breast in our case), is modelled and induced transmembrane voltage and pore densities were investigated. Effect of different parameters like cell membrane conductivity variation, amplitude of applied electric field, and time elapsed effect on electroporation were analyzed. The pore densities of normal and cancer cell after electroporation are differ by one order of magnitude and transmembrane potential of cancer cell is almost half as compare to normal cell. These results showed that under electroporation, the cell membrane of cancer cell become more permeabilized (due to many reasons discussed in later section) than its counterpart normal cell of same organ; with given constraints i.e., electrode shape, cell placement, and pulse parameters.
2. Materials and methods
2.1. Multilayer electric potential model for transmembrane voltage calculation
The non-permeable cell membrane with few nano-meter size pores prevent the exchange of content into and out of the cell's cytoplasm through the membrane. For EP, cell in electrolyte is placed between electrodes to apply external electric field. The nano-pores on the membrane of electroporated cells increases many folds after application of electric field; open then channels for exchange of contents between extracellular medium and cytoplasm.19 As single cell analysis give more insight into electrophysical phenomena;63 we considered spherical cell in electrolyte sandwiched between two semi-circular electrodes. The circular electrodes are considered in modelling due to more homogeneous exposure of electric field on cell membrane as compare to planar electrodes.64
The proposed multilayer analytical model is composed of three layers (electrolyte, cell membrane and cytoplasm) with different conductivities and permittivities. The proposed MEPM can be improved further by modelling cell organelles by increasing number of layers in model. The proposed model is not restricted to calculate potential distribution of biological cell and can be used in many other applications like potential distribution of multilayer capacitor, potential distribution of multilayer cable etc. Mostly the analytical modelling of potential distribution across cell is done in spherical coordinate system which resulted in complex solution.52,63 We derived simple analytical expressions for equivalent planar multilayer geometry instead of spherical geometry (Fig. 2(a)).
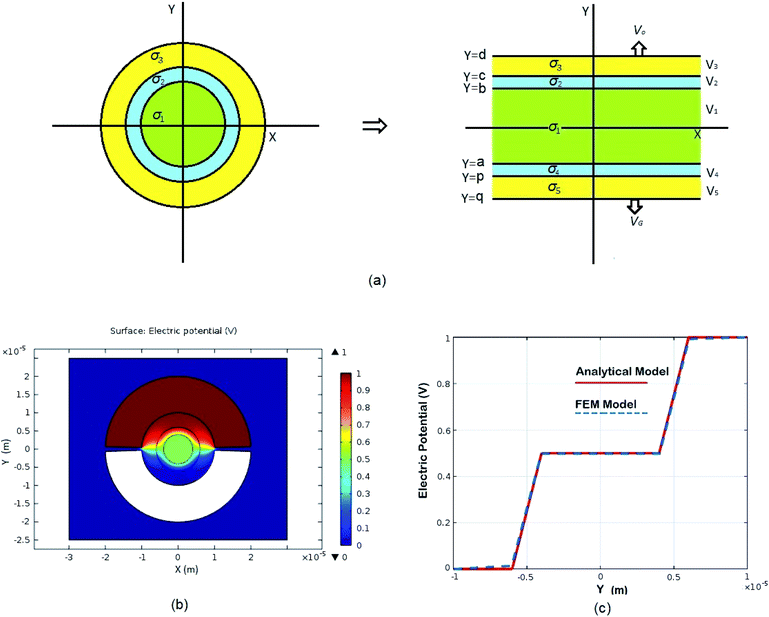 |
| | Fig. 2 Schematic of MEPM and FEM models with analysis. (a) This is a schematic for circular and its planar equivalent model of potential distribution across cell under certain conditions (i.e., for the validation of this model (1) we have to make the length of each electrode same. (2) We have to make the surfaces uniform. The uniform surfaces ensure uniform electric field which produce same potential distribution for planar model as circular model. Y = d represents the position of upper electrode (electrode of higher potential). Y = q represents the position of ground electrode. When we join region 2 to 4 and 3 to 5 circularly, they form cell membrane and cell exterior (cell medium) respectively, which gives σ3 = σ5 and σ2 = σ4. (b) FEM software results represent numerical model of general spherical biological cell encompassed by circular electrodes. (c) This is the comparison of electric potential distribution results of presented analytical model (MEPM) for biological cell under conditions and FEM model of general biological cell. | |
We derived analytical expressions for electrostatic potential distribution by solving the Laplace's equation over an equivalent planar multilayer geometry by solving the problem in Cartesian plane. The potential distribution for both planar and spherical geometries is made identical by applying two general conditions. The first condition is that the length of electrodes in each geometry should be same because by using different lengths we must solve it again in spherical domain or with conformal mapping which will make analytics more complex. The second condition is that we have to make the surfaces uniform as the uniform surfaces ensure uniform electric field which produce same potential distribution for planar model as in circular model65[ESI Fig. 1†]. If the above two conditions are not satisfied; the shape of electrode and potential applied will be non-symmetrical. In this case, the problem can be solved by the generic expression reported using conformal mapping.66
The model is solved by using Laplace equation; an extended form of Poisson equation which can be derived from Gauss's law. With the help of Gauss's law eqn (1), we obtain Poisson equation eqn (2). For source free region, the Passion's equation reduces to Laplace equation eqn (3).
| |
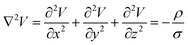 | (2) |
| |
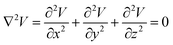 | (3) |
In order to find the potential at five different regions as you shown in Fig. 2(a). By integrating eqn (3), twice, for all five regions we get
where
V1 through
V5 represent potential in respective regions
Fig. 2(a) and the conductivity of different regions is represented with
σ1 through
σ5. The corresponding electric field intensities of each region are represented by
E1 through
E5. The
Fig. 2(a) shows a planar equivalent model of spherical biological cell. When we join region 2 to 4 and 3 to 5 circularly, they will form cell membrane and electrolyte respectively, which means in these regions the conductivity is same
i.e.,
σ3 =
σ5 and
σ2 =
σ4. By solving
eqn (4a), through
(4e) under following electrostatic boundary conditions:
| V5(q) = VG, V3(d) = VO(d), V1(b) = V2(b), |
| V2(c) = V3(c), V1(a) = V4(a), V4(p) = V5(p), |
| σ1E1(b) = σ2E2(b), σ1E1(a) = σ2E4(a), |
| σ2E2(c) = σ3E3(c), σ2E4(p) = σ3E5(p), |
All the unknowns can be found as follows:
| |
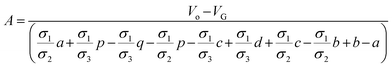 | (5a) |
| |
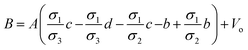 | (5b) |
| |
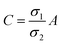 | (5c) |
| |
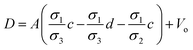 | (5d) |
| |
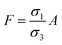 | (5e) |
| |
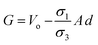 | (5f) |
| |
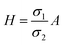 | (5g) |
| |
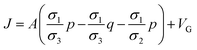 | (5h) |
| |
 | (5i) |
| |
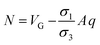 | (5j) |
The eqn (4a) through (4e) along with eqn (5a) though (5j), provides a complete analytical multilayer electric potential model (MEPM) which can be used to calculate the electric potential distribution of a spherical biological cell sandwiched in semi-circular electrodes with very simple and accurate analytics. Details of analytical modeling can be found in Appendix A of ESI document.†
2.1.1. Cell parameters determination. Electroporation of cell depends on properties of cell i.e., geometry, conductivity, permittivity, external medium, and applied electric field. Different type of cells has different electrical, physical, and geometric properties. In this paper, we will use breast normal and cancer cell parameters with spherical geometry for the modelling and simulation as the scope of paper is to develop a simple model to determine electric field distribution across cell and to analyze the contradistinctions of cancer and normal cells of particular organ under electroporation. The parameters used in the modelling and simulations in this paper are listed in Table 1.
Table 1 Values of constants and coefficients used in cancer's early detection model & in electroporation analysis
| References |
Parameters |
Description |
Values |
| 67 |
σn |
Conductivity of interior cell for MCF-10A |
0.3 S m−1 |
| 67 |
σc |
Conductivity of interior cell for MCF-7 |
0.23 S m−1 |
| 11 |
σe |
Conductivity of exterior cell medium |
0.14 S m−1 |
| |
ε0 |
Dielectric permittivity of free space |
8.85 × 10−12 As/Vm |
| 67, 68 |
εr,ni |
Permittivity of interior cell for MCF-10A |
80 |
| 68, 69 |
εr,ci |
Permittivity of interior cell for MCF-7 |
78.69 |
| |
εr,e |
Permittivity of exterior cell medium |
80 |
| 15 |
No |
Equilibrium pore density |
1.5 × 109 m−2 |
| 15 |
α |
Creation rate coefficient |
1 × 109 m−2 s−1 |
| 11 |
VEP |
Characteristic voltage of electroporation |
170 mV |
| 15 |
q |
Pore creation rate |
2.46 |
| 11, 39, 70 |
hn |
Ratio of membrane conductivity to thickness for MCF-10A |
100 S m−2 |
| 46 |
hc |
Ratio of membrane conductivity to thickness for MCF-7 |
243 S m−2 |
2.1.2. Numerical model of biological cell. As the cell membrane thickness is negligible as compare to cell size, it is very difficult to include such thin cell membrane into the numerical model. One approach is to use adaptive mesh or assign higher specific conductivity to membrane, but this will result in either exaggerated membrane thickness by few folds or an error which is difficult to estimate.In order to model cell membrane, the cell membrane is substituted by a surface and a boundary condition is assigned to this surface which is as follows:11
| |
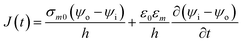 | (6) |
where
j represents the current density,
h is the thickness of membrane,
ε0 is the dielectric permittivity of free space,
εm is the relative membrane permittivity,
σm0 is the non-porated membrane conductivity,
ψi is potential inside the cell membrane surface while
ψo is potential outside the cell membrane surface. The current through the cell membrane is sum of conductive and capacitive components as shown in
eqn (6). By adopting this approach of replacing membrane with a surface to build model, we have avoided generation of very small finite elements adjacent to cell membrane. The current flows orthogonal to membrane surface as the specific conductivity of extracellular medium is higher by few order of magnitude as compare to membrane conductivity.
11 Although the cell membrane is replaced by surface, the boundary condition made sure that the electric potential drop at the surface is equivalent to the induced transmembrane potential on the membrane with
σm0 and
h.
2.2. Numerical model setup
In order to validate our MEPM analytical model, we determined the electric potential across cell in electrolyte between two semi-circular electrodes by using finite element method (FEM). For the comparison, the electric potential for normal human breast cells MCF-10A was determined using MEPM and FEM. The numerical simulations were performed in commercially available FEM package using the physics of electric current in time dependent domain. Different conductivities were assigned to cell interior (cytoplasm) and cell exterior (electrolyte) as given in Table 1. Fixed electric potential was assigned to electrodes; top electrode was assigned 1 V while the bottom electrode was set to ground. In order to compute electric potential interior and exterior of the cell, the following Poisson equation was solved:11| |
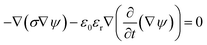 | (7) |
where ψ is electric potential, σ is the conductivity, εr is relative permittivity, and ε0 is the dielectric permittivity of free space.
2.3. Comparison of MEPM with its FEM equivalent model
MEPM analytical model can be used to determine electric potential distribution across spherical cell suspended in electrolyte in time efficient manner as compare to FEM simulations. The proposed analytical model (MEPM) can compute potential distribution in few seconds with any math simulator as we perform it in MATLAB R2017a, MathWorks®. In comparison, a good FEM simulator usually takes few tens of minutes to simulate potential distribution with high storage requirement. As the structure complexity, size and number of cells increases, the time and storage requirements by FEM simulator also increases. By using MEPM this can be achieved by varying conductivities and lengths or distances between layers in the model. We can compute potential distribution for any type of cell with different sizes with same time and resource requirement.
This MEPM analytical model can be used for modelling of different aspects of electrophysical biological processes which involve potential distribution determination. Transmembrane potential across cell membrane is required for computation of electroporation (EP) process and it can be determined from our model as the ITV is the difference between electric potential inside and outside of the cell membrane. Potential points in curve between cell medium and cell interior can give us transmembrane potential (ITV) Fig. 2(c). This model has been validated by simulating spherical cell in electrolyte between semi-circular electrode in a finite element method (FEM) for potential distribution Fig. 2(b). A negligible difference of potential is observed when we compared potential distribution determined by MEPM and its equivalent spherical FEM model as shown in Fig. 2(c).
2.4. Electroporation of cancer and normal cells – a hybrid analytical-numerical approach
When a biological cell is exposed to external electric field, transient hydrophilic pores are produced in lipid bilayer of the membrane. The density and size of pores depend on amplitude, duration and other parameters of applied electric field, the density and pore size normally increase by increasing intensity of applied electric field.19,71 Cancer cell membrane is more irregular, soft and loose than normal cells due to lack of fatty acids in phospholipid and lipoproteins in plasma membrane.40,41 Cancer cells are deficient in minerals and ions as these minerals and ions diffused out of the permeable membrane which is non-permeable and more rigid in normal cells.42,44,72 Due to altered cell membrane composition, cancer cells have low surface tension, low Young's modulus and less adhesion; cancer cells deformed more as compare to normal cells.41,42,43,73 Due to different biological, chemical and physical properties of cancer cells, their electrical properties are also different from normal cells. Cancer cell have overall low capacitance,45 higher membrane conductance,46 high permittivity, low transmembrane potential (ITV) and low impedance than normal cells.39,47–49 As electroporation is electrophysical phenomena, it can be used to discriminate cancer and normal cells due to their different physical and electrical properties.
2.4.1. Electroporation process. Electroporation process is generally divided in three stages that are non-permeable stage (NPS), primary-permeable stage (PPS) and secondary-permeable stage (SPS).74,75 During NSP stage, the applied electric field is below critical value, the hydrophobic tails of lipid bilayer membrane become tilted or starts to deform. At this stage, no mobilization across the membrane establishes. During PPS stage, hydrophobic pores forms and cell membrane become permeable under the influence of electric field above critical value. During SPS stage, hydrophobic pores transforms into hydrophilic pores and the cell membrane become more permeable and the conductivity of the cell membrane increases11,74,76 Fig. 1(b). If we further increase the intensity of the electric field, the pores will not be resealed after the removal of electric field, causes the permanent cell deformation or cell burst/cell lysis.77
2.4.2. Electroporation model. Pores size and density increase exponentially when intensity of applied electric field is above its critical value.75 The new conducting pathways are formed in the form of pores which result in inclusion of extra term in transmembrane current density J in eqn (6). The eqn (6) can be modified as:11| |
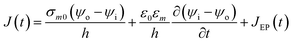 | (8) |
JEP can be written in the simplest form as JEP(t) = iEP(t) + N(t) where iEP is the current through the single pore15 and N is the pore density given by following differential equation:15,78
| |
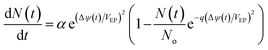 | (9) |
where
α is creation rate coefficient,
No is equilibrium pore density,
VEP is characteristic voltage of electroporation (EP) and
q is pore creation rate and Δ
ψ is induced transmembrane voltages given by
eqn (10). The values of constants for
eqn (9) is given in
Table 1. The realistic range of
α (0.9 × 10
9 m
−2 s
−1 to 2 × 10
9 m
−2 s
−1 (ref. 15)) did not affect the simulation results significantly, so we set the value of
α to 1 × 10
9 m
−2 s
−1. The pore conductivity (inside pore) and its radius were assumed constant in order to simulate
eqn (9).
11 Complete details regarding derivation of
eqn. (8) and
(9) and selection of different constants values can be found in
15,78, and.
11
The induced transmembrane potential was calculated as the difference between electric potential inside and outside the boundary surface as follows:
| | |
Δψ = Δψi(t) − Δψo(t)
| (10) |
where
ψi is potential inside the cell and
ψo is potential outside the cell. All the parameters used in numerical simulations are provided in
Table 1.
3. Results and discussion
3.1. Factors effecting electroporation
3.1.1. Effect of membrane conductance. Membrane conductivity of a normal cell ranges between 10−6–10−7 S m−1 (ref. 11, 79) depending upon cell membrane properties. Application of electric field on cell causes stress on cell surface [ESI Fig. 2 and 3†], which results in membrane conductivity increment that ultimately leads to pore formation.11 Membrane deformation of cancer cell affects its conductivity and adhesiveness.39,41 We simulated a normal breast cell MCF-10A model at different membrane conductivities starting from nonrealistic (10−3 S m−1) to realistic cell membrane conductivities (in this case 10−6 S m−1) and witnessed the effect of membrane conductivity on the pore formation and electric potential distributions on cell surface as shown in Fig. 3(a and b). We performed this simulation at low voltage to make sure that pore formation and electric potential distributions varies only due to the membrane conductivity and not by the electroporation itself. At such low voltage for realistic cell membrane conductivity (of the order of 10−6 S m−1), the pore density is almost identical to equilibrium pore density as shown in Fig. 3(c and d). Details are in [ESI Fig. 4†].
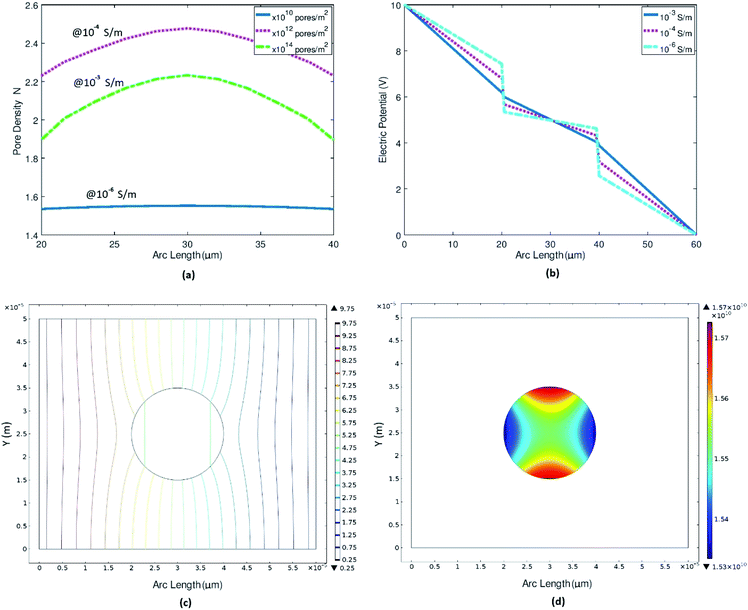 |
| | Fig. 3 Representing the trend of pore densities and electric potential with variation in the cell membrane conductivity. (a) Pore density variation w.r.t to cell membrane conductivities ranges from non-realistic 10−3 S m−1 to realistic 10−6 S m−1. (b) Electric potential distribution across cell surface at different cell membrane conductivities. (c) Electric potential contour plot at realistic cell membrane conductivity i.e., 10−6 S m−1. (d) Surface plot for pore density at realistic cell membrane conductivity. | |
When the conductivity is very high (of the order of 10−3 S m−1), we can see the total passage of potential through the cell [ESI Fig. 4†]. The resultant pore density is high as the membrane shows very low resistance or dielectric barrier which can be seen clearly in 1-D electric potential plot across the membrane region Fig. 3(b). As the membrane conductivity decreases and approaches realistic cell membrane conductivity, its show high dielectric barrier as shown in Fig. 3(b). Cancer cell loses its minerals like calcium, potassium, magnesium etc.; water become an excessive constituent44 and cancer cell membrane is more soft and more permeable as compare to normal cell membrane. Due to altered membrane composition, cancer cells have higher membrane conductance as compare to normal cell.46 These simulations clearly indicate that even at applied electric field lower than critical electric field required for EP, if the membrane conductivity is higher then pores form will also be higher, which validates our next part of numerical experiments i.e., pore density of cancer cells will be higher as compare to normal cells and even more higher after EP.
3.1.2. Effect of electric field. A test electric potential range is utilized to check its effect on electroporation (EP) from 5 V to 400 V or respective electric field (EF) almost 0 kV cm−1 to 70 kV cm−1 Fig. 4(a). Detail plots at all potential ranges are in [ESI Fig. 5†]. As you can see in Fig. 4(a), the 1-D plot that there is a nonlinear increase in the pore densities if you increase EF very high above the critical value as pore density is the function of ITV and ITV is the function of EF. This is because when we increase the EF, conductivity of the membrane increases11,80 which cause transmembrane potential (ITV) to decrease11,81 that leads to more pore formation. Induced transmembrane voltage (ITV) decrement is also analyzed as the no. of pore increases due to the increase in applied E-field showed in [ESI Fig. 6†]. Electric field in actual numerical experimentation of normal and cancer cell, 16 kV cm−1 is used.
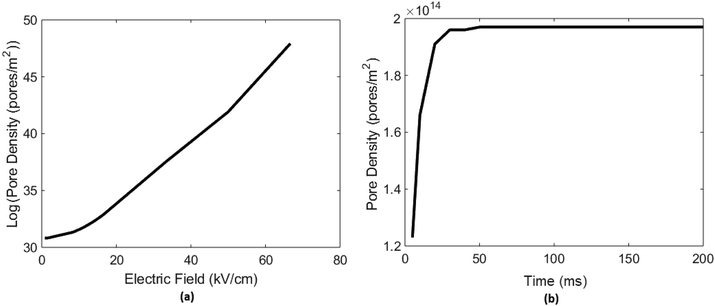 |
| | Fig. 4 Represents effect of electric field applied and time of applied pulse on electroporation or pore densities. (a) Shows variation of electroporation (EP) or pore densities with the increasing effect of applied electric field (EF) ranges up to 70 kV cm−1 (increment in EF cause increase in ITV which leads to EP or pore formation and once pores are form, ITV gradually decreases as pore density increases). (b) Represents if we increase the time of applied pulse 100 V here, pore density on cell surface increases up to a saturation level which is in this result is 50 ms. | |
3.1.3. Effect of applied pulse time. If the time of applied pulse is increased, no. of pores on cell surface increases up to a saturated level Fig. 4(b). After that there will be no increment in pore formation on cell surface until we increase the amplitude/intensity of E-Field applied which may lead to cell lysis or irreversible cell deformation then. A numerical analysis on cell electroporation (EP) vs time of applied pulse up to 200 ms is performed on breast cancer cell MCF-7, detailed plots at every time set can be found in ESI files [ESI Fig. 7†]. Results showed that no. of pores or pore density increased up to 50 ms and after that it became constant Fig. 4(b). On the basis of these results all simulations were performed for minimum 50 ms to get stabilized and constant results.The numerical model of electroporation (EP), by above mention equations, will lead us toward diversified multi-applications, one of them is understanding of why cancer cell behaves differently under electro-chemotherapy and calcium electroporation. By solving induced transmembrane voltage (ITV) and pore densities for cancer and normal cell pair with constant constraints; one can differentiate cancer and normal cell of particular organ clearly. Cancer cell shows more pore on its surface when undergo electroporation (EP) than normal cell and has less transmembrane voltages (ITV) than normal cell.
3.2. Pore densities & ITV of cancer and normal cell and comparison
It is observed as well as predicted in previous studies41,42,82 that cancer cells have discrete and more divergent biological, chemical, physical, electrical etc. properties than normal cells. But their effect is not truly utilized in biomedical engineering for cancer treatment.
So, two numerical experiments were performed with cancer and normal cell of same organ, breast in our case, to examine the clear contrast of their behavior under electroporation. As well as the normal and cancer cell counterparts (or both of same organ) were modeled for excellent scrutinizing and phenotyping. We made numerical model of normal breast cell MCF-10A and its cancerous counterpart MCF-7 which is a malignant breast carcinoma cell. Then we perform numerical electroporation (EP) experiment on them to observe the tendencies of pore densities and transmembrane potential (ITV). As you can see the Fig. 5, which show pore densities results of MCF-10A both 1-D and surface plots which portrays pore 1013 of the range per m sq. and for cancer cell is its observed at a range of 1014 per m sq.
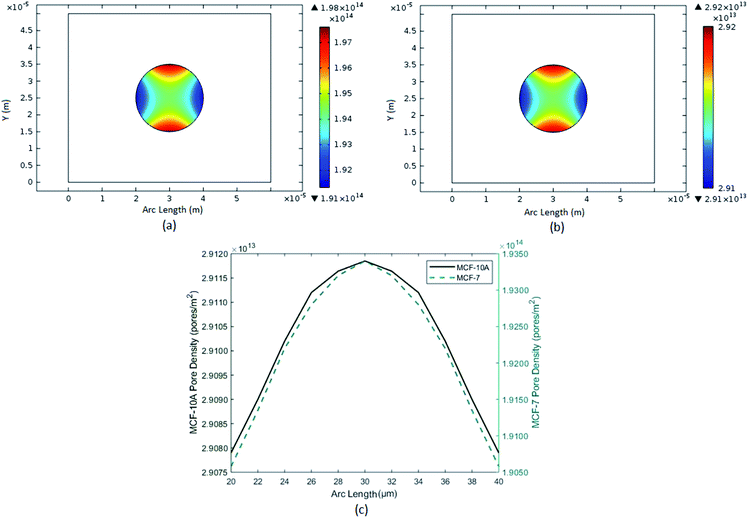 |
| | Fig. 5 Represent the pore densities of breast cancer cell MCF-7 and breast normal cell MCF-10A. (a) Surface plot of pore densities of breast cancer cell MCF-7. (b) Surface plot of pore densities of breast normal cell MCF-10A. (c) Comparison of 1-D plot of pore densities of breast cancer and normal cells. | |
Transmembrane potential (ITV) of cell is not same throughout the cell surface. Its shows maximum value where the EF intensity is high otherwise it tends to zero. Transmembrane potential (ITV) of normal breast cell MCF-10A Fig. 6, was in a range around 1.4 V but for cancerous breast cell MCF-7, it is more than 0.52 V. Combined plots of both findings are also attached for clear comparison.
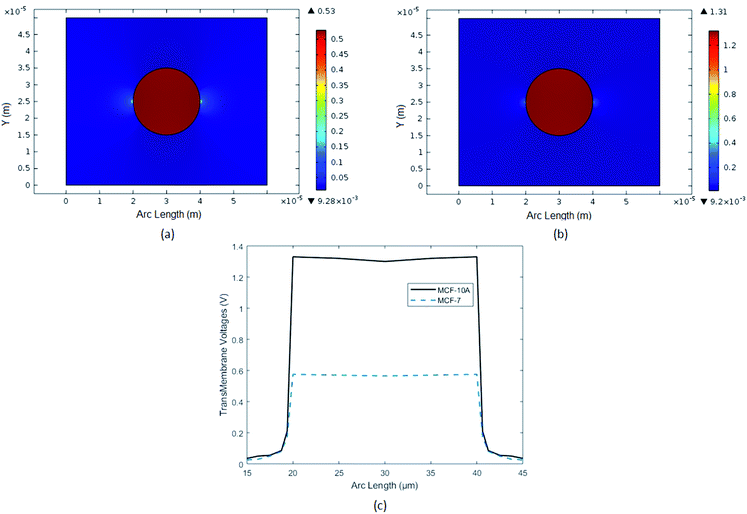 |
| | Fig. 6 In above figure, Induced Transmembrane Voltage (ITV) of breast cancer cell (MCF-7) and breast normal cell (MCF-10A) are analyzed. (a) Surface plot of ITV of breast cancer cell MCF-7. (b) Surface plot of ITV of breast normal cell MCF-10A. (c) Comparison with 1-D plots of ITV of breast cancer and normal cells. | |
3.3. Discussion
Cancer and normal cell contradistinctions as elaborated in previous works are categorized here in detail.
3.3.1. Electrical. Cancer cell have overall low capacitance45 and higher membrane conductance than normal cell.46 Cancer cells demonstrated greater permittivity, low transmembrane potential (ITV) and low impedance than normal cells.39,47–49
3.3.2. Physical and mechanical. Cancer cells have less adhesion or less sticky surfaces than normal cell due to lack of lipoproteins on membrane surface.41 Due to low surface tension and low Young's modulus, cancer cells are more vulnerable to deformation. Due to low Young's modulus, cancer cells are much softer than normal ones and keep on changing their shape.41–43,73 Plasma membrane become softer in cancer cells72 and because of that cell loses its rigidity.42
3.3.3. Biological and chemical. In cancer cells, the deficiency of lipoproteins e.g. E-cadherin, in plasma membrane40 and lack of fatty acids in phospholipid make membrane more diluted, deformed and alleviated41 as compare to normal cells. Permeability increases in cancer cells due to change in composition of phospholipids. The abnormal extracellular matrix (ECM) and intermediate filaments in cancer cell add direct stiffness to cell. The imbalance heat source ATP or GTP are also assumed to add stiffness indirectly in cancer cell. Consequently, deformed cell structure, relatively soft morphology and loose membrane results in carcinogenesis83,84 as shown in Fig. 1(a),.42 Membrane of cancer cell become soft and more permeable as the cell loses its minerals like calcium, potassium, magnesium etc.; water and sodium become an excessive constituent.44The above discussed behavior of cancer cell and healthy cell can lead us to clear and better understanding that why cancer cells behave differently under biological manipulations. Due to the differences of cell level statistics practitioner can make accurate predictions about disease proliferation and treatment method. Because cancer cells tend to show high pore densities and low transmembrane voltages due to many reasons of changed cell morphology discussed above with detail like high permittivity, low transmembrane voltages and low impedance etc. And high permittivity is an ability to resist the formation of electric potential. These are the perspicuous differences in the electrical properties of cancer cell which ultimately leads to more pore formation when the cancer cell comes under the influence of external EF; and less transmembrane voltages (ITV) as well. And due to decrement in the field gradient the free energy barrier decreases for pore formation.76,85 All these differences are because of some facts that are; cancer cells are much softer than the normal cells,42 when come under the influence of external force like EF etc. and undergo electroporation, this become one of the reason of more pore formation. Cancer cell's surface tension is much less than that of normal one and the water content is high. As discussed above that water is the primary source in the formation of pores on cell surface. Higher the water level, higher will be the tendency of pore formation and low transmembrane voltage (ITV) due to lack of ions formed by minerals86 and that become a cause which make them much more loose and less sticky which ultimately make them more prone to lose transmembrane potential (ITV) and high pore formation.
In the view of above discussions and these numerical experiments, the results obtained lead us to much better understanding of cancer cell morphology change under biological manipulation. Such results for cancer and normal cells of same organs are not yet reported with the technique of reversible electroporation (REP) for the analysis and investigation of heterogeneities. Some discrepancies observed those are, the difference of pore densities of cancer cell and normal cell should be a bit higher than that of reported and the transmembrane voltages (ITV) in case of cancer cell should be in the middle of 0.5 V and 1 V. Our results are pretty much close to this but not exactly match that is because of modeling limitations, that we did not model cell interior; like mitochondria, Golgi bodies, their membranes etc. This can be improved with much more detail modeling and we can get very interesting result by practically experimenting it as cheapest 3D Nano-spike electroporation device (NSP-EP) has been reported by us.16 So expensive equipment is no longer a big deal now.
4. Conclusion
A novel multilayer electric potential model (MEPM) of biological cell under electrodes boundary has been introduced which is primitive part of electroporation. The advantage of our model is that it is a simplistic model and applicable under both spherical and planar domain considering two conditions as discussed. The analytical MEMP model has been validated against potential distribution of numerical model of cell and the results were in good agreement. MEMP has been introduced to get an easy and flexible way to find potential distribution across the cell in short time instead of long-awaited FEM simulations. Electroporation of biological cell was explained in detail with the analysis of the factors by whom it influenced which includes; time of applied pulses, membrane conductivity variations and the amplitude of applied field. First time ever the electroporation of cancer and normal cell pair of same organ, breast cancer cell (MCF-7) and breast normal cell (MCF-10A), was numerically modeled to investigate the how and why cancer cell behave differently under biological manipulation. The results depicted that cancer cell get ten times more pores on its surface and less than half transmembrane potential than its normal counterpart. This assured that under biological manipulation cancer cell behaves as divergent unlike healthy cell. Indeed, it is a cheaper and much accurate way to analyze behavioral dissimilarities under the influence of electrical stimulus because it deals with cell level dissimilarities to examine fatal disease like cancer here. For future research, this method can be improved by introducing analytical model of pore formation and then testing electroporation model against practical experiment results using same organ's normal and malignant cells as we did numerically in this research, for correct understandings of cell abnormalities.
Conflicts of interest
There is no conflict of interest between authors.
Notes and references
- D. C. Chang, Guide to electroporation and electrofusion, Academic Press, 1992 Search PubMed.
- J. C. Weaver, IEEE Trans. Plasma Sci., 2000, 28, 24–33 CrossRef CAS.
- R. W. Glaser, S. L. Leikin, L. V. Chernomordik, V. F. Pastushenko and A. I. Sokirko, Biochim. Biophys. Acta, Biomembr., 1988, 940, 275–287 CrossRef CAS.
- A. Barnett and J. C. Weaver, Bioelectrochem. Bioenerg., 1991, 25, 163–182 CrossRef CAS.
- K. J. Müller, V. L. Sukhorukov and U. Zimmermann, J. Membr. Biol., 2001, 184, 161–170 CrossRef.
- B. Rubinsky, Technol. Cancer Res. Treat., 2007, 6, 255–260 CrossRef.
- P. G. K. Wagstaff, M. Buijs, W. van den Bos, D. M. de Bruin, P. J. Zondervan, J. J. M. C. H. de la Rosette and M. P. Laguna Pes, OncoTargets Ther., 2016, 9, 2437–2446 CrossRef CAS PubMed.
- B. Morshed, M. Shams and T. Mussivand, CRC Crit. Rev. Bioeng., 2013, 41, 37–50 Search PubMed.
- H. Lu, M. A. Schmidt and K. F. Jensen, Lab Chip, 2005, 5, 23–29 RSC.
- T. Kotnik, D. Miklavčič and T. Slivnik, Bioelectrochem. Bioenerg., 1998, 45, 3–16 CrossRef CAS.
- G. Pucihar, D. Miklavčič and T. Kotnik, IEEE Trans. Biomed. Eng., 2009, 56, 1491–1501 Search PubMed.
- J. Teissié and M. P. Rols, Biophys. J., 1993, 65, 409–413 CrossRef.
- T. Kotnik, G. Pucihar and D. Miklavčič, J. Membr. Biol., 2010, 236, 3–13 CrossRef CAS.
- J. C. Shillcock and U. Seifert, Biophys. J., 1998, 74, 1754–1766 CrossRef CAS.
- K. A. DeBruin and W. Krassowska, Biophys. J., 1999, 77, 1213–1224 CrossRef CAS.
- K. Riaz, S. F. Leung, Z. Fan and Y. K. Lee, Sens. Actuators, A, 2017, 255, 10–20 CrossRef CAS.
- W. G. Lee, U. Demirci and A. Khademhosseini, Integr. Biol., 2009, 1, 242–251 CrossRef CAS.
- S. B. Dev, D. P. Rabussay, G. Widera and G. A. Hofmann, IEEE Trans. Plasma Sci., 2000, 28, 206–223 CrossRef CAS.
- D. Miklavčič, Handbook of Electroporation, 2017, vol. 1–4 Search PubMed.
- Y. Isaka and E. Imai, Expert Opin. Drug Delivery, 2007, 4, 561–571 CrossRef CAS PubMed.
- A. K. Banga, Electrically assisted transdermal and topical drug delivery, Taylor & Francis Group, 1998 Search PubMed.
- Y. Mouneimne, P.-F. Tosi, R. Barhoumi and C. Nicolau, Biochim. Biophys. Acta, Biomembr., 1991, 1066, 83–89 CrossRef CAS.
- N. Crawford and N. Chronos, Semin. Interv. Cardiol., 1996, 1, 91–102 CAS.
- M. Ferguson, C. Byrnes, L. Sun, G. Marti, P. Bonde, M. Duncan and J. W. Harmon, World J. Surg., 2005, 29, S55–S59 CrossRef PubMed.
- M. Costa, M. Dottori, K. Sourris, P. Jamshidi, T. Hatzistavrou, R. Davis, L. Azzola, S. Jackson, S. M. Lim, M. Pera, A. G. Elefanty and E. G. Stanley, Nat. Protoc., 2007, 2, 792–796 CrossRef CAS.
- H. He, D. C. Chang and Y.-K. Lee, Bioelectrochemistry, 2007, 70, 363–368 CrossRef CAS PubMed.
- K. Riaz, S.-F. Leung, H. Shagoshtasbi, Z. Fan and Y.-K. Lee, in 10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, IEEE, 2015, pp. 263–267 Search PubMed.
- C. Jiang, R. V. Davalos and J. C. Bischof, IEEE Trans. Biomed. Eng., 2015, 62, 4–20 Search PubMed.
- M. Shahini and J. T. W. Yeow, in 10th IEEE International Conference on Nanotechnology, IEEE, 2010, pp. 607–610 Search PubMed.
- D. Miklavčič, G. Serša, E. Brecelj, J. Gehl, D. Soden, G. Bianchi, P. Ruggieri, C. R. Rossi, L. G. Campana and T. Jarm, Med. Biol. Eng. Comput., 2012, 50, 1213–1225 CrossRef PubMed.
- D. Miklavčič, B. Mali, B. Kos, R. Heller and G. Serša, Biomed. Eng. Online, 2014, 13, 1–20 CrossRef PubMed.
- R. V. Davalos, L. M. Mir and B. Rubinsky, Ann. Biomed. Eng., 2005, 33, 223–231 CrossRef CAS PubMed.
- G. Mernier, R. Martinez-Duarte, R. Lehal, F. Radtke and P. Renaud, Micromachines, 2012, 3, 574–581 CrossRef.
- H. Vega-Mercado, O. Martín-Belloso, B.-L. Qin, F. J. Chang, M. Marcela Góngora-Nieto, G. V. Barbosa-Cánovas and B. G. Swanson, Trends Food Sci. Technol., 1997, 8, 151–157 CrossRef CAS.
- K. Reineke, F. Schottroff, N. Meneses and D. Knorr, Front. Microbiol., 2015, 6, 400 Search PubMed.
- I. Álvarez, S. Condón and J. Raso, Microbial Inactivation by Pulsed Electric Fields, Springer, Boston, MA, 2006, pp. 97–129 Search PubMed.
- A. Županič and D. Miklavčič, Optimization and Numerical Modeling in Irreversible Electroporation Treatment Planning, Springer, Berlin, Heidelberg, 2010, pp. 203–222 Search PubMed.
- H. B. Kim, S. Lee, Y. Shen, P.-D. Ryu, Y. Lee, J. H. Chung, C. K. Sung and K. Y. Baik, Biochem. Biophys. Res. Commun., 2019, 517, 703–708 CrossRef CAS PubMed.
- S. Haltiwanger, The Rife 2003 International Conference in Seattle, Washington, 2003, vol. 17.06, pp. 7–23 Search PubMed.
- T. Betz, M. Lenz, J.-F. Joanny and C. Sykes, Proc. Natl. Acad. Sci. U. S. A., Early Ed., 2009, 106, 15320–15325 CrossRef CAS.
- M. Abercrombie and E. Ambrose, Cancer Res., 1962, 525–548 CAS.
- C. Alibert, B. Goud and J. B. Manneville, Biol. Cell., 2017, 109, 167–189 CrossRef PubMed.
- C. Händel, B. U. S. Schmidt, J. Schiller, U. Dietrich, T. Möhn, T. R. Kießling, S. Pawlizak, A. W. Fritsch, L.-C. Horn, S. Briest, M. Höckel, M. Zink and J. A. Käs, New J. Phys., 2015, 17, 083008 CrossRef.
- R. A. Charman, in Clayton's Electrotherapy, WB Saunders Company Ltd, 10th edn, 1996 Search PubMed.
- G. Qiao, W. Duan, C. Chatwin, A. Sinclair and W. Wang, J. Phys.: Conf. Ser., 2010, 224, 1 CrossRef.
- G. Bahrieh, M. Erdem and U. Gunduz, Analysis of changes in dielectric properties of doxorubicin-resistant breast cancer cell through electroporation of 3D electrodes, 2014, vol. 1, pp. 1–4 Search PubMed.
- R. C. Niemtzow 1942-, Transmembrane potentials
and characteristics of immune and tumor cells, ed. Richard C. Niemtzow, CRC Press, Boca Raton, Fla, 1985 Search PubMed.
- B. Blad and B. Baldetorp, Physiol Meas., 1996, 17(Suppl 4), A105–A115 CrossRef PubMed.
- R. G. Stern, B. N. Milestone and R. A. Gatenby, Med. Hypotheses, 1999, 52, 367–372 CrossRef CAS PubMed.
- H. P. Schwan, in Advances in biological and medical physics, Elsevier, 1957, vol. 5, pp. 147–209 Search PubMed.
- C. Grosse and H. P. Schwan, Biophys. J., 1992, 63, 1632–1642 CrossRef CAS PubMed.
- T. Kotnik and D. Miklavcic, IEEE Trans. Biomed. Eng., 2000, 47, 1074–1081 CrossRef CAS PubMed.
- C. Yao, D. Mo, C. Li, C. Sun and Y. Mi, IEEE Trans. Plasma Sci., 2007, 35, 1541–1549 CAS.
- M. Hibino, H. Itoh and K. Kinosita Jr, Biophys. J., 1993, 64, 1789 CrossRef CAS PubMed.
- O. Henao, V. Gómez, I. De Pava and J. Sánchez, Simulation of Normal and Cancerous T-cell Membrane Electroporation, 2014, pp. 1–4 Search PubMed.
- C. Yao, H. Liu, Y. Zhao, Y. Mi, S. Dong and Y. Lv, IEEE Trans. Plasma Sci., 2017, 45, 889–900 CAS.
- J. Bernhardt and H. Pauly, Biophysik, 1973, 10, 89–98 CAS.
- T. Kotnik and D. Miklavcic, Biophys. J., 2000, 79, 670 CrossRef CAS PubMed.
- J. Gimsa and D. Wachner, Biophys. J., 2001, 81, 1888–1896 CrossRef CAS PubMed.
- T. Murovec, D. C. Sweeney, E. Latouche, R. V Davalos and C. Brosseau, Biophys. J., 2016, 111, 2286–2295 CrossRef CAS PubMed.
- W. Yang, Y.-H. Wu, D. Yin, H. P. Koeffler, D. E. Sawcer, P. T. Vernier and M. A. Gundersen, Technol. Cancer Res. Treat., 2011, 10, 281–286 CrossRef CAS PubMed.
- S. K. Frandsen, M. B. Krüger, U. M. Mangalanathan, T. Tramm, F. Mahmood, I. Novak and J. Gehl, Cancer Res., 2017, 77, 4389–4401 CrossRef CAS PubMed.
- S. Movahed and D. Li, J. Membr. Biol., 2013, 246, 151–160 CrossRef CAS PubMed.
- M. Wang and W. Chang, Effect of Electrode Shape on Impedance of Single HeLa Cell: A COMSOL Simulation, BioMed Res. Int., 2015, 871603 Search PubMed.
- W. H. Hayt and J. J. A. Buck, 2001, ch. 3–4.
- S. B. Cahn, B. E. Nadgorny and P. D. Scholten, Am. J. Phys., 1995, 63, 861 CrossRef.
- J. An, J. Lee, S. H. Lee, J. Park and B. Kim, Anal. Bioanal. Chem., 2009, 394, 801–809 CrossRef CAS PubMed.
- M. P. Rols, C. Delteil, M. Golzio and J. Teissié, Eur. J. Biochem., 1998, 254, 382–388 CrossRef CAS PubMed.
- I. Guido, M. S. Jaeger and C. Duschl, Eur. Biophys. J., 2011, 40, 281–288 CrossRef PubMed.
- H. Watson, Essays Biochem., 2015, 59, 43–69 CrossRef PubMed.
- S. Kee, J. Gehl and E. Lee, Clinical Aspects of Electroporation, 2011, ch:1–6 Search PubMed.
- H. N. Green, Acta Unio Int. Cancrum, 1961, 17, 215 CAS.
- Y. Li, J. Schnekenburger and M. H. G. Duits, J. Biomed. Opt., 2009, 14, 064005 CrossRef PubMed.
- H. Shagoshtasbi, P. Deng and Y.-K. Lee, J. Lab. Autom., 2015, 20, 481–490 CrossRef CAS PubMed.
- K. Riaz, S.-F. Leung, Z. Fan and Y.-K. Lee, Sens. Actuators, A, 2017, 255, 10–20 CrossRef CAS.
- R. A. Böckmann, B. L. De Groot, S. Kakorin, E. Neumann and H. Grubmüller, Biophys. J., 2008, 95, 1837–1850 CrossRef PubMed.
- K. Riaz, S.-F. Leung, Z. Fan and Y.-K. Lee, J. Microelectromech. Syst., 2017, 26, 910–920 CAS.
- J. C. Neu and W. Krassowska, Phys. Rev. E, 1999, 59, 3471–3482 CrossRef CAS.
- R. Milo and R. Phillips, Cell Biology by the Numbers, 2015, ch. 1–2 Search PubMed.
- A. G. Pakhomov, D. Miklavcic and M. S. Markov, Advanced Electroporation Techniques in Biology and Medicine, 2010, ch. 10, p. 201 Search PubMed.
- A. G. Pakhomov, D. Miklavcic and M. S. Markov, Advanced Electroporation Techniques in Biology and Medicine, 2010, ch. 7, p. 141 Search PubMed.
- A. B. Harvey Lodish, B. Arnold and C. A. Kaiser and M. Krieger, Molecular Cell Biology, 2016, 8th edn, ch. 24, p. 1135 Search PubMed.
- D. Boss, A. Hoffmann, B. Rappaz, C. Depeursinge, P. J. Magistretti, D. van de Ville and P. Marquet, PLoS One, 2016, 32, 8574–8582 Search PubMed.
- P. G. Seeger and S. Wolz, Successful biological control of cancer by combat against the causes, Neuwieder Verlagsgesellschaft, 1992 Search PubMed.
- D. P. Tieleman, BMC Biochem., 2004, 5, 1–12 CrossRef PubMed.
- D. B. Agus, J. F. Alexander, W. Arap, S. Ashili, J. E. Aslan, R. H. Austin, V. Backman, K. J. Bethel, R. Bonneau, W. C. Chen, C. Chen-Tanyolac, N. C. Choi, S. A. Curley, M. Dallas, D. Damania, P. C. W. Davies, P. Decuzzi, L. Dickinson, L. Estevez-Salmeron, V. Estrella, M. Ferrari, C. Fischbach, J. Foo, S. I. Fraley, C. Frantz, A. Fuhrmann, P. Gascard, R. A. Gatenby, Y. Geng, S. Gerecht, R. J. Gillies, B. Godin, W. M. Grady, A. Greenfield, C. Hemphill, B. L. Hempstead, A. Hielscher, W. D. Hillis, E. C. Holland, A. Ibrahim-Hashim, T. Jacks, R. H. Johnson, A. Joo, J. E. Katz, L. Kelbauskas, C. Kesselman, M. R. King, K. Konstantopoulos, C. M. Kraning-Rush, P. Kuhn, K. Kung, B. Kwee, J. N. Lakins, G. Lambert, D. Liao, J. D. Licht, J. T. Liphardt, L. Liu, M. C. Lloyd, A. Lyubimova, P. Mallick, J. Marko, O. J. T. McCarty, D. R. Meldrum, F. Michor, S. M. Mumenthaler, V. Nandakumar, T. V. O'Halloran, S. Oh, R. Pasqualini, M. J. Paszek, K. G. Philips, C. S. Poultney, K. Rana, C. A. Reinhart-King, R. Ros, G. L. Semenza, P. Senechal, M. L. Shuler, S. Srinivasan, J. R. Staunton, Y. Stypula, H. Subramanian, T.
D. Tlsty, G. W. Tormoen, Y. Tseng, A. Van Oudenaarden, S. S. Verbridge, J. C. Wan, V. M. Weaver, J. Widom, C. Will, D. Wirtz, J. Wojtkowiak and P. H. Wu, Sci. Rep., 2013, 3, 1449 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra07428g |
| ‡ Co-first authors with equal contribution. |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Muhammad Qasim Mahmood and
Muhammad Zubair
*,
Muhammad Qasim Mahmood and
Muhammad Zubair *
*