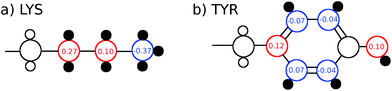Open Access Article
Open Access ArticleChanges in protein hydration dynamics by encapsulation or crowding of ubiquitin: strong correlation between time-dependent Stokes shift and intermolecular nuclear Overhauser effect
Philipp Honegger†
 ,
Esther Heid†
,
Esther Heid† ,
Stella Schmode
,
Stella Schmode ,
Christian Schröder
,
Christian Schröder and
Othmar Steinhauser
and
Othmar Steinhauser *
*
University of Vienna, Faculty of Chemistry, Department of Computational Biological Chemistry, Währingerstr. 17, A-1090 Vienna, Austria. E-mail: os@mdy.univie.ac.at
First published on 13th November 2019
Abstract
The local changes in protein hydration dynamics upon encapsulation of the protein or macromolecular crowding are essential to understand protein function in cellular environments. We were able to obtain a spatially-resolved picture of the influence of confinement and crowding on the hydration dynamics of the protein ubiquitin by analyzing the time-dependent Stokes shift (TDSS), as well as the intermolecular Nuclear Overhauser Effect (NOE) at different sites of the protein by large-scale computer simulation of single and multiple proteins in water and confined in reverse micelles. Besides high advanced space resolved information on hydration dynamics we found a strong correlation of the change in NOE upon crowding or encapsulation and the change in the integral TDSS relaxation times in all investigated systems relative to the signals in a diluted protein solution.
1 Introduction
The interactions of biomolecules such as proteins with the environment are crucial for their functionality. For example, the formation of hydrogen bonds to the surrounding water molecules is mandatory to build the three-dimensional protein structures responsible for biological activity.1 Furthermore, transport mechanisms strongly depend on processes like hydration and encapsulation, e.g. necessary to channel enzymes into a cell passing biomembranes.2During the last decades, the solvation of biomolecules such as proteins has been studied extensively, where mainly diluted samples in buffer solutions were examined.1,3–5 However, living matter usually features a crowded and confined matrix.6 In biological cells, a variety of solutes is present at high concentrations.7 The resulting macromolecular crowding was shown to induce a slowing down8–10 and/or diminishing11,12 of protein hydration. The encapsulation of biomolecules likewise affects the hydration behavior13,14 and was shown to suppress the hydrogen exchange between protein and water in NMR experiments.13,15 In order to understand protein function under real life conditions, it is therefore inevitable to examine the changes in protein hydration dynamics brought about by encapsulation, macromolecular crowding, or a combination of them. Since such changes are site-specific, a method to obtain local hydration dynamics at various sites around a protein is necessary. Experimentally, the time-dependent Stokes shift (TDSS), as well as the intermolecular Nuclear Overhauser Effect (NOE) between protein and water protons in principle offer (limited) site-specific hydration information as discussed in the following.
The TDSS is a frequently used observable to examine local hydration dynamics in the terahertz regime.16 This technique requires the incorporation of an optical probe into the molecular setup. The probe is excited by an ultrafast optical pump laser pulse, which induces an electrostatic perturbation to the system. The resulting rearrangement of the surroundings is monitored by probing the change in emission energy over time by a second ultrafast probe pulse. TDSS measurements and computer simulations were readily employed to characterize the dynamic properties of liquids in bulk phase,17–25 and close to biomolecules such as proteins.26–32 The TDSS is rather short-ranged (<6–7 Å),33,34 and can thus be employed as local probe of water dynamics. However, in recent investigations the use of TDSS was shown to be problematic for characterizing local hydration dynamics around large flexible biomolecules.35–41 The electrostatic perturbation of the probe not just affects water motions but flexible parts of the protein in its immediate vicinity as well. The absolute contribution of protein motion to the TDSS, as well as the respective timescales can not be subtracted from the overall signal, since they are usually unknown. Thus, the total TDSS is unable to reflect hydration dynamics due to the large direct and indirect contributions of protein motion.41 Nevertheless, the TDSS was used successfully to track changes in protein hydration caused by drug binding or dimerization,27,42,43 where instead of the absolute TDSS timescales only the respective relative changes were monitored. In fact, the change of the TDSS relative to a reference system may offer a chance to measure the retardation of the hydration dynamics timescales despite the inability of the TDSS to cover absolute timescales. The current study underlines this assumption. We are therefore not interested in the TDSS timescales of a single system, since they do not contain any usable information about hydration dynamics, but in the differences of TDSS timescales in two systems.
A different approach to measure local protein hydration dynamics, the intermolecular NOE between protein and water protons was proposed already decades ago,44–47 discarded later on48–51 and revived recently.52 In fact, we could show that the ratio σNOE/σROE between the NOE cross-relaxation rates in the laboratory and rotating frame, corresponding to NOESY and ROESY measurements respectively, is able to represent local hydration dynamics, namely the water residence times close to the respective proton.52 The cross-relaxation rates are calculated from a protein surface proton with respect to the spins of all water molecules. Although both σNOE and σROE are long-ranged, their ratio is rather short-ranged.53 In a previous study,52 we could show that the ratio σNOE/σROE correlates strongly with local water residence times at the protein surface. Thus, the intermolecular NOE can be employed to obtain a map of locally resolved protein hydration dynamics. However, for large systems like proteins in a realistic chemical environment the analysis of measured NOE data is challenging due to the enormous number of crowded NMR signals.
Another possibility of measuring local hydration dynamics, the Overhauser dynamic nuclear depolarization relaxometry, is physically equivalent to nuclear Overhauser enhancement with one of the spins being an electronic instead of a nuclear one. This method was shown to reveal site-specific hydration dynamics54–56 but necessarily requires the insertion of a radical label. To omit the addition of labels to our system we therefore only focus on TDSS and NOE calculations in this study.
Since both the change in TDSS, as well as the change in NOE upon alteration of the environment describe the change in the local hydration dynamics, we were interested in the amount of correlation between the two observables. Namely, can the local intermolecular NOE at a specific site of a protein be anticipated by measuring the TDSS at this site? This would require the protein motion to contribute about equally to the TDSS in the reference system and the investigated system, as well as negligible contributions from species only present in the investigated system but not in the reference system. Since NOE measurements are much more complicated and time-demanding than low-resolution TDSS measurements, such a correlation could be extremely useful. On the other hand, if intermolecular NOE information is available, the solvation dynamics as measured by the TDSS could be estimated easily also at sites that contain no natural chromophores, or no possibilities to attach a chromophore.
To investigate the extent of correlation, we calculated the TDSS and NOE at eight sites of the protein ubiquitin (UBQ) in different environments, namely in diluted aqueous solution, as well as in a crowded and/or encapsulated environment. UBQ is small (76 amino acids) and comprises different secondary structures, such as a five-stranded β-sheet, a long α-helix and a short 310 helix.13,57 Since UBQ participates in many protein–protein interactions in protein-degradation pathways,58 it is an ideal test case to study the effects of crowding and encapsulation, since the preferential side of interaction, the β-sheet, is known.15,58
2 Methods
2.1 Simulation setup
The UBQ structure was obtained from the RCSB Protein Data Bank,59 entry 1 UBQ.57 The cell environment was modeled via a reverse micelle (RM) where amphiphilic surfactant molecules surround a nanopool of water immersed in a medium of low polarity. Furthermore, different concentrations of UBQ were investigated, where either a single, or five proteins were encapsulated per RM, as described in the following.In total, five systems of varying UBQ concentration and RM composition were investigated, each consisting of five independent replica with a production length of 100 ns each, after hundreds of nanoseconds equilibration periods. For each system, furthermore different force field variations were applied, where protein–water interactions, as well as surfactant–water interactions were slightly scaled as suggested in literature.60,61 This was necessary to detect possible simulation artifacts since current force fields are optimized for one solvated protein and may yield considerable errors for crowded/confined systems, like exaggerated aggregation behaviour and incorrect solvation energies.60,62 The applied scaling was taken from Best and Mittal60 with λ = 1.1, where some van der Waals interactions are scaled by multiplying the respective well depth ε of the Lennard Jones potential by λ. The term ‘unscaled’ refers to the standard force field as described below. ‘Half-scaled’ corresponds to a scaling of protein–water interactions as suggested by Best and Mittal, whereas ‘full-scaled’ furthermore scales surfactant–water interactions. We note that the described effects of TDSS and NOE correlation were observed regardless of the use of force-field scaling, thus ruling out the influences of artifacts caused by force field defects.
An overview of all trajectories is given in Table 1 where the applied force-field scaling, the number of molecules, the box length a, the number of independent replica and the lengths of the equilibration and production runs are listed. Simulations of one UBQ in 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules were reused from ref. 63, as well as single UBQ64 and five UBQ molecules65 in a RM made up of uncharged surfactants. A mixture of the zwitterionic lauryldimethylamine-N-oxide (LDAO) and the neutral monoglyceride 1-decanoyl-rac-glycerol (DMAG) acted as surfactants. This novel surfactant mixture was developed by Wand et al. to facilitate mild and safe encapsulation of proteins.66 However, the most popular surfactant to date is the harsh anionic tensid sodium bis(2-ethylhexyl) sulfosuccinate (AOT), which leads to degradation of most proteins less robust than UBQ.67 Since important proof-of-concept encapsulation studies were performed with AOT,13,15 UBQ was also confined in a RM made up of AOT, where the trajectories were reused from ref. 53 and 68. Furthermore, trajectories of five UBQ molecules in water were partly reused from ref. 61, where additional 100 ns were calculated solely for this study to improve statistics. Simulation details are given in the respective references,53,61,63–65,68 and are only summarized in the following. The CHARMM36 force field69–72 was used to describe UBQ, as well as sodium and chloride ions. The SPC/E model was used in previous dielectric studies to describe water73 since it reproduces experimental dielectric observables better than the TIP3P water model,74,75 which is paramount to the accuracy of the dielectric analysis as a whole. While SPC/E water combines well with the CHARMM36 protein force field in practice,76 we want to add the caveat that force fields should not be mixed in general due to possible incompatibilities resulting in irreproducible outcomes. In this study, the two compared observables are calculated from the same trajectory hence the analysis is self-consistent in this regard.
000 water molecules were reused from ref. 63, as well as single UBQ64 and five UBQ molecules65 in a RM made up of uncharged surfactants. A mixture of the zwitterionic lauryldimethylamine-N-oxide (LDAO) and the neutral monoglyceride 1-decanoyl-rac-glycerol (DMAG) acted as surfactants. This novel surfactant mixture was developed by Wand et al. to facilitate mild and safe encapsulation of proteins.66 However, the most popular surfactant to date is the harsh anionic tensid sodium bis(2-ethylhexyl) sulfosuccinate (AOT), which leads to degradation of most proteins less robust than UBQ.67 Since important proof-of-concept encapsulation studies were performed with AOT,13,15 UBQ was also confined in a RM made up of AOT, where the trajectories were reused from ref. 53 and 68. Furthermore, trajectories of five UBQ molecules in water were partly reused from ref. 61, where additional 100 ns were calculated solely for this study to improve statistics. Simulation details are given in the respective references,53,61,63–65,68 and are only summarized in the following. The CHARMM36 force field69–72 was used to describe UBQ, as well as sodium and chloride ions. The SPC/E model was used in previous dielectric studies to describe water73 since it reproduces experimental dielectric observables better than the TIP3P water model,74,75 which is paramount to the accuracy of the dielectric analysis as a whole. While SPC/E water combines well with the CHARMM36 protein force field in practice,76 we want to add the caveat that force fields should not be mixed in general due to possible incompatibilities resulting in irreproducible outcomes. In this study, the two compared observables are calculated from the same trajectory hence the analysis is self-consistent in this regard.
| Scaling | #UBQ | #H2O | #Na+ | #Cl− | #AOT | #LDAO | #DMAG | #IOCT | a | #reps | t (equil.) | t (prod.) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UBQ in water (reference system) | ||||||||||||
| Unscaled | 1 | 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
150 | 150 | 0 | 0 | 0 | 0 | 110.9 Å | 5 | 100 ns | 100 ns |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| AOT reverse micelle | ||||||||||||
| Unscaled | 1 | 1500 | 105 | 5 | 100 | 0 | 0 | 4500 | 112.7 Å | 5 | 400 ns | 100 ns |
| Half-scaled | 1 | 1500 | 105 | 5 | 100 | 0 | 0 | 4500 | 112.7 Å | 5 | 400 ns | 100 ns |
| Full-scaled | 1 | 1500 | 105 | 5 | 100 | 0 | 0 | 4500 | 112.7 Å | 5 | 400 ns | 100 ns |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| LDAO/DMAG reverse micelle | ||||||||||||
| Unscaled | 1 | 1500 | 0 | 0 | 0 | 50 | 100 | 9000 | 140.07 Å | 5 | 300 ns | 100 ns |
| Half-scaled | 1 | 1500 | 0 | 0 | 0 | 50 | 100 | 9000 | 140.07 Å | 5 | 300 ns | 100 ns |
| Full-scaled | 1 | 1500 | 0 | 0 | 0 | 50 | 100 | 9000 | 140.07 Å | 5 | 300 ns | 100 ns |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| LDAO/DMAG reverse micelle, crowded | ||||||||||||
| Unscaled | 5 | 7500 | 0 | 0 | 0 | 250 | 500 | 9000 | 147.55 Å | 5 | 200 ns | 100 ns |
| Half-scaled | 5 | 7500 | 0 | 0 | 0 | 250 | 500 | 9000 | 147.55 Å | 5 | 200 ns | 100 ns |
| Full-scaled | 5 | 7500 | 0 | 0 | 0 | 250 | 500 | 9000 | 147.55 Å | 5 | 200 ns | 100 ns |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||||||
| Crowded, non-micellar system | ||||||||||||
| Unscaled | 5 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369 369 |
58 | 58 | 0 | 0 | 0 | 0 | 83.17 Å | 5 | 100 ns | 100 ns |
| Half-scaled | 5 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 369 369 |
58 | 58 | 0 | 0 | 0 | 0 | 83.17 Å | 5 | 100 ns | 100 ns |
Isooctane (IOCT) was modeled with the united atom force field from GROMOS 45A3 (ref. 77) with charges set to zero. This force field was devised for lipid aggregates like membranes and micelles and was demonstrated to yield accurate dielectric relaxation spectra,63 nuclear quadrupole resonance68 and terahertz absorption signals78 in conjunction with the force field setup explained above. LDAO and DMAG force fields were taken from ref. 79, as well as the AOT force field from ref. 68 with the aliphatic surfactant tails modelled with united atoms like the isooctane immersion medium and the polar head groups modelled atomistically.
The RMs used in this study were preassembled using the PACKMOL program with numerical seeds.80 Both the water loading w0 = [H2O]/[surfactant] = 15 for the UBQ bearing AOT RMs,13 w0 = 10 for the LDAO/DMAG RMs66 and the RM size81 were decided in accordance with experimental data for the 1-UBQ systems. For the 5-UBQ RM, the size was simply scaled up by a factor of 5 to facilitate better comparability without dilution effects.
All following simulation steps were carried out using DOMDEC CHARMM.82,83 The initial geometries were minimized by 2000 steps of steepest descent, then equilibrated as isothermal–isobaric ensembles (NPT) until the length of the cubic simulation box converged. The trajectory was then produced as a isothermal–isochoric ensemble (NVT) employing periodic boundary conditions with a temperature of T = 300 K kept constant with a Nosé–Hoover thermostat.84,85 The equations of motion were integrated using a leap-flog scheme.86 High-frequency oscillations of covalent bonds involving hydrogen were constraint with the SHAKE algorithm87 allowing for a time step of 2 fs with a total trajectory length of at least 200 ns and a write frequency of 1 ps. Non-bonded non-electrostatic interactions were cut off at 12 Å and long-ranged electrostatic interactions were calculated as Ewald sums using the Particle Mesh Ewald (PME) method88,89 on a 64 × 64 × 64 grid (bulk system) or else a 128 × 128 × 128 grid (crowded and RM systems) with cubic splines of order 6 and κ = 0.41 Å−1 (tinfoil boundary conditions).
In total, 60 simulations of 100 ns were analyzed, summing up to 6 μs, disregarding an even larger amount of additional equilibration periods. By employing such a wide variety of systems, we can investigate the changes in protein hydration brought about by encapsulation using neutral/zwitterionic or charged surfactants, as well as macromolecular crowding in great detail. The long equilibration periods and simulation times are furthermore necessary to sample a sufficiently large variety of conformations.
2.2 Analysis routines
The TDSS was calculated at eight amino acids at different locations and secondary structure elements, which were chosen to match the investigated sites in ref. 41 apart from histidine. In this work the TDSS is solely derived from equilibrium simulations via linear response theory (LRT). In ref. 41 we could show that LRT is valid for tyrosine and artificial lysine excitations, but not for histidine excitations. Lysine, although not a natural chromophore and thus not visible in experimental TDSS studies, was chosen since it is abundant in UBQ. Due to the hydrophilic character it is always located on the surface of the protein. Amino acids which are no chromophores were also used in literature to calculate an artificial TDSS.38,41 On the other hand, tyrosine is a natural chromophore in UBQ, and thus an obvious choice for TDSS calculations. NOE measurements of tyrosine, however, are tricky due to proton exchange reactions,13 which are absent in simulation.To obtain the TDSS at a chosen site, the (hypothetical) change in electrostatic interaction energy ΔU(t) between ground and excited state of the respective amino acid with the surroundings is monitored over time. Fig. 1 depicts the considered partial charge changes of lysine and tyrosine in the excited state. Since we rely on LRT, the amino acids never undergo an actual excitation, instead the solvent response is extrapolated from the (hypothetical) fluctuations around the mean change in interaction energy, δΔU(t) = ΔU(t) − 〈ΔU〉, if the amino acid would have been excited at timestep t. Thus, the analysis of the TDSS only requires ground-state trajectories in equilibrium with standard partial charges. We furthermore note that the chosen change in partial charge upon excitation does not affect the obtained TDSS timescales (only their magnitudes) if LRT is valid. However, the validity of LRT needs to be carefully evaluated for each system and excitation. In ref. 41 we could prove that LRT is valid for the excitations considered in this study. If LRT is applicable, the time correlation function S(t) of the fluctuations around the mean change in electrostatic interaction energy,
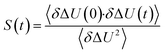 | (1) |
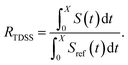 | (2) |
The intermolecular NOE is evaluated as the ratio between the homo-nuclear NOE cross-relaxation rates in the laboratory frame and the rotation frame
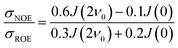 | (3) |
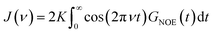 | (4) |
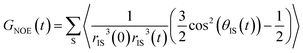 | (5) |
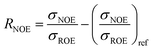 | (6) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) IS as described by eqn (5). We created 500 starting points evenly spaced on the analyzed trajectory. At each starting point, we positioned the UBQ molecule in the center of the simulation box to ensure minimum distance of the protein center-of-mass to all water molecules. This ensures that all the water molecules proximate to the protein residues due to periodic boundary conditions are spatially close as well. For each such correlation function, the box was unfolded individually to produce a no-jump trajectory. This allows for a natural diffusive motion of the protein–water pairs unperturbed by sudden coordinate jumps caused by periodic boundary conditions.
IS as described by eqn (5). We created 500 starting points evenly spaced on the analyzed trajectory. At each starting point, we positioned the UBQ molecule in the center of the simulation box to ensure minimum distance of the protein center-of-mass to all water molecules. This ensures that all the water molecules proximate to the protein residues due to periodic boundary conditions are spatially close as well. For each such correlation function, the box was unfolded individually to produce a no-jump trajectory. This allows for a natural diffusive motion of the protein–water pairs unperturbed by sudden coordinate jumps caused by periodic boundary conditions.
3 Results and discussion
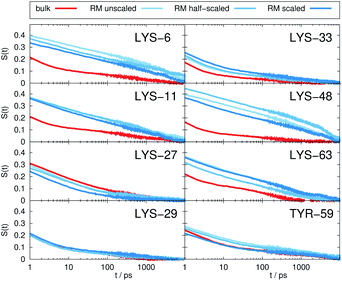
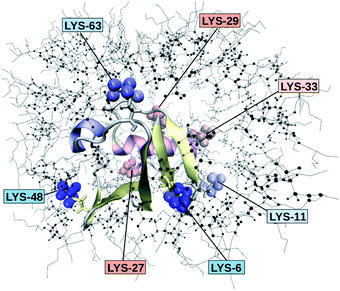
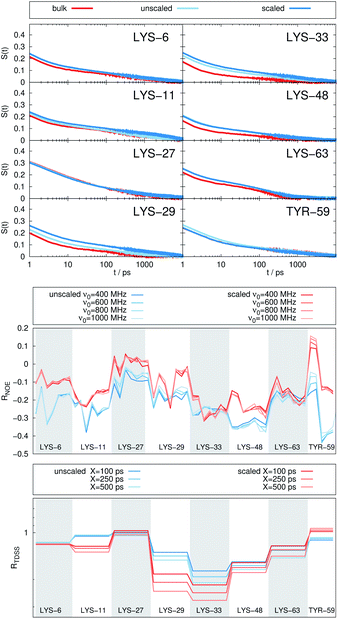
Fig. 2 depicts the TDSS around the seven lysine residues, as well as around tyrosine for a single proton of UBQ encapsulated in an AOT RM compared to the reference system. For LYS-27, LYS-29 and TYR-59, no or nearly no changes in TDSS occur upon encapsulation. This is directly connected to their respective positions, where LYS-27 and LYS-29 have access to water, but are located within the two pockets of UBQ,52,96 referred to as A and B site (c.f. ref. 41 and 52). Within the pockets, hydration dynamics is not affected by a change in environment. TYR-59 on the other hand is located in the interior of the protein and has only limited access to water.97,98 Thus, a change in environment does not change the solvation dynamics around tyrosine. The five other lysine residues are located at the protein surface and are not in proximity to any pockets. Thus, they sense the change in hydration dynamics brought about by encapsulation, with largest retardations at LYS-48 and LYS-6, followed by LYS-11. We note that we are only examining relative retardations compared to the dilute protein solution reference. On absolute terms, for example LYS-27, which is located in a pocket, shows much slower dynamics than the other amino acids.The retardation of σNOE/σROE (in the following simply referred to as NOE retardation) at the seven δ-, ε- and ζ lysine protons, and the aromatic and hydroxyl tyrosine protons upon encapsulation in the AOT RM is displayed in Fig. 3, where blue denotes large retardation and red no retardation. Note how the lysine residues on the β-sheet in proximity to the surfactant wall exhibit strong hydration retardation, while both the residues in water pockets (LYS-27, LYS-29) and the residue facing the bulk-like RM core (LYS-33) on the α-helix show no significant hydration dynamics slowdown compared to bulk diluted solution. A comparison of the TDSS retardation and the NOE retardation also confirms the selective retardation of some of the sites.
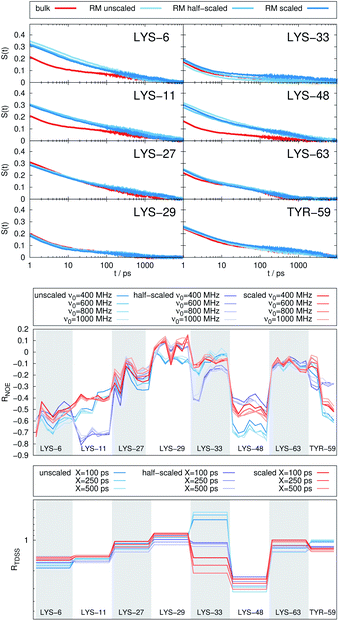
In Fig. 4, the NOE is plotted for four different spectrometer frequencies (top) and compared to the TDSS retardation factors at different upper limits of integration (bottom). We note that the spectrometer frequencies and integration limits only slightly affect the observed retardation in a quantitative, but not qualitative fashion. The NOE conveys the same information as already observed in the TDSS, namely LYS-48 and LYS-6 are largely retarded, followed by LYS-11, LYS-63 and LYS-33. An experimental study on NOE measurements of Wand and coworkers13 could show that mainly the β-sheet of UBQ shows very slow hydration when encapsulated in an AOT RM. Our computational results reproduce these experimental findings well. Both TDSS and NOE data confirm that the three most retarded sites are LYS-6, LYS-11 and LYS-48, which are all located in the β-sheet region. Indeed, 15N–1H NMR experiments of UBQ encapsulated in AOT carried out by Flynn et al. revealed increased Lipari–Szabo order parameters for β-sheet amino acids, indicative of an increased rigidity due to a direct β-sheet surfactant interaction.99–101
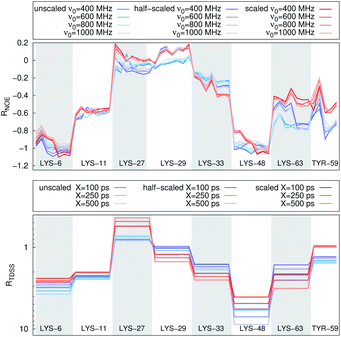 | ||
| Fig. 4 RNOE and RTDSS of ubiquitin encapsulated in the AOT reverse micelle. (Top) Change in intermolecular NOE at the lysine and tyrosine protons at different spectrometer frequencies ν0 (cf. eqn (6)). (Bottom) Change in the timescales of the time-dependent Stokes shift at different integration limits X (cf. eqn (2)). | ||
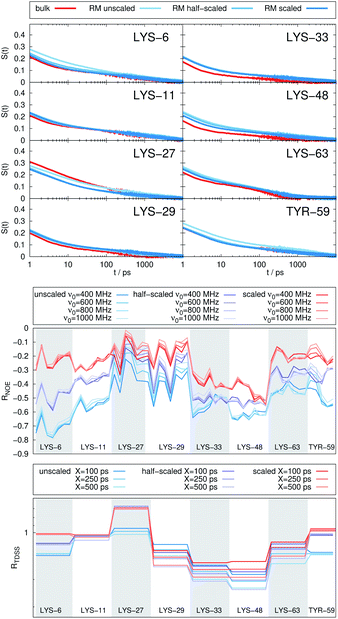
The TDSS and NOE of UBQ in the AOT RM thus correlate and also agree well with experimental results. However, this finding is only of interest if the observed correlation holds also for other systems and less strong retardations. The TDSS, as well as the TDSS retardation factors and changes in NOE timescales upon change in environment are given in Fig. 5 for a single UBQ in the LDAO/DMAG RM, in Fig. 7 for five UBQ molecules in the LDAO/DMAG RM and in Fig. 6 for five UBQ molecules in water without micelle. Each system is analyzed in detail in the following.
In the LDAO/DMAG RM holding a single UBQ molecule the retardation upon encapsulation is far less pronounced than in the AOT RM. Again, mainly the amino acids LYS-6, LYS-11 and LYS-48 are affected by the encapsulation, visible both in the TDSS and NOE signals since the position of the protein in the RM is similar irrespective of surfactant: The β-sheet site faces the surfactant wall, while the α-helix site is oriented towards the bulk-like core.
Switching from encapsulation to macromolecular crowding, Fig. 6 depicts the TDSS and NOE signals for five UBQ molecules in water without a micelle. This scenario models the effect of a high macromolecule concentration on the hydration dynamics of proteins without forming a complex. We see hydration retardation effects, i.e. TDSS ratios and NOE/ROE differences do also report on protein sites interacting with other proteins. Note that the retardations are very modest (between 0 and −0.4 for the NOE), which is much less than the previously observed retardations of up to −1.0. This is possibly due to rather short-lived protein–protein contacts as opposed to the continued interaction with the RM wall encountered in the case of the encapsulated UBQ. Also, the contact sites differ to some degree; while interactions with the β-sheet are still observed, crowding contacts take place via LYS-29 as well.
Combining crowding and encapsulation by increasing the protein loading of the LDAO/DMAG RM (from one molecule to five) we observe in Fig. 7 that the extent of retardation increases compared to bulk crowding, but is still lower than in the same RM containing just one UBQ and retardation can mainly be observed for LYS-6 and LYS-48. This is due to the UBQ molecules exploring a greater diversity of positions in the RM as opposed to the more simple single-protein system in constant contact with the surfactant wall. However, LYS-29 hydration dynamics is again more strongly retarded in the crowded RM than the single-protein one, probably due to protein–protein contacts.
Note that the crowded systems depend more strongly on the level of λ-scaling than the single-molecule ones. As presented in the methods section, λ-scaling was initially conceived to correct protein solvation/protein–protein aggregation behavior for standard force fields via non-bonded, non-charged interactions.60 We have shown previously that λ-scaling alters the mutual orientation of UBQ from parallel to orthogonal in bulk solution61 and from parallel/orthogonal to anti-parallel in crowded RMs.65 On the other hand, simple RM systems are governed mostly by other interactions, e.g. of electrostatic nature,79 thus λ-scaling only barely affects protein hydration dynamics.
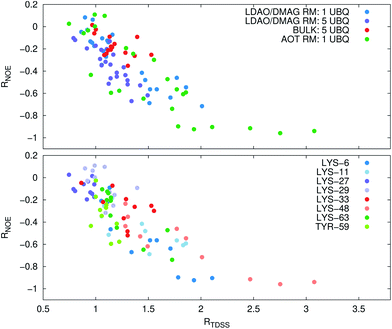
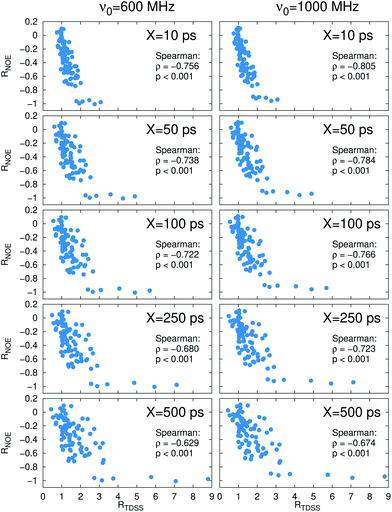
Now, is there a correlation between the observed retardation in TDSS and NOE throughout all investigated systems? Fig. 8 depicts RNOE at ν0 = 1000 MHz averaged over the protons in the respective amino acid (filled black circles in Fig. 1) versus RTDSS at X = 10 ps. The very small value of X increases the contribution of water motion (instead of protein motion) to the calculated RTDSS. Analogous plots for different values of X and ν0 are given in Fig. 9, as well as Spearman correlation coefficients for each combination, which range up to ρ = −0.81 for X = 10 ps and ν0 = 1000 MHz with p < 0.001. The p value indicates the probability that the observables are not correlated and their relationship was observed by chance. Larger X decrease the observed correlation to some extent. Ideally, the protein contribution to the TDSS would be the same in the observed and the reference system and thus cancel out in RTDSS. In that case, both small and large X should lead to the same results. From Fig. 4–7 we can infer that different X lead to slightly different RTDSS, thus the protein contribution to the TDSS changes to some extent upon encapsulation or crowding. Further, the surfactant molecules also contribute to the response, mainly on long timescales. To keep the influence of protein and surfactant motion to RTDSS as small as possible, a small X should be chosen. For ν0 = 1000 MHz and X = 10 ps, the correlation between RNOE and RTDSS is very strong (indicated by the large |ρ| value), of >99.9% confidence (indicated by the small p < 0.001), and negative, i.e. a lower RNOE corresponds to a larger RTDSS. In fact, taking into account the diversity of the investigated systems, the correlation is high. We furthermore note that RNOE cannot exceed −1.5, so that the observed correlation is not (and cannot be) of linear nature, and instead reaches a plateau for strong retardations, so that very large RTDSS yield the same RNOE. Also, the correlation between RTDSS and RNOE is rather qualitative (no, small or large water retardation at a protein site), instead of quantitative, and should be interpreted as such. We have therefore omitted an analytical expression of the correlation function.
The colors in the top panel of Fig. 8 refer to the four different systems. The largest changes in NOE and TDSS are observed for the AOT RM, which is known to create very harsh conditions due to the charged surfactants and large concentration of counter-ions.67 The mild LDAO/DMAG RM leads to less drastic changes in protein hydration dynamics if one UBQ is encapsulated, and even weaker effects in a crowded environment. The least effects are observed for the crowded, non-micellar system, where only moderate retardation is observed. The colors in the bottom panel of Fig. 8 refer to the respective amino acids. LYS-48 and LYS-6 are affected most by changes in the environment. They surround the hydrophobic patch (LEU-8, ILE-44, VAL-70) which is responsible for recognizing UBQ binding domains in other proteins.102–105 In confinement, this β-sheet region preferentially interacts with other interfaces, i.e. the RM wall with only a thin layer of water in between protein and surfactant molecules.53 We found this effect to take place both using the ionic AOT surfactant or the neutral LDAO/DMAG surfactant, in all independent replica and at all levels of λ-scaling. The same protein behaviour was reported previously by us,68 by another group employing a vastly different force field14,106 and by empirical NMR-experiments.100,101 Also, UBQ was found to bind to peptides preferably via the β-sheet, and especially via LYS-48.107 On the other side, LYS-27 and LYS-29, which are located in surface pockets, are barely influenced by encapsulation at all, reflecting the invariance of protein hydration in clefts or pockets to the surroundings. LYS-27 and LYS-29 are furthermore located in the α-helix part of UBQ, where the hydration dynamics were shown to be far less slowed-down in experiment.13
Now, should this correlation between relative TDSS and NOE have been expected? If so, why has it been overlooked previously? One the one hand, a correlation could have been expected since both the relative TDSS and intermolecular NOE report on pair-diffusive motion of charges and nuclear spins, respectively, by recording the temporal evolution of the protein–water connecting vectors ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) Thus, both methods inherently contain similar information about local hydration changes of a test system with regards to a reference system, although the TDSS is of more collective nature, and the NOE is summed over individual spins. On the other hand, the TDSS does not only monitor water motion, but the motion of all molecules surrounding the chromophore, including amino acids, surfactants or ions, while the NOE reports exclusively on water dynamics. The processing of the TDSS relaxation times, as well as the choice of reference system affects the ability of the TDSS to report on water dynamics. In this study, we observed that the TDSS only reports on water dynamics if one forms the ratio to a reference system to eliminate contributions from the protein scaffold.41 The TDSS of a single system cannot be used to infer NOE timescales. Also, the protein motion should not change largely compared to the reference system, otherwise its contributions will not cancel out. Furthermore, the contribution of species only present in the test system but not in the reference system must the low. In this study, the contribution of the wall, i.e. the surfactants, to the total TDSS affects the amount of correlation of TDSS and NOE to some extent. By choosing small integration limits X, the contributions from the wall can be kept low, since they occur mostly on long timescales. In general, we strongly recommend to use reference systems which are as similar as possible to the system of interest. Regarding the NOE, the correct processing of the raw signals is essential, too, since it is in principle long-ranged,48 and thus cannot directly convey information about local hydration dynamics. However, elimination of long-ranged protein–water contributions can be achieved by forming ratios, e.g. between the laboratory-frame NOE and the rotating frame NOE (ROE). Influences from the change in chemical environment can then be obtained by forming the difference of the two σNOE/σROE ratios.53 Following this protocol, a correlation between the relative TDSS and NOE can be observed.
Thus, both methods inherently contain similar information about local hydration changes of a test system with regards to a reference system, although the TDSS is of more collective nature, and the NOE is summed over individual spins. On the other hand, the TDSS does not only monitor water motion, but the motion of all molecules surrounding the chromophore, including amino acids, surfactants or ions, while the NOE reports exclusively on water dynamics. The processing of the TDSS relaxation times, as well as the choice of reference system affects the ability of the TDSS to report on water dynamics. In this study, we observed that the TDSS only reports on water dynamics if one forms the ratio to a reference system to eliminate contributions from the protein scaffold.41 The TDSS of a single system cannot be used to infer NOE timescales. Also, the protein motion should not change largely compared to the reference system, otherwise its contributions will not cancel out. Furthermore, the contribution of species only present in the test system but not in the reference system must the low. In this study, the contribution of the wall, i.e. the surfactants, to the total TDSS affects the amount of correlation of TDSS and NOE to some extent. By choosing small integration limits X, the contributions from the wall can be kept low, since they occur mostly on long timescales. In general, we strongly recommend to use reference systems which are as similar as possible to the system of interest. Regarding the NOE, the correct processing of the raw signals is essential, too, since it is in principle long-ranged,48 and thus cannot directly convey information about local hydration dynamics. However, elimination of long-ranged protein–water contributions can be achieved by forming ratios, e.g. between the laboratory-frame NOE and the rotating frame NOE (ROE). Influences from the change in chemical environment can then be obtained by forming the difference of the two σNOE/σROE ratios.53 Following this protocol, a correlation between the relative TDSS and NOE can be observed.
While shown here for the specific instances of macromolecular crowding and confinement of UBQ in comparison to bulk water, the correlation of relative TDSS and NOE is expected to hold for comparison of any two chemical environments involving a common protein, and not limited to crowding or confinement effects. For a different system, we thus expect a similar correlation function as obtained in this study, and are currently working on a generalization to other proteins, which will be the topic of a future article. If the observed RNOE versus RTDSS curves might look slightly different in a different system, they can be calibrated by measuring the TDSS and NOE at amino acids that can serve as intrinsic chromophores (tryptophan, phenylalanine), or extrinsic chromophores covalently linked to the protein, for an arbitrary combination of ν0 and X. We note that the employed chromophores in this study, lysine and tyrosine, led to the same correlation function between relative TDSS and NOE although they differed largely in size, degrees of flexibility and change of partial charges upon excitation. We therefore expect also other chromophores such as tryptophan or phenylalanine to exhibit this uniform behavior, i.e. that chromophore specific contributions to the TDSS cancel out upon forming the ratio to a reference system. A proof of this assumption is beyond the scope of this article and will be the topic of future studies, as well as the applicability of our results to extrinsic chromophores. In summary, by following the data processing proposed in this article, RTDSS can be interconverted to RNOE at sites that are invisible to NOE measurements. Analogously, RNOE can be interconverted to RTDSS at sites that are no chromophores and are thus not accessible in TDSS measurements. Although such a conversion cannot be made in a fully quantitative fashion, qualitative information (retardation of water dynamics at specific sites) can be obtained. In combination, this allows for a more detailed and comprehensive mapping of the changes of hydration properties upon a change in environment of a protein.
4 Conclusion
With our comparative approach for the first time we could correlate the change in TDSS to NOE data to show site selective hydration dynamics in a confined or crowded protein system. Both methods, in principle, can provide detailed space-resolved information on hydration dynamics, but come with severe limitations. Especially the absolute timescales of the TDSS are heavily influenced by protein dynamics, so that the TDSS is usually disregarded when investigating protein hydration dynamics. However, this obstacle can be partly overcome by comparing TDSS measurements or calculations to a reference system, i.e. by investigating relative instead of absolute timescales. In this case, both the TDSS and NOE reflect the changes in protein hydration dynamics caused by encapsulation or macromolecular crowding. The retarded hydration dynamics are caused by particularly slow water molecules caught interstitially between two surfaces.53 We furthermore observed that water molecules in clefts or pockets of the protein (measured via LYS-27 and LYS-29) are less affected by a change in environment than other water molecules at the protein surface.The localized dynamic data can be exploited to track the protein position inside the reverse micelle and elucidate whether a specific side of a protein is facing the surfactants. From that, we see that hydration dynamics not only slows down in proximity of interfaces and thus contains spatial information, but that the extent of slowing down is correlated when looking at fast hydration phenomena (TDSS time scale, <0.5 ns) or slow ones (NMR time scale, >1 ns). In a crowded environment, large retardations in the TDSS and NOE indicate that another protein is quite close to the respective site, thus slowing down water dynamics. Such information is invaluable to characterize protein hydration dynamics in a cellular environment, and could also be used to study ligand binding or dimerization processes.
In summary, the individual challenges of both methods including unpredictable contributions of protein dynamics to the TDSS and exorbitant long measurement times to generate crowded nearly inscrutable NMR spectra for the NOE analysis could be reduced by combining both techniques. The fundamental limitations of the TDSS to capture absolute hydration dynamics close to proteins can be overcome by calculating or measuring only comparative timescales, relative to a non-confined, non-crowded system. Thus, the TDSS can be used to obtain accurate relative timescales of water retardation upon a change in environment. The long-range contributions to the NOE can be eliminated by forming a ratio to the rotating frame NOE. The strong correlation between RNOE and RTDSS furthermore allows for time-intensive NOE measurements to be replaced or enhanced by TDSS measurements in large systems and at sites that are invisible to the NOE, whereas NOE measurements can help to estimate TDSS timescales at protein locations which hold no chromophore. A combination of NOE and TDSS experiments thus seems to be ideally suited to characterize protein hydration in different environments.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. H. is recipient of a DOC Fellowship of the Austrian Academy of Sciences at the Institute of Computational Biological Chemistry. S. S. acknowledges funding by the Austrian Science Fund FWF in the context of Project No. FWF-P28556-N34.References
- N. Nandi, K. Bhattacharyya and B. Bagchi, Chem. Rev., 2000, 100, 2013–2046 CrossRef CAS PubMed.
- R. Dutta, M. Gosh, A. Pyne and N. Sarkar, J. Phys. Chem. B, 2019, 123, 117–129 CrossRef CAS PubMed.
- R. J. Ellis, Trends Biochem. Sci., 2001, 26, 597–604 CrossRef CAS.
- T. I. Igumenova, K. K. Frederick and A. J. Wand, Chem. Rev., 2006, 106, 1672–1699 CrossRef CAS PubMed.
- M. Grossman, B. Born, M. Heyden, D. Tworowski, G. B. Fields, I. Sagi and M. Havenith, Nat. Struct. Mol. Biol., 2011, 18, 1102–1108 CrossRef CAS PubMed.
- A. P. Minton, J. Cell Sci., 2006, 119, 2863–2869 CrossRef CAS PubMed.
- S. B. Zimmerman and S. O. Trach, J. Mol. Biol., 1991, 222, 599–620 CrossRef CAS PubMed.
- P.-H. Wang, I. Yu, M. Feig and Y. Sugita, Chem. Phys. Lett., 2017, 671, 63–70 CrossRef CAS.
- S. Biswas, S. K. Mukherjee and P. K. Chowdhury, J. Phys. Chem. B, 2016, 120, 12501–12510 CrossRef CAS PubMed.
- S. K. Mukherjee, S. Gautam, S. Biswas, J. Kundu and P. K. Chowdhury, J. Phys. Chem. B, 2015, 119, 14145–14156 CrossRef CAS.
- E. Spiga, L. A. Abriata, F. Piazza and M. D. Peraro, J. Phys. Chem. B, 2014, 118, 5310–5321 CrossRef CAS PubMed.
- D. Karandur, K.-Y. Wong and B. M. Pettitt, J. Phys. Chem. B, 2014, 118, 9565–9572 CrossRef CAS PubMed.
- N. V. Nucci, M. S. Pometun and A. J. Wand, Nat. Struct. Mol. Biol., 2011, 18, 245–249 CrossRef CAS PubMed.
- J. Tian and A. E. Garcia, Biophys. J., 2009, 96, L57–L59 CrossRef CAS PubMed.
- N. V. Nucci, M. S. Pometun and A. J. Wand, J. Am. Chem. Soc., 2011, 133, 12326–12329 CrossRef CAS.
- Y. Xu and M. Havenith, J. Chem. Phys., 2015, 143, 170901 CrossRef PubMed.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1988, 89, 5044–5069 CrossRef CAS.
- R. Jimenez, G. R. Fleming, P. V. Kumar and M. Maroncelli, Nature, 1994, 369, 471–473 CrossRef CAS.
- N. Nandi, S. Roy and B. Bagchi, J. Chem. Phys., 1995, 102, 1390–1397 CrossRef CAS.
- S. J. Rosenthal, X. Xie, M. Du and G. R. Fleming, J. Chem. Phys., 1991, 95, 4715–4718 CrossRef CAS.
- M. Maroncelli, J. Chem. Phys., 1991, 94, 2084–2103 CrossRef CAS.
- P. V. Kumar and M. Maroncelli, J. Chem. Phys., 1995, 103, 3038–3060 CrossRef CAS.
- M. Maroncelli and G. R. Fleming, J. Chem. Phys., 1987, 86, 6221–6239 CrossRef CAS.
- C. F. Chapman, R. S. Fee and M. Maroncelli, J. Phys. Chem., 1995, 99, 4811–4819 CrossRef CAS.
- D. Bingemann and N. P. Ernsting, J. Chem. Phys., 1995, 102, 2691–2700 CrossRef CAS.
- S. K. Pal, D. Mandal, D. Sukul, S. Sen and K. Bhattacharyya, J. Phys. Chem. B, 2001, 105, 1438–1441 CrossRef CAS.
- S. K. Pal, J. Peon and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 15297–15302 CrossRef CAS PubMed.
- S. K. Pal, J. Peon and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 1763–1768 CrossRef CAS.
- S. K. Pal, J. Peon, B. Bagchi and A. H. Zewail, J. Phys. Chem. B, 2002, 106, 12376–12395 CrossRef CAS.
- S. M. Bhattacharyya, Z.-G. Wang and A. H. Zewail, J. Phys. Chem. B, 2003, 107, 13218–13228 CrossRef CAS.
- S. K. Pal and A. H. Zewail, Chem. Rev., 2004, 104, 2099–2124 CrossRef CAS.
- D. Zhong, S. K. Pal and A. H. Zewail, Chem. Phys. Lett., 2011, 503, 1–11 CrossRef CAS.
- M. Sajadi, F. Berndt, C. Richter, M. Gerecke, R. Mahrwald and N. P. Ernsting, J. Phys. Chem. Lett., 2014, 5, 1845–1849 CrossRef CAS PubMed.
- E. Heid and C. Schröder, Phys. Chem. Chem. Phys., 2018, 20, 10992 RSC.
- L. Nilsson and B. Halle, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13867–13872 CrossRef CAS PubMed.
- T. Li, A. A. Hassanali, Y.-T. Kao, D. Zhong and S. J. Singer, J. Am. Chem. Soc., 2007, 129, 3376–3382 CrossRef CAS PubMed.
- T. Li, A. A. Hassanali and S. J. Singer, J. Phys. Chem. B, 2008, 112, 16121–16134 CrossRef CAS PubMed.
- A. A. Golosov and M. Karplus, J. Phys. Chem. B, 2007, 111, 1482–1490 CrossRef CAS PubMed.
- B. Halle and L. Nilsson, J. Phys. Chem. B, 2009, 113, 8210–8213 CrossRef CAS PubMed.
- S. Mondal, S. Mukherjee and B. Bagchi, Chem. Phys. Lett., 2017, 683, 29–37 CrossRef CAS.
- E. Heid and D. Braun, Phys. Chem. Chem. Phys., 2019, 21, 4435–4443 RSC.
- B. E. Cohen, A. Pralle, X. Yao, G. Swaminath, C. S. Gandhi, Y. Nung Jan, B. K. Kobilka, E. Y. Isacoff and L. Y. Jan, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 965–970 CrossRef CAS.
- J. K. A. Kamal, L. Zhao and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 13411–13416 CrossRef CAS PubMed.
- G. Otting and K. Wüthrich, J. Am. Chem. Soc., 1989, 111, 1871–1875 CrossRef CAS.
- B. A. Messerle, G. Wider, G. Otting, C. Weber and K. Wüthrich, J. Magn. Reson., 1989, 85, 608–613 CAS.
- G. Otting, E. Liepinsh, B. T. Farmer and K. Wüthrich, J. Biomol. NMR, 1991, 1, 209–215 CrossRef CAS.
- G. Otting, E. Liepinsh and K. Wüthrich, Science, 1991, 254, 974–980 CrossRef CAS PubMed.
- B. Halle, J. Chem. Phys., 2003, 119, 12372–12385 CrossRef CAS.
- B. Halle, Philos. Trans. R. Soc., B, 2004, 359, 1207–1224 CrossRef CAS.
- K. Modig, E. Liepinsh, G. Otting and B. Halle, J. Am. Chem. Soc., 2004, 126, 102–114 CrossRef CAS.
- C. Mattea, J. Qvist and B. Halle, Biophys. J., 2008, 95, 2951–2963 CrossRef CAS.
- D. Braun, M. Schmollngruber and O. Steinhauser, J. Phys. Chem. Lett., 2017, 8, 3421–3426 CrossRef CAS.
- P. Honegger and O. Steinhauser, Phys. Chem. Chem. Phys., 2019, 21, 14571–14582 RSC.
- B. D. Armstrong, J. Choi, C. Lopez, D. A. Wesener, W. Hubbell, S. Cavagnero and S. Han, J. Am. Chem. Soc., 2011, 133, 5987–5995 CrossRef CAS PubMed.
- O. Fisette, C. Päslack, R. Barnes, J. M. Isas, R. Langen, M. Heyden, S. Han and L. V. Schäfer, J. Am. Chem. Soc., 2016, 138, 11526–11535 CrossRef CAS.
- J. H. Ortony, B. Qiao, C. J. Newcomb, T. J. Keller, L. C. Palmer, E. Deiss-Yehiely, M. O. de la Cruz, S. Han and S. I. Stupp, J. Am. Chem. Soc., 2017, 139, 8915–8921 CrossRef CAS PubMed.
- S. Vijay-Kumar, C. E. Bugg and W. J. Cook, J. Mol. Biol., 1987, 194, 531–544 CrossRef CAS.
- A. Hershko and A. Ciechanover, Annu. Rev. Biochem., 1998, 67, 425–479 CrossRef CAS PubMed.
- H. Berman, K. Henrick and H. Nakamura, Nat. Struct. Biol., 2003, 10, 980 CrossRef CAS.
- R. B. Best, W. Zheng and J. Mittal, J. Chem. Theory Comput., 2014, 10, 5113–5124 CrossRef CAS PubMed.
- P. Honegger, M. Schmollngruber and O. Steinhauser, Phys. Chem. Chem. Phys., 2018, 20, 19581–19594 RSC.
- D. Petrov and B. Zagrovic, PLoS Comput. Biol., 2014, 10, e1003638 CrossRef PubMed.
- D. Braun, M. Schmollngruber and O. Steinhauser, Phys. Chem. Chem. Phys., 2016, 18, 24620–24630 RSC.
- P. Honegger and O. Steinhauser, Phys. Chem. Chem. Phys., 2018, 20, 22932–22945 RSC.
- P. Honegger and O. Steinhauser, Phys. Chem. Chem. Phys., 2019, 21, 8108–8120 RSC.
- I. Dodevski, N. V. Nucci, K. G. Valentine, G. K. Sidhu, E. S. O'Brien, A. Pardi and A. J. Wand, J. Am. Chem. Soc., 2014, 136, 3465–3474 CrossRef CAS.
- I. Dodevski, N. V. Nucci, K. G. Valentine, G. K. Sidhu, E. S. O'Brien, A. Pardi and A. J. Wand, J. Magn. Reson., 2014, 241, 137–147 CrossRef PubMed.
- M. Schmollngruber, D. Braun, D. Oser and O. Steinhauser, Phys. Chem. Chem. Phys., 2016, 18, 3606–3617 RSC.
- D. Beglov and B. Roux, J. Chem. Phys., 1994, 100, 9050–9063 CrossRef CAS.
- A. D. MacKerell Jr, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef.
- A. D. MacKerell Jr, M. Feig and C. L. Brooks III, J. Am. Chem. Soc., 2004, 126, 698–699 CrossRef PubMed.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. MacKerell Jr, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- D. Braun, S. Boresch and O. Steinhauser, J. Chem. Phys., 2014, 140, 064107 CrossRef PubMed.
- M. Sega and C. Schröder, J. Phys. Chem. A, 2015, 119, 1539 CrossRef CAS PubMed.
- G. Schiro, F.-X. G. Y. Fichou, K. Wood, F. Gabel, M. Moulin, M. Härtlein, M. Heyden, J.-P. Colletier, A. Orecchini, A. Paciaroni, J. Wuttke, D. J. Tobias and M. Weik, Nat. Commun., 2015, 6, 6490 CrossRef CAS PubMed.
- L. D. Schuler, X. Daura and W. F. V. Gunsteren, J. Comput. Chem., 2001, 22, 1205–1218 CrossRef CAS.
- M. Schmollngruber, D. Braun and O. Steinhauser, Phys. Chem. Chem. Phys., 2016, 18, 30954 RSC.
- P. Honegger, M. Schmollngruber and O. Steinhauser, Phys. Chem. Chem. Phys., 2018, 20, 11454–11469 RSC.
- L. Martínez, R. Andrade, G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- I. R. Piletic, D. E. Moilanen, D. B. Spry, N. E. Levinger and M. D. Fayer, J. Phys. Chem. A, 2006, 110, 4985–4999 CrossRef CAS PubMed.
- B. R. Brooks, C. L. Brooks III, A. D. MacKerell Jr, L. Nilsson, R. J. Petrella, B. Roux, Y. Won, G. Archontis, C. Bartels, S. Boresch, A. Caflisch, L. Caves, Q. Cui, A. R. Dinner, M. Feig, S. Fischer, J. Gao, M. Hodoscek, W. Im, K. Kuczera, T. Lazaridis, J. Ma, V. Ovchinnikov, E. Paci, R. W. Pastor, C. B. Post, J. Z. Pu, M. Schaefer, B. Tidor, R. M. Venable, H. L. Woodcock, X. Wu, W. Yang, D. M. York and M. Karplus, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef CAS PubMed.
- A.-P. Hynninen and M. F. Crowley, J. Comput. Chem., 2014, 35, 406 CrossRef CAS PubMed.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed.
- R. W. Hockney, Methods Comput. Phys., 1970, 9, 135–211 Search PubMed.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577 CrossRef CAS.
- E. A. Carter and J. T. Hynes, J. Chem. Phys., 1991, 94, 5961–5979 CrossRef CAS.
- R. Zwanzig, Nonequilibrium Statistical Mechanics, Oxford Univ. Press, New York, 2001 Search PubMed.
- B. B. Laird and W. H. Thompson, J. Chem. Phys., 2007, 126, 211104 CrossRef PubMed.
- B. B. Laird and W. H. Thompson, J. Chem. Phys., 2011, 135, 084511 CrossRef PubMed.
- M. Roos, M. Hofmann, S. Link, M. Ott, J. Balbach, E. Rössler, K. Saalwächter and A. Krushelnitsky, J. Biomol. NMR, 2015, 63, 403–415 CrossRef CAS PubMed.
- T. Blochowicz, C. Tschirwitz, S. Benkhof and E. Rössler, J. Chem. Phys., 2003, 118, 7544–7555 CrossRef CAS.
- V. P. Denisov and B. Halle, J. Mol. Biol., 1995, 245, 682–697 CrossRef CAS PubMed.
- P. D. Cary, D. S. King, C. Crane-Robinson, E. M. Bradbury, A. Rabbani, G. H. Goodwin and E. W. Johns, Eur. J. Biochem., 1980, 112, 577–580 CrossRef CAS PubMed.
- S. Vijay-Kumar, C. E. Bugg, K. D. Wilkinson and W. J. Cook, Proc. Natl. Acad. Sci. U. S. A., 1985, 82, 3582–3585 CrossRef CAS PubMed.
- A. K. Simorellis and P. F. Flynn, J. Am. Chem. Soc., 2006, 128, 9580–9581 CrossRef CAS PubMed.
- W. D. V. Horn, A. K. Simorellis and P. F. Flynn, J. Am. Chem. Soc., 2005, 127, 13553 CrossRef PubMed.
- W. D. V. Horn, M. E. Oglivie and P. F. Flynn, J. Am. Chem. Soc., 2009, 131, 8030 CrossRef PubMed.
- W. I. Sundquist, H. L. Schubert, B. N. Kelly, G. C. Hill, J. M. Holton and C. P. Hill, Mol. Cell, 2004, 13, 783–789 CrossRef CAS PubMed.
- H. Teo, D. B. Veprintsev and R. L. Williams, J. Biol. Chem., 2004, 279, 28689–28696 CrossRef CAS PubMed.
- G. Prag, S. Lee, R. Mattera, C. N. Arighi, B. M. Beach, J. S. Bonifacino and J. H. Hurley, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 2334–2339 CrossRef CAS PubMed.
- P. Peschard, G. Kozlov, T. Lin, I. A. Mirza, A. M. Berghuis, S. Lipkowitz, M. Park and K. Gehring, Mol. Cell, 2007, 27, 474–485 CrossRef CAS PubMed.
- I. Tian and A. E. Garcia, J. Chem. Phys., 2011, 134, 225101 CrossRef PubMed.
- R. D. Fisher, B. Wang, S. L. Alam, D. S. Higginson, H. Robinson, W. I. Sundquist and C. P. Hill, J. Biol. Chem., 2003, 278, 28976–28984 CrossRef CAS PubMed.
Footnote |
| † These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2019 |