DOI:
10.1039/C9RA08294H
(Paper)
RSC Adv., 2019,
9, 37491-37496
Phonon–phonon scattering selection rules and control: an application to nanofriction and thermal transport†
Received
11th October 2019
, Accepted 4th November 2019
First published on 18th November 2019
Abstract
Phonon–phonon scattering processes are the crucial phenomena which account for phonon decay, thermal expansion, heat transfer, protein dynamics, spin relaxation and related quantities. In this work, we show how the symmetries of the system determine which scattering processes are allowed at any order of anharmonic approximation, irrespective of the chemical composition. We also discuss how to control the system symmetries to switch on and off any single scattering process. We apply the presented results to the study and control of nanoscale intrinsic friction and thermal transport in lamellar van der Waals transition metal dichalcogenides. Thanks to its general formulation, the presented framework expands the materials science tool set for the design of nanoengineered thermally-active materials, irrespective of the specific chemical composition and atomic topology.
Introduction
Lattice vibrations are usually described within the harmonic approximation of the potential energy, allowing Newton's equations of motion to be solved and to express atomic displacements as a superposition of sinusoidal functions, i.e., the normal modes of the system.1,2 However, such harmonic theory implies that: (i) a single lattice wave does not decay nor changes form with time because two lattice waves do not interact; (ii) there is no thermal expansion nor heat transfer; (iii) adiabatic and isothermal elastic constants are equal; (iv) elastic constants are independent of temperature and pressure; (v) the heat capacity becomes constant at high temperatures. In real materials, no such implications are strictly observed. Deviations are attributed to anharmonic terms in the interatomic displacements, which allow for phonon–phonon recombination processes. The fine tuning of such processes would allow selective and powerful control of a vast variety of phenomena such as spin relaxation,3,4 protein dynamics,5 thermoelectricity,6 phase transition,7 and thermal conductivity8 among others, which are the basis of the design of ordinary and meta-materials.9
In this work, we show how it is possible to state if a multi-phonon scattering process is allowed by means of symmetry arguments only, without the need to compute the actual value of the interaction strength. Symmetry properties are ordinarily exploited to identify selection rules which govern infrared and Raman transitions.10–15 Such rules are based on group theoretical arguments involving the symmetries of vibrational wave functions of the ground and excited states, and the Hamiltonian representing the external electric field inducing the transition; in this framework, the knowledge of the point group of the system under study is enough to predict which are the allowed transitions. Recent works on thermal transport in carbon nanotubes,16 graphene17 and Ba3N-derived materials18 pionereed the formulation of phonon recombination selection rules by means of symmetry arguments on the lattice potential energy expansion in terms of interatomic force constants; such selection rules can be applied to all processes involving flexural modes or acoustic and optical phonons in specific class of materials.
In what follows, we show that the knowledge of the point group of the system geometry is enough to determine which phonon recombination process is allowed; this result is general and does not have validity restrictions which depend on chemical composition, atom topology, phonon wave vector and branch of the material under study. We also discuss how to control the system symmetries to enable or forbid selected scattering processes; to this aim, we present the study case of nanoscale intrinsic friction and thermal transport in lamellar van der Waals transition metal dichalcogenides (TMDs), such phenomena being relevant in the assembly and functioning of micro- and nanoelectromechanical systems,19,20 photochemical water-splitting, smart health diagnostics and flexible electronics, among others.21
Method
We start by focusing on the first anharmonic term of the Taylor expansion of the potential energy of a system written in terms of normal coordinates; however, the theoretical result which we get is applicable to anharmonic terms of any order. The first anharmonic correction term Vpp reads| |
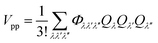 | (1) |
where λ = (q, j) represents the phonon mode with wave vector q and band index j, Qλ is the normal coordinate associated to the phonon λ, and Φλλ′λ′′ is the strength of interaction between the three phonons λ, λ′ and λ′′ involved in the scattering. Φλλ′λ′′ is explicitly written as2,22| |
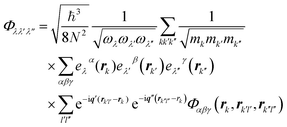 | (2) |
where ℏ is the Planck's constant, N is the number of unit cells, ωλ is the eigenfrequency of the mode λ, mk is the mass of the k-th atom, rk is the position of the k-th atom at the equilibrium, eλα(rk) is the α-th cartesian component of the eigenvector associated to the mode λ and to the k-th atom, rk′l′ (rk′′l′′) is the position of the k′-th (k′′-th) atom in the l′-th (l′′-th) cell replica, and Φαβγ is the third-rank cartesian tensor of the cubic anharmonic force constants.
If, in the initial state, the populations of λ, λ′ and λ′′ are nλ, nλ′ and nλ′′, respectively, then the transition probability with which the three phonons interact is22
| |
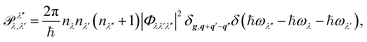 | (3) |
where
δg,q+q′−q′′ = 1(=0) if the sum of the three wave vectors
q,
q′ and
q′′ is (not) equal to a vector
g belonging to the reciprocal lattice,
23 and
δ(ℏ
ωλ′′ − ℏ
ωλ − ℏ
ωλ′) is the Dirac delta which guarantees the conservation of the energy. We here note that, while the populations depend on the temperature,
Φλλ′λ′′ is an intrinsic property of the system. According to
eqn (3),
λ +
λ′ +
λ′′ scattering is not allowed if
Φλλ′λ′′ is null. By a proper control of
Φλλ′λ′′, it is therefore possible to enable or forbid selected scattering processes.
We now show how it is possible to know if a specific phonon recombination is not allowed, that is if Φλλ′λ′′ is null, without evaulating eqn (2); it is worthy to note here that the result which we will obtain is analogous to the selection rules of infrared and Raman transitions.
As a first step, let's notice that the eigenvectors do not depend on the cell replica, that is eλβ(rk′) = eλβ(rk′l′) and eλγ(rk′′) = eλγ(rk′′l′′). If r is a generic vector spanning the cartesian space, then each eigenvector eλ(r) can be thought to be a function defined in this way:
| |
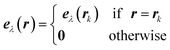 | (4) |
where
0 is the null vector. The quantity
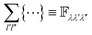
in
eqn (2) is a third rank tensor which corresponds to the Fourier transform of the cartesian anharmonic tensor
Φαβγ. Similarly to definition 4, we can then define the function
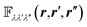
as
| |
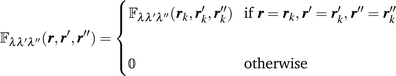 | (5) |
where

is the null third-rank tensor. We then consider the scalar function
M(
r,
r′,
r′′) defined as
| |
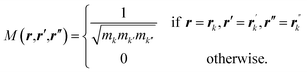 | (6) |
By using the definition of the triple inner product24 between three vectors and a third-rank tensor, we can then write eqn (2) in a more compact form as
| |
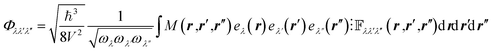 | (7) |
where we changed the sum over the atomic labels into an integral over the cartesian positions thanks to the definitions 4, 5 and 6. By exploiting a known result from group theory,
10 we can state that, if the integrand in
eqn (7) forms a basis for the totally symmetric representation, that is, if the direct product among the representations of each factor of the integrand contains the totally symmetric representation, then the integral is not null and the
λ +
λ′ =
λ′′ recombination is allowed.
25 The
M and
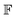
functions are both invariant under symmetry operations, since the former is a scalar and the latter depends only on the relative positions of the atoms; then, they both transform as the totally symmetric representation. Therefore, to know if
Φλλ′λ′′ can assume values different than zero, it is enough to check if the direct product of the irreducible representations of
eλ,
eλ′ and
eλ′′ contains the totally symmetric representation. In other words, given the irreducible representations
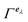
,
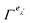
and
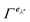
, for which the eigenvectors
eλ,
eλ′,
eλ′′ are respectively a basis, then
| |
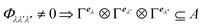 | (8) |
which states that if the direct product among the irreducible representations contain the totally symmetric representation
A, then the
λ +
λ′ =
λ′′ scattering is allowed. The magnitude of the allowed process depends on the actual numerical value of the interaction strength which, in turn, depends on the specific values of the anharmonic force constants. It is worthy to notice here that this result is general and also applies to scattering processes involving more than three phonons, corresponding to anharmonic terms of any order, since the relative interaction strength can be recast in a form analogous to
eqn (7). In fact, condition 8 can be generalized as
| |
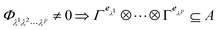 | (9) |
for a scattering process involving
p phonons. By controlling the symmetries of the eigenvectors
eλ, it is then possible to forbid/allow selected scattering processes. Moreover, condition 9 is a quick guide to identify which recombination processes are not null and at which order of anharmonic approximation.
Results and discussion
As showcase examples, we apply this result to the study of intrinsic friction and thermal conductivity in MX2 transition metal dichalcogenides. Related results are discussed in what follows.
Intrinsic friction
Nanoscale intrinsic friction in lamellar van der Waals MX2 transition metal dichalcogenides occurs during relative sliding of adjacent layers. We have already shown26–29 that all possible sliding directions can be represented by suitable combinations of few vibrational modes, namely sliding modes; moreover, the layer sliding occurs until such modes own enough energy, and therefore, the frictional forces are all those forces which activate dissipative processes producing a depopulation of the sliding modes.30 Such depopulation occurs via phonon–phonon scattering involving sliding and non-sliding, hence dissipative, modes; if such scattering is forbidden, then dissipation does not occur and sliding is longer active. In what follows, we show how symmetries determine which dissipation processes are allowed and suggest how to control them. Computational details and schematic of the discussed modes with relative irreducible representations are reported in the ESI.†
We choose the 2H polymorph crystalline MX2 compound as a reference structure (Fig. 1), with M = Mo, W and X = S, Se, Te and hexagonal P63/mmc symmetry (SG 194). Starting from such reference geometries, for each MX2 system, we truncate the structure along the c periodic direction and consider only 2, 3, 4, 5 and 6 adjacent layers. In this way, we build 5 model geometries that we name MX-nL, where n corresponds to the considered number of adjacent MX2 layers. The space group of the MX-nL systems is P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (#164) or P
m1 (#164) or P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (#187) if n is even or odd, respectively. Regardless the chemical composition, the sliding modes which mainly contribute to relative layer displacements have wave vector corresponding to the Γ point of the Brillouin zone (see ESI†). One of the main sources of energy dissipation preventing layer gliding is the recombination involving rigid lateral (Fig. 2a) and vertical (Fig. 2b) layer shifts. At increasing number of layers, more and more sliding modes are present other than rigid ones, thus increasing the number of possible recombination channels; however, some of the latter are not effective because the corresponding recombination process is forbidden by symmetry. For example, the scattering involving lateral layer sliding at different velocity (Fig. 2c) and vertical layer shift (Fig. 2b) is not allowed in systems with an even number of layers (point group
m2 (#187) if n is even or odd, respectively. Regardless the chemical composition, the sliding modes which mainly contribute to relative layer displacements have wave vector corresponding to the Γ point of the Brillouin zone (see ESI†). One of the main sources of energy dissipation preventing layer gliding is the recombination involving rigid lateral (Fig. 2a) and vertical (Fig. 2b) layer shifts. At increasing number of layers, more and more sliding modes are present other than rigid ones, thus increasing the number of possible recombination channels; however, some of the latter are not effective because the corresponding recombination process is forbidden by symmetry. For example, the scattering involving lateral layer sliding at different velocity (Fig. 2c) and vertical layer shift (Fig. 2b) is not allowed in systems with an even number of layers (point group ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), while it is active for odd number of layers (point group
m), while it is active for odd number of layers (point group ![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2), no matter the chemical composition of the system. In order to confirm such prediction, for all the considered compounds, we calculated the Φλλ′λ′′ matrix elements by means of eqn (2) with q = q′ = q′′ = Γ and band indices j, j′, j′′ spanning the integer value range [1, 3N], where N is the number of atoms in the system; indeed, the numerical values we obtain for allowed processes vary in the interval [10−9, 10−12] eV, while the magnitude of forbidden processes is of the order of 10−30 eV. Moreover, it is immediately apparent that the number of possible phonon recombinations involving sliding and dissipative modes, hence the relevant Φλλ′λ′′ values to be calculated, rapidly increases with the size of the system. In this respect, eqn (8) (in general Equation (9)) constitutes a fast tool to promptly identify which are the Φλλ′λ′′ coefficients, hence the recombination channels, which effectively contribute to the global dissipation process, thus avoiding unnecessary computational effort to evaluate anharmonic terms which will turn out to be null by symmetry.
m2), no matter the chemical composition of the system. In order to confirm such prediction, for all the considered compounds, we calculated the Φλλ′λ′′ matrix elements by means of eqn (2) with q = q′ = q′′ = Γ and band indices j, j′, j′′ spanning the integer value range [1, 3N], where N is the number of atoms in the system; indeed, the numerical values we obtain for allowed processes vary in the interval [10−9, 10−12] eV, while the magnitude of forbidden processes is of the order of 10−30 eV. Moreover, it is immediately apparent that the number of possible phonon recombinations involving sliding and dissipative modes, hence the relevant Φλλ′λ′′ values to be calculated, rapidly increases with the size of the system. In this respect, eqn (8) (in general Equation (9)) constitutes a fast tool to promptly identify which are the Φλλ′λ′′ coefficients, hence the recombination channels, which effectively contribute to the global dissipation process, thus avoiding unnecessary computational effort to evaluate anharmonic terms which will turn out to be null by symmetry.
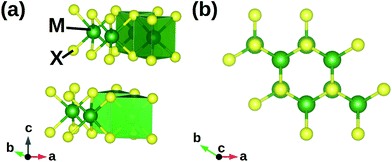 |
| | Fig. 1 Hexagonal P63/mmc structure of 2H polymorph MX2 model geometry. M–X bonds are arranged in a trigonal prismatic coordination forming MX2 layers bound together by van der Waals interactions. | |
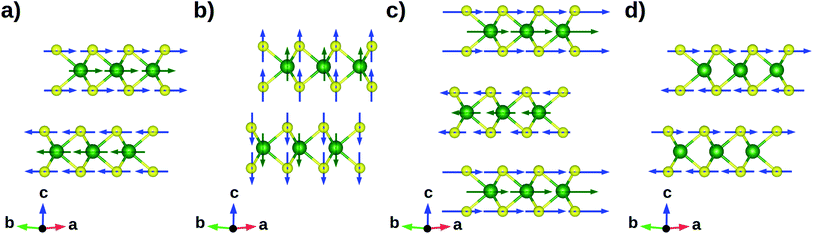 |
| | Fig. 2 Schematic representation of selected phonon modes: (a) rigid layer sliding, (b) rigid vertical shifting, (c) layer sliding at different velocity and (d) out-of-phase lateral shift of X anions. Displacement patterns represented in (a and c) and (b and d) correspond to sliding and dissipative modes, respectively. Larger arrow size indicates larger atomic displacement per time unit. Atom color code is the same as in Fig. 1. | |
The scattering involving rigid lateral and vertical layer shifts is allowed in finite n-layer systems but it is forbidden by symmetry in the bulk. In this latter case, one of the main dissipative processes involving the sliding modes is instead due to the dissipative mode corresponding to out-of-phase lateral shift of the X atom layers only (Fig. 2d). Since symmetries cannot be now adjusted by changing the number of layers (n = ∞ in bulk), we choose to perform a cation substitution in order to turn off this dissipation channel. We then consider the Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MoS2 system which we already identified as promising tribological material,26 with the symmetry of Cmcm (#63) space group. With such specific Ti → Mo substitution, the dissipative scattering which was allowed in the pristine MoS2 bulk, is now forbidden by symmetry (see ESI†).
MoS2 system which we already identified as promising tribological material,26 with the symmetry of Cmcm (#63) space group. With such specific Ti → Mo substitution, the dissipative scattering which was allowed in the pristine MoS2 bulk, is now forbidden by symmetry (see ESI†).
Thermal conductivity
The lattice thermal conductivity tensor 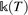 as a function of the temperature T can be written in terms of phonon modes of the system22 as
as a function of the temperature T can be written in terms of phonon modes of the system22 as| |
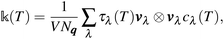 | (10) |
where V is the unit cell volume, Nq is the number of q points, τλ(T) is the relaxation time of the mode λ, vλ is the group velocity of the phonon λ and cλ(T) is the mode specific heat capacity. In bulk MX2 TMDs, lattice thermal conductivity is dominated by phonon recombination processes involving low- and high-frequency phonon bands.31,32 Inspection of eqn (10) suggests that one way to control such processes is to act on the group velocity vλ; indeed, this has already been achieved by inducing strain on the pristine structure via ion intercalation in the interlayer region, or by applying an external pressure.31–33 An other approach is to modify the relaxation time τλ. One of the factors determining the value of τλ is the phonon–phonon interaction strength, since| |
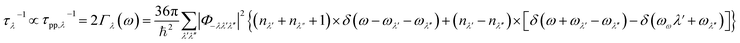 | (11) |
where τpp,λ is the phonon lifetime due to phonon–phonon scattering and Γλ(ω) is the self energy.34 From eqn (10) and eqn (11), it is apparent that the higher the number of non-null Φλλ′λ′′ elements, the shorter the lifetime of the phonon τλ and the lower the lattice thermal conductivity. We now show how the selection rule represented by eqn (8) can help to identify which interband scattering processes bring an effective contribution to the thermal conductivity. We first notice that each band j has a specific symmetry which does not depend on the considered q-point;35 all the allowed scattering processes can then be identified by means of eqn (8) at any q-point and are valid throughout the entire Brillouin zone, regardless of the chosen {q, q′, q′′} triplet. The phonon band structure of all the considered model systems of the bulk MX2 compounds is formed by 18 bands (since there are 6 atoms in the primitive unit cell), labeled with an increasing integer number j = 1⋯18; the low- and high-frequency bands are labeled as 1–6 and 7–18, respectively. The number of interband three-phonon processes is then 6 × 18 × 18 = 1944, which rapidly increases with the number of atoms in the unit cell.36 By applying eqn (8), we observe that the number of active interband processes is 1656, all the remaining one being forbidden by symmetry. In solving the Boltzmann transport equation, a mesh comprising at least about 4300 q-points is required, in order to obtain reliable values of the tensor 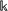 ;31 this corresponds to a maximum of about 8
;31 this corresponds to a maximum of about 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359
359![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 matrix elements to be evaluated; by using eqn (8), it is possible to precompute a list of effective transitions to be considered, and the number of Φλλ′λ′′ elements to determine is reduced by 15% (about 7
000 matrix elements to be evaluated; by using eqn (8), it is possible to precompute a list of effective transitions to be considered, and the number of Φλλ′λ′′ elements to determine is reduced by 15% (about 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121
121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 values).
000 values).
The detail of the microscopic mechanisms giving an effective contribution to the thermal conductivity can then be revealed by identifying the allowed phonon–phonon scattering processes. As an example, we consider the 1656 identified allowed processes in MoS2 and WS2, and calculate the average 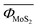 and
and 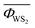 values of the corresponding Φλλ′λ′′ elements on a mesh of 19 × 19 × 12 = 4332 q-points; we obtain 1.92 × 10−14 and 1.79 × 10−14 eV for
values of the corresponding Φλλ′λ′′ elements on a mesh of 19 × 19 × 12 = 4332 q-points; we obtain 1.92 × 10−14 and 1.79 × 10−14 eV for 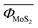 and
and 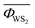 , respectively. This result can explain the higher thermal conductivity in bulk WS2 compared to bulk MoS2 discussed in a previous work,31 while the identified allowed processes constitute the microscopic origin of such difference. Once the allowed processes have been determined, it is possible to selectively control them. To show this, we here examine the case of the Ti
, respectively. This result can explain the higher thermal conductivity in bulk WS2 compared to bulk MoS2 discussed in a previous work,31 while the identified allowed processes constitute the microscopic origin of such difference. Once the allowed processes have been determined, it is possible to selectively control them. To show this, we here examine the case of the Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MoS2 bulk system already considered above. The Ti-doped MoS2 system is represented by a unit cell containing 24 atoms, 4 times larger than the unit cell of pristine MoS2, corresponding to a larger number of phonons hence interband recombinations (i.e., 124
MoS2 bulk system already considered above. The Ti-doped MoS2 system is represented by a unit cell containing 24 atoms, 4 times larger than the unit cell of pristine MoS2, corresponding to a larger number of phonons hence interband recombinations (i.e., 124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416); however, the induced change of the band symmetry reduces to 62
416); however, the induced change of the band symmetry reduces to 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 (about 50% less) the number of allowed transitions effectively contributing to
464 (about 50% less) the number of allowed transitions effectively contributing to 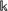 . The average
. The average 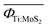 value which we obtain for such transitions is 6.54 × 10−14 eV; by comparing this value with those obtained for the MoS2 and WS2 systems, this compound is expected to show lower phonon lifetimes hence lower phonon contribution to the thermal conductivity.
value which we obtain for such transitions is 6.54 × 10−14 eV; by comparing this value with those obtained for the MoS2 and WS2 systems, this compound is expected to show lower phonon lifetimes hence lower phonon contribution to the thermal conductivity.
Conclusions
By exploiting the knowledge of the symmetries of the phonon modes of the stable structure, it is therefore possible to predict if a specific multi-phonon scattering process is allowed without the need to compute the corresponding interaction strength coefficient. As a consequence, by acting on the symmetries of the system, it is possible to switch on and off specific phonon channels. As a first example, we apply such result to the analysis of dissipative processes preventing layer sliding in lamellar var der Waals transition metal dichalcogenides. We find that, in finite systems, the number of layers determine the symmetries of the atom geometry, hence which specific dissipation channel is active. In bulk systems, where the number of layers in the unit cell is fixed, a viable solution to act on the symmetries is to perform a cation substitution. Other ways to switch on/off selected dissipation channels is the local control of the symmetries via atom dislocations, creation of vacancies, local distortion of the atomic geometry and introduction of geometric constraints (e.g. presence of fixed substrate). We then exploit the here presented selection rules to identify the effective contribution to the lattice thermal conductivity in bulk TMDs. We find that the number of active scattering processes is 85% of the total amount obtained without considering the symmetry restrictions on the involved eigenvectors. The number of effective phonon recombinations found in the considered bulk systems is further reduced by lowering the atomic site symmetries via cation substitution.
The specific value of the interaction strength, that is the magnitude of the scattering process, can be tuned via a fine control of the electronic structure or the lattice vibrations through collective descriptors such as orbital polarization,37,38 bond covalency39,40 and cophonicity.26 The present results can be exploited to build a simulative framework which combine symmetry, electronic and dynamical descriptors, in order to finely design scattering processes in solid state materials. Finally, the selection rule condensed in eqn (9) could help to further expedite the calculation of anharmonic terms in large automated libraries41 or software packages which compute physical quantities involving anharmonic corrections,34,42,43 where symmetry properties are already exploited in the calculation of phonon self-energies.44
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. C. gratefully thanks A. Togo for implementing some features in the PHONO3PY34 software which facilitated the analysis of the interaction strength coefficients. This work has been done with the support of the Czech Science Foundation (projects 17-24164Y), and the Ministry of Education, Youth and Sports with project “Novel nanostructures for engineering applications” No. CZ.02.1.01/0.0/0.0/16_026/0008396. This work was supported by The Ministry of Education, Youth and Sports from the Large Infrastructures for Research, Experimental Development and Innovations project “IT4Innovations National Supercomputing Center — LM2015070”.
Notes and references
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons Inc., 1971 Search PubMed.
- D. M. Wallace, Thermodynamics of Crystals, John Wiley & Sons Inc, United States of America, 1972 Search PubMed.
- A. Lunghi, F. Totti, R. Sessoli and S. Sanvito, Nat. Commun., 2017, 8, 14620 CrossRef PubMed.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275 RSC.
- A. Nicolaï, P. Delarue and P. Senet, Sci. Rep., 2015, 5, 18128 CrossRef PubMed.
- X. Lu, D. T. Morelli, Y. Xia, F. Zhou, V. Ozolins, H. Chi, X. Zhou and C. Uher, Adv. Energy Mater., 2013, 3, 342–348 CrossRef CAS.
- T. Matsunaga, N. Yamada, R. Kojima, S. Shamoto, M. Sato, H. Tanida, T. Uruga, S. Kohara, M. Takata, P. Zalden, G. Bruns, I. Sergueev, H. C. Wille, R. P. Hermann and M. Wuttig, Adv. Funct. Mater., 2011, 21, 2232–2239 CrossRef CAS.
- A. Shanker, C. Li, G.-H. Kim, D. Gidley, K. P. Pipe and J. Kim, Sci. Adv., 2017, 3, e1700342 CrossRef PubMed.
- M. Kadic, G. W. Milton, M. van Hecke and M. Wegener, Nature Reviews Physics, 2019, 1, 198–210 CrossRef.
- F. Cotton, Chemical Application of Group Theory, Wiley-Interscience, 3rd edn, 1990 Search PubMed.
- R. Evarestov and V. Smirnov, Site Symmetry in Crystals, Springer-Verlag, 1st edn, 1993 Search PubMed.
- L. M. Malard, M. H. D. Guimarães, D. L. Mafra, M. S. C. Mazzoni and A. Jorio, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 125426 CrossRef.
- A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401 CrossRef CAS PubMed.
- N. Kokanyan, M. Bazzan, L. Vittadello, D. Chapron, E. Kokanyan and M. D. Fontana, Sci. Rep., 2019, 9, 13408 CrossRef PubMed.
- A. Stupakiewicz, K. Szerenos, M. D. Davydova, K. A. Zvezdin, A. K. Zvezdin, A. Kirilyuk and A. V. Kimel, Nat. Commun., 2019, 10, 612 CrossRef CAS PubMed.
- L. Lindsay, D. A. Broido and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125407 CrossRef.
- L. Lindsay, D. A. Broido and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115427 CrossRef.
- T. Pandey, C. A. Polanco, V. R. Cooper, D. S. Parker and L. Lindsay, Phys. Rev. B, 2018, 98, 241405 CrossRef.
- B. Bhushan, Microelectron. Eng., 2007, 84, 387–412 CrossRef CAS.
- S. H. Kim, D. B. Asay and M. T. Dugger, Nano Today, 2007, 2, 22–29 CrossRef.
- G. Zhang and Y.-W. Zhang, J. Mater. Chem. C, 2017, 5, 7684–7698 RSC.
- J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, Oxford University Press, 2001 Search PubMed.
- If g is the null vector, this condition
is easily interpreted as conservation of momentum.
- The triple inner product of three generic vectors X, Y and Z with a generic third-rank tensor
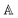 is defined as
is defined as 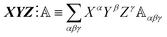 where the greek letter indices span the cartesian dimensions.22.
where the greek letter indices span the cartesian dimensions.22. - This general group theoretical result is based on the observation that the integration of a function f over the entire space is null if the function is not symmetric with respect to all possible symmetries. The property of f to be symmetric with respect to all possible symmetries is represented by the totally symmetric representation.
- A. Cammarata and T. Polcar, Inorg. Chem., 2015, 54, 5739–5744 CrossRef CAS PubMed.
- A. Cammarata and T. Polcar, RSC Adv., 2015, 5, 106809–106818 RSC.
- A. Cammarata and T. Polcar, Phys. Chem. Chem. Phys., 2016, 18, 4807–4813 RSC.
- A. Cammarata and T. Polcar, Phys. Rev. B, 2017, 96, 085406 CrossRef.
- A. Cammarata, P. Nicolini, K. Simonovic, E. Ukraintsev and T. Polcar, Phys. Rev. B, 2019, 99, 094309 CrossRef CAS.
- D. O. Lindroth and P. Erhart, Phys. Rev. B, 2016, 94, 115205 CrossRef.
- S. Chen, A. Sood, E. Pop, K. E. Goodson and D. Donadio, 2D Materials, 2019, 6, 025033 CrossRef CAS.
- X. Meng, T. Pandey, J. Jeong, S. Fu, J. Yang, K. Chen, A. Singh, F. He, X. Xu, J. Zhou, W.-P. Hsieh, A. K. Singh, J.-F. Lin and Y. Wang, Phys. Rev. Lett., 2019, 122, 155901 CrossRef CAS PubMed.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- A. Authier, International Tables for Crystallography Volume D: Physical properties of crystals, Kluwer Academic Publisher, 2013 Search PubMed.
- The interband scattering must involve at least one low-frequency phonon; if j is a low-frequency phonon, then it can assume any of the 6 different values corresponding to one of the low-frequency phonon labels (i.e., any value from 1 to 6), while j′ and j′′ can assume any value in the range [1, 18].
- M. J. Han, C. A. Marianetti and A. J. Millis, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 134408 CrossRef.
- A. Cammarata and J. M. Rondinelli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 155135 CrossRef.
- M.-H. Whangbo, H.-J. Koo, A. Villesuzanne and M. Pouchard, Inorg. Chem., 2002, 41, 1920–1929 CrossRef CAS PubMed.
- A. Cammarata and J. M. Rondinelli, J. Chem. Phys., 2014, 141, 114704 CrossRef PubMed.
- J. J. Plata, P. Nath, D. Usanmaz, J. Carrete, C. Toher, M. de Jong, M. Asta, M. Fornari, M. B. Nardelli and S. Curtarolo, npj Comput. Mater., 2017, 3, 45 CrossRef.
- A. Chernatynskiy and S. R. Phillpot, Comput. Phys. Commun., 2015, 192, 196–204 CrossRef CAS.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- L. Chaput, A. Togo, I. Tanaka and G. Hug, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 094302 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Model geometries, computational details, schematics and symmetry of the sliding and dissipative modes discussed along the text, and irreducible representation direct product tables. See DOI: 10.1039/c9ra08294h |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
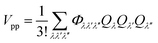
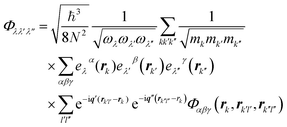
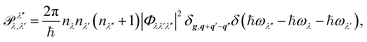
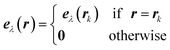
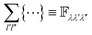 in eqn (2) is a third rank tensor which corresponds to the Fourier transform of the cartesian anharmonic tensor Φαβγ. Similarly to definition 4, we can then define the function
in eqn (2) is a third rank tensor which corresponds to the Fourier transform of the cartesian anharmonic tensor Φαβγ. Similarly to definition 4, we can then define the function 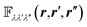 as
as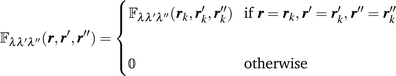
 is the null third-rank tensor. We then consider the scalar function M(r, r′, r′′) defined as
is the null third-rank tensor. We then consider the scalar function M(r, r′, r′′) defined as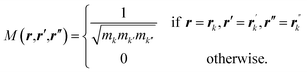
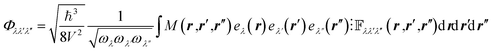
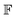 functions are both invariant under symmetry operations, since the former is a scalar and the latter depends only on the relative positions of the atoms; then, they both transform as the totally symmetric representation. Therefore, to know if Φλλ′λ′′ can assume values different than zero, it is enough to check if the direct product of the irreducible representations of eλ, eλ′ and eλ′′ contains the totally symmetric representation. In other words, given the irreducible representations
functions are both invariant under symmetry operations, since the former is a scalar and the latter depends only on the relative positions of the atoms; then, they both transform as the totally symmetric representation. Therefore, to know if Φλλ′λ′′ can assume values different than zero, it is enough to check if the direct product of the irreducible representations of eλ, eλ′ and eλ′′ contains the totally symmetric representation. In other words, given the irreducible representations 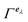 ,
, 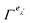 and
and 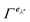 , for which the eigenvectors eλ, eλ′, eλ′′ are respectively a basis, then
, for which the eigenvectors eλ, eλ′, eλ′′ are respectively a basis, then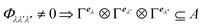
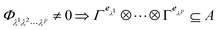
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1 (#164) or P
m1 (#164) or P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 (#187) if n is even or odd, respectively. Regardless the chemical composition, the sliding modes which mainly contribute to relative layer displacements have wave vector corresponding to the Γ point of the Brillouin zone (see ESI†). One of the main sources of energy dissipation preventing layer gliding is the recombination involving rigid lateral (Fig. 2a) and vertical (Fig. 2b) layer shifts. At increasing number of layers, more and more sliding modes are present other than rigid ones, thus increasing the number of possible recombination channels; however, some of the latter are not effective because the corresponding recombination process is forbidden by symmetry. For example, the scattering involving lateral layer sliding at different velocity (Fig. 2c) and vertical layer shift (Fig. 2b) is not allowed in systems with an even number of layers (point group
m2 (#187) if n is even or odd, respectively. Regardless the chemical composition, the sliding modes which mainly contribute to relative layer displacements have wave vector corresponding to the Γ point of the Brillouin zone (see ESI†). One of the main sources of energy dissipation preventing layer gliding is the recombination involving rigid lateral (Fig. 2a) and vertical (Fig. 2b) layer shifts. At increasing number of layers, more and more sliding modes are present other than rigid ones, thus increasing the number of possible recombination channels; however, some of the latter are not effective because the corresponding recombination process is forbidden by symmetry. For example, the scattering involving lateral layer sliding at different velocity (Fig. 2c) and vertical layer shift (Fig. 2b) is not allowed in systems with an even number of layers (point group ![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m), while it is active for odd number of layers (point group
m), while it is active for odd number of layers (point group ![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2), no matter the chemical composition of the system. In order to confirm such prediction, for all the considered compounds, we calculated the Φλλ′λ′′ matrix elements by means of eqn (2) with q = q′ = q′′ = Γ and band indices j, j′, j′′ spanning the integer value range [1, 3N], where N is the number of atoms in the system; indeed, the numerical values we obtain for allowed processes vary in the interval [10−9, 10−12] eV, while the magnitude of forbidden processes is of the order of 10−30 eV. Moreover, it is immediately apparent that the number of possible phonon recombinations involving sliding and dissipative modes, hence the relevant Φλλ′λ′′ values to be calculated, rapidly increases with the size of the system. In this respect, eqn (8) (in general Equation (9)) constitutes a fast tool to promptly identify which are the Φλλ′λ′′ coefficients, hence the recombination channels, which effectively contribute to the global dissipation process, thus avoiding unnecessary computational effort to evaluate anharmonic terms which will turn out to be null by symmetry.
m2), no matter the chemical composition of the system. In order to confirm such prediction, for all the considered compounds, we calculated the Φλλ′λ′′ matrix elements by means of eqn (2) with q = q′ = q′′ = Γ and band indices j, j′, j′′ spanning the integer value range [1, 3N], where N is the number of atoms in the system; indeed, the numerical values we obtain for allowed processes vary in the interval [10−9, 10−12] eV, while the magnitude of forbidden processes is of the order of 10−30 eV. Moreover, it is immediately apparent that the number of possible phonon recombinations involving sliding and dissipative modes, hence the relevant Φλλ′λ′′ values to be calculated, rapidly increases with the size of the system. In this respect, eqn (8) (in general Equation (9)) constitutes a fast tool to promptly identify which are the Φλλ′λ′′ coefficients, hence the recombination channels, which effectively contribute to the global dissipation process, thus avoiding unnecessary computational effort to evaluate anharmonic terms which will turn out to be null by symmetry.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MoS2 system which we already identified as promising tribological material,26 with the symmetry of Cmcm (#63) space group. With such specific Ti → Mo substitution, the dissipative scattering which was allowed in the pristine MoS2 bulk, is now forbidden by symmetry (see ESI†).
MoS2 system which we already identified as promising tribological material,26 with the symmetry of Cmcm (#63) space group. With such specific Ti → Mo substitution, the dissipative scattering which was allowed in the pristine MoS2 bulk, is now forbidden by symmetry (see ESI†).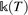 as a function of the temperature T can be written in terms of phonon modes of the system22 as
as a function of the temperature T can be written in terms of phonon modes of the system22 as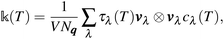
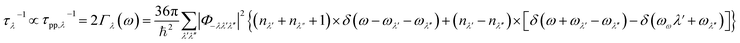
 ;31 this corresponds to a maximum of about 8
;31 this corresponds to a maximum of about 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 359
359![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 matrix elements to be evaluated; by using eqn (8), it is possible to precompute a list of effective transitions to be considered, and the number of Φλλ′λ′′ elements to determine is reduced by 15% (about 7
000 matrix elements to be evaluated; by using eqn (8), it is possible to precompute a list of effective transitions to be considered, and the number of Φλλ′λ′′ elements to determine is reduced by 15% (about 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 121
121![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 values).
000 values).
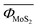 and
and 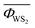 values of the corresponding Φλλ′λ′′ elements on a mesh of 19 × 19 × 12 = 4332 q-points; we obtain 1.92 × 10−14 and 1.79 × 10−14 eV for
values of the corresponding Φλλ′λ′′ elements on a mesh of 19 × 19 × 12 = 4332 q-points; we obtain 1.92 × 10−14 and 1.79 × 10−14 eV for 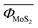 and
and 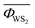 , respectively. This result can explain the higher thermal conductivity in bulk WS2 compared to bulk MoS2 discussed in a previous work,31 while the identified allowed processes constitute the microscopic origin of such difference. Once the allowed processes have been determined, it is possible to selectively control them. To show this, we here examine the case of the Ti
, respectively. This result can explain the higher thermal conductivity in bulk WS2 compared to bulk MoS2 discussed in a previous work,31 while the identified allowed processes constitute the microscopic origin of such difference. Once the allowed processes have been determined, it is possible to selectively control them. To show this, we here examine the case of the Ti![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MoS2 bulk system already considered above. The Ti-doped MoS2 system is represented by a unit cell containing 24 atoms, 4 times larger than the unit cell of pristine MoS2, corresponding to a larger number of phonons hence interband recombinations (i.e., 124
MoS2 bulk system already considered above. The Ti-doped MoS2 system is represented by a unit cell containing 24 atoms, 4 times larger than the unit cell of pristine MoS2, corresponding to a larger number of phonons hence interband recombinations (i.e., 124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416); however, the induced change of the band symmetry reduces to 62
416); however, the induced change of the band symmetry reduces to 62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 (about 50% less) the number of allowed transitions effectively contributing to
464 (about 50% less) the number of allowed transitions effectively contributing to 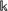 . The average
. The average 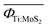 value which we obtain for such transitions is 6.54 × 10−14 eV; by comparing this value with those obtained for the MoS2 and WS2 systems, this compound is expected to show lower phonon lifetimes hence lower phonon contribution to the thermal conductivity.
value which we obtain for such transitions is 6.54 × 10−14 eV; by comparing this value with those obtained for the MoS2 and WS2 systems, this compound is expected to show lower phonon lifetimes hence lower phonon contribution to the thermal conductivity.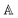 is defined as
is defined as 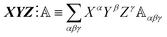 where the greek letter indices span the cartesian dimensions.22.
where the greek letter indices span the cartesian dimensions.22.