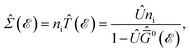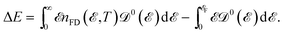DOI:
10.1039/C9RA08446K
(Paper)
RSC Adv., 2019,
9, 41569-41580
Schottky anomaly and Néel temperature treatment of possible perturbed hydrogenated AA-stacked graphene, SiC, and h-BN bilayers
Received
16th October 2019
, Accepted 20th November 2019
First published on 16th December 2019
Abstract
In this paper, the potential of engineering and manipulating the electronic heat capacity and Pauli susceptibility of pristine and perturbed hydrogenated AA-stacked graphene, SiC (silicon carbide), and h-BN (hexagonal boron nitride) bilayers is studied using a designed transverse Zeeman magnetic field and the dilute charged impurity. The tight-binding Hamiltonian model, the Born approximation and the Green’s function method describe the carrier dynamics up to a certain degree. The unperturbed results show that the heat capacity and susceptibility of all bilayers increase with different hydrogenation doping configurations. We also found that the maximum heat capacity and susceptibility relates to the chair-like and table-like configurations. Also, the graphene possesses the highest activity compared to SiC and h-BN lattices due to its zero on-site energies. For the Zeeman magnetic field-induced Schottky anomaly and the Néel temperature corresponding to the maximum electronic heat capacity, EHCMax., and Pauli spin paramagnetic susceptibility, PSPSMax., respectively, the pristine EHCMax. (PSPSMax.) decreases (increases) with the Zeeman field. On the other hand, the corresponding results for reduced table-like and reduced chair-like lattices illustrate that both EHCMax. and PSPSMax. decrease with the Zeeman field, on average. However, under the influence of the dilute charged impurity, the pristine EHCMax. of graphene (SiC and h-BN) decreases (increases) with impurity concentration for all configurations while the corresponding PSPSMax. fluctuates (decreases) for the pristine (reduced table-like and reduced chair-like) case. These findings introduce hydrogenated AA-stacked bilayers as versatile candidates for real applications.
1. Introduction
Graphene was discovered around fifteen years ago1–3 and opened the era of real 2D materials, for which the motion of carriers is limited completely in-plane. The special structure of graphene leads to unusual physical properties that are absent in conventional low-dimensional materials. Charged carriers in graphene are governed by the Dirac equation for massless fermions, resulting in high mobility, and high electrical and thermal conductivity. However, a disadvantage of graphene is related to its zero band gap because a finite band gap is necessary for logic devices. Therefore, in parallel with continuously exploring new properties in graphene and exploiting its potential applications, scientists have been seeking other materials to keep the desirable properties of graphene and to have a finite band gap, extinguishing the gapless nature of graphene as well as opening the era of atomically single-layer 2D materials.4–6
Researchers have been fabricating and designing many different materials based on monolayer structures. For example, by stacking certain monolayers, one can obtain multi-layer structures, such as bilayer graphene,7,8 bilayer SiC,9,10 bilayer h-BN,11–13 and other heterostructures composed of different kinds of materials.14–16 It has been shown that, compared to monolayers, bilayer structures have many interesting properties, which depend considerably on the stacking type and the twist angle between the layers.7,16 The main advantage of bilayer graphene is the possibility to induce locally a band gap and tune its magnitude by applying a strong electric field perpendicular to the carbon sheets, which is useful to design next-generation transistors that would work faster and use less energy; especially important for portable battery-powered devices. Besides, by cutting 2D monolayers into ribbons with a width on the order of nanometers, electron systems in one-dimensional nanoribbons are obtained. On the other hand, if we further limit the motion of electrons in the remained direction, we have 0D quantum dots.
Although the above-mentioned 2D materials possess their own fascinating physical and chemical features, there exist different ways to tailor their intrinsic properties. One of the ways is chemical functionalization by adding other atoms onto the system such as H, N, O, F, CH, or COOH. The purpose of the functionalization is to break the sp2-hybridization, and hence, modify the band gap of materials, which is an important consideration for other features. Also, hydrogenated graphene monolayers and bilayers have been reported.17–25 It has been shown that fully hydrogenated graphene has a band gap of 3.43 eV,26 making it a potential candidate in logic applications. Moreover, the ferromagnetic and antiferromagnetic ordering have been reported for different couplings between H and C atoms.21 The properties of hydrogenated graphene also depend on the hydrogenation configuration. It has been shown that fully hydrogenated graphene has different electronic properties in comparison with the half- or reduced hydrogenated form.18,27,28 Similarly, chemical functionalization has also been reported widely in SiC10,29–33 and h-BN.34
When such materials are affected by electronic and magnetic perturbations, for example, their electronic properties change significantly and accordingly other physical properties including thermodynamic properties will be affected. Studies of the effect of charged impurities on the densities of state and electronic phase transition in many graphene-like structures have been performed in detail.28 Like single-layer graphene, an electric field can be used to change the electronic structure of the bilayer. For example, the energy gap in bilayer graphene on the SiO2/Si wafer can be tuned using an electric field controlled by a double gate.35,36 The presence of a Zeeman magnetic field also changes dramatically the electronic properties of materials. The effect of an external Zeeman magnetic field on the electronic phase has been investigated in bilayer graphene.28 As a matter of fact, the displacement of the energy levels using the Zeeman magnetic field produces uniformly spaced multiplet splitting of the spectral lines, leading to an increase of a factor of two of the electron spin angular momentum. This, in turn, affects the orbital behavior of charge carriers and eventually leads to different physical properties.
Many studies have indicated that 2D materials (including graphene, SiC and h-BN) are potential candidates for heat dissipation and heat conduction technologies in modern electronic devices.13,37 The thermal conductivity and heat capacity of the bilayer graphene nanoribbons, bilayer boron nitride nanoribbons and graphene/boron nitride nanoribbons with different stacking types have been investigated theoretically.15,38 The results show that the thermal conductivity for all structures increases with temperature to its maximum value and then decreases with further increase of temperature. Also, the heat capacity of all structures shows a maximum value, implying the Schottky anomaly. M. Yarmohammadi39 calculated the electronic heat capacity in hydrogenated monolayer and bilayer graphene taking account of the contribution of hybridized orbitals by a Green’s function approach using a tight-binding Hamiltonian. The obtained results conclude that bilayer graphene can be a very promising material for thermoelectric applications. The results show the appearance of the maximum and minimum values in the Schottky anomaly, respectively, for hydrogenated bilayer AA-stacked and monolayer table-like configurations. However, the combined effect of the Zeeman magnetic field and charged impurities on the thermodynamic properties in hydrogenated graphene, h-BN, and SiC bilayers has not been considered yet.
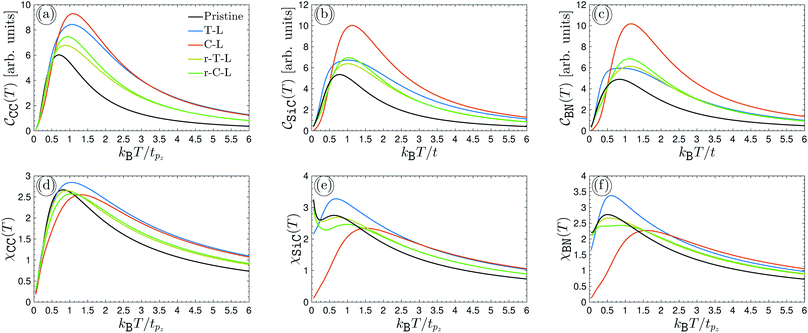
Due to their novel electronic properties under electronic and magnetic perturbation, the thermodynamic properties in the above-mentioned bilayer structures are expected to show many interesting behaviors and need to be studied, especially from a theoretical point of view. The purpose is to shed light on their new properties and to reveal their potential applications. In this work, we investigate the effects of a transverse Zeeman magnetic field and charged impurities on the electronic and thermodynamic properties of the hydrogenated-bilayer graphene, -bilayer SiC and -bilayer h-BN. The Zeeman magnetic field effect is obtained from the Green’s functions using a Hamiltonian in the tight-binding approximation. Also, the effect of charged impurities is taken into account via the electron–impurity interaction potential in the first Born approximation.
This paper is organized as follows. In section 2, we introduce the main Hamiltonian model of our system, in both the pristine and hydrogenated states. A detailed formulation of electronic DOS, EHC, and PSPS of AA-stacked hydrogenated bilayer states is discussed in section 3. Further, we demonstrate explicitly how the key remarks of our results are taken from the obtained EHC and PSPS. In section 4, we formulate the perturbed states in the presence of a transverse Zeeman magnetic field and dilute charged impurities. We discuss how the Schottky anomaly and the Néel temperature can be manipulated by these perturbations. We summarize our findings and discuss directions for our future research in section 5.
2. Tight-binding Hamiltonian model for the AA-stacked bilayer honeycomb lattice
2.1 Pristine state
In this section, we intend to describe the basic theoretical formulation of the present paper in detail using the tight-binding Hamiltonian model. In what follows, the physical constant ℏ is set to unity for simplicity. First, we focus on the pristine bilayer honeycomb lattices, see Fig. 1, and then the perturbations, transverse Zeeman magnetic field and dilute charged impurity, are considered. The real-space full-band Hamiltonian of such bilayers are given by| |
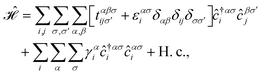 | (1) |
where the hopping between an electron with spin σ from sublattice α located at the unit cell i to another electron with spin σ′ from sublattice β in the unit cell j (with annihilation and creation operators 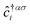 and
and 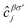 , respectively) is described by the coefficient
, respectively) is described by the coefficient 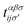 . In addition, εασi stands for the on-site energy of the sublattices. It should be noted that the index for the number of layers is omitted here because one can consider all four atoms {A1, B1, A2, B2} for α and β sublattice indices where needed, as well as the corresponding unit cells for the i and j indices. Note that the hopping and on-site energies are different for the graphene, SiC and h-BN cases;40–42 see Table 1. However, both energies for SiC and h-BN bilayers are normalized to the graphene values in the present paper. The on-site energy for carbon atoms in graphene are set to zero for simplicity, while the graphene hopping energy is
. In addition, εασi stands for the on-site energy of the sublattices. It should be noted that the index for the number of layers is omitted here because one can consider all four atoms {A1, B1, A2, B2} for α and β sublattice indices where needed, as well as the corresponding unit cells for the i and j indices. Note that the hopping and on-site energies are different for the graphene, SiC and h-BN cases;40–42 see Table 1. However, both energies for SiC and h-BN bilayers are normalized to the graphene values in the present paper. The on-site energy for carbon atoms in graphene are set to zero for simplicity, while the graphene hopping energy is 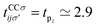 eV.1–3,43,44 Furthermore, the interlayer hopping parameter is defined by γαi, which is around 0.2 eV for graphene carbon atoms and different for other cases, see Table 1. As for the in-plane lattice constants, we deal with aC–C ≃ 1.42 Å, aSi–C ≃ 1.89 Å and aB–N ≃ 1.45 Å,1–3,40–44 while we approximate the distance between two layers as 3.35 Å, 3.5 Å and 3.22 Å, respectively, for graphene, SiC and h-BN.14,45–47
eV.1–3,43,44 Furthermore, the interlayer hopping parameter is defined by γαi, which is around 0.2 eV for graphene carbon atoms and different for other cases, see Table 1. As for the in-plane lattice constants, we deal with aC–C ≃ 1.42 Å, aSi–C ≃ 1.89 Å and aB–N ≃ 1.45 Å,1–3,40–44 while we approximate the distance between two layers as 3.35 Å, 3.5 Å and 3.22 Å, respectively, for graphene, SiC and h-BN.14,45–47
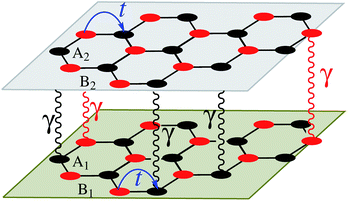 |
| | Fig. 1 Real-space description of atoms arranged in a bilayer honeycomb lattice with intralayer t and interlayer γ hopping energies. The atoms for the first layer are called A1 and B1, while the second layer contains A2 and B2 atoms. The hopping energies, as well as the atoms, are different for the graphene, SiC, and h-BN cases. | |
Table 1 Hopping energy and all on-site energies, taken from ref. 1–3 and 40–44 for graphene, SiC and h-BN simple bilayers
| Lattice |
t/eV |
γ/eV |
εαi/eV |
εβi/eV |
| Graphene |
2.90 |
0.20 |
0 |
0 |
| SiC |
1.42 |
0.15 |
0 |
−2.85 |
| h-BN |
1.95 |
0.17 |
0 |
−4.57 |
2.2 Hydrogenated state
The hydrogen contribution with spin up to the dynamics of carriers in simple AA-stacked bilayer honeycomb lattices should be included in both the on-site and hopping energy terms, however, we keep the on-site energy of sublattice unchanged in the presence of hydrogen. Since the coupling between sublattices and hydrogen atoms is perpendicular to each layer, the only orbital, pz, is considered in the contributed energy. However, between two hydrogen atoms doped on each sublattice, there also exists a hopping, which will be introduced later. Thus, the Hamiltonian for the hydrogenated AA-stacked bilayer honeycomb lattices can be written as| |
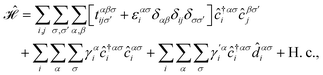 | (2) |
where the operator ![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) is used for the doped hydrogen atoms on the unit cell i and the sublattice α with the coupling strength γ′ ≃ 5.72 eV.48 Herein, four configurations for the hydrogenation doping are considered, namely table-like (T-L), chair-like (C-L), reduced table-like (r-T-L), and reduced chair-like (r-C-L). In the case of the table-like configuration, both sublattices in each layer are doped with hydrogen in the same direction, but opposite directions compared to other layers; for example, if the hydrogen is aligned to the +z axis for both sublattices in the upper layer, it is aligned to the −z axis for both sublattices in the lower layer. In the case of the chair-like configuration, hydrogen doping for the sublattices in each layer is different, meaning that if the hydrogen is aligned to the +z axis for the A sublattice, it is along the −z axis for the B sublattice, and in general this is reversed for other layers. Finally, in the case of reduced versions, the same configuration exists but only on one of the layers.39,49,50
is used for the doped hydrogen atoms on the unit cell i and the sublattice α with the coupling strength γ′ ≃ 5.72 eV.48 Herein, four configurations for the hydrogenation doping are considered, namely table-like (T-L), chair-like (C-L), reduced table-like (r-T-L), and reduced chair-like (r-C-L). In the case of the table-like configuration, both sublattices in each layer are doped with hydrogen in the same direction, but opposite directions compared to other layers; for example, if the hydrogen is aligned to the +z axis for both sublattices in the upper layer, it is aligned to the −z axis for both sublattices in the lower layer. In the case of the chair-like configuration, hydrogen doping for the sublattices in each layer is different, meaning that if the hydrogen is aligned to the +z axis for the A sublattice, it is along the −z axis for the B sublattice, and in general this is reversed for other layers. Finally, in the case of reduced versions, the same configuration exists but only on one of the layers.39,49,50
Now, we turn to the basic electronic and thermodynamic properties of the above-mentioned lattices in the absence and presence of perturbations, such as a transverse Zeeman magnetic field and impurity scattering.
3. Basic electronic and thermodynamic properties of the hydrogenated AA-stacked bilayer honeycomb lattice
As mentioned before, the main focus of this paper is on the hydrogenated bilayer systems. For this reason, we start with the eqn (2). The energy–momentum dispersions of the discussed lattices can be obtained via diagonalizing the reciprocal-space Hamiltonian (after taking into account the Fourier transformation computations) in eqn (2), given by a 5 × 5 matrix | |
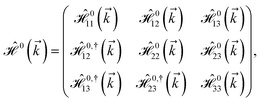 | (3) |
where index 1, 2 and 3 refers to the atoms in the first layer, atoms in the second layer and doped hydrogen atoms, respectively. Clearly, from the formulated kinetic and potential terms in the Hamiltonian, all elements are finite and non-zero. Therefore, the element 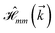 ,
, 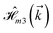 and
and 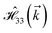 for m ∈ {1, 2} describes the possible coupling and interactions between atoms in the layer m, between the atoms in the layer m and hydrogen, and between the hydrogen atoms themselves, respectively. Using the geometry structure of lattices and simple lattice vectors, the elements are calculated as
for m ∈ {1, 2} describes the possible coupling and interactions between atoms in the layer m, between the atoms in the layer m and hydrogen, and between the hydrogen atoms themselves, respectively. Using the geometry structure of lattices and simple lattice vectors, the elements are calculated as| |
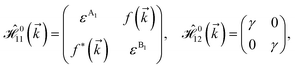 | (4a) |
| |
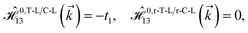 | (4b) |
| |
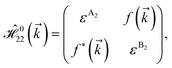 | (4c) |
| |
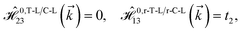 | (4d) |
| |
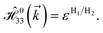 | (4e) |
where the structure factor is defined by f(![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = t(1 + exp[+i
) = t(1 + exp[+i![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ·
·![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) 1] + exp [+i
1] + exp [+i![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ·
·![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) 2]) and
2]) and 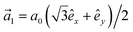 and
and 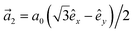 with a0 as the in-plane lattice constants. Also, t1 = t2 = 5.72 eV and εH1/H2 = −2.4 eV are, respectively, the hopping energy between sublattices and hydrogen, and hydrogen itself.
with a0 as the in-plane lattice constants. Also, t1 = t2 = 5.72 eV and εH1/H2 = −2.4 eV are, respectively, the hopping energy between sublattices and hydrogen, and hydrogen itself.
Having the Hamiltonian in the matrix-representation, the energy–momentum dispersion can be calculated easily via
| |
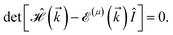 | (5) |
where
μ ∈ {1, ⋯, 5} stands for the band index, both conduction and valence, and
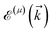
is the corresponding energy band. The dispersion energy is one of the fundamental quantities for studying the electronic features of a system. However, since we are interested in using the respective relation to electronic DOS, we switch to the DOS calculations to obtain the electronic heat capacity and Pauli spin paramagnetic susceptibility quantities. There are various ways to do so, however, we use the Green’s function approach to calculate the DOS, which helps us later when implementing the impurity effects. Using
eqn (3), the explicit form of non-interacting Green’s function matrix,
i.e. in the absence of external perturbations, can be calculated
via51| |
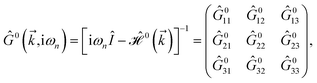 | (6) |
where
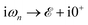
refers to the fermionic Matsubara frequency
51 and in the numerical calculation we use 0
+ = 5 meV for the root solving problem. The Green’s function obtained in
eqn (6) is used to find the DOS of the mentioned lattices by tracing out the imaginary part of the diagonal Green’s function elements in terms of Lehmann representation:
51| |
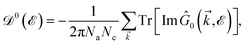 | (7) |
where
Na and
Nc refer to the number of atoms in the unit cell and the number of unit cells, respectively. As mentioned before, to further our purposes and to get close to the main aim of the present paper, the electronic DOS of all considered systems are calculated here. The explicit forms of the Green’s function elements are too lengthy and are not presented. Note that, we calculate the total DOS by summing over the whole first Brillouin zone (FBZ) for
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
= (
kx,
ky) with
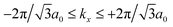
and −4π/3
a0 ≤
ky ≤ +4π/3
a0.
28 Let us use the calculated DOSs for the thermodynamic quantities.
It is well known that the heat capacity of solids can be divided into three contributions, the electronic part, the phononic part, and the magnonic part. In the present work, we restrict ourselves to the first contribution, i.e. the electronic heat capacity (EHC), and leave the two others for our future research to come. EHC appears as one of the most important thermodynamic properties of low-dimensional systems, which over a wide range of temperatures provides insight into the physics of the system. Therefore, it may provide the essential clue in the understanding of the microscopic behavior of pristine and perturbed hydrogenated AA-stacked bilayer honeycomb lattices.52 Consider if the system including N electrons observes a change in total energy ΔE when it undergoes a temperature change ΔT in the interval (0, T), thus, the EHC of this system can be expressed as53
| |
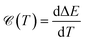 | (8) |
where
In the relation above, 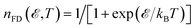 is the Fermi–Dirac distribution function and the number of electrons is given by
is the Fermi–Dirac distribution function and the number of electrons is given by 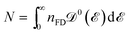 . Obviously, one observes that the electronic DOS
. Obviously, one observes that the electronic DOS 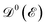 emerges in the heart of
emerges in the heart of 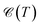 and in order to develop the microscopic theory of EHC a very careful evaluation of electron Green’s functions and DOS becomes essential. Rewriting ΔE as
and in order to develop the microscopic theory of EHC a very careful evaluation of electron Green’s functions and DOS becomes essential. Rewriting ΔE as
| |
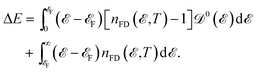 | (9) |
which possesses some benefits for separation of the needed energies to bring the electrons to the Fermi level from the levels beneath or to take the electrons from the Fermi level to the levels above. From
eqn (8), after taking into account the derivation of Δ
E with respect to the temperature, the EHC can be obtained as
| |
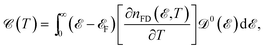 | (10) |
which is obvious that by taking the Fermi level as origin of energy
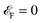
and considering all energies with respect to that, EHC could be restated as
| |
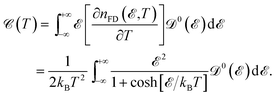 | (11) |
Now, we proceed to the subject of the Pauli spin paramagnetic susceptibility (PSPS) as another thermodynamic property. In the realm of magnetism, magnetization is considered as the response of the system to the external magnetic field; and these two are related by susceptibility χ. Every magnetic material has a linear response region for sufficiently small external perturbations wherein the linear response theory is applicable. To explain the itinerant moments, quasi-free conduction electrons carry a permanent moment of one Bohr magneton each. In this case, we deal with the Pauli paramagnetism, which is calculated by Nolting54
| |
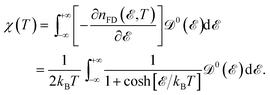 | (12) |
Thereby, the EHC and PSPS quantities of hydrogenated AA-stacked bilayer honeycomb lattices in the absence and presence of a transverse Zeeman magnetic field and dilute charged impurity are going to be discussed in the following.
It is necessary, first of all, to clarify the issues related to experiments and the conditions under which our results are appropriate. We have tried to choose logical and reliable values for all sets of parameters; however, although most of the theoretical frameworks for perturbations applied here are taken from valid models and techniques, our findings are theoretical predictions and may not be soon addressed absolutely by experiments. We start with the pristine cases. Concerning the model and the hydrogenated bilayer system, an illustration of 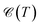 and χ(T) quantities is shown in Fig. 2(a)–(f).
and χ(T) quantities is shown in Fig. 2(a)–(f).
 |
| | Fig. 2 The electronic heat capacity [panels (a)–(c)] and the Pauli spin paramagnetic susceptibility [panels (d)–(f)] of pristine and hydrogenated AA-stacked bilayer honeycomb lattices, namely graphene, SiC and h-BN. The systems are in the absence of external perturbations. | |
As can be seen from panels (a)–(c), all three systems possess the same trend in the absence of perturbations. At first glance, although the different intensities for different configurations are observed, the EHC has a maximum value with a decreasing and increasing curve after and before this maximum point, the so-called Schottky anomaly. The physical meaning of this Schottky anomaly can be traced out from the entropy and probability transition of the states. The entropy decreases on cooling below the critical temperature corresponding to the anomaly, however, near the critical thermal energy, the entropy change is small, this must mean that only a very small fraction of electrons participate in the transition to the upper energy levels. For this reason, the EHC decreases after the critical thermal energy and approaches zero at high enough temperatures, implying that the thermal effects are dominant at higher temperatures and quantum ones die out gradually. For different configurations of hydrogen atom doping, one expects different treatments for EHC versus temperature due to different electronic states and electronic wave-functions. Depending on the type of hydrogen doping, the new emerged electronic states take place at different energy levels and consequently, EHC curves must not be the same, as illustrated in Fig. 2(a)–(f).
In Fig. 2(a)–(c), we anticipate some results for the pristine EHCs when hydrogen is doped differently. The initial intensity of EHCs in the case of AA-stacked non-hydrogenated bilayer lattices (black curve) becomes stronger in terms of hydrogenation independent of the lattice. However, the increasing rate in graphene (panel (a)) is more than the two others (panels (b) and (c)). SiC and h-BN lattices behave more or less the same and different from graphene, which can be understood from the zero and non-zero on-site energies of sublattices in graphene and SiC/h-BN, respectively. The non-zero on-site energies in SiC/h-BN come to play role in overlapping the strength of electronic wave functions as well as in screening effects between different sublattices. Although the units of EHCs are arbitrary throughout the present paper, we can report a percentage difference between the numbers of Schottky anomalies in different lattices. The percentage difference criterion translates the difference between two different values into a percentage, for which one needs a point of reference, commonly the most honest point of reference would be to use the average, or midpoint, of the two numbers.
The pristine case of graphene shows an 11.81% and 20.52% difference compared to pristine SiC and h-BN (black curves). The T-L hydrogenated bilayer graphene reports a 22.36% and 34.26% percentage difference compared to SiC and h-BN, respectively, while C-L gives rise to around 7.6% and 9.17%. These values for the case of r-T-L in graphene compared to SiC and h-BN can be extracted as, respectively, 6% and 9.82%, while for the r-C-L lattices, one obtains 7% and 8.5%. These percentage differences clarify that the capacity of graphene in response to the heat in all non-hydrogenated and hydrogenated cases is different from other SiC and h-BN systems. Furthermore, it is clear that the maximum EHC in all lattices is related to the C-L case (the red curves in panels (a)–(c)), i.e. the case for which the hydrogen doping for each sublattice in each layer is different. Another point refers to the changes in EHCs at high enough temperatures. As the formulations say, the T-L and C-L and on the other hand the r-T-L and r-C-L cases must lead to convergence at some point due to the similarity in their manner of hydrogenation. From Fig. 2(a)–(c), one sees that it is likely that this is the case and one observes a convergence at kBT/tpz ≥ 2.5 in graphene, at kBT/tpz ≥ 2.5 in r-T-L and r-C-L, and at kBT/tpz ≥ 6 in the T-L and C-L SiC/h-BN system. The evaluation of EHC with high temperature is unaffected due to the vanishing quantum effects. Of course, these were expected to be different for different lattices since the scattering rate and induced potential by thermal energy are different (stemming from different intra- and inter-layer hoppings).
Concerning the implementation of these lattices for the PSPS, since the formula presented in eqn (12) is similar to the one for EHC in eqn (11), thus, it is expected for PSPS be modified as EHC, as confirmed in Fig. 2(d)–(f). However, due to the thermal factors in EHC and PSPS, the same trends are not expected. We must report the variation of PSPS with temperature and hydrogenation doping way in another way. In contrast to the EHC quantity, a non-zero initial value is observed for the PSPS, i.e. PSPS at the zero temperature is not zero. On the other hand, the T-L configuration of hydrogen doping has the greatest contribution to the PSPSs, while this was the case for C-L in EHCs. These points allow us to conclude that the systems respond to the temperature changes differently in the absence and presence of the magnetic field, i.e. when dealing with both the spin and charge of carriers. As for the percentage differences, one achieves around 2.9% and 3.9% for maximum PSPS occurring at the thermal point, the so-called Néel temperature for such lattices, of pristine graphene compared to both pristine SiC and h-BN, respectively. However, T-L case reports around 14% and 17%. On the other hand, C-L differs with the percentages of 8.67% and 11.74%, respectively, for SiC and h-BN. Meanwhile, r-T-L shows a 1.5% and 0.52% difference between graphene, SiC, and h-BN; for the percentage differences in the case of r-C-L the values of 4.45% and 5.67% are calculated. These findings and comparisons are useful for experimentalists to choose which system is the best choice for some purposes. It is necessary to mention that these results are reported for the first time here and have not been reported already, which is one of the novelties of the present paper. Also, the amounts of PSPSs at zero temperature for different configurations will keep us active during further future researches, as they can be controlled with external perturbation for certain special aims.
The PSPS of SiC behaves differently compared to two other lattices. As is well-known, it is a semiconductor, while graphene and h-BN are a semi-metal and insulator, respectively. For this reason, it has non-zero transitions and responses even at fairly small temperatures, leading to many applications of silicon carbide, such as slide bearings, sealing rings, wear parts, sintering aids, crucibles, semiconductor applications, heating elements, burner nozzles, and heat exchangers. By this, we mean that the semiconducting behavior of SiC is the main reason for its different behavior compared to the two others. After interpreting the case of lattices in the absence of external perturbations, we are interested in seeing the alterations in EHC and PSPS at the Schottky anomaly and the Néel temperature points in the presence of external electronic and magnetic perturbations. To investigate the behavior of perturbed EHC and PSPS at the Schottky anomaly and the Néel temperature, respectively, for the systems above-configured (since the number of figures will be high and will lead to confusion for the reader), only three cases (pristine, r-T-L and r-C-L) are considered in what follows. In the next section, we will deal with them.
4. Perturbed hydrogenated AA-stacked bilayer honeycomb lattice
In this section, we formulate the requirements for our numerical results in the presence of the perturbations. We introduce the Hamiltonian of the transverse Zeeman magnetic field as well as the dilute charged impurities.
4.1 Transverse Zeeman magnetic field effects
In the presence of transverse Zeeman magnetic field (TZMF), only the spin degree of freedom is affected in the present paper, leading to spin-splitting effects. Eventually, the spintronic applications of such systems, besides the electronic logic applications, come to the board. The tight-binding Hamiltonian model for TZMF-induced AA-stacked bilayer honeycomb lattice is simply given by| |
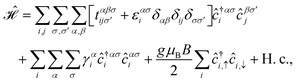 | (13) |
where gμBB is the applied transverse magnetic field potential which couples only to the electron spin, μB is the Bohr magneton, and g is the degeneracy number. Due to the spin-splitting effects, the dimensions of the Hamiltonian matrices in the reciprocal space are doubled. The 10 × 10 Hamiltonian matrix is written as| |
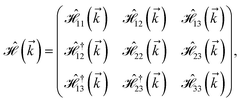 | (14) |
where, in the same manner, the elements can be calculated as| |
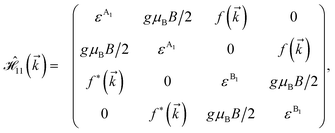 | (15a) |
| |
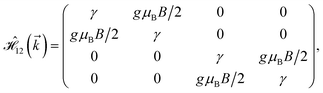 | (15b) |
| |
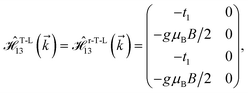 | (15c) |
| |
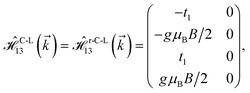 | (15d) |
| |
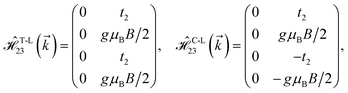 | (15e) |
| |
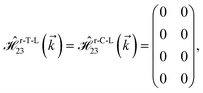 | (15f) |
| |
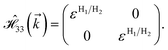 | (15g) |
Thus, the TZMF-induced Green’s functions, the so-called interacting Green’s functions, can be achieved
| |
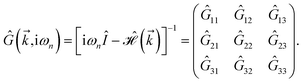 | (16) |
Following these new Green’s functions, the interacting DOS, EHC, and PSPS can easily be achieved with the aid of eqn (7), (11) and (12) with a summation over the imaginary parts of 10 diagonal Green’s functions. The behavior of the electrons of the systems coupled to the TZMF can be extracted from the exchange interaction between them to align the electron’s spin direction. The results are presented in Fig. 3. It is necessary to mention that, since the TZMF in the case of gμBB/tpz = 0 does not split the states and there is a degeneracy as expected, thus, the Schottky anomaly and Néel temperature amounts are doubled due to an added degeneracy factor of 2.
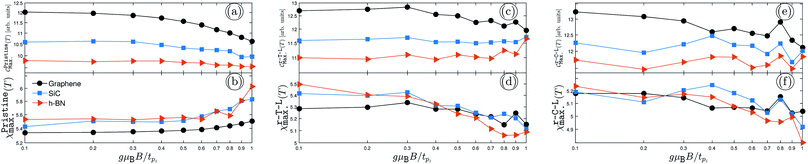 |
| | Fig. 3 The changes of EHCMax. and PSPSMax. of pristine {(a) and (b)}, r-T-L {(c) and (d)} and r-C-L {(e) and (f)} of graphene, SiC and h-BN with the TZMF. | |
In the same manner presented for the unperturbed systems, the changes of EHCMax. and PSPSMax. of pristine {(a) and (b)}, r-T-L {(c) and (d)} and r-C-L {(e) and (f)} of graphene, SiC and h-BN with the TZMF are represented in Fig. 3. Interestingly, notable evolutions are obtained targeting the TZMF-dependent thermal effects on the EHC and PSPS when the TZMF is set from 0 to tpz. Fig. 3 shows that both EHC and PSPS are affected under the TZMF with lattice-dependent change rates. In general, both SiC and h-BN structures contribute equally to the evolution of EHCMax. and PSPSMax., whilst there is a discrepancy between the behavior of graphene, which can be connected to the on-site and hopping energies dependencies of the structures. Let us focus on each panel separately.
In Fig. 3(a) and (b), we assess the TZMF-induced EHCMax. and PSPSMax. of pristine AA-stacked bilayer structures. It is necessary to remember that the graphene possesses a major (minor) contribution to the EHCMax. (PSPSMax.) and decreases (increases) for gμBB/tpz ≥ 0.4, implying that a high enough TZMFs for graphene is required to affect the response to the temperature changes and the external magnetic field. However, it seems that this TZMF strength is a critical point for all systems, such that the EHCMax. (PSPSMax.) of SiC and h-BN decreases (increases) after this potential point, shown by blue and red curves in panels (a) and (b). From the trends, one can see the intensities converge independently of the structure type, i.e. independently of the on-site and hopping energies at high enough TZMFs, which perhaps is far from reality and cannot be reported. Another remark is the behavior of PSPSMax. of SiC and h-BN at gμBB/tpz ≥ 0.7 and 0.9, which is perfectly independent of the sublattices.
From the hydrogenation doping point of view, the convergence point must be formed and appear when the system is hydrogenated because the hydrogen acts as a compressor for electronic wave functions (and in other words, for the atomic orbitals). As can be seen from Fig. 3(c) and (d), which corresponds to the same results as Fig. 3(a) and (b) but for r-T-L lattices, the convergence behavior of EHCMax. and PSPSMax. is confirmed as expected and all structures lead to almost the same value at high enough TZMFs. This is an interesting result, which confirms the role of hydrogen doping. On the other hand, graphene still has the greatest contribution to the EHCMax. at low TZMFs and the greatest contribution to the PSPSMax. is related to the h-BN structure. Also, there are some discrepancies between the results in Fig. 3(a), (b) and (c), (d), for which we deal with an increasing trend of EHCMax. for SiC and h-BN with gμBB/tpz as well as we deal with decreasing trends for all structures in the case of PSPSMax.. These are expected, as explained before, due to the role of hydrogen atoms, which add new electronic states, and eventually new transport treatments. For this reason, different responses come to play a role.
Furthermore, the EHCMax. and PSPSMax. of r-C-L also alter with gμBB/tpz and are located at different points compared to other pristine and r-T-L configurations depending on the TZMF strength, the reason for which can be traced back to their different hydrogen locations. As the final remark in this subsection, one could mention that the convergence emerges again but at higher TZMFs, which is not shown here; see Fig. 3(e) and (f). As in Fig. 3(c) and (d), on average, all EHCsMax. and PSPSsMax. decrease with TZMF. Depending on their requirements and purposes, experimentalists can use these theoretically predicted data. For example, the changes of EHCMax. help to obtain information about the electronic phase transition, while the changes of PSPSMax. leads to the magnetic phase transitions.28,38,55,56 Note that the different percentages reported in the previous sections are no longer valid in the presence of TZMF and can be calculated easily for all structures and both quantities.
Furthermore, we seek to study the impurity scattering effects. In the next subsection, we will formulate the dilute charged impurity effects to see how EHCMax. and PSPSMax. alter with the impurity concentration ni. It should be emphasized that throughout this work, a system of units is chosen such that most physical constants are equal to 1; thus the calculated quantities are in arbitrary units and show the qualitative behavior of the considered systems. We have organized the calculations in the framework of such a system of units.
4.2 Impurity scattering effects
In this section, the effects of external randomly doped impurities are considered using the Born approximation and T-matrix theory wherein the impurity concentration ni and impurity scattering potential νi are modeled simply. To keep the system stable under impurity doping, we mainly focus on the short-range noninteracting charged impurities, which can be modeled as a Dirac delta function potential with the constant parameter νi in the reciprocal space. It should be noted that the doping process can be performed with a single impurity or many impurities with low-density concentrations. The former case is not our interest and the latter will be considered here. Taking the average over the random local configuration of many impurities, we neglect the importance of the location of impurity in the present formulation.57–59 Thus, the impurity potential Û = νiÎ contains the non-zero elements in Î meaning that the impurity resides on the whole AA-stacked layers. The sign of νi affects the scattering process, such that the positive scattering potential νi binds up the negative electrons or positive holes, while negative νi attracts positive electrons. Consider a bilayer hydrogenated AA-stacked honeycomb lattice subjected to the charged impurity atoms. Within the scattering theory framework, new Green’s functions are required to describe the electronic correlations between scattered host electrons. Fortunately, the electronic self-energy describing the electronic correlation between guest electrons are responsible for this. For the local impurities, we deal with isotropic scatterings U, and the self-energy 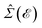 depends on the energy only, given by,51,60
depends on the energy only, given by,51,60| |
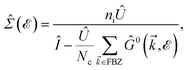 | (17) |
where ni = Ni/Vc is the density of Ni impurity atoms and Vc refers to the volume of all simulated unit cells. For more details, see the Appendix A. This expression leads to the interacting Green’s functions via the Dyson’s equation,51| |
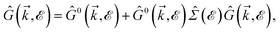 | (18) |
and eventually, in the same manner, the impurity-induced Green’s functions can be achieved as| |
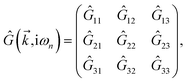 | (19) |
and again, these new Green’s functions lead to the impurity-induced DOS, EHC, and PSPS easily. The impurity scattering effects can be investigated in the absence and presence of TZMF, however, we will only focus on the individual effects of impurities here and will leave the combined effects of TZMF and impurity for our future research.
From the results of the TZMF effects, it can be inferred that the presence of impurities gives rise to different results but almost the same behavior for SiC and h-BN structures. One of the main important findings, i.e. the convergence limit, is here not valid any more, meaning that new midband and midgap states are added to the systems due to the presence of impurities and the hydrogen cannot control the convergence point significantly compared to the TZMF. Again, we take into account many impurities with low-density concentrations and take the average over their random local configuration. This implies that the location of the impurity does not matter in the formulation. Although one may consider the location of the impurity as well the distance away from the scattering center using the Fourier transform of Green’s functions, this is out of the scope of the present paper. In the present work, the positive ni and νi are studied and the negative ones are considered as well. Positive νi tends to bind negative electrons or positive holes, while negative νi attracts positive electrons. The sign of νi affects the scattering process, while the sign of ni just changes the sign of the energy at which the midband or midgap states take place. From eqn (7), we notice that the impurity-induced DOS is related to the poles of interacting Green’s functions given by eqn (19), containing the poles of self-energy 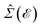 . Thus, the new poles associated with impurities come into play role in impurity-induced DOS at energy
. Thus, the new poles associated with impurities come into play role in impurity-induced DOS at energy  satisfying the equation
satisfying the equation
| |
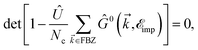 | (20) |
where the solution of this equation leads to the midband and midgap states.
To get a deeper understanding of the midband and midgap states effects, first of all, we consider pristine impurity-induced AA-stacked bilayer systems with the scattering potential νi = 0.5 eV, as presented in Fig. 4. The impurity concentrations ni = 0.05, 0.1 and 0.15 are examined. At first glance, the EHCMax., Fig. 4(a), decreases for graphene with ni, while it increases for SiC/h-BN. From the last values of the different structures, it is clear that the convergence does not take place for the dilute impurity limit. However, the PSPSMax., Fig. 4(b), shows different trends, such that it increases for graphene and h-BN with ni on the average, whist it decreases with ni for SiC. This can be understood from the fact that the zero and strong on-site energies are important for the response of the systems to the external magnetic field when the impurity is present. In addition to these main changes, it is simple to deduce that the relation EHCCCMax. > EHCSiCMax. > EHCBNMax. is always valid, while PSPSCCMax.PSPSSiCMax. < PSPSBNMax.. This general statement reconfirms that the structure- and atom-dependent on-site and hopping energies are more than important and for special purposes, the right one must be considered and examined. All these alterations in the presence of impurities together lead to different electronic and magnetic phases of the pristine systems, which has been reported already in the work by Hoi et al.28
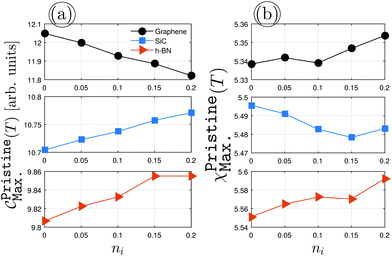 |
| | Fig. 4 The changes of EHCMax. (a) and PSPSMax. of pristine (b) of graphene (upper panels), SiC (middle panels) and h-BN (lower panels) with the dilute charge impurity concentration ni at the fixed scattering potential νi = 0.5 eV. | |
Generally, the path of propagating electronic waves is influenced by the impurity, affecting the scattering rate and dynamics of carriers. Let us turn to the other two configurations, i.e. AA-stacked hydrogenated bilayers r-T-L and r-C-L in the presence of impurity doping.
Fig. 5 demonstrates the impurity-induced EHCMax. and PSPSMax. of charge carriers on the AA-stacked hydrogenated bilayer r-T-L and r-C-L surfaces at νi = 0.5 eV. Similar behaviors to Fig. 4(a) appear, having gained a decreasing (an increasing) trend of graphene (SiC/h-BN) for EHCMax. around the Fermi energy; see Fig. 5(a) and (c). Applying impurity at νi = 0.5 eV, the midgap states appear and the spatial distribution of electronic waves breaks down. Nevertheless, in contrast to the pristine case, the PSPSMax. decreases for all structures with the impurity concentration, see Fig. 5(b) and (d). As a quick comparison between the upper and lower panels of Fig. 5 for r-T-L and r-C-L configurations, respectively, the difference percentage corresponding to the initial and final values of EHCMax. of r-T-L leads to 0.31%, 1.88% and 1.81% for graphene, SiC, and h-BN, respectively, while 0.53%, 1.21%, and 1.29% correspond to the EHCMax. of r-C-L. On the other hand, one finds quickly the percentages of 1.53% (1.06%), 2.04% (1.36%) and 1.86% (1.76%) for PSPSMax. of r-T-L (r-C-L). For a more accurate statement, however, we need to reach an electronic and magnetic phase transition condition so that the study of EHC and PSPS engineering can be fully addressed. This can be done by impurity doping in another way, i.e. in the way that the scattering potential νi varies, while the impurity concentration ni is fixed, however, the presented results here are those which are closer to experiment and from this point, we stop further investigations.
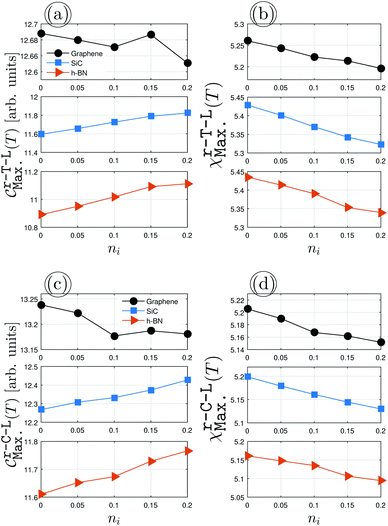 |
| | Fig. 5 The changes of EHCMax. and PSPSMax. of r-T-L {(a) and (b)} and r-C-L {(c) and (d)} of graphene (upper panels), SiC (middle panels) and h-BN (lower panels) with the dilute charge impurity concentration ni at the fixed scattering potential νi = 0.5 eV. | |
5. Conclusions
In conclusion, the perturbations are thought to be essential ingredients for tailoring the carrier dynamics of a system. For studying the transverse Zeeman magnetic field and dilute charged impurity effects on the electronic heat capacity and Pauli paramagnetic susceptibility of both pristine and hydrogenated AA-stacked graphene, SiC, and h-BN bilayers, the tight-binding model, Green’s function technique and the Born approximation are employed both analytically and numerically. Several hydrogenation model systems, namely table-like, chair-like, reduced table-like, and reduced chair-like are studied for all three structures. The table-like (chair-like) show a majority contribution to the heat capacity and susceptibility in the pristine non-hydrogenated structures. If certain commensurability Zeeman fields are met, besides the decreasing behavior of heat capacity and susceptibility for both reduced table-like and reduced chair-like configurations, a convergence at high enough Zeeman fields can be achieved. Also, we concluded that the non-hydrogenated systems show different behaviors compared to their hydrogenated counterparts in the presence of a dilute charged impurity, confirming the role of hydrogen doping. However, the results will not converge at high enough impurity concentrations, within the dilute regime, and to pave the way towards experimental verification, another approximation for the convergence is needed. Our findings provide useful routes to logic applications.
A. Appendix
In this appendix, we provide the derivation of eqn (17). Here we mainly focus on the short-range noninteracting charged impurities (note that this kind of impurity can be hydrogen adsorbed or other dopants for which the scattering potential is induced to the bilayer Dirac fermions), which can be modeled as a Dirac delta function potential| |
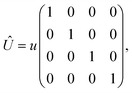 | (21) |
where the non-zero elements mean that the impurity resides on both sublattices. Consider the scattering potential  with two momenta
with two momenta ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and
and  , as the initial momentum of surface electrons and the momentum transferred by impurity scattering at the energy contour
, as the initial momentum of surface electrons and the momentum transferred by impurity scattering at the energy contour 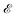 , respectively. Thus, the non-interacting Green’s function
, respectively. Thus, the non-interacting Green’s function 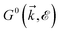 depends on both two momenta
depends on both two momenta ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and
and 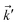 . Due to the broken translational invariance in the momentum space by the impurity, the perturbed Green’s function matrix is given by
. Due to the broken translational invariance in the momentum space by the impurity, the perturbed Green’s function matrix is given by| |
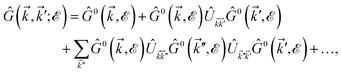 | (22) |
which can be simplified as| |
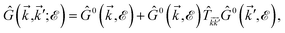 | (23) |
where the 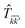 matrix is given by
matrix is given by| |
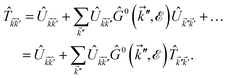 | (24) |
For the local impurities, we deal with isotropic scatterings Û; and ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) depends on the energy only as
depends on the energy only as
| |
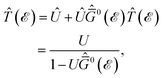 | (25) |
where
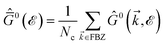
. After averaging over the random impurity distribution, the perturbed Green’s function matrix depends on the single momentum
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
and the combined effect of impurities is given by the self-energy
| |
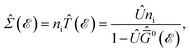 | (26) |
in which the impurity concentration is defined by
ni =
Ni/
Vc, where
Ni is the number of impurities and
Vc is the unit cell volume.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.01-2017.361.
References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Nature, 2005, 438, 197–200 CrossRef CAS PubMed.
- A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, Rev. Mod. Phys., 2009, 81, 109–162 CrossRef CAS.
- B. D. Hoi, M. Yarmohammadi and M. Davoudiniya, Solid State Commun., 2018, 271, 21–28 CrossRef.
- B. D. Hoi, M. Davoudiniya and M. Yarmohammadi, J. Magn. Magn. Mater., 2018, 452, 157–163 CrossRef CAS.
- B. D. Hoi, M. Davoudiniya and M. Yarmohammadi, Superlattices Microstruct., 2018, 113, 576–584 CrossRef CAS.
- A. Rozhkov, A. Sboychakov, A. Rakhmanov and F. Nori, Phys. Rep., 2016, 648, 1–104 CrossRef CAS.
- C. J. Tabert and E. J. Nicol, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075439 CrossRef.
- X. Lin, Y. Xu, S. Lin, A. A. Hakro, T. Cao, H. Chen and B. Zhang, 2012, arXiv:1205.5404.
- B.-L. Gao, B. Wang, Q.-Q. Xu and S.-J. Xiong, Phys. E, 2011, 43, 1394–1397 CrossRef CAS.
- H. Xu, J. Zhou, Y. Li, R. Jaramillo and J. Li, Nano Res., 2019, 12, 2634–2639 CrossRef CAS.
- A. V. Lebedev, I. V. Lebedeva, A. A. Knizhnik and A. M. Popov, RSC Adv., 2016, 6, 6423–6435 RSC.
- C. Wang, J. Guo, L. Dong, A. Aiyiti, X. Xu and B. Li, Sci. Rep., 2016, 6, 25334 CrossRef CAS PubMed.
- J. Sławińska, I. Zasada and Z. Klusek, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155433 CrossRef.
- S. Behzad, Phys. E, 2018, 103, 338–347 CrossRef CAS.
- S. Li, M. Sun, J.-P. Chou, J. Wei, H. Xing and A. Hu, Phys. Chem. Chem. Phys., 2018, 20, 24726–24734 RSC.
- D. C. Elias, R. R. Nair, T. M. G. Mohiuddin, S. V. Morozov, P. Blake, M. P. Halsall, A. C. Ferrari, D. W. Boukhvalov, M. I. Katsnelson, A. K. Geim and K. S. Novoselov, Science, 2009, 323, 610–613 CrossRef CAS PubMed.
- J. Zhou, Q. Wang, Q. Sun, X. S. Chen, Y. Kawazoe and P. Jena, Nano Lett., 2009, 9, 3867–3870 CrossRef CAS PubMed.
- D. Haberer, D. V. Vyalikh, S. Taioli, B. Dora, M. Farjam, J. Fink, D. Marchenko, T. Pichler, K. Ziegler, S. Simonucci, M. S. Dresselhaus, M. Knupfer, B. Büchner and A. Grüneis, Nano Lett., 2010, 10, 3360–3366 CrossRef CAS PubMed.
- R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Lægsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann and L. Hornekær, Nat. Mater., 2010, 9, 315–319 CrossRef CAS PubMed.
- M. V. Ulybyshev and M. I. Katsnelson, Phys. Rev. Lett., 2015, 114, 246801 CrossRef CAS PubMed.
- C. Lin, Y. Feng, Y. Xiao, M. Dürr, X. Huang, X. Xu, R. Zhao, E. Wang, X.-Z. Li and Z. Hu, Nano Lett., 2015, 15, 903–908 CrossRef CAS PubMed.
- K. M. McCreary, A. G. Swartz, W. Han, J. Fabian and R. K. Kawakami, Phys. Rev. Lett., 2012, 109, 186604 CrossRef PubMed.
- R. R. Nair, M. Sepioni, I.-L. Tsai, O. Lehtinen, J. Keinonen, A. V. Krasheninnikov, T. Thomson, A. K. Geim and I. V. Grigorieva, Nat. Phys., 2012, 8, 199–202 Search PubMed.
- M. Moaied, J. A. Moreno, M. J. Caturla, F. Ynduráin and J. J. Palacios, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 155419 CrossRef.
- Y. Li, Z. Zhou, P. Shen and Z. Chen, J. Phys. Chem. C, 2009, 113, 15043–15045 CrossRef CAS.
- J. O. Sofo, A. S. Chaudhari and G. D. Barber, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 153401 CrossRef.
- B. D. Hoi and M. Yarmohammadi, Phys. Lett. A, 2018, 382, 3298–3305 CrossRef CAS.
- A. Csóré, H. J. von Bardeleben, J. L. Cantin and A. Gali, Phys. Rev. B, 2017, 96, 085204 CrossRef.
- E. Bekaroglu, M. Topsakal, S. Cahangirov and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 075433 CrossRef.
- J. Kim, M. V. Fischetti and S. Aboud, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205323 CrossRef.
- B. R. Tuttle, Phys. Rev. B, 2018, 97, 045203 CrossRef CAS.
- N. Alaal, V. Loganathan, N. Medhekar and A. Shukla, Phys. Rev. Appl., 2017, 7, 064009 CrossRef.
- T.-H. Gao, S.-Q. Wu, P. Zhang and Z.-Z. Zhu, Acta Phys. Sin., 2014, 63(1), 016801 Search PubMed.
- J. B. Oostinga, H. B. Heersche, X. Liu, A. F. Morpurgo and L. M. K. Vandersypen, Nat. Mater., 2008, 7, 151–157 CrossRef CAS PubMed.
- E. V. Castro, K. S. Novoselov, S. V. Morozov, N. M. R. Peres, J. M. B. L. dos Santos, J. Nilsson, F. Guinea, A. K. Geim and A. H. C. Neto, Phys. Rev. Lett., 2007, 99, 216802 CrossRef PubMed.
- E. K. Sichel, R. E. Miller, M. S. Abrahams and C. J. Buiocchi, Phys. Rev. B: Solid State, 1976, 13, 4607–4611 CrossRef CAS.
- N. D. Hien, K. Mirabbaszadeh, M. Davoudiniya, B. D. Hoi, L. T. T. Phuong and M. Yarmohammadi, Sci. Rep., 2019, 9, 10651 CrossRef PubMed.
- M. Yarmohammadi, Chin. Phys. B, 2017, 26, 026502 CrossRef.
- K. Zhao, M. Zhao, Z. Wang and Y. Fan, Phys. E, 2010, 43, 440–445 CrossRef CAS.
- F.-L. Shyu, Phys. B, 2014, 452, 7–12 CrossRef CAS.
- B.-L. Gao, Q.-Q. Xu, S.-H. Ke, N. Xu, G. Hu, Y. Wang, F. Liang, Y. Tang and S.-J. Xiong, Phys. Lett. A, 2014, 378, 565–569 CrossRef CAS.
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, Nature, 2005, 438, 201–204 CrossRef CAS PubMed.
- C. Berger, Z. Song, X. Li, X. Wu, N. Brown, C. Naud, D. Mayou, T. Li, J. Hass, A. N. Marchenkov, E. H. Conrad, P. N. First and W. A. de Heer, Science, 2006, 312, 1191–1196 CrossRef CAS PubMed.
- W. Zan, W. Geng, H. Liu and X. Yao, J. Alloys Compd., 2016, 666, 204–208 CrossRef CAS.
- R. M. Ribeiro and N. M. R. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235312 CrossRef.
- G. Giovannetti, P. A. Khomyakov, G. Brocks, P. J. Kelly and J. van den Brink, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 073103 CrossRef.
- R. Grassi, T. Low and M. Lundstrom, Nano Lett., 2011, 11, 4574–4578 CrossRef CAS PubMed.
- M. Yarmohammadi, Phys. Lett. A, 2016, 380, 4062–4069 CrossRef CAS.
- M. Yarmohammadi, H. A. Kazzaz and M. S. Feali, Int. J. Mod. Phys. B, 2017, 31, 1750053 CrossRef CAS.
- G. D. Mahan, Many Particle Physics, Plenum Press, New York, 1993 Search PubMed.
- M. Yarmohammadi, Phys. Lett. A, 2017, 381, 1261–1267 CrossRef CAS.
- C. Kittel, Introduction to Solid State Physics, John Wiley and Sons, New York, 2004 Search PubMed.
- W. Nolting and A. Ramakanth, Quantum Theory of Magnetism, Springer Science and Business Media, Germany, 2009 Search PubMed.
- P. T. T. Le, M. Davoudiniya and M. Yarmohammadi, J. Appl. Phys., 2019, 125, 213903 CrossRef.
- H. D. Bui, M. Davoudiniya and M. Yarmohammadi, J. Appl. Phys., 2019, 126, 063902 CrossRef.
- P. Le, T. C. Phong and M. Yarmohammadi, Phys. Chem. Chem. Phys., 2019, 21, 21790 RSC.
- P. Le and M. Yarmohammadi, Phys. E, 2019, 107, 11–17 CrossRef CAS.
- H. D. Bui, L. T. T. Phuong and M. Yarmohammadi, Europhys. Lett., 2018, 124, 27001 CrossRef.
- G. Grosso and G. P. Parravicini, Solid State Physics, Academic Press, New York, 2014 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Vo T. Lamb,
Doan Q. Khoa*cd,
Tran Tiena,
Nguyen T. T. Binhe,
Huynh V. Phucf,
Nguyen N. Hieu
*a,
Vo T. Lamb,
Doan Q. Khoa*cd,
Tran Tiena,
Nguyen T. T. Binhe,
Huynh V. Phucf,
Nguyen N. Hieu e and
Chuong V. Nguyeng
e and
Chuong V. Nguyeng
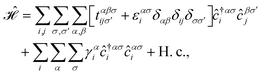
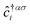 and
and 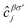 , respectively) is described by the coefficient
, respectively) is described by the coefficient 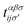 . In addition, εασi stands for the on-site energy of the sublattices. It should be noted that the index for the number of layers is omitted here because one can consider all four atoms {A1, B1, A2, B2} for α and β sublattice indices where needed, as well as the corresponding unit cells for the i and j indices. Note that the hopping and on-site energies are different for the graphene, SiC and h-BN cases;40–42 see Table 1. However, both energies for SiC and h-BN bilayers are normalized to the graphene values in the present paper. The on-site energy for carbon atoms in graphene are set to zero for simplicity, while the graphene hopping energy is
. In addition, εασi stands for the on-site energy of the sublattices. It should be noted that the index for the number of layers is omitted here because one can consider all four atoms {A1, B1, A2, B2} for α and β sublattice indices where needed, as well as the corresponding unit cells for the i and j indices. Note that the hopping and on-site energies are different for the graphene, SiC and h-BN cases;40–42 see Table 1. However, both energies for SiC and h-BN bilayers are normalized to the graphene values in the present paper. The on-site energy for carbon atoms in graphene are set to zero for simplicity, while the graphene hopping energy is 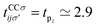 eV.1–3,43,44 Furthermore, the interlayer hopping parameter is defined by γαi, which is around 0.2 eV for graphene carbon atoms and different for other cases, see Table 1. As for the in-plane lattice constants, we deal with aC–C ≃ 1.42 Å, aSi–C ≃ 1.89 Å and aB–N ≃ 1.45 Å,1–3,40–44 while we approximate the distance between two layers as 3.35 Å, 3.5 Å and 3.22 Å, respectively, for graphene, SiC and h-BN.14,45–47
eV.1–3,43,44 Furthermore, the interlayer hopping parameter is defined by γαi, which is around 0.2 eV for graphene carbon atoms and different for other cases, see Table 1. As for the in-plane lattice constants, we deal with aC–C ≃ 1.42 Å, aSi–C ≃ 1.89 Å and aB–N ≃ 1.45 Å,1–3,40–44 while we approximate the distance between two layers as 3.35 Å, 3.5 Å and 3.22 Å, respectively, for graphene, SiC and h-BN.14,45–47
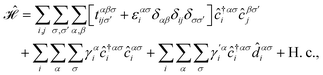
![[d with combining circumflex]](https://www.rsc.org/images/entities/i_char_0064_0302.gif) is used for the doped hydrogen atoms on the unit cell i and the sublattice α with the coupling strength γ′ ≃ 5.72 eV.48 Herein, four configurations for the hydrogenation doping are considered, namely table-like (T-L), chair-like (C-L), reduced table-like (r-T-L), and reduced chair-like (r-C-L). In the case of the table-like configuration, both sublattices in each layer are doped with hydrogen in the same direction, but opposite directions compared to other layers; for example, if the hydrogen is aligned to the +z axis for both sublattices in the upper layer, it is aligned to the −z axis for both sublattices in the lower layer. In the case of the chair-like configuration, hydrogen doping for the sublattices in each layer is different, meaning that if the hydrogen is aligned to the +z axis for the A sublattice, it is along the −z axis for the B sublattice, and in general this is reversed for other layers. Finally, in the case of reduced versions, the same configuration exists but only on one of the layers.39,49,50
is used for the doped hydrogen atoms on the unit cell i and the sublattice α with the coupling strength γ′ ≃ 5.72 eV.48 Herein, four configurations for the hydrogenation doping are considered, namely table-like (T-L), chair-like (C-L), reduced table-like (r-T-L), and reduced chair-like (r-C-L). In the case of the table-like configuration, both sublattices in each layer are doped with hydrogen in the same direction, but opposite directions compared to other layers; for example, if the hydrogen is aligned to the +z axis for both sublattices in the upper layer, it is aligned to the −z axis for both sublattices in the lower layer. In the case of the chair-like configuration, hydrogen doping for the sublattices in each layer is different, meaning that if the hydrogen is aligned to the +z axis for the A sublattice, it is along the −z axis for the B sublattice, and in general this is reversed for other layers. Finally, in the case of reduced versions, the same configuration exists but only on one of the layers.39,49,50
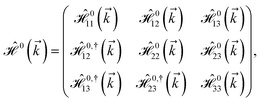
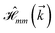 ,
, 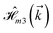 and
and 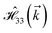 for m ∈ {1, 2} describes the possible coupling and interactions between atoms in the layer m, between the atoms in the layer m and hydrogen, and between the hydrogen atoms themselves, respectively. Using the geometry structure of lattices and simple lattice vectors, the elements are calculated as
for m ∈ {1, 2} describes the possible coupling and interactions between atoms in the layer m, between the atoms in the layer m and hydrogen, and between the hydrogen atoms themselves, respectively. Using the geometry structure of lattices and simple lattice vectors, the elements are calculated as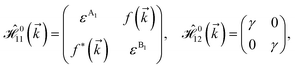
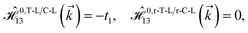
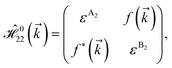
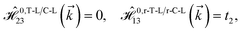
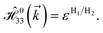
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) = t(1 + exp[+i
) = t(1 + exp[+i![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ·
·![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) 1] + exp [+i
1] + exp [+i![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ·
·![[a with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0061_20d1.gif) 2]) and
2]) and 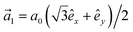 and
and 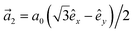 with a0 as the in-plane lattice constants. Also, t1 = t2 = 5.72 eV and εH1/H2 = −2.4 eV are, respectively, the hopping energy between sublattices and hydrogen, and hydrogen itself.
with a0 as the in-plane lattice constants. Also, t1 = t2 = 5.72 eV and εH1/H2 = −2.4 eV are, respectively, the hopping energy between sublattices and hydrogen, and hydrogen itself.
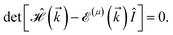
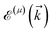 is the corresponding energy band. The dispersion energy is one of the fundamental quantities for studying the electronic features of a system. However, since we are interested in using the respective relation to electronic DOS, we switch to the DOS calculations to obtain the electronic heat capacity and Pauli spin paramagnetic susceptibility quantities. There are various ways to do so, however, we use the Green’s function approach to calculate the DOS, which helps us later when implementing the impurity effects. Using eqn (3), the explicit form of non-interacting Green’s function matrix, i.e. in the absence of external perturbations, can be calculated via51
is the corresponding energy band. The dispersion energy is one of the fundamental quantities for studying the electronic features of a system. However, since we are interested in using the respective relation to electronic DOS, we switch to the DOS calculations to obtain the electronic heat capacity and Pauli spin paramagnetic susceptibility quantities. There are various ways to do so, however, we use the Green’s function approach to calculate the DOS, which helps us later when implementing the impurity effects. Using eqn (3), the explicit form of non-interacting Green’s function matrix, i.e. in the absence of external perturbations, can be calculated via51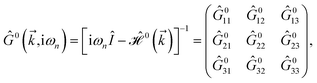
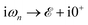 refers to the fermionic Matsubara frequency51 and in the numerical calculation we use 0+ = 5 meV for the root solving problem. The Green’s function obtained in eqn (6) is used to find the DOS of the mentioned lattices by tracing out the imaginary part of the diagonal Green’s function elements in terms of Lehmann representation:51
refers to the fermionic Matsubara frequency51 and in the numerical calculation we use 0+ = 5 meV for the root solving problem. The Green’s function obtained in eqn (6) is used to find the DOS of the mentioned lattices by tracing out the imaginary part of the diagonal Green’s function elements in terms of Lehmann representation:51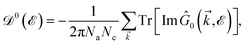
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) = (kx,ky) with
= (kx,ky) with 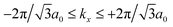 and −4π/3a0 ≤ ky ≤ +4π/3a0.28 Let us use the calculated DOSs for the thermodynamic quantities.
and −4π/3a0 ≤ ky ≤ +4π/3a0.28 Let us use the calculated DOSs for the thermodynamic quantities.
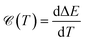
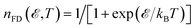 is the Fermi–Dirac distribution function and the number of electrons is given by
is the Fermi–Dirac distribution function and the number of electrons is given by 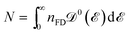 . Obviously, one observes that the electronic DOS
. Obviously, one observes that the electronic DOS 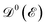 emerges in the heart of
emerges in the heart of 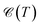 and in order to develop the microscopic theory of EHC a very careful evaluation of electron Green’s functions and DOS becomes essential. Rewriting ΔE as
and in order to develop the microscopic theory of EHC a very careful evaluation of electron Green’s functions and DOS becomes essential. Rewriting ΔE as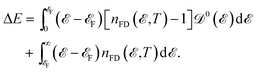
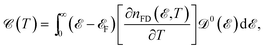
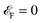 and considering all energies with respect to that, EHC could be restated as
and considering all energies with respect to that, EHC could be restated as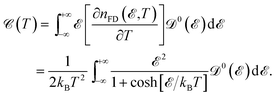
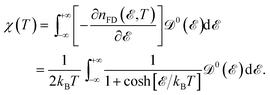
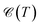 and χ(T) quantities is shown in Fig. 2(a)–(f).
and χ(T) quantities is shown in Fig. 2(a)–(f).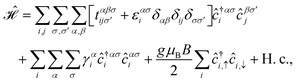
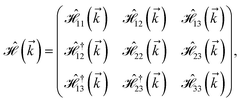
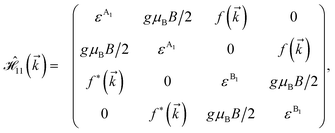
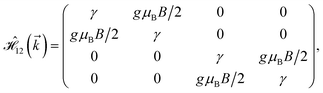
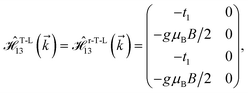
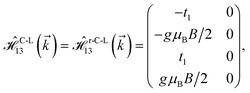
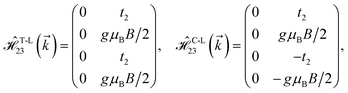
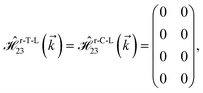
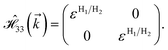
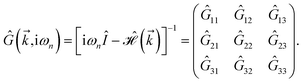

 depends on the energy only, given by,51,60
depends on the energy only, given by,51,60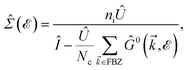
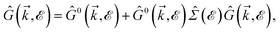
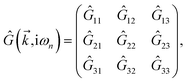
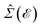 . Thus, the new poles associated with impurities come into play role in impurity-induced DOS at energy
. Thus, the new poles associated with impurities come into play role in impurity-induced DOS at energy  satisfying the equation
satisfying the equation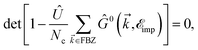
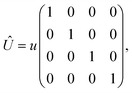
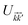 with two momenta
with two momenta ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and
and 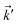 , as the initial momentum of surface electrons and the momentum transferred by impurity scattering at the energy contour
, as the initial momentum of surface electrons and the momentum transferred by impurity scattering at the energy contour 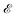 , respectively. Thus, the non-interacting Green’s function
, respectively. Thus, the non-interacting Green’s function 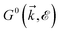 depends on both two momenta
depends on both two momenta ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and
and 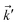 . Due to the broken translational invariance in the momentum space by the impurity, the perturbed Green’s function matrix is given by
. Due to the broken translational invariance in the momentum space by the impurity, the perturbed Green’s function matrix is given by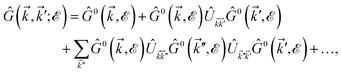
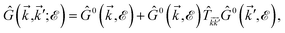
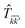 matrix is given by
matrix is given by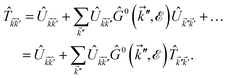
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) depends on the energy only as
depends on the energy only as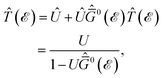
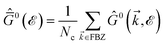 . After averaging over the random impurity distribution, the perturbed Green’s function matrix depends on the single momentum
. After averaging over the random impurity distribution, the perturbed Green’s function matrix depends on the single momentum ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) and the combined effect of impurities is given by the self-energy
and the combined effect of impurities is given by the self-energy