 Open Access Article
Open Access ArticleElectronic and optical properties of Janus ZrSSe by density functional theory
Tuan V. Vu ab,
Hien D. Tongc,
Duy Phu Tran
ab,
Hien D. Tongc,
Duy Phu Tran d,
Nguyen T. T. Binh*e,
Chuong V. Nguyen
d,
Nguyen T. T. Binh*e,
Chuong V. Nguyen f,
Huynh V. Phucg,
Hoat M. Doh and
Nguyen N. Hieu
f,
Huynh V. Phucg,
Hoat M. Doh and
Nguyen N. Hieu *e
*e
aDivision of Computational Physics, Institute for Computational Science, Ton Duc Thang University, Ho Chi Minh City, Viet Nam. E-mail: vuvantuan@tdtu.edu.vn
bFaculty of Electrical & Electronics Engineering, Ton Duc Thang University, Ho Chi Minh City, Viet Nam
cFaculty of Engineering, Vietnamese-German University, Binh Duong, Viet Nam
dFuture Industries Institute, ARC Centre of Excellence in Convergent Bio-Nano Science and Technology, University of South Australia, Mawson Lakes, Campus Mawson Lakes, South Australia 5095, Australia
eInstitute of Research and Development, Duy Tan University, Da Nang 550000, Viet Nam. E-mail: nguyentthanhbinh8@duytan.edu.vn; hieunn@duytan.edu.vn
fDepartment of Materials Science and Engineering, Le Quy Don Technical University, Ha Noi 100000, Viet Nam
gDivision of Theoretical Physics, Dong Thap University, Dong Thap, Viet Nam
hComputational Laboratory for Advanced Materials and Structures, Advanced Institute of Materials Science, Ton Duc Thang University, Ho Chi Minh City, Viet Nam
First published on 12th December 2019
Abstract
In the present work, we investigate systematically the electronic and optical properties of Janus ZrSSe using first-principles calculations. Our calculations demonstrate that the Janus ZrSSe monolayer is an indirect semiconductor at equilibrium. The band gap of the Janus ZrSSe is 1.341 eV using the Heyd–Scuseria–Ernzerhof hybrid functional, larger than the band gap of ZrSe2 monolayer and smaller than that of ZrS2 monolayer. Based on the analysis of the band edge alignment, we confirm that the Janus ZrSSe monolayer possesses photocatalytic activities that can be used in water splitting applications. While strain engineering plays an important role in modulating the electronic properties and optical characteristics of the Janus ZrSSe monolayer, the influence of the external electric field on these properties is negligible. The biaxial strain, εb, has significantly changed the band of the Janus ZrSSe monolayer, and particularly, the semiconductor–metal phase transition which occurred at εb = 7%. The Janus ZrSSe monolayer can absorb light in both visible and ultraviolet regions. Also, the biaxial strain has shifted the first optical gap of the Janus ZrSSe monolayer. Our findings provide additional information for the prospect of applying the Janus ZrSSe monolayer in nanoelectronic devices, especially in water splitting technology.
1 Introduction
Since the successful separation in 2004, graphene has become one of the top materials of interest to the scientific community due to its many extraordinary chemical and physical properties.1 The success of graphene in nanotechnology applications has led to a wide search for two-dimensional (2D) layered materials. In fact, many 2D graphene-like materials have been systematically studied, such as silicene, germanene, phosphorene and transition metal dichalcogenides,2–6 and in particular, van der Waals heterostructures.7–10 Recently, the Janus MoSSe monolayer, a new type of asymmetric transition metal dichalcogenide, was successfully synthesized through chemical vapour deposition.11,12 This has opened a new direction in the study of 2D materials. Several theoretical studies have focused on monolayers of Janus transition metal dichalcogenides13 and Janus monochalcogenide.14 The breaking of mirror symmetry in Janus transition metal dichalcogenides, which has been confirmed by scanning transmission electron microscopy,12 has given rise to many new physical properties with many promising applications in nanoelectronic and energy storage technologies.13,15,16Monolayer ZrS2 has been experimentally synthesized by Zeng and co-workers.17 Both ZrS2 and ZrSe2 are indirect semiconductors from first-principles calculations.15,18 Similar to other 2D layered materials, the electronic properties of the ZrS2 and ZrSe2 monolayers are very sensitive to external influences.19 Xin and co-workers indicated that semiconductor–metal transition was found at large elongation of biaxial strain.20 Besides, strain engineering can also lead to indirect–direct band gap in the ZrS2 monolayer.21 By replacing the bottom layer of S(Se) atoms in monolayer ZrS2(ZrSe2) with Se(S) atoms, we obtain the structure of the Janus ZrSSe monolayer. Using first-principles calculations, Guo and co-workers show that the Janus ZrSSe, an indirect semiconductor, is mechanically and dynamically stable.18 Janus ZrSSe may possess photocatalytic activities due to its high asymmetric arrangement.15 Also, the breaking of the inversion symmetry in the Janus structure of ZrSSe leads to a significant change in its piezoelectricity.22 It is well-known that spin–orbit coupling (SOC) plays an important role in the electronic properties of layered materials.23,24 When the SOC is included, the band gap of the Janus SnSSe24 and Janus transition metal dichalchogenide23 monolayers is reduced and a spin–orbit splitting was found at the Γ-point. This indicates that the spin–orbit splitting value depends strongly on the strain engineering.
In the present work, we focus on the electronic and optical properties of the Janus ZrSSe using first-principles calculations. To get a high level of accuracy in the energy gap problem, we used different functionals in our calculations. We also compared the results obtained from Janus ZrSSe with ZrS2 and ZrSe2 monolayers. The photocatalytic characteristics and catalytic activities of the Janus ZrSSe were also checked. The effects of strain engineering and the external electric field on the electronic and optical properties of the Janus ZrSSe have also been systematically studied in this work.
2 Computational details
In this study, all calculations are performed using density functional theory (DFT), which is implemented in the Quantum Espresso package25 within the projected augmented wave (PAW) method.26 The generalized gradient approximation (GGA) suggested by Perdew, Burke, and Ernzerhof (PBE)27,28 is chosen to describe the exchange–correction functional, and the SOC is included self consistently.29 Also, the Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional30 is used to solve the problems of band structure and band gap of the monolayers ZrS2, ZrSe2, and Janus ZrSSe. A semi-empirical DFT-D2 method proposed by Grimme31 is used to consider the long-range weak van der Waals interactions which exist in the monolayers. The cut-off energy is set to 500 eV, and the Brillouin zone is sampled by a 12 × 12 × 1 k-point grid. All the atoms are fully relaxed until the residue forces on each atom and total energy are converged to 0.001 eV Å−1 and 106 eV, respectively. To eliminate the interactions between neighbour layers, a vacuum space of 20 Å along the c-axis (perpendicular to the monolayer surface) is used.For calculations of the optical properties, we focus only on the dielectric function ε(ω) and the absorption coefficient α(ω) of the Janus ZrSSe monolayer. The imaginary part of the ε(ω) can be estimated via the sum of the transitions between occupied and unoccupied states and the real part can be calculated through the Kramers–Kronig relation.
To consider the effect of a biaxial strain on electronic and optical properties of monolayers ZrS2, ZrSe2, and Janus ZrSSe, we defined the strain elongation εb as εb = (l − l0)/l0, where l0 and l are, respectively, the lattice constants of pristine and strained monolayers. The plus and minus signs refer, respectively, to the tensile and compressive biaxial strains. To consider the influence of an electric field on the electronic and optical properties of the monolayers ZrS2, ZrSe2, and Janus ZrSSe, an electric field E is applied perpendicular to the 2D plane of the monolayers (c-axis). The negative field is applied so that the direction of the E is opposite to the positive direction of the c-axis. In this work, the applied biaxial strain, εb, is from −8% to 8% and the value of the external electric field is up to 5 V nm−1.
3 Results and discussion
The optimized atomic structure of Janus ZrSSe is shown in Fig. 1(a). We can build the structure of the Janus ZrSSe from the well-known ZrSe2 structure32 by replacing the bottom or top layer of the Se atoms by S atoms. The atomic structure of the ZrSe2 or ZrS2 monolayers belongs to the group symmetry![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) 3m1. Replacing the Se by S atoms results in distortion of the out-of-plane symmetry of the Janus ZrSSe. This causes the mirror symmetry to be broken with the absence of mirror planes perpendicular to the c-axis. The Janus ZrSSe belongs to a non-centrosymmetric group with space group symmetry P3m1. The structural parameters of the Janus ZrSSe, ZrSe2 and ZrS2 monolayers are listed in Table 1. After optimization, the lattice constant of Janus ZrSSe is a = 3.738 Å. This value is larger than the lattice constant of monolayer ZrS2 but smaller than that of monolayer ZrSe2. The bond lengths between the Zr atom and the S and Se atoms in the Janus ZrSSe are dZr–S = 2.572 Å and dZr–Se = 2.705 Å. Our obtained results are in good agreement with previous DFT calculations.18,22 Also, we have calculated the charge density as shown in Fig. 1(b) and (c). Previously, electrostatic potential differences at the surface of 2D Janus structures have been observed.33 We know that the difference in electrostatic potential can lead to a difference in the redox potential. This is very important in finding applicability in water splitting technology. In Fig. 2(a), we show the electrostatic potential along the c-axis for the Janus ZrSSe. To examine the dynamic stability, the phonon spectrum of the Janus ZrSSe is calculated as shown in Fig. 2(b). From Fig. 2(b) we can see that there is no soft mode (negative frequency) in the phonon spectrum of the Janus ZrSSe. This indicates that, at equilibrium, the Janus ZrSSe is dynamically stable.
3m1. Replacing the Se by S atoms results in distortion of the out-of-plane symmetry of the Janus ZrSSe. This causes the mirror symmetry to be broken with the absence of mirror planes perpendicular to the c-axis. The Janus ZrSSe belongs to a non-centrosymmetric group with space group symmetry P3m1. The structural parameters of the Janus ZrSSe, ZrSe2 and ZrS2 monolayers are listed in Table 1. After optimization, the lattice constant of Janus ZrSSe is a = 3.738 Å. This value is larger than the lattice constant of monolayer ZrS2 but smaller than that of monolayer ZrSe2. The bond lengths between the Zr atom and the S and Se atoms in the Janus ZrSSe are dZr–S = 2.572 Å and dZr–Se = 2.705 Å. Our obtained results are in good agreement with previous DFT calculations.18,22 Also, we have calculated the charge density as shown in Fig. 1(b) and (c). Previously, electrostatic potential differences at the surface of 2D Janus structures have been observed.33 We know that the difference in electrostatic potential can lead to a difference in the redox potential. This is very important in finding applicability in water splitting technology. In Fig. 2(a), we show the electrostatic potential along the c-axis for the Janus ZrSSe. To examine the dynamic stability, the phonon spectrum of the Janus ZrSSe is calculated as shown in Fig. 2(b). From Fig. 2(b) we can see that there is no soft mode (negative frequency) in the phonon spectrum of the Janus ZrSSe. This indicates that, at equilibrium, the Janus ZrSSe is dynamically stable.
 | ||
| Fig. 2 Electrostatic potential along the c-axis (a) and phonon dispersion relations (b) of the Janus ZrSSe at equilibrium. | ||
| a | dZr–S | dZr–Se | EPBEg | EPBE+SOCg | EHSEg | |
|---|---|---|---|---|---|---|
| ZrS2 | 3.699 | 2.584 | — | 1.104 | — | 1.871 |
| ZrSe2 | 3.790 | — | 2.697 | 0.479 | — | 1.079 |
| ZrSSe | 3.738 | 2.572 | 2.705 | 0.689 | 0.572 | 1.341 |
We first calculate the band structures and partial density of states (PDOS) of monolayers ZrS2 and ZrSe2 as shown in Fig. 3. We can see that both the ZrS2 and ZrSe2 are indirect semiconductors. The band gap of monolayer ZrS2 is larger than that of monolayer ZrSe2. At the PBE level, the band gaps of the monolayers ZrS2 and ZrSe2 are 1.104 eV and 0.479 eV, respectively. However, we know that, in the DFT calculations, the band gap problem of material depends greatly on the approach, i.e., which functional is used in the calculations. The PBE functional underestimates the band gap of insulators and semiconductors.34 The GW approximation35 or Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional30 was expected to be a suitable method to solve the band gap problem of the materials. Therefore, to accurately calculate the energy gap of the ZrS2, ZrSe2 and Janus ZrSSe monolayers, in this study we use also the HSE06 hybrid functional to estimate their band structure. The band gap of the monolayers ZrS2 and ZrSe2 are, respectively, 1.871 eV and 1.079 eV at the HSE06 level, quite larger than that calculated by the PBE functional.
 | ||
| Fig. 3 Band structures and PDOS of the monolayers ZrS2 (a), and ZrSe2 (b). The Fermi level is set to be zero. | ||
Band structure and PDOS of the Janus ZrSSe are shown in Fig. 4. We calculate the electronic structure of the Janus ZrSSe along the Γ–M–K–Γ high-symmetry direction in the energy region from −6 eV to 6 eV. As shown in Fig. 4, the Janus ZrSSe is an indirect semiconductor at equilibrium. The band gap of the Janus ZrSSe is EPBEg = 0.689 eV and EHSEg = 1.341 eV at the PBE and HSE06 levels, respectively. This result is in good agreement with previous calculations.18 From Fig. 4, we can see that at the equilibrium state, the conduction band minimum (CBM) is located at the M-point, while the valence band maximum (VBM) is located at the Γ-point. Focusing on analyzing the formation of electronic bands of the Janus ZrSSe, we performed the calculations for its PDOS as depicted in the right panel of Fig. 4. The electronic bands of the Janus ZrSSe were formed mainly by the contribution of S-p, Se-p, and Zr-d orbitals. The contribution of Zr-d orbitals to the conduction band is quite large, particularly in the energy range from 2 eV to 4 eV. The contribution of S-p and Se-p orbitals to the valence band is quite balanced. While the contribution of the Se-p orbitals to the valence band is dominant in the energy region from 1 eV to 3 eV, the S-p orbitals have a significant contribution to the valence bands in the energy region from 3 eV to 4 eV. The contribution of the s-orbital of S, Se, and Zr atoms to the electronic bands is quite small compared to other orbitals. Overall, the conduction band is largely contributed to by the orbitals of Zr atoms while the orbitals of S and Se atoms provide the dominant contribution to the valence band.
The redox potential of water splitting is dependent on the pH value.36 At pH = 00, the standard oxidation (O2/H2O) potential and reduction (H+/H2) potential for water splitting are Eoxi = −5.67 eV and Ered = −4.44 eV. In Fig. 5, we show the position of the CBM and VBM relative to the normal hydrogen electrode (NHE) of the ZrS2, ZrSe2 and Janus ZrSSe monolayers at pH = 0. The photocatalytic activity of the material depends greatly on the band gap. To possess the photocatalytic activity, the CBM must be higher than the standard hydrogen reduction potential of the H+/H2 and the VBM must be lower than the standard redox potential of the O2/H2O. At pH = 0, the standard oxidation potential of the O2/H2O is −5.67 eV vs. the vacuum level, or 1.23 eV vs. the NHE. This implies that to be able to possess photocatalytic activity, the minimum energy gap of the material must be at least 1.23 eV. As listed in Table 1, the band gaps of the ZrS2 (1.871 eV) and Janus ZrSSe (1.341 eV) monolayers are larger than 1.23 eV at the HSE06 level. Then, we examined the possibility of photocatalytic activity of these monolayers for water splitting via calculations for band edge alignment. The VBM and CBM edge alignment of ZrS2, ZrSe2, and Janus ZrSSe monolayers are shown in Fig. 5. From Fig. 5, we see that the photocatalytic activity of the ZrS2 monolayer is greatest. For the Janus ZrSSe, the VBM is right at the standard oxidation potential of the O2/H2O and the CBM is higher than the standard hydrogen reduction potential of the H+/H2. From this, we can conclude that, at the equilibrium state, the Janus ZrSSe monolayer possesses photocatalytic activity for water splitting applications.
 | ||
| Fig. 5 The VBM and CBM edge alignment of ZrS2, ZrSe2, and Janus ZrSSe monolayers. The horizontal dashed lines refer to the standard potentials for water splitting at pH = 0. | ||
Two-dimensional layered materials in general and monolayer transition metal dichalcogenides in particular, have electronic properties that are sensitive to external influences such as strain engineering or electric field. We next consider the effect of a biaxial strain, εb, on the electronic properties of the Janus ZrSSe. The calculations for the band structure of the strained Janus ZrSSe are performed at the PBE level. Band structures of the Janus ZrSSe under different levels of εb are shown in Fig. 6. Our DFT calculations demonstrate that in the presence of the tensile strain εb > 0 [see Fig. 6(a)], the Janus ZrSSe is still a semiconductor with an indirect band gap. In this case, the CBM and VBM of the tensile strained Janus ZrSSe are always at the M- and Γ-points, respectively. The tensile strain leads to a slight increase in the energy gap of the Janus ZrSSe. Unlike the case of tensile strain, the effect of compression strain (εb < 0), as shown in Fig. 6(b), on the band structure of the Janus ZrSSe is significant. The energy gap of the Janus ZrSSe decreases quickly when the compression biaxial strain is introduced. More interestingly, semiconductor–metal transitions were observed in the Janus ZrSSe at large biaxial strain of εb = −7%. The band gap of the Janus ZrSSe is equal to zero at the εb = −7% as depicted in Fig. 6(b).
 | ||
| Fig. 6 Band structure of the Janus ZrSSe under different levels of (a) tensile, and (b) compressive biaxial strains. | ||
To study the influence of an applied electric field E on the electronic properties of the Janus ZrSSe, the electric field is applied perpendicularly to the monolayer surface. The direction of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) is along the c-axis. The negative field (minus sign) implies that the
is along the c-axis. The negative field (minus sign) implies that the ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) is opposite to the c-axis. In contrast to the strain engineering, the influence of an external electric field on the band structure of the Janus ZrSSe is quite weak. As shown in Fig. 7, the band structure of the Janus ZrSSe is almost unchanged in the presence of the perpendicular electric field. Dependence of the band gap of the Janus ZrSSe on the strain engineering, εb, and external electric field E is depicted in Fig. 8. From Fig. 8, we can see that the electric field only slightly changes the band gap of the Janus ZrSSe. While a positive electric field increases its band gap slightly, a negative electric field reduces its energy. In the electric field from −5 V nm−1 to 5 V nm−1, the energy gap depends linearly on the electric field. However, as mentioned above, this change is very small. The band gaps of the Janus ZrSSe at E = −5 V nm−1 and E = +5 V nm−1 are, respectively, 0.664 eV and 0.720 eV. Fig. 7 also shows that the tensile strain increases the band gap of the Janus ZrSSe. However, the gap tends to increase slowly at large εb. The band gap of the Janus ZrSSe reaches 1.074 eV at εb = 8%. In the presence of biaxial strain, change tendency of the band gap of the Janus ZrSSe is similar to that of monolayer ZrS2. A previous study indicates that while compressive biaxial strain reduces the band gap of the monolayer ZrS2, the band gap of the monolayer ZrS2 is increased in the presence of tensile strain varying from 0 to 6%.37 However, compared with other transition metal dichalcogenide monolayers, we found that in the presence of tensile strain, while the band gap of the Janus ZrSSe increased slightly, the band gap of the transition metal dichalcogenide monolayers, such as PdS2, PdSe2, and PtSe2, was significantly reduced.38,39 In both cases of strain engineering and external electric field, from Fig. 6 and 7, we see that the change of band gap is due to the change of the conduction band. Indeed, the highest energy value of the valence band is always at the Fermi level EF = 0 and does not change in the presence of an electric field or biaxial strain. Controlling the band gap by strain, and particularly the occurrence of a semiconductor–metal transition due to strain engineering, can offer many opportunities for applications of the Janus ZrSSe in nanoelectronics technologies.
is opposite to the c-axis. In contrast to the strain engineering, the influence of an external electric field on the band structure of the Janus ZrSSe is quite weak. As shown in Fig. 7, the band structure of the Janus ZrSSe is almost unchanged in the presence of the perpendicular electric field. Dependence of the band gap of the Janus ZrSSe on the strain engineering, εb, and external electric field E is depicted in Fig. 8. From Fig. 8, we can see that the electric field only slightly changes the band gap of the Janus ZrSSe. While a positive electric field increases its band gap slightly, a negative electric field reduces its energy. In the electric field from −5 V nm−1 to 5 V nm−1, the energy gap depends linearly on the electric field. However, as mentioned above, this change is very small. The band gaps of the Janus ZrSSe at E = −5 V nm−1 and E = +5 V nm−1 are, respectively, 0.664 eV and 0.720 eV. Fig. 7 also shows that the tensile strain increases the band gap of the Janus ZrSSe. However, the gap tends to increase slowly at large εb. The band gap of the Janus ZrSSe reaches 1.074 eV at εb = 8%. In the presence of biaxial strain, change tendency of the band gap of the Janus ZrSSe is similar to that of monolayer ZrS2. A previous study indicates that while compressive biaxial strain reduces the band gap of the monolayer ZrS2, the band gap of the monolayer ZrS2 is increased in the presence of tensile strain varying from 0 to 6%.37 However, compared with other transition metal dichalcogenide monolayers, we found that in the presence of tensile strain, while the band gap of the Janus ZrSSe increased slightly, the band gap of the transition metal dichalcogenide monolayers, such as PdS2, PdSe2, and PtSe2, was significantly reduced.38,39 In both cases of strain engineering and external electric field, from Fig. 6 and 7, we see that the change of band gap is due to the change of the conduction band. Indeed, the highest energy value of the valence band is always at the Fermi level EF = 0 and does not change in the presence of an electric field or biaxial strain. Controlling the band gap by strain, and particularly the occurrence of a semiconductor–metal transition due to strain engineering, can offer many opportunities for applications of the Janus ZrSSe in nanoelectronics technologies.
 | ||
| Fig. 7 Band structure of the Janus ZrSSe under (a) positive, and (b) negative, external electric fields. | ||
It is well-known that the effect of the SOC on electronic properties of 2D layered materials is very important. In this work, the band structure, including SOC effects, of the Janus ZrSSe has been calculated using the PBE + SOC. In Fig. 9(a) and (b), we plot the band structures of the Janus ZrSSe using the PBE and PBE + SOC along the K–Γ–M–K high-symmetry direction. Our calculations indicate that at the equilibrium state the band gap of the Janus ZrSSe is reduced from EPBEg = 0.689 eV to EPBE+SOCg = 0.572 eV when the SOC effect is included. Besides, a spin–orbit splitting energy ΔE = 0.212 eV appeared at the high symmetry Γ-point in the valence band of the Janus ZrSSe monolayer. The effect of the biaxial strain and external electric field on the spin–orbit splitting value ΔE is also shown in Fig. 9(c). We can see that, similar to the band gap, the effect of the electric field on the spin–orbit splitting value ΔE is quite weak. Meanwhile, the influence of the SOC effect on band structure of the Janus ZrSSe is quite strong. The spin–orbit splitting values of the Janus ZrSSe at the εb = 0, εb = −8%, and εb = 8% are 0.212 eV, 0.235 eV and 0.175 eV, respectively.
In this part, we consider the optical characteristics of the Janus ZrSSe under strain engineering, εb, and external electric field E. We focus only on the dielectric function ε(ω), and the absorption coefficient α(ω) of the Janus ZrSSe. The dielectric function can be written as
| ε(ω) = ε1(ω) + iε2(ω). | (1) |
Usually, the imaginary part ε2(ω) is estimated first by the sum of the occupied–unoccupied transitions. The real part ε1(ω) can then be obtained via the Kramers–Kronig transformation. The imaginary part ε2(ω) of the dielectric function can be written as follows40,41
 | (2) |
![[p with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0070_20d1.gif) is the momentum operator, the |
is the momentum operator, the |![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) nσ〉 term refers to the wave-function of the crystal corresponding to energy, E
nσ〉 term refers to the wave-function of the crystal corresponding to energy, E![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) n.
n. ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) is the wave-vector and f
is the wave-vector and f![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) n is the function of the Fermi distribution.
n is the function of the Fermi distribution.
The absorption coefficient α(ω) can be calculated using the dielectric function which can be expressed as41,42
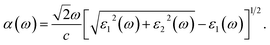 | (3) |
In our calculations, the incident light is polarized along the a-axis (parallel polarization) and is in the energy range from 0 to 10 eV. The calculated dielectric function of the Janus ZrSSe under biaxial strain, εb, and external electric field, E, is depicted in Fig. 9. We first focus on the effect of the εb on the dielectric function of the Janus ZrSSe as shown in Fig. 10(a). As shown in the imaginary part ε2(ω) [bottom panel of Fig. 10(a)], the first optical gap of the Janus ZrSSe is at 1.892 eV. It is in the visible light region. Our calculations demonstrate that the first optical gap of the Janus ZrSSe is significantly shifted under the effects of strain engineering, εb. While the compressive strain causes the first optical gap of the Janus ZrSSe to move towards the lower energy region, the tensile strain causes it to move towards the higher energy region. The tendency of the first optical gap of the Janus ZrSSe in the case of tensile strain is the opposite of that of the transition-metal dichalcogenide monolayers such as PdS2, PdSe2, and PtSe2, where both compressive and tensile strain cause the first optical peak to move towards the lower energy region.38 It is well-known that the ε2(ω) part of the ε(ω) is directly related to the absorption coefficient. Therefore, the optical gaps in the absorption spectrum of the Janus ZrSSe that we will discuss below will be closely related to this shifting. Similar to the electronic properties, the optical characteristics of the Janus ZrSSe are almost unaffected by the external electric field. Fig. 10(b) shows that parts of the dielectric constant are almost independent of the electric field, especially in the high energy region.
In Fig. 11, we show the calculated absorption coefficient α(ω) in the presence of the biaxial strain, εb, and external electric field, E. From Fig. 11, we can see that the Janus ZrSSe can sustainably absorb both visible and ultraviolet light. In the case of without strain or electric field, the maximum absorption coefficient is 9.483 × 104 cm−1 at the incident light energy of 5.795 eV. As mentioned-above, the optical gaps of the Janus ZrSSe shift with strain energy, εb, and the absorption coefficient also greatly depends on strain energy. Fig. 11 demonstrates that, while the tensile strain reduces maximum absorption coefficient, α(ω)max, the compressive strain increases the α(ω)max significantly. The maximum coefficient at εb = −7% is up to 1.005 × 105 cm−1 at the incident light energy of 6.672 eV. From Fig. 10(b) and 11(b), we can conclude that the effect of the external electric field on the optical characteristics of the Janus ZrSSe is negligible. With the ability to absorb light in both the visible and ultraviolet range, especially with high absorption coefficient, we believe that Janus ZrSSe has a lot of potential for applications in optoelectronic devices.
4 Conclusion
In summary, we systematically investigated the electronic and optical properties of the Janus ZrSSe monolayer under strain engineering and an external electric field using DFT calculations. Our calculated results demonstrate that the Janus ZrSSe is an indirect semiconductor and it can absorb both visible light and ultraviolet light. Interestingly, at the equilibrium state, the Janus ZrSSe possesses photocatalytic activity for water splitting. The effect of strain engineering on the electronic and optical properties of the Janus ZrSSe monolayer is significant, especially the semiconductor–metal transition which can be observed at certain εb. Besides, the biaxial strain is the cause of shifting optical gaps and the significantly changing absorption coefficient of the Janus ZrSSe monolayer. Possessing photocatalytic activities and being able to control electronic properties by strain engineering, the Janus ZrSSe monolayer has many advantages in its application prospects in nanoelectronic devices and water splitting technologies.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is funded by the Viet Nam National Foundation for Science and Technology Development (NAFOSTED) under Grant No. 103.01-2017.309.References
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666 CrossRef CAS PubMed.
- C. V. Nguyen, N. N. Hieu, N. A. Poklonski, V. V. Ilyasov, L. Dinh, T. C. Phong, L. V. Tung and H. V. Phuc, Phys. Rev. B, 2017, 96, 125411 CrossRef.
- C. V. Nguyen, N. N. Hieu, C. A. Duque, D. Q. Khoa, N. V. Hieu, L. V. Tung and H. V. Phuc, J. Appl. Phys., 2017, 121, 045107 CrossRef.
- P. T. T. Le, K. Mirabbaszadeh, M. Davoudiniya and M. Yarmohammadi, Phys. Chem. Chem. Phys., 2018, 20, 25044 RSC.
- C. V. Nguyen, N. N. Hieu, D. Muoi, C. A. Duque, E. Feddi, H. V. Nguyen, L. T. T. Phuong, B. D. Hoi and H. V. Phuc, J. Appl. Phys., 2018, 123, 034301 CrossRef.
- T. V. Vu, A. A. Lavrentyev, D. V. Thuan, C. V. Nguyen, O. Y. Khyzhun, B. V. Gabrelian, K. C. Tran, H. L. Luong, P. D. Tung, K. D. Pham, P. T. Dang and D. D. Vo, Superlattices Microstruct., 2019, 125, 205–213 CrossRef CAS.
- K. D. Pham, N. N. Hieu, H. V. Phuc, I. A. Fedorov, C. A. Duque, B. Amin and C. V. Nguyen, Appl. Phys. Lett., 2018, 113, 171605 CrossRef.
- K. D. Pham, L. G. Bach, B. Amin, M. Idrees, N. N. Hieu, H. V. Phuc, H. D. Bui and C. V. Nguyen, J. Appl. Phys., 2019, 125, 225304 CrossRef.
- P. T. T. Le, N. N. Hieu, L. M. Bui, H. V. Phuc, B. D. Hoi, B. Amin and C. V. Nguyen, Phys. Chem. Chem. Phys., 2018, 20, 27856 RSC.
- H. V. Phuc, V. V. Ilyasov, N. N. Hieu, B. Amin and C. V. Nguyen, J. Alloys Compd., 2018, 750, 765 CrossRef CAS.
- J. Zhang, S. Jia, I. Kholmanov, L. Dong, D. Er, W. Chen, H. Guo, Z. Jin, V. B. Shenoy, L. Shi and J. Lou, ACS Nano, 2017, 11, 8192 CrossRef CAS PubMed.
- A.-Y. Lu, H. Zhu, J. Xiao, C.-P. Chuu, Y. Han, M.-H. Chiu, C.-C. Cheng, C.-W. Yang, K.-H. Wei, Y. Yang, Y. Wang, D. Sokaras, D. Nordlund, P. Yang, D. A. Muller, M.-Y. Chou, X. Zhang and L.-J. Li, Nat. Nanotechnol., 2017, 12, 744 CrossRef CAS PubMed.
- L. Dong, J. Lou and V. B. Shenoy, ACS Nano, 2017, 11, 8242 CrossRef CAS PubMed.
- A. Huang, W. Shi and Z. Wang, J. Phys. Chem. C, 2019, 123, 11388 CrossRef CAS.
- N. N. Som and P. K. Jha, Int. J. Hydrogen Energy, 2019 DOI:10.1016/j.ijhydene.2019.09.033.
- W.-L. Tao, Y. Mu, C.-E. Hu, Y. Cheng and G.-F. Ji, Philos. Mag., 2019, 99, 1025 CrossRef CAS.
- Z. Zeng, Z. Yin, X. Huang, H. Li, Q. He, G. Lu, F. Boey and H. Zhang, Angew. Chem., Int. Ed., 2011, 50, 11093 CrossRef CAS PubMed.
- S.-D. Guo, Y.-F. Li and X.-S. Guo, Comput. Mater. Sci., 2019, 161, 16 CrossRef CAS.
- Q. Zhao, Y. Guo, K. Si, Z. Ren, J. Bai and X. Xu, Phys. Status Solidi B, 2017, 254, 1700033 CrossRef.
- Q. Xin, X. Zhao, X. Ma, N. Wu, X. Liu and S. Wei, Phys. E, 2017, 93, 87 CrossRef CAS.
- Y. Li, J. Kang and J. Li, RSC Adv., 2014, 4, 7396 RSC.
- Dimple, N. Jena, A. Rawat, R. Ahammed, M. K. Mohanta and A. De Sarkar, J. Mater. Chem. A, 2018, 6, 24885 RSC.
- S.-D. Guo and J. Dong, Semicond. Sci. Technol., 2018, 33, 085003 CrossRef.
- S.-D. Guo, X.-S. Guo, R.-Y. Han and Y. Deng, Phys. Chem. Chem. Phys., 2019, 21, 24620 RSC.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- A. H. MacDonald, W. E. Picket and D. D. Koelling, J. Phys. C: Solid State Phys., 1980, 13, 2675 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787 CrossRef CAS PubMed.
- M. J. Mleczko, C. Zhang, H. R. Lee, H.-H. Kuo, B. Magyari-Köpe, R. G. Moore, Z.-X. Shen, I. R. Fisher, Y. Nishi and E. Pop, Sci. Adv., 2017, 3, e1700481 CrossRef PubMed.
- C.-F. Fu, J. Sun, Q. Luo, X. Li, W. Hu and J. Yang, Nano Lett., 2018, 18, 6312 CrossRef CAS PubMed.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884 CrossRef CAS.
- L. Hedin, Phys. Rev., 1965, 139, A796 CrossRef.
- K. Ren, C. Ren, Y. Luo, Y. Xu, J. Yu, W. Tang and M. Sun, Phys. Chem. Chem. Phys., 2019, 21, 9949 RSC.
- H. Y. Lv, W. J. Lu, D. F. Shao, H. Y. Lu and Y. P. Sun, J. Mater. Chem. C, 2016, 4, 4538 RSC.
- S. Deng, L. Li and Y. Zhang, ACS Appl. Nano Mater., 2018, 1, 1932 CrossRef CAS.
- Y.-S. Lan, Q. Lu, C.-E. Hu, X.-R. Chen and Q.-F. Chen, Appl. Phys. A, 2019, 125, 33 CrossRef.
- A. Delin, P. Ravindran, O. Eriksson and J. Wills, Int. J. Quantum Chem., 1998, 69, 349 CrossRef CAS.
- S. Z. Karazhanov, P. Ravindran, A. Kjekshus, H. Fjellvag and B. G. Svensson, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155104 CrossRef.
- P. Ravindran, A. Delin, B. Johansson, O. Eriksson and J. M. Wills, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1776 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |






