Open Access Article
Open Access ArticleAtomic-level understanding of interface interactions in a halloysite nanotubes–PLA nanocomposite
Alexander Kruglikova,
Andrey Vasilchenkoa,
Anton Kasprzhitskiiab and
Georgy Lazorenko *ab
*ab
aRostov State Transport University, Narodnogo Opolcheniya Sq., Rostov-on-Don, 344038, Russia. E-mail: glazorenko@yandex.ru
bMineralica Limited Liability Company, Skolkovo Innovation Center, 42 Bolshoy Boulevard, Moscow, 121205, Russia
First published on 2nd December 2019
Abstract
To understand the nature of the bonding mechanism between poly(lactic acid) (PLA) and halloysite nanotubes (HNT), a first-principles DFT study was performed on the adsorption behavior of the PLA monomer, lactic acid (LA), on the outer, inner, and edge surfaces of the HNT. The role of LA functional groups, and its orientation behavior in the formation of bonds with HNT are systematically studied. Analysis of the adsorption energy, total and partial electron density of states (DOS), electric charge transfer between LA atoms and HNT mineral surfaces shows that van der Waals attraction governs their interaction. The calculations of the most stable adsorption configurations of LA show that the predominant number of hydrogen bonds is determined by the activity of the carboxyl functional group of LA on the hydroxylated surfaces of HNT. The important role of the –OH surface groups in the mechanism of lactic acid binding has been established; their absence on the external siloxane surface significantly reduces the LA affinity for HNT. The binding energy of lactic acid on the hydroxylated internal and edge surfaces of the HNT is much higher (by about 275%) than on the external siloxane surface. Mulliken population analysis showed that the formation of a hydrogen bond with the LA atomic groups leads to a more significant redistribution of charge on the inner and edge surfaces of the HNT in comparison with its outer surface. Van der Waals attraction between the LA and HNTs, as well as hydrogen bonds, is responsible for the formation of the bonding mechanism in halloysite nanotubes-PLA nanocomposite. Our results are in accord with available literature.
1. Introduction
Biopolymers obtained from renewable sources of raw materials are currently a promising alternative to traditional polymers of petrochemical origin since their use helps to solve pressing environmental problems and preserve fossil resources.1–3 From the point of view of price, poly(lactic acid) (PLA), which is a biodegradable, biocompatible, thermoplastic, aliphatic polyester, is today the most competitive biopolymer.4 Due to these features, the use of PLA is most relevant in two domains – the packaging industry, and medicine. It is used in the manufacture of films, rigid and semi-rigid containers for food and cosmetics.5,6 PLA is successfully used in tissue engineering,7 surgical sutures,8 orthopedic implants,9 and drug delivery systems.10However, PLA is not without significant flaws that limit its use. These include, in particular, fragility, a high diffusion coefficient of CO2 and barrier characteristics with respect to oxygen, low heat resistance, viscosity and elongation upon breaking.11 The use of polylactide for a wide range of industrial applications still requires the control and adaptation of its mechanical, thermal and barrier properties that meet the requirements of specific applications. One of the most effective ways to solve this problem, which has been developing significantly in recent years, is the inclusion of nanosized fillers of various shapes and chemical nature in the PLA polymer matrix which contribute to the formation of a nanocomposite.12 In particular, these include organically modified layered silicates,13,14 carbon nanotubes,15 graphene,16 nanocellulose,17 zinc and titanium oxides,6,18 silver nanoparticles.19
Recently, the attention of researchers has been attracted by halloysite nanotubes (HNT) as a new type of nanofillers for strengthening of the PLA matrix.20 Halloysite is an aluminosilicate, which is a multilayer nanotube with an external diameter of 30–190 nm, an internal diameter of 10–100 nm, and a length of up to 0.7–30 microns.21 The composition of HNT is similar to those of clay minerals kaolinite, dicite, or nacrite, with the chemical formula Al2Si2O5(OH)4·nH2O where n = 0 and 2, which correspond to dehydrated and hydrated forms.21 Halloysite, like many other clays, is non-toxic to living organisms and does not pollute the environment; due to this, as well as its structural features, HNT seems to be a promising and cheaper alternative to the above PLA nanofillers.
In the formation of properties of epy PLA-based nanocomposites, the nature of the interaction of the nanofiller with the polymer matrix plays a key role. Interactions at the interface between an individual filler nanoparticle and a matrix polymer forming a nanocomposite structure can include several types of bonds depending on the nanofiller surface structure. The description of these inter-phase interactions is difficult to quantify, and usually the structural description of a nanocomposite is limited by its morphology obtained from X-ray diffraction analysis, as well as by the nature of distribution of nanofiller in the polymer matrix, estimated by electron microscopy.15,22,23 Despite the growing number of publications in the field of HNT-PLA nanocomposites describing interesting new applications of these materials,20,24–35 only a small number of studies is related to the description of inter-phase interaction at the HNT-PLA interface. In papers20,25–27,33,34,36 atomic groups which can participate in bond formation between HNT and PLA were revealed according to FTIR-spectroscopy. As atomic surface groups of HNT involved in the interaction were considered: Si–O–Si,20,25 Al–O–Si,20,25 Si–O,33,36,37 Al–OH,36,37 and hydroxyl groups (–OH),20,25 arising on the edge surfaces and defects of HNT surfaces. In papers34,36,37 the possibility of special role of terminal hydroxyl groups (–OH) of PLA polymer chains, which can form hydrogen bond with HNT, is indicated. Interaction of atomic groups –CH3,20,25 –CO20,25,26 and –COH20,25 of PLA with HNT row is also possible. Thus, the mechanism of interphase interaction of HNT and PLA remains not fully explained. A deeper understanding these mechanisms can be obtained from quantum chemical calculations. However, today there are no such works. Thus, there is a need for a theoretical study of molecular aspects of the formation of inter-phase mechanisms of structure formation in polymer nanocomposites with a polylactide matrix filled with halloysite nanotubes.
In this work, within the framework of the density functional theory (DFT), a systematic study is carried out on the inter-phase interaction mechanism of binding the lactic acid, the PLA monomer, to the internal, external, and edge surfaces of halloysite nanotubes. In addition to energy characteristics of the binding process, structural characteristics were calculated, including the preferred adsorption sites on the HNT mineral surface and monomer orientation, as well as the electronic properties of the system – DOS, Mulliken bond population.
2. Computational details
In our study, the LA binding mechanism on all HNT mineral surfaces were studied using the density functional theory (DFT) with periodic boundary conditions38,39 realized via the Cambridge Serial Total Energy Package (CASTEP) plane-wave code.40,41 The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University.42,43 Calculation of exchange-correlation energy was performed in the generalized gradient approximation (GGA)44 using Perdew, Burke and Ernzerhof potential (PBE).45 The choice of GGA-PBE for solving this problem is due to the fact that it describes with high accuracy the energy characteristics of chemisorption and the formation of interatomic bonds of molecular systems with a mineral surface.46–48 Electron-ion interaction was calculated using the Vanderbilt ultra-soft pseudopotential,49 which has a wide range of applications50–53 and ensures high speed and accuracy of calculation.54 Valence electron configurations are Si 3s23p2, Al 3s23p1, C 2s22p2, and H 1s1. Structure optimization was performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm.55 Comparative test calculations of the studied models showed a difference in the total energies not exceeding 4 meV when using the basis of augmented plane waves with cutoff energies of more than 400 eV for the wave functions of the valence electrons, therefore this value was used as the cutoff energy in this study. Equilibrium atomic positions were determined in accordance with the following criteria: energy change per ion (10−5 eV); maximum force (0.03 eV Å−1); maximum stress (0.05 GPa); maximum displacement (10−3 Å). The iteration routine for minimizing the total energy of electronic system at each step of varying atomic positions continued until an accuracy of 10−6 eV per atom is achieved; its stability is ensured by mixing the electron density of a series of the last iterations using the conditionally conjugate gradient method with a participation coefficient of 0.5 (Pulay scheme).56 The contribution of non-covalent forces, such as hydrogen bonds and van der Waals interactions, which are critical in describing the adsorption of molecules on the mineral surface,57,58 is taken into account in the framework of the hybrid semi-empirical solution as damped atom-pairwise dispersion corrections of the form C6R−6 in the DFT formalism according to the Grimme scheme (DFT-D2 correction).59All HNT surfaces were simulated on the basis of a primitive kaolinite cell taken from paper.60 For the primitive cell with the parameters is 5.15 Å × 8.94 Å × 7.4 Å (basal spacing, c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β ∼ 7.16 Å and β ∼ 104.86°), DFT-bulk geometry and atomic relaxation was carried out. The models of the internal aluminol (001) (see Fig. 1a) and external siloxane (00
β ∼ 7.16 Å and β ∼ 104.86°), DFT-bulk geometry and atomic relaxation was carried out. The models of the internal aluminol (001) (see Fig. 1a) and external siloxane (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) (see Fig. 1b) surfaces were built using slabs with a (3 × 2) supercell with the parameters of 15.47 × 17.89 Å × 7.4 Å and with total number of atoms 204 was based on the primitive cell optimized. Each slab was separated from its periodic image in the z-direction by a vacuum space of 25 Å to be adequate to eliminate interaction between mineral slabs (see Fig. 1). The model of the edge (100) surface (see Fig. 1c) was built using a (3 × 2 × 1) supercell than was separated from its periodic image in the direction perpendicular to the (100) plane by a vacuum space of 25 Å. The dangling Si–O and Al–O bonds of the edge (100) surface were healed through the sorption of an integer number of water molecules to maintain the surface at the point of zero net proton charge. The under coordinated Si and Al atoms complete their coordination shell with OH groups.
) (see Fig. 1b) surfaces were built using slabs with a (3 × 2) supercell with the parameters of 15.47 × 17.89 Å × 7.4 Å and with total number of atoms 204 was based on the primitive cell optimized. Each slab was separated from its periodic image in the z-direction by a vacuum space of 25 Å to be adequate to eliminate interaction between mineral slabs (see Fig. 1). The model of the edge (100) surface (see Fig. 1c) was built using a (3 × 2 × 1) supercell than was separated from its periodic image in the direction perpendicular to the (100) plane by a vacuum space of 25 Å. The dangling Si–O and Al–O bonds of the edge (100) surface were healed through the sorption of an integer number of water molecules to maintain the surface at the point of zero net proton charge. The under coordinated Si and Al atoms complete their coordination shell with OH groups.
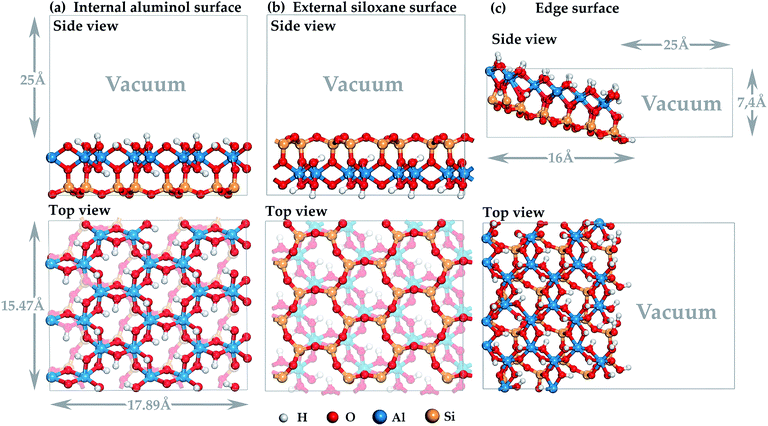 | ||
Fig. 1 Three-dimensional model of halloysite nanotube surface: (a) internal aluminol (001) surface; (b) external siloxane (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) surface; (c) edge (100) surface. ) surface; (c) edge (100) surface. | ||
The geometric structure of the monomeric unit of PLA, i.e. lactic acid (2-hydroxypropanoic acid, C3H6O3) used in the calculation was optimized in advance in a cell 40 × 40 × 40 Å in size with periodic boundary conditions and gamma-point was used in the reciprocal k-space. During optimization, the cell parameters were fixed.
The calculations were performed for the chosen models of HNT surfaces (see Fig. 1) with the periodic boundary conditions. A Monkhorst-Pack mesh of 2 × 2 × 1 k-points was used for the cell.61 During optimization, the cell parameters were fixed. The positions of all atoms were fully relaxed while calculating. The solutions were obtained in accordance with the convergency criteria.
The interaction between LA and HNT mineral surfaces was estimated on the basis of three calculated characteristics: adsorption energy ΔEads, magnitude of the change in charge Δqi on the atoms of the mineral surface and molecular adsorbate, and the electron density difference Δρ.
The adsorption energy ΔEads for LA on the HNT mineral surface is calculated as follows:
| ΔEads = ELA/SHNT − ELA − ESHNT, |
The change in the charge Δqi for a selected atom was determined in accordance with the formula:
| Δqi = qi,after adsorption − qi,before adsorption, |
For a qualitative analysis of intermolecular LA interactions, three-dimensional patterns of changes in the charge density were formed in order to verify the charge transfer between the LA atoms and the HNT mineral surface. To plot the patterns, the following equation was used:
| Δρ(r) = ρ(r)LA/HNT − ρ(r)HNT − ρ(r)LA, |
3. Results and discussion
3.1. Adsorption geometries and bonding
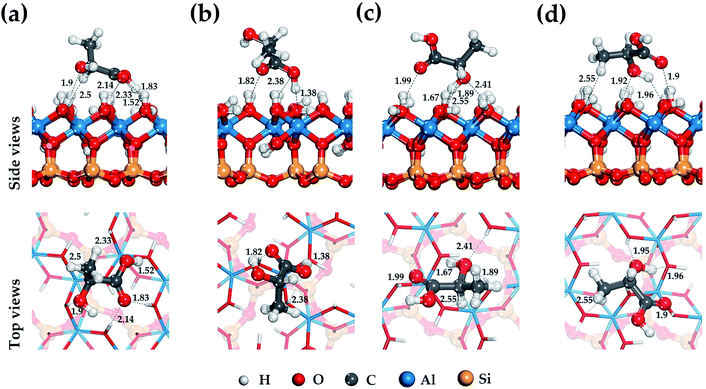
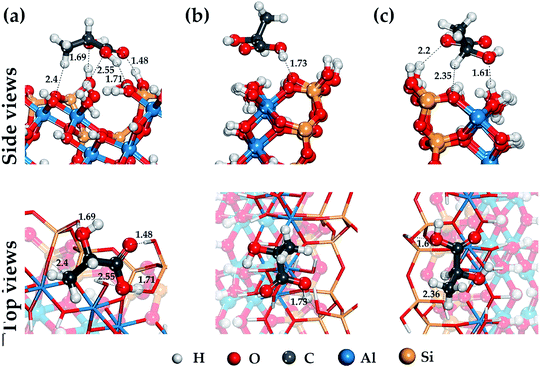
Lactic acid is a monobasic carboxylic acid containing functional carboxyl group (–COOH), methyl group (–CH3) and hydroxyl group (–OH), the nature of the interaction of which determines the mechanism of its binding to HNT mineral surfaces.Fig. 2–4 show the most stable and low-energy structures of lactic acid in the adsorbed state on the internal aluminol surface, edge surface, and external siloxane surface of HNT, respectively. The results of the analysis of the hydrogen bonds arising during the absorption of LA, and the LA functional groups are presented in Table 1. For their selection, the criteria for determining the hydrogen bond in accordance with62 were used: r(Oi⋯Hj) ≤ 2.45 Å; r(Oi⋯Oj) ≤ 3.60 Å; Φ ≤ 30°.
| Adsorption surface | Site of adsorbate lactic acid in Fig. 2–4 | Number of hydrogen bonds | ||||
|---|---|---|---|---|---|---|
| Total | –COOH | –CH | –OH | –CH3 | ||
| Internal aluminol surface | Position (a) | 6 | 4 | 1 | 1 | |
| Position (b) | 3 | 3 | ||||
| Position (c) | 5 | 1 | 1 | 3 | ||
| Position (d) | 5 | 1 | 3 | 1 | ||
| Edge surface | Position (a) | 4 | 2 | 1 | 1 | |
| Position (b) | 1 | 1 | ||||
| Position (c) | 3 | 1 | 1 | 1 | ||
| External siloxane surface | Position (a) | 0 | ||||
| Position (b) | 1 | 1 | ||||
The configuration of hydrogen bonds shown in Fig. 2–4 and their number as presented in Table 1 are the following: from 6 to 3 on the internal aluminol surface; from 5 to 3 on the edge surface and only from 1 to 0 hydrogen bonds on the external siloxane surface. The analysis shows that hydroxylated internal aluminol and edge surfaces can form a great number of hydrogen bonds with the participation of surface hydroxyl groups and functional groups of lactic acid with a variation in its orientation helping to maximize the number of hydrogen bonds (see Fig. 2 and 3).
In this case, the maximum binding of lactic acid is formed on the internal aluminol surface. The (–COOH) group is involved in the formation of hydrogen bonds on this mineral surface: two O atoms with bond lengths of 2.33 Å, 2.14 Å, 1.83 Å and a hydrogen atom with a bond length of 1.53 Å, an oxygen atom in (–OH) with a bond length of 1.9 Å, and also the hydrogen of (–CH) with a bond length of 2.49 Å (see Fig. 2). In this case, the role of the molecular adsorption center is played by the hydroxyl group forming three hydrogen bonds with the internal aluminol surface (see Table 1). Maximum binding of LA to the edge surface of the HNT is realized in the same manner (see Fig. 3). In this case, the carboxyl group (–COOH) forms two hydrogen bonds with the participation of the O atom with a bond length of 1.48 Å and the H atom with a bond length of 1.71 Å; in addition, one hydrogen bond is formed by: the O atom of the hydroxyl group (–OH) with a bond length of 1.69 Å, and the H atom of the methyl group (–CH3) with a bond length of 2.4 Å.
The configuration of thus formed hydrogen bonds with the atoms of the hydroxyl groups of LA and the hydroxylated surface of the HNT is in agreement with the results of studies of the behavior of water molecules on the surface of kaolinite.63,64 In this case, the hydroxyl groups of LA form three hydrogen bonds, two of them act as proton donors with an oxygen atom (–OH) LA, while the third one is a proton acceptor.
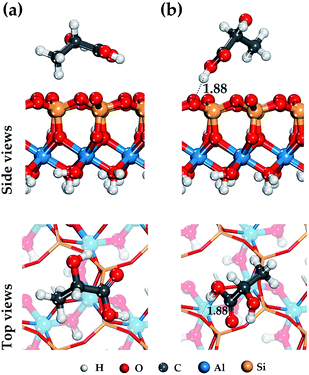
For the external siloxane surface, a significant decrease in the number of hydrogen bonds is observed, despite the presence of acceptor groups for the hydrogen atoms on the surface. As seen from Fig. 4, the adsorption behavior of LA on a siloxane surface is determined by the coordination of the hydrogen atoms of the functional groups (–CH3) and (–COOH), and the oxygen atom of the siloxane surface HNT.
In the case of the participation of the LA carboxyl functional group in adsorption on the HNT surface, the adsorbed molecule is located just above the center of the ditrigonal-tetrahedral hole and forms a single weak hydrogen bond 1.88 Å in length with one basal oxygen atom of the siloxane surface (see Fig. 4). This behavior is characteristic of hydroxyl groups; this is consistent with the results of previous studies.48,64 As shown in Fig. 4, the carboxyl group (–COOH) is centered relatively to the basal hydrogen atom. In case of other balanced states. Fig. 4 shows the adsorption state of LA with a coordinated methyl group (–CH3) just above the center of the ditrigonal-tetrahedral hole. In this case, the hydrogen atom of the LA methyl group (–CH3) in an optimized position forms an isosceles triangle with basal oxygen atoms on the external siloxane surface with equilibrium distances r(O⋯H) = 2.94 Å.
Analysis of the hydrogen bonds formation shows that their configuration depends on the functional groups of the adsorbate (see Fig. 2–4 and Table 1). The main role in the adsorption activity of LA on the HNT surface is played by the carboxyl functional group which forms a maximum number of hydrogen bonds with the surface in comparison with other functional groups of the adsorbate. This information allows one to supplement the experimental data of a number of studies25,37 on the participation of the carboxyl and hydroxyl groups of PLA in the mechanism of binding to HNT. In particular, the data in papers34,36,37 confirm the essential role of terminal hydroxyl groups (–OH) of PLA in the process of bond formation with HNT. In addition, occurring adsorption states of LA on the HNT surface are the most energetically favorable. In a number of alternative energetically less favorable cases, the concentration of hydrogen bonds on the hydroxyl functional group LA is observed (see Tables 1 and 2). The binding mechanism is also affected by HNT surface chemistry. Predominant number of hydrogen bonds formed on a hydroxylated HNT surfaces indicates the important role of the –OH surface groups in the mechanism of binding of LA the absence of which on the external siloxane surface of HNT significantly reduces the surface affinity for LA confirmed by the FTIR spectroscopy data in a number of studies.20,37,65
| Site of adsorbate lactic acid in Fig. 2–4 | Adsorption energy (kcal mol−1) | ||
|---|---|---|---|
| Internal aluminol surface | Edge surface | External siloxane surface | |
| a Adsorption energy after dispersion correction (DFT-D2). | |||
| Position (a) | −18,16 (−30,93)a | −20,12 (−27,99)a | −0,76 (−10,69)a |
| Position (b) | −17,69 (−26,33)a | −13,44 (−20,86)a | −1,72 (−9,52)a |
| Position (c) | −11,39 (−21,13)a | −7,56 (−16,21)a | |
| Position (d) | −9,63 (−20,42)a | ||
The obtained results specify the considerations of the atomic groups participating in bond formation. That is confirmed by the available experimental data: Al–O–Si,20,25 Al–OH,36,37 Si–O–Si,20,25 –CH3,20,25 –CO20,25,26 and –COH.20,25 The results also widen the considerations25,36,37 about the mechanism of bonding PLA with hydroxylated and syloxane HNT surfaces.
3.2. Binding energy
Table 2 shows the adsorption energies for the most stable adsorption configurations of LA on the surfaces of the halloysite nanotube. Accounting for the dispersion correction (DFT-D2) was performed for the total energies of the simulated systems; it is summarized in Table 2. The dispersion correction increases the adsorption energy which lies in the range of 8–12 kcal mol−1 for all mineral surfaces of halloysite. In this case, dispersion interactions dominate on the hydroxylated surfaces; this indicates that dispersion correction is also important for describing the interaction on halloysite surfaces, as well as for the formation of a hydrogen bond. Our results show that the adsorption energy of LA on the internal aluminol surface and edge surface is higher than on the external siloxane surface. For the most stable and energetically favorable state of LA in position (a) (see Table 2), the excess of adsorption energy on the internal aluminol surface and edge surface compared to the external siloxane surface is 2.89 and 2.62 times, respectively.This behavior is characteristic of the H2O molecule during its adsorption on the basal planes of kaolinite. The H2O adsorption energies on the (001) surface of kaolinite whose structure corresponds to the internal aluminol surface halloysite nanotube are much higher than on the (00![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) surface corresponding to the external siloxane surface of the halloysite nanotube.62,63,66 From the analysis of the hydrogen bond configuration that arise during LA adsorption (see Section 3.1), we can see their predominance on the hydroxylated HNT surfaces (see Table 1), that corresponds to the maximum value of adsorption energies (see Table 2).
) surface corresponding to the external siloxane surface of the halloysite nanotube.62,63,66 From the analysis of the hydrogen bond configuration that arise during LA adsorption (see Section 3.1), we can see their predominance on the hydroxylated HNT surfaces (see Table 1), that corresponds to the maximum value of adsorption energies (see Table 2).
Calculation results are in good agreement with experimental data. In particular, an experimental FTIR studies25,26 of the interaction of PLA and HNT indicates hydrogen-binding interactions between the carbonyl groups (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) of PLA and the hydroxyl groups of HNT. The papers20,36 indicate the possibility of interaction between the functional groups of PLA and mineral surface hydroxyls, which is due to the dipole–dipole interaction, van der Waals attraction forces, or the formation of hydrogen bonds. The authors67 of indicate an important role played by the hydroxyl groups on the HNT surface; their absence significantly reduces the strength of the interaction of the external mineral surface with an aliphatic polyester. These studies confirm the results obtained in this work (see Table 2). Thus, in comparison with the adsorption centers of the internal aluminol surface and edge surface, the binding of LA to the external siloxane surface halloysite nanotube is reduced due to the absence of hydrogen bonds (see Table 1). To increase the affinity of LA and HNT, it is necessary to increase the density of hydroxyl groups on the external siloxane surface.68,69
O) of PLA and the hydroxyl groups of HNT. The papers20,36 indicate the possibility of interaction between the functional groups of PLA and mineral surface hydroxyls, which is due to the dipole–dipole interaction, van der Waals attraction forces, or the formation of hydrogen bonds. The authors67 of indicate an important role played by the hydroxyl groups on the HNT surface; their absence significantly reduces the strength of the interaction of the external mineral surface with an aliphatic polyester. These studies confirm the results obtained in this work (see Table 2). Thus, in comparison with the adsorption centers of the internal aluminol surface and edge surface, the binding of LA to the external siloxane surface halloysite nanotube is reduced due to the absence of hydrogen bonds (see Table 1). To increase the affinity of LA and HNT, it is necessary to increase the density of hydroxyl groups on the external siloxane surface.68,69
3.3. Mulliken charges and DOS
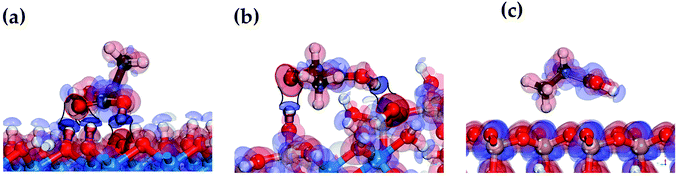
The mechanism of the LA adsorption on the HNT surface can be clarified by analyzing the electron transfer between the atoms participating in the formation of hydrogen bonds in the LA/HNT adsorption system. The electron density difference can be used to describe the electron rearrangement between pairs of atoms when a molecule is adsorbed on a surface. The electron density difference is determined for the most stable LA structures in the adsorbed state on the internal aluminol surface, external siloxane surface, and edge surface of HNT, are shown in Fig. 5.In Fig. 5, the electron density differences, represented by red and blue areas between the atoms forming the hydrogen bond correspond to the accumulation and loss of electrons, respectively. In this case, the larger the electron accumulation and electron loss areas, the stronger the interaction between the functional groups of LA and the HNT surface.
The participation of the LA carboxyl group in the formation of a hydrogen bond on hydroxylated internal aluminol and edge surfaces is accompanied by compensating charge transfer in the following directions: loss of the electron density of the H atom of the HNT surface (–OH) group and its redistribution (accumulation) on the O atom of the LA (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) carbonyl group (see Fig. 5a and b), and at the same time, redistribution of electron density from the LA (–C–OH) group H atom to the basal O atom. The remaining functional groups of LA during the formation of hydrogen bonds participate in unidirectional redistribution of electron charge. Thus, the LA hydroxyl group is involved in the formation of hydrogen bonds coming with the redistribution of electron density from the H atom of the surface (–OH) group and its accumulation on the O atom of LA (–OH). When LA interacts with an external siloxane surface, no significant charge transfer from LA functional groups to the surface is observed. The observed appearance of low-energy adsorption states in the absence of an apparent redistribution of electron density and charge transfer between the hydrogen atom of the LA hydroxyl group and surface oxygen atoms during the hydrogen bonds formation is due to the accumulation of electron density around oxygen atoms approaching the hydrogen atoms (see Fig. 5). The features of this process in terms of the behavior of the hydroxyl functional groups are consistent with the data for a water molecule.63,64
O) carbonyl group (see Fig. 5a and b), and at the same time, redistribution of electron density from the LA (–C–OH) group H atom to the basal O atom. The remaining functional groups of LA during the formation of hydrogen bonds participate in unidirectional redistribution of electron charge. Thus, the LA hydroxyl group is involved in the formation of hydrogen bonds coming with the redistribution of electron density from the H atom of the surface (–OH) group and its accumulation on the O atom of LA (–OH). When LA interacts with an external siloxane surface, no significant charge transfer from LA functional groups to the surface is observed. The observed appearance of low-energy adsorption states in the absence of an apparent redistribution of electron density and charge transfer between the hydrogen atom of the LA hydroxyl group and surface oxygen atoms during the hydrogen bonds formation is due to the accumulation of electron density around oxygen atoms approaching the hydrogen atoms (see Fig. 5). The features of this process in terms of the behavior of the hydroxyl functional groups are consistent with the data for a water molecule.63,64
The electron density redistribution on the HNT mineral surfaces caused by the formation of hydrogen bonds with LA is shown in Fig. 6. Compared to the original clear surface, the blue areas with negative values indicate the loss of charge while the red area with positive values show the increase in charge. These results clearly show that the hydroxylated surfaces undergo a more substantial charge redistribution around the hydrogen bond formation regions (red circles) compared to the siloxane surfaces.
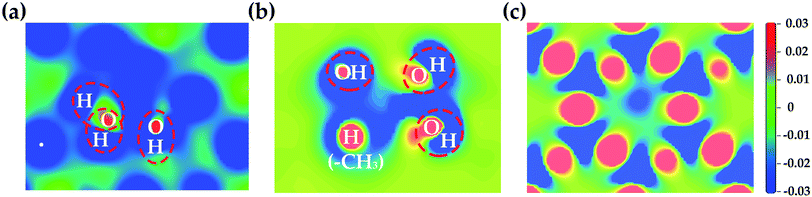 | ||
| Fig. 6 The electron density redistribution on internal aluminol surface (a), edge surface (b) and external siloxane surface (c) of HNT caused by the formation of hydrogen bonds. | ||
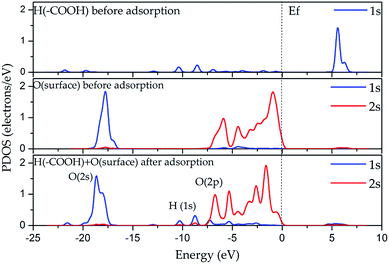
In the DOS analysis (see Fig. 7), the interaction between the hydrogen atom of the carboxyl group (–COOH) and the oxygen atom on the internal aluminol surface was taken as an example since in this case, the hydrogen bond is the strongest in all the considered cases presented in Section 3.1. The Fermi level (Ef) is set to be 0 eV. As shown in Fig. 7, the O 2p-states (internal aluminol surface) and 1s-state of H in (–COOH) are bound covalently and lie in the range from −11 to −1 eV. In this case, the bond is relatively weak after adsorption of LA on the internal aluminol surface HNT. Table 3 shows that the 1s state of the H atom of (–COOH) changed by 0.11e, and the total charge transferred to the LA surface is 0.02e. The magnitude of the charge obtained indicates that there are electrostatic interactions that arise between the internal aluminol surface and LA. However, electrostatic interactions are weak due to the transfer of smaller charge. This result means that the covalent interaction between LA and internal aluminol surface is insufficient. The discrepancy in the exchange of charges during LA adsorption by 0.09e does not allow one to completely describe the binding by electrostatic interaction. One can assume then that the van der Waals attractive forces are responsible for the interaction of internal aluminol surface and LA.
| Atoms | Adsorption status | Mulliken population | Charge (e) | ΔQ | ||
|---|---|---|---|---|---|---|
| s | p | Total | ||||
O(–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
Before | 1.83 | 4.73 | 6.56 | −0.56 | −0.05 |
| After | 1.82 | 4.79 | 6.61 | −0.61 | ||
| O(–C–OH) | Before | 1.82 | 4.87 | 6.69 | −0.69 | 0.05 |
| After | 1.79 | 4.85 | 6.64 | −0.64 | ||
| H(–C–OH) | Before | 0.45 | 0.45 | 0.55 | −0.11 | |
| After | 0.56 | 0.56 | 0.44 | |||
| H1(–CH3) | Before | 0.72 | 0.72 | 0.28 | 0.02 | |
| After | 0.70 | 0.70 | 0.30 | |||
| H2(–CH3) | Before | 0.71 | 0.71 | 0.29 | 0 | |
| After | 0.71 | 0.71 | 0.29 | |||
| H3(–CH3) | Before | 0.70 | 0.70 | 0.30 | −0.01 | |
| After | 0.71 | 0.71 | 0.29 | |||
| LA | Before | 0.01 | −0.08 | |||
| After | −0.07 | |||||
| Surface | Before | 0.06 | 0.02 | |||
| After | 0.08 | |||||
When analyzing the adsorption of LA on the external siloxane surface, Table 4 shows that for the atoms of the carboxyl group the following charge redistribution takes place: the O atom of (–C–OH) loses 0.01e, and the hydrogen atom 0.01e in the process of adsorption of the –COOH group. The hydrogens of methyl group lose 0.06e. These results indicate that there is a very weak electrostatic interaction between the external siloxane surface of the HNT and LA.
| Atoms | Adsorption status | Mulliken population | Charge (e) | ΔQ | ||
|---|---|---|---|---|---|---|
| s | p | Total | ||||
O(–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) O) |
Before | 1.83 | 4.73 | 6.56 | −0.56 | 0 |
| After | 1.83 | 4.73 | 6.56 | −0.56 | ||
| O(–C–OH) | Before | 1.82 | 4.87 | 6.69 | −0.69 | 0.01 |
| After | 1.82 | 4.86 | 6.68 | −0.68 | ||
| H(–C–OH) | Before | 0.45 | 0.45 | 0.55 | −0.01 | |
| After | 0.46 | 0.46 | 0.54 | |||
| H1(–CH3) | Before | 0.72 | 0.72 | 0.28 | −0.01 | |
| After | 0.73 | 0.73 | 0.27 | |||
| H2(–CH3) | Before | 0.71 | 0.71 | 0.29 | −0.04 | |
| After | 0.75 | 0.75 | 0.25 | |||
| H3(–CH3) | Before | 0.70 | 0.70 | 0.30 | −0.01 | |
| After | 0.71 | 0.71 | 0.29 | |||
| LA | Before | 0.01 | −0.03 | |||
| After | −0.02 | |||||
| Surface | Before | 0.09 | −0.01 | |||
| After | 0.08 | |||||
Summarizing the analysis performed, it can be seen that the amount of charge transferred during LA adsorption on the external siloxane surface is less than on the internal aluminol surface. Alongside with that, the leading role of carboxyl group of LA in the process of charge transfer with its maximum change on the H atom (see Table 3) is in high convergency with the data in papers.34,36,37 In combination with the results on the organization of hydrogen bonds (see Section 3.1), we can conclude that the van der Waals attractive forces affect the interaction of LA with the HNT surface.
4. Conclusions
In this work, the mechanism of the formation of lactic acid bonding with the inner, outer and edge surfaces of HNT using DFT calculations is investigated. The obtained results specify the considerations about atomic groups participating in bond formation and widen the considerations about the mechanism of bonding PLA with hydroxylated and syloxane HNT surfaces. The results obtained show that the main interaction between lactic acid and HNT, which determines the mechanism of their binding, is a hydrogen bond type of a non-bonded interaction dependent on the action of its functional groups. For the first time, it was shown that the principal role in the adsorption activity of lactic acid on HNT surfaces is played by the carboxyl functional group, which forms the maximum number of hydrogen bonds with the surface in comparison with other functional groups of the adsorbate. The essential role of terminal hydroxyl group of LA, included into carboxyl groups within the mechanism of binding with HNT, is revealed in the paper. For the most stable and energetically favourable states, a feature of the participation of the LA carboxyl group in the binding mechanism is the pair formation of hydrogen bonds on hydroxylated internal aluminol and edge surfaces accompanied by compensating charge transfer: for the first bond, from the H atom of the HNT surface atom to the O atom of the LA carbonyl group (–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), and for the second bond, from the H atom of LA (–C–OH) group to the basal O atom. The remaining functional groups of LA, as a rule, form an odd number of hydrogen bonds.
O), and for the second bond, from the H atom of LA (–C–OH) group to the basal O atom. The remaining functional groups of LA, as a rule, form an odd number of hydrogen bonds.
The predominant number of hydrogen bonds formed on hydroxylated HNT surfaces indicates the important role of the –OH surface groups in the lactic acid binding mechanism; their absence on the external siloxane surface significantly reduces LA affinity for HNT.
The results of the DOS analysis and the data on the exchange of electric charge between lactic acid and HNT surfaces indicate that the covalent bond and electrostatic interaction between lactic acid and the HNT surface is insufficient for providing their bonding interaction. The results showed that the van der Waals attractive forces regulate the interaction between LA and HNT particles.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Grant of the President of Russian Federation No. MK-3630.2018.8. The research is carried out using the equipment of the shared research facilities of HPC computing resources at Lomonosov Moscow State University.References
- B. Sharma, P. Malik and P. Jain, Mater. Today Commun., 2018, 16, 353–363 CrossRef CAS.
- I. Gan and W. S. Chow, Food Packag. Shelf Life, 2018, 17, 150–161 CrossRef.
- A. M. Youssef and S. M. El-Sayed, Carbohydr. Polym., 2018, 193, 19–27 CrossRef CAS PubMed.
- E. Castro-Aguirre, F. Iniguez-Franco, H. Samsudin, X. Fang and R. Auras, Adv. Drug Delivery Rev., 2016, 107, 333–366 CrossRef CAS PubMed.
- J.-M. Lagarón, in Multifunctional and nanoreinforced polymers for food packaging, ed, J.-M. Lagarón, Woodhead Publishing, Cambridge, 1st edn, 2011, vol. 17, pp. 485–497 Search PubMed.
- S. Shankar, L.-F. Wang and J.-W. Rhim, Mater. Sci. Eng. C, 2018, 93, 289–298 CrossRef CAS PubMed.
- I. Armentano, N. Bitinis, E. Fortunati, S. Mattioli, N. Rescignano, R. Verdejo, M. A. Lopez-Manchado and J. M. Kenny, Prog. Polym. Sci., 2013, 38, 1720–1747 CrossRef CAS.
- S. Farah, D. G. Anderson and R. Langer, Adv. Drug Delivery Rev., 2016, 107, 367–392 CrossRef CAS PubMed.
- D. da Silva, M. Kaduri, M. Poley, O. Adir, N. Krinsky, J. Shainsky-Roitman and A. Schroeder, Chem. Eng. J., 2018, 340, 9–14, DOI:10.1016/j.cej.2018.01.010.
- B. Tyler, et al., Adv. Drug Delivery Rev., 2016, 107, 163–175 CrossRef CAS PubMed.
- U. Sonchaeng, F. Iñiguez-Franco, R. Auras, S. Selke, M. Rubino and L.-T. Lim, Prog. Polym. Sci., 2018, 86, 85–121 CrossRef CAS.
- J.-M. Raquez, Y. Habibi, M. Murariu and P. Dubois, Prog. Polym. Sci., 2013, 38, 1504–1542 CrossRef CAS.
- M. Shabanian, M. Hajibeygi, K. Hedayati, M. Khaleghi and H. A. Khonakdar, Mater. Des., 2016, 110, 811–820 CrossRef CAS.
- G. Lazorenko, A. Kasprzhitskii and V. Yavna, Chem. Phys. Lett., 2018, 692, 264–270, DOI:10.1016/j.cplett.2017.12.054.
- Y. Zhou, L. Lei, B. Yang, J. Li and J. Ren, Polym. Test., 2018, 68, 34–38 CrossRef CAS.
- R. Scaffaro, L. Botta, A. Maio and G. Gallo, Composites, Part B, 2017, 109, 138–146 CrossRef CAS.
- L. K. Kian, N. Saba, M. Jawaid and M. T. H. Sultan, Int. J. Biol. Macromol., 2019, 121, 1314–1328 CrossRef CAS PubMed.
- C. Fonseca, A. Ochoa, M. T. Ulloa, E. Alvarez, D. Canales and P. A. Zapata, Mater. Sci. Eng. C, 2015, 57, 314–320 CrossRef CAS PubMed.
- M. Ramos, E. Fortunati, M. Peltzer, A. Jimenez, J. M. Kenny and M. C. Garrigós, Polym. Degrad. Stab., 2016, 132, 2–10 CrossRef CAS.
- S. Therias, M. Murariu and P. Dubois, Polym. Degrad. Stab., 2017, 145, 60–69 CrossRef CAS.
- P. Yuan, D. Tan and F. Annabi-Bergaya, Appl. Clay Sci., 2015, 112–113, 75–93 CrossRef CAS.
- R. Mansa, C.-T. Huang, A. Quintela, F. Rocha and C. Detellier, Appl. Clay Sci., 2015, 115, 87–96 CrossRef CAS.
- S. Mallick, Z. Ahmad, F. Touati, J. Bhadra, R. A. Shakoor and N. J. Al-Thani, Ceram. Int., 2018, 44, 16507–16513 CrossRef CAS.
- V. Bugatti, A. Sorrentino and G. Gorrasi, Eur. Polym. J., 2017, 93, 495–506 CrossRef CAS.
- M. Liu, Y. Zhang and C. Zhou, Appl. Clay Sci., 2013, 75–76, 52–59 CrossRef CAS.
- Y. Dong, J. Marshall, H. J. Haroosh, S. Mohammadzadehmoghadam, D. Liu, X. Qi and K.-T. Lau, Composites, Part A, 2015, 76, 28–36 CrossRef CAS.
- P. Krishnaiah, C. T. Ratnam and S. Manickam, Appl. Clay Sci., 2017, 135, 583–595 CrossRef CAS.
- M. K. Pierchala, M. Makaremi, H. L. Tan, J. Pushpamalar, S. Muniyandy, A. Solouk, S. M. Lee and P. Pasbakhsh, Appl. Clay Sci., 2018, 160, 95–105 CrossRef CAS.
- F. Wu, J. Zheng, Z. Li and M. Liu, Chem. Eng. J., 2019, 359, 672–683 CrossRef CAS.
- K. Lim, W. S. Chow and S. Y. Pung, J. Polym. Environ., 2019, 27, 1746–1759 CrossRef CAS.
- S. Sharma, A. A. Singh, A. Majumdar and B. S. Butola, J. Mater. Sci., 2019, 54, 8971–8983 CrossRef CAS.
- C. Venkatesh, O. Clear, I. Major, J. G. Lyons and D. M. Devine, Materials, 2019, 12, 1830 CrossRef PubMed.
- J. Guo, J. Qiao and X. Zhang, J. Appl. Polym. Sci., 2016, 133, 44272 Search PubMed.
- R. T. De Silva, P. Pasbakhsh, K. L. Goh, S. P. Chai and J. Chen, J. Compos. Mater., 2013, 48, 3705–3717 CrossRef.
- W. Xu, B. Luo, W. Wen, W. Xie, X. Wang, M. Liu and C. Zhou, J. Appl. Polym. Sci., 2015, 41451 Search PubMed.
- J. Matusik, E. Stodolak and K. Bahranowski, Appl. Clay Sci., 2011, 51, 102–109 CrossRef CAS.
- S. Zhou, X. Zheng, X. Yu, J. Wang, J. Weng, X. Li, B. Feng and M. Yin, Chem. Mater., 2007, 19, 247–253 CrossRef CAS.
- M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys., 1992, 64, 1045–1097 CrossRef CAS.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS PubMed.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr. - Cryst. Mater., 2005, 220, 567–570 CAS.
- M. D. Segall, P. J. D. Lindan, M. J. Probert, C. J. Pickard, P. J. Hasnip, S. J. Clark and M. C. Payne, J. Phys.: Condens. Matter, 2002, 14, 2717–2744 CrossRef CAS.
- V. Sadovnichy, A. Tikhonravov, Vl. Voevodin and V. Opanasenko, “Lomonosov”: Supercomputing at Moscow State University, in Contemporary High Performance Computing: From Petascale Toward Exascale, ed. J. S. Vetter, Chapman and Hall/CRC, Boca Raton, 1st edn, 2013, pp. 283–307 Search PubMed.
- Vl. Voevodin, A. Antonov, D. Nikitenko, P. Shvets, S. Sobolev, I. Sidorov, K. Stefanov, V. Voevodin and S. Zhumatiy, Supercomput. front. innov., 2019, 6, 4–11 Search PubMed.
- J. P. Perdew, K. Burke and Y. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16533–16539 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- P. Bechthold, J. S. Ardhengi, A. Juan, E. A. González and P. V. Jasen, Appl. Surf. Sci., 2014, 315, 467–474 CrossRef CAS.
- J. Wellendorff, T. L. Silbaugh, D. G. Pintos, J. K. Norskov, T. Bligaard, F. Studt and C. T. Campbell, Surf. Sci., 2015, 640, 36–44 CrossRef CAS.
- A. Kasprzhitskii, G. Lazorenko, V. Yavna and Ph. Daniel, J. Mol. Struct., 2016, 1109, 97–105 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895 CrossRef PubMed.
- A. D. Corso, A. Pasquarello and A. Baldereschi, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R11369–R11372 CrossRef.
- Y. Wang, W. Wang, K.-N. Fan and J. Deng, Surf. Sci., 2001, 490, 125–132 CrossRef CAS.
- V. A. Yavna, A. S. Kasprzhitskii, G. I. Lazorenko and A. G. Kochur, Opt. Spectrosc., 2015, 118, 529–536 CrossRef CAS.
- A. S. Kasprzhitskii, G. I. Lazorenko, S. N. Sulavko, V. A. Yavna and A. G. Kochur, Opt. Spectrosc., 2016, 121, 357–363 CrossRef CAS.
- K. F. Garrity, J. W. Bennett, K. M. Rabe and D. Vanderbilt, Comput. Mater. Sci., 2014, 81, 446–452 CrossRef CAS.
- B. G. Pfrommer, M. Cote, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240 CrossRef CAS.
- P. Pulay, Chem. Phys. Lett., 1980, 73, 393–398 CrossRef CAS.
- Z. Yanga, W. Liua, H. Zhanga, X. Jianga and F. Minb, Appl. Surf. Sci., 2018, 436, 58–65 CrossRef.
- G. Zhang, W. A. Al-Saidi, E. M. Myshakin and K. D. Jordan, J. Phys. Chem. C, 2012, 116, 17134–17141 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- R. B. Neder, M. Burghammer, T. Grasl, H. Schulz, A. Bram and S. Fiedler, Clays Clay Miner., 1999, 47, 487–494 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- A. Luzar and D. Chandler, J. Chem. Phys., 1993, 98, 8160–8173 CrossRef CAS.
- Y. Han, W. Liu and J. Chen, Appl. Surf. Sci., 2016, 370, 403–409 CrossRef CAS.
- D. Tunega, G. Haberhauer, M. H. Gerzabek and H. Lischka, Langmuir, 2002, 18, 139–147 CrossRef CAS.
- X. Li, D. Tan, L. Xie, H. Sun, S. Sun, G. Zhong and P. Ren, Appl. Clay Sci., 2018, 157, 218–226 CrossRef CAS.
- R. Šolc, M. H. Gerzabek, H. Lischka and D. Tunega, Geoderma, 2011, 169, 47–54 CrossRef.
- M. Tharmavaram, G. Pandey and D. Rawtani, Adv. Colloid Interface Sci., 2018, 261, 82–101 CrossRef CAS PubMed.
- P. Sun, G. Liu, D. Lv, X. Dong, J. Wu and D. Wang, RSC Adv., 2015, 5, 52916–52925 RSC.
- P. Luo, J. Zhang, B. Zhang, J. Wang, Y. Zhao and J. Liu, Ind. Eng. Chem. Res., 2011, 50, 10246–10252 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |