Open Access Article
Open Access ArticleA step forward in the development of superoxide dismutase mimetic nanozymes: the effect of the charge of the surface on antioxidant activity†
Álvaro Martínez-Camarena a,
José M. Llinares
a,
José M. Llinares ab,
Antonio Domenech-Carbó
ab,
Antonio Domenech-Carbó c,
Javier Alarcón
c,
Javier Alarcón d and
Enrique García-España
d and
Enrique García-España *a
*a
aICMol, Departamento de Química Inorgánica, Universidad de Valencia, C/Catedrático José Beltrán 2, 46980, Paterna, Spain. E-mail: enrique.garcia-es@uv.es
bDepartamento de Química Orgánica, Universidad de Valencia, C/Dr Moliner s/n, 46100, Burjassot, Spain
cDepartamento de Química Analítica, Universidad de Valencia, C/Dr Moliner s/n, 46100, Burjassot, Spain
dDepartamento de Química Inorgánica, Universidad de Valencia, C/Dr Moliner s/n, 46100, Burjassot, Spain
First published on 16th December 2019
Abstract
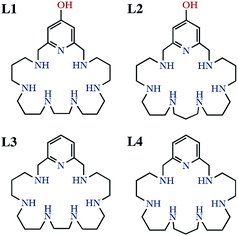
Two binucleating hezaaza macrocycles containing a pyridinol spacer have been prepared and characterised. Protonation studies indicate the deprotonation of the phenol group at relatively low pH values with the concomitant occurrence of a keto-enolic equilibrium. These ligands readily form binuclear Cu2+ and Zn2+ complexes as denoted by potentiometric and spectroscopic studies. The binding of the metals yields to the ready deprotonation of the phenol with the stabilisation of the keto form that results in complexes of greater stabilities than the analogous ones containing pyridine as spacer instead of pyridine. Mixed Cu2+–Zn2+-complexes were also detected in aqueous solutions containing equimolar amounts of Cu2+, Zn2+ and ligands. The binuclear Cu2+ complexes show significant SOD activity as proved by the McCord–Fridovich assays. The binuclear Cu2+ complexes of the ligands grafted to boehmite nanoparticles (BNPs) show a remarkable increase in SOD activity, which reaches 8-fold in one of the systems. The observed increase can be ascribed to the positive ζ-potential of the BNPs since the same complexes anchored to silica nanoparticles with negative ζ-potential do not show any apparent increase in activity. This behaviour is reminiscent of the positively charged funnel found in CuZnSOD, which has the electroactive copper ion at its end.
Introduction
It is well-known that the imbalance between the production and removal of reactive oxygen species in living systems generates oxidative stress, which is related to the occurrence of neurological disorders and, therefore, has profound consequences in aging and hence in life expectancy.1–4 Removal of excess amounts of oxygen reactive species (ROS) is carried out in healthy organisms by a battery of enzymes starting by the superoxide dismutase (SOD) family.5 SOD enzymes take care of the dismutation reaction of superoxide anionic radicals into dioxygen and hydrogen peroxide, which is then transformed into dioxygen and water by the action of the catalase family of enzymes (CATs).6,7 Although natural enzymes might be employed to remove ROS excesses,8–10 this procedure suffers from severe drawbacks such as lack of oral activity, immunogenicity, short half-life and low cell permeability.11,12 Therefore, low-molecular weight mimetics may be better suited than natural enzymes for this purpose owing to their lack of antigenicity, good tissue penetrance, high stability, longer half-life in solution, and low production cost.13,14 A number of these low molecular SOD mimetics are complexes of polyamine ligands of either cyclic or acyclic topology.15–20 In this respect, we have recently reported that several mononuclear or binuclear manganese and copper complexes of aza-macrocyclic ligands have SOD activities in vitro which rank among the highest ones so far reported for synthetic systems.21–23A plausible way of increasing SOD activity might be the attachment of the molecules to the surface of appropriate nanoparticles (NPs). Regarding this point, we have recently communicated that the Cu2+ binuclear complexes of the hexaazapyridinophane ligand L1 (Scheme 1) exhibited an 8-fold enhanced SOD activity when grafted to boehmite nanoparticles (BNPs).24 The reason for such a behaviour was in principle related to the accumulation of active sites in the surface of the BNPs.25 However, other factors may also influence the observed behaviour such as the charge of the nanoparticle surface. Boehmite has typically a positively charged surface that may attract the negatively charged superoxide anions towards the electroactive centres. This behaviour is somehow reminiscent of the funnel found in Cu2Zn2SOD, which has the electroactive copper ion at its end, and displays a gradient of increasing positive charge as the funnel approaches the electroactive centre.5,26 Herein we have prepared a novel hexazacyclophane receptor containing a continuous set of propylene chains between the amine groups linked to the 2,6-positions of a pyridinol ring through methylene groups (L2). We compare its Cu2+ and Zn2+ coordination behaviour with that of the parent ligand L1 and with those of the ligands having pyridine instead of pyridinol groups (L3 and L4 in Scheme 1). Moreover, we have grafted the new ligand to the surface of BNPs and we have estimated the SOD activity of the new system. In order to evaluate the influence the charge of the surface of the NPs we have measured the ζ-potential of either the BNPs alone or the BNPs grafted with either only the ligand or with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios of Cu2+. Finally, we have compared these systems with analogous ones in which we have attached our ligands to silica NPs (SNPs) that supposedly have a negatively charged surface.
1 molar ratios of Cu2+. Finally, we have compared these systems with analogous ones in which we have attached our ligands to silica NPs (SNPs) that supposedly have a negatively charged surface.
Results and discussion
Synthetic procedures
L2 has been synthesised in good yield by means of a modification of the Richman–Atkins procedure27 in which the tosylated amine 1,5,9,13,17,21-hexakis(ρ-tolylsulfonyl)-1,5,9,13,17,21-hexaazaheneicosane28,29 was reacted with 4-(benzyloxy)-2,6-bis(chloromethyl)pyridine30,31 in CH3CN using K2CO3 as a base. The removal of the tosyl and benzyl groups was performed using HBr/AcOH with an excess of phenol. Characterisation data of the compound are included in the ESI (Fig. S1–S6).†Boehmite nanoparticles (BNPs) were prepared by a two-step procedure already described.32 In the first step aluminium tert-butoxide was hydrolysed at 85 °C in water under strong stirring. After the alkoxide addition, a gel was formed almost instantaneously. In the second step a peptization process was carried out keeping the BNPs in HNO3 for several days at 95 °C. Characterization data of both the boehmite and the silica nanoparticles are included in the ESI (Fig. S7 and S8).†
The grafting of the macrocycles to the BNPs or SNPs was performed by condensation of the pyridinol groups with the terminal Al–OH or Si–OH groups at the surface of the nanoparticles. The amount of grafted macrocycle was measured by elemental microanalysis and 1H NMR using TSP as internal standard. The values obtained were [L1] = (3.5 ± 0.4) × 10−5 mol gBNP−1 and [L2] = (2.20 ± 0.02) × 10−4 mol gBNP−1 for the functionalised boehmite nanoparticles and [L1] = (2.3 ± 0.2) × 10−5 mol gSNP−1 and [L2] = (3.3 ± 0.3) × 10−5 mol gSBP−1 for the grafted silica ones (see Table S1 and Fig. S9–S18 in the ESI†). Furthermore, ICP-MS analysis showed that there were two moles of copper by every mole of grafted ligand (see ESI, Table S1†).
Acid-base behaviour
The protonation constants of L2 obtained by potentiometric titrations, as well as those we have previously reported for L1,24 are shown in Table 1. The representation of the distribution diagrams as a function of the pH are shown in Fig. 1. The protonation constants for the related pyridine containing cyclophanes L3 and L4, as well as their distribution diagrams, are collected in Table S2, Fig. S19 and S20 of the ESI.†| Reaction | L124 | L2 |
|---|---|---|
a Values in parentheses are standard deviations in the last significant figure.b log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = ∑log β = ∑log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. K. |
||
| H−1L− + H+ ⇄ H(H−1L) | 10.68(2)a | 10.03(2) |
| H(H−1L) + H+ ⇄ H2(H−1L)+ | 10.11(2) | 9.98(1) |
| H2(H−1L)+ + H+ ⇄ H3(H−1L)2+ | 9.36(1) | 8.99(2) |
| H3(H−1L)2+ + H+ ⇄ H4(H−1L)3+ | 7.97(1) | 7.94(2) |
| H4(H−1L)3+ + H+ ⇄ H5(H−1L)4+ | 6.13(1) | 6.61(2) |
| H5(H−1L)4+ + H+ ⇄ H5L5+ | 5.81(1) | 6.03(2) |
| H5L5+ + H+ ⇄ H6L6+ | 4.14(2) | 5.09(4) |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βb βb |
54.20 | 54.67 |
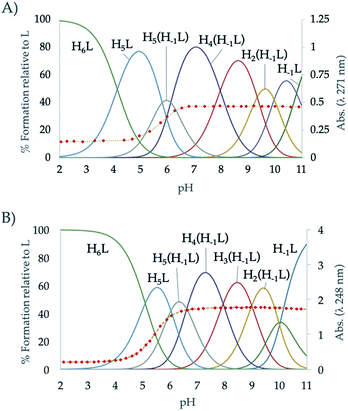 | ||
| Fig. 1 Distribution diagram of (A) L1 and (B) L2 as a function of the pH in aqueous solution. The absorbance at 248 nm in the UV-Vis spectra is represented overlaid as diamonds (♦). | ||
The potentiometric titrations allowed to determine 7 protonation constants ranging from 10.03 to 5.09 logarithmic units (Table 1). L2 follows the typical protonation behaviour usually found for cyclic polyamines, already shown for L1, which is based on the electrostatic repulsions between protonated amino groups, inductive effects of the alkyl and aromatic groups and statistic effects.29,33 The differences between the protonation constant values of L1 and L2,24 can be explained according to minimisation of charge repulsions and inductive effects.
L1, which has an ethylenic chain at the centre of the polyamine bridge, shows higher constant values for the first protonation steps, and smaller values for the last ones than L2. This effect can be explained attending to the separation between the amino groups in each ligand and its influence on intramolecular interactions. While the shorter ethylenic chains favours the stabilisation of the first protonations promoting the formation of intramolecular hydrogen bonds, the longer propylenic chains minimise the electrostatic repulsions in the last protonations.34
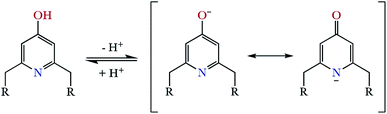
On the other hand, a comparison between the ligands with pyridinol or pyridine group and the same chain L1 vs. L3 and L2 vs. L4 (see Table S2 in the ESI†), reveals that the first constants of the pyridinol ligands, L1 and L2, show higher values than those corresponding to the pyridine receptors, L3 and L4, excluding the first protonation of L2. However, it is interesting to note that this tendency is reversed with the fourth protonation. Registration of the UV spectra at variable pH can give an explanation for this effect. While for the pyridine macrocycles L3 and L4 the band of the aromatic spacer at ∼260 nm does not change with pH, for the pyridinol ones it experiments a very significant hypochromism from pH 7 to 5 (Fig. 1). This can be attributed to the protonation of the phenolate that would occur coupled to the formation of the H5L5+ species, H5(H−1L)4+ + H+ ⇄ H5L5+ equilibrium. Deprotonation of the pyridinol moiety gives rise to a keto-enolic equilibrium (Fig. 2) whose ketonic form presents a negative charge located on the pyridinic nitrogen. Thus, the removal of the enolic hydrogen observed by the UV titrations could stabilise the first four protonations of the receptors through the formation of intramolecular ionic interactions (salt bridges), increasing the value of their constants.
Cu2+ complexation
The Cu2+ complexation constants of L2 determined by potentiometric titrations, as well as those of L1,24 are shown in Table 2. The stability constants of the pyridinophane ligands L3 and L4,29 are collected in Table S3 of the ESI.†| Entry | Reaction | L124 | L2 |
|---|---|---|---|
| a Values in parentheses are standard deviations in the last significant figure. | |||
| 1 | [CuH4(H−1L)]5+ + H+ ⇄ [CuH5(H−1L)]6+ | 3.79(6)a | 4.13(2) |
| 2 | [CuH3(H−1L)]4+ + H+ ⇄ [CuH4(H−1L)]5+ | 5.04(7) | 5.22(2) |
| 3 | [CuH2(H−1L)]3+ + H+ ⇄ [CuH3(H−1L)]4+ | 4.35(7) | 6.30(4) |
| 4 | [CuH(H−1L)]2+ + H+ ⇄ [CuH2(H−1L)]3+ | 6.16(4) | 7.34(4) |
| 5 | [Cu(H−1L)]+ + H+ ⇄ [CuH(H−1L)]2+ | 8.24(4) | 9.22(6) |
| 6 | H−1L− + Cu2+ ⇄ [Cu(H−1L)]+ | 23.56(4) | 19.25(4) |
| 7 | [Cu(H−1L)]+ + H2O ⇄ [Cu(H−1L)(OH)] + H+ | −10.11(5) | −10.71(3) |
| 8 | [Cu(H−1L)]+ + Cu2+ ⇄ [Cu2(H−1L)]3+ | 8.80(4) | 6.95(6) |
| 9 | [Cu2(H−1L)]3+ + H2O ⇄ [Cu2(H−1L)(OH)]2+ + H+ | −7.26(6) | −6.89(2) |
| 10 | [Cu2(H−1L)(OH)]2+ + H2O ⇄ [Cu2(H−1L)(OH)2]+ + H+ | −8.20(6) | −9.90(1) |
| 11 | Cu2+ + H(H−1L) ⇄ [CuH(H−1L)]2+ | 21.11(4) | 18.44(6) |
| 12 | 2Cu2+ + H(H−1L) ⇄ [Cu2H(H−1L)]4+ | 26.44(4) | — |
| 13 | [CuH(H−1L)]2+ + Cu2+ ⇄ [Cu2H(H−1L)]4+ | 5.33(4) | — |
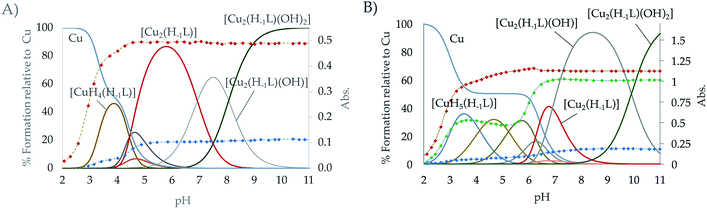
The speciation studies show the formation of mononuclear [CuHx(H−1L)](1+x)+ species with x ranging from 0 to 5 and binuclear species of [Cu2H(H−1L)]4+, [Cu2(H−1L)]3+, [Cu2(H−1L)(OH)]2+ and [Cu2(H−1L)(OH)2]+ stoichiometries. The distribution diagrams collected in Fig. 3 (and in Fig. S21–S26 in the ESI†) show that, while for Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L 1
L 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mole ratio only mononuclear species are present in solution in the pH covered in the studies (2.5–11.0), for a 2
1 mole ratio only mononuclear species are present in solution in the pH covered in the studies (2.5–11.0), for a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio the binuclear species prevail above pH 4 for L1 and above pH 6 for L2. Although inferring coordination numbers and geometries just from the stability constants values could be highly misleading, the combined analysis of these results with UV spectra recorded at variable pH of solutions with different Cu2+
1 ratio the binuclear species prevail above pH 4 for L1 and above pH 6 for L2. Although inferring coordination numbers and geometries just from the stability constants values could be highly misleading, the combined analysis of these results with UV spectra recorded at variable pH of solutions with different Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L mole ratios can give useful information. Thus, the variation of the pyridine band, centred at ∼260 nm, with pH for solutions with either 1
L mole ratios can give useful information. Thus, the variation of the pyridine band, centred at ∼260 nm, with pH for solutions with either 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 2
1 or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Cu2+
1 Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L mole ratio show that deprotonation of the pyridinol group takes place as soon as the first Cu2+ binds the macrocycle, which suggests that the pyridine nitrogen atom takes part in the coordination of the metal ions since the very beginning. This observation, along with the keto-enolic equilibrium of the pyridinol moiety, could explain the higher values of the constants for the formation of the [Cu(H−1L)]+ species shown by L1 and L2 (entry 6 in Table 2) in comparison with the pyridine ones (Cu2+ + L = CuL2+, log
L mole ratio show that deprotonation of the pyridinol group takes place as soon as the first Cu2+ binds the macrocycle, which suggests that the pyridine nitrogen atom takes part in the coordination of the metal ions since the very beginning. This observation, along with the keto-enolic equilibrium of the pyridinol moiety, could explain the higher values of the constants for the formation of the [Cu(H−1L)]+ species shown by L1 and L2 (entry 6 in Table 2) in comparison with the pyridine ones (Cu2+ + L = CuL2+, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 18.34 and 17.22 for L3 and L4, respectively).24,29 The pCu2+ values calculated for [L] = 1 × 10−5 M and [Cu2+] = 2 × 10−6 M confirm that the pyridinol complexes are more stable than the pyridine ones, being L1 the ligand that forms the most stable complexes (Fig. S27†).35 DFT calculations performed for the complex [Cu(H−1L1)]+ support this point since they show as most stable the complex in which the Cu2+ will be bound to the nitrogen of the aromatic moiety and to four secondary amines of the chain in a square pyramidal geometry (see Fig. S28†).
K = 18.34 and 17.22 for L3 and L4, respectively).24,29 The pCu2+ values calculated for [L] = 1 × 10−5 M and [Cu2+] = 2 × 10−6 M confirm that the pyridinol complexes are more stable than the pyridine ones, being L1 the ligand that forms the most stable complexes (Fig. S27†).35 DFT calculations performed for the complex [Cu(H−1L1)]+ support this point since they show as most stable the complex in which the Cu2+ will be bound to the nitrogen of the aromatic moiety and to four secondary amines of the chain in a square pyramidal geometry (see Fig. S28†).
The equilibrium constants found for the formation of the binuclear complexes from the mononuclear ones (entry 8 in Table 2) are rather low, suggesting either the participation of a lower number of nitrogen atoms in the coordination sphere of the second metal or a rearrangement of the coordination sites involving bond breaking and forming as DFT calculation on these systems indicate (see Fig. S28†). The variation of the spectra of the systems Cu2+–L2 and Cu2+–L1 in the UV region suggests the implication of the pyridinol ring in coordination as soon as the first complexes are formed. Coordination of the pyridinol group should lead to the deprotonation of the phenol group and to the formation of the quinone that would afford an increase of electron density on the donor group. The variation with pH of the spectra in the visible region show a profile with two plateaus corresponding to the formation of the mon- and binuclear complexes with extinction coefficients of ca. 123 and 339 M−1 cm−1, respectively. On the other and, the rather acidic values of the constants for the first hydrolysis of the [Cu2(H−1L)]3+ complexes (entry 9 in Table 2) support that the hydroxide anion is placed between the metal centres as a bridging ligand.
Zn2+ complexation
Since Zn2+ is also present in the active centre of Cu2Zn2SOD we next performed speciation studies for the binary Zn2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L systems. The complexation constants of L2 obtained by potentiometric titrations, as well as those we have previously reported for L1,24 are shown in Table S4.† The stability constants of the pyridinophane ligands L3 and L4,29 are collected in Table S5 of the ESI.†
L systems. The complexation constants of L2 obtained by potentiometric titrations, as well as those we have previously reported for L1,24 are shown in Table S4.† The stability constants of the pyridinophane ligands L3 and L4,29 are collected in Table S5 of the ESI.†
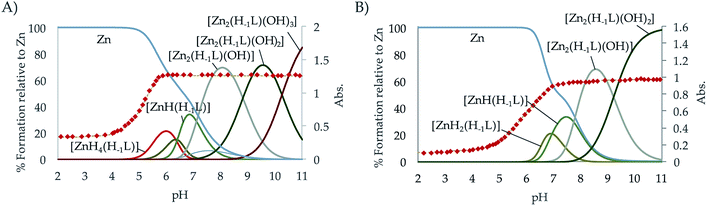
The distribution diagrams collected in Fig. 4 (and in Fig. S29–S34 in the ESI†) show that, analogously to Cu2+ although with a reduced range of protonation degrees and lower stabilities, different mono- and binuclear complexes are formed for both systems. As observed for Cu2+, the constant for the formation of the [Zn(H−1L)]+ is greater for L1 than for L2. However, in this case while the stability constant of the [Zn(H−1L2)]+ is greater than that of its analogue pyridine receptor L3, the opposite situation is found for L2 and L4.
Cu2+–Zn2+ complexation
Finally, the formation of mixed Cu2+–Zn2+–L complexes was investigated by potentiometry. To do so, solutions containing equimolar amounts of Cu2+, Zn2+ and of each one of the ligands were titrated with NaOH. To treat the data, as outlined in the Experimental section, in the first run the protonation and stability constants of the binary M2+–L systems already determined, were introduced as fixed parameters and the constants of the mixed Cu2+–Zn2+–L complexes were refined. In a second run, all titrations of both the binary Cu2+–L or Zn2+–L and ternary Cu2+–Zn2+–L systems were treated together refining, in this run, the constants of all the complexes formed independently if they were binary or ternary. The values obtained were self-consistent (Table 3); the differences observed with those constants derived only from the individual titrations fell within the standard deviations. As can be seen in the distribution diagrams (Fig. 5), the mixed systems predominate in both systems above pH 7, being the only species in solution at the pH of 7.4 where the evaluation of the oxidant activity is performed. It is also interesting to remark, that L2 with all propylenic chains presents more propensity to form mixed complexes than L1, which is likely related to the lower stability of its binary complexes.| Entry | Reaction | L124 | L2 |
|---|---|---|---|
| a Values in parentheses are standard deviations in the last significant figure. | |||
| 1 | [CuZnH2(H−1L)]5+ + H+ ⇄ [CuZnH3(H−1L)]6+ | — | 5.58(4) |
| 2 | [CuZnH(H−1L)]4+ + H+ ⇄ [CuZnH2(H−1L)]5+ | — | 7.11(4) |
| 3 | Cu2+ + Zn2+ + H−1L− + H+ ⇄ [CuZnH(H−1L)]4+ | — | 33.54(5) |
| 4 | Cu2+ + Zn2+ + H−1L− + H2O ⇄ [CuZn(H−1L)(OH)]2+ + H+ | 19.93(5) | 17.42(5) |
| 5 | Cu2+ + Zn2+ + H−1L− + 2H2O ⇄ [CuZn(H−1L)(OH)2]+ + 2H+ | 12.19(3) | 9.10(5) |
| 6 | Cu2+ + Zn2+ + H−1L− + 3H2O ⇄ [CuZn(H−1L)(OH)3] + 3H+ | 1.20(7) | — |
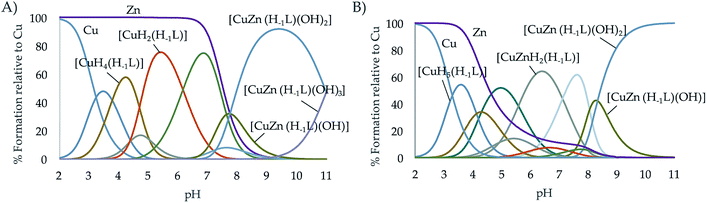 | ||
Fig. 5 Distribution diagram of the ternary systems Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn2+ Zn2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L systems for the ligands (A) L1 and (B) L2 as a function of the pH in aqueous solution ([Cu2+] = [Zn2+] = [L] = 10−3 M). L systems for the ligands (A) L1 and (B) L2 as a function of the pH in aqueous solution ([Cu2+] = [Zn2+] = [L] = 10−3 M). | ||
Electrochemical studies
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
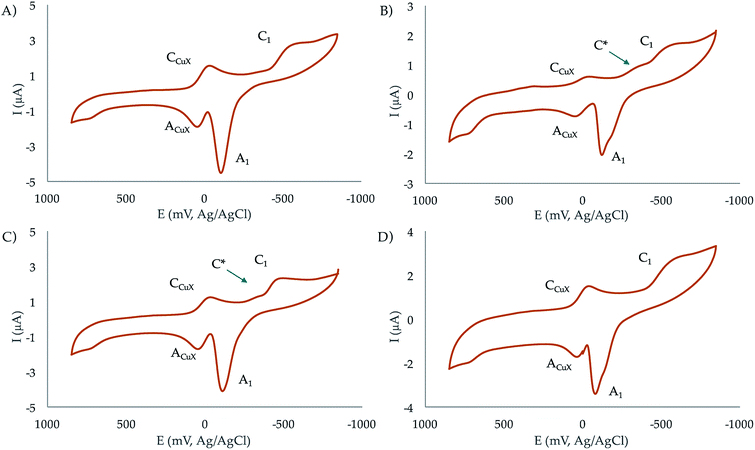
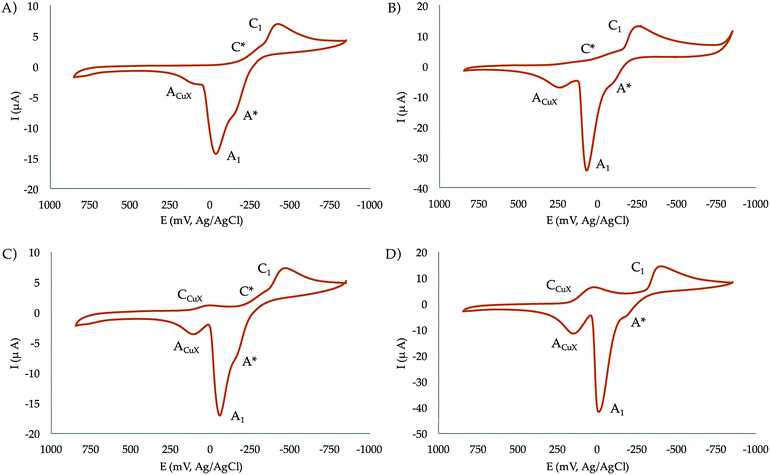
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratios at pH 7.4. In the initial cathodic scan, all complexes display a similar voltammetric pattern consisting of a reduction peak at ca. −0.45 V vs. Ag/AgCl (C1) preceded by a more or less marked shoulder around −0.30 V (C*). These peaks are followed, in the subsequent anodic scan, by an intense oxidation peak at −0.10 V (A1) often accompanied by a shoulder near −0.25 V (A*). The oxidation signal A1 is followed by a broad anodic wave at 0.15 V (ACuX) which is coupled, in the second and successive cathodic scans, by a reduction peak at ca. 0.05 V (CCuX).
1 molar ratios at pH 7.4. In the initial cathodic scan, all complexes display a similar voltammetric pattern consisting of a reduction peak at ca. −0.45 V vs. Ag/AgCl (C1) preceded by a more or less marked shoulder around −0.30 V (C*). These peaks are followed, in the subsequent anodic scan, by an intense oxidation peak at −0.10 V (A1) often accompanied by a shoulder near −0.25 V (A*). The oxidation signal A1 is followed by a broad anodic wave at 0.15 V (ACuX) which is coupled, in the second and successive cathodic scans, by a reduction peak at ca. 0.05 V (CCuX).
 | ||
| Fig. 6 Cyclic voltammograms at glassy carbon electrode of 10−3 M solutions of (a) CuL1, (b) Cu2L1, (c) CuL2, (d) Cu2L2 in 0.15 NaClO4 aqueous solutions at pH 7.4. Potential scan rate 50 mV s−1. | ||
The process A1 has the typical characteristics of the oxidative dissolution of metals (stripping processes), whereas the signals CCuX/ACuX define an essentially reversible one-electron couple which can be attributed to the Cu2+/Cu+ inter-conversion of copper–halide complexes formed as a result of the dissociation of the copper–receptor complexes during the electrochemical cycles.
When the potential range is restricted to the region between −0.10 and −0.30 V, it is possible to record a weak one-electron couple C*/A* (see Fig. S35 in the ESI†). Interestingly, the peak currents for C1 of the mononuclear complexes is just one half that of the binuclear ones. Although the mechanism of Cu2+ reduction in aqueous solution can be complicated,36–38 all these features can be interpreted in terms of the following scheme consistent with previous studies on Cu2+-macrocylic39 systems and the well-known electrochemistry of Cu2+–halide complexes:40,41
(a) Both the mononuclear and dinuclear Cu2+ complexes are reduced in a two-electron process to Cu0 via the process C1.
(b) In the case of dinuclear complexes, both metal centres are reduced simultaneously and independently; i.e., without electronic communication between them.
(c) The ACuX/CCuX couple corresponds to the one-electron reduction/oxidation of copper–halide complexes formed during electrochemical runs.
(d) The above ‘principal’ pathway is accompanied by a competing one involving the one-electron reduction of the parent Cu2+ complexes to Cu+. This pathway is defined by the C*/A* couple.
This scheme means that under electrochemical conditions the predominating route is the reduction of the Cu2+ complexes to Cu0. Under chemical and biochemical conditions, where different electronic and structural constraints can operate, there is possibility of the occurrence of the Cu2+/Cu+ couple as demanded by the ROS activity of the complexes (vide infra). This is supported by the values of the formal redox potentials of that couple (−270 mV for CuL2, −230 mV for Cu2L2, −265 mV for CuL1, and −140 mV for Cu2L1) determined as the half-sum of the peak potentials for the C*/A* peaks.
Antioxidant activity
Once known the main features of the Cu2+ and Zn2+ speciation in aqueous solutions, we proceeded to evaluate the antioxidant activity of our systems. We employed an indirect method based on the side production of superoxide anions by the enzyme xanthine oxidase and their capture by the dye nitroblue tetrazolium (NBT) to give formazan. A compound displaying SOD activity will decrease the flow of superoxide radical anions and thereby, the production of formazan (see Experimental section and the representation of the fitting of the data located in ESI, Fig. S38–S41†). Blank experiments were recorded with the ligands alone without observing any effect.The IC50 and kcat values shown in Table 4 allow deriving several conclusions. First, the SOD activity of the copper complexes of L1 and L2 is remarkable (see for example the comparative of kcat shown in Fig. S42†), showing the binuclear complexes much higher activity than the mononuclear ones. This can be attributed to the fact that, as above commented, the metal ion in the mononuclear complexes presents a rather saturated coordination sphere, which stabilises Cu2+ hampering the cycling between Cu2+ and Cu+ required for promoting the dismutation of the superoxide anions. However, since there are only seven nitrogen donors in the macrocycles, the second metal ion should be either bound to a lower number of nitrogen donors or its coordination should produce a rearrangement of the coordination spheres of both metal ions, which will be, in any case, non-saturated or completed by ancillary labile ligands, as water molecules; the first metal ion might be coordinated by the pyridine nitrogen and three neighbouring polyamine nitrogen atoms, whereas the second Cu2+ would be bound to the remaining three amine groups. DFT calculations for the system Cu2–L1 suggest the latter possibility as the most likely one (see Fig. S28†). The mixed Cu2+–Zn2+ complexes do not show significant differences in activity with respect to the mononuclear Cu2+ complexes.
| System | IC50 (μM) | kcat (106 M−1 s−1) |
|---|---|---|
| a Values in parenthesis are standard deviations in the last significant figure.b Taken from ref. 29.c Taken from ref. 42. | ||
| Cu–L1 | 1.4(5)a | 2.5 |
| CuZn–L1 | 1.6(2) | 2.1 |
| Cu2–L1 | 0.8(1) | 4.1 |
| Cu2–L2 | 0.37(4) | 9.3 |
| Cu2–BNP-L1 | 0.10(3) | 33.7 |
| Cu2–BNP-L2 | 0.12(1) | 28.7 |
| Cu2–SNP-L1 | 3.5(3) | 1.0 |
| Cu2–SNP-L2 | 0.45(3) | 8.2 |
| Cu2–L3b | 3.5(2) | 2.4 |
| Cu2–L4b | 0.11(2) | 27.0 |
| Cu(ClO4)2c | 1.1(1) | 2.7 |
| CuZn–SODc | 0.010(2) | 430 |
On the other hand, it has to be noted that none of these complexes seems to exhibit any catalase activity. The amount of H2O2 in solution was monitored following the evolution with time of its UV band at 229 nm (see Fig. 8 and S43†).
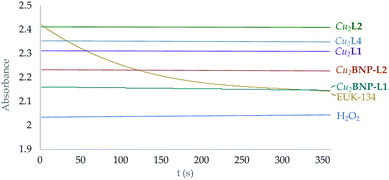 | ||
| Fig. 8 Representation of the variation of the absorbance intensity with time at 219 nm of H2O2 solutions with the presence of both the functionalised and free Cu2+ complexes in solution. Yellow line corresponds to the EUK-134 reference.12 | ||
However, the point of introducing a hydroxo group rightly disposed in the ligands was to permit their covalent anchorage to boehmite (γ-AlO(OH)) nanoparticles (BNPs) without loss of SOD activity. BNPs were chosen as support because we and others43 have shown its innocuous character that has permitted its use even as co-adjuvants in vaccines.44
Table 4 shows that the anchoring of the binuclear complexes of the macrocycles to the BNPs leads to very significant effects with an 8-fold increase in SOD activity in the case of Cu2–L1. Assays either performed with the non-grafted free NPs or with the NPs functionalised with the ligands but without the Cu2+ ions did not produce any activity.
This amplification of activity may be related, as previously described for other systems,25 to the pre-concentration of Cu2+ complexes on the surface of the BNPs that would favour their interaction with the substrate. However, as superoxide radicals are negatively charged the charge of the surface of the NPs may also have an important contribution to the observed enhancement. Therefore, we measured the ζ-potential of the BNPs either free or functionalised with only the macrocycles or with macrocycles plus Cu2+ ions (Table 5, Fig. S9 and S10†). First, it has to be remarked that our 58 nm sized BNPs have a positive ζ-potential of 32.1(8) mV and that the anchorage of the macrocycles produces a slight decrease for L1 while for the more basic and, thereby, more charged L2, the ζ-potential remains practically the same. Therefore, it seems that the positive charge of the NPs surface helps attracting the superoxide anions to the Cu2+ active centres favouring the catalytic process to occur. As noted in the introduction, this fact resembles somehow the attraction of superoxide anions exerted by the positively charged funnel of the CuZn–SOD family of enzymes.26
| System | ζ-Potential (mV) |
|---|---|
| a Values in parenthesis are standard deviations in the last significant figure. | |
| BNP | 32.1(8) |
| BNP-L1 | 23.9(2) |
| BNP-L2 | 35(2) |
| Cu2–BNP-L1 | 24.7(1) |
| Cu2–BNP-L2 | 32.0(7) |
| SNP | −18.1(9) |
| SNP-L1 | −14.9(2) |
| SNP-L2 | −5.6(2) |
| Cu2–SNP-L1 | −12(2) |
| Cu2–SNP-L2 | 0(2) |
In order to double check the effect of the surface charge of the NPs we grafted our macrocycles to silica nanoparticles (SNPs) which are known to have a negatively charged surface. In our case, the ζ-potential of the free SNPs was −18.1(9) mV. This ζ-potential became less negative when the macrocycles, particularly L2, were anchored. Moreover, in the case of L2 addition of two moles of Cu2+ per mol of ligand led to modified SNPs with a ζ-potential close to zero. The results in Tables 4, 5 and Fig. 9 show that while metal complex grafted SNPs with negative potential decrease the efficiency of superoxide dismutation, when they have potential close to zero there are not significant changes in activity with respect to the one displayed by the free metal complexes. Therefore, the results support that the electrostatic interaction between the surface of the NPs and the superoxide anionic substrates has a key role in the SOD activity increases or decreases exerted by the nanosystems.
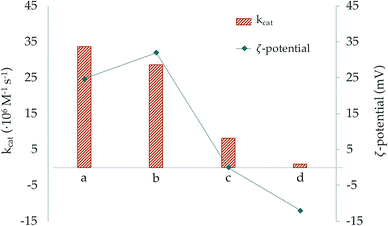 | ||
| Fig. 9 Representation of the catalytic constant (orange bars) and ζ-potential (blue dots) values of the systems (a) Cu2–BNP-L1, (b) Cu2–BNP-L2, (c) Cu2–SNP-L2 and (d) Cu2–SNP-L1. | ||
Conclusions
The binuclear Cu2+ complexes of two pyridinol hexaaza-macrocycles have shown to be extremely efficient in enhancing the dismutation rate of superoxide anions into hydrogen peroxide and dioxygen (SOD activity) while they do not show any catalase activity. The high SOD activity achieved is related to the unsaturated coordination sphere that the metal centres adopt with the entry of the second metal ion. Covalent grafting of the complexes to the surface of boehmite nanoparticles show a drastic enhancement in activity that can be mainly attributed to the positive charge of the nanoparticle that would help driving the anionic substrates to the active centre reminding the role played by the positively charged funnel of the CuZn–SOD family of enzymes. Studies performed with silica nanoparticles, which depending on the grafted molecules, show negative or close to zero ζ-potentials exhibit either decrease or similar activities to the free binuclear complexes. The studies here presented may represent an interesting to the develop nanozyme type materials with antioxidant properties.Experimental
Synthesis and characterisation
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CH3OH, 97
CH3OH, 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3). The product was obtained as a pale yellow solid (2.10 g, yield: 62%). 1H NMR (300 MHz, CDCl3), δ (ppm): 7.65 (d, J = 8.1 Hz, 4H), 7.62 (d, J = 8.1 Hz, 4H), 7.56 (d, J = 8.3 Hz, 4H), 7.43–7.23 (m, 17H), 6.92 (s, 2H), 5.01 (s, 2H), 4.27 (s, 4H), 3.22 (t, J = 7.0 Hz, 4H), 3.13–2.91 (m, 16H), 2.41 (s, 6H), 2.39 (s, 6H), 2.37 (s, 6H), 2.00–1.86 (m, 2H), 1.81–1.66 (m, 8H). 13C NMR (75.4 MHz, CDCl3) δ (ppm): 172.18, 158.64, 143.75, 137.46, 136.73, 136.07, 135.92, 130.21, 130.14, 129.09, 128.27, 127.63, 127.57, 127.55, 70.16, 54.25, 47.83, 31.03, 30.79, 29.92, 29.52, 28.93, 21.87. MS m/z (ESI) 1458.1 ([M + Na]+).
3). The product was obtained as a pale yellow solid (2.10 g, yield: 62%). 1H NMR (300 MHz, CDCl3), δ (ppm): 7.65 (d, J = 8.1 Hz, 4H), 7.62 (d, J = 8.1 Hz, 4H), 7.56 (d, J = 8.3 Hz, 4H), 7.43–7.23 (m, 17H), 6.92 (s, 2H), 5.01 (s, 2H), 4.27 (s, 4H), 3.22 (t, J = 7.0 Hz, 4H), 3.13–2.91 (m, 16H), 2.41 (s, 6H), 2.39 (s, 6H), 2.37 (s, 6H), 2.00–1.86 (m, 2H), 1.81–1.66 (m, 8H). 13C NMR (75.4 MHz, CDCl3) δ (ppm): 172.18, 158.64, 143.75, 137.46, 136.73, 136.07, 135.92, 130.21, 130.14, 129.09, 128.27, 127.63, 127.57, 127.55, 70.16, 54.25, 47.83, 31.03, 30.79, 29.92, 29.52, 28.93, 21.87. MS m/z (ESI) 1458.1 ([M + Na]+).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O 90
H2O 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 vol/vol mixture.
10 vol/vol mixture.Silica nanoparticles (SNPs) were provided by deference of Drs Juan Pastor and Rafael Abargues from INTENANOMAT of the Scientific Park of the University of Valencia.
Characterization data of both the boehmite and the silica nanoparticles are included in the ESI (Fig. S7 and S8).†
EMF measurements
The potentiometric titrations were carried out at 298.1 ± 0.1 K using NaClO4 0.15 M as supporting electrolyte. The experimental procedure (burette, potentiometer, cell, stirrer, microcomputer etc.) has been fully described elsewhere.45 The acquisition of the electromotive force (emf) data was performed with the computer program PASAT.46 The reference electrode was an Ag/AgCl electrode in saturated KCl solution. The glass electrode was calibrated as a hydrogen ion concentration probe by titration of previously standardised amounts of HCl with CO2-free NaOH solutions and the equivalent point determined by the Gran's method,47,48 which gives the standard potential, E°, and the ionic product of water (pKw = 13.73(1)). The computer program HYPERQUAD was used to calculate the protonation and stability constants.49 The HYSS50 program was used to obtain the distribution diagrams. The pH range investigated was 2.5–11.0. In the binary M2+/L systems the concentrations of Cu2+ or Zn2+ and the ligands ranged from 0.5 to 5 mM with M2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L molar ratios 1
L molar ratios 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 2
1 and 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In the ternary systems the Cu2+
1. In the ternary systems the Cu2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn2+
Zn2+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L molar ratio was 1
L molar ratio was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 with concentration of the reactants ca. 10−3 M. The titration curves for each system (at least two titrations, over 200 experimental points) were treated either as a single set or as separated curves without significant variations in the values of the stability constants. To check the consistency of the system, a final fitting of all the metal complex constants was carried out putting together all the titrations of the binary and ternary systems of a given ligand (1038 experimental points for L1, 778 experimental points for L2). The values of the constants obtained in this way agreed within the standard deviations with those retrieved from the treatment of the sets of binary and ternary systems alone.
1 with concentration of the reactants ca. 10−3 M. The titration curves for each system (at least two titrations, over 200 experimental points) were treated either as a single set or as separated curves without significant variations in the values of the stability constants. To check the consistency of the system, a final fitting of all the metal complex constants was carried out putting together all the titrations of the binary and ternary systems of a given ligand (1038 experimental points for L1, 778 experimental points for L2). The values of the constants obtained in this way agreed within the standard deviations with those retrieved from the treatment of the sets of binary and ternary systems alone.
NMR measurements
The 1H and 13C NMR spectra were recorded on a Bruker Advance DRX 500 spectrometer operating at 500 MHz for 1H and at 100.6 MHz for 13C. For the 13C NMR spectra, dioxane was used as a reference standard (δ 67.4 ppm), and for the 1H spectra, the solvent signal was used. Adjustments to the desired pH were made using drops of DCl or NaOD solutions. The pD was calculated from the measured pH values using the correlation, pH = pD − 0.4.51UV-Vis measurements
The solvents used were of spectroscopic or equivalent grade. Water was twice distilled and passed through a Millipore apparatus. The pH values were measured with a Metrohm 713 pH meter and adjustments of the hydrogen ion concentration of the solutions were made with diluted HCl and NaOH solutions. UV-Vis absorption spectra were recorded with an Agilent 8453 spectrometer.Electrochemical measurements
Cyclic voltammetric experiments in 10−3 M aqueous solutions of the receptors in the presence of different stoichiometric concentrations of Cu2+ were studied using 0.15 M NaClO4 as a supporting electrolyte. The pH was adjusted to 7.4 adding appropriate amounts of HClO4 and NaOH solutions. Electrochemical experiments were performed with a CHI 440 potentiostatic device using a conventional three-compartment cell with a Ag/AgCl (3 M NaCl) reference electrode, a platinum wire auxiliary electrode and a glassy-carbon working electrode (geometrical area 0.071 cm2). Prior to each voltammetric run, the electrode was polished with an aqueous suspension of alumina on a soft surface, rinsed with water and dried.ζ-Potential determination
The electric potential of the interfacial surface between the nanoparticles and the dispersion medium, also known as ζ-potential, was measured using a Malvern Mastersizer 2000 instrument. Solutions containing 1 mg of the NPs in 10 cm3 of a 10−4 M NaClO4 aqueous solution at pH 7.4 were employed in the measurements.Density functional theory (DFT) calculations
DFT calculations of the Cu2+ complexes were performed with DFT as a computational method using UB3LYP/6-311+G* and UB3LYP/LANDL2DZ combinations. Specifically, the 6-311+G* basis set was used for the nonmetallic atoms, while the LANDL2DZ was used for the transition metals, in which it has been generated ab initio effective core potentials to replace the Coulomb, core orthogonality, and exchange effects of the chemically inert core electrons in Cu2+. The Gaussian 09 (ref. 52) package was used for these DFT calculations and the Molden53 and Pymol54 package for the modelling analysis. The aqueous environment was implicitly considered by using the Self-Consistent Reaction Field (SCRF) method with a model of continuous polarization model with water as a solvent (Polarizable Continuum Model – PCM).55–57In vitro McCord–Fridovich SOD activity assays
SOD-like activity was determined by using the nitro blue tetrazolium (NBT) method.58–61 The assays were carried out in a pH = 7.4 50 mM HEPES buffer at 298 K. The xanthine (2.2 × 10−4 M) and xanthine oxidase system was used to generate a reproducible and constant flux of superoxide anions. The rate of reduction of NBT (7.3 × 10−5 M) to blue formazane was followed spectrophotometrically at 560 nm. Data in the absence of the complex were used as a reference. The rate of NBT reduction was progressively inhibited after the addition of the complex solutions at increasing concentrations prepared in 50 mM Tris–HCl buffer. The percentage of inhibition of the NBT reduction was used as a measure of the SOD activity of the compounds. The concentration of complex required to yield 50% inhibition of NBT reduction (IC50) was determined from a plot of percentage inhibition versus complex concentration. The IC50 data have been calculated from the mean values of (at least) three independent measurements. The catalytic constant was calculated from the IC50 using the equation kcat = kNBT[NBT]/IC50 where kNBT= (5.9 + 0.5) × 105 M−1 s−1.62–64Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the financial support by the Spanish MINECO and FEDER funds from the European Union (Project CTQ2016-78499-C6-1-R, CTQ2017-90852-REDC and Unidad de Excelencia María de Maeztu MDM-15-0538) and Generalitat Valenciana (PROMETEO II 2015-002). A. M.-C. wants to thank Spanish Ministry of Science, Research and Universities for the PhD grant FPU14/05098. We also acknowledge Mass Spectrometry, and NMR service from the Central Services for Experimental Research (SCSIE) of University of Valencia.References
- V. Dias, E. Junn and M. M. Mouradian, J. Parkinson's Dis., 2013, 3, 461 CAS.
- V. Chauhan and A. Chauhan, Pathophysiology, 2006, 13, 195 CrossRef CAS PubMed.
- A. Kumar and R. R. Ratan, J. Huntington's Dis., 2016, 5, 217 Search PubMed.
- Z. Liu, T. Zhou, A. C. Ziegler, P. Dimitrion and L. Zuo, Oxid. Med. Cell. Longevity, 2017, 2017, 1 CAS.
- I. A. Abreu and D. E. Cabelli, Biochim. Biophys. Acta, 2010, 1804, 263 CrossRef CAS PubMed.
- V. B. Djordjević, Int. Rev. Cytol., 2004, 237, 57 CrossRef.
- C. D. Putnam, A. S. Arvai, Y. Bourne and J. A. Tainer, J. Mol. Biol., 2000, 296, 295 CrossRef CAS PubMed.
- S. Gandhi and A. Y. Abramov, Oxid. Med. Cell. Longevity, 2012, 2012, 1 CrossRef PubMed.
- L. E. Scott and C. Orvig, Chem. Rev., 2009, 109, 4885 CrossRef CAS PubMed.
- M. T. Fodero-Tavoletti, V. L. Villemagne, C. C. Rowe, C. L. Masters, K. J. Barnham and R. Cappai, Int. J. Biochem. Cell Biol., 2011, 43, 1247 CrossRef CAS PubMed.
- J. M. McCord and M. A. Edeas, Biomed. Pharmacother., 2005, 59, 139 CrossRef CAS PubMed.
- I. Ivanović-Burmazović and M. R. Filipović, Adv. Inorg. Chem., 2012, 64, 53 CrossRef.
- P. A. Adlard, R. A. Cherny, D. I. Finkelstein, E. Gautier, E. Robb, M. Cortes, I. Volitakis, X. Liu, J. P. Smith, K. Perez, K. Laughton, Q.-X. Li, S. A. Charman, J. A. Nicolazzo, S. Wilkins, K. Deleva, T. Lynch, G. Kok, C. W. Ritchie, R. E. Tanzi, R. Cappai, C. L. Masters, K. J. Barnham and A. I. Bush, Neuron, 2008, 59, 43 CrossRef CAS PubMed.
- E. Crabb and E. A. Moore, Metals and Life, Royal Society of Chemistry, 2010 Search PubMed.
- K. Aston, N. Rath, A. Naik, U. Slomczynska, O. F. Schall and D. P. Riley, Inorg. Chem., 2001, 40, 1779 CrossRef CAS PubMed.
- G.-F. Liu, M. Filipović, F. W. Heinemann and I. Ivanović-Burmazović, Inorg. Chem., 2007, 46, 8825 CrossRef CAS PubMed.
- M. Tamura, Y. Urano, K. Kikuchi, T. Higuchi, M. Hirobe and T. Nagano, J. Organomet. Chem., 2000, 611, 586 CrossRef CAS.
- I. Szilágyi, I. Labádi, K. Hernadi, I. Pálinkó, N. V. Nagy, L. Korecz, A. Rockenbauer, Z. Kele and T. Kiss, J. Inorg. Biochem., 2005, 99, 1619 CrossRef PubMed.
- P. Failli, D. Bani, A. Bencini, M. Cantore, L. Di Cesare Mannelli, C. Ghelardini, C. Giorgi, M. Innocenti, F. Rugi, A. Spepi, R. Udisti and B. Valtancoli, J. Med. Chem., 2009, 52, 7273 CrossRef CAS PubMed.
- O. Singh, N. Tyagi, M. M. Olmstead and K. Ghosh, Dalton Trans., 2017, 46, 14186 RSC.
- M. P. Clares, S. Blasco, M. Inclán, L. del Castillo Agudo, B. Verdejo, C. Soriano, A. Doménech, J. Latorre and E. García-España, Chem. Commun., 2011, 47, 5988 RSC.
- J. González-García, Á. Martínez-Camarena, B. Verdejo, M. P. Clares, C. Soriano, E. García-España, H. R. Jiménez, A. Doménech-Carbó, R. Tejero, E. Calvo, L. Briansó-Llort, C. Serena, S. Trefler and A. García-España, J. Inorg. Biochem., 2016, 163, 230 CrossRef PubMed.
- L. Guijarro, M. Inclán, J. Pitarch-Jarque, A. Doménech-Carbó, J. U. Chicote, S. Trefler, E. García-España, A. García-España and B. Verdejo, Inorg. Chem., 2017, 56, 13748 CrossRef CAS PubMed.
- Á. Martínez-Camarena, E. Delgado-Pinar, C. Soriano, J. Alarcón, J. M. Llinares, R. Tejero and E. García-España, Chem. Commun., 2018, 54, 3871 RSC.
- C. Fasting, C. A. Schalley, M. Weber, O. Seitz, S. Hecht, B. Koksch, J. Dernedde, C. Graf, E. W. Knapp and R. Haag, Angew. Chem., Int. Ed., 2012, 51, 10472 CrossRef CAS PubMed.
- I. Bertini, S. Manganl and M. S. Viezzoli, Adv. Inorg. Chem., 1998, 45, 127 CrossRef CAS.
- J. E. Richman and T. J. Atkins, J. Am. Chem. Soc., 1974, 96, 2268 CrossRef CAS.
- B. Dietrich, M. W. Hosseini, J.-M. Lehn and R. B. Sessions, Helv. Chim. Acta, 1983, 66, 1262 CrossRef CAS.
- R. Belda, S. Blasco, B. Verdejo, H. R. Jiménez, A. Doménech-Carbó, C. Soriano, J. Latorre, C. Terencio and E. García-España, Dalton Trans., 2013, 42, 11194 RSC.
- E. Busto, A. González-Álvarez, V. Gotor-Fernández, I. Alfonso and V. Gotor, Tetrahedron, 2010, 66, 6070 CrossRef CAS.
- P. Froidevaux, J. M. Harrowfield and A. N. Sobolev, Inorg. Chem., 2000, 39, 4678 CrossRef CAS PubMed.
- R. Aucejo, P. Díaz, E. García-España, J. Alarcón, E. Delgado-Pinar, F. Torres, C. Soriano and M. C. Guillem, New J. Chem., 2007, 31, 44 RSC.
- J. Aguilar, M. G. Basallote, L. Gil, J. C. Hernández, M. A. Máñez, E. García-España and B. Verdejo, Dalton Trans., 2004, 94 RSC.
- A. Bencini, A. Bianchi, E. García-España, M. Micheloni and J. A. Ramirez, Coord. Chem. Rev., 1999, 188, 97 CrossRef CAS.
- W. R. Harris, K. N. Raymond and F. L. Weitl, J. Am. Chem. Soc., 1981, 103, 2667 CrossRef CAS.
- F. M. Hawkridge and H. H. Bauer, Anal. Chem., 1972, 44, 364 CrossRef CAS.
- J. L. Anderson and I. Shain, Anal. Chem., 1976, 48, 1274 CrossRef CAS.
- J. L. Anderson and I. Shain, Anal. Chem., 1978, 50, 163 CrossRef CAS.
- A. Doménech, E. García-España, S. V. Luis, V. Marcelino and J. F. Miravet, Inorg. Chim. Acta, 2000, 299, 238 CrossRef.
- G. Gunawardena, G. Hills and I. Montenegro, J. Electroanal. Chem., 1985, 184, 357 CrossRef CAS.
- J. Crousier and I. Bimaghra, Electrochim. Acta, 1989, 34, 1205 CrossRef.
- H. Ohtsu, Y. Shimazaki, A. Odani, O. Yamauchi, W. Mori, S. Itoh and S. Fukuzumi, J. Am. Chem. Soc., 2000, 122, 5733 CrossRef CAS.
- A. Rutenberg, V. V. Vinogradov and D. Avnir, Chem. Commun., 2013, 49, 5636 RSC.
- B. Sun and T. Xia, J. Mater. Chem. B, 2016, 4, 5496 RSC.
- E. Garcia-Espana, M. J. Ballester, F. Lloret, J. M. Moratal, J. Faus and A. Bianchi, J. Chem. Soc., Dalton Trans., 1988, 2, 101 RSC.
- M. Fontanelli and M. Micheloni, Proceedings of the I Spanish-Italian Congress on Thermodynamics of Metal Complexes, Peñíscola, España, 1990 Search PubMed.
- G. Gran, Analyst, 1952, 77, 661 RSC.
- F. J. C. Rossotti and H. Rossotti, J. Chem. Educ., 1965, 42, 375 CrossRef CAS.
- P. Gans, A. Sabatini and A. Vacca, Talanta, 1996, 43, 1739 CrossRef CAS PubMed.
- L. Alderighi, P. Gans, A. Ienco, D. Peters, A. Sabatini and A. Vacca, Coord. Chem. Rev., 1999, 184, 311 CrossRef CAS.
- A. K. Covington, M. Paabo, R. A. Robinson and R. G. Bates, Anal. Chem., 1968, 40, 700 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Version C.01, 2009 Search PubMed.
- G. Schaftenaar and J. H. Noordik, J. Comput.-Aided Mol. Des., 2000, 14, 123 CrossRef CAS PubMed.
- Schrödinger-LLC, The PyMOL Molecular Graphics System Version 1.8 Search PubMed.
- S. Miertuš, E. Scrocco and J. Tomasi, Chem. Phys., 1981, 55, 117 CrossRef.
- J. L. Pascual-ahuir, E. Silla and I. Tuñon, J. Comput. Chem., 1994, 15, 1127 CrossRef CAS.
- M. Cossi, G. Scalmani, N. Rega and V. Barone, J. Chem. Phys., 2002, 117, 43 CrossRef CAS.
- L. W. Oberley and D. R. Spitz, Oxygen Radicals in Biological Systems, Elsevier, 1984 Search PubMed.
- L. W. Oberley and D. R. Spitz, Handbook of methods of oxygen radicals research, CRC Press, Boca Raton, USA, 1986 Search PubMed.
- C. Beauchamp and I. Fridovich, Anal. Biochem., 1971, 44, 276 CrossRef CAS PubMed.
- J. Y. Zhou and P. Prognon, J. Pharm. Biomed. Anal., 2006, 40, 1143 CrossRef CAS.
- B. H. J. Bielski and H. W. Richter, J. Am. Chem. Soc., 1977, 99, 3019 CrossRef CAS.
- R. F. Pasternack and B. Halliwell, J. Am. Chem. Soc., 1979, 101, 1026 CrossRef CAS.
- S. Durot, C. Policar, F. Cisnetti, F. Lambert, J.-P. Renault, G. Pelosi, G. Blain, H. Korri-Youssoufi and J.-P. Mahy, Eur. J. Inorg. Chem., 2005, 3513 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Complete experimental procedure, supplementary NMR figures and analysis. See DOI: 10.1039/c9ra08992f |
| This journal is © The Royal Society of Chemistry 2019 |