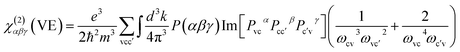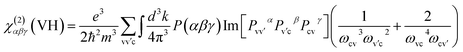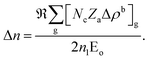Open Access Article
Open Access ArticleTheoretical investigation on the promotion of second harmonic generation from chalcopyrite family AIGaS2 to AIIGa2S4†
Alimujiang Yalikun a,
Ming-Hsien Leeb and
Mamatrishat Mamat
a,
Ming-Hsien Leeb and
Mamatrishat Mamat *a
*a
aSchool of Physics and Technology, Xinjiang University, Urumqi, Xinjiang 830046, P. R China. E-mail: mmtrxt@xju.edu.cn
bDepartment of Physics, Tamkang University, New Taipei 25137, Taiwan
First published on 17th December 2019
Abstract
The chalcopyrite structure is a rich source for the exploration of new IR materials. However, not all of the compounds with a chalcopyrite-type structure exhibit satisfactory optical properties, which may originate from their different microstructure features. In this work, we selected four classical chalcopyrite materials, AIGaS2 (AI = Ag, Cu) with normal structures and AIIGa2S4 (AII = Zn, Hg) with defect structures, to study their electronic structures, optical properties including the contribution of ions and ion groups to their band gaps, SHG responses and birefringences by the first-principles method. The results uncover that the different band gaps are mainly caused by the d orbitals of A* (A* = AI, AII)-site atoms and dp hybridizations between the A*-site and S atoms. In addition, the more powerful covalent bonds of AII–S and Ga–S in the AIIGa2S4 lead to the larger SHG responses of ZnGa2S4 and HgGa2S4. For the birefringences, the sizes of the A*-site atoms make sense, namely larger size will lead to higher distortion of tetrahedra, then result in large birefringences. All the above analyses conclude that the A*-site atoms in the chalcopyrite structures play a modulation role in determining the optical properties.
Introduction
As the key materials in the development of solid-state lasers by frequency-doubling conversion technology, nonlinear optical (NLO) materials have attracted considerable attention,1–6 that is attributed to their worthy applications in many advanced technological fields, such as infrared remote sensing, semiconductor photolithography, environmental monitoring, biological tissue imaging and minimal surgery. During the past few decades, a great number of famous materials applied in the ultraviolet (UV), deep ultraviolet (DUV) and visible regions have been synthesized such as KH2PO4 (KDP),7,8 KTiOPO4 (KTP),9 β-Ba2BO4 (BBO),10 LiB3O5 (LBO)11 and KBe2BOF2 (KBBF).12 However, the DUV materials are far from meeting the needs of the applications. Very recently, for DUV the novel deep UV (DUV) NLO fluorooxoborate crystals, which are represented by typical ABF families,13–15 have been successfully designed and achieved through using the first-principles method by Pan and Yang et al.'s group.16 Unfortunately, these materials cannot be utilized in the infrared (IR) region because of insufficient optical transparency and low SHG.17In IR region, metal chalcogenides AgGaQ2 (Q = S, Se) are classical NLO materials and generate large second harmonic generation (SHG) responses together with wide IR transparent ranges,18–20 but application prospects are seriously hindered by inherent performance defects, such as low laser damage, which is owing to their microcosmic functional building units like the anion groups21 in their structures. Generally, the criteria of an outstanding IR NLO material are as following: (1) long IR absorption edge, (2) large SHG response, (3) wide optical band gap, (4) high laser damage threshold (LDT) and easy to grow large-size single crystals. A wide band gap usually corresponds to low SHG responses in an IR crystal. Thus, the discovery of outstanding mid/far-infrared (IR) nonlinear optical (NLO) materials is still challenging, because of the difficulty in achieving a good balance between the band gap and second harmonic generation (SHG) effect. Under this circumstance, many promising IR NLO materials like, HgGa2S4,22 ZnGa2S4,23 SnGa4S7,24 PbGa4S7,25 BaGa4S7,26 BaGa4Se7,27 Na2Ga2GeS6,28 BaGa2GeX (X = S, Se),29 Li2Ga2PS6,30 Sr5ZnGa6S15 (ref. 31) are reported, which could satisfy the request mentioned above. By systematically investigating their microstructures, we discovered that GaQ4 tetrahedra are common functional anion groups. However, surprisingly we found the differences of the SHG responses between the chalcopyrite family AIGaS2 (AgGaS2 (AGS), CuGaS2 (CGS)) and AIIGa2S4 (HgGa2S4 (HGS), ZnGa2S4 (ZGS)), which have the same functional [GaS4] groups. Therefore, we focused on the theoretical study of the chalcopyrite system with different cations to offer a proposal for the experimental researchers. In the present research, based on the density functional theory, we investigate the origin of the property differences between the AGS, CGS and HGS, ZGS crystals. The results show that the covalent intensities of the Ga–S and A*–S (A* = AI, AII) bonds, the distortion of the [A*S4] and [GaS4] tetrahedra, have obvious differences among the four compounds and further lead to the difference of their optical properties.
Computational details
The present calculations were performed using the pseudo-potentials plane wave method, within density functional theory (DFT) as implemented in the CASTEP computer package.32 The exchange and correlation effects were considered under the generalized gradient approximation (GGA) scheme,33 with the Perdew–Burke–Ernzerhof (PBE) functional.34 Under the norm-conserving pseudo-potentials (NCP),35–37 the following orbital electrons were treated as valence electron: Ag 4d105s1, Cu 3d104s1, Hg 5d106s2, Zn 3d104s2 and Ga 4s24p1, S 3s23p4. To reach the convergence of calculation, the energy cutoff was set up to be 800 eV for AGS, HGS, ZGS, 880 eV for CGS, and Monkhorst–Pack scheme was set at 4 × 4 × 5 for AGS, 6 × 6 × 3 for CGS, and 5 × 5 × 3 for HGS, ZGS respectively in the primitive cell of the Brillouin zone (BZ). The imaginary part of dielectric function ε2 can be calculated based on the electronic structures and the real part is obtained by the Kramers–Kronig transform, accordingly the refractive indices and the birefringence (Δn) can be calculated. In addition, hybrid functional HSE06,38 was employed to describe band gap values, which was found in better agreement with experimental values.The so-called length-gauge formalism derived by Aversa and Sipe39 was performed to calculate the NLO properties. The SHG response is estimated through calculating the static second-order nonlinear susceptibilities at zero frequency. The second-order coefficients can be simplified as:40
| χ(2)αβγ = χ(2)αβγ(VE) + χ(2)αβγ(VH) |
Here, α, β, γ are Cartesian components, v and v′, denote valence bands, c and c′ denote conduction bands, and P(αβγ) denotes full permutation. The band energy difference and momentum matrix elements are denoted as ℏωij and pijα, respectively.
In REDA approximation, the birefringence can be estimated by the anisotropic valence bond of anionic groups as:41
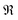 is the correction coefficient, Nc is the coordination number of the nearest neighbor cations to the central anion, Za is the formal chemical valence of the anion, Δρb is the difference between the maximum and minimum bonding electron density of covalent bond in an anionic group on the optical principal axes of a crystal, Eo is the optical band gap, and n1 is the minimum refractive index. In the formula,
is the correction coefficient, Nc is the coordination number of the nearest neighbor cations to the central anion, Za is the formal chemical valence of the anion, Δρb is the difference between the maximum and minimum bonding electron density of covalent bond in an anionic group on the optical principal axes of a crystal, Eo is the optical band gap, and n1 is the minimum refractive index. In the formula, 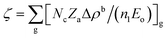 is called the REDA index which could be employed to characterize the optical anisotropy of materials.41
is called the REDA index which could be employed to characterize the optical anisotropy of materials.41
Results and discussion
Structure descriptions
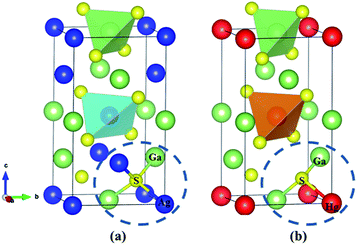
The ternary compounds AGS and CGS have a similar chemical formula AIGaS2, which are isostructural and belong to the same space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d of the tetragonal system. As seen in Fig. 1(a), each S atom is coordinated with two AI-cation and two Ga atoms in the structure. Besides, each AI-cation and Ga atom linked with four S atoms forming [AIS4] and [GaS4] tetrahedra, and the tetrahedra are arranging along the [111] direction. The isostructural compounds ZGS, HGS belong to the chalcopyrite family of AIIGa2S4, which crystalizing in the same nonlinear tetragonal I
2d of the tetragonal system. As seen in Fig. 1(a), each S atom is coordinated with two AI-cation and two Ga atoms in the structure. Besides, each AI-cation and Ga atom linked with four S atoms forming [AIS4] and [GaS4] tetrahedra, and the tetrahedra are arranging along the [111] direction. The isostructural compounds ZGS, HGS belong to the chalcopyrite family of AIIGa2S4, which crystalizing in the same nonlinear tetragonal I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) space group. As shown in Fig. 1(b), each AII-cation is coordinated with four S atoms in the unit cell. The Ga atoms take two different positions and each S atom linked with two Ga and one AII-cation, forming [AIIS4] and [GaS4] tetrahedra along [111] direction. It is clearly seen that [GaS4] tetrahedra contain all S atoms of the compounds. The only difference is that each S atom has four coordinations in AIGaS2 (normal structures), while in AIIGa2S4 each S atom has three coordinations, belonging to the defect chalcopyrite compounds. The unit cell parameters of the considered systems are listed (more calculated details in ESI Table S1†).
space group. As shown in Fig. 1(b), each AII-cation is coordinated with four S atoms in the unit cell. The Ga atoms take two different positions and each S atom linked with two Ga and one AII-cation, forming [AIIS4] and [GaS4] tetrahedra along [111] direction. It is clearly seen that [GaS4] tetrahedra contain all S atoms of the compounds. The only difference is that each S atom has four coordinations in AIGaS2 (normal structures), while in AIIGa2S4 each S atom has three coordinations, belonging to the defect chalcopyrite compounds. The unit cell parameters of the considered systems are listed (more calculated details in ESI Table S1†).
Band gap and electronic structure
The calculated band gaps are respectively 1.28 eV for AGS, 1.04 eV for CGS, 2.16 eV for ZGS and 1.64 eV for HGS, as shown (more calculated details in ESI Fig. S2†). In the band structure spectra, the highest point of the valence band (VB) and the lowest point of the conduction band (CB) are located at the same G point, which obviously demonstrates that the compounds are direct band gap compounds. The calculated band gaps are smaller than the experimental values (the data are shown in Table 1), which is common and mainly due to the discontinuity of exchange–correlation potential.42 Among the four compounds, ZGS exhibits the largest band gap both in theoretical and experimental results. To further investigate the reason, the total and partial density of states (TDOS and PDOS) were also analyzed, from which we can gain useful information such as the hybridization of orbitals and contributions of the states to the electronic band structures.| Space group | HSE06 | Band gap (eV) GGA | Exp. | SHG coefficients (pm V−1) | |
|---|---|---|---|---|---|
| a (Cal.) this work; a,43 b,44 c,45 d,46 e.47 | |||||
| AgGaS2 | I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d 2d |
2.74 | 1.28(Cal.) | 2.64(Exp.)a | d14 = 10.90 |
| d14 = 13a | |||||
| CuGaS2 | I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 2d 2d |
2.44 | 1.04(Cal.) | 2.43(Exp.)b | d14 = 9.11(0.7 × AGS) |
| d14 = 11 c | |||||
| ZnGa2S4 | I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) |
3.49 | 2.16(Cal.) | 3.60(Exp.)e | d14 = 13.2(1.01 × AGS) |
| d14 = 11.92(other cal.)d | |||||
| HgGa2S4 | I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) |
2.78 | 1.64(Cal.) | 2.84(Exp.)d | d14 = 21.3(1.64 × AGS) |
| d14 = 31.5(powder effect)d | |||||
As shown in Fig. 2, the VB of AGS can be divided into two major distinct regions: from −7.3 eV to −5 eV, the Ga-4s states totally overlap with S-3p states, showing strong Ga–S covalent features. Near the top of the VB from −5 eV to Fermi level is mainly contributions of Ag-4d and S-3p states. At the meantime, noted that there are hybridization between Ag-4d orbitals and S-3p orbitals at the −2 energy level.47 As for compound CGS, the energy band near the Fermi level was composed by three regions. The energy from −7.6 eV to −5.6 eV are contributed by Ga-4s states and S-3p states, which shows strong Ga–S covalent interactions. The region from −5.6 eV to −2.3 eV is mainly contribute from Cu-3d and S-3p orbitals, and the Cu-3d states overlap with the S-3p states at the −3 eV energy level, revealing the weak hybridization effect of Cu–S orbitals.48 The energy from −2.3 eV to the Fermi level is mainly contributed by Cu-3d states and S-3p states. It is worth noting that the hybridization effect between Cu-3d states with S-3p states is much stronger than that between Ag-4d and S-3p states, which may be the reason that CGS has a relatively smaller band gap than that of AGS.22 The same conclusion from population analysis could be obtained, which is shown in Table 2. The CB are similar in these isostructural compounds, which is mainly dominated by Ag-5s orbitals, Ga-3s, 4p orbitals and S-3p orbitals in AGS, Cu-4s states, Ga-3s, 4p orbitals and S-3p orbitals in CGS. The band gap is mainly determined by the edges of the valence band (VB) and conduction band (CB). From the Fig. 2(a and b), it is clear that the top of the VB band is mainly occupied by the S-p orbitals and the bottom of the CB is mainly occupied by the Ga-s orbitals. As a result, the Ga and S atoms maybe determine the band gap for these compounds. For the chalcopyrite family of AIIGa2S4, the density of states share almost the same feature, the energy band near the Fermi level was composed by three regions. In the region from −7 eV to −4 eV, the Hg-5d overlap with S-3p orbitals, revealing the weak hybridization effect of Hg–S in HGS. As for ZGS, Zn-4d orbitals overlap with S-3p orbitals, displaying the weak hybridization interactions. Meanwhile, there is little hybridization interaction between the Ga-4s states with S-3p states. Near the Fermi level (from −7 eV to Fermi level) is mainly composed of Ga-4s, 4p and S-3p states for ZGS and HGS. From the Fig. 2(c and d), it is clear that the top of the VB band is mainly occupied the S-p orbitals and the bottom of the CB is the Ga-s orbitals. Accordingly, the Ga-4p and S-3p orbitals determine the optical band gap of AIIGa2S4 compounds. For the AIIGa2S4 family, the only difference is that in the region from −7 eV to −4 eV, the Hg-5d hybridization interaction with the S-3p orbitals was stronger than those between Zn-3d and the S-3p orbitals, tending to develop a relatively narrow band gap.
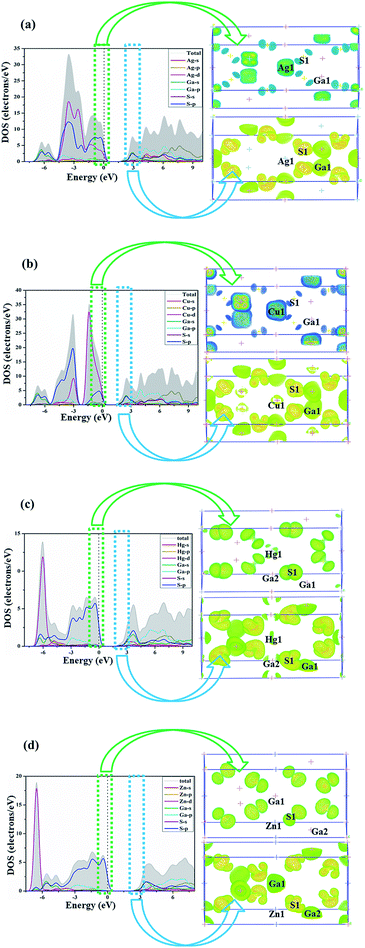 | ||
| Fig. 2 Partial density of states (PDOS) and orbitals for (a) AgGaS2, (b) CuGaS2, (c) HgGa2S4, (d) ZnGa2S4. | ||
| Compounds | Bond | Population (Q) |
|---|---|---|
| AgGaS2 | Ag–S | 0.36 |
| Ga–S | 0.47 | |
| CuGaS2 | Cu–S | 0.39 |
| Ga–S | 0.46 | |
| ZnGa2S4 | Zn–S | 0.46 |
| Ga–S | 0.53–0.58 | |
| HgGa2S4 | Hg–S | 0.44 |
| Ga–S | 0.52–0.56 |
Accordingly, it could be obviously discovered that their d orbitals positions in the energy zone are different, namely there is no d orbitals effect on the −3 eV to the Fermi level in ZGS, which lead to the largest band gap among the four compounds and may be caused by the high localization of the d orbitals of Zn.
Moreover, comparing the DOS of the two structural types of AIGaS2 and AIIGa2S4, it could be found that the dp interactions have a significant impact on the band gap. At the same energy level, strong dp hybridization makes the band gap smaller, near the Fermi level without the influence of the A-site cation d orbitals leads to increasing the band gap. The dp hybridization in AIGaS2-type compounds locate at a deeper energy level in VB, so they have wider band gap than AIIGa2S4-type compounds. To further approve the above discussion, and as well known the optical properties are correlated with electron transitions from VB and CB nearby Fermi level.49 We calculated the top of the orbitals in −3 eV to 3 eV region. As shown in Fig. 2, the highest occupied state levels respectively come from AI-cation 4d and S-3p orbitals, and the lowest unoccupied states mainly derived from both between Ga-4p and S-3p hybridization orbitals in the normal compounds. As for the AIIGa2S4 compounds, the highest occupied state levels are mainly contributed by the S-3p orbitals, Ga-4p and the lowest unoccupied states are composed of S-3p states, which match well with the PDOS analysis.
NLO coefficient and birefringence
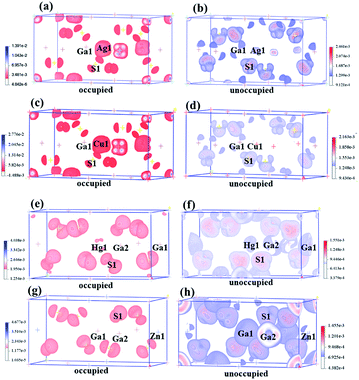
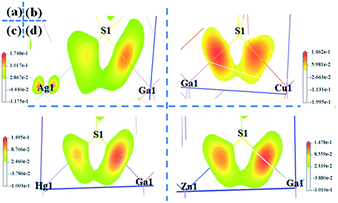
The birefringences of AGS, CGS, HGS and ZGS were obtained to be 0.066, 0.002, 0.044 and 0.008 @ 1064 nm, which is (more calculated details in ESI in Fig. S2†). In general, distortion in the tetrahedral groups can affect the optical anisotropy, which could be one of the reasons for the relative large birefringence. And the center-atom size and the divergences of the bond lengths and angles could relatively represent the distortion extent. Therefore, we compared the center-atom radius, the bond lengths and angles of the tetrahedra in AIGaS2, and AIIGa2S4. According to the periodic table of elements, the radius of the A*-site atoms in the two families have the following orders: rHg (1.76 Å) > rZn (1.53 Å) and rAg (1.75 Å) > rCu (1.57 Å), which matches well with their birefringences calculated in this work. To further observe the distortion of the MS4 (M = A*, Ga) tetrahedra, bond lengths and angles are made a careful comparison. In the structures of AIGaS2, the bond angles of S–AI–S present obvious differences (106°–116° for S–Ag–S and 109°–110° for S–Cu–S) while the angles of S–Ga–S are similar in both compounds. While in AIIGa2S4 type compounds, the angles among AII-site and S are similar (108°–111° for S–Hg–S and 109°–110° for S–Zn–S), however, the angles of S–Ga–S occur large differences (104°–117° in HGS and 106°–115° in ZGS). Therefore, it could be clearly seen that the AIS4 tetrahedra in AIGaS2 while GaS4 tetrahedra in AIIGa2S4 lead to the difference of the birefringence. To further verify this, we calculated the response electron distribution anisotropy index through the response electron distribution anisotropy REDA method proposed by Yang et al.50 The calculated REDA indexes and birefringences are listed in Table S2† and shown in Fig. S3.† It should be noted that exhibiting larger REDA index means more contributions to the birefringence. The results show that in AIGaS2 the REDA indexes of the AI–S bonds are both larger than those of Ga–S bonds (0.031 in AGS, −0.006 in CGS), and the Ag–S bond (0.329) lead to larger REDA index than Cu–S bonds (0.062). As for the AIIGaS2 compounds, the REDA indexes of Ga–S bonds (0.138 in HGS, 0.055 in ZGS) are larger than those of AII–S bonds (0.091 for Hg–S, 0.027 for ZGS), indicating the larger contribution to the birefringences.All about compounds belong to the asymmetric space group and exhibit relative SHG responses.51 We calculated the SHG coefficients of the four compounds by GGA with the scissors operators because of the common issue for underestimation, which is the difference between the calculated and the experimental values. The calculated SHG coefficients of all compounds are d14 = 10.90 pm V−1 for AGS, d14 = 9.11 pm V−1 for CGS, d14 = 13.2 pm V−1 for ZGS, d14 = 21.3 pm V−1 for HGS, listed in Table 1. In order to analyze the contribution of each atom to the SHG response, an SHG-density technique52 was used. Generally, there are two transition processes, namely VE and VH process. The obvious contribution of the VE process are predominant (>70%) for all compounds, so the SHG density are analyzed in the VE process. Fig. 3 shows the SHG densities of the four compounds at the occupied state and unoccupied states. The SHG-densit method is able to elucidate the SHG response in complex electron structure.53 The method ensures that the quantum state which give rise to SHG can be shown together as either occupied or unoccupied “SHG-density”. While the states irrelevant to SHG are not shown. Through the resulting distribution of such densities, thus the origin of SHG optical nonlinearity can be highlighted in real space.54 Hence, it could be seen that in the occupied states, A*-site atoms and S make the main contribution and in the unoccupied states, A*-site atoms together with Ga and S make contributions to the SHG response. Hence, we can tentatively deduce that the SHG response of AIGaS2 compounds may be the contribution of the [AIS4] and [GaS4] unit. There is the same result for the AIIGa2S4 compounds (the [AIIS4] and [GaS4] unit are the contribution of the SHG response).
Origin of the linear optical property
The stronger covalent bond will lead to a larger SHG effect.55 So the localized electron-density difference (EDD) is calculated, which is the difference between the assumed standard or model electron density and the actually observed or DFT calculated electron density to estimate the chemical bond characteristics in both families.56 As shown in Fig. 4, it could be clearly seen the electron cloud between the Ga–S and A*–S, indicating the covalent properties of them. To gain deep insight into the bonding behavior of the compounds, the bond character overlap population (Q) and bond distance analysis were performed, and the calculated results are displayed in Table 2. Bond population analysis can performed to get more information about the bonding character and to clarify the charge transfer between title compounds. Accordingly, we can see that bond population values between Ga with S and AII with S atoms in AIIGa2S4 type compounds is slightly larger than that between Ga with S and AI with S atoms in AIGaS2 type compounds. The result, may be the reason of AIIGa2S4 has larger SHG responses than AIGaS2.Conclusions
On a theoretical front, we made a comprehensive CASTEP study about the optical properties of AGS, CGS, ZGS and HGS, which agree well with the experimental observations. In all the compounds, [GaS4] unit determined the band gap however the dp interactions between A* and S atoms also play important roles. Moreover, the size effects of A*-site atom and the distortion extent of the tetrahedra have large influences on the birefringence. In addition, through analyzing the origin of the SHG effects, we find that the [GaS4] unit a main contribution of the SHG performance and the [A*S4] unit as well as have an important role in the SHG effect, and also the SHG response depends on the different cations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No. 61366001).Notes and references
- H. P. Wu, S. L. Pan, K. R. Poeppelmeier, H. Y. Li, D. Z. Jia, Z. H. Chen, X. Y. Fan, Y. Yang, J. M. Rondinelli and H. S. Luo, J. Am. Chem. Soc., 2011, 133, 7786–7790 CrossRef CAS PubMed.
- X. Su, Z. H. Yang, G. P. Han, Y. Wang, M. Wen and S. L. Pan, Dalton Trans., 2016, 45, 14394–14402 RSC.
- X. Y. Dong, Q. Jing, Y. J. Shi, Z. H. Yang, S. L. Pan, K. R. Poeppelmeier, J. H. Young and J. M. Rondinelli, J. Am. Chem. Soc., 2015, 137, 9417–9422 CrossRef CAS PubMed.
- H. G. Jo, S. J. Oh and K. M. ok, Dalton Trans., 2017, 46, 15628–15635 RSC.
- Y. X. Song, M. Luo, F. Liang, C. S. Lin, N. Ye, G. Y. Yan and Z. S. Lin, Dalton Trans., 2017, 46, 15228–15234 RSC.
- L. Huang, Q. Wang, F. F. He, X. Y. Liu, Z. W. Chen, W. He, X. Y. Luo, D. J. Gao, J. Bi and G. H. Zou, J. Alloys Compd., 2019, 771, 547–554 CrossRef CAS.
- J. J. De Yoreo, A. K. Burnham and P. K. Whitman, Int. Mater. Rev., 2002, 47, 113–152 CrossRef CAS.
- T. T. Tran, H. W. Yu, J. M. Rondinelli, K. R. Poeppelmeier and P. P. Halasyamani, Chem. Mater., 2016, 28, 5238–5258 CrossRef CAS.
- T. A. Driscoll, H. J. Hoffman and R. E. Stone, J. Opt. Soc. Am. B, 1986, 3, 683–686 CrossRef CAS.
- C. T. Chen, B. C. Wu, A. D. Jiang and G. M. You, Sci. Sin., Ser. B, 1985, 28, 235–244 Search PubMed.
- C. T. Chen, Y. C. Wu, A. D. Jiang, B. C. Wu, G. M. You, R. K. Li and S. J. Lin, J. Opt. Soc. Am., 1989, 6, 616–621 CrossRef CAS.
- C. T. Chen, Z. Y. Xu, D. Q. Deng, J. Zhang, G. K. L. Wong, B. C. Wu, N. Ye and D. Y. Tang, Appl. Phys. Lett., 1996, 68, 2930–2932 CrossRef CAS.
- G. Q. Shi, Y. Wang, F. F. Zhang, B. B. Zhang, Z. H. Yang, X. L. Hou, S. L. Pan and K. R. Poeppelmeier, J. Am. Chem. Soc., 2017, 139, 10645–10648 CrossRef CAS PubMed.
- M. D. Mutailipu, M. Zhang, B. B. Zhang, L. Y. Wang, Z. H. Yang, X. Zhou and S. L. Pan, Angew. Chem., Int. Ed., 2018, 57, 6095–6099 CrossRef CAS PubMed.
- Y. Wang, B. B. Zhang, Z. H. Yang and S. L. Pan, Angew. Chem., Int. Ed., 2018, 57, 2150–2154 CrossRef CAS PubMed.
- X. F. Wang, Y. Wang, B. B. Zhang, F. F. Zhang, Z. H. Yang and S. L. Pan, Angew. Chem., Int. Ed., 2017, 56, 14119–14123 CrossRef CAS PubMed.
- I. Chung and M. G. Kanatzidis, Chem. Mater., 2013, 26, 849–869 CrossRef.
- G. D. Boyd, E. Buehler and F. G. Storz, Appl. Phys. Lett., 1971, 18, 301–304 CrossRef CAS.
- G. D. Boyd, H. M. Kasper, J. H. Mcfee and F. G. Storz, IEEE J. Quantum Electron., 1972, 8, 900–908 CrossRef CAS.
- A. O. Okorogu, S. B. Mirov, W. Lee, D. I. Crouthamel, N. Jenkins, A. Y. Dergachev, K. L. Vodopyanov and V. V. Badikov, Opt. Commun., 1998, 155, 307–312 CrossRef CAS.
- C. T. Chen and G. Z. Liu, Annu. Rev. Mater. Sci., 1986, 16, 203–243 CrossRef CAS.
- J. N. Cheng, M. H. Lee and J. Zhang, J. Alloys Compd., 2018, 768, 883–888 CrossRef CAS.
- X. S. Jiang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 3–15 Search PubMed.
- Z. Z. Luo, C. S. Lin, H. H. Cui, W. L. Zhang, H. Zhang, Z. Z. He and W. D. Cheng, Chem. Mater., 2014, 26, 2743–2749 CrossRef CAS.
- X. S. Li, L. Kang, C. Li, Z. S. Lin, J. Y. Yao and Y. C. Wu, J. Mater. Chem. C, 2015, 3, 3060–3067 RSC.
- X. S. Lin, G. Zhang and N. Ye, Cryst. Growth Des., 2009, 9, 1186–1189 CrossRef CAS.
- J. Y. Yao, D. J. Mei, L. Bai, Z. S. Lin, W. L. Yin, P. Z. Fu and Y. C. Wu, Inorg. Chem., 2010, 49, 9212–9216 CrossRef CAS PubMed.
- S. F. Li, X. M. Jiang, B. W. Liu, D. Yan, H. Y. Zeng and G. C. Guo, Inorg. Chem., 2018, 57, 6783–6786 CrossRef CAS PubMed.
- X. S. Lin, Y. F. Guo and N. Ye, J. Solid State Chem., 2012, 195, 172–177 CrossRef CAS.
- J. H. Feng, C. L. Hu, B. X. Li and J. G. Mao, Chem. Mater., 2018, 30, 3901–3908 CrossRef CAS.
- H. Lin, B. X. Li, H. Chen, P. F. Liu, L. M. Wu, X. T. Wu and Q. L. Zhu, Inorg. Chem. Front., 2018, 5, 1458–1468 RSC.
- S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570 CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- A. M. Rappe, K. M. Rabe, E. Kaxiras and J. D. Joannopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1227–1230 CrossRef PubMed.
- J. S. Lin, A. Qteish, M. C. Payne and V. Heine, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 4174–4180 CrossRef.
- K. Liu, H. Q. Fan, P. R. Ren and C. Yang, J. Alloys Compd., 2011, 509, 1901–1905 CrossRef CAS.
- P. Deak, B. Aradi and T. Frauenheim, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155207 CrossRef.
- C. Aversa and J. E. Sipe, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14636–14645 CrossRef CAS PubMed.
- B. B. Zhang, M. H. Lee, Z. H. Yang, Q. Jing, S. L. Pan, M. Zhang, H. P. Wu, X. Su and C. S. Li, Appl. Phys. Lett., 2015, 106, 31906–31911 CrossRef.
- B. H. Lei, Z. H. Yang and S. L. Pan, Chem. Commun., 2017, 53, 2818–2821 RSC.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884–1887 CrossRef CAS.
- K. Wu and S. L. Pan, Coord. Chem. Rev., 2018, 377, 191–208 CrossRef CAS.
- M. G. Brik, J. Phys. Condens. Matter, 2009, 21, 485502 CrossRef CAS PubMed.
- G. D. Boyd, H. Kasper and J. H. McFee, IEEE J. Quantum Electron., 1971, 17, 563–573 CrossRef.
- F. Liang, L. Kang, Z. S. Lin, Y. C. Wu and C. T. Chen, Coord. Chem. Rev., 2017, 333, 57–70 CrossRef CAS.
- X. S. Jiang and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 35201 CrossRef.
- J. E. Jaffe and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1882 CrossRef CAS.
- Q. Jing, X. Y. Dong, Z. H. Yang, S. L. Pan, B. B. Zhang, X. C. Huang and M. W. Chen, J. Solid State Chem., 2014, 219, 138–142 CrossRef CAS.
- X. L. Chen, B. B. Zhang, F. F. Zhang, Y. Wang, M. Zhang, Z. H. Yang, K. R. Poeppelmeier and S. L. Pan, J. Am. Chem. Soc., 2018, 140, 16311–16319 CrossRef CAS PubMed.
- K. Iliopoulos, D. Kasprowicz, A. Majchrowski, E. Michalski, D. Gindre and B. Sahraoui, Appl. Phys. Lett., 2013, 103, 231103–231107 CrossRef.
- M. H. Lee, C. H. Yang and J. H. Jan, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–11 Search PubMed.
- C.-H. Lo, Master Degree thesis, Tamkang University, 2005 Search PubMed.
- B.-H. Lei, Q. Jing, Z. Yang, B. Zhang and S. Pan, J. Mater. Chem. C, 2015, 3, 1557–1566 RSC.
- C. T. Chen, Acta Phys. Sin., 1997, 26, 124 Search PubMed.
- C. Scheringer, D. Mullen and E. Hellner, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 2241–2243 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details about calculated and experimental crystal data and result of bond angles, REDA index, the calculated band structures and birefringence, for AIGaS2 (AI = Ag, Cu) and AIIGa2S4 (AII = Hg, Zn). See DOI: 10.1039/c9ra09109b |
| This journal is © The Royal Society of Chemistry 2019 |