Open Access Article
Open Access ArticleReaction induced diffusio-phoresis of ordinary catalytic particles
Aura
Visan
and
Rob G. H.
Lammertink
 *
*
Soft Matter, Fluidics and Interfaces, MESA+Institute for Nanotechnology, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands. E-mail: r.g.h.lammertink@utwente.nl; Tel: +31 (0)534892063
First published on 14th May 2019
Abstract
In this paper we demonstrate experimentally diffusio-phoresis of plain catalytic particles driven by the macroscopic concentration field that the particles generate by themselves. This introduces a general framework for heterogeneous catalysis where the driving force relies on solute gradients that are generated by a mere uneven distribution of catalytic particles. Whenever an inhomogeneity appears in the particle distribution, the higher particle density region will lower the reactant concentration more than the surrounding environment. This macroscopic concentration gradient propels the particles towards higher reactant concentration by surface driven flows. The nature of this flow originates from osmotic pressure differences and diffusion potentials in the case of charges species. This context of diffusio-phoresis demonstrates an additional transport mechanism for slurry reactors. We investigate the reaction induced particle movement for a photocatalytic degradation reaction using TiO2 suspensions in a co-flow microchannel. We have analyzed the experimental particle distribution by means of a numerical model that includes diffusio-phoretic movement of the catalytic particles. This model stresses the importance of particle characteristics, like surface potential, reactant and product interaction, and reaction kinetics with respect to the catalyst particle migration.
1 Introduction
Surface flows generated by concentration gradients and their particle propulsion analogue have been introduced by Derjaguin under the name of capillary osmosis and diffusio-phoresis. The phenomenon was speculated theoretically, starting from an extensive knowledge on surface science. Derjaguin rationalized that due to molecular interactions between solute and solid surface, a solution has a different chemical composition close to that solid surface which is susceptible to bulk concentration gradients. A gradient in osmotic pressure will develop within the interfacial layer where the interaction potential spans. Given that the diffusive part of the adsorption layer is mobile, it drives an osmotic flow parallel to the surface.1,2 Suspended particles will be propelled by such a surface flow in a solute concentration gradient. This propulsion mechanism is analogue to particle electro-phoresis in an external potential gradient. Derjaguin illustrated the theory regarding particle migration under electrolyte concentration gradients using an industrial example, namely the ionic deposition of latex particles under the dissolution of an electrolyte coating.3Following Derjaguin, Prieve and Anderson extended the theory in a series of papers. They derived the migration velocity of particles in gradients of neutral species while including other interaction potentials than the exponential profiles.4 They went on to prove that diffusio-phoresis in case of finite double layers will depend on the particle size.5 They corrected for the effect of strongly adsorbing solutes which affect the external concentration field.6 They also studied the effect of arbitrary distribution of zeta potential across the surface of the particle7 and, later on, they considered both non-spherical and non-uniformly charged particles with finite double layers.8
The theory was soon after validated in a series of experimental papers.9–19 Lechnick and Shaeiwitz accounted for the dependency of the zeta potential on the electrolyte concentration.13 Staffeld and Quinn inferred the particle–solute interaction potential by observing the diffusio-phoresis in gradients of neutral polymers (Dextran) and charged hard spheres (Percoll).15 More than three decades later, Shin et al. experimentally probed the effect of the finite Debye layer thickness and confirmed the theory of Prieve on the particle size dependent velocity.20 Paustian et al. looked into the particle migration under a gradient of solvent composition. They used hydrogel membranes to divide channels with different composition and monitored the translation of particles after stopping the flow.21 Nery-Azevedo et al. used the same device for tracking the migration of particles exposed to ionic surfactant gradients22 and Shi et al. used it under opposing gradients of different electrolytes23 where the neutralizing reaction leads to focusing of particles.
The examples mentioned above focused on the fundamental aspects of diffusio-phoresis, probing the chemical nature of the gradient with various solid-solute molecular interactions. These experimental endeavors served initially to confirm the theory and later on use it to infer surface properties and solute wall interactions. This increasing confidence in the theory helped transition to various applications. Shin et al. developed a very simple, but elegant experimental design using a dead-end channel to measure the zeta potential of walls and particles simultaneously.24,25 Due to the well-defined electrostatic interactions, one can use a plain electrolyte such as sodium chloride to infer the charge density of various surfaces by visualizing collective particle dynamics. Particle focusing and separation based on zeta potential was achieved by meticulous design of concentration profiles inside microchannels.26,27 Oil recovery can be enhanced by diffusio-phoresis of oil droplets out of the dead-end pores28 and membrane fouling due to particle deposition could be reduced by adding sodium carbonate particles, that by dissolving counteract the diffusion potential that appears due to the inherent salt rejection.29–31 Other applications using in situ gradient generation involve ion-exchange surfaces. Niu et al. uses ion-exchange particles for cargo transport32 while Florea et al. suggests an antifouling material application as a result of the migration of particles away from a Nafion ion-exchange membrane.33
There are two types of reaction induced phoretic phenomena that have been studied so far. The first is chemotaxis in biological systems where cells mostly react to the external composition. Their low activity has a small impact on the surrounding environment, such that the reactivity feedback on their dynamics is of lesser degree. The migration of cells towards higher nutrient sites is studied under externally imposed gradients while trying to decouple the contribution brought by their own activity.34–37 The second example is the migration of bimetallic particles that catalyze complementary redox reactions which leads to an uneven distribution of protons and hence an external electric field which electrophoretically drives the particles. This chemistry involves the production of charged species that are not being screened by counter-ions thanks to the “external” electron transport through the bimetallic particle. This phenomenon is based on spontaneous electrochemical reactions using particular chemicals, namely hydrogen peroxide or hydrazine, and Janus-type particles to provide the corresponding transport.38–43
In this paper, the driving force relies on solute gradients generated by the inhomogeneous distribution of otherwise homogeneous catalytic particles (Fig. 1). The spontaneously occurring surface flow can have a great impact on the overall conversion, as interfacial transport is a known limitation for heterogeneous catalysis. Reactant and product gradients are generated by an uneven distribution of catalytic particles, rather than by asymmetric particles (Janus type). The catalytic reactant consumption creates exceptional steep gradients. There is a synergy between the surface flow and the reaction rate with one enhancing the other that is particularly exciting.
The study describes the diffusio-phoresis of photocatalytic particles that catalytically generate macroscopic gradients caused by the uneven distribution of the particles. The migration of photocatalytic particles is studied systematically in a channel where an aqueous solution of an organic contaminant, methylthioninium chloride, is contacted under continuous flow with a particle suspension containing the same solute concentration. When UV light is turned on, the photocatalytic particles decompose the contaminant lowering its concentration inside the colloidal stream. The gradient in concentration that is photocatalytically generated leads to the migration of particles toward the higher concentration site. The effect of the reaction rate on the migration of particles is evaluated by changing both the light intensity and initial particle concentration. We analyze this experimentally observed migration mechanism by numerical simulations.
2 Methods
2.1 Experimental
Methylthioninium chloride, also known as methylene blue (MB) and Tris buffer were purchased from Sigma Aldrich and TiO2 suspension from Evonik. The particle agglomerates were measured to be 157 ± 70 nm in size. The Si-glass chip has been fabricated in a cleanroom using standard lithography, DRIE etching of silicon and anodic bonding. The channel has 55 × 600 μm cross-section (height × width) and is 10 mm in length. The design was inspired by the work of Abécassis et al.18,19 The two methylthioninium chloride solution streams are pumped at 1 μL min−1 using a Fluigent pressure pump where the flowrate is controlled by individual thermal sensors. The TiO2 suspension containing the same MB concentration is controlled at the same flowrate using a Nemesys syringe pump. All the solutions have been buffered at pH 8.15 using 1 mM Tris solution. The 365 nm monochromatic UV light is provided by 2 UV LEDs from Dr. Gröbel that allow a direct control of the intensity without changing the distance. The UV light intensity has been measured at the exact distance by a UVA sensor from the same company.2.2 Model
Mass transport is solved numerically for a two-dimensional domain of length L and width W. The macroscopic particle distribution was obtained by solving the species conservation equation for both the solute and catalytic particles. While the solute conservation equation includes advection, diffusion, and reaction terms, the particle transport is dictated by advection, migration and diffusion. Note that diffusion is insignificant as predicted by the Stokes–Einstein equation. A 3D model has also been built to verify the influence of the channel height. While the particle spreading shows a clear dependency on the z component, there was no specific feature of the integrated 3D particle profile that was additional to the 2D model. In dimensionless form the equations are:| ∇·(uc1) = ∇2c1 + R | (1) |
| ∇·(uc2) = D2∇2c2 + ∇·(uDOF·c2) | (2) |
![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i/
i/![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i,0 is the dimensionless concentration of species i which has diffusivity Di =
i,0 is the dimensionless concentration of species i which has diffusivity Di = ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) i/
i/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 1. Index i = 1 corresponds to the solute species, while particles are denoted by index i = 2. R is the normalised pseudo-homogeneous first order reaction rate, R = Da·c1, where Da = kW2/
1. Index i = 1 corresponds to the solute species, while particles are denoted by index i = 2. R is the normalised pseudo-homogeneous first order reaction rate, R = Da·c1, where Da = kW2/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 1 is the dimensionless Damköhler number. The apparent reaction rate constant, k, scales linearly with the particle density due to the linear proportionality of the catalytic surface area for a monodispersed suspension, k = k0·c2, where k0 is the intrinsic reaction rate constant. In this study we reference diffusivities to the diffusivity of methylthioninium chloride
1 is the dimensionless Damköhler number. The apparent reaction rate constant, k, scales linearly with the particle density due to the linear proportionality of the catalytic surface area for a monodispersed suspension, k = k0·c2, where k0 is the intrinsic reaction rate constant. In this study we reference diffusivities to the diffusivity of methylthioninium chloride ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 1 = 5.7 × 10−10 m2 s−1 and concentrations to their corresponding initial values,
1 = 5.7 × 10−10 m2 s−1 and concentrations to their corresponding initial values, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) i,0. The probed initial concentrations of methylthioninium chloride in DI water are
i,0. The probed initial concentrations of methylthioninium chloride in DI water are ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 1,0 = 10, 50 and 100 μM, while the initial particles densities are
1,0 = 10, 50 and 100 μM, while the initial particles densities are ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) 2,0 = 0.1, 0.5 and 1%. The diffusivity of the particles was estimate using Stokes–Einstein equation,
2,0 = 0.1, 0.5 and 1%. The diffusivity of the particles was estimate using Stokes–Einstein equation, ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 2 = 4.825 × 10−12 m2 s−1. Due to the high aspect ratio, velocity is assumed constant across the width and calculated based on the flowrate and channel dimensions. The x and y coordinates are scaled with respect to the width of the channel W = 6.00 × 10−4 m. The dimensionless velocity, u = 1.595 × 103, is referenced with respect to the diffusion velocity u = ũW/
2 = 4.825 × 10−12 m2 s−1. Due to the high aspect ratio, velocity is assumed constant across the width and calculated based on the flowrate and channel dimensions. The x and y coordinates are scaled with respect to the width of the channel W = 6.00 × 10−4 m. The dimensionless velocity, u = 1.595 × 103, is referenced with respect to the diffusion velocity u = ũW/![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) 1. The migration term, ∇·(uDOFc2), represents the diffusio-phoresis of particles where the diffusio-phoretic velocity, uDOF, scales with the normalized concentration gradient of the solute and has a mobility prefactor that depends on the zeta potential of the particles.44
1. The migration term, ∇·(uDOFc2), represents the diffusio-phoresis of particles where the diffusio-phoretic velocity, uDOF, scales with the normalized concentration gradient of the solute and has a mobility prefactor that depends on the zeta potential of the particles.44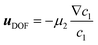 | (3) |
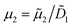 .
.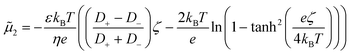 | (4) |
The three inlets are composed by two different boundary conditions. The side inlets have the reactant concentration 1 and 0 particle density, c1 = 1, c2 = 0, while the middle inlet has both reactant concentration and particle density 1, ci = 1. The outlet boundary condition is open flux, 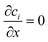 . The boundary conditions for the side walls are zero flux,
. The boundary conditions for the side walls are zero flux, 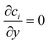 .
.
The governing equations are solved using Finite Element Analysis in COMSOL Multiphysics 5.3. The simulations were performed with a structured mesh, where 500 by 500 rectangular elements were used to ensure mesh independence.
3 Results and discussion
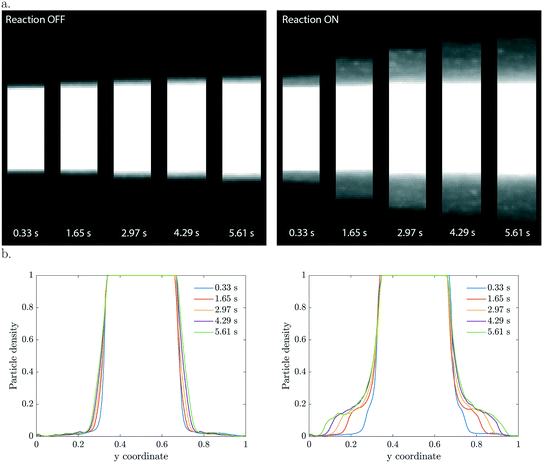
In the three co-flowing streams the initial methylthioninium chloride (MB) concentration is homogeneous. As long as the particles are passive such that they do not affect the reactant concentration, there is no driving force for diffusio-phoresis. Particle diffusion is negligible in the short 6 seconds residence time, as confirmed in the left panel of Fig. 2. The migration of particles becomes significant when the photocatalytic reaction is triggered by UV light. At this moment the particles start decomposing the methylthioninium chloride, lowering the concentration inside the colloidal stream. The concentration gradient that develops drives the particles towards higher MB concentrations by means of diffusio-phoresis (right Fig. 2). An experiment with the same distribution of particles and a homogeneous 1 mM Tris buffer solution under UV illumination displayed no diffusio-phoresis. We believe this rules out possible heating effects that could arise due to UV light absorption, any gradients generated by radical formation due to solvent (water) reactions that would affect particle migration, any additional gradients arising from Tris buffer oxidation and any pH gradients. Also, the μM MB concentration range ensures negligible change in density upon chemical conversion.The 2D and the corresponding width averaged 1D density profiles are shown in Fig. 2 for different residence times. Upon illumination, a MB gradient appears at the intersection between the streams. This leads to diffusio-phoresis of the catalytic particles from the center stream outwards, where the migrating cloud has a lower particle density compared to the center stream. The local MB conversion depends on the local particle density. As the particles migrate sideways the MB gradient is affected correspondingly. We want to stress the fact that these are plain catalytic particles which are not fluorescent and inherently will give less ideal imaging, including the saturation of the signal in the middle of the particle stream.
The concentration gradients sustained by active particles remain steeper than externally imposed gradients that relax due to diffusion. The particle velocities are extremely high, especially in the beginning when the contrast in particle density is the highest. For example, in the first micrograph slab which has a residence time of only 0.33 seconds, the displacement is already 30 μm which corresponds to a diffusio-phoretic velocity of ∼90 μm s−1. The enhancement in migration compared to pure particle diffusion is in the order of ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (103–104).
(103–104).
Given that the particle migration is dictated by the local solute gradient, any factor that is altering the concentration profile is affecting the particle distribution. The reaction rate, which is the source for gradient generation, depends on both particle density and light intensity (Fig. 3). The kinetics for the given particle density and light intensity were estimated from Visan et al.46 who investigated the same chemistry in an immobilized reactor. It also validates the possibility for neglecting the light intensity decay due to absorption by volume averaging the reaction rate constant, as it falls under the light independence criterion. Assuming that scattering is negligible compared to absorption at the 365 nm wavelength, this criterion stipulates that the height of the dispersion layer should be smaller than the inverse of the absorption coefficient (α = 5.1 × 103 m−1) for the used 1% TiO2 particle concentration. That is, for a thickness smaller than 200 μm, the absorption of light is less than 1 − 1/e (63.2%) of the incoming light.
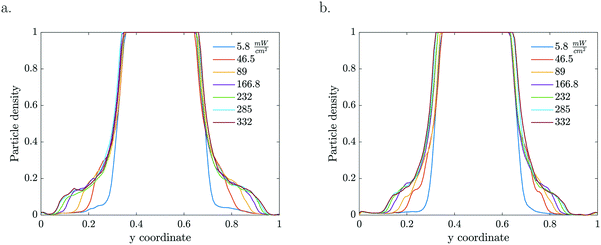 | ||
| Fig. 3 1D particle density profiles for various light intensities and particle concentrations ((a) 1 wt% TiO2, (b) 0.5 wt%, 50 μM MB, τ = 5.61 s). | ||
We have analyzed the particle distributions using a numerical model that includes the reactant concentration only and its interaction with the catalyst wall, expressed by the mobility (for details, see the Methods section). The motivation behind it is that the electro-phoretic contribution is most significant for the starting component as the contrast in diffusivity between the methylthioninium and chloride ions is the highest, i.e. the first term in eqn (4) dominates. We are aware that the magnitude of the velocity will depend on the collective contribution of all the chemical species present (reactants to intermediates and final products). For the electro-phoretic contribution, as long as the cation diffuses slower than the anion, the resulting electric field will be diminishing the one corresponding to the reactant, but will switch to being cumulative once the cation surpasses the diffusivity of the counter-ion (Cl- in this case). For the chemi-phoretic contribution which is dependent on the net interfacial concentration distribution, the product gradient will have an osmotic pressure gradient opposite to the reactant gradient in case of attractive interactions with the catalyst or additional in case of repulsive forces. The complete effect of species gradients on the resulting diffusio-phoretic flow involves many components and their interactions, which is beyond the scope of this paper. Here, we aim to demonstrate the relevance of diffusio-phoresis for heterogeneous catalytic systems.
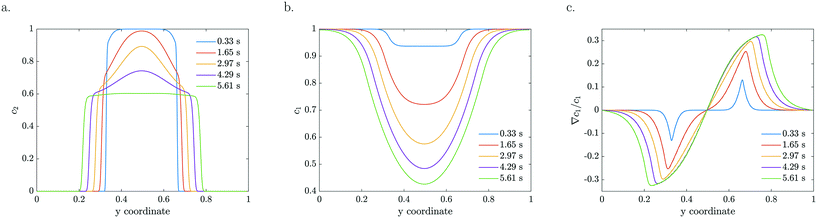
The model is based on advection, diffusion and reaction for MB, combined with advection, diffusion and diffusio-phoresis for the catalytic particles. As a starting model, we considered a constant zeta potential, thus constant mobility. The particle density and reactant concentration profiles are shown in Fig. 4 for k = 0.2 s−1 and ζ = −120 mV for the same residence times as the experimental profiles presented in Fig. 2. For a constant mobility, the particle density evens out as it is spreading. In the beginning, the relative gradient is localised at the edge of the colloidal stream, so only a thin region of particles feel the driving force (e.g.Fig. 4c at 0.33 s). As the particles spread further, the colloidal stream gets ‘diluted’ as the maximum relative gradient moves outwards with the edge of the stream and the leading particle density decreases. The reactant gets more depleted in the middle, near y = 0.5 in Fig. 4b, due to higher particle densities, causing these particles to accelerate and catch up with the leading front.
Clearly, the particle distribution does not match the experimental observations, even when the parameters were adjusted. The experimental particle density profiles can be retrieved in the numerical model only when the mobility is decreasing with MB concentration. The understanding behind a possible decrease in zeta potential with concentration relates to the specifics of the photocatalytic reaction. The degradation of MB follows a complex pathway47 that produces numerous ionic species which can potentially screen the surface charge. While a clear relationship between the degree of conversion and the zeta potential is difficult to infer a priori, a decrease in zeta potential with reactant concentration can be explained by an increase in the local ionic strength during reaction. Experiments using the same MB conversion, but with additional electrolytes (10 mM NaCl) confirmed the attenuation of diffusio-phoresis in high ionic strength media. Moreover, the particle dynamics showed experimentally an initial reactant concentration dependency which could not be explained by Langmuir–Hinshelwood kinetics verified numerically using the parameters determined in Houas et al.47 This finding suggests a correlation between the particle zeta potential and the reactant concentration for the illuminated state.
We employ a linear function to express the zeta potential in terms of reactant concentration which was also used by Lechnick et al., ζ = a + b·c1. The dependency of the zeta potential on the reactant concentration is an indirect method to account for the change in zeta potential that may be caused by the increase in reaction products. The dependency of the zeta potential on the conversion degree and thus on the reactant concentration is an empirical model that attempts to include the (opposing) product contribution on the driving force. A more theoretical model would entail a detailed understanding of the mechanism, that is, not only the identity of these intermediary species, but also their in situ interaction potential with the catalytic surface and the kinetics for all elementary reactions, i.e. the change in the distribution of these species with the conversion degree.
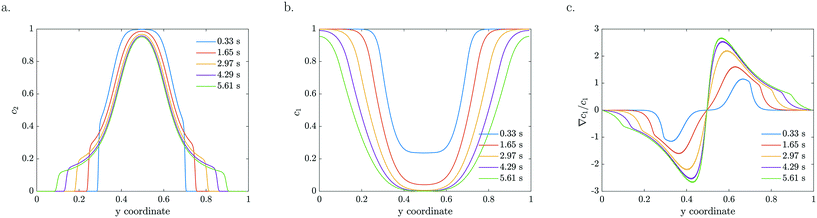
The particle density and reactant concentration profiles shown in Fig. 5 for k = 2 s−1 and a = 0 mV, b = −120 mV match the experimental shapes presented in Fig. 2. The fitted starting value (−120 mV) is relatively close to what has been reported in literature.48 Leroy et al. found a zeta potential of −90 mV for the same Evonik TiO2 particles at pH 8.15 corresponding to the conditions used in our experiments. The difference could be explained by an in situ increase in zeta potential upon UV light illumination which may originate from the same mechanism by which photocatalysis takes place, i.e. the generation of positive and negative charges that migrate to the surface. The concentration dependent zeta potential has the same initial magnitude, but decays very fast as the reactant is consumed which leads to a decreased mobility. It is very clear from Fig. 5c that the maximum in relative gradient does not move outwards with the edge of the particle stream, but instead remains deeper inside the particle stream. Here, the absolute reactant concentration is quite low, leading to a very strong relative gradient. However, due to the low reactant concentration in this middle region, the mobility is also very low. The consequence is not only a significantly reduced overall migration, but also a reduced particle density at the migrating front. Particles are continuously left behind as the spreading develops due to the steep decrease in reactant concentration in the migrating front. This gradual decline in the particle front density also reduces the driving force by relaxing the concentration gradient in Fig. 5c.
The particle dynamics are very sensitive to the interplay between the activity of the particles and their surface properties via the mobility. The mobility represents the sensitivity of the particle's response to the gradient (Fig. 6a). Enhanced zeta potentials are directly reflected in enhanced migration. For higher catalytic activities, steeper gradients develop which drive higher diffusio-phoretic velocities. Because the mobility depends on the local concentration, a change in the reaction rate constant will affect both the relative gradient as well as the mobility prefactor via the zeta potential which will couple back to the concentration profile in a nonlinear way (Fig. 6b).
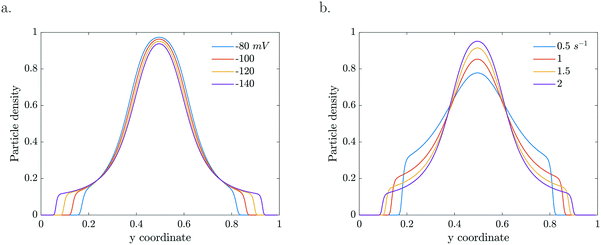 | ||
| Fig. 6 Particle density profiles at τ = 5.61 s for a. various concentration dependent ζ (k = 2 s−1) and b. various k (b = −120 mV). | ||
The spontaneous response of catalytic particles to the local reactant gradient enhances overall conversion. As they migrate towards regions of higher concentration, the local reaction rate increases. The conversion enhancement will depend on the extent of the particle migration, being a function of catalyst activity, its surface properties and residence time. As an example, given the parameters used in Fig. 5, the conversion doubles for the final residence time of 5.6 seconds with respect to a migration free scenario.
4 Conclusions
This work illustrates some intriguing aspects for reaction induced diffusio-phoresis of plain catalytic particles. While photocatalytic degradation of methylthioninium chloride may not pass as a standard industrial catalytic conversion, we consider the photocatalytic example to be an experimental proof for a general transport mechanism by which active particles migrate in response to local gradients that are produced by the particles themselves through their uneven distribution. We believe this phenomenon to be present for arbitrary chemical conversions whenever their kinetics are fast enough to preserve significant concentration gradients. While the phenomenon is general, we expect the particle migration signature to be specific to the catalytic system, depending on kinetics and interaction of all species involved. A simple numerical model is used to explore the details of the diffusio-phoretically driven process, confirming the relevance of the molecular interactions between the reactants/products and the catalyst surface.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Netherlands Center for Multiscale Catalytic Energy Conversion (MCEC), an NWO Gravitation programme funded by the Ministry of Education, Culture and Science of the government of the Netherlands. Rob Lammertink acknowledges the Vici project STW 016.160.312, financed by the Netherlands Organisation for Scientific Research (NWO).References
- B. V. Derjaguin, S. S. Dukhin and M. M. Koptelova, J. Colloid Interface Sci., 1972, 38, 584–595 CrossRef.
- B. V. Derjaguin, G. Sidorenkov, E. Zubashchenko and E. Kiseleva, Prog. Surf. Sci., 1993, 43, 138–152 CrossRef.
- B. Derjaguin, S. Dukhin and A. Korotkova, Prog. Surf. Sci., 1993, 43, 153–158 CrossRef.
- J. L. Anderson, M. E. Lowell and D. C. Prieve, J. Fluid Mech., 1982, 117, 107 CrossRef CAS.
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, J. Fluid Mech., 1984, 148, 247 CrossRef CAS.
- J. L. Anderson and D. C. Prieve, Langmuir, 1991, 7, 403–406 CrossRef CAS.
- J. L. Anderson, J. Colloid Interface Sci., 1985, 105, 45–54 CrossRef CAS.
- M. C. Fair and J. L. Anderson, J. Colloid Interface Sci., 1989, 127, 388–400 CrossRef CAS.
- R. E. Smith and D. C. Prieve, Chem. Eng. Sci., 1982, 37, 1213–1223 CrossRef CAS.
- J. P. Ebel, J. L. Anderson and D. C. Prieve, Langmuir, 1988, 4, 396–406 CrossRef CAS.
- P. O. Staffeld and J. A. Quinn, J. Colloid Interface Sci., 1989, 130, 69–87 CrossRef CAS.
- W. J. Lechnick and J. A. Shaeiwitz, J. Colloid Interface Sci., 1984, 102, 71–87 CrossRef CAS.
- W. J. Lechnick and J. A. Shaeiwitz, J. Colloid Interface Sci., 1985, 104, 456–470 CrossRef CAS.
- M. M. J. Lin and D. C. Prieve, J. Colloid Interface Sci., 1983, 95, 327–339 CrossRef CAS.
- P. O. Staffeld and J. A. Quinn, J. Colloid Interface Sci., 1989, 130, 69–87 CrossRef CAS.
- M. Kosmulski and E. Matuevi, J. Colloid Interface Sci., 1992, 150, 291–294 CrossRef CAS.
- M. Elimelech and C. R. O'Melia, Colloids Surf., 1990, 44, 165–178 CrossRef CAS.
- B. Abécassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, New J. Phys., 2009, 11, 075022 CrossRef.
- B. Abécassis, C. Cottin-Bizonne, C. Ybert, A. Ajdari and L. Bocquet, Nat. Mater., 2008, 7, 785–789 CrossRef PubMed.
- S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 257–261 CrossRef CAS PubMed.
- J. S. Paustian, C. D. Angulo, R. Nery-Azevedo, N. Shi, A. I. Abdel-Fattah and T. M. Squires, Langmuir, 2015, 31, 4402–4410 CrossRef CAS PubMed.
- R. Nery-Azevedo, A. Banerjee and T. M. Squires, Langmuir, 2017, 33, 9694–9702 CrossRef CAS PubMed.
- N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 1–5 Search PubMed.
- S. Shin, J. T. Ault, J. Feng, P. B. Warren and H. A. Stone, Adv. Mater., 2017, 29, 1–7 Search PubMed.
- J. T. Ault, P. B. Warren, S. Shin and H. A. Stone, Soft Matter, 2017, 13, 9015–9023 RSC.
- J. Palacci, B. Abécassis, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 104, 1–4 CrossRef PubMed.
- J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Soft Matter, 2012, 8, 980–994 RSC.
- A. Kar, T. Y. Chiang, I. Ortiz Rivera, A. Sen and D. Velegol, ACS Nano, 2015, 9, 746–753 CrossRef CAS PubMed.
- A. Kar, R. Guha, N. Dani, D. Velegol and M. Kumar, Langmuir, 2014, 30, 793–799 CrossRef CAS.
- R. Guha, X. Shang, A. L. Zydney, D. Velegol and M. Kumar, J. Membr. Sci., 2015, 479, 67–76 CrossRef CAS.
- J. J. McDermott, A. Kar, M. Daher, S. Klara, G. Wang, A. Sen and D. Velegol, Langmuir, 2012, 28, 15491–15497 CrossRef CAS.
- R. Niu, D. Botin, J. Weber, A. Reinmüller and T. Palberg, Langmuir, 2017, 33, 3450–3457 CrossRef CAS PubMed.
- D. Florea, S. Musa, J. M. R. Huyghe and H. M. Wyss, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 6554–6559 CrossRef CAS PubMed.
- X. Zhao, H. Palacci, V. Yadav, M. M. Spiering, M. K. Gilson, P. J. Butler, H. Hess, S. J. Benkovic and A. Sen, Nat. Chem., 2017, 10, 311 CrossRef PubMed.
- S. Sengupta, K. K. Dey, H. S. Muddana, T. Tabouillot, M. E. Ibele, P. J. Butler and A. Sen, J. Am. Chem. Soc., 2013, 135, 1406–1414 CrossRef CAS PubMed.
- K. K. Dey, X. Zhao, B. M. Tansi, W. J. Méndez-Ortiz, U. M. Córdova-Figueroa, R. Golestanian and A. Sen, Nano Lett., 2015, 15, 8311–8315 CrossRef CAS PubMed.
- H. Yu, K. Jo, K. L. Kounovsky, J. J. D. Pablo and D. C. Schwartz, J. Am. Chem. Soc., 2009, 131, 5722–5723 CrossRef CAS.
- W. F. Paxton, P. T. Baker, T. R. Kline, Y. Wang, T. E. Mallouk and A. Sen, J. Am. Chem. Soc., 2006, 128, 14881–14888 CrossRef CAS PubMed.
- Y. Wang, R. M. Hernandez, D. J. Bartlett, J. M. Bingham, T. R. Kline, A. Sen and T. E. Mallouk, Langmuir, 2006, 22, 10451–10456 CrossRef CAS.
- S. Ebbens, D. A. Gregory, G. Dunderdale, J. R. Howse, Y. Ibrahim, T. B. Liverpool and R. Golestanian, EPL, 2014, 106(5), 1–5 Search PubMed.
- J. L. Moran and J. D. Posner, J. Fluid Mech., 2011, 680, 31–66 CrossRef CAS.
- R. Golestanian, T. B. Liverpool and A. Ajdari, New J. Phys., 2007, 9(5), 126 CrossRef.
- R. Golestanian, T. B. Liverpool and A. Ajdari, Phys. Rev. Lett., 2005, 94, 1–4 CrossRef PubMed.
- J. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- D. G. Leaist, Can. J. Chem., 1988, 66, 2452–2457 CrossRef CAS.
- A. Visan, D. Rafieian, W. Ogieglo and R. G. Lammertink, Appl. Catal., B, 2014, 150–151, 93–100 CrossRef CAS.
- A. Houas, H. Lachheb, M. Ksibi, E. Elaloui, C. Guillard and J. M. Herrmann, Appl. Catal., B, 2001, 31, 145–157 CrossRef CAS.
- P. Leroy, C. Tournassat and M. Bizi, J. Colloid Interface Sci., 2011, 356, 442–453 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |