Open Access Article
Open Access ArticleA non-sacrificial method for the quantification of poly(ethylene glycol) grafting density on gold nanoparticles for applications in nanomedicine†
Jun
Lu
a,
Yao
Xue
a,
Rui
Shi
 b,
Jing
Kang
a,
Chao-Yang
Zhao
a,
Ning-Ning
Zhang
a,
Chun-Yu
Wang
b,
Jing
Kang
a,
Chao-Yang
Zhao
a,
Ning-Ning
Zhang
a,
Chun-Yu
Wang
 ab,
Zhong-Yuan
Lu
ab,
Zhong-Yuan
Lu
 *ab and
Kun
Liu
*ab and
Kun
Liu
 *a
*a
aState Key Laboratory of Supramolecular Structure and Materials, College of Chemistry, Jilin University, Changchun 130012, P. R. China. E-mail: kliu@jlu.edu.cn
bInstitute of Theoretical Chemistry, Jilin University, Changchun 130023, P. R. China. E-mail: luzhy@jlu.edu.cn
First published on 14th December 2018
Abstract
The grafting density of poly(ethylene glycol) (PEG) on nanoparticle (NP) surfaces is the most important parameter determining the interaction of nanoparticles with serum proteins, the subsequent sequestration of the nanoparticle from the bloodstream by the mononuclear phagocyte system, and the eventual delivery efficiency to tumor tissues. However, the majority of in vivo studies do not characterize or report the grafting density of PEG on nanoparticles due to a lack of feasible characterization methods, making it difficult to evaluate the published studies and reconcile apparent conflicting results. Herein, we develop a facile and non-sacrificial 1H NMR analytical approach for the quantitative characterization of grafting density of thiol-terminated PEG (HS-PEG) on gold NPs (GNPs). A multi-Lorentzian-splitting algorithm is used to distinguish the NMR signal of free PEG from those of the grafted ones, therefore allowing in situ monitoring of the grafting process to study the effects of GNP sizes, PEG molecular weights and NP capping ligands on grafting rates and grafting densities. The main advantage of this method is that it is not limited by the types of terminal functional groups on PEG, surface chemistry of the nanoparticles or their composition. It also provides a set of critical and standard guides for characterization of the PEG grafting density on nanoparticles for in vivo biological and biomedical studies.
Introduction
The extraordinary surface plasmon resonance property of gold nanoparticles (GNPs) and their proven ability to transform absorbed light into thermal energy make them promising candidates for a wide range of biological applications, such as bioimaging, medical diagnostics, and photothermal treatment for diseases.1–4 However, in vivo studies have shown that most administered GNPs are rapidly sequestered from the bloodstream by the mononuclear phagocyte system (MPS), leading to long-term accumulation of GNPs in the liver and spleen, and inadequate delivery and/or targeting of GNPs to the diseased tissues.5–8 The process of sequestration is triggered by opsonization of GNPs, which involves non-specific adsorption of plasma proteins onto the nanoparticle (NP) surface to form the so-called “protein corona”.9,10 The “protein corona” alters the size, aggregation state, and interfacial properties of GNPs, giving them a “biological identity” that governs the interactions with biomolecules and biological barriers while affecting the physiological immune response.11,12To suppress the sequestration by MPS, it is crucial to prevent non-specific protein adsorption onto the surface of GNPs. For this purpose, the surface of GNPs needs to be modified with charge-neutral, highly hydrophilic “anti-fouling” polymers, which can resist adsorption of biomolecules, cells, and microorganisms when NPs are injected into living organisms.13–15 Poly(ethylene glycol) (PEG) is the most commonly used “anti-fouling” polymer to modify GNPs in order to suppress non-specific protein attachment, prolong NP circulation time and improve delivery efficiency to diseased tissues. The grafting density of thiol-terminated PEG (HS-PEG) on the GNP surface (σ) is one of the most important parameters in determining the interaction of NPs with proteins, its subsequent sequestration from the bloodstream by the MPS, and the eventual delivery efficiency to tumours.16–19 However, studies on optimization of σ are relatively rare20,21 as the majority of in vivo studies use GNPs saturated with PEG chains but do not characterize or report σ. The lack of characterization is largely due to a lack of practical methods.
Several types of techniques have been utilized to quantify σ of PEG on the surface of NPs. Thermogravimetric analysis (TGA) is the most widely used tool to estimate σ of PEG on GNPs;22–25 this technique normally requires a large amount of GNPs and multiple centrifugation steps to remove unbound PEG chains, which may cause bound PEG to detach from the NP surface and result in an underestimation of σ. Additionally, TGA is a sacrificial method and impractical as a routine analytical approach for biomedical studies. Another commonly used strategy to characterize σ is based on the quantification of thiol end-group of unbound PEG by a stoichiometric reaction with 5,5′-dithiobis(2-nitrobenzoic acid).21 However, this method cannot quantify the concentration of disulphide bonds which are unavoidably formed in solution, leading to an overestimate of σ. Other approaches for characterizing σ include fluorescence26 and Raman27 spectroscopies (limited to HS-PEG molecules containing amino or Raman active end-groups) and other sacrificial methods such as inductively coupled plasma mass spectrometry (ICP-MS),28 total organic carbon (TOC) analysis,29 or X-ray photoelectron spectroscopy (XPS).30 On the other hand, one-dimensional proton nuclear magnetic resonance (1H NMR) spectroscopy is an easy-to-use, fast, and non-sacrificed quantification method to quantify σ. It can also be applied to analyse the ligand chemistry and monitor the grafting process in situ. However, using NMR to quantify σ and to simultaneously study the grafting process is quite rare.31,32 As such, a simple, robust, and universal NMR analytical method to accurately quantify σ in situ is highly desirable.
Herein, we report a facile and non-sacrificial 1H NMR analytical approach for the quantitative characterization of σ of HS-PEG on GNPs. We propose using a multi-Lorentzian-splitting algorithm based on the Akaike's information criterion (AIC), Bayesian information criterion (BIC) and maximum likelihood estimation in order to distinguish the NMR signal of free PEG from that of grafted PEG, which allows monitoring of the grafting process in situ. We demonstrate that this is an efficient method for studying the grafting rates and grafting densities for GNPs with varying dimensions, PEG with a range of molecular weights, and different types of original capping ligands on GNPs.
Results and discussion
Quantification of grafting density by multi-Lorentzian-splitting algorithm
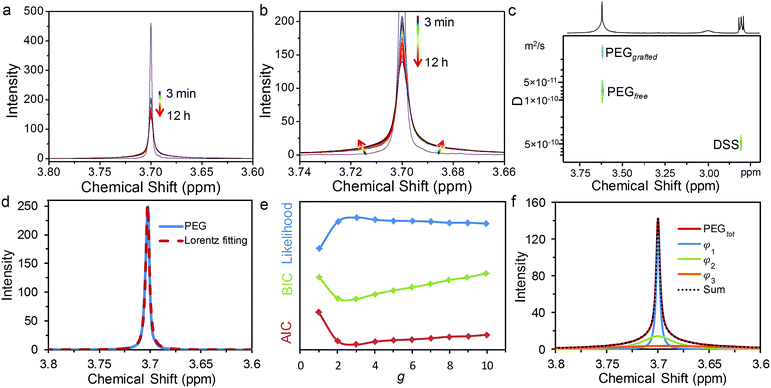
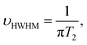
1H NMR spectroscopy was used to monitor the grafting-to process of HS-PEG on 13 nm GNPs with sodium 2,2-dimethyl-isotope-2-silapentane-5-sulfonate (DSS) as an external standard. Fig. 1 shows the temporal evolution of the 1H NMR spectra when excess HS-PEG (Mw of 5.0 kg mol−1, 0.50 mg mL−1) was grafted onto the surface of citrate-covered GNPs (78 nM) (Fig. S1†). Before grafting, HS-PEG in D2O exhibited a sharp peak at 3.70 ppm with a full width at half maximum (FWHM) of 0.00430 ppm. Three minutes after the GNPs and HS-PEG were mixed in D2O, the intensity of the peak was dropped dramatically to about half of its initial value. The peak intensity continued to decrease gradually for 12 hours. More interestingly during the grafting process, the bottom part of the peak broadened continuously while the top part remained sharp, suggesting the existence of two possible types of PEG chains in solution. The presence of two types of PEG chains was further confirmed by diffusion-ordered spectroscopy (DOSY) as two peaks appeared at 3.70 ppm (Fig. 1c and S2†). The diffusion coefficients of these two peaks were 8.07 × 10−11 (free PEG) and 1.39 × 10−11 m2 s−1 (grafted PEG); peak assignments were made after comparing the data with the diffusion coefficient of pure GNPs (1.91 × 10−11 m2 s−1), determined by dynamic light scattering measurements (Fig. S3†). On the basis of these results, the NMR peak at 3.70 ppm was a superposition of signals from free PEG molecules and PEG grafted on the NP surface.It is known that the attachment to NP surfaces causes the NMR signal of a ligand molecule to broaden and sometimes disappear, because the particle-bound ligand has faster transverse relaxation times (T2) leading to line shape broadening according to the following equation:33
 | (1) |
Once the concentration of free PEG was determined, the σ of PEG on the GNPs can be calculated as:
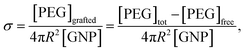 | (2) |
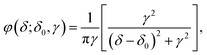 | (3) |
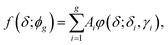 | (4) |
To isolate the Lorentzian function contribution from the free PEG, ϕg and the most probable number of components (g) need to be identified. For this purpose, we developed a multi-Lorentzian-splitting algorithm to estimate g and the corresponding Lorentzian functions. Firstly, Monte Carlo (MC) simulations with sufficient steps (>10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) were performed to generate samples from the original NMR data with chemical shifts in the range of 3.4 to 4.0 ppm. Afterwards, ϕg was fitted using the least-square algorithm for g ranging from one to ten components. Next, the fitting results were evaluated to find the most probable g using the criteria of the lowest Akaike's information criterion (AIC), the lowest Bayesian information criterion (BIC), and the maximum likelihood estimation.41–43 Noted that these three criteria may give different values of g because using AIC/BIC may give a value of g different from that using the maximum likelihood estimation. AIC and BIC are theoretically equivalent;43 therefore they are normally satisfied at the same time for a specific value of g. As the values from AIC and BIC heavily rely on specific dataset, the criterion with max difference between the values from BIC and AIC are always chosen for analysis in practical application. The maximum likelihood estimation is auxiliary to choose g. Its value is relatively small and easily affected by data fluctuations; therefore the maximum likelihood estimation is possible to give inconsistent results with AIC/BIC criteria. However, as the fluctuations of the NMR data are very small, these three criteria can give the same value of g.
000) were performed to generate samples from the original NMR data with chemical shifts in the range of 3.4 to 4.0 ppm. Afterwards, ϕg was fitted using the least-square algorithm for g ranging from one to ten components. Next, the fitting results were evaluated to find the most probable g using the criteria of the lowest Akaike's information criterion (AIC), the lowest Bayesian information criterion (BIC), and the maximum likelihood estimation.41–43 Noted that these three criteria may give different values of g because using AIC/BIC may give a value of g different from that using the maximum likelihood estimation. AIC and BIC are theoretically equivalent;43 therefore they are normally satisfied at the same time for a specific value of g. As the values from AIC and BIC heavily rely on specific dataset, the criterion with max difference between the values from BIC and AIC are always chosen for analysis in practical application. The maximum likelihood estimation is auxiliary to choose g. Its value is relatively small and easily affected by data fluctuations; therefore the maximum likelihood estimation is possible to give inconsistent results with AIC/BIC criteria. However, as the fluctuations of the NMR data are very small, these three criteria can give the same value of g.
Using the NMR spectrum at a grafting time of 720 minutes as an example, the AIC, BIC and maximum likelihood estimation all gave a g of 3 as the best fit (Fig. 1e). This result indicates that three peaks should be used for the multiple-Lorentzian splitting of the superposed NMR peak from both free and grafted PEG, including one sharp and two relatively broad peaks (Fig. 1f). The γ for the sharp peak is equal to 0.00210, which is very close to that of the pure PEG molecules (γ1 = 0.00215 in Fig. 1d), suggesting that the sharp peak should be assigned to free PEG. The other two peaks with higher γ values (0.0182 and 0.0680) are assigned to grafted PEG. After comparing the integral of free PEG with the standard curve of pure PEG, the concentrations of free PEG, grafted PEG and corresponding σ can be calculated.
Grafting process of HS-PEG onto gold nanoparticles
We used this in situ NMR spectroscopy to analyse the grafting process of PEG onto the surface of GNPs (Fig. 2). Fig. 2a shows the temporal evolution of the 1H NMR spectra of free PEG, isolated from the NMR spectra in the grafting process (Fig. 1) via the multi-Lorentzian-splitting algorithm. Based on the integral of free PEG in 1H NMR spectra, concentrations of free PEG at any time during the grafting process can be calculated. Fig. 2b shows the evolution of σ with grafting time. The σ was determined to be 1.34 chains per nm2 at t = 3 minutes, indicating the grafting process was fairly quick due to the strong affinity between gold and sulphur atoms.44 For longer grafting times of several minutes to about 180 minutes, σ gradually increased to 1.53 chains per nm2. At the end of the grafting process (720 min), σ eventually reached a maximum of 1.55 chains per nm2 for full coverage.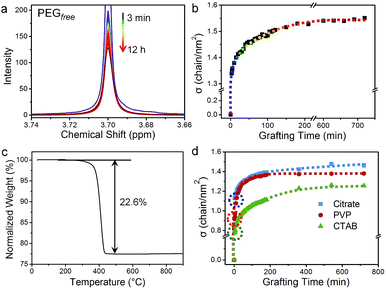 | ||
| Fig. 2 Grafting process for HS-PEG onto the surface of GNPs analysed by the multi-Lorentzian-splitting algorithm. Temporal evolution of 1H NMR spectra of (a) free PEG and (b) σ in the grafting-to process of HS-PEG onto the surface of citrate-capped GNPs. The colour of the lines corresponds to the same time points as Fig. 1. (c) Thermal curve from thermal gravimetric analysis (TGA) of HS-PEG grafted GNPs. (d) Temporal evolution of σ for HS-PEG grafted onto the surface of GNPs capped by citrate (blue squares), PVP (red circles), and CTAB (green triangles). Dotted circles on the curves in (d) highlight σ at the grafting time of 3 min. | ||
We also evaluated the accuracy and precision of the multi-Lorentzian splitting method. The accuracy of this approach was verified by a post-centrifugation strategy in which the GNPs with grafted PEG was removed from the solution by multiple centrifugation to obtain free PEG supernatant for 1H NMR quantification (Fig. S5a†). Using GNPs (13 nm, capped by citrate) grafted with HS-PEG (Mw of 5.0 kg mol−1) as an example, the NMR peak of free PEG from the multi-Lorentzian-splitting algorithm was highly coincided with that from the post-centrifugation strategy, and the calculated σ at saturation (1.55 chains per nm2) was almost identical with that from the post-centrifugation strategy (1.53 chains per nm2) (Fig. S5b and Table S1†). The accuracy of the multi-Lorentzian-splitting algorithm can also be confirmed by comparison with other quantification methods such as TGA, TOC and analytical ultracentrifugation (AUC). The value of σ (1.55 chains per nm2) determined from the multi-Lorentzian-splitting method is very close to that from TGA (1.44 chains per nm2, Fig. 2c). It should be noted σ determined from TGA could be underestimated as PEG can potentially detach from GNPs during repeated centrifugations. This σ for 13 nm GNPs determined from NMR spectroscopy is also in reasonable agreement with σ reported for the same HS-PEG on 11 nm GNPs (measured by TOC and AUC; 1.77 chains per nm2), where the smaller GNPs allow for denser packing and a higher σ.29 Next, the precision of the multi-Lorentzian-splitting method was evaluated via repeated measurements under identical experimental and analytical conditions, i.e. three replicas for quantifying σ of GNPs with different sizes and PEG with different molecular weights (Fig. 3). The majority of the standard deviation values obtained with this method were less than 5%, and the maximum standard deviation was no more than 8%. These results prove that the multi-Lorentzian-splitting method is highly accurate with excellent reproducibility.
Effect of capping ligands
The capping ligands on the surface of GNPs play a critical role during ligand exchange with the HS-PEG molecules. To study the effect of ligands on the grafting process, GNPs capped with three different kinds of ligands, i.e. citrate, cetyltrimethylammonium bromide (CTAB), and polyvinylpyrrolidone (PVP), were reacted with HS-PEG under identical grafting conditions. 13 nm citrate-coated GNPs were obtained referred to the standard Turkevich method.45 The other two types of GNPs of the same size were prepared via ligand exchange of CTAB or PVP with the citrate-covered GNPs, made possible as CTAB and PVP possess stronger binding affinity for GNPs than citrate.26 The successful ligand exchanges were confirmed by UV and zeta-potential measurements (Fig. S6†).The grafting processes of HS-PEG onto citrate-, CTAB-, and PVP-covered GNPs were monitored by 1H NMR spectroscopy and analysed with the multi-Lorentzian-splitting algorithm (Fig. S7†). Fig. 2d shows the temporal evolution of σ for HS-PEG (Mw of 5.0 kg mol−1) grafted onto the surfaces of GNP@citrate, GNP@PVP and GNP@CTAB, respectively. At the grafting time of 3 min, σ decreased in the order of GNP@citrate (1.13 chains per nm2) > GNP@PVP (0.92 chains per nm2) > GNP@CTAB (0.78 chains per nm2), indicating that the grafting rate was inversely correlated to the binding affinity of the original capping ligand on the surface of GNPs (CTAB > PVP > citrate).26 As grafting continued, σ of these GNPs capped by different ligands exhibited a similar trend such that σ increased progressively from several minutes to about 180 min, and then reached a full coverage state. The maximum σ attained decreased in the order of GNP@citrate (1.46 chains per nm2) > GNP@PVP (1.38 chains per nm2) > GNP@CTAB (1.26 chains per nm2), which was the opposite of the binding affinity trend observed for the original capping ligands, revealing that the maximum σ was also inversely correlated to the binding affinity of the capping ligands on GNPs.
Effect of nanoparticle size
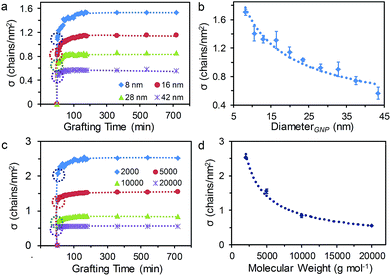
It is well known that the size of NPs, i.e. the curvature of NP surface, plays an important role on grafting density. However, studies on the effect of NP sizes on grafting rate are very rare due to a lack of practical characterization methods.31 To further demonstrate the power of our method, we exploited this multi-Lorentzian-splitting algorithm to evaluate the effect of GNP sizes on the grafting process. For this purpose, monodisperse CTAB-capped GNPs with average diameters ranging from 8 to 42 nm and standard deviations of less than 10% were conjugated with HS-PEG in D2O solutions (Mw of 5.0 kg mol−1, [PEG] of 0.60 mg mL−1) (Fig. S8 and S9†). For each GNP size, the initial [GNP] used was inversely proportional to the surface area of NPs (the square of the diameter) to keep the total surface area of GNPs the same. The multi-Lorentzian-splitting algorithm was then used to calculate σ for each NP size. Fig. 3a shows the temporal evolution of σ for HS-PEG on GNPs with average diameters (d) of 8.5, 16.2, 28.0, and 41.9 nm. At the grafting time (t) of 3 min, σ decreased with increasing size of GNPs, calculated as 1.08, 0.82, 0.69 and 0.48 chains per nm2 for dGNP of 8.5, 16.2, 28.0, and 41.9 nm, respectively. Note that [GNP]d=8.5 was almost 25 times greater than [GNP]d=41.9, meaning that the relative ratio of HS-PEG to GNPs for smaller GNPs was much less than that of larger GNPs. The higher σ observed for smaller GNPs indicates that the grafting rate is strongly dependent on the diffusion rate of GNPs, which is inversely proportional to their diameters (Stokes–Einstein equation).46 The grafting time to achieve a fully covered GNP surface with HS-PEG decreased from 180 to 50 min with increasing GNP sizes, primarily a result of the much denser surface coverage (i.e. higher σ at saturation) of smaller GNPs compared to larger ones. As expected, the plot σ at saturation against the diameter of GNPs revealed that σ decreased from 1.70 to 0.56 chains per nm2 while d increased from 8.5 to 41.9 nm (Fig. 3b). This indicates that the grafting efficiency of PEG onto the surface of GNPs was reduced with increasing curvature of GNPs. This result is qualitatively consistent with previous studies of other ligands bound to the surface of nanocrystals.47–49Effect of the molecular weight of HS-PEG
We also used this method to study the effect of HS-PEG molecular weights on the grafting process. Fig. 3c and S10† show the temporal evolution of σ and the NMR signal, respectively, for a series of HS-PEG with increasing molecular weight (Mw of 2.0, 5.0, 10.0 and 20.0 kg mol−1, [PEG] of 0.50 mg mL−1) grafting onto 13 nm citrate-capped GNPs. These experiments revealed that the grafting process was dramatically affected by the HS-PEG chain length. Similar to the trend of σ for decreasing GNP sizes, the grafting rate increased with decreasing HS-PEG chain length. This result suggests the grafting process is dependent on the diffusivity of free HS-PEG molecules, which decreases exponentially in water as the chain length is increased.49 This observation is also consistent with our previous study on the grafting process of HS-PEG on a flat Au surface.50 Plotting the σ at saturation (i.e. equilibrium) against the molecular weights demonstrated that σ decreased in the order of 2.53, 1.55, 0.84, 0.55 chains per nm2 for Mw of 2.0, 5.0, 10.0 and 20.0 kg mol−1, respectively. The data confirmed that σ at saturation decreased with increasing molecular weight (Fig. 3d), which is consistent with previous studies of σ for various polymer molecular weights.29,51Limitations of the multi-Lorentzian-splitting algorithm
The limitations of our method are mainly determined by the following aspects: (1) the size of gold nanoparticles, (2) the molecular weight of PEG molecules, and (3) the fraction of free PEG among all PEG molecules in reaction solutions. For the multi-Lorentzian-splitting algorithm, the separation of the NMR signals of free PEG from the grafted ones is dependent on their peak-width difference, which is caused by the slow diffusion of PEG on the nanoparticle surface. Therefore, the multi-Lorentzian-splitting algorithm is not suitable for the scenario when the diffusion of grafted PEG or part of it is similar to that of free PEG, that is when the size of nanoparticles is too small, or the molecular weight of PEG is too large.For the limitation of GNP size, we determined the lower limit of nanoparticle size by comparing the grafting density obtained by the multi-Lorentzian-splitting algorithm and post-centrifugation methods (Fig. S11†). The latter is highly accurate for the quantification of final grafting densities, but not capable for monitoring the grafting process. Fig. S11† reveals that the lower limit of nanoparticle size of the multi-Lorentzian-splitting algorithm increases with the molecular weight of PEG molecules. For example, the lower limit of nanoparticle size for PEG-5K is ca. 10 nm, while that for PEG-20K is ca. 23 nm. In principle, there is no upper limit of nanoparticle size for the multi-Lorentzian-splitting algorithm, as the difference of diffusion between free PEG and grafted one can only increase with the size of nanoparticles. It should be noticed that when the size of nanoparticles is too large, the NMR signal of grafted PEG will become too broad to distinguish from the spectral baseline. Therefore, one can directly quantify the amount of free PEG from the NMR peak of PEG in reaction solutions.
For biomedical applications of PEGylated Au nanoparticles, the molecular weight of PEG is generally in the range of 2.0 to 20 kg mol−1. We found the multi-Lorentzian-splitting is suitable for the PEG in this range. The grafting density of PEG with shorter chain lengths (i.e. molecular weight less than 2.0 kg mol−1) could be determined by the previous methods developed for small molecular ligands. For PEG with longer chain lengths (i.e. molecular weight higher than 20 kg mol−1), the multi-Lorentzian-splitting algorithm can be used to determine the grafting density of PEG on NPs with sizes above the lower limit for each molecular weight.
In addition, the multi-Lorentzian-splitting algorithm method is more appropriate for the scenario when the NMR signal of free PEG is not significantly larger than that of grafted ones, that is the fraction of free PEG among all PEG is relatively small. In a controlled experiment, we continuously added free PEG-5K into a solution of PEGlyated GNPs (size of 13 nm) with saturate and known grafting density of the same PEG (1.53 chains per nm2). The 1H NMR signals for the solution with different free/total PEG ratios were interpreted by the multi-Lorentzian-splitting algorithm to obtain the calculated grafting density, which were compared to the known value as shown in Fig. S12.† The comparison result reveals that once the fraction of free PEG was beyond 60%, the calculated grafting density determined by the multi-Lorentzian-splitting algorithm became inconsistent with the actual known value. In the scenario when the fraction of free PEG is much larger than that of the grafted ones, the grafting density will become saturated and can be easily determined by the post-centrifugation method.
Quantification of PEG grafting-to SiO2 encapsulated gold nanorods
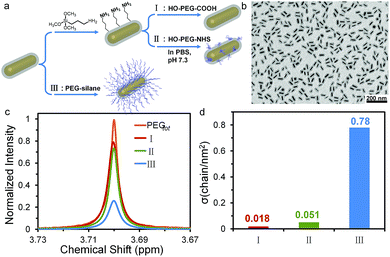
The grafting-to process of PEG on NP surfaces is a thermodynamically-driven adsorption/desorption process, and should be affected by the activity of the adsorption reaction of ligands with the NP surfaces. Despite the reaction of thiol with gold, other adsorptions through supramolecular interactions or covalent reactions can co-exist and the corresponding grafting densities need to be quantified. In order to verify the universal applicability of our multi-Lorentzian-splitting algorithm to other types of adsorption reactions, we selected the PEGylation of SiO2 encapsulated gold nanorods (GNR@SiO2) as an example because of their potential biomedical applications such as photothermal therapy,52 photoacoustic imaging,53 biosensing,54 and drug delivery.55 Three typical adsorption reactions were used to graft PEG chains (Mw of 5.0 kg mol−1) onto GNR@SiO2 surfaces (Fig. 4a, b and S13†). The first reacted amine-functionalized GNR@SiO2 (GNR@SiO2–NH2) with α-methoxy-ω-carboxyl poly(ethylene glycol) (PEG-COOH) via electronic interactions (Route I). The second employed GNR@SiO2–NH2 to interact with α-methoxy-ω-N-hydroxysuccinimide-polyethylene glycol (PEG-NHS) by the formation of active esters (Route II). The third involved a hydrolysis reaction of 2-[methoxy(polyethyleneoxy)propyl]trimethoxysilane (PEG-silane) on SiO2 shells covered GNRs under acidic conditions (Route III).56In order to quantify the grafting density for each route, the multi-Lorentzian-splitting algorithm was applied to isolate the free PEG signal from the mixture containing grafted PEG after the grafting-to process reached equilibrium. Fig. 4c shows the NMR spectra of free PEG calculated via the multi-Lorentzian-splitting method. The grafting density for each route was determined by comparing the integral of the free PEG signal with the standard curve of pure PEG (Fig. 4d). Route III yielded the highest grafting efficiency with σ up to 0.78 chain per nm2, which was 43 and 15 times larger than that of routes I (0.018 chain per nm2) and II (0.051 chain per nm2), respectively; this revealed that the hydrolysis of PEG-silane is a much more effective way to graft PEG chains onto SiO2 shells covered GNRs. It should be noted that during the hydrolysis reaction, there is no by-products, i.e. PEG micelles, observed by the 1H NMR and dynamic light scattering (DLS) studies (Fig. S14, Table S2 and the discussion in ESI†). Additionally, σ achieved through Route I and II were similar to σ of HS-PEG on CTAB-covered GNRs, which was determined as 0.034 chain per nm2 by the same multi-Lorentzian-splitting algorithm (Fig. S15†). Taken together, these results indicate that the multi-Lorentzian-splitting algorithm is well-suited to quantify the coverage from PEG ligands in various adsorption reactions with NP surfaces and is not limited by the NP shapes.
Conclusions
In summary, we report a facile and non-sacrificial 1H NMR analytical approach to quantitatively characterize PEG grafting density on GNPs. In order to distinguish the NMR signal of free PEG from that of grafted molecules, a multi-Lorentzian-splitting algorithm is proposed and allows monitoring of the grafting process in situ. Using this method, the grafting rates and grafting densities can be efficiently studied for GNPs with different dimensions, PEG with different molecular weights, and different types of the original capping ligand on GNPs. This method is not limited by the types of terminal functional group of PEG, the surface chemistry of nanoparticles, or the composition of nanoparticles, and can be applied to other polymer ligands capping different types of nanoparticles. More importantly, our methods provide a set of critical and standard guide for characterization of the PEG grafting density on nanoparticles (the most important parameter in biological interactions) for in vivo biological and biomedicine studies.57,58Conflicts of interest
There are no conflicts to declare.Acknowledgements
K. L. and Z.-Y. L. gratefully acknowledge financial support from the National Natural Science Foundation of China (21534004). K. L. thanks the National Natural Science Foundation of China (21474040, 21674042) and China’s Thousand Talent Plan for financial support.Notes and references
- C. J. Murphy, A. M. Gole, J. W. Stone, P. N. Sisco, A. M. Alkilany, E. C. Goldsmith and S. C. Baxter, Acc. Chem. Res., 2008, 41, 1721 CrossRef CAS PubMed.
- N. L. Rosi and C. A. Mirkin, Chem. Rev., 2005, 105, 1547 CrossRef CAS PubMed.
- Z. Zhang, J. Wang and C. Chen, Adv. Mater., 2013, 25, 3869 CrossRef CAS PubMed.
- C. Tu, S. Das, A. B. Baker, J. Zoldan and L. J. Suggs, ACS Nano, 2015, 9, 3436 CrossRef CAS PubMed.
- S. Wilhelm, A. J. Tavares, Q. Dai, S. Ohta, J. Audet, H. F. Dvorak and W. C. W. Chan, Nat. Rev. Mater., 2016, 1, 16014 CrossRef CAS.
- J. Lazarovits, Y. Y. Chen, E. A. Sykes and W. C. W. Chan, Chem. Commun., 2015, 51, 2756 RSC.
- J. W. Nichols and Y. H. Bae, Nano Today, 2012, 7, 606 CrossRef CAS PubMed.
- E. Blanco, H. Shen and M. Ferrari, Nat. Biotechnol., 2015, 33, 941 CrossRef CAS PubMed.
- I. Lynch and K. A. Dawson, Nano Today, 2008, 3, 40 CrossRef CAS.
- M. Lundqvist, J. Stigler, G. Elia, I. Lynch, T. Cedervall and K. A. Dawson, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 14265 CrossRef CAS PubMed.
- C. D. Walkey and W. C. W. Chan, Chem. Soc. Rev., 2012, 41, 2780 RSC.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543 CrossRef CAS PubMed.
- S. M. Moghimi, A. C. Hunter and J. C. Murray, Pharmacol. Rev., 2001, 53, 283 CAS.
- X. Yang, M. Yang, B. Pang, M. Vara and Y. Xia, Chem. Rev., 2015, 115, 10410 CrossRef CAS PubMed.
- J. S. Suk, Q. Xu, N. Kim, J. Hanes and L. M. Ensign, Adv. Drug Delivery Rev., 2016, 99, 28 CrossRef CAS PubMed.
- V. C. F. Mosqueira, P. Legrand, J.-L. Morgat, M. Vert, E. Mysiakine, R. Gref, J.-P. Devissaguet and G. Barratt, Pharm. Res., 2001, 18, 1411 CrossRef CAS.
- J. V. Jokerst, T. Lobovkina, R. N. Zare and S. S. Gambhir, Nanomedicine, 2011, 6, 715 CrossRef CAS PubMed.
- R. Gref, M. Lück, P. Quellec, M. Marchand, E. Dellacherie, S. Harnisch, T. Blunk and R. H. Müller, Colloids Surf., B, 2000, 18, 301 CrossRef CAS PubMed.
- L. D. Unsworth, H. Sheardown and J. L. Brash, Langmuir, 2008, 24, 1924 CrossRef CAS PubMed.
- Q. Yang, S. W. Jones, C. L. Parker, W. C. Zamboni, J. E. Bear and S. K. Lai, Mol. Pharmaceutics, 2014, 11, 1250 CrossRef CAS.
- C. H. J. Choi, C. A. Alabi, P. Webster and M. E. Davis, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 1235 CrossRef CAS PubMed.
- M. Maccarini, G. Briganti, S. Rucareanu, X.-D. Lui, R. Sinibaldi, M. Sztucki and R. B. Lennox, J. Phys. Chem. C, 2010, 114, 6937 CrossRef CAS.
- E. Mansfield, A. Kar, T. P. Quinn and S. A. Hooker, Anal. Chem., 2010, 82, 9977 CrossRef CAS.
- M. K. Corbierre, N. S. Cameron, M. Sutton, K. Laaziri and R. B. Lennox, Langmuir, 2005, 21, 6063 CrossRef CAS PubMed.
- H. Zhang, W. Wang, S. Mallapragada, A. Travesset and D. Vaknin, Nanoscale, 2017, 9, 164 RSC.
- X. Xia, M. Yang, Y. Wang, Y. Zheng, Q. Li, J. Chen and Y. Xia, ACS Nano, 2012, 6, 512 CrossRef CAS.
- C. S. Levin, S. W. Bishnoi, N. K. Grady and N. J. Halas, Anal. Chem., 2006, 78, 3277 CrossRef CAS PubMed.
- H. Hinterwirth, S. Kappel, T. Waitz, T. Prohaska, W. Lindner and M. Lämmerhofer, ACS Nano, 2013, 7, 1129 CrossRef CAS PubMed.
- D. N. Benoit, H. Zhu, M. H. Lilierose, R. A. Verm, N. Ali, A. N. Morrison, J. D. Fortner, C. Avendano and V. L. Colvin, Anal. Chem., 2012, 84, 9238 CrossRef CAS PubMed.
- V. B. Damodaran, C. J. Fee, T. Ruckh and K. C. Popat, Langmuir, 2010, 26, 7299 CrossRef CAS PubMed.
- A. M. Smith, L. E. Marbella, K. A. Johnston, M. J. Hartmann, S. E. Crawford, L. M. Kozycz, D. S. Seferos and J. E. Millstone, Anal. Chem., 2015, 87, 2771 CrossRef CAS.
- K. A. Johnston, A. M. Smith, L. E. Marbella and J. E. Millstone, Langmuir, 2016, 32, 3820 CrossRef CAS PubMed.
- M. H. Levitt, Spin Dynamics: Basics of Nuclear Magnetic Resonance, John Wiley & Sons Ltd., West Sussex, England, 2nd edn, 2008 Search PubMed.
- M. J. Hostetler, J. E. Wingate, C.-J. Zhong, J. E. Harris, R. W. Vachet, M. R. Clark, J. D. Londono, S. J. Green, J. J. Stokes, G. D. Wignall, G. L. Glish, M. D. Porter, N. D. Evans and R. W. Murray, Langmuir, 1998, 14, 17 CrossRef CAS.
- E. Tavasoli, Y. Guo, P. Kunal, J. Grajeda, A. Gerber and J. Vela, Chem. Mater., 2012, 24, 4231 CrossRef CAS.
- C.-C. Lin, Y. Guo and J. Vela, ACS Catal., 2015, 5, 1037 CrossRef CAS.
- O. Kohlmann, W. E. Steinmetz, X.-A. Mao, W. P. Wuelfing, A. C. Templeton, R. W. Murray and C. S. Johnson, J. Phys. Chem. B, 2001, 105, 8801 CrossRef CAS.
- L. E. Marbella and J. E. Millstone, Chem. Mater., 2015, 27, 2721 CrossRef CAS.
- Z. Hens and J. C. Martins, Chem. Mater., 2013, 25, 1211 CrossRef CAS.
- J. D. Roo, N. Yazdani, E. Drijvers, A. Lauria, J. Maes, J. S. Owen, I. V. Driessche, M. Niederberger, V. Wood, J. C. Martins, I. Infante and Z. Hens, Chem. Mater., 2018, 30, 5485 CrossRef.
- D. F. Findley, Ann. Inst. Stat. Math., 1991, 43, 505 CrossRef.
- H. Akaike, IEEE Trans. Autom. Control, 1974, 19, 716 CrossRef.
- G. J. McLachlan and S. Rathnayake, WIREs Data Mining and Knowledge Discovery, 2014, 4, 341 CrossRef.
- H. Häkkinen, Nat. Chem., 2012, 4, 443 CrossRef.
- J. Turkevich, P. C. Stevenson and J. Hillier, J. Phys. Chem., 1953, 57, 670 CrossRef CAS.
- Z. Hens, I. Moreels and J. C. Martins, ChemPhysChem, 2005, 6, 2578 CrossRef CAS.
- H. D. Hill, J. E. Millstone, M. J. Banholzer and C. A. Mirkin, ACS Nano, 2009, 3, 418 CrossRef CAS PubMed.
- C. D. Walkey, J. B. Olsen, H. Guo, A. Emili and W. C. W. Chan, J. Am. Chem. Soc., 2012, 134, 2139 CrossRef CAS PubMed.
- K. Rahme, L. Chen, R. G. Hobbs, M. A. Morris, C. O'Driscoll and J. D. Holmes, RSC Adv., 2013, 3, 6085 RSC.
- H.-M. Gao, H. Liu, H.-J. Qian, G.-S. Jiao and Z.-Y. Lu, Phys. Chem. Chem. Phys., 2018, 20, 1381 RSC.
- B. Shi, C. Fang and Y. Pei, J. Pharm. Sci., 2006, 95, 1873 CrossRef CAS.
- S. Shen, H. Tang, X. Zhang, J. Ren, Z. Pang, D. Wang, H. Gao, Y. Qian, X. Jiang and W. Yang, Biomaterials, 2013, 34, 3150 CrossRef CAS.
- Y.-S. Chen, W. Frey, S. Kim, K. Homan, P. Kruizinga, K. Sokolov and S. Emelianov, Opt. Express, 2010, 18, 8867 CrossRef CAS PubMed.
- C. Wang, Z. Ma, T. Wang and Z. Su, Adv. Funct. Mater., 2006, 16, 1673 CrossRef CAS.
- E. Choi, M. Kwak, B. Jang and Y. Piao, Nanoscale, 2013, 5, 151 RSC.
- W.-C. Wu and J. B. Tracy, Chem. Mater., 2015, 27, 2888 CrossRef CAS PubMed.
- M. Faria, M. Bjornmalm, K. J. Thurecht, S. J. Kent, R. G. Parton, M. Kavallaris, A. P. R. Johnston, J. J. Gooding, S. R. Corrie, B. J. Boyd, P. Thordarson, A. K. Whittaker, M. M. Stevens, C. A. Prestidge, C. J. H. Porter, W. J. Parak, T. P. Davis, E. J. Crampin and F. Caruso, Nat. Nanotechnol., 2018, 13, 777 CrossRef CAS PubMed.
- The code of multi-Lorentzian-splitting algorithm is available at: http://https://github.com/Shirui816/MultipleDistributionFitting, The audiences with nonprofit objectives can cite this article to use the code for free.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc02847h |
| This journal is © The Royal Society of Chemistry 2019 |