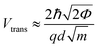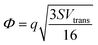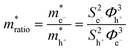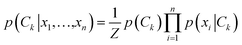Nucleotide and structural label identification in single RNA molecules with quantum tunneling spectroscopy

Abstract

Although a number of advances have been made in RNA sequencing and structural characterization, the lack of a method for directly determining the sequence and structure of single RNA molecules has limited our ability to probe heterogeneity in gene expression at the level of single cells. Here we present a method for direct nucleotide identification and structural label mapping of single RNA molecules via Quantum Molecular Sequencing (QMSeq). The method combines non-perturbative quantum tunneling spectroscopy to probe the molecular orbitals of ribonucleotides, new experimental biophysical parameters that fingerprint these molecular orbitals, and a machine learning classification algorithm to distinguish between the ribonucleotides. The algorithm uses tunneling spectroscopy measurements on an unknown ribonucleotide to determine its chemical identity and the presence of local chemical modifications. Combining this with structure-dependent chemical labeling presents the possibility of mapping both the sequence and local structure of individual RNA molecules. By optimizing the base-calling algorithm, we show a high accuracy for both ribonucleotide discrimination (>99.8%) and chemical label identification (>98%) with a relatively modest molecular coverage (35 repeat measurements). This lays the groundwork for simultaneous sequencing and structural mapping of single unknown RNA molecules, and paves the way for probing the sequence–structure–function relationship within the transcriptome at an unprecedented level of detail.

---

Introduction

Ribonucleic acid (RNA) plays a central role in a number of crucial biological processes, including transcription, translation, and catalysis. Just as with DNA and proteins, the structure and chemical properties of each RNA molecule are primarily dictated by its sequence. Unique to RNA, however, is its ability to both encode genetic information and carry out diverse chemical functions within the cell.¹ While traditional sequencing methods target DNA, which is the primary information carrier in cells, genomic sequencing does not access information about gene expression levels, splicing, and other modifications that occur after transcription. Several methods currently exist for indirectly sequencing RNA molecules,² and they typically rely on reverse transcription into cDNA, which can then be sequenced conventionally. However, these methods have limited sensitivity, and no method so far is capable of directly determining the sequence of individual RNA molecules, which will be crucial for measuring gene heterogeneity, detecting rare transcripts, and improving the sensitivity and accuracy of gene expression profiling in single cells.^3,4

Going beyond sequencing, the diversity of cellular roles played by RNA motivates a large-scale effort to achieve a more comprehensive understanding of the relationship between sequence, structure, and function in the transcriptome.⁵ Accurate prediction of three-dimensional RNA structure from the sequence using computational methods is still not trivial,⁶ and typically relies on experimental data to impose constraints on the large conformational space available to a molecule. Traditional methods of biomolecular structure determination, such as X-ray crystallography⁷ and NMR,⁸ require considerable sample preparation, are low-throughput, and are not universally applicable to all native RNA molecules. Thus the vast majority of transcripts remain structurally uncharacterized.⁵ Alternatively, methods based on chemical labeling or enzymatic probing can be used to measure structure-dependent properties such as solvent accessibility and conformational flexibility along the molecule, and these methods have shown broad applicability and considerably higher throughput.⁹ In particular, the SHAPE (Selective 2′-Hydroxyl Acylation analyzed by Primer Extension) technique has proven to be an especially versatile and powerful tool for RNA secondary and tertiary structure elucidation.^10,11 The ability of SHAPE to probe local flexibility at single-nucleotide resolution in a parallel and high-throughput manner has allowed for comprehensive RNA structural mapping studies, including whole transcriptome¹² and viral genome analysis.¹³ However, despite its strengths the SHAPE method still relies on measuring average nucleotide reactivity within a large ensemble of molecules via reverse transcription and cDNA analysis, and thus cannot resolve distinct structural populations that may exist for a particular molecule. To date, no method has been capable of determining the native structure of individual RNA molecules.

Here we describe a method that uses scanning tunneling spectroscopy (STS) measurements to identify individual nucleotides and structure-dependent chemical labels of single RNA molecules. By probing the molecular orbitals of each ribonucleotide via non-perturbative quantum tunneling spectroscopy, combined with an identification algorithm that uses machine learning to recognize unique electronic fingerprints for each base, we have been able to correctly discriminate between the four RNA bases (A, G, C, U) with a single-base accuracy of >99.8%. In addition, we have adapted the SHAPE method for probing the structure of single RNA molecules by combining the conformation-dependent acylation of SHAPE with our nanoelectronic fingerprinting approach.

Results and discussion

QMSeq method and STS measurements

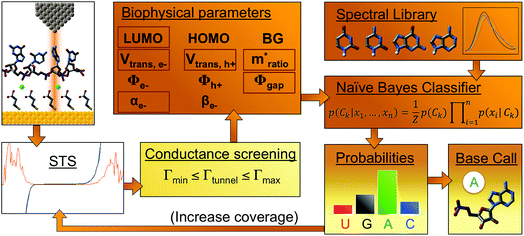
We successfully identified ribonucleotides in single RNA molecules using the quantum molecular sequencing (QMSeq) method, a technique that our group previously developed for identification of DNA nucleobases.^14,15 In this method, the molecules are adsorbed onto a metal substrate and electronically probed using STS, which encodes information about the molecular orbitals of each base in the tunneling spectra. A molecular identification algorithm based on machine learning is then applied to both identify each ribonucleotide as well as discriminate between chemically labeled and unlabeled bases within the molecule. When combined with structure-dependent chemical labeling, this represents a method for simultaneous sequence identification and structural characterization of individual RNA molecules and will pave the way for mapping the transcriptome with a level of detail that has been previously unattainable.

In recent years a number of potential single-molecule sequencing platforms based on nanoelectronic measurements have emerged.¹⁶ In contrast to nanopore sequencing methods that rely on electronic measurements of a molecule as it threads through a pore,^17–19 our method first immobilizes the molecules onto a flat metal substrate, allowing for both STM imaging and repeated tunneling spectroscopy measurements along the molecule. While reproducibility in STS measurements of nucleobases has previously been hindered by poor control over molecular orientation, leading to high entropy states and a broadening of measured energy levels,^20–22 our method relies on tailored surface chemistry to immobilize the RNA and limit conformational freedom on the surface. As illustrated in Fig. 1a, the surface consists of a self-assembled monolayer of 3-mercaptopropionic acid (MPA) on an atomically flat Au (111) substrate.²³ The presence of divalent metal cations (M²⁺) in solution during the adsorption step promotes an attractive interaction between the terminal carboxylate groups of the monolayer and the negatively charged phosphate groups of the RNA molecules, effectively forming a salt bridge between the nucleic acids and the surface.²⁴ This electrostatic attraction results in strong immobilization of the RNA on the substrate, as has been reported previously for DNA on similar carboxylate-terminated alkanethiol monolayers²⁵ (see STM images in Fig. 1, S1†). STS measurements on a clean MPA/M²⁺ monolayer produce primarily conductive spectra with no apparent bandgap, for example as shown in Fig. 1b. In contrast, STS measurements on the same surface after adsorption of RNA produce a mixture of conductive spectra, as observed on clean MPA, and spectra displaying a characteristic bandgap of ∼1.5 eV (Fig. 1c), corresponding to the molecular orbitals of the nucleobases within the adsorbed RNA. This permits unambiguous discrimination between spectra acquired over nucleotides and those acquired over the background. The density of states can then be plotted by taking the first derivative of the I–V spectrum, which allows for identification of the highest occupied and lowest unoccupied molecular orbital (HOMO & LUMO) energy levels as the first major peaks in the negative and positive voltage regions, respectively (Fig. 1c). The measured HOMO, LUMO, and the resulting bandgap, BG = LUMO − HOMO, are unique biophysical parameters that are expected to differ slightly for each RNA base due to differences in their molecular orbitals.^14,15,22 However, because of small shifts in the energy levels resulting from different molecular conformations and substrate interactions, in practice the measured levels are smeared out and show significant overlap in their distributions (Fig. S2†), making it difficult to discriminate between bases using these three parameters alone.

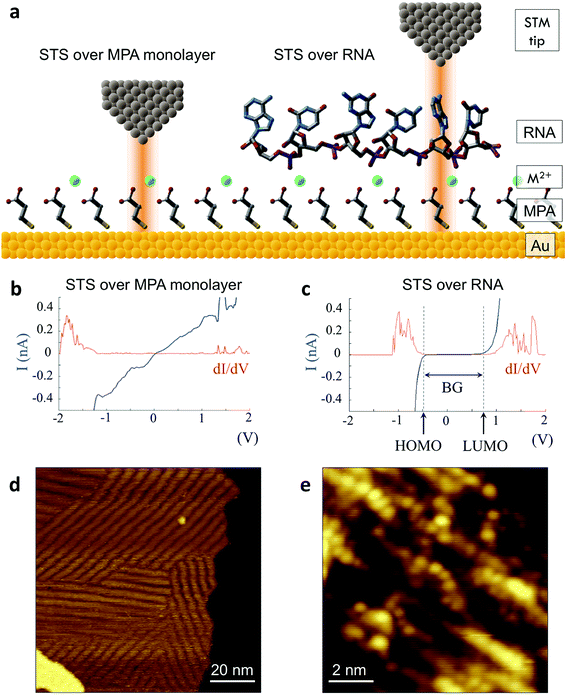Fig. 1 Tunneling spectroscopy measurements of individual RNA molecules (a) illustration of the experimental approach used. RNA molecules are electrostatically adsorbed onto the MPA/Au substrate, and their nucleobase molecular orbitals are then probed via STS. (b) Measurements acquired over the background monolayer result in conductive spectra with no apparent bandgap. (c) In contrast, measurements acquired over ribonucleotides show a characteristic bandgap of ∼1.5 V, with HOMO and LUMO levels that can be identified from peaks in the plot of dI/dV vs. V. (d) STM image of the MPA monolayer, with several atomic steps and terraces are visible, as well as the previously observed threefold-symmetric striped domains.⁴⁰ (e) High-resolution STM image of a densely packed layer of poly-(dC)₁₀₀ molecules adsorbed onto a positively charged monolayer.

Additional biophysical parameters as fingerprints

Previous work from our group showed that accuracy in discriminating between DNA bases with STS could be drastically improved by introducing an additional six biophysical parameters that are derived from transition voltage spectroscopy (TVS).¹⁵ TVS provides a means to characterize charge tunneling through a metal–molecule–metal junction, which in this case is formed between the STM tip, the ribonucleotide, the underlying monolayer, and the gold substrate. TVS analysis is performed by plotting the I–V data as ln(I/V²) vs. 1/V, also known as a Fowler–Nordheim (FN) plot.²⁶ For metal–molecule–metal junctions with a relatively small tunneling barrier height, there is an inflection point in the FN plot as the charge transport mechanism transitions from direct tunneling (low-bias) to field emission (high bias).²⁷ This transition voltage V_trans depends on the difference between the HOMO of the molecule and the Fermi level of the metal, and is related to the tunneling barrier height Φ via the following equation:
where ħ is the reduced Planck constant, q is the elementary charge, d is the tunneling distance, and m is a convolution of the effective mass m^* and the electron rest mass m_e. As there are distinct transition voltages for the positive bias region (electron tunneling, V_trans(e⁻)) and the negative bias region (hole tunneling, V_trans(h⁺)), this provides two additional measurable parameters that depend on the identity of the molecule within the junction. Furthermore, the tunneling barrier height Φ can be determined from the transition voltage using the following relation:
where S is the measured slope of the high-bias region of the FN plot.¹⁵ The barriers for electron tunneling Φ_e⁻ and hole tunneling Φ_h⁺ can both be extracted from TVS, and can be summed to give the total tunneling barrier height Φ_gap, representing three additional biophysical parameters. Finally, once the tunneling barriers are known, the effective mass ratio of electrons to holes, 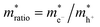, can be determined from the following relation:
Ultimately this results in a set of nine unique biophysical parameters (HOMO, LUMO, BG, V_trans(e⁻), V_trans(h⁺), Φ_e⁻, Φ_h⁺, Φ_gap, and 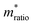) that depend on the molecule within the junction and can be extracted from each tunneling spectrum. Comparison of the distributions of the additional six parameters shows that although there is still a significant overlap between the four bases, there are also base-dependent shifts in the distributions (Fig. S2†). These differences enable a prediction of the likelihood that a particular STS measurement belongs to each of the four bases by comparing the values of the nine parameters from that measurement to the corresponding distributions of those parameters for each of the bases in a library. This was previously developed into a DNA base-calling algorithm,¹⁵ and here we extend this approach for RNA base calling and structural label identification, as described below.

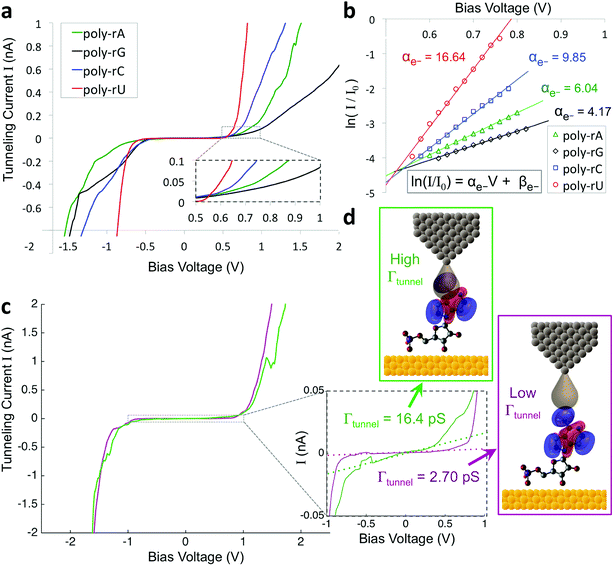
To improve the accuracy in discriminating between different nucleotides as well as identification of chemical modifications, we sought to incorporate additional biophysical parameters into our model to characterize higher energy molecular orbitals. While the previously described parameters relate to interactions between the tunneling electrons and the frontier molecular orbitals, there should also be information about higher- and lower-lying molecular orbitals contained in the tunneling spectrum. Density functional theory (DFT) calculations show differences in the higher-lying molecular orbitals that can potentially be used to help distinguish between the different nucleobases, and also to characterize modifications of the sugar backbone that may be difficult to identify by probing only the frontier orbitals (Fig. S3†). In an STS study of short DNA oligonucleotides on a Cu (111) surface, Yoshida et al. observed differences between the different DNA bases in the tunneling current behavior at bias voltages just above the bandgap.²⁸ More specifically, they fit a straight line to the log of the current vs. bias voltage, and observed shifts in the slope and intercept values between some of the DNA bases, likely arising from differences in the energy level spacing for LUMO + 1, LUMO + 2, etc. We performed a similar analysis on our STS data, as shown in Fig. 2 for an example spectrum for each of the four bases. After identifying the bandgap from the I–V plot (Fig. 2a), we then plotted the log of the current as a function of bias voltage for the region just above the bandgap, performed a linear fitting, and extracted the slope and intercept parameters α_e⁻ and β_e⁻ (Fig. 2b), such that

ln(I/I₀) = α_e⁻V + β_e⁻

where I₀ = 1.0 nA. When comparing distributions of α_e⁻ and β_e⁻ values for the different bases (Fig. S2†), we observed that although there is significant overlap, there are also small shifts in the average values that are useful in discriminating between the bases. Thus we included α_e⁻ and β_e⁻ as two additional parameters in our base-calling algorithm.

Fig. 2 Extracting additional biophysical parameters from the tunneling spectra. (a) Selected tunneling spectra for each of the four ribonucleotides. Inset shows a zoomed-in view of the region just above the bandgap. (b) A plot of ln(I/I₀) vs. V for the same spectra shown in (a). The open symbols are experimental data, and the solid lines represent linear fits to the data, with the values of the slope parameter α_e⁻ shown. (c) Examples of two STS measurements on the same poly-rA₇ sample that show a very similar bandgap but an order of magnitude difference in the tunneling conductance Γ_tunnel. Inset shows a zoomed-in view of the bandgap region, along with a linear fit to the current inside the bandgap (dotted lines). (d) Proposed qualitative model of the effect of tip–molecule orbital overlap on the tunneling conductance. The monolayer has been omitted for clarity.

Given the significant overlap in the distributions of all 11 biophysical parameters observed between the different bases, it is desirable to minimize the smearing of energy levels due to molecular entropy.²⁹ However, in practice, it is currently not possible to eliminate this smearing experimentally, leading to broadening in the measured parameter distributions that is unavoidable.²² To address this challenge we sought to identify an independent parameter that could serve as a classifier of the extent of molecular energy level smear in a given measurement. For this purpose, we introduced a twelfth parameter, the tunneling conductance Γ_tunnel, which corresponds to the measured conductance within the bandgap due to tunneling of charges through the tip–molecule–surface junction. We extracted the tunneling conductance from STS measurements by fitting a line to the I–V points within the bandgap for each of the tunneling spectra and measuring the slope of the line, as shown in Fig. 2c. This conductance, while exceedingly small (<100 pS), is still expected to vary as a result of a number of factors affecting the nature of the charge conduction pathway, including different conformations of the molecule and different molecule/substrate arrangements (e.g. adjacency to an atomic step edge, vacancy, or other defect).^30–33 While a detailed model of the relationship between Γ_tunnel and the molecular arrangement is beyond the scope of this paper, in a simplified picture the tunneling conductance may reflect the extent of orbital overlap between the tip, molecule, and surface, with larger overlap leading to larger Γ_tunnel values (Fig. 2d). When comparing STS measurements on all four RNA bases, we observed a large variation in the tunneling conductance values, with most measurements falling within the range of 1–10 pS (Fig. S2†). This presents the opportunity to use Γ_tunnel not just as a twelfth biophysical parameter, but also as a metric for screening out measurements in which the nucleotide molecular orbitals were strongly perturbed by an unfavorable tip–molecule–substrate geometry. If the tunneling conductance does indeed serve as an indicator of the degree of perturbation of the molecular orbitals, then the incorporation of Γ_tunnel into the base-calling algorithm is expected to help reduce the errors that result from broadening and overlap of the other 11 parameters between the different ribonucleotides.

Nucleobase identification algorithm

As a first step in developing a tunneling spectroscopy RNA base-calling algorithm, we created a spectral library consisting of several hundred individual STS measurements of each of the four unmodified ribonucleotides. To do this, we deposited poly-(rN)₇ RNA homopolymers (N = A, G, C, or U) onto an MPA/Au substrate at high surface-coverage, and collected a large number (>10 000) of STS measurements on each sample. The STS measurements were collected pointwise on grids across the surface, and as a result, the majority of the measurements were not directly over an RNA nucleobase. Thus we found it necessary to exclude spectra that did not display a sufficiently large bandgap (BG < 0.5 eV), which were assumed to be measurements over the background monolayer.¹⁵ In addition, spectra that showed primarily insulating behavior (BG > 3 eV) were assumed to be from multi-layered molecules or surface contaminants, and were also excluded. Finally, spectra that did not show a clearly identifiable transition voltage in the FN plot were considered to be ionic impurities exhibiting Frenkel–Poole conduction,³⁴ and were also filtered out. The remaining spectra were analyzed in order to extract the twelve biophysical parameters outlined above, which were added to the library.

We then implemented a machine learning algorithm based on a modified naïve Bayes classifier in order to predict which of the four bases a randomly selected ‘unknown’ STS measurement belongs to (see ESI† for details of the algorithm).¹⁵ Briefly, the probability p that an unknown measurement belongs to the k^th class C_k (corresponding to rA, rG, rC, or rU) is estimated using the following equation:

where x_i represents the measured value for the i^th biophysical parameter (from 1–12), and Z is a normalization factor. The parameter-specific probabilities p(x_i|C_k) are determined from the kernel density estimate of the observed distribution of parameter i for class C_k. After calculating a probability for each of the four classes (bases), the class with the highest probability is chosen, producing a base call. While making base calls from single measurements has some important advantages, in practice, it is desirable to improve both the accuracy and the confidence by incorporating multiple measurements (or reads) on the same sample into a single base call. This is in analogy to sequence coverage (or depth) in traditional sequencing methods, and is made possible here by the fact that the molecules are immobilized on a surface and can be repeatedly measured by STS.

The results from applying our base-calling algorithm to the ribonucleotide library are shown in Fig. 3. As a first pass, we performed classification with HOMO and LUMO as the only parameters. This resulted in poor recall for all four bases (Fig. 3a), with a low overall base-calling accuracy even at high coverage (<40% at 35X coverage). This is not surprising, given the significant overlap observed between the bases for both the HOMO and LUMO distributions. Next, we repeated the classification using all 12 biophysical parameters, which resulted in significantly improved recall for all four bases (Fig. 3b). Although adenine still showed relatively low recall, using 12 parameters increased the overall accuracy to 82% at 35X coverage. This improvement is due to the improved ability of the classification algorithm to distinguish between the bases when using a larger set of parameters, and is consistent with what was found previously with DNA.¹⁵ The previous study also found that accuracy could be further improved by narrowing down to an optimal parameter subset for each base that includes only some of the biophysical parameters.¹⁵ In this case, we modified the algorithm to test different parameter subsets along with probability weighting coefficients, which were then numerically optimized to give the best accuracy when applied to training and testing data sets. Using the optimized parameter subsets along with the weighting coefficients, the recall shows significant improvement at all coverages (Fig. 3c), with overall accuracy increasing to 93% at 35X coverage. While it may seem counterintuitive that discarding some of the parameters would increase the accuracy, this can be explained by the fact that some parameters are more useful than others for identifying specific bases, owing to better separation and less overlap with the other bases in their distributions. To explore this further, we tested the base-calling algorithm using only single parameters, as well as systematically removing or replacing individual parameters from optimized parameter subsets, and observed a large variation in the relative importance of the different parameters as defined by the relative change in base-calling accuracy when removing or replacing a given parameter (Fig. S4†). The use of weighting coefficients and numerical optimization then allows for the determination of the optimal parameter sets without any prior assumptions about the importance of each parameter. Shown in Fig. 3d is a comparison of the overall accuracies at selected coverages when performing base calling with HOMO and LUMO only, with all 12 parameters, and with optimal parameter sets. In order to avoid overtraining the classification algorithm, the libraries consisting of several hundred measurements per nucleobase were randomly split into fourths for 4-fold cross-validation of results (see ESI and Fig. S5 for further details†).

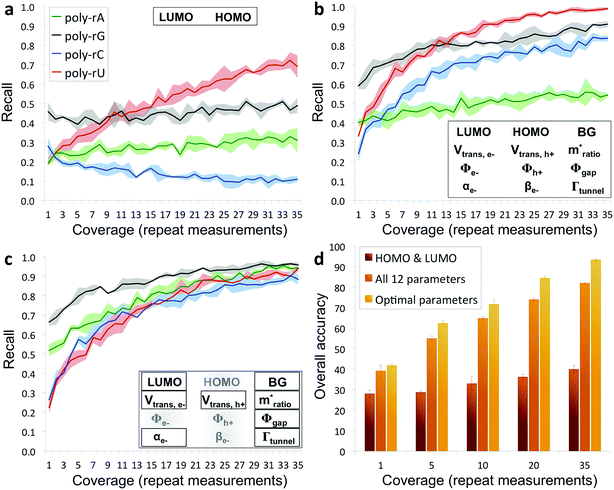Fig. 3 Recall and accuracy results from the RNA base-calling algorithm. (a) Correct recall vs. coverage for base calling with HOMO and LUMO as the only parameters used by the algorithm. (b) Correct recall vs. coverage for base calling with all 12 biophysical parameters. (c) Correct recall vs. coverage for base calling with optimized subsets of the parameters along with probability weighting coefficients. (d) Overall base-calling accuracy at selected coverage values with the algorithm using only HOMO and LUMO, using all 12 parameters, or using optimal parameter subsets (additional details in the ESI†).

Non-perturbative tunneling spectroscopy

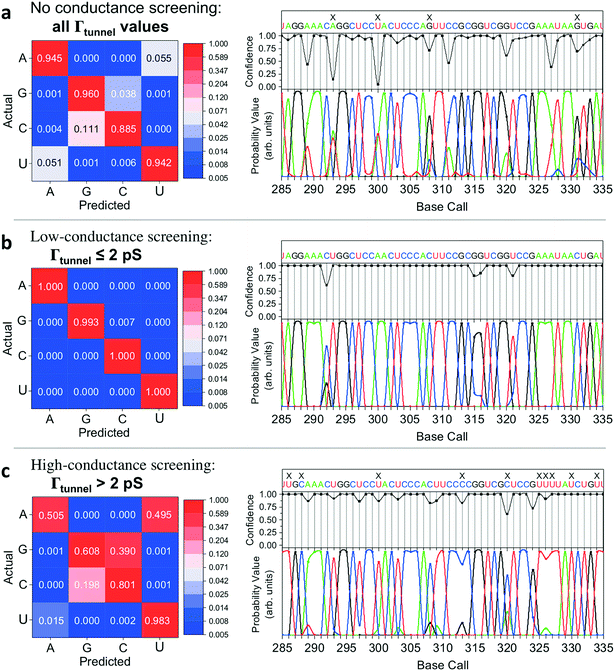
In implementing the base-calling algorithm described above, the tunneling conductance Γ_tunnel was simply included as a twelfth biophysical parameter. Going one step further, we sought to use Γ_tunnel as a metric for screening out measurements that were significantly perturbed by the tip and substrate in a way that hinders accurate base calling. To test whether Γ_tunnel can serve as a classifier for the extent of molecular smear in a given measurement, we next modified the algorithm to include a tunneling conductance screening step prior to any base calling. In this step, only measurements that fall within a specified range of Γ_tunnel values are passed to the base-calling algorithm. We hypothesized that STS measurements showing a low tunneling conductance would lead to better discrimination between ribonucleotides, given that such measurements presumably correspond to a lower degree of perturbation by the tip and substrate. In order to compare how the modified algorithm performs in the context of sequence identification, we generated a random ‘unknown’ sequence of bases, then pulled measurements from the library for each unknown ribonucleotide in the sequence and fed them into the base-calling algorithm to produce a predicted sequence. The predicted sequence was then compared to the actual sequence of the randomly produced unknown in order to generate a sequence trace plot and corresponding confusion matrix. Shown in Fig. 4a are the resulting confusion matrix and an example section of a trace plot from implementing the algorithm, using the optimal parameter sets but without any conductance screening, at 35X coverage (see Fig. S6–S8† for full trace plots). Note that although the accuracy is high, there are still several calls made with low confidence along with a number of errors in the predicted sequence (as marked by an ‘X’). To test the effect of the proposed conductance screening on base-calling accuracy, we next modified the algorithm to use only measurements for which Γ_tunnel was less than a threshold value of 2 pS (Fig. 4b). The results are striking—when applied to the same unknown sequence, the modified algorithm shows a dramatic increase in both accuracy and confidence. At 35X coverage, the overall accuracy increased from 93% without screening to over 99.8% with low-conductance screening. This is consistent with the hypothesis that the low-conductance measurements correspond to less perturbation by the tip and substrate, and are therefore more useful for base calling. As a further test of our hypothesis we reversed the selection criteria, using only high-conductance measurements for which Γ_tunnel was greater than the threshold value of 2 pS. While this may still aid somewhat in base calling by narrowing to a subset of spectra with similar Γ_tunnel values, the molecular smear is expected to be larger for these high-conductance measurements, which likely leads to greater overlap and more incorrect calls. Indeed, when applied to the same unknown sequence, the high-conductance screening algorithm shows significantly worse performance (Fig. 4c), with a drop in overall accuracy to 72% at 35X coverage. Interestingly, the high-conductance screening led to making base calls with both higher confidence and more frequent mistakes than the same algorithm with no screening. In other words, when using only high-conductance measurements the algorithm seems to be confusing the bases more easily. Taken together, these results support the idea that tunneling conductance can serve as an important metric for characterizing the extent of energy level smear in STS measurements, and thus can reduce the error rate in molecular identification from tunneling spectra. Combining this approach with improvements in surface engineering to minimize heterogeneity and reduce conformational entropy should further increase the ability to distinguish between similar molecular species via their electronic fingerprints. Fig. 5 shows a schematic diagram depicting an overview of the base-calling algorithm that we have presented here.

Fig. 4 Perturbation analysis and improved RNA base calling at 35X coverage. Confusion matrices (left) and selected sequencing trace plots (right) from applying the base-calling algorithm to identify a randomly generated ‘unknown’ sequence from STS measurements. The trace plots show the predicted sequence at the top, with an ‘X’ indicating incorrect base calls. The middle shows base-calling confidence at each position, with final probability values for each of the four bases shown at the bottom. (a) Results at 35X coverage from applying the algorithm without any conductance screening. (b) Results at 35X coverage from using a low-conductance screening filter, where only STS measurements with Γ_tunnel ≤ 2 pS were included. (c) Results at 35X coverage from using a high-conductance screening filter, where only STS measurements with Γ_tunnel > 2 pS were included.

Fig. 5 Schematic flow diagram depicting the modified QMSeq base-calling algorithm. First, a number of tunneling spectra are acquired over the molecule of interest. Next, the spectra pass through a conductance screening filter, which passes on only measurements for which Γ_tunnel falls within the specified range. Next, the full set of biophysical parameters are extracted from the spectra, which are then fed into a machine learning classification algorithm along with values from a spectral library. The resulting probabilities are then used to make a base call. Coverage is increased by feeding in additional spectra from the same molecule to improve the accuracy.

Structural label mapping

The capability of directly sequencing individual RNA molecules represents a new and powerful tool for single-cell transcriptomics. Going beyond sequencing, the possibility of probing the three-dimensional structure of RNA is arguably even more valuable, given the importance of RNA structure to its biological function. Since the QMSeq method described above relies on measurable differences in charge tunneling through molecular orbitals to discriminate between the bases, we hypothesized that we could use the same approach to detect shifts in the molecular orbital energy levels resulting from the site-specific and structure-dependent addition of chemical labels to the RNA molecules. Of the various chemical-labeling methods, SHAPE has proven to be both versatile and robust, allowing for parallel and high-throughput analysis of local flexibility at single-nucleotide resolution.³⁵ Thus we chose to adapt the SHAPE methodology for probing the structure of single RNA molecules. A schematic illustration of our proposed nanoelectronic method of RNA structural mapping is shown in Fig. 6a. As with SHAPE, the first step is to fold the RNA into its native structure, followed by selective acylation with N-methylisatoic anhydride (NMIA, Fig. 6b), a nucleophile that reacts with the ribose 2′-hydroxyl group of RNA in regions that exhibit sufficient conformational flexibility (i.e., are not constrained by base-pairing or secondary structure).¹⁰ NMIA treatment thus leads to selective labeling in unstructured, flexible regions of the molecule. In traditional SHAPE, this is followed by reverse transcription of the labeled RNA into cDNA (primer extension), during which the transcription is terminated at labeled sites, leading to a collection of truncated transcripts that can be analyzed by gel electrophoresis to generate a structural map of the molecule. The SHAPE method has since been extended for probing distinct structural subpopulations within an ensemble of RNA,³⁶ but due to the requirement of enzymatic amplification, it is still unable to directly detect the positions of all labeled regions within individual RNA molecules. In contrast, rather than relying on amplification, our method uses STS to directly identify the labeled nucleotides within each RNA molecule by detecting systematic shifts in the measured biophysical parameters that result from the modification of the sugar to form a 2′-O-adduct. Importantly, this opens up the possibility of creating full structural maps of individual RNA molecules.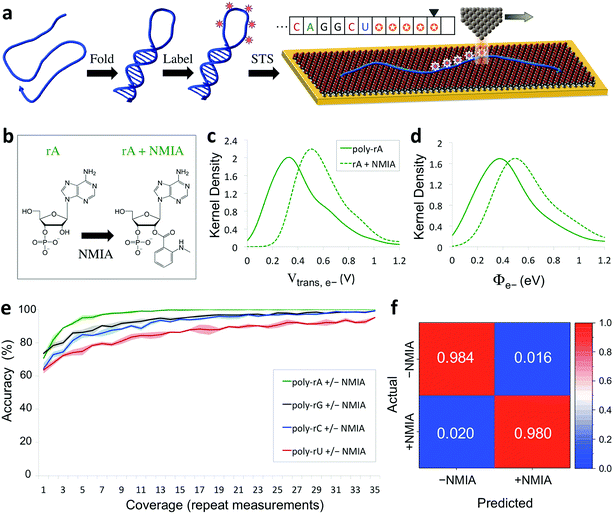

Fig. 6 Nanoelectronic identification of structure-dependent chemical labels in RNA. (a) Schematic illustration of the experimental approach used. An RNA molecule is first folded into its native structure, then undergoes a structure-dependent chemical labeling step before being adsorbed onto the MPA/Au substrate and measured with STS. (b) Chemical structure of an adenine ribonucleotide before and after selective acylation by NMIA. (c, d) Selected examples of kernel density plots for the V_trans(e⁻) and Φ_e⁻ parameters for poly-rA₇ RNA, both before (solid line) and after (dashed line) NMIA labeling. (Full results shown in Fig. S9–S12†). (e) Plot of the accuracy vs. coverage for NMIA identification for each of the four RNA bases. (f) Confusion matrix for discrimination between NMIA-labeled and unlabeled nucleotides without prior knowledge of the identity of each nucleobase.

Our proposed method of structurally mapping single RNA molecules relies on discrimination between labeled and unlabeled ribonucleotides via STS. To this end, we sought to detect and characterize changes in the charge tunneling properties of the four nucleobases resulting from modification of the adjacent ribose sugar. To do this, we collected a second spectral library consisting of STS measurements on short RNA homopolymers that had been fully labeled with NMIA. We used short molecules (7 nt), a high-temperature denaturation step (95 °C), and a large excess concentration of NMIA during labeling to ensure saturation of the unstructured molecules with the label. Selected examples of the results of our QMSeq measurements on labeled RNA are shown in Fig. 6c, d (full results in Fig. S9–S12†). Compared to the unlabeled RNA, the NMIA-labeled molecules display subtle shifts in several of the measured parameter distributions for all four bases, particularly for the electron-tunneling parameters V_trans(e⁻) and Φ_e⁻. This confirms that the ribose 2′-O-adduct does influence the molecular orbitals of the nucleobases to a measurable degree. To adapt our base-calling algorithm for distinguishing between labeled and unlabeled nucleotides, we reduced the number of classes in the algorithm from four (rA, rG, rC, rU) to two (rN ± NMIA), taking advantage of the fact that in structure studies the sequence is often known already, or else can be determined beforehand using the sequencing method described above. We then used the new library to re-optimize the parameter set for each base to give the best discrimination between labeled and unlabeled nucleotides.

The plots of correct recall vs. coverage for each of the four bases are shown in Fig. 6e. For label identification with only two classes the error rate is lower, with the overall accuracy reaching 85% after just 5X coverage, and exceeding 98% at 35X coverage, without using any conductance screening. This demonstrates that structure-dependent RNA modifications can also be identified via STS with high accuracy. Going further, we tested whether our algorithm could successfully discriminate between labeled and unlabeled nucleotides without any prior knowledge of the identity of the nucleobase, as would be necessary for simultaneous sequencing and structural mapping of molecules with an unknown sequence. In this case, we combined the data from all four nucleobases and broadly divided the data into two classes: labeled (+NMIA) and unlabeled (−NMIA). This data was then classified using the label identification algorithm without using any information about the nucleotide identity. The results shown in Fig. 6f demonstrate that even without knowledge of the RNA nucleobase sequence, we are still capable of identifying NMIA-labeled nucleotides with an accuracy of over 98% at 35X coverage. Thus each nucleotide position can be measured with STS and first classified as labeled or unlabeled, followed by sequence identification for unlabeled bases, simultaneously yielding a partial sequence and full structural label map (see Fig. 6a, inset). This structural map can then be aligned to the complete sequence of the molecule, which is either already known or can be determined by sequencing the unlabeled RNA molecules. These steps combined then fully characterize the sequence and structural labelling of single RNA molecules. Ultimately this structural labeling study serves as a demonstration of the ability to combine our proposed tunneling spectroscopy method with machine learning using biophysical parameters as molecular fingerprints in order to identify chemically labeled nucleotides for RNA structure determination.

Conclusion

We have presented a powerful new method for directly identifying individual ribonucleotides and local structural labels in single RNA molecules. Using the QMSeq technique, we have demonstrated the ability to discriminate between the four ribonucleotides within individual RNA molecules with an overall accuracy of >99.8% at relatively modest coverage (35X). Furthermore, we have shown that by probing the electronic states of the ribonucleotides we can identify the presence of chemical modifications of the sugar moiety. This will enable structural characterization of single RNA molecules using a combination of structure-dependent chemical labeling and tunneling spectroscopy measurements, in analogy with the widely successful SHAPE method.¹⁰ Importantly, this presents the possibility of simultaneous sequencing and structural mapping of individual RNA molecules, which will be an unprecedented tool in understanding the sequence–structure–function relationship for this centrally important biomolecule. We recognize that there are additional challenges when translating this method into a full sequencing approach, including the difficulty of correlating the extracted nucleotide information with the position of each measurement along an unknown molecule in order to derive the true sequence.³⁷ One promising solution is to carry out simultaneous STM imaging and STS mapping of the region containing the molecule, allowing the spectral grid to be mapped onto a high-resolution image of each segment of the molecule. Another challenge pertains to the speed of the proposed sequencing approach. Using a small voltage window (±1 V) and a fast sweep rate (∼200 V s⁻¹) allows for single-nucleotide measurement times of ∼0.5 s (30 sweeps per measurement), with an estimated sequencing speed of ∼8 min kb⁻¹ when using a single tip. However this speed could be dramatically improved by using an array of tips scanning a much larger area in parallel.³⁸ We also expect this approach to be more broadly applicable to other biologically relevant chemical alterations of nucleotides, including epigenetic modifications and oxidative damage. We anticipate that our new single-molecule characterization platform could help to address some of the more challenging problems in transcriptomics, including deconvoluting cellular heterogeneity, mapping developmental trajectories, and understanding the role of stochasticity in transcriptional mechanics.³⁹

Experimental methods

RNA handling

Precautions were taken to minimize enzymatic degradation of the RNA. All solutions coming into contact with RNA were prepared with ultrapure deionized (DI) water (Barnstead Thermolyne NANOpure Diamond purification system, water resistivity > 18 MΩ cm). Prior to handling RNA, the workbench, gloves, pipets and other surfaces were cleaned with RNaseZAP™ RNase inhibitor solution (Ambion, Inc, USA). RNA solutions were stored long-term at −80 °C and short-term at −20 °C in small aliquots, and were thawed on ice immediately before use.

NMIA labeling of RNA

RNA labeling was carried out following a procedure adapted from the originally published SHAPE protocol.¹¹ RNA (50 pmol) was diluted in 40 μL of 0.5X TAE buffer (1X TAE = 40 mM Tris acetate, 1 mM ethylenediaminetetraacetic acid, pH ∼ 8.3) in a 200 μL PCR tube. The RNA solution was heated to 95 °C for 2 min to fully denature any secondary structure, then immediately placed on ice. Next 5 μL of 10X TAE buffer was added, followed by 5 μL of 10X NMIA solution (100 mM in DMSO, freshly prepared), to give final concentrations of 1 μM RNA, 10 mM NMIA, and 1.4X TAE. The solution was heated to 37 °C for 45 min (or roughly five NMIA hydrolysis half-lives), then cooled to 4 °C and immediately purified using a QIAquick Nucleotide Removal Kit (QIAGEN, Germany).

Substrate preparation

Measurements were carried out on the (111) facet of a single-crystal Au substrate. The substrate was cleaned by rinsing and brief sonication in acetone and methanol and rinsing with ultrapure DI water (resistivity > 18 MΩ cm), followed by immersion in hot nitric acid for 10–15 min. Then, it was rinsed thoroughly with ultrapure water, blown dry, and briefly annealed under a hydrogen flame. After cooling under a stream of nitrogen gas, the substrate was immersed into a freshly prepared ethanolic solution of 3-mercaptopropionic acid (MPA, 1 mM) containing 3% v/v acetic acid. The container was backfilled with N₂ gas, sealed with Parafilm, and kept in the dark at room temperature to minimize thiol oxidation. After overnight monolayer assembly (typically 16–20 h), the sample was removed from the solution, briefly sonicated in ethanol (10 s), rinsed with ethanol, and blown dry.

RNA adsorption

The MPA/Au substrate was exposed to an aqueous solution containing the RNA oligonucleotides (1.0–100 nM) along with 5 mM Ni(II) acetate for an adsorption time t_ads of 1–5 min. The solution was then removed and the sample was blown dry and immediately transferred to the STM vacuum chamber. The initial high surface-coverage experiments on unmodified RNA used 100 nM RNA and t_ads = 5 min, while the low surface-coverage experiments on RNA ± NMIA used 1.0 nM RNA and t_ads = 1 min.

STM

Imaging and spectroscopy were carried out on an R9 model STM (RHK Technologies, USA), operating in constant current mode under ultra-high vacuum (UHV, ∼8 × 10⁻¹⁰ Torr) at room temperature (∼294 K). STM probes were made in-house by carefully cutting a short length of platinum-iridium wire to mechanically form a sharp tip. Tip sharpness was verified by imaging the characteristic herringbone reconstruction on a clean Au (111) substrate (see Fig. S1a†). Imaging was performed at a bias of −500 mV with a current setpoint of 100–200 pA. The high-resolution image in Fig. 1e was obtained at low temperature (12 K) using a bias of 1.5 V with a current setpoint of 200 pA.

Tunneling spectroscopy

STS measurements were collected pointwise on 64 × 64 or 128 × 128 grids across different areas of the sample, with a grid point spacing of at least 1.25 nm. During the measurement, the STM tip was moved sequentially to each grid point under constant-current feedback. Then after a stabilization delay of 200 ms, the feedback was switched off and the bias voltage was swept from −3.0 V to + 3.0 V at a rate of 120 V s⁻¹ while monitoring the current. Each I/V spectrum consists of 301 data points with a resolution of 20 mV.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

The authors acknowledge funding for this work from W. M. Keck Foundation, and partial support through National Science Foundation Soft Materials MRSEC at the University of Colorado through NSF Award DMR 1420736. L. E. K. and P.·B.·O. acknowledge financial support from National Science Foundation Graduate Research Fellowship Program under Grant No. DGE 1144083.

References

1. E. J. Strobel, K. E. Watters, D. Loughrey and J. B. Lucks, Curr. Opin. Biotechnol., 2016, 39, 182–191.
2. X. Adiconis, D. Borges-Rivera, R. Satija, D. S. DeLuca, M. A. Busby, A. M. Berlin, A. Sivachenko, D. A. Thompson, A. Wysoker and T. Fennell, Nat. Methods, 2013, 10, 623–629.
3. A. K. Shalek, R. Satija, J. Shuga, J. J. Trombetta, D. Gennert, D. Lu, P. Chen, R. S. Gertner, J. T. Gaublomme and N. Yosef, Nature, 2014, 510, 363.
4. A. A. Kolodziejczyk, J. K. Kim, V. Svensson, J. C. Marioni and S. A. Teichmann, Mol. Cell, 2015, 58, 610–620.
5. S. A. Mortimer, M. A. Kidwell and J. A. Doudna, Nat. Rev. Genet., 2014, 15, 469–479.
6. Z. Miao and E. Westhof, Annu. Rev. Biophys., 2017, 46, 483–503.
7. F. E. Reyes, A. D. Garst and R. T. Batey, Methods Enzymol., 2009, 469, 119–139.
8. B. Fürtig, C. Richter, J. Wöhnert and H. Schwalbe, ChemBioChem, 2003, 4, 936–962.
9. K. M. Weeks, Curr. Opin. Struct. Biol., 2010, 20, 295–304.
10. E. J. Merino, K. A. Wilkinson, J. L. Coughlan and K. M. Weeks, J. Am. Chem. Soc., 2005, 127, 4223–4231.
11. K. A. Wilkinson, E. J. Merino and K. M. Weeks, Nat. Protoc., 2006, 1, 1610–1616.
12. K. M. Kutchko and A. Laederach, Wiley Interdiscip. Rev.: RNA, 2017, 8, e1374.
13. J. M. Watts, K. K. Dang, R. J. Gorelick, C. W. Leonard, J. W. Bess Jr, R. Swanstrom, C. L. Burch and K. M. Weeks, Nature, 2009, 460, 711–716.
14. J. C. Ribot, A. Chatterjee and P. Nagpal, J. Phys. Chem. B, 2015, 119, 4968–4974.
15. L. E. Korshoj, S. Afsari, S. Khan, A. Chatterjee and P. Nagpal, Small, 2017, 13, 1603033.
16. M. Di Ventra and M. Taniguchi, Nat. Nanotechnol., 2016, 11, 117.
17. J. Lagerqvist, M. Zwolak and M. Di Ventra, Nano Lett., 2006, 6, 779–782.
18. D. Branton, D. W. Deamer, A. Marziali, H. Bayley, S. A. Benner, T. Butler, M. Di Ventra, S. Garaj, A. Hibbs and X. Huang, Nat. Biotechnol., 2008, 26, 1146.
19. M. Krems, M. Zwolak, Y. V. Pershin and M. Di Ventra, Biophys. J., 2009, 97, 1990–1996.
20. E. Shapir, H. Cohen, A. Calzolari, C. Cavazzoni, D. A. Ryndyk, G. Cuniberti, A. Kotlyar, R. Di Felice and D. Porath, Nat. Mater., 2008, 7, 68.
21. S. Huang, J. He, S. Chang, P. Zhang, F. Liang, S. Li, M. Tuchband, A. Fuhrmann, R. Ros and S. Lindsay, Nat. Nanotechnol., 2010, 5, 868.
22. T. Ahmed, S. Kilina, T. Das, J. T. Haraldsen, J. J. Rehr and A. V. Balatsky, Nano Lett., 2012, 12, 927–931.
23. T. Sawaguchi, Y. Sato and F. Mizutani, Phys. Chem. Chem. Phys., 2001, 3, 3399–3404.
24. H. G. Hansma and D. E. Laney, Biophys. J., 1996, 70, 1933–1939.
25. G. R. Abel Jr, E. A. Josephs, N. Luong and T. Ye, J. Am. Chem. Soc., 2013, 135, 6399–6402.
26. R. H. Fowler and L. Nordheim, Electron emission in intense electric fields, The Royal Society, 1928.
27. J. M. Beebe, B. Kim, J. W. Gadzuk, C. D. Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801.
28. Y. Yoshida, Y. Nojima, H. Tanaka and T. Kawai, J. Vac. Sci. Technol., B: Microelectron. Nanometer Struct.--Process., Meas., Phenom., 2007, 25, 242–246.
29. L. E. Korshoj, S. Afsari, A. Chatterjee and P. Nagpal, J. Am. Chem. Soc., 2017, 139, 15420.
30. Z. J. Donhauser, B. A. Mantooth, K. F. Kelly, L. A. Bumm, J. D. Monnell, J. J. Stapleton, D. W. Price Jr, A. M. Rawlett, D. L. Allara, J. M. Tour and P. S. Weiss, Science, 2001, 292, 2303–2307.
31. L. Venkataraman, J. E. Klare, C. Nuckolls, M. S. Hybertsen and M. L. Steigerwald, Nature, 2006, 442, 904–907.
32. X. Li, J. He, J. Hihath, B. Xu, S. M. Lindsay and N. Tao, J. Am. Chem. Soc., 2006, 128, 2135–2141.
33. C. Li, I. Pobelov, T. Wandlowski, A. Bagrets, A. Arnold and F. Evers, J. Am. Chem. Soc., 2008, 130, 318–326.
34. S. M. Sze and K. K. Ng, Physics of semiconductor devices, John Wiley & Sons, 2006.
35. S. A. Mortimer and K. M. Weeks, Nat. Protoc., 2009, 4, 1413–1421.
36. P. J. Homan, O. V. Favorov, C. A. Lavender, O. Kursun, X. Ge, S. Busan, N. V. Dokholyan and K. M. Weeks, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 13858–13863.
37. H. Tanaka and T. Kawai, Nat. Nanotechnol., 2009, 4, 518.
38. S. Hasegawa, in Scanning Probe Microscopy, ed. S. Kalinin and A. Gruverman, Springer, 2007, pp. 480–505.
39. S. Liu and C. Trapnell, F1000Research, 2016, 5, 182.
40. M. Petri, D. M. Kolb, U. Memmert and H. Meyer, Electrochim. Acta, 2003, 49, 175–182.

---

Footnote

† Electronic supplementary information (ESI) available: Details of the base-calling algorithm and additional figures as described in the text. See DOI: 10.1039/c8sc03354d

---