Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Do water's electrons care about electrolytes?†
Marvin N.
Pohl
 ab,
Eva
Muchová
ab,
Eva
Muchová
 c,
Robert
Seidel
c,
Robert
Seidel
 de,
Hebatallah
Ali
de,
Hebatallah
Ali
 ab,
Štěpán
Sršeň
ab,
Štěpán
Sršeň
 c,
Iain
Wilkinson
*d,
Bernd
Winter
c,
Iain
Wilkinson
*d,
Bernd
Winter
 *a and
Petr
Slavíček
*a and
Petr
Slavíček
 *c
*c
aFritz-Haber-Institut der Max-Planck-Gesellschaft, Faradayweg 4-6, D-14195 Berlin, Germany. E-mail: winter@fhi-berlin.mpg.de
bFachbereich Physik, Freie Universität Berlin, Arnimallee 14, D-14195 Berlin, Germany
cDepartment of Physical Chemistry, University of Chemistry and Technology, Technická 5, 16628 Prague, Czech Republic. E-mail: petr.slavicek@vscht.cz
dHelmholtz-Zentrum Berlin für Materialien und Energie, Hahn-Meitner-Platz 1, D-14109 Berlin, Germany. E-mail: iain.wilkinson@helmholtz-berlin.de
eHumboldt-Universität zu Berlin, Department of Chemistry, Brook-Taylor-Str. 2, D-12489 Berlin, Germany
First published on 1st November 2018
Abstract
Ions have a profound effect on the geometrical structure of liquid water and an aqueous environment is known to change the electronic structure of ions. Here we combine photoelectron spectroscopy measurements from liquid microjets with molecular dynamical and quantum chemical calculations to address the reverse question, to what extent do ions affect the electronic structure of liquid water? We study aqueous solutions of sodium iodide (NaI) over a wide concentration range, from nearly pure water to 8 M solutions, recording spectra in the 5 to 60 eV binding energy range to include all water valence and the solute Na+ 2p, I− 4d, and I− 5p orbital ionization peaks. We observe that the electron binding energies of the solute ions change only slightly as a function of electrolyte concentration, less than 150 ± 60 meV over an ∼8 M range. Furthermore, the photoelectron spectrum of liquid water is surprisingly mildly affected as we transform the sample from a dilute aqueous salt solution to a viscous, crystalline-like phase. The most noticeable spectral changes are a negative binding energy shift of the water 1b2 ionizing transition (up to −370 ± 60 meV) and a narrowing of the flat-top shape water 3a1 ionization feature (up to 450 ± 90 meV). A novel computationally efficient technique is introduced to calculate liquid-state photoemission spectra using small clusters from molecular dynamics (MD) simulations embedded in dielectric continuum. This theoretical treatment captured the characteristic positions and structures of the aqueous photoemission peaks, reproducing the experimentally observed narrowing of the water 3a1 feature and weak sensitivity of the water binding energies to electrolyte concentration. The calculations allowed us to attribute the small binding energy shifts to ion-induced disruptions of intermolecular electronic interactions. Furthermore, they demonstrate the importance of considering concentration-dependent screening lengths for a correct description of the electronic structure of solvated systems. Accounting for electronic screening, the calculations highlight the minimal effect of electrolyte concentration on the 1b1 binding energy reference, in accord with the experiments. This leads us to a key finding that the isolated, lowest-binding-energy, 1b1, photoemission feature of liquid water is a robust energetic reference for aqueous liquid microjet photoemission studies.
1. Introduction
More than a hundred years ago, Arrhenius, Ostwald, and van't Hoff revolutionized chemistry by establishing the ionic theory of electrolytes.1 Yet, the molecular understanding of ion–solvent interactions still exhibits surprising gaps.2 Even the geometric structure of liquid water itself remains a subject of ongoing controversy, with conflicting views emerging from different experimental and theoretical approaches.3–11 Still less is known about electrolyte solutions.12–14In the present work, we focus on the effects of dissolved atomic ions, particularly Na+ and I−, at high concentration on the electronic structure of liquid water. The electrolytes are expected to induce significant electrostatic effects and disruptions of hydrogen bonding networks, especially for highly concentrated solutions.11,15–17 The iodide anion has been found to have an exceptional influence on the extended hydrogen bond (HB) network due to its large polarizability, allowing charge to be delocalized to water molecules.18 Further understanding of the associated effects on the electronic structure of water are important from a fundamental perspective as well as for applications. For instance, from a practical standpoint, highly concentrated electrolyte solutions extend the water electrochemical window from 1.5 eV to 3.0 eV, prompting recent suggestions to apply such solutions in a variety of safe and environmentally friendly devices, such as aqueous-solution based batteries.19–21 Also, the (anomalous) increase in screening length that follows the classical decrease of the Debye screening length in dilute electrolytes is of substantial relevance to chemistry, biology, and energy storage.22–24 Furthermore, as aqueous phase photoelectron (PE) spectroscopy measurements are often performed at relatively high solute concentrations and energy-referenced to the binding energies of liquid water, such screening effects are of great importance to the interpretation of liquid-phase PE spectroscopy measurements, as will be shown in the following text.
The ground-state electronic wave function of isolated water is dominated by a (1a1)2(2a1)2(1b2)2(3a1)2(1b1)2 electronic configuration (adopting a C2v representation). Within this description, the highest-energy electrons are associated with the 1b1 orbital, which is essentially an oxygen p orbital with a nodal plane coinciding with the molecular plane. The lower-lying non-bonding 3a1 orbital is again of the oxygen p-orbital type. The 1b2 electrons dominantly contribute to the O–H bonds while the inner-valence 2a1 orbital has prevailing oxygen 2s orbital parentage. The electrons of isolated, gas-phase water molecules are relatively tightly bound, with the first binding energy (BE) of the neutral molecule occurring at 12.6 eV (![[X with combining tilde]](https://www.rsc.org/images/entities/char_0058_0303.gif) 2A1, (1b1)−1), and higher vertical valence BEs occurring at 14.8 eV (Ã2A1, (3a1)−1), 18.6 eV (
2A1, (1b1)−1), and higher vertical valence BEs occurring at 14.8 eV (Ã2A1, (3a1)−1), 18.6 eV (![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) 2B2, (1b2)−1) and 32.6 eV (
2B2, (1b2)−1) and 32.6 eV (![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) 2A1 (2a1)−1).25–29 The electron BEs are shifted by approximately 1.2–1.4 eV to lower values in liquid water, with water-cluster BEs bridging these energetic shifts.30–32 The distribution of electron BEs is broader in liquid water than for isolated gas-phase molecules due to the continuum of hydration configurations that can be adopted in liquid water at ambient temperatures. However, we cannot interpret the liquid water photoemission spectrum as a shifted and broadened spectrum of the monomer – the intermolecular interactions do measurably alter the electronic structure of the water molecule. These interactions may be conceptually described by considering individual water molecules as “superatomic orbitals”, interacting via the bonding and antibonding interactions of their frontier molecular orbitals (1b1, 3a1, 1b2, 2a1 – the ‘superatomic orbitals’). This effect is highlighted by the splitting of the 3a1 peak of the monomer to form a doublet peak structure in liquid water that cannot be fit with a single Gaussian peak (for such valence features, a Gaussian line shape is commonly adopted as the spectral intensity profiles primarily reflect environmental inhomogeneous and instrumental resolution limit broadening terms33–35). The observed unusual spectral shape arises from intermolecular orbital interactions, predominantly 3a1–3a1 interactions between neighboring molecules.34–36 This peak splitting is known to be less pronounced than for crystalline ice, with the differences in the ice and liquid water spectra interpreted as a consequence of the varying local geometries in the disordered structure of liquid water.34
2A1 (2a1)−1).25–29 The electron BEs are shifted by approximately 1.2–1.4 eV to lower values in liquid water, with water-cluster BEs bridging these energetic shifts.30–32 The distribution of electron BEs is broader in liquid water than for isolated gas-phase molecules due to the continuum of hydration configurations that can be adopted in liquid water at ambient temperatures. However, we cannot interpret the liquid water photoemission spectrum as a shifted and broadened spectrum of the monomer – the intermolecular interactions do measurably alter the electronic structure of the water molecule. These interactions may be conceptually described by considering individual water molecules as “superatomic orbitals”, interacting via the bonding and antibonding interactions of their frontier molecular orbitals (1b1, 3a1, 1b2, 2a1 – the ‘superatomic orbitals’). This effect is highlighted by the splitting of the 3a1 peak of the monomer to form a doublet peak structure in liquid water that cannot be fit with a single Gaussian peak (for such valence features, a Gaussian line shape is commonly adopted as the spectral intensity profiles primarily reflect environmental inhomogeneous and instrumental resolution limit broadening terms33–35). The observed unusual spectral shape arises from intermolecular orbital interactions, predominantly 3a1–3a1 interactions between neighboring molecules.34–36 This peak splitting is known to be less pronounced than for crystalline ice, with the differences in the ice and liquid water spectra interpreted as a consequence of the varying local geometries in the disordered structure of liquid water.34
Analogous to intermolecular bonding interactions in liquid water, electrolyte species may have a profound effect on the electronic structure of liquid water. Indeed, at high concentrations, the effect of ions may be stronger than the electrostatic effects of the water molecular dipoles. Moreover, such ionic effects might be specific as different ions have a propensity to adopt different proximities to individual water molecules.11 It is noted that the effects of ions on nearby water molecules are considerably greater for gaseous species when compared to liquid water, the latter exhibiting a surprising screening ability that has been demonstrated for various organic and inorganic solutes.37 For example, BEs obtained from PE spectroscopy measurements of solvated nucleic acid bases, nucleosides, and nucleotides are almost identical, in contrast to the BEs of the gas phase or micro-hydrated molecules.38–41 Na+ counterions have been shown to have a minor effect on BEs of multiply charged anions, in contrast to the strong effect of protonation of these anionic species.42 In addition to the dielectric screening effect of the solvent, the electrostatic attenuation brought about by the ions (i.e., Debye–Hückel screening43) must be also explicitly considered. Such screening abilities will depend on the electrolyte concentration; an effect that is poorly explored for extremely high concentrations. Considering all the above-mentioned aspects, it is by no means clear to what extent water's electronic structure can be tuned by electrolyte addition.
Experimentally, the electronic structure of liquid water can be accessed by various means,13,44–49 with several types of X-ray emission spectroscopies and PE spectroscopy being the most powerful techniques.9,44,50–53 However, the energy-dispersive PE spectroscopy requirement of a vacuum environment is not readily met with highly volatile samples such as aqueous solutions. Hence, early PE spectroscopy measurements were only possible from highly concentrated aqueous salt solutions, where the electrolyte induced a significant reduction of the water vapor pressure.54–56 Later, using total electron yield measurements which did not require a vacuum environment or energy-dispersive detection, the (lowest) ionization onsets of several aqueous solutions were determined.57–59 Because the electron mean free path in water and aqueous solutions is on the order of just a few molecular layers (it has not been determined quantitatively yet60), the application of energy-dispersive PE spectroscopy to an aqueous solution required the development of concepts that increase the electron travel length through the water vapor. The first development of this kind was the liquid microjet technique,51,61 where one exploits the fact that the vapor pressure of the solution rapidly decreases with distance from a liquid jet. When the sample jet has a micrometer-scale diameter, the electrons emitted from the liquid phase can reach a differentially pumped electron detection chamber unperturbed at an increased transfer length of ∼1 mm under typical experimental conditions. Another way to increase the electron transfer length is via so-called ambient-pressure PE spectroscopy, where the lower gas-phase pressure results from efficient differential pumping in the vicinity of the irradiated sample.62–64 With these experimental developments, valence- and core-electron BEs, as well as energies of second-order electrons, have been measured for more than a decade.33,65 Thus far, absolute energy scale probes of the valence electronic structure of aqueous samples have almost exclusively relied on the liquid microjet technique. Associated valence PE spectroscopy data has recently been reviewed along with recent advances in related theoretical modeling approaches.60 However, despite the rapid development of the liquid-jet valence PE spectroscopy technique over the last decade and its application to a wide range of solutions, there is a crucial but almost neglected detail regarding the accuracy of the reported valence electron BEs from aqueous solutions.
In all studies, an assumption was made that the BE of a solute species can be obtained with reference to the peak of the lowest BE feature (1b1, 11.16 ± 0.04 eV BE (ref. 33); a value of 11.31 eV has been reported in a later study66 but this has no effect on the present work, as further detailed below) of the liquid water PE spectrum. The reason to continue to adopt this assumption is not ignorance, but rather a reflection of several experimental peculiarities of liquid-jet PE spectroscopy. Since the first liquid jet PE spectroscopy measurements51,61 it was known that a neat liquid water jet will be almost inevitably charged;67 some of the underlying contributions to such charging have been discussed.66,68,69 Distinction and quantification of the different charging contributions and their effects on PE spectra is currently beyond our experimental capabilities and awaits dedicated liquid-jet designs. We note that small amounts of electrolyte are generally added to aqueous samples to mitigate such charging effects, and any uncompensated charge would lead to an energetic shift of the whole PE spectrum; the residual effect being equivalent to applying a small voltage to a (conductive) crystalline sample. A notable remaining point is that in the majority of liquid-jet PE spectroscopy instruments, the electric field that exists between a charged liquid jet and the grounded electron detector is ill-defined. A well-known consequence of this effect is that the peak position of the gas-phase water 1b1, or any other gas-phase ionizing transition, depends on the given experimental setup, and hence is generally an inappropriate reference for assigning liquid-phase binding energies. This is another issue that was addressed in the early liquid jet PE studies.
In the present work we analyze valence PE spectra of aqueous NaI solutions (ranging from very low to very high concentrations), and we identify and quantify specific (small) differential changes of the electronic structure of liquid water, as opposed to constant (charge-induced) energy shifts of the entire spectrum; see ref. 67. We contrast this goal with a more common objective to interrogate how water affects the electronic structure of solute species, which is typically discussed with reference to gas-phase BEs of the respective solute molecules.33 Furthermore, we critically assess the common procedure of energetically referencing aqueous-phase PE spectra by aligning the water 1b1 peak to the 11.16 eV BE value for neat liquid water. The observed small but experimentally measurable changes of the water electronic structure are interpreted with ab initio and molecular dynamics (MD) simulations, and we discuss the implications for dielectric screening at large electrolyte concentrations. We emphasize that the present study is not designed to verify the accuracy of the value of the water 1b1 BE (11.16 ± 0.04 eV).70 The actual value of this reference energy is rather irrelevant here as we explore to what extent the energies of other water orbitals as well as the solute orbitals may change with respect to water's lowest ionization energy.
2. Experimental approach: photoemission spectroscopy
PE spectra from 0.05 M, 0.5 M, 1.0 M, 2.5 M, 3.0 M, 4.0 M, 5.0 M, 6.0 M, 7.0 M and 8.0 M NaI aqueous solutions were measured from a ∼24 μm diameter vacuum liquid–water jet. Solutions were prepared by dissolving NaI of ≥99% purity (Sigma-Aldrich, #793558) in highly demineralized water (conductivity ∼0.2 μS cm−1). The jet velocity was approximately 80 m s−1, and the jet temperature was 8 °C. The main reason for using an iodide salt here is that unlike for all other halide ions in water, the lowest electron detachment peak (I− 5p) is well separated from water's lowest ionization energy peak (1b1).60 Furthermore, in X-ray absorption spectroscopy measurements, of all of the halide anions, iodide has been observed to have the largest effect on the electronic structure of liquid water.18 Ionization photon energies of 180 eV/198 eV were applied in relatively surface-sensitive experiments; in this case the inelastic mean free path (IMFP) of the photoelectrons (approximately 169 eV/187 eV respective kinetic energies for water 1b1 ionization) is approximately 1 nm, as defined at the 1/e level.60,71 Two different photon energies were used in several experimental runs, and even at different beamlines, over the course of one year. In order to probe deeper into the solutions and to ensure any observed BE shifts were not due to interfacial effects we used 650 eV photons, corresponding to an approximately 5 nm IMFP.60 With this procedure we were able to observe changes in the water valence band BEs when increasing the NaI concentration. The measurements at 198 eV and 650 eV photon energies were conducted at the U49/2 PGM1 undulator beamline of BESSY II at the Helmholtz-Zentrum Berlin. Spectra at 180 eV incident photon energy were measured during the first measurement period at the U41 PGM undulator beamline of BESSY II. In all experiments electrons were detected with a hemispherical electron-energy analyzer at normal angle with respect to the polarization direction of the linearly polarized incident light. A small X-ray focal size, 80 × 22 μm2, at the U49 beamline (23 × 12 μm2 at the U41), ensured that the gas-phase signal amounted to less than 10% of the total (photo)electron signal during all measurements. The liquid jet was placed at a ∼500 μm distance from the analyzer entrance orifice (500 μm diameter).The energy resolution of both beamlines was better than 340 meV for 650 eV photon energies, and better than 60 meV for 198 eV energies. For the 180 eV photon energy, the resolution of the U41 beamline was better than 20 meV. The resolution of the electron analyzer was constant with kinetic energy (about 20 meV, at 20 eV pass energy). However, from fitting analyses of the 3a1, 1b2, and 1b1 PE peaks in multiple data sets, we conclude that water peak positions and widths can generally be determined with ±40–60 meV uncertainties in both our ∼200 eV and 650 eV photon energy data sets. Similar uncertainties are obtained for the more intense and spectrally separated solute peaks (Na+ 2p and I− 4d). In situations where solute peaks overlap with other features (I− 5p and 5s peaks) and solute concentrations are relatively low, our BE determination uncertainties are dominated by fitting errors in the range of ± 0.04–0.40 eV. This will be shown below in Table 2 when we present the experimental data.
3. Simulation protocol: IEDC with Mulliken projection
We studied the effects of ions on the liquid water PE spectra with small cluster models (water heptamers) embedded in a dielectric continuum. To account for the structural variations encountered in solutions, we extracted cluster geometric configurations from molecular dynamics simulations for neat water and 3 M and 8 M NaI solutions. The clusters were extracted as follows: we randomly selected one water molecule and found the closest six water molecules and the closest sodium and iodide ions. For neat water clusters, we simply extracted a central water molecule and six closest neighbors. In total we selected 500 structures for each concentration. We also performed calculations of idealized water pentamers in which the central water molecule is perfectly tetrahedrally solvated (similarly to a previous study72), results are provided in the ESI section.†The MD simulations were performed using the GROMACS 4.6.7 package73 with a non-polarizable force field where water was represented by the SPC/E model.74 The parameters for the ions73 are summarized in Table 1. The simulation box contained (i) 2240 water molecules in a 3.29177 × 3.29177 × 6.19806 nm3 box for the neat water simulations, (ii) 2496 water molecules, 155 iodide ions, and 155 sodium ions in a 3.47095 × 3.47095 × 7.14514 nm3 box for the 3 M simulations, and (iii) 1540 water molecules, 350 iodide ions, and 350 sodium ions in 3.36427 × 3.36427 × 6.43305 nm3 box for the 8 M simulations. The total length of the simulation was 10 ns, the time step for the propagation was set to 1 fs, and 3D periodic boundary conditions were employed. All simulations were performed under a constant pressure of 1 bar which was controlled by the Parrinello–Rahman barostat75 with a coupling constant of 1 ps and a constant temperature of 300 K which was controlled by the Nosé–Hoover thermostat76,77 with a coupling constant of 1 ps. Constraints were applied to all bonds via the Lincs algorithm of fourth order.78 The van der Waals interactions were truncated at 1.2 nm; the long-range electrostatic interactions were calculated by the particle mesh Ewald method.79 The local structure of the solutions is described via the tetrahedral order parameter, q.80 The parameter focuses on the four closest neighbors of the water oxygen atoms and is sensitive only to angular order. The average value of q varies between 0 for an ideal gas to 1 for an ideal tetrahedral arrangement. The parameter describing the variance of distances between a central water molecule and its closest neighbors is the translational tetrahedral order parameter, Sk, defined in ref. 81. Sk is 0 for an ideal tetrahedron; if the configuration deviates from ideal tetrahedrality, Sk increases and reaches a maximum value of 1 for an ideal gas.
| R min/2 [Å] | ε [kcal mol−1] | |
|---|---|---|
| I− | 2.919 | 0.0427845 |
| Na+ | 1.212 | 0.3526418 |
The BEs for all clusters were calculated with a recently introduced ionization-as-an-excitation-into-a-distant-center (IEDC) approach.83 Briefly, the method is based on modelling the ionization from a selected orbital space as an excitation into a continuum using time-dependent density functional (TDDFT) theory. As DFT is in principle an exact many-body theory, we can obtain correlated orbital energies.84 In all calculations the long-range corrected Perdew–Burke–Ernzerhof functional (LC-ωPBE)85 was employed with the range-separation parameter, ω, set to 0.45 a0−1, which was optimized for the water clusters.31
We specifically focus on the electronic structure of the fully solvated central water unit. For this purpose we employ the Mulliken-type population analysis86 to evaluate the fraction of the selected moiety, fFr, contributing to each of the orbitals:
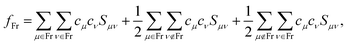 | (1) |
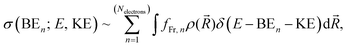 | (2) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) ) is the nuclear density evaluated with the classical MD simulations, BEn is the binding energy of the ejected electron, KE is the kinetic energy of an ejected electron, E is the incident photon energy, and fFr,n is the contribution from the n-th electron of the fragment of interest. In the modelled photoemission spectra we included solvent spectral broadening via the reflection principle with an additional broadening scheme (RP-AB),89i.e., each point is broadened with a Gaussian function with a variance reflecting the reorganization energy calculated by means of dielectric continuum methods.
) is the nuclear density evaluated with the classical MD simulations, BEn is the binding energy of the ejected electron, KE is the kinetic energy of an ejected electron, E is the incident photon energy, and fFr,n is the contribution from the n-th electron of the fragment of interest. In the modelled photoemission spectra we included solvent spectral broadening via the reflection principle with an additional broadening scheme (RP-AB),89i.e., each point is broadened with a Gaussian function with a variance reflecting the reorganization energy calculated by means of dielectric continuum methods.
As the models used are of a rather limited size, we account for the remaining water molecules via the dielectric continuum model represented by a conductor-like polarizable continuum (C-PCM).90–92 We use the non-equilibrium model of solvation (NEPCM) for the ionized states, i.e., only the fast part of the dielectric constant of water (the “optical” dielectric constant is 1.78) follows ionization while the slow part remains unchanged as in the ground state.93–95 We employed the state specific (SS) scheme as implemented in the Q-Chem 4.1 code.96 We note here that inclusion of the solvation effects in the ionization potential theorem is non-trivial. The embedding of the non-equilibrium response of the solvent to the Kohn–Sham orbital energies has been a subject of a debate, so far attempts were made mainly in different directions.97,98 The IEDC approach is fully consistent in this respect.83
The use of a dielectric continuum model parameterized for water should be further discussed. Indeed, the screening ability of electrolyte solutions is different from that of water.99–102 Since the electrolyte solutions are conductive, the use of the concept of dielectric screening cannot be fully justified. However, a frequency-dependent permittivity constant is still defined. The low frequency limit of the real part yields the static permittivity (dielectric constant, εr) and its value for a wide range of salts decreases as the electrolyte concentration is increased; a phenomenon called a dielectric decrement. The phenomenon is attributed to excluded volume effects and to the formation of hydration shells around ions and ion pairs (ion dipoles) which prevents orientation of these water molecules in the external electric field. The dielectric properties of electrolytes are still a subject of independent research, far beyond the scope of the present work. In our work we adopted a pragmatic approach, correcting the permittivity for concentrated solutions according to experimental and model data for NaCl (data for NaI are not available in the investigated concentration range103,104) that were extrapolated to high concentrations.105,106 The permittivity for an 8 M solution has to be taken as approximate. The 3 M and 8 M solution permittivity was set to, εr = 46 and εr = 22, respectively, compared to εr = 78.39 for pure water. The optical dielectric constant, εopt, was set according to the dependence of the refractive index on salt concentration107 to 1.78 for pure water, 1.86 for the 3 M solution, and 2.01 for the 8 M solution.108,109
The nature and characteristics of hydrogen bonding in clusters in a polarizable continuum were described in terms of a natural bond orbital110 (NBO) analysis. In this scheme, the orthogonal natural orbitals are constructed as eigenvalues of the density matrix obtained from the converged SCF calculation. The orbitals are classified in terms of Lewis structures as bonding, lone pairs, core (for occupied orbitals), and Rydberg and antibonding (for unoccupied orbitals). The donor–acceptor character of hydrogen bonds can be described in terms of a charge transfer from a high-energy occupied orbital of donor (lone pair of oxygen for water, lone pair of the iodide anion) to an unoccupied orbital of the acceptor unit (σ*(O–H) orbital for water111). The electronic occupancy of the σ*(O–H) orbital can be used as a possible parameter for quantification of the hydrogen bonding.
4. Experimental results
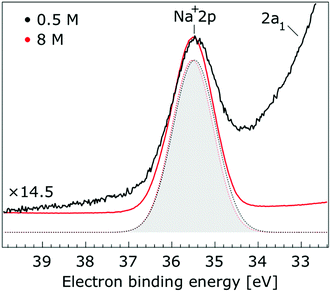
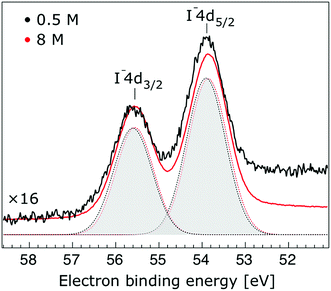
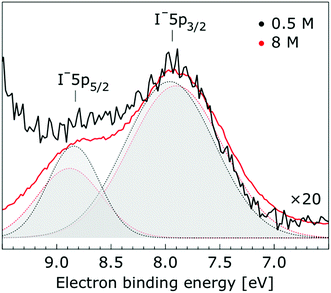
In Fig. 1, we present PE spectra from 0.5 M and 8.0 M NaI aqueous solutions measured at a 198 eV incident photon energy, covering the 5–60 eV BE range. This data was recorded at the U49 beamline with a focal spot size of the order of the liquid jet dimensions. At this photon energy, this resulted in the largest gas-phase water spectral contribution of all of the spectra reported here. Both spectra in Fig. 1 have been shifted in energy to match the established 11.16 eV lowest vertical ionization energy (1b1) of liquid water;60 this procedure by which the 1b1 energy is an inherently fixed reference energy, not subjected to any change upon concentration variation is explained in the next paragraph. In addition, we subtracted a linear background signal to minimize contributions from inelastically scattered electrons. The relative intensities of the two spectra are set to yield the best overlap of the 1b1 liquid water spectral contributions. Peaks at 13.5 eV, 17.3 eV, and 30.9 eV BE, primarily corresponding to ionization of the liquid water 3a1, 1b2, and 2a1 orbitals, respectively, are in agreement with previous work.33 The large peak at 35.0 eV BE arises from ionization of the Na+ 2p orbital. Peaks near 8.0 eV and 55.0 eV BEs are due to ionization of the I− 5p1/2, 3/2 and I− 4d3/2, 5/2 orbitals, respectively.51,60 Observed relative peak intensities in Fig. 1 reflect solute concentrations weighted by relative partial photoionization cross-sections, the PE angular distributions of the respective water and solute ionization processes, and the electron collection/detection geometry.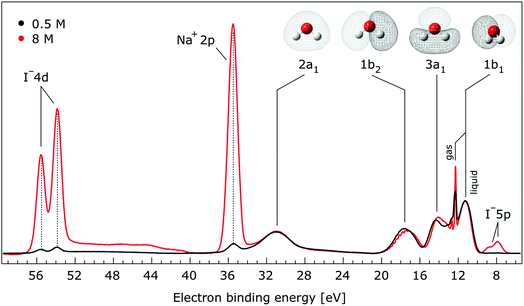 | ||
| Fig. 1 Valence photoelectron spectra of 0.5 M (black) and 8.0 M (red) NaI (aq.) measured at a 198.0 eV photon energy at the U49 beamline. A linear background was subtracted from both spectra in order to account for the contributions of the inelastically scattered electrons. Both spectra appear to be closely energetically aligned at the Na+ 2p and I− 4d peaks after shifting the peak of the liquid water 1b1 peaks to 11.16 eV, as indicated by dashed lines. Small plateau features in the 41–52 eV BE region for the 8 M solution can be assigned to energy loss processes where Na+ 2p photoelectrons excite quasi-optical transitions of water.112 Schematics of the valence molecular orbitals of water are reprinted from ref. 139 in the top right of the figure. | ||
We find, from Fig. 1, that when the liquid 1b1 peaks are energetically aligned, all other water peaks, as well as the solute peaks, are close to aligned for the two solution concentrations. This good overlap suggests that our choice of a fixed 1b1 energy reference is reasonable but at the same time our procedure imposes an inability to quantify any possible energy shifts of the water 1b1 orbital. Unfortunately, there is little to improve as any other treatment of the as-measured spectra – affected by liquid charging, true and apparent (scattering-related) BE shifts – would require careful quantification and correction of electrolyte-concentration-dependent sample-analyzer electric field gradients and potentially theoretical corrections for scattering effects, both of which would be subject to relatively large uncertainties. In fact, a strong argument in favor of the spectral alignment at the water 1b1 peak is that the best overlap of all peak positions considered in the spectra, including all solute and water peaks, is achieved in this case. That is, the sum of all spectral shifts is smallest with this spectral alignment procedure. We now show that small energetic shifts of the solute peaks are indeed in good agreement with an aligned water 1b1 peak. Furthermore, our experimental observations, based on the fixed water 1b1 energy, are well corroborated by our computations.
Thorough spectral analysis of Fig. 1 (simultaneous fitting of all spectral features) reveals a small energetic shift of the water 1b2 peak (with respect to the 1b1 peak) and a change of the spectral shape of the water 3a1 peak. A detailed analysis of the water 2a1 peak will not be presented here; as shown in Fig. 1 this peak position is well-aligned at low and high concentrations. The subtler effects on the solute spectral features are more clearly seen in Fig. 2–4, which present enlarged views of the two Na+ 2p (aq.) spectra (Fig. 2), I− 4d (aq.) spectra (Fig. 3), and I− 5p (aq.) spectra (Fig. 4). Fig. 2–4 also show respective Gaussian fits to the data; in the case of Na+ 2p (aq.), the 0.5 M spectrum has been subtracted from the 8.0 M spectrum to remove the contributions from the water 2a1 electrons. Under the aforementioned conditions, we find that the respective Gaussian peak positions are shifted to slightly lower BEs with increasing concentration (maximum energetic shifts of 110 ± 70 meV with variances in the peak widths < 30 ± 50 meV). The energetic shifts are significantly less than those of the water 1b2 feature discussed below. We summarize the obtained experimental BEs of the solute orbitals in Table 2 (Top) where we also present similar data for crystalline NaI;113 the valence I− 5p orbitals form the valence band in the crystalline phase and hence, their BEs are not included. We emphasize that all reported BE values correspond to aqueous ground neutral state – aqueous cation/free electron state energy gaps, as referenced to the best of our experimental capabilities to the vacuum level, and that experimental differentiation between initial and final state contributions to any electrolyte-induced BE shifts are not possible.
| Peak | BE [eV] | ||||
|---|---|---|---|---|---|
| 0.5 M | 8.0 M | ΔE | NaI crystal | ||
| Interface | I− 5p3/2 | 7.83 ± 0.04 | 7.72 ± 0.05 | −0.11 ± 0.07 | — |
| I− 5p1/2 | 8.70 ± 0.11 | 8.67 ± 0.05 | −0.03 ± 0.12 | — | |
| Na+ 2p | 35.39 ± 0.04 | 35.41 ± 0.04 | +0.02 ± 0.06 | 29.29 | |
| I− 4d5/2 | 53.84 ± 0.04 | 53.74 ± 0.04 | −0.10 ± 0.06 | 47.68 | |
| I− 4d3/2 | 55.52 ± 0.04 | 55.44 ± 0.06 | −0.08 ± 0.07 | 49.35 | |
| Bulk | I− 5p3/2 | 7.82 ± 0.04 | 7.71 ± 0.04 | −0.11 ± 0.06 | — |
| I− 5p1/2 | 8.71 ± 0.10 | 8.67 ± 0.04 | −0.04 ± 0.11 | — | |
| I− 5s | Not detectable | 19.6 ± 0.4 | Not detectable | 11.21 | |
| Na+ 2p | 35.44 ± 0.04 | 35.41 ± 0.04 | −0.03 ± 0.06 | 29.29 | |
| I− 4d5/2 | 53.89 ± 0.04 | 53.74 ± 0.04 | −0.15 ± 0.06 | 47.68 | |
| I− 4d3/2 | 55.57 ± 0.04 | 55.44 ± 0.04 | −0.13 ± 0.06 | 49.35 | |
In order to quantify the small spectral changes of the water valence band, which displays significant overlap among the spectral peaks, we consider the series of spectra spanning 0.05 M to 8.00 M NaI concentrations shown in Fig. 5. These spectra were recorded with a 180 eV photon energy, a higher energy resolution, and a smaller focal spot size at the U41 beamline (see the Experimental approach section), resulting in lower gas-phase spectral contributions with respect to Fig. 1. The 0.05 M solution is representative of neat water, with the fairly small amount of salt serving to achieve sufficient electric conductivity for high-acquisition-rate PE spectroscopy experiments.51 Note that over the large concentration variation, from 0.05 M to 8.00 M, the viscosity of the aqueous solution increases, potentially leading to the liquid jet experiencing small (μm) changes in position which will alter the relative liquid-to-gas signal intensity ratio. With the water 1b1 peaks aligned to 11.16 eV, a shift to lower BE up to 370 ± 60 meV is observed for the water 1b2 peak across the concentration range shown in Fig. 5. The evolution of the 1b2 peak shift, as obtained from Gaussian fits, is displayed in Fig. 6. Indicated error bars were determined from uncertainties of the fitting procedure. A 1b2 peak-width analysis, presented in Fig. SI-1 in the ESI,† reveals no noticeable trends, and this quantity is not further considered here.
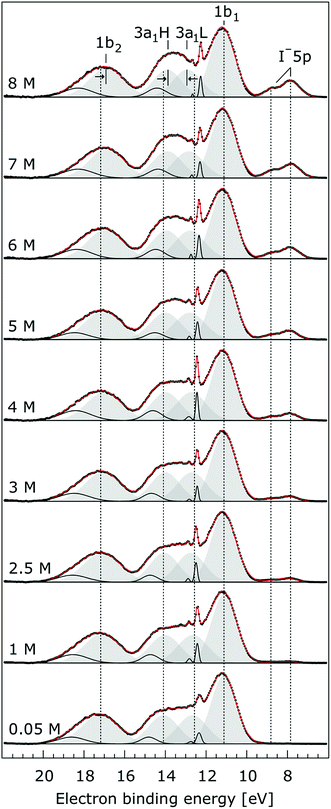 | ||
| Fig. 5 Valence photoelectron spectra from NaI aqueous solutions as a function of concentration, 0.05 M to 8.0 M. The high energy resolution spectra were recorded at the U41 beamline with a photon energy of 180 eV. Intensities are displayed to yield the same liquid water 1b1 peak heights for each solution. Peaks in grey are the Gaussian fits representing the photoelectron contributions primarily due to ionization of the four liquid water valence orbitals. Solid black lines are Gaussian fits of gas-phase water signal contributions. For the lowest concentration, the fit parameters previously reported for water32 were used. For the higher concentrations, the energetic positions and widths of all peaks were allowed to vary. Both 3a1 Gaussian fit component peaks (3a1 L and 3a1 H, see the main body of the text for details) are constrained so that they exhibit similar widths and heights in each spectrum. | ||
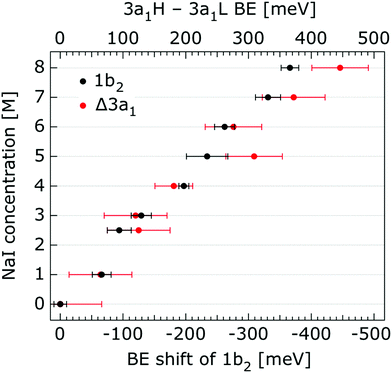 | ||
| Fig. 6 Decrease of the water 1b2 binding energy (with respect to that of 1b1), and decreasing 3a1 splitting in NaI aqueous solutions as a function of concentration, 0.05 M to 8.0 M. All data were extracted from Fig. 5. The error bars represent the uncertainties of the fitting procedure. | ||
The other, and more notable, spectral change occurs for the water 3a1 peak, in the 12–16 eV BE region. At low concentrations, the flat-top profile typical for neat liquid water, represented by the two aforementioned Gaussians, is observed. (Note that the 3a1 flat-top profile is obscured in Fig. 1 due to overlap with gas-phase spectral contributions.) With increasing concentration, the 3a1 flat-top feature evolves into a broad maximum. The 3a1 feature comprises of two orbital components that are primarily associated with intermolecular bonding and non-bonding interactions between water molecules, and have been formerly referred to as the 3a1 L and 3a1 H bands, respectively.35,66 Accordingly, we consider the 3a1 peak change with concentration a consequence of a varying energetic spacing between the 3a1 L and 3a1 H bands. To quantify such an effect, the 3a1 peak profiles were fit using a pair of Gaussian components, starting with the 0.05 M NaI solution, and using the well-established water peak widths and energies.33 Fixing the 3a1 L and 3a1 H peak widths to equal values and ensuring equal spectral contributions to the fit, we find that a small shift to higher BEs of the 3a1 L peak, and a small shift to lower BEs of the 3a1 H peak nicely represents the evolving overall 3a1 peak shape. In going from a 0.05 M to 8.00 M concentration, the 3a1 peak-splitting reduces by 450 ± 90 meV. The evolution of the 3a1 peak-splitting is also shown in Fig. 6A and is of similar magnitude to the concentration-dependent differential peak shift observed for the 1b2 PE features.
So far, the experimental results have been presented for the rather low photon energies 180 eV and 198 eV which produce photoelectrons with relatively short IMFPs,60 allowing us to primarily probe the liquid–vacuum interface. Our previous liquid-jet PE studies on the dissociation of HNO3 at the aqueous solution surface114 or on the molecular propensity of amine aqueous solutes with different dominant protonation states to concentrate at an interface115 highlighted that uniquely interfacial behavior can be detected when electrons are produced with kinetic energies near 100 eV. This finding is consistent with the shortest electron IMFPs in water,71,116 which is believed to be approximately 1 nm, for energies in the approximately 50–200 eV range. When increasing the kinetic energy by ∼400–500 eV one rather obtains spectra characteristic of the bulk aqueous solution. In order to ascertain whether the observed spectral changes discussed so far are properties of the interface, we have also measured the valence PE spectra at a 650 eV photon energy, corresponding to an approximate electron IMFP of 5 nm.117,118 We show the results from the 650 eV photon energy measurements in Fig. 7.
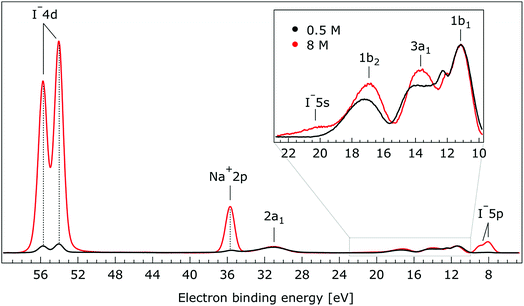 | ||
| Fig. 7 Valence photoelectron spectra of 0.5 M (black) and 8.0 M (red) NaI (aq.) measured at a 650.0 eV photon energy. Inset: enlarged region associated with the outer-valence spectrum. | ||
The most important observation from Fig. 7 is that the solute and water BEs do not change significantly with increasing salt concentration in these bulk-sensitive measurements; similar to the interfacially-sensitive results shown in Fig. 1. However, upon close inspection, slight shifts to lower BE of the solute peaks of up to 150 ± 60 meV are observed with increasing concentration in the bulk sensitive data. The associated shifts can be seen more clearly in the enlarged views of the Na+ 2p, I− 4d, and I− 5p BE regions shown in Fig. SI-2 to SI-4,† respectively. The positions and concentration-dependent peak shifts of the individual solute peaks are also summarized in Table 2 (bottom). Considering the water PE spectrum features, the 1b2 and 3a1 peaks are observed to display qualitatively similar behavior in the aqueous bulk as at the vacuum–liquid interface. From Gaussian fits to the 1b2 PE features in Fig. 7, a 330 ± 60 meV shift to lower BE is extracted when the NaI concentration is raised from 0.5 M to 8.0 M. Similarly to the analysis of the data shown in Fig. 5, pairs of constrained Gaussians were fit to the 3a1 features in the 0.5 M and 8.0 M spectra. As the concentration was increased, the 3a1 L and 3a1 H fit components were found to shift to higher and lower energies, respectively, resulting in a narrowing of the peak separation by 310 ± 120 meV. Collectively considering the concentration-dependent BE changes extracted from Fig. 7, we conclude that equivalent results are obtained from the vacuum–liquid interface and aqueous-bulk-sensitive measurements. This is an interesting finding, suggesting that differences in the interfacial and bulk-solution structure have no (detectable) effect on the spectral positions of the reported valence PE spectra.
5. Theoretical results
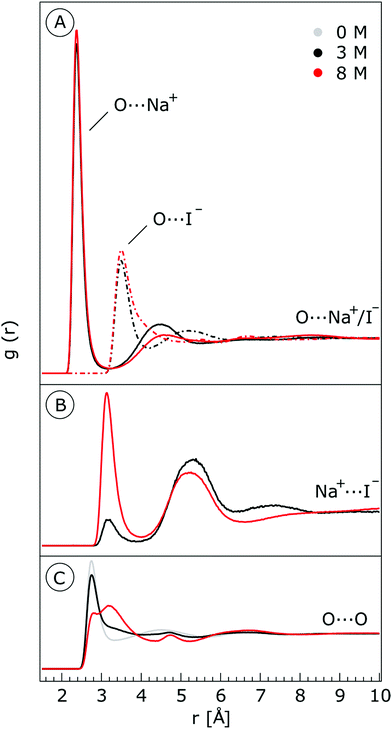
We characterize the molecular structure of the highly concentrated solutions with classical molecular dynamics (MD) simulations. We start by considering the radial distribution functions (RDFs) in the aqueous solutions; see Fig. 8. Note that all the presented results correspond to molecules in the bulk, i.e., we do not focus on the vacuum–liquid interface. The first peak of the O–Na+ RDF shown in Fig. 8A occurs at 2.37 Å; the first peak for the O–I− RDF occurs at 3.50 Å. Both are in good agreement with previous MD studies.82,119 The Na+–I− RDF shown in Fig. 8B exhibits two peaks and a broad third peak. The first one at ∼3 Å corresponds to the contact ion pair, the second at ∼5 Å corresponds to the solvent-shared ion pair configurations. The third broad peak corresponds to the solvent-shared ion pair, which is typically observed for salt solutions. The precise fraction between contact-ion pairs and solvent-shared ion pairs is a point of ongoing debate, with distinct results obtained for the different force field models used.82,120,121 The total fraction of ion-pair structures, however, undoubtedly increases significantly when passing from 3 M to 8 M solution. We also show the RDF for O–O in Fig. 8C. As can be inferred from the figure, the water structure is slightly altered in the 3 M solution (similar to previous findings, e.g., in ref. 122). However, for the 8 M solution, the RDF for O–O is dramatically different. We have to note here that the MD simulations do not necessarily provide a quantitatively correct evaluation of the liquid molecular structure for the highly concentrated solution, but the observed trends are still relevant.For a 3 M solution, the coordination numbers of the ions around water are 0.450 for an iodide anion and 0.329 for a sodium cation (see Table 3). The coordination numbers are calculated as 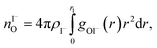 where ρI− is the I− number density, gOI− is the radial distribution function of O–I− with the first minimum at r1. Analogous O–Na+ calculations were also performed. The tetrahedral order parameter and translational tetrahedral order parameters are collected in Table 3 as well. As can be inferred from the table, both parameters (q and Sk) indicate that the 3 M solution structure has a less tetrahedral character compared to bulk water (q decreases and Sk increases). The structures of the 500 (H2O)7Na+I− clusters extracted from the simulations reflect bulk properties; the sodium cation is within the first coordination shell (distance smaller than 3.2 Å from the central water molecule) for 33% of structures, yet only 15% of the structures have sodium coordinated in a tetrahedral position (angle H–O⋯Na+ in the range 109° ± 20°). The iodide anion is within the first coordination shell (at distances less than 4.5 Å from the central water molecule) for 44% of the structures and in 27% of the structures the anion forms a HB with the central water molecule (O–H⋯I− in the range 180° ± 20°). Less than 5% of the structures have both sodium and iodide ions tetrahedrally coordinated in the first coordination shell. For the 8 M solution, the coordination numbers are 1.00 for Na+, and 2.69 for I−. Therefore, a randomly selected water molecule has a sodium cation in its first coordination shell at a distance less than 3.2 Å from the central water molecule. The first minimum on the O⋯I RDF is localized at a distance of 4.5 Å; i.e., the coordination shell is larger than for Na+ and more than two iodide anions are typically found within the shell. Both order parameters in Table 3 show that the tetrahedrality of the solution further decreases compared to the 3 M solution, the local structure of the solution is clearly affected by the ions. Here again, the 500 clusters extracted from the MD simulations reflect the bulk structural properties, 80% of (H2O)7Na+I− structures have a sodium cation within 3.2 Å and 100% of the structures have an iodide anion within 4.5 Å. 35% of the structures have a sodium cation tetrahedrally coordinated to the central water molecule, 55% of the structures have the iodide anion hydrogen-bonded to the central water molecule, and 20% of all structures have both iodide and sodium ions coordinated tetrahedrally in the first solvation shell.
where ρI− is the I− number density, gOI− is the radial distribution function of O–I− with the first minimum at r1. Analogous O–Na+ calculations were also performed. The tetrahedral order parameter and translational tetrahedral order parameters are collected in Table 3 as well. As can be inferred from the table, both parameters (q and Sk) indicate that the 3 M solution structure has a less tetrahedral character compared to bulk water (q decreases and Sk increases). The structures of the 500 (H2O)7Na+I− clusters extracted from the simulations reflect bulk properties; the sodium cation is within the first coordination shell (distance smaller than 3.2 Å from the central water molecule) for 33% of structures, yet only 15% of the structures have sodium coordinated in a tetrahedral position (angle H–O⋯Na+ in the range 109° ± 20°). The iodide anion is within the first coordination shell (at distances less than 4.5 Å from the central water molecule) for 44% of the structures and in 27% of the structures the anion forms a HB with the central water molecule (O–H⋯I− in the range 180° ± 20°). Less than 5% of the structures have both sodium and iodide ions tetrahedrally coordinated in the first coordination shell. For the 8 M solution, the coordination numbers are 1.00 for Na+, and 2.69 for I−. Therefore, a randomly selected water molecule has a sodium cation in its first coordination shell at a distance less than 3.2 Å from the central water molecule. The first minimum on the O⋯I RDF is localized at a distance of 4.5 Å; i.e., the coordination shell is larger than for Na+ and more than two iodide anions are typically found within the shell. Both order parameters in Table 3 show that the tetrahedrality of the solution further decreases compared to the 3 M solution, the local structure of the solution is clearly affected by the ions. Here again, the 500 clusters extracted from the MD simulations reflect the bulk structural properties, 80% of (H2O)7Na+I− structures have a sodium cation within 3.2 Å and 100% of the structures have an iodide anion within 4.5 Å. 35% of the structures have a sodium cation tetrahedrally coordinated to the central water molecule, 55% of the structures have the iodide anion hydrogen-bonded to the central water molecule, and 20% of all structures have both iodide and sodium ions coordinated tetrahedrally in the first solvation shell.
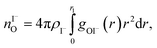 where ρI− is the I− number density, gOI− is the radial distribution function of O–I− with the first minimum at r1. The O–Na+ mean coordination numbers were analogously calculated. The position of the first minima for I− for 3 M concentration is 4.5 Å and for 8 M it is 5.04 Å, which explains a dramatic increase in coordination number. For Na+, the increase in the coordination number corresponds to the increase in concentration; the position of the first minima is 3.2 Å for both 3 M and 8 M
where ρI− is the I− number density, gOI− is the radial distribution function of O–I− with the first minimum at r1. The O–Na+ mean coordination numbers were analogously calculated. The position of the first minima for I− for 3 M concentration is 4.5 Å and for 8 M it is 5.04 Å, which explains a dramatic increase in coordination number. For Na+, the increase in the coordination number corresponds to the increase in concentration; the position of the first minima is 3.2 Å for both 3 M and 8 M
| Concentration | Coord. number I− | Coord. number Na+ | q | S k | Number of H-bonds/molecule |
|---|---|---|---|---|---|
| 0 M | — | — | 0.6300(0.0050) | 0.00122(0.00003) | 3.58 |
| 3 M | 0.450 | 0.329 | 0.5076(0.0051) | 0.00205(0.00003) | 2.73 |
| 8 M | 2.691 | 1.001 | 0.3266(0.0076) | 0.00326(0.00004) | 1.16 |
The average number of HBs formed per water molecule with other water molecules is collected in the last column of Table 3. We follow a geometrical definition of a HB, i.e., the O⋯H distance is smaller than 2.3 Å and the Oj –Oi⋯Hi angle is smaller than 30°. The higher number of HBs in neat water reflects the fact that ions substitute tetrahedrally coordinated water; the number therefore decreases with increasing the electrolyte concentration.123 For the 8 M solution, the calculated average number is only 1.16 per water molecule.
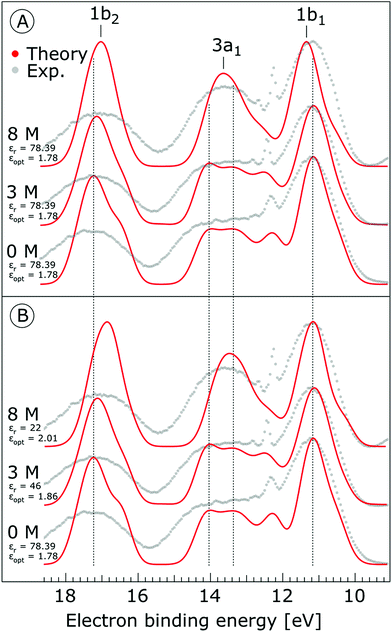
The photoemission spectra were calculated for 500 representative (H2O)7Na+I− (or (H2O)7 for neat water) clusters extracted from the MD simulations. We present the calculated PE spectra for neat water, 3 M and 8 M NaI aqueous solutions in Fig. 9. Panels A and B show the PE spectra obtained for different dielectric continuum permittivities. In order to explore the effect of dielectric screening, the spectra were calculated for a dielectric continuum mimicking pure water, i.e., assuming εr ∼ 78 (presented in Fig. 9A), and also for corrected dielectric constants (Fig. 9B) to account for the screening ability of highly concentrated solutions. We further comment on the details of the spectra in the discussion section.
We performed the NBO analysis to obtain additional insight into the effects of the electrolyte on the electronic structure of the solvated water molecule. We performed the analysis for the 500 clusters extracted from the MD simulations for various concentrations. The clusters were embedded in the polarizable continuum with adjusted dielectric constants corresponding to neat water, 3 M and 8 M NaI solutions. The changes in electron densities of water were almost negligible for the 3 M solution (compared to neat water) while some effect of the electrolyte is observed for the 8 M NaI solution. The analysis showed that the occupation numbers of the oxygen lone pairs of the central water molecule are on average higher in the electrolyte – there is negligible charge transfer from the water lone pair to the sodium cation. The occupation numbers of the σ*(O–H) orbitals of the central water molecule are also little changed upon adding the electrolyte, with somewhat lower occupations in these orbitals (see the ESI, Fig. SI-6†). These observations are consistent with electrolyte-induced disruptions of the HB network. However, the observed approach of the 3a1 L and 3a1 H ionization energies on the one side and the 1b2 and 1b1 ionization energies can be traced to the stabilization of the lone pair electrons by sodium cations and destabilization of the electrons in the water bonding orbitals by iodide anions.
We also explored the effect of the environment and ions on the water ionization energies separately using idealized tetrahedral cluster models. These results may help to understand the molecular origin of the shifts in electron binding energies, and are discussed in more detail in the ESI.† The largest shifts in the BEs are found to be due to the interactions with sodium cations; the observed shifts are generally much larger than for the clusters obtained from the MD simulations. This is attributed to the local structure from the MD simulations rarely being ideally tetrahedral.
6. Discussion
In the following, we interpret our experimental liquid phase PE spectra with the help of the theoretical calculations. We first consider our experimental results. As described above (see ref. 67), without a fully characterized electric field between a sample liquid jet and an electron detector, global (sample-concentration-dependent) spectral shifts for given aqueous solutions may occur that cannot be accurately interpreted. However, it is possible to circumvent this effect by energetically aligning the spectra from the different NaI concentration samples at the positions of the spectrally isolated liquid water 1b1 peaks. Notably, such a treatment is only applicable when the entire PE spectrum experiences a uniform energetic shift, as if a bias voltage had been applied to the sample. As mentioned above, this is almost the case. Within this framework, peaks which do not align at different concentrations, as observed for the 1b2 and 3a1, identify orbitals that are affected by explicit water–water and ion–water interactions. Unfortunately, due to our spectral alignment methodology, the small spectral shifts that may also occur for the 1b1 energy cannot be captured in our analysis.Initially we focus on the BEs of the solute ions, as extracted from Fig. 2–4 and SI-2–4† and summarized in Table 1. We find the BEs of the Na+ cation PE features to be independent of electrolyte concentration within our error bounds. In contrast, the anion BEs are observed to shift to slightly lower energies over the same concentration range. Comparing the vacuum/liquid interface and bulk-sensitive measurement results shown in Fig. 1 and 7, the concentration behavior of the solute BEs is found to be independent of our experimental probe depth. Significant differences between the relative intensities of the solute spectral features are observed between the vacuum/liquid-interface and bulk-sensitive data sets, however. These changes are due to the dependence of the partial ionization cross-sections and PE angular distributions on photon energy. Most prominent is the large increase of the I− 4d to Na+ 2p intensity ratio, where the initially larger Na+ peak height becomes much smaller than the I− peak height. This is primarily due to the steep increase of the I− 4d anisotropy parameter, β, between 200 eV and 600 eV electron kinetic energy and our light polarization/electron detection geometry.116
Collectively analyzing the BE results extracted from different Na+I− samples – including 0.5 M and 8.0 M aqueous solutions and crystalline solid NaI113 – we note near-identical intraspectral energetic separations between the Na+ 2p, I− 4d, and I− 5p PE features across environments. Additionally, despite the aqueous surface activity of I−,124–127 equivalent spectra are obtained from the aqueous vacuum/liquid-interface-sensitive and primarily bulk-sensitive data sets. This weak sensitivity to the solute surroundings is a clear indication of a minimal effect of solvation on the electronic structure of the ionic constituents.
In contrast to a previous investigation of the concentration dependence of aqueous alkali halide PE spectra,127 the I– solute BEs reported here were found to vary slightly with electrolyte concentration (up to 150 ± 60 meV over a 7.5 M range). This discrepancy can likely be attributed to the lower energy resolution and the narrower concentration range adopted in the previous study. We note that under the previously adopted experimental conditions, the solute peak shifts reported here would be undetectable. The origin of the slight, I− peak shifts observed here remain to be explored. However, one may speculate that these shifts are caused by the electrolyte-induced hydrogen-bonding network disruption and associated changes in charge donation by the polarizable I− anions to the water antibonding, σ*(O–H), orbitals as the electrolyte concentration is increased.18 In contrast, the charge-dense Na+ ions are relatively unaffected as the electrolyte concentration increases, simply coordinating to the oxygen atoms of the solvent molecules in greater number. The theoretical NBO results support this interpretation, showing that the electron density of the sodium cation is unaffected as the electrolyte concentration is increased, while the iodide anion exhibits small charge transfer to water molecule.
In shifting our attention to ionic effects on the electronic structure of the liquid water solvent, we focus on the series of more liquid–vacuum-interface-sensitive spectra shown in Fig. 5. Here, spectral contamination from gas-phase water is minimized and trends in electrolyte concentration-dependent solvent spectral changes can be discerned. The observed shift to lower BE of the 1b2 feature relative to the 1b1 peak (of up to 370 ± 60 meV) with increasing electrolyte concentration is highlighted in Fig. 6. The apparent respective shifts to higher and lower BE of the 3a1 L and 3a1 H spectral components and increased spectral component overlap with increasing electrolyte concentration (differential component shift, Δ3a1, up to 450 ± 90 meV) is also highlighted in Fig. 6. In combination with the observation that the Na+ 2p, I− 4d, and I− 5p feature BEs are affected to a lesser degree by the increase in electrolyte concentration (see Fig. 2–4 and Table 2), these findings facilitate the following inferences. First, the 1b2 relative energetic shift with concentration can likely be considered an absolute energetic shift as the relative separations of the solute PE spectra features and the liquid water 1b1 feature all remain relatively unaltered over the studied concentration range. Given the opposite charges of the solute components, the coordination of the lone-pair 1b1 electrons to other water molecules or Na+ ions, and the intermolecular bonding character of the 1b2 orbital, the alternative explanation that the 1b2 PE feature remains fixed in energy while the solute and 1b1 solvent features shift is deemed unlikely. Second, the observation that the 1b2 and 3a1 PE features are discernibly affected as the electrolyte concentration is increased implies that any intermolecular water–water and water–ion interactions primarily involve these molecular orbitals.
The bulk-sensitive measurements shown in Fig. 7 reaffirm the aforementioned observations from the interfacially-sensitive data, albeit with an additional complication. Small differences in the behavior of the water 1b2 peak in the high photon energy, bulk-sensitive measurements may be partially obscured by additional spectral contributions from iodide (undetected in the 180/198 eV measurements) that overlap with this water peak at the high-BE side. This additional signal at 19.6 ± 0.4 eV BE (according to our fits) is attributed to ionization of the I− 5s orbital, in agreement with the computed BE value of 20.2 ± 0.2 eV. Our assignment is also in accord with the expected ∼20% relative peak height compared to the I− 4d signal intensity; here we have quantitatively accounted for the smaller ionization cross-section of I− 5s compared to I− 5p at a 650 eV photon energy, and we also considered the lower emission intensity for s-orbital ionization with respect to p-orbital ionization (based on values for atomic iodine128) in the adopted detection geometry, i.e., with electron detection perpendicular to the light polarization. We have also accounted for the different electron occupancies. Despite the observed I− 5s and water 1b2 spectral overlap, we were able to extract the 1b2 peak shift to lower BEs arising from the 0.5 M to 8.0 M NaI concentration increase. Based on multi-peak Gaussian fits to the I− 5s and water 1b2 PE features, a 330 ± 60 meV 1b2 peak shift was extracted, in good agreement with the value (370 ± 60 meV) extracted over the larger concentration range (0.05 M to 8.00 M) associated with the interfacially-sensitive measurement results shown in Fig. 5. Using a similar analysis to that adopted for Fig. 5, we extracted a narrowing of the 3a1 L and 3a1 H peak splitting of 310 ± 120 meV from the lower concentration range data shown in Fig. 7. Considering our experimental uncertainties, this is consistent with the 450 ± 90 meV result extracted from the interfacially-sensitive spectra. On the other hand, the observed differences may arise from the different ion hydration structures at the surface and in the bulk. Unfortunately, our experimental uncertainties are too large to definitively identify any such surface and bulk hydration differences. Notably, differences are expected between surface and bulk hydration structures for such aqueous salt solutions,129 and these effects may contribute to the differences observed between the interfacially- and bulk-sensitive spectra.
As shown in Fig. 9, the calculated 1b1, 3a1, and 1b2 water valence peaks coincide well with the experimental results, although the theoretical peaks are narrower due to the classical nature of the MD simulations used in the present study.31 Small peaks in the 3a1 band at 12.2 eV or apparent shoulders in the spectra represent minor artefacts of the classical calculations. The theoretical spectra were shifted to lower energies by 0.3 eV in order to align those spectra representing neat water with the water 1b1 peak (11.16 eV BE). The simulations correctly reproduce the flat-top structure of the overlapping 3a1 H and 3a1 L peaks that are characteristic of the interatomic interactions predominantly described by 3a1 – 3a1 bonding (although the 1b1, 1b2 and 2a1 orbitals also contribute) between water molecules, as found experimentally for neat water. Furthermore, we qualitatively reproduce the change of the 3a1 peak shape as a function of concentration in the simulation. This change results from weakened 3a1 – 3a1 interactions upon addition of salt. Proton vibrations of the hydrogen-bond donor unit apparently modulate the electronic interaction, i.e., the interaction is different for different minute geometric arrangements of the solution. When some of the associated water units are replaced by ions, the intermolecular bonding interaction is weakened, resulting in a narrowing of the 1b1 and 3a1 PE features, as observed experimentally. The electrolyte clearly disrupts the intermolecular electronic wave function overlap. The observed narrowing of the 3a1 BE peak is the most robust manifestation of ionic influence on the electronic and molecular structure of liquid water. It confirms that the unusual spectral shape of the 3a1 peak stems from hydrogen bonding; yet it does not result from the electrostatics but rather from the electronic interactions. Notably, similar ionic effects on the structure of liquid water are indicated by a range of other spectroscopies.11,14,130–137
Next, we discuss the energetic shifts of the calculated water BEs with increasing electrolyte concentrations in detail. We shall focus on the role of the dielectric continuum treatment in the calculations. The differences in the spectra are rather small but the effect is observable. In Fig. 9A, where the concentration dependence of the dielectric constant was neglected, we see that for the 3 M solution the 1b1 peak aligns with neat water and the 1b2 peak shifts by less than 0.1 eV to lower energies compared to neat water. For an 8 M solution, the 1b1 peak shifts to slightly higher energy (by 0.2 eV compared to neat water), and the 1b2 peak shifts to lower BEs by 0.2 eV compared to neat water. Interestingly, the relative energetic shift between the 1b1 and 1b2 peaks is close to that observed in the experiments. We can qualitatively understand this observation in terms of stabilization of the non-bonding 1b1 electron by the sodium cation, and destabilization of the 1b2 electron by the iodide anion when the dielectric constants are fixed to values associated with neat water. When accounting for concentration-dependent variations of εr and εopt (see the Method section), the 1b1 peak shift almost disappears; see Fig. 9B. Once we account for the variations of the effective dielectric constant with concentration, with εr (3 M) = 46 and εopt (3 M) = 1.86, and εr (8 M) = 22 and εopt (8 M) = 2.01, the 1b1 peaks line up closely, and only the 1b2 peak exhibits a small energetic shift of ∼0.34 eV to lower energies. Hence, these simulations are also in agreement with the experimental results. The spectra calculated with concentration-dependent dielectric constants correctly capture the BE peak positions, the structure of the peaks and their dependence on the electrolyte concentration. Contrary to the experiment, the theoretical calculations also provide the absolute energetics of the spectra. Spectra in Fig. 9B clearly show that the liquid water 1b1 peak position remains unaltered with increasing electrolyte concentration, which supports the experimental energetic referencing procedure. Indeed, collectively the experimental and theoretical results support the adoption of the spectrally isolated 1b1(l) PE peak as a robust energetic reference for liquid-phase PE spectroscopy measurements.
The theoretical analysis presented in the ESI† shows that the main effect of the electrolyte is caused by the sodium cation. The iodide anion is much bigger than the sodium cation, its coordination distance is larger due to Pauli repulsion and consequently, the electrostatic interaction between the anion and the water is within the model smaller.
7. Conclusions
Most photoemission studies focus on how the solvent affects the solute. Here, we have explored the reverse, i.e., the effects of electrolytes on water. We rely on the fact that the PE spectrum of water is very well known, and we can interpret even subtle variations. We observed that the electron binding energies of liquid water are only mildly affected even for a highly concentrated electrolyte solution. Our findings that the large change in the liquid structure, i.e., the transformation from the dilute aqueous solution to the viscous almost crystalline-like phase, has so little effect on the water PE spectra are clearly surprising. Both the PE spectroscopy experiments and theoretical calculations show that the solute and solvent peak positions in the PE spectra are surprisingly stable with respect to increasing electrolyte concentrations. The directly observed variations are the small negative, relative energetic shifts of the I− solute peaks (≤150 ± 60 meV) and water 1b2 (370 ± 60 meV) peak and the reduced spacing of the water 3a1 H and 3a1 L peak components (450 ± 90 meV). One important consequence from an experimental and practical viewpoint is that the present results fully justify the common procedure of aligning liquid-jet PE spectra from dilute or concentrated aqueous solutions using the well-resolved liquid water 1b1 peak. As the relative energetics of the solute peaks – that are energetically-referenced to the 1b1 peak – are found to be relatively insensitive to ion concentration, by extension the water 1b1 BE can also be inferred to be relatively insensitive to ion concentration. Through our analysis, we have determined an 150 ± 60 meV upper limit for the 1b1 BE shift over an ∼8 M solute concentration range. Given the large concentration range studied here, our results abate previous conjecture that an energetic shift of the water 1b1 PE peak position of up to 0.57 eV could be expected in going from (nearly) neat water to a 1 M NaCl aqueous solution.138 In defining still more robust energetic references for liquid PE spectroscopy experiments, the dielectric-constant-corrected PE spectra simulation results shown in Fig. 9B are encouraging. Indeed, the simulated few-tens-of-meV stability window of the water 1b1 BE is similar to the precisions with which liquid phase BEs can currently be determined. Further measurements dedicated to defining liquid water reference (1b1) and solute BEs, over large solute concentration ranges and with these high precisions, are ongoing in our laboratories.It follows from the present work that the energetics of the individual ionizing transitions and the associated electrons do not change significantly during the solvation process – the relative BEs of the ions are essentially the same for dilute solutions, concentrated solutions, and crystalline NaI. This is consistent with the almost isoenthalpic nature of NaI dissolution. The solvation enthalpy for infinite dilution is only −7.53 kJ mol−1, and this number further decreases with increasing electrolyte concentration.139 As the total energy of the system varies little with electrolyte concentration, we cannot expect significant variations in the energetics of the electronic subsystems. On the other hand, the small variations in the BEs show that we are, in principle, able to investigate and detect the effects of solvation on the ionizing transitions and hence on the associated electrons.
Another crucial, although barely addressed question that arises regards the nature of PE spectroscopy's apparent insensitivity to the geometric structure of the aqueous solution. This behavior may surprise in the light of the X-ray PE spectroscopy technique's high sensitivity to a local atomic (chemical) environment which can lead to core-level (chemical) energy shifts of several electron volts.54,140 The insensitivity of the present spectra points toward the impressive screening ability of polar liquids and the more delocalized nature of the valence electrons on which we focus here. The experimental results presented indicate that aqueous-phase valence electron BEs are quite insensitive to purely electrostatic interactions between molecules over a wide range of concentrations. We can contrast this result with Auger electron energetics that have been shown to be much more sensitive towards ion pairing.141,142 On the other hand, aqueous-phase valence BEs have been shown to sensitively reflect changes in the covalent bonding of solute species. Valence binding energies of aqueous-phase PO43−, HPO42− and H2PO4− are, for example, very different while the BE of PO43− and its sodiated analogues remain almost identical.42 While adding NaCl to water will hardly change the binding energies of water molecules, a significant change will occur upon dissolving HCl in water; new covalently bonded species such as H3O+ emerge with completely different electronic structure characteristics. Comparatively, the electronic structure of water in electrolyte solutions is modified in a subtler way. Liquid water represents a collection of water molecules, which electronically interact within a shell of nearest neighbors. Upon increasing the electrolyte concentration, we disrupt these interactions and we tend towards “electronically isolated” water units embedded in a dielectric continuum.
Finally, an important finding of our work is the realization that the PE spectra of aqueous solutions can be reliably simulated using a relatively thrifty dielectric continuum approach. There are several important aspects. First, the nearest neighbors of the investigated water molecule have to be included in the calculations. Second, we need to focus only on the fully solvated water units. The IEDC approach is excellently suited for this purpose. The present technique does not require demanding ab initio MD calculations, and yet the results are reliable. Here, an important aspect is the proper treatment of the dielectric continuum. First, the non-equilibrium character of the ionization process has to be acknowledged.37,89 Second, we should adjust the dielectric continuum model to reflect the finite ionic strength of the studied solution. A number of studies that worked towards this goal have recently been published,105,143,144 and the present study is supportive of these concepts. Furthermore, these new aspects of photoemission data can be useful for testing classical MD simulations. Most of the employed force fields do not directly aim to describe highly concentrated solutions. The ability to describe the intermolecular bonding interactions that lead to the 3a1 water peak variations, which are the crucial experimentally observable quantities, can be utilized to develop improved dielectric continuum models. This would require investing some effort into getting the right results for the right reasons. For example, simulations taking into account the quantum character of the atomic nuclei and corresponding force fields should then be used.31,145 We also point out that the present data are relevant for the discussion of increased screening length at high electrolyte concentrations where Debye–Hückel theory is no longer applicable. A particularly interesting question is how the (Debye) decay length connects to the dielectric-scaled ion density; here the polarizability of the ions is expected to play a crucial role,22 signatures of which may be detectable in further liquid jet PE spectroscopy measurements and interpretable using the IEDC methodology.
Conflicts of interest
Acknowledgements
E. M., Š. S. and P. S. acknowledge the support by the Czech Science Foundation, project number 18-23756S. Š. S. is a student of the International Max Planck Research School for “Many-Particle Systems in Structured Environments”. B. W. and M. N. P. acknowledge the support from the Deutsche Forschungsgemeinschaft (DFG) via the DFG Research Unit FOR 1789. B. W. and R. S. furthermore acknowledge support from the DFG through the Collaborative Research Center 1109. R. S. also gratefully acknowledges an Emmy-Noether Young Investigator stipend through the DFG (project SE 2253/3-1). H. A. thanks the Egyptian Ministry of Higher Education and Ain Shams University for her PhD grant and the Egyptian Culture Office in Berlin for support. We thank the Helmholtz-Zentrum Berlin (HZB) for the allocation of synchrotron radiation beamtime and the BESSY II staff for support during the beamtime.References
- P. Coffey, Cathedrals of Science – The personalities and rivalries that made modern chemistry, Oxford University Press, 2008 Search PubMed.
- L. G. M. Pettersson, R. H. Henchman and A. Nilsson, Chem. Rev., 2016, 116, 7459–7462 CrossRef CAS PubMed.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. A. Naslund, T. K. Hirsch, L. Ojamae, P. Glatzel, L. G. M. Pettersson and A. Nilsson, Science, 2004, 304, 995–999 CrossRef CAS PubMed.
- J. D. Smith, C. D. Cappa, K. R. Wilson, B. M. Messer, R. C. Cohen and R. J. Saykally, Science, 2004, 306, 851–853 CrossRef CAS PubMed.
- C. Huang, K. T. Wikfeldt, T. Tokushima, D. Nordlund, Y. Harada, U. Bergmann, M. Niebuhr, T. M. Weiss, Y. Horikawa, M. Leetmaa, M. P. Ljungberg, O. Takahashi, A. Lenz, L. Ojamae, A. P. Lyubartsev, S. Shin, L. G. M. Pettersson and A. Nilsson, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15214–15218 CrossRef CAS PubMed.
- G. N. I. Clark, C. D. Cappa, J. D. Smith, R. J. Saykally and T. Head-Gordon, Mol. Phys., 2010, 108, 1415–1433 CrossRef CAS.
- R. H. Henchman and S. J. Cockram, Faraday Discuss., 2013, 167, 529–550 RSC.
- T. D. Kühne and R. Z. Khaliullin, Nat. Commun., 2013, 4, 1450 CrossRef PubMed.
- Y. Harada, J. Miyawaki, H. Niwa, K. Yamazoe, L. G. M. Pettersson and A. Nilsson, J. Phys. Chem. Lett., 2017, 8, 5487–5491 CrossRef CAS PubMed.
- P. Gallo, K. Arnann-Winkel, C. A. Angell, M. A. Anisimov, F. Caupin, C. Chakravarty, E. Lascaris, T. Loerting, A. Z. Panagiotopoulos, J. Russo, J. A. Sellberg, H. E. Stanley, H. Tanaka, C. Vega, L. M. Xu and L. G. M. Pettersson, Chem. Rev., 2016, 116, 7463–7500 CrossRef CAS PubMed.
- H. Bakker, Chem. Rev., 2008, 108, 1456–1473 CrossRef CAS PubMed.
- Y. L. Jeyachandran, F. Meyer, S. Nagarajan, A. Benkert, M. Bar, M. Blum, W. L. Yang, F. Reinert, C. Heske, L. Weinhardt and M. Zharnikov, J. Phys. Chem. Lett., 2014, 5, 4143–4148 CrossRef CAS PubMed.
- Z. Yin, L. Inhester, S. T. Veedu, W. Quevedo, A. Pietzsch, P. Wernet, G. Groenhof, A. Föhlisch, H. Grubmüller and S. Techert, J. Phys. Chem. Lett., 2017, 8, 3759–3764 CrossRef CAS PubMed.
- K. Tielrooij, N. Garcia-Araez, M. Bonn and H. Bakker, Science, 2010, 328, 1006–1009 CrossRef CAS PubMed.
- A. W. Omta, M. F. Kropman, S. Woutersen and H. J. Bakker, Science, 2003, 301, 347–349 CrossRef CAS PubMed.
- Y. Marcus, Chem. Rev., 2009, 109, 1346–1370 CrossRef CAS PubMed.
- Z. Yin, I. Rajkovic, K. Kubicek, W. Quevedo, A. Pietzsch, P. Wernet, A. Föhlisch and S. Techert, J. Phys. Chem. B, 2014, 118, 9398–9403 CrossRef CAS PubMed.
- I. Waluyo, D. Nordlund, U. Bergmann, D. Schlesinger, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2014, 140, 244506 CrossRef PubMed.
- L. M. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. L. Fan, C. Luo, C. S. Wang and K. Xu, Science, 2015, 350, 938–943 CrossRef CAS PubMed.
- Y. Yamada, K. Usui, K. Sodeyama, S. Ko, Y. Tateyama and A. Yamada, Nat. Energy, 2016, 1, 16129 CrossRef CAS.
- R. S. Kuhnel, D. Reber and C. Battaglia, ACS Energy Lett., 2017, 2, 2005–2006 CrossRef CAS.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Faraday Discuss., 2017, 199, 239–259 RSC.
- Z. A. H. Goodwin and A. A. Kornyshev, Electrochem. Commun., 2017, 82, 129–133 CrossRef CAS.
- R. Sankari, M. Ehara, H. Nakatsuji, Y. Senba, K. Hosokawa, H. Yoshida, A. De Fanis, Y. Tamenori, S. Aksela and K. Ueda, Chem. Phys. Lett., 2003, 380, 647–653 CrossRef CAS.
- M. S. Banna, B. H. McQuaide, R. Malutzki and V. Schmidt, J. Chem. Phys., 1986, 84, 4739–4747 CrossRef CAS.
- J. E. Reutt, L. S. Wang, Y. T. Lee and D. A. Shirley, J. Chem. Phys., 1986, 85, 6928–6939 CrossRef CAS.
- R. H. Page, R. J. Larkin, Y. R. Shen and Y. T. Lee, J. Chem. Phys., 1988, 88, 2249–2263 CrossRef CAS.
- S. Y. Truong, A. J. Yencha, A. M. Juarez, S. J. Cavanagh, P. Bolognesi and G. C. King, Chem. Phys., 2009, 355, 183–193 CrossRef CAS.
- S. Barth, M. Ončák, V. Ulrich, M. Mucke, T. Lischke, P. Slavíček and U. Hergenhahn, J. Phys. Chem. A, 2009, 113, 13519–13527 CrossRef CAS PubMed.
- D. Hollas, E. Muchová and P. Slavíček, J. Chem. Theory Comput., 2016, 12, 5009–5017 CrossRef CAS PubMed.
- A. P. Gaiduk, M. Govoni, R. Seidel, J. H. Skone, B. Winter and G. Galli, J. Am. Chem. Soc., 2016, 138, 6912–6915 CrossRef CAS PubMed.
- B. Winter, R. Weber, W. Widdra, M. Dittmar, M. Faubel and I. V. Hertel, J. Phys. Chem. A, 2004, 108, 2625–2632 CrossRef CAS.
- D. Nordlund, M. Odelius, H. Bluhm, H. Ogasawara, L. G. M. Pettersson and A. Nilsson, Chem. Phys. Lett., 2008, 460, 86–92 CrossRef CAS.
- K. Nishizawa, N. Kurahashi, K. Sekiguchi, T. Mizuno, Y. Ogi, T. Horio, M. Oura, N. Kosugi and T. Suzuki, Phys. Chem. Chem. Phys., 2011, 13, 413–417 RSC.
- J. H. Guo and Y. Luo, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 181–191 CrossRef CAS.
- E. Pluhařová, P. Slavíček and P. Jungwirth, Acc. Chem. Res., 2015, 48, 1209–1217 CrossRef PubMed.
- P. Slavíček, B. Winter, M. Faubel, S. E. Bradforth and P. Jungwirth, J. Am. Chem. Soc., 2009, 131, 6460–6467 CrossRef PubMed.
- C. A. Schroeder, E. Pluhařová, R. Seidel, W. P. Schroeder, M. Faubel, P. Slavíček, B. Winter, P. Jungwirth and S. E. Bradforth, J. Am. Chem. Soc., 2015, 137, 201–209 CrossRef CAS PubMed.
- E. Pluhařová, C. Schroeder, R. Seidel, S. E. Bradforth, B. Winter, M. Faubel, P. Slavíček and P. Jungwirth, J. Phys. Chem. Lett., 2013, 4, 3766–3769 CrossRef.
- E. Pluhařová, P. Jungwirth, S. E. Bradforth and P. Slavíček, J. Phys. Chem. B, 2011, 115, 1294–1305 CrossRef PubMed.
- E. Pluhařová, M. Ončák, R. Seidel, C. Schroeder, W. Schroeder, B. Winter, S. E. Bradforth, P. Jungwirth and P. Slavíček, J. Phys. Chem. B, 2012, 116, 13254–13264 CrossRef PubMed.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206 CAS.
- T. Fransson, Y. Harada, N. Kosugi, N. A. Besley, B. Winter, J. J. Rehr, L. G. M. Pettersson and A. Nilsson, Chem. Rev., 2016, 116, 7551–7569 CrossRef CAS PubMed.
- C. G. Elles, C. A. Rivera, Y. Zhang, P. A. Pieniazek and S. E. Bradforth, J. Chem. Phys., 2009, 130 Search PubMed.
- C. G. Elles, I. A. Shkrob, R. A. Crowell and S. E. Bradforth, J. Chem. Phys., 2007, 126, 164503 CrossRef PubMed.
- G. D. Kerr, M. W. Williams, R. D. Birkhoff, R. N. Hamm and L. R. Painter, Phys. Rev. A, 1972, 5, 2523 CrossRef.
- A. Bernas, C. Ferradini and J. P. JayGerin, Chem. Phys., 1997, 222, 151–160 CrossRef CAS.
- A. Nilsson, D. Nordlund, I. Waluyo, N. Huang, H. Ogasawara, S. Kaya, U. Bergmann, L. A. Naslund, H. Ostrom, P. Wernet, K. J. Andersson, T. Schiros and L. G. M. Pettersson, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 99–129 CrossRef CAS.
- L. Weinhardt, O. Fuchs, M. Blum, M. Bär, M. Weigand, J. D. Denlinger, Y. Zubavichus, M. Zharnikov, M. Grunze, C. Heske and E. Umbach, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 206–211 CrossRef CAS.
- B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211 CrossRef CAS PubMed.
- A. Pietzsch, F. Hennies, P. S. Miedema, B. Kennedy, J. Schlappa, T. Schmitt, V. N. Strocov and A. Föhlisch, Phys. Rev. Lett., 2015, 114, 088302 CrossRef CAS PubMed.
- A. Nilsson and L. G. M. Pettersson, Chem. Phys., 2011, 389, 1–34 CrossRef CAS.
- B. Winter, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 601, 139–150 CrossRef CAS.
- H. Siegbahn and K. Siegbahn, J. Electron Spectrosc. Relat. Phenom., 1973, 2, 319–325 CrossRef CAS.
- M. Lundholm, H. Siegbahn, S. Holberg and M. Arbman, J. Electron Spectrosc. Relat. Phenom., 1986, 40, 163–180 CrossRef CAS.
- P. Delahay and K. Von Burg, Chem. Phys. Lett., 1981, 83, 250–254 CrossRef CAS.
- K. Von Burg and P. Delahay, Chem. Phys. Lett., 1981, 78, 287–290 CrossRef CAS.
- P. Delahay and A. Dziedzic, J. Chem. Phys., 1984, 80, 5793–5798 CrossRef CAS.
- R. Seidel, B. Winter and S. E. Bradforth, in Annu. Rev. Phys. Chem., ed. M. A. Johnson and T. J. Martinez, 2016, vol. 67, pp. 283–305 Search PubMed.
- M. Faubel, B. Steiner and J. P. Toennies, J. Chem. Phys., 1997, 106, 9013–9031 CrossRef CAS.
- M. Salmeron and R. Schlögl, Surf. Sci. Rep., 2008, 63, 169–199 CrossRef CAS.
- D. E. Starr, Z. Liu, M. Haevecker, A. Knop-Gericke and H. Bluhm, Chem. Soc. Rev., 2013, 42, 5833–5857 RSC.
- C. H. Wu, R. S. Weatherup and M. B. Salmeron, Phys. Chem. Chem. Phys., 2015, 17, 30229–30239 RSC.
- B. Winter, E. F. Aziz, U. Hergenhahn, M. Faubel and I. V. Hertel, J. Chem. Phys., 2007, 126, 124504 CrossRef PubMed.
- N. Kurahashi, S. Karashima, Y. Tang, T. Horio, B. Abulimiti, Y.-I. Suzuki, Y. Ogi, M. Oura and T. Suzuki, J. Chem. Phys., 2014, 140 Search PubMed.
- There are two major sources of liquid jet charging, (1) electrokinetic charging, and (2) the low conductivity and charge screening capability of neat liquid water. As stated in the main body of the text, both of these effects can be mitigated by adding electrolyte to a solution to increase its conductivity, the latter effect can also be assuaged by decreasing the light intensity. In addition, a third effect (3), the possible change or evolution of the solution surface potential due to a molecular dipole layer must be taken into account. This effect is associated with the orientation of molecules at the water/aqueous solution – vacuum interface. A related effect is the possible larger surface propensity of one type of charged species (even an atomic ion such as iodide) compared to its counter ion, an effect that will give rise to an electrical double layer. It is perhaps useful to recall that molecular adsorption on a single-crystal surface (typically investigated by PE spectroscopy in ultra-high vacuum) is well known to cause changes of the sample’s work function. As of yet, for aqueous-solution PE spectroscopy, this effect has never been considered or detected. We note that any of the listed three effects will influence the kinetic energies of the photoelectrons (the position of the PE peak) that are measured in the experiment..
- N. Preissler, F. Buchner, T. Schultz and A. Lübcke, J. Phys. Chem. B, 2013, 117, 2422–2428 CrossRef CAS PubMed.
- D. N. Kelly, R. K. Lam, A. M. Duffin and R. J. Saykally, J. Phys. Chem. C, 2013, 117, 12702–12706 CrossRef CAS.
- It is perhaps interesting to mention that the accuracy of the reported water 1b1 BE may be challenged when realizing that inelastic scattering of the photoelectrons can lead to a measured (apparent) BE that differs from the actual (genuine) BE. Such effects have recently been observed in BE measurements of the hydrated electron in liquid jet photoelectron spectroscopy studies [Yamamoto et al., Phys. Rev. Lett., 112, 2014, 187603 and Luckhaus et al., Sci. Adv., 3, 2017, e1603224]. However, one must consider that these experiments adopted ionization photon energies of 3.6–13.6 eV, corresponding to relatively low electron kinetic energies of approximately 0–11 eV. Under such conditions, electron-phonon and electron-electron inelastic scattering cross-sections were found to be highly electron kinetic energy dependent. We note that in the experiments reported here, photoelectrons are produced and detected at significantly higher kinetic energies in the 120–193 eV and 590–645 eV ranges. At such kinetic energies, electron-electron inelastic scattering processes are expected to dominate, with inelastic scattering cross-sections and their energy dependences differing in the two probed electron kinetic energy ranges71 [Dingfelder et al., Radiat. Phys. Chem., 53, 1998, 1]. Based on the calculated differential electron energy transfer cross-sections of liquid water at 100 eV and 500 eV, [Dingfelder et al., Radiat. Chem. Phys., 53, 1998, 1] the apparent water 3a1 and 1b2 PE features may be expected to shift to lower BEs as the electron kinetic energy is increased from ∼160 eV to ∼620 eV. Such effects were not observed in the experimental data reported here, suggesting that such inelastic scattering effects have a, thus far, unmeasurable effect on aqueous valence electron BEs recorded using such high energy photons. In any event, the explicit treatment of such inelastic scattering and peak distortion effects requires more precise measurements of (electron kinetic energy dependent) inelastic mean free paths and inelastic scattering cross-sections in liquid water.60,117,118 Accordingly, such scattering effects and their influence on measured BEs are not considered explicitly in the present work, i.e., we assume that the differential inelastic scattering cross-section is uniform over the electron kinetic energy and BE ranges considered here..
- H. T. Nguyen-Truong, J. Phys.: Condens. Matter, 2018, 30, 155101 CrossRef PubMed.
- P. Slavíček, B. Winter, L. S. Cederbaum and N. V. Kryzhevoi, J. Am. Chem. Soc., 2014, 136, 18170–18176 CrossRef PubMed.
- B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4, 435–447 CrossRef CAS PubMed.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS.
- S. Nose, Mol. Phys., 1984, 52, 255–268 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- J. R. Errington and P. G. Debenedetti, Nature, 2001, 409, 318 CrossRef CAS PubMed.
- P.-L. Chau and A. Hardwick, Mol. Phys., 1998, 93, 511–518 CrossRef CAS.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS PubMed.
- M. Rubešová, E. Muchová and P. Slavíček, J. Chem. Theory Comput., 2017, 13, 4972–4983 CrossRef PubMed.
- R. J. Bartlett and D. S. Ranasinghe, Chem. Phys. Lett., 2017, 669, 54–70 CrossRef CAS.
- M. Levy, J. P. Perdew and V. Sahni, Phys. Rev. A, 1984, 30, 2745–2748 CrossRef.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840 CrossRef CAS.
- F. Della Sala, R. Rousseau, A. Gorling and D. Marx, Phys. Rev. Lett., 2004, 92, 183401 CrossRef PubMed.
- M. Ončák, L. Šištík and P. Slavíček, J. Chem. Phys., 2010, 133, 174303–174309 CrossRef PubMed.
- M. Rubešová, V. Jurásková and P. Slavíček, J. Comput. Chem., 2017, 38, 427–437 CrossRef PubMed.
- M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681 CrossRef CAS PubMed.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CrossRef CAS.
- T. N. Truong and E. V. Stefanovich, Chem. Phys. Lett., 1995, 240, 253–260 CrossRef CAS.
- B. Jagoda-Cwiklik, P. Slavíček, L. Cwiklik, D. Nolting, B. Winter and P. Jungwirth, J. Phys. Chem. A, 2008, 112, 3499–3505 CrossRef CAS PubMed.
- Z. Q. You, J. M. Mewes, A. Dreuw and J. M. Herbert, J. Chem. Phys., 2015, 143, 204104 CrossRef PubMed.
- C. A. Guido, D. Jacquemin, C. Adamo and B. Mennucci, J. Chem. Theory Comput., 2015, 11, 5782–5790 CrossRef CAS PubMed.
- J. M. Mewes, Z. Q. You, M. Wormit, T. Kriesche, J. M. Herbert and A. Dreuw, J. Phys. Chem. A, 2015, 119, 5446–5464 CrossRef CAS PubMed.
- T. B. de Queiroz and S. Kummel, J. Chem. Phys., 2015, 143, 034101 CrossRef PubMed.
- A. Boruah, M. P. Borpuzari, Y. Kawashima, K. Hirao and R. Kar, J. Chem. Phys., 2017, 146, 164102 CrossRef PubMed.
- F. E. Harris and C. T. O'Konski, J. Phys. Chem., 1957, 61, 310–319 CrossRef CAS.
- J. Hasted, D. Ritson and C. Collie, J. Chem. Phys., 1948, 16, 1–21 CrossRef CAS.
- G. Haggis, J. Hasted and T. Buchanan, J. Chem. Phys., 1952, 20, 1452–1465 CrossRef CAS.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CrossRef CAS.
- P. Winsor IV and R. H. Cole, J. Phys. Chem., 1982, 86, 2486–2490 CrossRef.
- J. Hasted and G. Roderick, J. Chem. Phys., 1958, 29, 17–26 CrossRef CAS.
- X. F. Guan, M. M. Ma, Z. C. Gan, Z. L. Xu and B. Li, Phys. Rev. E, 2016, 94, 053312 CrossRef PubMed.
- B. Li, J. Y. Wen and S. G. Zhou, Commun. Math. Sci., 2016, 14, 249–271 CrossRef CAS PubMed.
- H. A. Clark and B. R. Sutherland, Exp. Fluids, 2009, 47, 183–193 CrossRef CAS.
- B. Mennucci, R. Cammi and J. Tomasi, J. Chem. Phys., 1998, 109, 2798–2807 CrossRef CAS.
- M. Cossi and V. Barone, J. Phys. Chem. A, 2000, 104, 10614–10622 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- A. Reed, Chem. Rev., 1988, 88, 899 CrossRef CAS.
- B. Winter, R. Weber, P. M. Schmidt, I. V. Hertel, M. Faubel, L. Vrbka and P. Jungwirth, J. Phys. Chem. B, 2004, 108, 14558–14564 CrossRef CAS.
- S. P. Kowalczyk, F. R. McFeely, L. Ley, R. A. Pollak and D. A. Shirley, Phys. Rev. B: Condens. Matter Mater. Phys., 1974, 9, 3573–3581 CrossRef CAS.
- T. Lewis, B. Winter, A. C. Stern, M. D. Baer, C. J. Mundy, D. J. Tobias and J. C. Hemminger, J. Phys. Chem. C, 2011, 115, 21183–21190 CrossRef CAS.
- T. Lewis, M. Faubel, B. Winter and J. C. Hemminger, Angew. Chem., Int. Ed., 2011, 50, 10178–10181 CrossRef CAS PubMed.
- N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth and B. Winter, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 60–70 CrossRef CAS.
- S. Thürmer, R. Seidel, M. Faubel, W. Eberhardt, J. C. Hemminger, S. E. Bradforth and B. Winter, Phys. Rev. Lett., 2013, 111, 173005 CrossRef PubMed.
- Y.-I. Suzuki, K. Nishizawa, N. Kurahashi and T. Suzuki, Phys. Rev. E, 2014, 90, 010302 CrossRef PubMed.
- D. Horinek, S. I. Mamatkulov and R. R. Netz, J. Chem. Phys., 2009, 130, 124507 CrossRef PubMed.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2009, 113, 13279–13290 CrossRef CAS PubMed.
- K. P. Jensen and W. L. Jorgensen, J. Chem. Theory Comput., 2006, 2, 1499–1509 CrossRef CAS PubMed.
- D. Di Tommaso, E. Ruiz-Agudo, N. H. de Leeuw, A. Putnis and C. V. Putnis, Phys. Chem. Chem. Phys., 2014, 16, 7772–7785 RSC.
- R. Hartkamp and B. Coasne, J. Chem. Phys., 2014, 141, 124508 CrossRef PubMed.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2001, 105, 10468–10472 CrossRef CAS.
- P. Jungwirth and D. J. Tobias, J. Phys. Chem. B, 2002, 106, 6361–6373 CrossRef CAS.
- D. F. Liu, G. Ma, L. M. Levering and H. C. Allen, J. Phys. Chem. B, 2004, 108, 2252–2260 CrossRef CAS.
- N. Ottosson, J. Heyda, E. Wernersson, W. Pokapanich, S. Svensson, B. Winter, G. Öhrwall, P. Jungwirth and O. Björneholm, Phys. Chem. Chem. Phys., 2010, 12, 10693–10700 RSC.
- J.-J. Yeh, Atomic Calculations of Photoionization Cross Sections and Asymmetry Parameters, Gordon and Breach, Langhorne, PA, 1993 Search PubMed.
- P. Jungwirth and D. J. Tobias, Chem. Rev., 2006, 106, 1259–1281 CrossRef CAS PubMed.
- J. D. Smith, R. J. Saykally and P. L. Geissler, J. Am. Chem. Soc., 2007, 129, 13847–13856 CrossRef CAS PubMed.
- Y. Wang and Y. Tominaga, J. Chem. Phys., 1994, 101, 3453–3458 CrossRef CAS.
- K. Mizoguchi, T. Ujike and Y. Tominaga, J. Chem. Phys., 1998, 109, 1867–1872 CrossRef CAS.
- Y. Amo and Y. Tominaga, Phys. Rev. E, 1998, 58, 7553 CrossRef CAS.
- T. Ujike, Y. Tominaga and K. Mizoguchi, J. Chem. Phys., 1999, 110, 1558–1568 CrossRef CAS.
- P. Foggi, M. Bellini, D. P. Kien, I. Vercuque and R. Righini, J. Phys. Chem. A, 1997, 101, 7029–7035 CrossRef CAS.
- K. Tielrooij, S. Van Der Post, J. Hunger, M. Bonn and H. Bakker, J. Phys. Chem. B, 2011, 115, 12638–12647 CrossRef CAS PubMed.
- J. T. O'Brien and E. R. Williams, J. Am. Chem. Soc., 2012, 134, 10228–10236 CrossRef PubMed.
- G. Olivieri, A. Goel, A. Kleibert, D. Cvetko and M. A. Brown, Phys. Chem. Chem. Phys., 2016, 18, 29506–29515 RSC.
- O. Madelung, New series group III, 1987, vol. 22, 63, p. 117 Search PubMed.
- S. Hüfner, Photoelectron Spectroscopy: Principles and Applications, Springer-Verlag, Berlin, Heidelberg, New York, London, Paris, Tokyo, Hong Kong, Barcelona, Budapest, 1995 Search PubMed.
- M. N. Pohl, C. Richter, E. Lugovoy, R. Seidel, P. Slavíček, E. F. Aziz, B. Abel, B. Winter and U. Hergenhahn, J. Phys. Chem. B, 2017, 121, 7709–7714 CrossRef CAS PubMed.
- I. Unger, R. Seidel, S. Thürmer, M. N. Pohl, E. F. Aziz, L. S. Cederbaum, E. Muchová, P. Slavíček, B. Winter and N. V. Kryzhevoi, Nat. Chem., 2017, 9, 708 CrossRef CAS PubMed.
- A. W. Lange and J. M. Herbert, J. Chem. Phys., 2011, 134, 204110 CrossRef PubMed.
- V. Frecer and S. Miertus, Int. J. Quantum Chem., 1992, 42, 1449–1468 CrossRef CAS.
- C. McBride, C. Vega, E. G. Noya, R. Ramirez and L. M. Sese, J. Chem. Phys., 2009, 131, 024506 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc03381a |
| This journal is © The Royal Society of Chemistry 2019 |