Open Access Article
Open Access ArticleAn essential descriptor for the oxygen evolution reaction on reducible metal oxide surfaces†
Xiang
Huang‡
ab,
Jiong
Wang‡
c,
Hua Bing
Tao‡
c,
Hao
Tian
a and
Hu
Xu
 *a
*a
aDepartment of Physics, Southern University of Science and Technology, Shenzhen 518055, China. E-mail: xuh@sustc.edu.cn
bSchool of Physics and Technology, Wuhan University, Wuhan 430072, China
cSchool of Chemical and Biomedical Engineering, Nanyang Technological University, 62 Nanyang Drive, Singapore 637459, Singapore
First published on 1st February 2019
Abstract
The development of a universal activity descriptor like the d-band model for transition metal catalysts is of great importance to catalyst design. However, due to the complicated electronic structures of metal oxides, the correlation of the binding energies of reaction intermediates (*OH, *O, and *OOH) in the oxygen evolution reaction (OER) with experimentally controllable properties of metal oxides has not been well established. Here we demonstrate that excess electrons are the essential factor that governs the binding properties of intermediates on the surfaces of reducible metal oxides. We propose that the number of excess electrons (NEE) is an essential activity descriptor toward the OER activities of these oxides, which perfectly reproduces the volcano curve plotted using the descriptor ΔGO − ΔGOH, so that tuning NEE can effectively tailor the OER activities of reducible metal oxide based catalysts. Guided by this descriptor, we predict a novel non-precious catalyst with an overpotential of 0.54 eV, which could be a potential alternative to current Ru or Ir based catalysts.
Introduction
Electrochemical splitting of water has gained enormous interest as a green technique to convert and store renewable energies, such as sunlight and wind, as hydrogen fuels.1,2 However, this process is severely hindered by the oxygen evolution reaction (OER) generally catalyzed by metal oxides at the anode, because of the mismatch in the binding energies of the involved oxygen-containing intermediates (OCI, including *OH, *O, and *OOH).3,4 Substantial efforts have been devoted to clarifying the adsorption behavior of OCI and fundamental insights into the OER on a broad variety of metal oxides.3,5,6To achieve an optimal OER catalyst, it is of primary importance to screen the different structures of metal oxides based on a universal activity descriptor.7–10 So far, a widely accepted descriptor is the difference in binding energies of *O and *OH (ΔGO − ΔGOH), because of the scaling relation existing between the binding energies of *OH and *OOH, i.e., ΔGOOH − ΔGOH = 3.2 ± 0.2 eV.3,4,11,12 The descriptor ΔGO − ΔGOH has been verified to well describe the trend of OER activities on various metal oxide surfaces.1,3 Nonetheless, it has not been fully understood yet which essential factors govern the binding energies of OCI on metal oxide surfaces. Several characteristics of electronic and geometric structures have been observed to correlate with adsorption properties, for instance, the transition metal eg filling,13 σ*-band filling,14 p-band center of oxygen atoms,13,15 and coordinatively unsaturated metal cations.16 However, due to the diversity of the structures of metal oxides (e.g., perovskite, spinel, rutile, rock salt, and bixbyite oxides) and their distinct electronic properties,3 a unified model that can describe the surface reactivity of these different oxides has not been found yet, thus limiting the rational design of OER catalysts.
As is well known, metal oxides can be classified into two main categories: reducible and non-reducible oxides, depending on their capabilities to generate oxygen-deficient structures.17,18 TiO2 is a prototypical reducible oxide. As reported, even if TiO2 is annealed in an oxygen atmosphere up to 1000 °C, the stoichiometric ratio of Ti/O remains to be 1.995;19,20 the reported concentration of surface oxygen vacancies ranges from 2.5% to 14%.21 Namely, the growth of TiO2 naturally accompanies the formation of O vacancies or Ti interstitials. It is noted that such defects lead to the creation of excess electrons in TiO2,20,22–25 which can induce significant changes in the surface reactivity of TiO2(110).22,26–29
Here, we carry out extensive first-principles calculations to investigate the OER on reducible metal oxide surfaces. We demonstrate that excess electrons are the essential factor that governs the binding energies of OCI on the surfaces of reducible metal oxides. Significantly, through tuning the number of excess electrons (NEE) in TiO2, the OER activities of the resultant TiO2(110) surfaces show a volcano correlation with the NEE. Moreover, it perfectly reproduces the volcano curve plotted using the descriptor ΔGO − ΔGOH. Similar volcano correlations are observed when the proposed tuning strategy is extended to other reducible metal oxides. These results indicate that the NEE is an essential activity descriptor for the OER activities of reducible metal oxides. Applying this descriptor, we predict a novel non-precious catalyst (Mo@TiO2(110)) with a theoretical overpotential of 0.54 V, which is lower than that of many good catalysts such as RuO2 and IrO2, and thus it could become a promising alternative to current Ru or Ir based catalysts.
Computational methods
Spin-polarized density functional theory (DFT) calculations are performed using generalized gradient approximation (GGA) in the form of revised Perdew–Burke–Ernzerhof (RPBE) for the exchange–correlation potentials,30–32 the projector augmented wave method,33 and a plane-wave basis set of 450 eV, as implemented in the Vienna ab initio simulation package (VASP).34,35 The OERs are carried out on the surfaces of several typical reducible metal oxides including TiO2, SnO2, NiO, WO3, and ZnO. Different combinations of pseudo-hydrogen atoms with different numbers of valence electrons such as 0.25 e, 0.33 e, 0.42 e, 0.5 e, 0.58 e, 0.66 e, 0.75 e and 1 e are used to tune the excess electrons in these systems. We consider that the OER follows a four-electron mechanism.3,36 The free energy of a pair of proton and electron (H+ + e−) is calculated as a function of applied potential relative to reversible hydrogen electrode (U vs. RHE), i.e., μ(H+ + e−) = 0.5μ(H2) − eU, according to the computational hydrogen electrode (CHE) model proposed by Nørskov et al.36 The potential determining step (pds) is defined as the last step to become downhill in free energy along the OER pathway with the increase of potential.3 The approach of introducing excess electrons and the additional computational details are given in the Methods section and Tables S1–S3 in the ESI.†Results and discussion
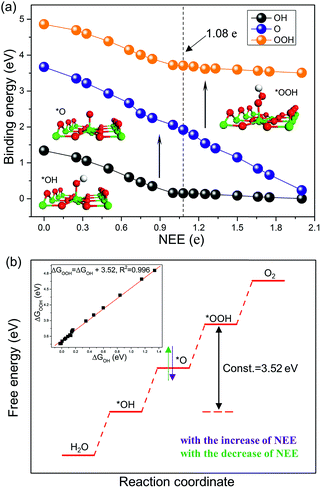
The excess electron environments are simulated by introducing pseudo-hydrogen atoms with different numbers of valence electrons to chemisorb on bridge oxygen atoms on the TiO2(110) surface (Fig. S1†). Considering that each O vacancy brings in two excess electrons in TiO2,20,22–24,26 it is reasonable that one chemisorbed H atom could bring in excess electrons in the same quantity as that of its valence electrons.37–39We first investigate the stable adsorption configurations of *OH, *O, and *OOH on the TiO2(110) surface with tuning the NEE from 0 to 2 e, and then plot their binding energies as a function of NEE, as shown in Fig. 1a. At NEE = 0 (corresponding to a stoichiometric surface), *O prefers to bind with two adjacent five-coordinated Ti atoms (termed Ti5c) and a surface O atom of TiO2(110) simultaneously.40,41 However, with the increase of NEE, *O favors locating above one Ti5c atom via Ti–O bonding. Such cases are distinct from the adsorption of *OH and *OOH, for which the excess electrons do not change their adsorption configurations. Both of them are energetically favorable to occupy the top site of the Ti5c atom.
The NEE has a significant influence on the binding energies of OCI on the TiO2(110) surface. As shown in Fig. 1a, with the increase of NEE from 0 to 1 e, the binding energies of *OH and *OOH species linearly strengthen with slopes of −1.23 eV per e and −1.20 eV per e, respectively (Fig. S2a and b†), while they become nearly zero when the NEE is in the range from 1 e to 2 e, showing an inflection point at NEE = 1 e. In contrast, the binding energy of *O species keeps linearly enhancing from an NEE of 0 to 2 e with a slope of −1.75 eV per e (Fig. S2c†), and the inflection point does not arise until the NEE increases to 2 e (Fig. S3†). As the NEE ranges from 0 to 2 e, the binding energies of *OH, *O, and *OOH are strengthened by 1.33 eV, 3.43 eV, and 1.35 eV, respectively. This is further confirmed by local density of states analysis (Fig. S4†).
These adsorption properties can be explained by the octet rule.42,43 According to this rule, *OH and *OOH need to accept 1 e while *O requires to accept 2 e to form eight-electron outer shells. Therefore, it is comfortable for *OH and *OOH (*O) to capture electrons when the NEE is less than 1 e (2 e). However, their capturing abilities will become weak once the eight-electron outer shells are formed. This explains the occurrence of inflection points and that the observed slopes become smaller (close to zero) after the inflection points. In addition, the slopes of *OH and *OOH in the interval of [0, 1 e] or [1 e, 2 e] are nearly the same, whereas the slope of *O in the interval of [0, 2 e] is remarkably larger than that of *OH and *OOH (−1.23 eV per e and −1.20 eV per e versus −1.75 eV per e). This indicates that *O has a stronger electron capturing ability compared to *OH and *OOH. Overall, these results illustrate that the NEE in TiO2 can essentially determine the binding energies of *OH, *O and *OOH on TiO2(110).
The slopes of the binding energies of *OH and *OOH as a function of NEE are nearly the same in the intervals of [0, 1 e] or [1 e, 2 e]. We thus plot the binding energy of *OOH as a function of that of *OH. The fitting slope is close to 1 (Fig. S2d†), suggesting that they exhibit similar binding properties for binding with the Ti5c atom. For example, both are chemically bound with Ti5c atoms via a single Ti–O bond. The obtained intercept is ΔGOOH − ΔGOH = 3.52 eV (Fig. 1b), which is free from the influence of NEE. It is worth noting that although the intercept proposed in prior studies is 3.2 ± 0.2 eV,3,11,12 our calculations clearly show that the intercept is closely related to the coverage of *OOH and *OH species. At a moderate coverage, e.g., 0.5 ML, the intercept is within the range of 3.2 ± 0.2 eV. However, with the decrease of coverage, it deviates from this value and ultimately converges to 3.52 eV (Fig. S5 and Table S4†).
The intercept ΔGOOH − ΔGOH = 3.52 eV is constant with the variation of NEE. Therefore, tuning the NEE actually changes the relative free energy of *O with respect to that of *OH and *OOH (Fig. 1b). To clarify the effect of excess electrons on the OER activity of the TiO2(110) surface, we constructed the OER free energy diagrams at an NEE of 0, 1.08 e, and 2 e, respectively, as seen in Fig. 2. When the NEE is 0, the reaction is limited by the oxidation of *OH to *O because of the very weak Ti–O bonding. At NEE = 2 e, the Ti–O bonding becomes very strong, leading to the restriction of reaction by the formation of *OOH. An optimal OER activity of the TiO2(110) surface is achieved at an NEE of ∼1.08 e, where ΔGO is nearly equal to half of ΔGOOH + ΔGOH. Significantly, a volcano plot is achieved when the negative overpotentials (−η) of the OER are depicted as a function of NEE, and it is nearly identical to the volcano curve achieved when ΔGO − ΔGOH is applied as the descriptor. As clarified above (Fig. 1a), because NEE essentially governs the binding energies of OCI, such a descriptor should provide a deeper insight into the OER activity compared to ΔGO − ΔGOH. As can be seen from Fig. 3, the potential determining step (pds) clearly changes at NEE = ∼1.08 e. When NEE is less/more than 1.08 e, the pds corresponds to the transformation of *OH to *O/*O to *OOH, represented by the right/left leg of the volcano curve. This indicates that tuning of NEE is able to tailor the OER activity of TiO2(110). We further verify the NEE's effect on the OER activities of TiO2(100) and TiO2(101), which are the other two important surfaces of rutile TiO2. The established volcano curves using the NEE as the descriptor are also nearly identical to those plotted using ΔGO − ΔGOH, which is similar to the case of TiO2(110) (Fig. S6†). All of these results indicate that the OER activity of TiO2 is tailored by tuning NEE.
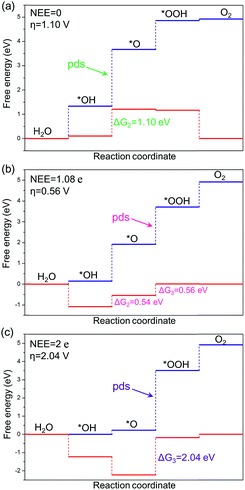 | ||
| Fig. 2 Free energy diagrams of the OER on the TiO2(110) surface at potentials of U = 0 V (blue line) and 1.23 V (red line) vs. RHE with NEE of (a) 0, (b) 1.08 e, and (c) 2 e, respectively. | ||
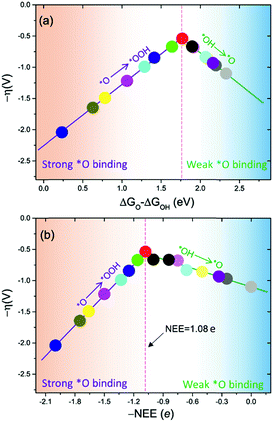 | ||
| Fig. 3 OER activities plotted as a function of (a) ΔGO − ΔGOH and (b) negative NEE (−NEE). The points in (a) and (b) with the same color denote the same set of data. | ||
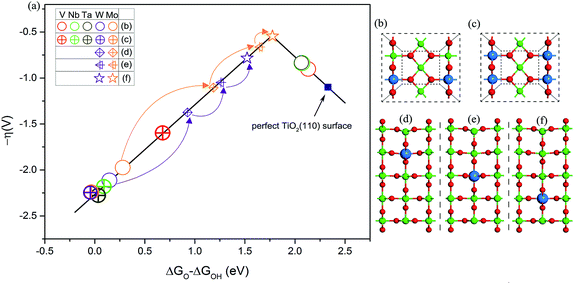
Guided by this descriptor, we next consider applying a doping strategy to introduce excess electrons into TiO2 for the practical design of catalysts. V, Nb, Ta, Mo, and W atoms are applied to substitute the six-coordinated Ti atom in TiO2(110). Compared to the valence of Ti (+4) in TiO2, the common valence of V, Nb, and Ta is +5 and that of Mo and W is +6. This suggests that each substituted V, Nb, or Ta atom should provide an NEE of 1 e and each Mo or W atom should provide an NEE of 2 e in principle. As shown in Fig. 4a and b, the OER activities of V, Nb, or Ta atom doped TiO2(110) lie on the right leg. This is because the NEE provided by V, Nb, or Ta atoms is less than 1.08 e, corresponding to the weak Ti–O bonding. By contrast, the OER activities of Mo or W atom doped TiO2(110) are located on the left leg, which is attributed to the strong Ti–O bonding, because a Mo or W atom can provide an NEE of more than 1.08 e. Additionally, we use the same two dopants to substitute two six-coordinated Ti atoms on the surface (Fig. 4c). As a result, all the OER activities are located on the left leg of the volcano curve. This is because two V, Nb, or Ta atoms can also provide NEE of 2 e, significantly enhancing the binding energy of *O compared to the cases with one heteroatom as the dopant. However, for the case of doping with two Mo or W atoms, the OER activity of TiO2(110) slightly decreases. This is explained that upon an O atom accommodating 2 e, the additional NEE does not severely affect the binding energy of *O species, as discussed above (Fig. 1a). All these results fully support our proposed mechanism.
To further improve the OER activity of TiO2(110), we chose one Mo or W atom to substitute the Ti atom located at the second, third, and fourth layers of TiO2(110). The motivation is based on an assumption that the NEE captured by intermediates is related to the distance from the active site (surface Ti5c atom) to the dopant.22,44–46 On the surface, due to a short distance between the dopant and active site, the excess electrons are easily transferred to intermediates.44,45,47 However, with the increase of distance, the NEE available for intermediates is speculated to be 2δ e (0 ≤ δ ≤ 1).22,48 In other words, the OER activity can be tailored via changing the distance between the dopant and active site. With changing the location of a Mo or W atom from the surface to the second, third, and fourth layers of TiO2(110), the OER activities of the resultant surfaces progressively improved (Fig. 4a and Table S5†). In particular, the surface with a Mo atom doped at the fourth layer of TiO2(110) exhibits OER activity nearly close to the peak of the volcano curve with an overpotential of 0.54 V, which is lower than that of many good catalysts such as Co3O4 (ref. 49) and is even comparable to that of RuO2 and IrO2.2,3,50–52 Considering that the Mo dopant is non-precious and resistant to acid corrosion, this designed catalyst (named Mo@TiO2(110)) could become a potential alternative to current Ru or Ir based proton exchange membrane water electrolyzers, the most advanced device for water splitting.
Similar to TiO2, WO3 is another typical reducible metal oxide and is widely used in chemical sensors.53 We investigate the variation of OER activity of the WO3(001) surface by tuning the NEE from 0 to 2 e. As expected, a volcano curve for WO3(001) also appears and the optimal activity is achieved at NEE = ∼1.16 e (Fig. S7†). In addition, we test the influence of excess electrons on other typical reducible metal oxides, including NiO, ZnO, and SnO2. The NEE reproduces the volcano curves of NiO(001), ZnO(10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 0), and SnO2(110) plotted using ΔGO − ΔGOH (Fig. S8†). These results provide solid evidence that tuning the NEE is able to tailor the OER activities of reducible metal oxide based catalysts.
0), and SnO2(110) plotted using ΔGO − ΔGOH (Fig. S8†). These results provide solid evidence that tuning the NEE is able to tailor the OER activities of reducible metal oxide based catalysts.
Conclusion
In summary, we investigated the effect of excess electrons on the OER activities on the surfaces of reducible metal oxides. We demonstrate that excess electrons are the essential factor governing the binding energies of OCI on the surfaces of these metal oxides. When using NEE as a descriptor, it exhibits a volcano correlation with OER activities of reducible metal oxides. Moreover, it perfectly reproduces the volcano curve plotted using the descriptor ΔGO − ΔGOH, indicating that NEE is an essential activity descriptor toward the OER activities of reducible metal oxide based catalysts. Guided by this descriptor, we predict a non-precious catalyst (Mo@TiO2(110)) with an overpotential as low as 0.54 eV, which could thus become a potential alternative to Ru or Ir based proton exchange membrane water electrolyzers. Our findings provide a deep insight into understanding the design of OER catalysts based on reducible metal oxides.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (NSFC, Grant Nos. 11674148 and 11334003), the Guangdong Natural Science Funds for Distinguished Young Scholars (No. 2017B030306008), and the Center for Computational Science and Engineering of Southern University of Science and Technology.References
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- I. Katsounaros, S. Cherevko, A. R. Zeradjanin and K. J. J. Mayrhofer, Angew. Chem., Int. Ed., 2014, 53, 102–121 CrossRef CAS PubMed.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. A. Hansen, J. I. Martínez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Nørskov and J. Rossmeisl, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- M. T. M. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- J. Rossmeisl, Z. W. Qu, H. Zhu, G. J. Kroes and J. K. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- W. T. Hong, R. E. Welsch and Y. Shao-Horn, J. Phys. Chem. C, 2016, 120, 78–86 CrossRef CAS.
- S. Trasatti, J. Electroanal. Chem. Interfacial Electrochem., 1980, 111, 125–131 CrossRef CAS.
- S. Trasatti, Electrochim. Acta, 1984, 29, 1503–1512 CrossRef CAS.
- H. Xu, D. Cheng, D. Cao and X. C. Zeng, Nat. Catal., 2018, 1, 339–348 CrossRef.
- R. Christensen, H. A. Hansen, C. F. Dickens, J. K. Nørskov and T. Vegge, J. Phys. Chem. C, 2016, 120, 24910–24916 CrossRef CAS.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS.
- J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385 CrossRef CAS PubMed.
- Y. Matsumoto, S. Yamada, T. Nishida and E. Sato, J. Electrochem. Soc., 1980, 127, 2360–2364 CrossRef CAS.
- J. H. Montoya, A. D. Doyle, J. K. Norskov and A. Vojvodic, Phys. Chem. Chem. Phys., 2018, 20, 3813–3818 RSC.
- H. B. Tao, L. Fang, J. Chen, H. B. Yang, J. Gao, J. Miao, S. Chen and B. Liu, J. Am. Chem. Soc., 2016, 138, 9978–9985 CrossRef CAS PubMed.
- A. Ruiz Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7, 6493–6513 CrossRef CAS.
- Y. Wang, Y. Li and T. Heine, J. Am. Chem. Soc., 2018, 140, 12732–12735 CrossRef CAS PubMed.
- T. Bak, J. Nowotny and M. K. Nowotny, J. Phys. Chem. B, 2006, 110, 21560–21567 CrossRef CAS PubMed.
- P. Deák, B. Aradi and T. Frauenheim, Phys. Rev. B, 2015, 92, 045204 CrossRef.
- M. A. Henderson, W. S. Epling, C. H. F. Peden and C. L. Perkins, J. Phys. Chem. B, 2003, 107, 534–545 CrossRef CAS.
- Y.-Y. Yu and X.-Q. Gong, ACS Catal., 2015, 5, 2042–2050 CrossRef CAS.
- C. M. Yim, C. L. Pang and G. Thornton, Phys. Rev. Lett., 2010, 104, 036806 CrossRef CAS PubMed.
- Z. Helali, A. Jedidi, O. A. Syzgantseva, M. Calatayud and C. Minot, Theor. Chem. Acc., 2017, 136, 100 Search PubMed.
- M. Setvin, U. Aschauer, J. Hulva, T. Simschitz, B. Daniel, M. Schmid, A. Selloni and U. Diebold, J. Am. Chem. Soc., 2016, 138, 9565–9571 CrossRef CAS PubMed.
- H. Tian, B. Xu, J. Fan and H. Xu, J. Phys. Chem. C, 2018, 122, 8270–8276 CrossRef CAS.
- A. C. Papageorgiou, N. S. Beglitis, C. L. Pang, G. Teobaldi, G. Cabailh, Q. Chen, A. J. Fisher, W. A. Hofer and G. Thornton, Proc. Natl. Acad. Sci., 2010, 107, 2391–2396 CrossRef PubMed.
- R. Schaub, P. Thostrup, N. Lopez, E. Lægsgaard, I. Stensgaard, J. K. Nørskov and F. Besenbacher, Phys. Rev. Lett., 2001, 87, 266104 CrossRef CAS PubMed.
- S. Wendt, P. T. Sprunger, E. Lira, G. K. H. Madsen, Z. Li, J. Ø. Hansen, J. Matthiesen, A. Blekinge-Rasmussen, E. Lægsgaard, B. Hammer and F. Besenbacher, Science, 2008, 320, 1755–1759 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B, 1999, 59, 7413–7421 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- C. Di Valentin, G. Pacchioni and A. Selloni, Phys. Rev. Lett., 2006, 97, 166803 CrossRef PubMed.
- Z.-T. Wang, J. C. Garcia, N. A. Deskins and I. Lyubinetsky, Phys. Rev. B, 2015, 92, 081402 CrossRef.
- N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2009, 113, 14583–14586 CrossRef CAS.
- H. Xu and S. Y. Tong, Surf. Sci., 2013, 610, 33–41 CrossRef CAS.
- Á. Valdés, Z. W. Qu, G. J. Kroes, J. Rossmeisl and J. K. Nørskov, J. Phys. Chem. C, 2008, 112, 9872–9879 CrossRef.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Phys. Rev. Lett., 2012, 108, 116103 CrossRef CAS PubMed.
- I. Langmuir, J. Am. Chem. Soc., 1919, 41, 868–934 CrossRef CAS.
- Y. Yoon, Y.-G. Wang, R. Rousseau and V.-A. Glezakou, ACS Catal., 2015, 5, 1764–1771 CrossRef CAS.
- Y. Yoon, Y. Du, J. C. Garcia, Z. Zhu, Z.-T. Wang, N. G. Petrik, G. A. Kimmel, Z. Dohnalek, M. A. Henderson, R. Rousseau, N. A. Deskins and I. Lyubinetsky, ChemPhysChem, 2015, 16, 313–321 CrossRef CAS PubMed.
- S. Wendt, P. T. Sprunger, E. Lira, G. K. H. Madsen, Z. Li, J. Ø. Hansen, J. Matthiesen, A. Blekinge-Rasmussen, E. Lægsgaard, B. Hammer and F. Besenbacher, Science, 2008, 320, 1755–1759 CrossRef CAS PubMed.
- N. A. Deskins, R. Rousseau and M. Dupuis, J. Phys. Chem. C, 2010, 114, 5891–5897 CrossRef CAS.
- Y.-F. Li, U. Aschauer, J. Chen and A. Selloni, Acc. Chem. Res., 2014, 47, 3361–3368 CrossRef CAS PubMed.
- M. García-Mota, M. Bajdich, V. Viswanathan, A. Vojvodic, A. T. Bell and J. K. Nørskov, J. Phys. Chem. C, 2012, 116, 21077–21082 CrossRef.
- L. G. V. Briquet, M. Sarwar, J. Mugo, G. Jones and F. Calle-Vallejo, ChemCatChem, 2017, 9, 1261–1268 CrossRef CAS.
- C. F. Dickens and J. K. Nørskov, J. Phys. Chem. C, 2017, 121, 18516–18524 CrossRef CAS.
- R. R. Rao, M. J. Kolb, N. B. Halck, A. F. Pedersen, A. Mehta, H. You, K. A. Stoerzinger, Z. Feng, H. A. Hansen, H. Zhou, L. Giordano, J. Rossmeisl, T. Vegge, I. Chorkendorff, I. E. L. Stephens and Y. Shao-Horn, Energy Environ. Sci., 2017, 10, 2626–2637 RSC.
- G. Eranna, B. C. Joshi, D. P. Runthala and R. P. Gupta, Crit. Rev. Solid State Mater. Sci., 2004, 29, 111–188 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Computational methods. See DOI: 10.1039/c8sc04521f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2019 |