Population analysis to increase the robustness of molecular computational identification and its extension into the near-infrared for substantial numbers of small objects

Abstract

The first population analysis is presented for submillimetric polymer beads which are tagged with five multi-valued logic gates, YES, 2YES + PASS 1, YES + PASS 1, YES + 2PASS 1 and PASS 1 with H⁺ input, 700 nm near-infrared fluorescence output and 615 nm red excitation light as the power supply. The gates carry an azaBODIPY fluorophore and an aliphatic tertiary amine as the H⁺ receptor where necessary. Each logic tag has essentially identical emission characteristics except for the H⁺-induced fluorescence enhancement factors which consistently map onto the theoretical predictions, after allowing for bead-to-bead statistical variability for the first time. These enhancement factors are signatures which identify a given bead type within a mixed population when examined with a ‘wash and watch’ protocol under a fluorescence microscope. This delineates the scope of molecular computational identification (MCID) for encoding objects which are too small for radiofrequency identification (RFID) tagging.

---

Introduction

Molecular logic-based computation^1–10 is a field where molecules perform Boolean and related operations usually belonging to semiconductor-based information processors. Recent developments include gate concatenation,^11–13 combinatorial sensing,^14,15 multi-analyte sensing,^16–22 gaming,^23–26 logical materials,^27–31 human-level computation^32–34 and cryptography.^35–37 An intrinsic strength of molecular logic is that the gates are nanometric in size and therefore capable of operating in nanospaces. The first demonstration of a molecular logic operation in a small space which was barred to semiconductor devices was ion-driven intra-micellar AND logic with fluorescence output.³⁸ The first robust application of molecular logic-based computation which could not be carried out by semiconductor-based computation was molecular computational identification (MCID).^39–41 A powerful application area for molecular logical computation is inside living cells^42–47 where semiconductor-based devices have various incompatibilities.

There is a need for identifying small objects within a population in several fields of science. Such situations can arise during cell diagnostics or during the analysis of combinatorial chemistry libraries.^49–52 Although coloured or fluorescent tags can be used for this purpose,⁵⁰ the number of objects which can be distinguished is very limited. We proposed MCID at the proof-of concept level,³⁹ where it is possible to employ fluorescent tags whose output signal is controlled by external conditions such as pH. Such input–output relationships can be put on a Boolean logic basis. Many Boolean logic gates are available for exploitation in this way. Being an identification technique, MCID has security implications for the object populations under study. Even large biomolecules have been suggested as such objects.⁴⁸ Each logic descriptor becomes a signature. The substantial diversity of Boolean logic gate types, when combined with the large diversity of chemical species and their interactions, can be employed to build large sets of tags. Such sets are further amplified when pairs of them are employed to double-tag the objects. Fluorescence readout is employed to interrogate the tagged objects.

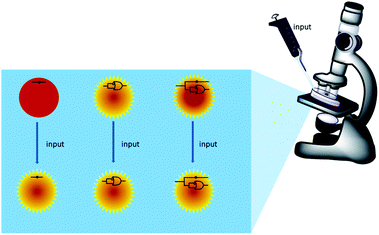
Scheme 1 summarizes the approach. A mixture of polymer beads carrying various logic tags such as YES, PASS 1 and YES + PASS 1 are held on a microscope stage. These tags employ chemical inputs such as H⁺ and fluorescence output. The bead carrying the YES gate responds to ‘high’ H⁺ levels by switching its fluorescence from ‘low’ to ‘high’. The bead labelled with the PASS 1 gate has ‘high’ fluorescence whatever the H⁺ level. The double-labelled bead with the YES + PASS 1 tag possesses an intermediate enhancement of the fluorescence signal upon acidification. The polymer beads are carefully acidified during microscopic observation and different bead types respond with different H⁺-induced fluorescence enhancement ratios (FE_H+ values).

Scheme 1 Illustration of the molecular computational identification method. For instance, YES, PASS 1 and YES + PASS 1 logic tags driven by H⁺ input and showing a fluorescence output are attached to polymer beads so that they can be identified under a microscope when acid is carefully added with a pipet. The physical electronic symbols of these gates are shown. Although the fluorescence of the YES logic tag is initially weak, acidification causes a strong signal. The PASS 1 logic tag remains highly emissive before and after acidification. YES + PASS 1 logic tag is partially emissive before acidification but becomes fully fluorescent after acid is added. YES, PASS 1 and YES + PASS 1 logic tags give rise to large, no and intermediate H⁺-induced fluorescence enhancements respectively.

However, the original proof-of-concept paper³⁹ only had one pair of micrographs for single-bead logic operations. The standard range of FE_H+ values for each logic type could not be established. In other words, the practical limits of applicability of the MCID method could not be established. Now we present the first testing of small but substantial populations of these under microscopy conditions, which extends the scope of MCID by reliably and unambiguously identifying tags of five logic types. We also present the first near-infra red (NIR) logic tags so that extra spectral bandwidth becomes exploitable by the MCID technique.

Results and discussion

Strategy

In order to strengthen the foundation of the MCID approach, it is critical to establish its scope under practical conditions. We do this now by studying significant populations of identical copies of beads tagged with a given logic type under fluorescence microscopy conditions before going on to identifications of sub-sets in mixed bead populations. In particular, we study tags which emit in the NIR region which is notorious for having poorly switchable fluorescence owing to the low excited state energies involved. However, success in this spectral range will be highly rewarding since it will open up much bandwidth previously unavailable to MCID and related logic switching applications.

Spectroscopy

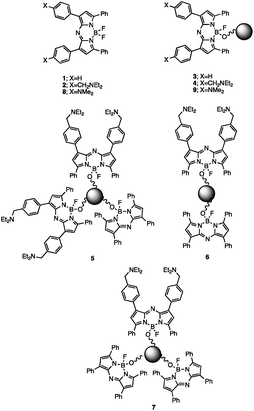
AzaBODIPY (azaborondipyrromethene) dyes^53–69 are highly photostable NIR fluorophores, some of which show environmental sensitivity. NIR fluorophores are particularly desirable because of their biocompatibility in terms of high transmission of their signals through tissue and many other materials without much interference from autofluorescence. Fluorescent PET (photoinduced electron transfer) sensors^70,71 have been built by attaching suitable methylene spacers and amine receptors to these fluorophores.^54,56,64 Fluorescent ICT (internal charge transfer) sensors^70,72 have also been built by direct attachment of receptors.^57–62 These studies inspired us to build H⁺-driven PASS 1 logic gate 1⁵³ and YES logic gate 2⁵⁴ (Fig. 1 and ESI†) and to construct TentaGel™ S–OH bead-bound versions 3 and 4 respectively according to a procedure developed by O'Shea⁵⁸ so that NIR MCID tags for substantial populations of objects could be introduced. The double-labelled cases 5–7 were prepared by attaching 1 and 2 in the appropriate molar ratios to the beads. As shown in Table 2, this is an easy way to build logic gate arrays which are integrated in parallel. In contrast, serial integration of molecular logic gates is still achievable by the community only in relatively small numbers and configurations.

Fig. 1 Structure of the free logic gates and those tagged on the TentaGel™ S–OH beads.

The fluorescent characterization of the logic tags are conducted in solution before attachment to the beads. As seen in Table 1, the wavelengths in absorption and emission of 1 and diprotonated 2 are essentially identical. The quantum yields of fluorescence in methanol : water for 1 and diprotonated 2 are found to be 0.11 and 0.17 respectively (by using 1 in CHCl₃ as the standard⁵³). Aggregation of the rather hydrophobic 1 in mixed aqueous solution causes the significant downward deviation but this problem disappears when the fluorophores are bound on beads (see below). Such similarities are pre-requisites for the MCID method to be used in its most versatile form.

Table 1 pH-dependent fluorescence properties of logic gates when free in solution or when tagged onto TentaGel™ S–OH beads^a

Logic	λ acid/nm	λ base/nm	FEH+^b(ideal)	pKa*^c	m
a 10^−6 M free logic gates or tagged on TentaGel™ S–OH beads at 1% total loading in methanol : water (1 : 1, v/v) excited at 615 nm. b H^+-induced fluorescence enhancement factor. This is ideally infinity for H^+-driven YES and 1.0 for H^+-driven PASS 1 gates respectively, if PET is a much faster deexcitation process than fluorescence.^70 The ideal FEH+ values for the combined gates are calculated from the multi-valued logic tables (Table 2), along with the following assumptions: (i) the gate proportion on-bead is the same as the gate feed ratio during synthesis, (ii) the fluorescence quantum yields of the gates on-bead are unchanged from those found in free solution, (iii) on-bead inter-gate interactions, if any, have negligible optical consequences. c by analysis of IF-pH data according to the equation, log[(IFmax − IF)/(IF − IFmin)] = m. pH − m. pKa*, where m = 1 ideally.^73 The correlation coefficient (R^2) is >0.99 in all cases.
YES (free) [2]	679	673	6.2 (∞)	8.1	0.83
PASS 1 (free) [1]	673	671	1.4 (1.0)	—	—
YES [4]	704	710	5.8 (∞)	6.1	0.93
2YES + PASS 1 [5]	700	706	3.8 (3.0)	5.9	0.85
YES + PASS 1 [6]	700	705	2.3 (2.0)	6.1	0.92
YES + 2PASS 1 [7]	702	704	2.1 (1.5)	6.2	0.85
PASS 1 [3]	697	696	1.0 (1.0)	—	—

---

The bead-bound logic tags are characterized next. The bead-bound 3 and 4 possess fluorescence emission wavelengths close to those seen in the free-solution cases, except for a small apparent red-shift caused by inner-filtering of the blue edge of the emission band due to the high local concentration of these fluorophores with small Stokes-shifts.⁴¹ Although absolute quantum yields are difficult to measure for solids, the fluorescence quantum yield ratio between 3 and 4 (in its diprotonated form) is 1.16 : 1.00, which is close to the assumptions in Table 1.

Characterization of the pH-dependence of fluorescence is the next logical step. The pK_a value of 2 is found to be 8.1 by Henderson-Hasselbalch analysis of the pH-dependent fluorescence intensity.⁷³ As expected of a H⁺-driven YES gate, the fluorescence only switches ‘on’ when the H⁺-level is high. The thermodynamics of the PET process from the diethylaminomethyl side-chain to the azaBODIPY fluorophore (ΔG_PET) can be estimated from the Weller eqn (1)⁷⁴ as being −0.3 eV.

ΔG_PET =−E_{ex fluorophore} − E_{red fluorophore} + E_{ox receptor} − 0.1 (1)

where E_{ex fluorophore} is excited state energy of the fluorophore (1.77 eV for ca. 700 nm emission of on-bead gates), E_{red fluorophore} is the reduction potential of the fluorophore (−0.41 V vs. sce)^68,75,76 and E_{ox receptor} is the oxidation potential of the amine receptor (+1.19 V vs. sce).⁷⁷ Protonation of the amine receptor renders ΔG_PET large and positive. Because of the suppression of PET from the amine to the fluorophore upon protonation, the fluorescence intensity of 2 switches ‘on’ by a factor of 6.2. Unsurprisingly, the fluorescence emission of 1 is largely pH-independent and corresponds to a PASS 1 gate action. The significant deviations from ideal behaviour are due to time-dependent aggregation of the rather hydrophobic 1 in mixed aqueous solution, as seen above for the fluorescence quantum yields. Such time-dependent aggregation effects disappear when the gates are bound onto the beads.

Does the molecular logic behaviour of the tags survive the bead-attachment? The logic behaviour is indeed found to be carried over to the bead-bound forms, where the YES gate 4 displays a similar H⁺-induced fluorescence enhancement (FE_H+) factor of 5.8 (Fig. 2). The generally lower polarity of the bead surface environment when compared to the mixed aqueous medium has no significant effect on PET rates in our case,^{56,64,78–80} probably because of the rather exergonic PET process (as calculated for acetonitrile solution where ΔG_PET = −0.3 eV). In other words, PET probably remains exergonic in the bead surface environment. In general, FE_H+ values can be >1000 under optimal conditions,^81,82e.g. in water solution, so that the infinity value simply calculated in Table 2 for a YES gate is defendable. The assumptions, mentioned in Table 1, underlying such ideal calculations are reasonably realistic since the correlation between observed and ideal FE_H+ values is described by the eqn (2), with a R² value of 0.96 for 4 data points. The data point for YES itself, containing an infinity term, is not included.

FE_H+observed = 1.24FE_H+ideal (2)

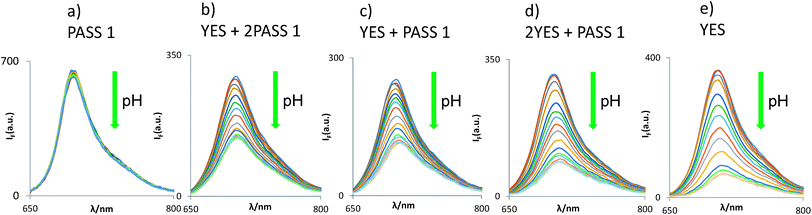Fig. 2 pH-dependent fluorescence spectra of five types of logic gates when tagged onto TentaGel™ S–OH beads. Each of the panels (a)–(e) concerns beads of the specified logic type only.

Table 2 Multi-valued logic tables for parallel gate combinations whose outputs are summed for observation

In	YES	PASS 1	2YES + PASS 1	YES + PASS 1	YES + 2PASS 1
	Out	Out	ΣOut	ΣOut	ΣOut
0	0	1	1	1	2
1	1	1	3	2	3
	FEH+ = ∞	FEH+ = 1	FEH+ = 3	FEH+ = 2	FEH+ = 1.5
	Binary	Binary	Quaternary	Ternary	Quaternary

---

On the other hand, the pK_a* value is shifted to lower values by 2.0 pH units when the YES gate is transferred onto the bead surface, owing to the preferential destabilization of its diprotonated form by the apolar environment.

The excellent compatibility of 3 and 4 in terms of their spectral parameters (as expected of well-behaved fluorescent PET sensors^83–85), underpins our construction of bead-bound gates of the following types: H⁺-driven 2YES + PASS 1 (5), YES + PASS 1 (6) and YES + 2PASS 1 (7). Their logical basis is given in Table 2 and their spectra are shown in Fig. 2. As seen in Table 1, these cases produce essentially constant pK_a* values, which is gratifying. Spectroscopically measured FE_H+ factors are also reasonably close to the ideal values. Importantly, each of the five multi-valued logic types⁸⁶ examined can be distinguished by their FE_H+ values as expected for the successful application of the MCID method.

It is worth emphasizing that multi-valued logic is avoided in a majority of current semiconductor devices because numbers larger than 0 and 1 begin to lose their distinguishability because of error build-up over many serial operations and because of noise accumulation during data transmission.⁸⁷ Importantly, our MCID method has neither of these two difficulties. Indeed, the experiments in this paper will delineate the level of multi-valued logic that can be tolerated under our experimental conditions.

H⁺-driven YES logic gate 8^57,58 is a known fluorescent ICT-based pH sensor^70,72 with a shorter synthesis route than 1. So we also test this for potential MCID tag behaviour. In free solution, it has λ_acid = 683 nm, λ_base = 680 nm, FE_H+ = 7.1 and pK_a* = 1.7. This low pK_a* value is not surprising since it involves an aromatic amine receptor joined to an electron-withdrawing moiety but it does not augur well for a bead-based tag since the apolar environment would push its pK_a* to impracticably low values. Indeed, the bead-immobilized version (9) has λ_acid = 682 nm, λ_base = 695 nm, FE_H+ >2.3 and pK_a* < 1.3. Some tag leaching is also seen due to acid hydrolysis under these extreme conditions, which is a further reason to preclude 8 and 9 from our current MCID application.

Microscopy

Now that the spectroscopic evaluation is available, we can proceed to the fluorescent microscopic examination of the small objects so that each object can be assessed for its H⁺ input – fluorescence output behaviour. The original MCID study had access to only a single pair of fluorescence micrographs,³⁹ so that statistics of the objects could not be evaluated. Logic-tagged beads (diameter 0.1–0.2 mm) are now studied extensively, and in parallel, under an inverted fluorescence microscope as individuals in a population according to a ‘wash and watch’ protocol.³⁹ Restrained beads, lightly pressed between a pair of cover slips, initially swollen under basic conditions (pH 10) are gently infused with acid (1 M HCl) upon the microscope stage until the image intensities reach equilibrium. While significant movement of the beads are seen on occasion, these displacements are small enough to maintain the relative positions of the beads.

First, populations of identical copies are considered to evaluate the reliability of microscopy FE_H+ values as a MCID signature. FE_H+ can serve as a rather robust signature because it is a ratio of the steady-state mean fluorescence intensities of a bead after and before acid infusion. In particular, we measure mean intensities within a circle of half the bead radius drawn about the bead centre. This procedure minimizes errors in the mean intensities caused by bead–bead overlap effects under the nearly close-packed conditions. Such fluorescence ratiometry⁸⁹ is a time-honoured way of minimizing object-to-object variation in optical path length, illumination intensity, fluorophore density, quencher density, fluorophore photodegradation and other inhomogeneities.

Some reductions of the spectroscopically determined FE_H+ values (Table 1) are to be expected when measured under microscopy conditions because of the lower spectral resolution of commonly available excitation and emission filters available for microscopes at reasonable prices and because of their mismatch with azaBODIPY characteristic wavelengths. Analysis of the micrograph pairs in acid and base for 3–7 (Fig. 3a–e) allows the extraction of FE_H+ values for each individual bead of each logic type. A series of micrographs in acid annotated with these FE_H+ values is also shown in the third row of Fig. 3a–e. When this dataset is analyzed further according to a histogram (Fig. 4) 3–7 are found to have average FE_H+ values of 1.02 ± 0.02 (n = 14), 2.20 ± 0.11 (n = 12), 1.50 ± 0.05 (n = 13), 1.33 ± 0.02 (n = 15) and 1.20 ± 0.03 (n = 12) respectively, where the standard deviation of the bead-to-bead variation is given as the uncertainty and where the number of beads analyzed is given in parentheses. These average values and standard deviations of FE_H+ values are the most important advance made by this paper because they show the extent of practical applicability of each MCID logic type as an ID tag. In other words, these values show how many separate MCID logic types can be fitted into a given interval of FE_H+ values without sacrificing the accuracy of unambiguous identification.

Fig. 3 Fluorescence micrographs of TentaGel™ S–OH beads, each set tagged with one of five types of logic gates. Each of the panels (a)–(e) concerns beads of the specified logic type only. The excitation filter passes 545–580 nm and the emission filter passes >610 nm. The initial basic solution is at pH 10, which is then infused with 1 M HCl. Only those beads whose perimeters are essentially fully visible are analysed.

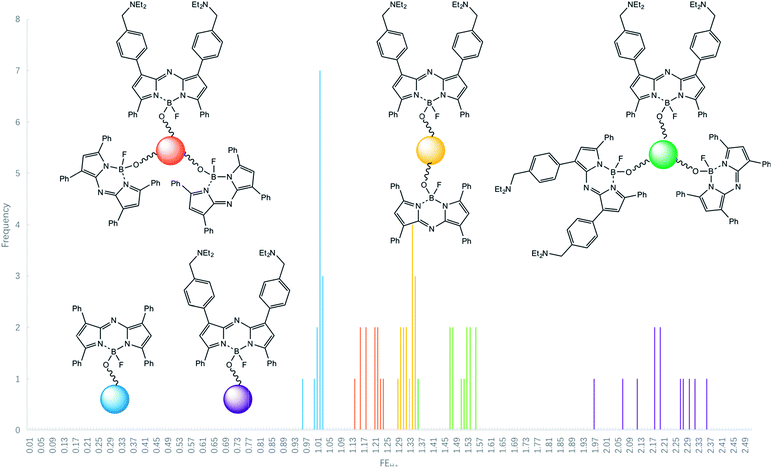Fig. 4 Histogram for the occurrence of various FE_H+ values in logic-tagged beads for samples of identical copies.

The histogram includes the bins 0.00–1.00 because this region will be occupied in the future by NOT gates (FE_H+ being ideally 0.00) and NOT + PASS 1 gates (FE_H+ = 0.50) for example. We note that a Gaussian-type distribution of each bead type cannot be expected to emerge fully (Fig. 4) in the relatively small populations (ca. 12 of each logic type) studied here. Although the FE_H+ values are significantly reduced under our practical microscopy conditions, the five types of logic tags examined here remain distinguishable. It is noticeable, however, that an outlier of the 2YES + PASS 1 tagged set comes close to the YES + PASS 1 set. The correlation between the FE_H+ values obtained from spectroscopy of bulk bead samples (Fig. 2) and the average FE_H+ values obtained from microscopy of individual beads under our conditions (Fig. 3) is described by eqn (3), with a R² value of 0.96 for 5 data points. Its non-zero intercept shows that the microscopy experiments carry a significant background, as might be expected.

FE_H+microscopy = 0.24FE_{H+spectrosopy} + 0.73 (3)

We also note that the current uncertainties would make it hard for us to use a logic tag like quinary (YES + 3PASS 1) alongside quaternary (YES + 2PASS 1) for instance. Nevertheless, better-endowed laboratories should be able to reduce background signals and to improve the resolution of logic signatures reported here by employing excitation lamps/LEDs and excitation and emission filters more closely matched to azaBODIPY fluorophores so that multiple-valued logic gates of higher order will become available as MCID tags. Such laboratories will also be able to analyze the micrographs obtained under lower magnification so that larger numbers of beads are observed in parallel. We have refrained from doing this so that each bead in the images occupies suitably large numbers of pixels to allow its mean intensity to be measured with sufficient accuracy with our resources. Overall, the practical limits noted in this paper can be reduced by others in the community to make the MCID approach more powerful for identification purposes.

We are now in position to apply the contextualized FE_H+ values for microscopy under ‘wash and watch’ conditions to a population of mixed beads. Fig. 5a and b display a micrograph pair in base and acid of such a sample containing equal weights of each of the five bead types. The microscopy FE_H+ values of all beads fall into one of five groups (Fig. 5c) and this allows each bead to be unambiguously identified as one of the five logic types (Fig. 5d). Because this demonstrator only considers five MCID tags in bead populations of about 12 in each micrograph, there will naturally be a degree of redundancy when the beads are identified individually. Furthermore, each bead type cannot be expected to occur at equal frequencies within the relatively small population (12). Nevertheless, this study clearly shows how a single fluorophore can give rise to not one,⁵⁰ but at least five microscopically distinguishable logic tags by employing just two parent Boolean gates (YES and PASS 1) under microscopy conditions. Other parent gates, e.g. NOT,³⁹ AND³⁹etc, other-coloured fluorophores⁵⁰ and other inputs can be applied similarly in future studies so that each object within an arbitrarily large population can receive a unique MCID identifier. The statistical basis of the current demonstrator puts us well on the road to that goal.

Fig. 5 Fluorescence micrographs of a mixed population containing PASS 1, YES, 2 YES + PASS 1, YES + PASS 1 and YES + 2 PASS 1 logic tagged beads in (a) base, (b) acid, (c) acid micrograph annotated with FE_H+ values and (d) acid micrograph annotated with the logic types assigned with the aid of Fig. 4.

Experimental

Compounds 1⁵³ and 2⁵⁴ were synthesized essentially according to the literature (ESI†). The pH-dependent fluorescence spectra for the tagged-beads were obtained by allowing the swollen beads to settle under gravity in a quartz UV-vis absorption cell with 2 mm path and then by interrogating the cell in a front-surface accessory. This approach, though requiring a 0.6 mL of swollen beads, is easy to set up. We formerly used a quartz fibre optic accessory on much smaller bead volumes but this method required much painstaking setting up.³⁹ pH-dependent micrographs were recorded on swollen beads held between coverslips. The mean intensities of each complete bead in the field-of-view were measured in basic and acidic solution as explained previously. While this approach is sufficient for our present purpose, it is a pleasure to note more elegant ways of restraining beads while they are being interrogated by solvent vapours.⁹⁰

Conclusions

Molecular computational identification (MCID) is practically validated for encoding submillimetric objects by demonstrating that the statistical variability of a given logic tag does not interfere with the unambiguous assignment of each object in a small but substantial population to one of five logic types. Future studies should be able to extend the number of logic types and the population size. The present work also extends the spectral range of the logic tags for the previously known blue^39–41 and green⁴¹ out into the particularly advantageous near-infrared. The availability of a range of MCID tag logic types in a range of colours strengthens the field of object encoding.^91–97

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We are grateful to the China Scholarship Council, Queen's University Belfast, B. Liu, X. G. Ling, L. H. Wang, G. M. Yao and F. F. Huang for support and help. We thank Professor Donal O'Shea for encouragement.

Notes and references

1. A. P. de Silva, H. Q. N. Gunaratne and C. P. McCoy, Nature, 1993, 364, 42.
2. Molecular and Supramolecular Information Processing, ed. E. Katz, Wiley-VCH, Weinheim, 2012.
3. Biomolecular Information Processing, ed. E. Katz, Wiley-VCH, Weinheim, 2012.
4. K. Szacilowski, Infochemistry, Wiley, Chichester, 2012.
5. A. P. de Silva, Molecular Logic-based Computation, Royal Society of Chemistry, Cambridge, 2013.
6. V. Balzani, A. Credi and M. Venturi, Molecular Devices and Machines. VCH, Weinheim, 2nd ed., 2008.
7. J. Andreasson and U. Pischel, Chem. Soc. Rev., 2015, 44, 1053.
8. A. P. de Silva, Y. Leydet, C. Lincheneau and N. D. McClenaghan, J. Phys.: Condens. Matter, 2006, 18, S1847.
9. B. Daly, J. Ling, V. A. D. Silverson and A. P. de Silva, Chem. Commun., 2015, 51, 8403.
10. S. Erbas-Cakmak, S. Kolemen, A. C. Sedgwick, T. Gunnlaugsson, T. D. James, J. Y. Yoon and E. U. Akkaya, Chem. Soc. Rev., 2018, 47, 2228.
11. J. Andreasson, U. Pischel, S. D. Straight, T. A. Moore, A. L. Moore and D. Gust, J. Am. Chem. Soc., 2011, 133, 11641.
12. E. T. Ecik, A. Atilgan, R. Guliyev, T. B. Uyar, A. Gumus and E. U. Akkaya, Dalton Trans., 2014, 43, 67.
13. M. Elstner, J. Axthelm and A. Schiller, Angew. Chem., Int. Ed., 2014, 53, 7339.
14. J. Hatay, L. Motiei and D. Margulies, J. Am. Chem. Soc., 2017, 139, 2136.
15. Z. Pode, R. Peri-Naor, J. M. Georgeson, T. Ilani, V. Kiss, T. Unger, B. Markus, H. M. Barr, L. Motiei and D. Margulies, Nat. Nanotechnol., 2017, 12, 1161.
16. G. C. Van de Bittner, C. R. Bertozzi and C. J. Chang, J. Am. Chem. Soc., 2013, 135, 1783.
17. A. Romieu, Org. Biomol. Chem., 2015, 13, 1294.
18. S. Debieu and A. Romieu, Org. Biomol. Chem., 2015, 13, 10348.
19. L. Yi, L. Wei, R. Y. Wang, C. Y. Zhang, J. Zhang, T. W. Tan and Z. Xi, Chem. - Eur. J., 2015, 21, 15167.
20. C. Y. Ang, S. Y. Tan, S. J. Wu, Q. Y. Qu, M. F. E. Wong, Z. Luo, P. –Z. Li, S. T. Selvan and Y. L. Zhao, J. Mater. Chem. C, 2016, 4, 2761.
21. M. L. Odyniec, A. C. Sedgwick, A. H. Swan, M. Weber, T. M. S. Tang, J. E. Gardiner, M. Zhang, Y. –B. Jiang, G. Kociok-Kohn, R. B. P. Elmes, S. D. Bull, X. –P. He and T. D. James, Chem. Commun., 2018, 54, 8466.
22. A. C. Sedgwick, H. –H. Han, J. E. Gardiner, S. D. Bull, X. –P. He and T. D. James, Chem. Sci., 2018, 9, 3672.
23. M. N. Stojanovic and D. Stefanovic, Nat. Biotechnol., 2003, 21, 1069.
24. R. Pei, E. Matamoros, D. Stefanovic and M. N. Stojanovic, Nat. Nanotechnol., 2010, 5, 773.
25. M. N. Stojanovic, D. Stefanovic and S. Rudchenko, Acc. Chem. Res., 2014, 47, 1845.
26. M. Elstner and A. Schiller, J. Chem. Inf. Model., 2015, 55, 1547.
27. H.-J. Schneider, T. J. Liu, N. Lomadze and B. Palm, Adv. Mater., 2004, 16, 613.
28. H. Komatsu, S. Matsumoto, S. I. Tamaru, K. Kaneko, M. Ikeda and I. Hamachi, J. Am. Chem. Soc., 2009, 131, 5580.
29. S. J. Bradberry, J. P. Byrne, C. P. McCoy and T. Gunnlaugsson, Chem. Commun., 2015, 51, 16565.
30. L. K. Truman, S. J. Bradberry, S. Comby, O. Kotova and T. Gunnlaugsson, ChemPhysChem, 2017, 18, 1746.
31. B. A. Badeau, M. P. Comerford, C. K. Arakawa, J. A. Shadish and C. A. DeForest, Nat. Chem., 2018, 10, 251.
32. J. Ling, G. W. Naren, J. Kelly, T. S. Moody and A. P. de Silva, J. Am. Chem. Soc., 2015, 137, 3763.
33. J. Ling, G. W. Naren, J. Kelly, D. B. Fox and A. P. de Silva, Chem. Sci., 2015, 6, 4472.
34. J. Ling, G. W. Naren, J. Kelly, A. Qureshi and A. P. de Silva, Faraday Discuss., 2015, 185, 337.
35. T. Sarkar, K. Selvakumar, L. Motiei and D. Margulies, Nat. Commun., 2016, 7, 11374.
36. A. C. Boukis, K. Reiter, M. Frölich, D. Hofheinz and M. A. R. Meier, Nat. Commun., 2018, 9, 1439.
37. J. Andreasson and U. Pischel, Chem. Soc. Rev., 2018, 47, 2266.
38. S. Uchiyama, G. D. McClean, K. Iwai and A. P. de Silva, J. Am. Chem. Soc., 2005, 127, 8920.
39. A. P. de Silva, M. R. James, B. O. F. McKinney, D. A. Pears and S. M. Weir, Nat. Mater., 2006, 5, 787.
40. G. J. Brown, A. P. de Silva, M. R. James, B. O. F. McKinney, D. A. Pears and S. M. Weir, Tetrahedron, 2008, 64, 8301.
41. B. O. F. McKinney, B. Daly, C. Y. Yao, M. Schroeder and A. P. de Silva, ChemPhysChem, 2017, 18, 1760.
42. M. N. Win and C. D. Smolke, Science, 2008, 322, 456.
43. D. P. Murale, H. Liew, Y. H. Suh and D. G. Churchill, Anal. Methods, 2013, 5, 2650.
44. M. Prost and J. Hasserodt, Chem. Commun., 2014, 50, 14896.
45. I. Takashima, R. Kawagoe, I. Hamachi and A. Ojida, Chem. - Eur. J., 2015, 21, 2038.
46. B. Finkler, I. Riemann, M. Vester, A. Grüter, F. Stracke and G. Jung, Photochem. Photobiol. Sci., 2016, 15, 1544.
47. I. S. Turan, G. Gunaydin, S. Ayan and E. U. Akkaya, Nat. Commun., 2018, 9, 805.
48. R. Webb, Nature, 2006, 443, 39.
49. K. S. Lam, S. E. Salmon, E. M. Hersh, V. J. Hruby, W. M. Kazmierski and R. J. Knapp, Nature, 1991, 354, 82.
50. Smith Kline Beecham Corp, US Pat., 6,210,900 B1, 3 April 2001.
51. Combinatorial Peptide and Nonpeptide Libraries, ed. G. Jung, VCH, Weinheim, 1996.
52. Combinatorial Chemistry, Synthesis and Application, ed. S. R. Wilson and A. W. Czarnik, Wiley, New York, 1997.
53. A. Gorman, J. Killoran, C. O'Shea, T. Kenna, W. M. Gallagher and D. F. O'Shea, J. Am. Chem. Soc., 2004, 126, 10619.
54. S. O. McDonnell, M. J. Hall, L. T. Allen, A. Byrne, W. M. Gallagher and D. F. O'Shea, J. Am. Chem. Soc., 2005, 127, 16360.
55. M. J. Hall, S. O. McDonnell, J. Killoran and D. F. O'Shea, J. Org. Chem., 2005, 70, 5571.
56. M. J. Hall, L. T. Allen and D. F. O'Shea, Org. Biomol. Chem., 2006, 4, 776.
57. J. Killoran, S. O. McDonnell, J. F. Gallagher and D. F. O'Shea, New J. Chem., 2008, 32, 483.
58. A. Palma, M. Tasior, D. O. Frimannsson, T. T. Vu, R. Meallet-Renault and D. F. O'Shea, Org. Lett., 2009, 11, 3638.
59. J. Murtagh, D. O. Frimannsson and D. F. O'Shea, Org. Lett., 2009, 11, 5386.
60. M. Grossi, M. Morgunova, S. Cheung, D. Scholz, E. Conroy, M. Terrile, A. Panarella, J. C. Simpson, W. M. Gallagher and D. F. O'Shea, Nat. Commun., 2016, 7, 10855.
61. C. Ali, M. D. Yilmaz and E. U. Akkaya, Org. Lett., 2007, 9, 607.
62. T. Jokic, S. M. Borisov, R. Saf, D. A. Nielsen, M. Kuhl and I. Klimant, Anal. Chem., 2012, 84, 6723.
63. X. D. Jiang, J. Zhang, X. M. Shao and W. L. Zhao, Org. Biomol. Chem., 2012, 10, 1966.
64. X. –X. Zhang, Z. Wang, X. Y. Yue, Y. Ma, D. O. Kiesewetter and X. Y. Chen, Mol. Pharmaceutics, 2013, 10, 1910.
65. G. Sathyamoorthi, M. L. Soong, T. W. Ross and J. H. Boyer, Heteroat. Chem., 1993, 4, 603.
66. Y. Kataoka, Y. Shibata and H. Tamiaki, Chem. Lett., 2010, 39, 953.
67. X. D. Jiang, R. N. Gao, Y. Yue, G. T. Sun and W. L. Zhao, Org. Biomol. Chem., 2012, 10, 6861.
68. A. N. Amin, M. E. El-Khouly, N. K. Subbaiyan, M. E. Zandler, S. Fukuzumi and F. D'Souza, Chem. Commun., 2012, 48, 206.
69. D. Collado, Y. Vida, F. Najera and E. Perez-Inestrosa, RSC Adv., 2014, 4, 2306.
70. A. P. de Silva, H. Q. N. Gunaratne, T. Gunnlaugsson, A. J. M. Huxley, C. P. McCoy, J. T. Rademacher and T. E. Rice, Chem. Rev., 1997, 97, 1515.
71. B. Daly, J. Ling and A. P. de Silva, Chem. Soc. Rev., 2015, 44, 4203.
72. B. Valeur and M. N. Berberan-Santos, Molecular Fluorescence, Wiley-VCH, Weinheim, 2nd edn, 2012.
73. A. P. de Silva, H. Q. N. Gunaratne, P. L. M. Lynch, A. L. Patty and G. L. Spence, J. Chem. Soc., Perkin Trans. 2, 1993, 1611.
74. Z. R. Grabowski and J. Dobkowski, Pure Appl. Chem., 1983, 55, 245.
75. S. Kumar, H. B. Gobeze, T. Chatterjee, F. D'Souza and M. Ravikanth, J. Phys. Chem. A, 2015, 119, 8338.
76. V. V. Pavlishchuk and A. W. Addison, Inorg. Chim. Acta, 2000, 298, 97.
77. H. Siegerman, in Technique of Electroorganic Synthesis, ed. N. L. Weinberg, Wiley, New York, 1975.
78. R. A. Bissell, A. P. de Silva, W. T. M. L. Fernando, S. T. Patuwathavithana and T. K. S. D. Samarasinghe, Tetrahedron Lett., 1991, 32, 425.
79. C. J. Fahrni, L. C. Yang and D. G. VanDerveer, J. Am. Chem. Soc., 2003, 125, 3799.
80. T. Y. Liu, X. G. Liu, D. R. Spring, X. H. Qian, J. N. Cui and Z. C. Xu, Sci. Rep., 2014, 4, 5418.
81. R. A. Bissell, E. Calle, A. P. de Silva, S. A. de Silva, H. Q. N. Gunaratne, J. L. Habib-Jiwan, S. L. A. Peiris, R. A. D. D. Rupasinghe, T. K. S. D. Samarasinghe, K. R. A. S. Sandanayake and J.-P. Soumillion, J. Chem. Soc., Perkin Trans. 2, 1992, 1559.
82. M. E. Huston, K. W. Haider and A. W. Czarnik, J. Am. Chem. Soc., 1988, 110, 4460.
83. R. A. Bissell, A. P. de Silva, H. Q. N. Gunaratne, P. L. M. Lynch, G. E. M. Maguire and K. R. A. S. Sandanayake, Chem. Soc. Rev., 1992, 21, 187.
84. A. P. de Silva, T. P. Vance, M. E. S. West and G. D. Wright, Org. Biomol. Chem., 2008, 6, 2468.
85. A. P. de Silva, T. S. Moody and G. D. Wright, Analyst, 2009, 134, 2385.
86. B. Hayes, Am. Sci., 2001, 89, 490.
87. R. W. Keyes, Rev. Mod. Phys., 1989, 61, 279.
88. V. Bandi, M. E. El-Khouly, K. Ohkubo, V. N. Nesterov, M. E. Zandler, S. Fukuzumi and F. D'Souza, Chem. - Eur. J., 2013, 19, 7221.
89. R. Y. Tsien, Am. J. Physiol., 1992, 263, C723.
90. D. R. Walt, Chem. Soc. Rev., 2010, 39, 38.
91. M. H. J. Ohlmeyer, R. N. Swanson, L. W. Dillard, J. C. Reader, G. Asouline, R. Kobayashi, M. Wigler and W. C. Still, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 10922.
92. S. R. Nicewarner-Pena, R. G. Freeman, B. D. Reiss, L. He, D. J. Pena, I. D. Walton, R. Cromer, S. D. Keating and M. J. Natan, Science, 2001, 294, 137.
93. M. Han, X. Gao, J. Z. Su and S. Nie, Nat. Biotechnol., 2001, 19, 631.
94. B. J. Battersby, G. A. Lawrie, A. P. R. Johnston and M. Trau, Chem. Commun., 2002, 1435.
95. F. He, T. Gaedt, I. Manners and M. A. Winnik, J. Am. Chem. Soc., 2011, 133, 9095.
96. R. S. Bilan, V. A. Krivenkov, M. A. Berestovoy, A. E. Efimov, I. I. Agapov, P. S. Samokhvalov, I. Nabiev and A. Sukhanova, ChemPhysChem, 2017, 18, 1.
97. S. Shikha, T. Salafi, J. T. Cheng and Y. Zhang, Chem. Soc. Rev., 2017, 46, 7054.

---

Footnote

† Electronic supplementary information (ESI) available: synthesis and characterization of 2 and related compounds, where ref. 88 is mentioned; bead tagging procedures; pH values used in Fig. 2. See DOI: 10.1039/c8sc05548c

---