Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Using sulfur bridge oxidation to control electronic coupling and photochemistry in covalent anthracene dimers†
Chad D.
Cruz
a,
Jennifer
Yuan
 b,
Clàudia
Climent
b,
Clàudia
Climent
 c,
Nathan T.
Tierce
a,
Peter R.
Christensen
c,
Nathan T.
Tierce
a,
Peter R.
Christensen
 b,
Eric L.
Chronister
a,
David
Casanova
b,
Eric L.
Chronister
a,
David
Casanova
 *de,
Michael O.
Wolf
*de,
Michael O.
Wolf
 *b and
Christopher J.
Bardeen
*b and
Christopher J.
Bardeen
 *a
*a
aDepartment of Chemistry, University of California Riverside, 501 Big Springs Road, Riverside, California 92521, USA. E-mail: christopher.bardeen@ucr.edu
bDepartment of Chemistry, University of British Columbia, 2036 Main Mall, Vancouver, BC, Canada V6T 1Z1
cDepartamento de Física Teórica de la Materia Condensada, Universidad Autónoma de Madrid, E-28049 Madrid, Spain
dDonostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia, Euskadi, Spain
eIKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Euskadi, Spain
First published on 17th June 2019
Abstract
Covalently tethered bichromophores provide an ideal proving ground to develop strategies for controlling excited state behavior in chromophore assemblies. In this work, optical spectroscopy and electronic structure theory are combined to demonstrate that the oxidation state of a sulfur linker between anthracene chromophores gives control over not only the photophysics but also the photochemistry of the molecules. Altering the oxidation state of the sulfur linker does not change the geometry between chromophores, allowing electronic effects between chromophores to be isolated. Previously, we showed that excitonic states in sulfur-bridged terthiophene dimers were modulated by electronic screening of the sulfur lone pairs, but that the sulfur orbitals were not directly involved in these states. In the bridged anthracene dimers that are the subject of the current paper, the atomic orbitals of the unoxidized S linker can actively mix with the anthracene molecular orbitals to form new electronic states with enhanced charge transfer character, different excitonic coupling, and rapid (sub-nanosecond) intersystem crossing that depends on solvent polarity. However, the fully oxidized SO2 bridge restores purely through-space electronic coupling between anthracene chromophores and inhibits intersystem crossing. Photoexcitation leads to either internal conversion on a sub-20 picosecond timescale, or to the creation of a long-lived emissive state that is the likely precursor of the intramolecular [4 + 4] photodimerization. These results illustrate how chemical modification of a single atom in the covalent bridge can dramatically alter not only the photophysics but also the photochemistry of molecules.
1. Introduction
The application of conjugated organic molecules in solar energy conversion and electroluminescence requires the development of complex chromophores and control of their assembly. The geometric arrangement of molecular chromophores determines their ability to interact electronically and generate various types of exciton and charge transfer (CT) states.1–5 One way to control the interaction between chromophore molecules is to tether two of them together using a covalent linker group. This structural motif allows the geometrical arrangement between the chromophores to be defined and the electronic interaction to be controlled. Such dimers or bichromophores form the smallest subunit of larger chromophore assemblies such as polymers and are useful for basic studies of phenomena relevant to organic electronic materials. For example, bichromophores have been used to study energy and charge transfer,6–14 as well as singlet exciton fission15–25 and triplet–triplet annihilation.26,27 They can also support intramolecular CT states that give rise to enhanced charge separation and thermally activated delayed fluorescence.28–30 Their unique properties may eventually lead to applications in technologies including light-emitting diodes and photovoltaics.One of the most important scientific questions regarding covalent bichromophores concerns the role of the linker. In one limit, it functions as a passive structural element that positions the two chromophores to interact purely via through-space Coulombic effects. But in many cases, it can actively participate in the electronic coupling through its own electronic states.31–34 Separating these two effects can be challenging because alterations to the linker's chemical structure to modify its electronic properties typically changes the molecular geometry and the through-space interaction simultaneously. Wolf and coworkers developed a way around this problem by using a sulfur atom as a bichromophore bridge.35,36 Changing the oxidation state of the sulfur from S to SO to SO2 allows modification of the electronic properties of the bridge while maintaining almost identical molecular conformations, as determined from the crystal structures. Modification of the electronic structure of the bridge resulted in dramatic changes in the photophysical properties of bichromophores based on pyrene, naphthalene and terthiophene. In the case of terthiophene dimers, oxidation of the sulfur bridge turned off the intersystem crossing (ISC) that normally limits the fluorescence yields of monomeric terthiophene.14 When the bridge was fully oxidized, both experimental and computational results indicated that an excited state with appreciable CT character could be formed in the dimers. This low-lying state limits ISC and generated fluorescence with a quantum yield of 52% in polar solvents, as compared to 6% for monomeric terthiophene. The main physical insight that emerged from that work was that the electron pairs on the bridging sulfur atom could be used to modulate the chromophore–chromophore interaction. The presence of the lone pair electrons between the two molecular π systems hinders π–π interactions and suppresses intramolecular CT states. Replacing the lone pairs with polarized S![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds prevents them from screening out the Coulombic stabilization of intramolecular CT states, enabling the formation of longer-lived emissive excited states.
O bonds prevents them from screening out the Coulombic stabilization of intramolecular CT states, enabling the formation of longer-lived emissive excited states.
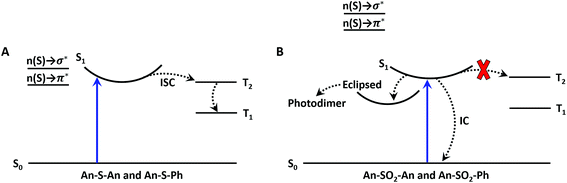
We were interested to see if the principles derived from the terthiophene work can be extended to dimeric systems composed of other chromophores. We chose anthracene (An) because it is a conjugated organic molecule whose photophysics and photochemistry have been extensively explored.37–39 Unlike terthiophene, it does not possess an intrinsic heavy atom like sulfur, so ISC is weaker in the monomeric form. Moreover, An can undergo photochemical reactions in solution, specifically [4 + 4] photocycloaddition between neighboring An rings. This capability opens up the possibility of using the linker group to modify the photoreactivity of the bichromophore as well. The An-based bichromophores used in this study are shown in Chart 1. The current study was motivated by our preliminary study of the An–SOx–An (x = 0, 1, 2) linked dimers, where it was shown that their photoreactivity depended on the linker oxidation state.36 Under UV excitation An–SO2–An formed a photodimer containing an episulfone ring whereas An–S–An was unreactive.36 We note that An–SO–An was explored in the previous study as well and was found to have unique photochemistry in which the bridging sulfoxide was lost and 9,9′-bianthryl was formed. We did not include the sulfoxide linker in the current work because (1) the efficient and irreversible photochemistry makes obtaining reliable photophysical data challenging; and (2) we wanted to concentrate on the limiting cases of S (not oxidized) versus SO2 (fully oxidized).
Electron donating and withdrawing substituents have been widely used to modify the photophysics of An derivatives.40–46 In most cases, the substituent can undergo an electron transfer reaction with the photoexcited An core, leading to the formation of the An radical cation or anion. Subsequent charge recombination can lead to triplet formation and interesting photochemistry.47,48 Here, we are interested in a subtler effect: the use of the linker atom to modulate the excited state structure via CT interactions while avoiding full electron transfer. The ability to generate novel excited states without ionization can be expected to lead to new photophysical behavior. In this paper, we combine organic synthesis, spectroscopy and theory to understand the origin of the differences in reactivity for the An-based bichromophores. Dimers with different bridge oxidation states (S versus SO2) and constituent chromophores (Anversus phenyl (Ph)) are prepared in order to isolate bridge and chromophore effects. Steady-state and time-resolved spectroscopy measurements are used to characterize the excited state dynamics, while time-dependent density functional theory (TD-DFT) calculations are used to characterize the nature of the electronic states. At the start of this study, we expected that the role of the oxidation state of the bridging S atom would be similar to that in the terthiophene bichromophores, where the bridge lone pair orbitals modulate the electronic interactions between the An chromophores without participating in the electronic states. However, we find that this separation does not hold for the S-bridge, whose orbitals do participate in the optically accessible excited states and contribute to rapid ISC in both An–S–An and An–S–Ph bichromophores. The SO2-bridged dimers exhibit more complex dynamics, with rapid internal conversion and, in the An–SO2–An molecules, the generation of a long-lived emissive state that is likely the precursor to the intramolecular [4 + 4] photocycloaddition. Intramolecular reactivity in covalent anthracene assemblies is usually assumed to be completely controlled by steric effects and geometry, for example through the topochemical principle.49–53 Our results suggest that electronic state engineering, which can be accomplished by changing the chemical structure of a single atom in the assembly, provides a new chemical strategy for controlling the photochemical behavior of covalent molecular assemblies.
2. Experimental
The symmetric sulfur-bridged anthracene dimers An–S–An and An–SO2–An are synthesized in accordance with a previously reported method.36 The synthetic scheme to make An–S–Ph and An–SO2–Ph is given in Scheme S1 and described in detail in the ESI.†Steady-state absorption measurements of each compound in dilute solutions of cyclohexane (∼30 μM), CH2Cl2 (∼100 μM), and acetonitrile (∼50 μM) are performed with a Varian Cary 500 spectrophotometer. Steady-state photoluminescence (PL) spectra of the same solutions are recorded in a right-angle configuration with a PTI QM-400 fluorimeter.
Time-resolved PL experiments are performed by frequency doubling the 800 nm output of a 1 kHz repetition rate Coherent Libra Ti:sapphire laser system. The PL signal is detected using a Hamamatsu C4334 Streakscope which has a time resolution of 25 ps and a wavelength resolution of 2.5 nm. The sample solutions are contained in a 1 cm quartz cuvette and the emitted light is collected in a front-face configuration utilizing magic angle polarization. A 420 nm long wave pass filter is placed before the detector to minimize laser scatter in the signal. Each solution is degassed by bubbling argon gas through the cuvette for 15 minutes prior to the measurement.
Femtosecond transient absorption (TA) measurements are performed using the 1 kHz laser system described above. The 400 nm beam is used as the pump and a small portion of the 800 nm fundamental beam is focused onto a CaF2 plate to generate the white light continuum probe beam. The pump and probe beams are overlapped in a 1 mm pathlength quartz flow cell. The probe beam is detected with a fiber optic coupled to an Ocean Optics S2000 spectrometer. The Ultrafast Systems Helios program is used to control the delay stage as well as generate the difference spectrum. The solvent response is also measured and nonresonant contributions to the TA signal are removed with Ultrafast Systems Surface Xplorer software. Pump-pulse fluences are kept between 0.6–3 mJ cm−2. The time resolution of these experiments is estimated to be ∼150 fs based on the width of the pump-probe cross correlation signal from the neat solvent.
Electronic structure calculations for the ground and excited states are performed within the framework of density functional theory (DFT)54,55 and its time-dependent version (TD-DFT)56,57 respectively. To account for weak interactions and important electronic redistribution between the anthracene moieties and the SOx bridge upon photoexcitation, the ωB97X-D functional58 is used together with the 6-31+G(d) basis set. CH2Cl2 solvent effects are accounted for with the polarizable continuum model using the C-PCM variant.59 Critical points on the ground state potential energy surface (PES) are optimized with no restrictions. Computation of the diabatic states is performed by means of the Edmiston–Ruedenberg localization scheme.60 Energy crossing points are optimized within the spin-flip DFT (SF-DFT) approximation61 with the BHHLYP functional.62,63 All calculations are performed with the Q-Chem program.64
3. Results and discussion
3.1 Steady-state spectroscopy
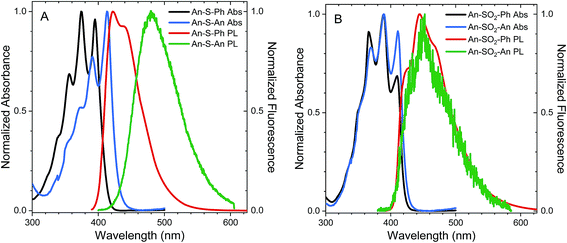
The steady state absorption spectra of An–S–An, An–S–Ph, An–SO2–An and An–SO2–Ph in cyclohexane are shown in Fig. 1. The absorption spectra of all sulfur-bridged anthracenes display vibronic structure which is reminiscent of unsubstituted An. The enhanced relative intensity of the 0–0 vibronic peaks in both the An-terminated dimers indicates the presence of excitonic interaction between chromophores.4 This enhancement of the 0–0 peak is more pronounced for An–S–An than for An–SO2–An, which also undergoes a 20 nm redshift that is not observed for the oxidized species. The absorption redshift and 0–0 peak enhancement is indicative of J-type excitonic coupling in An–S–An. For all compounds, the absorption spectra are relatively insensitive to solvent polarity, with acetonitrile and CH2Cl2 causing only a slight broadening of the spectra (ESI, Fig. S4†).The steady-state photoluminescence (PL) of the Ph-terminated compounds is measured in cyclohexane, CH2Cl2 and acetonitrile after 400 nm excitation. The PL spectra for the An–SOx–An compounds are extracted from the time-resolved measurements in order to avoid a long-lived impurity emission that contaminated the steady-state spectra reported in our earlier work.36 The PL spectrum of An–S–Ph peaks at 420 nm in cyclohexane with a small shoulder present at 440 nm (Fig. 1A). In solutions of CH2Cl2 and acetonitrile, the spectra are featureless and red-shift slightly ∼20 nm (ESI, Fig. S5†). When the Ph group is replaced by An, the PL of An–S–An in cyclohexane has a strong, featureless PL centered at 475 nm (Fig. 1A). This feature red-shifts to ∼540 nm and ∼560 nm in CH2Cl2 and acetonitrile respectively (ESI, Fig. S5†), suggesting that the emissive state possesses significant CT character. The PL spectrum of An–SO2–Ph in cyclohexane is similar to that of An–S–Ph (Fig. 1B), again broadening in polar solvents and shifting to lower energies (ESI, Fig. S5†). However, when the Ph group is replaced by An, the high sensitivity to the second chromophore and solvent polarity is not observed. Unlike the S-bridge, the PL spectra of An–SO2–An is similar to that of An–SO2–Ph and barely shifts with solvent polarity, although a slight broadening of the spectra is observed in CH2Cl2 and acetonitrile (ESI, Fig. S5†). The spectra retain much of the structure observed in the cyclohexane spectrum and the broadened red portions seen in the polar solvents are likely due to a species with some CT character in the excited state as they resemble excimer PL observed in methyl bridged anthracene dimers.65
The different behaviors observed in the steady-state spectra suggest that there are significant differences between the S- and SO2-bridged compounds. These differences become even more pronounced when the time-resolved data is analyzed. For this reason, in the following sections we analyze the dynamic behavior of the S- and SO2-bridged compounds separately before comparing them in the theoretical section of this paper.
3.2 Excited state dynamics of An–S–Ph and An–S–An
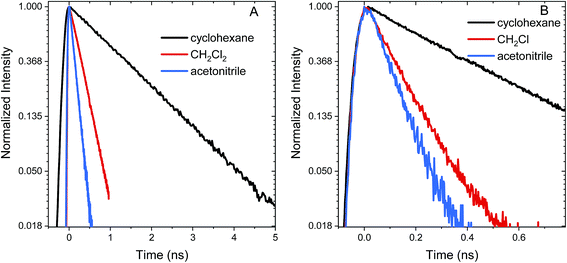
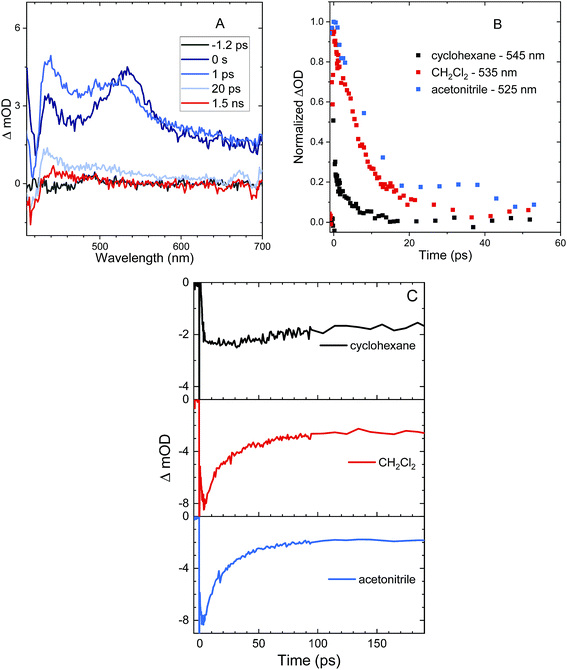
Excited state relaxation in unsubstituted An is caused by a combination of ISC, internal conversion, and radiative relaxation.43 ISC in anthracene is efficient (∼70% triplet quantum yield) and contributes to a relatively short PL lifetime of ∼4 ns.43 The addition of the S–Ph moiety leads to shorter PL lifetimes of 1.4 ns in cyclohexane, 300 ps in CH2Cl2 and 130 ps in acetonitrile (Fig. 2A). Replacing the Ph by An quenches the PL more effectively with PL lifetimes of 400 ps in cyclohexane, 120 ps in CH2Cl2 and 90 ps in acetonitrile (Fig. 2B). The decays are mono-exponential at earlier times, with a slight deviation at later times caused by residual fluorescent impurities (ESI, Fig. S6†). For both S-bridged dimers, the solvent-dependent PL lifetimes suggest that an excited state with some CT character undergoes much more rapid nonradiative relaxation than monomeric An.Femtosecond transient absorption (fs-TA) can help elucidate the mechanism which leads to rapid PL quenching in all S-bridged molecules. The behavior of all S-bridged compounds is similar. A representative example of the TA data is shown in Fig. 3A for An–S–An in acetonitrile. At early times, a broad positive feature centered at ∼600 nm is assigned to the singlet S1 → SN induced absorption. By 30 ps a new positive feature emerges at ∼430 nm, similar to the triplet T1 → TN feature observed in An and its derivatives.66–68 By 100 ps the T1 → TN feature dominates the spectrum while the singlet absorption has decayed. In cyclohexane and CH2Cl2 the same features emerge in the TA spectra, but the triplet transition appears more slowly, mirroring the trend found in the PL decays (ESI, Fig. S7†). In all solvents, a clear isosbestic point between the singlet and triplet induced absorptions is seen, indicating that a population transfer is occurring between these two well-defined electronic states. A global analysis of the TA data for both An–S–An and An–S–Ph yields a fit that best describes the data with two species associated spectra (ESI, Fig. S7 and S8†). One spectrum corresponds to the singlet feature which decays with a lifetime closely matching the PL lifetime. The second spectral component has an extremely long lifetime and represents the triplet feature which does not decay during the experiment. An example of this fitting of the fs-TA decays is shown in Fig. 3B. For all the S-bridged compounds, ISC appears to be the dominant mechanism that removes the S1 population.
The relaxation constants measured for An–S–Ph and An–S–An in the different solvents are summarized in Table 1. For all compounds, the time constants obtained from independently fitting the PL decays and the fs-TA evolution are the same to within 10%. This good correspondence indicates that we are not missing an important relaxation channel in our analysis. In all of the S-bridged compounds, singlet state relaxation is dominated by ISC and we assume that the singlet decay rate reflects the ISC rate (kISC). The increase in kISC with increasing solvent polarity for An–S–An and An–S–Ph is shown in Fig. 4. Qualitatively, this behavior is consistent with the involvement of a singlet state that is stabilized in polar solvents and by the presence of a larger, more polarizable chromophore. These trends, combined with the fluorescence spectra in Fig. 1A, suggest that the singlet state has appreciable CT character. As the energy of this state decreases, it moves closer to the low-lying triplet of An and presumably facilitates ISC. Note that if the bridging S atom was merely an innocent bystander that only contributed to electronic screening of the An–An interaction (i.e. analogous to the terthiophene system) we would expect An–S–Ph and An–S–An to exhibit behavior similar to monomeric An. The large deviations already indicate that the An dimer system behaves differently from the terthiophene system.
| Cyclohexane | CH2Cl2 | Acetonitrile | ||
|---|---|---|---|---|
| An–S–Ph | PL (ps) | 1390 ± 5 | 303 ± 5 | 132 ± 3 |
| TA (ps) | 1743 | 280 ± 110 | 136 ± 97 | |
| An–S–An | PL (ps) | 407 ± 5 | 118 ± 2 | 87 ± 2 |
| TA (ps) | 416 ± 153 | 128 ± 24 | 84 ± 16 | |
| An–SO2–Ph | PL (ps) | 3560 ± 6 | 229 ± 2 | 130 ± 2 |
| TA (ps) | >1500 | 226 ± 6 | 144 ± 13 | |
| An–SO2–An | PL (ns) | 11.2 ± 0.12 | 16.8 ± 0.5 | 10.9 ± 0.03 |
| TA (ps) | NA | 23.8 ± 0.7 | 19.6 ± 0.3 |
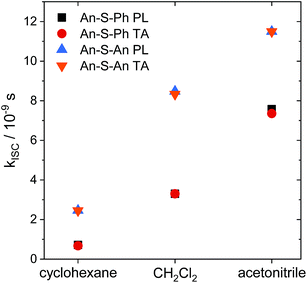 | ||
| Fig. 4 Intersystem crossing rates (kISC) as a function of solvent polarity (cyclohexane, ε = 2.02; CH2Cl2, ε = 8.93; acetonitrile, ε = 36.64)83 for An–S–Ph calculated from the PL lifetimes (black squares) and TA lifetimes (red circles) compared with the rates for An–S–An calculated from the PL lifetimes (blue up triangles) and TA lifetimes (orange down triangles). Intersystem crossing is faster in more polar solvents and faster for An–S–An than for An–S–Ph. | ||
3.3 Excited state dynamics of An–SO2–Ph and An–SO2–An
The SO2-bridged compounds (An–SO2–Ph and An–SO2–An) behave similarly to the S-bridged compounds in that their PL decays also depend on solvent polarity. The PL time traces of An–SO2–Ph are mono-exponential with lifetimes of 3.6 ns in cyclohexane, 230 ps in CH2Cl2 and 130 ps in acetonitrile (Fig. 5A). However, the PL time traces for An–SO2–An are biexponential in all solvents, with a prompt decay component that cannot be resolved within the instrument response function of the streak camera. The long-lived tail of the decay has the same emission spectrum as the prompt component but with a lifetime on the order of 10 ns, accounting for roughly 50% of the total decay amplitude (Fig. 5B).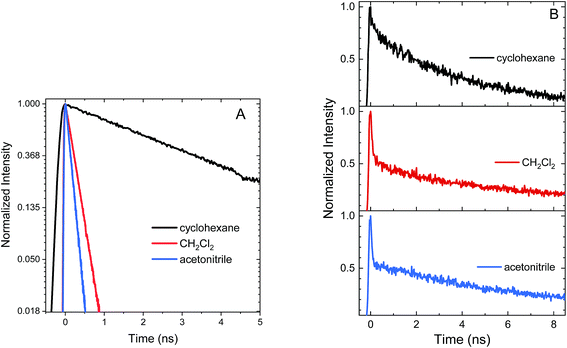 | ||
| Fig. 5 Normalized PL time traces integrated over all wavelengths for (A) An–SO2–Ph shown on a natural log scale and (B) An–SO2–An in cyclohexane, CH2Cl2, and acetonitrile. | ||
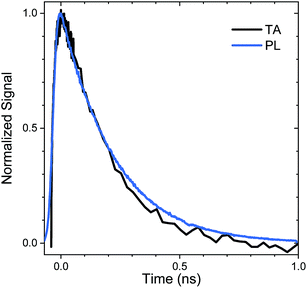
The relaxation of the singlet state for the SO2-bridged compounds is much faster than that observed for the S-bridged compounds, but ISC is not the culprit in this case. In the TA spectra of An–SO2–Ph, only a short-lived S1 → SN feature is observed in each solvent (ESI, Fig. S9†). In polar solvents there is a slight blue shift of the S1 → SN feature, but it disappears on the same time scale as the PL lifetime. No signature T1 → TN features appear as the singlet disappears, which indicates that ISC does not play a major role. When probed at 400 nm, the recovery of the ground state absorption mirrors the PL decay, as the comparison in Fig. 6 shows. This correlation suggests that internal conversion to the ground state must be the nonradiative pathway that quenches the PL. The rate of internal conversion becomes more rapid as the solvent polarity is increased. This type of solvent polarity enhanced internal conversion has been previously reported for carotenoid derivatives and attributed to an excited singlet with some CT character.69,70 It is also possible that the internal conversion proceeds through an intermediate state with CT character whose decay rate is much more rapid than its population rate from the initially excited singlet state (inverted kinetics).71–73
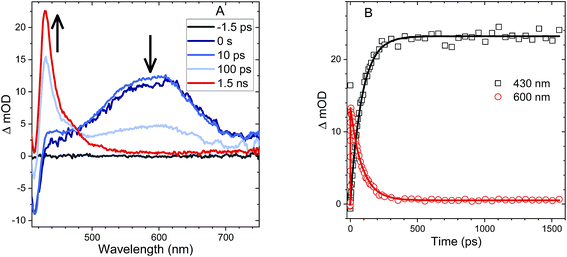
The behavior of the An–SO2–An bichromophore is more complicated. The femtosecond TA spectra for An–SO2–An in CH2Cl2 is shown in Fig. 7A. It is similar to that of An–SO2–Ph, with broad S1 → SN features that are present at early times but disappear in less than 100 ps. Unlike An–S–An or An–S–Ph, the decay is slower in more polar solvents with the singlet absorption decaying within 3 ps in cyclohexane, 9 ps in CH2Cl2 and 15 ps in acetonitrile (Fig. 7B). The rapid disappearance of the singlet absorption in the visible spectral range raises the question of where the population may be going. Again, the absence of a T1 → TN feature suggests that ISC is not a major factor. To see if the population is returning directly to the ground state as observed in An–SO2–Ph, we monitored the bleach signal at 400 nm.
Kinetic traces of the 400 nm TA bleach features of An–SO2–An show that there is a rapid (<100 ps) ground state recovery component in all three solvents, followed by a much longer-lived component. The amplitude of the rapid component is much smaller for cyclohexane than for CH2Cl2 and acetonitrile (Fig. 7C). The smaller magnitude of the picosecond bleach recovery in cyclohexane is consistent with the PL data in Fig. 5B, where the fast decay component is smaller than in CH2Cl2 and acetonitrile. The rapid initial decay of the singlet state is limited by the instrument response in the PL measurements, but is clearly resolved in the visible and 400 nm fs-TA data. From the TA and PL data, An–SO2–An appears to decay by two different pathways. One part of the population relaxes via rapid internal conversion directly to the ground state, similar to An–SO2–Ph. But another portion ends up in an emissive state that survives for 10 ns or longer. Unfortunately, this long-lived state does not appear to have a strong absorption signature in the 400–700 nm range. Based on the broadened emission spectrum, it probably involves CT between the An moieties and is the likely precursor for the photocycloaddition reaction between neighboring anthracene rings. Several workers have shown that this type of excimer state can have a strong absorption signature in the near-infrared, and it is possible that a TA experiment that probes this region would reveal the spectroscopic signature of this long-lived state.74–79
3.4 Theoretical analysis
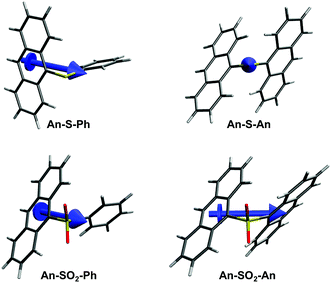
The different behavior of the S- and SO2-bridged compounds cannot be rationalized in terms of the screening model previously developed for the terthiophene bichromophores, in which the presence of sulfur lone pairs decreased the amount of excited-state CT character by preventing Coulomb stabilization.14 For example, the An–S–An excited state appears to have significantly more CT character than An–SO2–An, which is the opposite of what was observed for the terthiophene compounds. In order to explain these discrepancies, we analyze the excited state structure of the molecules using TD-DFT. Optimization of the molecular ground state geometries is described in the ESI.† All molecules rest in a “displaced” geometry with C2 symmetry, with the An and Ph moieties rotated so that the π systems are offset from each other. These structures are consistent with the crystal structure data and there is no evidence that the molecules adopt a significantly different conformation in solution.| ΔE | Strength | Δμ | Composition | |
|---|---|---|---|---|
| An–S–An | 3.46 | 0.42 | −1.01 | 68 (H → L), 26 (H−1 → L+1) |
| An–SO2–An | 3.48 | 0.29 | −0.20 | 53 (H → L), 42 (H−1 → L+1) |
| An–S–Ph | 3.65 | 0.28 | −0.70 | 93 (H → L) |
| An–SO2–Ph | 3.61 | 0.25 | −0.29 | 94 (H → L) |
From Table 2, the oscillator strengths for the transition to S1 are very similar in all cases, except for An–S–An, which has a noticeably larger transition probability. Transition dipole moments (Fig. 9) of both Ph-substituted dimers correspond to an An localized transition (La state) with the transition dipole along the An short molecular axis. In An–SO2–An, the orientation of the total transition dipole moment is as expected for an H-type aggregate of two An molecules whose transition dipole moments are oriented side-by-side and add out-of-phase. On the other hand, the transition dipole moment to S1 in An–S–An is oriented perpendicular to that of An–SO2–An and corresponds to the in-phase combination of local dipoles, as expected for a J-type dimer. Again, this is consistent with the redshift and enhanced 0–0 vibronic peak in the An–S–An absorption spectrum (Fig. 1).
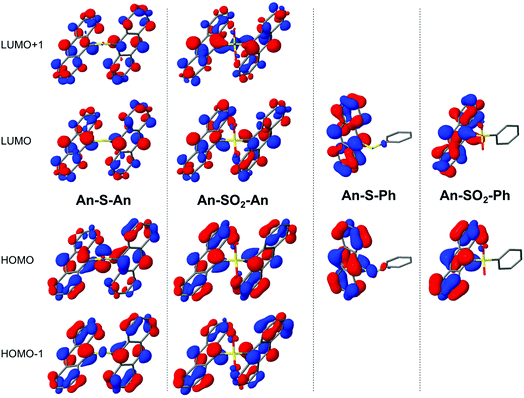
Varying the oxidation state dramatically changes the degree of CT and the excitonic coupling between the An chromophores (Table 2 and Fig. 9). Enhanced excitonic coupling increases the total oscillator strength of the An–S–An transition, which now reflects contributions from both An chromophores. To further characterize the nature of the S1 state in An–S–An and An–SO2–An and to understand the differences between S and SO2 linkers, we decompose the transition to S1 in terms of diabatic contributions (ESI†). The lowest state in An–SO2–An is mainly obtained as the linear combination of local excitations (LE) of the two anthracenes. The excitation to S1 in An–SO2–An is almost purely of LE character, with a very small contribution of π → π* CT between anthracenes. The π → π* CT contributions in An–S–An are estimated to account for 5% of the transition, slightly higher than in the SO2-bridged dimer. But the S-bridged dimer also receives a sizeable contribution of electron transfer from the lone-pair electrons of the sulfide bridge to the anthracene units, i.e. n(S) → π* (CTB). The involvement of the lone-pair electrons in the transition to the lowest singlet has been observed in a computational study of a sulfur-bridged naphthalene dimer (Naph–S–Naph),80 but not for the terthiophene counterpart (T3–S–T3).14 In T3–S–T3 the n(S) orbitals lie much lower in energy than the HOMOs of the two terthiophene moieties. As a result, there is no sizeable contribution from n(S) in the transition to lowest excited states of T3–S–T3, i.e. no relevant n(S) → π* (CTB) excitations within the computed lowest 10 excited singlet states.
Vertical de-excitation energies from the displaced and eclipsed S1 minima are given in the ESI.† The character of the S1 emission in the Ph-terminated compounds holds strong π → π* character localized on the An with a CTB contribution in the S-bridged case (similar to the S0 → S1 transition at the Franck–Condon region), in agreement with the weak solvent dependence of emission peak maxima. The computed Stokes shifts are on the order of 0.6–0.7 eV, and transition strengths are close to the values computed at the ground state geometry. When the Ph group is replaced by An, calculations also predict strong Stokes shifts for displaced forms (∼0.9 eV) that are even larger for the eclipsed minima (1.4 eV and 1.8 eV for An–S–An and An–SO2–An, respectively). Furthermore, the eclipsed oscillator strengths are considerably lower with respect to the strengths at the absorbing Franck–Condon region. All the calculated Stokes shift values are much larger than the experimentally observed Stokes shifts in Fig. 1, and it is likely that our TD-DFT calculations overestimate the energy differences between the absorbing and relaxed geometries. The important point is that theory shows that there are two distinct excited state minima for the An–SOx–An compounds, both with diminished oscillator strengths, in contrast to the single relaxed state in the An–SOx–Ph compounds.
To efficiently relax to the triplet state via ISC, two requirements need to be satisfied, that is: (1) a small energy gap between initial (singlet) and final (triplet) states, and (2) sizeable spin–orbit coupling (SOC). At the local excited state minimum the displaced conformer of An–S–An presents a large singlet–triplet gap (Table 3). The S1–T1 relative energy is also large for the Ph-substituted and the eclipsed form of An–S–An, while the energy difference with respect to T2 is reduced, although for An–S–Ph the ISC process is energetically uphill. The computed SOCs to T1 and T2 for the S-bridged dimers are considerably larger than for anthracene and the SO2-bridged compounds. Interestingly, the elongated conformer is calculated to have an extremely large SOC (159 and 178 cm−1 for An–S–An and An–S–Ph respectively), suggesting that it could also play a role in ISC. These results, which can be rationalized by means of El-Sayed's rule82 (ESI†), support the idea of faster ISC in S-bridged dimers. Moreover, the CTB character of the n(S) → π* and n(S) → σ* orbitals agrees with the solvent polarity dependence of the ISC rate observed in Fig. 4 for the S-bridged compounds.
| S1/T1 | S1/T2 | |||
|---|---|---|---|---|
| ΔE | SOC | ΔE | SOC | |
| Anthracene | 1.63 | 0.00 | 0.02 | 0.01 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| An–S–Ph | ||||
| Displaced | 1.48 | 2.63 | −0.23 | 1.75 |
| Elongated | 0.53 | 0.82 | 0.27 | 178.37 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| An–S–An | ||||
| Displaced | 1.04 | 2.68 | 0.89 | 8.23 |
| Eclipsed | 0.98 | 0.02 | 0.27 | 4.10 |
| Elongated | 0.52 | 2.74 | 0.31 | 158.59 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| An–SO2–Ph | ||||
| Displaced | 1.48 | 0.15 | −0.17 | 1.07 |
| Eclipsed | 1.46 | 0.06 | −0.28 | 1.25 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| An–SO2–An | ||||
| Displaced | 1.07 | 0.30 | 0.92 | 1.15 |
| Eclipsed | 0.89 | 0.01 | 0.02 | 0.57 |
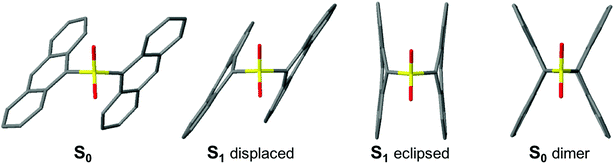 | ||
| Fig. 10 Optimized geometries of An–SO2–An. From left to right: S0, S1 displaced, S1 eclipsed and S0 dimer. | ||
While the lack of ISC explains how An–SO2–An can support a long-lived singlet state, the time-resolved measurements indicate that both SO2-bridged compounds experience rapid internal conversion to the ground state as well. The origin of the fast internal conversion channel that dominates the An–SO2–Ph relaxation and accounts for a substantial fraction of the An–SO2–An relaxation is intriguing. The ability of the SO2 group to induce rapid internal conversion, especially in An–SO2–Ph, is unexpected since this highly oxidized group should be electronically inert. Searches on the excited state potential energy surfaces of these two molecules uncovered no obvious signs of conical intersections that would provide a path to the ground state. However, the solvent dependence shows that the partitioning of population to the ground state is enhanced in polar environments, suggesting an intermediate with CT character may be involved. One scenario is that the SO2 bridge can support different types of CT states in solution, possibly due to relaxation into different conformations. If one CT conformation undergoes rapid charge recombination on a sub-nanosecond timescale, it would lead to an apparent rapid internal conversion, as described above. This conformation would be dominant for AnSO2Ph, but only about 50% for the AnSO2An molecule, with the remainder of the population residing in a CT conformation that supports the long-lived emission and the photodimerization reaction. Locating these different excited state conformations would be a considerable challenge for theory, so this explanation must be regarded as tentative for now.
4. Conclusions
The ability to tune the oxidation state of the sulfur bridge provides a way to investigate the role of the bridge electronic structure in modulating electronic interactions between chromophores. When the bridge and chromophore orbitals are closer in energy, as in the case of anthracene, orbital mixing can lead to unexpected effects, as seen for An–S–An, where this mixing leads to enhanced excited state CT character, a change from H-type to J-type excitonic coupling, and rapid ISC. When the bridge orbitals are shifted away by bridge oxidation, behavior is recovered that is more representative of two independent chromophores that interact primarily via through-space Coulomb terms. In this case, the bridge affects the excitonic state primarily through geometrical factors and electronic screening, as demonstrated in our previous work on terthiophene dimers.14 The present work demonstrates the ability of the linker to tune not only the photophysical but also the photochemical properties of the covalent assembly. In An–SO2–An, tying up the lone pairs on the S prevents them from short-circuiting the photochemistry by ISC. The ability to engineer the photophysical and photochemical properties of molecular assemblies by tuning the linker electronic structure may prove useful for the design of functional organic optoelectronic materials.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the Basque Government (IT588-13) and the Spanish Government MINECO/FEDER (CT2016-80955-P). C. C. is indebted to the European Research Council (ERC-2016-STG-714870) for a postdoctoral contract. M. O. W. acknowledges support from the Natural Sciences and Engineering Research Council. C. J. B. acknowledges support from the National Science Foundation grant CHE-1800187.References
- M. Kasha, H. R. Rawls and M. Ashraf El-Bayoumi, Pure Appl. Chem., 1965, 11, 371–392 CAS.
- K. Liang, M. S. Farahat, J. Perlstein, K.-Y. Law and D. G. Whitten, J. Am. Chem. Soc., 1997, 119, 830–831 CrossRef CAS.
- F. C. Spano, Annu. Rev. Phys. Chem., 2006, 57, 217–243 CrossRef CAS PubMed.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- C. J. Bardeen, MRS Bull., 2013, 38, 65–71 CrossRef.
- D. S. McClure, Can. J. Chem., 1958, 36, 59–71 CrossRef CAS.
- G. D. Scholes, K. P. Ghiggino, A. M. Oliver and M. N. Paddon-Row, J. Phys. Chem., 1993, 97, 11871–11876 CrossRef CAS.
- N. A. v. Dantzig, D. H. Levy, C. Vigo and P. Piotrowiak, J. Chem. Phys., 1995, 103, 4894–4906 CrossRef.
- G. Grabner, K. Rechthaler and G. Köhler, J. Phys. Chem. A, 1998, 102, 689–696 CrossRef CAS.
- L. Lu, R. J. Lachicotte, T. L. Penner, J. Perlstein and D. G. Whitten, J. Am. Chem. Soc., 1999, 121, 8146–8156 CrossRef CAS.
- N. Asami, T. Takaya, S. Yabumoto, S. Shigeto, H.-o. Hamaguchi and K. Iwata, J. Phys. Chem. A, 2010, 114, 6351–6355 CrossRef CAS PubMed.
- M. T. Whited, N. M. Patel, S. T. Roberts, K. Allen, P. I. Djurovich, S. E. Bradforth and M. E. Thompson, Chem. Commun., 2012, 48, 284–286 RSC.
- C. Trinh, K. Kirlikovali, S. Das, M. E. Ener, H. B. Gray, P. Djurovich, S. E. Bradforth and M. E. Thompson, J. Phys. Chem. C, 2014, 118, 21834–21845 CrossRef CAS PubMed.
- C. D. Cruz, P. R. Christensen, E. L. Chronister, D. Casanova, M. O. Wolf and C. J. Bardeen, J. Am. Chem. Soc., 2015, 137, 12552–12564 CrossRef CAS PubMed.
- A. M. Müller, Y. S. Avlasevich, W. W. Schoeller, K. Müllen and C. J. Bardeen, J. Am. Chem. Soc., 2007, 129, 14240–14250 CrossRef PubMed.
- J. C. Johnson, A. J. Nozik and J. Michl, Acc. Chem. Res., 2013, 46, 1290–1299 CrossRef CAS PubMed.
- K. Aryanpour, A. Shukla and S. Mazumdar, J. Phys. Chem. C, 2015, 119, 6966–6979 CrossRef.
- S. N. Sanders, E. Kumarasamy, A. B. Pun, M. T. Trinh, B. Choi, J. Xia, E. J. Taffet, J. Z. Low, J. R. Miller, X. Roy, X. Y. Zhu, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2015, 137, 8965–8972 CrossRef CAS PubMed.
- X. Feng, D. Casanova and A. I. Krylov, J. Phys. Chem. C, 2016, 120, 19070–19077 CrossRef CAS.
- N. V. Korovina, S. Das, Z. Nett, X. Feng, J. Joy, R. Haiges, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2016, 138, 617–627 CrossRef CAS PubMed.
- E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2016, 8, 1120 CrossRef CAS PubMed.
- J. C. Dean, R. Zhang, R. K. Hallani, R. D. Pensack, S. N. Sanders, D. G. Oblinsky, S. R. Parkin, L. M. Campos, J. E. Anthony and G. D. Scholes, Phys. Chem. Chem. Phys., 2017, 19, 23162–23175 RSC.
- E. Kumarasamy, S. N. Sanders, M. J. Y. Tayebjee, A. Asadpoordarvish, T. J. H. Hele, E. G. Fuemmeler, A. B. Pun, L. M. Yablon, J. Z. Low, D. W. Paley, J. C. Dean, B. Choi, G. D. Scholes, M. L. Steigerwald, N. Ananth, D. R. McCamey, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2017, 139, 12488–12494 CrossRef CAS PubMed.
- M. Chen, Y. J. Bae, C. M. Mauck, A. Mandal, R. M. Young and M. R. Wasielewski, J. Am. Chem. Soc., 2018, 140, 9184–9192 CrossRef CAS PubMed.
- N. V. Korovina, J. Joy, X. Feng, C. Feltenberger, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2018, 140, 10179–10190 CrossRef CAS PubMed.
- D. V. Kozlov and F. N. Castellano, Chem. Commun., 2004, 2860–2861 RSC.
- X. Guo, Y. Liu, Q. Chen, D. Zhao and Y. Ma, Adv. Opt. Mater., 2018, 6, 1700981 CrossRef.
- Q. Zhang, J. Li, K. Shizu, S. Huang, S. Hirata, H. Miyazaki and C. Adachi, J. Am. Chem. Soc., 2012, 134, 14706–14709 CrossRef CAS PubMed.
- Q. Zhang, B. Li, S. Huang, H. Nomura, H. Tanaka and C. Adachi, Nat. Photonics, 2014, 8, 326–332 CrossRef CAS.
- A. N. Bartynski, M. Gruber, S. Das, S. Rangan, S. Mollinger, C. Trinh, S. E. Bradforth, K. Vandewal, A. Salleo, R. A. Bartynski, W. Bruetting and M. E. Thompson, J. Am. Chem. Soc., 2015, 137, 5397–5405 CrossRef CAS PubMed.
- V. Balaji, L. Ng, K. D. Jordan, M. N. Paddon-Row and H. K. Patney, J. Am. Chem. Soc., 1987, 109, 6957–6969 CrossRef CAS.
- M. D. Newton, Chem. Rev., 1991, 91, 767–792 CrossRef CAS.
- K. D. Jordan and M. N. Paddon-Row, Chem. Rev., 1992, 92, 395–410 CrossRef CAS.
- G. D. G. Scholes, K. P. Ghiggino, A. M. Oliver and M. N. Paddon-Row, J. Am. Chem. Soc., 1993, 115, 4345–4349 CrossRef CAS.
- P. R. Christensen, J. K. Nagle, A. Bhatti and M. O. Wolf, J. Am. Chem. Soc., 2013, 135, 8109–8112 CrossRef CAS PubMed.
- P. R. Christensen, B. O. Patrick, E. Caron and M. O. Wolf, Angew. Chem., Int. Ed. Engl., 2013, 52, 12946–12950 CrossRef CAS PubMed.
- H. D. Becker, Chem. Rev., 1993, 93, 145–172 CrossRef CAS.
- H. Bouas-Laurent, A. Castellan, J.-P. Desvergne and R. Lapouyade, Chem. Soc. Rev., 2000, 29, 43–55 RSC.
- H. Bouas-Laurent, A. Castellan, J.-P. Desvergne and R. Lapouyade, Chem. Soc. Rev., 2001, 30, 248–263 RSC.
- S. Franzen, W. Ni and B. Wang, J. Phys. Chem. B, 2003, 107, 12942–12948 CrossRef CAS.
- C. V. Suneesh and K. R. Gopidas, J. Phys. Chem. C, 2009, 113, 1606–1614 CrossRef CAS.
- T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS PubMed.
- J. B. Birks, Photophysics of Aromatic Molecules, Wiley - Interscience, New York, 1970 Search PubMed.
- J. Lukacs, R. A. Lampert, J. Metclafe and D. Phillips, J. Photochem. Photobiol., A, 1992, 63, 59–65 CrossRef CAS.
- T. C. Werner and J. Rodgers, J. Photochem., 1986, 32, 59–68 CrossRef CAS.
- W. Rodríguez-Córdoba, R. Noria-Moreno, P. Navarro and J. Peon, J. Lumin., 2014, 145, 697–707 CrossRef.
- I. R. Gould, J. A. Boiani, E. B. Gaillard, J. L. Goodman and S. Farid, J. Phys. Chem. A, 2003, 107, 3515–3524 CrossRef CAS.
- H. J. van Willigen, G. Jones and M. S. Farahat, J. Phys. Chem., 1996, 100, 3312–3316 CrossRef CAS.
- E. Heller and G. M. J. Schmidt, Isr. J. Chem., 1971, 9, 449–462 CrossRef CAS.
- G. Wegner, Pure Appl. Chem., 1977, 49, 443–454 CAS.
- V. Ramamurthy and K. Venkatesan, Chem. Rev., 1987, 87, 433–481 CrossRef CAS.
- H. Ihmels, D. Leusser, M. Pfeiffer and D. Stalke, Tetrahedron, 2000, 56, 6867–6875 CrossRef CAS.
- T. Salzillo, E. Venuti, R. G. Della Valle and A. Brillante, J. Raman Spectrosc., 2017, 48, 271–277 CrossRef CAS.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- M. E. Casida, in Recent Advances in Density Functional Methods, World Scientific, 1995, vol. 1, pp. 155–192 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- J. Liu and W. Liang, J. Chem. Phys., 2013, 138, 024101 CrossRef PubMed.
- J. E. Subotnik, R. J. Cave, R. P. Steele and N. Shenvi, J. Chem. Phys., 2009, 130, 234102 CrossRef PubMed.
- Y. Shao, M. Head-Gordon and A. I. Krylov, J. Chem. Phys., 2003, 118, 4807–4818 CrossRef CAS.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef CAS PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2014, 113, 184–215 CrossRef.
- W. Rettig, B. Paeplow, H. Herbst, K. Müllen, J.-P. Desvergne and H. Bouas-Laurent, New J. Chem., 1999, 23, 453–460 RSC.
- R. Bensasson and E. J. Land, Trans. Faraday Soc., 1971, 67, 1904–1915 RSC.
- Y. H. Meyer, R. Astier and J. M. Leclercq, J. Chem. Phys., 1972, 56, 801–815 CrossRef CAS.
- R. H. Compton, K. T. V. Grattan and T. Morrow, J. Photochem., 1980, 14, 61–66 CrossRef CAS.
- J. A. Bautista, R. E. Connors, B. B. Raju, R. G. Hiller, F. P. Sharples, D. Gosztola, M. R. Wasielewski and H. A. Frank, J. Phys. Chem. B, 1999, 103, 8751–8758 CrossRef CAS.
- Y. Pang, M. A. Prantil, A. J. Van Tassle, G. A. Jones and G. R. Fleming, J. Phys. Chem. B, 2009, 113, 13086–13095 CrossRef CAS PubMed.
- M. Fakis, J. S. Beckwith, K. Seintis, E. Martinou, C. Nançoz, N. Karakostas, I. Petsalakis, G. Pistolis and E. Vauthey, Phys. Chem. Chem. Phys., 2018, 20, 837–849 RSC.
- D. Villamaina, S. V. Bhosale, S. J. Langford and E. Vauthey, Phys. Chem. Chem. Phys., 2013, 15, 1177–1187 RSC.
- C. Högemann and E. Vauthey, J. Phys. Chem. A, 1998, 102, 10051–10059 CrossRef.
- R. Katoh, E. Katoh, N. Nakashima, M. Yuuki and M. Kotani, J. Phys. Chem. A, 1997, 101, 7725–7728 CrossRef CAS.
- M. A. J. Rodgers, Chem. Phys. Lett., 1972, 12, 612–614 CrossRef CAS.
- M. F. M. Post, J. Langelaar and J. D. W. van Voorst, Chem. Phys. Lett., 1971, 10, 468–472 CrossRef CAS.
- H. Saigusa, S. Sun and E. C. Lim, J. Phys. Chem., 1992, 96, 10099–10101 CrossRef CAS.
- S. I. Druzhinin, N. P. Ernsting, S. A. Kovalenko, L. P. Lustres, T. A. Senyushkina and K. A. Zachariasse, J. Phys. Chem. A, 2006, 110, 2955–2969 CrossRef CAS PubMed.
- O. F. Mohammed and E. Vauthey, J. Phys. Chem. A, 2008, 112, 5804–5809 CrossRef CAS PubMed.
- C. Climent, M. Barbatti, M. O. Wolf, C. J. Bardeen and D. Casanova, Chem. Sci., 2017, 8, 4941–4950 RSC.
- K. C. Woo, D. H. Kang and S. K. Kim, J. Am. Chem. Soc., 2017, 139, 17152–17158 CrossRef CAS PubMed.
- M. A. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838 CrossRef CAS.
- J. R. Rumble, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, 99th edn, 2018 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sc05598j |
| This journal is © The Royal Society of Chemistry 2019 |