Open Access Article
Open Access ArticleCrystallization kinetics of amorphous calcium carbonate in confinement†
Jack
Cavanaugh
 ,
Michael L.
Whittaker‡
,
Michael L.
Whittaker‡
 and
Derk
Joester
and
Derk
Joester
 *
*
Department of Materials Science and Engineering, Northwestern University, Evanston, IL, 60208 USA. E-mail: d-joester@northwestern.edu
First published on 11th April 2019
Abstract
Phase transformations of carbonates are relevant to a wide range of biological, environmental, and industrial processes. Over the past decade, it emerged that crystallization pathways in these systems can be quite complex. Metastable intermediates such as amorphous calcium carbonate (ACC) were found to greatly impact composition, structure, and properties of more stable phases. However, it has been challenging to create predictive models. Rapid transformation of ACC in bulk has been one obstacle in the determination of nucleation rates. Herein, it is reported that confinement in microfluidic droplets allows separating in time the precipitation of ACC and subsequent nucleation and growth of crystalline CaCO3. An upper limit of 1.2 cm−3 s−1 was determined for the steady-state crystal nucleation rate in the presence of ACC at ambient conditions. This rate has implications for the formation of calcium carbonate in biomineralization, bio-inspired syntheses, and carbon sequestration.
Introduction
Pathways involving metastable carbonates are thought to be integral to the construction of intricately designed functional materials in biomineralizing organisms.1 They are increasingly used in bio-inspired syntheses to generate structures and compositions far from equilibrium,2 and play an important role in carbon sequestration by precipitation of CaCO3.3–5 It is therefore of general interest to improve our understanding of carbonate crystallization pathways and the associated rates of phase transformation, especially in confinement.Amorphous calcium carbonate (ACC), a precursor to all three crystalline polymorphs of CaCO3,6 is perhaps the most widely characterized amorphous intermediate. In bulk systems, synthetic ACC typically transforms to calcite via vaterite within ∼5 minutes of ACC precipitation.7 ACC persists much longer in confinement, even in the absence of stabilizing additives.8,9 Increased lifetime may be the result of thermodynamic stabilization of ACC by interfacial or particle size effects,10 a kinetic trap,8 and/or the absence of powerful heterogeneous nucleators.11 It has been proposed that hindering the removal of water from ACC can reduce the rate of phase transformation,12,13 although it is unclear whether this mechanism fits within the classical description.
Given that the many proposed crystallization pathways may compete with each other,13,14 it is highly desirable to determine nucleation rates for each active pathway.15 Microfluidic techniques have enabled the study of crystal growth via ACC in small reaction chambers with well-defined surfaces and geometry as well as at the interface of solutions under laminar flow.16 Droplet microfluidic devices are particularly well-suited for characterizing crystallization in real-time and with large sample sizes17,18 We report here on the phase transformation kinetics of ACC confined in droplets.
We used a hydrodynamic flow-focusing device19 (Fig. S1†) made of PDMS to produce aqueous droplets in a fluorocarbon oil (HFE7500) containing 2 wt% surfactant.20 The surfactant is a triblock copolymer comprised of two perfluoropolyether (PFPE) “tails” separated by a polyethylene glycol (PEG) head group. Droplets of aqueous calcium chloride (1 M) had low polydispersity and were stable against coalescence for >7 days. However, colloidal stability was lost following precipitation of CaCO3 (not shown). To address this issue, and inspired by devices used in protein crystallization,22 we developed the ‘droplet orchard’ (Fig. 1 and S2†). This device consists of cubic wells connected to a channel with rectangular cross section (100 μm width, 50 μm height).
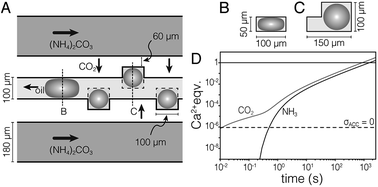 | ||
| Fig. 1 (A) Schematic drawing of the droplet orchard device. In the oil channel, droplets take an ellipsoidal shape (B), but can relax on entering the wells (C). (D) Plot of stoichiometric equivalents of CO2 and NH3 delivered to the droplet versus time, predicted by finite element modeling. Droplets are supersaturated for ACC (pKsp = 6.04, ref. 21) the dashed horizontal line. | ||
Results
Droplets (d = 100 μm) were generated in a decoupled flow focusing device (at ∼300 μL per hour), captured in PTFE tubing, and loaded into the droplet orchard (at ∼5 μL per hour). Droplets are trapped in the wells primarily due to the reduction in interfacial energy as they relax from an ellipsoidal to a spherical shape (Fig. 1B and C, Movie S1†).Precipitation of CaCO3 inside the droplets was induced by flowing aqueous ammonium carbonate ((NH4)2CO3, 1.5 M, 200 μL h−1) through two channels flanking the central storage channel (Fig. 1A). Transport kinetics of CO2 and NH3 from the ammonium carbonate channel to the droplet were estimated by finite element analysis (Fig. 1D, ESI†). In the case of entirely diffusive transport, i.e. without convective mixing in the oil, this model predicts that supersaturation with respect to ACC is established within 500 ms. Assuming fast chemical equilibration and precipitation in the droplets, this model further indicates that delivery of stoichiometric amounts of CO2 and NH3 for the precipitation of virtually all Ca2+ takes less than 30 min.
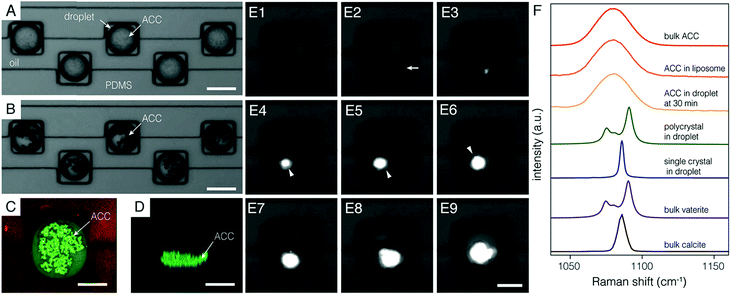
In good agreement with the FE model, many non-birefringent particles appeared throughout the volume of each droplet within five minutes of the initiation of (NH4)2CO3 flow (Fig. 2A). Particles grew over the course of ∼30 min and sank to the bottom (Fig. 2B–D, Movie S2†). We confirmed that these precipitates were ACC using confocal Raman micro-spectroscopy (Fig. 2F). Specifically, the center of the most intense carbonate ν1 mode appeared at 1080 cm−1, with a full width at half maximum of 19 cm−1, and was indistinguishable from bulk ACC powder and ACC stabilized in liposomes8 (see Fig. S3† for full spectra).
Growth of ACC particles became imperceptible after ∼30 minutes, suggesting that supersaturation with respect to ACC became negligible. Under these conditions, precipitates may still increase in average size through coarsening, but the total volume of ACC remains constant. ACC is then, to a close approximation, in metastable equilibrium with the encapsulated solution. The supersaturation with respect to the more stable polymorphs of calcium carbonate, vaterite, aragonite, and calcite is therefore fixed by ACC solubility (ESI†).
We followed the transformation of ACC to crystalline CaCO3 by time-resolved polarized light microscopy. Onset of crystallization was detected by a strong increase in brightness, consistent with the formation of birefringent crystals (Fig. 2E). A depletion zone free of ACC surrounding the birefringent particle developed within 5 minutes of the random timepoint at which crystallization was observed. While this does not rule out other mechanisms at earlier times, most of the mineral volume transformed by dissolution-reprecipitation. Crystalline precipitates had either an irregular or a faceted habit, with diameters that ranged from 10–30 μm. Droplets and their cargo rotated slowly in the confinement of the wells (∼5 rpm). Rotating faceted particles extinguished regularly when viewed between crossed polarizers, consistent with single crystals. Irregular precipitates did not extinguish uniformly, consistent with a polycrystalline mass (Movies S3 and S4†). Confocal Raman microscopy performed offline identified polycrystals as vaterite and faceted single crystals as calcite (Fig. 2F and S4†).
Irrespective of polymorph, crystalline precipitates were 1–10 μm in their largest dimension at first detection, and grew until all ACC was consumed, typically within one hour (Fig. 2E, Movies S5–S7†). Based on the growth rate observed over this time frame, we predict that a nucleus grows to a detectable size within minutes (ESI†). Uncertainty in determining the time of nucleation would therefore be commensurate with the inverse frame rate (5 min).
Discussion
Assuming nucleation events occur continuously and independently at a steady-state nucleation rate, J, an exponential distribution describes the time between nucleation events. The cumulative probability, P0(t), that nucleation has not occurred in a volume V at time t is given by the exponential failure distribution:18| P0(t) = e−JVt ≈ N0/N | (1) |
We recorded the time-to-detection of nucleation events in three independent experiments (N = 99, 97, and 95). Based on their habit, 42 of 48 crystals (87.5%) contained vaterite. As we cannot exclude that vaterite formed prior to calcite for the remaining 6 (12.5%), we calculated N0/N independent of polymorph. The spread in N0/N between the three experiments may appear broad (Fig. 3A); however, for the small number of observations in each experiment (6, 22, and 20 crystals detected, respectively), wide variability is expected between samples drawn from the same population. A 3-sample Anderson–Darling test failed to reject the null hypothesis that the three sets of observations were drawn from the same distribution (α = 0.010; p = 0.013; ESI†).
 | ||
| Fig. 3 Kinetics of crystallization of ACC. (A) Plot of N0/N versus t for three experiments (open symbols) and 68%, 95%, and 99.7% (shaded regions) of Monte Carlo simulations (105 experiments; 97 droplets; Δt = 1 h; J = 1.2 cm−3 s−1). (B) Aggregated data for all 291 droplets in (A), curve representing the nucleation rate determined by maximum-likelihood estimation (dashed line), and 99% confidence interval (dotted lines). (C) Plot of the time τ predicted to elapse before crystallization occurs in 1% (dotted line), 50% (dashed line), and 99% (solid line) of containers with volume V, given a steady state nucleation rate of J = 1.2 cm−3 s−1. Note that τ is found by rearranging eqn (1) for P0(τ). The equivalent dimension for spherical (diameter, d) and cubic (edge length) containers is provided. | ||
We therefore chose to aggregate the datasets and model the experiments with a single nucleation rate like in eqn (1), which is consistent with classical nucleation theory.18 Indeed, a 1-sample Anderson–Darling test failed to reject the null hypothesis (α = 0.010; p = 0.211) that the aggregated data come from an exponential distribution. In other words, we lack statistical evidence that would recommend against modelling the aggregated data using eqn (1). Although nucleation events were recorded in just 16% of all droplets, the remainder of droplets were included in the model by right-censoring, using the latest observation time. Maximum-likelihood estimation predicted that J = 1.2 cm−3 s−1 with a 99% confidence interval (CI) from 0.8–1.7 cm−3 s−1 (Fig. 3B).
While a single nucleation rate is consistent with the notion that calcite forms via vaterite, it is also possible that the nucleation rate for calcite is too low to significantly affect the experimental results. If, instead, we assume that calcite does not form via vaterite, maximum-likelihood estimation predicts nucleation rates for vaterite Jvat = 1.1 cm−3 s−1 (99%-CI: 0.7–1.5 cm−3 s−1) and calcite Jcal = 0.15 cm−3 s−1 (0.04–0.36 cm−3 s−1).
We explored the expected spread in N0/N over time between many identical experiments using Monte Carlo (MC) simulations (ESI†). Crystallization in each droplet was treated as a random process, with the probability, that crystallization does not occur during a time increment Δt = 1 hour calculated for J = 1.2 cm−3 s−1 (P0(Δt) = 0.998). The bounds of 99.7% of 105 97-droplet MC experiments include the three experiments from which J was calculated (Fig. 3A). In other words, the observed experimental scatter is within expectations given the size and duration of the experiment. In the absence of any evidence to suggest otherwise, we are therefore confident that modelling all observations from the three droplet orchard experiments with a single nucleation rate is appropriate.
However, we cannot exclude that the rate we found represents a population of “fast” droplets. The presence of “slow” droplets would manifest as a systematic deviation of the experimental data points from the fitted curve (dashed line in Fig. 3B) at long times.23 We therefore conclude that we have established an upper limit for J for the nucleation of vaterite from ACC confined in droplets. A further caveat is that it was not possible to identify the nucleation site inside the droplet. Therefore, we cannot distinguish between homogeneous and heterogeneous nucleation, nor can we identify nucleating surfaces. It should, however, be possible to determine whether J scales with the droplet volume or the surface area of the droplets or the ACC precipitates confined in them.
For J = 1.2 cm−3 s−1 and assuming the rate does scale with volume, one could expect about 103 years to elapse before ACC crystallizes in merely 1% of vesicles with 1 μm diameter. More than 106 years would elapse before ACC crystallizes in 1% of vesicles with 100 nm diameter (Fig. 3C). This is consistent with the report that ACC was not observed to crystallize in liposomes in the same size range.24 We note, however, that ACC was always observed within 15 minutes in liposomes with a diameter as small as ∼100 nm, meaning that if it forms by nucleation (rather than spinodal decomposition),25 the nucleation rate is higher by a factor of at least 2 × 1010.
When calcium carbonate forms intracellularly, for instance in coccoliths,26 sea urchin embryo spicules,27 or cystoliths6—or abiotically, yet confined to volumes of similar dimensions8—we expect ACC to be the default product if its supersaturation is exceeded. ACC would also be apparently “stable”, i.e. very unlikely to crystallize during the lifetime of the organism or the duration of a typical experiment. However, on breaking the confinement, and introducing ACC to heterogeneous nucleators in the environment, rapid phase transformation is expected. This is indeed observed in some systems.6,8 Organisms clearly have found solutions to accelerate nucleation when that is desired. Likely candidates are heterogeneous nucleators that are introduced into the compartments in which biomineralization occurs. These nucleators are then ideally positioned to also control crystal polymorph and orientation.
Conclusions
Looking forward, we expect that the device we describe herein is well suited to quantify the role of a wide range of additives on the transformation of ACC. It should also be relatively straightforward to adapt it to transformations of other phases. In fact, using microfluidic droplet confinement strategies may open pathways to synthesis of a host of amorphous precursor materials that could then be transformed into crystalline materials with structures and compositions far from equilibrium. In combination with a systematic evaluation of the effect of droplet size and temperature, our approach is well positioned to generate deep insights into the kinetics of phase transformations, and the thermodynamic barriers that control these rates. Therefore, we expect that it will become useful not only in biomineralization, but also, for instance, in carbon capture and sequestration, and bio-inspired materials synthesis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the NSF (DMR-1508399) and ARO (W911NF-16-1-0262). This work made use of: the EPIC facility of Northwestern University's NUANCE Center, which has received support from the Soft and Hybrid Nanotechnology Experimental (SHyNE) Resource (NSF ECCS-1542205); the MRSEC Program (NSF DMR-1121262) at the Materials Research Center; the International Institute for Nanotechnology (IIN); the Keck Foundation; and the State of Illinois, through the IIN. The authors acknowledge Prof. Seth Fraden and Dr Achini Opathalage for training in microfluidic fabrication.Notes and references
- J. J. De Yoreo, P. U. Gilbert, N. A. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Colfen and P. M. Dove, Science, 2015, 349, aaa6760 CrossRef PubMed.
- S. A. Kondrat, P. J. Smith, P. P. Wells, P. A. Chater, J. H. Carter, D. J. Morgan, E. M. Fiordaliso, J. B. Wagner, T. E. Davies, L. Lu, J. K. Bartley, S. H. Taylor, M. S. Spencer, C. J. Kiely, G. J. Kelly, C. W. Park, M. J. Rosseinsky and G. J. Hutchings, Nature, 2016, 531, 83–87 CrossRef CAS PubMed; M. L. Whittaker, P. J. M. Smeets, H. Asayesh-Ardakani, R. Shahbazian-Yassar and D. Joester, Angew. Chem., Int. Ed. Engl., 2017, 56, 16028–16031 CrossRef PubMed.
- J. Matter, et al. , Science, 2016, 352, 1312–1314 CrossRef CAS PubMed.
- J. J. Vericella, S. E. Baker, J. K. Stolaroff, E. B. Duoss, J. O. t. Hardin, J. Lewicki, E. Glogowski, W. C. Floyd, C. A. Valdez, W. L. Smith, J. H. Satcher Jr, W. L. Bourcier, C. M. Spadaccini, J. A. Lewis and R. D. Aines, Nat. Commun., 2015, 6, 6124 CrossRef CAS PubMed.
- M. T. Dunstan, A. Jain, W. Liu, S. P. Ong, T. Liu, J. Lee, K. A. Persson, S. A. Scott, J. S. Dennis and C. P. Grey, Energy Environ. Sci., 2016, 9, 1346–1360 RSC.
- L. Addadi, S. Raz and S. Weiner, Adv. Mater., 2003, 15, 959–970 CrossRef CAS.
- J. D. Rodriguez-Blanco, S. Shaw and L. G. Benning, Nanoscale, 2011, 3, 265–271 RSC; P. Bots, L. G. Benning, J.-D. Rodriguez-Blanco, T. Roncal-Herrero and S. Shaw, Cryst. Growth Des., 2012, 12, 3806–3814 CrossRef CAS.
- C. C. Tester, M. L. Whittaker and D. Joester, Chem. Commun., 2014, 50, 5619 RSC.
- C. J. Stephens, Y.-Y. Kim, S. D. Evans, F. C. Meldrum and H. K. Christenson, J. Am. Chem. Soc., 2011, 133, 5210–5213 CrossRef CAS PubMed.
- A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12096–12101 CrossRef CAS PubMed.
- D. Turnbull, J. Appl. Phys., 1950, 21, 1022–1028 CrossRef CAS; M. L. Whittaker, P. M. Dove and D. Joester, MRS Bull., 2016, 41, 361–362 CrossRef.
- A. V. Radha, T. Z. Forbes, C. E. Killian, P. U. P. A. Gilbert and A. Navrotsky, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16438–16443 CrossRef CAS PubMed.
- J. Ihli, W. C. Wong, E. H. Noel, Y.-Y. Kim, A. N. Kulak, H. K. Christenson, M. J. Duer and F. C. Meldrum, Nat. Commun., 2014, 5, 3169 CrossRef PubMed.
- A. J. Giuffre, A. C. Gagnon, J. J. De Yoreo and P. M. Dove, Geochim. Cosmochim. Acta, 2015, 165, 407–417 CrossRef CAS; Y. Politi, R. A. Metzler, M. Abrecht, B. Gilbert, F. H. Wilt, I. Sagi, L. Addadi, S. Weiner and P. U. P. A. Gilbert, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 17362–17366 CrossRef PubMed; M. H. Nielsen, S. Aloni and J. J. De Yoreo, Science, 2014, 345, 1158–1162 CrossRef PubMed.
- A. J. Giuffre, L. M. Hamm, N. Han, J. J. De Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9261–9266 CrossRef CAS PubMed; L. M. Hamm, A. J. Giuffre, N. Han, J. Tao, D. Wang, J. J. De Yoreo and P. M. Dove, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1304–1309 CrossRef PubMed.
- X. Gong, Y.-W. Wang, J. Ihli, Y.-Y. Kim, S. Li, R. Walshaw, L. Chen and F. C. Meldrum, Adv. Mater., 2015, 27, 7395–7400 CrossRef CAS PubMed; Y.-Y. Kim, C. L. Freeman, X. Gong, M. A. Levenstein, Y. Wang, A. N. Kulak, C. Anduix-Canto, P. A. Lee, S. Li, L. Chen, H. K. Christenson and F. C. Meldrum, Angew. Chem., Int. Ed., 2017, 56, 11885–11890 CrossRef PubMed; Y. Zeng, J. Cao, Z. Wang, J. Guo and J. Lu, Cryst. Growth Des., 2018, 18, 1710–1721 CrossRef.
- S. Li, M. Zeng, T. Gaule, M. J. McPherson and F. C. Meldrum, Small, 2017, 13, 1702154 CrossRef PubMed.
- R. P. Sear, CrystEngComm, 2014, 16, 6506–6522 RSC.
- S. L. Anna, N. Bontoux and H. A. Stone, Appl. Phys. Lett., 2003, 82, 364–366 CrossRef CAS.
- C. Holtze, A. C. Rowat, J. J. Agresti, J. B. Hutchison, F. E. Angilè, C. H. J. Schmitz, S. Köster, H. Duan, K. J. Humphry and R. A. Scanga, Lab Chip, 2008, 8, 1632 RSC.
- J. R. Clarkson, T. J. Price and C. J. Adams, J. Chem. Soc., Faraday Trans., 1992, 88, 243–249 RSC.
- J.-U. Shim, G. Cristobal, D. R. Link, T. Thorsen, Y. Jia, K. Piattelli and S. Fraden, J. Am. Chem. Soc., 2007, 129, 8825–8835 CrossRef CAS PubMed.
- S. V. Akella, A. Mowitz, M. Heymann and S. Fraden, Cryst. Growth Des., 2014, 14, 4487–4509 CrossRef CAS.
- C. C. Tester, C.-H. Wu, S. Weigand and D. Joester, Faraday Discuss., 2012, 159, 345–356 RSC.
- Z. Zou, W. J. E. M. Habraken, L. Bertinetti, Y. Politi, A. Gal, S. Weiner, L. Addadi and P. Fratzl, Adv. Mater. Interfaces, 2017, 4, 1600076 CrossRef.
- S. Sviben, A. Gal, M. A. Hood, L. Bertinetti, Y. Politi, M. Bennet, P. Krishnamoorthy, A. Schertel, R. Wirth, A. Sorrentino, E. Pereiro, D. Faivre and A. Scheffel, Nat. Commun., 2016, 7, 11228 CrossRef CAS PubMed.
- E. Beniash, J. Aizenberg, L. Addadi and S. Weiner, Proc. R. Soc. London, Ser. B, 1997, 264, 461–465 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials and methods and supplemental figures, movies and discussion. See DOI: 10.1039/c8sc05634j |
| ‡ Current address: Earth and Environmental Sciences Area, Lawrence Berkeley National Laboratory, 1 Cyclotron Rd., Berkeley, CA 94720. |
| This journal is © The Royal Society of Chemistry 2019 |