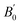Gold(I) sulfide: unusual bonding and an unexpected computational challenge in a simple solid

Abstract

We report the experimental high-pressure crystal structure and equation of state of gold(I) sulfide (Au₂S) determined using diamond-anvil cell synchrotron X-ray diffraction. Our data shows that Au₂S has a simple cubic structure with six atoms in the unit cell (four Au in linear, and two S in tetrahedral, coordination), no internal degrees of freedom, and relatively low bulk modulus. Despite its structural simplicity, Au₂S displays very unusual chemical bonding. The very similar and relatively high electronegativities of Au and S rule out any significant metallic or ionic character. Using a simple valence bond (Lewis) model, we argue that the Au₂S crystal possesses two different types of covalent bonds: dative and shared. These bonds are distributed in such a way that each Au atom engages in one bond of each kind. The multiple arrangements in space of dative and shared bonds are degenerate, and the multiplicity of configurations imparts the system with multireference character, which is highly unusual for an extended solid. The other striking feature of this system is that common computational (DFT) methods fail quite spectacularly to describe it, with 20% and 400% errors in the equilibrium volume and bulk modulus, respectively. We explain this by the poor treatment of static correlation in common density-functional approximations. The fact that the solid is structurally very simple, yet presents unique chemical bonding and is unmodelable using current DFT methods, makes it an interesting case study and a computational challenge.

---

1 Introduction

Chemical bonding in solids is traditionally understood in terms of four bonding patterns: ionic, covalent, metallic, and van der Waals.^1–5 Simple binary non-molecular solids in particular are elegantly classified according to their ionic/covalent/metallic character using van Arkel–Ketelaar triangle diagrams.^6–8 In these diagrams, each of the ideal bonding patterns occupies a corner in the triangle, and real solids are assigned points on the inside using a pair of quantitative bonding indices. In the traditional textbook diagram, these indices are the electronegativity difference (|χ_A − χ_B|) and the average electronegativity ((χ_A + χ_B)/2) of both atoms,⁸ although alternatives using indices obtained computationally have been proposed.^2,9 If the electronegativities of atoms A and B are similar, then the solid is metallic (low χ_A and χ_B) or covalent (high χ_A and χ_B). Furthermore, if the solid is covalent, then atoms in the periodic structure are arranged in such a way that they acquire a closed-shell electron configuration via electron sharing with their neighbors.

Simple binary solids are also quite well described by computational methods. Common approximations in density-functional theory^10,11 (DFT), the most popular class of computational methods for the solid state, predict lattice parameters and bulk moduli of simple solids with an average error relative to experiment of approximately 0.05 Å and 5 GPa, regardless of their ionic, covalent, or metallic character.^12,13 Only the case of molecular crystals, in which binding is dominated by intermolecular van der Waals interactions, is problematic for common density functionals. However, in the past two decades many solutions to this problem have been proposed and the computational description of molecular crystals does not present the challenge it once did.^14,15

In this article, we report the unusual behavior of a simple binary solid, gold(I) sulfide (Au₂S). Diamond-anvil cell (DAC) synchrotron X-ray diffraction (XRD) experiments were performed on Au₂S to determine its high-pressure crystal structure and equation of state. Our experimental evidence shows that this is a simple binary solid with cuprite-type structure and a relatively low bulk modulus. Despite its apparent simplicity, this system is unmodelable by common DFT-based methods typically used in solids, which grossly overestimate the equilibrium volume and bulk modulus.

In order to explain the large discrepancy between theory and experiment, we examine the nature of the chemical bonding in this crystal, via molecular models that mimic bulk Au₂S. Gold has a number of unusual properties owing to very large relativistic effects.¹⁶ Among them, the electronegativity of gold is quite high, and similar to that of sulfur. This places Au₂S in the covalent region of the van Arkel–Ketelaar diagram but, unlike elements from the p-block with similar electronegativity, gold only has one valence electron available to engage in covalent bonding. This observation explains the observed tendency of Au to form linear coordination compounds^16,17 and ultimately the abundance of cases where gold compounds engage in weak Au(I)–Au(I) closed-shell interactions^18,19 (aurophilicity).

By constructing a simple Lewis model, we propose that Au–S bonds in bulk Au₂S are an average of two distinct types of single bonds (dative and shared), and that the ground-state of this crystal is a combination of degenerate configurations with different spatial arrangements of these bonds. Our interpretation explains the electronic structure of molecular models that mimic bulk Au₂S and the failure of common density-functional approximations (DFA) to describe the equation of state of bulk Au₂S. To our knowledge, this is the first case of a solid with multireference character arising strictly from its periodic nature.

2 Experimental details

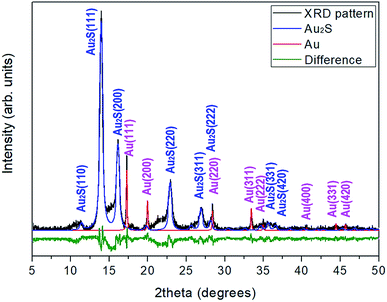
Gold sulfide (Au₂S) was synthesized by bubbling H₂S through a KAu(CN)₂ solution.²⁰ The XRD characterization of the dark brown reaction product was performed using a STOE X-ray powder diffractometer with monochromatic Kα₁ molybdenum radiation (λ = 0.7093 Å). The XRD pattern shows relatively broad Au₂S diffraction peaks and a diffuse scattering halo in the range 2θ = 13–18°, which point to a limited crystallinity. In addition, the sample coexists with gold metal, with approximately a 12 : 1 Au₂S : Au molar ratio (see Fig. 1). The presence of gold in this proportion provides a good internal pressure gauge for the high-pressure XRD experiments.

Fig. 1 Rietveld refinement of the X-ray diffraction pattern of the synthesized Au₂S sample plus elemental gold at room conditions (using λ_Cu = 1.5406 Å). Black: observed pattern. Blue: calculated profile for Au₂S. Red: calculated profile for metallic gold. Green: difference between observed and calculated patterns.

High-pressure angle-dispersive XRD experiments were conducted at room temperature at the I15 beamline of the Diamond Light Source with an incident monochromatic wavelength of 0.4246 Å focused to 30 × 30 μm². Three different runs were conducted. In the first run, measurements up to 10 GPa were performed in an ETH(BGI)-type DAC with diamond culets of 700 μm. Au₂S powder was loaded in a 300 μm diameter hole of a tungsten gasket preindented to a thickness of about 70 μm. A 4 : 1 methanol–ethanol mixture was used as the pressure-transmitting medium. In the second and third runs, measurements up to 29 GPa were performed in a LeToullec-type membrane-DAC (Sanchez Technologies) with 400 μm-culet diamonds. The sample was loaded in a 250 μm diameter hole of a rhenium gasket preindented to a thickness of about 35 μm. Neon was loaded in a 1500 bar gas-loading facility and used as the pressure-transmitting medium.

Pressure was determined using both the ruby fluorescence technique²¹ and the equation of state (EOS) of gold.²² The pressure difference between both scales is below 0.2 GPa at the maximum pressure studied. XRD images covering a 2θ range of up to 18° were collected using a PerkinElmer flat panel. Detector calibration, correction of distortion, and integration to conventional 2θ-intensity data were carried out with the Dioptas software.²³ The indexing and refinement of the powder patterns were performed using the FULLPROF²⁴ and POWDERCELL²⁵ program packages.

3 Computational details

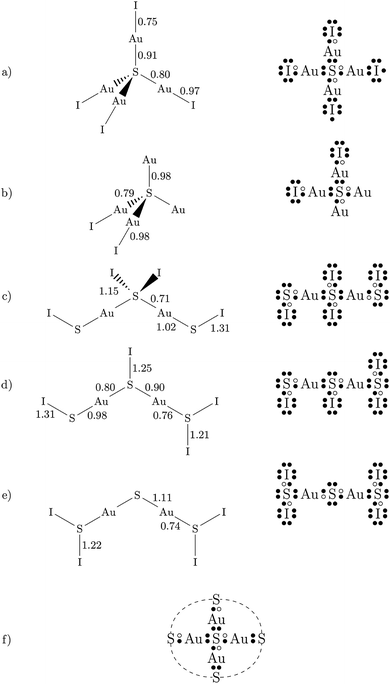
Most DFT calculations were carried out using the projector-augmented wave (PAW) method²⁶ implemented in the Quantum ESPRESSO package.²⁷ Scalar-relativistic PAW datasets were used for both S and Au from the pslibrary repository.²⁸ The latter dataset contains 11 valence electrons (5d¹⁰ 6s¹), but a harder 19-electron dataset with additional 5s² and 5p⁶ electrons in the valence was used for some tests. Various functionals were employed (see Table 1). The energy cutoffs for the plane wave and density expansions were 80 and 800 Ry, respectively, and we used a 6 × 6 × 6 uniform k-point grid. This ensures a convergence in the total energy to less than 0.1 mRy and in the stress tensor to ≈0.01 GPa. Due to the very small distortions and forces involved, we used very tight convergence criteria for the geometry relaxations: 10⁻⁶ Ry in the total energy, 10⁻⁵ Ry per bohr in the atomic forces, and 0.05 GPa in the pressure. Some tests were conducted using Cococcioni and de Gironcoli's simplified version²⁹ of the DFT+U method,^30–32 using different values of the U parameter and with the correction applied to the Au atom.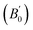

Table 1 Zero-pressure volumes (V₀), bulk moduli (B₀), and first derivatives with respect to pressure , obtained experimentally and computationally (the references containing the definition of each functional are given; all values reported are from this work). The parameters for the experimental data set using Ne as the pressure-transmitting medium were obtained from: (i) the whole pressure range (0–29 GPa) or (ii) two different pressure regimes (low pressure, 0–8 GPa; high pressure, 8–29 Gpa). The theoretical data corresponds to the static approximation (no lattice vibrations)

	V 0 (Å^3)	B 0 (GPa)
a No energy minimum found in the range. b Small core pseudopotential with 33 electrons in the valence (4f^145s^25p^65d^106s^1). c Including spin–orbit interactions.
Ne data set
0–8 GPa	129.4(3)	18.6(11)	6.3(5)
0–29 GPa	126.2(8)	30(2)	3.9(2)
8–29 GPa	116.3(5)	61(2)	2.37(9)
MeOH : EtOH data set
1–10 GPa	128.7(3)	16.4(9)	8.4(6)
Computational results
LDA^53	141.36	90.0	5.1
PBE^35	153.22	67.5	5.3
PBEsol^54	145.52	80.7	5.2
revPBE^55	157.50	60.0	5.4
B86bPBE^35,56	154.59	65.7	5.3
BP86 ^57,58	153.88	67.1	5.3
PW91 ^59	152.91	68.3	5.3
PBE-D2 ^60,61	144.33	120.3	4.9
PBE-D3 ^62	147.87	84.6	5.2
PBE-XDM^63,64	149.92	76.1	5.7
rVV10 ^65,66	154.22	70.4	5.2
vdw-DF2 ^67^a	>163	—	—
PBE(sc)^b	150.97	68.7	5.4
PBE/LAPW	150.29	64.5	6.2
PBE/LCAO(HF)	>163	—	—
PBE/LCAO(WB)	152.70	71.2	7.5
PBE/LCAO(DF)	152.42	71.9	7.5
B3LYP/LCAO^68,69	158.49	68.3	−1.7
HF/LCAO^a	>163	—	—
PBE-U (3 eV)	155.34	63.5	5.4
PBE-U (5 eV)	156.94	60.7	5.4
PBE-U (7 eV)	158.64	58.0	5.4
PBE(SO)^c	151.19	70.2	5.3

---

Equilibrium volumes and bulk moduli were calculated using fixed-volume geometry optimizations on a volume grid with 31 points between 118.5 ų and 163.0 ų. This range encompasses the experimental volume³³ (128.4 ų) and the calculated equilibrium volumes for most functionals. Phonon vibration frequencies were calculated at each of these points using density-functional perturbation theory³⁴ (DFPT) and the Perdew–Burke–Ernzerhof (PBE) functional.³⁵ We used a 2 × 2 × 2 regular q-point grid that was then interpolated to a 10 × 10 × 10 grid. Thermodynamic properties were computed either in the static approximation (V₀, B₀, 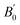) or using the total energies and phonon density of states on the volume grid in the quasiharmonic approximation (QHA), as implemented in the gibbs2 program.^36,37

Additional tests were performed with other computational techniques. The crystal17 program³⁸ was used to perform calculations employing linear combinations of atomic orbitals (LCAO). In this case, a 4 × 4 × 4 uniform k-point grid and the pob-TZVP triple-ζ basis set³⁹ were used. The core electrons in Au were replaced with Stuttgart–Dresden effective-core potentials and the effect of relativity was studied using their non-relativistic⁴⁰ (HF), quasi-relativistic⁴¹ (WB), and fully relativistic⁴² (DF) forms. The linearized augmented plane-waves (LAPW) calculations were carried out using the elk program,⁴³ version 4.3.06. The calculation parameters were: 4 × 4 × 4 uniform k-point grid, R^MT_min × max(|G + k|) = 9.0, and R^MT = 2.8 a.u. for gold and 2.2 a.u. for sulphur. Molecular calculations were carried out using Gaussian16.⁴⁴

Bader atomic charges^45,46 and delocalization indices⁴⁷ were calculated for some systems. We used the critic2 program⁴⁸ and the Yu–Trinkle integration method⁴⁹ for solids and the aimall program⁵⁰ for molecules. In solids, the DIs were calculated via maximally localized Wannier functions (MLWF), obtained from the wannier90 program,⁵¹ using a recently published method.⁵²

4 Experimental results

At ambient conditions, the XRD pattern of Au₂S corresponds to a cubic cuprite-type structure (space group Pn3̄m, number 224) with lattice parameter a = 5.0443(6) Å (Z = 2, V = 128.36(5) Å), which is consistent with previous studies.^20,33 The structure is shown in Fig. 2. Au atoms are in linear 2-fold coordination with S (S–Au–S) and S atoms are in tetrahedral 4-fold coordination with Au (d_Au–s = 2.16 Å). The structure is an interpenetration of a face-centered cubic (fcc) lattice of gold and a body-centered cubic (bcc) lattice of sulphur, relatively displaced by 1/4 along the main diagonal.

Fig. 2 Structure of cubic cuprite-like Au₂S. Large gray and small yellow spheres represent Au and S atoms, respectively. The Au–S and the Au–Au contacts are depicted as red and blue solid lines. The cubic unit cell is shown with black lines.

Four reflections of the cubic Au₂S structure, (111), (200), (220) and (311), can be easily identified at low pressure in the synchrotron XRD patterns. At high pressure, no new Bragg peaks were observed up to 29 GPa, indicating the absence of a first-order phase transition. However, the sample undergoes a clear and progressive pressure-induced amorphization (PIA) that reverses upon decompression. The loss of local atomic order is already visible at low pressure. The (111) reflection was always present up to the maximum pressure reached in this study, the (220) reflection only disappeared above 8 GPa, whereas the (200) and (311) were not visible above 3.5 GPa. Although tangential to the subject of this work, the analysis of the PIA has interest in itself; more details are given in the ESI.†

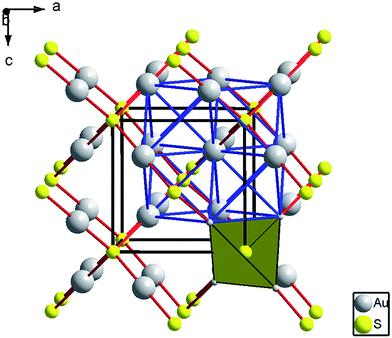
The lattice parameter of the cubic unit cell varies smoothly with increasing pressure (Fig. 3), also supporting the absence of first-order phase transitions in the studied pressure range. The least-squares fits of third-order Birch–Murnaghan (BM) EOS⁷⁰ to our experimental pressure-volume data are collected in Table 1. Gold sulfide has a low bulk modulus, comparable to the low-pressure phases of alkali-metal binary sulfides^71–75 and slightly lower than bulk moduli of the low-pressure phases of other group 11 sulfides such as Cu₂S,^76,77 AgCuS,⁷⁸ and Ag₂S.⁷⁹ The experimental data cannot be properly fitted using a third-order BM-EOS due to the existence of two different pressure regimes: below and above 8 GPa. The Au₂S crystal is considerably more compressible at low pressures (see Table 1). Fig. 3 also shows that there is a large hysteresis in the volume during decompression, the degree of which is dependent on the maximum pressure and/or the pressure-transmitting media. A third-order BM fit to the decompression P–V data gives V₀ = 130(3) ų, B₀ = 8(3) GPa, and 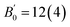. The ESI† contains more details regarding the experimental fitting procedure. We will use the experimental V₀ and B₀ values in boldface in Table 1 for the comparison to our computational data.

Fig. 3 Au₂S pressure-volume data from high-pressure XRD experiments. Run 1 (black symbols and line) used a 4 : 1 methanol : ethanol mixture as the pressure medium. Runs 2 and 3 (red symbols and line) used Ne as the pressure medium. During decompression there is a large hysteresis in the volume, which also depends on the maximum pressure reached and/or the pressure-transmitting medium. The green star symbol corresponds to the sample outside the DAC under ambient conditions.

5 Computational results

Our experimental results show that Au₂S has an unusually low bulk modulus compared to sulfides of other metals in the same group. Our original aim was to gain understanding of this observation by conducting a series of DFT calculations. The calculated static equilibrium volumes (V₀), bulk moduli (B₀), and pressure-derivatives of the bulk moduli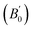 using different functionals are shown in Table 1. The experimental equilibrium volume and the bulk modulus are greatly overestimated in all cases (by about 20% and 400%, respectively), and our values agree with previous theoretical calculations on Au₂S.^80,81 Such a large disagreement between DFT and experiment is highly unusual for such a simple solid.^12,13 As an illustration, we calculated and compared the bulk moduli of other simple solids to the experimental values. In simple binary sulfides: Li₂S (calc. 40.6 GPa, expt. 41 GPa  ⁸²), Na₂S (calc. 28.1 GPa, expt. 28 GPa  ⁸²), high-pressure AgCuS (calc. 81.0 GPa, expt. 80 GPa;⁷⁸ the bulk modulus of the zero-pressure phase was not found experimentally), high-pressure Ag₂S (calc. 74.3 GPa,⁷⁹ expt. 82 GPa;⁷⁹ there are difficulties fitting the equation of state for the low-pressure phase). Likewise, in Cu₂O, which has the same structure as Au₂S, the calculated bulk modulus is 108.8 GPa and the experimental value is 114.4 GPa.⁸³ Deviations much smaller than 20% between calculated and experimental equilibrium volumes are typical as well: Li₂S (calc. 185.9 ų, expt. 184.2–186.7 ų (ref. 82)), Na₂S (calc. 283.3 ų, expt. 274.6–279.5 ų (ref. 82)), AgCuS (calc. 233 ų (ref. 78), expt. 215.3 ų (ref. 78)), high-pressure Ag₂S (calc. 225.5 ų (ref. 79), expt. 217.2 ų (ref. 79)), and Cu₂O (calc. 80.6 ų, expt. 77.8 ų (ref. 80)). Clearly, chemically and structurally similar solids do not present the same challenge as Au₂S. In the rest of the article we attempt to explain this failure.

In a first step, we evaluated all possible contributions to the disagreement. For instance, the static volume and bulk moduli are not directly comparable to the experimental counterparts because of vibrational effects. To evaluate their impact, we conducted a series of phonon frequency calculations at the grid volumes using the PBE functional. Examination of the phonon density of states reveals that a mechanical instability develops with increasing pressure, in agreement with the experimentally observed amorphization. Subsequent total-energy relaxation revealed that, at a static pressure of around 4 GPa, the cubic phase becomes unstable and undergoes a rhombohedral deformation. This is accompanied by a significant drop in crystal compressibility, and a change of regime in the E(V) and p(V) curves, in agreement with experimental observations above 8 GPa. This loss of symmetry happens by distortion of the [AuS₄] tetrahedra that, in our calculations, leads to the formation of a phase with Au monolayers and interstitial S atoms. The calculated Au–Au distances are much shorter in the distorted structure (3.1 Å at 10 GPa, cf. 3.8 Å at 0 GPa) and similar to the Au–Au distance in metallic gold (2.9 Å).

These observations could be used to explain the experimentally observed partial decomposition into elemental gold under pressure, but the incorporation of vibrational effects does not explain the disagreement between calculated and experimental V₀ and B₀. The calculated ambient-conditions V and B_T in the quasiharmonic approximation are 153.54 ų and 58.0 GPa, respectively, using the PBE functional. The quasiharmonic approximation (QHA) volume is slightly larger and the bulk modulus slightly smaller than the static counterparts, but still much higher than the experimental values. Interestingly, our QHA calculations also predict that Au₂S in the low-pressure regime shows negative thermal expansion up to a temperature of ≈250 K.

Since the incorporation of vibrational effects has a relatively minor effect on the volume and bulk modulus, we will compare the static quantities with the experimental values directly for simplicity. Table 1 gives a list of the different methods and corrections that were tried. The application of a dispersion correction decreases the equilibrium volume relative to PBE, but increases the bulk modulus, and does not improve the agreement with experiment. PBE-D2, in particular, doubles the predicted bulk modulus because of the very high value of the leading dispersion coefficient (C₆) for gold in this implementation (2818.3 a.u., cf. 634.3 a.u. for D3 and 197.5 a.u. for XDM). Non-local functionals such as rVV10 or vdw-DF2 increase the V₀ and B₀ relative to PBE, moving further away from experiment. The vdw-DF2 functional, in particular, does not have an energy minimum in the examined volume range.

Using methods other than the plane-waves/PAW approach changes the equilibrium volume and bulk modulus negligibly. Table 1 shows the results of our tests using PAW and a small-core pseudopotential for Au (33 electrons in the valence), an LCAO approach with different types of pseudopotentials, and the LAPW method. All PBE results are consistent, with all V₀ and B₀ values in a range of a few ų and GPa. Using fully relativistic pseudopotentials in the LCAO approach also has a negligible impact, whereas deactivating relativistic effects in the pseudopotential (PBE/LCAO(HF)) results in the disappearance of the energy minimum.

Given the internal consistency between our PAW and LCAO results, we employ the LCAO approach to examine the effect of incorporating exact exchange into the functional. A Hartree–Fock (HF) calculation results in a crystal that is not bound in the considered volume range. Admixture of only a fraction of exact exchange, as in the B3LYP functional, also increases the equilibrium volume and degrades the agreement with the experimental values significantly, while still overestimating the bulk modulus.

Finally, we performed a few tests with the Hubbard's U energy correction. We applied the correction term to the Au atom using different values of U. Table 1 shows that the equilibrium quantities are mostly unaffected by the inclusion of this energy term, which is not surprising given that Au is formally closed-shell in Au₂S. The inclusion of spin–orbit corrections in the calculation does not change the results significantly.

6 Bonding in gold(I) sulfide and the failure of density-functional approximations

From the preceding discussion we conclude that neither vibrational effects nor the usual shortcomings (dispersion, delocalization error⁸⁴) are responsible for the failure of generalized gradient approximation (GGA) functionals to reproduce the experimental data. All basis sets (atomic orbitals, linearized augmented plane waves, plane waves) and functionals tested overestimate the experimental volume and bulk modulus. It is revealing that the LCAO results predict that the disagreement increases with the fraction of exact exchange in the functional, to the point where HF does not even show an energy minimum in the E(V) curve. This behavior is characteristic of static (also known as non-dynamical) correlation problems^84–88 that appear in systems with multireference character, where the ground-state wavefunction is best represented as a linear combination of near-degenerate configurations. A simple example of this is a H₂ molecule stretched to its dissociation limit, where the wavefunction is a linear combination of two degenerate Slater determinants, with opposite-spin electrons localized on each H atom. All common density functionals fail to describe the dissociation of H₂ in a spin-restricted approach, with Hartree–Fock showing particularly poor performance. A common feature of the HF and common DFAs for multireference systems is that their description is improved (in terms of energy) by allowing spin-polarization of the wavefunction to arrive at the lower-energy broken-spin-symmetry self-consistent solution. In stretched H₂, for instance, unrestricted Hartree–Fock (UHF) gives the correct dissociation energy. The spin-polarized wavefunction, however, lacks any physical significance since it is not an eigenfunction of the spin operator.

The existence of an restricted (RHF) to unrestricted (UHF) Hartree–Fock instability in the wavefunction that leads to a lower-energy spin-contaminated wavefunction is a clear indicator of static-correlation character in a system. In a solid, the broken-symmetry ground state can be reached by using an initial guess with non-zero atomic magnetizations. However, all our attempts at finding a broken-symmetry ground state in bulk Au₂S proved unsuccessful. Therefore, if the static correlation problem is behind the experiment/DFT disagreement, then Au₂S is also unusual in that a lower-energy broken-symmetry ground state is not available, and this absence must be explained. Importantly, our DFPT calculations show that PBE has no negative phonon frequencies at the equilibrium geometry, indicating that the structure is mechanically stable. Our GGA calculations also predict the system is an insulator, with a band gap of 2.13 eV (PBE). The band structure is given in the ESI.†

To find our explanation for the DFT/experiment disagreement, we examine the chemical bonding in the solid. Let us first consider the nature of bonding in small molecular Au(I) complexes. In the +1 oxidation state, Au strongly prefers linear coordination,¹⁷ with typical complexes being [Au(PH₃)₂]⁺ and [AuCl(PH₃)]. Bonding in these complexes can be understood as a two-stage process. First, the 6s¹ electron in Au forms a σ covalent bond with a ligand that has one unpaired electron (for instance, Cl). Then, a Lewis base, such as PH₃, forms a dative bond with the σ-hole of the first bond, further stabilizing the molecule. A simple calculation in [AuCl(PH₃)] using B3LYP^68,69/Def2-TZVPP^41,89 predicts both steps stabilize the complex by 49.1 and 61.8 kcal mol⁻¹, respectively (a similar value for the second step has been reported¹⁷). In the rest of the discussion we will call these two types of bonds the “shared” and “dative” bonds, respectively. The [Au(PH₃)₂]⁺ complex has a similarly simple interpretation, but in that case the 6s¹ electron is missing and both bonds are dative.

The Au–S bonds in bulk Au₂S are particular in that the Pauling electronegativities of both atoms are very similar (Au = 2.54, S = 2.58), so we expect this crystal to show very little ionic character. This is confirmed by integration of the atomic charges, which gives a charge of +0.136 on each Au (using the PBE functional at the equilibrium geometry). Therefore, the 6s¹ electron on the Au atom has, for the most part, not been transferred to the neighboring S atoms. Since our band structure predicts a non-zero band gap, we conclude that the 6s¹ electron is used in forming covalent bonds. This situation is similar to the [AuCl(PH₃)] molecular example above, but we expect bonds in Au₂S to be much weaker, given the small amount of charge transfer present.

The simple bonding picture for the Au(I) metal complexes can be extended to simple molecular models for the Au₂S crystal (Fig. 4). Let us consider the tetrahedral [S(AuI)₄] molecule (Fig. 4a), with S and Au in the same coordination as in Au₂S. Iodine has been chosen as the capping atom because its electronegativity (2.66) is similar those of Au and S, in order to minimize charge transfer and molecular polarization. In [S(AuI)₄], the central S atom has two unpaired electrons, and the 6s¹ electrons from two neighboring Au atoms must be invested in forming two shared bonds. The other two Au–S bonds are dative. This leaves two iodine atoms with unpaired electrons, giving this molecule a multireference (biradical) character. Analysis of the stability of the restricted wavefunction (HF/Def2-TZVPP) reveals a lower-energy broken-symmetry spin-contaminated wavefunction with an unpaired α electron on one of the I atoms and an unpaired β electron on another. The delocalization indices (DIs) show a distribution of dative and shared bonds entirely consistent with our Lewis diagram. Shared bonds correspond to a higher DI than dative bonds, in agreement with our bond strength estimates for the [AuCl(PH₃)] complex. The two I atoms with the biradical character in the broken-symmetry wavefunction bond more weakly to the Au than the others. In turn, the Au atoms to which the I with radical character are attached bond more strongly with the central S atom.

Fig. 4 Lewis dot diagram for several molecular models (a–e) and for bulk Au₂S (f). The closed circles (●) are electrons from S and the open circles (○) are electrons from Au. The numbers indicate the calculated Bader's delocalization indices (DIs) at the HF/def2-TZVPP level in the broken-symmetry ground state. The dashed line represents equivalence under translational symmetry.

If we consider the same tetrahedral complex without two of the terminal I atoms ([S(AuI)₂Au₂], Fig. 4b), our Lewis diagrams predict that the molecule will be a stable closed-shell singlet, which is confirmed by HF/Def2-TZVPP calculations. The calculated DIs are again consistent with the Lewis diagram and the [S(AuI)₄] biradical results. Geometry relaxation of the [S(AuI)₂Au₂] complex with B3LYP/Def2-TZVPP allows the calculation of bond lengths and bond strengths: 24.0 kcal mol⁻¹ (2.32 Å) for the dative bond and 35.4 kcal mol⁻¹ (2.29 Å) for the shared bond. As expected, these bonds are much weaker than in [AuCl(PH₃)], which indirectly justifies the tendency of solid Au₂S to decompose. We explored several other simple molecular models of Au₂S and found that their broken-symmetry wavefunctions are also explained by our Lewis diagrams. Fig. 4c–e shows three Au₂S₃I₄ molecules that our model correctly predicts are closed-shell singlets (HF/Def2-TZVPP). The calculated DIs are consistent with the predicted character of each bond: shared bonds have higher DI, and are therefore stronger, than dative bonds.

Based on the success of our simple Lewis model in predicting the behavior of Au/S molecular systems, it is reasonable to assume that it will describe bulk Au₂S itself. The Lewis dot diagram for Au₂S is shown in Fig. 4f. The central S atom forms two dative bonds and two shared bonds with its four neighboring Au. The distribution of these four bonds determines the character (dative or shared) of the rest of the bonds in the cell and, by extension, the whole crystal. There are six possible ways to arrange the bonds in the central atom, and thus there are six possible ground-state configurations for this crystal if translational symmetry is imposed. If we consider a non-primitive supercell, then there would be additional possible bond arrangements based on the number of S atoms in the supercell.

Given that these two bonds are not equivalent (they have different bond strengths and bond lengths), we expect that all degenerate electronic configurations contribute to the ground state of Au₂S equally, which makes this system multireference in character. Our GGA calculations predict a ground state where all bonds are equivalent, and approximately average between the shared and the dative bonds (the calculated bonded Au–S DIs in the solid using the PBE functional are 0.94). If we used the exact exchange-correlation functional, the energy of this average would equal the energy of any of the contributing configurations.⁸⁴ However, all approximate density functionals in Table 1 violate this condition, and therefore the failure of common DFAs to reproduce the equation of state in Au₂S can be attributed to the erroneous treatment of static correlation.

In comparison with other typical static correlation error cases like stretched H₂, Au₂S possesses unique features. First, it is a periodic solid, and the multireference character of the ground state is a direct consequence of the periodicity. Second, all degenerate configurations that enter the density average⁸⁴ are closed-shell singlets, which explains why it is not possible to arrive at a lower-energy broken-symmetry solution in the bulk. Another consequence of this observation is that it is difficult to cast this problem in terms of fractional-spin behavior, like in stretched H₂ or systems with a biradical character. Finally, given its simple structure (cubic, high symmetry, six atoms in the unit cell, no internal degrees of freedom), Au₂S is both an excellent test case for the development of new density functional approximations and a crystal with unique chemical bonding.

7 Conclusions

In this article, we present an experimental/theoretical study of gold(I) sulfide (Au₂S), which is shown to be an anomalous solid in a number of ways. The structural properties of Au₂S at ambient conditions and under pressure were studied using diamond-anvil cell synchrotron X-ray diffraction experiments. The zero-pressure phase of Au₂S is cubic (space group Pn3̄m) with 6 atoms in the unit cell and no internal atomic degrees of freedom. The system undergoes a progressive pressure-induced amorphization above 3 GPa, but the crystalline and amorphous phases coexist up to 29 GPa. In addition, the amorphous phase reverts, at least partially, to the ordered cubic phase upon decompression.

The most interesting characteristics of Au₂S, however, are its unique chemical bonding and the fact that it is a challenge for DFT methods. All common density functionals fail to reproduce the experimental volume (V₀) and bulk modulus (B₀) quite spectacularly, with an overestimation of the unit cell volume by around 20% and an equilibrium bulk modulus around 400% higher than the experimental value. We examined the usual reasons for such a discrepancy but none of them explain the disagreement. Vibrational effects have a small impact on the calculated V₀ and B₀. All examined functionals, including dispersion-corrected and non-local, display the same failure. The V₀ and B₀ calculated using different basis sets (plane waves, atomic orbitals, augmented plane-waves) and the same functional are consistent with each other, but wrong. Inclusion of exact exchange degrades the agreement with experiment even further, and the Hartree–Fock E(V) curve does not have a minimum in the volume range considered.

These observations, particularly the response to the inclusion of exact exchange, suggest that static correlation error is behind the discrepancy. The electronegativities of Au and S are almost exactly the same, which negates any charge transfer within the crystal and makes the bonding in Au₂S almost purely covalent. In view of this, we proposed a simple Lewis model and applied it to explain the ground-state electronic configuration of simple molecular models similar to bulk Au₂S. In these systems, Au(I) forms two kinds of bonds: dative (both electrons come from the ligand) and shared (one electron from the ligand and one from Au). These two bonds are not equivalent and have different bond lengths and strengths, although both are relatively weak. By applying the same model to bulk Au₂S, we propose that the ground state of Au₂S is best described as a linear combination of several closed-shell singlet electron configurations that differ in how the dative and shared bonds are arranged. The system is therefore multireference in character and static correlation is important in its description, which explains the failure of common density-functional approximations in reproducing the experimental results. Our interpretation also explains why it is possible to find a broken spin-symmetry state of lower energy than the restricted ground state in molecular models but not in the solid. Au₂S is a very simple system, yet a large challenge to current density-functional approximations. We hope that it will serve as a test case for future development.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the Spanish Ministerio de Economía y Competitividad (MINECO), the Generalitat Valenciana, the Spanish Research Agency (AEI), and the European Fund for Regional Development (FEDER) for their financial support (MAT2016-75586-C4-3-P, and MAT2015-71070-REDC (MALTA Consolider), and Prometeo/2018/123 (EFIMAT)). D. S.-P., A. O. R. and J. R.-F. acknowledge MINECO for two Ramón y Cajal (RyC-2014-15643 and RyC-2016-20301) and a Juan de la Cierva (IJCI-2014-20513) contracts. E. R. J. thanks the Natural Sciences and Engineering Research Council of Canada (NSERC) for financial support. The authors also thank the Diamond Light Source for beamtime allocation at I15 line (EE16212).

References

1. C. Kittel, Introduction to solid state physics, John Wiley & Sons, New York, 8th edn, 1996.
2. W. P. Anderson, J. K. Burdett and P. T. Czech, J. Am. Chem. Soc., 1994, 116, 8808–8809.
3. L. C. Allen and J. F. Capitani, J. Am. Chem. Soc., 1994, 116, 8810.
4. L. C. Allen, J. F. Capitani, G. A. Kolks and G. D. Sproul, J. Mol. Struct., 1993, 300, 647–655.
5. W. B. Jensen, J. Chem. Educ., 1995, 72, 395.
6. A. E. Arkel, Molecules and crystals in inorganic chemistry, Interscience Publishers, 1956.
7. J. A. A. Ketelaar, Chemical constitution: an introduction to the theory of the chemical bond, Elsevier Publishing Company, 1958.
8. W. B. Jensen, Bull. Hist. Chem., 1992, 13, 47–59.
9. P. Mori-Sánchez, A. Martín Pendás and V. Luaña, J. Am. Chem. Soc., 2002, 124, 14721–14723.
10. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864.
11. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133.
12. P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 085104.
13. G. I. Csonka, J. P. Perdew, A. Ruzsinszky, P. H. Philipsen, S. Lebègue, J. Paier, O. A. Vydrov and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 155107.
14. G. A. DiLabio and A. Otero-de-la-Roza, Rev. Comput. Chem., 2016, 29, 1–97.
15. Non-covalent Interactions in Quantum Chemistry and Physics, ed. A. Otero-de-la-Roza and G. DiLabio, Elsevier, 2017, in press.
16. P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412–4456.
17. P. Schwerdtfeger, H. L. Hermann and H. Schmidbaur, Inorg. Chem., 2003, 42, 1334–1342.
18. P. Pyykkö, Chem. Rev., 1997, 97, 597–636.
19. A. Otero-de-la-Roza, J. D. Mallory and E. R. Johnson, J. Chem. Phys., 2014, 140, 18A504.
20. H. Hirsch, A. Decugnac, M. Gadet and J. Pouradier, C. R. Seances Acad. Sci., Ser. B, 1966, 263, 1328.
21. H. Mao, J.-A. Xu and P. Bell, J. Geophys. Res., Solid Earth Planets, 1986, 91, 4673–4676.
22. A. Dewaele, P. Loubeyre and M. Mezouar, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 094112.
23. C. Prescher and V. B. Prakapenka, High Pressure Res., 2015, 35, 223–230.
24. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
25. W. Kraus and G. Nolze, Powder Diffr., 1998, 13, 256.
26. P. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
27. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901.
28. A. Dal Corso, Comput. Mater. Sci., 2014, 95, 337–350.
29. M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
30. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943.
31. V. I. Anisimov, I. Solovyev, M. Korotin, M. Czyżyk and G. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 16929.
32. A. Liechtenstein, V. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467.
33. K. Ishikawa, T. Isonaga, S. Wakita and Y. Suzuki, Solid State Ionics, 1995, 79, 60–66.
34. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515.
35. J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. A. Otero-de-la-Roza and V. Luaña, Comput. Phys. Commun., 2011, 182, 1708–1720.
37. A. Otero-de-la-Roza, D. Abbasi-Pérez and V. Luaña, Comput. Phys. Commun., 2011, 182, 2232–2248.
38. R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rerat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, Torino, 2017.
39. M. F. Peintinger, D. V. Oliveira and T. Bredow, J. Comput. Chem., 2012, 451–459.
40. P. Schwerdtfeger, M. Dolg, W. E. Schwarz, G. A. Bowmaker and P. D. Boyd, J. Chem. Phys., 1989, 91, 1762–1774.
41. D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Theor. Chim. Acta, 1990, 77, 123–141.
42. D. Figgen, G. Rauhut, M. Dolg and H. Stoll, Chem. Phys., 2005, 311, 227–244.
43. K. Dewhurst, S. Sharma, et al., The Elk FP-LAPW code, http://elk.sourceforge.net/.
44. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian˜16 Revision B.01, 2016, Gaussian Inc, Wallingford CT.
45. R. F. W. Bader, Atoms in Molecules.A Quantum Theory, Oxford University Press, Oxford, 1990.
46. R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15.
47. R. F. Bader and M. E. Stephens, J. Am. Chem. Soc., 1975, 97, 7391–7399.
48. A. Otero-de-la-Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
49. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.
50. T. A. Keith, AIMAll (Version 14.06.21), TK Gristmill Software, Overland Park KS, USA, 2014, aim.tkgristmill.com.
51. A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699.
52. A. Otero-de-la-Roza, A. Martín Pendás and E. R. Johnson, J. Chem. Theory Comput., 2018, 14, 4699–4710.
53. J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048.
54. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
55. Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890.
56. A. Becke, J. Chem. Phys., 1986, 85, 7184.
57. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
58. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
59. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
60. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
61. V. Barone, M. Casarin, D. Forrer, M. Pavone, M. Sambi and A. Vittadini, J. Comput. Chem., 2009, 30, 934–939.
62. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
63. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
64. A. Otero-de-la-Roza and E. R. Johnson, J. Chem. Phys., 2012, 136, 174109.
65. O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103.
66. R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108.
67. K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101.
68. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
69. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
70. F. Birch, J. Geophys. Res., 1978, 83, 1257–1268.
71. A. Grzechnik, A. Vegas, K. Syassen, I. Loa, M. Hanfland and M. Jansen, J. Solid State Chem., 2000, 154, 603–611.
72. A. Vegas, A. Grzechnik, K. Syassen, I. Loa, M. Hanfland and M. Jansen, Acta Crystallogr., Sect. B: Struct. Sci., 2001, 57, 151–156.
73. A. Vegas, A. Grzechnik, M. Hanfland, C. Mühle and M. Jansen, Solid State Sci., 2002, 4, 1077–1081.
74. D. Santamaria-Perez, A. Vegas, C. Muehle and M. Jansen, Acta Crystallogr., Sect. B: Struct. Sci., 2011, 67, 109–115.
75. D. Santamaria-Perez, A. Vegas, C. Muehle and M. Jansen, J. Chem. Phys., 2011, 135, 054511.
76. D. Santamaria-Perez, G. Garbarino, R. Chulia-Jordan, M. Dobrowolski, C. Mühle and M. Jansen, J. Alloys Compd., 2014, 610, 645–650.
77. D. Zimmer, J. Ruiz-Fuertes, W. Morgenroth, A. Friedrich, L. Bayarjargal, E. Haussühl, D. Santamaría-Pérez, S. Frischkorn, V. Milman and B. Winkler, Phys. Rev. B, 2018, 97, 134111.
78. D. Santamaria-Perez, A. Morales-Garcia, D. Martinez-Garcia, B. Garcia-Domene, C. Muhle and M. Jansen, Inorg. Chem., 2012, 52, 355–361.
79. D. Santamaría-Pérez, M. Marqués, R. Chuliá-Jordán, J. M. Menendez, O. Gomis, J. Ruiz-Fuertes, J. A. Sans, D. Errandonea and J. M. Recio, Inorg. Chem., 2012, 51, 5289–5298.
80. A. Kirfel and K. Eichhorn, Acta Crystallogr., Sect. A: Found. Adv., 1990, 46, 271–284.
81. J. A. Suárez, J. J. Plata, A. M. Márquez and J. F. Sanz, Theor. Chem. Acc., 2016, 135, 70.
82. J. Schön, Ž. Čančarević and M. Jansen, J. Chem. Phys., 2004, 121, 2289–2304.
83. M. Beg and S. Shapiro, Phys. Rev. B: Solid State, 1976, 13, 1728.
84. A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2011, 112, 289–320.
85. D. H. Ess, E. R. Johnson, X. Hu and W. Yang, J. Phys. Chem. A, 2011, 115, 76–83.
86. A. J. Cohen, P. Mori-Sánchez and W. Yang, J. Chem. Phys., 2008, 129, 121104.
87. A. D. Becke, J. Chem. Phys., 2003, 119, 2972–2977.
88. T. Ziegler, A. Rauk and E. J. Baerends, Theor. Chim. Acta, 1977, 43, 261–271.
89. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.

---

Footnote

† Electronic supplementary information (ESI) available: Analysis of the pressure-induced amorphization in Au₂S and calculated band structure. See DOI: 10.1039/c9sc00371a

---