Open Access Article
Open Access ArticleExperimental and theoretical investigation of overall energy deposition in surface-induced unfolding of protein ions†
Micah T.
Donor
a,
Austin M.
Mroz
a and
James S.
Prell
 *ab
*ab
aDepartment of Chemistry and Biochemistry, 1253 University of Oregon, Eugene, OR 97403-1253, USA
bMaterials Science Institute, University of Oregon, 1252 University of Oregon, Eugene, OR 97403-1252, USA. E-mail: jprell@uoregon.edu; Fax: +1 541 346 4643; Tel: +1 541 346 2597
First published on 6th March 2019
Abstract
Recent advances in native mass spectrometry have enabled its use to probe the structure of and interactions within biomolecular complexes. Surface-induced dissociation, in which inter- and intramolecular interactions are disrupted following an energetic ion-surface collision, is a method that can directly interrogate the topology of protein complexes. However, a quantitative relationship between the ion kinetic energy at the moment of surface collision and the internal energy deposited into the ion has not yet been established for proteins. The factors affecting energy deposition in surface-induced unfolding (SIU) of protein monomers were investigated and a calibration relating laboratory-frame kinetic energy to internal energy developed. Protein monomers were unfolded by SIU and by collision-induced unfolding (CIU). CIU and SIU cause proteins to undergo the same unfolding transitions at different values of laboratory-frame kinetic energy. There is a strong correlation between the SIU and CIU energies, demonstrating that SIU, like CIU, can largely be understood as a thermal process. The change in internal energy in CIU was modeled using a Monte Carlo approach and theory. Computed values of the overall efficiency were found to be approximately 25% and used to rescale the CIU energy axis and relate nominal SIU energies to internal energy. The energy deposition efficiency in SIU increases with mass and kinetic energy from a low of ∼20% to a high of ∼68%, indicating that the effective mass of the surface increases along with the mass of the ion. The effect of ion structure on energy deposition was probed using multiple stages of ion activation. Energy deposition in SIU strongly depends on structure, decreasing as the protein is elongated, due to decreased effective protein-surface collisional cross section and increased transfer to rotational modes.
Introduction
The ability of electrospray ionization (ESI) to preserve native-like non-covalent interactions into the gas phase has led to the study of a range of important biological systems using native mass spectrometry. Native ion mobility-mass spectrometry (IM-MS), which can be used to characterize the overall shape and size of an ion by determining its collisional cross section (CCS) in a buffer gas, is a powerful tool for the investigation of high-order structure.1 Various gas-phase dissociation methods can be used to disrupt covalent and/or non-covalent interactions in order to probe structural characteristics such as sequence,2–4 location of ligand binding or post-translational modifications,3–5 connectivity of subunits in a complex,6–8 and differences in stability between closely-related structures.9,10 These dissociation methods vary as to how the ion is activated, i.e., via charge transfer/recombination,11–14 collisions with neutral species,15 or absorption of photons.16–18Collision induced dissociation (CID), in which ions are slowly heated by many low energy collisions with a neutral gas (e.g. Ar), is the most commonly-used method for interrogating protein complex composition using mass spectrometry. The products of CID for a non-covalently bound assembly such as a protein oligomer with n subunits are typically an ejected monomer and remaining (n − 1)-mer.9,19 For protein assembly ions, the charge of the complex is typically partitioned asymmetrically between the products – the monomer is often unfolded and carries a share of the charge that is larger than its share of the mass of the complex.9,20,21 This provides useful information about the identity of the subunits in a complex but imparts only limited information about the quaternary structure of the complex.
By contrast, surface induced dissociation (SID) is an alternative dissociation method that can yield more information about the high-order structure of protein complexes than is typically obtained in CID.22,23 In SID, dissociation is caused by a single high-energy collision event with a rigid surface, usually a gold electrode coated with a self-assembled monolayer of perfluorinated alkanethiol (FSAM). Unlike CID, SID often fragments native-like protein complexes such that the products remain compact on the millisecond timescale of the experiment and the charge is partitioned symmetrically.22,24,25 Seminal results from the Wysocki group for a variety of protein homo- and heterooligomers indicate that the SID products in many cases reflect the quaternary structure of the complex observed in condensed-phase data (e.g. a hexamer with an X-ray crystal structure indicative of a dimer of trimers will dissociate into two trimers upon SID), and thus that SID can probe the high-order structure of protein complexes.6–8,26,27 For protein complexes, correlation between the surface area of the interfaces broken and the SID collision energy required to break them has been reported,26 but the challenge of translating the nominal laboratory frame energies to internal energies has limited quantitative determination of protein–protein interfacial areas directly from SID data. SID has been implemented on a number of different mass spectrometry platforms, including FT-ICR28,29 and Q-TOF30 instruments. In partnership with Waters Corp., the Wysocki group has developed a kit that enables routine application of SID on Waters Synapt Q-IM-TOF instruments, making this platform a testbed for SID of native protein complexes.
The energetics of SID have been previously characterized, both experimentally31–33 and computationally,34,35 for small monomeric molecules and peptides. In general, the kinetics of product formation from these precursor ions after relatively low-energy surface collision can be well-described using unimolecular RRKM theory, indicating that the dissociation process occurs away from the surface following picosecond-timescale34,36 thermalization of the energy deposited by the collision. Multiple studies have shown that approximately 20% of the ion's laboratory frame kinetic energy is converted to internal energy of the ion for collisions with the typical FSAM surfaces.31,32,34,35 This fraction varies little with the angle of incidence, which instead modulates the proportion of the laboratory frame kinetic energy transferred out of the ion's translational modes or into the surface, with shallower angles decreasing transfer into the surface and increasing the amount of translational energy remaining after surface collision.31 For some peptide ions, fragments that appear at very short reaction times suggest that “shattering” is an alternate dissociation pathway at high incident kinetic energies (such that greater than 10 eV is transferred to internal modes),33,37 a result supported by simulations of glycine38 and octaglycine39 SID showing that specific collision orientations lead to shattering. Shattering, in which fragmentation is nearly instantaneous following surface impact (ps timescale), is also commonly observed for small molecules and large non-covalent clusters of atoms and small molecules (e.g. Ar, ammonium) colliding with the surface at high (transonic) velocities.40–43
Due to the vast number of degrees of freedom present in proteins and protein complexes, energy deposition and dissociation in SID can be much more difficult to study quantitatively using the same methods employed for peptides. Proteins and protein complexes also differ from peptides in that the observed fragments result from the disruption of many non-covalent interactions that can be distributed across a large surface area, rather than a single covalent bond. This raises the possibility that, when a small portion of a large species traveling at high velocity collides with the surface, shear forces and other mechanical effects may play a large role, leading to dissociation of some of these non-covalent interactions before thermalization is complete. Multiple collisions of the ion with the surface may also occur, further complicating the study of SID dynamics both computationally and experimentally.35
A first step towards understanding SID of protein complexes more quantitatively is to understand how surface collisions deposit energy into proteins more generally. Here, unfolding of protein monomers, as measured by ion mobility after surface collision, is used to investigate energy deposition upon surface collision. We demonstrate that proteins subjected to collision- and surface-induced unfolding (CIU and SIU, respectively) undergo the same unfolding transitions and quantify the relationship between their nominal laboratory-frame energy scales. Monte Carlo simulations and theoretical modeling of CIU enable calibration of the internal energy deposited for CIU, which in turn is used to calibrate overall energy deposition in SIU. We show that the efficiency of SIU, defined as the proportion of laboratory-frame kinetic energy converted to internal energy of the ion, can be nearly three times the efficiency of CIU for large monomeric proteins. Finally, SIU is shown to depend strongly on the structure of the precursor ion, with more unfolded ions having a smaller effective protein-surface CCS and lower energy transfer efficiency.
Methods
Sample preparation
Myoglobin, β-lactoglobulin, concanavalin A, carbonic anhydrase, alcohol dehydrogenase, albumin, bovine serum albumin, and transferrin were acquired from Sigma-Aldrich. Two protein components of anthrax lethal toxin, protective antigen, PA63, and the N-terminal domain of lethal factor, LFN, were graciously provided by Dr Bryan Krantz at the University of Maryland. Lyophilized proteins were reconstituted in ultrapure (18 MΩ) water. Protein samples were exchanged into either 200 mM ammonium acetate 10 mM ammonium bicarbonate pH 8 (PA63) or 200 mM ammonium acetate pH 7 (all other proteins) using Micro Bio-Spin 6 desalting columns (BioRad).Ion mobility-mass spectrometry
All ion mobility-mass spectra were collected using a Synapt G2-Si ion mobility-mass spectrometer (Waters Corp.) equipped with a nanoelectrospray (nanoESI) source. NanoESI emitters with a tip ID of approximately 1 μm were pulled from borosilicate capillaries with an ID of 0.78 mm using a Flaming-Brown P-97 micropipette puller (Sutter Instruments). For mass spectrometry analysis, 3–5 μL of sample was loaded into an emitter, and electrospray was initiated by applying a potential (relative to instrument ground) of +0.7–1.1 kV to a platinum wire in electrical contact with the solution. All experiments were conducted in “Sensitivity” mode with the source equilibrated to ambient temperature and a backing pressure of 3.7 mbar. Traveling wave velocities of 400–550 m s−1 and wave heights of 18–25 V were used in all experiments. Nitrogen was used as the buffer gas in ion mobility experiments, and the helium cell and nitrogen gas flows were set to 100 mL min−1 and 50 mL min−1, respectively. Measured arrival time distributions were converted to collisional cross sections using an established literature procedure.44,45 Cytochrome C, β-lactoglobulin, avidin, bovine serum albumin, and concanavalin A were used as ion mobility calibrants.Collision-induced unfolding
Collisional activation in the Waters Synapt G2-Si occurs in the “Trap” region of the instrument, located between the quadrupole and the ion mobility cell. A single charge state was isolated using the quadrupole with the LM Resolution set to 4.0 and the HM Resolution to 15. Collision-induced unfolding was performed by increasing the acceleration voltage (Trap CE) in 5 V increments, starting at 5 V and ending when significant fragmentation of the precursor ion was observed. The Trap gas flow was set to 5 mL min−1 for all collision-induced unfolding experiments. Arrival time distributions for each acceleration voltage were extracted using MassLynx 4.1 (Waters) and “fingerprint” images were generated using Igor Pro (WaveMetrics). For each acceleration voltage, the Multi Peak Fitting package in Igor Pro was used to fit the arrival time distribution with a number of Gaussian functions corresponding to the number of conformer families present. The area of each peak was computed to determine the relative abundance of each conformer family. For transitions resulting in at least 50% conversion to the more unfolded conformer family in both SIU and CIU, appearance energies were determined by summing the relative abundances of each conformer family with a larger CCS than that of the initial family for the transition (i.e. for the transition out of conformer family 1, sum the abundances of families 2, 3, and 4), and fitting that data with a sigmoidal function using Igor Pro – the appearance energy is the energy value at the intersection between the line tangent to the midpoint of the sigmoid and the x-axis.Surface-induced unfolding
In the Synapt G2-Si, the SID device is located between the Trap and the ion mobility cell.25 Single charge state precursors were isolated in the manner described in the preceding section. Surface-induced unfolding was performed by increasing the SID acceleration potential in 5 V increments, starting at 20 V (the lowest SID voltage accessible) and continuing until fragmentation was observed. SID on this platform is accomplished by holding the surface at a fixed potential and then raising the potentials of all the instrument optics up to and including the exit electrode of the Trap by changing the “Trap DC Bias” value. Tuning of the entrance optics in the SID device is required to maintain ion transmission while causing the ions to hit the surface. The SID acceleration potential is calculated as the difference between the exit electrode of the Trap and the surface electrode. Minimally-activating conditions in the Trap were used: 5 V potential and 5 mL min−1 gas flow. Surface-induced unfolding data were analyzed using the procedure described for the collision-induced unfolding data.Combined unfolding: source + CIU or source + SIU
On the Synapt G2-Si platform, activation prior to the quadrupole is readily accomplished by increasing the sampling cone voltage near the ion source. This value was set to either 130 V or 175 V for the experiments with BSA to produce mildly or moderately activated precursors, respectively, that were subsequently subjected to either collision- or surface-induced unfolding following the procedures outlined above. For the experiments combining in-source activation with SIU, the gas flow in the Trap was reduced to 1 mL min−1 to minimize any ion heating or cooling in that region.Monte Carlo and theoretical modeling of CIU
For each protein and charge state studied experimentally, the CIU process was simulated at acceleration voltages from 10–200 V in 5 V increments using argon as the collision gas and two models of the activation process, one with a cooling mechanism and one without. A value of 0.9 was used for the per-collision efficiency of converting center-of-mass frame kinetic to internal energy, based on results for nonapeptides.46 Gas velocities were sampled from a Boltzmann distribution at a temperature of 298 K, and collision geometries were sampled from an isotropic distribution. The collision probability at each time step was sampled from an exponential distribution consistent with the mean free path of the ion as derived from its CCS and the gas pressure in the Trap. The model for the on-axis electrical potential due to the traveling wave was adapted from Mortensen et al.47 To avoid undercounting collisions, the simulation time step was set to 1/20th of the mean time between field free collisions at the highest initial kinetic energy for each protein simulated. Additionally, an analytic expression for the total internal energy deposited was derived in the limit of a large number of collisions and averaging over all possible collision geometries and gas velocities: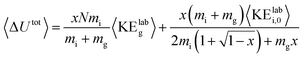 | (1) |
Results and discussion
A major challenge in using SID (and CID) to determine quantitative energetic information is relating the nominal, laboratory-frame kinetic energy to the internal energy deposited into the ion. Because all of these experiments were performed on a Synapt G2-Si platform, the “laboratory-frame kinetic energy” (KElab) is defined here as an ion's charge state multiplied by the voltage difference between either the FSAM-gold surface electrode and the exit electrode of the Trap in SID, or the entrance electrode of the Trap and exit electrode of the quadrupole in CID. The overall SIU or CIU efficiency is defined as the ratio of the initial KElab and the final internal energy following the collision(s) or interaction with the surface. The relationship between initial KElab and final internal energy may depend on factors such as the identity of the collision partner and number of collisions, and the mass, size, and shape of the ion.CIU and SIU access the same unfolding transitions
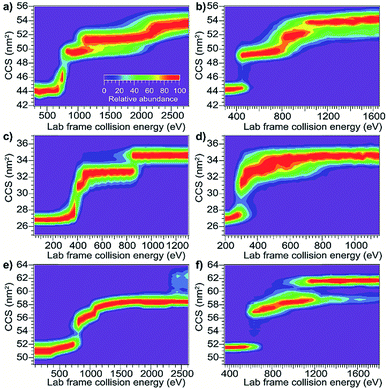
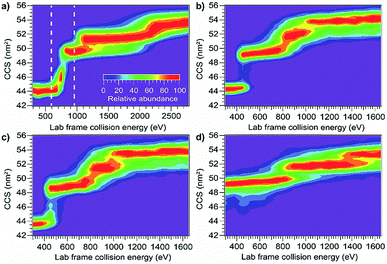
Using the same instrumentation as for CID of protein complexes, accelerating a native-like protein monomer ion through a buffer gas often causes the ion to unfold and adopt one or more extended conformations at collision energies below those required for fragmentation.10 The size and shape of these conformations can be assessed by ion mobility spectrometry prior to mass analysis. This technique, termed collision-induced unfolding (CIU), has been demonstrated to yield useful information about a variety of protein structural characteristics.10,48,49 Analogous protein unfolding using surface activation (surface-induced unfolding, SIU) has not yet been extensively studied. Comparing CIU and SIU for the same protein monomer ions is one approach to better understand the energy deposition (activation) process in SIU. Because CID typically partitions charge asymmetrically while SID partitions charge symmetrically, they often yield different products even for protein dimers.22,24 Since protein ions in CIU and SIU experiments do not significantly change mass or charge, their unfolding products and energies can be more directly compared than can dissociation products of protein oligomer ions.As the first step in calibrating the internal energy deposited by SIU, 10 native-like protein ions, ranging in size from 17–80 kDa, were unfolded using CIU and SIU. Results for three of these, bovine serum albumin (BSA15+, 66 kDa), the N-terminal domain of anthrax lethal factor (LFN10+, 31 kDa), and transferrin (TF18+, 80 kDa) are illustrated in Fig. 1 as examples. For BSA15+, three structural transitions are observed in the CIU “fingerprint” between a native-like and three successively more unfolded conformer families as the nominal KElab is increased from 300 to 2775 eV (Fig. 1a). In the SIU “fingerprint” one native-like and three unfolded conformer families are observed with the same CCSs as in the CIU experiment, suggesting that the same unfolding transitions to the same unfolded states are taking place in both CIU and SIU of BSA (Fig. 1b). Similarly, LFN10+ exhibits unfolding transitions from a native-like to three successively more unfolded conformer families in both CIU and SIU, with virtually identical CCSs in both data sets (Fig. 1c and d). In the case of TF, CIU causes a complete transition to the conformer family at approximately 58 nm2, and only minimal conversion to the conformer family at approximately 62 nm2 (Fig. 1e). However, SIU results in complete transitions to both unfolded conformer families (Fig. 1f), consistent with results from the Wysocki group showing that SID/SIU are able to effect greater activation on the timescale of the experiment than CID/CIU at the same KElab.7 Similar CIU and SIU analysis of the remainder of the protein monomers investigated shows that CIU and SIU produce unfolded states with the same CCSs for a variety of proteins and charge states (Fig. S1†).
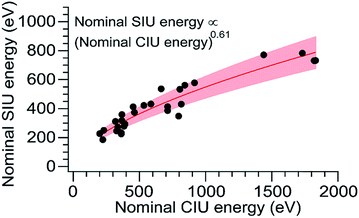
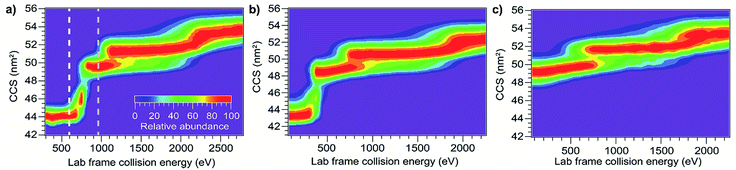
Although CIU and SIU access the same conformer families, they do not produce identical unfolding “fingerprints” as a function of KElab. For each of the proteins studied, the CIU and SIU transitions occur at different acceleration voltages and thus different nominal laboratory frame kinetic energies. Additionally, the differences between the lab-frame appearance energies for successive structural transitions are not the same in CIU and SIU. However, defining the transition “appearance energy” as the energy at which the more unfolded conformer is detected (determined as described in the Methods section), extracting appearance energies for each transition, and plotting the nominal SIU energies against the nominal CIU energies reveals a correlation between SIU and CIU appearance energies (Fig. 2). The trend is clearly non-linear and can be empirically fit to a power law relationship with an exponent of 0.61 ± 0.05 (energy uncertainties are propagated from the uncertainty in the fit). Some of the scatter in the data set arises from uncertainty in the measurement of SIU or CIU energies (approximately 5%, arising primarily from voltage fluctuations and uncertainty in the sigmoidal fits), but protein-specific factors, such as structure, almost certainly cause deviations from the fitted curve. However, neither the amount of α-helical or β-sheet structure, the number of salt bridges, nor the ratios of CCS to mass, charge to mass, and charge to CCS correlate with deviations from the fitted curve (Fig. S6†). The implication of the exponent being less than 1 is that SIU is relatively more efficient at causing unfolding than is CIU at higher KElab values under these instrumental conditions, due to an increase in SIU efficiency, a decrease in CIU efficiency, or some combination of both. Kinetic shifts may be present in both CIU and SIU on this instrument; however, the time for unfolding after activation is likely shorter in SIU because the SID device is located closer to the detector than is the Trap, where CIU occurs. This difference alone should result in a smaller kinetic shift for SIU compared to CIU. Furthermore, if kinetic shift alone were responsible for the non-linear trend observed in Fig. 2, the curvature of the trend should be in the opposite direction from what is observed. Thus, other factors beyond kinetic shift dominate the observed trend. The fit also intersects the origin, which implies that any other activation taking place that is not a function of the CIU or SIU potential is approximately the same for both processes under the conditions used here.
Calibrating SIU energy deposition by modeling CIU energy deposition
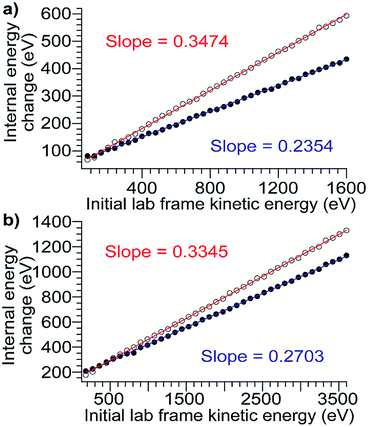
To relate the nominal SIU and CIU energies to the overall internal energy deposited into the ion by each process, the CIU process was modeled and used to calibrate the internal energy scale of the SIU data. The physics of the individual collisions involved in the CID/CIU process have been investigated previously, and a number of theoretical models describing the rate of ion heating and dissociation in multiple-collision CID have been introduced.50–53 In the Synapt G2-Si, in addition to the acceleration potential that injects ions into the collision cell there is a time-dependent electric field (traveling wave potential) that helps elute the ions out of the Trap. In order to model trajectories and energetics for protein ions undergoing CIU it is necessary to add this component to models describing the ion-gas collisions in a field-free environment, e.g., Douglas' model.51 At the pressures used for CID/CIU in this instrument (approximately 2.6 × 10−2 mbar), these protein ions experience from several hundred to several thousand collisions as they traverse the collision cell. Implementing a Monte Carlo simulation of the collision geometry and distance between collisions (a similar approach to that of Nesatyy and Laskin)50 enables consideration of both internal energy gain and kinetic energy loss due to energetic collisions.For all proteins and charge states studied experimentally, the change in internal energy in both the presence and absence of cooling mechanisms is modeled for each 5 V increment of the acceleration potential from 10–200 V. The internal energy change increases linearly with KElab, and the slope of the trend line gives the overall CIU efficiency (Fig. 3). The overall CIU efficiency, defined as the maximum fraction of KElab converted to internal energy, was found to be approximately 34% and decrease slightly with ion mass in the absence of a cooling mechanism, compared to 25% with a slight increase with ion mass with a cooling mechanism (Fig. S2†). These values provide upper and lower bounds to the energy deposition, since in our simulations collisional cooling occurs at the maximum possible rate. We expect that the actual amount of energy deposited is close to that computed in the simulations with cooling. When the collisions are highly inelastic (as in these experiments), the traveling wave has a small effect (<2%) on the overall CIU efficiency (Fig. S3d†), but does contribute to the non-zero intercepts of the plots in Fig. 3. Values of the total internal energy change and overall efficiency computed using eqn (1) are in excellent agreement with the results from Monte Carlo simulations without a cooling mechanism (Fig. S3a–c†).
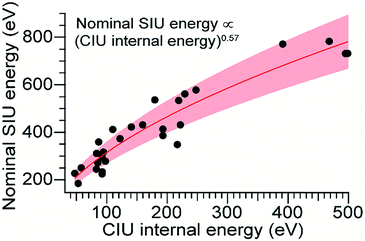
Using the computed values for internal energy deposited during CIU (from the simulations with cooling), the energy axis for the data shown in Fig. 2 was calibrated (Fig. 4), with energy uncertainties in Fig. 4 propagated from the uncertainty in the fit. After this re-calibration, it is clear that energy deposition at higher laboratory frame collision energies is typically more efficient for SIU than for CIU, and SIU is more efficient for high-mass protein ions than for those with lower masses, reaching a maximum of ∼68% conversion to internal energy for the highest–energy transitions (using the CIU calibration with no cooling mechanism yields a value of ∼85%, which we interpret as an extreme upper bound for energy deposition in SIU). Computational results for collisions of dialanine with an FSAM surface suggest that a maximum of 16% of initial KElab remains in translational modes after surface collision,35 leaving 84% or more of the energy to be partitioned between ion internal modes and the surface; an even lower fraction of the energy remains in translational modes for nanoscale polystyrene latex spheres after surface collision.54 Our maximum value falls within this upper bound, and suggests that energy transfer to internal modes dominates over energy transfer to the surface under these conditions. The nominal SIU energy vs. calibrated CIU energy trend can be fit to a power law relationship, with an exponent of 0.57 ± 0.04. The fact that the energy scale in SIU can be well-described by relation to CIU data implies that SIU, like CIU, can be understood as a primarily thermal process, in which the observed extent of unfolding in SIU is determined in large part by the amount of energy deposited into and equilibrated among the ion's internal modes. This result is in agreement with the majority of previous experimental and theoretical work on SID of small molecules, peptides, and proteins.30,31,55–57
Laskin and Futrell showed that in SID of peptides the efficiency of conversion to ion internal energy was approximately 20% and largely invariant to acceleration voltage.32,33 Thus, increased mass is likely to be primarily responsible for the observed increase in efficiency in our experiments. Previously published results for small molecules and peptides up to 1 kDa have shown that energy deposition efficiency varies little in this size range.32 The observed increase in overall SIU efficiency with mass in these experiments suggests that proteins of the size studied here fall into a different regime. Note that the SIU energy calibration presented here probes the overall deposition of energy into the ion and not dynamical details of how SIU energy deposition occurs, such as whether the ion interacts one or multiple times with the surface.
In-source activation effects on SIU behavior
Besides mass and initial kinetic energy, other factors that can in principle affect energy deposition in SID are the initial internal energy and structure of the protein ion. In-source ion activation followed by SIU was used to probe the influence of these factors. Applying a cone voltage of 130 V at a backing pressure of 3.7 mbar activates BSA15+ as much as possible without causing observable unfolding on the timescale of these experiments (see Fig. S8† for full in-source CIU fingerprint). Subjecting this activated precursor to SIU produces a remarkably similar unfolding “fingerprint” to that obtained without in-source activation (Fig. 5), and causes a 0.5% to 3.5% change in the unfolding transition appearance energies (Table 1). Thus, for a precursor with a given CCS, SIU under these conditions does not depend strongly on the degree of activation prior to the surface collision. This is in contrast to CIU, in which ions pre-activated in the source region require less energy to unfold in the Trap (Fig. 6), with each transition shifted lower in energy. Interestingly, the size of the shift is the same for the first two unfolding transitions and half as large for the third unfolding transition (Table 1). These data indicate that in CIU ions retain a high internal temperature or already have many of their native non-covalent interactions disrupted as they enter the Trap. Decreased adduction following in-source activation may also contribute to the observed destabilization, as adducts have been shown to have a slight stabilizing effect in CIU,58–61 and in-source activation in these experiments dissociates approximately 225 Da of adducts. However, for SIU, in-source activation has no significant effect on unfolding appearance energies, suggesting that these ions cool prior to SIU. Minimal cooling is observed for CIU with the same instrumental conditions between the source and the Trap, and SIU following pre-activation in the Trap produces the same result as in-source pre-activation (Fig. S9†). Thus, cooling of the ions between the source and collision surface in SIU is likely due to collisions with helium or nitrogen leaking from the ion mobility cell.| Activation method | Sampling cone voltage | Appearance energies (eV) | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| CIU | 25 V | 713 | 916 | 1731 |
| 130 V | 296 | 514 | 1518 | |
| 175 V | 288 | 1241 | ||
| SIU | 25 V | 386 | 578 | 783 |
| 130 V | 377 | 598 | 779 | |
| 175 V | 649 | 953 | ||
Markedly different behavior is observed when the protein monomers studied here were measurably unfolded in the source region prior to SIU. For example, applying a cone voltage of 175 V with a backing pressure of 3.7 mbar causes BSA15+ to undergo an unfolding transition to the first unfolded conformer family (Fig. 5). The SIU fingerprint of this species is dramatically different from that generated without source unfolding (Fig. 5): the KElab value required to precipitate the second unfolding transition increases by 71 eV, and the third unfolding transition is shifted higher in energy by 170 eV (Table 1). Considering that the ions enter the Trap region partially unfolded, it is remarkable that more energy is required to precipitate the second and third unfolding transitions than without in-source activation, and cooling in the Trap cannot explain these differences. Thus, conversion of kinetic energy of the surface collision to internal energy of the protein must be much less efficient for these initially unfolded, relatively low-charge structures. The differences between the first and second and between the second and third transition appearance energies have increased by approximately 50%, demonstrating that SIU is highly sensitive to the structure of the precursor ion; a 12% increase in CCS leads to this dramatic reduction in the energy deposition efficiency. In simulations of triglycine SID, folded and extended structures differed little in energy deposition efficiency,34 again indicating that proteins of the size studied here fall into a different regime than peptides.
Contrasting behavior is observed in CIU, where in-source unfolding followed by CIU causes the second and third unfolding transition appearance energies to decrease by 628 and 490 eV, respectively (Table 1). These results agree with those for in-source activation without unfolding followed by CIU, and demonstrate that overall internal energy deposition efficiency for these ions in CIU depends on ion CCS to a much lesser extent than in SIU. This conclusion is supported by calculations of the overall CIU efficiency with cooling included, which show that although overall CIU efficiency depends non-linearly on CCS and has its maximum at the experimental CCS value of the native-like conformation (Fig. S4†), changing the CCS of BSA15+ by the amounts observed experimentally changes the overall CIU efficiency by only 1–5% (Fig. S5†). Simulations of collisional activation of peptides do show a small decrease in energy transfer for extended structures, a finding consistent with our results.62 SIU of pre-activated TF18+ provides a corroborating result, with in-source unfolding causing the appearance energy of the next transition to increase significantly (Fig. S10†).
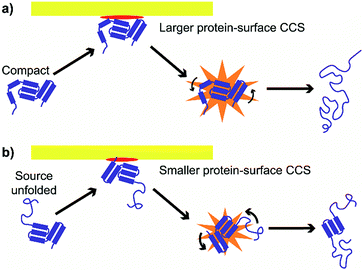
These results suggest at least two mechanisms that contribute to the reduction in energy deposition efficiency for unfolded proteins in SIU (Fig. 7). First, the effective protein-surface CCS can be smaller for unfolded proteins than for folded proteins, even though the protein-gas CCS is larger. That is, in many cases, an ion that is more elongated will on average interact with a smaller area of the surface than an ion with the same mass that is compact (Fig. 7). This reduces the effective center-of-mass frame kinetic energy of the collision and thus decreases the amount of energy transferred to internal modes. The increased flexibility of the unfolded protein ions in these experiments relative to the compact, native-like conformers likely also contributes to the lower energy conversion efficiency, because energy can be more efficiently transferred into rotational motion for more elongated structures.62 As rotation is less efficient than vibrational energy at causing further unfolding,63 this will increase the amount of KElab required to cause further unfolding. Multiple interactions of the ion with the surface may further complicate energy deposition.
Conclusion
The energy deposition process in SID of proteins was studied by comparing unfolding of protein monomers by collisional and surface activation and by investigating the effect of in-source pre-activation on CIU and SIU. CIU and SIU cause similar unfolding transitions and the conformer families observed have the same CCS. The nominal energy scales of CIU and SIU are correlated and follow a power law relationship, with SIU being more efficient than CIU at higher KElab values and for larger ions, but significant scatter from this trend indicates other protein-specific factors also play a significant role, although no correlations in deviations from the trend were found with respect to secondary structure content, number of salt bridges, or the ratios of charge to mass, charge to CCS, or CCS to mass. These factors may be structural or may be related to the mechanical protein-surface interaction. The average overall efficiency for conversion of initial KElab to internal energy for CIU determined by Monte Carlo simulations including both ion heating and cooling is approximately 25%, increasing slightly with ion mass. These calculated data are used to calibrate the SIU energy scale, leading to computed efficiency values for SIU of up to 68% for the largest ions studied (80 kDa). Alternatively, this is equivalent to the effective mass of the surface during the collision, defined as the mass of the effective two-body collision partner required to impart a center-of-mass frame energy equal to the calibrated CIU internal energy,55 increasing with protein size. Previous determinations of the effective mass of the surface in peptide SID experiments were a few tens of Da,55,56 a result corroborated by atomistic simulations of peptide SID showing that the peptide interacts with a single –CF3 group (mass of 69 Da).35 Our data suggest that the effective mass of the surface grows with the mass of the protein (Fig. S11†).When in-source pre-activation is followed by CIU, for both degrees of in-source activation (unfolded and not unfolded), subsequent unfolding transitions are shifted to lower energies by an amount commensurate with the amount of in-source activation. This indicates that effects of activation, i.e. an elevated internal temperature or disruption of non-covalent interactions, can be preserved as the protein ions travel from the source region to the entrance of the Trap. In contrast, pre-activation without unfolding has little effect on SIU, indicating that protein ions are cooled between the end of the Trap and the SID device. Protein ions unfolded in the source require significantly more energy to further unfold in SIU than their compact counterparts, showing that energy deposition in SID is sensitive to ion CCS, with reduced conversion efficiency for more unfolded ions due to a smaller effective protein-surface CCS and increased transfer to rotational modes. The Wysocki group has combined in-source activation with SID of protein tetramers and demonstrated that when partially-unfolded complexes are subjected to SID they produce fragments akin to those produced by CID.64 The results obtained here parallel those and provide quantitative insights into the effect of structure on the SID energy deposition process. Future experiments probing the energy required to dissociate pre-activated protein complexes could elucidate how the effects demonstrated here change with varying complex size and number of subunits. We anticipate that calibration of energy deposition in SID using a strategy similar to that reported here may enable more quantitative calibration of SID appearance energies with respect to the disrupted protein–protein interfacial areas, facilitating rapid characterization of protein–protein interactions in previously unexamined complexes, including membrane protein complexes. Future investigation of the role of protein structure as well as mechanical effects of the surface collision, including those revealed by sophisticated chemical dynamics simulations,65 are expected to shed light on protein-specific deviations from the SIU–CIU calibration curve described here.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors thank Jeff Cina for helpful conversations. M. T. D. acknowledges support from a National Science Foundation Graduate Research Fellowship (DGE-1309047). Research reported in this publication was supported by the National Institutes of Health under award number R21AI125804 (to J. S. P.). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Science Foundation or the National Institutes of Health.References
- F. Lanucara, S. W. Holman, C. J. Gray and C. E. Eyers, Nat. Chem., 2014, 6, 281–294 CrossRef CAS PubMed.
- A. Resemann, D. Wunderlich, U. Rothbauer, B. Warscheid, H. Leonhardt, J. Fuchser, K. Kuhlmann and D. Suckau, Anal. Chem., 2010, 82, 3283–3292 CrossRef CAS PubMed.
- N. Siuti, M. J. Roth, C. A. Mizzen, N. L. Kelleher and J. J. Pesavento, J. Proteome Res., 2006, 5, 233–239 CrossRef CAS PubMed.
- J. B. Shaw, W. Li, D. D. Holden, Y. Zhang, J. Griep-Raming, R. T. Fellers, B. P. Early, P. M. Thomas, N. L. Kelleher and J. S. Brodbelt, J. Am. Chem. Soc., 2013, 135, 12646–12651 CrossRef CAS PubMed.
- J. N. Rabuck-Gibbons, J. E. Keating and B. T. Ruotolo, Int. J. Mass Spectrom., 2018, 427, 151–156 CrossRef CAS.
- X. Ma, J. A. Loo and V. H. Wysocki, Int. J. Mass Spectrom., 2015, 377, 201–204 CrossRef CAS PubMed.
- X. Ma, M. Zhou and V. H. Wysocki, J. Am. Soc. Mass Spectrom., 2014, 25, 368–379 CrossRef CAS PubMed.
- Y. Song, M. T. Nelp, V. Bandarian and V. H. Wysocki, ACS Cent. Sci., 2015, 1, 477–487 CrossRef CAS PubMed.
- J. L. P. Benesch, J. A. Aquilina, B. T. Ruotolo, F. Sobott and C. V. Robinson, Chem. Biol., 2006, 13, 597–605 CrossRef CAS PubMed.
- S. M. Dixit, D. A. Polasky and B. T. Ruotolo, Curr. Opin. Chem. Biol., 2018, 42, 93–100 CrossRef CAS PubMed.
- R. A. Zubarev, Curr. Opin. Biotechnol., 2004, 15, 12–16 CrossRef CAS PubMed.
- R. A. Zubarev, N. L. Kelleher and F. W. McLafferty, J. Am. Chem. Soc., 1998, 120, 3265–3266 CrossRef CAS.
- J. J. Coon, J. Shabanowitz, D. F. Hunt and J. E. P. Syka, J. Am. Soc. Mass Spectrom., 2005, 16, 880–882 CrossRef CAS PubMed.
- J. E. P. Syka, J. J. Coon, M. J. Schroeder, J. Shabanowitz and D. F. Hunt, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 9528–9533 CrossRef CAS PubMed.
- S. A. McLuckey, J. Am. Soc. Mass Spectrom., 1992, 3, 599–614 CrossRef CAS PubMed.
- J. S. Brodbelt, Chem. Soc. Rev., 2014, 43, 2757–2783 RSC.
- J. P. Reilly, Mass Spectrom. Rev., 2009, 28, 425–447 CrossRef CAS PubMed.
- J. S. Brodbelt and J. J. Wilson, Mass Spectrom. Rev., 2009, 28, 390–424 CrossRef CAS PubMed.
- B. L. Schwartz, J. E. Bruce, G. A. Anderson, S. A. Hofstadler, A. L. Rockwood, R. D. Smith, A. Chilkoti and P. S. Stayton, J. Am. Soc. Mass Spectrom., 1995, 6, 459–465 CrossRef CAS PubMed.
- J. C. Jurchen and E. R. Williams, J. Am. Chem. Soc., 2003, 125, 2817–2826 CrossRef CAS PubMed.
- S. V. Sciuto, J. Liu and L. Konermann, J. Am. Soc. Mass Spectrom., 2011, 22, 1679 CrossRef CAS PubMed.
- R. L. Beardsley, C. M. Jones, A. S. Galhena and V. H. Wysocki, Anal. Chem., 2009, 81, 1347–1356 CrossRef CAS PubMed.
- M. Zhou, S. Dagan and V. H. Wysocki, Analyst, 2013, 138, 1353–1362 RSC.
- C. M. Jones, R. L. Beardsley, A. S. Galhena, S. Dagan, G. Cheng and V. H. Wysocki, J. Am. Chem. Soc., 2006, 128, 15044–15045 CrossRef CAS PubMed.
- M. Zhou, S. Dagan and V. H. Wysocki, Angew. Chem., Int. Ed., 2012, 51, 4336–4339 CrossRef CAS PubMed.
- R. S. Quintyn, J. Yan and V. H. Wysocki, Chem. Biol., 2015, 22, 583–592 CrossRef CAS PubMed.
- M. Zhou, C. M. Jones and V. H. Wysocki, Anal. Chem., 2013, 85, 8262–8267 CrossRef CAS PubMed.
- J. Yan, M. Zhou, J. D. Gilbert, J. J. Wolff, Á. Somogyi, R. E. Pedder, R. S. Quintyn, L. J. Morrison, M. L. Easterling, L. Paša-Tolić and V. H. Wysocki, Anal. Chem., 2017, 89, 895–901 CrossRef CAS PubMed.
- J. Laskin, E. V. Denisov, A. K. Shukla, S. E. Barlow and J. H. Futrell, Anal. Chem., 2002, 74, 3255–3261 CrossRef CAS PubMed.
- A. S. Galhena, S. Dagan, C. M. Jones, R. L. Beardsley and V. H. Wysocki, Anal. Chem., 2008, 80, 1425–1436 CrossRef CAS PubMed.
- J. Žabka, Z. Dolejšek and Z. Herman, J. Phys. Chem. A, 2002, 106, 10861–10869 CrossRef.
- J. Laskin and J. H. Futrell, J. Chem. Phys., 2002, 116, 4302–4310 CrossRef CAS.
- J. Laskin and J. H. Futrell, J. Am. Soc. Mass Spectrom., 2003, 14, 1340–1347 CrossRef CAS PubMed.
- O. Meroueh and W. L. Hase, J. Am. Chem. Soc., 2002, 124, 1524–1531 CrossRef CAS PubMed.
- S. Pratihar, S. C. Kohale, D. G. Bhakta, J. Laskin and W. L. Hase, Phys. Chem. Chem. Phys., 2014, 16, 23769–23778 RSC.
- T. Raz and R. D. Levine, Chem. Phys., 1996, 213, 263–275 CrossRef CAS.
- J. Laskin, T. H. Bailey and J. H. Futrell, J. Am. Chem. Soc., 2003, 125, 1625–1632 CrossRef CAS PubMed.
- S. O. Meroueh, Y. Wang and W. L. Hase, J. Phys. Chem. A, 2002, 106, 9983–9992 CrossRef CAS.
- K. Park, B. Deb, K. Song and W. L. Hase, J. Am. Soc. Mass Spectrom., 2009, 20, 939–948 CrossRef CAS PubMed.
- E. Hendell, U. Even, T. Raz and R. D. Levine, Phys. Rev. Lett., 1995, 75, 2670–2673 CrossRef CAS PubMed.
- T. Raz and R. D. Levine, J. Chem. Phys., 1996, 105, 8097–8102 CrossRef CAS.
- R. D. Beck, C. Warth, K. May and M. M. Kappes, Chem. Phys. Lett., 1996, 257, 557–562 CrossRef CAS.
- D. G. Schultz and L. Hanley, J. Chem. Phys., 1998, 109, 10976–10983 CrossRef CAS.
- M. F. Bush, Z. Hall, K. Giles, J. Hoyes, C. V. Robinson and B. T. Ruotolo, Anal. Chem., 2010, 82, 9557–9565 CrossRef CAS PubMed.
- B. T. Ruotolo, J. L. P. Benesch, A. M. Sandercock, S.-J. Hyung and C. V. Robinson, Nat. Protoc., 2008, 3, 1139–1152 CrossRef CAS PubMed.
- E. M. Marzluff, S. Campbell, M. T. Rodgers and J. L. Beauchamp, J. Am. Chem. Soc., 1994, 116, 6947–6948 CrossRef CAS.
- D. N. Mortensen, A. C. Susa and E. R. Williams, J. Am. Soc. Mass Spectrom., 2017, 28, 1282–1292 CrossRef CAS PubMed.
- Y. Tian, L. Han, A. C. Buckner and B. T. Ruotolo, Anal. Chem., 2015, 87, 11509–11515 CrossRef CAS PubMed.
- Y. Zhong, L. Han and B. T. Ruotolo, Angew. Chem., Int. Ed., 2014, 53, 9209–9212 CrossRef CAS PubMed.
- V. J. Nesatyy and J. Laskin, Int. J. Mass Spectrom., 2002, 221, 245–262 CrossRef CAS.
- D. J. Douglas, J. Am. Soc. Mass Spectrom., 1998, 9, 101–113 CrossRef CAS.
- A. Hoxha, C. Collette, E. De Pauw and B. Leyh, J. Phys. Chem. A, 2001, 105, 7326–7333 CrossRef CAS.
- E. Uggerud and P. J. Derrick, J. Phys. Chem., 1991, 95, 1430–1436 CrossRef CAS.
- B. D. Adamson, M. E. C. Miller and R. E. Continetti, EPJ Techniques and Instrumentation, 2017, 4, 2 CrossRef.
- J. Laskin, E. Denisov and J. Futrell, J. Am. Chem. Soc., 2000, 122, 9703–9714 CrossRef CAS.
- J. Laskin, E. Denisov and J. Futrell, J. Phys. Chem. B, 2001, 105, 1895–1900 CrossRef CAS.
- V. S. Rakov, E. V. Denisov, J. Laskin and J. H. Futrell, J. Phys. Chem. A, 2002, 106, 2781–2788 CrossRef CAS.
- L. Han, S.-J. Hyung, J. J. S. Mayers and B. T. Ruotolo, J. Am. Chem. Soc., 2011, 133, 11358–11367 CrossRef CAS PubMed.
- L. Han, S.-J. Hyung and B. T. Ruotolo, Angew. Chem., Int. Ed., 2012, 51, 5692–5695 CrossRef CAS PubMed.
- J. Freeke, C. V. Robinson and B. T. Ruotolo, Int. J. Mass Spectrom., 2010, 298, 91–98 CrossRef CAS.
- N. D. Wagner, D. Kim and D. H. Russell, Anal. Chem., 2016, 88, 5934–5940 CrossRef CAS PubMed.
- O. Meroueh and W. L. Hase, Int. J. Mass Spectrom., 2000, 201, 233–244 CrossRef CAS.
- T. Baer, W. L. Hase, W. L. Hase and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press, USA, 1996 Search PubMed.
- R. S. Quintyn, M. Zhou, J. Yan and V. H. Wysocki, Anal. Chem., 2015, 87, 11879–11886 CrossRef CAS PubMed.
- S. Pratihar, S. C. Kohale, S. A. Vázquez and W. L. Hase, J. Phys. Chem. B, 2014, 118, 5577–5588 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc00644c |
| This journal is © The Royal Society of Chemistry 2019 |