Open Access Article
Open Access ArticleSingle-ion anisotropy and exchange coupling in cobalt(II)-radical complexes: insights from magnetic and ab initio studies†
Gemma K.
Gransbury
 a,
Marie-Emmanuelle
Boulon
a,
Marie-Emmanuelle
Boulon
 b,
Richard A.
Mole
b,
Richard A.
Mole
 c,
Robert W.
Gable
c,
Robert W.
Gable
 a,
Boujemaa
Moubaraki
d,
Keith S.
Murray
a,
Boujemaa
Moubaraki
d,
Keith S.
Murray
 d,
Lorenzo
Sorace
d,
Lorenzo
Sorace
 b,
Alessandro
Soncini
b,
Alessandro
Soncini
 *a and
Colette
Boskovic
*a and
Colette
Boskovic
 *a
*a
aSchool of Chemistry, University of Melbourne, Parkville, Victoria 3010, Australia. E-mail: c.boskovic@unimelb.edu.au
bUdR INSTM, Department of Chemistry “U. Schiff”, University of Florence, 50019 Sesto Fiorentino (FI), Italy
cAustralian Nuclear Science and Technology Organisation, Locked Bag 2001, Kirrawee DC, New South Wales 2232, Australia
dSchool of Chemistry, Monash University, Clayton, Victoria 3800, Australia
First published on 30th July 2019
Abstract
The concurrent effects of single-ion anisotropy and exchange interactions on the electronic structure and magnetization dynamics have been analyzed for a cobalt(II)-semiquinonate complex. Analogs containing diamagnetic catecholate and tropolonate ligands were employed for comparison of the magnetic behavior and zinc congeners assisted with the spectroscopic characterization and assessment of intermolecular interactions in the cobalt(II) compounds. Low temperature X-band (ν ≈ 9.4 GHz) and W-Band (ν ≈ 94 GHz) electron paramagnetic resonance spectroscopy and static and dynamic magnetic measurements have been used to elucidate the electronic structure of the high spin cobalt(II) ion in [Co(Me3tpa)(Br4cat)] (1; Me3tpa = tris[(6-methyl-2-pyridyl)methyl]amine, Br4cat2− = tetrabromocatecholate) and [Co(Me3tpa)(trop)](PF6) (2(PF6); trop− = tropolonate), which show slow relaxation of the magnetization in applied field. The cobalt(II)-semiquinonate exchange interaction in [Co(Me3tpa)(dbsq)](PF6)·tol (3(PF6)·tol; dbsq− = 3,5-di-tert-butylsemiquinonate, tol = toluene) has been determined using an anisotropic exchange Hamiltonian in conjunction with multistate restricted active space self-consistent field ab initio modeling and wavefunction analysis, with comparison to magnetic and inelastic neutron scattering data. Our results demonstrate dominant ferromagnetic exchange for 3+ that is of similar magnitude to the anisotropy parameters of the cobalt(II) ion and contains a significant contribution from spin–orbit coupling. The nature of the exchange coupling between octahedral high spin cobalt(II) and semiquinonate ligands is a longstanding question; answering this question for the specific case of 3+ has confirmed the considerable sensitivity of the exchange to the molecular structure. The methodology employed will be generally applicable for elucidating exchange coupling between orbitally-degenerate metal ions and radical ligands and relevant to the development of bistable molecules and their integration into devices.
Introduction
Elucidating exchange interactions involving orbitally-degenerate metal ions is an ongoing and considerable challenge, due to the comparable magnitude of single-ion anisotropy and anisotropic exchange.1–3 Compounds that combine orbitally-degenerate metals with radical ligands are increasingly being explored for new magnetic and multifunctional materials, including those that behave as single-molecule magnets (SMMs),2,4–20 single-chain magnets,21–23 hard permanent magnets,24 antiferromagnets,14 spin crossover compounds,25 and valence tautomeric compounds.26–30 These systems are being investigated for various potential applications, including as molecular-based memories or switches and for molecular electronics and spintronics. The rational design of optimized materials requires a comprehensive understanding of the correlation between molecular and electronic structure. For example, the SMM property of slow magnetic relaxation is critically linked to single-ion anisotropy.31 Recent studies on lanthanoid(III)-radical31,32 and Co(II)-radical8,12,33–35 SMMs have revealed how exchange interactions can be important for suppressing or enhancing key relaxation processes, such as quantum tunneling of the magnetization (QTM).17 If SMMs are to be employed in spintronics, metal-radical exchange plays a key role in mediating the interaction at the interfaces within the devices.36,37 Furthermore, the presence of an exchange-coupling interaction can also be exploited to address electronic and nuclear quantum states associated with lanthanoid complexes integrated into single-molecule spin transistors.38–41The issue of metal-radical exchange coupling involving orbitally-degenerate metals is also relevant for cobalt-dioxolene valence tautomeric materials. These systems undergo a thermally-induced intramolecular electron transfer between redox-active metal and redox-active ligand, accompanied by a spin transition at the cobalt center.26,42,43 The nature of the exchange coupling in the pseudo-octahedral high spin (HS) Co(II)-sq (sq− = semiquinonate) tautomer has been an enduring question in the literature,44,45 with both ferromagnetic and antiferromagnetic coupling claimed, in tandem with potentially anisotropic exchange interactions.46,47 In most cases the metal-radical exchange coupling in these systems cannot be determined directly by experiment; however, this can be required to assess the relative amounts of the two redox isomers.
A complete description of the electronic structure of exchange-coupled systems involving orbitally-degenerate metal ions requires modeling the anisotropic electronic structure of the metal, often determined by empirical comparison to analogous compounds with diamagnetic ligands.44,48 Most commonly, only the sign of the exchange is inferred from the qualitative shape of the curve in a plot of the product of the molar magnetic susceptibility and temperature (χMT) vs. temperature.4,5,49 In some cases, the metal–ligand exchange coupling has been estimated by fitting the data for a spin-only analog.17 In other cases, the metal–ligand exchange can be determined directly,50,51 such as in the limit of strong spin–orbit coupling (SOC) where Kramers ions, such as Co(II), possess a spin doublet ground state (Kramers doublet, KD) that acts as a pseudo-spin S′ = 1/2 with anisotropic g-values.52 Here a metal–ligand interaction can be modeled as anisotropic exchange between the pseudo-spin S′ = 1/2 and the radical true S = 1/2 spin.44,53 This model is limited to low temperatures when only the ground KD is populated and to situations where the radical coupling with the next highest energy metal-based state is negligible.45 Modeling exchange interactions using pseudo-spins has proved particularly successful in Co(II) coordination clusters and dinuclear lanthanoid(III) complexes, for which transitions between exchange-coupled states have been directly observed by inelastic neutron scattering (INS) and electron paramagnetic resonance (EPR) spectroscopy.1,54–57
Even computationally, modeling metal-radical exchange in spin–orbit coupled systems is extremely challenging.53 Density functional theory (DFT) employing the Broken Symmetry (BS) approximation and the Yamaguchi equation, or the “spin-flip” approach, has been used to calculate isotropic exchange coupling, neglecting SOC contributions.58–62 In the case of highly anisotropic lanthanoid(III) ions, this can be related to the Ising-type anisotropic exchange.63,64 However, DFT has limited applicability in determining exchange coupling in transition metals as it cannot capture SOC contributions to exchange. Furthermore, exchange constants determined using the BS method are dependent on the DFT functional used.62,65,66 Multiconfigurational ab initio calculations on orbitally-degenerate metal-radical systems are computationally expensive and rare, there are a few reports with lanthanoid complexes and none with octahedral Co(II).36,53,67,68 Recently, Sarkar and van Slageren et al. reported multiconfigurational calculations on a radical bridged dinuclear tetrahedral Co(II) complex, for which SOC acts at the second order.69 Most often multiconfigurational techniques are used to define the metal electronic state only in the absence of the radical.2,34,63,64,70–74
A multi-technique experimental approach combined with a multiconfigurational ab initio study is thus required to clarify the nature and the magnitude of the interactions in anisotropic metal-radical coupled systems and the way they can be varied to design improved bistable materials. Advances in computational methods and in magnetic and spectroscopic data analysis now allow us to resolve this issue for Co(II)-semiquinonate complexes, which we propose as a case study to demonstrate the advantages of this approach and the many pitfalls to be avoided.
Herein we have used pseudo-octahedral HS-Co(II) reference complexes containing diamagnetic ligands (Chart 1), [Co(Me3tpa)(Br4cat)] (1; Br4cat2− = tetrabromocatecholate; Me3tpa = tris[(6-methyl-2-pyridyl)methyl]amine) and [Co(Me3tpa)(trop)]+ (2+; trop− = tropolonate), to aid in the investigation of the pseudo-octahedral HS-Co(II)-radical complex [Co(Me3tpa)(dbsq)]+, (3+; dbsq− = 3,5-di-tert-butylsemiquinonate). For complex 2+, the tropolonate ligand, already reported for [Co(Me4cyclam)(trop)](PF6) (Me4cyclam = 1,4,8,11-tetramethyl-1,4,8,11-tetraazacyclotetradecane), allows access to a monopositive cobalt-dioxolene complex with a diamagnetic ligand.45 We have also synthesized the zinc analogs (1-Zn, 2-Zn+ and 3-Zn+) for dilution studies, and employed them to assist the spectroscopic (EPR and INS), magnetic and electronic structure characterization of the Co(II) compounds.
Experimental section
Synthetic procedures
Synthetic procedures are detailed in the ESI.† The syntheses of 1, [Zn(Me3tpa)(Br4cat)](1-Zn) and [Co(Me3tpa)(dbsq)](PF6) (3(PF6)) have been previously reported,42,75 and the syntheses of new compounds [Co(Me3tpa)(trop)](PF6) (2(PF6)), [Zn(Me3tpa)(trop)](PF6) (2-Zn(PF6)), [Zn(Me3tpa)(dbsq)](PF6) (3-Zn(PF6)) and 1-Co0.05 (5% 1 in 1-Zn) have been adapted from the syntheses of 1, 3(PF6) and [Co(Me4cyclam)(trop)](PF6).45X-ray data collection and structure solution
Single crystal X-ray diffraction data for 1-Co0.05, 2(PF6), 3-Zn(PF6)·tol (Table 1; tol = toluene), 2(PF6)-II, 2(PF6)·1.5tol-III, 2(PF6)·tol-IV and 2-Zn(PF6)·1.5tol-III (Table S1†; phases II–IV are minor structural phases of 2(PF6) and 2-Zn(PF6)) were collected at 130 K using a Rigaku Oxford Diffraction SuperNova Dual Wavelength diffractometer with mirror monochromated Cu-Kα radiation (λ = 1.5418 Å). The crystal structures of 1 and 1-Zn have been reported by some of us previously.75 The crystal structure of 3(PF6)·tol has been reported previously, at 150 K and from a crystal whose quality was less than ideal (final R1: 0.084).42 As this structure was to be the focus of ab initio calculations, we have recollected the data using a better quality crystal at 100 K using a Rigaku XtaLAB Synergy-S Dual Microfocus X-ray diffractometer using Cu-Kα radiation (Table 1).42 All crystals were transferred directly from the mother liquor to protective oil before mounting on the diffractometer. For each structure data reduction was carried out using CrysAlisPro,76 with numerical absorption corrections based on Gaussian integration over a multifaceted crystal. All structures were solved with SHELXT using intrinsic phasing and refined using a full-matrix least square procedure based upon F2 using SHELXL in OLEX2.77–79 The positions of all non-hydrogen atoms were refined using anisotropic displacement factors. Hydrogen atoms were placed geometrically, and their positions were constrained to geometrical estimates using the riding model. Details on modeling the disorder of the anion, solvent and tert-butyl substituents are given in the ESI.†| 1-Co0.05 | 2(PF6) | 3(PF6)·tol | 3-Zn(PF6)·tol | |
|---|---|---|---|---|
| Formula | C27H24Br4Co0.06Zn0.94N4O2 | C28H29CoN4O2PF6 | C42H52CoN4O2PF6 | C24H52ZnN4O2PF6 |
| fw/g mol−1 | 821.12 | 657.45 | 848.77 | 855.21 |
| Cryst syst | Monoclinic | Monoclinic | Monoclinic | Monoclinic |
| Space group | P21/n | P21/c | P21/c | P21/c |
| a/Å | 11.3060(2) | 9.5661(1) | 11.57434(4) | 11.5686(1) |
| b/Å | 13.5277(2) | 14.0025(2) | 31.7531(1) | 31.8810(4) |
| c/Å | 18.5746(3) | 21.2941(3) | 22.05467(7) | 22.0748(2) |
| β/deg | 92.550(1) | 94.929(1) | 94.1148(3) | 94.031(1) |
| V/Å3 | 2838.06(8) | 2841.78(6) | 8084.67(5) | 8121.5(1) |
| T/K | 130.0(1) | 130.0(1) | 100.0(1) | 130.0(1) |
| Z | 4 | 4 | 8 | 8 |
| R int | 0.0261 | 0.0335 | 0.0808 | 0.0290 |
| ρ calc/g cm−3 | 1.922 | 1.537 | 1.395 | 1.399 |
| μ/mm−1 | 8.279 | 5.926 | 4.292 | 1.799 |
| Reflns measd | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 997 997 |
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 711 711 |
324![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 842 842 |
61![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 398 398 |
| Data/restraints/param | 5938/0/347 | 5667/0/382 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 195/85/1083 195/85/1083 |
17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 012/100/1082 012/100/1082 |
| R 1[I > 2σ(I)] | 0.0237 | 0.0316 | 0.0424 | 0.0427 |
| wR2 (all data) | 0.0634 | 0.0831 | 0.1167 | 0.1191 |
| GOF on F2 | 1.067 | 1.035 | 1.052 | 1.037 |
| Residual density/e Å−3 | 0.42/−0.70 | 0.26/−0.36 | 0.69/−0.69 | 0.84/−0.78 |
In isolation, the X-ray diffraction data of 1-Co0.05 contained insufficient evidence of the presence of Co, with the freely refined Zn atom giving an occupancy of 0.987(2). However, the orange color of single crystals of 1-Co0.05, compared to red for 1 and yellow for 1-Zn (Fig. S1†) indicated the presence of Co doped on the scale of a single crystal. This was also confirmed by EPR spectroscopy (see below). Refining the relative occupancy factors of both Zn and Co with coincident atom positions and identical anisotropic displacement parameters resulted in a Co contribution of 6(1)%.
X-ray powder diffraction data were measured on the Rigaku Oxford Diffraction SuperNova Dual Wavelength diffractometer using Cu-Kα radiation at 130 K. Powder samples were prepared by crushing the samples gently and loading them in a glass capillary for measurement. Data were collected to 2θ = 80° with an exposure time of 60 s per frame and were processed using CrysAlisPro.76
Electron paramagnetic resonance spectroscopy
X-band (ν ≈ 9.4 GHz) and W-Band (ν ≈ 94 GHz) EPR spectra were recorded on a Bruker Elexsys E500 spectrometer (X-band) with an SHQ cavity and a Bruker E600 spectrometer (W-band). Low temperature measurements were obtained using Oxford Instruments ESR900 (X-band) and Oxford CF935 (W-band) continuous flow helium cryostats controlled by Oxford Intelligent Temperature Controllers, at temperatures of 10 K (X-band) and 11 K (W-band). EPR spectra were simulated using the pepper suite in EasySpin software.80 In the simulation of the X- and W-band EPR spectra of 2(PF6), the same broadening was assumed at both frequencies and the following constraint was applied: g1/A1 = g2/A2 = g3/A3 (where A1, A2 and A3 represent the effective hyperfine interactions), to enable fitting without resolved hyperfine coupling observed.Magnetic measurements
Static magnetic measurements were performed on two different Quantum Design MPMS-XL SQUID magnetometers, in Florence and Monash. Magnetic susceptibility data were acquired for microcrystalline samples of 1 and 2(PF6), restrained in eicosane, in the temperature range 2–300 K with an applied field of 0.1 T, together with magnetization data with fields up to 5 T and temperature between 2 and 5.5 K. Raw data were corrected for the sample holder using a constant value across the temperature range and for the intrinsic diamagnetism of the sample, estimated by Pascal's constants.81Magnetic susceptibility data were acquired for microcrystalline samples of 3(PF6)·tol and 3-Zn(PF6)·tol, restrained by pressing into pellets with polytetrafluoroethylene (PTFE) tape. Measurements were corrected for the diamagnetic contribution of the PTFE tape and diamagnetic contribution of the compounds using Pascal's constants.81 Magnetic susceptibility data were acquired in the temperature range 1.8–300 K with an applied field of 0.1 T (T < 30 K) or 1 T (T > 30 K), together with magnetization data with fields up to 5 T and temperature between 1.9 and 4.5 K. Magnetic data acquired for 3(PF6)·tol restrained in eicosane under the same conditions as for 1 and 2(PF6) were similar to those of the PTFE restrained sample (Fig. S16†); however, the diamagnetic correction for the PTFE pellet is more accurate and has been used for analysis purposes.
Dynamic magnetic measurements (10–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz) were measured using a Quantum Design PPMS (Physical Property Measurement System), equipped with an alternating current susceptometer inset for microcrystalline samples of 1, 2(PF6) and 3(PF6)·tol, restrained in eicosane.
000 Hz) were measured using a Quantum Design PPMS (Physical Property Measurement System), equipped with an alternating current susceptometer inset for microcrystalline samples of 1, 2(PF6) and 3(PF6)·tol, restrained in eicosane.
Inelastic neutron scattering
Inelastic neutron scattering (INS) experiments were performed on the PELICAN cold neutron time-of-flight spectrometer.82 Measurements were performed on microcrystalline samples of 3(PF6)·tol and 3-Zn(PF6)·tol. Approximately 2 g of sample was loaded into an annular aluminum can of thickness 0.5 mm to minimize multiple scattering. Samples were then cooled using a closed cycle cryostat. Data were collected using λ = 4.69 Å neutrons, the choppers were also re-phased to obtain the higher order wavelength 2.345 Å. Data were collected at 1.5 K, 5 K, 10 K, 25 K, 50 K and 100 K for 3(PF6)·tol and 1.5 K, 10 K, 25 K, 50 K and 100 K for 3-Zn(PF6)·tol. The signal of an empty can was subtracted as background and all data were normalized to vanadium. All data manipulations were carried out using the freely available LAMP software.83Other measurements
Elemental analyses were performed by the Campbell Microanalytical Laboratory, Chemistry Department, University of Otago, New Zealand. High resolution mass spectra (HR-MS) were performed on an Agilent 6520 Accurate-Mass Q-TOF spectrometer. Thermogravimetric analyses were performed on a Mettler Toledo thermal analyzer using a ramp rate of 7 °C min−1 up to a maximum temperature of 700 °C. Ultraviolet-visible (UV-Vis) absorption spectra were recorded on an Agilent Cary 60 UV-Vis spectrophotometer in the range 220–1000 nm. Near infra-red (NIR) absorption spectra were recorded on a PerkinElmer Lambda 1050 UV/Vis/NIR spectrophotometer in the range 800–1330 nm. Electronic absorption spectra are discussed in the ESI (Fig. S13, Table S4†). Infrared spectra (KBr disk) were recorded on a Bruker Tensor 27 FTIR spectrometer. Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES) was performed on a PerkinElmer Optima 4300 DV Optical Emission Spectrometer. Wavelengths chosen for analysis were 228.616 nm for Co and 206.200 nm for Zn, with five replicate measurements performed at each wavelength. The sample (3.0 mg) was digested in 1 mL reverse aqua regia and diluted with water prior to analysis.Ab initio calculations
Ab initio state-averaged RASSCF calculations were performed on the Co(II) complexes, followed by the restricted-active-space-state-interaction including the spin–orbit interaction (RASSI-SO), as implemented in the MOLCAS quantum chemistry package (version 8.1).84 The X-ray structures of the Co(II) complexes were used without optimization, with each crystallographically independent cobalt complex treated in a separate calculation (Tables S19–S26†). For positional disorder of one tert-butyl substituent in a molecule of 3(PF6)·tol (later termed molecule 3+-B) the major orientation was used (0.86 occupancy). All atoms were described by relativistic atomic natural orbital (ANO-RCC) basis sets,85,86 with contractions of [5s4p2d1f] for Co, [5s4p2d1f] for Br, [3s2p1d] for C, N and O and [2s1p] for H for calculations on 1 and 2+. Calculations on hypothetical [CoII(Me3tpa)(dbcat)] (3; dbcat2− = 3,5-di-tert-butylcatecholate) and 3+ used contractions of [6s5p3d2f1g] for Co, [3s2p1d] for C, N and O and [2s1p] for H. Scalar relativistic effects were included in the basis set contraction using the Douglas–Kroll–Hess Hamiltonian.87–90 Cholesky decomposition of the two-electron integrals was employed to save disk space and speed-up the calculations, with a decomposition threshold of δ = 10−6 au.91,92The shorthand notation RAS(n,a) is used where n is the number of active electrons, and a is the total number of active orbitals. The longer notation RAS(n,l,m;i,j,k) is also used, where l is the maximum number of holes allowed in RAS1, m is the maximum number of electrons in RAS3 and the subpartitions of the active space i, j, k indicate the number of active orbitals in RAS1, RAS2 and RAS3, respectively (i + j + k = a). The spin-only wavefunctions resulting from the RASSCF method (Fig. S26, S27, S29–S32, Tables S7 and S14†), were used as basis states for the addition of SOC within RASSI-SO (Tables S8–S11 and S15†). The SINGLE_ANISO routine was used to compute the magnetic properties (magnetic susceptibility, magnetization) of all complexes and g tensors of the Kramer's doublets in the case of 1, 2+ and 3.93 For 3+, the lowest three quintet and triplet states were optimized separately in the RASSCF method, and then combined in the RASSI-SO and SINGLE_ANISO routine.94,95
Results and discussion
Syntheses
The mononuclear Co(II) compounds 1, 2(PF6) and3(PF6) were prepared by combining equimolar amounts of a Co(II) salt, Me3tpa and the corresponding dioxolene or tropolone ligand—first deprotonated by triethylamine—in methanolic solution. Compound 1 precipitates directly from the reaction solution as a red solid and was recrystallized from DMF/diethyl ether.75 Compound 2(PF6) precipitates as a pale orange solid. A series of small-scale recrystallizations of 2(PF6) with toluene were performed to obtain single crystals of diffraction quality. Slight variations in the solution concentration and cooling rate resulted in crystals of one of four phases: 2(PF6)-I, 2(PF6)-II, 2(PF6)·1.5tol-III and 2(PF6)·tol-IV (see Structure description section and ESI† for further details). A bulk recrystallization of 2(PF6) was performed to use for future measurements, and this sample was identified as phase I by PXRD (Fig. S11†); all references to 2+ and 2(PF6) in this work refer to phase I unless specified otherwise. Recrystallisation from toluene gave 3(PF6)·tol as a dark green solid.42 The solvation of 1, 2(PF6) and 3(PF6)·tol were confirmed by elemental analysis and thermogravimetric analysis (Fig. S2†).The mononuclear Zn(II) compounds 1-Zn, 2-Zn(PF6) and 3-Zn(PF6)·tol were synthesized as per their cobalt analogs; however, using zinc(II) chloride in place of the cobalt salt and a larger volume of methanol to account for its lower solubility. As 1-Zn is isomorphous with 1, the diluted analog with 5% cobalt doped in zinc, 1-Co0.05, was synthesized using the procedure from 1 with appropriate amounts of zinc(II) chloride and cobalt(II) chloride.75 The mole % of Co was determined to be 4.68(4)% by ICP-OES, a value that is consistent with the structural analysis. While PXRD indicates the bulk sample of 2-Zn(PF6) is predominantly isomorphous with 2(PF6), the bulk sample with 5% dilution of cobalt in zinc (2-Co0.05(PF6)) resulted in a mixture of phases (Fig. S11†) and was not pursued further. A single crystal structure of 2-Zn(PF6)·1.5tol-III was also obtained that was isomorphous with 2(PF6)·1.5tol-III. Infrared spectra confirm that 1-Zn, 2-Zn(PF6) and 3-Zn(PF6)·tol are isostructural with their cobalt analogs (see ref. 75 and Fig. S3 and S4†).
Structure description
Compounds 1, 1-Co0.05 and 1-Zn are isomorphous and crystallize in the monoclinic space group P21/n with one unique complex in the asymmetric unit. Phase I and II of 2(PF6) both crystallize solvent free but differ in the space group and number of crystallographically unique metal complexes. Phase I of 2(PF6) crystallizes in the monoclinic space group P21/c with one metal complex and one PF6− anion in the asymmetric unit. Phase II of 2(PF6) crystallizes in the triclinic space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) with two unique metal complexes and two PF6− anions in the asymmetric unit. Toluene-solvated phases III and IV of 2(PF6) crystallize in the monoclinic space groups P21/c and P21, respectively. Phases III and IV differ in the number of toluene molecules in the asymmetric unit: 1.5 and 1 toluene molecule, respectively, in addition to the single unique metal complex and single PF6− anion. Further discussion of 2(PF6) will focus on phase I, which represents the bulk sample; structural details of 2+ in phases II, III and IV are reported in Table S2.† Compound 2-Zn(PF6)·1.5tol-III crystallizes in the monoclinic space group P21/c and is isomorphous with 2(PF6)·1.5tol-III. Compounds 3(PF6)·tol and 3-Zn(PF6)·tol crystallize in the monoclinic space group P21/c and are isomorphous, with two crystallographically independent metal complexes in the unit cell (molecules 3+-A and 3+-B), along with two PF6− anions and two toluene molecules.
with two unique metal complexes and two PF6− anions in the asymmetric unit. Toluene-solvated phases III and IV of 2(PF6) crystallize in the monoclinic space groups P21/c and P21, respectively. Phases III and IV differ in the number of toluene molecules in the asymmetric unit: 1.5 and 1 toluene molecule, respectively, in addition to the single unique metal complex and single PF6− anion. Further discussion of 2(PF6) will focus on phase I, which represents the bulk sample; structural details of 2+ in phases II, III and IV are reported in Table S2.† Compound 2-Zn(PF6)·1.5tol-III crystallizes in the monoclinic space group P21/c and is isomorphous with 2(PF6)·1.5tol-III. Compounds 3(PF6)·tol and 3-Zn(PF6)·tol crystallize in the monoclinic space group P21/c and are isomorphous, with two crystallographically independent metal complexes in the unit cell (molecules 3+-A and 3+-B), along with two PF6− anions and two toluene molecules.
Complexes 1, 2+, 3+ and their zinc analogs share a common structural motif. The complexes consist of a 6-coordinate metal with an N4O2 coordination sphere comprised of three pyridyl N and one tertiary amine N from the tripodal tetradentate ligand, Me3tpa, and two cis O atoms from the alpha-hydroxy keto ligand (Fig. 1). Examination of the Co coordination spheres for 1, 2+ and 3+ indicate Co–O, Co–Namine and Co–Npy bond distances in the ranges 1.985(1)–2.105(1), 2.116(2)–2.129(2) and 2.149(2)–2.286(2) Å, respectively (Table 2), consistent with HS-Co(II) centers.43 The coordination sphere is distorted octahedral in all cases, with an axial elongation along N3–Co–N4, a compression along N1–Co–O1, and C1 symmetry (see Fig. 1 for labelling). The degree of distortion is similar between 1, 2+ and 3+ as evidenced by octahedral SHAPE indices in the narrow range 1.72–1.81 and similar octahedral distortion parameters Σ and Θ (Table 2).96–98
| 1 | 2(PF6) | 3(PF6)·tol | 3(PF6)·tol | ||
|---|---|---|---|---|---|
| 3+-A | 3+-B | ||||
| a Minimum intramolecular Co⋯Co distance. b SHAPE index for octahedral geometry, calculated in SHAPE 2.1.96,97 c where αi are the twelve cis-O/N–Co–O/N angles about the cobalt atom.98 d where θj are the 24 unique O/N–Ca–Cb–O/N dihedral angles, |θj| < 120°. Ca and Cb are the centroids of two triangular faces that are opposite on the octahedron such that Ca–Cb represents their common pseudo-threefold axis.98 e Metrical Oxidation State, as described in main text.99 | |||||
| Intramolecular and interatomic distances and angles | |||||
| Co–O1/Å | 1.985(1) | 2.024(1) | 2.027(1) | 2.015(1) | |
| Co–O2/Å | 2.061(1) | 2.077(1) | 2.075(1) | 2.105(1) | |
| Co–N1/Å | 2.129(2) | 2.127(1) | 2.118(2) | 2.116(2) | |
| Co–N2/Å | 2.229(2) | 2.167(1) | 2.149(2) | 2.171(2) | |
| Co–N3/Å | 2.267(2) | 2.233(1) | 2.240(2) | 2.216(2) | |
| Co–N4/Å | 2.253(2) | 2.242(1) | 2.280(2) | 2.286(2) | |
| C1–O1/Å | 1.313(2) | 1.285(2) | 1.287(2) | 1.290(2) | |
| C2–O2/Å | 1.296(2) | 1.276(2) | 1.282(2) | 1.278(2) | |
| C1–C2/Å | 1.451(3) | 1.480(2) | 1.463(2) | 1.465(2) | |
| O1–Co–O2/deg | 82.65(6) | 78.07(4) | 79.17(5) | 78.99(5) | |
| Co⋯Coa/Å | 7.9296(4) | 7.8765(6) | 8.3580(9) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Distortion parameters and oxidation state parameter | |||||
| SHAPE (Oh)b | 1.730 | 1.715 | 1.737 | 1.810 | |
| Σ /deg | 101.0 | 101.7 | 98.1 | 103.7 | |
| Θ /deg | 172.6 | 173.6 | 181.3 | 183.8 | |
| MOSe | −1.5(2) | n/a | −0.96(2) | −0.94(4) | |
The empirical metrical oxidation state (MOS) of dioxolene ligands, proposed by Brown et al. uses a least squares fitting of C–C and C–O bond lengths to assign an apparent oxidation state: −1 for a semiquinonate ligand and −2 for a catecholate ligand.99 The dioxolene ligand exists in the semiquinonate oxidation state for complex 3+ as indicated by MOS values of around −1 (Table 2) for molecule 3+-A and 3+-B. Compound 3-Zn+ also contains a semiquinonate ligand, with a MOS value of −0.85(3) and −0.86(4) for molecules 3-Zn+-A and 3-Zn+-B, respectively. The MOS values for Br4cat2− in 1 and 1-Zn are −1.5(2);75 however, the MOS is considered unreliable for electron-poor catecholates.99 Divalent metals and the formal dianionic charge on Br4cat2− compared to monoanionic dbsq− and trop− enforces neutral complexes with Br4cat2− instead of monocationic complexes.
The crystallographically independent cobalt complexes in 3(PF6)·tol are very similar, with the main differences relating to the angle of the pendant pyridine arms (Fig. 1). The Br4cat2− and trop− ligands are reasonable surrogates for dbsq−, with bite angles at the Co differing by less than 3.7° and 1.1°, respectively, and bonds in the O1–C1–C2–O2 fragment varying by less than 0.026 Å (Table 2). Overlaying the [Co(Me3tpa)(L)]n+ fragments reveals that 1 and 2+ differ most significantly from 3+-A and 3+-B by a bending of the pyridine and dioxolene/tropolonate rings (Fig. S5†). In compound 1 and 2(PF6) the dioxolene/tropolonate plane is at an angle of 7.4 and 13.1°, respectively, to the (Co, O1, O2) plane compared to −4.7 and −5.9° in 3(PF6)·tol. The polymorphs of 2(PF6) show similar deviations in pyridine and tropolonate ring orientations (Fig. S6†), resulting in Co–O/N bonds that vary by up to 0.084 Å and octahedral SHAPE indices in the range 1.51–1.73 (Table S2†).
The shortest intermolecular Co⋯Co distances of 7.93, 7.88 and 8.36 Å for compounds 1, 2(PF6) and 3(PF6)·tol, respectively (Table 2), are potentially sufficient to propagate observable dipolar interactions. Networks of intermolecular interactions including anion-complex interactions for 2(PF6) are responsible for the close packing and short Co⋯Co distances in 1 and 2(PF6) (Fig. S7†). As noted previously42 additional noncovalent interactions are present in 3(PF6)·tol, including slipped π⋯π interactions between Me3tpa pyridine rings and C–H⋯π interactions between Me3tpa pyridine and semiquinonate rings, resulting in chains of 3+ molecules stacked along the b-axis (Fig. 2, S8 and S9, Table S3†).
Electron paramagnetic resonance spectroscopy
Low temperature X-band EPR spectra of ground powders of 1 and 2(PF6) present broad transitions indicating significant intermolecular dipole coupling (Fig. S14†). In the case of 1, the spectrum is dominated by an asymmetric band centered at g ≈ 4.1 in addition to a feature at g ≈ 2.2. The diluted sample 1-Co0.05 was prepared to remove the effects of intermolecular interactions observed for 1, thereby improving g-factor resolution, and to investigate hyperfine coupling in the compound. The X-band EPR spectrum of 1-Co0.05 at 10 K (Fig. 3) is rhombic and indeed allows resolution of the hyperfine coupling to the 59Co nucleus (I = 7/2). A simulation of an effective S′ = 1/2 including only anisotropic g-values (Table 3), g-strains and hyperfine A-values (Table S5†) can reproduce all the key features of the spectrum (Fig. 3). The same parameters give a reasonable reproduction of the X-band EPR spectrum of 1, with the addition of H-strain to account for unresolved hyperfine coupling (Fig. S14, Table S5†).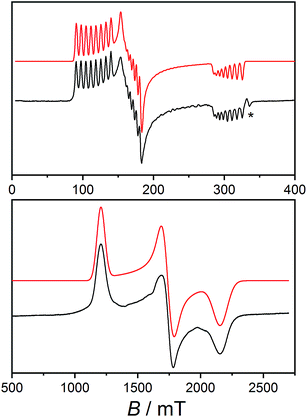 | ||
| Fig. 3 Solid state EPR spectra (black): X-band spectrum of 1-Co0.05 measured at 10 K (top) and W-band spectrum of 2(PF6) measured at 11 K (bottom) and simulations using the parameters indicated in Table S5† (red). Asterisk indicates the signal from an unavoidable impurity at g = 2.00. | ||
| Compound | Origin | g 1 | g 2 | g 3 |
|---|---|---|---|---|
| a g-Values resulting from the fit of eqn (1) to magnetic susceptibility, magnetization and experimental g-values. | ||||
| 1-Co0.05 | EPR | 5.815 | 3.975 | 2.190 |
| 1 | Magnetica | 5.654 | 3.791 | 2.200 |
| Ab initio | 5.692 | 3.930 | 2.709 | |
| 2(PF6) | EPR | 5.579 | 3.872 | 3.118 |
| 2+ | Magnetica | 5.491 | 3.798 | 3.037 |
| Ab initio | 5.646 | 3.687 | 3.177 | |
X-band EPR spectrum of 2(PF6) presents an asymmetric band centered at g ≈ 3.8 (Fig. S14†). However, the absence of the second feature at high field suggests that the pattern of g-values of the ground KD is significantly different for 1 and 2+.
Unfortunately, the isostructural diluted analog could not be obtained for 2(PF6) and we instead used higher frequency EPR to obtain a better resolved spectrum and more precise effective g-values. The W-band spectrum for 2(PF6) was then measured at 11 K (Fig. 3) resulting in three clearly resolved features. The 2(PF6) spectra could be reproduced with an anisotropic g- and H-strain model as used for 1 with parameters indicated in Tables 3 and S4 (Fig. 3 and S14†). As any other Co(II)-sq complex reported up to date, compound 3(PF6)·tol is EPR silent, due to the combined effect of the integer spin state and large anisotropy.
Static magnetic properties
The product of the molar susceptibility χM and the temperature for 1 decreases gradually upon cooling, from χMT[300 K] = 2.87 cm3 K mol−1 at room temperature until 130 K. Below this, χMT decreases more rapidly to reach a value of 1.56 cm3 K mol−1 at 2 K (Fig. 4) due to the depopulation of the Co(II) spin–orbit-coupled states derived from the low-symmetry ligand field states. The χMT[300 K] product is larger than the calculated spin-only value for an S = 3/2 spin with g = 2 (1.875 cm3 K mol−1), consistent with HS-Co(II) complexes with significant orbital angular momentum contributions. The field dependent magnetization data are close to saturating at high field and low temperature, with a limit of 2.12 NμB (Fig. 4). The reduced magnetization shows almost superimposed M vs. B/T curves, indicating an isolated magnetic ground state.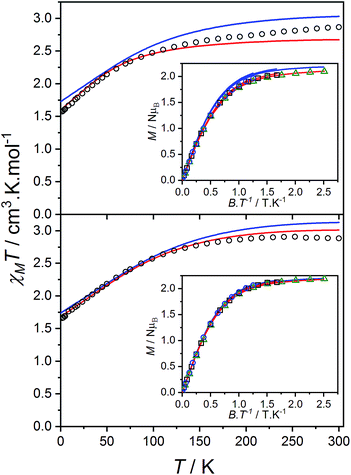 | ||
| Fig. 4 Plots of χMT versus T for 1 (top) and 2(PF6) (bottom) with inset: M versus B/T at 1.9 (black circles), 2.5 (blue square) and 4.5 K (green triangle). Overlaid fits to eqn (1) (red line, parameters in text) and ab initio simulations for 1 and 2+ (blue line). | ||
Pseudo-octahedral HS-Co(II) can be modeled using the Griffith approach, adapted for axial symmetry by Sakiyama and implemented with rhombic symmetry in PHI.52,100–104 In this approach the 4T1g ground state, which arises from the 4F free ion term in octahedral symmetry, is treated as an effective orbital moment of Leff = 1, spin S = 3/2 with explicit SOC using the T, P isomorphism.73,105,106 A combined orbital reduction parameter, α, is also included, which incorporates the isomorphism coefficient (−3/2) and reduction of the orbital angular momentum (Leff ≤ 1) due to the mixing of higher energy states into the ground state and metal–ligand bond covalency (α varies from −3/2 for a weak ligand field to −1 for a strong ligand field).52 The spin–orbit coupling constant, λSO, is expected to take values in the range −90 to −180 for six-coordinate Co(II) complexes.52 To avoid overparameterization when fitting experimental data, λSO, was fixed at −170 cm−1, a value approximating the free ion one for Co(II).73 The low symmetry of the complex splits and mixes the J = 1/2, 3/2 and 5/2 spin–orbit coupled states to give six doublets. Low symmetry is described by effective crystal field parameters for axial (B02) and rhombic (B22) distortions from octahedral symmetry.73,104,105
According to the Griffith model, the magnetic susceptibility and magnetization data and EPR effective g-values for 1 were simultaneously fit to a phenomenological Hamiltonian (eqn (1), where I is the identity matrix) in the program PHI.104
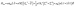 | (1) |
The overall best fit was achieved with the following parameters: α = −1.113(8), B02 = 161(5) cm−1 and |B22| = 111(5) cm−1, resulting in a residual of 5.23 × 10−5. The residual is defined as the product of the individual sum of squares absolute errors for each data set, and the uncertainties in the parameters correspond to a 5% increase in the residual with all other parameters fixed. The best fit closely matched the magnetization data; however, the effective g-values deviate from the EPR experimental values by up to 0.2 (Fig. 4, Table 3) and at higher temperatures, χMT departs from the experimental values.
The magnetic data for 2(PF6) are also typical for HS-Co(II) complexes with significant orbital angular momentum contributions. The χMT profile of 2(PF6) remains approximately constant at 2.88 cm3 K mol−1 from 300 K until 150 K, below which it decreases to 1.66 cm3 K mol−1 at 2 K. The reduced magnetization curves saturate at 2.19 NμB at low temperature (Fig. 4). Using the same approach as for 1, the experimental data can be fit with the following parameters: α = −1.254(7), B02 = −66(1) cm−1 and |B22| = 49(3) cm−1, resulting in a residual of 1.06 × 10−5. The magnetic data could be closely reproduced for 2(PF6) with effective g-values agreement to within 0.09 (Fig. 4, Table 3). It was noted that for both 1 and 2(PF6), the magnetization and magnetic susceptibility data could be fit in isolation using only the α and B02 parameters; however, this is not a realistic representation of the system given the rhombic EPR spectra. Only simultaneous consideration of magnetization, magnetic susceptibility and EPR g-values enabled the determination of |B22| without overparameterization, and thus accurate modeling of the system.
The orbital reduction parameter is larger for 1 than for 2(PF6), indicating a stronger ligand field or higher degree of covalency.52 This is consistent with the greater negative charge on Br4cat2− compared to trop−. The magnitude of the crystal field parameters is comparable to the SOC parameter, especially for 1. For 2(PF6), the states arising from splitting of the orbital doublet, quartet and sextet are clearly separated (Table S9†), while the large B02 term in 1 significantly splits the orbital quartet states by 410 cm−1 such that the second Kramer's doublet (KD), arising from the orbital quartet, is only 139 cm−1 above the ground KD (Table S8†). We also note that the different B02 sign for the two derivatives is consistent with the EPR pattern, with dominant easy-plane g pattern observed for 1-Co0.05 and dominant easy-axis one for 2(PF6). The best fit Bqk parameters obtained for 1 and 2(PF6) are consistent with a strong rhombicity of the cobalt complexes which is supported by electronic absorption spectral analysis (Fig. S13, Table S4†).
Ab initio calculations were performed on 1 and all polymorphs of 2+ (outlined in the ESI,† Section 11). Theoretical calculations provided excellent reproduction of magnetic and spectroscopic experimental data (Table 3, Fig. 4). However, slight variations in the Co coordination geometry of the polymorphs of 2+ were found to significantly impact the calculated ground state anisotropy (Table S11†). Furthermore, despite the qualitative similarity in the χMT vs. T plots measured for 1 and 2(PF6), markedly different Co(II) anisotropy parameters were obtained for the two species. Thus, despite the apparently similar molecular structures, the Co(II) electronic structure cannot be assumed to be the same for 1, 2+ and 3+ and we conclude that the diamagnetic substitution method is not suitable for the present case.
Compound 3(PF6)·tol has a room temperature χMT[300 K] value of 3.40 cm3 K mol−1, which is significantly larger than the expected spin-only value for an uncoupled S = 3/2 and S = 1/2 (2.25 cm3 K mol−1), but lies in the typical range of 2.5–3.8 cm3 K mol−1 for HS-Co(II)-sq complexes (Fig. 5).42,107 The increase of 0.52 cm3 K mol−1 between χMT[300 K] for 3(PF6)·tol and 2(PF6) is greater than the expected increase of 0.375 cm3 K mol−1 for the introduction of a non-interacting radical with S = 1/2. This suggests that the effect of the Co(II)-dbsq exchange coupling is not negligible even at room temperature, despite the temperature independence of χMT value of 3(PF6)·tol above 100 K. Below this temperature, χMT decreases gradually until an abrupt downturn at 10 K to reach a value of 1.44 cm3 K mol−1 at 1.8 K. Overall the observed behavior is in agreement with that previously reported for the ethanol solvate of 3(PF6).42 The reduced magnetization data of 3(PF6)·tol (Fig. 5) does not saturate at high field and low temperature and the M vs. B/T curves do not superimpose, indicating a magnetic ground state with a low-lying excited state. There are too many parameters required to adequately describe the Co(II) anisotropy and Co(II)-dbsq exchange coupling to uniquely fit the relatively featureless magnetic data.
Co(II)-radical ab initio calculations
| 2(PF6) Griffith | 2+ ab initio | 30-A ab initio | 30-B ab initio | 3+-A ab initio | 3+-B ab initio |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 6.587 | 5.702 |
| — | — | — | — | 55.008 | 33.141 |
| — | — | — | — | 63.306 | 54.142 |
| 244.511 | 282.193 | 253.267 | 294.315 | 298.415 | 270.322 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 1004.59 | 1053.75 | 1290.46 | 1215.17 | 1271.70 | 1294.15 |
Exchange parameters can be extracted from the ab initio results by fitting the simulated magnetization, magnetic susceptibility and spin–orbit energy levels to a simplified model of 3+. The isolated 3+ complex is modeled as an exchange coupled SCo = 3/2, LCo,eff = 1 of Co(II), subject to ligand field effect, and Ssq = 1/2 of the radical, termed the 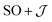 model:
model:
| Ĥtot = ĤCo + Ĥsq + Ĥex | (2) |
 and Ĥex modeling the exchange interaction between Co(II) and semiquinonate radical. The exchange interaction between orbitally-degenerate ions and radicals is often treated as an isotropic Lines exchange between the true spins of the ions and radicals involved, for example in the case of nitronyl nitroxide complexes of HS-Co(II).12,100,108 Here we define the exchange interaction in eqn (3) as completely anisotropic.104
and Ĥex modeling the exchange interaction between Co(II) and semiquinonate radical. The exchange interaction between orbitally-degenerate ions and radicals is often treated as an isotropic Lines exchange between the true spins of the ions and radicals involved, for example in the case of nitronyl nitroxide complexes of HS-Co(II).12,100,108 Here we define the exchange interaction in eqn (3) as completely anisotropic.104 | (3) |
The Hamiltonian (2) involves seven free parameters; to reduce the parameter space we sought to fix ĤCo parameters λSO, α, B02 and B22 prior to fitting data for 3+. The Co(II) electronic structure parameters are highly sensitive to slight changes in geometry, vide supra. To obtain single-ion Co(II) parameters, we first performed calculations on the structures of 3+-A and 3+-B with the charge distribution HS-Co(II)-dbcat2– (3, not observed experimentally). The CAS(7,5) calculations included the metal-based orbitals of the RAS(20,17) calculations on 3+. The resulting magnetic susceptibility, magnetization, energy levels and g-values were then fit104 to eqn (1) (Tables S10, S12 and S13†), leaving λSO as a free variable. This gave the following parameters: α = −1.416(7), λSO = −180.9(2) cm−1, B02 = −72(2) cm−1 and |B22| = 43(4) cm−1 for 3-A and α = −1.422(8), λSO = −180(1) cm−1, B02 = −95.8(4) cm−1 and |B22| = 72(4) cm−1 for 3-B. Errors were determined from fits of three out of four sets of data.
The ab initio simulated magnetic susceptibility, magnetization and energy levels of 3+-A and 3+-B were then fit104 to eqn (2) with the Co(II) parameters fixed to the values for 3-A and 3-B, respectively. For molecule 3+-A, a good reproduction of ab initio simulated data could be obtained with 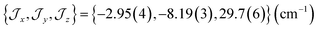 , representing a dominant F Ising-type exchange along the axis defined by B02 with significant anisotropic in-plane exchange contributions (Table S15, Fig. S28†).
, representing a dominant F Ising-type exchange along the axis defined by B02 with significant anisotropic in-plane exchange contributions (Table S15, Fig. S28†).
The 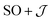 model can help us to understand how the exchange interactions control the energy level splitting. In the
model can help us to understand how the exchange interactions control the energy level splitting. In the 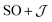 model where
model where 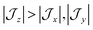 , the composition of the ground pseudo-doublet is controlled by
, the composition of the ground pseudo-doublet is controlled by 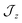 , and the
, and the 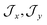 parameters affect the energy of the second level in the ground pseudo-doublet (E2). For
parameters affect the energy of the second level in the ground pseudo-doublet (E2). For 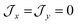 , the lowest two states become a true degenerate doublet, while non-zero in-plane exchange components mix other small components into the ground state. The radical perturbation on Co(II) therefore acts to double the number of energy levels, but will remove the electronic degeneracy in the presence of in-plane exchange interactions (Table 4).
, the lowest two states become a true degenerate doublet, while non-zero in-plane exchange components mix other small components into the ground state. The radical perturbation on Co(II) therefore acts to double the number of energy levels, but will remove the electronic degeneracy in the presence of in-plane exchange interactions (Table 4).
There are limitations to the 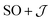 model: the fit for 3+-Bab initio data is significantly poorer (Fig. S28†)—the best exchange parameters
model: the fit for 3+-Bab initio data is significantly poorer (Fig. S28†)—the best exchange parameters 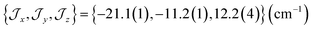 are unable to reproduce the energy of the third spin–orbit state (|3B〉), giving an energy of 10 cm−1 compared to 33 cm−1 in ab initio simulations (Table S15†).
are unable to reproduce the energy of the third spin–orbit state (|3B〉), giving an energy of 10 cm−1 compared to 33 cm−1 in ab initio simulations (Table S15†).
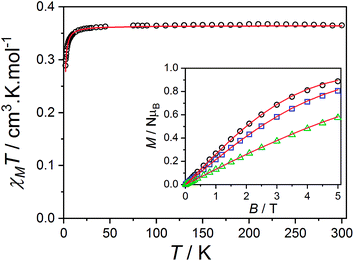
Zn-radical analog
The magnetic data reported per mole of 3-Zn(PF6)·tol are shown in Fig. 7: at room temperature the value of χMT[300 K] = 0.364 cm3 K mol−1 is very close to that expected for a simple S = 1/2 radical. On lowering the temperature below 40 K there is a downturn in χMT, consistent with an antiferromagnetic intermolecular interaction between semiquinonate radical ligands. The magnetic susceptibility and magnetization data were separately fit assuming an isotropic dimer model104 (eqn (4)) or a regular antiferromagnetic chain model using the Bonner–Fisher approximation.106 | (4) |
The dimer model (Fig. 7) provides the best fit values 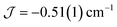 and g = 1.971(2), whereas the chain model (Fig. S17†) gives
and g = 1.971(2), whereas the chain model (Fig. S17†) gives 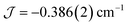 and g = 1.978(3) (deviation of g from the expected g = 2.00 value can be accounted for by a mass error of ∼1%). The Curie–Weiss plot is also linear (Fig. S18†) with a small AF Weiss constant of −0.48 ± 0.06 K. Intermolecular interactions were confirmed by the presence of an EPR half-field transition up to 20 K (Fig. S15†).
and g = 1.978(3) (deviation of g from the expected g = 2.00 value can be accounted for by a mass error of ∼1%). The Curie–Weiss plot is also linear (Fig. S18†) with a small AF Weiss constant of −0.48 ± 0.06 K. Intermolecular interactions were confirmed by the presence of an EPR half-field transition up to 20 K (Fig. S15†).
These results provide unequivocal confirmation of the intermolecular radical–radical exchange interaction in 3-Zn+. The exchange coupling might propagate through non-covalent interactions described in the structural section, resulting in an antiferromagnetic spin chain. Thus, in the isomorphous cobalt analog 3+, intermolecular interactions cannot be assumed to be negligible and should be considered in the modeling of the magnetic data and electronic structure.
Inelastic neutron scattering
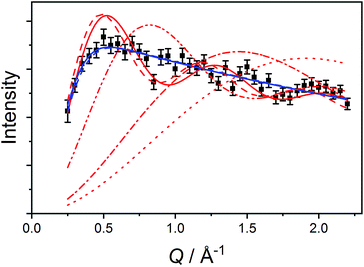
The data measured for 3(PF6)·tol at 1.5 K with neutrons of wavelength 4.69 Å exhibit several distinct features. At an energy transfer of E = 6.00(8) cm−1 there is a sharp, approximately resolution-limited peak (Fig. 8). Examination of the scattering factor, S(Q,E), reveals that this feature does not show dispersion, consistent with a magnetic excitation (Fig. S20†). Above 10 cm−1 is a broad excitation that extends to higher energies and has its maximum at 16 cm−1. As the sample is warmed, the intensity of the 6.00(8) cm−1 peak reduces while the 16 cm−1 peak increases (Fig. 8). Determination of the Q-dependence of these excitations shows that the 6.00(8) cm−1 peak has a maximum at Q ∼ 0.55 Å−1 followed by a decay in intensity with increasing Q, while the 16 cm−1 transition shows a quadratic increase in intensity with Q (Fig. 9 and S21†). Consideration of both the temperature- and Q-dependence together indicates that the 6.00(8) cm−1 feature is magnetic in origin, while the 16 cm−1 peak is due to a phonon. The 16 cm−1 phonon peak is confirmed by INS spectra of isomorphous 3-Zn(PF6)·tol, while spectra measured to 110 cm−1 on 3(PF6)·tol and 3-Zn(PF6)·tol are also dominated by phonon modes (ESI, Fig. S23–S25†). The low-resolution neutron powder diffraction obtained while cooling the sample indicates that no phase transition or valence tautomeric transition occurs upon lowering the temperature (Fig. S22†).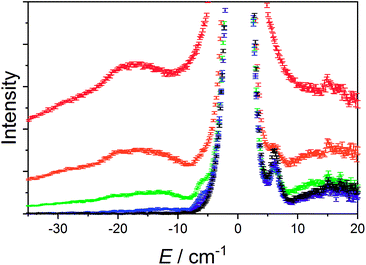 | ||
| Fig. 8 Variable temperature INS of 3(PF6)·tol with integration over the whole Q-range. Color code: 1.5 K, black; 5 K, purple; 10 K, blue; 25 K, green; 50 K, orange; 100 K, red. | ||
First, we attempted to reproduce the Q-dependence of the 6.00(8) cm−1 transition in 3(PF6)·tol using a simple dimer model—using the interference term from Güdel and Furrer:109
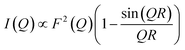 | (5) |
Free refinement of the R parameter in model (5) gave a reasonable fit to the data with a large R value of 8.3(2) Å (Fig. 9, solid red line). Although the observed data do not exhibit the same oscillations the model, the general trend in the low-Q region, and the prediction of an initial maximum around Q = 0.5 Å−1 is correct. Referring to the crystal structure, this refined distance is close to the intermolecular distance between Co-dbsq species, ∼8.963 Å (Table S3;† red dashed line in Fig. 9). Thus, the best fit corresponds to a “giant spin” scenario where the semiquinonate ligand and Co(II) ion in each molecule are coupled to produce Co(II)-dbsq “giant spins” that exhibit intermolecular coupling with each other. The lack of oscillations in the Q-dependence is likely due to the unpaired electrons being distributed across the Co-dbsq unit, so the data are not fit well by a single distance.
We then modeled the data to a function that represents an interaction over a range of lengths, in a similar manner to the analysis of jump diffusion in quasi-elastic neutron scattering:111,112
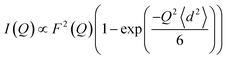 | (6) |
Intermolecular interaction model
The Q-dependence of the 6.00(8) cm−1 INS transition is inconsistent with the ab initio RASSCF/RASSI-SO predicted |1A〉 → |2A〉 or |1B〉 → |2B〉 transitions of the isolated molecules 3+-A and 3+-B (Table S6†); furthermore, the low temperature magnetic susceptibility is poorly reproduced by ab initio calculations on isolated molecules. Analysis of the 6.00(8) cm−1 INS transition in 3(PF6)·tol provides direct evidence of coupling between pairs of Co-dbsq units; thus, the theoretical model must be revised to consider these intermolecular interactions. Magnetic and EPR studies on 3-Zn(PF6)·tol indicate exchange interactions occur between the radical moieties.In the intermolecular interaction model we couple the radical spin component of the ab initio RASSCF/RASSI-SO pseudo-doublet states |1A〉 and |2A〉 with energies 0 and E2A on molecule 3+-A and corresponding states |1B〉 and |2B〉 with energies 0 and E2B on molecule 3+-B. To avoid excessive complication, we use a dimer interaction model between molecules 3+-A and 3+-B, which have the closest slipped π–π interaction, as measured by the minimum C⋯C distance (Fig. 2, Table S3†). The spin system is then described by the Hamiltonian:
 | (7) |
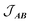 is the intermolecular interaction exchange parameter in cm−1, the only free parameter in the intermolecular exchange Hamiltonian (7). The Hamiltonian is diagonalized to obtain eigenvectors |1AB〉, |2AB〉, |3AB〉, |4AB〉 with corresponding energies ε1, ε2, ε3, ε4 and the magnetic susceptibility can be corrected for the exchange coupled states as follows:
is the intermolecular interaction exchange parameter in cm−1, the only free parameter in the intermolecular exchange Hamiltonian (7). The Hamiltonian is diagonalized to obtain eigenvectors |1AB〉, |2AB〉, |3AB〉, |4AB〉 with corresponding energies ε1, ε2, ε3, ε4 and the magnetic susceptibility can be corrected for the exchange coupled states as follows: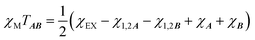 | (8) |
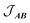 , with a value of +1.1(1) cm−1 providing the best reproduction of the data (Fig. 10). The simulation of low temperature χMT indicates a very good fit of the low energy states, which are the most important for interpreting intra- and inter-molecular exchange interactions. The intermolecular interaction model resulted in the dimer eigenfunctions (linear combinations of the product state basis):
, with a value of +1.1(1) cm−1 providing the best reproduction of the data (Fig. 10). The simulation of low temperature χMT indicates a very good fit of the low energy states, which are the most important for interpreting intra- and inter-molecular exchange interactions. The intermolecular interaction model resulted in the dimer eigenfunctions (linear combinations of the product state basis):| |1AB〉 = 0.9938|1A1B〉 + (−0.1009 − 0.0471i)|2A2B〉 |
| |2AB〉 = (−0.0495 − 0.5886i)|2A1B〉 + 0.8069|1A2B〉 |
| |3AB〉 = 0.8069|2A1B〉 + (0.0495 − 0.5886i)|1A2B〉 |
| |4AB〉 = (0.1009 − 0.0471i)|1A1B〉 + 0.9938|2A2B〉 |
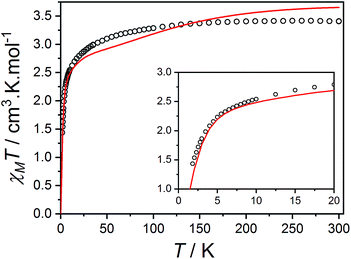 | ||
Fig. 10 Plot of χMT versus T for 3(PF6)·tol (circles) and overlaid simulation (line) using eqn (7) and (8) with 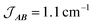 . Inset: expansion of the low-temperature region. . Inset: expansion of the low-temperature region. | ||
The final picture of the 3(PF6)·tol system is that of two Co-dbsq units featuring an anisotropic exchange interaction between the Co(II) ion and semiquinonate ligand, which results in a dominant ferromagnetic ground state. The exchange is of similar magnitude to crystal field effects and has significant contributions from SOC, which mixes the Co-dbsq states. Pairs of Co-dbsq units exhibit a weak intermolecular ferromagnetic interaction, via the semiquinonate radicals. The intermolecular interaction is of opposite sign to the semiquinonate coupling in 3-Zn(PF6)·tol and does not arise from dipolar interactions alone, as dipolar coupling of the pseudo-doublet states results in a very weak −0.016 cm−1 antiferromagnetic interaction along the g3 direction (Fig. 2, eqn (S7)†).
Dynamic magnetic measurements
As stated in the introduction, the accurate determination of the electronic structure in orbitally-degenerate metal-radical systems is of paramount importance for understanding the magnetization relaxation dynamics in SMMs and optimizing SMM performance. Field-induced cobalt(II)-based SMMs are commonly found with geometries including linear, tetrahedral, square pyramidal, octahedral, trigonal prismatic and pentagonal bipyramidal.74,113–116 Recently, Long et al. reported a linear Co(II) zero-field SMM with a high angular momentum ground state and an effective thermal barrier to the reversal of the magnetization of 450 cm−1, the highest yet for a transition metal complex.116 Zero-field Co(II) SMMs are less common, and only one pseudo-octahedral Co(II) example has been reported to date, diluted in Zn.117Pseudo-octahedral field-induced SMMs have been reported with both easy-plane and easy-axis anisotropies (in the case of quenched orbital angular momentum) as well as rhombic electronic structures.73,74,117–119Dynamic magnetic properties were measured for 1, 2(PF6) and 3(PF6)·tol to explore the dependence of potential SMM behavior on single-ion anisotropy and exchange effects. In the absence of a direct current (DC) field, no out-of-phase alternating current (AC) signal was observed for 1 or 2(PF6), potentially due to QTM promoted by intermolecular interactions or hyperfine coupling to the Co nucleus (I = 7/2). The optimum DC field (BDC) to suppress such relaxation pathways was determined for each compound at 2.5 K by varying the field from 0 to 300 mT. Compounds 1 and 2(PF6) display a non-zero out-of-phase magnetic susceptibility (χ′′) under optimum DC fields of 120 and 75 mT, respectively (Fig. 11).
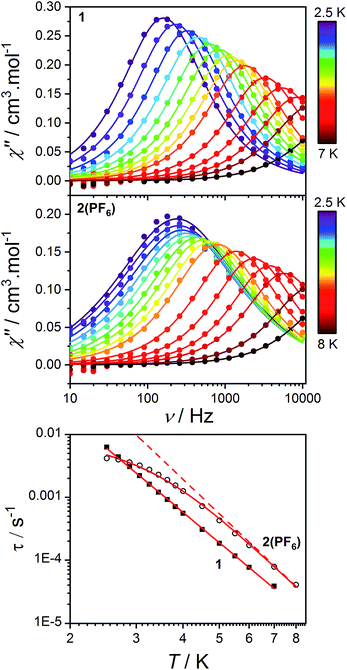 | ||
| Fig. 11 Frequency-dependence of the out-of-phase AC magnetic susceptibility (solid circles) for 1 (top) and 2(PF6) (middle) under applied fields of 120 and 75 mT, respectively and at different temperatures. Lines indicate fits to the generalized Debye model (9). Bottom: log–log plot of relaxation times as a function of temperature for 1 (solid squares) and 2(PF6) (empty circles). Solid lines indicate fits to the relaxation eqn (10) as discussed in the text. The dashed line indicates the Raman component of the relaxation equation for 2(PF6). | ||
Alternating current susceptibilities as a function of frequency (ν) were measured for a range of temperatures for 1 and 2(PF6) in the presence of BDC. The angular frequency (ω = 2πν) – dependent χ′′ were fit to the generalized Debye eqn (9) to obtain the characteristic relaxation time (τ) and lifetime distribution (η) at each temperature (Fig. 11).
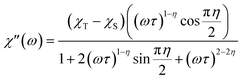 | (9) |
| τ−1 = CTw + BT | (10) |
Compound 3(PF6)·tol does not display a non-zero out-of-phase AC magnetic susceptibility with or without an applied field (0–0.3 T, Fig. S19†). We attribute this lack of SMM behavior to the absence of a bistable ground state due to the in-plane magnetic exchange components between the Co(II) ion and the semiquinonate radical ligand, evidenced by our analysis. Although in some cases intramolecular exchange between a metal center and a radical ligand can enhance SMM properties, by shifting the zero field QTM,2,4,5,17,31 in the present case it inhibits them, since the ground state is a singlet with a gap to the first excited state on the order of a few wavenumbers. We suggest that suppressing in-plane exchange components to achieve Ising-type exchange could restore the degeneracy of the ground state. This might be achieved by improving the easy axis nature of the Co(II) center, in much the same way as Ln-based SMMs.11 Alternatively, metal-radical systems with an odd total number of unpaired electrons could be targeted, to retain Kramers' degeneracy, as has been achieved for symmetric radical-bridged Co(II) and lanthanoid(III) systems previously.2,4–9,11,12,69
Conclusions
We have demonstrated that tackling the challenging problem of elucidating exchange interactions involving orbitally-degenerate metal ions requires the application of several experimental techniques and complementary advanced computational methods. This approach enabled us to answer the long-debated question about the nature of exchange in Co(II)-semiquinonate systems, for the specific case of 3(PF6)·tol. The ground state of 3+ is a pseudo-doublet with dominant ferromagnetic exchange contributions in the ground state wavefunctions. However, we stress that this exchange is not simply ferromagnetic or antiferromagnetic, as suggested by DFT calculations. The exchange coupling is anisotropic, of similar magnitude to the single-ion anisotropy parameters of the Co(II) ion and contains significant contributions from SOC. It is clear from our study that the outcome will depend on the specific system investigated, since exchange paths and contributions of ligand field and SOC are highly sensitive to coordination geometry. Thus, there is no simple, generally applicable, answer to the exchange coupling question for all Co(II)-semiquinonate systems. This result explains the wide variety of χMT values reported for the high temperature HS-Co(II)-semiquinonate valence tautomer in cobalt-dioxolene valence tautomeric systems, even when comparing differently solvated forms of a single compound.128We have also demonstrated that, despite the very similar molecular structures and charge distribution, the electronic structure of the Co(II) single ions cannot be assumed to be the same for 1, 2+ and 3+. It is clear, that care should be taken when employing the diamagnetic substitution method to empirically obtain information for this type of system. Furthermore, intermolecular exchange plays an important role in determining the magnetic behavior of the present system and should not be neglected, as is often the case.
With regard to SMM behavior, an anisotropic metal center gives rise to anisotropic exchange interactions and we have found that the anisotropic exchange suppresses SMM behavior when comparing 3(PF6)·tol to non-radical containing analogs 1 and 2(PF6). An improved understanding of exchange interactions in orbitally-degenerate metal ion-radical systems may enable not only the design of improved SMMs, but may also engender the ability to modulate the SMM-surface/electrode communication channels that are essential for the realization of SMM-based spintronics devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Australian Research Council for financial support to CB and LS through DP150100353. GKG acknowledges the support of an Elizabeth and Vernon Puzey Scholarship from the University of Melbourne and an Australian Government Research Training Scholarship. LS and MEB acknowledge the financial support from Italian MIUR through Project No. PRIN 2015-HYFSRT. The authors wish to thank Dr Willem Van den Heuvel for guidance on ab initio calculations, Mr Edward Nagul for running ICP-OES and Dr Nick Chilton for helpful discussions. This research was supported by use of the NeCTAR Research Cloud, a collaborative Australian research platform supported by the National Collaborative Research Infrastructure Strategy (NCRIS).References
- M. J. Giansiracusa, E. Moreno-Pineda, R. Hussain, R. Marx, M. Martínez Prada, P. Neugebauer, S. Al-Badran, D. Collison, F. Tuna, J. van Slageren, S. Carretta, T. Guidi, E. J. L. McInnes, R. E. P. Winpenny and N. F. Chilton, J. Am. Chem. Soc., 2018, 140, 2504–2513 CrossRef CAS PubMed.
- P. Zhang, M. Perfetti, M. Kern, P. P. Hallmen, L. Ungur, S. Lenz, M. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Chem. Sci., 2018, 9, 1221–1230 RSC.
- F. Gendron, J. Autschbach, J.-P. Malrieu and H. Bolvin, Inorg. Chem., 2019, 58, 581–593 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542 CrossRef CAS PubMed.
- F.-S. Guo and R. A. Layfield, Chem. Commun., 2017, 53, 3130–3133 RSC.
- S. Demir, M. Nippe, M. I. Gonzalez and J. R. Long, Chem. Sci., 2014, 5, 4701–4711 RSC.
- X. Ma, E. A. Suturina, S. De, P. Négrier, M. Rouzières, R. Clérac and P. Dechambenoit, Angew. Chem., Int. Ed., 2018, 57, 7841–7845 CrossRef CAS PubMed.
- S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549 CrossRef CAS PubMed.
- E. M. Fatila, M. Rouzières, M. C. Jennings, A. J. Lough, R. Clérac and K. E. Preuss, J. Am. Chem. Soc., 2013, 135, 9596–9599 CrossRef CAS PubMed.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144 CrossRef PubMed.
- T. J. Woods, M. F. Ballesteros-Rivas, S. M. Ostrovsky, A. V. Palii, O. S. Reu, S. I. Klokishner and K. R. Dunbar, Chem.–Eur. J., 2015, 21, 10302–10305 CrossRef CAS PubMed.
- Z.-X. Xiao, H. Miao, D. Shao, H.-Y. Wei, Y.-Q. Zhang and X.-Y. Wang, Chem. Commun., 2018, 54, 9726–9729 RSC.
- S. Kanegawa, S. Karasawa, M. Maeyama, M. Nakano and N. Koga, J. Am. Chem. Soc., 2008, 130, 3079–3094 CrossRef CAS PubMed.
- S. Kanegawa, S. Karasawa, M. Nakano and N. Koga, Chem. Commun., 2004, 1750–1751 RSC.
- S. Karasawa, G. Zhou, H. Morikawa and N. Koga, J. Am. Chem. Soc., 2003, 125, 13676–13677 CrossRef CAS PubMed.
- S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176 CrossRef CAS.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006 Search PubMed.
- Single-Molecule Magnets and Related Phenomena, ed. R. Winpenny, Springer-Verlag Berlin Heidelberg, 2006 Search PubMed.
- B. S. Dolinar, S. Gómez-Coca, D. I. Alexandropoulos and K. R. Dunbar, Chem. Commun., 2017, 53, 2283–2286 RSC.
- A. Caneschi, D. Gatteschi, N. Lalioti, C. Sangregorio, R. Sessoli, G. Venturi, A. Vindigni, A. Rettori, M. G. Pini and M. A. Novak, Angew. Chem., Int. Ed., 2001, 40, 1760–1763 CrossRef CAS PubMed.
- L. Bogani, A. Vindigni, R. Sessoli and D. Gatteschi, J. Mater. Chem., 2008, 18, 4750–4758 RSC.
- X. Liu, Y. Zhang, W. Shi and P. Cheng, Inorg. Chem., 2018, 57, 13409–13414 CrossRef CAS PubMed.
- N. Ishii, Y. Okamura, S. Chiba, T. Nogami and T. Ishida, J. Am. Chem. Soc., 2008, 130, 24–25 CrossRef CAS PubMed.
- M. Graf, G. Wolmershäuser, H. Kelm, S. Demeschko, F. Meyer and H.-J. Krüger, Angew. Chem., Int. Ed., 2010, 49, 950–953 CrossRef CAS PubMed.
- T. Tezgerevska, K. G. Alley and C. Boskovic, Coord. Chem. Rev., 2014, 268, 23–40 CrossRef CAS.
- O. Sato, A. Cui, R. Matsuda, J. Tao and S. Hayami, Acc. Chem. Res., 2007, 40, 361–369 CrossRef CAS PubMed.
- A. Dei and L. Sorace, Appl. Magn. Reson., 2010, 38, 139–153 CrossRef CAS.
- R. D. Schmidt, D. A. Shultz, J. D. Martin and P. D. Boyle, J. Am. Chem. Soc., 2010, 132, 6261–6273 CrossRef CAS PubMed.
- I. L. Fedushkin, O. V. Maslova, A. G. Morozov, S. Dechert, S. Demeshko and F. Meyer, Angew. Chem., Int. Ed., 2012, 51, 10584–10587 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and L. Sorace, in Handbook on the Physics and Chemistry of Rare Earths, ed. J.-C. G. Bünzli and V. K. Pecharsky, Elsevier, 2016, vol. 50, pp. 91–139 Search PubMed.
- D. Komijani, A. Ghirri, C. Bonizzoni, S. Klyatskaya, E. Moreno-Pineda, M. Ruben, A. Soncini, M. Affronte and S. Hill, Phys. Rev. Mater., 2018, 2, 024405 CrossRef CAS.
- Y. Wang, J. Li, L. Zhang, C. Chen, R. Feng, Y. Zhao, Y.-Q. Zhang, G. Tan, Y. Song and X. Wang, Dalton Trans., 2018, 47, 17211–17215 RSC.
- S. Fortier, J. J. Le Roy, C.-H. Chen, V. Vieru, M. Murugesu, L. F. Chibotaru, D. J. Mindiola and K. G. Caulton, J. Am. Chem. Soc., 2013, 135, 14670–14678 CrossRef CAS PubMed.
- J. Wang, J.-N. Li, S.-L. Zhang, X.-H. Zhao, D. Shao and X.-Y. Wang, Chem. Commun., 2016, 52, 5033–5036 RSC.
- S. Marocchi, A. Candini, D. Klar, W. Van den Heuvel, H. Huang, F. Troiani, V. Corradini, R. Biagi, V. De Renzi, S. Klyatskaya, K. Kummer, N. B. Brookes, M. Ruben, H. Wende, U. del Pennino, A. Soncini, M. Affronte and V. Bellini, ACS Nano, 2016, 10, 9353–9360 CrossRef CAS PubMed.
- A. Candini, D. Klar, S. Marocchi, V. Corradini, R. Biagi, V. De Renzi, U. del Pennino, F. Troiani, V. Bellini, S. Klyatskaya, M. Ruben, K. Kummer, N. B. Brookes, H. Huang, A. Soncini, H. Wende and M. Affronte, Sci. Rep., 2016, 6, 21740 CrossRef CAS PubMed.
- C. Godfrin, S. Thiele, A. Ferhat, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, ACS Nano, 2017, 11, 3984–3989 CrossRef CAS PubMed.
- M. Urdampilleta, S. Klayatskaya, M. Ruben and W. Wernsdorfer, ACS Nano, 2015, 9, 4458–4464 CrossRef CAS PubMed.
- S. Thiele, F. Balestro, R. Ballou, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Science, 2014, 344, 1135 CrossRef CAS PubMed.
- R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Nature, 2012, 488, 357 CrossRef CAS PubMed.
- A. Beni, A. Dei, S. Laschi, M. Rizzitano and L. Sorace, Chem.–Eur. J., 2008, 14, 1804–1813 CrossRef CAS PubMed.
- K. G. Alley, G. Poneti, P. S. D. Robinson, A. Nafady, B. Moubaraki, J. B. Aitken, S. C. Drew, C. Ritchie, B. F. Abrahams, R. K. Hocking, K. S. Murray, A. M. Bond, H. H. Harris, L. Sorace and C. Boskovic, J. Am. Chem. Soc., 2013, 135, 8304–8323 CrossRef CAS PubMed.
- A. Caneschi, A. Dei, D. Gatteschi and V. Tangoulis, Inorg. Chem., 2002, 41, 3508–3512 CrossRef CAS PubMed.
- A. Bencini, A. Beni, F. Costantino, A. Dei, D. Gatteschi and L. Sorace, Dalton Trans., 2006, 722–729 RSC.
- D. Ruiz, J. Yoo, D. N. Hendrickson, I. A. Guzei and A. L. Rheingold, Chem. Commun., 1998, 2089–2090 RSC.
- M. W. Lynch, R. M. Buchanan, C. G. Pierpont and D. N. Hendrickson, Inorg. Chem., 1981, 20, 1038–1046 CrossRef CAS.
- A. Caneschi, A. Dei, D. Gatteschi, S. Poussereau and L. Sorace, Dalton Trans., 2004, 1048–1055 RSC.
- T. Mehdoui, J.-C. Berthet, P. Thuéry, L. Salmon, E. Rivière and M. Ephritikhine, Chem.–Eur. J., 2005, 11, 6994–7006 CrossRef CAS PubMed.
- M. L. Kahn, R. Ballou, P. Porcher, O. Kahn and J.-P. Sutter, Chem.–Eur. J., 2002, 8, 525–531 CrossRef CAS.
- A. Palii, B. Tsukerblat, S. Klokishner, K. R. Dunbar, J. M. Clemente-Juan and E. Coronado, Chem. Soc. Rev., 2011, 40, 3130–3156 RSC.
- F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Inorg. Chim. Acta, 2008, 361, 3432–3445 CrossRef CAS.
- F. Ortu, J. Liu, M. Burton, J. M. Fowler, A. Formanuik, M.-E. Boulon, N. F. Chilton and D. P. Mills, Inorg. Chem., 2017, 56, 2496–2505 CrossRef CAS PubMed.
- E. Moreno Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2014, 5, 5243 CrossRef CAS PubMed.
- J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, C. Giménez-Saiz, H.-U. Güdel, A. Sieber, R. Bircher and H. Mutka, Inorg. Chem., 2005, 44, 3389–3395 CrossRef CAS PubMed.
- H. Andres, J. M. Clemente-Juan, R. Basler, M. Aebersold, H.-U. Güdel, J. J. Borrás-Almenar, A. Gaita, E. Coronado, H. Büttner and S. Janssen, Inorg. Chem., 2001, 40, 1943–1950 CrossRef CAS PubMed.
- A. B. Boeer, A.-L. Barra, L. F. Chibotaru, D. Collison, E. J. L. McInnes, R. A. Mole, G. G. Simeoni, G. A. Timco, L. Ungur, T. Unruh and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2011, 50, 4007–4011 CrossRef CAS PubMed.
- K. Yamaguchi, H. Fukui and T. Fueno, Chem. Lett., 1986, 15, 625–628 CrossRef.
- D. M. Adams, L. Noodleman and D. N. Hendrickson, Inorg. Chem., 1997, 36, 3966–3984 CrossRef CAS.
- A. Bencini, A. Caneschi, C. Carbonera, A. Dei, D. Gatteschi, R. Righini, C. Sangregorio and J. van Slageren, J. Mol. Struct., 2003, 656, 141–154 CrossRef CAS.
- A. A. Starikova, M. G. Chegerev, A. G. Starikov and V. I. Minkin, Comput. Theor. Chem., 2018, 1124, 15–22 CrossRef CAS.
- A. Witt, F. W. Heinemann, S. Sproules and M. M. Khusniyarov, Chem.–Eur. J., 2014, 20, 11149–11162 CrossRef CAS PubMed.
- Y.-Q. Zhang, C.-L. Luo, B.-W. Wang and S. Gao, J. Phys. Chem. A, 2013, 117, 10873–10880 CrossRef CAS PubMed.
- Y.-Q. Zhang, C.-L. Luo and Q. Zhang, J. Comput. Chem., 2014, 35, 904–909 CrossRef CAS PubMed.
- F. Neese, Coord. Chem. Rev., 2009, 253, 526–563 CrossRef CAS.
- H. Paulsen, V. Schüenemann and J. A. Wolny, Eur. J. Inorg. Chem., 2013, 2013, 628–641 CrossRef CAS.
- C. H. Booth, M. D. Walter, D. Kazhdan, Y.-J. Hu, W. W. Lukens, E. D. Bauer, L. Maron, O. Eisenstein and R. A. Andersen, J. Am. Chem. Soc., 2009, 131, 6480–6491 CrossRef CAS PubMed.
- C. H. Booth, D. Kazhdan, E. L. Werkema, M. D. Walter, W. W. Lukens, E. D. Bauer, Y.-J. Hu, L. Maron, O. Eisenstein, M. Head-Gordon and R. A. Andersen, J. Am. Chem. Soc., 2010, 132, 17537–17549 CrossRef CAS PubMed.
- U. Albold, H. Bamberger, P. P. Hallmen, J. van Slageren and B. Sarkar, Angew. Chem., Int. Ed., 2019, 58, 9802–9806 CrossRef CAS PubMed.
- J. O. Moilanen, N. F. Chilton, B. M. Day, T. Pugh and R. A. Layfield, Angew. Chem., Int. Ed., 2016, 55, 5521–5525 CrossRef CAS PubMed.
- R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896–5898 CrossRef CAS PubMed.
- J. Li, Y. Han, F. Cao, R.-M. Wei, Y.-Q. Zhang and Y. Song, Dalton Trans., 2016, 45, 9279–9284 RSC.
- J. P. S. Walsh, G. Bowling, A.-M. Ariciu, N. F. M. Jailani, N. F. Chilton, P. Waddell, D. Collison, F. Tuna and L. J. Higham, Magnetochemistry, 2016, 2, 23 CrossRef.
- D. Sertphon, K. S. Murray, W. Phonsri, J. Jover, E. Ruiz, S. G. Telfer, A. Alkaş, P. Harding and D. J. Harding, Dalton Trans., 2018, 47, 859–867 RSC.
- G. K. Gransbury, M.-E. Boulon, S. Petrie, R. W. Gable, R. J. Mulder, L. Sorace, R. Stranger and C. Boskovic, Inorg. Chem., 2019, 58, 4230–4243 CrossRef CAS PubMed.
- CrysAlisPro 1.171.37.35 or 1.171.38.43, Rigaku Oxford Diffraction, Yarnton, Oxfordshire, England, 2015 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532–536 CrossRef CAS.
- D. Yu, R. Mole, T. Noakes, S. Kennedy and R. Robinson, J. Phys. Soc. Jpn., 2013, 82, SA027 CrossRef.
- D. Richard, M. Ferrand and G. J. Kearley, J. Neutron Res., 1996, 4, 33–39 CrossRef.
- F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. F. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P.-Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579 CrossRef CAS PubMed.
- B. O. Roos, R. Lindh, P.-Å. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858 CrossRef CAS.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748 CrossRef CAS PubMed.
- B. O. Roos and P.-Å. Malmqvist, Phys. Chem. Chem. Phys., 2004, 6, 2919–2927 RSC.
- M. Reiher and A. Wolf, J. Chem. Phys., 2004, 121, 10945–10956 CrossRef CAS PubMed.
- F. Aquilante, T. B. Pedersen and R. Lindh, J. Chem. Phys., 2007, 126, 194106 CrossRef PubMed.
- T. B. Pedersen, F. Aquilante and R. Lindh, Theor. Chem. Acc., 2009, 124, 1–10 Search PubMed.
- L. F. Chibotaru and L. Ungur, J. Chem. Phys., 2012, 137, 064112 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur and A. Soncini, Angew. Chem., Int. Ed., 2008, 47, 4126–4129 CrossRef CAS PubMed.
- L. F. Chibotaru, L. Ungur, C. Aronica, H. Elmoll, G. Pilet and D. Luneau, J. Am. Chem. Soc., 2008, 130, 12445–12455 CrossRef CAS PubMed.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, New J. Chem., 2002, 26, 996–1009 RSC.
- M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE 2.1, Universitat de Barcelona, Barcelona, Spain, 2013 Search PubMed.
- M. A. Halcrow, Chem. Soc. Rev., 2011, 40, 4119–4142 RSC.
- S. N. Brown, Inorg. Chem., 2012, 51, 1251–1260 CrossRef CAS PubMed.
- M. E. Lines, J. Chem. Phys., 1971, 55, 2977–2984 CrossRef CAS.
- M. E. Lines, Phys. Rev., 1963, 131, 546–555 CrossRef CAS.
- H. Sakiyama, R. Ito, H. Kumagai, K. Inoue, M. Sakamoto, Y. Nishida and M. Yamasaki, Eur. J. Inorg. Chem., 2001, 2027–2032 CrossRef CAS.
- H. Sakiyama, R. Ito, H. Kumagai, K. Inoue, M. Sakamoto, Y. Nishida and M. Yamasaki, Eur. J. Inorg. Chem., 2001, 2705 CrossRef CAS.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, J. Comput. Chem., 2013, 34, 1164–1175 CrossRef CAS PubMed.
- S. Roy, I. Oyarzabal, J. Vallejo, J. Cano, E. Colacio, A. Bauza, A. Frontera, A. M. Kirillov, M. G. B. Drew and S. Das, Inorg. Chem., 2016, 55, 8502–8513 CrossRef CAS PubMed.
- O. Kahn, Molecular Magnetism, VCH Publishers, Inc., New York, NY, 1993 Search PubMed.
- F. Yu, M. Xiang, Q.-g. Wu, H. He, S.-q. Cheng, X.-y. Cai, A.-h. Li, Y.-m. Zhang and B. Li, Inorg. Chim. Acta, 2015, 426, 146–149 CrossRef CAS.
- D. Luneau, F. M. Romero and R. Ziessel, Inorg. Chem., 1998, 37, 5078–5087 CrossRef CAS.
- A. Furrer and H. U. Güdel, Phys. Rev. Lett., 1977, 39, 657–660 CrossRef CAS.
- R. E. Watson and A. J. Freeman, Acta Crystallogr., 1961, 14, 27–37 CrossRef CAS.
- P. L. Hall and D. K. Ross, Mol. Phys., 1981, 42, 673–682 CrossRef CAS.
- H. Jobic and D. N. Theodorou, Microporous Mesoporous Mater., 2007, 102, 21–50 CrossRef CAS.
- M. Murrie, Chem. Soc. Rev., 2010, 39, 1986–1995 RSC.
- G. A. Craig and M. Murrie, Chem. Soc. Rev., 2015, 44, 2135–2147 RSC.
- R. F. Higgins, B. N. Livesay, T. J. Ozumerzifon, J. P. Joyce, A. K. Rappé and M. P. Shores, Polyhedron, 2018, 143, 193–200 CrossRef CAS.
- P. C. Bunting, M. Atanasov, E. Damgaard-Møller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, Science, 2018, 362, eaat7319 CrossRef CAS PubMed.
- L. Rigamonti, N. Bridonneau, G. Poneti, L. Tesi, L. Sorace, D. Pinkowicz, J. Jover, E. Ruiz, R. Sessoli and A. Cornia, Chem.–Eur. J., 2018, 24, 8857–8868 CrossRef CAS PubMed.
- Y. Peng, V. Mereacre, C. E. Anson, Y. Zhang, T. Bodenstein, K. Fink and A. K. Powell, Inorg. Chem., 2017, 56, 6056–6066 CrossRef CAS PubMed.
- G. Novitchi, S. Jiang, S. Shova, F. Rida, I. Hlavička, M. Orlita, W. Wernsdorfer, R. Hamze, C. Martins, N. Suaud, N. Guihéry, A.-L. Barra and C. Train, Inorg. Chem., 2017, 56, 14809–14822 CrossRef CAS PubMed.
- A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Dover Publications, Inc, Mineola, NY, 1986 Search PubMed.
- X. Liu, X. Ma, P. Cen, F. An, Z. Wang, W. Song and Y.-Q. Zhang, New J. Chem., 2018, 42, 9612–9619 RSC.
- M. A. Palacios, J. Nehrkorn, E. A. Suturina, E. Ruiz, S. Gómez-Coca, K. Holldack, A. Schnegg, J. Krzystek, J. M. Moreno and E. Colacio, Chem.–Eur. J., 2017, 23, 11649–11661 CrossRef CAS PubMed.
- A. K. Mondal, S. Khatua, K. Tomar and S. Konar, Eur. J. Inorg. Chem., 2016, 2016, 3545–3552 CrossRef CAS.
- R. Orbach, Proc. R. Soc. London, Ser. A, 1961, 264, 458 CrossRef CAS.
- A. Singh and K. N. Shrivastava, Phys. Status Solidi B, 1979, 95, 273–277 CrossRef CAS.
- K. N. Shrivastava, Phys. Status Solidi B, 1983, 117, 437–458 CrossRef CAS.
- E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130–9134 CrossRef CAS PubMed.
- D. M. Adams, A. Dei, A. L. Rheingold and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 8221–8229 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional characterization and discussion, crystallography, UV-Vis-NIR, INS, EPR, magnetic measurements, ab initio details and calculations on 1 and 2+ and details of models discussed in the main text. CCDC 1896298–1896305. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc00914k |
| This journal is © The Royal Society of Chemistry 2019 |

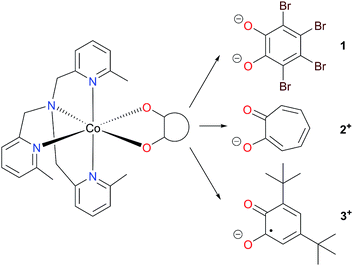
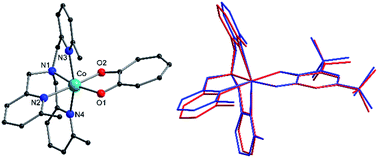
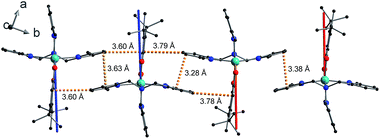
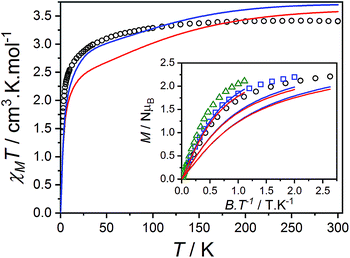
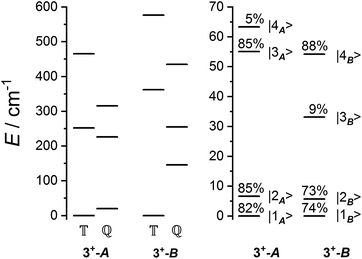
![[Doublestruck Q]](https://www.rsc.org/images/entities/char_e174.gif) ) and triplet (
) and triplet (![[Doublestruck T]](https://www.rsc.org/images/entities/char_e177.gif) ) spin-only states are indicated, and spin–orbit states are labelled with quintet composition. The next highest energy spin–orbit states have energies >270 cm−1.
) spin-only states are indicated, and spin–orbit states are labelled with quintet composition. The next highest energy spin–orbit states have energies >270 cm−1.