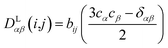Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Configuration determination by residual dipolar couplings: accessing the full conformational space by molecular dynamics with tensorial constraints†
Pavleta
Tzvetkova
 ,
Ulrich
Sternberg‡
,
Ulrich
Sternberg‡
 ,
Thomas
Gloge
,
Armando
Navarro-Vázquez§
,
Thomas
Gloge
,
Armando
Navarro-Vázquez§
 * and
Burkhard
Luy
* and
Burkhard
Luy
 *
*
Institute of Organic Chemistry and Institute for Biological Interfaces 4 – Magnetic Resonance, Karlsruhe Institute of Technology (KIT), Fritz-Haber-Weg 6, 76131 Karlsruhe, Germany. E-mail: armando.deus@gmail.com; burkhard.luy@kit.edu
First published on 29th July 2019
Abstract
Residual dipolar couplings (RDCs) and other residual anisotropic NMR parameters provide valuable structural information of high quality and quantity, bringing detailed structural models of flexible molecules in solution in reach. The corresponding data interpretation so far is directly or indirectly based on the concept of a molecular alignment tensor, which, however, is ill-defined for flexible molecules. The concept is typically applied to a single or a small set of lowest energy structures, ignoring the effect of vibrational averaging. Here, we introduce an entirely different approach based on time averaged molecular dynamics with dipolar couplings as tensorial orientational restraints that can be used to solve structural problems in molecules of any size without the need of introducing an explicit molecular alignment tensor into the computation. RDC restraints are represented by their full 3D interaction tensor in the laboratory frame, for which pseudo forces are calculated using a secular dipolar Hamiltonian as the target. The resulting rotational averaging of each individual tensorial restraint leads to structural ensembles that best fulfil the experimental data. Using one-bond RDCs, the approach has been implemented in the force field procedures of the program COSMOS and extensively tested. A concise theoretical introduction, including the special treatment of force fields for stable and fast MD simulations, as well as applications regarding configurational analyses of small to medium-sized organic molecules with different degrees of flexibility, is given. The observed results are discussed in detail.
1 Introduction
Residual dipolar couplings (RDCs) are an efficient tool for the determination of the relative configuration of small organic molecules.1–5 The use of RDCs has been boosted by the availability of weak aligning media compatible with standard organic solvents such as CDCl3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6–10 or DMSO-d6,11–18 and most other common NMR solvents.19–22 While it is widely recognized that residual anisotropic NMR parameters are suited for the determination of dynamics in biomolecules,23,24 they are equally amenable to the structure elucidation of small molecules with inherent flexibility. However, physically sound data interpretation is difficult, especially in the case of small to medium sized molecules in which typically only a single alignment medium is employed and, although in principle a multitude of internuclear couplings exists, the amount of practically accessible RDCs is limited. Vibrations and slow conformational changes in molecules significantly complicate the situation. For small, rigid molecules simple harmonic modes can be obtained from DFT calculations and have been successfully applied,25 but for most cases the corresponding contributions are either neglected or treated using considerable approximations. Here, instead, we introduce molecular dynamics with RDC-based orientational tensorial constraints applied in the laboratory frame as a physically sound method for the determination of relative configurations of molecules with inherent flexibility.
6–10 or DMSO-d6,11–18 and most other common NMR solvents.19–22 While it is widely recognized that residual anisotropic NMR parameters are suited for the determination of dynamics in biomolecules,23,24 they are equally amenable to the structure elucidation of small molecules with inherent flexibility. However, physically sound data interpretation is difficult, especially in the case of small to medium sized molecules in which typically only a single alignment medium is employed and, although in principle a multitude of internuclear couplings exists, the amount of practically accessible RDCs is limited. Vibrations and slow conformational changes in molecules significantly complicate the situation. For small, rigid molecules simple harmonic modes can be obtained from DFT calculations and have been successfully applied,25 but for most cases the corresponding contributions are either neglected or treated using considerable approximations. Here, instead, we introduce molecular dynamics with RDC-based orientational tensorial constraints applied in the laboratory frame as a physically sound method for the determination of relative configurations of molecules with inherent flexibility.
Since RDCs, in contrast to locally determined NMR parameters like NOEs or J-couplings, depend on the global orientation of the internuclear vectors with respect to the external magnetic field, they provide information that can become crucial for the solution of relative configuration problems, in particular in the case of stereogenic centres too distant from each other. The technique has been successfully applied to the structure elucidation of several natural26–33 and synthetic compounds.34–37 In the case of rigid molecules, the analysis is based on fitting the experimental data to global molecular order or alignment tensors S for each possible configuration, which are then ranked according to the fitting between the experimental and back computed values. This fitting is accomplished in most of the cases by a least squares solution of a set of linear equations using singular value decomposition (SVD)38 – although other techniques can be employed.38–45 Nevertheless, in many cases the studied compounds have some degree of conformational flexibility which needs to be taken into account when analysing the data. It has been known for decades that vibrational corrections need to be applied for accurate RDC interpretation,46,47 as the full enthalpically and entropically driven conformational space contributes to the alignment. But these contributions are difficult to include in everyday applications. The currently employed approaches are mostly based on fitting RDC data to a discrete ensemble of lowest energy conformations obtained typically by a force-field-based stochastic conformational search, a procedure that we will call here the “static” approximation. Other physically more sound models involve the detailed treatment of a defined, limited set of flexible bonds, or the use of restrained molecular dynamics (r-MD) methodologies, usually applied with RDCs as scalar restraints in an alignment tensor frame of reference.
The “static” method uses in most cases the “single tensor” approximation,48–50i.e. the assumption that different conformers share a common global molecular order tensor, which is mostly called the Saupe tensor or alignment tensor (we refer to this method throughout the paper as the alignment tensor method). Sharing a common order tensor, the populations of different conformations can be estimated through different optimization techniques.43,50–52 Although the procedure is based on a rough approximation, its use is reasonable when the conformational changes do not cause a significant change of the global shape of the molecule. As only low energy conformers are included in the data interpretation, experimental RDCs are practically never fulfilled within the experimental error. The use of the single tensor approximation requires the definition of a common frame for all conformations, which is usually accomplished by overlay of the atomic coordinates,48,50,51 but which is generally ill-defined in the presence of flexibility.
Static multi tensor approaches, where an order tensor is determined for each conformation considered, have been scarcely used in structure determination problems since the large number of unknown parameters to be fitted makes the problem usually bad conditioned. Vibrational averaging is not considered and the populations of different conformations cannot be determined, unless a common degree of order is assumed for all determined tensors.50,53 Alternatively, populations can be derived from other NMR constraints such as scalar couplings or NOE-derived distances.29 Another approach is based on the maximum entropy (ME) method that attempts to explain the experimental data with the bare minimum of information, therefore maximizing the freedom on the rotational global and internal degrees of freedom. The original unconstrained ME54 frequently leads to too flat conformational spaces, and in fact wrongly predicts a complete freedom around internal coordinates in the isotropic limit. This is due to the fact that the method ignores the enthalpy contributions to the total entropy coming from the different potential energies of different conformational states. The method has also been extended to include all kinds of constraints to obtain a minimum set of conformations to fulfil sparse experimental data and to include a priori structural information.55
Based on the Marcelja molecular mean-field approximation,56 a successful and physically sound approach to the flexibility problem is the additive potential (AP) method,57 which is very well suited for the analysis of torsional distributions in simple molecules. The method requires the definition of a functional form for the isotropic limit conformational distribution and allows the separate treatment of molecular fragments. It has been considerably enhanced by the introduction of Gaussian angular distributions into the so-called AP-DPD approach.46,57 A clear comparison of the AP and ME methods was reported by Emsley et al.58 However, the method unfortunately is computationally demanding, currently limiting the application to systems with less than 60 atoms. The combined APME method proposed by Maliniak and coworkers combines the two methods and avoids the use of a functional form for the isotropic limit distribution by simultaneous fitting to J-coupling and NOE distances.59,60
All methods described so far are based on providing a single structure or an ensemble of structures with the lowest energies that is used for fitting experimental data to a single tensor or a sum of individual alignment tensors. More sophisticated approaches incorporate vibrational averaging based on harmonic approximations to further enhance the fitting procedure. With the exception of a number of quite small molecules, however, the amount of accessible experimental parameters does not match the number of fitting parameters, which invokes additional approximations like the ME approach. Very different from this procedure, the conformationally accessible space, including excited states and entropic contributions, is inherently sampled in restrained molecular dynamics (r-MD) approaches, where RDCs are used as constraints.
In most cases, RDCs as scalar constraints are introduced in steepest descent or r-MD simulations based on protocols using axial and rhombic parameters of an alignment tensor that has been estimated initially and RDCs were used as angular as well as combined angular and distance restraints.61–65 A clear advantage is the direct combination with other NMR observables such as scalar couplings or NOE-derived distances as constraints.26,37,66 r-MD simulations have been used in combination with floating chirality protocols67,68 which allow the computation to directly lead to the best fitting configuration.69–71 A fundamental problem with all scalar procedures, however, is the approximation to a single alignment tensor in a molecular frame of reference, which per se is potentially a rough estimate. The obtained ensembles might fulfil experimental constraints, but at the same time not resemble the actually physically existing structural ensembles.
Molecular dynamics and Monte Carlo-type calculations have also been used in different ways to characterize intrinsically disordered proteins as a highly flexible class of molecules. The flexible meccano approach72 uses an unrestrained approach for generating a structural ensemble for which populations are refined using the prediction of an alignment tensor for each conformation, similar to the tramite approach;42 and finally the ϑ-method73–75 uses angles derived from RDCs as relative scalar constraints for the refinement of structures in the laboratory frame, where a principle of replica-averaging in the framework of the maximum entropy is used in line with a linear scaling factor to replace the alignment tensor.
In a radically different MD approach Sternberg et al.76–78 have proposed the analysis of anisotropic NMR properties, such as quadrupolar couplings, chemical shifts or dipolar couplings, by performing molecular dynamics with orientational constraints (MDOC). This method is based on tensorial constraints which individually have to fulfil the secular dipolar interaction Hamiltonian in the laboratory frame without the assumption of an overall order or alignment tensor. It has been originally applied to the analysis of 2H quadrupolar splitting in several membrane-bound peptides.79,80 In the present work we demonstrate on a number of molecules with different complexities how this procedure can be applied to the analysis of RDC data and the determination of relative configuration in small molecules. As the approach does not make any assumptions on the molecular shape or the corresponding overall alignment, it can equally be applied to any kind of molecule and lead to structural ensembles that fully comply with the experimental data as vibrational averaging and other conformational variabilities are included in the calculation.
2 Theory
In the following we will briefly review the MDOC methodology with an emphasis on the analysis of one bond 1DCH RDCs and special extensions to data originating from weakly aligned molecules. Due to its dependence on the relative orientation between the internuclear vector and the external magnetic field, the dipolar coupling between two nuclei i and j in the laboratory frame is expressed as a second rank symmetric tensor DL(i,j). In the laboratory frame, the z-axis is assumed to be parallel to the B0 external field, and at an arbitrarily chosen time point t0 the components of DL(i,j) in rad/s are of the form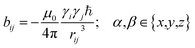 | (1) |
2.1 Averaged dipolar couplings
Experimental dipolar couplings are always an average of the different vibrational states, conformations, and orientations being populated during the course of the measurement. Restricting ourselves to dipolar couplings between directly bonded nuclei, we will neglect the stretching components of vibrations, as the corresponding changes in the bond length are very small and occur on the order of femtoseconds and can be taken care of by a stretching averaged distance rij. All other contributions lead to changes in orientation that will be treated in the following manner.The preferred dipolar coupling associated coordinate system is chosen in such a way that the new z′-axis points along the vector rij and the dipolar coupling tensor has a diagonal representation according to
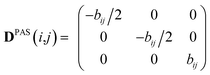 | (2) |
The tensorial components in this principal axis system (PAS) are transformed into the laboratory frame by a rotation matrix T(i,j). This transformation is expressed by a double sum over the components of the transformation matrix Tαβ (coupling sites i and j are omitted)
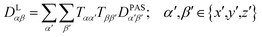 | (3) |
Due to rotational diffusion and other contributions, the orientation of the internuclear vector with respect to the external field changes with time and, therefore, the rotation matrix T becomes time dependent. In the case of partially aligned samples, where such rotations are dominated by rotational tumbling – that takes place on the order of the correlation time τc, i.e. picoseconds to nanoseconds – dipolar couplings are observed as significantly downscaled time averaged values called residual dipolar couplings (RDCs). Considering a rigid molecule, the averaging of the zz-component of the dipolar coupling tensor can be described by an overall order matrix, the so-called Saupe matrix or alignment tensor,81,82 according to
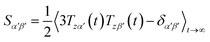 | (4) |
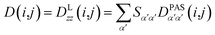 | (5) |
However, RDCs may be further averaged by conformational dynamics. Therefore, the products of the rotation matrix elements Tαα′Tββ′ contain valuable information not only about the global molecular rotational tumbling but also about the typically much slower internal motions. In this context it is of practical use to introduce local (segmental) order tensors S(i,j) for each coupling in the molecule with the components
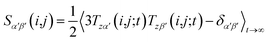 | (6) |
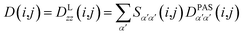 | (7) |
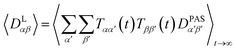 | (8) |
The MDOC method uses the whole coupling tensors 〈DLαβ(i,j)〉t averaged over the time span t of the MD trajectory as an approximation and utilizes them as restraints for calculating further transformation matrices at every MD step as described in the following sections.
2.2 Dipolar coupling tensor scaling
The approach derived in the previous sections could be used directly to simulate the time averaging of full residual dipolar coupling tensors of every spin pair i and j. However, experimental RDC data are obtained using the so-called alignment media that scale down the dipolar coupling tensors by a factor of approximately 1000 in order to maintain chemical shift dispersion in the corresponding spectra. Apparently, for the majority of the time, the molecule of interest is isotropically averaged and only a small fraction contributes to the measured RDCs. This scaling of anisotropy may conveniently be described by the factor sexpAM. As the isotropic averaging can be neglected in the corresponding MDOC simulations, we can now introduce a scaling factor| 1 ≥ sAM ≥ sexpAM | (9) |
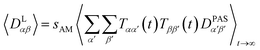 | (10) |
Note, however, that sAM should not be so low that experimental couplings are not attainable in the simulations. sAM should always be chosen a factor 2–10 higher than the largest component of an estimated Saupe matrix Sαβ to allow for both overall alignment of the assumedly rigid molecule and averaging of the alignment due to internal conformational changes.
2.3 Weighted time averaging
In simulations with constraints depending on the molecular orientations, the values of DL(i,j;t) are not relevant at every time step t and only their mean values obtained from molecular reorientations can be compared to experimental constraints. This is a general problem for all conformationally averaged NMR properties, such as NOE distance restraints or scalar couplings. Torda and van Gunsteren114,115 introduced the idea of averaging properties using an exponential decay function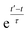 , allowing the system to “forget” past events and therefore be able to experience deviations from the instantaneous computed value to the average value. This technique, at first introduced for the averaging of NOE based distances, has been later extended to scalar coupling restraints83 and alignment-tensor-based scalar RDC constraints.61 Following this methodology, time averaged dipolar coupling tensors are given by
, allowing the system to “forget” past events and therefore be able to experience deviations from the instantaneous computed value to the average value. This technique, at first introduced for the averaging of NOE based distances, has been later extended to scalar coupling restraints83 and alignment-tensor-based scalar RDC constraints.61 Following this methodology, time averaged dipolar coupling tensors are given by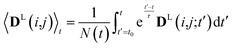 | (11) |
The introduction of the time average with exponential memory according to eqn (11) effectively introduces a new time scale for rotational reorientations and fluctuations. This time scale represents the lifetime of the orientation of the molecule or a mobile segment. The so-called memory time constant is denoted with τ and N is the norm of the integral. The memory time function ensures that contributions from past events are “forgotten” within the time averaging of D.
To further illustrate this point, an abstract system with two states A and B (representing for instance two conformers of the molecule) is considered, where in the NMR experiment the mean value of these two states is measured and used as a constraint. If the simple (arithmetic) time mean value is calculated and the system is half of the time in state A and the other half in state B, then the pseudo energy vanishes and an undefined time is needed before a difference between the constraint and calculated mean value builds up. The natural behaviour targeted in MD simulations is of a system jumping between different conformational states many times during the trajectory. In most cases, the conformational exchange has to surmount relatively large barriers and the transition events cannot be recorded in the course of standard MD procedures. Using eqn (11) we have merely to wait a time period on the order of the memory time τ until a difference between the constraint and time mean value develops and the pseudo forces can flip the system from A to B or vice versa. Therefore τ is the effective time scale of the accelerated MDOC simulation and we have to wait about 5τ before obtaining an ensemble average. Only in the case of very high barriers longer simulation times may be necessary. In practice, this can be tested by inspecting the time development of averaged dipolar couplings over a trajectory. If the average converges to a constant value, one can be certain that the overall simulation time is sufficient.
Since in conventional MD simulations the equations of motion are integrated in finite time steps Δt, the integral in eqn (11) is practically implemented as a discrete sum. During the MD simulation, the sum 〈DL(i,j)〉(m+1)Δt at time t = (m + 1)Δt is calculated from the previous time step 〈DL(i,j)〉mΔt in a recursive manner for each time step Δt according to
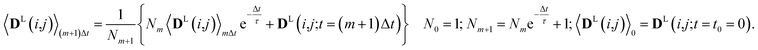 | (12) |
2.4 Pseudo energy
To carry out MD simulations driven by experimental constraints, pseudo energy terms are added to the molecular energy provided by the force field. These pseudo energies are defined as a function of the difference between the experimental and calculated tensor properties: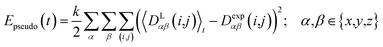 | (13) |
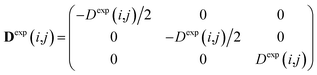 | (14) |
2.5 Pseudo forces
In MD simulations, the equations of motion are solved in a discrete step by step manner and pseudo forces F have to be calculated from the respective pseudo energy contributions. They are obtained as derivatives of the energies with respect to the Cartesian coordinates of the atoms. In the case of orientational pseudo forces, we have to derive the transformation matrices T(i,j) with respect to the coordinates of the atoms that were used in their definition (for details see e.g. Sternberg et al.77). The transformation matrices are constructed from the unit vectors that define the actual orientation of the dipolar systems: the unit vector ez′ = e(i,j) points along the direction of the nuclei i and j (i.e. along the C–H bond direction) and two additional, arbitrarily defined vectors ex′ and ey′ perpendicular to ez′. The transformation matrices T(i,j;t) at time t is then constructed with the unit vectors being columns T = (ex′, ey′, ez′). The pseudo forces in the Cartesian directions x, y and z (denoted with the Greek index γ) are then given by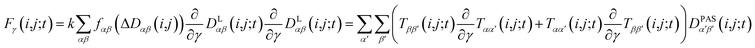 | (15) |
The calculation of the orientational pseudo forces is thus reduced to determining the derivatives of the elements of the transformation matrices T(i,j;t) with respect to the Cartesian coordinates of atoms i and j at time t. The direction of pseudo forces is calculated from the actual orientations of the dipolar i,j-system (e.g. a CH-vector), while the magnitude of pseudo forces depends on the difference between exponentially weighted 〈DLαβ(i,j)〉t and the corresponding experimental dipolar coupling tensor components Dexpαβ(i,j) as expressed by the function fαβ(ΔDαβ(i,j)).
2.6 Adapted pseudo force strength
In geometry optimization with NMR constraints, the standard harmonic form of the pseudo energy as given in eqn (13) is useful, especially if we are near the pseudo energy minimum. For the situation in MD simulations far from minima, however, the harmonic potential leads to rapidly growing forces and therefore to unrealistic structures and motions. These unrealistically large pseudo forces can be avoided by multiplying their values with a hyperbolic tangent weighting function, leading to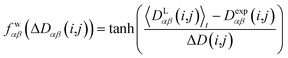 | (16) |
In this case, the width of the potential ΔD(i,j) is chosen ideally to be proportional to the estimated experimental error ΔDexp(i,j) derived from the coupling measurement, ΔD(i,j) ≈ ΔDexp(i,j). As long as the condition 〈DLαβ(i,j)〉t − Dexpαβ(i,j) < ΔD(i,j) is fulfilled, the function behaves similarly to the derivative of the original energy expression from eqn (13) divided by the experimental error, i.e. a linear dependence according to 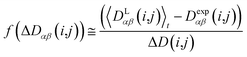 ; but it gives rise to nearly constant forces if 〈DLαβ(i,j)〉t − Dexpαβ(i,j) exceeds the threshold ΔD(i,j).76
; but it gives rise to nearly constant forces if 〈DLαβ(i,j)〉t − Dexpαβ(i,j) exceeds the threshold ΔD(i,j).76
The value of the pseudo force constant k is critical for the setup of successful MD simulations. Too big values may lead to unrealistic molecular motions, whereas too small values may result in insufficient sampling of the relevant conformations in reasonable computing times. A value of k = 10−4 kJ Hz−2 is usually a good starting compromise. The final pseudo force constants may vary between 10−3 and 10−5 kJ Hz−2, depending on the particular simulation. As long as the most favourable configurations do not exceed χ−2min values of 1 (eqn (21)), k should be increased to ensure proper sampling. Too high values for k can be identified by monitoring the temperature development during the course of an MDOC simulation: while a temperature rise can be tolerated as long as a dynamic equilibrium is reached, a steadily increasing temperature during the simulation is a clear sign of too large force constants.
Although dipolar couplings are downscaled with the scaling factor sAM, pseudo forces especially in the beginning of the MD simulation may become too strong. The molecules could surmount high barriers that separate configurations or form conformers which do not occur at ambient temperatures. Therefore an additional function is introduced that starts with zero and asymptotically reaches a value of one controlled by an additional time constant ρ, resulting in an overall weighting function of the form.
| fαβ(ΔDαβ(i,j)) = (1 − e−t/ρ)fwαβ(ΔDαβ(i,j)). | (17) |
Typical values for ρ are on the order of 200 ps, which lead to sufficient initial damping over the time course of the memory decay time constant τ of a similar duration.
2.7 Treatment of methyl groups
In the case of freely rotating X-CH3 groups51 the averaging of the dipolar couplings of these groups is taken into account by computing the value for a virtual CH (vCH) vector pointing along the X–C rotation axis and then applying the resulting forces on the methyl carbon and its α-substituent X using the relation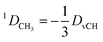 | (18) |
3 Materials and methods
3.1 NMR spectroscopy
Four example molecules with different properties have been chosen to demonstrate the capabilities of the MDOC simulations with respect to prochiral assignment, conformation, and determination of the relative configuration (see Fig. 1): norcamphor 1 and a synthetic spiroindene derivative 2 as rigid systems, staurosporine 3 as an example for a molecule with several potential conformations, and oidiolactone B 4 as a molecule with inherent flexibility on the NMR time-scale. The RDC data for compound 1 aligned in PEOMMA/TFE,19 compound 2 aligned in CDCl3/PDMS,8 and compound 3 aligned in dPS/CDCl310 were taken from the literature. Oidiolactone B (4) was aligned in polyacrylonitrile/DMSO-d6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 using a rubber-based stretching device.84,85 The assignment of 1H and 13C chemical shifts as well as the measured proton–proton scalar couplings are provided as the ESI.† Note that the assignment and RDC data for oidiolactone B are given using the carbon numbering shown in Fig. 1. The known absolute stereochemistry of oidiolactone B is 5S7R8R9S13S. All dipolar couplings are defined as the difference D = T − J between the measured splittings under aligned and isotropic conditions. Both 1TCH and 1JCH couplings for 4 have been obtained from CLIP-HSQC experiments86 in a stretched gel and in pure isotropic DMSO-d6, respectively.
16 using a rubber-based stretching device.84,85 The assignment of 1H and 13C chemical shifts as well as the measured proton–proton scalar couplings are provided as the ESI.† Note that the assignment and RDC data for oidiolactone B are given using the carbon numbering shown in Fig. 1. The known absolute stereochemistry of oidiolactone B is 5S7R8R9S13S. All dipolar couplings are defined as the difference D = T − J between the measured splittings under aligned and isotropic conditions. Both 1TCH and 1JCH couplings for 4 have been obtained from CLIP-HSQC experiments86 in a stretched gel and in pure isotropic DMSO-d6, respectively.
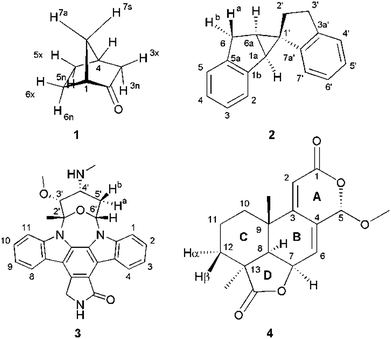 | ||
| Fig. 1 Structure and numbering of the four test molecules: norcamphor (1), a synthetic spiroindene derivative (2), staurosporine (3) and oidiolactone B (4). | ||
3.2 Molecular dynamics simulations
MDOC simulations were performed using the COSMOS 6.0 implementation of the COSMOS-NMR force field.87,88 Atomic partial charges are recomputed every 2 fs by using bond polarization theory (BPT).89,90 For the more rigid systems norcamphor 1 and spiroindene 2, 10 ns MDOC simulations were employed whereas for the more flexible staurosporine 3 and oidiolactone B 4 longer MDOC simulations of 20 ns were necessary to reach equilibrium. One bond C–H distances in norcamphor and spiroindene were fixed using the SHAKE algorithm,91 which allowed an integration time step of up to 2 fs. A memory decay time constant τ of 200 ps was employed in all cases. A force reaction time ρ for the uprising of the pseudo forces was set to 200 ps. The optimal values for the pseudo force constant k and the scaling factor sAM change from system to system and have been subjected to optimization. In the case of the force constant k we increased its value successively until the best configurations fulfilled experimental constraints within errors and checked at random that only physically meaningful structures were obtained. Also the optimization of the scaling factor sAM is crucial for the outcome of the simulations as it determines the maximum difference ΔDαβ at any given time t. A large factor sAM will increase the effective pseudo forces similar to the force constant k, so the interdependence of the two factors must be taken into account. But even if the product k sAM is kept constant, the size of the scaling factor has a strong influence on the populated conformations. If sAM is too large, ΔDαβ can be on the order of kHz, so that small deviations of RDCs of a few Hz are easily compensated by very small angular changes of e.g. 1° and below. As a result, essentially a single major conformation is populated with only slight vibration-like variations in individual bonds that cannot fulfil all experimental constraints. Too small factors sAM < sexpAM, on the other hand, have a similar effect as the largest experimental constraints can never be attained and the corresponding bond vector will essentially be fixed along the z-axis. The best results are obtained for scaling factors on the order of 2–10 times sexpAM, where the latter can be estimated by the largest component of an approximate Saupe matrix Sαβ, as mentioned above. As a rule of thumb, also the largest absolute value of experimental RDCs can be used as a good initial estimate: the largest values of approximately 10, 20, and 30 Hz showed good performance with sAM values of 0.001, 0.002, and 0.003, respectively.The simulations were performed in the NVT ensemble with the temperature typically being set to 300 K and controlled via a proper thermostat.92
3.3 Data interpretation
All reported averaged properties are computed by discarding the first nanosecond of the MD simulations. The fit of computed dipolar couplings to the experimental ones is expressed by two overall quality criteria that turn out to be very useful for the evaluation of how far the structural models are consistent with the experimental data. Both criteria are based on χ2, a well-known quantity that reliably describes the difference of calculated vs. experimental data with respect to the error of the experiment. For each coupling between spins i and j, a corresponding individual criterion can be formulated according to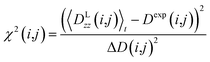 | (19) |
The first overall quality criterion we use to describe the overall fit with the experimental data is the inverse normalized χ2 factor27
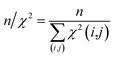 | (20) |
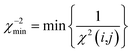 | (21) |
Only if this criterion is equal to or greater than 1, the structure fulfils all experimental data within the given error. We also give the number of outliers, i.e. the number of spin pairs with 1/χ2(i,j) < 1 that violate the structure, as an additional parameter for the evaluation of a particular structure within parentheses.
4 Results and discussion
In the current work we have evaluated the performance and capabilities of molecular dynamics with orientational constraints (MDOC) simulations as implemented in COSMOS 6.0 to assign the relative configuration of stereogenic and prochiral centres in small organic molecules. We have selected a set of four compounds with varying degrees of conformational mobility, starting from a rigid skeleton through semi-rigid cases to fully flexible systems in fast exchange (Fig. 1). In the following, the MDOC setup and results for the different cases are given in detail and discussed, including the corresponding standard alignment tensor analyses.4.1 Conformationally rigid systems: norcamphor
The bridged ring system of norcamphor 1 is an example molecule with an assumedly rigid skeleton. All possible 1DCH values of 1 in a PEOMMA/TFE gel have been measured using a CLIP-HSQC experiment19,86 (see Table 1). Thus previously reported experimental RDCs define a complete set of independent RDCs for a thorough RDC data evaluation.| Sites | Experiment | Expt. Err. | MDOC | SVD |
|---|---|---|---|---|
| D exp /Hz | ΔDb/Hz | 〈DLzz〉tc/Hz | D calc /Hz | |
| a Experimental values for 1DCH residual dipolar couplings. b Corresponding experimental maximum error estimates,93 corresponding to roughly three times the standard deviation. c Time averaged computed RDCs from the MDOC trajectory using the correct assignment. d Back calculated RDCs using the SVD-based alignment tensor approach implemented in the program MSpin52 and the correct assignment. | ||||
| C1H1 | 1.4 | 0.5 | 1.4 | 0.8 |
| C3H3x | 6.0 | 0.7 | 5.6 | 5.9 |
| C3H3n | 5.0 | 0.7 | 4.6 | 5.8 |
| C4H4 | −2.9 | 0.3 | −2.8 | −2.3 |
| C5H5x | −10.5 | 0.5 | −10.0 | −10.6 |
| C5H5n | 5.3 | 0.5 | 5.3 | 5.0 |
| C6H6x | −1.9 | 0.5 | −2.1 | −1.9 |
| C6H6n | 1.5 | 0.2 | 1.4 | 1.0 |
| C7H7s | 5.8 | 0.2 | 5.7 | 5.8 |
| C7H7a | −7.1 | 0.2 | −6.9 | −7.0 |
The conformationally stable structure of norcamphor allows to establish a basic protocol and to evaluate the performance of the method without significant complications and ambiguities arising from conformational averaging of the RDC data. It will also allow the determination of the influence of vibrational averaging and how far MDOC computations can be used to create an ensemble of conformers that fulfil the experimental data. Norcamphor has ten C–H vectors, where eight are part of four methylene groups, out of which three are having diastereotopic endo-/exo-positions and one a syn-/anti-position (Fig. 1, Table 1). The assignment of the endo-/exo- and syn-/anti-positions can be unambiguously achieved based on scalar coupling and NOE data. However, for the evaluation of MDOC simulations, we also have performed the prochiral assignment by means of analysis via1DCH RDCs.
As a first step, a starting geometry of 1 was optimized at the AM1 level of theory,94 from which an input file for COSMOS was built containing the molecular geometry and connectivities, along with atom definitions, dipolar coupling data and control keywords (see the ESI†). The aliphatic C–H bond distances were fixed to 1.093 Å, the default value for the corresponding tensorial COSMOS force field, using the SHAKE algorithm.91 Additionally, all distances from each methylene proton to the respective β-carbons and the methylene interproton distances were fixed during the MDOC simulation.
We then started MDOC simulations with ten tensorial constraints from the experimental 1DCH couplings, varying the pseudo force strength k and the scaling factor sAM. Good conditions, as judged by the introduced quality criteria and the equilibration of the trajectory, were obtained for k = 6 × 10−4 kJ Hz−2 and sAM = 10−3.
In the MDOC simulation with the correct prochiral assignment, all the computed dipolar couplings converged to the experimental values within the error limits (see Table 1). A closer look at the time evolution of the corresponding DLzz(i,j) values reveals that convergence is reached in a time interval of approximately 250 ps, i.e. slightly longer than the time period ρ = 200 ps for the uprising of the pseudo forces (Fig. 2A). After convergence is reached, only small fluctuations of the computed RDC values are visible. The effect can also be seen in the overall quality criterion n/χ2 over the course of the trajectory as shown in Fig. 2B. A plateau value for the quality criterion above 1 is found after ca. 150 ps of the MD simulations, indicating averaged orientations that potentially fulfil the experimental constraints as soon as the corresponding pseudo forces are active. To be on the safe side, we decided in the following to just use converged time steps for subsequent structure analysis by discarding the first nanosecond of the trajectory. The resulting averaged plateau value for n/χ2 is 3.314 (Table 2 and the dashed line in Fig. 2B).
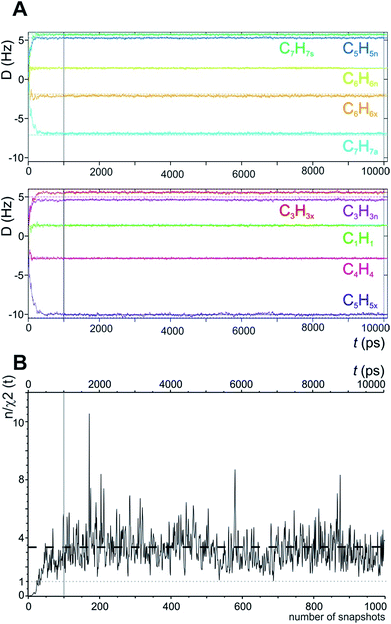 | ||
| Fig. 2 (A) Time course of individual simulated RDC values during the 10 ns MDOC simulation of norcamphor. The individual RDCs are assigned and colour coded with the experimental values given as horizontal dotted lines. Shortly after the start of the MDOC simulation, i.e. after approximately 250 ps, all 1DCH values fluctuate within or near the corresponding error ranges. (B) Evolution of the quality criterion n/χ2 over the MDOC simulation of norcamphor using the correct assignment: After 500 ps for every snapshot with weighted time averaging according to eqn (10), n/χ2 is always larger than 1 (grey dotted line). The dashed horizontal line shows the final value of the quality criterion (3.314). The first nanosecond is needed for building up the correct orientational and structural averaging and is left out from the final analysis (vertical solid lines in A and B). | ||
| Swapa | MDOC | SVD | ||
|---|---|---|---|---|
| n/χ2b | χ −2min | n/χ2d | χ −2min | |
| a Carbon position at which the assignment of two methylene protons is exchanged relative to the correct assignment. b Initial overall quality criterion applied to the MDOC simulations. c Strict overall quality criterion for the MDOC run, the number of outliers is given within brackets. d Corresponding overall quality criterion computed from the MSpin alignment tensor results. e Corresponding strict overall criterion for MSpin results. | ||||
| 3.314 | 1.160 (0) | 0.671 | 0.137 (4) | |
| X3 | 2.700 | 0.828 (1) | 1.017 | 0.207 (3) |
| X5 | 0.017 | 0.002 (7) | 0.008 | 0.003 (10) |
| X6 | 0.937 | 0.119 (1) | 0.190 | 0.034 (6) |
| X7 | 0.004 | 0.001 (5) | 0.005 | 0.001 (8) |
For a first demonstration of the capabilities of MDOC in structural analysis, we had a closer look at the potential to determine the prochiral assignment within methylene groups. Ample examples have been reported previously that prochiral assignments can be achieved using 1DCH couplings in alignment tensor calculations as long as the two methylene RDCs differ sufficiently.95,96 A straightforward method is the comparison of quality criteria for the two possibilities of the prochiral assignment. There are four methylene groups in norcamphor, so we constructed four additional data sets by swapping the two 1DCH values of a single methylene group in each set. We refer to the data sets as X3, X5, X6, and X7 for the C3, C5, C6, and C7 prochiral carbons, for which the assignment of attached protons has been exchanged. An MDOC simulation was performed for each of these data sets using the already optimized parameters. As can be seen in Table 2, only the MDOC simulations corresponding to the correct assignment and the swapping at position C3 (X3) fulfil the quality criterion n/χ2 > 1, whereas in all other cases the prochiral assignment can be excluded. The weak discrimination in the case of the C3 carbon, on the other hand, is expected since the two 1DCH couplings (C3H3x and C3H3n) present close values. The strict χ−2min criterion exhibits a slightly improved discrimination as it reveals a better fit of the correct structure while one outlier is detected for the X3 assignment (see Tables 1 and 2).
For a fair comparison with state-of-the-art techniques, the different data sets were also fitted to a single MMFF94 (ref. 97) optimized geometry using the well-established SVD-based alignment tensor approach as implemented in MSpin.52 The averaged back calculated RDCs for the correct assignment are listed in Table 1 next to the MDOC-derived RDCs. An n/χ2 value of 0.671 from the back calculated values and a condition number in the SVD decomposition of 2.72 are obtained, indicating that the order tensor could be confidently calculated from the data set. The MSpin-fitted data generally correlate very well with the experimental data, but a closer look also reveals that four RDCs are clearly outside the error range of the experiment. The outliers imply that the structural model does not completely fulfil the experimental data. Apparently, the experimental RDC values cannot be obtained with the computed conformation, which leads to the conclusion that either the static structural model on the MMFF94 level is incorrect, or, more likely, the significant deviations result from missing vibrational averaging and are therefore inherent to the static method. Regarding the determination of the prochiral assignment, the alignment tensor approach implemented in MSpin equally works in discarding the assignments X5, X6, and X7. Interestingly, the n/χ2 and χ−2min values slightly favour the wrong assignment X3 (1.067 and 0.207 using MSpin) over the correct assignment (0.671 and 0.137, respectively).
4.2 Conformationally rigid systems: a spiroindene derivative
A second test on the ability of the COSMOS implementation of MDOC to discriminate between diastereoisomeric structures is performed on spiroindene 2 (Fig. 1). The configuration of the molecule, according to X-ray analysis,98 has been determined to be 1S1aS6aR, which corresponds to configuration 2b (Fig. 3). A previous RDC analysis of 2 using 1DCH couplings obtained in a stretched cross linked poly(dimethylsiloxane)/CDCl3 gel resulted in data that could be fitted well using the SVD-fitting procedure as well as the steric prediction method implemented in PALES.45 A good discrimination between 2a (1R1aS6aR) and its diastereoisomer 2b was observed.85 In the following we use this well-studied test case to evaluate the ability of the MDOC simulations to discriminate the diastereoisomers 2a and 2b.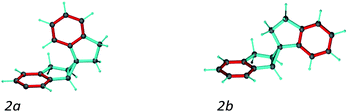 | ||
| Fig. 3 Spiroindene with the incorrect (2a) and correct (2b) relative configurations used in the MDOC simulations. | ||
As in the norcamphor case, the distances between methylene protons and their respective β-carbons were fixed with the SHAKE algorithm. Equally, all C–H vectors were fixed to the COSMOS standard distances for 1DCH couplings. The first MDOC test runs showed that the influence of the orientational pseudo-forces on the tetrahedral geometry of the quaternary carbon in the cyclopropyl ring cannot be compensated by the standard force field implemented in COSMOS. As a result, unphysically flattened structures appeared, followed by a drastic increase in temperature and premature ending of the MDOC simulations without convergence. To circumvent this problem and preserve the tetrahedral geometry, we fixed the distances between the pairs of carbons next to the quaternary spiro-carbon using SHAKE. With these additional distance constraints, the geometries of both 2a and 2b were well maintained during all MDOC simulations. Optimization of the pseudo forces and scaling factor led to k = 4.5 × 10−5 kJ Hz−2 and sAM = 2 × 10−3, which were used for the final MDOC simulations of the two possible relative configurations.
The spiroindene experimental data as shown in Table 3 contain RDC values within a range of 10 Hz (−3.5 to 6.4 Hz) and relatively large experimental errors (1.0 to 2.0 Hz). Since the individual experimental error values are used within the MDOC simulations to determine the width of the potentials for the constraints, it could be expected that the discrimination of the diastereoisomers will be less pronounced as with the alignment tensor approach using a single rigid structure. Nevertheless, as can be seen in Table 3, the averaged calculated RDC values during the MDOC simulation for the correct diastereoisomer very well reproduce the experimental ones and the comparison of the final n/χ2 values of 0.268 for 2a and 11.280 for 2b allows a clear differentiation between the diastereomers and the presence of 7 outliers for 2a and no outliers for 2b leave no doubt about the correct relative configuration. For completeness, we repeated a previously published SVD-based alignment tensor analysis with the program MSpin,52 which essentially led to identical results as previously published. It should be noted that the impact of the vibrational averaging in the analysis can safely be neglected as the large relative experimental errors of up to 30% in the experimental data render it irrelevant (Table 4).
| Sites | Experiment | MDOC | SVD | |
|---|---|---|---|---|
| D exp /Hz | ΔDb/Hz | 〈DLzz〉tc/Hz | D calc /Hz | |
| a Experimental values for 1DCH residual dipolar couplings. b Corresponding experimental error estimates.93 c Time averaged computed RDCs from the MDOC trajectory using the correct assignment. d Back calculated RDCs using the SVD-based alignment tensor approach implemented in the program MSpin52 and the correct assignment. | ||||
| C2H2 | −2.2 | 1.0 | −1.8 | −2.2 |
| C3H3 | −0.3 | 1.0 | −0.2 | 0.2 |
| C4H4 | 4.9 | 1.0 | 4.9 | 5.5 |
| C5H5 | −2.1 | 2.0 | −1.8 | −2.3 |
| C1aH1a | −2.0 | 2.0 | −2.1 | −2.0 |
| C6Ha6 | −1.9 | 1.0 | −2.3 | −2.1 |
| C6Hb6 | −3.5 | 1.0 | −3.0 | −3.0 |
| C6aH6a | −0.2 | 2.0 | −0.2 | −1.4 |
| C4′H4′ | −1.7 | 1.0 | −1.3 | −1.4 |
| C5′H5′ | 6.4 | 1.5 | 5.8 | 5.6 |
| C6′H6′ | −1.3 | 1.0 | −0.8 | −0.4 |
| C7′H7′ | −1.1 | 2.0 | −1.3 | −1.4 |
| Config. | MDOC | SVD | ||
|---|---|---|---|---|
| n/χ2a | χ −2min | n/χ2c | χ −2min | |
| a Overall MDOC quality criterion. b Strict overall quality criterion for the MDOC simulation; the number of outliers is given within brackets. c Same overall quality criterion computed from the MSpin alignment tensor results. d Same strict overall criterion for MSpin results. | ||||
| 2a | 0.268 | 0.047 (7) | 0.178 | 0.035 (8) |
| 2b | 11.280 | 4.623 (0) | 5.276 | 1.678 (0) |
4.3 Conformational variability: staurosporine
The next well-studied model molecule, this time with four stereogenic centres and conformational freedom in a six-membered ring, is staurosporine 3 (Fig. 1). Staurosporine is a protein kinase inhibitor isolated from Streptomyces staurosporeus. Its absolute configuration has been determined by single crystal X-ray analysis of its N-methyl iodide derivative to be 2′S3′R4′R6′R.991DCH RDCs have been measured for staurosporine aligned in stretched perdeuterated polystyrene/CDCl3 gels.10 In its analysis the authors have shown that next to the stereochemistry two possible conformational states for the six-membered ring, chair and boat, have to be considered as well. An SVD-based fit of RDCs showed the best correlation with the chair conformation.10For the MDOC simulations, the geometry of the correct configuration was initially optimized using the MM2 force field (Chemdraw 3D, Cambridge Software). Then, as in the previous examples, the distances between methylene protons and their respective β-carbons were fixed with the SHAKE algorithm and all C–H vectors were fixed to the COSMOS standard distances for 1DCH couplings. The pseudo force constant and the scaling factor were optimized for the molecule to k = 2 × 10−3 kJ Hz−2 and sAM = 1 × 10−3, respectively. For a conformational search and for input in the SVD-based alignment tensor approach in MSpin, all low-energy geometries for the different combinations of configurations and conformations were optimized at the DFT BP86 level.
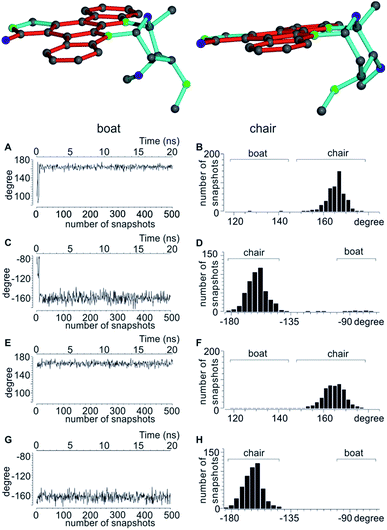
In accordance to previous RDC analysis we evaluated all possible relative configurations on the 2′, 3′, 4′ and 6′ stereogenic centres taking into account both conformations (chair and boat) in every case. Using the program Avogadro, all structural isomers were produced and geometry optimized. For visualization, the boat and chair conformations for the correct configuration are shown in Fig. 4. As the nomenclature for the various configurations of 3, a simple stereogenic descriptor in the order of the numbering is given, such that the SRRR configuration of the six-membered ring corresponds to the correct configuration 2′S3′R4′R6′R. The conformation of the six-membered ring is abbreviated with either b for boat or c for chair.
As shown in Table 5, both MDOC and MSpin derived RDCs correlate well with the experiment. MSpin, using rigid structures and essentially five RDCs for defining the six-membered ring with the four stereogenic centres as input, can clearly distinguish SRRRc as the best structural model. SRSRc as the second best fitting structure still achieves an n/χ2 > 1, but it shows also three outliers as compared to only one for the correct structure and can be excluded therefore (Table 6). Again, most likely due to missing vibrational averaging in the static approach, even the correct structure cannot fully represent all RDCs within their relatively large experimental errors. Using MDOC, the five one-bond RDCs with relatively large error ranges are barely sufficient to define the flexible ring. They leave a large conformationally unrestricted space that will be entirely used to fulfil the averaged RDCs. Considering this freedom in conformational space, we were positively surprised that the MDOC simulations still show a fair discrimination capability between the trial configurations. The correct configuration and chair conformation SRRRc has a total n/χ2 value of 4.139, and the closest competitor, the SRSR stereoisomer with the boat conformation, has a total n/χ2 of 2.657, not allowing any discrimination per se. However, only the correct structure fulfils all constraints, while SRSRb displays a χ−2min of 0.481, i.e. not all experimental RDCs are fulfilled within the error range. Equally, for all other structures at least one outlier is observed and the corresponding χ−2min values are even smaller. It can be concluded that despite the much larger molecular flexibility inherent to the MDOC approach compared to the discrete conformational SVD-based fit, the correct configuration can still be distinguished from the incorrect ones.
| Sites | Experiment | MDOC | SVD | |
|---|---|---|---|---|
| D exp /Hz | ΔDb/Hz | 〈DLzz〉tc/Hz | D calc /Hz | |
| a Experimental values for 1DCH residual dipolar couplings. b Corresponding experimental maximum error estimates derived as described in ref. 93. c Time averaged computed RDCs from the MDOC trajectory using the correct configuration and chair conformation. d Back calculated RDCs using the SVD-based alignment tensor approach implemented in the program MSpin using the correct configuration and chair conformation. | ||||
| C2′CH3 | −3.2 | 1.0 | −2.7 | −2.7 |
| C3′H3′ | −19.8 | 5.0 | −15.0 | −20.8 |
| C4′H4′ | −3.7 | 1.0 | −3.7 | −4.2 |
| C5′H5′a | 7.5 | 3.2 | 7.4 | 7.4 |
| C6′H6′ | 5.8 | 1.1 | 5.1 | 5.7 |
| C1H1 | −27.2 | 2.5 | −25.8 | −27.8 |
| C2H2 | −11.1 | 7.6 | −8.4 | −10.6 |
| C3H3 | 1.7 | 4.2 | 1.2 | 0.6 |
| C4H4 | −27.1 | 1.0 | −26.5 | −27.1 |
| C8H8 | −25.3 | 1.0 | −24.8 | −25.1 |
| C9H9 | −12.9 | 5.4 | −10.9 | −13.5 |
| C10H10 | 2.6 | 3.6 | 2.2 | 2.6 |
| C11H11 | −25.4 | 1.1 | −24.8 | −24.0 |
| Config.a | MDOC | SVD | ||
|---|---|---|---|---|
| n/χ2b | χ −2min | n/χ2d | χ −2min | |
| a Indicates the different configurations, where the order of the labelling for the stereogenic centres is kept according to 2′, 3′, 4′ and 6′; b and c indicate boat or chair starting conformations of the flexible ring. b Overall MDOC quality criterion. c Strict overall quality criterion for the MDOC simulation; the number of outliers is given within brackets. d Same overall quality criterion computed from the MSpin alignment tensor results. e Same strict criterion for MSpin results. f Boat conformation changes to mainly chair conformation during the MDOC simulation. | ||||
| SRRRb | 3.344f | 0.905 (1)f | 0.108 | 0.014 (8) |
| SRRRc | 4.139 | 1.074 (0) | 5.392 | 0.617 (1) |
| SRSRb | 2.657f | 0.481 (1)f | 0.049 | 0.004 (5) |
| SRSRc | 2.469 | 0.446 (1) | 1.377 | 0.160 (3) |
| SSRRb | 2.454f | 0.374 (1)f | 0.032 | 0.005 (10) |
| SSRRc | 1.573 | 0.184 (2) | 0.118 | 0.014 (7) |
| SSSRb | 1.601f | 0.220 (2)f | 0.116 | 0.017 (8) |
| SSSRc | 1.575 | 0.219 (2) | 0.085 | 0.023 (10) |
A significant difference of the MDOC simulations compared to the MSpin single structure fits is the lack of distinction of different starting conformers, as all stereoisomers show very similar overall quality criteria for the two different starting conformers. The reason becomes clear when we look at Fig. 4, where two torsion angles representative of the boat and chair conformations are observed over the course of the trajectory for the SRRRb and SRRRc starting structures: after less than 1 ns the boat conformation flips into the chair conformation, where it stays for most of the rest of the simulation. Because of the change into the preferred chair conformation, the MDOC simulation with the SRRRb starting structure is practically indistinguishable from the one starting with SRRRc, as the MDOC calculations for the two starting conformations evaluated in Table 6 essentially contain the same conformational distribution as long as the initial 1 ns is discarded. It is therefore a good example for demonstrating that the MDOC procedure can induce strong enough pseudo forces to overcome the relatively high energy barriers associated with ring pseudo rotations, and thus to drive the molecule into its preferred conformations that best fulfil RDC constraints. Similar to the configuration shown, the starting boat conformations of the other stereoisomers always undergo a transition to the preferred chair conformations in the corresponding MDOC simulations.
4.4 Conformational flexibility: oidolactone B
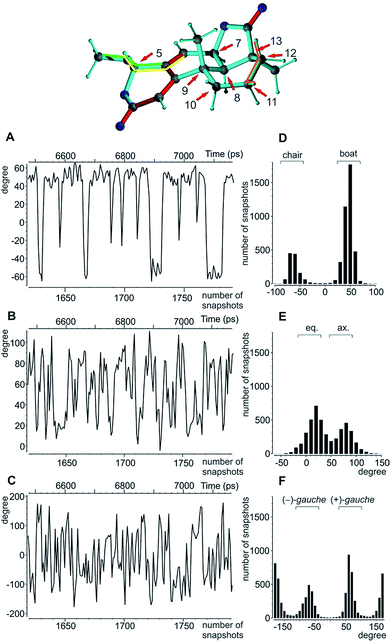
A real life example for the MDOC analysis with an apparent degree of flexibility is oidiolactone B (4). The mould isolated compound100,101 shows activity against human fungal infections and cancer cell lines.102 The absolute configuration of its five stereogenic centres has been established as 5S7R8R9S13S (Fig. 1) via total synthesis and X-ray analysis.103 In the following, configurations are defined by the stereogenic descriptor in the order of the numbering, i.e. the correct configuration is given as SRRSS. It should be noted that methylene protons of 4 are labelled α, when they are situated behind the plain, while β labels indicate protons in front of the paper plain as shown in Fig. 1.Conformational flexibility within this molecule may arise from pseudo rotation of the six-membered saturated and lactone rings (rings C and A), as well as the rotation of the methoxy group. MMFF94 conformational analysis showed the boat and chair forms of ring C to be energetically very close (ΔE ≈ 0.2 kcal mol−1). The vicinal scalar coupling values of ca. 7 Hz measured for the protons in the six-membered ring C (see the ESI† for more information) clearly show that averaging between different ring conformations takes place in solution. In addition, some of the cross peaks from the NOESY spectra can only be explained by the presence of a boat-type conformation for the saturated six-membered ring C (see the top of Fig. 5 and 6). Experimental information on ring A is more limited, as only the relatively isolated protons H2 and H5 and the methoxy group are accessible and no defined evidence for the averaging behaviour is available. An NOE contact between the methyl group CH3-9 and H5 indicates that the pseudo-equatorial position of the methoxy group should be significantly populated (see the ESI†). Only pseudo-equatorial O–Me conformations were found in the conformational search for the correct SRRSS configuration in a large 5.0 kcal mol−1 energy window using the MMFF94 force field. Hence the molecular modelling procedure associated with the single tensor SVD approach discards a priori any pseudo-axial structures. Note that the universal force field (UFF)104 favours a pseudo-axial conformation and DFT M062X supports the pseudo-equatorial conformation, but only with an energy gap ΔE = 1.8 kcal mol−1. In addition, a close look at the possible conformations of the methyl group in the methoxy moiety reveals that the pseudo-axial conformation implies an almost free rotation about the C5–O axis, while the rotation is severely hindered in the pseudo-equatorial conformer. Therefore a potential entropic contribution favouring the pseudo-axial orientation must be taken into account. In summary, the exact distribution of populations of the different conformers of ring A and the methoxy group are not defined, but it will be likely dominated by a pseudo-equatorial O–Me conformation.
Using the program MSpin, initially a single tensor fitting has been performed for the single lowest energy conformation (see Table 8). In this case, only a poor quality of the fit is achieved (n/χ2 = 0.091) with 10 RDCs being outside the experimental uncertainty, which proves that conformational averaging is present and the corresponding data cannot be represented by a single conformer. Using the full set of four conformers found in the MMFF94 search, the overall fit to experimental RDCs improved dramatically with an overall value of n/χ2 = 1.543 for the best structural ensemble. However, a χ−2min value of 0.444 and 3 outliers still violating the experimental data are present, indicating that averaging over additional conformers is necessary. The distribution of the boat vs. chair conformation in ring C from the multiple conformer/single tensor fit is ca. 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which differs from the MMFF94-predicted distribution of approximately 3
1, which differs from the MMFF94-predicted distribution of approximately 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. As the selected conformations possess the pseudo-equatorial conformation at the methoxy group, ring A has essentially been treated as rigid.
1. As the selected conformations possess the pseudo-equatorial conformation at the methoxy group, ring A has essentially been treated as rigid.
For MDOC calculations, again, the distances between methylene protons and their respective β-carbons were fixed with the SHAKE algorithm and all C–H vectors were fixed to the COSMOS standard distances for 1DCH couplings. The pseudo force constant and the scaling factor were optimized for the molecule to k = 1.2 10−3 kJ Hz−2 and sAM = 0.002, respectively.
The MDOC simulations for the correct SRRSS configuration lead to RDC values which perfectly agree with the experimentally determined values within the experimental uncertainty (see Table 7). A detailed examination of the obtained structural ensembles based on dihedral angles reveals that continuous jumps between different populated conformers occur. Even relatively low pseudo forces can trigger the boat/chair transition, and therefore allow the proper calculation of time averaged RDCs (Fig. 5A and D). A histogram analysis of the dihedral angle H11β-C11-C12-H12β shows the conformational jumps between chair (H11β-C11-C12-H12β < 0) and boat forms (H11β-C11-C12-H12β > 0). It is important to note that jumps take place very frequently within the memory time window τ, which ensures that proper time-averaged values are computed. Similarly, monitoring of the MeO-C5-C4-C6 dihedral angle (Fig. 5B and E) shows a distribution of pseudo-equatorial and pseudo-axial positions of the anomeric methoxy groups and frequent jumps between conformers. Monitoring of C4-C5-O-CH3 shows that all three angles corresponding to +/− gauche and trans are populated with a clear preference for +gauche and trans, reflecting a hindered rotation of the methoxy group in the pseudo-equatorial conformation. As the population of pseudo-axial and pseudo-equatorial conformers is not well-determined, we also performed MDOC simulations with ring A being fixed in the pseudo-equatorial conformation. The resulting structural ensembles equally fitted all experimental constraints within the experimental errors.
| Sites | Experiment | MDOC | SVD (single conf.) | SVD (mult. conf) | |
|---|---|---|---|---|---|
| D exp /Hz | ΔDb/Hz | 〈DLzz〉tc/Hz | D calc /Hz | D calc /Hz | |
| a Experimental values for 1DCH residual dipolar couplings. b Corresponding experimental maximum error estimates.93 c Time averaged computed RDCs from the MDOC trajectory using the correct assignment. d Back calculated RDCs using the single conformer single alignment tensor SVD procedure. e Back calculated RDCs using the multiple conformer single alignment tensor SVD procedure. | |||||
| C2H2 | −10.4 | 0.4 | −10.3 | −12.0 | −10.3 |
| C5H5 | 5.8 | 0.4 | 5.7 | 4.1 | 6.0 |
| C6H6 | −10.1 | 2.0 | −9.9 | −11.2 | −11.0 |
| C7H7 | −0.8 | 0.4 | −0.8 | −0.7 | −0.3 |
| C8H8 | 18.2 | 1.0 | 17.5 | 11.9 | 16.7 |
| CH3-9 | −4.7 | 1.0 | −4.5 | −3.1 | −4.1 |
| C10H10α | 15.6 | 1.5 | 14.3 | 14.7 | 16.9 |
| C10H10β | −1.3 | 1.0 | −1.7 | −4.0 | −2.3 |
| C11H11α | 0.5* | 2.5 | 0.3 | 4.9 | 0.7 |
| C11H11β | 0.8* | 2.5 | 1.8 | 1.0 | 1.2 |
| C12H12α | −0.3 | 1.0 | −0.2 | −4.2 | −0.8 |
| C12H12β | 10.3 | 1.5 | 9.6 | 11.9 | 9.1 |
| CH3-13 | 0.4 | 0.2 | 0.4 | 1.7 | 0.1 |
| CH3-5 | 2.8 | 0.4 | 2.8 | 1.5 | 2.7 |
Altogether sixteen diastereoisomers are possible for oidiolactone B and three methylene groups require diastereotopic assignment. Two of the stereogenic centres are part of the flexible saturated six-membered ring C and one is at the torsionally flexible methoxy group at C5. Conformational spaces were generated for all diastereoisomeric structures at the MMFF94 level. MDOC simulations were started from different conformers, but all simulations lead to basically identical results, indicating that in all cases the experimental constraints were the determining factor for the simulations.
When using the best diastereotopic assignment of CH2 groups, the single conformer SVD-based fit for the different configurations results in very low quality factors, indicating in principle the robustness of RDC data interpretation. Also a correct diastereotopic assignment is achieved at methylene groups C10 and C12 – only the almost identical RDCs for the two protons attached to C11 does not allow an unambiguous assignment. The multiple conformer/single tensor fit leads to a further improved distinction of the correct configuration despite the fact that none of the structures fulfils the experimental data within errors. The conformation at C5 in all MMFF94-derived structures is pseudo-equatorial and the corresponding fit to a single alignment tensor helps dramatically in defining all residual stereogenic centres as it fixes the orientation of the tensor axes (see Fig. 6A and B). Due to the restriction to a single alignment tensor and the negligence of vibrational motions, on the other hand, the ability to fully fit experimental data is strongly limited and must result in deviating RDCs. Importantly, the MDOC procedures do not suffer from a priori limitations on the selection of particular conformations, associated with the SVD method, although this has the disadvantage of a lower capability for discrimination of the configuration.
In the MDOC simulations the full accessible conformational space is taken into account, leaving no restriction with respect to the number of conformers or the number of alignment tensors being present. In principle, the approach may result in a different alignment tensor for each measured RDC. Again, all sixteen possible configurations of the molecule were compared for their performance using exclusively the fourteen 1DCH values as MDOC constraints. Based on the χ−2min value of the MDOC simulations, the most wrong configurations can be falsified, but a few configurations remain as potential competitors (Table 8). No constraints are violated for the correct stereochemistry (SRRSS) and the epimer at C5 (RRRSS). A detailed analysis of the structural ensembles reveals that both favour pseudo-equatorial conformations of the methoxy group, in which case the C5-H5 RDC will lead to identical values. However, as no single, common alignment tensor is used in the calculation, the RDC at C5 does not decisively influence the configuration determination in ring C. A change in the configuration at positions C7 and C9 both result in χ−2min values slightly below 0.9 with at least one outlier. Apparently, these configurations result in C–H vector orientations that are very similar to the correct structure if the full conformational space is accessible. Nevertheless, a difference larger than 0.4 in χ−2min clearly favours the correct configuration.
| Config.a | MDOC | χ −2min | SVD (single conf.) | SVD (mult. conf.) | SVD (single conf.) | SVD (mult. conf.) |
|---|---|---|---|---|---|---|
| n/χ2b | n/χ2d | χ −2min | n/χ2d | χ −2min | ||
| a Different diastereoisomers given in a five letter code and exchange of prochiral assignment by X and the carbon position. b Overall MDOC quality criterion. c Strict quality criterion for the MDOC simulation; the number of outliers is given within brackets. d Same overall quality criterion computed from the MSpin alignment tensor results. e Same strict criterion for MSpin results. f Configurations with an inversion of chirality at position C5 can be excluded from the NOE-derived distance between H5 and 9-CH3. | ||||||
| SRRSS | 6.788 | 1.314 (0) | 0.091 | 0.025 (10) | 1.543 | 0.444 (3) |
| RRRSS | 6.863 | 1.367 (0) | 0.022 | 0.002 (9) | 0.062 | 0.017 (10) |
| SSRSS | 2.596 | 0.882 (1) | 0.014 | 0.001 (10) | 0.013 | 0.001 (10) |
| SRSSS | 1.304 | 0.240 (3) | 0.013 | 0.001 (10) | 0.012 | 0.001 (8) |
| SRRRS | 4.598 | 0.866 (1) | 0.022 | 0.007 (13) | 0.053 | 0.005 (7) |
| SRRSR | 1.429 | 0.247 (2) | 0.012 | 0.002 (13) | 0.011 | 0.002 (12) |
| RSRSS | 2.526 | 0.918 (2) | 0.009 | 0.001 (13) | 0.014 | 0.014 (9) |
| RRSSS | 1.222 | 0.230 (3) | 0.007 | 0.001 (11) | 0.007 | 0.001 (11) |
| RRRRS | 4.914 | 0.939 (1) | 0.009 | 0.001 (13) | 0.047 | 0.006 (9) |
| RRRSR | 1.272 | 0.232 (2) | 0.007 | 0.002 (13) | 0.005 | 0.000 (12) |
| SSSSS | 1.478 | 0.220 (4) | 0.016 | 0.004 (13) | 0.013 | 0.002 (12) |
| SSRRS | 0.482 | 0.063 (4) | 0.021 | 0.004 (9) | 0.021 | 0.003 (10) |
| SSRSR | 1.021 | 0.160 (2) | 0.016 | 0.003 (13) | 0.015 | 0.002 (13) |
| SRSRS | 0.998 | 0.117 (4) | 0.024 | 0.006 (8) | 0.024 | 0.003 (12) |
| SRSSR | 0.597 | 0.099 (4) | 0.012 | 0.002 (11) | 0.012 | 0.002 (11) |
| SRRRR | 0.999 | 0.169 (2) | 0.017 | 0.003 (13) | 0.016 | 0.001 (11) |
| X10 | 1.544 | 0.158 (2) | 0.017 | 0.002 (11) | 0.018 | 0.003 (10) |
| X11 | 6.943 | 1.369 (0) | 0.094 | 0.026 (10) | 1.446 | 0.367 (2) |
| X12 | 5.087 | 0.891 (1) | 0.030 | 0.010 (12) | 0.118 | 0.012 (6) |
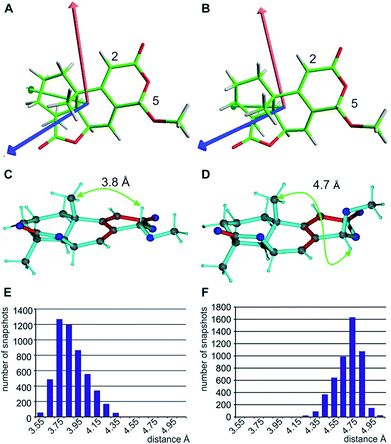
With respect to CH2 groups, the diastereotopic assignment with MDOC shows the same result as that with MSpin, allowing the correct assignment of methylene protons at C10 and C12, while the very similar RDCs for C11 lead to practically identical results for the two possible assignments. Finally, it should be noted that the RRRSS epimer cannot be excluded from one bond RDC data alone, but the structural ensemble from the corresponding MDOC simulations may be used to back calculate other experimentally accessible NMR parameters. Correspondingly, the distance distribution of H5 to the methyl group attached to C9 corresponds well to the measured NOE with an average distance of approximately 3.7 Å for the correct configuration, while the C5 epimer results in a distance distribution of around 4.7 Å (see Fig. 6C–F and annotation f in Table 8).
5 Conclusion and outlook
In summary, a novel way of using residual anisotropic NMR parameters as orientational constraints in molecular dynamics simulations (MDOC) is introduced using one-bond residual dipolar couplings (RDCs) as the most easily accessible spectroscopic quantity. In contrast to classical alignment tensor based methods, MDOC is entirely calculated in the laboratory frame, therefore avoiding issues with the treatment of flexibility where a common frame of reference for the alignment tensor is usually not accurately defined. A full description of the underlying theory is given, including rotational averaging, the tensorial force field, and the exponential decay of constraints over time. In the second part of the paper, the possibilities and limitations are explored for several example molecules with different degrees of flexibility.It should be noted that Salvi et al. recently pointed out that methods in the laboratory frame only relying on the projection onto the principal axis of alignment and magnetic field, the z-axis, do not allow sufficient angular sampling to produce valid structural ensembles.105 The MDOC method, however, is based on tensorial constraints and therefore provides angular sampling with respect to x-, y-, and z-axes as well as the combined xy, yx, xz, zx, yz, and zy components of the dipolar interaction of each coupled spin pair in the laboratory frame. As such, full angular sampling is provided and valid structural ensembles obtained.
During MDOC simulations, rotational averaging of each coupled spin pair is achieved individually via pseudo forces mainly originating from non-zero off-diagonal elements of the weighted time averaged dipolar coupling tensor. This directly allows the description of any kind of flexibility as MDOC will rapidly sample the locally available conformational ensemble that best fulfils the NMR parameters. For the correct structural model, the approach usually leads to a structural and orientational ensemble which matches all experimental constraints within the experimental error. If, on the other hand, a structure cannot simultaneously fulfil all experimental constraints, it can be safely neglected. A single “outlier”, i.e. a single NMR parameter that does not fulfil experimental data within experimental errors, is sufficient to discriminate or exclude structures. When the approach is applied to the determination of the relative configuration of small molecules, its advantage seems to be the straightforward usage and the avoidance of over interpretation of data as the full available conformational space is sampled. This conformational space per se includes structures of low-populated conformations as well as short and long amplitude vibrational contributions. In this way, MDOC simulations also include entropic contributions to the Gibbs free energy (Fig. 7). The MDOC approach, as mentioned above, practically always leads to a very good correspondence of the resulting structural ensemble with experimental constraints, as demonstrated here for a number of cases with known correct structures. On the other hand, the discrimination of configurations is potentially reduced compared to single alignment tensor models since the number of accessible conformers is significantly restricted in the latter. However, this discrimination capability of the SVD approach comes at the expense that even the correct configuration often cannot fulfil experimental constraints within errors, rendering the structural ensemble questionable for further calculations.
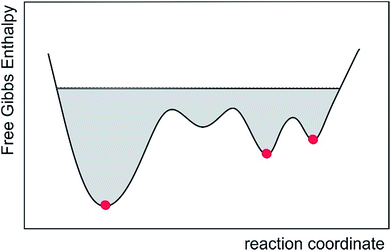
Vibrational contributions are not considered and high-energy conformations might be missed out. Even worse, in cases of large structural rearrangements, the single alignment tensor approximation will fail. This will be of particular interest if molecules with flexible chain-like elements,29 including e.g. intrinsically disordered proteins,106 are studied. To avoid such potential misinterpretation, the MDOC approach provides a physically sound and viable alternative as long as sufficient experimental constraints for the molecular dynamics simulations are available. Due to the orientational degeneracy of anisotropic parameters, sparsely conditioned MDOC simulations may lead also to wrong conformations included in a structural ensemble. While this only leads to reduced distinction of relative configurations, with the correct structure still among the allowed ones, the direct interpretation of a structural ensemble as physical reality might be compromised. This effect, however, is not inherent to the method, but depends solely on the number and quality of experimental constraints. As the number of 1DCH RDCs is usually restricted, we had to limit the application of the MDOC approach to molecules with local flexibility. In all example molecules studied here, the correct configuration could be identified with a structural ensemble that can be used to calculate further molecular properties. For the most flexible molecule under study, oidiolactone B, the fourteen one-bond RDCs alone were not sufficient to exclude the epimer at position C5, but back calculation of the average distance from the resulting structural ensembles and comparison with NOE data clearly excluded the wrong configuration. However, such distances can also be introduced as additional constraints in a molecular dynamics simulation. Even more, isotropic scalar J-couplings, by employing a variety of Karplus relationships,107 or anisotropic parameters such as long-range RDCs, residual quadrupolar couplings and residual chemical shift anisotropies should be applicable. RCSAs have been measured successfully using a variety of methods,108–110 and they should result in particularly valuable restraints in protonless spin systems as long as the corresponding CSA tensors can be estimated.111,112 We are currently working on the corresponding extensions of the COSMOS program. The aim for the future is therefore the inclusion of as many constraints to the MDOC approach as possible. We foresee that most organic molecules, including classes with substantial inherent flexibility, will be amenable to both configurational and conformational analyses using the combined power of experimentally derived anisotropic and isotropic NMR parameters as well as theoretically derived constraints.113
Conflicts of interest
U. S. has written the program COSMOS and was the co-founder of COSMOS-software, Jena, Germany.Abbreviations
| r-MD | Restrained molecular dynamics |
| MDOC | Molecular dynamics with orientational constraints |
| SVD | Singular value decomposition |
| RDC | Residual dipolar coupling |
Acknowledgements
All authors are indebted to Dr Sebastian Ehni (formerly KIT, now Carbogen Amcis, Hunzenschwil, Switzerland) who made most valuable contributions to the presented research. We also thank Dr Maria Enrica Di Pietro (KIT) for carefully correcting the manuscript. B. L. thanks the Fonds der Chemischen Industrie, the Deutsche Forschungsgemeinschaft (LU 835/11-1, project C3 of the SFB 1176, and instrumentation facility Pro2NMR), and the HGF programme BIFTM for financial resources. A. N. V. thanks the Karlsruhe Institute of Technology for a Gastdozenten fellowship. Part of this work was performed on the computational resource bwUniCluster funded by the Ministry of Science, Research and Arts and the Universities of the State of Baden-Württemberg, Germany, within the framework program bwHPC.References
- E. Troche-Pesqueira, C. Anklin, R. R. Gil and A. Navarro-Vazquez, Angew. Chem., Int. Ed., 2017, 56, 3660–3664 CrossRef CAS PubMed.
- Y. Liu, J. Sauri, E. Mevers, M. W. Peczuh, H. Hiemstra, J. Clardy, G. E. Martin and R. T. Williamson, Science, 2017, 356, eaam5349 CrossRef PubMed.
- G. Kummerlöwe and B. Luy, TrAC, Trends Anal. Chem., 2009, 28, 483–493 CrossRef.
- B. Böttcher and C. M. Thiele, in eMagRes, John Wiley & Sons, Ltd, 1st edn, 2007, DOI:10.1002/9780470034590.emrstm1194.
- R. R. Gil, C. Griesinger, A. Navarro-Vázquez and H. Sun, in Structure Elucidation in Organic Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, 2015, pp. 279–324, DOI:10.1002/9783527664610.ch8.
- P. Kaden, J. C. Freudenberger and B. Luy, Magn. Reson. Chem., 2012, 50, S22–S28 CrossRef CAS PubMed.
- C. Gayathri, N. V. Tsarevsky and R. R. Gil, Chem.–Eur. J., 2010, 16, 3622–3626 CrossRef CAS PubMed.
- J. C. Freudenberger, P. Spiteller, R. Bauer, H. Kessler and B. Luy, J. Am. Chem. Soc., 2004, 126, 14690–14691 CrossRef CAS PubMed.
- B. Luy, K. Kobzar and H. Kessler, Angew. Chem., Int. Ed., 2004, 43, 1092–1094 CrossRef CAS PubMed.
- G. Kummerlowe, S. Knör, A. O. Frank, T. Paululat, H. Kessler and B. Luy, Chem. Commun., 2008, 5722–5724 RSC.
- U. M. Reinscheid, J. Farjon, M. Radzom, P. Haberz, A. Zeeck, M. Blackledge and C. Griesinger, ChemBioChem, 2006, 7, 287–296 CrossRef CAS PubMed.
- J. C. Freudenberger, S. Knör, K. Kobzar, D. Heckmann, T. Paululat, H. Kessler and B. Luy, Angew. Chem., Int. Ed., 2005, 44, 423–426 CrossRef CAS PubMed.
- G. Kummerlöwe, M. Behl, A. Lendlein and B. Luy, Chem. Commun., 2010, 46, 8273–8275 RSC.
- W. Zong, G. W. Li, J. M. Cao, X. X. Lei, M. L. Hu, H. Sun, C. Griesinger and R. X. Tan, Angew. Chem., Int. Ed., 2016, 55, 3690–3693 CrossRef CAS PubMed.
- P. Haberz, J. Farjon and C. Griesinger, Angew. Chem., 2005, 117, 431–433 CrossRef.
- G. Kummerlowe, J. Auernheimer, A. Lendlein and B. Luy, J. Am. Chem. Soc., 2007, 129, 6080–6081 CrossRef PubMed.
- X. Lei, Z. Xu, H. Sun, S. Wang, C. Griesinger, L. Peng, C. Gao and R. X. Tan, J. Am. Chem. Soc., 2014, 136, 11280–11283 CrossRef CAS PubMed.
- D. S. Carvalho, D. G. B. da Silva, F. Hallwass and A. Navarro-Vázquez, J. Magn. Reson., 2019, 302, 21–27 CrossRef CAS PubMed.
- C. Merle, G. Kummerlöwe, J. C. Freudenberger, F. Halbach, W. Stower, C. L. Gostomski, J. Hopfner, T. Beskers, M. Wilhelm and B. Luy, Angew. Chem., Int. Ed., 2013, 52, 10309–10312 CrossRef CAS PubMed.
- C. M. Thiele, Concepts Magn. Reson., Part A, 2007, 30, 65–80 CrossRef.
- G. Kummerlöwe and B. Luy, in Ann. Rep. NMR Spectrosc., ed. G. A. Webb, 2009, vol. 68, pp. 193–232 Search PubMed.
- V. Schmidts, Magn. Reson. Chem., 2017, 55, 54–60 CrossRef CAS PubMed.
- O. F. Lange, N. A. Lakomek, C. Fares, G. F. Schroder, K. F. A. Walter, S. Becker, J. Meiler, H. Grubmuller, C. Griesinger and B. L. de Groot, Science, 2008, 320, 1471–1475 CrossRef CAS PubMed.
- V. Ozenne, R. Schneider, M. X. Yao, J. R. Huang, L. Salmon, M. Zweckstetter, M. R. Jensen and M. Blackledge, J. Am. Chem. Soc., 2012, 134, 15138–15148 CrossRef CAS PubMed.
- G. Celebre, G. De Luca, M. Longeri and G. Pileio, Mol. Cryst. Liq. Cryst., 2007, 465, 289–299 CrossRef CAS.
- J. Klages, C. Neubauer, M. Coles, H. Kessler and B. Luy, ChemBioChem, 2005, 6, 1672–1678 CrossRef CAS PubMed.
- D. Intelmann, G. Kummerlöwe, G. Haseleu, N. Desmer, K. Schulze, R. Fröhlich, O. Frank, B. Luy and T. Hofmann, Chem.–Eur. J., 2009, 15, 13047–13058 CrossRef CAS PubMed.
- A. Schuetz, J. Junker, A. Leonov, O. F. Lange, T. F. Molinski and C. Griesinger, J. Am. Chem. Soc., 2007, 129, 15114–15115 CrossRef CAS PubMed.
- H. Sun, U. M. Reinscheid, E. L. Whitson, E. J. d'Auvergne, C. M. Ireland, A. Navarro-Vazquez and C. Griesinger, J. Am. Chem. Soc., 2011, 133, 14629–14636 CrossRef CAS PubMed.
- M. E. Garcia, S. Pagola, A. Navarro-Vazquez, D. D. Phillips, C. Gayathri, H. Krakauer, P. W. Stephens, V. E. Nicotra and R. R. Gil, Angew. Chem., Int. Ed., 2009, 48, 5670–5674 CrossRef CAS PubMed.
- H. M. Ge, H. Sun, N. Jiang, Y. H. Qin, H. Dou, T. Yan, Y. Y. Hou, C. Griesinger and R. X. Tan, Chem.–Eur. J., 2012, 18, 5213–5221 CrossRef CAS PubMed.
- V. Schmidts, M. Fredersdorf, T. Lubken, A. Porzel, N. Arnold, L. Wessjohann and C. M. Thiele, J. Nat. Prod., 2013, 76, 839–844 CrossRef CAS PubMed.
- W. Waratchareeyakul, E. Hellemann, R. R. Gil, K. Chantrapromma, M. K. Langat and D. A. Mulholland, J. Nat. Prod., 2017, 80, 391–402 CrossRef CAS PubMed.
- M. J. Riveira, C. Gayathri, A. Navarro-Vazquez, N. V. Tsarevsky, R. R. Gil and M. P. Mischne, Org. Biomol. Chem., 2011, 9, 3170–3175 RSC.
- H. Sun, E. J. d'Auvergne, U. M. Reinscheid, L. Carlos Dias, C. K. Z. Andrade, R. Oliveira Rocha and C. Griesinger, Chem.–Eur. J., 2011, 17, 1811–1817 CrossRef CAS PubMed.
- G. Kummerlowe, B. Crone, M. Kretschmer, S. F. Kirsch and B. Luy, Angew. Chem., Int. Ed., 2011, 50, 2643–2645 CrossRef PubMed.
- M. U. Kiran, A. Sudhakar, J. Klages, G. Kummerlöwe, B. Luy and B. Jagadeesh, J. Am. Chem. Soc., 2009, 131, 15590–15591 CrossRef CAS PubMed.
- J. A. Losonczi, M. Andrec, M. W. Fischer and J. H. Prestegard, J. Magn. Reson., 1999, 138, 334–342 CrossRef CAS PubMed.
- A. O. Frank, J. C. Freudenberger, A. K. Shaytan, H. Kessler and B. Luy, Magn. Reson. Chem., 2015, 53, 213–217 CrossRef CAS PubMed.
- A. Ferrarini, J. Phys. Chem. B, 2003, 107, 7923–7931 CrossRef CAS.
- E. E. Burnell and C. A. de Lange, Chem. Rev., 1998, 98, 2359–2387 CrossRef CAS PubMed.
- H. F. Azurmendi and C. A. Bush, J. Am. Chem. Soc., 2002, 124, 2426–2427 CrossRef CAS PubMed.
- P. Trigo-Mouriño, M. C. de la Fuente, R. R. Gil, V. M. Sánchez-Pedregal and A. Navarro-Vázquez, Chem.–Eur. J., 2013, 19, 14989–14997 CrossRef PubMed.
- L. N. Wirz and J. R. Allison, J. Biomol. NMR, 2015, 62, 25–29 CrossRef CAS PubMed.
- M. Zweckstetter and A. Bax, J. Am. Chem. Soc., 2000, 122, 3791–3792 CrossRef CAS.
- G. Celebre, G. De Luca, J. W. Emsley, E. K. Foord, M. Longeri, F. Lucchesini and G. Pileio, J. Chem. Phys., 2003, 118, 6417–6426 CrossRef CAS.
- J. W. Emsley, Liq. Cryst., 2010, 37, 913–921 CrossRef CAS.
- E. E. Burnell and C. A. de Lange, J. Magn. Reson., 1980, 39, 461–480 CAS.
- E. E. Burnell and C. A. Delange, Chem. Phys. Lett., 1980, 76, 268–272 CrossRef CAS.
- C. M. Thiele, V. Schmidts, B. Bottcher, I. Louzao, R. Berger, A. Maliniak and B. Stevensson, Angew. Chem., Int. Ed., 2009, 48, 6708–6712 CrossRef CAS PubMed.
- V. M. Sanchez-Pedregal, R. Santamaria-Fernandez and A. Navarro-Vazquez, Org. Lett., 2009, 11, 1471–1474 CrossRef CAS PubMed.
- A. Navarro-Vázquez, Magn. Reson. Chem., 2012, 50, S73–S79 CrossRef PubMed.
- C. Pérez-Balado, H. Sun, C. Griesinger, Á. R. de Lera and A. Navarro-Vázquez, Chem.–Eur. J., 2011, 17, 11983–11986 CrossRef PubMed.
- D. Catalano, L. D. Bari, C. A. Veracini, G. N. Shilstone and C. Zannoni, J. Chem. Phys., 1991, 94, 3928–3935 CrossRef CAS.
- R. Berardi, F. Spinozzi and C. Zannoni, J. Chem. Phys., 1998, 109, 3742–3759 CrossRef CAS.
- S. Marčelja, J. Chem. Phys., 1974, 60, 3599–3604 CrossRef.
- J. W. Emsley, G. R. Luckhurst and C. P. Stockley, Proc. R. Soc. London, Ser. A, 1982, 381, 117–138 CrossRef CAS.
- J. W. Emsley, I. D. Wallington, D. Catalano, C. A. Veracini, G. Celebre and M. Longeri, J. Phys. Chem., 1993, 97, 6518–6523 CrossRef CAS.
- B. Stevensson, D. Sandström and A. Maliniak, J. Chem. Phys., 2003, 119, 2738–2746 CrossRef CAS.
- B. Stevensson, C. Landersjö, G. Widmalm and A. Maliniak, J. Am. Chem. Soc., 2002, 124, 5946–5947 CrossRef CAS PubMed.
- B. Hess and R. M. Scheek, J. Magn. Reson., 2003, 164, 19–27 CrossRef CAS PubMed.
- J. Meiler, N. Blomberg, M. Nilges and C. Griesinger, J. Biomol. NMR, 2000, 17, 185 CrossRef CAS.
- G. M. Clore, A. M. Gronenborn and A. Bax, J. Magn. Reson., 1998, 133, 216–221 CrossRef CAS PubMed.
- H. J. Sass, G. Musco, S. J. Stahl, P. T. Wingfield and S. Grzesiek, J. Biomol. NMR, 2001, 21, 275–280 CrossRef CAS PubMed.
- N. Tjandra, J. Marquardt and G. M. Clore, J. Magn. Reson., 2000, 142, 393–396 CrossRef CAS PubMed.
- C. Farès, J. Hassfeld, D. Menche and T. Carlomagno, Angew. Chem., Int. Ed., 2008, 47, 3722–3726 CrossRef PubMed.
- T. A. Holak, D. Gondol, J. Otlewski and T. Wilusz, J. Mol. Biol., 1989, 210, 635–648 CrossRef CAS PubMed.
- P. L. Weber, R. Morrison and D. Hare, J. Mol. Biol., 1988, 204, 483–487 CrossRef CAS PubMed.
- A. Schuetz, T. Murakami, N. Takada, J. Junker, M. Hashimoto and C. Griesinger, Angew. Chem., Int. Ed., 2008, 47, 2032–2034 CrossRef CAS PubMed.
- G. Cornilescu, R. F. R. Alvarenga, T. P. Wyche, T. S. Bugni, R. R. Gil, C. C. Cornilescu, W. M. Westler, J. L. Markley and C. D. Schwieters, ACS Chem. Biol., 2017, 12, 2157–2163 CrossRef CAS PubMed.
- S. Immel, M. Köck and M. Reggelin, Chem.–Eur. J., 2018, 24, 13918–13930 CrossRef CAS PubMed.
- V. Ozenne, F. Bauer, L. Salmon, J. R. Huang, M. R. Jensen, S. Segard, P. Bernadó, C. Charavay and M. Blackledge, Bioinformatics, 2012, 28, 1463–1470 CrossRef CAS PubMed.
- C. Camilloni and M. Vendruscolo, J. Phys. Chem. B, 2015, 119, 653–661 CrossRef CAS PubMed.
- L. N. Wirz and J. R. Allison, J. Phys. Chem. B, 2015, 119, 8223–8224 CrossRef CAS PubMed.
- G. Tomba, C. Camilloni and M. Vendruscolo, Methods, 2018, 148, 4–8 CrossRef CAS PubMed.
- R. Witter, W. Priess and U. Sternberg, J. Comput. Chem., 2002, 23, 298–305 CrossRef CAS PubMed.
- U. Sternberg, R. Witter and A. S. Ulrich, J. Biomol. NMR, 2007, 38, 23–39 CrossRef CAS PubMed.
- U. Sternberg and R. Witter, J. Biomol. NMR, 2015, 63, 265–274 CrossRef CAS PubMed.
- U. Sternberg, M. Klipfel, S. L. Grage, R. Witter and A. S. Ulrich, Phys. Chem. Chem. Phys., 2009, 11, 7048–7060 RSC.
- D. Grasnick, U. Sternberg, E. Strandberg, P. Wadhwani and A. S. Ulrich, Eur. Biophys. J., 2011, 40, 529–543 CrossRef CAS PubMed.
- F. Kramer, M. V. Deshmukh, H. Kessler and S. J. Glaser, Concepts Magn. Reson., 2004, 21A, 10–21 CrossRef.
- A. Saupe, Z. Naturforsch. A, 1964, 19, 161–171 Search PubMed.
- A. E. Torda, R. M. Brunne, T. Huber, H. Kessler and W. F. van Gunsteren, J. Biomol. NMR, 1993, 3, 55–66 CrossRef CAS PubMed.
- P. W. Kuchel, B. E. Chapman, N. Muller, W. A. Bubb, D. J. Philp and A. M. Torres, J. Magn. Reson., 2006, 180, 256–265 CrossRef CAS PubMed.
- G. Kummerlowe, E. F. McCord, S. F. Cheatham, S. Niss, R. W. Schnell and B. Luy, Chemistry, 2010, 16, 7087–7089 CrossRef PubMed.
- A. Enthart, J. C. Freudenberger, J. Furrer, H. Kessler and B. Luy, J. Magn. Reson., 2008, 192, 314–322 CrossRef CAS PubMed.
- M. Möllhoff and U. Sternberg, J. Mol. Model., 2001, 7, 90–102 CrossRef.
- U. Sternberg, F.-T. Koch, M. Bräuer, M. Kunert and E. Anders, J. Mol. Model., 2001, 7, 54–64 CrossRef CAS.
- U. Sternberg, F. T. Koch and M. Möllhoff, J. Comput. Chem., 1994, 15, 524–531 CrossRef CAS.
- R. Witter, M. Möllhoff, F. T. Koch and U. Sternberg, J. Chem., 2015, 908204, DOI:10.1155/2015/908204.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- D. Evans and G. Morriss, Statistical Mechanics of Nonequilibrium Liquids, Academic, London, 1990, 1995 Search PubMed.
- G. Kummerlöwe, S. Schmitt and B. Luy, Open Spectrosc. J., 2010, 4, 16–27 CrossRef.
- M. J. S. Dewar, E. G. Zoebisch, E. F. Healy and J. J. P. Stewart, J. Am. Chem. Soc., 1985, 107, 3902–3909 CrossRef CAS.
- C. M. Thiele and S. Berger, Org. Lett., 2003, 5, 705–708 CrossRef CAS PubMed.
- B. Luy, K. Kobzar, S. Knör, J. Furrer, D. Heckmann and H. Kessler, J. Am. Chem. Soc., 2005, 127, 6459–6465 CrossRef CAS PubMed.
- T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519 CrossRef CAS.
- J. Jovanovic, W. Elling, M. Schurmann, H. Preut and M. Spiteller, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2002, 58, o815–o816 CrossRef CAS.
- A. Furusaki, N. Hashiba, T. Matsumoto, A. Hirano, Y. Iwai and S. Omura, J. Chem. Soc., Chem. Commun., 1978, 800–801 RSC.
- G. A. Ellestad, R. H. Evans and M. P. Kunstmann, J. Am. Chem. Soc., 1969, 91, 2134–2136 CrossRef CAS PubMed.
- G. A. Ellestad, R. H. Evans, Jr, M. P. Kunstmann, J. E. Lancaster and G. O. Morton, J. Am. Chem. Soc., 1970, 92, 5483–5489 CrossRef CAS PubMed.
- G. R. Pettit, R. Tan, D. L. Herald, J. Hamblin and R. K. Pettit, J. Nat. Prod., 2003, 66, 276–278 CrossRef CAS PubMed.
- S. Hanessian, N. Boyer, G. J. Reddy and B. Deschênes-Simard, Org. Lett., 2009, 11, 4640–4643 CrossRef CAS PubMed.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
- N. Salvi, L. Salmon and M. Blackledge, J. Am. Chem. Soc., 2017, 139, 5011–5014 CrossRef CAS PubMed.
- P. E. Wright and H. J. Dyson, Nat. Rev. Mol. Cell Biol., 2015, 16, 18–29 CrossRef CAS PubMed.
- A. Navarro-Vazquez, R. Santamaria-Fernandez and F. J. Sardina, Magn. Reson. Chem., 2018, 56, 505–512 CrossRef CAS PubMed.
- G. Kummerlowe, S. L. Grage, C. M. Thiele, I. Kuprov, A. S. Ulrich and B. Luy, J. Magn. Reson., 2011, 209, 19–30 CrossRef PubMed.
- N. Nath, M. Schmidt, R. R. Gil, R. T. Williamson, G. E. Martin, A. Navarro-Vazquez, C. Griesinger and Y. Z. Liu, J. Am. Chem. Soc., 2016, 138, 9548–9556 CrossRef CAS PubMed.
- F. Hallwass, M. Schmidt, H. Sun, A. Mazur, G. Kummerlöwe, B. Luy, A. Navarro-Vázquez, C. Griesinger and U. M. Reinscheid, Angew. Chem., Int. Ed., 2011, 50, 9487–9490 CrossRef CAS PubMed.
- I. Jakovkin, M. Klipfel, C. Muhle-Goll, A. S. Ulrich, B. Luy and U. Sternberg, Phys. Chem. Chem. Phys., 2012, 14, 12263–12276 RSC.
- U. Sternberg, R. Witter and A. S. Ulrich, Advances in Solid State NMR Studies of Materials and Polymers, 2004, 52, 53–104 CAS.
- A. Navarro-Vazquez, R. R. Gil and K. Blinov, J. Nat. Prod., 2018, 81, 203–210 CrossRef CAS PubMed.
- A. E. Torda, R. M. Scheek and W. F. van Gunsteren, Chem. Phys. Lett., 1989, 157, 289–294 CrossRef CAS.
- A. E. Torda and W. F. van Gunsteren, Comput. Phys. Commun., 1991, 62, 289–296 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01084j |
| ‡ Present address: COSMOS-Software, Jena, Germany. |
| § Present address: Departamento de Química Fundamental, Universidade Federal de Pernambuco, Cidade Universitária, Recife, PE 50740-560, Brazil. |
| This journal is © The Royal Society of Chemistry 2019 |