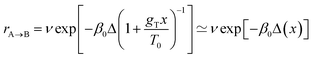Open Access Article
Open Access ArticleControlling the preferential motion of chiral molecular walkers on a surface†
David
Abbasi-Pérez
 *a,
Hongqian
Sang
*a,
Hongqian
Sang
 ab,
Lluïsa
Pérez-García
ab,
Lluïsa
Pérez-García
 c,
Andrea
Floris
c,
Andrea
Floris
 d,
David B.
Amabilino
d,
David B.
Amabilino
 e,
Rasmita
Raval
f,
J. Manuel
Recio
e,
Rasmita
Raval
f,
J. Manuel
Recio
 g and
Lev
Kantorovich
g and
Lev
Kantorovich
 *a
*a
aDepartment of Physics, King's College London, London, WC2R 2LS, UK. E-mail: stqa8038@kcl.ac.uk; david.abbasi_perez@kcl.ac.uk
bInstitute for Interdisciplinary Research, Jianghan University, Wuhan 430056, China
cSchool of Pharmacy, University of Nottingham, University Park, Nottingham, NG7 2RD, UK
dSchool of Chemistry, University of Lincoln, Brayford Pool, Lincoln LN6 7TS, UK
eSchool of Chemistry, GSK Carbon Neutral Lab. for Sustainable Chemistry, University of Nottingham, Triumph Road, NG7 2TU, UK
fSurface Science Research Centre, Department of Chemistry, University of Liverpool, Liverpool L69 3BX, UK
gMALTA-Consolider Team and Department of Analytical and Physical Chemistry, Universidad de Oviedo, Oviedo, 33006, Spain
First published on 14th May 2019
Abstract
Molecular walkers standing on two or more “feet” on an anisotropic periodic potential of a crystal surface may perform a one-dimensional Brownian motion at the surface–vacuum interface along a particular direction in which their mobility is the largest. In thermal equilibrium the molecules move with equal probabilities both ways along this direction, as expected from the detailed balance principle, well-known in chemical reactivity and in the theory of molecular motors. For molecules that possess an asymmetric potential energy surface (PES), we propose a generic method based on the application of a time-periodic external stimulus that would enable the molecules to move preferentially in a single direction thereby acting as Brownian ratchets. To illustrate this method, we consider a prototypical synthetic chiral molecular walker, 1,3-bis(imidazol-1-ylmethyl)-5(1-phenylethyl)benzene, diffusing on the anisotropic Cu(110) surface along the Cu rows. As unveiled by our kinetic Monte Carlo simulations based on the rates calculated using ab initio density functional theory, this molecule moves to the nearest equivalent lattice site via the so-called inchworm mechanism in which it steps first with the rear foot and then with the front foot. As a result, the molecule diffuses via a two-step mechanism, and due to its inherent asymmetry, the corresponding PES is also spatially asymmetric. Taking advantage of this fact, we show how the external stimulus can be tuned to separate molecules of different chirality, orientation and conformation. The consequences of these findings for molecular machines and the separation of enantiomers are also discussed.
1 Introduction
The controlled movement of molecules, either through intramolecular switching or binding and release between molecules, is a challenging contemporary goal. Hence, development of novel methods for controlling molecular motion on surfaces is necessary. The related area of research known as molecular motors1–7 has also become a topic of significant interest. These molecular motors (or machines) under certain conditions are capable of a net unidirectional motion. In biology motor proteins such as kinesin,8–10 myosin11 or dynein12 “walk” along one-dimensional tracks thereby performing specific tasks in the cells. Inspired by these biological systems, successful DNA track nano-walkers have been developed.13–15 The behaviours of many other molecules have also been investigated in terms of their ability to walk or rotate preferentially in a particular direction either driven by a laser pulse,16 chemical reactions,17–20 electric field,21–24 temperature,25 or a combination of different stimuli.26 A ratchet-like behaviour has been observed in colloidal particles,27 an artificial motor system designed to replicate a realistic motor protein,28 cold atoms in optical lattices,29–31 nanoparticles in solution,32,33 SQUIDs,34 soliton transport,35 nanopores in polymer films,36 polarons in diatomic molecular chains,37 superparamagnetic particles,38 and many other cases.Fundamental principles leading to unidirectional motion of molecules are well understood.2,39–43 If in thermal equilibrium a Brownian particle is placed in a periodic potential of a lattice in a single dimension 1D (which could be achieved, e.g., on surfaces with strong anisotropy, such as the Cu(110) surface44), then it would diffuse on average equally likely in both directions along that dimension even though the corresponding potential energy surface (PES) may consist of asymmetric periodic parts (or waveforms). This is because at equilibrium the principle of detailed balance is at work not allowing a net mass transport in any particular direction without doing any work (since that would contradict the second law of thermodynamics). In order to enforce unidirectional mass transport, one has to break the thermal equilibrium. This can be achieved by applying an external stimulus, e.g. an external field or temperature fluctuation, or, as is the case in biological systems, by performing work on the molecules via a chemical reaction. Alongside the application of a time-periodic stimulus (e.g. a field or temperature gradient), an additional condition of broken symmetry is required. For instance, for a unidirectional movement the PES must consist of asymmetric periodic waveforms.
Our main objective is to propose a method based on applying external time-periodic stimuli which would enable one to enforce preferential motion of molecular walkers. As an illustration of our method and a proof of principle, in this paper we explore the Brownian motion of a realistic small bipedal molecule 1,3-bis(imidazol-1-ylmethyl)-5(1-phenylethyl)benzene (BIPEB) on the Cu(110) surface, see Fig. 1. Alongside the most stable geometry, a different conformer is also considered that is slightly less stable. The surface consists of parallel rows of protruding Cu atoms making it highly anisotropic. Consequently the molecules diffuse mostly along the rows; this is similar to a small molecular walker considered previously44 that encounters much higher diffusion barriers across the rows than along the rows. The molecules diffuse along the rows by stepping separately with the rear “foot” and then with the front one akin to the inchworm mechanism,44 and yield a PES consisting of two-peak periodic waveforms with barriers of different heights, i.e. these waveforms lack spatial symmetry.
The plan of the paper is as follows. In the next section we shall briefly consider the computational methods employed. Then the molecules are introduced and their PES is calculated and discussed in Section 3.1. In Section 3 results of the kinetic Monte Carlo simulations without and with various static and time-periodic external stimuli are discussed. Finally, conclusions are drawn in Section 4.
2 Methods
The geometry of the molecules on the surface was relaxed using an ab initio density functional theory (DFT) method as implemented in the CP2K computer code,45 which uses Goedecker–Teter–Hutter (GTH) pseudopotentials to describe atomic core electrons, and a hybrid scheme based on both Gaussian orbitals and plane waves (GPWs) as the basis set for valence electrons. Exchange–correlation interactions were described by the Perdew–Burke–Ernzerhof density functional,46 while the dispersion interaction was described by the rVV10 functional.47 The energy cutoff used was 400 Rydberg. To perform these calculations we used a periodic slab of the Cu(110) surface containing 2 layers of Cu atoms with a vacuum gap of 13 Å (138 atoms altogether), with atoms of the upper layer allowed to relax. As our calculations serve to yield mostly a general qualitative picture, this number of layers is considered sufficient. The 9 × 5 lateral size of the periodic unit cell with a single molecule on its surface was chosen such that the interactions between molecular images are negligible. Only the k = 0 (Γ) point was used in our calculations. The geometry relaxation was stopped when the forces on atoms were less than 1 meV Å−1.To calculate the PES of the molecules associated with a single translation along the Cu rows between two equivalent lowest energy positions, the climbing image nudged elastic band (CI-NEB)48,49 method was applied; in some cases the dimer method50 was used to optimise the geometry of the transition state. The path was split into two separate NEB simulations by an intermediate geometry found (see Section 3.2). The spring constant used varied between 2 and 5 eV Å−2. The NEB calculations were considered converged when the maximum force on the atoms of the band was less than 10 meV Å−1.
As for the computational tool used for investigating the molecules' dynamics, we chose the kinetic Monte Carlo (KMC) method51,52 as a simple and practical alternative to the method based on the Fokker–Planck equation,2,42 which has been widely used in studies on Brownian ratchets. This is because the application of the latter method to realistic multi-atomic molecules is highly difficult due to the many degrees of freedom the whole system possesses. Moreover, when using the KMC method, we benefit from the advanced electronic structure methods, such as those based on DFT, and are able to calculate the corresponding transition rates. For this we have used harmonic transition state theory (HTST)51,53 according to which the transition rate rA→B between two states A and B is calculated via rA→B = v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βΔ), where ν is the frequency pre-factor, β = 1/kBT is the inverse temperature, kB is the Boltzmann constant, and Δ is the energy barrier. The pre-factors can in principle be calculated from the vibrational frequencies of the system in the minimum and saddle point (transition state) using the Vineyard formula.53 However, as this calculation is rather expensive, it was performed only for one molecule (see the ESI†), and then fixed pre-factors were chosen at a value of v = 10 ps−1 for all transitions, with or without the stimulus. This simplification should not affect our conclusions as the transition rates are exponentially more sensitive to the energy barriers rather than to the pre-factors.
exp(−βΔ), where ν is the frequency pre-factor, β = 1/kBT is the inverse temperature, kB is the Boltzmann constant, and Δ is the energy barrier. The pre-factors can in principle be calculated from the vibrational frequencies of the system in the minimum and saddle point (transition state) using the Vineyard formula.53 However, as this calculation is rather expensive, it was performed only for one molecule (see the ESI†), and then fixed pre-factors were chosen at a value of v = 10 ps−1 for all transitions, with or without the stimulus. This simplification should not affect our conclusions as the transition rates are exponentially more sensitive to the energy barriers rather than to the pre-factors.
Now we have to discuss how the energy barriers in the presence of a weak external stimulus were calculated. We have two types of stimuli in mind in this study: (i) a uniform external electric field E,21–24 and (ii) a spatially uniform temperature gradient gT = ∇T.25 In the former case the molecule must be charged, and its PES would then be directly affected by the field causing the energy barriers to respond to it. Indeed, let E be the electrostatic field along the direction x of the Cu rows on the surface, measured in eV Å−1. The electrostatic potential across this direction, V(x) = −Ex, changes linearly with the distance and has to be added to the potential energy of the molecule calculated with DFT. As a result of this, the potential energy barriers Δ(x) of the transitions linearly change with x. Note that for this mechanism to work, it is not sufficient for the molecule to have only a dipole moment (e.g. due to charge exchange with the metal surface), as in this case the contribution of the field to the PES will be spatially uniform and hence would not affect the energy barriers in a desirable way. It is easy to see that the effect of the field is such that the barriers in the direction of the field are reduced, while those in the opposite direction are increased.
In the second case of the temperature gradient the PES is affected indirectly via an effective change of the energy barriers. Indeed, for a constant gradient gT, one has the temperature proportional to the distance x via T(x) = T0 + gTx, with T0 being the temperature somewhere in the middle of a molecular track (we assume that these tracks are of finite length λ such that |gTλ| ≪ T0). Then, the transition rate can be approximately written as
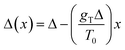 . The effect of this stimulus is that the effective energy barriers in the direction of the temperature gradient (assuming gT > 0) are increased, while those in the opposite direction are reduced. This change can also be approximately treated as being caused by an effective ‘electrostatic’ field
. The effect of this stimulus is that the effective energy barriers in the direction of the temperature gradient (assuming gT > 0) are increased, while those in the opposite direction are reduced. This change can also be approximately treated as being caused by an effective ‘electrostatic’ field 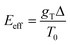 with Δ being some ‘average’ energy barrier.
with Δ being some ‘average’ energy barrier.
Hence, both cases can be considered on the same footing, and in the following we shall interchangeably use both words, ‘stimulus’ and ‘field’, depending on the context.
Since the main purpose of this study is to understand the qualitative effects of the time-periodic stimulus on the molecular ratchet, the following approximate method, which mimics all the essential features of the realistic calculation, has been used. Since due to the field Eeff the energy barriers change linearly with the distance x along the Cu rows on the surface and are increased in one direction and reduced in the opposite one, this can be imagined by the final PES of a molecule being tilted one or the other way, depending on the direction of the field. As the only meaningful quantities responsible for the net mass transport are the transition rates, it is sufficient to shift the energy barriers up/down by an appropriate amount (see Section 3.2 for details, especially Fig. 4(c)).
Finally, since in our simulations the external driving changes with time, additional care should be taken when running KMC simulations. This is because in the standard formulation of KMC it is assumed that the rates remain constant over time, which is obviously not the case in our simulations, where the rates depend on time due to the time dependent external stimulus modifying the energy barriers in real time. Therefore, we use here an approach54 in which this assumption is lifted. In contrast with the standard algorithm in which the rates for the system to jump into all available states from the given state are used and the timestep is chosen at random from the exponential distribution, in the method we used, the timestep Δt is fixed to 100 ps and probabilities to jump as well as to remain in the current state over this time are employed. Otherwise, the two algorithms are very similar.
3 Results
3.1 Isomers and their potential energy surface
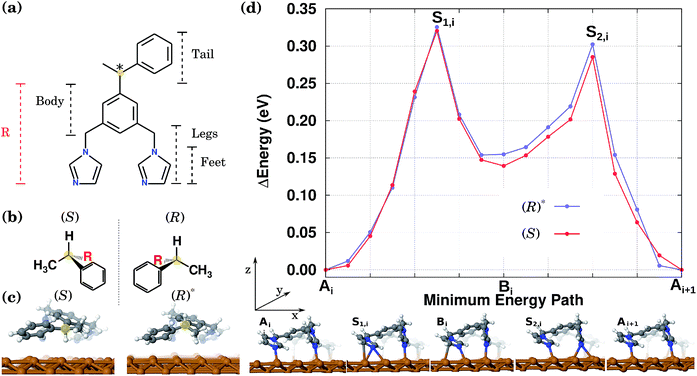
The preferential directional motion of a synthetic walking molecule is an important goal which can be achieved in the minimalist walker molecule on the copper surface described here based on two conditions: (i) selective and directional adsorption on the Cu(110) surface and (ii) the application of an external stimulus. This effect can be seen in its simplest case by considering the energy minimum structures of two enantiomers that when arranged with their “tails” along the same normal to the copper atom rows will present mirror image potential energy surfaces.In this study, as a prototypical molecular walker, we consider a (electrically neutral) synthetic bipedal molecule 1,3-bis(imidazol-1-ylmethyl)-5(1-phenylethyl)benzene (BIPEB) shown in Fig. 1(a). We refer to different parts of the molecule as body, tail and legs, as indicated in the scheme; the body is the benzene group, and the tail (1-phenylethyl) and the legs (imidazol-1-ylmethyl groups) are attached to it. Within the legs, the imidazole moieties are the feet. The molecule possesses a stereogenic carbon atom in its tail, shown in yellow, leading to the existence of two enantiomers, (R) and (S), Fig. 1(b); both adopt a 3D geometry in the gas phase. When placed on the Cu(110) surface, several adsorption geometries were found for either of the two (the geometries of (R) being mirror reflections of those of (S)), with the most energetically favourable structure shown for the (S) enantiomer in Fig. 1(c). The molecule is strongly bound to the surface with a binding energy of 3.61 eV (after inclusion of the basis set superposition error (BSSE) employing the counterpoise method55).
Here we also consider a competitive geometry that, as compared to (S), has the H atom and the methyl group attached to the stereogenic carbon swapped with each other, which changes its chirality from (S) to (R). The H atom is pointing outwards from the surface, while in (S) it is directed towards it (the methyl group in both cases is pointed in the opposite direction to the H atom). Therefore, this metastable geometry is to be considered as another conformer of the (R) enantiomer, and will be referred to hereafter as the conformer (R)*, Fig. 1(c). It is 0.1 eV less stable than the (S) or (R) geometries. It is important to note that the calculated energy difference of 0.1 eV between the two conformers (R) and (R)* (and similarly between (S) and (S)*) is due to the existence of the stereogenic centre in the BIPEB molecule. The three point model for binding describes this situation well, and is a consequence of the “handedness”, or rather “footedness”56 of the molecule.
These two conformations can generate other equivalent geometries related by mirror symmetry due to a plane perpendicular to the surface. This symmetry operation does not change the absolute value of the energy, but can change the shape of the PES. The mirror reflection of the (S) enantiomer with respect to a plane perpendicular to the Cu row leads to the (R) enantiomer. This operation also mirrors the PES. If the mirror plane is parallel to the Cu row, we transform the (S) enantiomer into (R), but this time the tail points towards the opposite direction. We call this the (R)r enantiomer, as it is equivalent to rotating the enantiomer (R) by 180° with respect to an axis perpendicular to the surface. This operation does not change the shape of the PES. Hence, enantiomers (S) and (R) have identical orientations but mirrored PESs, while enantiomers (S) and (R)r have identical PESs but different orientations. The same procedure can be applied to the (R)* conformer. Due to these symmetry relations, calculating the PES only for one enantiomer and one of its conformers allows us to obtain the PES for the rest of the geometries. All eight conformations are presented in Fig. 2, with their corresponding PES to show how it is modified after each reflection.
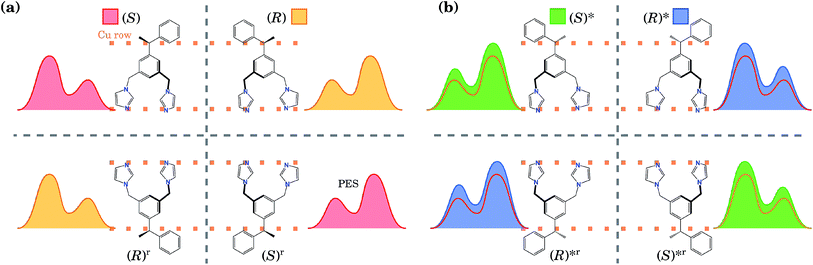 | ||
| Fig. 2 (a) Schematics (the top view) of the four most energetically favourable equivalent configurations that the BIPEB molecule can adopt when adsorbed on the surface, shown with the schematics of their corresponding PES. By symmetry, these four configurations have exactly the same energy. The four geometries are connected by mirror symmetry operations (grey dashed lines). Every reflection transforms the molecule into its enantiomer, but only the reflection over the planes perpendicular to the Cu rows transforms the PES by reflecting it. The rotated configurations (bottom line) (S)r and (R)r are equivalent to the (S) and (R) enantiomers, respectively, and are obtained by a 180° rotation about the axis perpendicular to the surface. (b) Conformers and their PESs shown in filled colour. For comparison, we also show with the line of appropriate colour the PES of the corresponding competitive molecule from (a), which has the closest PES shape (but slightly different barriers). This colour code for each isomer is used throughout the paper: red, yellow, green and blue represent the isomers (S), (R), (S)* and (R)*, respectively. Note that for clarity the schematic PESs shown here do not correspond exactly to the calculated ones shown in Fig. 1(d). | ||
In all geometries, the BIPEB molecule shows two N–Cu interactions44 similar in nature to the nitrogen atom surface (NAS) interactions we have recently reported for a p-terphenyl m-dicarbonitrile molecule on the Ag(111) surface.57 This is clearly seen in the electron density difference (EDD) maps shown in Fig. 3. The imidazole groups of the molecule interact with the surface via their nucleophilic nitrogen atoms that act as their feet, which bind to two non-adjacent Cu atoms in the same close-packed row. The NAS interactions are strong enough to noticeably lift up the interacting Cu atoms from their relaxed positions on the surface. At the same time, the tail of the molecule interacts with a neighbouring Cu row; however, this binding is much weaker than that of the imidazole feet as the EDD maps illustrate and hence this connection to the surface is less important and in most cases can be ignored, except when the two geometries are compared with each other as we discuss below. Comparing the EDD of (S) and (R)*, we can see that the (S) enantiomer has an extra interaction with the surface via the H atom attached to the stereogenic C, which is missing in (R)*. This interaction appears in the EDD in a “kebab”-like form, i.e. via alternating regions of excess and depletion of the electronic density along the straight line connecting the atoms participating in the bond, and is highlighted in Fig. 3. This fact yields slightly different barrier heights for both geometries along the asymmetric PES, which will be exploited later on for their separation.
In the stable equilibrium geometries for both (S) and (R)* the imidazole feet are separated by a single Cu atom along the same row. We have also found another adsorption geometry for both conformers in which there are no Cu atoms between the feet, see geometry Bi at the bottom of Fig. 1(d). This configuration is less favourable by 0.15 eV and appears as an intermediate state between the more stable equilibrium geometries labelled A and Ai+1 (see below). Note that other adsorption geometries are also possible when both feet stand on the neighbouring Cu rows or the tail is rotated. However, these are much less favourable and hence are much less relevant when considering the molecules’ diffusion and will be ignored hereafter.
To calculate the diffusion path between the two most favourable geometries in Fig. 1(c), we first run NEB calculations between these two states via two different mechanisms: one, in which the molecule slides as a whole along the Cu row in a one-step motion, and the other, the so-called inchworm mechanism, in which the molecule follows a two-step movement whereby first its rear foot moves forward and then its front one. Interestingly enough, the latter calculation indicated the existence of an intermediate minimum in the middle of the path. After relaxation of the geometry in that minimum, the second geometry mentioned above (labelled Bi at the bottom of Fig. 1(d)) was found. Hence, the whole path was split into two, and two separate CI-NEB simulations were run with 9 images each, to characterize both elementary steps. This computational scheme was applied to both (S) and (R)*. The resulting PES for the complete inchworm path between two equivalent states (Ai and Ai+1) that passes through an intermediate minimum Bi is shown at the top of Fig. 1(d) for both enantiomers. A selection of geometries along the path of (R)* is shown at the bottom. The PES for the other molecules can be obtained by applying the corresponding symmetry operations, as shown in Fig. 2. While the NEB calculation for the sliding mechanism revealed a one-step diffusion with an energy barrier of 0.55 eV, in the inchworm mechanism the diffusion occurs via a two-step diffusion path where the highest barrier was found to be below 0.34 eV. Hence, it is evident that the diffusion of either of the molecules is manifested by the inchworm walking mechanism,44 where imidazole groups act like feet that step on top of the Cu atoms along the row: to move forward, first the rear foot moves one surface lattice constant (Ai → Bi), then the front foot moves forward one lattice constant (Bi → Ai+1) bringing the molecule to an equivalent state displaced by one lattice constant.
Thus, the PES of the two conformers by moving one lattice constant along the Cu row is a waveform consisting of two peaks. In both cases the peaks heights, measured from the geometries A or B, are slightly different rendering the expected diffusion of the two conformers to be slightly different as well. This difference originates from the slightly different interaction of the tails of the two molecules with the surface. The calculated energy barriers between the minima are shown in Table 1 and are found to be indeed different by around 19 meV from Ai to Bi and 31 meV for Ai+1 to Bi, for both conformers. Therefore, the PES of the molecules along a Cu row consists of an infinite periodic sequence of such two-peak waveforms. We conclude that the PES of either of the molecules is spatially asymmetric, even though the difference in peaks heights is small.
| Description | Δ (eV) | |
|---|---|---|
| (R)* | (S) | |
| From Ai to Bi (to the right) | 0.339 | 0.320 |
| From Ai+1 to Bi (to the left) | 0.316 | 0.285 |
| From Bi to Ai+1 (to the right) | 0.147 | 0.146 |
| From Bi to Ai (to the left) | 0.170 | 0.181 |
For performing KMC simulations, a periodic sequence of states A and B was in all cases considered with all possible transitions between neighbouring states. When a molecule moves the whole lattice constant to the right, i.e. Ai → Bi → Ai+1, then +1 (in units of the lattice constant) is added to its position along the row; when the molecule moves the whole lattice constant to the left, i.e. Ai+1 →Bi → Ai, then −1 is added to its position, see Fig. 1(d).
A final note is in order related to the fact that when performing NEB simulations the molecule was not charged: the above calculation (and the dynamic simulations described in the following sections) corresponds directly only to the case of the temperature gradient as the stimulus. One may think that the PES calculated in our NEB simulation is irrelevant then to the first type of the stimulus, an external electric field, since in this case the molecule has to possess a charge. We argue that even in this case the NEB calculation makes perfect sense, at least qualitatively. Indeed, the two-peak PES of the molecule is related primarily to the fact that the molecule stands on two ‘feet’ and diffuses via the inchworm mechanism. An extra charge on the molecule does not affect the former point (see the ESI†), and hence the latter point must be valid as well as a consequence. Therefore, if the molecule is charged, the energy barriers would somewhat change numerically; at the same time, the dynamical behaviours we obtain will remain qualitatively exactly the same.
3.2 Diffusion with zero and constant external stimulus
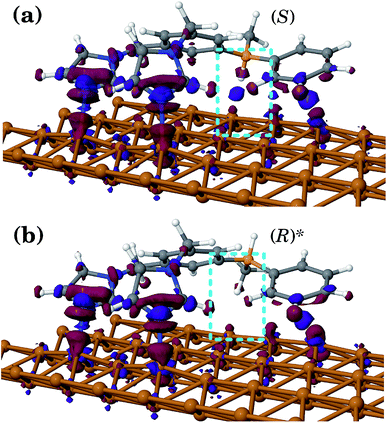
Consider first the diffusion of all conformers without being driven by any external field. The position of the molecules along the Cu row during the course of a selected number of KMC simulations is shown in Fig. 4(a). One can clearly see that there is no preference for the molecules to go in one or the opposite direction in spite of the fact that the waveform of their PES is asymmetric. After 50 ms, the average distance walked by the molecules is zero within the accuracy of our calculations.The obtained results agree with the fundamental principle of detailed balance (following from the second law of thermodynamics) that at thermal equilibrium there should be no such preference.2,40,42,43 In order for the molecules to move preferentially in a single direction, one has to break the equilibrium condition, e.g., by applying an external field or temperature gradient. In what follows, the latter method will directly be exploited, although, as was said above, qualitatively our simulations are valid for the former method as well.
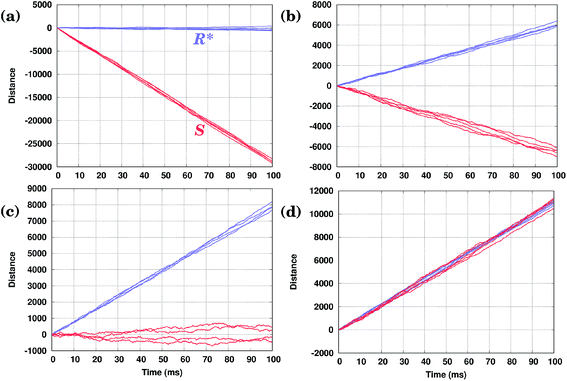
In Fig. 4(b) calculated KMC paths are shown for the equally oriented enantiomers under constant values of the field Eeff = ±0.02 eV/a, where a = 2.56 Å is the Cu–Cu distance along the Cu row. As expected, the application of a constant field forces the molecules to perform preferential unidirectional movement in the direction of the field. Note that all conformers would move preferentially along the field. Moreover, each enantiomer may adopt two orientations on the same Cu row, the second being obtained from the first by rotating the molecule by 180° about the vertical axis. Because either of the PESs is tilted in the same direction (either to the right or left, depending on the sign of Eeff), preferential diffusion along the field is observed irrespective of the orientation of the molecules, so the separation is difficult in this case.
Application of a permanent field along one direction of the copper rows will lead to motion of the molecules, but because of the differences in the potential energy surfaces the (R) and (S) enantiomers will move at different speeds, i.e. the distance travelled in a certain time is actually different when going to the right (positive distance values) or to the left (negative distance values), Fig. 4(b). Indeed, if we look at the curves for the enantiomers (S) and (R), red and yellow respectively, the (S) molecule moves to the right (Eeff > 0) slower than (R) in the case of the opposite direction of the field (to the left, Eeff < 0) (S) moves faster than (R): after 50 ms (S) travels around 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 lattice constants to the right and 26
500 lattice constants to the right and 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lattice constants to the left, while (R) travels 26
000 lattice constants to the left, while (R) travels 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 lattice constants to the right and 17
000 lattice constants to the right and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 to the left. This can be explained in the following way. Suppose one direction of the field forces the molecules to move preferentially along the field and in that direction the smaller peak of the PES comes first, while the opposite direction of the field makes the molecules preferentially move in the opposite direction when the higher peak of the PES comes first. In this case the molecules would move faster in the former case than in the latter since overcoming a sequence of two smaller barriers (Ai+1 → Bi → Ai) is on the whole ‘easier’ than moving in the opposite direction, Ai → Bi → Ai+1, which requires climbing a larger energy barrier first, Fig. 4(c).
500 to the left. This can be explained in the following way. Suppose one direction of the field forces the molecules to move preferentially along the field and in that direction the smaller peak of the PES comes first, while the opposite direction of the field makes the molecules preferentially move in the opposite direction when the higher peak of the PES comes first. In this case the molecules would move faster in the former case than in the latter since overcoming a sequence of two smaller barriers (Ai+1 → Bi → Ai) is on the whole ‘easier’ than moving in the opposite direction, Ai → Bi → Ai+1, which requires climbing a larger energy barrier first, Fig. 4(c).
Even though the application of a constant field cannot be used for molecular separation (all molecules go together displaying almost identical trajectories in each case, albeit with different speeds), the effect of the sign of the field on the velocity of the molecules in performing unidirectional movement appears to be crucial for developing methods which are capable of achieving the desired separation of the molecules via their unidirectional motion.
3.3 Separation of molecules using oscillating fields
We have seen that the application of a constant field (stimulus) is trivially able to cause unidirectional diffusion of the molecules along the field; because of the asymmetry of the PES, the speed with which the molecules move depends on the direction of the field. This effect can now be exploited in order to propose an external stimulus that is able to separate the molecules with respect to their chirality on the Cu rows. Note that the PES of an enantiomer is obtained simply by mirroring the PES corresponding to the original molecule, see Fig. 2. This is also true for molecules rotated by 180°.The idea is to apply a time-periodic (but still spatially uniform) external field Eeff(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt). In this case for any sensible choice of the parameters A and ω molecules of different chiralities will move in the opposite directions with the same speed, as shown in Fig. 4(d). Indeed, if in the case of a constant field molecules moved in the direction of the field, when applying an oscillatory field, molecules move preferentially in the direction in which they move faster (see our discussion above). As the (S) enantiomer moves faster to the left and (R) to the right in the presence of a field, the application of an oscillating field will drive the enantiomers (S) to the left and (R) to the right, achieving a separation of enantiomers. Moreover, in the case of the molecules with opposite orientations their movement will be also a mirror reflection of each other. Note that the actual trajectories shown in Fig. 4(d) are not exactly the mirror images of each other as they represent a sample of stochastic KMC trajectories.
sin(ωt). In this case for any sensible choice of the parameters A and ω molecules of different chiralities will move in the opposite directions with the same speed, as shown in Fig. 4(d). Indeed, if in the case of a constant field molecules moved in the direction of the field, when applying an oscillatory field, molecules move preferentially in the direction in which they move faster (see our discussion above). As the (S) enantiomer moves faster to the left and (R) to the right in the presence of a field, the application of an oscillating field will drive the enantiomers (S) to the left and (R) to the right, achieving a separation of enantiomers. Moreover, in the case of the molecules with opposite orientations their movement will be also a mirror reflection of each other. Note that the actual trajectories shown in Fig. 4(d) are not exactly the mirror images of each other as they represent a sample of stochastic KMC trajectories.
Hence, by applying a properly adjusted oscillating field, in a racemic mixture with equally oriented molecules, one should be able to separate the enantiomers. On the other hand, in an enantiopure system, it is possible to separate the molecules based on their orientation.
3.4 Separation of competitive conformers
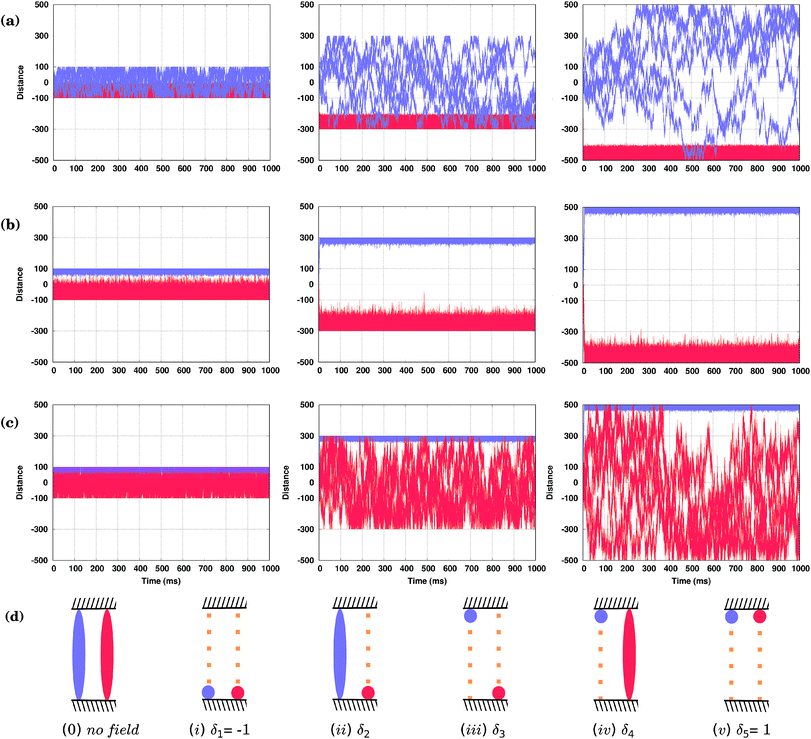
As shown in Fig. 4(d), both conformers (S) and (R)* (or (R) and (S)*), at least for the molecules considered here, would move in the same direction; only their velocities will be different. Hence, the oscillating field considered so far is not appropriate to separate them. This is because the field has an equal duration in both positive and negative directions. In other words, a time-symmetric stimulus does not allow one to fully resolve the molecules of different conformations. In order to separate two competitive geometries (conformers with similar PESs but slightly different energy barriers), it is necessary to allow the field to operate in one direction longer (or shorter) than in the other, i.e. the time symmetry must be broken. This asymmetry of the field can be easily created by applying, e.g., a shifted field, Eeff(t) = A[sin(ωt) + δ], where the relative displacement −1 ≤ δ ≤ 1. By properly fine-tuning the parameters of the field, it is possible to exploit the difference in the conformer velocities. We can either make one conformer stay around the initial position while the other moves away, Fig. 5(a) and (c), or make them move with the same velocity, Fig. 5(d). Finally, we can make them move in the opposite directions, i.e. to separate them, as shown in Fig. 5(b). Note that by taking the value of the parameter δ to be around the value used in Fig. 5(d), one can make the two molecules move in the same direction, but with different velocities (not shown).Hence, by applying a properly shifted (asymmetric) field it is possible to separate molecules of different conformations.
3.5 Fences
Brownian molecular motion on surfaces may be conditioned by the intrinsic features of the molecules, the anisotropy of the surface or the existence of natural barriers such as steps and/or local defects (e.g. impurities). Molecular fences, e.g. such as the filaments of porphyrins described in ref. 44, provide realistic spatial constraints for the walkers, adding new possibilities to the resolution of racemic mixtures. In particular, these fences could be used as a practical tool in collecting the molecules of either one orientation, conformation or, possibly, even chirality.Now we shall describe our KMC simulations in which two infinite parallel fences were placed perpendicular to the Cu rows, and the molecules are placed between them. It was assumed in our KMC simulations that the molecules cannot move across the fences, but can ideally be reflected upon them. How the distance between these barriers affects the separation of the conformers, when external fields differing only by the value of the shift parameter δ are applied, is illustrated in Fig. 6. In Fig. 6(a) and (c), with δ2 = 0.021294 and δ4 = 0.02800, respectively, the applied fields are able to fuel one of the conformers in less than two milliseconds to one fence, while the second conformer remains broadly distributed between the fences. Note, however, that for distant fences at long simulation times the second molecule would spend more of its time at the other fence, as it is still under the influence of the field that biases its movement, see right panels in Fig. 6(a) and (c). Applying a different field with δ3 = 0.02638, Fig. 6(b), the two conformers are fully separated by the top (R) and bottom (S) fences, but due to the stochastic nature of the movement, molecules confined near one fence may still reach the opposite fence if the distance between them is not large enough, see the left panel in Fig. 6(b). Note that by increasing the frequency ω of the field, molecules can be confined at narrower spaces and kept separated between even closer placed fences (not shown). For our system, a distance between fences of around 600 lattice constants (the middle column in (a–c)) would allow there to be five different states in the presence of the field, Fig. 6(d): (i) both conformers at the lower fence (δ1 = −1), (ii) the conformer (S) at the lower fence while (R)* moves broadly within the confined space (δ2 = 0.02194), (iii) both conformers separated at opposite fences (δ3 = 0.026380), (iv) conformer (R)* confined at the upper fence while (S) moves everywhere (δ4 = 0.02800), and finally, (v) both conformers at the upper fence (δ5 = 1). Note that all of these states are achievable by just changing the δ parameter of the field. Simulations were run for long times, up to one second, and show that these states are stable over time as long as the field is kept. Obviously, when the field is switched off, all molecules move freely between the fences.
4 Discussion and conclusions
In this work, we have explored the unidirectional motion of a prototypical molecular walker under an external time-periodic stimulus such as a weak uniform temperature gradient which acts as an effective uniform field linearly distorting the molecular PES. Our results must also be directly relevant to the other type of the stimulus, an external uniform electric field, although in this case the calculated parameters of the field that influence the unidirectional motion are expected to be numerically slightly different. Practical ways of charging molecules on surfaces are discussed in ref. 58 and 59.The particular chiral molecule considered is 1,3-bis(imidazol-1-ylmethyl)-5(1-phenylethyl)benzene that has two enantiomers, (R) and (S). We demonstrated that both enantiomers diffuse on the Cu(110) surface via a walking mechanism akin to the inchworm motion where the molecule's first step is with its rear foot and then with its front one. Consequently, the PES of the molecule on the Cu(110) surface consists of a periodic sequence of slightly asymmetric waveforms containing two peaks each associated with the stepping of a single foot. In contrast with common computational approaches in which Brownian molecular ratchets are studied using oversimplified molecular models by means of, e.g., the Fokker–Planck equation, we propose a method that is based on running KMC simulations. The obvious advantage of our theoretical approach is that it is able to consider dynamics of realistic systems (both molecules and surfaces) with adsorption geometries and diffusion rates calculated using modern ab initio methods.
It has been shown that despite the spatial asymmetry in the PES of the molecules, no preferential motion towards a particular direction along the Cu rows is observed, which is in accordance with the second law of thermodynamics and the principle of detailed balance. However, unidirectional motion is achieved by the application of an external field, and we have shown that small differences in the heights of the two peaks in the PES waveforms yield different diffusion velocities of the molecules on the surface, according to the sign of the field. The central result of this study is that when applying a uniform time-periodic (sinusoidal) external field, the molecules diffuse preferentially towards the direction they move faster. This effect is general and would be applicable to a wide class of surface-molecule systems, being of principal importance for the separation of the molecules. If we have a racemic mixture, where all molecules are equally oriented in the same direction and hence have mirror-symmetric PESs, they will diffuse in opposite directions in the presence of an oscillating field. It is also possible to separate molecules of the same kind (i.e. in an enantiopure system) but of opposite orientation as they would preferentially diffuse in the opposite directions along the Cu rows, thereby ensuring their separation.
Hence, we have shown that the molecules can be separated according to either their chirality or their orientation by applying an appropriate external stimulus.
In reality, for a chiral molecule and the surface like the one we considered here, there will be four types of isomers on the surface after deposition (see Fig. 2): (S), (R), (S)r and (R)r (and this is also true for each conformer), all present in equal quantities. Therefore, by applying our method, we should be able to separate these molecules into two groups: (i) (S) and (R)r, and (ii) (R) and (S)r, which corresponds only to a partial separation. However, if in the presence of the same field the PES of the molecules in different orientations is different (e.g. by applying an extra weak field acting in the direction perpendicular to the direction of motion), then using an appropriate modification of our method it should be possible to achieve full separation of the molecules with respect to both their chirality and orientation.
Furthermore, we have demonstrated that when the PES is not mirror-symmetric but has a similar shape with slightly different energy barriers, the diffusion direction of the molecules can still be controlled. By combining a constant field with an oscillating one, so that the times during which the field points in both directions are different, one can fine-tune the parameters of such a field to achieve various effects in the diffusion of the enantiomers. For instance, one can ensure that one enantiomer moves faster (or slower) than the other while moving in the same direction, or one would on average not move at all while the other moves. Most intriguingly, however, we have shown that one can also adjust the parameters of the field (its constant component) in such a way that two competitive molecules, when oriented in the same way on the surface, would move in opposite directions.
The possibility to control the movement of the molecules in a confined system, like between fences, can have potential applications at the nanoscale. It could be used as a tool for molecular control. If fences for example are not only physical barriers that only block the diffusion, but molecules or electrodes, or even individual entities that can perform an action according to the presence (or absence) of the molecules, then, the application of the field could rearrange the molecules in that hypothetical device and trigger a certain response. If this is applied in a more complicated device, these molecules could act as information carriers or molecular relays, activated by the shape of the external fields if instead of an inert fence there is a nanodevice capable of triggering a reaction according to the presence or absence of the molecules. Also, the possibility to control diffusion at the molecular level could allow seeding of enantiopure regions on a surface to start growing enantiopure self-assembled monolayers.
Our findings open a way for enantiomer separation with exciting applications in physics and chemistry. Understanding molecular ratchets provides a novel route to designing efficient methods to separate various molecules, with particular relevance to racemic mixtures of enantiomers where preferential crystallization works sporadically.60 In particular, we have shown that by providing parallel fences44 perpendicular to the Cu rows, one can collect molecules of the same orientation and/or chirality near different fences.
We hope that this study will be useful to a wide community of physicists and chemists working in different areas related to studying molecules on surfaces and in the field of molecular motors and nanoscale devices. Furthermore, it may contribute to solving exciting questions like why proteins and, by extension, life are stereospecific. Perhaps this relationship between directional motion and chirality could be part of the answer.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431), this work used both the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) and the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/P020194). This research was supported by the UK EPSRC grant EP/J019844/1 and in part by EP/N023587/1. H. S. would like to acknowledge the support from the National Natural Science Foundation of China (Grant No. 21603086) and the China Scholarship Council (Grant No. 201608420186). J. M. R. thanks the Spanish MINECO and FICYT for financial support (Projects CTQ2015-67755-C2-2-R, FC-GRUPIN-IDI/2018/000177) and Universidad de Oviedo for a mobility grant to visit King's College London.References
- M. Schliwa and G. Woehlke, Nature, 2003, 422, 759–765 CrossRef CAS PubMed.
- P. Hänggi and F. Marchesoni, Rev. Mod. Phys., 2009, 81, 387–442 CrossRef.
- M. von Delius and D. A. Leigh, Chem. Soc. Rev., 2011, 40, 3656–3676 RSC.
- S. Erbas-Cakmak, D. A. Leigh, C. T. McTernan and A. L. Nussbaumer, Chem. Rev., 2015, 115, 10081–10206 CrossRef CAS PubMed.
- S. Kassem, T. van Leeuwen, A. S. Lubbe, M. R. Wilson, B. L. Feringa and D. A. Leigh, Chem. Soc. Rev., 2017, 46, 2592–2621 RSC.
- C. Pezzato, C. Cheng, J. F. Stoddart and R. D. Astumian, Chem. Soc. Rev., 2017, 46, 5491–5507 RSC.
- R. D. Astumian, Chem. Commun., 2018, 54, 427–444 RSC.
- R. D. Vale, T. Funatsu, D. W. Pierce, L. Romberg, Y. Harada and T. Yanagida, Nature, 1996, 380, 451–453 CrossRef CAS PubMed.
- S. M. Block, Biophys. J., 2007, 92, 2986–2995 CrossRef CAS PubMed.
- A. Gennerich and R. D. Vale, Curr. Opin. Cell Biol., 2009, 21, 59–67 CrossRef CAS PubMed.
- R. Sellers and C. Veigel, Curr. Opin. Cell Biol., 2006, 18, 68–73 CrossRef PubMed.
- K. Oiwa and H. Sakakibara, Curr. Opin. Cell Biol., 2005, 17, 98–103 CrossRef CAS PubMed.
- I. Y. Loh, J. Cheng, S. R. Tee, A. Efremov and Z. Wang, ACS Nano, 2014, 8, 10293–10304 CrossRef CAS PubMed.
- Q. Y. Yeo, I. Y. Loh, S. R. Tee, Y. H. Chiang, J. Cheng, M. H. Liu and Z. S. Wang, Nanoscale, 2017, 9, 12142–12149 RSC.
- Y. H. Chiang, S. L. Tsai, S. R. Tee, O. L. Nair, I. Y. Loh, M. H. Liu and Z. S. Wang, Nanoscale, 2018, 10, 9199–9211 RSC.
- K. Hoki, M. Yamaki and Y. Fujimura, Angew. Chem., 2003, 115, 3084–3086 CrossRef.
- M. von Delius, E. M. Geertsema and D. A. Leigh, Nat. Chem., 2010, 2, 96–101 CrossRef CAS PubMed.
- S. Otto, Nat. Chem., 2010, 2, 75–76 CrossRef CAS.
- E. M. Perez, Angew. Chem., Int. Ed., 2011, 50, 3359–3361 CrossRef CAS.
- C. J. Martin, A. T. L. Lee, R. W. Adams and D. A. Leigh, J. Am. Chem. Soc., 2017, 139, 11998–12002 CrossRef CAS.
- R. D. Astumian, Science, 1997, 276, 917–922 CrossRef CAS.
- T. Kudernac, N. Ruangsupapichat, M. Parschau, B. Macià, N. Katsonis, S. R. Harutyunyan, K.-H. Ernst and B. L. Feringa, Nature, 2011, 479, 208–211 CrossRef CAS.
- A. V. Akimov and A. B. Kolomeisky, J. Phys. Chem. C, 2012, 116, 22595–22601 CrossRef CAS.
- J. Neumann, K. E. Gottschalk and R. D. Astumian, ACS Nano, 2012, 6, 5242–5248 CrossRef CAS PubMed.
- N. A. Wasio, C. J. Murphy, D. A. Patel, D. Wei, D. S. Sholl and E. C. H. Sykes, Tetrahedron, 2017, 73, 4858–4863 CrossRef CAS.
- M. J. Barrell, A. G. Campana, M. von Delius, E. M. Geertsema and D. A. Leigh, Angew. Chem., Int. Ed., 2011, 50, 285–290 CrossRef CAS PubMed.
- F. Martinez-Pedrero, H. Massana-Cid, T. Ziegler, T. H. Johansen, A. V. Straubeae and P. Tierno, Phys. Chem. Chem. Phys., 2016, 18, 26353–26357 RSC.
- N. Arai, K. Yasuoka, T. Koishi, T. Ebisuzaki and X. C. Zeng, J. Am. Chem. Soc., 2013, 135, 8616–8624 CrossRef CAS.
- P. H. Jones, M. Goonasekera and F. Renzoni, Phys. Rev. Lett., 2004, 93, 073904 CrossRef CAS PubMed.
- R. Gommers, S. Denisov and F. Renzoni, Phys. Rev. Lett., 2006, 96, 240604 CrossRef CAS PubMed.
- R. Gommers, V. Lebedev, M. Brown and F. Renzoni, Phys. Rev. Lett., 2008, 100, 040603 CrossRef CAS PubMed.
- S.-H. Wu, N. Huang, E. Jaquay and M. L. Povinelli, Nano Lett., 2016, 16, 5261–5266 CrossRef CAS.
- P. Tierno, S. V. Reddy, M. G. Roper, T. H. Johansen and T. M. Fischer, J. Phys. Chem. B, 2008, 112, 3833–3837 CrossRef CAS PubMed.
- S. Weiss, D. Koelle, J. Müller, R. Gross and K. Barthel, Europhys. Lett., 2000, 51, 499 CrossRef CAS.
- M. Borromeo and F. Marchesoni, Chaos, 2005, 15, 026110 CrossRef CAS PubMed.
- E. Kalman, K. Healy and Z. S. Siwy, Europhys. Lett., 2007, 78, 28002 CrossRef.
- L. S. Brizhik, A. A. Eremko, B. M. A. G. Piette and W. J. Zakrzewski, J. Phys.: Condens. Matter, 2008, 20, 255242 CrossRef.
- F. Liu, L. Jiang, H. M. Tan, A. Yadav, P. Biswas, J. R. C. van der Maarel, C. A. Nijhuis and J. A. van Kan, Biomicrofluidics, 2016, 10, 064105 CrossRef PubMed.
- B. Robertson and R. Astumian, Biophys. J., 1990, 58, 969–974 CrossRef CAS PubMed.
- M. O. Magnasco, Phys. Rev. Lett., 1993, 71, 1477–1481 CrossRef PubMed.
- R. D. Astumian and B. Robertson, J. Am. Chem. Soc., 1993, 115, 11063–11068 CrossRef CAS.
- P. Reimann, Phys. Rep., 2002, 361, 57–265 CrossRef CAS.
- P. Reinmann and P. Hänggi, Appl. Phys. A, 2002, 75, 169–178 CrossRef.
- S. Haq, B. Wit, H. Sang, A. Floris, Y. Wang, J. Wang, L. Pérez-García, L. Kantorovich, D. B. Amabilino and R. Raval, Angew. Chem., Int. Ed., 2015, 54, 7101–7105 CrossRef CAS.
- J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108 CrossRef.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. Nitzan, Chemical Dynamics in Condensed Phases: Relaxation, Transfer, and Reactions in Condensed Molecular Systems, Oxford University Press, 2014 Search PubMed.
- K. A. Fichthorn and W. H. Weinberg, J. Chem. Phys., 1991, 95, 1090 CrossRef CAS.
- G. H. Vineyard, J. Phys. Chem. Solids, 1957, 3, 121 CrossRef CAS.
- L. Kantorovich, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 75, 064305 CrossRef.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- A. G. Mark, M. Forster and R. Raval, ChemPhysChem, 2011, 12, 1474–1480 CrossRef CAS PubMed.
- D. Abbasi-Pérez, J. Manuel Recio and L. Kantorovich, Phys. Chem. Chem. Phys., 2015, 17, 11182–11192 RSC.
- R. B. Cody, J. A. Laramee and H. D. Durst, Anal. Chem., 2005, 77, 2297–2302 CrossRef CAS PubMed.
- C. L. Feider, A. Krieger, R. J. DeHoog and L. S. Eberlin, Anal. Chem., 2019, 91, 4266–4290 CrossRef CAS PubMed.
- A. Otero-de-la Roza, B. H. Cao, I. K. Price, J. E. Hein and E. R. Johnson, Angew. Chem., Int. Ed., 2014, 53, 7879–7882 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01135h |
| This journal is © The Royal Society of Chemistry 2019 |