Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Counting loops in sidechain-crosslinked polymers from elastic solids to single-chain nanoparticles†
Junpeng
Wang
a,
Rui
Wang
b,
Yuwei
Gu
a,
Alexandra
Sourakov
a,
Bradley D.
Olsen
 *b and
Jeremiah A.
Johnson
*b and
Jeremiah A.
Johnson
 *a
*a
aDepartment of Chemistry, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: jaj2109@mit.edu
bDepartment of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA. E-mail: bdolsen@mit.edu
First published on 1st May 2019
Abstract
The vast differences in material properties accessible via crosslinking of sidechain-functionalized polymers are driven by topology. For example, vulcanized rubbery networks feature intermolecular connections and loop topologies of various orders while single-chain nanoparticles (SCNPs) are comprised, in principle, entirely of primary loops. Despite this fact, precise quantification of loops in sidechain crosslinked polymers has not been accomplished. Here, it is demonstrated that by introducing cleavable linkers and mass labels onto the pendant functional groups of reactive polymers, the number of primary loops in sidechain crosslinked materials ranging from rubbery networks (gels) to soluble SCNPs can be precisely quantified. This study sheds new light on the topology of sidechain-crosslinked networks, providing design principles for augmenting the properties of this industrially and academically important class of materials through topological control.
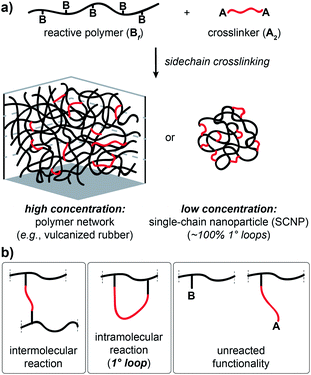
Crosslinked polymers are widely used in applications including gas storage and separation,1–4 water purification,5–7 soft robotics8,9 and additive manufacturing.10–12 Sidechain-crosslinked networks made from reactive polymers with f functional groups (Bf) and crosslinkers (A2) represent a particularly useful class of polymer networks (Fig. 1a). Perhaps the most famous example is vulcanized rubber, which is formed by crosslinking of polyisoprene natural rubber with sulphur.13 Single-chain nanoparticles (SCNPs) are another type of side-chain crosslinked polymer that have attracted extensive attention.14–18 Notably, the difference between vulcanized rubber, which is an elastic solid that is insoluble in solvents, and SCNPs, which are nano-scale soluble materials, is one of topology:19 vulcanized rubber is formed via mostly intermolecular reactions (Fig. 1b), while SCNPs are, in principle, comprised of only primary (1°) loops (i.e., “self-crosslinking” or “internal crosslinking”20 where both ends of the A2 crosslinker are connected to the same Bf macromolecule, Fig. 1b). Thus, it is important to quantify and control the topology of sidechain-crosslinked polymers to fully understand their structure and engender novel properties for emerging applications.21
Network disassembly spectrometry (NDS) is a powerful tool for precisely counting loops of various orders in end-linked polymer networks.22–26 NDS is based on the concept of a crossover experiment, wherein mass-labeled precursors are used to construct networks where the mass labels will distribute uniquely at loops of a specific order compared to all other network topologies. Chemical degradation of the networks and mass spectrometry of the labeled fragments provides the loop fractions. Compared to other methods for quantifying polymer network topology,27–29 NDS can selectively and unambiguously quantify loops of a specific order. Nevertheless, due to the requirement for mass-labeled components, NDS has so far only been used in the context of end-linked model networks; developing an analogous approach for studying the topology of sidechain-crosslinked polymers would provide new insights into the structure of these ubiquitous materials. In particular, NDS for such networks would provide a fundamentally new way to quantify the topological purity of SCNPs, which hitherto has been inferred by measurement of macromolecular size.
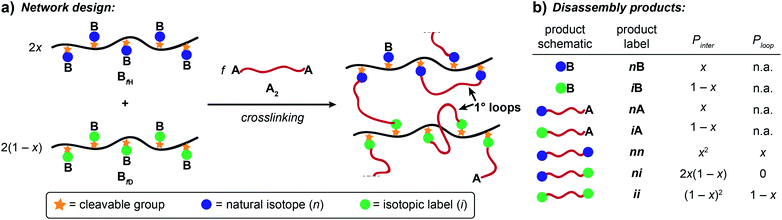
Here, we present an NDS approach for counting 1° loops in sidechain-crosslinked polymers (Fig. 2). By introducing cleavable groups and mass labels adjacent to the pendant functional groups of reactive polymers BfH and BfD (Fig. 2a), the 1° loop fraction, ϕλ, in networks derived from crosslinking a mixture of 2xBfH and 2(1 − x) BfD with bifunctional crosslinker A2 can be obtained from the mass distribution of the degradation products nn, ni, and ii (Fig. 2b) viaeqn (1) and (2).
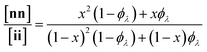 | (1) |
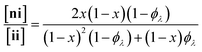 | (2) |
It is shown that ϕλ in sidechain-crosslinked rubbery networks can be exceptionally high; due to the high functionality of Bf, these networks are “loop defect tolerant” similar to other high branch functionality networks.30,31 Moreover, as for end-linked networks,21,26ϕλ plays a major role in determining the shear storage modulus (G′) of sidechain-crosslinked rubbery networks. At high dilution, soluble networks with ϕλ > 0.7 are obtained. Notably, even at very low concentrations (<1 mg mL−1 of Bf) that are often used for the synthesis of SCNPs, NDS reveals the presence of a small fraction (∼3–7%) of intermolecular reactions that strongly depends on the length of A2. Based on these results, NDS should be applied broadly to elucidate the topological purity of SCNPs.
To demonstrate the concepts outlined in Fig. 2, nitroxide-mediated polymerization of styrene and 4-vinylbenzyl acetate (5.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio) was conducted to provide random copolymer32,331 (Mn = 14
1 ratio) was conducted to provide random copolymer32,331 (Mn = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600, Đ = 1.16, Fig. 3a), which was hydrolyzed to form hydroxyl-functionalized copolymer 2. Coupling 2 with acids 3H or 3D, which contain either C4H8 or C4D8 labels, respectively, and an azide end group, yielded copolymers B20H and B20D with mass labels and azide pendant functional groups (Fig. 3a) (Mn = 17
600, Đ = 1.16, Fig. 3a), which was hydrolyzed to form hydroxyl-functionalized copolymer 2. Coupling 2 with acids 3H or 3D, which contain either C4H8 or C4D8 labels, respectively, and an azide end group, yielded copolymers B20H and B20D with mass labels and azide pendant functional groups (Fig. 3a) (Mn = 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300, Đ = 1.17, average number of azide groups per polymer = 20, see ESI† for details). B20H and B20D were combined in a 1
300, Đ = 1.17, average number of azide groups per polymer = 20, see ESI† for details). B20H and B20D were combined in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
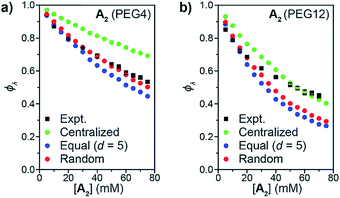
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, and this mixture was used to generate two sets of sidechain crosslinked polymer networks from A2 crosslinkers of different length (PEG4 and PEG12, Fig. 3b) via copper-catalyzed azide–alkyne cycloaddition (CuAAC).34–39 The resulting materials were hydrolyzed, and the degradation products (Fig. 3b, far right) were analyzed by LC/MS (Fig. 3c and d). Conversion was >95% for all samples (unreacted functionalities will appear as LC/MS peaks with unique masses, see Fig. 2b, allowing their facile quantification). ϕλ values for networks derived from both PEG4 and PEG12 A2 at different concentrations were obtained (Fig. 3e) from eqn (1) and (2). Similar to end-linked networks,23 the tendency to form loops in these sidechain crosslinked materials strongly depends on A2 length: networks prepared from the longer PEG12 A2 consistently had fewer loops than those prepared from PEG4 A2. In both sets of materials, the maximum ϕλ for which gelation could occur was ∼0.7; above this value, soluble materials were obtained. Based on Monte Carlo simulations, it was previously reported that gelation can occur in tetrafunctional end-linked networks (A2 + B4) when ϕλ < ∼0.35.40 Given that the maximum ϕλ for gelation increases with the junction functionality (n in this study), the observation of a critical ϕλ of ∼0.7 for gelation suggests that the effective functionality of Bf is much larger than 4, which is consistent with its chemical structure (n = 20). The ability to form robust rubbery networks even with quite high 1° loop densities, i.e., “loop defect tolerance,” is a hallmark of high branch functionality polymer networks.30,31
1 ratio, and this mixture was used to generate two sets of sidechain crosslinked polymer networks from A2 crosslinkers of different length (PEG4 and PEG12, Fig. 3b) via copper-catalyzed azide–alkyne cycloaddition (CuAAC).34–39 The resulting materials were hydrolyzed, and the degradation products (Fig. 3b, far right) were analyzed by LC/MS (Fig. 3c and d). Conversion was >95% for all samples (unreacted functionalities will appear as LC/MS peaks with unique masses, see Fig. 2b, allowing their facile quantification). ϕλ values for networks derived from both PEG4 and PEG12 A2 at different concentrations were obtained (Fig. 3e) from eqn (1) and (2). Similar to end-linked networks,23 the tendency to form loops in these sidechain crosslinked materials strongly depends on A2 length: networks prepared from the longer PEG12 A2 consistently had fewer loops than those prepared from PEG4 A2. In both sets of materials, the maximum ϕλ for which gelation could occur was ∼0.7; above this value, soluble materials were obtained. Based on Monte Carlo simulations, it was previously reported that gelation can occur in tetrafunctional end-linked networks (A2 + B4) when ϕλ < ∼0.35.40 Given that the maximum ϕλ for gelation increases with the junction functionality (n in this study), the observation of a critical ϕλ of ∼0.7 for gelation suggests that the effective functionality of Bf is much larger than 4, which is consistent with its chemical structure (n = 20). The ability to form robust rubbery networks even with quite high 1° loop densities, i.e., “loop defect tolerance,” is a hallmark of high branch functionality polymer networks.30,31
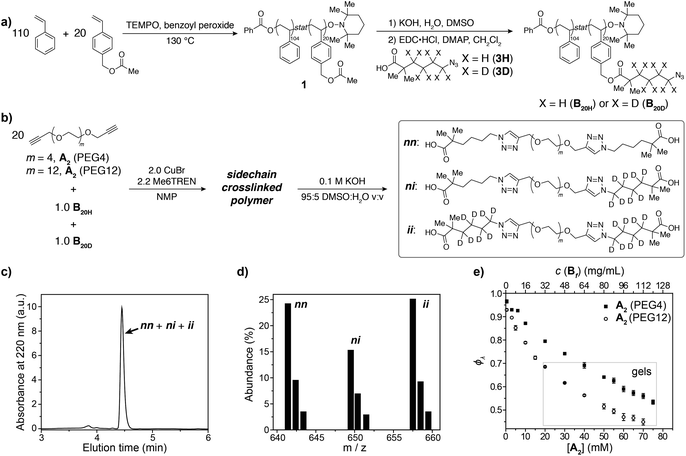 | ||
| Fig. 3 (a) Synthesis of azide-functionalized statistical copolymers B20H and B20D. (b) Synthesis and degradation of sidechain-crosslinked polymer networks derived from B20H and B20D and A2 (PEG4 or PEG12) crosslinkers provides three different doubly reacted products nn, ni, ii that vary by their isotopic labeling pattern. (c) Absorbance (220 nm) vs. elution time LC trace for degraded network formed from A2 PEG4. The major peak corresponds to the mixture of products nn, ni, and ii. (d) Representative mass spectrum showing the products nn, ni, and ii. The ratios of these products are dependent on ϕλviaeqn (1) and (2). (e) Measured ϕλ for networks derived from A2 PEG4 and PEG12 at different concentrations. Gels are formed when ϕλ < 0.7 and soluble networks are formed when ϕλ > 0.7. The material formed from A2 PEG4 at 0.8 mg mL−1 of polymer has ϕλ = 0.97 ± 0.01. | ||
When ϕλ > ∼0.7 in these materials, the preponderance of 1° loops precludes the gel point and soluble networks are obtained. Depending on the polymer mass concentration (c), a wide range of ϕλ values were observed. When c < 5 mg mL−1, ϕλ was >0.9. As described above, SCNPs are defined as sidechain-crosslinked polymers with 100% 1° loops. Previous studies by Kuhn and Balmer on crosslinking of polyvinyl alcohol and terephthalaldehyde suggested that 1° loop formation dominated when the polymer concentration was ∼1 mg mL−1 or lower.20 Moreover, SCNPs are typically formed at c ∼ 1 mg mL−1.16 Here, in the PEG4 and PEG12 materials formed at 0.8 mg mL−1, ϕλ was 0.97 ± 0.01 and 0.93 ± 0.01, respectively. Thus, even at c < 1 mg mL−1 the 1° loop fraction is not 100%. In addition, these results demonstrate that the formation of SCNPs with 100% topological purity becomes significantly more challenging as the crosslinker (here, A2) becomes larger.
When the statistics of functional group placements are appropriately captured, the experimentally measured ϕλ is qualitatively reproduced by Monte Carlo simulations without any adjustable parameters (see ESI section† for a detailed description of the MC algorithm). To explore how the distribution of groups on Bf affects 1° loop formation, three conditions were explored: point crosslinkers (centralized), where Bf is viewed as a point with 20 reactive groups (this approach is equivalent to previous studies using end-linked networks41), functional groups equally spaced by d monomers (equal), and randomly distributed functional groups (random). As shown in Fig. 4a and b, the centralized model significantly overestimated ϕλ, which is not surprising since the close proximity of the reactive groups in this model should favor intramolecular reactions. In contrast, the equal model using d = 5 based on the DP of unfunctionalized PS = 100 and n = 20 underestimated ϕλ for high concentrations. Since the pendant functional groups are not evenly distributed along the statistical copolymers used experimentally, this discrepancy highlights the impact of randomness on ϕλ, particularly overlooking pairs of reactive groups that randomly occur very close together on the polymer chain. This finding suggests that methods for precision polymerization, wherein reactive groups are precisely spaced along a polymer backbone, should provide a means for controlling the topology of sidechain-crosslinked networks and SCNPs.42–47 Finally, the random model, which describes Bf as a perfectly random copolymer, gave the best agreement with experimental data, particularly for the PEG4 materials (Fig. 4a). There was still a discrepancy between experiment and simulations for PEG12 when [A2] > 30 mM or (c > 48 mg mL−1) (Fig. 4b). The extent of this discrepancy increased with polymer concentration, and it only occurred in the gelation regime, not in the soluble network regime. Kinetic and thermodynamic considerations not incorporated into the Monto Carlo simulations may explain these observations. Regarding the former, slower diffusion of the larger PEG12 A2 crosslinker may hinder interchain crosslinking leading to an increase in ϕλ at high c values. This hypothesis was tested by lowering the catalyst loading for CuAAC from 1.0 equiv. to 0.2 equiv., which extended the gelation time by ∼5-fold. The ϕλ values for networks prepared under these two conditions were not significantly different (see ESI† for details), which is consistent with studies of end-linked networks showing that gelation kinetics have little effect on ϕλ.48 Thus, diffusion limitations may not be the main cause of the observed variation between simulation and experiment in this work. An alternative explanation could be poor mixing between A2 and Bf, which may be amplified for the longer, more polar, Bf. In the future, exploration of even longer A2 crosslinkers and crosslinkers of different composition should provide further insights into this phenomenon; here, we note that without a direct measurement of ϕλ such discrepancies between simulation and experiment would be impossible to discern.
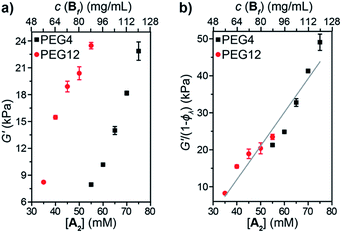
Oscillatory rheology was used to study the impact of 1° loops on G′ in these materials (Fig. 5a). In order to achieve the same G′, gels derived from PEG4 required higher concentrations compared to those derived from PEG12, which is consistent with the higher ϕλ and corresponding lower crosslinking density for the same concentration of PEG4 compared to PEG12. Normalizing G′ by 1 − ϕλ (Fig. 5b) provided a line with a slope of 910 J mol−1. According to eqn (3):
| G′ = CνeffkT = Cν0kT(1 − ϕλ) | (3) |
In summary, a conceptual framework that enables the precise quantification of 1° loops in sidechain-crosslinked polymers is presented and reduced to practice. Measurements of the primary loop fraction, ϕλ, were made for networks derived from polymers bearing ∼20 reactive groups and two different crosslinkers of varied length (PEG12 and PEG28). In both sets of materials, gels could not form when the loop fraction is >∼0.7. Moreover, ϕλ was >0.9 when polymer concentrations of 5 mg mL−1 or lower were used. Notably, even at the lowest concentration tested (0.8 mg mL−1), which is within a range commonly used to form SCNPs, the largest value of ϕλ measured (for PEG4) was 0.97 ± 0.01, and this value was significantly lower for the samples derived from PEG12. These findings suggest that the topological purity of SCNPs is very sensitive to the size of the crosslinker used, and should motivate the use of NDS methods to characterize SCNPs in the future. Monte Carlo simulations show that the distance between the pendant functional groups (d) and the randomness of the functional group distribution should both be considered for predicting ϕλ. The simulation results for the PEG4 A2 materials matched well with experimental values, but not for the PEG12 A2 materials, which highlights the importance of the chemical dissimilarity between polymer Bf and crosslinker A2 when the length of crosslinker increases. Rheology studies suggest that while primary loops considerably impact the shear storage modulus (G′), higher-order loops and the distribution of pendant functional groups also play significant roles. Altogether, these results shed new light on the topology of one of the most widely used and studied classes of materials, and should guide the design of next generation sidechain-crosslinked networks and SCNPs.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We acknowledge the support from a National Science Foundation (NSF) (CHE-1629358) and the Center for the Chemistry of Molecularly Optimized Networks, an NSF Center for Chemical Innovation (CHE-1832256). This work was supported in part by the MRSEC Program of the NSF under award number DMR-1419807.References
- N. B. McKeown and P. M. Budd, Chem. Soc. Rev., 2006, 35, 675 RSC.
- D. Q. Yuan, W. G. Lu, D. Zhao and H. C. Zhou, Adv. Mater., 2011, 23, 3723 CrossRef CAS PubMed.
- Q. Chen, M. Luo, P. Hammershoj, D. Zhou, Y. Han, B. W. Laursen, C. G. Yan and B. H. Han, J. Am. Chem. Soc., 2012, 134, 6084 CrossRef CAS PubMed.
- R. Dawson, A. I. Cooper and D. J. Adams, Prog. Polym. Sci., 2012, 37, 530 CrossRef CAS.
- A. Alsbaiee, B. J. Smith, L. Xiao, Y. Ling, D. E. Helbling and W. R. Dichtel, Nature, 2015, 529, 190 CrossRef.
- L. Xiao, Y. Ling, A. Alsbaiee, C. Li, D. E. Helbling and W. R. Dichtel, J. Am. Chem. Soc., 2017, 139, 7689 CrossRef CAS PubMed.
- C. Rizzo, S. Marullo, P. R. Campodonico, I. Pibiri, N. T. Dintcheva, R. Noto, D. Millan and F. D'Anna, ACS Sustainable Chem. Eng., 2018, 6, 12453 CrossRef CAS.
- S. A. Morin, R. F. Shepherd, S. W. Kwok, A. A. Stokes, A. Nemiroski and G. M. Whitesides, Science, 2012, 337, 828 CrossRef CAS PubMed.
- D. Rus and M. T. Tolley, Nature, 2015, 521, 467 CrossRef CAS.
- J. R. Tumbleston, D. Shirvanyants, N. Ermoshkin, R. Janusziewicz, A. R. Johnson, D. Kelly, K. Chen, R. Pinschmidt, J. P. Rolland, A. Ermoshkin, E. T. Samulski and J. M. DeSimone, Science, 2015, 347, 1349 CrossRef CAS PubMed.
- T. Jungst, W. Smolan, K. Schacht, T. Scheibel and J. Groll, Chem. Rev., 2016, 116, 1496 CrossRef CAS.
- M. Chen, Y. Gu, A. Singh, M. Zhong, A. M. Jordan, S. Biswas, L. T. J. Korley, A. C. Balazs and J. A. Johnson, ACS Cent. Sci., 2017, 3, 124 CrossRef CAS PubMed.
- M. Rubinstein and R. H. Colby, Polymer physics, Oxford University Press, Oxford, United Kingdom, 2011 Search PubMed.
- M. Gonzalez-Burgos, A. Latorre-Sanchez and J. A. Pomposo, Chem. Soc. Rev., 2015, 44, 6122 RSC.
- O. Altintas and C. Barner-Kowollik, Macromol. Rapid Commun., 2016, 37, 29 CrossRef CAS PubMed.
- A. M. Hanlon, C. K. Lyon and E. B. Berda, Macromolecules, 2016, 49, 2 CrossRef CAS.
- S. Mavila, O. Eivgi, I. Berkovich and N. G. Lemcoff, Chem. Rev., 2016, 116, 878 CrossRef CAS PubMed.
- J. Rubio-Cervilla, E. Gonzalez and J. A. Pomposo, Nanomaterials, 2017, 7, 341 CrossRef PubMed.
- Y. Gu, J. Zhao and J. A. Johnson, Trends in Chemistry, 2019 DOI:10.1016/j.trechm.2019.02.017.
- W. Kuhn and G. Balmer, J. Polym. Sci., 1962, 57, 311 CrossRef CAS.
- M. Zhong, R. Wang, K. Kawamoto, B. D. Olsen and J. A. Johnson, Science, 2016, 353, 1264 CrossRef CAS PubMed.
- H. Zhou, J. Woo, A. M. Cok, M. Wang, B. D. Olsen and J. A. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 19119 CrossRef CAS PubMed.
- H. X. Zhou, E. M. Schon, M. Z. Wang, M. J. Glassman, J. Liu, M. Zhong, D. Díaz Díaz, B. D. Olsen and J. A. Johnson, J. Am. Chem. Soc., 2014, 136, 9464 CrossRef CAS PubMed.
- K. Kawamoto, M. Zhong, R. Wang, B. D. Olsen and J. A. Johnson, Macromolecules, 2015, 48, 8980 CrossRef CAS.
- Y. Gu, K. Kawamoto, M. Zhong, M. Chen, M. J. A. Hore, A. M. Jordan, L. T. J. Korley, B. D. Olsen and J. A. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 4875 CrossRef CAS PubMed.
- J. Wang, T.-S. Lin, Y. Gu, R. Wang, B. D. Olsen and J. A. Johnson, ACS Macro Lett., 2018, 7, 244 CrossRef CAS.
- F. Lange, K. Schwenke, M. Kurakazu, Y. Akagi, U. Chung, M. Lang, J. Sommer, T. Sakai and K. Saalwächter, Macromolecules, 2011, 44, 9666 CrossRef CAS.
- F. J. Stadler, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1972 CrossRef CAS PubMed.
- B. D. Olsen and J. A. Johnson, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, E1973 CrossRef CAS.
- A. V. Zhukhovitskiy, M. Zhong, E. G. Keeler, V. K. Michaelis, J. E. P. Sun, M. J. A. Hore, D. J. Pochan, R. G. Griffin, A. P. Willard and J. A. Johnson, Nat. Chem., 2015, 8, 33 CrossRef PubMed.
- Y. Gu, E. A. Alt, H. Wang, X. Li, A. P. Willard and J. A. Johnson, Nature, 2018, 560, 65 CrossRef CAS PubMed.
- P. J. M. Stals, T. N. T. Phan, D. Gigmes, T. F. E. Paffen, E. W. Meijer and A. R. A. Palmans, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 780 CrossRef CAS.
- E. M. Doerffler and T. E. Patten, Macromolecules, 2000, 33, 8911 CrossRef CAS.
- H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004 CrossRef CAS PubMed.
- D. Díaz Díaz, S. Punna, P. Holzer, A. K. McPherson, K. B. Sharpless, V. V. Fokin and M. G. Finn, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 4392 CrossRef.
- J. A. Johnson, D. R. Lewis, D. Díaz Díaz, M. G. Finn, J. T. Koberstein and N. J. Turro, J. Am. Chem. Soc., 2006, 128, 6564 CrossRef CAS PubMed.
- C. Li and M. G. Finn, J. Polym. Sci., Part A: Polym. Chem., 2006, 44, 5513 CrossRef CAS.
- D. Fournier, R. Hoogenboom and U. S. Schubert, Chem. Soc. Rev., 2007, 36, 1369 RSC.
- Y. Liu, D. Díaz Díaz, A. A. Accurso, K. B. Sharpless, V. V. Fokin and M. G. Finn, J. Polym. Sci., Part A: Polym. Chem., 2007, 45, 5182 CrossRef CAS.
- R. Wang, T.-S. Lin, J. A. Johnson and B. D. Olsen, ACS Macro Lett., 2017, 6, 1414 CrossRef CAS.
- R. Wang, A. Alexander-Katz, J. A. Johnson and B. D. Olsen, Phys. Rev. Lett., 2016, 116, 188302–188311 CrossRef PubMed.
- M. Porel and C. A. Alabi, J. Am. Chem. Soc., 2014, 136, 13162 CrossRef CAS.
- J. C. Barnes, D. J. C. Ehrlich, A. X. Gao, F. A. Leibfarth, Y. Jiang, E. Zhou, T. F. Jamison and J. A. Johnson, Nat. Chem., 2015, 7, 810 CrossRef CAS.
- Y. Jiang, M. R. Golder, H. V.-T. Nguyen, Y. Wang, M. Zhong, J. C. Barnes, D. J. C. Ehrlich and J. A. Johnson, J. Am. Chem. Soc., 2016, 138, 9369 CrossRef CAS PubMed.
- W. R. Gutekunst and C. J. Hawker, J. Am. Chem. Soc., 2015, 137, 8038 CrossRef CAS PubMed.
- G. Li and N. S. Sampson, Macromolecules, 2018, 51, 3932 CrossRef CAS PubMed.
- M. R. Golder, Y. Jiang, P. E. Teichen, H. V.-T. Nguyen, W. Wang, N. Milos, S. A. Freedman, A. P. Willard and J. A. Johnson, J. Am. Chem. Soc., 2018, 140, 1596 CrossRef CAS PubMed.
- Y. Gu, D. Schauenburg, J. W. Bode and J. A. Johnson, J. Am. Chem. Soc., 2018, 140, 14033 CrossRef CAS PubMed.
- Given that at each reacted site (i.e., triazole) two segments from Bf are connected to one from A2, the value of v0 is 3 times the concentration of A2.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic procedures, methods and materials, and characterization data; Monte Carlo simulation algorithm for obtaining ϕλ for side-chain crosslinked polymer networks. See DOI: 10.1039/c9sc01297d |
| This journal is © The Royal Society of Chemistry 2019 |