Generalizing metallocene mechanochemistry to ruthenocene mechanophores

Abstract

Recent reports have shown that ferrocene displays an unexpected combination of force-free stability and mechanochemical activity, as it acts as the preferred site of chain scission along the backbone of highly extended polymer chains. This observation raises the tantalizing question as to whether similar mechanochemical activity might be present in other metallocenes, and, if so, what features of metallocenes dictate their relative ability to act as mechanophores. In this work, we elucidate polymerization methodologies towards main-chain ruthenocene-based polymers and explore the mechanochemistry of ruthenocene. We find that ruthenocene, in analogy to ferrocene, acts as a highly selective site of main chain scission despite the fact that it is even more inert. A comparison of ruthenocene and ferrocene reactivity provides insights as to the possible origins of metallocene mechanochemistry, including the relative importance of structural and thermodynamic parameters such as bond length and bond dissociation energy. These results suggest that metallocenes might be privileged mechanophores through which highly inert coordination complexes can be made dynamic in a stimuli-responsive fashion, offering potential opportunities in dynamic metallo-supramolecular materials and in mechanochemical routes to reactive intermediates that are otherwise difficult to obtain.

---

Introduction

A mechano-responsive polymer exhibits a specific response triggered by an external stress.^1–11 One class of mechano-responsive polymers relies on stress-responsive entities termed mechanophores that are connected to the polymer or polymer matrix such that stored tension is coupled to a specific chemical response.^12,13 A common feature of these mechanophores is that the more responsive functional groups typically have lower intrinsic activation energies associated with the chemical response of interest, leading to the selective scission of bonds that can be either covalent or coordination.^13,14 There is often a trade-off between force-free stability and mechanical lability.

Mechanophores with weak coordination bonds are usually organometallic compounds.^15–18 In contrast to most organometallic mechanophores, metallocenes, one of the most classical organometallic motifs,^19–21 are commonly regarded as being highly inert, mostly due to their thermodynamic stability. For example, ferrocene has been commonly regarded as a stable “covalent” compound based on its high bond dissociation energy (BDE).^22–25 One might therefore expect ferrocene to hold little promise as a mechanophore. Very recently, however, Fromm and Weder and we independently reported that ferrocene mechanophores embedded in polymer backbones can be mechanically activated under sonication.^26,27 We further quantified the mechanical strength of ferrocene, and found that it displays remarkable mechanochemical lability despite its substantial thermal BDE.²⁷ This counterintuitive result inspired us to question whether the mechanical lability is universal to the metallocene family, or more generally what features of metallocenes dictate their relative ability to act as mechanophores.

Ruthenocene, for example, is isoelectronic to ferrocene. The Ru–cyclopentadienyl (Cp) bond distance (metal to Cp centroid distance, 1.823 Å) is significantly larger than the Fe–Cp distance in ferrocene (1.661 Å).²⁸ Furthermore, ruthenocene is reported to have an even higher thermodynamic BDE than ferrocene (Table 1) for both a homolytic and a heterolytic dissociation process,^29–31 although comparable thermodynamic data are only available for the complete dissociation of the complexes.

Table 1 Thermodynamic bond dissociation energy (BDE) of metallocenes based on dissociation mechanisms

Metallocene	Homolytic full dissociation (kcal mol^−1)		Heterolytic full dissociation (kcal mol^−1)
	Exp	Theo	Exp	Theo
Ferrocene	158 (ref. 32)	131–156 (ref. 29, 33 and 34)	635 (ref. 31 and 35)	615–689 (ref. 29, 31, 34–37)
Ruthenocene	172 (ref. 32)	187–249 (ref. 30)	—	679–750 (ref. 30, 31 and 35)

---

Herein we report the first synthesis of ruthenocene polymers with a main-chain topology by site-specific atom transfer radical polymerization (ATRP) and ring-opening metathesis polymerization (ROMP). Ultrasonication is employed to study the mechanical activity of these ruthenocene-containing polymers. Various spectroscopic evidence and control experiments demonstrate that ruthenocene is the preferential scission site of the mechanophore along the polymer chain. The relative mechanical strength of ruthenocene is experimentally quantified through the competition between the bond scission and the non-scissile ring-opening of gem-dichlorocyclopropane mechanophores along the same polymer backbone. The scission is further elucidated by calculations.

Results and discussion

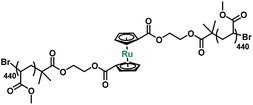
When a polymer solution is exposed to an acoustic field, the resulting cavitation events generate extensional flow fields through which the center of the polymer chain experiences the largest mechanical force.^14,38,39 To test the mechanical susceptibility of ruthenocene, a difunctional ATRP initiator 2 was prepared by esterification of 1,1′-ruthenocene dicarboxylic acid and 2-hydroxyethyl 2-bromoisobutyrate with a yield of ∼60% (Scheme S1†). Subsequent ATRP of methyl acrylate afforded poly(methyl acrylate) (PMA, P1, Scheme S1†) with high molecular weight and low dispersity (M_n = 76 400 Da, Đ = 1.06, Table 2) for sonication studies.

Table 2 Main-chain ruthenocene-containing polymers used in this study

Polymer	Structure	M n (Da)	Đ	Labeling molar ratio
P1		76 400	1.06	0.11%
P2		56 500	1.02	0.15%
P3		113 000	1.61	2.8%
P4		104 000	1.52	11%
P5		86 800	1.58	5.0%

---

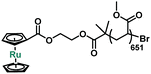
Sonication of P1 was conducted in acetonitrile at a concentration of 2 mg mL⁻¹. One cumulative hour of sonication led to a decrease of molecular weight to 52 600 Da, or 54% of chains broken. The activation of ruthenocene was quantified by the change in relative integration of ¹H NMR peaks from 4.7–5.3 ppm (Fig. S1†). The analysis shows that 58 ± 2% of ruthenocene has disappeared. The correlation between apparent number of ruthenocene scission and chain scission events indicates that ruthenocene is the preferential scission site along the polymer chain. Similar to ferrocene, new peaks (δ = 7.5–6.6 ppm, Fig. S1†) were observed after sonication, consistent with the mechanical generation of dissociated Cp ligands.^27,40–42 These freshly formed Cp ligands led us to speculate that the mechanism of ruthenocene dissociation might resemble that previously attributed to ferrocene dissociation, namely the mechanical generation and subsequent protonation of Cp anions.²⁷ In order to validate that the activity of ruthenocene originates from the coupled mechanical stress, a control polymer P2 with ruthenocene located at the chain terminus (Table 1, Scheme S1†) was prepared from ruthenocene-based ATRP monofunctional initiator 3. After sonication under the same conditions as P1, P2 showed no changes in its ¹H NMR spectra associated with ruthenocene dissociation (Fig. S2†). We therefore rule out dissociation mechanisms based on heating and/or the production of reactive species independent of tension along the polymer chain.^4,13

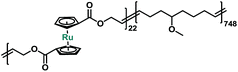
In order to better probe and quantify the mechanochemical reactivity of ruthenocene, we turned to a multi-mechanophore labeling strategy that has previously proven to be useful.⁴³ Entropy-driven ring-opening metathesis polymerization (ROMP) serves as a robust tool to incorporate main-chain functionalities.⁴³ The cyclic olefin monomers of mechanophores can be obtained through the versatile ring-closing metathesis (RCM) of terminal dienes. It should be noted that for the preparation of metallocene-based cyclic olefins, the size of macrocycles and substituents should be carefully considered, as these factors strongly affect the interplay of entropy and enthalpy during ring closing.⁴⁴ Our synthetic approach is described in Scheme S2.† Copolymerization of 5 with 5-methoxycyclooctene yielded copolymer P3 with multiple ruthenocene moieties on the polymer backbone. Sonication of P3 was conducted in tetrahydrofuran (THF) at a concentration of 2 mg mL⁻¹. Similar to P1, ruthenocene in copolymer P3 was the preferential scission site during sonication based on the normalized ¹H NMR spectra, as shown in Fig. S4 in ESI.†

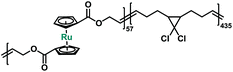
Macrocycle 5 was then copolymerized with gem-dichlorocyclopropane (gDCC) based cyclooctene to yield polybutadiene-like (PB-like) polymers P4 and P5. Under sonication, the mechanochemical ring opening of non-scissile gDCC serves as an internal standard that competes with ruthenocene scission to report the bond strength of ruthenocene (Fig. 1a). This methodology has been successfully used to estimate the mechanical strength of weak bonds including ferrocene.^27,45 The extent of ring opening per scission cycle (Φ_i) describes the ratio of ring opening that accompanies a representative weak bond scission. As Fig. 1b shows, the slopes of ruthenocene-containing polymers (P4 and P5) are each lower than that of poly(gDCC), which means the Ru–Cp bond is more susceptible to mechanical force than the poly(gDCC) backbone, consistent with the observed preference for ruthenocene scission. The reduction in Φ_i from P5 (0.52) to P4 (0.43) is due to the increased incorporation of the ruthenocene (5% vs. 11%).

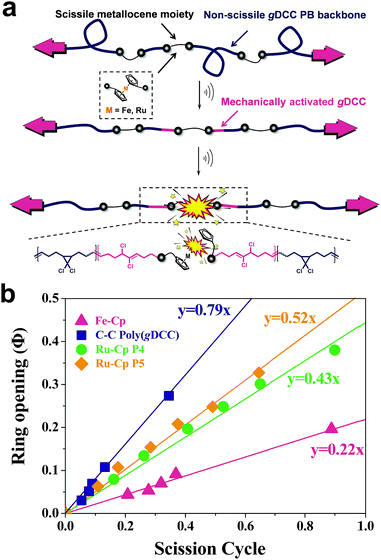Fig. 1 (a) Scheme of a multi-mechanophore polymer system to examine ruthenocene scission and gDCC ring opening; (b) fraction of ring opening of gDCC versus scission cycle for poly(gDCC),²⁷ ferrocene-containing polymer (labeling ratio: 10%)²⁷ and ruthenocene-containing polymers.

When compared to ferrocene with a similar labeling ratio (Φ_i = 0.22 at 10% ferrocene),²⁷P4 shows considerably higher Φ_i (0.43), indicating that the mechanical strength of ruthenocene is higher than ferrocene. This result is contradictory to an empirical rule that rupture forces usually decrease when bond length increases because the longer bond length suggests softer potential, which in general would be more easily deformable,¹⁴ but aligns well with the relative thermodynamic strength of the two metallocenes (Table 1). The nascent bond strengths, rather than bond lengths, appear from the data to be the better predictors of the relative mechanical strength of metallocenes. The Φ_i value allows one to compare the mechanical strength of ruthenocene to other known covalent bonds. In particular, the Φ_i of the carbon–sulfur bond of a thioether (BDE = 54 kcal mol⁻¹) is 0.43 at a labeling ratio of 12%.^45,46 Ruthenocene therefore appears to be effectively indistinguishable from a thioether in terms of its mechanical lability during sonication, even though the BDE of the Ru–Cp bond is much greater (see Table 1). This result also suggests the tantalizing possibility that mechanical lability may be a common feature of metallocenes in general.

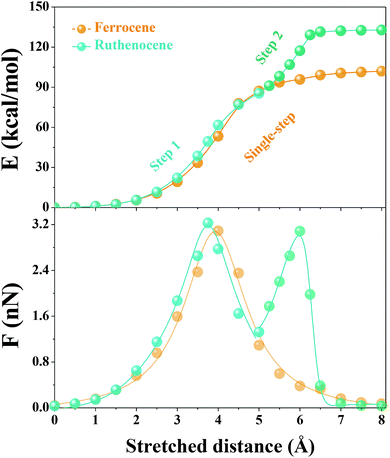
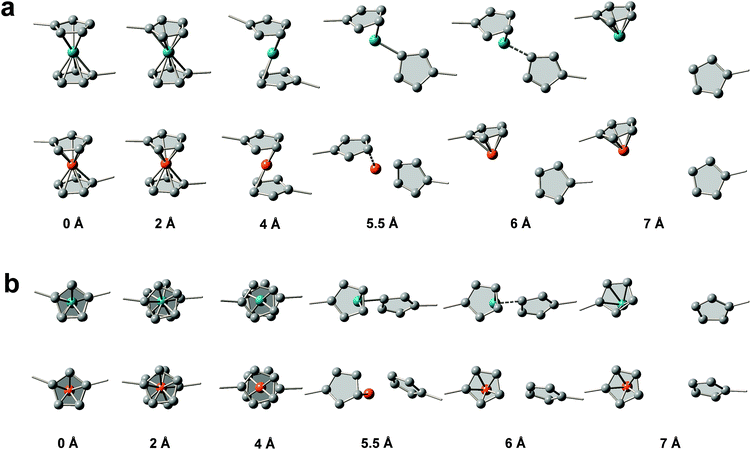
We then used constrained geometries simulated external force (COGEF) simulations⁴⁷ to provide more mechanistic insights into the mechanochemical process of ruthenocene dissociation to see how the interplay of bond length and bond strength plays out. The DFT computational details (functionals, pseudopotential and basis sets) are summarized in the ESI.† Briefly, the reaction is simulated by artificially stretching the end-to-end distance of a model molecule to a fixed value whereas the other structural geometries remain fully relaxed, yielding potential energy and force of the constrained molecule as a function of end-to-end distance as shown in Fig. 2. Simultaneously, the structural evolution of the reaction can be obtained, some representative structures are shown in Fig. 3.

Fig. 2 COGEF potential and force as a function of stretched distance for ruthenocene and ferrocene model compounds (the substituents on Cp are omitted for viewing clarity). The stretched distance defined as 0 Å when no stress is applied.

Fig. 3 (a) Front view and (b) top view for structural evolution of metallocene model compounds (the substituents on Cp were not displayed) as a function of elongated distance. Grey ball represents carbon atom, blue ball represents ruthenium atom and orange ball represents iron atom.

Surprisingly, the COGEF potential of ruthenocene model compound shows a two-step dissociation process that is quite different from the single-step dissociation of ferrocene. When no stress is applied on the ruthenocene, the two Cp rings align in an eclipsed geometry (Fig. 3b). Initial stretching twists the Cp rings to a staggered geometry due to low energy barrier for Cp rotation.⁴⁸ Then two Cp rings come to a staggered geometry along the stretching direction. Beyond this point (2 Å), stretching leads to a rapid increase in energy due to bond angle distortion and bond length changes, until the maximum slope of the COGEF potential curve and thus the maximum force is reached (3.75 Å, a peak value in force profile of Fig. 2). This first step in the dissociation process for ruthenocene is quite similar to that of ferrocene, resulting in a similar COGEF potential curve (Fig. 2). Notably, the COGEF potential as well as the force plot is slightly contracted in ruthenocene relative to ferrocene; its inflection point occurs at a smaller extension and has a larger slope (corresponding to a maximum sustainable force). This observation is somewhat counterintuitive to us, as the larger Ru–Cp bond length in ruthenocene suggested a softer bonding potential that is not reflected along the COGEF coordinate. We hypothesize that the reason that the initial COGEF potential of ruthenocene is so similar to that of ferrocene may be due at least in part to the fact that the pulling direction (and therefore the COGEF potential) is nearly perpendicular to the orientation of the metal–Cp bond. Because the COGEF dissociation coordinate is not necessarily the same as the reaction coordinate for force-free metal–Cp dissociation, electronic factors that lead to differences in ruthenocene and ferrocene bonding need not be directly reflected in the force-coupled dissociation pathways.

In contrast, striking differences in behavior are observed upon further extension. When the stretching distance of ferrocene comes to 5.5 Å, pronounced Cp⁻ and [CpFe]⁺ cleavage takes place, and further stretching leads to a complete separation of the two fragments. In comparison, the complete dissociation of ruthenocene has not yet occurred even when the stretching distance comes to 5.5 Å. Further stretching of ruthenocene maintains a barrier to dissociation, and the force value increases to a second maximum (Fig. 2). As seen in Fig. 3, this second stage of mechanically induced dissociation can be attributed to the rich coordination structure that is available in ruthenium but not in row 2 organic covalent bonding. In particular, the observed structures are reminiscent of ring-slippage chemistry that has been observed in other transition-metal cyclopentadienyl complexes.⁴⁹

Beyond the stretching distance of 5.5 Å, the distance between one carbon atom of detached Cp and ruthenium is still within the range of coordination bonding modes because of its nascent high BDE, making the Cp still “sticky” to ruthenium. Further stretching to 6 Å leads to the Ru–C bond elongation and reaches a second inflection point (local maximum sustainable force) on the COGEF potential energy surface, resulting in a delayed fragmental separation. Ultimately, [RuCp]⁺ and Cp⁻ are well separated after an extension of ∼7 Å, and the calculated potential comes to a plateau with force release following the sequential two-step dissociation process, leading to higher mechanical BDE than the single-step dissociation in ferrocene.²⁷

Next, the bond cleavage mechanism of ruthenocene is examined. A molecular electrostatic potential (ESP) plot mapped onto a molecular surface gives intuitive guidance about the charge distribution during dissociation.^51–53 ESP maps of the ruthenocene model are shown as a function of stretching distance in Fig. 4a. Prior to Cp slippage, the ESP distribution is centrosymmetric. When it was stretched to 5 Å where the Cp ring slippage is discernable, the left segment ([RuCp]⁺) possesses more positive ESP, and the right segment (dissociated Cp⁻) picks up negative charge density. Further stretching results in a complete dissociation and charge separation of ruthenocene, as signified by peak positive potential (blue color) in the ESP located on the ruthenium atom. The ESP analysis supports the conclusion drawn from experiments that ruthenocene dissociation is likely heterolytic in nature, with substantial charge separation at the point of scission.

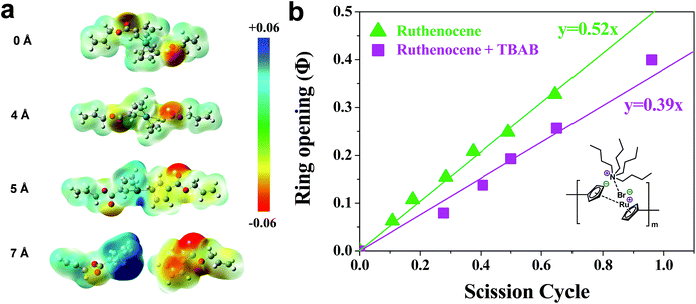Fig. 4 (a) Electrostatic potential map as a function of stretched distance. The contour surface is defined based on the van der Waals surface with an electron density of 0.001 e/Bohr³ proposed by Bader.⁵⁰ (b) Fraction of ring opening of gDCC vs. ruthenocene scission cycles for P5 with/without the presence of TBAB.

Experimentally, we also hypothesized that the Ru–Cp bond cleavage is heterolytic and involves a charge separation process to produce [CpRu]⁺ and Cp⁻ in solution. In THF solvent with relative low dielectric constant, the dissociation energy would include a contribution from the charge separation. Excess tetrabutylammonium bromide (TBAB) was mixed with P5 to stabilize the charge separation and/or facilitate ligand exchange. As shown in Fig. 4b, the presence of TBAB lowers Φ_i of ruthenocene from 0.52 to 0.39, but has no measurable effect on polybutadiene-like backbone cleavage in the absence of ruthenocene.²⁷ These experiments support a heterolytic mechanism of ruthenocene dissociation. The presence of a heterolytic dissociation might seem at odds with the relative energies of heterolytic and homolytic processes reported in Table 1, but it is important to note that the experimental/computational values in Table 1 are gas phase values. In the condensed phase, solvent dielectric effects and/or coordination to the exposed metal center will have a substantial, albeit unquantified, stabilizing effect on the charged products of heterolytic dissociation. Thus, it is possible that the heterolytic pathway is the energetically preferred dissociation pathway under the conditions of the sonication experiments.

Conclusions

In summary, we prepared single and multiple ruthenocene-labeled main-chain polymers based on site-specific ATRP and entropy-driven ROMP. Despite its thermodynamic stability, ruthenocene is the selective site of mechanical scission, in a manner similar to ferrocene previously observed, suggesting that metallocenes might be a privileged class of mechanophores that possess intriguing combinations of force-free thermal stability and mechanical lability. The fact that both computational and experimental mechanistic studies show striking similarities in the mechanochemistry of the two mechanophores further support the idea that metallocene mechanochemistry holds rich potential for stress-responsive metallo-polymers and as a tool in metallocene synthesis.

Whereas there are similarities in the mechanochemistry of ruthenocene and ferrocene, the current studies also reveal important variations in behaviors that hint at mechanisms through which to tune metallocene mechanochemistry and that motivate further studies. In particular, the existence of multiple discrete coordination states as intermediates on the ring-slip dissociation pathway provides a potential avenue to tune metallocene mechanochemistry, for example, by adjusting metal and/or ligand electronics to bias the relative contributions of the two modes of interactions. Ruthenocene is shown here to be less reactive under both force-free and force-coupled conditions, but it might be possible to design metallocenes that are even more inert thermally while also being more active mechanically. Similarly, one can imagine gaining access to new modes of organometallic reactivity, either through the complete dissociation of ligands that are otherwise difficult to remove or by accessing “partial slip” states of unusual coordination as observed here in ruthenocene. Given the breadth of metallocene structures available in this classical set of compounds, we see the possibility of even richer behaviors yet to be uncovered.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is partially supported by the National Science Foundation (OIA-1655740 to C. T.) and by the US Army Research Laboratory and the Army Research Office (Grant W911NF-15-0143 to S. L. C).

References

1. Z. Chen, J. A. M. Mercer, X. Zhu, J. A. H. Romaniuk, R. Pfattner, L. Cegelski, T. J. Martinez, N. Z. Burns and Y. Xia, Science, 2017, 357, 475–478.
2. K. Ishizuki, D. Aoki, R. Goseki and H. Otsuka, ACS Macro Lett., 2018, 7, 556–560.
3. M. J. Robb, T. A. Kim, A. J. Halmes, S. R. White, N. R. Sottos and J. S. Moore, J. Am. Chem. Soc., 2016, 138, 12328–12331.
4. D. A. Davis, A. Hamilton, J. L. Yang, L. D. Cremar, D. Van Gough, S. L. Potisek, M. T. Ong, P. V. Braun, T. J. Martinez, S. R. White, J. S. Moore and N. R. Sottos, Nature, 2009, 459, 68–72.
5. J. M. Clough, A. Balan, T. J. van Daal and R. P. Sijbesma, Angew. Chem., Int. Ed., 2016, 55, 1445–1449.
6. Y. L. Chen, A. J. H. Spiering, S. Karthikeyan, G. W. M. Peters, E. W. Meijer and R. P. Sijbesma, Nat. Chem., 2012, 4, 559–562.
7. M. Karman, E. Verde-Sesto, C. Weder and Y. C. Simon, ACS Macro Lett., 2018, 7, 1099–1104.
8. H. Zhang, X. Li, Y. Lin, F. Gao, Z. Tang, P. Su, W. Zhang, Y. Xu, W. Weng and R. Boulatov, Nat. Commun., 2017, 8, 1147.
9. G. De Bo, Chem. Sci., 2018, 9, 15–21.
10. N. Willis-Fox, E. Rognin, T. A. Aljohani and R. Daly, Chem, 2018, 4, 2499–2537.
11. K. M. Herbert, S. Schrettl, S. J. Rowan and C. Weder, Macromolecules, 2017, 50, 8845–8870.
12. K. L. Berkowski, S. L. Potisek, C. R. Hickenboth and J. S. Moore, Macromolecules, 2005, 38, 8975–8978.
13. J. Li, C. Nagamani and J. S. Moore, Acc. Chem. Res., 2015, 48, 2181–2190.
14. M. K. Beyer and H. Clausen-Schaumann, Chem. Rev., 2005, 105, 2921–2948.
15. A. Piermattei, S. Karthikeyan and R. P. Sijbesma, Nat. Chem., 2009, 1, 133–137.
16. J. M. J. Paulusse and R. P. Sijbesma, Chem. Commun., 2008, 4416–4418.
17. S. Karthikeyan, S. L. Potisek, A. Piermattei and R. P. Sijbesma, J. Am. Chem. Soc., 2008, 130, 14968.
18. J. M. J. Paulusse and R. P. Sijbesma, Angew. Chem., Int. Ed., 2004, 43, 4460–4462.
19. J. Zhang, Y. Yan, M. W. Chance, J. Chen, J. Hayat, S. Ma and C. Tang, Angew. Chem., Int. Ed., 2013, 52, 13387–13391.
20. Y. Yan, J. Zhang, L. Ren and C. Tang, Chem. Soc. Rev., 2016, 45, 5232–5263.
21. C. G. Hardy, J. Zhang, Y. Yan, L. Ren and C. Tang, Prog. Polym. Sci., 2014, 39, 1742–1796.
22. A. Haaland, Acc. Chem. Res., 1979, 12, 415–422.
23. R. A. Musgrave, A. D. Russell, D. W. Hayward, G. R. Whittell, P. G. Lawrence, P. J. Gates, J. C. Green and I. Manners, Nat. Chem., 2017, 9, 743–750.
24. T. Zhu, Y. Sha, J. Yan, P. Pageni, M. A. Rahman, Y. Yan and C. Tang, Nat. Commun., 2018, 9, 4329.
25. T. Zhu, S. Xu, A. Rahman, E. Dogdibegovic, P. Yang, P. Pageni, M. P. Kabir, X. Zhou and C. Tang, Angew. Chem., Int. Ed., 2018, 57, 2388–2392.
26. M. Di Giannantonio, M. A. Ayer, E. Verde-Sesto, M. Lattuada, C. Weder and K. M. Fromm, Angew. Chem., Int. Ed., 2018, 57, 11445–11450.
27. Y. Sha, Y. Zhang, E. Xu, Z. Wang, T. Zhu, S. L. Craig and C. Tang, ACS Macro Lett., 2018, 7, 1174–1179.
28. M. Swart and J. G. Snijders, Theor. Chem. Acc., 2003, 110, 34–41.
29. K. Pierloot, B. J. Persson and B. O. Roos, J. Phys. Chem., 1995, 99, 3465–3472.
30. Q. M. Phung, S. Vancoillie, A. Delabie, G. Pourtois and K. Pierloot, Theor. Chem. Acc., 2012, 131, 1238.
31. M. Swart, Inorg. Chim. Acta, 2007, 360, 179–189.
32. M. F. Ryan, J. R. Eyler and D. E. Richardson, J. Am. Chem. Soc., 1992, 114, 8611–8619.
33. J. Frunzke, M. Lein and G. Frenking, Organometallics, 2002, 21, 3351–3359.
34. M. Lein, J. Frunzke, A. Timoshkin and G. Frenking, Chem.–Eur. J., 2001, 7, 4155–4163.
35. M. J. Mayor-Lopez and J. Weber, Chem. Phys. Lett., 1997, 281, 226–232.
36. P. Quan Manh, S. Vancoillie and K. Pierloot, J. Chem. Theory Comput., 2012, 8, 883–892.
37. C. H. W. Kelly and M. Lein, Phys. Chem. Chem. Phys., 2016, 18, 32448–32457.
38. M. M. Caruso, D. A. Davis, Q. Shen, S. A. Odom, N. R. Sottos, S. R. White and J. S. Moore, Chem. Rev., 2009, 109, 5755–5798.
39. T. Stanch and A. Dreuw, Chem. Rev., 2016, 116, 14137–14180.
40. M. Tanabe and I. Manners, J. Am. Chem. Soc., 2004, 126, 11434–11435.
41. S. Top, J. S. Lehn, P. Morel and G. Jaouen, J. Organomet. Chem., 1999, 583, 63–68.
42. G. L. Grunewald and D. P. Davis, J. Org. Chem., 1978, 43, 3074–3076.
43. B. H. Bowser and S. L. Craig, Polym. Chem., 2018, 3583–3593.
44. Y. Sha, Y. Zhang, T. Zhu, S. Tan, Y. Cha, S. L. Craig and C. Tang, Macromolecules, 2018, 51, 9131–9139.
45. B. Lee, Z. Niu, J. Wang, C. Slebodnick and S. L. Craig, J. Am. Chem. Soc., 2015, 137, 10826–10832.
46. J. A. Hawari, D. Griller and F. P. Lossing, J. Am. Chem. Soc., 1986, 108, 3273–3275.
47. M. K. Beyer, J. Chem. Phys., 2000, 112, 7307–7312.
48. D. Astruc, Eur. J. Inorg. Chem., 2017, 6–29.
49. J. M. Oconnor and C. P. Casey, Chem. Rev., 1987, 87, 307–318.
50. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
51. F. A. Bulat, A. Toro-Labbe, T. Brinck, J. S. Murray and P. Politzer, J. Mol. Model., 2010, 16, 1679–1691.
52. P. Politzer and J. S. Murray, Theor. Chem. Acc., 2002, 108, 134–142.
53. T. Brinck, J. S. Murray and P. Politzer, Mol. Phys., 1992, 76, 609–617.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sc01347d

‡ These authors contributed equally.

---