Conformational diversity induces nanosecond-timescale chemical disorder in the HIV-1 protease reaction pathway

Abstract

The role of conformational diversity in enzyme catalysis has been a matter of analysis in recent studies. Pre-organization of the active site has been pointed out as the major source for enzymes' catalytic power. Following this line of thought, it is becoming clear that specific, instantaneous, non-rare enzyme conformations that make the active site perfectly pre-organized for the reaction lead to the lowest activation barriers that mostly contribute to the macroscopically observed reaction rate. The present work is focused on exploring the relationship between structure and catalysis in HIV-1 protease (PR) with an adiabatic mapping method, starting from different initial structures, collected from a classical MD simulation. The first, rate-limiting step of the HIV-1 PR catalytic mechanism was studied with the ONIOM QM/MM methodology (B3LYP/6-31G(d):ff99SB), with activation and reaction energies calculated at the M06-2X/6-311++G(2d,2p):ff99SB level of theory, in 19 different enzyme:substrate conformations. The results showed that the instantaneous enzyme conformations have two independent consequences on the enzyme's chemistry: they influence the barrier height, something also observed in the past in other enzymes, and they also influence the specific reaction pathway, which is something unusual and unexpected, challenging the “one enzyme–one substrate–one reaction mechanism” paradigm. Two different reaction mechanisms, with similar reactant probabilities and barrier heights, lead to the same gem-diol intermediate. Subtle nanosecond-timescale rearrangements in the active site hydrogen bonding network were shown to determine which reaction the enzyme follows. We named this phenomenon chemical disorder. The results make us realize the unexpected mechanistic consequences of conformational diversity in enzymatic reactivity.

---

Introduction

As is the case with very large molecules, enzymes have a very large number of internal degrees of freedom. Their structures fluctuate significantly over time at physiological temperature, resulting in many interchanging conformations.^1–3 There are many enzyme conformations, well populated, which can be the starting point of the corresponding catalytic reactions. In the same way, these reactant conformations may lead to transition states and products with different geometries, or different energetics for similar transition states and products. Due to the time scale of typical bond-breaking and bond-forming processes (femtoseconds), enzyme conformations remain mostly unchanged during the event of barrier crossing. The experimental reaction rate is usually measured on macroscopic amounts of proteins and over macroscopic time scales, and reflects a weighted average over all these possible barriers arising from different instantaneous reactant conformations. Single-molecule kinetic measurements confirmed this picture.⁴ As these experiments measure chemical turnovers, the diversity of the observed activation barriers was limited to those that are crossed during the time of the experiment. It is tempting to speculate that, in these experiments, instantaneous barriers that lead to turnovers slower than the experimental timescale will always pass unnoticed, as the enzyme will change to lower-barrier conformations before a barrier crossing can be observed. Enzymatic studies using computational methods may easily be performed on single structures to measure barriers that are insurmountable in the time scale of experiments and clearly isolate this effect from the macroscopic average, something that experimentally is very difficult to do.

The influence of enzyme conformations on reactivity

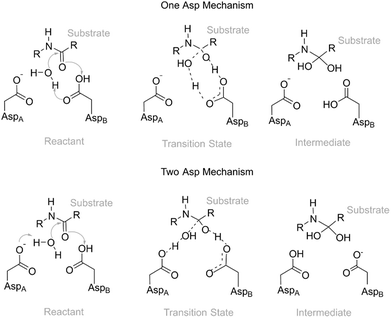
Active site pre-organization has been surfacing as the most relevant factor behind the origin of an enzyme's catalytic power.^5,6 Chemical reactions in enzymes only occur on physiologically useful timescales when the active site residues are in a suitable pre-organization position/orientation to promote the reaction; otherwise the energetic barriers will be very high, and the reaction will not take place. Enzymes are very proficient in keeping the residues in an orientation that specifically stabilizes the transition structures, as they fold in a way to lock them in those orientations. However, the position of the key residues and, in particular, the distances between the residues and the reacting substrate atoms still fluctuate significantly in the ps–ns timescale, and even at larger timescales due to greater global enzyme movements, caused by thermal motion. This strong dependence of the reactivity on specific enzyme conformations has been demonstrated by different computational studies, in which the activation barriers were calculated for several different initial conformations of the same enzyme.^7–16 For example, in ketosteroid isomerase, the barriers change is about 20 kcal mol⁻¹ due to a structural variation on the active site, which determines its closure and, consequently, the progress of the catalyzed reaction.¹² In fluoroacetate dehalogenase, twenty snapshots in three different systems were used, and it was found that the barrier of each reaction varies by up to 15 kcal mol⁻¹. These energetic fluctuations were associated with structural parameters of the active site.¹³ In the reaction catalyzed by P450, variations up to 17 kcal mol⁻¹ were also found.¹⁴ Our previous study on α-amylase showed that the position of a buried water molecule highly influences the barrier of activation for this enzyme. Values from 9.3 to 28.6 kcal mol⁻¹ were calculated. The fluctuations in the barrier were caused, to a very significant extent, by the fluctuations in the position and orientation of this water molecule and of the two active-site reactive residues.⁷ These are only a few of a number of studies in which this phenomenon was studied in detail. Combining all these barriers into a single, observed one is a matter of intense research.^8,17–19 The main difficulty lies in the necessary extensive sampling that is needed to obtain good statistical convergence in the barrier height and to determine the contribution of each of the individual barriers to the final observed barrier. The thermodynamic ensembles generated by molecular mechanics force field based molecular dynamics (MM-MD) simulations from which the structures are extracted can be well balanced, but there is no guarantee that this good balance will be retained when the ensemble is reduced to a few tenths of snapshots and the MM force field is transformed into a QM/MM Hamiltonian. However, the objective of these studies is not to calculate an accurate value for the “macroscopic barrier” but instead to shed light on the fine structural requirements for a reaction to take place with a low activation barrier. Other methods, such as QM/MM MD, implicitly deal with and average these instantaneous barrier fluctuations. However, in these cases, the Hamiltonian used to describe the catalytic region is usually simplified, and the size of the QM region is reduced, in order to calculate the energies of very many structures generated by these methods.^20–25 Recent state-of-the-art studies have already calculated potentials of mean force with high-level hybrid–meta Hamiltonians, even though the size of the QM region is still reduced and the MD time, despite being remarkable, is still smaller than the timescale of many enzyme structural fluctuations, due to insurmountable CPU limitations.²⁶ In these excellent studies, the effects of conformational diversity are accounted for implicitly, through the sampling made in each point along the reaction coordinate, and thus not used to gain understanding of the nature of the fluctuations in the interactions that stabilize the transition structures, which is the major purpose of this study and other studies of this kind.

In the present work, we have studied the first, rate-limiting step of the catalytic mechanism of HIV-1 PR (Fig. 1). This reaction step was found to take place through either the One Asp mechanism (Fig. 1, top) or the Two Asp mechanism (Fig. 1, bottom), depending on the reactant's conformation. We have thus tried to identify correlations between enzyme:substrate structural fluctuations and the reaction mechanism (and reaction rate), to understand the factors that led to this mechanistic divergence.

Fig. 1 The first step of the One Asp (top) and Two Asp (bottom) catalytic mechanisms on the carbonyl carbon of the substrate scissile bond, forming a tetrahedral intermediate. In the One Asp mechanism, the same aspartate residue (AspB) deprotonates the hydrolytic water molecule and protonates the peptide oxygen – one carboxylate oxygen acts as an acid and the other as a base. In the Two Asp mechanism, which is most widely accepted, one of the two active site aspartates (AspB) protonates the oxyanion generated by the water attack, while the other (AspA) deprotonates the nucleophilic water. Conventionally, AspB is the residue that is considered to be protonated – the two chains are equivalent.

Earlier studies^27–29 systematically favored the Two Asp mechanism, where the Asp25 from a chain acts as a base and the Asp25 from the other chain acts as an acid, over the One Asp mechanism, in which a single Asp25 takes on the two roles. Here we investigate the extent to which the preference for the Two Asp mechanisms could have been caused by the insufficient conformational space explored in these earlier studies.

To do so, one of the possible approaches is to sample several reaction paths with QM(DFT)/MM methods, using different initial structures of the enzyme:substrate complex gathered from a long MM-MD simulation, which can span much larger timescales than a QM/MM MD. In that sense, ONIOM QM/MM calculations were performed on HIV-1 PR, starting from 19 different initial structures taken from a 130 ns MM-MD simulation, as well as the X-ray structure. This system was selected for two main reasons: (a) the size of this enzyme is small, and its structure is relatively simple and well known, composed of two identical amino acid chains, with 99 residues in each one; (b) its catalytic mechanism is well studied, both experimentally and theoretically, and can easily be transposed to similar, also well-studied, aspartic proteases.^8,15,29

The results were analyzed focusing on the understanding of the relationship between reaction pathways and activation energies obtained from each reactant conformation, and specific interactions that occur in that same conformation. We related the obtained activation barriers with structural parameters of each conformation, analyzing in particular the main enzyme–substrate distances of the active site. The results showed that the fine-level structural organization of the active site hydrogen bonding network is determinant to define the pathway of the chemical reaction. Different conformations of the active site led not only to different barriers but also to two different reaction paths with comparable barrier heights. This kind of mechanistic divergence took place at the nanosecond timescale in which the conformations were sampled.

Methods

The computational protocol used in this work was very similar to the one used in one of our previous studies:³⁰ we started by modeling the enzyme–substrate complex using the 4HVP PDB structure,³¹ added hydrogen atoms to the structure with the software xleap³² (standard protonation states were predicted by PropKa,³³ except for Asp25B, which is known to be neutral at physiological pH), inserted the system into a pre-equilibrated rectangular water box whose faces were at least 12 Ångstrom away from any protein atom (details in the ESI†), equilibrated the system with a short MM-MD heating run, from 0 to 300 K in 40 ps, and subsequently performed a 130 ns MM-MD simulation in the NPT ensemble to sample the conformational space of the system. All the modeling and MD details can be found in the ESI.† Next, we studied the first step of the HIV-1 protease catalytic mechanism using a QM/MM methodology, starting from 30 different structures, collected from the latter MM-MD simulation. From these, 19 were possible to characterize with full convergence criteria, and over the latter we performed a structural analysis of the active site residues, correlating their structural fluctuations with the obtained activation energies. Different snapshots from the MM-MD simulation were taken based on the simulation time. We started by selecting some structures from the initial nanoseconds of the MM-MD simulation. However, the results associated with these structures were discarded due to very high barriers. We associated these results with an incorrect position of the catalytic water molecule (not present in any X-ray structure), modeled in the active site by us. Taking this into account, we decided to select well-equilibrated snapshots at regular intervals (1 ns) subsequent to the first 100 ns of MM-MD simulation.

Fig. S1† shows the distribution of energies of the reactant state in the MM-MD simulation (grey bars). The purple line indicates how many structures from each MM-MD energy range were extracted, as a full protein:substrate plus water shell model, and changed to the QM/MM level, to calculate the reaction mechanism and activation barriers. As can be seen, the structures taken from the MM-MD simulation belong to well-populated areas of the MM-MD ensemble and follow the MM-MD distribution reasonably well, even though direct comparison should be made with caution due to the change in the system's Hamiltonian. Both distributions do not need to be “superimposable”, but only “reasonably similar”. In fact, the reaction rate depends linearly on the conformation populations but exponentially on the activation free energy and, therefore, differences between the distributions only have an impact on the reaction rate if they amount to orders of magnitude.

Similar QM/MM models, applying an ONIOM scheme as implemented in the Gaussian 09 software package,³⁴ were defined for each enzyme:substrate complex. All the prepared systems contained a total of 6232 atoms with 90 atoms in the QM layer and the remaining system in the MM layer. The QM layer contained the two catalytic aspartates, the nucleophilic water molecule, seventeen atoms of the substrate, two other water molecules and some residues around the groups that actively participate in the reaction (Ala28B, Gly27B, Thr26B, Gly27A, Ala28A, and the carbonyl group of Thr26A). A cap of 1000 water molecules (∼3 Å around the protein) was kept in the model. The water molecules were frozen during all the calculations, except the ones present in the high layer. The freezing scheme was shown to be adequate in an earlier study.³⁰ The interaction between the layers was treated with the electrostatic embedding scheme. The QM layer was optimized with the density functional B3LYP³⁵ and 6-31G(d) basis set. Hydrogen atoms were used as link atoms where QM covalent bonds were truncated. The reaction path was studied in the same manner for all models, using the same reaction coordinate (the distance between the oxygen of the nucleophilic water molecule and the carbonyl carbon of the scissile peptide bond of the substrate) for an initial exploitation. The structures with the highest energy in the performed scans were used as starting guesses for a full optimization of the transition structure geometry. Nuclear vibrational frequencies were determined to confirm the nature of the stationary points (absence of imaginary frequencies in minima and one imaginary frequency in each transition state). Zero-point energies were computed at the B3LYP/6-31G(d) level of theory,^36–38 using the harmonic oscillator/rigid rotor formalism.^39,40 Intrinsic reaction coordinate (IRC) calculations were performed to obtain reactant, transition state and product structures in the same relative minimum. Single point energy calculations were performed using the M06-2X density functional and a higher basis set (6-311++G(2d,2p)). This theoretical level was used because we have seen in earlier benchmarks that it provides excellent results for main group chemistry reactions in enzymes.^41–44 The final results were represented as QM/MM energies plus ZPE. All the calculations were performed using the ONIOM scheme⁴⁵ as implemented in the Gaussian 09 software package.³⁴

Moving from the MM-MD simulation to the QM/MM studies implies methodological differences that are important to have in mind. First of all, the molecular model is different. While in an MM-MD simulation the system is studied as periodic, with explicit solvent, in QM/MM calculations a single protein:substrate system in a small cap of constrained water molecules is used. The Hamiltonian, which is used to treat the system, is also different in both methodologies. These factors, together with the (still) limited QM/MM sampling, make it difficult to assign a rigorous relative weight to each of the calculated barriers. Despite these limitations, the methodology used here is obviously adequate to help us understand the influence of enzyme thermal conformational fluctuations on the chemical pathway and the activation barrier.

Results and discussion

The MM-MD performed in this work generated an isothermic–isobaric ensemble distribution of different microstates, in the reactant state. We studied the barriers of a significant number of structures and used them as a “reduced ensemble” of initial structures to study the rate-limiting step of the reaction (Fig. 1). Enzyme conformational rearrangements occurring in a larger time scale than that covered during the MM-MD simulation (130 ns) were not explored. This is a general limitation of MM-MD simulations, due to the large timescale of enzyme motions, which easily goes beyond milliseconds. A more thorough conformational space of the active site requires invoking advanced sampling techniques such as parallel tempering and related methods^46,47 or collective coordinate based sampling methods.⁴⁸ Out of the 30 selected initial structures, only 19 were used in our analysis. These were the ones where the calculations and analysis were possible to carry out with rigor. The remaining 11 had to be excluded due to optimization problems or difficulties in characterizing the stationary points (reactants or transition states). The transition state for this step is particularly difficult to optimize, due to the intricate network of hydrogen bonds; despite having the active site residues and substrate properly positioned to react, some specific structures are so difficult to optimize that computationally it becomes more economical to start with a large number of structures and afterwards just discard the most problematic ones.

Spread of the activation barriers and chemical disorder

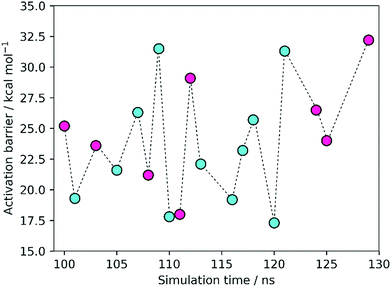
The results showed activation barriers (ΔE + ΔZPE) ranging from 17.3 to 32.2 kcal mol⁻¹ at the M06-2X/6-311++G(2d,2p):ff99SB level of theory (Fig. 2), covering a span of 15 kcal mol⁻¹. More importantly, two different reaction mechanisms (One Asp mechanism and Two Asp mechanism) were observed, the occurrence of which depended on the specific reactant structure (Fig. 3). The activation barriers changed widely in the nanoseconds time scale, as did the reaction mechanisms. The energy barrier, obtained using the structure taken after 120 ns of MM-MD simulation, was the lowest among all our measurements, and corresponds to 17.3 kcal mol⁻¹. Just 1 ns later, the activation barrier was above 30 kcal mol⁻¹.

Fig. 2 Activation barriers for the snapshots selected from the MM-MD simulation. These barriers corresponded to zero-point corrected total energies , calculated at the M06-2X/6-311++G(2d,2p):ff99SB level of theory. The purple and cyan points correspond to structures that react through the One Asp mechanism and the Two Asp mechanism, respectively. The lowest activation barrier (17.3 kcal mol⁻¹) was obtained, starting from the structure taken after 120 ns of MM-MD simulation. The dashed line provides a visual guidance for the chronological order of the barriers and does not correspond to an interpolation of the energies between them.

Fig. 3 (a) Reactant state from the structure taken after 120 ns of MM-MD simulation, which is associated with the lowest energetic barrier. Only the QM layer was represented for simplicity. Important active site distances (explained in the main text above) are highlighted. (b) 2D representation of the relevant active-site interactions.

Small changes in the position/orientation of the active site residues, as well as small movements of the catalytic water molecule, seem to justify, to a great extent, the propensity for each of the two different mechanisms. The conformational fluctuations do not correspond to changes in global folding (which take place in much larger timescales), but instead to much more subtle changes (mostly hydrogen bonding distances) that, despite being small, can modify the very important chemical interactions between the substrates and the active site, leading to a change in the reaction pathway.

The turnover of HIV-1 PR takes place in seconds, a timescale at least nine orders of magnitude slower than the fluctuations of the barrier. This means that the experimentally observed kinetics could be a consequence of the overcoming of a few low barriers that occur at well-defined conformations and generate perfectly pre-organized active site conformations. Despite the limited sampling achieved here, due to the high-level theoretical methods and large QM regions employed, the high frequency at which these low-barrier structures appear (7 out of 19, with barriers smaller than 22 kcal mol⁻¹) is more than enough to overcome the very high Boltzmann penalties associated with the more frequent, high-barrier structures, and thus the former should determine the reaction kinetics. In this regard, it is important to keep in mind that the turnover rate depends linearly on the frequency of reactive conformations and exponentially on the barrier heights, meaning that the turnover rate is much more sensitive to the latter than to the former. The conclusion is consistent with other previous studies, where low-energy barriers were not found in the majority of the explored conformations but still in a very reasonable number of cases.^7,8,49 In analogy to the concept of “static/dynamic/instantaneous disorder” coined in the past for the dispersion in k_cat arising from folding fluctuations at several timescales,^50–53 we refer to the phenomenon seen herein as “chemical disorder”, with the adjective “instantaneous” due to the nanosecond timescale in which it takes place.

Two different reaction mechanisms

The Two Asp mechanism is well described and widely accepted in the literature, for HIV-1 PR and other similar aspartic proteases.^27,28,54,55 Considering that the Asp25 that is known to be protonated is the one from chain B (conventionally since the chains are equivalent), the mechanism is characterized by a nucleophilic attack of the water molecule present between both catalytic Asp25 residues, on the carbonyl carbon of the scissile bond, while it loses a proton to Asp25A. During the same reaction step the carboxylate of Asp25B protonates the carbonyl oxygen of the peptide bond. In the One Asp mechanism, the Asp25A does not participate directly in the reaction, even though it is still fundamental because it raises the pK_a of Asp25B, making it neutral at the beginning of the reaction. In this mechanism, the unprotonated oxygen of Asp25B abstracts the water proton when the water molecule attacks the carbonyl carbon, while the Asp25B acidic proton is transferred to the carbonyl oxygen. These two mechanisms present a similar chemistry, the main difference being whether a single Asp residue acts as an acid and a base in the same step, or if the two functions are divided by two equivalent Asp residues, and whether a negative or a neutral Asp acts as a base. The fact that their chemistry is similar may be the reason why the enzyme was found to stabilize both transition states to a comparable extent.

Equivalent low barriers were found in both mechanisms, provided that the conformation of the active site is adequate. For example, the structure taken after 109 ns of MM-MD simulation is associated with a high barrier of 31.5 kcal mol⁻¹, which means that this structure is not adequate to initiate the reaction mechanism. However, after 1 ns of MM-MD simulation (110 ns), small fluctuations on the enzyme and substrate structure enable the reaction (activation barrier of 17.8 kcal mol⁻¹) to take place. For these two structures, the reaction occurs via the Two Asp mechanism. The structure found just one nanosecond later (111 ns) reacted, in turn, via the One Asp mechanism with a favorable activation barrier of 18.0 kcal mol⁻¹. A structural analysis comparing both mechanisms and correlating the enzyme–substrate structure with them, and with the activation barriers, was performed and is detailed in the next section.

Why two mechanisms?

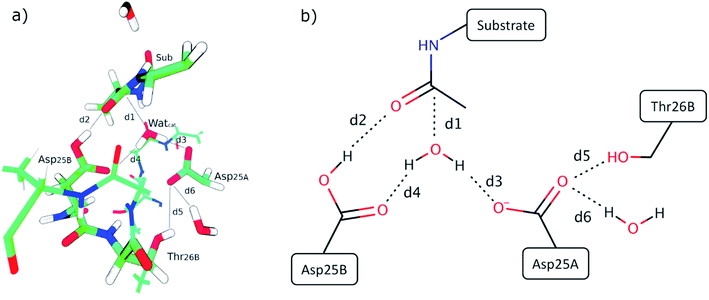
Fig. 3 presents the QM layer used in the QM/MM calculations, highlighting the most relevant distances for the reaction, which we analyzed to understand the origin of the propensity for each of the two mechanisms. These specific distances were chosen because they correspond to all the bond-breaking/bond-forming distances and first-shell interactions with reacting atoms. For simplicity, we only represent the QM layer from the structure that reacted with the smallest barrier (120 ns – 17.3 kcal mol⁻¹). Six distances were selected for analysis, which encompass interactions between reacting atoms (d1 to d4) and fundamental hydrogen bonds that tune the pK_a of the reacting groups (d5 and d6, which tune the pK_a of Asp25A). d1 is the distance between the oxygen of the catalytic water and the carbonyl carbon of the substrate scissile bond (Met201); d2 is the distance between the acidic hydrogen atom from the Asp25B carboxylic group and the oxygen atom from the carbonyl group of Met201 that will be protonated; d3 corresponds to the smallest distance between a (basic) oxygen from the Asp25A carboxylic group and a proton from the catalytic water molecule; d4 corresponds to the distance between the non-protonated oxygen from the carboxylic group of Asp25B and the catalytic water molecule; d5 is the distance between the hydroxyl proton of Thr26B and the carboxyl oxygen from the Asp25A and, finally, d6 is the hydrogen bond distance between a carboxyl oxygen atom from Asp25A and a buried water molecule present at the active site. These structural parameters were evaluated in the optimized reactant structures (after IRC calculations) and in the optimized transition structures.

Table S1† summarizes the results, indicating the reaction mechanism that corresponds to each reactant structure, and the obtained activation barriers, as well as the d1–d6 values. The obtained barriers ranged from 17.3 kcal mol⁻¹ to 32.2 kcal mol⁻¹. This range was similar for both mechanisms: 17.3–31.5 kcal mol⁻¹ for the Two Asp mechanism, and 18.0–32.2 kcal mol⁻¹ for the One Asp mechanism. The barriers for the two mechanisms can be considered as equivalent within the accuracy of the method.

It is evident that the “instantaneous” propensity of each of the two mechanisms will depend on the geometry of the whole protein system and solvent at that specific moment. The question that arises is whether some (few) of the interactions of the whole system have a very preponderant role in determining the mechanistic route. It is expectable that the local interactions around the reactive atoms represent most of the determining effect, but it remains to be known if these are dominant enough to allow explaining the mechanistic route just by themselves. After all, it is not easy to reduce a whole protein, having many thousand degrees of freedom, plus the solvent, to only six active-site degrees of freedom, and still explain the observed effects just based on the latter.

Therefore, to understand the origin of the propensity for the two reaction mechanisms, we investigated if any of the individual key distances d1–d6 for the reaction correlated with the tendency for a specific mechanism. However, no correlation was found. Additionally, all the individual distances of each structure were represented against the respective barrier. The results showed that there is no evident correlation between the individual distances and the energetic barriers (see Fig. S2 and S3 in the ESI†).

The instantaneous active site hydrogen-bonding network determines the chemical mechanism

The previous results show that the propensity to follow a given reaction mechanism is too complex to be captured by a single internal degree of freedom, a single chemical interaction. Instead, this tendency seems to depend on the overall pre-organization of the whole active site. To test if this is the case, we hypothesized what would be the chemical interactions that would drive the reaction through each of the two mechanisms, basing ourselves on the principles of chemical reactivity and transition state stabilization.

It is expectable from the point of view of chemical reactivity that the pK_a of Asp25A is relevant in this regard, as in the Two Asp mechanism it should act as a base but in the One Asp mechanism it should not. Therefore, low pK_a values should deviate the chemical flow from the Two Asp mechanism, due to a less competent Asp25A base. It is also evident that the strength of the two hydrogen bonds established between the Asp25A carboxylate and the Thr26B and the structural water molecule will be relevant to tune the Asp25A pK_a – the shorter the hydrogen bonds, the lower the pK_a.

A second aspect that will determine the reaction pathway is how close a basic Asp25 is from the hydrolytic water, and how far the competing Asp25 is from the same water. For example, the One Asp mechanism will be promoted when Asp25B is close to the hydrolytic water (distance d4), making easier the water deprotonation by this residue and, similarly, when the competing Asp25A base and the hydrolytic water are far apart (distance d3), as the water deprotonation by the competing Asp25A becomes increasingly difficult.

Looking at the active site interactions shown in Fig. 3, there do not seem to exist any more differentiating interactions from the point of view of chemical reactivity. The remaining interactions are related to the attack of the hydrolytic water on the peptide bond (d1) and protonation of the peptide oxygen (d2). As these reactions take place in both mechanisms, they are not expected to exert a discriminatory effect that selectively drives the system through one chemical pathway over the other.

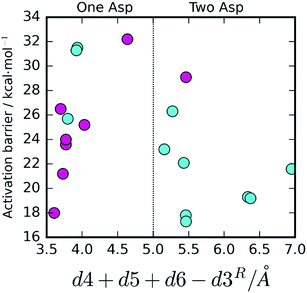
The effect of the active site hydrogen bonding on the Asp25B pK_a can be summarized by the variable d5 + d6 (the smaller the sum, the stronger the hydrogen bonds, and the lower the pK_a will be); the difference between the proximity of the two competing Asp25 bases and the hydrolytic water can be interpreted by analyzing the variable d4 − d3 (the smaller this value is, the closer is Asp25B to the water molecule in relation to Asp25A). Overall, the collective variable d_col = d4 + d5 + d6 − d3 expresses the two conditions together; therefore, it is expectable that small d_col values should represent an active site pre-organized to drive the reaction through the One Asp and large d_col values express an active site pre-organized to drive the reaction through the Two Asp mechanism.

To confirm that this is the case, we plotted d_col against the barrier height (Fig. 4). A very clear distinction between the two mechanisms emanates, with the One Asp mechanism being dominant at low d_col values and the Two Asp mechanism being dominant at high coordinate values, as anticipated, confirming that the specific interactions pointed out have a very prominent role in determining the reaction pathway. As their distances fluctuate, due to thermal motion, the chemical pathway changes as a consequence, bringing nanosecond-timescale “instantaneous” chemical disorder to the system.

Fig. 4 Activation barrier, chemical pathway and d_col (d4 + d5 + d6 − d3). A very clear correlation between the value of d_col and the reaction pathway is visible. The One Asp mechanism is correlated with small values of d5 + d6 (stronger hydrogen bonding to Asp25A and, consequently, lower Asp25A pK_a) as well as small values of d4 and large values of d3, promoting water deprotonation by Asp25B over competing Asp25A. The opposite tendency is observed for the Two Asp mechanism. In the three exceptional cases where these conditions were not fulfilled, the barriers were far too high for any of the two mechanisms to take place.

The origin of the barrier fluctuations in each reaction mechanism

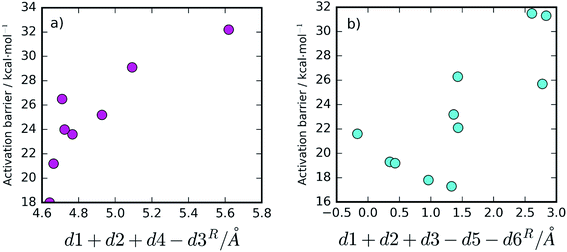
Besides the existence of chemical disorder, leading to two different chemical pathways, it is also interesting to analyze the barrier fluctuations within each pathway. In both mechanisms, low activation barriers are expected to be promoted by reactant conformations having short distances between the atoms that will react. These are the distance between the hydrolytic water and the peptide carbon atom (d1) and the distance between the substrate's carbonyl oxygen and the Asp25B that will protonate it (d2).

Additionally, for the One Asp mechanism, the hydrogen bond distance between the hydrolytic water and Asp25B (d4) is important for the barrier, as Asp25B has to deprotonate this water. Short hydrogen bonds will be associated with smaller barriers. Larger distances between Asp25A and the hydrolytic water (large d3) will also promote small barriers in this mechanism, by reducing the electrostatic repulsion between the negative Asp25A and the hydroxide ion that is formed in the transition state. These proposals, based on chemical principles of reactivity, can be tested by correlating the variable d^{one Asp}_col = d1 + d2 + d4 − d3 (that summarizes all the hypotheses) with the activation barrier heights (Fig. 5a). As expected, the correlation is very clear, confirming that the described network of hydrogen bonds has a relevant role in defining the barrier height.

Fig. 5 Correlation between the collective variable d^{one Asp}_col = d1 + d2 + d4 − d3, for the One Asp mechanism (a), and d^{two Asp}_col = d1 + d2 + d3 − d5 − d6, for the Two Asp mechanism (b), and the activation barriers. A correlation can be seen in the first one, with the barrier growing as d^{one Asp}_col grows, as expected, almost without exception. For the second, there is a clear tendency for finding high barriers when d^{two Asp}_col is above ∼1.5 Å, but additional factors not contemplated in d^{two Asp}_col may find some relevance for smaller values.

For the Two Asp mechanism, short distances between the hydrolytic water and the Asp25A base (small d3) are expected to promote water deprotonation by Asp25A; longer hydrogen bonds to Asp25A formed by the catalytic water and by Thr26B (large d5 and d6, respectively) should also be important to promote this mechanism as they increase the Asp25A pK_a, making it a better base. These criteria can be tested by correlating d^{two Asp}_col = d1 + d2 + d3 − d5 − d6 with the barrier (Fig. 5b). In this case, the correlation is not as clear as in the previous ones, in particular for small d^{two Asp}_col values, but it is still quite clear that values larger than ∼1.5 Å for this collective variable lead to high activation barriers, making difficult the progress of the reaction. The correlation seems to indicate that other geometric aspects, not incorporated into the already complex collective variable, may also be making a substantial contribution for short d^{two Asp}_col values.

We note that it is tempting to make a multiple linear regression of the d1–d6 distances (or for many other possible distances) and the activation barriers, for the discrimination between mechanisms. A recent study by Lodola et al.⁵⁶ has shown that interesting information can be extracted from the reactant conformation using principal component analysis, partial least squares regression analysis, and multiple linear regression analysis. We avoided doing so here because the number of independent observables was not large enough for automated methods to extract better information than the one obtained by an expert analysis based on chemical reactivity principles. The number of independent measurements (19) and the number of variables to be fitted (6) might easily lead to overfitting, in particular when the 19 barriers were split between two mechanisms (11 for one and 8 for the other). The purpose for relating collective variables with the barrier height or reaction mechanism was to demonstrate that a very significant fraction of the origin of the fluctuations and the origin of the preference between mechanisms was related to these key interatomic interactions (that make sense from a chemical point of view) and to their thermal fluctuations, and not to reproduce the barriers or the choice between mechanisms through a fitted function. In summary, our purpose was to achieve “chemical understanding” and use the collective variables to test the chemical insights, and not the contrary.

Finally, it is important to discuss the use of the X-ray conformation (the most abundant conformation) for the determination of the chemical mechanism and barrier height. A very large body of studies^19,57–63 shows that a correct X-ray conformation almost always provides barrier heights in agreement with experiments, and chemical mechanisms that are widely accepted to also be correct. This is particularly true for X-ray structures co-crystallized with a substrate/transition state analogue. Here, the use of X-ray structures is futile, as the catalytic water molecule is never present in the experimental structures, and it is its exact position that determines the outcome of the reaction mechanism and barrier height. Therefore, the very act of modeling this missing molecule (with all the involved assumptions and ambiguities) would mostly determine the result of the calculation. As such, the best solution here was to embark on a multi-PES study.

Conclusions

The aim of this work was to understand the effect of conformational fluctuations on the reaction mechanism followed by HIV-1 PR. A total of 19 different structures, collected from a long classical MM-MD simulation were used as initial reactants to study the reaction path of the first step of this mechanism, with QM/MM calculations.

The results showed that the different conformations of the enzyme in the reactant state lead to two different reaction mechanisms. We studied the reasons behind this effect, which we have named chemical disorder. We found that fast rearrangements in the hydrogen bonding network of the active site push the chemical reaction through one way or the other of this mechanistic bifurcation. As these interactions fluctuate at the nanosecond timescale, due to thermal motions, the most favorable mechanism also changed, according to the instantaneous enzyme conformations, bringing nanosecond-timescale “chemical disorder” to this amazing enzyme, a phenomenon very rare in enzymatic systems that challenges the “one enzyme–one substrate–one reaction mechanism” paradigm.

The competent activation barriers for both mechanisms were similar, as well as the populations for the reactants that drive the mechanism through each of the pathways.

The One Asp mechanism was considered as less probable in the past, due to the large barriers found by other authors.⁸ The Two Asp mechanism is well described and accepted in previous studies of HIV-1 PR and other proteases. The One Asp mechanism was found to take place when Asp25A is well stabilized through hydrogen bonds with a structural water molecule and Thr26B, lowering its pK_a and making it a weaker base. The relative proximity between the competing Asp25A and Asp25B bases and the hydrolytic water proton, which fluctuates due to thermal motion, also influences which of them will deprotonate it, and thus the outcome in terms of the reaction pathway. The role of this structural water molecule was not documented before, even though its prevalence during the MM-MD simulation is consistent with its relevance to the HIV-1 PR mechanism. The results provide a very interesting glimpse into the intricacies of an apparently well-known enzyme, revealing the underlying richness of HIV-1 PR chemistry. The extent to which chemical disorder is prevalent in the general enzymatic world is yet to be known.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by UID/MULTI/04378/2019 with funding from FCT/MCTES through national funds. The authors acknowledge financing from Fundação para a Ciência e Tecnologia through the project PTDC/QUI-QFI/28714/2017. A. R. Calixto would like to thank FCT for her PhD Fellowship SFRH/BD/95962/2013.

References

1. K. Henzler-Wildman and D. Kern, Dynamic Personalities of Proteins, Nature, 2007, 450(7172), 964–972.
2. P. Hanoian, C. T. Liu, S. Hammes-Schiffer and S. Benkovic, Perspectives on Electrostatics and Conformational Motions in Enzyme Catalysis, Acc. Chem. Res., 2015, 48(2), 482–489.
3. A. G. Palmer III, Enzyme Dynamics from NMR Spectroscopy, Acc. Chem. Res., 2015, 48(2), 457–465.
4. W. Min, B. P. English, G. Luo, B. J. Cherayil, S. C. Kou and X. S. Xie, Fluctuating Enzymes: Lessons from Single-Molecule Studies, Acc. Chem. Res., 2005, 38(12), 923–931.
5. A. Warshel, Electrostatic Origin of the Catalytic Power of Enzymes and the Role of Preorganized Active Sites, J. Biol. Chem., 1998, 273(42), 27035–27038.
6. A. Warshel, P. K. Sharma, M. Kato, Y. Xiang, H. Liu and M. H. Olsson, Electrostatic Basis for Enzyme Catalysis, Chem. Rev., 2006, 106(8), 3210–3235.
7. D. Santos-Martins, A. R. Calixto, P. A. Fernandes and M. J. Ramos, A Buried Water Molecule Influences Reactivity in α-Amylase on a Subnanosecond Time Scale, ACS Catal., 2018, 8(5), 4055–4063.
8. A. N. J. Ribeiro, D. Santos-Martins, N. Russo, M. J. Ramos and P. A. Fernandes, Enzymatic Flexibility and Reaction Rate: A QM/MM Study of HIV-1 Protease, ACS Catal., 2015, 5(9), 5617–5626.
9. R. A. Mata, H. J. Werner, S. Thiel and W. Thiel, Toward Accurate Barriers for Enzymatic Reactions: QM/MM Case Study on P-Hydroxybenzoate Hydroxylase, J. Chem. Phys., 2008, 128(2), 025104.
10. R. Lonsdale, S. Hoyle, D. T. Grey, L. Ridder and A. J. Mulholland, Determinants of Reactivity and Selectivity in Soluble Epoxide Hydrolase from Quantum Mechanics/Molecular Mechanics Modeling, Biochemistry, 2012, 51(8), 1774–1786.
11. Y. Li, R. Zhang, L. Du, Q. Zhang and W. Wang, How Many Conformations of Enzymes Should Be Sampled for DFT/Mm Calculations? A Case Study of Fluoroacetate Dehalogenase, Int. J. Mol. Sci., 2016, 17(8), 1372.
12. M. W. van der Kamp, R. Chaudret and A. J. Mulholland, QM/MM Modelling of Ketosteroid Isomerase Reactivity Indicates That Active Site Closure is Integral to Catalysis, FEBS J., 2013, 280(13), 3120–3131.
13. Y. Li, R. Zhang, L. Du, Q. Zhang and W. Wang, Catalytic Mechanism of C–F Bond Cleavage: Insights from QM/MM Analysis of Fluoroacetate Dehalogenase, Catal. Sci. Technol., 2016, 6(1), 73–80.
14. J. C. Schöneboom, H. Lin, N. Reuter, W. Thiel, S. Cohen, F. Ogliaro and S. Shaik, The Elusive Oxidant Species of Cytochrome P450 Enzymes: Characterization by Combined Quantum Mechanical/Molecular Mechanical (QM/MM) Calculations, J. Am. Chem. Soc., 2002, 124(27), 8142–8151.
15. S. Piana and P. Carloni, Conformational Flexibility of the Catalytic Asp Dyad in HIV-1 Protease: An Ab Initio Study on the Free Enzyme, Proteins, 2000, 39(1), 26–36.
16. P. Saura, I. Kaganer, D. Heydeck, J. M. Lluch, H. Kuhn and A. Gonzalez-Lafont, Mutagenesis of Sequence Determinants of Truncated Porcine Alox15 Induces Changes in the Reaction Specificity by Altering the Catalytic Mechanism of Initial Hydrogen Abstraction, Chem.–Eur. J., 2018, 24(4), 962–973.
17. A. M. Cooper and J. Kästner, Averaging Techniques for Reaction Barriers in QM/MM Simulations, ChemPhysChem, 2014, 15(15), 3264–3269.
18. R. Lonsdale, J. N. Harvey and A. J. Mulholland, Compound I Reactivity Defines Alkene Oxidation Selectivity in Cytochrome P450cam, J. Phys. Chem. B, 2009, 114(2), 1156–1162.
19. S. F. Sousa, A. J. Ribeiro, R. P. Neves, N. F. Brás, N. M. Cerqueira, P. A. Fernandes and M. J. Ramos, Application of Quantum Mechanics/Molecular Mechanics Methods in the Study of Enzymatic Reaction Mechanisms, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7(2), e1281.
20. K.-Y. Wong and J. Gao, The Reaction Mechanism of Paraoxon Hydrolysis by Phosphotriesterase from Combined QM/MM Simulations, Biochemistry, 2007, 46(46), 13352–13369.
21. M. Repič, R. Vianello, M. Purg, F. Duarte, P. Bauer, S. C. Kamerlin and J. Mavri, Empirical Valence Bond Simulations of the Hydride Transfer Step in the Monoamine Oxidase B Catalyzed Metabolism of Dopamine, Proteins, 2014, 82(12), 3347–3355.
22. A. Maršavelski, D. a. Petrović, P. Bauer, R. Vianello and S. C. L. Kamerlin, Empirical Valence Bond Simulations Suggest a Direct Hydride Transfer Mechanism for Human Diamine Oxidase, ACS Omega, 2018, 3(4), 3665–3674.
23. A. Barrozo, Q. Liao, M. Esguerra, G. Marloie, J. Florián, N. H. Williams and S. C. L. Kamerlin, Computer Simulations of the Catalytic Mechanism of Wild-Type and Mutant B-Phosphoglucomutase, Org. Biomol. Chem., 2018, 16(12), 2060–2073.
24. P. Hu and Y. Zhang, Catalytic Mechanism and Product Specificity of the Histone Lysine Methyltransferase Set7/9: An Ab Initio QM/MM-Fe Study with Multiple Initial Structures, J. Am. Chem. Soc., 2006, 128(4), 1272–1278.
25. M. Reis, C. N. Alves, J. Lameira, I. Tuñón, S. Martí and V. Moliner, The Catalytic Mechanism of Glyceraldehyde 3-Phosphate Dehydrogenase from Trypanosoma Cruzi Elucidated Via the QM/MM Approach, Phys. Chem. Chem. Phys., 2013, 15(11), 3772–3785.
26. M. Prieß, H. Göddeke, G. Groenhof and L. V. Schäfer, Molecular Mechanism of Atp Hydrolysis in an Abc Transporter, ACS Cent. Sci., 2018, 4(10), 1334–1343.
27. A. Brik and C.-H. Wong, HIV-1 Protease: Mechanism and Drug Discovery, Org. Biomol. Chem., 2003, 1(1), 5–14.
28. S. Piana, D. Bucher, P. Carloni and U. Rothlisberger, Reaction Mechanism of HIV-1 Protease by Hybrid Car-Parrinello/Classical MD Simulations, J. Phys. Chem. B, 2004, 108(30), 11139–11149.
29. S. Piana, P. Carloni and M. Parrinello, Role of Conformational Fluctuations in the Enzymatic Reaction of HIV-1 Protease, J. Mol. Biol., 2002, 319(2), 567–583.
30. A. R. Calixto, M. J. Ramos and P. A. Fernandes, Influence of Frozen Residues on the Exploration of the Pes of Enzyme Reaction Mechanisms, J. Chem. Theory Comput., 2017, 13(11), 5486–5495.
31. M. Miller, J. Schneider, B. K. Sathyanarayana, M. V. ToTH, G. R. Marshall, L. Clawson, L. Selk, S. Kent and A. Wlodawer, Structure of Complex of Synthetic HIV-1 Protease with a Substrate-Based Inhibitor at 2.3 a Resolution, Science, 1989, 246(4934), 1149–1152.
32. D. Case, T. Darden, T. Cheatham III, C. Simmerling, J. Wang, R. Duke, R. Luo, R. Walker, W. Zhang and K. Merz, AMBER 12, University of California, San Francisco, 2012, vol. 2010, pp. 1–826.
33. M. H. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, Propka3: Consistent Treatment of Internal and Surface Residues in Empirical pKa Predictions, J. Chem. Theory Comput., 2011, 7(2), 525–537.
34. M. Frisch, G. Trucks, H. Schlegel, G. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. Petersson, Gaussian 09, Revision D. 01, Gaussian. Inc., Wallingford, CT, 2009.
35. A. D. Becke, Density-functional thermochemistry. III. The Role of Exact Exchange, J. Chem. Theory Comput., 1993, 98(7), 5648–5652.
36. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785.
37. K. Raghavachari, Perspective on “Density Functional Thermochemistry. III. The Role of Exact Exchange”, Theor. Chem. Acc., 2000, 103(3–4), 361–363.
38. J. D. Dill and J. A. Pople, Self-Consistent Molecular Orbital Methods. Xv. Extended Gaussian-Type Basis Sets for Lithium, Beryllium, and Boron, J. Chem. Phys., 1975, 62(7), 2921–2923.
39. J. W. Ochterski, Thermochemistry in Gaussian, Gaussian Inc, 2000, pp. 1–19.
40. D. A. McQuarrie and J. D. Simon, Molecular Thermodynamics, University Science Books, Sausalito, CA, 1999, vol. 63.
41. A. J. Ribeiro, M. J. Ramos and P. A. Fernandes, Benchmarking of DFT Functionals for the Hydrolysis of Phosphodiester Bonds, J. Chem. Theory Comput., 2010, 6(8), 2281–2292.
42. N. F. Brás, M. A. Perez, P. A. Fernandes, P. J. Silva and M. J. Ramos, Accuracy of Density Functionals in the Prediction of Electronic Proton Affinities of Amino Acid Side Chains, J. Chem. Theory Comput., 2011, 7(12), 3898–3908.
43. R. P. Neves, P. A. Fernandes, A. N. J. Varandas and M. J. Ramos, Benchmarking of Density Functionals for the Accurate Description of Thiol–Disulfide Exchange, J. Chem. Theory Comput., 2014, 10(11), 4842–4856.
44. A. T. Pereira, A. J. Ribeiro, P. A. Fernandes and M. J. Ramos, Benchmarking of Density Functionals for the Kinetics and Thermodynamics of the Hydrolysis of Glycosidic Bonds Catalyzed by Glycosidases, Int. J. Quantum Chem., 2017, 117(18), e25409.
45. T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery Jr, K. Morokuma and M. J. Frisch, Combining Quantum Mechanics Methods with Molecular Mechanics Methods in Oniom, J. Chem. Theory Comput., 2006, 2(3), 815–826.
46. Y. Sugita and Y. Okamoto, Replica-Exchange Molecular Dynamics Method for Protein Folding, Chem. Phys. Lett., 1999, 314(1–2), 141–151.
47. P. Liu, B. Kim, R. A. Friesner and B. J. Berne, Replica Exchange with Solute Tempering: A Method for Sampling Biological Systems in Explicit Water, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(39), 13749–13754.
48. S. Awasthi and N. N. Nair, Exploring High-Dimensional Free Energy Landscapes of Chemical Reactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9(3), e1398.
49. E. F. Oliveira, N. M. Cerqueira, M. J. Ramos and P. A. Fernandes, QM/MM Study of the Mechanism of Reduction of 3-Hydroxy-3-Methylglutaryl Coenzyme a Catalyzed by Human Hmg-Coa Reductase, Catal. Sci. Technol., 2016, 6(19), 7172–7185.
50. H. P. Lu, L. Xun and X. S. Xie, Single-Molecule Enzymatic Dynamics, Science, 1998, 282(5395), 1877–1882.
51. Q. Xue and E. S. Yeung, Differences in the Chemical Reactivity of Individual Molecules of an Enzyme, Nature, 1995, 373(6516), 681–683.
52. R. D. Smiley and G. G. Hammes, Single Molecule Studies of Enzyme Mechanisms, Chem. Rev., 2006, 106(8), 3080–3094.
53. B. P. English, W. Min, A. M. Van Oijen, K. T. Lee, G. Luo, H. Sun, B. J. Cherayil, S. Kou and X. S. Xie, Ever-Fluctuating Single Enzyme Molecules: Michaelis–Menten Equation Revisited, Nat. Chem. Biol., 2006, 2(2), 87–94.
54. A. R. Calixto, N. F. Bras, P. A. Fernandes and M. J. Ramos, Reaction Mechanism of Human Renin Studied by Quantum Mechanics/Molecular Mechanics (QM/MM) Calculations, ACS Catal., 2014, 4(11), 3869–3876.
55. N. F. Brás, M. J. Ramos and P. A. Fernandes, The Catalytic Mechanism of Mouse Renin Studied with QM/MM Calculations, Phys. Chem. Chem. Phys., 2012, 14(36), 12605–12613.
56. A. Lodola, J. Sirirak, N. Fey, S. Rivara, M. Mor and A. J. Mulholland, Structural Fluctuations in Enzyme-Catalyzed Reactions: Determinants of Reactivity in Fatty Acid Amide Hydrolase from Multivariate Statistical Analysis of Quantum Mechanics/Molecular Mechanics Paths, J. Chem. Theory Comput., 2010, 6(9), 2948–2960.
57. N. Cerqueira, P. Fernandes and M. J. Ramos, Protocol for Computational Enzymatic Reactivity Based on Geometry Optimisation, ChemPhysChem, 2018, 19(6), 669–689.
58. M. J. Ramos and P. A. Fernandes, Computational Enzymatic Catalysis, Acc. Chem. Res., 2008, 41(6), 689–698.
59. S. F. Sousa, P. A. Fernandes and M. J. Ramos, Computational Enzymatic Catalysis–Clarifying Enzymatic Mechanisms with the Help of Computers, Phys. Chem. Chem. Phys., 2012, 14(36), 12431–12441.
60. F. Himo, Recent Trends in Quantum Chemical Modeling of Enzymatic Reactions, J. Am. Chem. Soc., 2017, 139(20), 6780–6786.
61. P. E. Siegbahn and F. Himo, The Quantum Chemical Cluster Approach for Modeling Enzyme Reactions, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1(3), 323–336.
62. H. M. Senn and W. Thiel, QM/MM Methods for Biomolecular Systems, Angew. Chem., Int. Ed., 2009, 48(7), 1198–1229.
63. J. Llano and J. W. Gauld, Mechanistics of Enzyme Catalysis: From Small to Large Active-Site Models, Quantum Biochem., 2010, 643–666.

---

Footnotes

† Electronic supplementary information (ESI) available: Methodology used in the initial model and MM-MD simulations; Fig. S1 – energy distribution of the NPT ensemble generated by the MM-MD calculations and of the microstates extracted for the QM/MM calculations; Fig. S2 – correlations between six selected active site distances from reactant structures and the corresponding activation barriers; Fig. S3 – correlations between six selected active site distances from transition state structures and the corresponding activation barriers (PDF). Geometries of the optimized stationary points (ZIP file). See DOI: 10.1039/c9sc01464k

‡ Present Address: Ana Rita Calixto – Department of Chemistry – BMC, Uppsala University, Box 576, Uppsala S-751 23, Sweden.

---