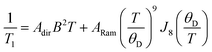Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
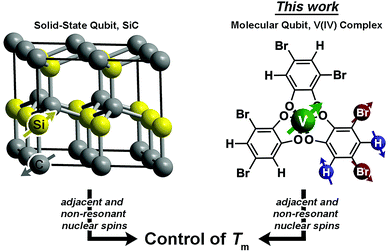
Nuclear-spin-pattern control of electron-spin dynamics in a series of V(IV) complexes†
Cassidy E.
Jackson
a,
Chun-Yi
Lin‡
a,
Spencer H.
Johnson
a,
Johan
van Tol
b and
Joseph M.
Zadrozny
 *a
*a
aDepartment of Chemistry, Colorado State University, Fort Collins, CO 80523, USA. E-mail: joe.zadrozny@colostate.edu
bNational High Magnetic Field Laboratory, Tallahassee, FL 32310, USA
First published on 29th July 2019
Abstract
Achieving control of phase memory relaxation times (Tm) in metal ions is an important goal of molecular spintronics. Herein we provide the first evidence that nuclear-spin patterning in the ligand shell is an important handle to modulate Tm in metal ions. We synthesized and studied a series of five V(IV) complexes with brominated catecholate ligands, [V(C6H4−nBrnO2)3]2− (n = 0, 1, 2, and 4), where the 79/81Br and 1H nuclear spins are arranged in different substitutional patterns. High-field, high-frequency (120 GHz) pulsed electron paramagnetic resonance spectroscopic analysis of this series reveals a pattern-dependent variation in Tm for the V(IV) ion. Notably, we show that it is possible for two molecules to have starkly different (by 50%) Tm values despite the same chemical composition. Nuclear magnetic resonance analyses of the protons on the ligand shell suggest that relative chemical shift (δ), controlled by the patterning of nuclear spins, is an important underlying design principle. Here, having multiple ligand-based protons with nearly identical chemical shift values in the ligand shell will, ultimately, engender a short Tm for the bound metal ion.
Introduction
Magnetic molecules are next-generation components of many different technological arenas, ranging from magnetic resonance imaging (MRI)1,2 to quantum information processing.3–11 Utility in any of these applications requires long spin-lattice relaxation times (T1 > 1 ms) and phase-memory relaxation times (Tm§ > 100 μs). T1 defines the lifetime of an excited spin and is the upper limit of Tm. In contrast, Tm is the lifetime of the electron spin superposition, or coherence time. Designing systems where both of these parameters are long is an acute challenge because of the ubiquitous spin bath (nearby electronic spins or nuclear spins), which produces a chaotic local magnetism that shortens T1 and Tm from spin–spin interactions.12–15 To circumvent the spin bath challenge, significant efforts are made to engineer environments with less noise from the spin bath. This engineering is done by dilution of the paramagnetic species, using smaller-magnetic-moment isotopic substitution (e.g.2H, μ = 0.86μN for 1H, μ = 2.79μN), or complete elimination of nuclear spins.3,16–20 However, large-moment environmental spins are a critical part of utility in nearly all applications. For example, MRI applications require function in proton-rich biological environments, and information processing applications will likely feature stray magnetic fields from moving charges or other proximate magnetic materials in a device. Hence, understanding how to design complexes with long T1 and Tm in magnetic environments is a necessary advance for future technologies.Herein, we demonstrate the first control of Tmvia patterning of ligand-based nuclear spins in a metal complex (Fig. 1). In molecules, ligand nuclear spins are a critical component of the nuclear spin bath and control electron spin dynamics through nuclear spin diffusion.14,15,21 In this phenomena, pairs of resonant nuclear spins (those that require identical quantities of energy to flip) engage in energy-conserving flip-flop motions, wherein two oppositely oriented spins simultaneously flip, or exchange spin.22 This process generates local magnetic noise and shortens Tm for a magnetic ion.23–26 In the absence of a nuclear spin bath, Tm will approach and exceed millisecond lifetimes.27–30 However, in spin-rich environments, lifetimes are typically less than 100 μs (ref. 31) and more frequently less than 10 μs.19,23,32–52
A recent breakthrough in the study of paramagnetic defects in SiC might hold the key to longer relaxation times in nuclear spin-rich baths (Fig. 1).53–55 The defects in SiC display longer Tm values than nitrogen vacancy centers in diamond despite higher nuclear spin concentration in the former (1.1% 13C and 4.7% 29Si in SiC; 1.1% 13C in diamond).56 The relative enhancement in Tm stems from a particular structural feature – each Si atom is surrounded by C and each C atom is surrounded by Si.53–55,57 This interstitial patterning increases Tm in two ways. First, two Si nuclear spins are never adjacent (likewise for C), and nuclear spin diffusion decreases for spins held far apart from one another.12 Second, the difference in the nuclear gn factors for C and Si ensures that, even when adjacent, spin diffusion will not occur between the nonresonant 13C and 29Si nuclei. These results suggest specific positioning of nuclear spins as a potential method of Tm control via synthetic chemistry.
Drawing inspiration from SiC, we address the questions: can patterning of nuclear spins on ligand shells influence the electronic Tm of a ligated metal? Freedman and co-workers showed that separation between an open-shell ion and nuclear spins is important,58 and there is significant literature demonstrating the impacts on replacement of 1H (μ = 2.79μN) with low-moment magnetic nuclei e.g.2H (μ = 0.86μN).19,42,46 In this paper we probe a different question: can the impacts of high-magnetic-moment nuclei on Tm be mitigated instead by controlling nuclear spin to nuclear spin interactions in a molecule? To address these questions, we prepared and investigated, via pulsed EPR spectroscopy, a series of Bu3NH+ salts of the canonical tris(catecholato)vanadate(IV) complex [V(C6H4O2)3]2−: (n-Bu3NH)2[V(C6H4O2)3] (1), (n-Bu3NH)2[V(4-Br-C6H3O2)3] (2), (n-Bu3NH)2[V(3,5-Br2-C6H2O2)3] (3), (n-Bu3NH)2[V(4,5-Br2-C6H2O2)3] (4), and (n-Bu3NH)2[V(C6Br4O2)3] (5). In this series, the specific pattern of 1H and 79/81Br is varied on each ligand (Fig. 2 and 3). These nuclear spins have significantly different resonance frequencies,56 and, on this basis, we hypothesized that ligand-based nuclear-spin diffusion would be modulated in 1–5. Furthermore, we predicted that such change would lead to a variation in V(IV) Tm dependent on the exact substitutional pattern of H and Br on the ligand. In this report, we show for the first time that this patterning design strategy is an effective means of influencing Tm. Importantly, these studies also include the first investigation of the pulsed EPR spectroscopic properties of the V(IV) ion at very high field and frequency (>4.0 T, 120 GHz).
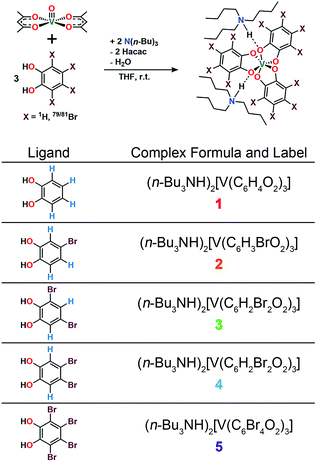 | ||
| Fig. 2 General synthetic scheme for 1–5 and labelling scheme for the studied complexes in this manuscript. See ESI† for additional synthetic information. | ||
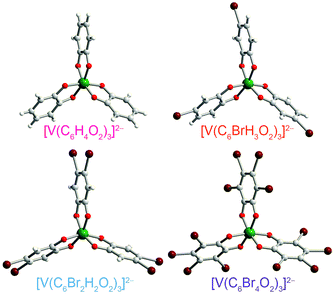 | ||
| Fig. 3 Molecular structures of the V(IV) complexes in 1 (ref. 40), 2, 4, and 5, as determined from the crystal structures of these compounds. Counter ions are omitted for clarity. Green, maroon, red, gray, and white spheres represent vanadium, bromine, oxygen, carbon, and hydrogen atoms, respectively. | ||
Results and discussion
Preparation of the targeted complexes proceeded via a simple ligand metathesis scheme using VO(acac)2, tri-n-butylamine, and the ligands shown in Fig. 2 (see also ESI, Fig. S1–S4†). The general scheme for these syntheses follows previous reports of the triscatecholato complex of V(IV).18,41,59–62 Recrystallization afforded crystals suitable for single crystal X-ray diffraction of 2, 4, and 5 (but not 3, see Fig. 3, Tables S1–S3, and ESI†). Single crystal X-ray diffraction experiments on crystals of 1,402, 4, and 5 (Fig. 3) reveal similar molecular structures of the VO6 core. In these structures, all vanadium(IV) ions are in a six-coordinate environment, with average V–O bond lengths varying over a tight range across the series, from 1.938(4) Å for 1 to 1.943(9) Å for 5. The continuous-shape-measurement (CSM) analyses using SHAPE 2.0 software63,64 of 1–5 provide symmetry measures for an octahedron of 1.67, 2.39, 3.97, and 1.41 for 1, 2, 4, and 5, respectively (here, a value of 0 corresponds to a perfect octahedron). The symmetry measures for a trigonal prismatic geometry are much higher (>5), indicating that 1, 2, 4, and 5 are better described as slightly distorted octahedra (Table S4†). Beyond the first coordination sphere, all molecules exist hydrogen-bonded to two n-Bu3NH+ cations through the O atoms of the catecholate ligands (Fig. S5†). This interaction is similar across 1, 2, 4, and 5, with an average V⋯HNBu3+ distance of 2.99(6) Å. Prior experiments demonstrate that this association persists in solution (Fig. S5†).40One critical aspect of the tested design principle relies on a difference between the spin-flip energies of the 1H and 79/81Br nuclear spins. On this merit, high-field and high-frequency EPR (120 GHz) was selected for studying 1–5. With this technique, the differences in Larmor frequencies between 1H (ca. 187 MHz) and 79/81Br (ca. 47 and 51 MHz, respectively) at 4.4 T are large relative to those at the more conventional EPR frequency, X-band (0.4 T): 1H (ca. 17.0 MHz) and 79/81Br (ca. 4.3 and 4.6 MHz, respectively).65 Importantly, such conditions will decouple not only the 1H and 79/81Br nuclear spins, but potentially 79Br from 81Br due to the bigger difference in Larmor frequencies (ca. 4 MHz) – rendering the Br atoms inert spin blocks to disrupt 1H nuclear-spin diffusion. High-field, high-frequency investigations of the relaxation times of V(IV) are, to the best of our knowledge, unprecedented.
Echo-detected EPR spectra of 1–5 were collected to test for variation in the spin-Hamiltonian parameters as a function of ligand. To do so, 1–5 were dissolved in d14-o-terphenyl (d14-OTP) at a 1 mM concentration, leveraging the solubility in nonpolar media afforded by the tri-n-butylammonium cations.40 The echo-detected, field-swept (EDFS) spectra of 1–5 were then collected at 5 K and 120 GHz (Fig. 4, S6 and Table S5†). The recorded spectra starkly differ in appearance from the 100 mT-wide, eight-line patterns observed at X-band frequency (Fig. 4). Instead, each 120 GHz spectrum reveals a single broad transition, spanning from 4.3–4.5 T. Such spectral width is attributed to enhanced broadening of the electronic g-factor (“g-strain”) at high magnetic fields.15 Simulations of the spectra were performed using Easyspin66 and the following spin Hamiltonian:
| Ĥ = geμBBŜ − gNμNBÎ + ÎAŜ + ÎQÎ |
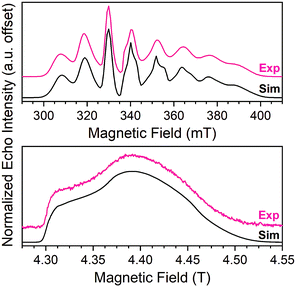 | ||
| Fig. 4 (Top) X-band (9.460 GHz) echo-detected, field-swept spectra of 1 (1 mM in OTP, color line) at 5 K and simulation (black). Data taken from ref. 40. (Bottom) 120 GHz echo-detected, field-swept spectra of 1 mM 1 in OTP solution (color) at 5 K and simulation (black). | ||
Spin-lattice relaxation rates (1/T1) were obtained as the first step toward understanding the impact of ligand nuclear-spin patterning on the V(IV) spin dynamics. To determine these rates for 1–5, variable-temperature inversion recovery experiments were performed at the highest-intensity peaks in the 120 GHz EDFS spectra at 5 K, which is B0 = 4.4 T for all five complexes (Fig. 5, S7–S11 and Table S6†). For 1–5, 1/T1 is slowest at low temperature, with an average 1/T1 of 0.88(6) ms−1 at 5 K. With increasing temperature, T1 rapidly decreases for 1–5, in concert with a rapidly hastening relaxation rate, 1/T1. Owing to instrumental limitations related to the deadtime, performance of these experiments was precluded above 40 K. An immediate observation from these data is the near-two-orders-of-magnitude enhancement of 1/T1 (average 1/T1 = 0.88(6) ms−1) at 120 GHz versus the 5 K, 9.4 GHz 1/T1 of 1: 0.0141(4) ms−1.40,41,43 Comparison of 1/T1 across the series of complexes, in contrast, reveals remarkable similarity between the temperature-dependent curves at this field/frequency.
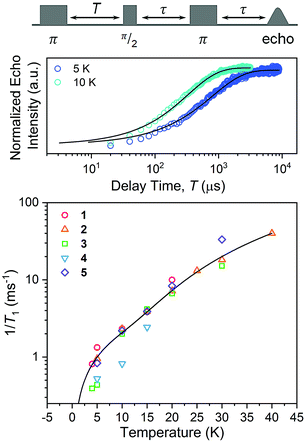 | ||
| Fig. 5 (Top) Selected variable temperature inversion recovery curves (color traces) and fits (black traces) for 1. (Bottom) Variable-temperature 1/T1 data for 1–5. Data were collected at 120 GHz frequency on samples of ca. 1 mM concentration in d14-OTP glass. The black trace is the fit to the direct and Raman processes. Error bars are generally under the width of the symbols – exact uncertainties are tabulated and depicted in the ESI.† | ||
The enhancement of spin-lattice relaxation rates (1/T1) at high field/frequency gives valuable information about the dominant high-field relaxation process for V(IV). Indeed, there are a collection of different mechanisms potentially responsible for spin-lattice relaxation: direct, Raman, local-mode, tunneling, and thermally activated processes.15,71 Yet, only direct, tunneling, and thermally activated processes are field-dependent. Of these, tunneling is typically suppressed under an applied field and thermally activated processes are likely precluded for V(IV) owing to the absence of low-lying excited states for this S = 1/2 ion. Hence, we hypothesized that a dominant direct process is responsible for the stark shortening of T1. To test this hypothesis, we modelled the temperature-dependence of the spin-lattice relaxation rate (1/T1) at 120 GHz. We found that the data for all complexes were readily modeled using the sum of a direct and Raman process in the following equation (see Fig. 5 and S12†):15
Nuclear spin diffusion is expected to exert the greatest impact on Tm, not T1.3,12,21,23 Hence, Tm was measured for 1–5 to test for a pattern-dependent effect. Variable-temperature, two-pulse Hahn echo experiments were performed on 1–5 in d14-OTP at 1 mM concentration to evaluate the echo decay as a function of ligand (Fig. 6 and S13–S17†). Stretched exponential functions were fit to these decays to extract Tm and the stretch parameter, β, (see ESI, Table S6†) which can give mechanistic insight into the decay of the superposition. All complexes display the longest Tms at the lowest temperatures. At 5 K, the Tm values of 1, 2, 3, and 5 range from 4.36(8) to 5.36(9) μs. For 4, Tm is about 2 μs shorter, 2.75(3) μs. With increasing temperatures, Tm drops sharply for 1–5. By 20 K, the Tm of 4 is 0.7(1) μs, which precluded pulsed measurements at any higher temperatures owing to low signal to noise. In contrast, Tm remains appreciable for 1–3 and 5 up to at least 30 K. Interestingly, above 20 K, Tm for 3 is slightly higher than the other complexes. The stretch parameters increase with increasing temperatures for 1–5. For 1–3 and 5, β ranges over 0.6 to 0.8 at the lowest temperatures, and venture closer to 1 at the highest temperatures. For 4, however, β is close to 1 at the lowest temperature and only increases with higher temperatures.
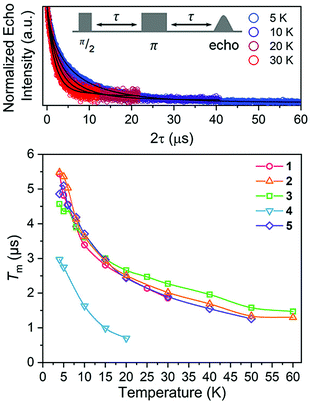 | ||
| Fig. 6 (Top) Selected variable temperature Hahn echo decay curves (color traces) and fits (black traces) for 1. The pulse sequence is inset. (Bottom) Variable-temperature Tm data for 1–5. Data were collected at 120 GHz frequency on samples of ca. 1 mM concentration o-terphenyl glass. Error values are generally within the width of the data symbols – exact uncertainties are tabulated and depicted in the ESI.† | ||
The difference in Tm for 4 relative to 3, and 3, 4 relative to 1, 2, and 5, represent two significant findings. First, these data, particularly for 3 (Tm = 4.36(8) μs) and 4 (Tm = 2.75(3) μs), reveal for the first time that two substitutional isomers of the same magnetic metal complex can have significantly different Tm values. Second, the data for 3versus the rest of the series highlight the possibility of enhancing Tmvia patterns that avoid two adjacent protons (though that impact is modest in the present system). However, in that context, it is particularly puzzling that 4 demonstrates a significantly shorter Tm than 1 and 5, which possess the highest number of adjacent 1H and 79/81Br spins, respectively. It is further puzzling that 4 displays a shorter Tm than 3, when the protons in 4 are clearly further separated than those of 3. Changes in geometry of the coordination site and electronic structure are powerful mechanisms for adjusting Tm.12 However, the similarity of the spin-Hamiltonian parameters, crystallographic data, and T1 values for 1–5 suggests that the different substitutional patterns of the ligands do not affect these aspects of the V(IV) ion. These results thus suggest that the impact of the pattern on Tm is truly magnetic in nature, stemming from the 1H and 79/81Br ligand nuclear spins (vide infra).
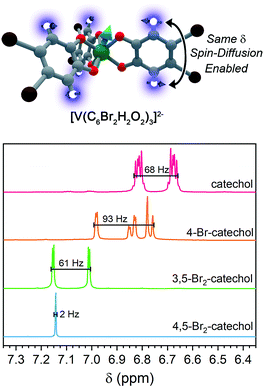
For ligand-based nuclear spin diffusion to operate efficiently, the nuclear spins should have the same resonant NMR frequency (chemical shift). To probe the environment of nuclear spins for the molecules in this paper, we collected the 1H NMR spectra of the ligands.3,15 The 400 MHz (= 9.4 T field) 1H NMR spectra of the ligands of 1, 2, and 3 demonstrate peaks of varying multiplicity over a range of chemical shifts (in frequency, 68, 93, and 61 Hz, respectively) (Fig. 7). The observed range of 1H chemical shifts in the ligands of 1–3 is a consequence of two factors. First, the presence of different quantities and arrangements of bromine on the ligands adjust the 1H chemical shifts. Second, J-coupling between the aromatic 1H protons split the individual 1H peaks into multiplets. In contrast, the aromatic protons of 4,5-dibromocatechol (the ligand of 4) yield a single peak with a full-width half-maximum of 2 Hz. The protons in this ligand are constrained to this tight chemical-shift window by the two-fold rotational symmetry and weak J-coupling (0–1 Hz) for aromatic 3,6 protons.72,73
On the basis of the NMR data, we rationalize the observed Tm data in terms of synthetic control via ligand-shell nuclear spin diffusion. First, the high symmetry of the 4,5-dibromocatechol and weak J-coupling ensure nearly identical chemical shifts for the aromatic 1H nuclei. In the other ligands, in contrast, asymmetry and stronger 1H–1H J-coupling spread the 1H chemical shifts out over >60 Hz. Owing to the relatively tight range (2 Hz) of the 1H frequencies in the ligand of 4 relative to 1–3, we posit that a given ligand proton in 4 is significantly more likely to have a proximate nucleus (across the aromatic ring) with the same chemical shift. Hence, the ligand-based protons in 4 are more likely to engage in nuclear spin diffusion and impact Tm. In the other complexes, J-coupling and differing chemical shifts spread the spin-flip frequencies of the 1H protons over a wider range, ensuring a lower probability that a given 1H will have a neighbor with precisely the same chemical shift. Hence, 1–3, with non-resonant 1H spins, would be expected to display less-efficient spin diffusion and show a longer Tm. This effect may also be operative for the ligand bromines, due to the different isotopes of bromine (79Br and 81Br). Hence, this argument may explain why 5 has a Tm in the same range of 1–3. We note that the stretch parameters β are slightly higher for 4 relative to 1–3 and 5, suggesting that nuclear spin-diffusion may be more operative for 4 (and consistent with our rationale).21 However, the typical values of β for dominant nuclear-spin diffusion are closer to 2–2.5,12 and this discrepancy may be related to the limitation of Tm by the short T1 in 1–5. Given the fast spin-lattice relaxation at high field, lower-field measurements may engender stronger nuclear-spin-diffusion control by pushing ligand-based nuclear spin resonant frequencies closer together.69,74–77 Such measurements are exciting next studies.
Conclusions and outlook
The foregoing results demonstrate, for the first time, that control of phase memory relaxation times is possible via nuclear-spin patterning within a molecule. Importantly, we interpret our data to suggest that tuning relative chemical shifts, which are dictated by the symmetry and chemical make-up of the molecule, are a key future design strategy for manipulating Tm in magnetic complexes. However, multiple new avenues of work are necessary to fully test the presented design strategy. In particular, learning how to harness said strategy to improve Tm is a pressing concern. Indeed, we note that the “optimally patterned” species 3 only exhibits a slight enhancement of Tm over a fully-protonated complex and the most dramatic impact is a shortening, not lengthening of Tm. Toward the understanding to use this mechanism to lengthen Tm, our future work spans studying the nuclear spin dynamics (in particular, the time constants for spin diffusion and spin–spin relaxation) of the ligands and metal complexes. In this context, an important absence in the above analyses is a direct picture of the spin dynamics of the 79/81Br nuclear spins, which is extremely challenging to obtain with solution-phase NMR. A system patterned with 19F nuclei is in contrast particularly advantageous since 19F NMR is readily performed.78–80 It is in these directions that we are now working.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was performed with the support of Colorado State University (CSU) and the National Science Foundation (CHE-1836537). Standard molecular characterization experiments were performed at the CSU Central Instrument Facility, which is supported by an NIH-SIG award (1S10OD021814-01) and the CSU-CORES Program. C. E. J. and J. M. Z. thank Mr J. Joyce and Prof. Sandra Eaton for helpful insight. A portion of this work was performed at the National High Magnetic Field Laboratory, which is supported by the National Science Foundation Cooperative Agreement No. DMR-1644779 and the State of Florida.Notes and references
- M. C. Heffern, L. M. Matosziuk and T. J. Meade, Chem. Rev., 2014, 114, 4496–4539 CrossRef CAS PubMed.
- G. Tircs and Z. Baranyai, The Chemistry of Contrast Agents in Medical Magnetic Resonance Imaging Stability and Toxicity of Contrast Agents, John Wiley & Sons, 2013 Search PubMed.
- M. J. Graham, J. M. Zadrozny, M. S. Fataftah and D. E. Freedman, Chem. Mater., 2017, 29, 1885–1897 CrossRef CAS.
- M. Affronte, F. Troiani, A. Ghirri, A. Candini, M. Evangelisti, V. Corradini, S. Carretta, P. Santini, G. Amoretti, F. Tuna, G. Timco and R. E. P. Winpenny, J. Phys. D: Appl. Phys., 2007, 40, 2999–3004 CrossRef CAS.
- G. Aromí, D. Aguilà, P. Gamez, F. Luis and O. Roubeau, Chem. Soc. Rev., 2012, 41, 537–546 RSC.
- F. Troiani and M. Affronte, Chem. Soc. Rev., 2011, 40, 3119 RSC.
- L. Escalera-Moreno, J. J. Baldoví, A. Gaita-Ariño and E. Coronado, Chem. Sci., 2018, 9, 3265–3275 RSC.
- P. C. E. Stamp and A. Gaita-Ariño, J. Mater. Chem., 2009, 19, 1718–1730 RSC.
- A. Gaita-Ariño, F. Luis, S. Hill and E. Coronado, Nat. Chem., 2019, 11, 301–309 CrossRef PubMed.
- R. E. P. Winpenny, Angew. Chem., Int. Ed., 2008, 47, 7992–7994 CrossRef CAS PubMed.
- M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, 2010 Search PubMed.
- L. J. Berliner, G. R. Eaton and S. S. Eaton, Distance Measurements in Biological Systems by EPR, Springer US, 2002 Search PubMed.
- S. K. Misra, Multifrequency Electron Paramagnetic Resonance: Theory and Applications, Wiley-VCH, 2011 Search PubMed.
- S. S. Eaton, G. R. Eaton and L. J. Berliner, Biomedical EPR. Part A, Free radicals, Metals, Medicine and Physiology, Springer, 2011 Search PubMed.
- D. Goldfarb and S. Stoll, EPR Spectroscopy: Fundamentals and Methods, Wiley, 2018 Search PubMed.
- K. Bader, S. H. Schlindwein, D. Gudat and J. van Slageren, Phys. Chem. Chem. Phys., 2017, 19, 2525–2529 RSC.
- K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304 CrossRef CAS PubMed.
- J. J. L. Morton, A. M. Tyryshkin, A. Ardavan, K. Porfyrakis, S. A. Lyon and G. A. D. Briggs, Phys. Rev. B: Solid State, 2007, 76, 085418 CrossRef.
- C. J. Wedge, G. A. Timco, E. T. Spielberg, R. E. George, F. Tuna, S. Rigby, E. J. L. McInnes, R. E. P. Winpenny, S. J. Blundell and A. Ardavan, Phys. Rev. Lett., 2012, 108, 107204 CrossRef CAS PubMed.
- A. Ardavan, O. Rival, J. J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Phys. Rev. Lett., 2007, 98, 057201 CrossRef PubMed.
- G. R. Eaton and S. S. Eaton, in Characterization of Materials, John Wiley & Sons, Inc., Hoboken, NJ, USA, 2012, pp. 1–13 Search PubMed.
- S. S. Eaton and G. R. Eaton, in eMagRes, John Wiley & Sons, Ltd, Chichester, UK, 2016, pp. 1543–1556 Search PubMed.
- S. Lenz, K. Bader, H. Bamberger and J. van Slageren, Chem. Commun., 2017, 53, 4477–4480 RSC.
- W. M. Witzel and S. Das Sarma, Phys. Rev. B: Solid State, 2007, 76, 241303 CrossRef.
- W. M. Witzel, R. de Sousa and S. Das Sarma, Phys. Rev. B: Solid State, 2005, 72, 161306 CrossRef.
- W. M. Witzel and S. Das Sarma, Phys. Rev. B: Solid State, 2006, 74, 035322 CrossRef.
- J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492 CrossRef CAS PubMed.
- C.-J. Yu, M. J. Graham, J. M. Zadrozny, J. Niklas, M. D. Krzyaniak, M. R. Wasielewski, O. G. Poluektov and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 14678–14685 CrossRef CAS PubMed.
- G. Balasubramanian, P. Neumann, D. Twitchen, M. Markham, R. Kolesov, N. Mizuochi, J. Isoya, J. Achard, J. Beck, J. Tissler, V. Jacques, P. R. Hemmer, F. Jelezko and J. Wrachtrup, Nat. Mater., 2009, 8, 383–387 CrossRef CAS PubMed.
- G. Wolfowicz, A. M. Tyryshkin, R. E. George, H. Riemann, N. V. Abrosimov, P. Becker, H.-J. Pohl, M. L. W. Thewalt, S. A. Lyon and J. J. L. Morton, Nat. Nanotechnol., 2013, 8, 561–564 CrossRef CAS PubMed.
- A. M. Ariciu, D. H. Woen, D. N. Huh, L. Nodaraki, A. Kostopoulos, C. A. P. Goodwin, N. F. Chilton, E. J. L. McInnes, R. E. P. Winpenny, W. J. Evans and F. Tuna, Nat. Commun., 2019, 10(1), 3330 CrossRef PubMed.
- J. Yang, Y. Wang, Z. Wang, X. Rong, C.-K. Duan, J.-H. Su and J. Du, Phys. Rev. Lett., 2012, 108, 230501 CrossRef PubMed.
- F. Moro, D. Kaminski, F. Tuna, G. F. S. Whitehead, G. A. Timco, D. Collison, R. E. P. Winpenny, A. Ardavan and E. J. L. McInnes, Chem. Commun., 2014, 50, 91–93 RSC.
- G. Mitrikas, Y. Sanakis, C. P. Raptopoulou, G. Kordas and G. Papavassiliou, Phys. Chem. Chem. Phys., 2008, 10, 743–748 RSC.
- M. Warner, S. Din, I. S. Tupitsyn, G. W. Morley, A. M. Stoneham, J. A. Gardener, Z. Wu, A. J. Fisher, S. Heutz, C. W. M. Kay and G. Aeppli, Nature, 2013, 503, 504–508 CrossRef CAS PubMed.
- K. S. Pedersen, A.-M. Ariciu, S. McAdams, H. Weihe, J. Bendix, F. Tuna and S. Piligkos, J. Am. Chem. Soc., 2016, 138, 5801–5804 CrossRef CAS PubMed.
- D. Aguilà, L. A. Barrios, V. Velasco, O. Roubeau, A. Repollés, P. J. Alonso, J. Sesé, S. J. Teat, F. Luis and G. Aromí, J. Am. Chem. Soc., 2014, 136, 14215–14222 CrossRef PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Nature, 2016, 531, 348–351 CrossRef CAS PubMed.
- M. S. Fataftah, J. M. Zadrozny, S. C. Coste, M. J. Graham, D. M. Rogers and D. E. Freedman, J. Am. Chem. Soc., 2016, 138, 1344–1348 CrossRef CAS PubMed.
- C.-Y. Lin, T. Ngendahimana, G. R. Eaton, S. S. Eaton and J. M. Zadrozny, Chem. Sci., 2019, 10, 548–555 RSC.
- M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Inorg. Chem., 2018, 57, 731–740 CrossRef CAS PubMed.
- S. Lenz, H. Bamberger, P. P. Hallmen, Y. Thiebes, S. Otto, K. Heinze and J. van Slageren, Phys. Chem. Chem. Phys., 2019, 21, 6976–6983 RSC.
- M. Atzori, E. Morra, L. Tesi, A. Albino, M. Chiesa, L. Sorace and R. Sessoli, J. Am. Chem. Soc., 2016, 138, 11234–11244 CrossRef CAS PubMed.
- G. R. Eaton and S. S. Eaton, J. Magn. Reson., 1999, 136, 63–68 CrossRef CAS PubMed.
- J. J. Baldoví, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and H. Prima-García, Chem. Commun., 2013, 49, 8922 RSC.
- K. Bader, M. Winkler and J. van Slageren, Chem. Commun., 2016, 52, 3623–3626 RSC.
- M. J. Martínez-Pérez, S. Cardona-Serra, C. Schlegel, F. Moro, P. J. Alonso, H. Prima-García, J. M. Clemente-Juan, M. Evangelisti, A. Gaita-Ariño, J. Sesé, J. van Slageren, E. Coronado and F. Luis, Phys. Rev. Lett., 2012, 108, 247213 CrossRef PubMed.
- C. Schlegel, J. van Slageren, M. Manoli, E. K. Brechin and M. Dressel, Phys. Rev. Lett., 2008, 101, 147203 CrossRef CAS PubMed.
- J. P. S. Walsh, S. B. Meadows, A. Ghirri, F. Moro, M. Jennings, W. F. Smith, D. M. Graham, T. Kihara, H. Nojiri, I. J. Vitorica-Yrezabal, G. A. Timco, D. Collison, E. J. L. McInnes and R. E. P. Winpenny, Inorg. Chem., 2015, 54, 12019–12026 CrossRef CAS PubMed.
- J. Ferrando-Soria, E. Moreno Pineda, A. Chiesa, A. Fernandez, S. A. Magee, S. Carretta, P. Santini, I. J. Vitorica-Yrezabal, F. Tuna, G. A. Timco, E. J. L. McInnes and R. E. P. Winpenny, Nat. Commun., 2016, 7, 11377 CrossRef CAS PubMed.
- A. J. Fielding, S. Fox, G. L. Millhauser, M. Chattopadhyay, P. M. H. Kroneck, G. Fritz, G. R. Eaton and S. S. Eaton, J. Magn. Reson., 2006, 179, 92–104 CrossRef CAS PubMed.
- Y. Krupskaya, R. Zaripov, E. Vavilova, V. Miluykov, I. Bezkishko, D. Krivolapov, O. Kataeva, O. Sinyashin, E. Hey-Hawkins, V. Voronkova, K. Salikhov, V. Kataev and B. Büchner, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 092402 CrossRef.
- A. L. Falk, B. B. Buckley, G. Calusine, W. F. Koehl, V. V. Dobrovitski, A. Politi, C. A. Zorman, P. X.-L. Feng and D. D. Awschalom, Nat. Commun., 2013, 4, 1819 CrossRef PubMed.
- J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. Van de Walle and D. D. Awschalom, J. Appl. Phys., 2011, 109, 102417 CrossRef.
- W. F. Koehl, B. B. Buckley, F. J. Heremans, G. Calusine and D. D. Awschalom, Nature, 2011, 479, 84–87 CrossRef CAS PubMed.
- J. R. Rumble, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics: a Ready-Reference Book of Chemical and Physical Data, CRC Press, Boca Raton, 99th edn, 2018 Search PubMed.
- G. Pacchioni, Nat. Rev. Mater., 2017, 2, 17052 CrossRef.
- M. J. Graham, C.-J. Yu, M. D. Krzyaniak, M. R. Wasielewski and D. E. Freedman, J. Am. Chem. Soc., 2017, 139, 3196–3201 CrossRef CAS PubMed.
- S. R. Cooper, Y. B. Koh and K. N. Raymond, J. Am. Chem. Soc., 1982, 104, 5092–5102 CrossRef CAS.
- M. Branca, G. Micera, A. Dessi, D. Sanna and K. N. Raymond, Inorg. Chem., 1990, 29, 1586–1589 CrossRef CAS.
- C. Milsmann, A. Levina, H. H. Harris, G. J. Foran, P. Turner and P. A. Lay, Inorg. Chem., 2006, 45, 4743–4754 CrossRef CAS PubMed.
- B. A. Borgias, S. R. Cooper, Y. B. Koh and K. N. Raymond, Inorg. Chem., 1984, 23, 1009–1016 CrossRef CAS.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Coord. Chem. Rev., 2005, 249, 1693–1708 CrossRef CAS.
- S. Alvarez, D. Avnir, M. Llunell and M. Pinsky, New J. Chem., 2002, 26, 996–1009 RSC.
- N. J. Stone, At. Data Nucl. Data Tables, 2005, 90, 75–176 CrossRef CAS.
- S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55 CrossRef CAS PubMed.
- J. Telser, J. Krzystek and A. Ozarowski, J. Biol. Inorg Chem., 2014, 19, 297–318 CrossRef CAS PubMed.
- J. van Tol, G. W. Morley, S. Takahashi, D. R. McCamey, C. Boehme and M. E. Zvanut, Appl. Magn. Reson., 2009, 36, 259–268 CrossRef PubMed.
- S. Takahashi, R. Hanson, J. van Tol, M. S. Sherwin and D. D. Awschalom, Phys. Rev. Lett., 2008, 101, 047601 CrossRef PubMed.
- B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Applications, Wiley-VCH, 2000 Search PubMed.
- D. Gatteschi and R. Sessoli, Angew. Chem., Int. Ed., 2003, 42, 268–297 CrossRef CAS PubMed.
- E. L. Hahn, A. Abragam and D. M. S. Bagguley, Pulsed Magnetic Resonance: NMR, ESR, and Optics: A Recognition of E.L. Hahn, Clarendon Press, 1992 Search PubMed.
- L. M. Jackman and S. Sternhell, Application of Nuclear Magnetic Resonance Spectroscopy in Organic Chemistry, Pergamon Press, New York, 2nd edn, 1969 Search PubMed.
- S. Takahashi, I. S. Tupitsyn, J. van Tol, C. C. Beedle, D. N. Hendrickson and P. C. E. Stamp, Nature, 2011, 476, 76–79 CrossRef CAS PubMed.
- T. D. Ladd, D. Press, K. De Greve, P. L. McMahon, B. Friess, C. Schneider, M. Kamp, S. Höfling, A. Forchel and Y. Yamamoto, Phys. Rev. Lett., 2010, 105, 107401 CrossRef PubMed.
- N. V. Prokof’ev and P. C. E. Stamp, Rep. Prog. Phys., 2000, 63, 669–726 CrossRef.
- P. C. E. Stamp, Stud. Hist. Philos. Mod. Phys., 2006, 37, 467–497 CrossRef.
- C. Dalvit and A. Vulpetti, J. Med. Chem., 2019, 62, 2218–2244 CrossRef CAS PubMed.
- A. H. Schmieder, S. D. Caruthers, J. Keupp, S. A. Wickline and G. M. Lanza, Engineering, 2015, 1, 475–489 CrossRef CAS PubMed.
- H. Kovacs and Ē. Kupče, Magn. Reson. Chem., 2016, 54, 544–560 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Methods, additional characterization and discussion. CCDC 1921675–1921677. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9sc02899d |
| ‡ Now at the Department of Chemistry, National Cheng Kung University, Taiwan. |
| § In this paper, we use Tm to describe the time constant associated with the decay of the echo intensity in a Hahn-echo experiment. This parameter is frequently also labelled T2, the spin–spin relaxation. However, the T2 designation is typically ascribed to relaxation in the xy-plane primarily from electronic spin flip-flop motions. In contrast, Tm is a broader, all-encompassing term for all relaxation processes that affect relaxation in the xy-plane. The Tm designation is particularly appropriate in this manuscript because there may be other factors controlling Tm (e.g. a short T1) under the experimental conditions. Further reading on this distinction can be found in ref. 12. |
| This journal is © The Royal Society of Chemistry 2019 |