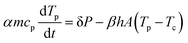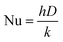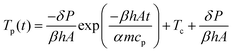DOI:
10.1039/C8SM02081G
(Paper)
Soft Matter, 2019,
15, 1373-1387
Laser sintering of polymer particle pairs studied by in situ visualization†
Received
11th October 2018
, Accepted 17th December 2018
First published on 18th December 2018
Abstract
Merging of particle pairs during selective laser sintering (SLS) of polymers is vital in defining the final part properties. Depending on the sintering conditions, polymers can undergo full or partial sintering whereby incomplete sintering results in poor mechanical properties. At present, the underlying mechanisms and related conditions leading to various consolidation phenomena of polymer particles are not well understood. In the present work, a novel in-house developed experimental setup is used to perform laser sintering experiments on polystyrene (PS) particle doublets while performing in situ visualization of the sintering dynamics. From the recorded images, the evolution of the growth of the neck radius formed between both particles is analyzed as a function of time. Sintering conditions such as heating chamber temperature, laser pulse energy and duration, laser spot size and particle size are precisely controlled and systematically varied. A non-isothermal viscous sintering model is developed that allows qualitative prediction of the observed effects of the various parameters. It is shown that the sintering kinetics is determined by a complex interplay between the transient rheology caused by the finite relaxation times of the polymer and the time-dependent temperature profile which also affects the polymer viscosity. The combination of a full material characterization with sintering experiments under well-defined conditions has resulted in a general understanding of the effects of material and process parameters on laser sintering. Thereby a strong foundation is laid for the route towards rational design of laser sintering.

Ruth Cardinaels
| Ruth Cardinaels obtained her PhD at KU Leuven (Belgium) in 2010. After her PhD, she continued to work there in the Soft Matter Rheology and Technology section as a postdoctoral research fellow of the Research Foundation – Flanders. During this period she was also a visiting postdoctoral researcher at the Mechanical Engineering department of Princeton University (USA). Since 2014 she is an Assistant Professor in the Polymer Technology section of Prof. P. Anderson in the Mechanical Engineering Department at Eindhoven University of Technology (The Netherlands). Her research involves the study of multiphasic soft matter systems by means of optical, rheological, rheo-optical and rheo-dielectric techniques. |
1. Introduction
Selective laser sintering (SLS) is an additive manufacturing technique that offers the possibility to produce intricate geometries and freeform surfaces from polymer powder without the use of a mould.1,2 This provides economic benefits and opens up new options for producing complex functional parts, which are currently being limited by traditional techniques like injection moulding. In SLS, a bed of polymer powder is heated below the glass transition temperature (Tg) and melting temperature (Tm) of amorphous and semi-crystalline polymers respectively. A laser beam selectively heats and thereby sinters specific areas corresponding to the coordinates provided by a computer-aided design (CAD) model. After lowering the work platform, another layer of powder is added and the process is repeated, thus, the part geometry is created layer by layer.3–6 However, a number of limitations exist in the SLS process and associated products. Some of the commonly found defects like porosity and poor layer-to-layer adhesion lead to poor mechanical properties of the final printed parts as compared to products produced by traditional polymer processing methods.7,8 Furthermore, a limited control over process parameters and an incomplete understanding of the effects of the processing conditions on the consolidation phenomena of the polymer powder have further hampered the production of parts with reproducible product properties.9
In the literature, different approaches have been taken to overcome these previously mentioned adversaries. Extensive research using commercial SLS machines has shown that varying the processing conditions allows changes in the final part morphology and crystalline microstructure.10–13 The heating chamber temperature, particle size and size distribution, laser energy and scan speed all have been shown to affect the final properties.7 For instance, it was observed that at a constant laser speed and powder bed temperature, gradually increasing the laser power allowed to achieve better consolidation of the polymer powder whereas a low power yielded fragile parts with poor mechanical properties.6,14 However, due to the fact that global process parameters rather than local conditions are controlled and spatial as well as temporal variability in parameters such as temperature may occur, the reported observations are mostly specific to each machine. Furthermore, the information is limited to the final morphology obtained and insight into the actual structure development during processing is still lacking.
Another approach has been the study of the coalescence process on the scale of particle doublets, allowing a simplified representation of the complex process. When two particles in contact reach their melting point, they tend to flow with a progressively increasing contact region (neck).15–17 This particle sintering on the level of a particle doublet has been investigated by means of hot stage microscopy, which has enabled to study the coalescence process and to relate it with existing analytical models. It was reported that capillary forces drive an outwards polymer flow,18 which was later verified for polypropylene (PP) particles,19 by tagging the inter-particle neck and tracking the flow along the weld line. The temperature dependence of the sintering rate was experimentally verified for PMMA and PP particles showing that the rate and type of flow depend on the sintering temperature.19,20 Frenkel derived a simple scaling relation allowing description of the early sintering stages by assuming Newtonian flow and a constant strain rate.21 The Frenkel theory was later modified by Pokluda et al.15 by balancing the work of surface tension and that of viscous dissipation, while taking into account volume conservation. Thus the obtained model was found to be suitable to describe the complete sintering process of viscous liquids. The dependence of the sintering process on the rheological fluid parameters was shown experimentally by measuring the inter-particle neck thicknesses for PEEK and PEK polymer particles of different viscosity at a fixed temperature,22 indicating that the sintering rate is affected by the viscosity and elasticity of the polymer and a faster coalescence was observed for the less viscous polymer.23 A model considering the viscoelastic nature of the sintered materials was developed by Bellehumeur et al.17 by using an upper convected Maxwell model for the calculation of the work of viscous dissipation. By using a quasi-steady state approach to isolate the effects of the elastic stresses, they could show that melt elasticity slows down sintering. This was later also experimentally verified by Muller et al.24 for a range of viscoelastic Boger fluids. Subsequently, Scribben et al.25 applied the Bellehumeur model under full transient conditions, thereby showing that due to time effects of the viscosity, increasing the relaxation time of the material can accelerate sintering. This acceleration due to the transient rheology has also been confirmed by Balemans et al. using fully resolved numerical simulations.26
Although the different observations and models allow an understanding of sintering phenomena in processing techniques such as rotational moulding, they do not fully represent the laser sintering process. To date, experimental studies focusing on the laser-stimulated heating and sintering of particle doublets are lacking. Also, the available analytical models consider isothermal conditions, neglecting thermal effects on the viscosity of the polymer. However, with a laser being the heat source that locally binds particles together, inhomogeneous and non-isothermal temperature profiles are obtained.27–29 A recent numerical study has shown that a judicious choice of the different sintering parameters would allow significant optimization of the sintering process.30 The objective of the present work is to provide insight in the sintering dynamics during laser sintering of an amorphous polymer, in this case polystyrene. We use a novel in-house developed experimental setup which incorporates the main features of an SLS device and at the same time facilitates optical visualization of the sintering dynamics with precise control over all processing parameters. Based on a systematic experimental study of the effects of the various processing parameters, the relationships between on the one hand material properties and processing conditions and on the other hand the sintering of polymer particle doublets have been investigated.
2. Experimental setup
Fig. 1a depicts the experimental setup for in situ laser sintering experiments. It consists of a home-build heated sample chamber in which sintering takes place while optical imaging via the top and side is possible with two separate optical trains. Laser light is guided into the chamber from the top. A visible light (λ = 532 nm) continuous wave (CW) laser (Genesis MX) from Coherent is used, with a spatial TEM00 mode, which provides a Gaussian intensity distribution. The small wavelength laser with stable beam parameters, low noise and high power-stability ensures a well-defined spot size and precise control over the laser impact energy. One of the key components in the setup is the acousto-optic modulator (AOM, Isomet), whose main functionality is to pulse the laser. The laser beam is diverted through the AOM, and by switching on and off the modulation within the AOM, the CW laser beam can be pulsed whereby excess energy is diverted to the beam dump. The precise control over the laser impact parameters namely the pulse duration as well as the pulse energy, allows simulation of various laser scanning speeds encountered during an actual laser sintering process.
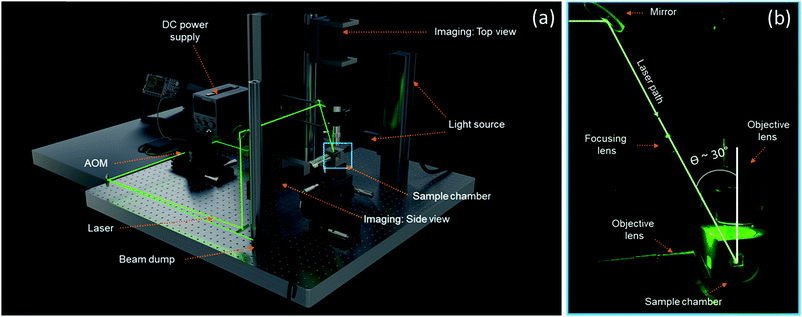 |
| | Fig. 1 (a) Rendered image of the experimental setup highlighting the main components. (b) Close-up of the sample chamber depicting the laser path. | |
The design of the sample chamber ensures the possibility to perform in situ laser sintering with simultaneous visualization of the sintering dynamics by incorporation of quartz windows on the top and sides. A mirror polished stainless steel sample substrate holds the particle pairs to be sintered and visualized. The chamber is built from aluminum walls fitted with heating rods on each side, as well as in the substrate. A low thermal conductivity (0.4 W (mK)−1 at 400 °C) isolation around the box limits the heat loss to the environment. Furthermore, two thermocouples measure the temperature of the substrate and the chamber air respectively. The thermocouples and heating rods are connected to a temperature-control unit (Hasco), which ensures that the sample temperature can be controlled within 1 °C. In the present work, the temperatures of the heating chamber and the substrate were always kept at the same value. Custom made optical trains were designed, to capture the fast sintering dynamics and relatively small length scales of the formed particle bridges that dominate during the sintering process. The main components of the optical train are the Pixelink (PL-D725MU-T) CMOS camera and an infinity corrected objective lens with 20× magnification from Mitutoyo (NA 0.28). Design considerations were made as such that the heat loss from the sample chamber does not affect the performance of the imaging train and at the same time allows a minimum possible angle of incidence of the laser light (30°) with respect to the objective lens (Fig. 1b). A well-defined focal spot was achieved by placing a focusing lens with known focal length along the laser path, as shown in Fig. 1b. An animation illustrating the features of the experimental setup can be found in the ESI.†
3. Materials and methods
3.1 Materials and material characterization
Spherical polystyrene (PS) particles were prepared from standard low molecular weight polystyrene (Sigma Aldrich). The PS particles contained 2 wt% of the Nubian black PC-0870 dye (Orient Chemical Industries co., Ltd), which enables visible-light laser energy to be absorbed. This dye has a molecular weight of Mw ∼ 397 g mol−1. The thermal conductivity k, density ρ and surface tension Γ of polystyrene are respectively 0.167 W (mK)−1, 1040 kg m−3 and 35.6 mN m−1 at 115 °C.31–33
To select suitable sintering parameters and to analyze the sintering process, the thermal, optical and rheological properties of the used material are required. Differential scanning calorimetry measurements (Mettler Toledo 823e/700 DSC module) at a heating rate of 10 °C min−1 were performed to determine the glass transition temperature (Tg) and specific heat capacity (cp) of PS. Thereto, the DSC was calibrated for the heat flux and melting enthalpy with indium. Rheological measurements were carried out on a strain-controlled rheometer (TA instruments RDAIII) equipped with a convection oven using a plate–plate geometry of 25 mm diameter. Strain sweep experiments at 1 Hz determined the linear viscoelastic regime and at temperatures sufficiently above the Tg of the polymer, frequency sweep experiments at four different temperatures were performed. The absorption properties of the dyed polymer at the laser wavelength were characterized by measuring the intensity of the transmitted and reflected light through thin polymer sheets. Thereto, polymer samples containing different concentrations of dye (0–3 wt%) were prepared by solution mixing in acetone. The required amounts of polymer and dye were dissolved in acetone by first mixing with a magnetic stirrer and subsequently using ultrasonication (each for one hour). The resulting mixture was poured into a petri dish, wherein the dyed polymer was obtained after acetone evaporation. Compression moulded disks of various thicknesses (50–230 μm) were prepared between glass microscope slides using a Fontyne plate press used at 10 kPa and 165 °C. For the absorption experiments, the sample was placed in the laser path on a sample holder with the possibility to vary the incoming angle of the laser light on the sample. Using a continuous beam with a light intensity of 0.04 W mm−2, the intensity of both transmitted and reflected light was measured using an XLP12 thermopile at an incoming angle of 30°. Furthermore, the transmission was measured for an incoming angle of 0°.
3.2 Micromanipulation
At the start of a sintering experiment, two polymer particles of roughly the same size and in contact at their interface, should be placed on the heating bed. To accomplish this, we have developed a manipulation technique that allows picking and placing the polymer particles independent of their size. Similarly sized polymer particles are selected and subsequently deposited on a mirror polished stainless steel substrate placed on an xyz translation stage. The first polymer particle is brought in the field of view and in the focus of the camera. Subsequently, a tungsten probe with a tip diameter of 100 μm, also connected to an xyz translation stage, is positioned within the field of view of the camera, as can be seen in Fig. 2a. Then, a voltage is applied between the probe and the substrate by means of a DC power supply, which creates a non-uniform electrostatic field. When a dielectric polymer particle is present in this field a dielectrophoresis force is exerted on it, which attracts the particle to the probe, as illustrated in Fig. 2b and c and allows it to be lifted up (Fig. 2d). By translating the substrate in the xyz direction, similarly sized particles can be found, as shown in Fig. 2e. The probe with the particle is then positioned close to the second particle and the voltage is switched off, after which the first particle is released onto the substrate next to the second particle being in contact at their interface, as shown in Fig. 2f–h. This particle doublet now forms the starting point for a sintering experiment.
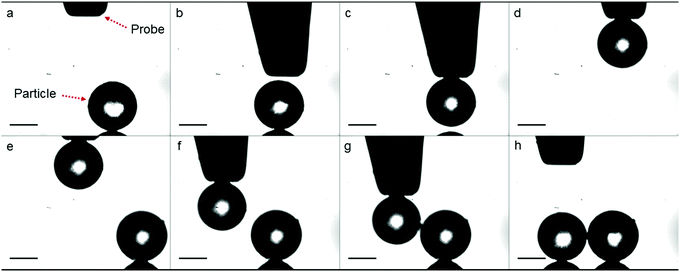 |
| | Fig. 2 Image sequence illustrating micromanipulation of PS particles in a non-destructive manner. Scale bar represents 100 μm. | |
3.3 Experimental protocol and data analysis
Before the start of the experiment, the laser-beam spot is focused at the correct location for visualization of the sintering process. In this work, the beam spot diameter is fixed at 40 μm, as verified by optical imaging and fitting of a Gaussian profile on the spatial intensity distribution. Subsequently, the substrate with a particle pair was placed in the sample chamber and brought in focus on both cameras thereby ensuring correct alignment with respect to the laser beam. Subsequently, the chamber was heated to the required temperature (below the Tg of PS) at a relatively low heating rate, thereby avoiding temperature overshoots and allowing sufficient time to reach thermal equilibrium. Then, a single laser pulse is sent onto the particles while the sintering process is optically visualized. The obtained images are analyzed by means of a custom-made Matlab® code. The code uses the circle-Hough transform to detect circles in the images and to determine the particle diameter at each time instant.34 For determining the size of the bridge between the polymer particles, the edge points are placed in an array and the point with the lowest distance perpendicular to the line connecting both particle centers is used to determine the neck radius.
4. Results and discussion
4.1 Determination of laser sintering parameters
To avoid sintering of the polymer particles in the absence of laser light, the temperature of the sample chamber should remain sufficiently below the glass transition temperature of the polymer, similar to actual SLS printing. Fig. 3 shows the DSC thermograph of the used PS containing 2 wt% dye, from which the Tg was determined as the mid-point of the inflection of the thermogram. It can be concluded that the used PS has a Tg of 62 °C and specific heat capacity cp of 1320 J (kg K)−1 in the liquid state. This Tg value corresponds to a molecular weight of around 3000 g mol−1.35 It should be noted that the effect of the dye on Tg was found to be minor, thereby indicating limited plasticization effects of the dye. To allow sintering, a sufficient amount of laser energy should be transferred to the particle pair. Neglecting heat losses and assuming full conversion of the visible light laser energy into heat, an estimation of the amount of laser energy required to raise the temperature of a single particle can be made by the following equation:where Q is the heat energy (J), m is the particle mass (kg), cp is the specific heat of polystyrene (J (kg K)−1) and ΔT is the temperature difference (K). For a particle radius of 60 μm, this means that the energy required Q to heat a single particle by 20 K is estimated to be 25 μJ. Based on this material information, the bed temperatures for the sintering experiments were fixed between 30 °C and 53 °C and the laser pulse energies were varied from 19–29 μJ.
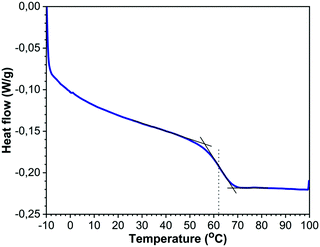 |
| | Fig. 3 DSC thermogram (heating cycle) of PS containing 2 wt% dye using the midpoint of the inflection to determine Tg. | |
Viscosity plays a vital role in consolidation during laser sintering.36 Since laser sintering is a non-isothermal process, the temperature-dependent viscosity is required to understand the sintering dynamics. Using the fact that simple polymers obey the Cox–Merz rule, the complex viscosity η* is used to characterize the flow behaviour. To determine the steady state zero-shear viscosity ηso as a function of temperature, a time-temperature superposition of the frequency-sweep experiment is first performed. This results in a master curve and shift factor aT that obeys the Williams–Landel–Ferry (WLF) equation:37
| | 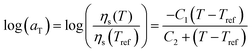 | (2) |
where
C1 and
C2 are constants,
Tref is the reference temperature,
ηs(
Tref) is the steady state viscosity at the reference temperature,
T is the measurement temperature and
ηs(
T) is the steady state viscosity at the measurement temperature. The WLF equation is typically used to describe the time-temperature behavior of polymers near the glass transition temperature.
37 Using
Tg as the reference temperature, values for
C1 and
C2 of 13.05 and 147.1 °C are obtained, respectively, which is in reasonable agreement with literature values for PS.
38 Hence, the DSC and rheology results are consistent.
Fig. 4a shows the complex viscosity
η*
versus angular frequency
ω at a reference temperature of 100 °C for PS containing 2 wt% dye. With this reference temperature,
C1 and
C2 are equal to 10.37 and 185.07 °C, respectively. Subsequently, the master curve of complex viscosity is fitted with the cross model:
37| | 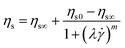 | (3) |
where
ηs∞ is the steady state shear viscosity at infinite shear rate,
ηs0 is the steady state zero-shear viscosity,
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)
is the shear rate,
m is a constant and
λ is the cross time constant with 1/
λ corresponding to the shear rate at the onset of shear thinning. This results in a zero-shear viscosity of 2119 Pa s at the reference temperature of 100 °C.
Fig. 4b provides the zero-shear viscosity values at different temperatures together with the WLF fit that is used to determine the viscosity at other temperatures. Based on the measured viscosities, the expected timescale of the sintering process, using the characteristic timescale of the Frenkel model, which is (
ηs0a0)/
Γ where
Γ is the surface tension of PS,
ηs0 the steady state zero-shear viscosity and
a0 the initial particle radius,
15 is on the order of 3 s for a particle radius of 60 μm and a temperature of 100 °C. By fitting the small-amplitude dynamic moduli with a multimode Maxwell model (
Fig. 4a),
37 the relaxation time distribution of the polymer is determined.
Table 1 provides the different relaxation times and their respective contributions. Based on the data in
Table 1, the viscosity average relaxation time is 6.1 s and the zero-shear viscosity is 2207 Pa s at 100 °C. From the sintering model of Bellehumeur
et al.,
17 which considers an upper convected Maxwell model for the polymer rheology under quasi-steady state conditions for sintering (neglecting transient viscosity effects), it is concluded that for
λ ≈ 2(
ηs0a0)/
Γ as is the case here, the effect of the viscoelastic stresses on the sintering dynamics can be neglected. However, transient effects of the viscosity buildup after the start of the flow are expected to play a role.
25
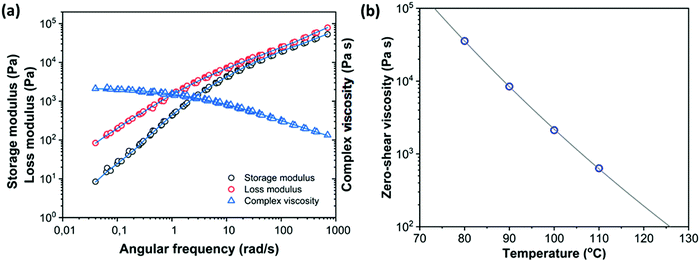 |
| | Fig. 4 (a) Master curves for dynamic moduli and complex viscosity of PS containing 2 wt% dye at a reference temperature of 100 °C obtained from frequency-sweep measurements at 80 °C, 90 °C, 100 °C and 110 °C. The viscosity is fitted with a cross model and the dynamic moduli are fitted with a multimode Maxwell model (lines) (b) temperature dependent zero-shear viscosity values fitted with the WLF equation (line). | |
Table 1 Relaxation time distribution at 100 °C for PS containing 2 wt% dye based on a multimode Maxwell model
|
λ
i
|
η
si
|
| 0.00171 |
73.36 |
| 0.0104 |
164.32 |
| 0.0509 |
364.44 |
| 0.229 |
558.76 |
| 1.02 |
493.68 |
| 5.63 |
245.71 |
| 37.3 |
306.26 |
To estimate the required dye content to allow for significant absorption of the laser energy, the transmission and reflection of laser light by PS sheets with various thicknesses and dye contents were analyzed. From this the absorption was determined since these three contributions together should be equal to the intensity of the incoming laser light. Fig. 5a presents the results for the 100 μm thick PS sheets as a function of the dye content. The amount of reflection is very small (around 5%) which corresponds to the prediction of Fresnel's law. Moreover, due to the nearly equal refractive indices of glass and PS (1.5 versus 1.59) the presence of the microscope slides on both sides of the sample, which was required due to sample brittleness, cannot be noticed on the reflection data, as was verified using a plane sheet of high molecular weight PS. Both the transmission TI as a function of dye weight percent (Fig. 5a) as well as the transmission TI as a function of sample thickness (Fig. 5b) follow the Lambert–Beer law:
| | 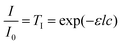 | (4) |
where
I0 is the intensity of the incoming light,
I is the transmitted intensity,
l is the path length through the sample,
c is the concentration of the dye and
ε is the extinction coefficient. Fitting both data sets with this equation resulted in an extinction coefficient
ε of 1172 m
2 mol
−1, which makes it possible to determine the light absorption as a function of sample thickness and dye concentration. Finally,
Fig. 5b shows that the effect of the angle of incidence of the laser light is negligible, if the increased path length through the sample due to the sample orientation is taken into account. This is caused by the fact that reflection only constitutes a minor part of the total response. Based on the absorption values, a fixed dye content of 2 wt% was chosen for particle radii ranging from 30 to 105 μm. This leads to an absorption value close to 90% of the incoming laser light.
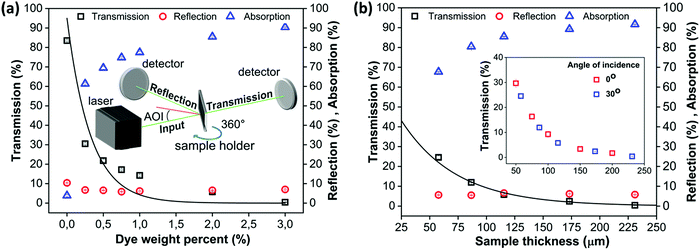 |
| | Fig. 5 (a) Transmission, reflection and absorption of visible light (532 nm) as a function of dye weight% for a sample thickness of 100 μm and an angle of incidence (AOI) of 30°, (b) transmission, reflection and absorption of visible light (532 nm) as a function of sample thickness perpendicular to the laser path for a dye-weight percent of 2% and an angle of incidence of 30°. The inset compares the transmission at angles of incidence of 0° and 30°. Lines indicate fits with the Lambert–Beer law. | |
4.2 Representative sintering behaviour
Fig. 6 presents image sequences obtained in the top and side views during a typical sintering experiment. Movies of the sintering process in the top and side views are available in the ESI.† The laser pulse is applied at time t = 0 s. In general, sintering consists of three stages.16 Upon initial softening of the material due to heating above Tg, small deformation of the contact region will create a finite contact surface. Subsequently a neck is formed due to the merging of both polymer particles at the contact surface and the disappearance of the intermediate liquid–air interface. Finally, neck growth occurs during which the particle doublet transforms its shape towards a single sphere under the driving force of surface tension. Within the resolution of the optical train, we can only analyze the neck growth stage of the sintering process, starting from the neck radius to particle radius ratio (x/a0) of 0.2, as shown in Fig. 6. A gradual growth of the neck radius is observed in the image sequence. The images in Fig. 6 also show that the particles remain pinned to the substrate during the major part of the sintering process as they do not liquefy completely. Only towards the end of the sintering process, wetting of the polymer on the substrate starts to occur, which is however halted rapidly due to solidification at the end of the laser pulse. For the viscous sintering of liquid droplets, it has been shown that the wetting of the polymer on the substrate can affect the sintering kinetics, whereby enhanced wetting results in an acceleration of the sintering kinetics.39 In our case, the substrate that is relevant for the actual sintering process in laser sintering would be polystyrene. However, the mirror polished steel substrate provides a twofold advantage: it facilitates the applied particle manipulation technique and also avoids stray reflections in the optical images. The wetting behavior of liquids on solids can be estimated from the wetting parameter S:39where Γs is the surface energy of the substrate, Γsl is that of the substrate–liquid interface and Γl is the surface tension of the liquid. If S > 0 the liquid will favorably wet the substrate. Since stainless steel is a material with a very high surface energy, a good wetting will be obtained. Similarly, polystyrene droplets will wet a polystyrene substrate. Hence, the wetting behavior of polystyrene droplets on a polystyrene substrate and a stainless steel substrate are expected to be similar, which was also experimentally verified. Thus, all further experiments were performed on the steel substrate, but are also representative for sintering of polystyrene on polystyrene.
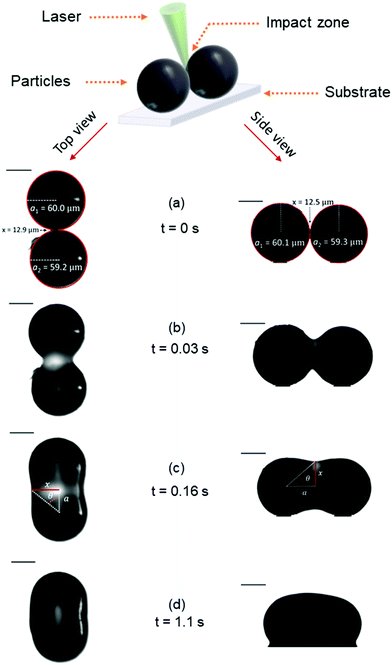 |
| | Fig. 6 Image sequence of a typical sintering experiment with a particle radius of a0 = 60 μm, heating chamber temperature of Tc = 53 °C, pulse energy of Ep = 28 μJ and pulse duration of tL = 800 ms. | |
Using the image sequence of Fig. 6, the neck radius as a function of time is determined and is given in Fig. 7a and b for the top and side view, respectively. The experimental reproducibility is very high, as is seen from the repeat experiments in Fig. 7. Additional reproducibility checks at other values of the pulse energy are shown in Fig. S1 in the ESI.† Furthermore, Fig. 7 shows that the kinetics exhibited in the top view and side view are identical. For all sintering experiments performed in this work, there was no systematic effect of analyzing the data from either the top or the side view. The final obtained neck radius was exactly the same in both cases. Therefore, only the side view results are shown in the remaining part of the work, as they were captured with a faster camera. This axisymmetric behavior of the neck region and thus absence of any effects of the substrate on the sintering kinetics can most probably be attributed to the fact that the particle contact point with the substrate remains solid during the major part of the sintering process.
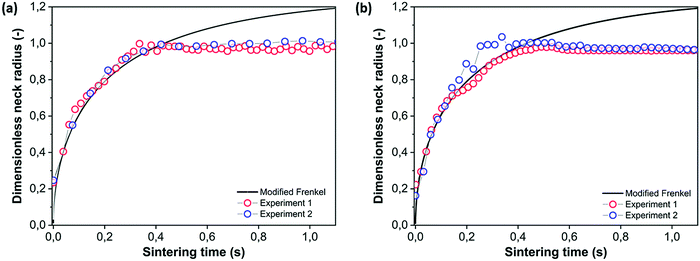 |
| | Fig. 7 Dimensionless neck radius versus sintering time fitted with the modified Frenkel model (lines) with a particle radius a0 = 60 μm, heating chamber temperature Tc = 53 °C, pulse energy Ep = 28 μJ and pulse duration tL = 800 ms. (a) Top view, (b) side view. | |
The evolution of the neck radius in Fig. 7 was fitted with the modified Frenkel model for viscous sintering of liquids under isothermal conditions, given by:15
| | 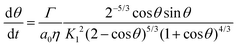 | (6) |
where
Γ is the surface tension,
η is the viscosity,
a0 is the particle radius,
θ is the angle between the line connecting the particle centers and that connecting a particle center with the extreme point of the neck, as indicated in
Fig. 6c, and
K1 is given by:
25| | 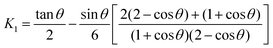 | (7) |
which is the expression derived by Scribben
et al.25 for arbitrary
θ values. From
θ the dimensionless neck radius
x/
a0 can be obtained:
15| | 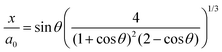 | (8) |
Thereby, the viscosity
η was used as a fitting parameter. It can be seen from
Fig. 7 that this model is well suited to describe the initial sintering kinetics, even though it was developed for isothermal sintering of viscous liquids. The resulting fit value for the viscosity is 143 Pa s, which with the given WLF parameters corresponds to a temperature of 122 °C. Starting from a bed temperature of 53 °C, the resulting temperature increase would require a total energy of 86 μJ per particle to heat up to 122 °C, which is higher than the applied energy of 28 μJ thereby suggesting that both particles are not fully heated up to a homogeneous temperature. In addition, it suggests that the conversion of visible light energy into heat is rather efficient. At the last sintering stage, the modified Frenkel model predicts a final dimensionless neck radius of 2
1/3, which is 1.26, and corresponds to a spherical particle with radius
a02
1/3. In the laser sintering experiment, the dimensionless neck radius levels off at a lower value since the particle doublet is not able to fully relax to a spherical droplet. This can be attributed to the limited energy supply, which hampers sufficient fluidity of the complete particles to retract into a spherical shape. During thermal sintering in a homogeneously heated chamber or upon continuous application of a three times higher laser energy, complete sintering up to a spherical droplet was observed.
It is interesting that, despite the expected non-isothermal characteristics of the sintering process, both in time as well as in space, the modified Frenkel model allows to capture the initial sintering kinetics rather well. Concerning the spatial distribution of the temperature profile, it should be noted that the ratio of laser spot radius (20 μm) to particle radius (60 μm) is 0.33 at this particle size, thereby a large area of the particles is illuminated. Moreover, the heat diffusion time from the laser illuminated area to the surrounding region of the particles can be estimated using the characteristic time for heat diffusion given by:40
| | 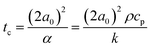 | (9) |
where
α is the thermal diffusivity and
ρ,
cp and
k are the respective density, heat capacity and thermal conductivity of PS. For a particle radius of 60 μm,
tc equals 0.12 s. This indicates a relatively fast heat diffusion throughout the particles, which suggests that the neck region will most probably attain a relatively homogeneous temperature during sintering. However, even though spatial gradients within the sintering neck region are expected to be limited, temporal variations in temperature will be present due to the continuous heating of the neck region by the supplied laser energy.
4.3 Effect of particle size
With the main characteristics of the sintering kinetics being set out in Section 4.2, the effects of several parameters relevant in laser sintering are systematically explored via experimental characterization of the sintering process. First, the particle size is varied, with the radii ranging between 30 and 105 μm. This corresponds to the typical particle size range of laser sintering materials.7 The results of the neck growth kinetics presented in Fig. 8 show two main effects. Firstly it can be seen that increasing the particle size substantially slows down the sintering kinetics. This is qualitatively the expected trend according to the scaling of the modified Frenkel model,15 as increasing the particle radius reduces the driving force originating from the surface tension which is maximal for a highly curved meniscus.41 Second, Fig. 8a shows that due to the slower sintering kinetics, only partial neck growth is attained by the time the laser pulse ends, which results in partially sintered doublets, as shown in Fig. 8b. During actual laser sintering, such partially sintered doublets would result in porosity of the printed parts.
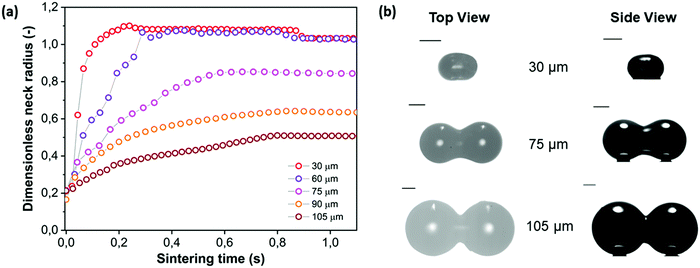 |
| | Fig. 8 Effect of particle radius on sintering kinetics with heating chamber temperature Tc = 53 °C, pulse energy Ep = 29 μJ and pulse duration tL = 800 ms. (a) Dimensionless neck radius in side view and (b) particle doublets at the end of the sintering process. | |
To analyze whether the effects of particle radius follow the typical scaling of the modified Frenkel model, the sintering time is scaled with the characteristic Frenkel time (ηa0/Γ where Γ is the surface tension of polystyrene, η the viscosity and a0 the particle radius whereby η was kept the same as that obtained for a particle radius of 60 μm in Fig. 7), as shown in Fig. 9a. It can be seen that even after applying this scaling, the sintering of the larger particles is slower than that of the smaller ones. This indicates that the heat diffusion from the laser illuminated area to the surrounding particle region plays a significant role, as already concluded in Section 4.2. When increasing the particle radius from 30 to 105 μm, the ratio of the laser spot size to particle size decreases from 0.66 to 0.19. Since for large particles a larger part of the heat energy flows to the non-illuminated regions, the temperature increase in the neck region will be less, resulting in a higher viscosity and thus a slower sintering kinetics. For the cases resulting in incomplete sintering, it can also be seen that the sintering kinetics slows down at the later sintering stages, thereby no longer allowing a description of the kinetics using the modified Frenkel model. This is caused by the effect of the transient rheology, resulting from the finite relaxation time of the polymer, which leads to a larger viscosity at later timescales, for which complete sintering is already obtained in the case of smaller particles. At the end of the laser pulse (at t = 800 ms in Fig. 8a), an almost instantaneous solidification of the neck region is noticed. This phenomenon is analyzed by an estimation of the cooling rate of the particles. First, the Biot number was estimated as follows:40
| | 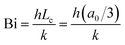 | (10) |
where
h is the heat transfer coefficient,
k is the thermal conductivity,
Lc is the characteristic length scale which is defined as volume/surface area and
a0 is the particle radius. This allows the determination of the relative contributions of external convection and internal heat conduction. Due to the small length scales involved, Bi ≪ 0.1 and once the laser is switched off, the cooling of the particle will occur more or less homogeneously throughout the particle without the generation of additional temperature gradients within the particle. Moreover, the timescale for cooling can be estimated from an energy balance considering only heat loss due to convection:
| | 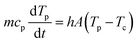 | (11) |
where
m is the particle mass,
cp is the heat capacity,
Tp is the particle temperature,
h is the heat transfer coefficient,
A is the particle surface area and
Tc is the temperature of the heating chamber. Using a typical value for
h of 50 W m
−2 K
−1 (Section 4.7), it can be calculated that cooling from the estimated sintering temperature of 122 °C occurs rather fast whereby more than a 10 °C temperature drop is obtained within 100 ms. Moreover, especially in the case of fully sintered particles with a large contact area between the particles and the substrate, additional heat loss to the heating chamber substrate will occur. The final reached neck radius is an important characteristic of the final sintered product and the dimensionless final neck radius (
xf/
a0) is provided as a function of the particle radius in
Fig. 9b. It can be seen that once incomplete sintering is obtained, the final dimensionless neck radius decreases approximately linearly with the overall particle radius. The sintering process is halted when the polymer viscosity exceeds a critical value whereby the work of the surface tension becomes insufficient to overcome the viscous loss during flow.
15 Since the evolution of the polymer viscosity with time critically depends on the different rheological parameters of the material, the exact relation between the final dimensionless neck radius and the particle size will depend on the polymer rheology.
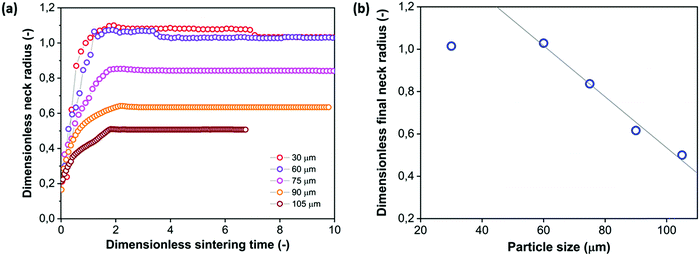 |
| | Fig. 9 Effect of particle radius on sintering kinetics with heating chamber temperature Tc = 53 °C, pulse energy Ep = 29 μJ and pulse duration tL = 800 ms. (a) Dimensionless neck radius in side view versus time rescaled with Frenkel timescale, (b) dimensionless final neck radius versus particle size. | |
4.4 Effect of heating chamber temperature
The optimal heating chamber temperature in selective laser sintering is generally considered to be the highest temperature that does not result in consolidation of the powder outside the laser area. This way, the required laser energy is minimal whereas thermal gradients and thermal expansion are also minimized.7 The effect of varying the heating chamber temperatures from close to Tg to far below it, keeping all other parameters fixed, is depicted in Fig. 10. A priori, two effects of decreasing the heating chamber temperature would be expected. With a lower heating chamber temperature and at the same laser energy, the temperature in the sintering region would be lower, resulting in a higher viscosity and thus lower sintering speed. In addition, once the laser energy is not sufficient anymore to heat the polymer above the glass transition temperature, solidification and cessation of the sintering process will be observed. It can be seen in Fig. 10 that mainly at the lowest heating chamber temperature of 30 °C, the initial sintering speed is significantly slowed down. However, the reduction of the sintering speed is much less as compared to what would be expected from the increase of the steady state viscosity due to a temperature reduction of 23 °C in the sintering region (as can be derived from a scaling of the x axis with the Frenkel timescale taking into account the steady state viscosity effect being 143 Pa s at 122 °C versus 2094 Pa s at 99 °C, results not shown). This is caused by the fact that during the initial stages of sintering, the effect of temperature on the viscosity can be much less as compared to the temperature effect at the steady state. For the other heating chamber temperatures, the lower sintering kinetics is noticed only at timescales above 200 ms, which may indicate that initially the limiting step is the distribution of heat to the particle region outside the laser spot area. Moreover, at timescales that are sufficiently short with respect to the polymer relaxation time, the effects of temperature on the viscosity can become insignificant. This is caused by the fact that increasing the temperature lowers both the steady state viscosity as well as the relaxation time.42 The dependence of the final obtained dimensionless neck radius on the heating chamber temperature is depicted in Fig. 10b. It can be seen that the sensitivity to the heating chamber temperature is rather limited within a relatively wide range of heating chamber temperatures.
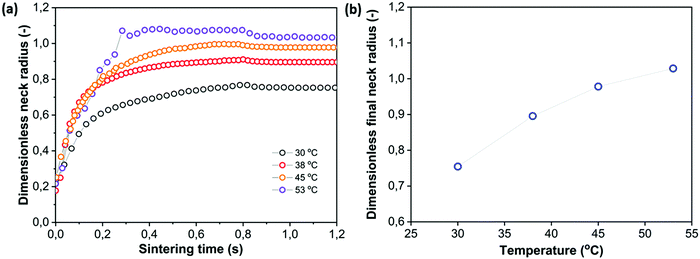 |
| | Fig. 10 Effect of heating chamber temperature on sintering kinetics with pulse energy Ep = 29 μJ, pulse duration tL = 800 ms and particle radius a0 = 60 μm. (a) Dimensionless neck radius in side view and (b) dimensionless final neck radius versus heating chamber temperature. | |
4.5 Effect of pulse duration
A third parameter that is of relevance during laser sintering is the laser pulse duration. With typical scanning speeds ranging between 10 and 1000 mm s−1 and particle diameters in the range of 50 to 500 μm,7 the typical duration of laser impact on a particle is in the range of 0.05–50 ms. However, since the laser scan spacing is mostly chosen about 3 to 6 times smaller than the laser beam diameter, the effective laser impact time on each location is larger.7 To be able to perform a systematic study of the effects of laser pulse duration, we selected a range of pulse durations, ranging from much shorter than the characteristic sintering time, to longer than this time. The total energy within each pulse was kept constant. Fig. 11a demonstrates that the main effect of shorter pulse durations is a premature cessation of the neck growth process occurring nearly instantaneously after switching off the laser pulse. On the other hand, even though at the same total pulse energy the longest pulse duration corresponds to a more than ten-fold lower power as compared to the shortest pulse (0.036 versus 1.16 mW), the kinetics of the growth of the neck radius is relatively insensitive to this parameter. This may suggest that at the shortest pulse durations the limiting factor for the kinetics is the distribution of heat over the sintering area rather than the effective laser power. In addition, the higher instantaneous laser power would result in larger temperature gradients within the particle doublet, thereby leading to more heat flow to the outer particle regions as compared to the case in which there is a slower heating of the sintering region. In addition, during the initial sintering stages, the effect of temperature on the polymer viscosity can be very limited, even though the steady state viscosity shows a high temperature dependence. The dependence of the final obtained neck radius as a function of laser pulse duration is shown in Fig. 11b. Since the sintering kinetics is relatively insensitive to the applied laser pulse duration (or correspondingly the laser power), the dependence of the final dimensionless neck radius xf/a0 follows a similar trend as x/a0 for the case of the longest applied pulse duration. This is caused by the fact that the final neck radius is only determined by the time point at which sintering was halted by the end of the laser pulse. These results clearly show that, using the same total pulse energy, distributing this energy over a longer time results in more efficient sintering.
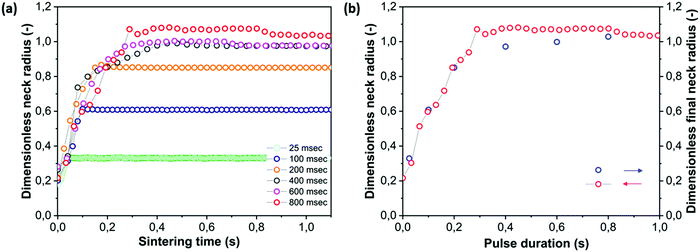 |
| | Fig. 11 Effect of pulse duration on sintering kinetics with heating chamber temperature Tc = 53 °C, pulse energy Ep = 29 μJ and particle radius a0 = 60 μm. (a) Dimensionless neck radius in side view and (b) dimensionless final neck radius versus pulse duration. | |
4.6 Effect of laser energy
Finally, the laser sintering process is affected by the laser energy. As typical spot sizes in commercial laser sintering devices are much larger than 40 μm, the fluence or laser energy per unit area will be used for comparison purposes. In the present work, the laser energy values were varied between 19 and 29 μJ, which corresponds to fluence values of 3800–5800 J m−2. For amorphous polymers such as polystyrene, typical values of the fluence can be estimated from the laser power, scan speed and scan spacing, which for instance results in a value in the order of 2000–3000 J m−2 for the sintering of high impact polystyrene.11Fig. 12 shows that decreasing the laser energy at a constant pulse duration (thus reducing the laser power from 0.036 to 0.024 mW) results in a slowing down of the sintering kinetics for the lowest pulse energies whereas for the highest values, the initial slope remains the same up to 200 ms, which corresponds to the trend observed in Fig. 11 showing the effect of pulse duration, for values resulting in higher power values as those observed in Fig. 12. This suggests that there is a critical power value above which the power is no longer the limiting factor at the initial stages of the sintering process. At the lowest applied laser energy values, the initial sintering kinetics is slower but it also appears that sintering is nearly halted already before the end of the laser pulse (at 800 ms). This suggests that the supplied energy is so low that the viscosity decrease due to the increase in temperature is less pronounced than the viscosity increase due to transient effects. Hence, sintering can only occur in the initial stages when the driving force is very large due to the high curvature and viscosity buildup is still ongoing whereas after some time, sintering slows down substantially due to the high viscosity. Fig. 12b shows the evolution of the final dimensionless neck radius with the applied laser energy. The dependence on laser energy is very strong in the studied range of energy values whereby the lowest values are clearly not enough to obtain a sufficient temperature increase for sintering. A linear relation between the laser energy and the dimensionless final neck radius is obtained for the whole range of relevant laser energies, ranging from those resulting in nearly no sintering to those leading to complete sintering. However, similar to the effects of particle size, the exact relation between both parameters depends on the complex time and temperature dependent rheology of the polymer.
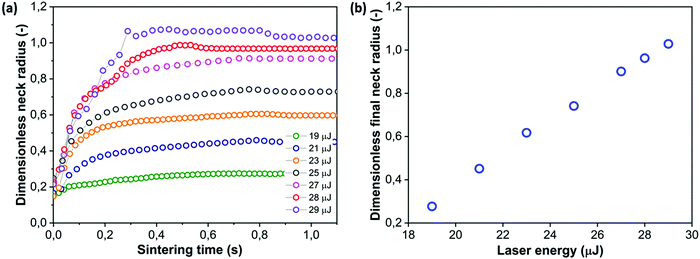 |
| | Fig. 12 Effect of laser energy on sintering kinetics with a heating chamber temperature Tc = 53 °C, pulse duration tL = 800 ms and particle radius a0 = 60 μm. (a) Dimensionless neck radius in side view and (b) dimensionless final neck radius versus laser energy. | |
4.7 Main physical phenomena summarized in a non-isothermal sintering model
To date, viscous sintering models have been used to describe the sintering kinetics in the case of isothermal sintering processes in a heated chamber. However, as mentioned above, during laser sintering, a continuous increase in the temperature of the neck region is expected. Since such a temperature evolution results in a changing rheological behavior during sintering, this should be taken into account in the sintering model. Scribben et al.25 generalized the modified Frenkel model to become valid for any rheological constitutive equation, resulting in:| | 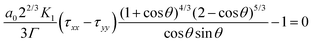 | (12) |
where a0 is the particle radius, Γ is the surface tension, τxx and τyy are the normal stresses in two perpendicular directions and K1 is defined in eqn (7). In the model derivation, it was assumed that sintering results in a purely biaxial extensional flow with a homogeneous extension rate throughout the fluid volume. Hence, the extension rate 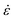 depends on the sintering kinetics, according to:15
depends on the sintering kinetics, according to:15| | 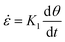 | (13) |
Since the stress values in eqn (12) depend on the rheological parameters as well as the extension rate, the rheological constitutive equation and sintering equation thus form a coupled set of equations. Based on eqn (13) and the sintering kinetics shown in Fig. 7, extension rates in our study range up to 4 s−1, depending on the applied laser sintering conditions. Hence, a full analysis of the sintering problem would require a non-linear constitutive equation, as quasi-linear models such as the upper convected Maxwell model may fail due to the fact that the extensional viscosity becomes unbounded for 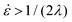 .42 However, in that case, a full numerical approach, such as that applied in the work of Balemans et al.,30 using a finite element method, might be more suitable. Hence, we neglect non-linear rheological effects and describe the rheology of the polymer with the linear viscoelastic Maxwell model. Thereby, qualitative insights into the effects of the different laser sintering parameters on the neck growth process, via their effects on the polymer rheology, will be provided. In the linear viscoelastic case, the rheology and sintering kinetics is decoupled. Hence, first the evolution of the viscosity with time is calculated from the Maxwell model with temperature-dependent parameters:
.42 However, in that case, a full numerical approach, such as that applied in the work of Balemans et al.,30 using a finite element method, might be more suitable. Hence, we neglect non-linear rheological effects and describe the rheology of the polymer with the linear viscoelastic Maxwell model. Thereby, qualitative insights into the effects of the different laser sintering parameters on the neck growth process, via their effects on the polymer rheology, will be provided. In the linear viscoelastic case, the rheology and sintering kinetics is decoupled. Hence, first the evolution of the viscosity with time is calculated from the Maxwell model with temperature-dependent parameters:| | 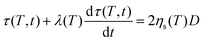 | (14) |
where τ is the stress tensor, D is the rate of deformation tensor, λ is the relaxation time and ηsis the steady state viscosity. As shown in Fig. 4, the PS polymer behaves thermorheologically simply, hence the temperature dependence of ηs and λ can be described by means of the temperature shift factor aT (eqn (2)). The resulting viscosity evolution with time is governed by two counteracting effects. Gradual heating of the particles leads to a decrease in the viscosity with time. Simultaneously, the finite relaxation time of the polymer causes a viscosity buildup with time. The resulting viscosity η as a function of time, defined as:| | 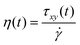 | (15) |
where ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the shear rate and τxy the shear stress, are substituted in eqn (6), which is equivalent to eqn (12) when a linear viscoelastic constitutive equation is used.
the shear rate and τxy the shear stress, are substituted in eqn (6), which is equivalent to eqn (12) when a linear viscoelastic constitutive equation is used.
To determine the evolution of the temperature as a function of time during the heating by means of the laser pulse, an energy balance is used. First, it should be noted that due to the limited temperature difference between the particles and the heating chamber, heat loss by radiation is negligible as compared to that by convection.40 Hence, the temperature evolution of the particles is governed by the supplied laser energy and the heat loss to the environment by means of free convection:
| | 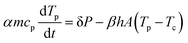 | (16) |
where
m is the particle mass,
cp is the heat capacity,
Tp is the particle temperature,
P is the power of the laser given by the pulse energy
Ep divided by the pulse duration
tL,
h is the heat transfer coefficient,
A is the particle surface area and
Tc is the temperature of the heating chamber. The parameters
α,
δ and
β allow to correct for the facts that not the whole particle is heated, that the conversion from laser energy to heat energy is not complete and that there may be additional heat loss to the environment by conduction into the heating chamber substrate. The heat transfer coefficient
h can be estimated from heat transfer correlations for free convection over an object. Based on the dimensionless Rayleigh number, which is on the order of 10
−6 for the studied conditions, it is concluded that buoyancy-driven flows are negligible and the heat transfer is dominated by conduction.
40 In that case, the heat transfer coefficient is obtained from the fact that the Nusselt number Nu for conduction equals two with the Nusselt number being defined as:
| | 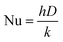 | (17) |
where
h is the heat transfer coefficient,
D is the characteristic length scale which in this case is the particle diameter and
k is the thermal conductivity of air.
40 This results in a value for the heat transfer coefficient on the order of 50 W mK
−1. Depending on the contact area between the particle and the heating chamber substrate, additional heat loss to the heating chamber substrate may play a role, which can be taken into account by means of parameter
β in
eqn (16). From the energy balance stated in
eqn (16), the temperature evolution in the particle can be obtained as:
| | 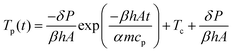 | (18) |
Using this model, the effect of the various parameters that affect the sintering process, namely the particle size, heating chamber temperature, laser energy and laser pulse duration can be investigated. Model predictions are calculated for the sintering parameters shown in Fig. 7, using the reference viscosity and reference relaxation time obtained in Section 4.1 and keeping the correction factors α, β and δ in eqn (16) and (18) at one. The results for the temperature and viscosity evolution as a function of time for various values of the laser pulse energy are shown in Fig. 13a and b. Fig. 13a demonstrates that increasing the laser energy results in a more pronounced temperature increase. Moreover, after a certain time, the particle temperature becomes so high that the heat loss equals the energy supplied by the laser and thus the temperature reaches a plateau value. The corresponding viscosity evolution is shown in Fig. 13b. In general, the viscosity exhibits an increasing trend as a function of time, which is caused by the transient effects from the polymer relaxation time. With increasing temperature, the rising trend of the viscosity becomes less pronounced. However, the temperature effects at initial times are clearly less pronounced than those at later times and under the steady state conditions. When the supplied energy is high enough, the viscosity even exhibits a non-monotonous trend, which first increases due to the dominant effect of viscoelasticity followed by a decrease due to the dominant effect of the temperature rise.
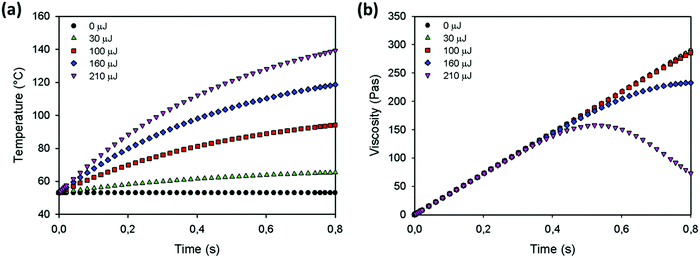 |
| | Fig. 13 Model predictions at various laser energies for (a) temperature and (b) viscosity as a function of time for a particle radius a0 = 60 μm, heating chamber temperature Tc = 53 °C, pulse duration tL = 800 ms, ηref = 2119 Pa s, λref = 6.1 s, α = 1, β = 1 and δ = 1. | |
Fig. 14a shows the sintering kinetics for the parameter values for which the temperature and viscosity evolution are shown in Fig. 13a and b. This figure clearly indicates that using the experimental parameter values, the obtained sintering kinetics is much faster as compared to the behavior observed in the experiments. This discrepancy can most probably be attributed to the fact that the solid polymer behavior below Tg is not incorporated in the model and the liquid behavior and corresponding viscosities and relaxation times at these temperatures are extrapolated from the WLF behavior, which does not hold below Tg. Hence, whereas our model predicts an initial viscosity of zero that builds up with a very long relaxation time, the actual polymer will be a viscoelastic solid during the initial stages of sintering. Due to the pronounced sintering at very short sintering times, the final obtained dimensionless neck radius is nearly independent of the supplied laser energy in this case. By reducing the relaxation time of the polymer, a faster increase of the viscosity results, as shown in Fig. 14b. This faster viscosity build-up suppresses the sintering process, as shown in Fig. 14a. Since the model predictions do not allow quantitative matching of the experimental sintering behavior, the model cannot be used to describe the experimental data but rather to indicate the relevant governing phenomena.
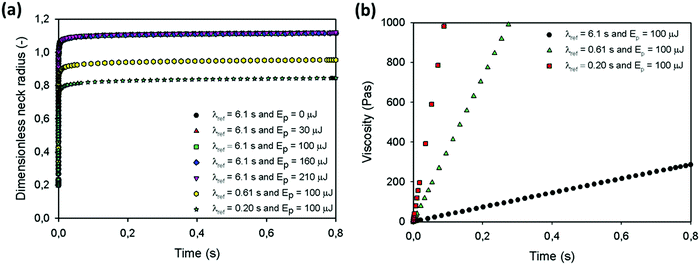 |
| | Fig. 14 Model predictions for (a) dimensionless neck radius versus time for a particle radius a0 = 60 μm and (b) viscosity versus time, heating chamber temperature Tc = 53 °C, pulse duration tL = 800 ms, ηref = 2119 Pa s, α = 1, β = 1 and δ = 1. | |
In conclusion, the performed model calculations indicate that the balance between the relaxation time and the temperature dependence of the viscosity has a significant contribution to the sintering behavior. Faster sintering is obtained when the polymer viscosity is low. A low viscosity can be obtained from a steady state viscosity that drops significantly with increasing temperature but also from a large relaxation time that provides a slow viscosity build-up. Since in typical polymers both the viscosity and the relaxation time show a similar drop with increasing temperature, use of more complex materials, e.g. multiphasic materials, is expected to allow an enhanced optimization of the material rheology for the laser sintering process. From the point of view of process parameters, it can be concluded that the various parameters that affect the sintering kinetics all act through changes of the temperature and thereby viscosity of the material. Hence, a correct understanding and modelling of the temporal and spatial temperature profiles is crucial to capture the actual sintering kinetics. Clearly, due to the complex interaction between the temperature and time-dependent rheological behavior, merely increasing the temperature by using a higher laser power or chamber temperature, does not always improve the sintering speed, which is counter-intuitive.
5. Conclusions
Laser sintering of polystyrene is studied on the scale of a single particle doublet by using a novel in-house developed experimental setup. This setup allowed the particle doublet to be subjected to a well-defined laser pulse while performing optical visualization of the growth of the neck radius between the particles, both from the top as well as from the sides. A visible light laser modulated with an acousto-optic modulator was used to create laser pulses focused on the particle doublet with a well-defined small spot size. Thereby, the scanning of the laser over the particles in the actual laser sintering devices can be mimicked. By using spherical polystyrene particles of various sizes the ratio of laser spot size to particle size was varied between 0.66 and 0.19. The thermal, rheological and laser light absorption properties of the used polystyrene were characterized a priori. This allowed the determination of the suitable parameter range for the heating chamber temperature, laser pulse duration and laser pulse energy. Subsequently, a systematic study of the effects of the main laser sintering parameters on the sintering dynamics, quantified as the evolution of the neck radius between both particles with time, was performed. This allowed, for the first time, the provision of time-resolved information on the laser sintering of polymer particles. The initial sintering kinetics as a function of time can be described with the modified Frenkel model for isothermal sintering of viscous liquids, whereby the characteristic viscosity depends on the applied process conditions. However, the overall sintering kinetics is determined by a complex interplay between the temperature and time effects on the viscosity. Contrary to thermal sintering in a homogeneously heated chamber, laser-induced particle sintering can slow down and even completely halt at later stages. This is caused by the viscosity build-up as a function of time due to the finite relaxation time of the material. Hence, if the supplied laser energy is not sufficient to cause a substantial temperature increase, only partial sintering occurs. Considering the complexity of the sintering process that is characterized by a non-uniform and time-dependent temperature profile as well as complex flow fields, further studies will involve a combination of experimental and numerical work to provide complementary information on the global as well as local scale. Moreover, the effects of the presence of surrounding particles on the sintering kinetics will be studied to be able to extend our results to actual sintering in a polymer powder bed. In the case of viscous sintering, it has already been shown that the sintering of nearby particles affects the kinetics.43 Finally, since laser sintering of polymers often concerns semi-crystalline materials, the experimental approach will be extended to allow in situ characterization of the crystallization process during sintering.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work forms part of the research programme of the Brightlands Materials Center (BMC). We thank the ICMS, TU Eindhoven, for providing us with the rendered image and animation of the experimental setup. The undergraduate student Loek Trimbach is acknowledged for the development of the Matlab® code for image analysis.
References
-
J. P. Kruth, M. C. Leu and T. Nakagawa, Progress in additive manufacturing and rapid prototyping, 1998, pp. 525–540 Search PubMed.
- E. Radstok, Rapid Prototyp. J., 1999, 5(4), 164–168 CrossRef.
-
C. R. Deckard, Method and apparatus for producing parts by selective sintering, 1989 Search PubMed.
- S. Kumar, JOM, 2003, 55(10), 43–47 CrossRef CAS.
- J. P. Kruth, P. Mercelis, J. Van Vaerenbergh, L. Froyen and M. Rombouts, Rapid Prototyp. J., 2005, 11(1), 26–36 CrossRef.
- I. Gibson and D. P. Shi, Rapid Prototyp. J., 1997, 3(4), 129–136 CrossRef.
- R. D. Goodridge, C. J. Tuck and R. J. M. Hague, Prog. Mater. Sci., 2012, 57(2), 229–267 CrossRef CAS.
- Y. Shi, Z. Li, H. Sun, S. Huang and F. Zeng, Proc. Inst. Mech. Eng., Part L, 2004, 218(L3), 247–252 CAS.
- N. Hopkinson, C. E. Majewski and H. Zarringhalam, CIRP Ann., 2009, 58(1), 197–200 CrossRef.
- T. H. C. Childs, M. Berzins, G. R. Ryder and A. Tontowi, Proc. Inst. Mech. Eng., Part B, 1999, 213(4), 333–349 CrossRef.
- Y. S. Shi, Y. Wang, J. B. Chen and S. H. Huang, J. Appl. Polym. Sci., 2008, 108(1), 535–540 CrossRef CAS.
- M. Schmidt, D. Pohle and T. Rechtenwald, CIRP Ann., 2007, 56(1), 205–208 CrossRef.
-
D. Drummer, K. Wudy, F. Kuhnlein and M. Drexler, Polymer Blends for Selective Laser Sintering: Material and Process Requirements, in Laser Assisted Net Shape Engineering 7, ed. M. Schmidt, F. Vollertsen and M. Geiger, 2012, vol. 39, pp. 509–517 Search PubMed.
- K. H. Tan, C. K. Chua, K. F. Leong, C. M. Cheah, P. Cheang, M. S. Abu Bakar and S. W. Cha, Biomaterials, 2003, 24(18), 3115–3123 CrossRef CAS PubMed.
- O. Pokluda, C. T. Bellehumeur and J. Vlachopoulos, AIChE J., 1997, 43(12), 3253–3256 CrossRef CAS.
- C. T. Bellehumeur, M. K. Bisaria and J. Vlachopoulos, Polym. Eng. Sci., 1996, 36(17), 2198–2207 CrossRef CAS.
- C. T. Bellehumeur, M. Kontopoulou and J. Vlachopoulos, Rheol. Acta, 1998, 37(3), 270–278 CrossRef CAS.
- N. Rosenzweig and M. Narkis, Polymer, 1980, 21(9), 988–989 CrossRef CAS.
- P. R. Hornsby and A. S. Maxwell, J. Mater. Sci., 1992, 27(9), 2525–2533 CrossRef CAS.
- G. C. Kuczynski, B. Neuville and H. P. Toner, J. Appl. Polym. Sci., 1970, 14(8), 2069–2077 CrossRef CAS.
- J. Frenkel, J. Phys., 1945, 9(5), 385–391 Search PubMed.
- S. Berretta, Y. Wang, R. Davies and O. R. Ghita, J. Mater. Sci., 2016, 51(10), 4778–4794 CrossRef CAS.
- S. Aid, A. Eddhahak, Z. Ortega, D. Froelich and A. Tcharkhtchi, J. Mater. Sci., 2017, 52(19), 11725–11736 CrossRef CAS.
- J. D. Muller, M. Bousmina and A. Maazouz, Macromolecules, 2008, 41(6), 2096–2103 CrossRef CAS.
- E. Scribben, D. Baird and P. Wapperom, Rheol. Acta, 2006, 45(6), 825–839 CrossRef CAS.
- C. Balemans, M. A. Hulsen and P. D. Anderson, Appl. Sci., 2017, 7, 5 Search PubMed.
- N. K. Tolochko, T. Laoui, Y. V. Khlopkov, S. E. Mozzharov, V. I. Titov and M. B. Ignatiev, Rapid Prototyp. J., 2000, 6(3), 155–160 CrossRef.
- C. W. Buckley and T. L. Bergman, J. Heat Transfer, 2001, 123(3), 586–592 CrossRef CAS.
- D. T. Pham and R. S. Gault, Int. J. Mach. Tool Manufact., 1998, 38(10–11), 1257–1287 CrossRef.
- C. Balemans, N. O. Jaensson, M. Hulsen and P. D. Anderson, Addit. Manufact., 2018, 24, 528–542 CrossRef CAS.
- A. D. Pasquino, J. Polym. Sci., Part B: Polym. Lett., 1964, 2(3PB), 253–255 CrossRef CAS.
- H. Hocker, G. J. Blake and P. J. Flory, Trans. Faraday Soc., 1971, 67(584), 2251–2257 RSC.
-
S. Wu, Polymer interface and adhesion, Marcel Dekker, 1982 Search PubMed.
- D. H. Ballard, Pattern Recogn., 1981, 13(2), 111–122 CrossRef.
- J. Hintermeyer, A. Herrmann, R. Kahlau, C. Goiceanu and E. A. Rossler, Macromolecules, 2008, 41(23), 9335–9344 CrossRef CAS.
- J. P. Kruth, G. Levy, F. Klocke and T. H. C. Childs, CIRP Ann., 2007, 56(2), 730–759 CrossRef.
-
C. Macosko, Rheology Principles, measurements and applications, Wiley-VCH, 1994 Search PubMed.
- P. Lomellini, Polymer, 1992, 33(23), 4983–4989 CrossRef CAS.
- J. D. Muller, K. Lamnawar and A. Maazouz, J. Mater. Sci., 2012, 47(1), 121–131 CrossRef CAS.
-
W. M. Rohsenow, J. P. Hartnett and Y. I. Cho, Handbook of heat transfer, McGraw-Hill, 1998 Search PubMed.
- J. Eggers, J. R. Lister and H. A. Stone, J. Fluid Mech., 1999, 401, 293–310 CrossRef CAS.
-
F. Morrison, Understanding rheology, Oxford University Press, 2001 Search PubMed.
- F. Varnik, A. Rios, M. Gross and I. Steinbach, Modell. Simul. Mater. Sci. Eng., 2013, 21(2), 025003 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02081g |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Patrick D.
Anderson
a,
Patrick D.
Anderson
 a and
Ruth
Cardinaels
a and
Ruth
Cardinaels
 *a
*a



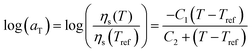
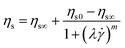
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, m is a constant and λ is the cross time constant with 1/λ corresponding to the shear rate at the onset of shear thinning. This results in a zero-shear viscosity of 2119 Pa s at the reference temperature of 100 °C. Fig. 4b provides the zero-shear viscosity values at different temperatures together with the WLF fit that is used to determine the viscosity at other temperatures. Based on the measured viscosities, the expected timescale of the sintering process, using the characteristic timescale of the Frenkel model, which is (ηs0a0)/Γ where Γ is the surface tension of PS, ηs0 the steady state zero-shear viscosity and a0 the initial particle radius,15 is on the order of 3 s for a particle radius of 60 μm and a temperature of 100 °C. By fitting the small-amplitude dynamic moduli with a multimode Maxwell model (Fig. 4a),37 the relaxation time distribution of the polymer is determined. Table 1 provides the different relaxation times and their respective contributions. Based on the data in Table 1, the viscosity average relaxation time is 6.1 s and the zero-shear viscosity is 2207 Pa s at 100 °C. From the sintering model of Bellehumeur et al.,17 which considers an upper convected Maxwell model for the polymer rheology under quasi-steady state conditions for sintering (neglecting transient viscosity effects), it is concluded that for λ ≈ 2(ηs0a0)/Γ as is the case here, the effect of the viscoelastic stresses on the sintering dynamics can be neglected. However, transient effects of the viscosity buildup after the start of the flow are expected to play a role.25
is the shear rate, m is a constant and λ is the cross time constant with 1/λ corresponding to the shear rate at the onset of shear thinning. This results in a zero-shear viscosity of 2119 Pa s at the reference temperature of 100 °C. Fig. 4b provides the zero-shear viscosity values at different temperatures together with the WLF fit that is used to determine the viscosity at other temperatures. Based on the measured viscosities, the expected timescale of the sintering process, using the characteristic timescale of the Frenkel model, which is (ηs0a0)/Γ where Γ is the surface tension of PS, ηs0 the steady state zero-shear viscosity and a0 the initial particle radius,15 is on the order of 3 s for a particle radius of 60 μm and a temperature of 100 °C. By fitting the small-amplitude dynamic moduli with a multimode Maxwell model (Fig. 4a),37 the relaxation time distribution of the polymer is determined. Table 1 provides the different relaxation times and their respective contributions. Based on the data in Table 1, the viscosity average relaxation time is 6.1 s and the zero-shear viscosity is 2207 Pa s at 100 °C. From the sintering model of Bellehumeur et al.,17 which considers an upper convected Maxwell model for the polymer rheology under quasi-steady state conditions for sintering (neglecting transient viscosity effects), it is concluded that for λ ≈ 2(ηs0a0)/Γ as is the case here, the effect of the viscoelastic stresses on the sintering dynamics can be neglected. However, transient effects of the viscosity buildup after the start of the flow are expected to play a role.25
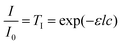

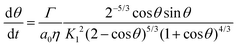
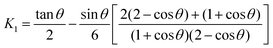
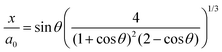
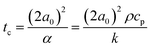
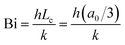
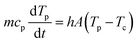
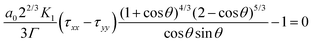
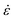 depends on the sintering kinetics, according to:15
depends on the sintering kinetics, according to:15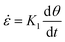
 .42 However, in that case, a full numerical approach, such as that applied in the work of Balemans et al.,30 using a finite element method, might be more suitable. Hence, we neglect non-linear rheological effects and describe the rheology of the polymer with the linear viscoelastic Maxwell model. Thereby, qualitative insights into the effects of the different laser sintering parameters on the neck growth process, via their effects on the polymer rheology, will be provided. In the linear viscoelastic case, the rheology and sintering kinetics is decoupled. Hence, first the evolution of the viscosity with time is calculated from the Maxwell model with temperature-dependent parameters:
.42 However, in that case, a full numerical approach, such as that applied in the work of Balemans et al.,30 using a finite element method, might be more suitable. Hence, we neglect non-linear rheological effects and describe the rheology of the polymer with the linear viscoelastic Maxwell model. Thereby, qualitative insights into the effects of the different laser sintering parameters on the neck growth process, via their effects on the polymer rheology, will be provided. In the linear viscoelastic case, the rheology and sintering kinetics is decoupled. Hence, first the evolution of the viscosity with time is calculated from the Maxwell model with temperature-dependent parameters: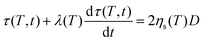
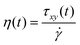
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) the shear rate and τxy the shear stress, are substituted in eqn (6), which is equivalent to eqn (12) when a linear viscoelastic constitutive equation is used.
the shear rate and τxy the shear stress, are substituted in eqn (6), which is equivalent to eqn (12) when a linear viscoelastic constitutive equation is used.