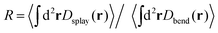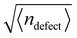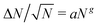The interplay between activity and filament flexibility determines the emergent properties of active nematics†
Abhijeet
Joshi
,
Elias
Putzig
,
Aparna
Baskaran
* and
Michael F.
Hagan
 *
*
Martin Fisher School of Physics, Brandeis University, Waltham, MA 02453, USA. E-mail: aparna@brandeis.edu; hagan@brandeis.edu
First published on 29th November 2018
Abstract
Active nematics are microscopically driven liquid crystals that exhibit dynamical steady states characterized by the creation and annihilation of topological defects. Motivated by differences between previous simulations of active nematics based on rigid rods and experimental realizations based on semiflexible biopolymer filaments, we describe a large-scale simulation study of a particle-based computational model that explicitly incorporates filament semiflexibility. We find that energy injected into the system at the particle scale preferentially excites bend deformations, reducing the apparent filament bend modulus. The emergent characteristics of the active nematic depend on activity and flexibility only through this activity-renormalized bend ‘modulus’, demonstrating that apparent values of material parameters, such as the Frank ‘constants’, depend on activity. Thus, phenomenological parameters within continuum hydrodynamic descriptions of active nematics must account for this dependence. Further, we present a systematic way to estimate these parameters from observations of deformation fields and defect shapes in experimental or simulation data.
I. Introduction
Active nematics are a class of non-equilibrium liquid crystalline materials in which the constituent particles transduce energy into stress and motion, driving orientationally inhomogeneous dynamical steady states characterized by generation, annihilation, and streaming of topological defects.1–7 Being intrinsically far-from-equilibrium, active nematics enable developing materials with capabilities that would be thermodynamically forbidden in an equilibrium system. However, such applications require understanding how an active nematic's macroscale material properties depend on the microscale features of its constituent nematogens.The challenge in this task can be illustrated by considering the shape of a defect. Defects have been the subject of intense research in equilibrium nematics, since they must be eliminated for display technologies, and controlled for applications such as directed assembly and biosensing.8–10 Theory and experiments10–12 have shown that defect morphologies depend on the relative values of the bend and splay elastic moduli, k33 and k11 (Fig. 1a), defined in the Frank free energy density for a 2D nematic as fF = k11(∇·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) )2 + k33(
)2 + k33(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) × (∇ ×
× (∇ × ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) ))2 with
))2 with ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) the director field.13,14 Different experimental realizations of active nematics also exhibit variations in defect morphologies (e.g.Fig. 1c and d). However, relating these defect morphologies to material constants is much less straightforward than in equilibrium systems. Since moduli are an equilibrium concept, they cannot be rigorously defined in a non-equilibrium system such as an active nematic. If it is possible to define ‘effective moduli’ in active systems, there is currently no systematic way to measure them, and it is unclear whether and how they may depend on activity.
the director field.13,14 Different experimental realizations of active nematics also exhibit variations in defect morphologies (e.g.Fig. 1c and d). However, relating these defect morphologies to material constants is much less straightforward than in equilibrium systems. Since moduli are an equilibrium concept, they cannot be rigorously defined in a non-equilibrium system such as an active nematic. If it is possible to define ‘effective moduli’ in active systems, there is currently no systematic way to measure them, and it is unclear whether and how they may depend on activity.
 | ||
| Fig. 1 (a and b) The equilibrium director field configuration near a +½ defect for (a) bend modulus larger than splay modulus k33/k11 = 3.4, leading to pointed defects and (b) splay modulus larger than bend k33/k11 = 0.3 leading to rounded defects. In each case the director field was calculated by numerically minimizing the Frank free energy around a separated ±½ defect pair. (c and d) Typical defect morphologies observed in (c) a vibrated granular nematic5 and (d) a microtubule-based active nematic.1,40 | ||
Computational and theoretical modeling could overcome these limitations. Symmetry-based hydrodynamic theories15–17 have led to numerous insights about active nematics, including describing defect dynamics (e.g.ref. 18–23), induced flows in the suspending fluid (e.g.ref. 24–26), and how confinement in planar27–30 and curved geometries31–34 controls defect proliferation and dynamics. However, hydrodynamic theories cannot predict how material constants or emergent behaviors depend on the microscale properties of individual nematogens. Further, while simulations of active nematics composed of rigid rods2,35–37 have elucidated emergent morphologies, these models do not account for internal degrees of freedom available to flexible nematogens.1,38,39
In this work, we perform large-scale simulations on a model active nematic composed of semiflexible filaments, and determine how its emergent morphology depends on filament stiffness and activity. Fig. 2 shows representative simulation outcomes. We find that the intrinsic bending modulus of nematogens κ undergoes an apparent softening in an active nematic, according κeff ∼ κ/(fa)2, where fa is a measure of its activity. Furthermore, the characteristics of the active nematic texture – the defect density, magnitudes and characteristic scales of bend and splay deformations, the shape of motile 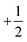 defects, and number fluctuations – depend on activity and rigidity only through the apparent nematogen rigidity κeff. Moreover, we show that one can define effective bend and splay moduli analogous to their equilibrium counterparts, but that the apparent bend modulus is proportional to κeff. This observation demonstrates that activity preferentially dissipates into particular modes within an active material, depending on the internal degrees of freedom of its constituent units. Further, these results suggest revisiting assumptions underlying existing hydrodynamic theories of active matter, since a microscopic model for an active fluid results in macroscopic properties that depend on activity in nontrivial ways, which cannot be simply described by an active stress. Finally, we present a method of parameterizing defect shapes, which enables estimating the relative magnitudes of apparent bend and splay constants from experimental observations of defects, and thus allows direct experimental testing of our prediction.
defects, and number fluctuations – depend on activity and rigidity only through the apparent nematogen rigidity κeff. Moreover, we show that one can define effective bend and splay moduli analogous to their equilibrium counterparts, but that the apparent bend modulus is proportional to κeff. This observation demonstrates that activity preferentially dissipates into particular modes within an active material, depending on the internal degrees of freedom of its constituent units. Further, these results suggest revisiting assumptions underlying existing hydrodynamic theories of active matter, since a microscopic model for an active fluid results in macroscopic properties that depend on activity in nontrivial ways, which cannot be simply described by an active stress. Finally, we present a method of parameterizing defect shapes, which enables estimating the relative magnitudes of apparent bend and splay constants from experimental observations of defects, and thus allows direct experimental testing of our prediction.
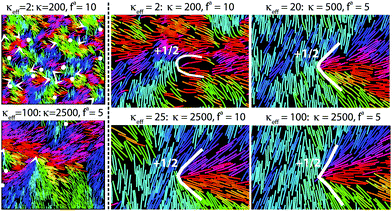 | ||
| Fig. 2 A visual summary of how active nematic emergent properties depend on the activity parameter fa and the filament modulus κ. The left panel in each row shows 1/16th of the simulation box for indicated parameter values, with white arrows indicating positions and orientations of +½ defects and white dots indicating positions of -½ defects. Filament beads are colored according to the orientations of the local tangent vector. The right 4 panels are each zoomed in on a +½ defect, with indicated parameter values. The white lines are drawn by eye to highlight defect shapes. Animations of corresponding simulation trajectories are in the ESI.†41 The box size is (840 × 840σ2) for all simulations in this work. Other parameters are τ1 = 0.2τ and kb = 300kBTref/σ2. | ||
II. Methods
We seek a minimal computational model that captures the key material properties and symmetries of active nematics, namely extensile activity, nematic inter-particle alignment and semiflexibility. We model active filaments as semiflexible bead-spring polymers, each containing M beads of diameter σ, with flexibility controlled by a harmonic angle potential between successive bonds that sets the filament bending modulus κ. Activity is implemented as a force of magnitude fa acting on each filament bead along the local tangent to the filament. To make activity nematic, the active force on every bead within a given filament reverses direction after a time interval chosen from a Poisson distribution with mean τ1. The Langevin equations governing the system dynamics were integrated using a modified version of LAMMPS.42 The model combines features of recent models for polar self-propelled polymers43 and the reversing rods approach to rigid active nematic rods.36Equations of motion and interaction potentials
We simulate the dynamics according to the following Langevin equation for each filament α and bead i (with filaments indexed by Greek letters, α = 1,…,N, and beads within a filament indexed in Roman, i = 1,…,M):m![[r with combining umlaut]](https://www.rsc.org/images/entities/b_char_0072_0308.gif) α,i = faα,i − γṙα,i − ∇rα,iU + Rα,i(t). α,i = faα,i − γṙα,i − ∇rα,iU + Rα,i(t). | (1) |
The interaction potential includes three contributions which respectively account for non-bonded interactions between all bead pairs, stretching of each bond, and the angle potential between each pair of neighboring bonds:
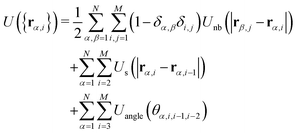 | (2) |
| Unb(r) = 4ε((σ/r)12 − (σ/r)6 + 1/4)Θ(21/6σ − r) | (3) |
Us(r) = −1/2kbR02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(1 − (r/R0)2) ln(1 − (r/R0)2) | (4) |
| Uangle(θ) = κ(θ − π)2 | (5) |
Finally, activity is modeled as a propulsive force on every bead directed along the filament tangent toward its head. To render the activity nematic, the head and tail of each filament are switched at stochastic intervals so that the force direction on each bead rotates by 180 degrees. In particular, the active force has the form, faα,i(t) = ηα(t)fatα,i, where fa parameterizes the activity strength, and ηα(t) is a stochastic variable associated with filament α that changes its values between 1 and −1 on Poisson distributed intervals with mean τ1, so that τ1 controls the reversal frequency.
Simulations and parameter values
Since we are motivated by systems sufficiently large that boundary effects are negligible (e.g.ref. 2), we performed simulations in a A = 840 × 840σ2 periodic simulation box, with N = 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 404 filaments, each with M = 20 beads, so that the packing fraction ϕ = MNσ2/A ≈ 0.55. Fixing all other model parameters, we varied the filament stiffness, κ ∈ [102, 104]kBTref and the magnitude of the active force, fa ∈ [5, 30]kBTref/σ, where the units are set by the thermal energy at a reference state kBTref, and the filament diameter σ. Time is measured in units of
404 filaments, each with M = 20 beads, so that the packing fraction ϕ = MNσ2/A ≈ 0.55. Fixing all other model parameters, we varied the filament stiffness, κ ∈ [102, 104]kBTref and the magnitude of the active force, fa ∈ [5, 30]kBTref/σ, where the units are set by the thermal energy at a reference state kBTref, and the filament diameter σ. Time is measured in units of 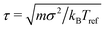 . We set mass of the each bead to m = 1, the damping coefficient to γ = 2, and the temperature to T = 3.0kBTref. With these parameters inertia is non-negligible. In the future, we plan to systematically investigate the effect of damping. We set the repulsion parameter ε = kBTref (the results are insensitive to the value of ε provided it is sufficiently high to avoid filament overlap), and used a time step of δt = 10−3τ.
. We set mass of the each bead to m = 1, the damping coefficient to γ = 2, and the temperature to T = 3.0kBTref. With these parameters inertia is non-negligible. In the future, we plan to systematically investigate the effect of damping. We set the repulsion parameter ε = kBTref (the results are insensitive to the value of ε provided it is sufficiently high to avoid filament overlap), and used a time step of δt = 10−3τ.
In the FENE bond potential, R0 is set to 1.5σ and kb = 300kBTref/σ2 for the simulations reported in the main text (except in Fig. 3). These parameters lead to a mean bond length of b ≈ 0.84σ, which ensures that filaments are non-penetrable for the parameter space explored in this work. We have fixed the filament length at M = 20 beads, so L = (M − 1)b is the mean filament length. Varying M does not change the scaling of observables, although it shifts properties such as the defect density since the total active force per filament goes as faM. Also, the maximum persistence length above which scaling laws fail is proportional to M (see Results). In the semiflexible limit, the stiffness κ in the discrete model is related to the continuum bending modulus 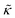 as
as 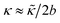 , and thus the persistence length is given by lp = 2bκ/kBT.
, and thus the persistence length is given by lp = 2bκ/kBT.
We performed two sets of simulations. Initially, we set the FENE bond strength kb = 30kBTref/σ2 and τ1 = τ. However, for these parameters we discovered that interpenetration of filaments becomes possible at large propulsion velocities, thus limiting the simulations to fa ≤ 10. To enable investigating higher activity values, we therefore performed a second set of simulations (those reported in Fig. 4–7 of the main text) with higher FENE bond strength, kb = 300kBTref/σ2 and shorter reversal timescale τ1 = 0.2, with κ ∈ [100, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000]kBTref. This enables simulating activity values up to fa ≤ 30.
000]kBTref. This enables simulating activity values up to fa ≤ 30.
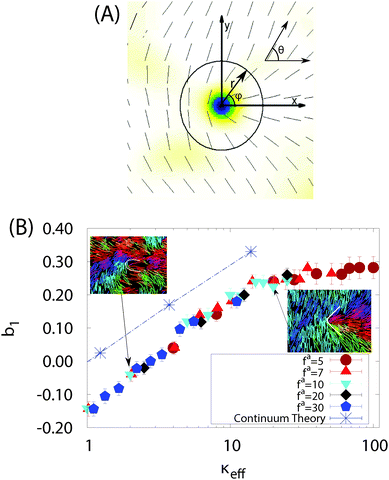 | ||
Fig. 5 Defect shape depends on the effective bending rigidity. (A) Schematic showing the defect-centered coordinate system defined in the text, with azimuthal angle ϕ and director angle θ(r, ϕ). Note that the x-axis is chosen along the orientation vector of the +1/2 defect given by the angle θ0′ defined in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41 (B) Mode of defect shape parameter b1 for +½ defects as a function of κeff for fa ∈ [7, 30] and κ ∈ [100, 10 41 (B) Mode of defect shape parameter b1 for +½ defects as a function of κeff for fa ∈ [7, 30] and κ ∈ [100, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000], with b1(r) values evaluated at a radial distance r = 12.6σ from the defect core. The dashed line and blue asterisk symbols show values of b1 calculated for isolated defects from equilibrium continuum elastic theory, with the ratio of bend and splay moduli k33/k11 for each κeff set according to the measured ratio R of bend and splay deformations in Fig. 4. Images of defects at two indicated parameter sets are shown. Other parameters are τ1 = 0.2τ and kb = 300kBTref/σ2. 000], with b1(r) values evaluated at a radial distance r = 12.6σ from the defect core. The dashed line and blue asterisk symbols show values of b1 calculated for isolated defects from equilibrium continuum elastic theory, with the ratio of bend and splay moduli k33/k11 for each κeff set according to the measured ratio R of bend and splay deformations in Fig. 4. Images of defects at two indicated parameter sets are shown. Other parameters are τ1 = 0.2τ and kb = 300kBTref/σ2. | ||
The shorter reversal timescale was needed to keep the system in the nematic regime at large fa. When the product faτ exceeds a characteristic collision length scale the self-propulsion becomes polar in nature and model is no longer a good description of an active nematic. In particular, the filaments behave as polar self-propelled rods, as evidenced by the formation of polar clusters.46–50 Interestingly, increasing kb increases the rate of defect formation and decreases the threshold value of faτ above which phase separation occurs. We monitored the existence of phase separation by measuring local densities within simulation boxes (see ref. 41). We found no significant phase separation (except on short scales) or formation of polar clusters for any of the simulations described here, indicating the systems were in the nematic regime. Within the nematic regime, increasing kb does not qualitatively change results or scaling relations, although it does quantitatively shift properties such as the defect density. Additional plots for the simulation set with kb = 30 are shown in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41
41
Initialization
We initialized the system by first placing the filaments in completely extended configurations (all bonds parallel and all bond lengths set to b), on a rectangular lattice with filaments oriented along one of the lattice vectors. We then relaxed the initial configuration for 104τ, where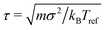 , before performing production runs of ∼4 × 104τ. The equilibration time of 104τ was chosen based on the fact that in all simulated systems the defect density had reached steady state by this time. We also confirmed that other observables of interest have reached steady state at this time. In the limit of high stiffness or low activity, the unphysical crystalline initial condition did not relax on computationally accessible timescales. In these cases, we used an alternative initial configuration, with filaments arranged into four rectangular lattices, each placed in one quadrant of the simulation box such that adjacent (non-diagonal) lattices were orthogonal.
, before performing production runs of ∼4 × 104τ. The equilibration time of 104τ was chosen based on the fact that in all simulated systems the defect density had reached steady state by this time. We also confirmed that other observables of interest have reached steady state at this time. In the limit of high stiffness or low activity, the unphysical crystalline initial condition did not relax on computationally accessible timescales. In these cases, we used an alternative initial configuration, with filaments arranged into four rectangular lattices, each placed in one quadrant of the simulation box such that adjacent (non-diagonal) lattices were orthogonal.
III. Results and discussion
To understand how the interplay between filament flexibility and activity determines the texture of an active nematic, we analyzed our simulation results using multiple metrics for the deformations in nematic order.Before reporting these results, let us first consider the basic physics governing the emergent phenomenology in our system. Deforming a nematogen causes an elastic stress that scales ∼κ, the filament bending modulus. This elastic stress must be balanced by stresses arising from interparticle collisions. These collisional stresses have two contributions. First there are the passive collisional stresses, which are ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (1) in our units (as we have chosen the thermal energy and the particle size σ as the energy and length scales). Then there are active collisional stresses that arise due to the self-replenishing active force of magnitude fa acting on each monomer. The active collisional stress will scale as νcollΔpcoll, i.e., the collision frequency times the momentum transfer at each collision. Both the collision frequency and momentum transfer will scale with the self-propulsion velocity,51 which in our model is set by fa. Thus, the collisional stresses will scale ∼(1 + (fa)2). So, the system properties will be controlled by a parameter which measures the ratio of elastic to collisional stresses, κeff ≡ κ/(1 + (fa)2).
(1) in our units (as we have chosen the thermal energy and the particle size σ as the energy and length scales). Then there are active collisional stresses that arise due to the self-replenishing active force of magnitude fa acting on each monomer. The active collisional stress will scale as νcollΔpcoll, i.e., the collision frequency times the momentum transfer at each collision. Both the collision frequency and momentum transfer will scale with the self-propulsion velocity,51 which in our model is set by fa. Thus, the collisional stresses will scale ∼(1 + (fa)2). So, the system properties will be controlled by a parameter which measures the ratio of elastic to collisional stresses, κeff ≡ κ/(1 + (fa)2).
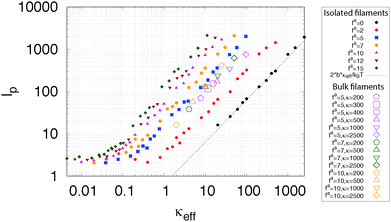
Persistence length
To test this scaling, we measured the tangent fluctuations of individual filaments within our computational active nematic. We then determined the effective persistence length from the Fourier spectrum of these fluctuations (see ref. 41, Section S4 and Fig. S2, ESI†). Fig. 3 shows estimated persistence lengths over a range of filament bending modulus values κ ∈ (200, 2500), and activity parameter values fa ∈ (5, 10) from two sets of simulations: isolated chains (small solid symbols) and chains from the bulk active nematic (large open symbols). Note that the result for an isolated equilibrium polymer (fa = 0,![[pentagon filled]](https://www.rsc.org/images/entities/char_e13d.gif) symbols) perfectly matches the expected relationship lp = 2bκeff/kBT. For the bulk active chains we observe data collapse over all of these parameters when the persistence length is plotted as a function of κeff, with persistence length scaling as lp ∼ κeff. In contrast, the effective persistence length for isolated active chains does not exhibit data collapse; the persistence length scales linearly with κ but exhibits a different dependence on activity. This result supports the proposal that the apparent softening of filaments in bulk active nematics arises due to inter-chain collisions.
symbols) perfectly matches the expected relationship lp = 2bκeff/kBT. For the bulk active chains we observe data collapse over all of these parameters when the persistence length is plotted as a function of κeff, with persistence length scaling as lp ∼ κeff. In contrast, the effective persistence length for isolated active chains does not exhibit data collapse; the persistence length scales linearly with κ but exhibits a different dependence on activity. This result supports the proposal that the apparent softening of filaments in bulk active nematics arises due to inter-chain collisions.
Note that we restrict the analysis to fa ≥ 5 because the system loses nematic order for smaller activity values (see Fig. S5C (ESI†)41 and ‘Comparison with Equilibrium’ below). The results in Fig. 3 were performed on our initial data set with τ1 = τ and kb = 30kBTref/σ2 and thus are limited to fa ≤ 10 (see Methods).
We now test whether the arguments proposed above can describe the collective behaviors of an active nematic, using several metrics for deformations in the nematic order: the distribution of energy in splay and bend deformations, defect shape, defect density, and number fluctuations. As shown in Fig. 4–7, all of these quantities depend on bending rigidity and activity only through the combination κeff. We performed the analysis of active nematics textures (described next) on the second parameter set with τ1 = 0.2τ and kb = 300kBTref/σ2, which allowed fa ≤ 30.
Splay and bend deformations
We first determine whether it is possible to define quantities analogous to splay and bend moduli in an active nematic. We emphasize that moduli cannot be rigorously defined in a non-equilibrium system, but we will see that the relative amounts of energy in bend and splay deformations, and all other steady-state properties of an active nematic, can be described by ‘effective moduli’ if the effect of activity is accounted for.In a 2D nematic, any arbitrary deformation of the director field can be decomposed into a bend deformation dbend = (![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) (r) × (∇ ×
(r) × (∇ × ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) (r))) and a splay deformation dsplay = (∇·
(r))) and a splay deformation dsplay = (∇·![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) (r)). We define associated strain energy densities Dbend = ρS2|dbend|2 and Dsplay = ρS2dsplay2, which measure how the system's elastic energy distributes into the two linearly independent deformation modes. The prefactors of density ρ and order S allow the definitions to be valid in regions such as defect cores and voids that occur in the particle simulations.
(r)). We define associated strain energy densities Dbend = ρS2|dbend|2 and Dsplay = ρS2dsplay2, which measure how the system's elastic energy distributes into the two linearly independent deformation modes. The prefactors of density ρ and order S allow the definitions to be valid in regions such as defect cores and voids that occur in the particle simulations.
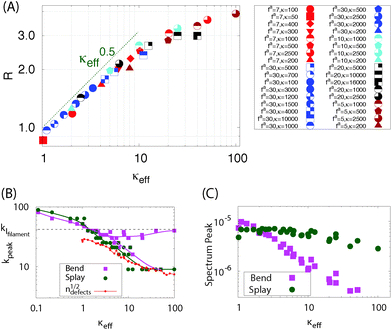
To compare the splay and bend deformations to their form in an equilibrium nematic, let us consider the ratio of total strain energy in splay deformations to those in bend, 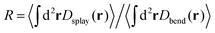 . In equilibrium, equipartition requires that this ratio satisfy Req = k33/k11. In our simulations, we observe that R depends strongly on activity; however, the data for all parameter sets collapses when plotted as a function of the effective filament bend modulus κeff. This result is consistent with the concept of effective moduli, but shows that their values depend on activity.
. In equilibrium, equipartition requires that this ratio satisfy Req = k33/k11. In our simulations, we observe that R depends strongly on activity; however, the data for all parameter sets collapses when plotted as a function of the effective filament bend modulus κeff. This result is consistent with the concept of effective moduli, but shows that their values depend on activity.
To understand why the apparent modulus values depend on activity, we analyzed the power spectra associated with these strain energies (Fig. S4 in ref. 41). The power spectra exhibit two features: (1) Fig. 4B shows that for the smallest simulated effective rigidity, κeff = 2, the peak of the power spectrum kpeak is on the filament scale, indicating that most deformation energy arises due to bending of individual filaments. But for all higher values of κeff, a peak arises at the defect spacing scale, indicating that the defect density controls the texture in this active nematic. (2) Fig. 4C shows the magnitude of the power spectrum at the characteristic scale kpeak. The splay energy density is nearly independent of the effective filament stiffness, while the amount of bend decreases linearly with κeff for κeff ≲ κmaxeff, where κmaxeff ≈ 30 is the point at which the effective persistence length of the filaments is equal to their contour length. This observation demonstrates that energy injected into the system at the microscale due to activity preferentially dissipates into bend modes.
Defect shape
Let us now consider a striking feature of the texture of an active nematic, the shape of a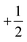 defect. A quantitative descriptor of defect shape can be developed as follows. We choose a coordinate system with its origin at the center of the defect core, with the x-axis pointing along the defect orientation (see Fig. 5A). We work in polar coordinates, with r the radial distance from the defect core and ϕ as the azimuthal angle with respect to the x-axis. We define θ as the angle of the director field with respect to the x-axis. At any position, we can then express θ(r, ϕ) as a Fourier expansion in ϕ ∈ {−π:π}.
defect. A quantitative descriptor of defect shape can be developed as follows. We choose a coordinate system with its origin at the center of the defect core, with the x-axis pointing along the defect orientation (see Fig. 5A). We work in polar coordinates, with r the radial distance from the defect core and ϕ as the azimuthal angle with respect to the x-axis. We define θ as the angle of the director field with respect to the x-axis. At any position, we can then express θ(r, ϕ) as a Fourier expansion in ϕ ∈ {−π:π}.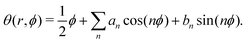 | (6) |
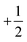 defect well, so the descriptor simplifies to
defect well, so the descriptor simplifies to 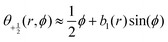 , and the result is insensitive to r provided the measurement is performed outside of the defect core (see Fig. S10 (ESI†)41). Thus, the parameter b1 uniquely describes the defect shape; in particular, larger values of b1 correspond to pointier defects. Note that Zhang et al.12 and Cortese et al.22 recently proposed similar approaches to characterizing defect shapes. An advantage of our approach is that the shape can be described by a single number, b1.
, and the result is insensitive to r provided the measurement is performed outside of the defect core (see Fig. S10 (ESI†)41). Thus, the parameter b1 uniquely describes the defect shape; in particular, larger values of b1 correspond to pointier defects. Note that Zhang et al.12 and Cortese et al.22 recently proposed similar approaches to characterizing defect shapes. An advantage of our approach is that the shape can be described by a single number, b1.
Fig. 5B shows that the mode of b1 calculated from defects within our simulations depends only on κeff, thus demonstrating that defect shape is controlled by the apparent bending rigidity. Moreover, b1 increases logarithmically with κeff; i.e., defects become more pointed as the bending rigidity increases, consistent with the previous observations of highly pointed defects in rigid rod simulations.2,35,52
Defect density
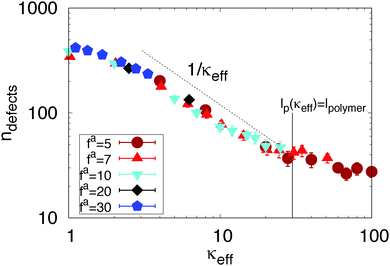
We next consider a well-studied property of an active nematic, the steady-state defect density.19,24,28,53Fig. 6 shows that the defect density collapses onto a single curve when plotted as a function of κeff, and scales roughly as 1/κeff under parameter values for which the apparent persistence length lies between the monomer scale and filament contour length, 1.5 ≲ κeff ≲ κmaxeff. We observe the same scaling for our other data set (Fig. S1, ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41). Hydrodynamic theories such as ref. 19, 24, 28 and 53 predict that the defect density scales as α/K, where α is the measure of active stress in the hydrodynamic theories and K is a Frank elastic constant. The scaling collapse observed in our simulations indicates that these hydrodynamic parameters are directly related to their microscopic analogs, namely the filament elastic constant κ and the collisional active stress ∼(1 + (fa)2). Note that we could not measure defect densities in systems with both extremely high activity and high bare bending rigidity (fa ≥ 20 and κ ≳ 5000) because our defect detection algorithm breaks down (see Section S8 of ref. 41).
41). Hydrodynamic theories such as ref. 19, 24, 28 and 53 predict that the defect density scales as α/K, where α is the measure of active stress in the hydrodynamic theories and K is a Frank elastic constant. The scaling collapse observed in our simulations indicates that these hydrodynamic parameters are directly related to their microscopic analogs, namely the filament elastic constant κ and the collisional active stress ∼(1 + (fa)2). Note that we could not measure defect densities in systems with both extremely high activity and high bare bending rigidity (fa ≥ 20 and κ ≳ 5000) because our defect detection algorithm breaks down (see Section S8 of ref. 41).
Number fluctuations
Finally, previous work has shown that active nematics are susceptible to phase separation36,54–56 and giant number fluctuations (GNFs).5,54,57–59 We find that flexibility suppresses phase separation except at molecular scales (Fig. S8, ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41), but that number fluctuations are governed by the apparent modulus. We monitored number fluctuations by measuring the number of pseudoatoms within square subsystems with side lengths ranging from 20σ to 840σ. At equilibrium, in a region containing on average N particles the standard deviation of the number of particles ΔN scales as
41), but that number fluctuations are governed by the apparent modulus. We monitored number fluctuations by measuring the number of pseudoatoms within square subsystems with side lengths ranging from 20σ to 840σ. At equilibrium, in a region containing on average N particles the standard deviation of the number of particles ΔN scales as 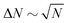 , while previous studies of active nematics have identified higher scaling, as large as ΔN ∼ N. Fig. S9 (ESI†)41 shows measured number fluctuations for different values of the effective bending modulus. We see that for small κeff = 2 the result is constant with subsystem size, indicating equilibrium-like fluctuations, but the slope increases for larger effective modulus values, indicating a progression toward GNFs. At all κeff the fluctuations are eventually suppressed on scales comparable to the defect spacing (N ≳ 104), at which scale the system is essentially isotropic, consistent with Narayan et al.5
, while previous studies of active nematics have identified higher scaling, as large as ΔN ∼ N. Fig. S9 (ESI†)41 shows measured number fluctuations for different values of the effective bending modulus. We see that for small κeff = 2 the result is constant with subsystem size, indicating equilibrium-like fluctuations, but the slope increases for larger effective modulus values, indicating a progression toward GNFs. At all κeff the fluctuations are eventually suppressed on scales comparable to the defect spacing (N ≳ 104), at which scale the system is essentially isotropic, consistent with Narayan et al.5
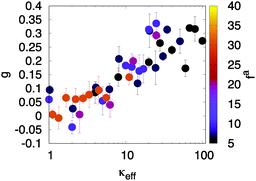
To determine the dependence on κeff, we fit the data for each simulation in the range N ≤ 104 to the form aNg, so that g = 0 indicates equilibrium-like fluctuations and g = 0.5 would indicate linear scaling of fluctuations with system size. As shown in Fig. 7, g increases with κeff, with g = 0 for small κeff and g ≈ 0.3 for the largest effective bending rigidity values investigated; i.e. ΔN ∼ N0.8. The fact that g < 0.5 for the parameters we consider may reflect suppression of fluctuations even for N < 104. Importantly, estimated values of g at different fa and κ collapse onto a single function of κeff, consistent with the observations of the other characteristics of an active nematic shown above.
Comparison with equilibrium
For small values of κeff, the bend/splay ratio in our model active nematic roughly scales as R ∼κ1/2eff (Fig. 4). This differs from the scaling of an equilibrium nematic, where the moduli scale as k33 ∼ κ and k11 ∼ κ1/3,60,61 giving Req ∼ κ2/3. We confirmed this scaling by calculating the equilibrium moduli for our system (Fig. S5, ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41) using the free energy perturbation technique of ref. 62. Analysis of simulation trajectories suggests that the difference in scaling arises because the active systems have much higher nematic order than the equilibrium systems (when compared at the same values of effective bending rigidity). In an equilibrium system, increasing the filament flexibility decreases order, resulting in a transition from the nematic to isotropic phase as κ decreases below 5 at the density used in our simulations.63 In contrast, the active systems remain deep within the nematic phase (S ≳ 0.8) for all parameter sets (Fig. S5c in ref. 41). We empirically found that normalizing the bend–splay ratio by the degree of order, using the form R/S2, roughly collapses the equilibrium and active results onto a single curve (Fig. S5b, ESI†
41) using the free energy perturbation technique of ref. 62. Analysis of simulation trajectories suggests that the difference in scaling arises because the active systems have much higher nematic order than the equilibrium systems (when compared at the same values of effective bending rigidity). In an equilibrium system, increasing the filament flexibility decreases order, resulting in a transition from the nematic to isotropic phase as κ decreases below 5 at the density used in our simulations.63 In contrast, the active systems remain deep within the nematic phase (S ≳ 0.8) for all parameter sets (Fig. S5c in ref. 41). We empirically found that normalizing the bend–splay ratio by the degree of order, using the form R/S2, roughly collapses the equilibrium and active results onto a single curve (Fig. S5b, ESI†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 41). Although we cannot rationalize the form of the normalization, this result implies that the differences in scaling between active and equilibrium cases arise from the increased nematic order in the active simulations.
41). Although we cannot rationalize the form of the normalization, this result implies that the differences in scaling between active and equilibrium cases arise from the increased nematic order in the active simulations.
Returning to the defect shape measurements, the dashed line in Fig. 5B shows the defect shape parameter values b1 calculated by minimizing the continuum Frank free energy for an equilibrium system containing a separated pair of 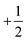 and
and 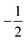 defects. Here we have fixed the continuum modulus k11 and varied k33 so that
defects. Here we have fixed the continuum modulus k11 and varied k33 so that 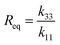 matches the value obtained from our microscopic simulations at the corresponding value of effective stiffness: Req(k33) = R(κeff). Although the equilibrium b1 values are shifted above the simulation results, consistent with the discrepancy in R between the active and passive systems described above, we observe the same scaling with bending rigidity in the continuum and simulation results. Thus, the defect shape measurement provides a straightforward means to estimate effective moduli in simulations or experiments on active nematics.
matches the value obtained from our microscopic simulations at the corresponding value of effective stiffness: Req(k33) = R(κeff). Although the equilibrium b1 values are shifted above the simulation results, consistent with the discrepancy in R between the active and passive systems described above, we observe the same scaling with bending rigidity in the continuum and simulation results. Thus, the defect shape measurement provides a straightforward means to estimate effective moduli in simulations or experiments on active nematics.
IV. Conclusions
In active materials, energy injected at the particle scale undergoes an inverse cascade, manifesting in collective spatiotemporal dynamics at larger scales. The nature of this emergent behavior depends crucially on which modes the active energy dissipates into. Our simulations show that activity within a dry active nematic preferentially dissipates into bend modes, thus softening the apparent bend modulus. Consequently, the value of the apparent bend modulus depends strongly on activity. However, we show that once this dependence on activity is accounted for, this effective modulus dictates all collective behaviors that we investigated – the relative amounts of bend and splay, defect density, defect shape, and giant number fluctuations. The dependence of multiple characteristics on this single parameter suggests that material properties such as apparent moduli can be meaningfully assessed in an active nematic and related to their values at equilibrium, provided their dependence on activity is accounted for. Finally, our technique to parameterize defect shapes allows estimating the relative magnitudes of these effective moduli in any experimental or computational system that exhibits defects.Experimental confirmation of the predicted dependence of effective bend and splay moduli on activity
After a preprint of our manuscript first appeared, ref. 64 presented elegant experimental results confirming that the ratio of apparent bend and splay moduli depend on activity as predicted here.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Brandeis Center for Bioinspired Soft Materials, an NSF MRSEC, DMR-1420382 (AJ, EP, AB, MFH) and NSF DMR-1149266 (AB). Computational resources were provided by NSF XSEDE computing resources (MCB090163, Stampede) and the Brandeis HPCC which is partially supported by DMR-1420382.References
- T. Sanchez, D. T. N. Chen, S. J. Decamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS PubMed.
- S. J. DeCamp, G. S. Redner, A. Baskaran, M. F. Hagan and Z. Dogic, Nat. Mater., 2015, 14, 1110–1115 CrossRef CAS PubMed.
- C. Peng, T. Turiv, Y. Guo, Q.-H. Wei and O. D. Lavrentovich, Science, 2016, 354, 882–885 CrossRef CAS.
- S. Zhou, A. Sokolov, O. D. Lavrentovich and I. S. Aranson, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 1265–1270 CrossRef CAS PubMed.
- V. Narayan, S. Ramaswamy and N. Menon, Science, 2007, 317, 105–108 CrossRef CAS.
- V. Narayan, N. Menon and S. Ramaswamy, J. Stat. Mech.: Theory Exp., 2006, 2006, P01005 Search PubMed.
- G. Duclos, C. Erlenkämper, J.-F. Joanny and P. Silberzan, Nat. Phys., 2017, 13, 58 Search PubMed.
- D. J. Broer, Nat. Mater., 2010, 9, 99–100 CrossRef CAS.
- I.-h. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. de Pablo and N. L. Abbott, Science, 2011, 332, 1297–1300 CrossRef CAS PubMed.
- M. Kleman, Rep. Prog. Phys., 1989, 52, 555–654 CrossRef CAS.
- S. Zhou, S. V. Shiyanovskii, H.-S. Park and O. D. Lavrentovich, Nat. Commun., 2017, 8, 14974 CrossRef PubMed.
- R. Zhang, N. Kumar, J. L. Ross, M. L. Gardel and J. J. de Pablo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E124–E133 CrossRef CAS PubMed.
- F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19 RSC.
- C. W. Oseen, Trans. Faraday Soc., 1933, 29, 883–899 RSC.
- R. A. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101 CrossRef PubMed.
- M. C. Marchetti, J. F. Joanny, S. Ramaswamy, T. B. Liverpool, J. Prost, M. Rao and R. A. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- L. Giomi, M. J. Bowick, X. Ma and M. C. Marchetti, Phys. Rev. Lett., 2013, 110, 228101 CrossRef PubMed.
- L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek and M. Cristina Marchetti, Philos. Trans. R. Soc., A, 2014, 372, 20130365 CrossRef PubMed.
- A. Doostmohammadi, T. N. Shendruk, K. Thijssen and J. M. Yeomans, Nat. Commun., 2017, 8, 15326 CrossRef CAS PubMed.
- A. U. Oza and J. Dunkel, New J. Phys., 2016, 18, 093006 CrossRef.
- D. Cortese, J. Eggers and T. B. Liverpool, Phys. Rev. E, 2018, 97, 022704 CrossRef.
- T. N. Shendruk, K. Thijssen, J. M. Yeomans and A. Doostmohammadi, Phys. Rev. E, 2018, 98, 010601 CrossRef PubMed.
- S. P. Thampi, R. Golestanian and J. M. Yeomans, EPL, 2014, 105, 18001 CrossRef.
- L. Giomi, Phys. Rev. X, 2015, 5, 031003 Search PubMed.
- L. M. Lemma, S. J. Decamp, Z. You, L. Giomi and Z. Dogic, arXiv preprint arXiv:1809.06938, 2018.
- T. N. Shendruk, A. Doostmohammadi, K. Thijssen and J. M. Yeomans, Soft Matter, 2017, 13, 3853–3862 RSC.
- M. M. Norton, A. Baskaran, A. Opathalage, B. Langeslay, S. Fraden, A. Baskaran and M. F. Hagan, Phys. Rev. E, 2018, 97, 012702 CrossRef PubMed.
- T. Gao, M. D. Betterton, A.-S. Jhang and M. J. Shelley, Phys. Rev. Fluids, 2017, 2, 093302 CrossRef.
- P. Guillamat, J. Ignés-Mullol and F. Sagués, Nat. Commun., 2017, 8, 564 CrossRef CAS PubMed.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Science, 2014, 345, 1135–1139 CrossRef CAS PubMed.
- R. Zhang, Y. Zhou, M. Rahimi and J. J. De Pablo, Nat. Commun., 2016, 7, 13483 CrossRef CAS PubMed.
- P. W. Ellis, D. J. G. Pearce, Y.-W. Chang, G. Goldsztein, L. Giomi and A. Fernandez-Nieves, Nat. Phys., 2017, 14, 85 Search PubMed.
- F. Alaimo, C. Köhler and A. Voigt, Sci. Rep., 2017, 7, 5211 Search PubMed.
- T. Gao, R. Blackwell, M. A. Glaser, M. D. Betterton and M. J. Shelley, Phys. Rev. Lett., 2015, 114, 048101 CrossRef PubMed.
- X.-q. Shi and Y.-q. Ma, Nat. Commun., 2013, 4, 3013 CrossRef.
- S. Henkes, M. C. Marchetti and R. Sknepnek, Phys. Rev. E, 2018, 97, 042605 CrossRef PubMed.
- Y. Sumino, K. H. Nagai, Y. Shitaka, D. Tanaka, K. Yoshikawa, H. Chaté and K. Oiwa, Nature, 2012, 483, 448 CrossRef CAS PubMed.
- P. Guillamat, J. Ignés-Mullol and F. Sagués, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 5498–5502 CrossRef CAS.
- Image provided by Linnea Metcalf, Achini Opathalage and Zvonimir Dogc and used with their permission.
- ESI† to this paper is provided at DOI: 10.1039/c8sm02202j.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- K. R. Prathyusha, S. Henkes and R. Sknepnek, Phys. Rev. E, 2018, 97, 022606 CrossRef CAS PubMed.
- J. D. Weeks, D. Chandler and H. C. Andersen, J. Chem. Phys., 1971, 54, 5237–5247 CrossRef CAS.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- F. Peruani, A. Deutsch and M. Bär, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 030904 CrossRef PubMed.
- S. R. McCandlish, A. Baskaran and M. F. Hagan, Soft Matter, 2012, 8, 2527–2534 RSC.
- S. Weitz, A. Deutsch and F. Peruani, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012322 CrossRef PubMed.
- F. Ginelli, F. Peruani, M. Bär and H. Chaté, Phys. Rev. Lett., 2010, 104, 184502 CrossRef PubMed.
- F. Peruani, J. Starruß, V. Jakovljevic, L. Søgaard-Andersen, A. Deutsch and M. Bär, Phys. Rev. Lett., 2012, 108, 098102 CrossRef PubMed.
- A. Baskaran and M. C. Marchetti, Phys. Rev. Lett., 2008, 101, 268101 CrossRef PubMed.
- X.-q. Shi, H. Chaté and Y.-q. Ma, New J. Phys., 2014, 16, 035003 CrossRef.
- E. Putzig, G. S. Redner, A. Baskaran and A. Baskaran, Soft Matter, 2015, 12, 1–5 Search PubMed.
- S. Mishra and S. Ramaswamy, Phys. Rev. Lett., 2006, 97, 090602 CrossRef PubMed.
- S. Ngo, A. Peshkov, I. S. Aranson, E. Bertin, F. Ginelli and H. Chaté, Phys. Rev. Lett., 2014, 113, 038302 CrossRef PubMed.
- E. Putzig and A. Baskaran, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 90, 042304 CrossRef PubMed.
- S. Ramaswamy, R. A. Simha and J. Toner, Europhys. Lett., 2003, 62, 196–202 CrossRef CAS.
- H. Chaté, F. Ginelli and R. Montagne, Phys. Rev. Lett., 2006, 96, 180602 CrossRef PubMed.
- H. P. Zhang, A. Be'er, E.-L. Florin and H. L. Swinney, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13626–13630 CrossRef CAS PubMed.
- J. V. Selinger and R. F. Bruinsma, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 2910–2921 CrossRef.
- M. Dijkstra and D. Frenkel, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 51, 5891–5898 CrossRef.
- A. A. Joshi, J. K. Whitmer, O. Guzmán, N. L. Abbott and J. J. de Pablo, Soft Matter, 2014, 10, 882–893 RSC.
- Note that this 2D system with soft-core interactions should exhibit quasi-long-range order in the nematic phase,65–67 and thus S decays with system size. Since we are interested in the degree of order on the scale of typical bend and splay fluctuations, we report S values measured within regions of size 10 × 10σ2 (see ref. 41).
- N. Kumar, R. Zhang, J. J. de Pablo and M. L. Gardel, Sci. Adv., 2018, 4, eaat7779 CrossRef PubMed.
- J. P. Straley, Phys. Rev. A: At., Mol., Opt. Phys., 1971, 4, 675–681 CrossRef.
- D. Frenkel and R. Eppenga, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1776–1787 CrossRef CAS.
- J. M. Kosterlitz and D. J. Thouless, J. Phys. C: Solid State Phys., 1973, 6, 1181 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8sm02202j |
| This journal is © The Royal Society of Chemistry 2019 |