Polymer nanocomposite capsules formed by droplet extraction: spontaneous stratification and tailored dissolution

Abstract

We report the formation of polymeric and nanocomposite capsules via droplet solvent extraction, focusing on the interplay between solvent exchange and removal, demixing and directional solidification kinetics. We investigate a model system of sodium poly(styrene sulfonate), NaPSS and silica nanoparticles in aqueous solution, whose phase behaviour is experimentally measured, and examine a series of selective extraction solvents (toluene, butyl acetate, ethyl acetate and methyl ethyl ketone), ranging from 0.04 to 11% v/v water solubility. Tuning the rate of solvent exchange is shown to provide an effective means of decoupling demixing and solidification timescales, and thereby tunes the internal microstructure of the capsule, including hollow, microporous, core–shell, and bicontinuous morphologies. In turn, these determine the capsule dissolution mechanism and kinetics, ranging from single to pulsed release profiles of nanoparticle clusters (at intermediate solubilities), to minimal dissolution (at either extremes). These findings provide facile design and assembly strategies for functional capsules with time-varying release profiles.

---

1 Introduction

Polymeric capsules are extensively used to contain and subsequently deliver active ingredients following an external trigger. A range of industries rely on this technology for the long-term, stable encapsulation and modulated release of medical drugs, biologically active species, and fragrances,^1–3 as well as within emerging self-healing materials.⁴ The performance of capsules depends fundamentally on their external and internal morphology and dimensions, and barrier and release properties, which are further governed by solution thermodynamics and non-equilibrium transfer processes.^5–7

Common approaches for encapsulation include spray drying,⁸ emulsion polymerisation,⁹ photopolymerization,⁷ solvent displacement,¹⁰ and layer-by-layer assembly,¹¹ as well as the more recent flash nanoprecipitation.¹² The advent of droplet microfluidics, and single and multiple emulsification has provided exceptional capability for templating solute droplets, with relatively high throughput, enabling capsules to be formed by initiating polymerization, phase change, solvent evaporation/extraction or directed solidification.^13–15 In solvent evaporation, solute-containing liquid droplets are concentrated by osmotic removal of the solvent in liquid or gas phase. In addition, their internal microstructure can be spontaneously generated by demixing, coarsening and eventual kinetic arrest upon solidification. This methodology has been employed in the fabrication of porous capsules with various architectures, including isolated micropores as well as interconnected domains,^16,17 using multi-step processes. Single-step approaches able to spontaneously control capsule microstructure and triggered delivery of active agents are evidently attractive and have remained elusive.

We have previously demonstrated the formation of spherical and non-spherical polymeric particles with prescribed internal micropore structure and size distribution, via microfluidic extraction.^18,19 The roles of polymer molecular mass M_w and water solubility (the good solvent), and starting composition (with respect to overlap and concentrated crossovers) and solution viscosity were investigated.²⁰ In addition, we reported an approach for anisotropic polymer–nanocomposite capsule design, mapping accessible shapes and morphologies. Internally bicontinuous capsules were found to exhibit pulsed cargo release, in a series of bursts.²¹ Here, we seek to elucidate the role of the extraction solvent in modulating microcapsule architecture and, in turn, the release mechanism and kinetics of nanoparticle cargo. We therefore investigate a series of extraction solvents and carry out a comparative study of their effect in both capsule formation and dissolution. Our hypothesis is that the timescale for nanocomposite capsule formation can be decoupled into competitive solidification and demixing timescales, such that the microstructure of capsules could be tailored precisely by design of the extraction process.

2 Experimental section

System

Sodium poly(styrene sulfonate) (NaPSS) with average molecular weight M_w ≃ 70 kg mol⁻¹, and 22 nm diameter silica SiO₂ suspension (Ludox AS-40, 40% w/v in H₂O, pH 9–9.5) were obtained from Sigma-Aldrich; in water, these form surface silanol groups which partly deprotonate under alkaline conditions, yielding a negative particle charge and thus electrostatic stabilization of the suspension. Toluene (ACS, Reag. Ph. Eur., ≥99.9%, T), butyl acetate (puriss. p.a., Reag. Ph. Eur., ≥99%, BA), methyl ethyl ketone (puriss. p.a., ACS reagent, ≥99.5%, MEK) were obtained from Sigma-Aldrich, ethyl acetate (HiperSolv Chromanorm, ≥99.8%, EA) from VWR International, and deionized (DI) water was from a Centra ELGA filtration system. All reagents were used as received.

Phase mapping

Phase diagrams were obtained by turbidity measurements after two weeks of sample preparation. Silica solutions from 1 to 40% w/v were prepared; polymer was added, in 0.1 g increments, to nanoparticle solutions, agitated to ensure mixing and allowed to equilibrate at 21 ± 2 °C for two weeks. In total, over 100 samples of different compositions were employed to locate the phase boundaries of the NaPSS/SiO₂/H₂O system with ±5% precision.

Microfluidics and extraction

A microfluidic device with flow-focussing junction was fabricated by frontal photopolymerisation (FPP) of thiolene NOA 81, using a previously reported procedure.^22,23 The microchannels were 100 μm deep and 650 μm wide, with a focussing constriction of 300 μm. Channel surfaces were rendered hydrophobic by exposure to a 10% w/v solution of octadecyltrichlorosilane (OTS ≥ 90%, Sigma-Aldrich) in toluene for 1 h, followed by 24 h in a convection oven at 110 °C. Inlets were connected with silicone tubing to 10 mL syringes mounted on syringe pumps (Braintree BS-8000) and the outlet tube was immersed in the non-solvent bath. The dispersed phase was the polymer/nanoparticle aqueous mixture, while the continuous (carrier) phase was hexadecane. For microfluidic emulsification, 2–5% v/v of Span80 was employed to minimize coalescence and found to have minimal impact in capsule formation (for comparison, surfactant-free droplets were also produced using a 5 mL syringe fitted with a 30 G × 1/2′′ needle). Initial droplet radius was varied by changing the flow rate of the continuous phase, F_c, within 50 to 90 μL min⁻¹ while the dispersed phase flow rate, F_d, was kept constant at 10 μL min⁻¹, corresponding to Reynolds number (Re = ρUL/η, where ρ is the density, U is the flow velocity, L is the characteristic length and η is the viscosity) between 0.17 and 0.3.

Droplet extraction and capsule characterisation

Droplets were precipitated into external non-solvent baths (MEK, EA, BA, T) with large excess volume (20 mL), within a glass Petri dish. The surface of the glass dish was rendered hydrophobic by treating with a 10 wt% OTS solution in toluene for 1 h, followed by 24 h in a forced air convection oven at 110 °C. Droplet shrinkage and evolution of internal morphology during solvent extraction were monitored using an upright reflection microscope (Olympus BX41M) and CCD camera (Allied technologies, Mantra F-145, 1392 × 1040 pixels, 20 fps) and analyzed with ImageJ. The resulting capsules were dried for 24 h, sectioned or crushed between glass plates, and coated with chromium before SEM imaging and EDX analysis. Their internal structure was characterized with a LEO 1525 Field Emission Scanning Electron Microscope (SEM) at accelerating voltage 5 kV. Energy dispersive X-ray spectroscopy (EDX) spectra were acquired for 60 s with a silicon–lithium, Si(Li), detector.

3 Results and discussion

3.1 Bulk polymer–colloid phase behavior

We select a water soluble polyelectrolyte, sodium poly(styrene sulfonate), NaPSS, with average molecular mass M_w ≃ 70 kg mol⁻¹, and colloidal silica (radius R_NP ≃ 11 nm) as respectively, the model polymer matrix and nanoparticle (NP) cargo. The radius of gyration of the polymer is evaluated as R_g = (3M_w/C_p*4πN_A)^1/3 ≃ 10.6 ± 2.0 nm, where C_p* = 0.0238 g mL⁻¹ is the polymer overlap concentration, estimated as the reciprocal of intrinsic viscosity [η] at dilute polymer concentration C_p.²⁴ The conformation of the polymer was investigated by small angle neutron scattering (SANS) and viscosity measurements (ESI,† Fig. S1) showing characteristic neutral polymer behavior, as expected for polyelectrolyte solutions in the presence of salt (estimated salt to monomer ratio of 1 : 3 to 1 : 4). The system can thus be expected to behave as non-adsorbing neutral polymer chains in the presence of charged nanoparticles in aqueous solution. The thermodynamics of (non-adsorbing) polymer–colloid solutions has been extensively studied^25–28 in terms of the range and strength of interactions, ratio between polymer and nanoparticle dimensions q_R ≡ R_g/R_NP, and solute concentration. For this system, q_R ≃ 0.97 ± 0.18. In systems with long-range interactions (q_R ≥ 0.3), two phase (gas–liquid and fluid–crystal) as well as three phase (gas–liquid–crystal) regions are expected, and spinodal decomposition can occur following a quenching from the stable region.²⁹

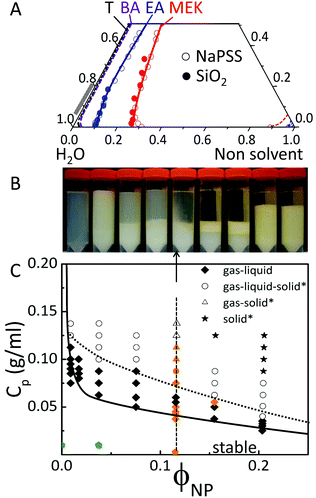
With these ideas in mind, we first establish the solution thermodynamics for ternary systems, comprising solvent (water), non-solvent (MEK, EA, BA and T) and neat NaPSS or SiO₂ by turbidimetry, as shown in Fig. 1A. The obtained binodal lines approximately follow the solubility limit of the neat solvent pairs (provided in ESI,† Table S1), providing a simple means to estimate the stability lines. The solubility of water in the various non-solvents ranges from ≃11 to 0.04% v/v, respectively from MEK to T. Demixing of the aqueous solutions by non-solvent addition is therefore expected to occur at progressively smaller concentrations of MEK, EA, BA and T as shown in Fig. 1A. Initial droplet compositions of interest are shown by the grey band (0.8–1) along the H₂O:solute line on the phase diagram. The non-solvent quality appears thus to be an effective means of precisely selecting the location of the demixing trigger along the solvent extraction pathway of a droplet. However, given that solvent extraction will be correspondingly slower for poorer selective solvents, the interplay between demixing and extraction kinetics is a priori not obvious. Recent phase field simulations by Tree, Fredrickson and co-workers³⁰ are able to qualitatively capture many features of the morphological evolution of non-solvent induced phase separation (NIPS) in a planar geometry, although not yet kinetic arrest upon coarsening, or two solute systems, such as those considered next, as relevant for encapsulation.

Fig. 1 (A) Ternary phase diagram for NaPSS/H₂O/NS (open circles) and SiO₂/H₂O/NS (filled circles) with non-solvents methyl ethyl ketone (MEK) and ethyl acetate (EA); dashed lines show estimated phase boundaries for butyl acetate (BA) and toluene (T). The hatched band on the left, between 0.8–1.0 H₂O:solute, represents NaPSS and SiO₂ compositions shown in (C). (B) Photograph of phase separated mixtures of NaPSS/SiO₂/H₂O with ϕ_NP = 0.12, and varying C_p 0.025, 0.0375, 0.0425, 0.045, 0.05, 0.075, 0.088, 0.100, 0.1125 g mL⁻¹ [L–R]. (C) Phase diagram of NaPSS/SiO₂ mixtures in water plotted as a function of nanoparticle volume fraction ϕ_NP and polymer concentration C_p in the sample. The symbols represent the final state of the system observed at each composition: gas–liquid coexistence, gas–liquid–solid coexistence, gas–solid coexistence, and solid phases. The samples composition of panel (B) are indicated by the coloured markers along the dashed line. Initial droplet compositions from neat NaPSS and NaPSS:SiO₂ are indicated by the green markers.

The phase behaviour of ternary mixtures of NaPSS/SiO₂/H₂O as a function of composition, at 20 °C, in terms of the polymer concentration C_p and nanoparticle volume fraction ϕ_NP is shown in Fig. 1B and C. Cross-sectional images of mixtures with constant ϕ_NP = 0.12 and increasing C_p (left to right) are provided in Fig. 1B, corresponding to the vertical line in Fig. 1C. Upon increasing C_p, initially homogeneous and stable mixtures become biphasic, exhibiting a bottom, liquid-phase, of higher ϕ_NP and a top, cloudy, gas phase. Coexisting three phases are observed upon further increasing C_p, corresponding to a bottom (solid), middle (liquid), and a top gas phase. At sufficiently high ϕ_NP and C_p, solid phases span the entire sample volume. The gas–liquid and solid–liquid interfaces were identified following the method by Faers and Luckham,³¹ by tilting demixed sample vials at a 30° angle and observing the interface tilt with respect to the vial, as well as its flow response; phase assignment was further confirmed by densitometry. Phase separation and coarsening in our system reached equilibrium after approximately two weeks, and the extent of the demixed regions did not change noticeably after 8 months. Crystal regions were not observed in our experiments probably due to the polydispersity of the silica dispersion and polymer chain lengths. It has been shown that even modest polydispersities suppress crystallization and fluid–solid transition, and introduce multiple solid phases,^32,33 while gas–liquid demixing is less sensitive to polydispersity. We summarise our findings in a phase diagram, mapping out stable and immiscible compositions as shown in Fig. 1C.

3.2 Droplet formation and extraction

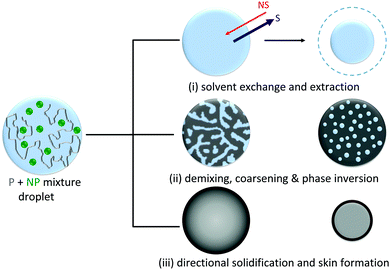
To produce droplets with precise dimensions and relatively high frequency, we employ a flow focusing microfluidic device, fabricated by frontal photopolymerization.^22,23 Droplets containing polymer/nanoparticle aqueous solutions are first generated within an immiscible carrier phase, hexadecane, and then subjected to selective solvent extraction in a variety of external bath solvents to yield particles and capsules. The choice of extraction solvent is therefore not trivial. These must be immiscible with the solute (polymer or nanoparticle) but partially miscible with the solvent within the droplet, in order to control kinetics while preserving the droplet template. Further, for emulsification, the extraction solvent must also be miscible with the carrier phase (which in turn must be immiscible with the droplet solvent). We have therefore selected the series MEK, EA, BA, and T as extraction solvents for this study, since these are all non-solvents for the polymer and colloidal silica, but good solvents for the carrier phase and partially miscible with the droplet phase (water); hexadecane is employed as carrier phase.

The capsule formation process is expected to involve three simultaneous processes: solvent exchange and extraction, phase separation (via nucleation and growth or spinodal decomposition) and coarsening, and eventual phase inversion and solidification resulting in the formation of solid capsules, illustrated in the schematic presented in Fig. 2. Extraction is initiated by immersion of droplets in the non-solvent bath enabling solvent exchange at the interface, and a net osmotic removal of H₂O, increasing both the polymer and/or nanoparticle concentration within the droplet. Non-solvent ingress within the droplet causes the solution to cross its phase boundaries, depicted in Fig. 1A, driving phase separation, beginning at the interface where the solvent composition gradient is highest, and continuing temporally as further extraction and internal recirculation flows occur. Eventually, kinetic arrest is expected when the solute concentration in one phase is sufficiently high to cause phase inversion and precipitation (as extensively employed in membrane fabrication^30,34,35).

Fig. 2 Schematic of the capsule formation mechanism, illustrating the three governing, simultaneous processes: (i) solvent exchange and extraction, resulting in drop shrinkage, (ii) droplet demixing, initiated by ingress of non-solvent, proceeding via spinodal decomposition or nucleation and growth, and (iii) eventual phase inversion and directional solidification, generally resulting in the formation of a smooth skin and internal microstructure.

The pathway and kinetics of capsule formation are therefore expected to depend on an interplay between mutual affinity and diffusion between solvent and selective solvent, droplet concentration and dimensions, the rich phase behaviour of polymer–nanoparticle solutions, and eventual kinetic arrest. With these ideas in mind, we design drop shrinkage experiments to yield a range of effective Péclet numbers, estimated as Pe = [(dR/dt)R₀]/D, where dR/dt is the initial shrinkage rate, R₀ is the initial droplet radius, and D is the Stokes–Einstein diffusivity of the solute (detailed in ESI†). This dimensionless mass transport number characterises the relative rates of diffusion and convection, and ranges from Pe ≃ 0.9 to 60, for T to MEK, depending on solute content. Spray dried^36–38 and solvent-extracted,³⁹ single- and multi-component droplets can be expected to yield dimpled, hollow, or crumpled capsules under rapid extraction (Pe ≫ 1), while dense compact capsules have been reported for comparatively slow extraction (Pe ≪ 1).

3.3 Extraction data analysis and descriptive model

To isolate the impact of the polymer and nanoparticle solutes within droplets, and solvent/non-solvent miscibility, droplets of 1% w/v NaPSS and 1% w/v NaPSS + 10% w/v SiO₂ were extracted in all four solvents. Representative time series of the extraction of NaPSS/SiO₂/H₂O droplets of similar initial radius R₀, following immersion in MEK, EA, BA and T, measured by optical microscopy, are shown in Fig. 3.

Fig. 3 Time series of solvent extraction from polymer/nanoparticle droplets with composition 1% w/v NaPSS + 10% w/v SiO₂ immersed in non-solvents (A) methyl ethyl ketone. MEK, (B) ethyl acetate, EA, (C) butyl acetate, BA, and (D) toluene, T. Spinodal decomposition is observed in droplets immersed in EA (E) and BA (F). Coarsening proceeds to a larger extent in droplets immersed in BA and a core–shell capsule is formed (G). The initial radius for all droplets was ≃250 μm.

At all conditions, droplet radii decrease monotonically with time and eventual solidification results in capsule formation which, under these conditions, remain largely spherical. Internal convection is observed within droplets, in particular for the faster extractions (ESI,† Supplementary movie S1). The external morphology of capsules obtained using MEK appears somewhat crumpled, which is expected for fast extractions (higher Pe) and shell formation at earlier times,²¹ followed by subsequent buckling upon continuous solvent removal. Buckling is driven by the unconstrained decrease in compressive stresses generated on the shell wall during droplet volume reduction.⁴⁰

Notably, the timescales for extraction and solidification vary by more that two orders of magnitude from MEK to T, following the variation in H₂O miscibility, depicted in Fig. 1A. The droplets exchanged with the solvents with intermediate miscibilities, EA and BA, exhibit clear demixed structures during extraction (ESI,† Supplementary movies S2 and S3). Fig. 3E shows a clear spinodal structure, which appears transiently and coarsens around t ∼ 140 s for an EA extraction. According to the phase diagram (Fig. 1C), the two internal phases are assigned to nanoparticle-rich and -poor, as expected for a quench into the unstable gas–liquid region, resulting in bicontinuous domains (Fig. 3E and F) as previously reported.²⁹ In polymer–colloid demixing, the polymer component has been found to preferentially partition to the colloid-poor phase.²⁷ We therefore assign the bicontinuous matrix phase and capsule skin as originating from the polymer-rich (colloid-poor) gas-phase, and the internal bicontinuous phase to the nanoparticle-rich liquid phase, validated by EDX measurements discussed below.

While the process is qualitatively similar in BA, spinodal demixing now occurs around t ∼ 1000 s (shown in Fig. 3F); further, given the lower H₂O:BA miscibility, extraction takes considerably longer and thus coarsening of the structure can happen over longer timescales. Eventually, a well-defined skin layer (shell thickness of ∼10 μm) emerges upon approaching the solidification stage, depicted in Fig. 3G, which we interpret as resulting from the comparatively prolonged phase coarsening and stratification of the polymer-rich phase to the interface.

For the fastest extraction (MEK), a bicontinuous phase is not observed, which we interpret as due to the high Pe number resulting in rapid skin formation and precipitation, likely circumventing the spinodal pathway and leading to a hollow morphology examined below. At the other extreme of slow extraction, associated with the low solubility of H₂O in T miscibility, and Pe ≃ 0.8, we obtain compact, dense particles with no visible demixed structure (ESI,† Supplementary movie S4), interpreted as due to the slow shrinkage aided by recirculation flows that enable gradual equilibration until kinetic arrest.

These observations are quantified by the evolution of droplet radius R(t) during the extraction process as shown in Fig. 4. The lines are empirical fits to 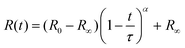, where R₀ is the initial droplet radius, R_∞ is the (final) capsule radius, τ is the extraction time (when R ceases to change), and α is a parameter accounting for non-Fickian diffusion, introduced previously.^18,19 In agreement with the expected impact of solvent solubility on dissolution profile,^41–43 extraction timescales ranging from tens to thousands of seconds can be readily tuned by the extraction medium. Further, the extraction timescale τ is found to depend linearly on R₀ (ESI,† Fig. S3) with a prefactor which depends, as expected,^18–20 on solute content.

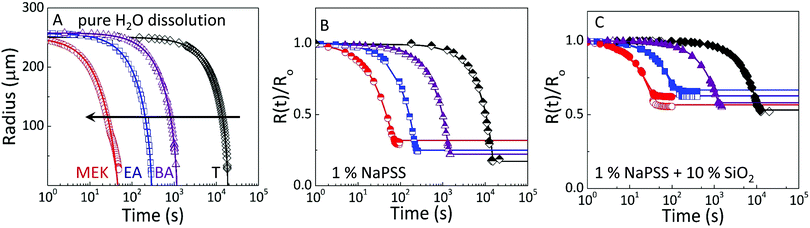Fig. 4 Droplet extraction kinetics in selected solvents, methyl ethyl ketone (MEK), ethyl acetate (EA), butyl acetate (BA), and toluene (T). Evolution of droplet radius with time for (A) pure H₂O, (B) 1% (w/v) NaPSS, and (C) 1% w/v NaPSS + 10% w/v SiO₂. Initial droplet radius R₀ for data shown ranges between 250–270 μm. In (B and C), the radius is normalised by R₀ to facilitate comparison. The raw data are provided in ESI,† Fig. S2. The open and closed symbols in (C) capture minor deviations from sphericity, by plotting both dimensions of the spheroid. Lines shown are empirical fits to the data, described in the text.

3.4 Correlation with H₂O solubility in extraction solvent

Comparative experiments were then carried out with pure H₂O droplets, to quantify the relation between solvent/non-solvent miscibility and extraction timescale, as shown in Fig. 4A, providing an estimate of the mutual diffusion of solvents across the interface in the absence of solute. With the poorest extraction solvent (T), complete dissolution of a 250 μm pure H₂O droplet is achieved in ∼10 000 seconds, decreasing to a few tens of seconds for MEK.

Similar trends are observed with neat 1% w/v NaPSS (Fig. 4B) and 1% w/v NaPSS + 10% w/v SiO₂ (Fig. 4C) droplets. Obviously, in these cases, instead of full dissolution and R(t) → 0, a final particle or capsule size R_∞ is obtained. This size follows a dependence with the opposite sign to that of τ, and smaller (thus more compact) particles are attained with poorer extraction solvents, as demonstrated above.

A summary of these observations is presented in Fig. 5 in terms of final capsule size R_∞ and extraction time τ. We find that droplet extraction kinetics τ are remarkably governed by solvent/non-solvent miscibility (summarised in ESI,† Table S1), regardless of solute (neat solvents, polymer or polymer/nanoparticle solutions) which has a comparably smaller effect. From droplets of comparable initial radius (selected in Fig. 5A for R₀ ≃ 250–270 μm), the resulting capsule size R_∞ also depends monotonically, approximately linearly, on H₂O solubility, with minor variations likely due to surface and crowding droplet effects during extraction. Further, R_∞ also scales monotonically with polymer and/or nanoparticle content.^18,19 For reference, raw data are provided in ESI,† Fig. S2. Therefore, it emerges that R₀, solute content and, to some extent solvent/non-solvent miscibility, largely control R_∞, while the extraction time scale τ is largely governed by solvent/non-solvent miscibility, with solute content playing a comparatively minor role, and τ ∝ R₀, the initial droplet size. The inverse relation between R_∞ and τ can be qualitatively rationalized in the context that larger capsules form upon faster extractions, due to an early onset of skin formation. However, a theoretical framework to describe the phenomena requires the coupling of extraction (and mutual diffusion), demixing and directional solidification and is currently not available beyond the descriptive model introduced above and parameterized by these experiments. These parameters provide a facile strategy to design capsule size and formation timescale by osmotic solvent extraction, while the demixing processes described are expected to impact the internal microstructure.

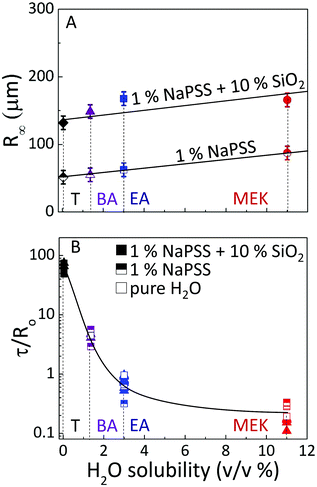Fig. 5 Dependence of (A) capsule radius, R_∞, and (B) extraction time, τ, normalised by R₀, on the solvent/nonsolvent solubility limit for neat polymer and polymer/nanoparticle droplets. Data shown in (A) include only droplets with initial droplet radius R₀ ≃ 250–270 μm. Lines shown are guides to the eye. Selective solvents methyl ethyl ketone (MEK), ethyl acetate (EA), butyl acetate (BA), and toluene (T) were investigated. Additional data showing the linear dependence of τ on R₀ for NaPSS and NaPSS:SiO₂ droplets immersed in EA are provided in ESI,† S3.

3.5 Capsule microstructure: correlation between extraction solvent and cargo release

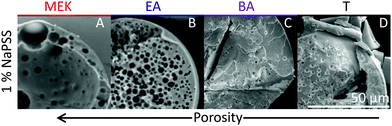
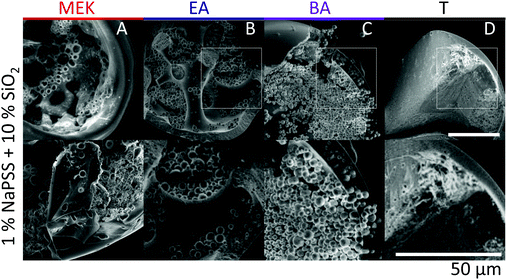
Scanning electron microscopy (SEM) is employed to characterise the cross-sectional structure of capsules. Neat polymer capsules formed within the various extraction solvents are found to exhibit progressively higher porosities as the extraction solvent quality increases, as shown in Fig. 6. Under otherwise identical conditions, pores diameters as small as ≈2 μm and as large ≈60 μm are observed in capsules fabricated with T and MEK, respectively. This somewhat counterintuitive result correlates well with the higher Pe and the interplay between rapid skin formation and ensuing internal phase coarsening.

Fig. 6 SEM images of the internal microstructure of neat polymer capsules obtained from droplets with initial concentration 1% w/v immersed in (A) methyl ethyl ketone, MEK, (B) ethyl acetate, EA, (C) butyl acetate, BA, and (D) toluene, T. Initial droplet radius R₀ ≃ 250 μm for all capsules.

The counterpart internal structures of polymer–nanocomposite capsules are shown in Fig. 7 as a function of extraction solvent. In this case, the morphology is not only determined by the polymer-rich and -poor phase, but also by the demixing between polymer and nanoparticle phase in solution. Upon decreasing extraction solvent quality a succession of capsule microstructures is found, namely hollow, bicontinuous, core–shell, and compact, in good agreement with optical microscopy observations. SEM and EDX (show in ESI,† Fig. S4) measurements reveal that the internal spherical clusters, of ≈1–5 μm in diameter, are precipitated silica aggregates, bound by trace amounts of polymer. Varying extraction time is found to effectively tune structural coarsening time and thus internal architecture, demonstrated by the formation of a bicontinuous (Fig. 7B) or core–shell capsule (Fig. 7C) achieved using EA and BA respectively as non-solvents. At the extremes of solubility, hollow (larger) capsules and dense (compact) capsules are obtained for the fastest and slowest extraction rates, in MEK and T, respectively (Fig. 7A and D).

Fig. 7 SEM images of the internal microstructure of composite polymer–nanoparticle capsules obtained from droplets with initial concentration 1% w/v NaPSS + 10% w/v SiO₂ immersed in (A) methyl ethyl ketone, MEK, (B) ethyl acetate, EA, (C) butyl acetate, BA, and (D) toluene, T. Initial droplet radius R₀ ≃ 250–270 μm for all capsules. High magnification images of highlighted sections of the capsules are provided on the bottom row.

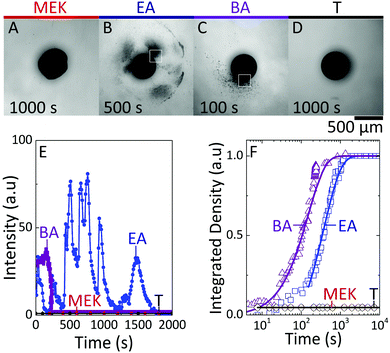
Finally, we examine the consequence of capsule morphology on nanoparticle release. The dissolution of nanocomposite capsules in DI H₂O is shown in Fig. 8. Minimal release of nanoparticle clusters is observed from capsules extracted in MEK and T, as shown in Fig. 8A and D, within the timescales probed up to 10⁴ s, and this intensity could not be resolved optically. Internally bicontinuous capsules formed by EA extraction (Fig. 8B), are found to release the encapsulated nanoparticle clusters in a series of bursts from specific sites around the capsule surface, over long timescales (ESI,† Supplementary movie S5), as shown in Fig. 8E. During release, the capsule's scaffold retains its integrity, thereby enabling the multiple bursts from internal compartments over time.²¹ Core–shell capsules, formed by BA extraction, possessing a large single compartment filled with nanoparticle clusters, releases from only one active site and in a single burst, at a comparatively shorter time (ESI,† Supplementary movie S6). We estimate nanoparticle cluster release from active sites of EA and BA capsules (indicated in Fig. 8B and C) and the overall release by computing the integrated release density over time, as shown in Fig. 8E and F. We interpret the minimal release observed in the most compact and least compact capsules as due to the formation of dense polymer–nanoparticle composites: in the case of fast extraction, at the capsule shell, while for slow extraction within the bulk volume. Short-range attractions between nanoparticle clusters are expected to hinder dissolution, in the absence of strong agitation. However, at intermediate solubilities, likely due to the gradually stratified structure and larger inter-particle distance, capsules exhibit tunable release profiles. These observations corroborate the proposed correlation between internal architecture and release of ‘cargo’, following from the simple design strategies outlined for capsule formation.

Fig. 8 Optical images of dissolution of polymer/nanocomposite capsules following immersion in DI water at pH 5–6; droplets extracted in (A) methyl ethyl ketone, MEK, (B) ethyl acetate, EA, (C) butyl acetate, BA, and (D) toluene, T, from an initial composition 1% w/v NaPSS + 10% w/v SiO₂. (E) Release profile of nanoparticle clusters from marked active sites over time, and (F) overall release intensities of the respective capsules.

4 Conclusions

Selective solvent extraction is shown to provide an effective route to the controlled assembly of polymer and polymer-composite particles and capsules. Specifically, we have examined the role of the extraction solvent in the process, comprising (i) droplet shrinkage by solvent exchange and removal, (ii) demixing and coarsening, and (iii) eventual directed solidification and kinetic arrest. We select NaPSS (R_g ≃ 10 nm) as the polymer phase, since it is water-soluble and extensively studied in terms of conformation, solution properties and rheology, and ubiquitous silica (R ≃ 11 nm) as the nanoparticle suspension. As expected, we find that decreasing extraction solvent quality (measured by water solubility in the extraction phase) monotonically leads to longer extraction times. This yields a facile lever to tune extraction kinetics, beyond the initial polymer radius (τ ∝ R₀). In turn, longer extraction times result in more compact, thus smaller, solid particles, which we interpret as being enabled by the additional time for coarsening and densification. The extraction timescale τ is largely controlled by the solvent miscibility, with the addition of polymer and/or nanoparticle having a comparatively minor effect. This feature provides an opportunity to decouple demixing and coarsening to kinetic arrest, which we exploit to controllably design particle and capsule microstructure. For neat polymer particles, the process is comparatively simple: faster extraction leads to early skin formation (at higher Pe number) and thus greater internal porosity. For polymer-composite particles, the effects are more subtle, as the microstructure is, in addition, governed by the thermodynamics of polymer and nanoparticle. At intermediate extraction times (or solubility), demixing takes place by spinodal decomposition and particles extracted with EA yield internally bicontinuous capsules with a polymer-rich skin. Further decreasing solvent quality (BA) allows for further coarsening to take place, resulting in the spontaneous formation of core–shell particles comprising a polymer-rich skin and a particle rich core. These design strategies open a range of possibilities in predictive microcapsule design by solvent extraction.

To examine the functional consequences of this design, capsules were subsequently immersed in good solvent (water). At the two extreme solubilities (MEK, T) no appreciable dissolution takes place over long times (≥24 h) under quiescent conditions (i.e. in the absence of agitation), interpreted as due to the formation of a compact skin or compact (bulk) particle in MEK and T, respectively. At the intermediate solubilities, with BA we find a single burst release at early times, compatible with the formation of a single large, particle reservoir, due to coarsening of the internal morphology; the bicontinuous structure formed by EA extraction (at faster timescales), releases over a series of pulses, and from multiple locations, reflecting its internal compartmentalized morphology. Polymer–nanoparticle thermodynamic and tuneable solvent extraction kinetics are therefore also shown to provide a means to modulate the dissolution of capsules. Further control can likely be exercised by employing solvent mixtures, across a large R₀ range (typically 1–1000 μm) available via microfluidics.

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

C. U. thanks the Department of Chemical Engineering, Imperial College London for a PhD studentship. We thank the Seventh Framework Programme of the European Commission, Grant Agreement No. 618333, and the Engineering and Physical Sciences Research Council (EPSRC), EP/L020564/1, for financial support. Discussions with Carlos G. Lopez, Axel Huerre, William Sharratt, and Paul Luckham are gratefully acknowledged. We thank the Institut Laue-Langevin, Grenoble, France for beam time, and Lionel Porcar for assistance during SANS experiments (data reported in ESI†).

References

1. F. Lim and A. M. Sun, Science, 1980, 210, 908–910.
2. R. Langer, Nature, 1998, 392, 5–10.
3. I. Hofmeister, K. Landfester and A. Taden, Macromolecules, 2014, 47, 5768–5773.
4. J. D. Rule, E. N. Brown, N. R. Sottos, S. R. White and J. S. Moore, Adv. Mater., 2005, 17, 205–208.
5. J. A. Champion, Y. K. Katare and S. Mitragotri, J. Controlled Release, 2007, 121, 3–9.
6. O. D. Velev, A. M. Lenhoff and E. W. Kaler, Science, 2000, 287, 2240–2243.
7. H. C. Shum, A. R. Abate, D. Lee, A. R. Studart, B. Wang, C.-H. Chen, J. Thiele, R. K. Shah, A. Krummel and D. A. Weitz, Macromol. Rapid Commun., 2010, 31, 108–118.
8. A. Gharsallaoui, G. Roudaut, O. Chambin, A. Voilley and R. Saurel, Food Res. Int., 2007, 40, 1107–1121.
9. J. Ugelstad, K. H. Kaggerud, F. K. Hansen and A. Berge, Die Makromolekulare Chemie, 1979, 180, 737–744.
10. S. Freitas, H. P. Merkle and B. Gander, J. Controlled Release, 2005, 102, 313–332.
11. V. Salgueirino-Maceira, M. Correa-Duarte and M. A. Farle, Small, 2005, 1, 1073–1076.
12. C. Zhang, V. J. Pansare, R. K. Prud'homme and R. D. Priestley, Soft Matter, 2012, 8, 86–93.
13. E. Kumacheva and P. Garstecki, Microfluidic Reactors for Polymer Particles, John Wiley & Sons, Inc., 1st edn, 2011.
14. J. Wan, A. Bick, M. Sullivan and H. A. Stone, Adv. Mater., 2008, 20, 3314–3318.
15. Q. Xu, M. Hashimoto, T. T. Dang, T. Hoare, D. S. Kohane, G. M. Whitesides, R. Langer and D. G. Anderson, Small, 2009, 5, 1575–1581.
16. S. Liu, M. Cai, R. Deng, J. Wang, R. Liang and J. Zhu, Korea-Aust. Rheol. J., 2014, 26, 63–71.
17. M. F. Haase, K. J. Stebe and D. Lee, Adv. Mater., 2015, 27, 7065–7071.
18. T. Watanabe, C. G. Lopez, J. F. Douglas, T. Ono and J. T. Cabral, Langmuir, 2014, 30, 2470–2479.
19. C. E. Udoh, V. Garbin and J. T. Cabral, Langmuir, 2016, 32, 8131–8140.
20. W. N. Sharratt, A. Brooker, E. S. J. Robles and J. T. Cabral, Soft Matter, 2018, 14, 4453–4463.
21. C. E. Udoh, J. T. Cabral and V. Garbin, Sci. Adv., 2017, 3, eaao3353.
22. J. T. Cabral, S. D. Hudson, C. Harrison and J. F. Douglas, Langmuir, 2004, 20, 10020–10029.
23. C. Harrison, J. T. Cabral, C. M. Stafford, A. Karim and E. J. Amis, J. Micromech. Microeng., 2004, 14, 153–158.
24. M. Rubenstein and R. H. Colby, Polymer Physics, Oxford University Press Inc., New York, 2003.
25. P. R. Sperry, J. Colloid Interface Sci., 1984, 99, 97–108.
26. A. P. Gast, W. Russel and C. K. Hall, J. Colloid Interface Sci., 1986, 109, 161–171.
27. H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, Europhys. Lett., 1992, 20, 559–564.
28. V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811–815.
29. A. E. Bailey, W. C. K. Poon, R. J. Christianson, A. B. Schofield, U. Gasser, V. Prasad, S. Manley, P. N. Segre, L. Cipelletti, W. V. Meyer, M. P. Doherty, S. Sankaran, A. L. Jankovsky, W. L. Shiley, J. P. Bowen, J. C. Eggers, C. Kurta, T. Lorik, P. N. Pusey and D. A. Weitz, Phys. Rev. Lett., 2007, 99, 205701.
30. D. R. Tree, K. T. Delaney, H. D. Ceniceros, T. Iwama and G. H. Fredrickson, Soft Matter, 2017, 13, 3013–3030.
31. M. A. Faers and P. F. Luckham, Langmuir, 1997, 13, 2922–2931.
32. M. Fasolo and P. Sollich, J. Chem. Phys., 2005, 122, 074904.
33. M. Fasolo and P. Sollich, J. Phys.: Condens. Matter, 2005, 17, 797–812.
34. H. Strathmann and K. Kock, Desalination, 1977, 21, 241–255.
35. C. Smolders, A. Reuvers, R. Boom and I. Wienk, J. Membr. Sci., 1992, 73, 259–275.
36. V. R. Gundabala, W. B. Zimmerman and A. F. Routh, Langmuir, 2004, 220, 8721–8727.
37. J. Bahadur, D. Sen, S. Mazumder, B. Paul, H. Bhatt and S. G. Singh, Langmuir, 2012, 1914–1923.
38. C. Sadek, P. Schuck, Y. Fallourd, N. Pradeau, C. Le Floch-Fouéré and R. Jeantet, Dairy Sci. Technol., 2014, 95, 771–794.
39. N. Tsapis, D. Bennett, B. Jackson, D. A. Weitz and D. A. Edwards, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12001–12005.
40. S. S. Datta, H. C. Shum and D. A. Weitz, Langmuir, 2010, 26, 18612–18616.
41. J. T. Su and D. Needham, Langmuir, 2013, 29, 13339–13345.
42. P. B. Duncan and D. Needham, Langmuir, 2006, 22, 4190–4197.
43. D. L. Bitterfield, A. Utoft and D. Needham, Langmuir, 2016, 12749–12759.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm00708c

---