 Open Access Article
Open Access ArticleThe intimate relationship between the dielectric response and the decay of intermolecular correlations and surface forces in electrolytes†
Roland
Kjellander

Department of Chemistry and Molecular Biology, University of Gothenburg, SE-412 96 Gothenburg, Sweden. E-mail: roland.kjellander@gu.se; Tel: +46 31 7869027
First published on 10th June 2019
Abstract
A general, exact theory for the decay of interactions between any particles immersed in electrolytes, including surface forces between macroscopic bodies, is derived in a self-contained, physically transparent manner. It is valid for electrolytes at any density, including ionic gases, molten salts, ionic liquids, and electrolyte solutions with molecular solvent at any concentration. The ions, the solvent and any other particles in the system can have any sizes, any shapes and arbitrary internal charge distributions. The spatial propagation of the interactions in electrolytes has several decay modes with different decay lengths that are given by the solutions, κν, ν = 1, 2,…, to a general equation for the screening parameter κ; an equation that describes the dielectric response. There can exist simultaneous decay modes with plain exponential decay and modes with damped oscillatory exponential decay, as observed experimentally and theoretically. In the limit of zero ionic density, the decay length 1/κν of the mode with the longest range approaches the Debye length 1/κD. The coupling between fluctuations in number density and charge density, described by the density–charge correlation function HNQ(r), makes all decay modes of pair correlations and interaction free energies identical to those of the screened electrostatic potential, and hence they have the same values for the screening parameters. The density–density and charge–charge correlation functions, HNN(r) and HQQ(r), also have these decay modes. For the exceptional case of charge-inversion invariant systems, HNQ(r) is identically zero for symmetry reasons and HNN(r) and HQQ(r) have, instead, decay modes with different decay lengths.
1 Introduction
Electrolytes are prevalent in various systems of great importance in physics, chemistry, biosciences, surface and colloid sciences and many applied fields, including industrial applications. Such systems have been studied theoretically and experimentally for a very long time, but recently some unexpected experimental observations have been made, in particular the existence of long-range interactions in systems with high ion densities like ionic liquids and concentrated electrolyte solutions. These observations have renewed the interest in the basics of interactions in electrolytes.Oscillatory pair distribution functions and, consequently, oscillatory free energy of intermolecular interaction (potential of mean force) are well-established features of dense electrolytes like molten salts. The recent discovery1,2 of monotonic, exponentially decaying long-range forces with decay lengths of 4–11 nm in ionic liquids was therefore quite surprising, not least because traditional theories of electrolytes give screening lengths that are orders of magnitude shorter under the conditions in question. Such forces with long decay lengths have been observed for various systems with high ionic densities, like ionic liquids and concentrated electrolyte solutions.3–10 Simultaneously, there are often oscillatory contributions with shorter decay lengths simultaneously present in the force curves for such systems.
These observations are conceptually important because exponentially decaying forces between surfaces in electrolyte solutions have often been taken as an experimental verification of the correctness of the Poisson–Boltzmann (PB) approximation for surface interactions, which predicts such forces for large distances. The PB expressions that are commonly used contain adjustable parameters like surface charge density, surface potential etc. that can be fitted to the experimental data. However, any reasonable theory gives exponentially decaying forces in electrolytes at least for low ionic densities and exact analysis of statistical mechanics of fluids says that the forces must be exponential under such conditions – apart from contributions due to dispersion interactions that have power law decay and therefore ultimately must dominate the forces for sufficiently large distances. Therefore the mere existence of an exponential decay says nothing about the validity of the PB approximation. In this connection we should note that an exponential decay of the interactions in planar geometry, i.e., proportional to e−κℓ, where ℓ is the distance and κ is the screening parameter, translates for spherical geometry into a Yukawa function decay, e−κr/r, where r is the radial distance. Furthermore, it is a statistical mechanical fact that the exponential decay of surface forces for large separations has the same parameter κ as the pair correlations in the bulk fluid in equilibrium with the fluid in the slit between the surfaces. The same applies for exponentially damped oscillatory forces.
Another test of whether the PB approximation is applicable or not is the magnitude of the decay length, which in this approximation is given by the Debye length 1/κD where the Debye screening parameter κD is defined for electrolyte solutions from
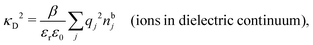 | (1) |
The PB approximation is quite accurate for low ionic densities. The actual decay length for the electrolyte approaches 1/κD when the ion density goes to zero and the importance of the ion–ion correlations decreases. A pertinent question is how low the ion density must be for the correlations to be unimportant. In fact, long-range electrostatic ion–ion correlations can give substantial deviation from the Debye length also for low ion densities provided the electrostatic coupling is sufficiently strong, for instance for multivalent ions in dilute aqueous solution as we will see later.
Furthermore, in contrast to the PB prediction of monotonic exponential decay with a single decay length, there appear in general more than one decay length and/or exponentially damped oscillatory decay. This can be illustrated by a simple approximation11,12 that is valid for simple ionic fluids with rather low electrostatic coupling, for example ionic fluids at very high temperatures or electrolyte solutions in the primitive model at high εr for the dielectric continuum solvent; typical examples are monovalent ions in aqueous solution at room temperature and such ions in vacuum at T = 23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 K (these systems have the same value of εrT). For a symmetric electrolyte with ionic diameter d this approximation gives the following expression for the screening parameter κ
400 K (these systems have the same value of εrT). For a symmetric electrolyte with ionic diameter d this approximation gives the following expression for the screening parameter κ
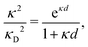 | (2) |
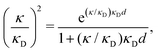 | (3) |
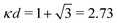 at this point), which for monovalent ions corresponds to a molar concentration of (4.10/d)2 when d is measured in Å. For κDd > 1.35, the solutions are complex-valued; the two solutions are then complex conjugates to each other: κ = κℜ + iκℑ and κ′ = κℜ − iκℑ, where i is the imaginary unit. The appearance of the complex solutions, marked by a filled symbol in the figure, means that there is a cross-over from a plain exponential decay to an oscillatory exponential one, that is, proportional to e−κℜℓ
at this point), which for monovalent ions corresponds to a molar concentration of (4.10/d)2 when d is measured in Å. For κDd > 1.35, the solutions are complex-valued; the two solutions are then complex conjugates to each other: κ = κℜ + iκℑ and κ′ = κℜ − iκℑ, where i is the imaginary unit. The appearance of the complex solutions, marked by a filled symbol in the figure, means that there is a cross-over from a plain exponential decay to an oscillatory exponential one, that is, proportional to e−κℜℓ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(κℑℓ + γ) in planar geometry and e−κℜr
cos(κℑℓ + γ) in planar geometry and e−κℜr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(κℑr + γ)/r in spherical geometry, where γ is a phase shift. This behavior is well-known and is called a Kirkwood cross-over,13 named after John G. Kirkwood who already in the 1930s showed14,15 the existence of such a change to oscillatory behavior for electrolytes. Since then, several expressions for κ with the same behavior have been obtained, for example in the Mean Spherical Approximation (MSA), the Linearized Modified PB (LMPB) approximation by Outhwaite16,17 and the generalized MSA.13 This behavior has also been verified many times in the past in numerical calculations, including simulations.
cos(κℑr + γ)/r in spherical geometry, where γ is a phase shift. This behavior is well-known and is called a Kirkwood cross-over,13 named after John G. Kirkwood who already in the 1930s showed14,15 the existence of such a change to oscillatory behavior for electrolytes. Since then, several expressions for κ with the same behavior have been obtained, for example in the Mean Spherical Approximation (MSA), the Linearized Modified PB (LMPB) approximation by Outhwaite16,17 and the generalized MSA.13 This behavior has also been verified many times in the past in numerical calculations, including simulations.
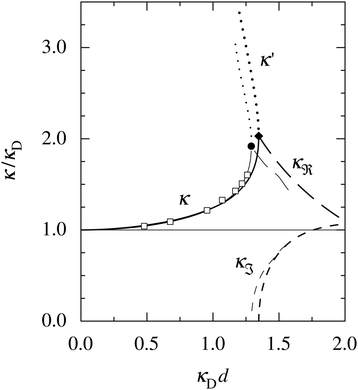 | ||
Fig. 1 A plot of the screening parameters divided by the Debye parameter κD for a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 aqueous electrolyte solution at room temperature as functions of κDd, which is proportional to the square root of the electrolyte concentration. The decay length is smaller than the Debye length when κ/κD > 1. The full curves show the screening parameter κ that gives the leading decay length 1/κ for low concentrations. The other curves show the screening parameters for other decay modes of the system (see text). The thick curves are the results of the simple approximation in eqn (2), while the thin curves are from HNC calculations18–20 that are very accurate for this system. The open symbols show Monte Carlo data18 for the same system. The filled symbols show the cross-over point between monotonic exponential and exponentially damped oscillatory decays, i.e., real and complex screening parameters, respectively, as calculated in the HNC approximation and from eqn (2). 1 aqueous electrolyte solution at room temperature as functions of κDd, which is proportional to the square root of the electrolyte concentration. The decay length is smaller than the Debye length when κ/κD > 1. The full curves show the screening parameter κ that gives the leading decay length 1/κ for low concentrations. The other curves show the screening parameters for other decay modes of the system (see text). The thick curves are the results of the simple approximation in eqn (2), while the thin curves are from HNC calculations18–20 that are very accurate for this system. The open symbols show Monte Carlo data18 for the same system. The filled symbols show the cross-over point between monotonic exponential and exponentially damped oscillatory decays, i.e., real and complex screening parameters, respectively, as calculated in the HNC approximation and from eqn (2). | ||
The simple expression in eqn (2) is surprisingly accurate, considering its humble origin; in the figure its predictions are compared with the results from Monte Carlo (MC) simulations18 and Hypernetted Chain (HNC) calculations18–20 and it is seen that the agreement is nearly quantitative. For the oscillatory decay, the decay length 1/κℜ increases quite rapidly with electrolyte concentration after the cross-over point. The wavelength 2π/κℑ immediately after the cross-over is very long (κℑ = 0 at the cross-over point), much longer than the decay length, so in practice the oscillations would not be observable. However, the wavelength decreases very rapidly with increased concentration and is quite soon comparable to the decay length. Therefore, for the forces between particles or between surfaces at increasing separations, some oscillations should be seen before their magnitude is too small.
The important points here are that there exist more than one decay mode, one with decay length 1/κ and one with 1/κ′ and, furthermore, that the decay modes predicted by the equation for κ can be oscillatory. The objective of the simple expression (2) is to give a simple illustration of these facts. In the general case, other decay modes are also simultaneously present in electrolytes. These matters constitute the main theme of the current work. We will see how the decay modes can be treated in formally exact theory that is valid for much more complex systems. Such modes have a major role for the interactions in electrolytes for all conditions from low to high ionic densities and all temperatures (provided that the system remains fluid).
The approximation behind eqn (2) is not sufficient for higher electrostatic coupling than that of the example in the figure, i.e., lower temperatures, lower εr and/higher ionic valencies. For divalent ions in aqueous solution at room temperature, results from HNC calculations and MC simulations18–20 show that the decay length at low ion densities is appreciably longer than the Debye length. In a plot as that in Fig. 1, the curve for κ/κD then lies below the value 1 for small κDd; for example, for divalent ions with diameter d = 4.6 Å, κ/κD reaches a minimal value ≈0.84 before it increases to values above 1, whereafter the qualitative behavior is similar to that for the monovalent case. In fact, the results from the HNC approximation show that κ/κD lies below the value 1 for very small κDd also for the monovalent ions,12,20 but this is not visible for monovalent electrolytes on the scale in Fig. 1.
It is quite significant that deviations in decay length from the Debye length occur not only for dense electrolytes. This is a fundamental property of electrolytes because in the limit of low ionic density, the ratio κ/κD for a z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) z electrolyte (z is the valency) satisfies the exact limiting law20,21
z electrolyte (z is the valency) satisfies the exact limiting law20,21
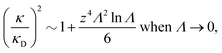 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Λ is negative for small Λ, so formula (4) shows that the decay length is larger than the Debye length for low electrolyte concentrations in agreement with the numerical theoretical results mentioned above.
Λ is negative for small Λ, so formula (4) shows that the decay length is larger than the Debye length for low electrolyte concentrations in agreement with the numerical theoretical results mentioned above.
This law was recently verified experimentally by Smith et al.23 for dilute 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 3
2 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 electrolytes in aqueous solution. Large negative deviations of κ/κD from the value 1 were observed for electrolyte concentrations in the interval 0.1–10 mM and the agreement with eqn (4) was nearly quantitative for a large part of this interval. For aqueous 1
3 electrolytes in aqueous solution. Large negative deviations of κ/κD from the value 1 were observed for electrolyte concentrations in the interval 0.1–10 mM and the agreement with eqn (4) was nearly quantitative for a large part of this interval. For aqueous 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 electrolytes, however, the deviation from the value 1 was very small.
1 electrolytes, however, the deviation from the value 1 was very small.
The effect described by eqn (4) is not included in the approximation given in eqn (2) or in any other linear theory like MSA and LMPB, so κ/κD > 1 for small κDd in these approximations. However, if one includes nonlinear terms,12 one obtains agreement with eqn (4) in the limit of small Λ. Since the HNC approximation is nonlinear, it is in agreement with eqn (4). The difference between κ/κD from eqn (2) and from the HNC approximation for small κDd is very small for the monovalent electrolyte in Fig. 1. Due to the factor of z4 in eqn (4) the deviation from the Debye length increases rapidly with ionic valency for systems at low ion densities. For systems with much lower εr and/or lower temperatures, the deviation will be substantial also for monovalent ions.
Other very relevant illustrations of the subject that is studied formally in the current work can be taken from the computer simulation work by Keblinski et al.,24 where they investigate NaCl for a large variety of conditions from thin gases to molten salt for various temperatures. They used an empirical, realistic model for the pair interaction potential for NaCl that has been shown to reproduce quite well the thermodynamic, structural and other properties of molten NaCl.
Keblinski and coworkers calculated the charge–charge and density–density correlation functions, HQQ(r) and HNN(r) respectively,¶ and determined the decay lengths, wavelengths and other characteristics of the dominant contributions to these functions for various conditions. They found that the leading term of the asymptotic decay for large r of the correlation functions can dominate also for shorter distances – in some cases down to a distance of one or two particle diameters. Their Fig. 1 in ref. 12 shows that in molten NaCl at 1000 K, the leading asymptotic term in HQQ(r), which decays like e−κℜr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(κℑr + γ)/r, is practically indistinguishable from HQQ(r) down to r ≈ 2d, where d is the average ion diameter. Furthermore, it gives a very good description of HQQ(r) down to r ≈ d. This means that an asymptotic analysis of the correlation function gives important information not only for very large r, but also for a quite wide range of shorter distances. It can in many cases be sufficient to include a couple of leading decay modes in the asymptotic analysis. Such a dominance of the leading asymptotic terms has also been found in earlier studies of other electrolyte systems.18,20,25
cos(κℑr + γ)/r, is practically indistinguishable from HQQ(r) down to r ≈ 2d, where d is the average ion diameter. Furthermore, it gives a very good description of HQQ(r) down to r ≈ d. This means that an asymptotic analysis of the correlation function gives important information not only for very large r, but also for a quite wide range of shorter distances. It can in many cases be sufficient to include a couple of leading decay modes in the asymptotic analysis. Such a dominance of the leading asymptotic terms has also been found in earlier studies of other electrolyte systems.18,20,25
The simulations by Keblinski and coworkers also included a study of the Kirkwood cross-over and they showed explicitly the presence of two exponentially decaying modes in in HQQ(r) with decay lengths 1/κ and 1/κ′ (in our notation) for densities lower than the cross-over point and the leading oscillatory mode after the cross-over (see Fig. 5 in ref. 24). Furthermore, they showed the existence of two simultaneous decay modes of different types in the pair distribution function gij(r), an oscillatory mode decaying as e−κℜr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(κℑr + γ)/r and a monotonic one decaying as e−κ″r/r. The decay lengths 1/κℜ and 1/κ″ vary with ion density so that for some densities 1/κℜ is smaller than 1/κ″ and for other densities the reverse is true (see Fig. 7 in ref. 24, where 1/κℑ is denoted by λQ and 1/κ″ is denoted by λG). The density where the decay lengths are equal is a so-called Fisher–Widom cross-over point,13 where changes in the decay lengths of gij(r) make an oscillatory term to become leading for large distances instead of a monotonic term or vice versa. For NaCl at T = 3000 K, which is close to the critical temperature, this cross-over occurs at the density nbtot = nb+ + nb− ≈ 0.1d−3. The monotonic term has the largest decay length for nbtot < 0.1d−3, which is due to the proximity of criticality where the density–density correlations have a long range, and the oscillatory term has the largest decay length above this density.
cos(κℑr + γ)/r and a monotonic one decaying as e−κ″r/r. The decay lengths 1/κℜ and 1/κ″ vary with ion density so that for some densities 1/κℜ is smaller than 1/κ″ and for other densities the reverse is true (see Fig. 7 in ref. 24, where 1/κℑ is denoted by λQ and 1/κ″ is denoted by λG). The density where the decay lengths are equal is a so-called Fisher–Widom cross-over point,13 where changes in the decay lengths of gij(r) make an oscillatory term to become leading for large distances instead of a monotonic term or vice versa. For NaCl at T = 3000 K, which is close to the critical temperature, this cross-over occurs at the density nbtot = nb+ + nb− ≈ 0.1d−3. The monotonic term has the largest decay length for nbtot < 0.1d−3, which is due to the proximity of criticality where the density–density correlations have a long range, and the oscillatory term has the largest decay length above this density.
In their analysis of the simulation data, Keblinski and coworkers extracted the decay length for the oscillatory decay mode from HQQ(r) and that for the monotonic mode from HNN(r). Therefore they denoted the former as the “screening length” λQ and the latter as the “density–density correlation length” λG. A very important point to be made here is that there are terms in both correlation functions with these decay lengths, i.e., there is an oscillatory term in both HQQ(r) and HNN(r) with decay length λQ and likewise a monotonic term in both functions with decay length λG. The magnitude of the prefactor for the term with decay length λQ in HNN(r) is, however, small for the NaCl system and likewise the term with decay length λN is small in HQQ(r), so these contributions are rather insignificant numerically. As we will see, this is due to the fact that g++(r) ≈ g−−(r) in this system. For other systems the magnitudes of these kinds of terms in HQQ(r) and HNN(r) do not differ that much in general. In some cases they can have similar magnitudes.
In general, the leading terms of HQQ(r) and HNN(r) for large r have the same decay length. This has been shown for binary electrolytes with spherical ions of different sizes or different valencies in ref. 13, 25 and 26. We will show in the current work that this applies to all decay modes in electrolytes of almost any kind, so the decay lengths are therefore both screening lengths and density–density correlation lengths – in this work they are simply called “screening lengths” and the κ parameters are called “screening parameters.”
As we will see, there exist a few exceptions, for example model systems where the anions and cations are identical apart from the sign of their charges. The restricted primitive model (RPM) is such a model because all ions are charged hard spheres of equal diameter and have the same absolute valency. Then g++(r) = g−−(r) and, as a consequence of this symmetry, the density–charge correlation function HNQ(r) is identically equal to zero and HQQ(r) and HNN(r) have different decay lengths. It is quite astounding that the most common model for electrolytes is an exception as regards its screening behavior! However, as we saw from the case of NaCl where g++(r) ≈ g−−(r), terms in HQQ(r) and HNN(r) with the same decay length have very different magnitudes and one dominates over the other, which means that results from models with g++(r) = g−−(r) may be quite reasonable as an approximation. These matters will be investigated for the general case in the current work and we will see that the class of systems that constitute this kind of exception consists of systems that are invariant when one reverses the sign of all charges in the system (including those in polar molecules). They will be called “charge-inversion invariant systems.”
The normal, realistic cases are, of course, systems that do not have such an invariance. Anions and cations virtually always differ by much more than the sign of their charges and, in addition, the positive and negative parts of the solvent molecules (if present) normally differ a lot apart from the sign of the charge. Thus HQQ(r) and HNN(r) normally have contributions with exactly the same set of decay lengths as the electrostatic potential and so do gij and the free energy of interaction. It may appear puzzling that HQQ(r) and HNN(r) have the same decay length also in cases where long-range density fluctuations arise upon approach to a critical point. Since both functions have equal range, HQQ(r) is also an equally long-range function but we will see that the ratio HQQ(r)/HNN(r) for large r decreases quickly with increasing decay length, so the influence of HQQ(r) vanishes when the decay length diverges. We must, however, emphasize that the present analysis does not cover critical phenomena, so critical points are not included.
As mentioned earlier, simultaneous decay modes with long-range monotonic and shorter-range oscillatory exponential decays have been observed in ionic liquids and concentrated electrolyte solutions. The presence of oscillatory, exponentially damped contributions to the correlation functions reflect in many cases the granularity of the system at the molecular level. The wavelength can have about the same magnitude as the average molecular size or, for ionic systems, a combination of the anion and cation diameters. This is, however, not always the case, for example when the particle sizes are very different or when the electrostatic correlations dominate.
It is important to note that oscillatory surface forces that extend several oscillations, like those observed in electrolyte solutions and ionic liquids, have decay lengths and wavelengths that are the same as those in the bulk fluid in equilibrium with the fluid between the surfaces. It is common to think of such oscillations as being specifically caused by a layered structure close to the surfaces, but the corresponding structuring is present also for the pair distributions in the bulk. A specific structure may be induced by the surfaces that causes a few oscillations in the surface force for very short surface separations, but in order for the oscillations to continue when the separation is increased, they must be supported by a decay mode of the bulk phase. As we have seen, the leading modes of the decay of the correlation functions often dominate not only for very large distances, but also for surprisingly short ones. This applies also for surface forces. Therefore, the bulk properties of electrolytes that are analyzed in the current work have great significance also for surface forces.
Oscillatory contributions are expected for most dense liquid systems, including dilute electrolyte solutions with molecular solvent. The oscillations are then dominated by the structure of the solvent. This has been observed experimentally by Smith et al.9 in surface force experiments for mixtures of an ionic liquid and a polar solvent. Simultaneously, there was a monotonic long-range decay mode. Their findings regarding the oscillatory contributions (but not the long-range monotonic one) have been illustrated theoretically in calculations by Coupette et al.27,28 for a semi-primitive model of electrolyte solutions, where the monovalent ions and the solvent are hard spheres. They studied systems with equally-sized ions,27 where the model is a charge-inversion invariant system, and systems with unequally-sized ions.28 Several decay modes were found and analyzed. For the case of equally-sized ions, the charge–charge and the density–density correlations have different decay lengths and different wavelengths, while for unequally-sized ions all correlation functions have common lengths. The wavelengths and the decay lengths were determined by the bulk phase, as always when the oscillations are maintained for increased surface separation. These observations are in agreement with the findings in the current work and in ref. 29 and 31. The presence of multiple decay modes and the behavior of the decay lengths for this system are also in line with previous studies of the primitive model (without discrete solvent) in ref. 13, 18–20 and 25.
The oscillatory contributions due to solvent molecules must be present also for dilute aqueous solutions of simple salts and, as argued in ref. 29, such oscillatory forces determined by the bulk phase have been observed in both surface force experiments and in theoretical investigations of bulk systems with discrete water molecules; the oscillatory surface forces are therefore not caused by “hydration forces” specifically associated with the surfaces. Thus, for dilute electrolyte solutions in general, there are simultaneous decay modes with long-range monotonic decay (i.e., the traditional decay mode with κ ≈ κD) and a shorter-range oscillatory exponential decay mode with a complex-valued screening parameter – the latter mode due primarily to the structure of the solvent. Most importantly, both of these decay modes are present in the correlation functions, the mean electrostatic potential and the interaction free energy.
The fact that the coupling between fluctuations in number density and fluctuations in charge density leads to equal decay lengths for the screened electrostatic potential, and all correlation functions, including HNN(r), are analyzed thoroughly in the present work. We will prove that all decay modes in electrolytes, both the monotonic and the oscillatory exponential ones, originate in the general case from the same fundamental equation, which describes the relevant dielectric response of the system and involves the static dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), where k is the wave number. This equation, which constitutes the general exact equation for the screening parameter κ, can be written in several equivalent manners. Perhaps the most appealing manner is the following expression30,31 that is similar to eqn (1) for the Debye parameter
(k), where k is the wave number. This equation, which constitutes the general exact equation for the screening parameter κ, can be written in several equivalent manners. Perhaps the most appealing manner is the following expression30,31 that is similar to eqn (1) for the Debye parameter
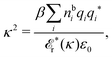 | (5) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) is called the dielectric factor, which is obtained from
r*(κ) is called the dielectric factor, which is obtained from ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) in a manner described later. Since the unknown variable κ appears on both sides in the expression, it is an equation for κ. The different solutions κν, ν = 1, 2,…, to this equation comprise the set of screening parameters for the various decay modes. There exist in general both real and complex-valued solutions to the equation, which give rise to the monotonic and the oscillatory modes, respectively. An equivalent manner to write eqn (5) is, as we will see,
(k) in a manner described later. Since the unknown variable κ appears on both sides in the expression, it is an equation for κ. The different solutions κν, ν = 1, 2,…, to this equation comprise the set of screening parameters for the various decay modes. There exist in general both real and complex-valued solutions to the equation, which give rise to the monotonic and the oscillatory modes, respectively. An equivalent manner to write eqn (5) is, as we will see, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0, which explicitly involves the static dielectric function. The physical meaning of the appearance of the imaginary unit i in k = iκ is that the dielectric response is evaluated for an exponentially decaying field rather than a sinusoidal one (the latter corresponds to real k).
(iκ) = 0, which explicitly involves the static dielectric function. The physical meaning of the appearance of the imaginary unit i in k = iκ is that the dielectric response is evaluated for an exponentially decaying field rather than a sinusoidal one (the latter corresponds to real k).
The exact theory presented in the present paper is very general and is valid for electrolytes from low to high ion densities: from thin gases to dense liquids and from dilute to concentrated electrolyte solutions with molecular solvent. The ions, the solvent and any other particles can have any sizes, arbitrary shapes, any internal charge distributions and can interact with any reasonable nonelectrostatic pair interactions. For simplicity, the particles are, however, assumed to be rigid and unpolarizable. The theory is a generalization of the Dressed Ion Theory (DIT)21,25,32 and the Dressed Molecule Theory (DMT)33–35 and it extends previous related work on the interactions in electrolytes.29–31 The basis of the theory is derived in the present paper in a new self-contained manner, which allows it to be done in a physically intuitive, yet correct way without use of advanced statistical mechanics. This derivation should allow a much broader readership than otherwise would be possible. It also allows a gradual introduction of the principally new results of the present work in an equally transparent manner. Although this theory treats quite complex phenomena and therefore is intrinsically complicated, the introduction of the concept of dressed particles, which is a key element, allows the general exact features of electrolytes to be cast in a form that is much simpler than otherwise is possible.
The contents of the paper are as follows. Section 2 contains a treatment of the linear polarization response of electrolytes due to the effect of weak external electrostatic fields. This is done in a special manner which focuses on the free energy of interaction for each constituent particle in the fluid and is formulated such that it is suitable as a basis for the general treatment of interparticle interactions in electrolytes. The nonlocal nature of electrostatic interactions in electrolytes is thereby demonstrated in a straightforward manner and is contrasted to the treatment of electrolytes in the PB approximation. The relationship to the static dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) is given. In Section 3, the concept of a dressed particle is defined from an elementary analysis of the polarization response of electrolytes. The charge density of a dressed particle of species i is denoted by ρi* and it is an entity that is involved in all major aspects of screened interactions in electrolytes. The screened Coulomb potential ϕCoul*(r), which describes the spatial propagation of electrostatic interactions in electrolytes, is defined for the general case and can be expressed in terms of
(k) is given. In Section 3, the concept of a dressed particle is defined from an elementary analysis of the polarization response of electrolytes. The charge density of a dressed particle of species i is denoted by ρi* and it is an entity that is involved in all major aspects of screened interactions in electrolytes. The screened Coulomb potential ϕCoul*(r), which describes the spatial propagation of electrostatic interactions in electrolytes, is defined for the general case and can be expressed in terms of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) in a simple manner. It is shown that one can use ϕCoul*(r) and ρi* in Coulomb's law to calculate the mean electrostatic potential ψi due to the particle. The general exact eqn (5) for the screening parameters κν of the decay modes of ϕCoul*(r) is derived. The potential ψi has the same set of decay modes as ϕCoul*(r) and the different magnitudes of the modes of ψi are determined by projections of ρi* on each mode. The projections can be interpreted in terms of “effective” charges, as we will see. Section 4 deals with the pair distribution function gij and the free energy of interaction wij between particles in electrolytes, i.e., the pair potential of mean force. The distribution functions gij* of the dresses of the particles are also obtained. It is shown that all decay modes of wij and gij are, in general, the same as those of ϕCoul*(r) and are hence determined by the dielectric response of the electrolyte. This is caused by the coupling between charge density and number density fluctuations and implies that HQQ(r), HNN(r) and HNQ(r) also have the same set of decay modes. The exception is charge-inversion invariant systems where the modes of HNN(r) differ from those of HQQ(r) and of ϕCoul*(r) since charge and density fluctuations in this case are independent of each other for symmetry reasons. Such invariant systems are investigated in some detail. Finally, the decays of HQQ(r), HNN(r) and HNQ(r) for large r are investigated for the general case. Section 5 contains a summary of the conclusions of this work and also some perspectives on the use of the results in experimental and theoretical investigations.
(k) in a simple manner. It is shown that one can use ϕCoul*(r) and ρi* in Coulomb's law to calculate the mean electrostatic potential ψi due to the particle. The general exact eqn (5) for the screening parameters κν of the decay modes of ϕCoul*(r) is derived. The potential ψi has the same set of decay modes as ϕCoul*(r) and the different magnitudes of the modes of ψi are determined by projections of ρi* on each mode. The projections can be interpreted in terms of “effective” charges, as we will see. Section 4 deals with the pair distribution function gij and the free energy of interaction wij between particles in electrolytes, i.e., the pair potential of mean force. The distribution functions gij* of the dresses of the particles are also obtained. It is shown that all decay modes of wij and gij are, in general, the same as those of ϕCoul*(r) and are hence determined by the dielectric response of the electrolyte. This is caused by the coupling between charge density and number density fluctuations and implies that HQQ(r), HNN(r) and HNQ(r) also have the same set of decay modes. The exception is charge-inversion invariant systems where the modes of HNN(r) differ from those of HQQ(r) and of ϕCoul*(r) since charge and density fluctuations in this case are independent of each other for symmetry reasons. Such invariant systems are investigated in some detail. Finally, the decays of HQQ(r), HNN(r) and HNQ(r) for large r are investigated for the general case. Section 5 contains a summary of the conclusions of this work and also some perspectives on the use of the results in experimental and theoretical investigations.
2 Polarization response and nonlocal electrostatics in electrolytes
2.1 Polarization and external electrostatic potential
Consider an inhomogeneous electrolyte that is exposed to an external electrostatic potential Ψext(r) from a source outside the system. The source may be a macroscopic body in contact with the electrolyte or a particle of any size and shape immersed in the electrolyte. The body or particle that is external to the system contains an arbitrary internal charge distribution that gives rise to Ψext. Let us change the external potential somewhat by changing this charge distribution, so the system is instead exposed to the external potential Ψext(r) + δΨext(r) where δΨext(r′) is assumed to be small everywhere in the electrolyte. Initially the charge distribution of the inhomogeneous fluid phase is ρ(r′), which can be obtained from the density distribution of constituent particles of the electrolyte. For the case of spherically symmetric ions with a point charge at the center, we have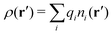 , where ni(r′) is the number density distribution of ion species i (the corresponding formula for nonspherical ions and other particles will be given later). The change δΨext in external potential makes the charge distribution become ρ(r′) + δρ(r′), where
, where ni(r′) is the number density distribution of ion species i (the corresponding formula for nonspherical ions and other particles will be given later). The change δΨext in external potential makes the charge distribution become ρ(r′) + δρ(r′), where 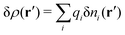 and δni is the variation in number density induced by the change in Ψext. For reasons that soon will be apparent, this variation of ρ will be called a polarization charge density induced by δΨext, so we have δρpol ≡ δρ.
and δni is the variation in number density induced by the change in Ψext. For reasons that soon will be apparent, this variation of ρ will be called a polarization charge density induced by δΨext, so we have δρpol ≡ δρ.
The total electrostatic potential in the system is equal to Ψ(r) given by
| δΨ(r) = δΨext(r) + δΨpol(r). | (6) |
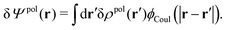 | (7) |
The density distribution ni(r′) can be expressed in terms of the potential of mean force Wi(r′) as the Boltzmann relationship
| ni(r′) = nbie−βWi(r′), | (8) |
| δni(r′) = −βni(r′)δWi(r′), | (9) |
For the special case of a bulk electrolyte, which is the main subject in this work, the density of species i is equal to nbi and we have ρ(r) = 0. Then, the electrostatic potential Ψ is constant and we set it equal to zero by convention. Likewise we initially have Ψext = 0. Let us expose the system to an external electrostatic potential δΨext(r) that is small everywhere in the electrolyte. This potential polarizes the bulk electrolyte and gives rise to a polarization charge density δρpol and hence to nonzero δΨpol and δΨ given by eqn (6) and (7). Henceforth, when we consider the polarization of a bulk electrolyte, all functions with a δ, like δρpol, δΨpol, δΨ and δΨext, denote entities that are weak everywhere in the electrolyte; in principle they are infinitesimally small.
For a bulk fluid eqn (9) becomes
| δni(r′) = −βnbiδWi(r′) | (10) |
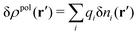 can be determined when we know δWi. Thereby, a central question is: how can δWi be determined from δΨext or, in other words, what is the free energy of interaction δWi(r′) of an i-ion at r′ when it interacts with the weak electrostatic potential δΨext?
can be determined when we know δWi. Thereby, a central question is: how can δWi be determined from δΨext or, in other words, what is the free energy of interaction δWi(r′) of an i-ion at r′ when it interacts with the weak electrostatic potential δΨext?
As we will show below
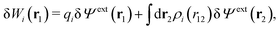 | (11) |
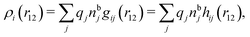 | (12) |
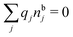 , which follows from charge electroneutrality of the bulk phase. Eqn (11) says that the potential of mean force δWi is given by the interactions of δΨext with the i-ion itself, that is, with the charge qi at the center of the ion [the first term on the right-hand side (rhs)], and with the ion cloud with density ρi [the integral], whereby the latter interaction affects the i-ion via the ion–ion correlations. Eqn (11) is an exact result, so it is precisely in this manner that ion–ion correlations enter into δWi. For reasons that will be apparent in the following sections, we will, however, need to express the effects of such correlations in a more useful manner later.
, which follows from charge electroneutrality of the bulk phase. Eqn (11) says that the potential of mean force δWi is given by the interactions of δΨext with the i-ion itself, that is, with the charge qi at the center of the ion [the first term on the right-hand side (rhs)], and with the ion cloud with density ρi [the integral], whereby the latter interaction affects the i-ion via the ion–ion correlations. Eqn (11) is an exact result, so it is precisely in this manner that ion–ion correlations enter into δWi. For reasons that will be apparent in the following sections, we will, however, need to express the effects of such correlations in a more useful manner later.
To show eqn (11) we will make use of an exact relationship in statistical mechanics for fluids called Yvon's first equation. It says that for a bulk fluid mixture that we expose to a weak external potential δvj(r2) acting on the various species j, we have
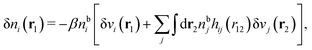 | (13) |
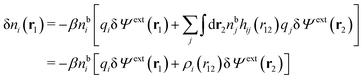 | (14) |
We can write the central charge qi of the ion as a charge density qiδ(3)(r), where δ(3)(r) is the three-dimensional Dirac delta function. By introducing ρtoti(r) = qiδ(3)(r) + ρi(r), which is the total charge density of the ion itself and the surrounding ion cloud, we can write eqn (14) as
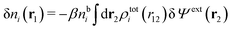 | (15) |
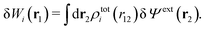 | (16) |
From eqn (15) it follows that the polarization charge density for a bulk electrolyte exposed to the weak electrostatic potential Ψext is given by
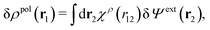 | (17) |
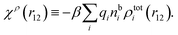 | (18) |
We can express this as χρ(r12) = −βqe2HQQ(r12), where qe is the elementary (protonic) charge and HQQ is the charge–charge correlation function. The latter gives the correlation between fluctuations in charge densities at r1 and r2 irrespectively of which species the charges belong to and is for spherical ions equal to the square bracket divided by qe2. Its Fourier transform is equal to the charge–charge structure factor. These results for χρ and HQQ are well-known, but we have derived them here in a manner that is suitable for further development of the exact theory for electrolytes done later in this work.
Let us now turn to electrolytes consisting of nonspherical ions and other particles, for example solvent molecules. We will for simplicity solely treat the case of rigid, unpolarizable particles, but for each species i, the particle size, shape and internal charge density σi are arbitrary. For a particle with center of mass at r3 and orientation ω3, the internal charge density at point r1 is given by σi(r1|r3,ω3). We use a normalized orientation variable ω so that 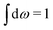 where the integral is taken over all orientations.|| The charge of the particle is
where the integral is taken over all orientations.|| The charge of the particle is 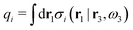 , which is independent of r3 and ω3. Note that σj(r1|r3,ω3) for a given ω3 is a function of only r31 = r1 − r3, where the vector r31 starts at the center of the particle. To simplify the notation we will henceforth write (rν,ων) ≡ Rν whereby we have σi(r1|r3,ω3) ≡ σi(r1|R3), which is the charge density at r1 for a particle with coordinates R3.
, which is independent of r3 and ω3. Note that σj(r1|r3,ω3) for a given ω3 is a function of only r31 = r1 − r3, where the vector r31 starts at the center of the particle. To simplify the notation we will henceforth write (rν,ων) ≡ Rν whereby we have σi(r1|r3,ω3) ≡ σi(r1|R3), which is the charge density at r1 for a particle with coordinates R3.
The pair interaction potential is uij = uelij + uneij, which is the sum of the electrostatic (el) and nonelectrostatic (ne) interaction. The former is given by Coulomb's law as
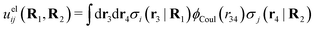 | (19) |
The number density of particles with center of mass at r3 and orientation ω3 is equal to ni(r3,ω3) ≡ ni(R3) and we have ni(R3) = nbie−βWi(R3). The charge density of the system is
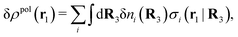 | (20) |
As shown in Appendix A, the equation that corresponds to eqn (15) for a bulk fluid of nonspherical particles exposed to a weak external electrostatic potential δΨext is
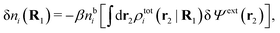 | (21) |
| ρtoti(r2|R1) = σi(r2|R1) + ρi(r2|R1) | (22) |
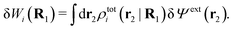 | (23) |
The physical interpretation of this formula is identical to that for spherical particles.
For nonspherical particles the expression for the polarization response function χρ is somewhat more complicated than eqn (18). By inserting eqn (21) into eqn (20) we obtain
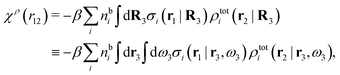 | (24) |
We can write eqn (24) as
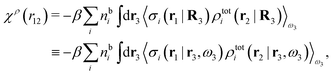 | (25) |
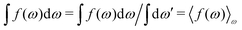 . Note that χρ(r12) depends only on the distance r12 because the average over orientations is taken.
. Note that χρ(r12) depends only on the distance r12 because the average over orientations is taken.
2.2 Polarization and total electrostatic potential
To continue we note that Ψext is the electrostatic potential due to the external source in the absence of the electrolyte, while Ψ is the total potential in the presence of the electrolyte. This means that Ψ is the mean potential that actually exists in the electrolyte. Since this is the system that we are interested in, it is a relevant task to express δρpol in terms of δΨ rather than in terms of δΨext as in eqn (17). Thereby we will obtain a relationship that can be used as an alternative to the latter equation.The fact that the functions δΨext, δρpol, and δΨ are linearly related to each other implies that there exists a function χ*(r) that expresses the linear relationship between δρpol and δΨ as
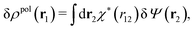 | (26) |
In fact, for a given χρ(r), the function χ*(r) is the solution to the equation
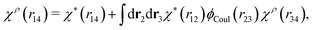 | (27) |
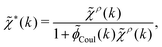 | (28) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k) = 1/(ε0k2). We define the Fourier transform
Coul(k) = 1/(ε0k2). We define the Fourier transform ![[f with combining tilde]](https://www.rsc.org/images/entities/i_char_0066_0303.gif) (k) of a function f(r) as
(k) of a function f(r) as 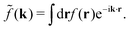 For a function f(r) that only depends on r we have
For a function f(r) that only depends on r we have 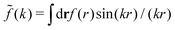 where k = |k|.
where k = |k|.
Eqn (27) is easily derived as follows. By inserting (6) into eqn (26) and then using eqn (7) we obtain
Since the left-hand side (lhs) is equal to 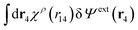 and δΨext(r4) is arbitrary, eqn (27) follows.
and δΨext(r4) is arbitrary, eqn (27) follows.
It is illustrative to see what the PB approximation says about the polarization response. In this approximation we have for spherical ions δWi(r1) = qiδΨ(r1) and hence from eqn (10) we obtain δni(r1) = −βnbiqiδΨ(r1). Therefore
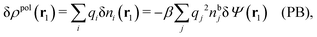 | (29) |
and by comparing with the expression (26) for χ*, we can identify
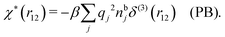 | (30) |
In reality, we have nonlocal electrostatics in the sense that the polarization at one point r1 is influenced by the electrostatic potential at other points in the surroundings. This can be seen in eqn (26). The polarization response function χ*(r12) is nonzero for r12 ≠ 0 so δρpol(r1) is influenced by δΨ(r2) for all points r2 in the neighborhood of r1. This feature is caused by the correlations between the particles in the electrolyte. The nonlocal nature of the response can be understood in the following manner. Any ion located at r2 interacts with the electrostatic potential and since this ion correlates with other ions it will affect the probability for ions to be at r1. The density of ions at r1 accordingly depends on the potential elsewhere. In other words, the potential of mean force δwi(r1) and hence the charge density δρpol(r1) depend on the values of δΨ(r2) for all points r2 in the vicinity of r1. This fact is expressed by the nonlocality in the general exact relationships we have obtained.
The response functions χρ(r) and χ*(r) are closely related to the dielectric response of the electrolyte in terms of the static dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), where k is a wave number. To see this we introduce the electrostatic fields corresponding to Ψ(r) and Ψext, which are E(r) = −∇Ψ(r) and Eext(r) = −∇Ψext(r), respectively. E is sometimes called the Maxwell field and Eext can be expressed in terms of the displacement field D given by D(r) = ε0Eext(r), but we will use Eext in the present work. As we have seen Eext is the field from the external source in the absence of the fluid. The reasoning is performed most easily in Fourier space, so we will consider Ẽ(k) and Ẽext(k).
(k), where k is a wave number. To see this we introduce the electrostatic fields corresponding to Ψ(r) and Ψext, which are E(r) = −∇Ψ(r) and Eext(r) = −∇Ψext(r), respectively. E is sometimes called the Maxwell field and Eext can be expressed in terms of the displacement field D given by D(r) = ε0Eext(r), but we will use Eext in the present work. As we have seen Eext is the field from the external source in the absence of the fluid. The reasoning is performed most easily in Fourier space, so we will consider Ẽ(k) and Ẽext(k).
The static (longitudinal) dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) relates these electrostatic fields when they are weak and therefore linearly related to each other. In general we have for a homogeneous and isotropic fluid
(k) relates these electrostatic fields when they are weak and therefore linearly related to each other. In general we have for a homogeneous and isotropic fluid
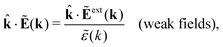 | (31) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k is a unit vector and where the field components along the wave vector k (the longitudinal components) are projected out. In electrostatics Ẽ and Ẽext are parallel to k, which can be seen from the fact that in Fourier space we have Ẽ(k) = −ik
= k/k is a unit vector and where the field components along the wave vector k (the longitudinal components) are projected out. In electrostatics Ẽ and Ẽext are parallel to k, which can be seen from the fact that in Fourier space we have Ẽ(k) = −ik![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (k) (the factor ik corresponds to ∇ in ordinary space) and likewise for Ẽext. Hence we have
(k) (the factor ik corresponds to ∇ in ordinary space) and likewise for Ẽext. Hence we have ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ·Ẽ(k) = −i
·Ẽ(k) = −i![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ·k
·k![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (k) = −ik
(k) = −ik![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) (k) and
(k) and ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ·Ẽext(k) = −ik
·Ẽext(k) = −ik![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ext(k). Therefore only the longitudinal components of the fields matter. In electrodynamics the transversal components, which are perpendicular to
ext(k). Therefore only the longitudinal components of the fields matter. In electrodynamics the transversal components, which are perpendicular to ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) , also matter, but in the present work we limit ourselves to the static equilibrium case. The frequency dependence of the dielectric function, that is commonly considered in the study of the polarization of fluids, is therefore not included in the treatment.
, also matter, but in the present work we limit ourselves to the static equilibrium case. The frequency dependence of the dielectric function, that is commonly considered in the study of the polarization of fluids, is therefore not included in the treatment.
In line with the notation above, when we expose the electrolyte to a weak field we put a δ on the potentials ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) and
and ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ext. Therefore we write δ
ext. Therefore we write δ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) and δ
and δ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ext instead of
ext instead of ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) and
and ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ext, whereby eqn (31) implies
ext, whereby eqn (31) implies
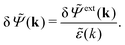 | (32) |
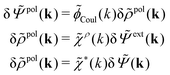 | (33) |
![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) = δ
= δ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ext + δ
ext + δ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) pol we obtain
pol we obtainBy comparing the last two equations with eqn (32) we can identify
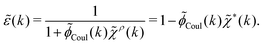 | (34) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) in terms of
(k) in terms of ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) ρ(k) and
ρ(k) and ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(k) are equivalent to standard expressions for
*(k) are equivalent to standard expressions for ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) given in ref. 36–38.
(k) given in ref. 36–38.
The nonlocal nature of electrostatics in the microscopic domain, which is described by the nonlocal response functions χρ(r) and χ*(r), is hence included in the k dependence of the dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k). In the PB approximation, where electrostatics is local, we have from eqn (30)
(k). In the PB approximation, where electrostatics is local, we have from eqn (30)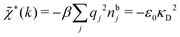 , where κD is the Debye screening parameter for ions in vacuum given by
, where κD is the Debye screening parameter for ions in vacuum given by
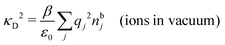 | (35) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(k) is independent of k in the PB case and we obtain
*(k) is independent of k in the PB case and we obtain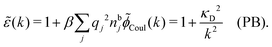 | (36) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) originates from the Coulomb potential
(k) originates from the Coulomb potential ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k).
Coul(k).
For completeness, we note that in electrostatics it is common to use the electric susceptibility χe, which gives the polarization density P in terms of the total field as ![[P with combining tilde]](https://www.rsc.org/images/entities/b_char_0050_0303.gif) = ε0
= ε0![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) eẼ for weak fields.†† In our notation we have P = −ε0Epol, where Epol(r) = −∇Ψpol(r). For weak fields we thus have −ε0δẼpol = ε0
eẼ for weak fields.†† In our notation we have P = −ε0Epol, where Epol(r) = −∇Ψpol(r). For weak fields we thus have −ε0δẼpol = ε0![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) eδẼ or in terms of potentials δ
eδẼ or in terms of potentials δ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) pol = −
pol = −![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) eδ
eδ![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) . By comparing with eqn (33) we see that
. By comparing with eqn (33) we see that
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) as
as ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = 1 +
(k) = 1 + ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) e(k) as usual. In traditional treatments of polar media, P expresses dipolar polarization, while in the general case, including electrolytes, Epol and hence P originate from all kinds of polarization, for example from changes in dipolar, quadrupolar, octupolar orientations and ion distributions.31 For a pure polar fluid (no ions), the dielectric constant (relative dielectric permittivity) is defined microscopically as
e(k) as usual. In traditional treatments of polar media, P expresses dipolar polarization, while in the general case, including electrolytes, Epol and hence P originate from all kinds of polarization, for example from changes in dipolar, quadrupolar, octupolar orientations and ion distributions.31 For a pure polar fluid (no ions), the dielectric constant (relative dielectric permittivity) is defined microscopically as 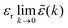 and in this limit solely the dipolar polarization contributes. In the case of electrolytes this limit does not exist since
and in this limit solely the dipolar polarization contributes. In the case of electrolytes this limit does not exist since ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) diverges at k = 0 and, as we will see, other k values matter a lot.
(k) diverges at k = 0 and, as we will see, other k values matter a lot.
To minimize the number of symbols we use, we will refrain ourselves from using ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) e in what follows. Instead we use
e in what follows. Instead we use ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(k) [in ordinary space χ*(r)], which plays a central role in the present work. Obviously,
*(k) [in ordinary space χ*(r)], which plays a central role in the present work. Obviously, ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) * has a prominent role also in ordinary electrostatics.
* has a prominent role also in ordinary electrostatics.
3 Dressed particles and screened electrostatic interactions
3.1 Definition of dressed particles
The potential of mean force δWi due to a weak external electrostatic potential δΨext was expressed in eqn (23) as the interaction energy between δΨext and the total charge density ρtoti associated with an i-particle, where ρtoti is the sum of the internal charge densities σi of the particle and ρi of the surrounding ion/solvent cloud, i.e., the surrounding cloud of particles of any kind present in the system. We will now determine the corresponding relationship between δWi and the total electrostatic potential δΨ. Thereby we are led to the definition of the concept of dressed particles and the corresponding charge density ρi*, which plays a fundamental role in the understanding of interactions in electrolytes.By inserting δΨext(r) = δΨ(r) − δΨpol(r) into eqn (23) we obtain
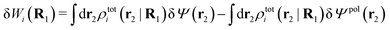 | (37) |
where
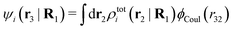 | (38) |
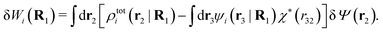 | (39) |
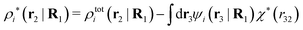 | (40) |
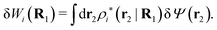 | (41) |
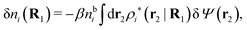 | (42) |
We will now interpret the physical meaning of ρi*. Let us immerse a particle of species i with orientation ω1 into a bulk electrolyte at the point r1. Initially the charge density is zero and after the immersion the density at r2 is ρtoti(r2|R1). We have ρtoti = σi + ρi [eqn (22)] and ρi can be regarded as the total polarization charge density that the particle induces in the surrounding electrolyte due to all kinds of interactions between this particle and the other particles (not only the polarization due to electrostatic interactions). Since these interactions are strong close to the particle, one cannot treat the polarization by linear response. If, however, the total electrostatic potential ψi due to the particle were weak, we would according to eqn (26) have the polarization charge density due to this potential
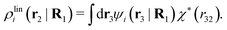 | (43) |
| ρi*(r2|R1) = ρtoti(r2|R1) − ρlini(r2|R1), | (44) |
| ρi*(r2|R1) = σi(r2|R1) + ρdressi(r2|R1), | (45) |
The density ρi* plays a key role in what follows. For instance, as we have seen from eqn (23) and (41), the dressed charge density ρi* has the same role vis-à-vis the total potential δΨ as the total charge density ρtoti has vis-à-vis the external potential δΨext. Eqn (41) says that in the linear domain, the free energy of interaction δWi of the i-ion with the total electrostatic field is equal to the electrostatic interaction energy between δΨ and the dressed particle charge–density ρi* associated with the ion. As we will see ρi* has very important roles in the interparticle interactions in electrolytes.
Note that ρi* for each i can be expressed in terms of ρtotj for all j viaeqn (40) where ψi is given in terms of ρtoti by eqn (38) and where χ* can be expressed in terms of χρviaeqn (28) and finally in terms of ρtotjviaeqn (25). Thus, given ρtotj for all j, one can calculate ρi* at least in principle.
Let us now return to the case when a bulk electrolyte is polarized by a weak electrostatic potential. Then, δni is given by eqn (42) and we can readily derive
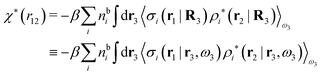 | (46) |
We can write eqn (46) in Fourier space by introducing the notation
| f(r12,ω1) ≡ f(r2|r1,ω1) = f(r2|R1) | (47) |
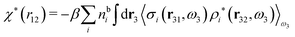 | (48) |
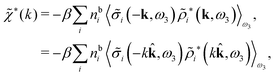 | (49) |
![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) i since the integral over r3 in eqn (48) becomes a convolution when r31 is replaced by −r13 = r31. Since we take the average over ω3, the direction of the unit vector
i since the integral over r3 in eqn (48) becomes a convolution when r31 is replaced by −r13 = r31. Since we take the average over ω3, the direction of the unit vector ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k is arbitrary. Eqn (49) implies that the dielectric function
= k/k is arbitrary. Eqn (49) implies that the dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = 1 −
(k) = 1 − ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(k)
*(k)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k) can be expressed as
Coul(k) can be expressed as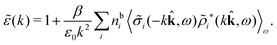 | (50) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = 1 +
(k) = 1 + ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k)
Coul(k)![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) ρ(k) can likewise be expressed in terms of
ρ(k) can likewise be expressed in terms of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) toti and thereby in terms of HQQvia the Fourier transform of eqn (24). The latter is the usual path to
toti and thereby in terms of HQQvia the Fourier transform of eqn (24). The latter is the usual path to ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), while we will see that eqn (50) is much more useful.
(k), while we will see that eqn (50) is much more useful.
Let us yet again connect with the PB approximation. For this purpose we apply the general, exact equations above to the special case of spherical ions with a charge qi at the center, whereby eqn (43) becomes
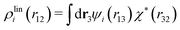 | (51) |
| ρi*(r12) = σi(r12) + ρdressi(r12) = qiδ(3)(r12) + ρdressi(r12), | (52) |
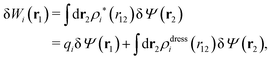 | (53) |
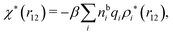 | (54) |
Let us consider a single nonspherical j-particle immersed in an electrolyte consisting of spherical ions of equal sizes. In this case the PB approximation says that
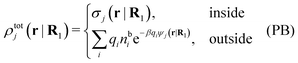 | (55) |
From eqn (43) with χ*(r) given by eqn (30) we have
so from eqn (44) it follows that
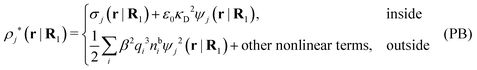 | (56) |
As noted earlier, these results in the PB approximation apply only to a single particle in an electrolyte. The surrounding ions are treated as bare point ions that do not correlate with each other, so they do not have any ion clouds of their own and no dresses. For these ions the potential of mean force is qiψj as assumed in the exponent of eqn (55). When the distribution of ions around an ion is calculated in the PB approximation, i.e., the pair distributions, one accordingly treats the latter ion differently than the rest. This unequal treatment leads to an infamous feature that gij ≠ gji in the (nonlinear) PB approximation.
As we saw in the simple example in Fig. 1 based on the approximation in eqn (2), if we instead treat all ions on an equal basis so all have dresses and, as we will see, therefore have effective charges different from the bare charges, the consequences are quite dramatic with the appearance of multiple screening parameters and oscillatory decay instead of a simple screening parameter κD.
3.2 The screened Coulomb potential in the general case
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) [eqn (50)]. We will now see that the dressed particle charge–density has yet another important role, namely as the source of the screened electrostatic potential from a particle.
(k) [eqn (50)]. We will now see that the dressed particle charge–density has yet another important role, namely as the source of the screened electrostatic potential from a particle.
The mean electrostatic potential ψi(r|R1) from a particle with coordinates R1 can be obtained from the total charge density ρtoti associated with the particle via Coulomb's law as expressed in eqn (38). This potential satisfies Poisson's equation
| −ε0∇2ψi(r|R1) = ρtoti(r|R1) | (57) |
| −ε0∇2ψi(r|R1) − ρlini(r|R1) = ρtoti(r|R1) − ρlini(r|R1) ≡ ρi*(r|R1) |
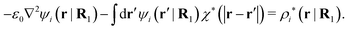 | (58) |
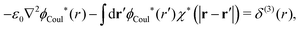 | (59) |
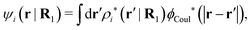 | (60) |
Incidentally we note that in the PB approximation, where χ*(r) given by eqn (30), eqn (59) becomes
| −ε0[∇2ϕCoul*(r) − κD2ϕCoul*(r)] = δ(3)(r) (PB), | (61) |
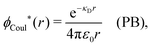 | (62) |
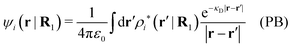 | (63) |
In the general case, by taking the Fourier transform of eqn (59) we obtain
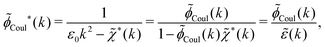 | (64) |
![[capital Psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11c.gif) ext(k) = δq
ext(k) = δq![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k) that the resulting total potential is δΨ(r) = δqϕCoul*(r) ≡ Ψ{δq}(r) at least if r is sufficiently large and δq is sufficiently small, so the linear response is adequate. In this sense we may say that
Coul(k) that the resulting total potential is δΨ(r) = δqϕCoul*(r) ≡ Ψ{δq}(r) at least if r is sufficiently large and δq is sufficiently small, so the linear response is adequate. In this sense we may say thatfor r > 0.
The right hand side (rhs) of eqn (60) has the same form as Coulomb's law in eqn (38), which is no surprise since the usual (unscreened) Coulomb potential ϕCoul(r) is a Green's function of Poisson's equation (57). Note that ψi(r|R1) given by eqn (38) and (60) is exactly the same for all r; what differs in the two equations is the following: when ψi is expressed in terms of ϕCoul(r) the source is ρtoti while when it is expressed in terms of ϕCoul*(r) the source is ρi*.
We can write eqn (38) and (60) in Fourier space by using the notation in eqn (47), whereby we obtain
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) i(k,ω1) = i(k,ω1) = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) toti(k,ω1) toti(k,ω1)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k) = Coul(k) = ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i*(k,ω1) i*(k,ω1)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k). Coul*(k). | (65) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) =
Coul*(k) = ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k)/
Coul(k)/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = 1/|ε0k2
(k) = 1/|ε0k2![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k)] we see from the last equality that
(k)] we see from the last equality that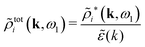 | (66) |
In the PB approximation where ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) is given by eqn (36) we have
(k) is given by eqn (36) we have
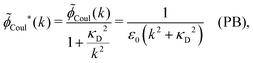 | (67) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) has simple poles at k = ±iκD. This holds in general,‡‡ so a pair of simple zeros k = ±iκ of the denominator of eqn (64) corresponds to a term in ϕCoul*(r) that decays as e−κr/r. At such zeros, i.e., poles of
Coul*(k) has simple poles at k = ±iκD. This holds in general,‡‡ so a pair of simple zeros k = ±iκ of the denominator of eqn (64) corresponds to a term in ϕCoul*(r) that decays as e−κr/r. At such zeros, i.e., poles of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k), we have
Coul*(k), we have[ε0k2 − ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(k)]k=±iκ = 0, *(k)]k=±iκ = 0, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (±iκ) = 0, (±iκ) = 0, | (68) |
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) is the Fourier transform of a real function of r,
Coul*(k) is the Fourier transform of a real function of r, ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) is an even function of k and therefore it is sufficient to consider a pole at iκ, whereby the pole at −iκ follows.
Coul*(k) is an even function of k and therefore it is sufficient to consider a pole at iκ, whereby the pole at −iκ follows.
In order to see what these facts lead to, let us first consider an electrolyte consisting of spherical simple ions in vacuum. From the Fourier transform of eqn (54) we see that ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) has a pole k = iκ when
Coul*(k) has a pole k = iκ when
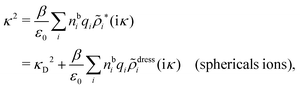 | (69) |
When the density of the ions goes to zero, the charge density ρi(r) of the ion cloud goes to zero for each r and likewise the linear part ρlini(r), so ρdressi ≡ ρi − ρlini goes to zero. Thus κ/κD → 1 in this limit and the PB result is approached. Likewise, in the same limit we have δWi(r1) ≈ qiδΨ(r1) from eqn (53), so the PB approximation is reasonable at least where the electrostatic potential is sufficiently small.
At finite densities the pole at k = iκ gives, as we will see, the leading term in the decay of ϕCoul*
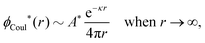 | (70) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) and use the condition
(k) and use the condition ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0 in eqn (68) for the pole of
(iκ) = 0 in eqn (68) for the pole of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k). Since
Coul*(k). Since ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = 1 −
(k) = 1 − ![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(k)
*(k)![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k) we can write
Coul(k) we can write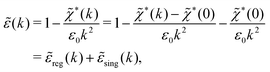 | (71) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) into two parts
(k) into two parts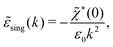 | (72) |
![[small chi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e11b.gif) *(0) ≠ 0), and
*(0) ≠ 0), and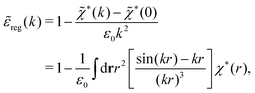 | (73) |
These integrals converge provided χ*(r) decays to zero sufficiently rapidly with increasing r.
For the case of spherical simple ions we have from the Fourier transform of eqn (54)
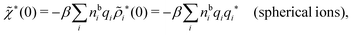 | (74) |
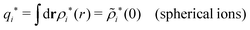 | (75) |
because the total charge of ρtoti(r) is zero due to the local electroneutrality condition. Since ρlini is the linear part of the polarization response due to ψi from the ion, qi* is normally nonzero and has the same sign as qi. It is, however, possible for qi* for a species to change sign and thereby attain the opposite sign to qi, so in rare cases qi* for a species can fortuitously be zero for certain parameter values of the system. One can show§§ that
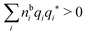 for electrolytes, so it is not possible to have qiqi* < 0 for all ionic species simultaneously. In Appendix A of ref. 31 it is described how ρi*(r) and qi* can be calculated from ρtotj(r) for all j or from the pair distribution functions gij(r).
for electrolytes, so it is not possible to have qiqi* < 0 for all ionic species simultaneously. In Appendix A of ref. 31 it is described how ρi*(r) and qi* can be calculated from ρtotj(r) for all j or from the pair distribution functions gij(r).
For nonspherical particles eqn (49) yields for k = 0
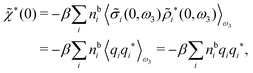 | (76) |
which is independent of the orientation ω3, and the corresponding relationship for σi. Again, qi* is the total charge of the dressed particle charge–density ρi*. Thus we always have
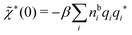 , where qi* is the dressed particle charge.
, where qi* is the dressed particle charge.
By inserting this result into eqn (72) we obtain
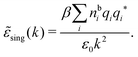 | (77) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) sing(k), the dielectric function
sing(k), the dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) for electrolytes diverges to infinity when k → 0. This divergence is commonly called perfect screening.
(k) for electrolytes diverges to infinity when k → 0. This divergence is commonly called perfect screening.
Using eqn (77) we see that the condition for a pole, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) =
(iκ) = ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) reg(iκ) +
reg(iκ) + ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) sing(iκ) = 0, is
sing(iκ) = 0, is
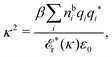 | (78) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) = r*(κ) = ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) reg(iκ) reg(iκ) | (79) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0. Note that eqn (78), which is an exact equation for κ with general applicability, has an appearance very similar to the definition of the Debye parameter κD; only the factor qi* and the presence of
(iκ) = 0. Note that eqn (78), which is an exact equation for κ with general applicability, has an appearance very similar to the definition of the Debye parameter κD; only the factor qi* and the presence of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) in the denominator differ. From eqn (73) it follows that
r*(κ) in the denominator differ. From eqn (73) it follows that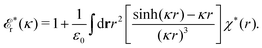 | (80) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) is a function of κ is crucial for the understanding of the properties of electrolytes. When the particle density goes to zero, we have qi* → qi and
r*(κ) is a function of κ is crucial for the understanding of the properties of electrolytes. When the particle density goes to zero, we have qi* → qi and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) → 1 with screening parameter κ near zero, so eqn (78) approaches the expression for κD in eqn (35) which implies that κ/κD → 1 in this limit. For electrolyte models with a dielectric continuum solvent, the initial 1 on the rhs of eqn (80) should be replaced by εr for the solvent.
r*(κ) → 1 with screening parameter κ near zero, so eqn (78) approaches the expression for κD in eqn (35) which implies that κ/κD → 1 in this limit. For electrolyte models with a dielectric continuum solvent, the initial 1 on the rhs of eqn (80) should be replaced by εr for the solvent.
For a binary electrolyte, the deviation in κ from κD can be obtained from
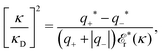 | (81) |
Since the denominator is zero for k = ±iκ we can write
where A* is given by
Here
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) reg′(k) = d
reg′(k) = d![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) reg(k)/dk and we have used l'Hospital's rule to obtain the last equality. If we define
reg(k)/dk and we have used l'Hospital's rule to obtain the last equality. If we define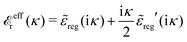 | (82) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ)] and hence we have
effr(κ)] and hence we have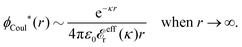 | (83) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ). In addition there is a change in the value of the screening parameter from κD to κ. Note that
effr(κ). In addition there is a change in the value of the screening parameter from κD to κ. Note that ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) differs from
effr(κ) differs from ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) by the last term in eqn (82).
r*(κ) by the last term in eqn (82).
Alternative expressions for ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr are
effr are
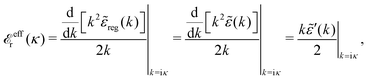 | (84) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0 to obtain the last equality. From eqn (73) and the first equality in eqn (84) we readily obtain
(iκ) = 0 to obtain the last equality. From eqn (73) and the first equality in eqn (84) we readily obtainwhich can be compared with eqn (80). When the density of the particles in the electrolyte goes to zero, we have
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) → 1. Since κ/κD → 1 in this limit, eqn (83) approaches the PB result for ϕCoul*(r) in eqn (62), at least for sufficiently large r. (For electrolyte models with a dielectric continuum solvent, the initial 1 on the rhs should be replaced by εr for the solvent.)
effr(κ) → 1. Since κ/κD → 1 in this limit, eqn (83) approaches the PB result for ϕCoul*(r) in eqn (62), at least for sufficiently large r. (For electrolyte models with a dielectric continuum solvent, the initial 1 on the rhs should be replaced by εr for the solvent.)
These results can be applied to the case of an electrolyte solution with a molecular solvent consisting of polar, uncharged molecules. Since such molecules have qi = 0 they do not contribute to ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) sing(k), so the sum in eqn (77) runs in practice over the ionic species only. Furthermore, since these molecules have no net charge they do not contribute to qi* for any species i. In the expression for κ, eqn (78), the solvent molecules solely contribute to the dielectric factor
sing(k), so the sum in eqn (77) runs in practice over the ionic species only. Furthermore, since these molecules have no net charge they do not contribute to qi* for any species i. In the expression for κ, eqn (78), the solvent molecules solely contribute to the dielectric factor ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) [apart from their indirect influence on the distribution functions and other entities, of course].
r*(κ) [apart from their indirect influence on the distribution functions and other entities, of course].
For a pure polar solvent without ions, ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) sing(k) vanishes so
sing(k) vanishes so ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) =
(k) = ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) reg(k). As mentioned earlier the dielectric constant of a pure polar medium is defined microscopically as
reg(k). As mentioned earlier the dielectric constant of a pure polar medium is defined microscopically as 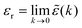 , so we have εr =
, so we have εr = ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (0) =
(0) = ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) reg(0). In a very dilute electrolyte solution κ ≈ 0 and hence
reg(0). In a very dilute electrolyte solution κ ≈ 0 and hence ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) ≈
r*(κ) ≈ ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(0) ≈ εr. Eqn (78) then becomes
r*(0) ≈ εr. Eqn (78) then becomes
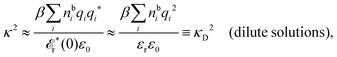 | (85) |
In dilute solutions we have ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) ≈
effr(κ) ≈ ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(0) ≈ εr since the last term in eqn (82) vanishes when κ → 0 because of the prefactor iκ. This implies that we approximately have when r → ∞
effr(0) ≈ εr since the last term in eqn (82) vanishes when κ → 0 because of the prefactor iκ. This implies that we approximately have when r → ∞
For electrolyte solutions in general, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) and
effr(κ) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) contain, as we have seen, contributions from the ions. Since 1/
r*(κ) contain, as we have seen, contributions from the ions. Since 1/![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) determines the magnitude of the screened Coulomb potential for large r,
effr(κ) determines the magnitude of the screened Coulomb potential for large r, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) can be designated as the effective relative dielectric permittivity of the entire electrolyte solution. Likewise, the dielectric factor
effr(κ) can be designated as the effective relative dielectric permittivity of the entire electrolyte solution. Likewise, the dielectric factor ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) acts as a kind of relative dielectric permittivity of the solution since it takes the role that the dielectric constant of the pure solvent has in the expression for κD. Remember that
r*(κ) acts as a kind of relative dielectric permittivity of the solution since it takes the role that the dielectric constant of the pure solvent has in the expression for κD. Remember that ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) and
effr(κ) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) are different from each other in general.
r*(κ) are different from each other in general.
The only difference between the general equation for the screening parameter κ, eqn (78), and the definition (35) of the Debye parameter κD is, apart from the factor ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ), that the former contains the factor qiqi* instead of qi2. While κD is given solely in terms of the system parameters ni, qi, and T, the actual screening parameter κ depends on the state-dependent entities qi* and
r*(κ), that the former contains the factor qiqi* instead of qi2. While κD is given solely in terms of the system parameters ni, qi, and T, the actual screening parameter κ depends on the state-dependent entities qi* and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ). The latter are, as we have seen, defined in terms of dressed charge densities or, equivalently, in terms of ρtoti for all i via its relationship to ρi* as explained earlier.
r*(κ). The latter are, as we have seen, defined in terms of dressed charge densities or, equivalently, in terms of ρtoti for all i via its relationship to ρi* as explained earlier.
In the expression (78) for κ, the dressed ion charge qi* is a constant for each system with given system parameters, but the dielectric factor ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) is a function of κ. The latter fact makes a huge difference compared to the predictions of the PB approximation. While this approximation predicts a unique screening parameter κD from eqn (35), the exact equation, eqn (78), is an equation for κ. Apart from the solution κ, which gives the longest decay length, eqn (78) has in general several other solutions κ′, κ″ etc. (the three solutions can alternatively be denoted κν, for ν = 1, 2 and 3). Each solution gives rise to a term in ϕCoul*(r) like the rhs of eqn (83), so we have¶¶
r*(κ) is a function of κ. The latter fact makes a huge difference compared to the predictions of the PB approximation. While this approximation predicts a unique screening parameter κD from eqn (35), the exact equation, eqn (78), is an equation for κ. Apart from the solution κ, which gives the longest decay length, eqn (78) has in general several other solutions κ′, κ″ etc. (the three solutions can alternatively be denoted κν, for ν = 1, 2 and 3). Each solution gives rise to a term in ϕCoul*(r) like the rhs of eqn (83), so we have¶¶
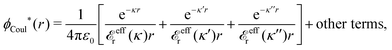 | (86) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr.
effr.
Furthermore, solutions to eqn (78) can be complex-valued, in the case of which there are always two solutions that are complex conjugates to each other, say, κ = κℜ + iκℑ and κ′ = κℜ + iκℑ, where κℜ and κℑ are real. Since the sum of a complex number Z and its complex conjugate ![[Z with combining low line]](https://www.rsc.org/images/entities/i_char_005a_0332.gif) is given by Z +
is given by Z + ![[Z with combining low line]](https://www.rsc.org/images/entities/i_char_005a_0332.gif) = 2ℜ(Z), where ℜ(Z) stands for the real part of Z, we then have
= 2ℜ(Z), where ℜ(Z) stands for the real part of Z, we then have
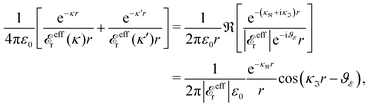 | (87) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κℜ + iκℑ) = |
effr(κℜ + iκℑ) = |![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr|e−iϑ
effr|e−iϑ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) with a real ϑ
with a real ϑ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) . The two poles hence give rise to an exponentially decaying, oscillatory term with decay length 1/κℜ, wavelength 2π/κℑ and phase shift −ϑ
. The two poles hence give rise to an exponentially decaying, oscillatory term with decay length 1/κℜ, wavelength 2π/κℑ and phase shift −ϑ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) . We will denote such a function as an “oscillatory Yukawa function.” The function e−κr/r with real κ will be designated as a “monotonic Yukawa function.”
. We will denote such a function as an “oscillatory Yukawa function.” The function e−κr/r with real κ will be designated as a “monotonic Yukawa function.”
Thus there exist several decay modes for the screened electric potential, some that give monotonic and others that give oscillatory decay. In the limit of low ionic densities, one of the modes approaches the single mode that is included in the PB approximations. Henceforth, we will use the term “screening parameters” to denote a set like κ, κ′, κ″ etc. that are solutions to eqn (78), so this term includes the inverse decay lengths κ or κℜ and the inverse wavelengths κℑ/2π of all monotonic and oscillatory Yukawa function contributions to ϕCoul*. More generally, the concept of “decay parameters” denotes the inverse decay lengths and inverse wavelengths of all kinds of contributions to the various functions.
A well-known example of the occurrence of an oscillatory term as in eqn (87) is the Kirkwood cross-over13 mentioned in the Introduction, where two real solutions turn into two complex-valued solutions when a system parameter like the ion density is changed. We take the example of two real solutions κ and κ′, where κ is the smallest and κ′ is the second smallest solution, i.e., for large r they give the two leading terms in ϕCoul*(r) as given by eqn (86) and we have
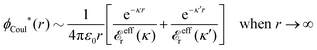 | (88) |
Recall that eqn (78) is equivalent to ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0, so before the cross-over κ and κ′ are two consecutive zeros of
(iκ) = 0, so before the cross-over κ and κ′ are two consecutive zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iξ) as a function of the real variable ξ. As we have seen,
(iξ) as a function of the real variable ξ. As we have seen, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) > 0 for low ion densities, so from the rhs of eqn (84) we see that
effr(κ) > 0 for low ion densities, so from the rhs of eqn (84) we see that ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ′(iξ) > 0 for ξ = κ. The next zero of
′(iξ) > 0 for ξ = κ. The next zero of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iξ) must have an opposite derivative, so
(iξ) must have an opposite derivative, so ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) ′(iξ) < 0 for ξ = κ′, which implies that
′(iξ) < 0 for ξ = κ′, which implies that ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ′) < 0. Thus the two terms in eqn (88) have opposite signs. At the the cross-over point, where the two zeros of
effr(κ′) < 0. Thus the two terms in eqn (88) have opposite signs. At the the cross-over point, where the two zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iξ) merge, we must have
(iξ) merge, we must have ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ) =
effr(κ) = ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ′) = 0 but the sum of the two terms remains finite there.
effr(κ′) = 0 but the sum of the two terms remains finite there.
There may also appear another kind of cross-over between a monotonic and an oscillatory Yukawa function decay, namely the Fisher–Widom cross-over13 mentioned in the Introduction. Say that the term with screening parameter κ″ in eqn (86) initially has a shorter decay length 1/κ″ than the oscillatory term we have just discussed. When the ionic density is increased it is possible that the former term becomes the leading term because 1/κ″ becomes larger than the decay length 1/κℜ of the latter. This means that the decay behavior of ϕCoul*(r) for large r changes from oscillatory to monotonic at the density value where 1/κ″ and 1/κℜ are equal. This kind of cross-over may, of course, also occur in the reverse direction, i.e., the decay changes from monotonic to oscillatory.
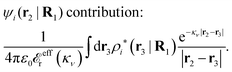 | (89) |
Let us investigate some consequences of eqn (89) and we start with real κν. We will use the fact that
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) = r/r. By setting r = r12 and r′ = r13 (note that r − r′ = r2 − r3) and using the notation introduced in eqn (47), we can conclude from eqn (89) in the limit r12 → ∞
= r/r. By setting r = r12 and r′ = r13 (note that r − r′ = r2 − r3) and using the notation introduced in eqn (47), we can conclude from eqn (89) in the limit r12 → ∞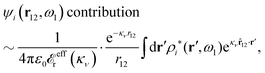 | (90) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 in the exponent.
12 in the exponent.
For a spherically symmetric particle, the integral becomes
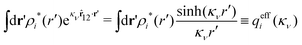 | (91) |
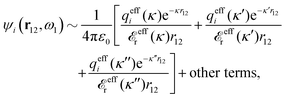 | (92) |
In the general case of nonspherical particles eqn (90) implies that
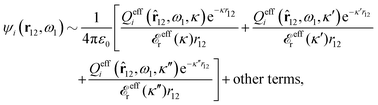 | (93) |
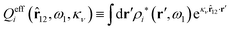 | (94) |
where
![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effi(κ) = 〈Qeffi( effi(κ) = 〈Qeffi(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ,ω,κ)〉ω ,ω,κ)〉ω | (95) |
![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effi can be described as a kind of monopolar effective charge of the particles. The rest of Qeffi(
effi can be described as a kind of monopolar effective charge of the particles. The rest of Qeffi(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12,ω1,κν) has an orientational angle dependence with a combination of dipolar, quadrupolar and higher multipolar characteristics.34 Note that electroneutral particles, like solvent molecules, acquire nonzero
12,ω1,κν) has an orientational angle dependence with a combination of dipolar, quadrupolar and higher multipolar characteristics.34 Note that electroneutral particles, like solvent molecules, acquire nonzero ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effi due to the presence of ions in their neighborhood, so they have nonzero effective charges in general.
effi due to the presence of ions in their neighborhood, so they have nonzero effective charges in general.
For a pair of complex-valued screening parameters, there is an oscillatory Yukawa term in ψi with a direction dependent coefficient that can be determined from eqn (93) in a similar manner as in eqn (87).
Since the theory is valid for particles of any size and shape, the result in eqn (93) is also applicable to macroscopic particles. Therefore the decay of the potential from, for example, a planar surface is also given by the same decay modes. In such cases the effective particle charges can be translated into effective surface charge densities by dividing by the surface area.30
The results in eqn (93) and (94) can alternatively be obtained in Fourier space where ψi is given by [eqn (65)]
![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k), that is, zero of
Coul*(k), that is, zero of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), we obtain a contribution to ψi(r12,ω1) that decays as e−κνr/r with the same prefactor 1/[4πε0
(k), we obtain a contribution to ψi(r12,ω1) that decays as e−κνr/r with the same prefactor 1/[4πε0![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κν)] as in eqn (86) times the factor
effr(κν)] as in eqn (86) times the factor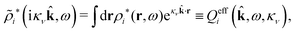 | (96) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) =
= ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 since the origin is selected at the particle center. We see that Qeffi for the mode with screening parameter κν is the projection of ρi* on this mode.
12 since the origin is selected at the particle center. We see that Qeffi for the mode with screening parameter κν is the projection of ρi* on this mode.
There exists an intimate relationship between the screening parameters κν and the effective charges, i.e., qeffi for spherical and Qeffi for nonspherical particles. The parameter κ is a solution to ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0 and, equivalently, to the general equation for κ, eqn (78). By inserting k = iκ into the expression (50) for
(iκ) = 0 and, equivalently, to the general equation for κ, eqn (78). By inserting k = iκ into the expression (50) for ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) we obtain
(k) we obtain
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0 we find that
(iκ) = 0 we find that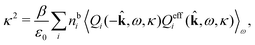 | (97) |
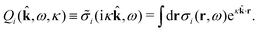 | (98) |
For a spherical ion with charge qi at the center we have ![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) i(k) = qi so we have Qi(−
i(k) = qi so we have Qi(−![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ,ω,κ) = qi and Qeffi(
,ω,κ) = qi and Qeffi(![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ,ω,κ) = qeffi(κ). When we deal with a system consisting solely of such ions, eqn (97) becomes [cf.eqn (69)]
,ω,κ) = qeffi(κ). When we deal with a system consisting solely of such ions, eqn (97) becomes [cf.eqn (69)]
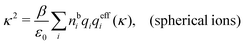 | (99) |
![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) in the denominator. Incidentally, we may note that for spherical ions we have
r*(κ) in the denominator. Incidentally, we may note that for spherical ions we have 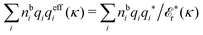 , but in general qeffi(κ) ≠ qi*/
, but in general qeffi(κ) ≠ qi*/![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ). For a binary electrolyte of spherical ions, the deviation in κ from κD can be obtained from
r*(κ). For a binary electrolyte of spherical ions, the deviation in κ from κD can be obtained from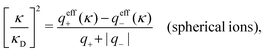 | (100) |
For the special case of a binary symmetric electrolyte nb+ = nb− ≡ nb and q+ = −q− ≡ q. If the spherical anions and cations differ only by the sign of their charges, as in the restricted primitive model, we have qeff+(κ) = −qeff−(κ) ≡ qeff and q+* = −q−* ≡ q*. In this case qeff(κ) = q*/![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κ) and from eqn (100) it follows that
r*(κ) and from eqn (100) it follows that
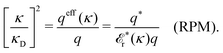 | (101) |
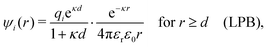 | (102) |
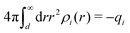 . We can identify the effective charge as qeffi = qieκd/(1 + κd) whereby we have ψi(r) = qeffie−κr/[4πεrε0r]. In the PB approximation, only the central ion has qeffi ≠ qi while all ions in its ion cloud are assumed to be bare, so for them qeffi = qi and eqn (101) yields κ/κD = 1. However, since all ions should be treated on the same basis, they should all have qeffi ≠ qi. If we in eqn (101) set qeff equal to the value from the LPB case but with κ ≠ κD, we obtain the approximation in eqn (2).
. We can identify the effective charge as qeffi = qieκd/(1 + κd) whereby we have ψi(r) = qeffie−κr/[4πεrε0r]. In the PB approximation, only the central ion has qeffi ≠ qi while all ions in its ion cloud are assumed to be bare, so for them qeffi = qi and eqn (101) yields κ/κD = 1. However, since all ions should be treated on the same basis, they should all have qeffi ≠ qi. If we in eqn (101) set qeff equal to the value from the LPB case but with κ ≠ κD, we obtain the approximation in eqn (2).
We finally note that each Yukawa function term for nonspherical particles is always accompanied by terms that decay as e−κr/rl with l = 2, 3,… and have different orientational dependencies.34 The term with l = 2 has an orientational angle dependence with a combination of dipolar, quadrupolar and higher multipolar characteristics, but lacks a monopolar part, while the term with l = 3 has quadrupolar and higher multipolar orientational characteristics, but no monopolar and dipolar parts. This applies for all screening parameter values, κ, κ′, κ″ etc. These higher order terms are included in “other terms” above.
When κ → 0, the term with l = 2 goes over to a purely dipolar term that decays with distance as 1/r2 and the term with l = 3 goes to a purely quadrupolar term that decays as 1/r3. Thereby the usual multipole expansion is obtained, which applies to the electrostatic potential from a fixed charge distribution immersed in a pure polar liquid.
4 Screened interactions in electrolytes in the general case
4.1 The main case: all decay modes of the correlations are determined by the dielectric function
As we saw earlier, the electrostatic potential from a particle can be regarded as an external potential for the system even when the particle belongs to the same species as one of the constituent ones. The total mean potential ψj(r|R2) from a j-particle with coordinates R2 can then be treated in the same manner as Ψ(r) and when ψj is weak, the pair potential of mean force wij(R1,R2) for a particle of species i with coordinates R1 satisfies according to eqn (41)provided that the screened electrostatic interactions between the two particles dominate in wij. Here wij has taken the role of δWi and ψi that of δΨ in eqn (41). With this in mind, we define in the general case the screened electrostatic part of the potential of mean force as
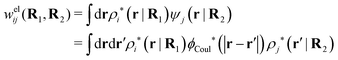 | (103) |
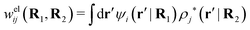 . The integral on the rhs of eqn (103) has the same form as a Coulomb interaction energy between the charge densities ρi* and ρj*, but with the screened Coulomb potential ϕCoul*(r) instead of the usual unscreened one. As we will see welij has a central role for the interparticle interactions in electrolytes. For spherically symmetric particles we have
. The integral on the rhs of eqn (103) has the same form as a Coulomb interaction energy between the charge densities ρi* and ρj*, but with the screened Coulomb potential ϕCoul*(r) instead of the usual unscreened one. As we will see welij has a central role for the interparticle interactions in electrolytes. For spherically symmetric particles we have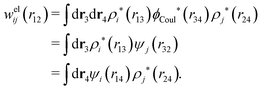 | (104) |
A very important task is to relate the decay behavior of ϕCoul*(r) to that of wij and the pair distribution functions gij = 1 + hij = e−βwij. We have the expansions
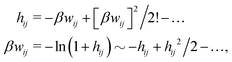 | (105) |
To find the connection between the decays of ϕCoul* and hij, let us introduce another pair correlation function hij*, which for spherical simple ions is defined by
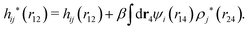 | (106) |
We will now show that the dressed ion charge density is given by
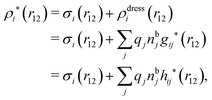 | (107) |
where we have used eqn (54) to obtain the last equality. The rhs of this equation is equal to ρi*(r12) according to its definition (40), so eqn (107) follows.
In the general case we define in an analogous manner
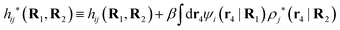 | (108) |
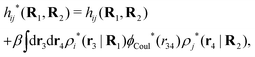 | (109) |
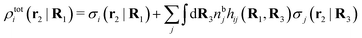 | (110) |
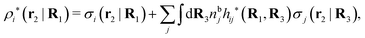 | (111) |
By using the definition (103) of welij we see that eqn (109) can be written as
| hij(R1,R2) = hij*(R1,R2) − βwelij(R1,R2). | (112) |
The pair correlation function hij has accordingly been split into two parts: the function hij* of the dresses and the part −βwelij that contains the screened Coulomb interaction. As we will see, the electrostatic term welij determines the decay behavior of pair correlation function hij in terms of Yukawa functions. More precisely, in the overwhelming number of cases
(i) the term −βwelij in eqn (112) gives rise to all contributions to hij (and thereby to −βwij) that decays exponentially like a monotonic Yukawa function e−ar/r or an oscillatory one e−aℜr![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(aℑr + ϑ)/r [with aℜ = ℜ(a) and aℑ = ℑ(a), the imaginary part] and
cos(aℑr + ϑ)/r [with aℜ = ℜ(a) and aℑ = ℑ(a), the imaginary part] and
(ii) the decay parameter a of each such contribution satisfies ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (ia) = 0, which means that a is a solution to the general eqn (78) for κ, so a is a screening parameter. This implies that hijhas the same set of screening parameters as ϕCoul*(r) and that the various a are equal to κ, κ′ etc. in eqn (86).
(ia) = 0, which means that a is a solution to the general eqn (78) for κ, so a is a screening parameter. This implies that hijhas the same set of screening parameters as ϕCoul*(r) and that the various a are equal to κ, κ′ etc. in eqn (86).
Thus, for each Yukawa term in eqn (86) there is a corresponding contribution in hij with the same screening parameters (but with different prefactor and phase shift, if any). The first term in eqn (112), the function hij*, also has contributions that decay like Yukawa functions (with other values of the decay parameters), but as shown below they do not give any contribution to hij (apart from some rare exceptions to be described later). Thus, the screened Coulomb potential and the pair correlation function normally have the same decay modes, each mode having its own values of the screening parameter, dielectric factor, effective relative dielectric permittivity and effective charges.
As we have seen, a contribution that decays like a monotonic or oscillatory Yukawa function corresponds to a simple pole in complex k-space. Let us therefore investigate the functions in Fourier space. Since the pair correlation function hij(R1,R2) in the bulk phase depends on the separation vector r12 = r2 − r1 we can write hij(R1,R2) = hij(r12,ω1,ω2), so in Fourier space we obtain from eqn (103) and (112)
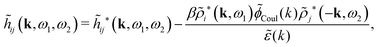 | (113) |
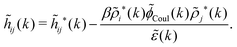 | (114) |
An important result of the current work is that the coupling between fluctuations in charge density and in number density, which normally takes place, makes all poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij to be given by the zeros of
ij to be given by the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), whereby they coincide with the poles of
(k), whereby they coincide with the poles of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k). This follows from the fact, shown in Appendix C, that
Coul*(k). This follows from the fact, shown in Appendix C, that ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij and
ij and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* cannot have poles for the same k values (apart from a few exceptional cases that will be treated in Section 4.2). This result is a consequence of the fact that each pole of
ij* cannot have poles for the same k values (apart from a few exceptional cases that will be treated in Section 4.2). This result is a consequence of the fact that each pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* is cancelled by a corresponding pole in the last term in eqn (113), as shown explicitly in Appendix C. For binary simple electrolytes this cancellation in eqn (114) has previously been found.25 Since
ij* is cancelled by a corresponding pole in the last term in eqn (113), as shown explicitly in Appendix C. For binary simple electrolytes this cancellation in eqn (114) has previously been found.25 Since ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i* and
i* and ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) j* are given by linear combinations of
j* are given by linear combinations of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*, their poles are also poles of
ij*, their poles are also poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and cannot coincide with any pole of
ij* and cannot coincide with any pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij. Therefore, all poles of the rhs of eqn (113) [for spherical ions eqn (114)] originate from the zeros of
ij. Therefore, all poles of the rhs of eqn (113) [for spherical ions eqn (114)] originate from the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) in the denominator and the assertions in (i) and (ii) above follow. The dielectric function
(k) in the denominator and the assertions in (i) and (ii) above follow. The dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) is also a linear combination of
(k) is also a linear combination of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* since
ij* since ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i* in eqn (50) is such a linear combination. The poles and zeros of
i* in eqn (50) is such a linear combination. The poles and zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) occur, of course, for different k values.
(k) occur, of course, for different k values.
For spherical particles, these results and eqn (114) imply that [cf.eqn (92)]
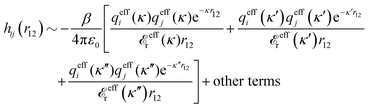 | (115) |
For nonspherical particles, an expression for hij(r12,ω1,ω2) analogous to that in eqn (115) applies when r12 → ∞
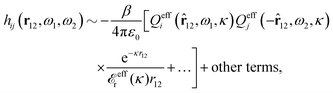 | (116) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 in Qeffi and −
12 in Qeffi and −![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12 in Qeffj point towards the center of the other particle along the connecting line. As noted in Section 3.2.4, for these kinds of systems, each Yukawa function term is always accompanied by terms that decay as e−κr/rl with l = 2, 3,… They are included in “other terms” together with additional terms that will be discussed at the end of this section.
12 in Qeffj point towards the center of the other particle along the connecting line. As noted in Section 3.2.4, for these kinds of systems, each Yukawa function term is always accompanied by terms that decay as e−κr/rl with l = 2, 3,… They are included in “other terms” together with additional terms that will be discussed at the end of this section.
When κ is complex, the κ and κ′ terms combine and form an oscillatory term [cf.eqn (87)]. By writing Qeffl(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ,ω,κ) = |Qeffl(
,ω,κ) = |Qeffl(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ,ω,κ)|e−iγl(
,ω,κ)|e−iγl(![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) ,ω,κ) with a real-valued γl for l = i, j, we then have for r12 → ∞
,ω,κ) with a real-valued γl for l = i, j, we then have for r12 → ∞
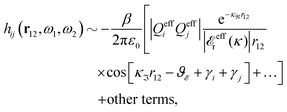 | (117) |
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12,ω1,κ), γj = γj(−
12,ω1,κ), γj = γj(−![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) 12,ω2,κ) and where we likewise have suppressed the arguments of Qeffi and Qeffj. Both γl and |Qeffl| depend on orientation. This kind of oscillatory term is, of course, formed from any pair of complex conjugate screening parameters κν that are solutions to eqn (78), say, κν and
12,ω2,κ) and where we likewise have suppressed the arguments of Qeffi and Qeffj. Both γl and |Qeffl| depend on orientation. This kind of oscillatory term is, of course, formed from any pair of complex conjugate screening parameters κν that are solutions to eqn (78), say, κν and 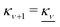 .
.
As noted in Section 3.2.4, the theory is valid for particles of any size and shape. Therefore results in eqn (116) and (117) are applicable for the correlations between, for example, a macroparticle and an ion. Thereby the potential of mean force acting on the ion as a function of distance from the macroparticle decays as wij ∼ −β−1hij. Likewise, the results can be applied for the interaction between two macroparticles, for example, the surface forces between two macroscopic surfaces,29,30 which hence have the decay modes that are determined by the bulk electrolyte that the fluid phase between the surfaces is in equilibrium with.
The density–density, charge–charge, density–charge correlation functions, HNN(r), HQQ(r) and HNQ(r) defined in Appendix B, have the same poles in Fourier space as ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij, which are in general determined by the zeros of
ij, which are in general determined by the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k). This can be realized as follows.
(k). This can be realized as follows. ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NN(k), given in Appendix B, eqn (138), is a linear combination of
NN(k), given in Appendix B, eqn (138), is a linear combination of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij,
ij,
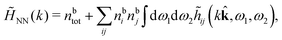 | (118) |
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij. By inserting eqn (66) into
ij. By inserting eqn (66) into ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) QQ(k) given in eqn (136) and
QQ(k) given in eqn (136) and ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NQ(k) given in eqn (140) we obtain
NQ(k) given in eqn (140) we obtain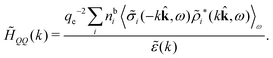 | (119) |
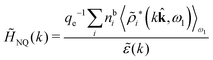 | (120) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) are poles of these functions. Thus HNN(r), HQQ(r), HNQ(r), hij, wij and ϕCoul*(r) have the same screening parameters, apart from in the exceptional cases mentioned earlier. They will be treated in the next section.
(k) are poles of these functions. Thus HNN(r), HQQ(r), HNQ(r), hij, wij and ϕCoul*(r) have the same screening parameters, apart from in the exceptional cases mentioned earlier. They will be treated in the next section.
As mentioned earlier there always exist terms in eqn (115) that have a different r dependence than Yukawa functions. They appear because when hij(r) and therefore wij(r) contain a term that decays as e−κr/r with real κ, it follows from eqn (105) that hij(r) contains terms that decay as [e−κr/r]2, [e−κr/r]3etc. and that this also applies to wij(r). These higher order terms that appear because the system is intrinsically nonlinear have decay lengths (2κ)−1, (3κ)−1etc. so they decay faster than the “original” Yukawa function term, with the same κ, that has generated them.|||| Therefore they give important contributions mainly for small r. For large r some of them can, however, dominate over Yukawa function terms with larger κ values in eqn (115), for example the term with e−κ′r/r provided κ′ > 2κ. There also exist terms that decay as ζ(r)[e−κr/r]l, where ζ(r) is a slowly varying function and l ≥ 2.21 Furthermore, there are cross-terms from two or more Yukawa functions with different decay lengths. All these higher order terms are included in “other terms” in eqn (115) and it is not worthwhile to consider more than the leading ones individually and explicitly. For complex-valued κ, similar conclusions are valid for exponentially decaying oscillatory terms and the same applies in eqn (116) for nonspherical particles.
All of these contributions are generated by the set of fundamental decay modes with screening parameters κν that are solutions to the general eqn (78) for κ and, equivalently, solutions to ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκν) = 0 and to eqn (97). Thus, the decay behaviors of both the screened electrostatic potential and the correlation functions originate from fundamental decay modes.
(iκν) = 0 and to eqn (97). Thus, the decay behaviors of both the screened electrostatic potential and the correlation functions originate from fundamental decay modes.
In cases where the non-electrostatic pair interactions uneij(r) do not have a short range (contrary to our assumptions earlier), but instead have a power law decay like the r−6 dispersion interactions, the functions hij(r), wij(r) and ϕCoul*(r) ultimately decay like a power law when r → ∞.35 These functions still have Yukawa function terms*** that are given by the present formalism and the power law terms are included in “other terms” in the various equations. The Yukawa terms can give dominant contributions for short to intermediate r values, but they can never dominate for very large r because they decay faster than any power law. In many cases the Yukawa function terms have a dominant influence in hij(r) for most r. This is, for example, seen in the simulation results by Keblinski et al.24 mentioned in the Introduction for the realistic model for NaCl that includes dispersion interactions. Their calculations show that the monotonic and oscillatory Yukawa function terms give the dominant contributions.
4.2 Exceptions; charge-inversion invariant systems
Let us now turn to the exceptional cases, that is, cases where![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij and
ij and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* can have poles for the same k values and where Yukawa function contributions to hij therefore originate both from the last term in eqn (113) and from
ij* can have poles for the same k values and where Yukawa function contributions to hij therefore originate both from the last term in eqn (113) and from ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*. As shown in Appendix D of ref. 29 this can occur for most systems at exceptional points in the system's parameter space (for instance a critical point).††† This will not be dealt with any further because the systems behave in the way we have just described for all other parameter values.
ij*. As shown in Appendix D of ref. 29 this can occur for most systems at exceptional points in the system's parameter space (for instance a critical point).††† This will not be dealt with any further because the systems behave in the way we have just described for all other parameter values.
The other exceptional case is a category of systems where ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*, in contrast to the main case, always gives Yukawa function contributions to hij, namely model systems that are invariant when we invert the sign of all charges of the particles. Such systems, which we will call charge-inversion invariant systems, remain exactly the same when one does such a charge inversion, whereby the internal charge distribution σi(r|R1) for each particle changes to −σi(r|R1) (positive regions become negative and vice versa without change in the absolute value of σi for each r). This means, for example, that the anions become cations and vice versa during charge inversion. For an invariant system, for each cation species there must exist an anion species that is identical in all respects apart from the sign of σi(r|R1), like the same size, same shape and same nonelectrostatic interactions with other particles, and have the same number density. Examples of such systems include the restricted primitive model, where the anions and cations of the same absolute valency are charged hard spheres of equal size. As soon as there is any difference, however small, between anions and cations apart from the sign of their charges, the main result applies, so all Yukawa function terms in hij originate from the last term in eqn (113) and all poles of
ij*, in contrast to the main case, always gives Yukawa function contributions to hij, namely model systems that are invariant when we invert the sign of all charges of the particles. Such systems, which we will call charge-inversion invariant systems, remain exactly the same when one does such a charge inversion, whereby the internal charge distribution σi(r|R1) for each particle changes to −σi(r|R1) (positive regions become negative and vice versa without change in the absolute value of σi for each r). This means, for example, that the anions become cations and vice versa during charge inversion. For an invariant system, for each cation species there must exist an anion species that is identical in all respects apart from the sign of σi(r|R1), like the same size, same shape and same nonelectrostatic interactions with other particles, and have the same number density. Examples of such systems include the restricted primitive model, where the anions and cations of the same absolute valency are charged hard spheres of equal size. As soon as there is any difference, however small, between anions and cations apart from the sign of their charges, the main result applies, so all Yukawa function terms in hij originate from the last term in eqn (113) and all poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij arises from the zeros of
ij arises from the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k). For charge-inversion invariant electrolyte systems, all electroneutral species present must also satisfy invariance conditions. Examples include electrolyte models with explicit solvent where the solvent molecules turn into themselves during a charge inversion, for instance spherical particles with a dipole at the center.
(k). For charge-inversion invariant electrolyte systems, all electroneutral species present must also satisfy invariance conditions. Examples include electrolyte models with explicit solvent where the solvent molecules turn into themselves during a charge inversion, for instance spherical particles with a dipole at the center.
The reason why charge-inversion invariant systems are exceptions is that the extreme symmetry forces the density–charge correlation function HNQ(r) to be identically zero, so fluctuations in charge density and in number density are uncoupled from each other. It is simple to realize that HNQ(r) must be identically equal to zero in such systems. Suppose that HNQ(r) is, say, positive for a certain r value and we invert all charges in the system, HNQ(r) would become negative but since the system is charge-inversion invariant HNQ(r) must remain the same, which implies that HNQ(r) must be zero. Alternatively, this can be realized when we consider correlations between fluctuations in density and fluctuations in charge at two points separated by distance r, because for a given fluctuation in density, the probability for positive and negative fluctuations in charge must be equal, so the fluctuations will average to zero. Mathematically, the fact that HNQ(r) ≡ 0 can be realized from the rhs of the definition of HNQ(r) in Appendix B [eqn (139)]. For each positive contribution on the rhs there must exist an equally large negative contribution due to the charge-inversion invariance. This can likewise be realized from eqn (140). Exactly the same argument applies to eqn (120) because during a charge inversion ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i*(k,ω1) for each particle changes to −
i*(k,ω1) for each particle changes to −![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i*(k,ω1), so we must have
i*(k,ω1), so we must have
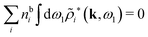 | (121) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NQ(k)
NQ(k)![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) 0.
0.
Let us now consider the density–density correlation function for charge-inversion invariant systems. By inserting ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij from eqn (113) into eqn (118) we see that the contribution from the last terms in eqn (113) cancels identically in
ij from eqn (113) into eqn (118) we see that the contribution from the last terms in eqn (113) cancels identically in ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NN(k) because of eqn (121). Therefore we have
NN(k) because of eqn (121). Therefore we have
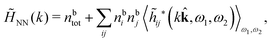 | (122) |
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NN(k) must be poles of
NN(k) must be poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*. Eqn (119) for
ij*. Eqn (119) for ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) QQ(k) remains, however, valid and the poles of
QQ(k) remains, however, valid and the poles of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) QQ(k) are hence given by the zeros of
QQ(k) are hence given by the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) also in the present case. Thus there are two different sets of poles that are relevant, the poles of
(k) also in the present case. Thus there are two different sets of poles that are relevant, the poles of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) QQ(k) [zeros of
QQ(k) [zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k)] and those of
(k)] and those of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NN(k). The poles of the pair correlation function
NN(k). The poles of the pair correlation function ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij belong to both sets, but as we will see they enter in
ij belong to both sets, but as we will see they enter in ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij in different manners.
ij in different manners.
Consider two species of ions that swap their identities as anions and cations during a charge inversion. Let us call them A+ and A−, so we have σA+(r|R1) = −σA−(r|R1). The common notation A indicates that they are identical apart from the sign of their internal charge distributions. We likewise consider two other species of ions B+ and B− with σB+(r|R1) = −σB−(r|R1). They are also identical to each other apart from the sign of σi. The charge-inversion invariance implies that we have the symmetry
We now define hS,AB(r,ω1,ω2), hD,AB(r,ω1,ω2) and the corresponding h* functions from
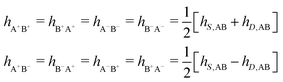 | (123) |
Due to the charge-inversion invariance we have ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A+* = −
A+* = −![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A−* ≡
A−* ≡ ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A*, which defines
A*, which defines ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) A*, and likewise for
A*, and likewise for ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) B*. Therefore we have from eqn (113)
B*. Therefore we have from eqn (113)
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) S,AB(k,ω1,ω2) = S,AB(k,ω1,ω2) = ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) S,AB*(k,ω1,ω2) S,AB*(k,ω1,ω2) | (124) |
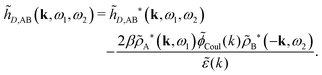 | (125) |
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and
ij* and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij, it follows that
ij, it follows that ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) D,AB* cannot have poles common to
D,AB* cannot have poles common to ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) D,AB so the poles of
D,AB so the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) D,AB are due to the zeros of
D,AB are due to the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) [possibly apart from exceptional points in the system's parameter space]. The functions hS,AB and hD,AB have different decay parameters; the poles of
(k) [possibly apart from exceptional points in the system's parameter space]. The functions hS,AB and hD,AB have different decay parameters; the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) S,AB belong to one of the sets mentioned earlier [the poles of
S,AB belong to one of the sets mentioned earlier [the poles of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NN(k)] and those of
NN(k)] and those of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) D,AB belong to the other set [the poles of
D,AB belong to the other set [the poles of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) QQ(k)]. Thus only hD,AB has the same screening parameters as ϕCoul*(r) and hD,AB/2 decays analogously to the rhs of eqn (115)–(117). The contribution from hD,AB in eqn (123) appears with a plus sign for ions of the same sign of charge and with a minus sign for ions of opposite sign. The function hS,AB (with different decay parameters than hD,AB) appears with a plus sign in eqn (123) for all ions irrespectively of their signs of charge.
QQ(k)]. Thus only hD,AB has the same screening parameters as ϕCoul*(r) and hD,AB/2 decays analogously to the rhs of eqn (115)–(117). The contribution from hD,AB in eqn (123) appears with a plus sign for ions of the same sign of charge and with a minus sign for ions of opposite sign. The function hS,AB (with different decay parameters than hD,AB) appears with a plus sign in eqn (123) for all ions irrespectively of their signs of charge.
In fact, HNN(r) is a linear combination of the S-functions and HQQ(r) is a linear combination of the D-functions (including those for any electroneutral particles, if present). Furthermore, the total particle density 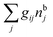 around each of the particles in charge-inversion invariant systems is determined by S-functions and the total charge density ρtoti is determined by D-functions, so these two entities have different decay parameters.
around each of the particles in charge-inversion invariant systems is determined by S-functions and the total charge density ρtoti is determined by D-functions, so these two entities have different decay parameters.
All these facts are well-known for the restricted primitive model where there are only two species A+ and A− in a dielectric continuum solvent, but the new findings here are that this applies in general for charge-inversion invariant systems with any number of components including solvent molecules and other electroneutral particles. All particles can have any shape, size, internal charge density and nonelectrostatic interactions subject to the conditions of charge-inversion invariance.
In the RPM, where we have 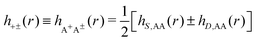 , it can happen that hS,AA(r) has a longer decay length than hD,AA(r) when the ion density is high.19,20,39 Then, the tail of hij(r) for large r has the same sign irrespective of the signs of the i and j-ions. This has been denoted as “core dominance,”39 because hS,AA(r) is decoupled from electrostatics and is mainly determined by the hard core packing of the ions. For low ion densities, where hD,AA(r) has the longest decay length, the tails of h++(r) and h+−(r) have different signs and there is “electrostatic dominance.” Such strict distinction between core dominance and electrostatic dominance exists only in charge-inversion invariant systems.
, it can happen that hS,AA(r) has a longer decay length than hD,AA(r) when the ion density is high.19,20,39 Then, the tail of hij(r) for large r has the same sign irrespective of the signs of the i and j-ions. This has been denoted as “core dominance,”39 because hS,AA(r) is decoupled from electrostatics and is mainly determined by the hard core packing of the ions. For low ion densities, where hD,AA(r) has the longest decay length, the tails of h++(r) and h+−(r) have different signs and there is “electrostatic dominance.” Such strict distinction between core dominance and electrostatic dominance exists only in charge-inversion invariant systems.
It is interesting to consider systems that are close to being charge-inversion invariant. This is the case, for example, in the primitive model of binary symmetric electrolyte solutions when anions and cations have equal absolute valency but differ slightly in size. Then, there is no longer a decoupling between electrostatic and nonelectrostatic correlations, so there is electrostatic coupling in the decay modes where hard core packing of the ions dominates and vice versa. Systems close to charge-inversion invariance also occur in more realistic models of symmetric electrolytes where the anions and cations have nearly the same nonelectrostatic pair interactions with their own species une++(r) ≈ une−−(r), as in the model for NaCl mentioned in the Introduction. Another example is a model with explicit solvent where anions and cations are identical apart from their signs but the solvent molecules are modeled as spheres with a radially aligned dipole that lies somewhat off-center.
For these systems all poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij are given by the zeros of
ij are given by the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), while for charge-inversion invariant systems the decay parameter values of hij belong, as we have seen, to two distinct sets: those that are due to poles of
(k), while for charge-inversion invariant systems the decay parameter values of hij belong, as we have seen, to two distinct sets: those that are due to poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and those that are due to zeros of
ij* and those that are due to zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k). Since the two kinds of systems differ very little from each other, their decay parameters must be closely related and vary continuously when one changes a system from being nearly charge-inversion invariant to being invariant or vice versa. This must apply not only for the decay parameters that are given by zeros of
(k). Since the two kinds of systems differ very little from each other, their decay parameters must be closely related and vary continuously when one changes a system from being nearly charge-inversion invariant to being invariant or vice versa. This must apply not only for the decay parameters that are given by zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) all the time, but also for those that initially are due to such zeros and then, for the invariant system, belong to the set that are due to poles of
(k) all the time, but also for those that initially are due to such zeros and then, for the invariant system, belong to the set that are due to poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* but not zeros of
ij* but not zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k). In Appendix C it is shown why and how this happens. One can visualize the findings by following the “trajectories” of the poles of
(k). In Appendix C it is shown why and how this happens. One can visualize the findings by following the “trajectories” of the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij and
ij and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* as functions of the system parameters like ion sizes etc. For a system that is nearly charge-inversion invariant, it is found in the appendix that there exist one set of poles of
ij* as functions of the system parameters like ion sizes etc. For a system that is nearly charge-inversion invariant, it is found in the appendix that there exist one set of poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij [zeros of
ij [zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k)] where each pole is close to a pole of
(k)] where each pole is close to a pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and where the trajectories of the poles of
ij* and where the trajectories of the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij and
ij and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* cross each other at the point where the system become invariant. At the crossing point the pole of
ij* cross each other at the point where the system become invariant. At the crossing point the pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij ceases to be a zero of
ij ceases to be a zero of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) and becomes instead a pole of both
(k) and becomes instead a pole of both ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and
ij* and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij. The second set of poles of
ij. The second set of poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij do not have such crossings and these poles remain zeros of
ij do not have such crossings and these poles remain zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) throughout. These two sets correspond to the sets for the invariant system introduced above.
(k) throughout. These two sets correspond to the sets for the invariant system introduced above.
More precisely, it is shown in the appendix that there exist zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) for the nearly invariant system that lie close to the poles of
(k) for the nearly invariant system that lie close to the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* for the same system. The latter are not poles of
ij* for the same system. The latter are not poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij while the zeros of
ij while the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) are such poles. Each of these zeros moves continuously with the system parameters so that when the system is turned into a charge-inversion invariant one, it merges with the corresponding pole of
(k) are such poles. Each of these zeros moves continuously with the system parameters so that when the system is turned into a charge-inversion invariant one, it merges with the corresponding pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and ceases to be a zero of
ij* and ceases to be a zero of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) but remains as a pole of
(k) but remains as a pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij.
ij.
4.3 The decay of HQQ(r), HNN(r) and HNQ(r)
Let us now return to the general case of systems without charge-inversion symmetry, which is the normal, realistic case since anions and cations virtually always differ by much more than the sign of their charge and since the positive and negative parts of the solvent molecules normally differ a lot apart from the sign of the charge.Let us consider cases where the leading term in hij is given by the monotonic Yukawa term shown explicitly in eqn (116). This term originates from the last term in eqn (113) evaluated at the leading zero of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), i.e., k = iκ and we assume that κ is real. We will investigate the leading term when r → ∞ for HNN(r), HQQ(r) and HNQ(r), respectively. The decay length is 1/κ for all three functions and we will find that the magnitudes of the leading term of these functions are interdependent via common prefactors, which can be obtained from the effective multipole charges Qeffi. We will also show that the intimate relationship between the screening parameter κ and Qeffi found in Section 3.2.4 has direct consequences for the relative importance of the different correlation functions.
(k), i.e., k = iκ and we assume that κ is real. We will investigate the leading term when r → ∞ for HNN(r), HQQ(r) and HNQ(r), respectively. The decay length is 1/κ for all three functions and we will find that the magnitudes of the leading term of these functions are interdependent via common prefactors, which can be obtained from the effective multipole charges Qeffi. We will also show that the intimate relationship between the screening parameter κ and Qeffi found in Section 3.2.4 has direct consequences for the relative importance of the different correlation functions.
These results can be obtained from eqn (118)–(120) together with eqn (116) and we obtain for r → ∞
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) due to the average over the orientations,
due to the average over the orientations,where we can select
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) =
= ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_char_0072_0302.gif) [cf.eqn (94) and (96)] and where Qi is defined in eqn (98). The Yukawa function factor arises from 1/
[cf.eqn (94) and (96)] and where Qi is defined in eqn (98). The Yukawa function factor arises from 1/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = k2εr
(k) = k2εr![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) evaluated in r space. By defining the average entities
Coul*(k) evaluated in r space. By defining the average entities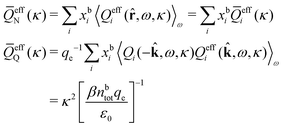 | (126) |
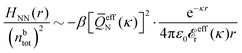 | (127) |
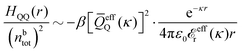 | (128) |
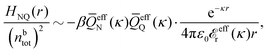 | (129) |
![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN is simply the average over all particles of the orientation independent part of Qeffi [eqn (95)],
effN is simply the average over all particles of the orientation independent part of Qeffi [eqn (95)], ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ contains a weighing with respect to Qi that depends on the bare charge density σi of the particles [see eqn (98)].
effQ contains a weighing with respect to Qi that depends on the bare charge density σi of the particles [see eqn (98)].
H
NN(r), HNQ(r) and HQQ(r) have the same decay length, but depending on the values of the system parameters the leading term of HQQ(r) can be larger than that of HNN(r) or vice versa. Since κ2 = βnbtotqe![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ(κ)/ε0, the decay length 1/κ is directly linked to the magnitude of HQQ(r), while the magnitude of HNN(r) does not have such a direct link. For a situation with long-range density–density correlations, the screening parameter κ is small and the charge–charge correlations must be small and become even smaller when the decay length increases. This is, for example, relevant when a critical point is approached, whereby the charge–charge correlations become less and less significant although they have the same decay length as the density–density correlations. In the present analysis we do, however, avoid the immediate neighborhood of critical points, where other considerations have to be made. We may, however, note that in the limit of 1/κ → ∞ the charge–charge correlations vanish as they must do.
effQ(κ)/ε0, the decay length 1/κ is directly linked to the magnitude of HQQ(r), while the magnitude of HNN(r) does not have such a direct link. For a situation with long-range density–density correlations, the screening parameter κ is small and the charge–charge correlations must be small and become even smaller when the decay length increases. This is, for example, relevant when a critical point is approached, whereby the charge–charge correlations become less and less significant although they have the same decay length as the density–density correlations. In the present analysis we do, however, avoid the immediate neighborhood of critical points, where other considerations have to be made. We may, however, note that in the limit of 1/κ → ∞ the charge–charge correlations vanish as they must do.
For charge-inversion invariant systems ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN ≡ 0 and HNQ(r) ≡ 0, while the decay of HNN(r) can be obtained from
effN ≡ 0 and HNQ(r) ≡ 0, while the decay of HNN(r) can be obtained from
Returning to the general case, the conclusions above expressed in eqn (127)–(129) are valid for the leading term in HNN(r), HNQ(r) and HQQ(r) when κ is real. Analogous conclusions are valid for the Yukawa terms with other κν values in these correlation functions, so similar relationships to these equation are valid for all decay modes (including the oscillatory case where there is also a cosine factor). The relative magnitudes of |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN| and |
effN| and |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ| varies for the different modes, so the contributions with some decay lengths may have |
effQ| varies for the different modes, so the contributions with some decay lengths may have |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN| > |
effN| > |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ| while the reverse can be true for those with other decay lengths. In this regard it is particularly illustrative to consider systems that are close to being charge-inversion invariant, but let us start with the corresponding invariant systems.
effQ| while the reverse can be true for those with other decay lengths. In this regard it is particularly illustrative to consider systems that are close to being charge-inversion invariant, but let us start with the corresponding invariant systems.
For charge-inversion invariant systems we have seen that there are two distinct sets of poles for ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij: the poles of
ij: the poles of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) NN(k) [poles of
NN(k) [poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*] and those of
ij*] and those of ![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) QQ(k) [zeros of
QQ(k) [zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k)]. This implies that the Yukawa function terms in HNN(r) and HQQ(r) have distinct decay parameter values; a Yukawa term that is present in HNN(r) is absent in HQQ(r) and vice versa. A system that is close to being charge-inversion invariant has, however, all such terms present in both HNN(r) and HQQ(r). These two functions then have the same decay parameters and, as we saw at the end of Section 4.2, when one breaks the charge-inversion invariance all decay parameters vary continuously with the system parameters. We also saw that the two sets of poles for
(k)]. This implies that the Yukawa function terms in HNN(r) and HQQ(r) have distinct decay parameter values; a Yukawa term that is present in HNN(r) is absent in HQQ(r) and vice versa. A system that is close to being charge-inversion invariant has, however, all such terms present in both HNN(r) and HQQ(r). These two functions then have the same decay parameters and, as we saw at the end of Section 4.2, when one breaks the charge-inversion invariance all decay parameters vary continuously with the system parameters. We also saw that the two sets of poles for ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij remain in the sense that each pole in one set is close to a pole of
ij remain in the sense that each pole in one set is close to a pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* (and merge with it for the invariant system) and the other set consists of poles that do not behave in this manner and are poles of
ij* (and merge with it for the invariant system) and the other set consists of poles that do not behave in this manner and are poles of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) throughout. For continuity reasons, the magnitudes of the Yukawa terms in HQQ(r) with decay parameters in the first set must be close to zero (they are exactly zero for the invariant system), while the magnitudes of the terms in HNN(r) belonging to the second set must be close to zero for the same reason. Thus |
(k) throughout. For continuity reasons, the magnitudes of the Yukawa terms in HQQ(r) with decay parameters in the first set must be close to zero (they are exactly zero for the invariant system), while the magnitudes of the terms in HNN(r) belonging to the second set must be close to zero for the same reason. Thus |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN| ≫ |
effN| ≫ |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ| for the first set and |
effQ| for the first set and |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN| ≪ |
effN| ≪ |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ| for the second. This is the situation for the NaCl system mentioned in the Introduction.
effQ| for the second. This is the situation for the NaCl system mentioned in the Introduction.
Finally, we will turn to dilute electrolyte solutions with molecular solvent. The leading term in hij for large distances then has a decay parameter κ that approaches the Debye parameter κD at high dilution, as we saw in eqn (85). In a dilute solution where κ is small we have ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effi(κ) ≈ qi, which implies that nbtot
effi(κ) ≈ qi, which implies that nbtot![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN(κ) is very small because
effN(κ) is very small because 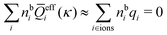 due to electroneutrality (qsolvent = 0 since the solvent molecules are uncharged). Thus, the leading term in HNN(r), which is proportional to [nbtot
due to electroneutrality (qsolvent = 0 since the solvent molecules are uncharged). Thus, the leading term in HNN(r), which is proportional to [nbtot![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN(κ)]2, is very small. HQQ(r) is much larger because its coefficient is proportional to the square of
effN(κ)]2, is very small. HQQ(r) is much larger because its coefficient is proportional to the square of
As in other systems, there exist other decay modes with terms of different decay lengths in the correlation functions, for example contributions where the density–density fluctuations of the solvent are prominent. In contrast to the very small terms in HNN(r) with decay length 1/κ that we investigated above, these contributions to HNN(r) are accordingly substantial. Such solvent-dominated contributions are given by Yukawa functions with screening parameters κν that satisfy eqn (78) and each mode yields terms in HNN(r), HNQ(r) and HQQ(r) with the same decay length. As we saw from the examples in the Introduction, for dilute electrolyte solutions at least one pair of these screening parameters is complex-valued and gives rise to an oscillatory component of the correlation functions that reflects the structure of the molecular solvent.
In the limit of zero electrolyte concentration, the screened Coulomb potential decays as ϕCoul*(r) ∼ 1/(4πε0εrr) which originates from the leading term e−κr/(4πε0![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κ)r) when κ → 0. However, the solvent-dominated decay modes make ϕCoul*(r) oscillatory for small to intermediate r values as discussed in more detail for aqueous systems in ref. 29. These oscillations dominate in ϕCoul*(r) for pure water up to quite large r values where 1/r tail eventually takes over.
effr(κ)r) when κ → 0. However, the solvent-dominated decay modes make ϕCoul*(r) oscillatory for small to intermediate r values as discussed in more detail for aqueous systems in ref. 29. These oscillations dominate in ϕCoul*(r) for pure water up to quite large r values where 1/r tail eventually takes over.
At higher concentrations of electrolyte, one cannot clearly distinguish between contributions to the correlation functions that are solvent-dominated and those that are electrolyte-dominated because there is an intricate coupling between the different constituents of the solution. In all cases there are several decay modes with different screening parameters that are simultaneously present.
5 Summary and concluding remarks
In this section we will give an overview of the key results and also give some perspectives on their usage in experimental and theoretical investigations.Perhaps the most important finding in this work is the fact that all decay modes in electrolytes, with the exception of charge-inversion invariant electrolyte systems, are governed by the dielectric response and that the decay lengths hence are determined by the parameters κν that are solutions to eqn (5), which are the screening parameters for the electrostatic potential. Accordingly, all decay modes of the pair potential of mean force wij for the particles are the same as for the screened Coulomb potential ϕCoul*(r); the latter modes are shown explicitly in eqn (86). This applies for both the monotonic and the oscillatory exponential modes, including those that are dominated by “packing” of molecules in dense liquids. It also applies to the long-range monotonic modes at high ionic densities and the long-range density–density correlations on approach of criticality (but not at the critical point itself). All these facts are a consequence of the coupling between fluctuations in charge density and fluctuations in number density.
Another very significant result is that each decay mode has its own value of the effective relative dielectric permittivity ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κν), which determines the magnitude of the mode's contribution to ϕCoul*(r) [eqn (86)] and, for oscillatory modes, determines also the phase.
effr(κν), which determines the magnitude of the mode's contribution to ϕCoul*(r) [eqn (86)] and, for oscillatory modes, determines also the phase. ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κν) is the physical entity for electrostatic interactions in electrolytes that corresponds to the dielectric constant εr for pure polar fluids and other nonelectrolytes. In contrast to εr it is not given by the infinite wavelength dielectric response (k → ∞) and does not solely contain the dipolar orientational dielectric polarization. As discussed in more detail in ref. 31, the values of the effective dielectric permittivities result from all kinds of polarizations: orientational polarizations (dipolar, quadrupolar, octupolar etc.) and from changes in ion distributions, including transient aggregate formations like ion pairing. The value of
effr(κν) is the physical entity for electrostatic interactions in electrolytes that corresponds to the dielectric constant εr for pure polar fluids and other nonelectrolytes. In contrast to εr it is not given by the infinite wavelength dielectric response (k → ∞) and does not solely contain the dipolar orientational dielectric polarization. As discussed in more detail in ref. 31, the values of the effective dielectric permittivities result from all kinds of polarizations: orientational polarizations (dipolar, quadrupolar, octupolar etc.) and from changes in ion distributions, including transient aggregate formations like ion pairing. The value of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κν) reflects the polarization response of the electrolyte to an exponentially decaying disturbance with decay parameter κν.
effr(κν) reflects the polarization response of the electrolyte to an exponentially decaying disturbance with decay parameter κν.
Furthermore, the dielectric factor ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κν) that appears in the expression for the screening parameter κν, eqn (5), has different values for the various modes. As we have seen,
r*(κν) that appears in the expression for the screening parameter κν, eqn (5), has different values for the various modes. As we have seen, ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κν) replaces the dielectric constant εr that appears in the expression for the Debye parameter κD [eqn (1)]. It is not correct to use a dielectric permittivity obtained from the dielectric polarization response at infinite wavelength instead of
r*(κν) replaces the dielectric constant εr that appears in the expression for the Debye parameter κD [eqn (1)]. It is not correct to use a dielectric permittivity obtained from the dielectric polarization response at infinite wavelength instead of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr(κν) and
effr(κν) and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κν), except possibly as an approximation for modes with long decay lengths. Thus, when κν is not close to zero, one cannot use experimental “dielectric constants” for electrolytes evaluated macroscopically at k = 0 from measurements at low frequencies. Furthermore, theoretical estimates of such dielectric constants based on dipolar polarizations including the effect of ions on dipolar orientations are clearly inadequate, since they leave out the polarization from changes in ion distributions and multipole orientations.
r*(κν), except possibly as an approximation for modes with long decay lengths. Thus, when κν is not close to zero, one cannot use experimental “dielectric constants” for electrolytes evaluated macroscopically at k = 0 from measurements at low frequencies. Furthermore, theoretical estimates of such dielectric constants based on dipolar polarizations including the effect of ions on dipolar orientations are clearly inadequate, since they leave out the polarization from changes in ion distributions and multipole orientations.
It is shown in Section 4.1 that the decay modes of hij and wij are determined by the screened electrostatic pair interaction welij, which is a part of wij. The entity welij is equal to the electrostatic interaction energy of the dressed particles of species i and j (with charge densities ρi* and ρj*) as mediated by the screened Coulomb potential ϕCoul*(r) [eqn (103) and (104)], that is, welij = ρi* ⊛ ϕCoul* ⊛ ρj*, where ⊛ denotes a convolution integral. Alternatively this can be expressed as follows: welij is equal to the interaction energy between the mean electrostatic potential ψi due to the particle of species i and the charge distribution ρj* of a dressed particle of species j (or vice versa). Thereby we have used the fact that ψi = ρi* ⊛ ϕCoul*, that is, ψi is obtained via Coulomb's law for the screened potential, eqn (60), where ρi* is the source for ψi.
The screened Coulomb potential ϕCoul*(r) is a Green's function that describes the spatial propagation of electrostatic interactions in electrolytes. It is closely related to the dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k); in Fourier space we have
(k); in Fourier space we have ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) =
Coul*(k) = ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k)/
Coul(k)/![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), where
(k), where ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul(k) = 1/(ε0k2) is the Fourier transform of the ordinary unscreened Coulomb potential ϕCoul(r). The decay modes of ϕCoul*(r) are given by the poles of
Coul(k) = 1/(ε0k2) is the Fourier transform of the ordinary unscreened Coulomb potential ϕCoul(r). The decay modes of ϕCoul*(r) are given by the poles of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) in complex k-space, i.e., the zeros of
Coul*(k) in complex k-space, i.e., the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), whereby the screening parameter κ satisfies
(k), whereby the screening parameter κ satisfies ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0, where the imaginary unit i appears because the dielectric response is evaluated for an exponentially decaying field. The condition
(iκ) = 0, where the imaginary unit i appears because the dielectric response is evaluated for an exponentially decaying field. The condition ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0 is equivalent to the general exact equation for the screening parameter, eqn (5).
(iκ) = 0 is equivalent to the general exact equation for the screening parameter, eqn (5).
In analyses of experimental measurements of interparticle interactions in electrolytes, including surface force measurements, it is important to realize the existence of the various decay modes with different values of the screening parameter κν. It is therefore suitable to analyze the data using several decay modes with various decay lengths and, when appropriate, wavelengths. Thereby, the various modes may dominate in different distance intervals.
In both experimental and theoretical work, one can make curve fits to force curves and similar data plots on a log scale in order to find the decay lengths and the wavelengths. In cases where the decay modes have quite different decay lengths, it should be feasible to identify the modes, but if, say, two modes have nearly the same decay lengths, it is in general difficult to distinguish them. It can also be difficult to know if one has determined the functions for sufficiently large distances so the results cover the ultimate decay where the mode with the largest decay length dominates. Furthermore, if the magnitude of a mode is small it may not be possible to detect it.
In theoretical work, including simulations, one should, if practically feasible, solve eqn (5) for the decay parameter or the equivalent equation ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκ) = 0 in order to determine the various κν. One can then also determine modes that are difficult to detect by fitting. For spherical ions, eqn (99) is an option. The solutions should then be compared with the decay parameters obtained by fitting. Thereby, one has two independent ways to determine the decay modes. Ref. 18 gives examples of how this can be done in practice in simulations of electrolytes with spherical ions.
(iκ) = 0 in order to determine the various κν. One can then also determine modes that are difficult to detect by fitting. For spherical ions, eqn (99) is an option. The solutions should then be compared with the decay parameters obtained by fitting. Thereby, one has two independent ways to determine the decay modes. Ref. 18 gives examples of how this can be done in practice in simulations of electrolytes with spherical ions.
For binary electrolytes, in particular, it can be useful to plot κν/κD as a function of, for example, temperature or concentration since this ratio has a simple relationship to qi* and ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) r*(κν), see eqn (81). For spherical ions there is also a simple relationship to the effective ionic charges, see eqn (100).
r*(κν), see eqn (81). For spherical ions there is also a simple relationship to the effective ionic charges, see eqn (100).
A central theme of the present work is the demonstration of the fact that when one deals with the screened electrostatic interactions in electrolytes, it is appropriate and often advantageous to use the concept of a dressed particle instead of the entity composed of the particle together with the entire ion/solvent cloud that surrounds it. This cloud consists of the charge distribution ρi due to excess ions and solvent molecules close to the particle, including the effects of their orientational ordering due to interactions. A dressed particle is the particle together with its dress, which has a charge distribution ρdressi that is different from ρi. The total charge density of the particle and its surrounding cloud is ρtoti = σi + ρi, where σi is the internal charge density of the particle. Likewise, we have ρi* = σi + ρdressi. While the ion/solvent cloud ρi is described by the pair distribution functions gij = hij + 1, the dress ρdressi is described by the distribution functions gij* = hij* + 1 that are related to the former by the simple relationship gij* = gij + βwelij [eqn (112)]. The dressed particle charge qi* that occurs in eqn (5) for the screening parameter is the total charge of ρi*.
The reason why it is appropriate to use dressed particles is apparent already when considering the linear polarization response of the bulk electrolyte due to a weak external electrostatic potential δΨext, as discussed in Section 2. This response can be described microscopically from the point of view of the free energy of interaction for each constituent particle in the fluid (ion, solvent molecule or any other particle). The interactional free energy δWi for a particle of species i is simply equal to the electrostatic interaction energy δWi = ρtoti ⊛ δΨext between δΨext and ρtoti [eqn (16) and (23)]. However, δΨext is the potential from the external charges in the absence of the electrolyte, while the total potential δΨ, which also includes the potential δΨpol from the induced polarization charge density, is the actual potential in the presence of the electrolyte. The latter gives the real situation for the particles in the system and, as shown in Section 3, the free energy δWi is equal to the electrostatic interaction δWi = ρi* ⊛ δΨ between δΨ and ρi* [eqn (41)]. Thus, the use of dressed particles reflects the actual conditions for the particles in the weakly polarized electrolyte.
The strong, nonlinear polarization in the immediate neighborhood of the i-particle, which is due to the interactions between the particle and its surroundings, is included in the dress. The linear part of the electrostatic polarization due to the particle, ρlini, is included in ρtoti but not in ρi*, and we have ρtoti = ρi* + ρlini [eqn (44)]. The contribution from this linear part to the potential of mean force δWi = ρi* ⊛ δΨ is instead included in the factor δΨ via the collective response to the external potential from all particles in the electrolyte.
A similar decomposition in linear and nonlinear parts of the electrostatic polarization due to a particle is done in the calculation of ψivia Coulomb's law. The mean potential ψi can be obtained from ρtoti by using the usual unscreened Coulomb potential, ϕCoul(r) = 1/(4πε0r) in this law [eqn (38)]. As mentioned above, exactly the same potential ψi can alternatively be obtained from ρi* by using ϕCoul*(r) in Coulomb's law [eqn (60)]. The difference is that the linear part of the electrostatic polarization in the latter case is included via ϕCoul*(r), which contains an electrostatic linear response via ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), while in the former case the linear part is included in ρtoti.
(k), while in the former case the linear part is included in ρtoti.
The decay modes of ψi are always the same as those of ϕCoul*(r). The magnitude of each of these decay modes of ψi is proportional to a kind of effective charge Qeffi of the dressed i-particle, which has different values for the different modes, and inversely proportional to ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) effr [eqn (93)]. The values of Qeffi are determined by the projections of ρi* on the various modes, which define Qeffi for each mode [eqn (94)]. For the oscillatory modes there is also a phase shift determined by ρi*. In this case, Qeffi is complex-valued and its absolute value gives the magnitude of the mode and its phase gives the phase shift. It is clear that the concept of dressed particle has a fundamental role since ρi* directly determines the magnitudes and the phase shifts of the modes of ψi. For a nonspherical particle, the effective charge and the phase shift are direction dependent quantities which reflect the anisotropy of the mean potential ψi. The former is therefore denoted as the “multipolar effective charge” [Section 3.2.4].
effr [eqn (93)]. The values of Qeffi are determined by the projections of ρi* on the various modes, which define Qeffi for each mode [eqn (94)]. For the oscillatory modes there is also a phase shift determined by ρi*. In this case, Qeffi is complex-valued and its absolute value gives the magnitude of the mode and its phase gives the phase shift. It is clear that the concept of dressed particle has a fundamental role since ρi* directly determines the magnitudes and the phase shifts of the modes of ψi. For a nonspherical particle, the effective charge and the phase shift are direction dependent quantities which reflect the anisotropy of the mean potential ψi. The former is therefore denoted as the “multipolar effective charge” [Section 3.2.4].
The fundamental role of the dressed particles is further accentuated from their appearance in welij as mentioned earlier and the fact that welij in general determines all decay modes of hij and wij. The magnitude of each decay mode of hij and wij is proportional to the product QeffiQeffj as evaluated for each mode [eqn (116)]. For oscillatory modes the phase shift contains the sum of the phases of Qeffi and Qeffj [eqn (117)].
The correlation functions HNN(r), HNQ(r) and HQQ(r) have in general the same set of decay modes as welij and all three functions therefore have the same decay lengths. Their magnitudes are proportional to a set of prefactors ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN and
effN and ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ that constitute averages of the effective charges of the particles in the electrolyte [eqn (126)]. The modes of HNN(r) are proportional to (
effQ that constitute averages of the effective charges of the particles in the electrolyte [eqn (126)]. The modes of HNN(r) are proportional to (![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN)2, those of HNQ(r) proportional to
effN)2, those of HNQ(r) proportional to ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN
effN![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ and those of HQQ(r) proportional to (
effQ and those of HQQ(r) proportional to (![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ)2 [eqn (127)–(129)].
effQ)2 [eqn (127)–(129)].
For charge-inversion invariant systems, where HNQ(r) is identically equal to zero, the decay modes of HQQ(r) are determined by welij, but those for HNN(r) are different. The latter are instead determined by the correlation functions hij* of the dresses [eqn (122)], so the concept of dressed particles has in this case yet another fundamental role. The decay modes of HNN(r) are here given by the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*, which are different from the poles of
ij*, which are different from the poles of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k). Only in charge-inversion invariant systems there is a strict distinction between “electrostatic dominance” and so-called “core dominance” (in the latter, packing effects dominate), for example in the restricted primitive model.39 The former kind of dominance occurs when HQQ(r) has the longest decay length and the latter when HNN(r) has the longest one.
Coul*(k). Only in charge-inversion invariant systems there is a strict distinction between “electrostatic dominance” and so-called “core dominance” (in the latter, packing effects dominate), for example in the restricted primitive model.39 The former kind of dominance occurs when HQQ(r) has the longest decay length and the latter when HNN(r) has the longest one.
There exist electrolytes that are nearly charge-inversion invariant, for example the NaCl system mentioned in the Introduction and any binary system in the primitive model that have anions and cations of the same valency but with slightly different sizes. For such systems, the conclusions for the main case apply and hij, wij, ϕCoul*(r), HNN(r), HQQ(r) and HNQ(r) have the same set of decay modes. In this case the poles of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) [i.e., zeros of
Coul*(k) [i.e., zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k)] can be divided into two categories depending on what takes place when the system is converted into one that is charge-inversion invariant; in the given primitive model example this happens when the ion sizes are made equal. Each pole in the first category lies close to a pole of
(k)] can be divided into two categories depending on what takes place when the system is converted into one that is charge-inversion invariant; in the given primitive model example this happens when the ion sizes are made equal. Each pole in the first category lies close to a pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and the two poles move towards each other when the system is converted into an invariant one. When the system becomes invariant the pole of
ij* and the two poles move towards each other when the system is converted into an invariant one. When the system becomes invariant the pole of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) vanishes. The decay mode remains but is instead determined by the pole of
Coul*(k) vanishes. The decay mode remains but is instead determined by the pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* for the invariant case. Each pole of
ij* for the invariant case. Each pole of ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) in the second set continues to be such a pole throughout. For the decay modes given by first set of poles |
Coul*(k) in the second set continues to be such a pole throughout. For the decay modes given by first set of poles |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN| ≫ |
effN| ≫ |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ| and
effQ| and ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ becomes zero when the system becomes charge-inversion invariant, while for the second set |
effQ becomes zero when the system becomes charge-inversion invariant, while for the second set |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN| ≪ |
effN| ≪ |![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effQ| and
effQ| and ![[Q with combining macron]](https://www.rsc.org/images/entities/i_char_0051_0304.gif) effN becomes zero for the invariant case. Thereby, the various modes are smoothly changed when the electrolyte is turned into a charge-inversion invariant one.
effN becomes zero for the invariant case. Thereby, the various modes are smoothly changed when the electrolyte is turned into a charge-inversion invariant one.
Conflicts of interest
There are no conflicts to declare.Appendices
A Response due to variation in external electrostatic potential for the nonspherical case
For an inhomogeneous fluid of nonspherical particles Yvon's first equation isand for a bulk fluid perturbed by the weak external potential δvj(R) ≡ δvj(r,ω) this becomes
When the external potential is solely due to the electrostatic potential δΨext(r) we have
and hence we obtain
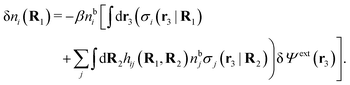 | (130) |
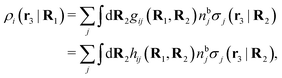 | (131) |
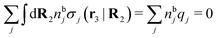 that follows from electroneutrality. Note that
that follows from electroneutrality. Note that  , where σj(r23,ω2) ≡ σj(r3|r2,ω2) for given ω2 is a function of r23 only. Thus we can write eqn (130) as
, where σj(r23,ω2) ≡ σj(r3|r2,ω2) for given ω2 is a function of r23 only. Thus we can write eqn (130) aswhere ρtoti is the total charge density of the particle and its surroundings. The change in charge density, δρ(r4) at a point r4, is hence given by
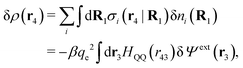 | (132) |
B The HQQ, HNN and HNQ correlation functions
The charge–charge correlation function HQQ is defined as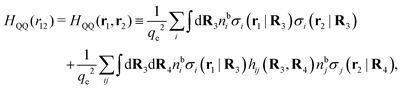 | (133) |
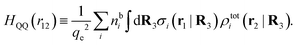 | (134) |
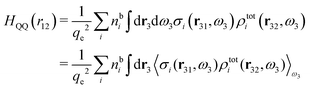 | (135) |
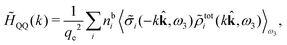 | (136) |
![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) = k/k.
= k/k.
The density–density correlation function HNN is defined as
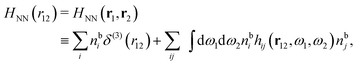 | (137) |
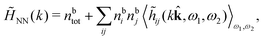 | (138) |
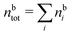 .
.
Finally, the density–charge correlation function HNQ ≡ HQN is defined as
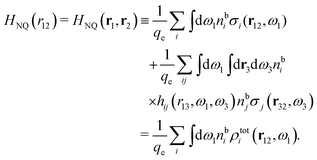 | (139) |
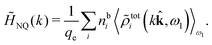 | (140) |
C Relationships between the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0068_0303.gif) ij* and
ij* and ![[h with combining tilde]](https://www.rsc.org/images/entities/h3_i_char_0068_0303.gif) ij
ij
In this appendix we will investigate the relationships between the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij and
ij and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*. In particular we will show that each pole of
ij*. In particular we will show that each pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*(k) in eqn (113) is normally cancelled by a corresponding pole in the last term of this equation. This implies that
ij*(k) in eqn (113) is normally cancelled by a corresponding pole in the last term of this equation. This implies that ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij and
ij and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* cannot have poles for the same k values (apart from some exceptional cases treated in detail in Section 4.2). We will also investigate some cases where poles of
ij* cannot have poles for the same k values (apart from some exceptional cases treated in detail in Section 4.2). We will also investigate some cases where poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* can influence where the poles of
ij* can influence where the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij appear.
ij appear.
The existence of a simple pole for ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* at k = ±iα means that
ij* at k = ±iα means that ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* diverges like
ij* diverges like
![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ij(k
ij(k![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ,ω1,ω2) is a function that is finite at k = ±iα. One can show that
,ω1,ω2) is a function that is finite at k = ±iα. One can show that ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) ij factorizes§§§ at k = iα as
ij factorizes§§§ at k = iα as 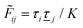 , where τl for l = i, j is a function of orientation for a given α and
, where τl for l = i, j is a function of orientation for a given α and ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) and where K = K(α) is a constant, and we have
and where K = K(α) is a constant, and we have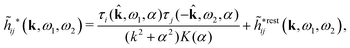 | (141) |
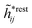 is a part of
is a part of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* that stays finite at k = iα. This means that this pole gives a term in hij* in ordinary space that decays as
ij* that stays finite at k = iα. This means that this pole gives a term in hij* in ordinary space that decays aswhen r → ∞.
The factorization in eqn (141) is crucial for the cancellation of poles as we now will see. The Fourier transform of eqn (111) is given by the first line in the following equation and by inserting eqn (141) we obtain the second line
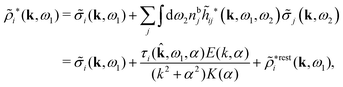 | (142) |
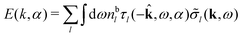 | (143) |
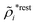 is the part of
is the part of ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i* originating from
i* originating from 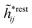 . E(k,α) does not depend on the direction of
. E(k,α) does not depend on the direction of ![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) due to the averaging over ω. The dielectric function
due to the averaging over ω. The dielectric function ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) [given by eqn (50)] can be written as the first line in the following equation and by inserting eqn (142) we obtain the second line
(k) [given by eqn (50)] can be written as the first line in the following equation and by inserting eqn (142) we obtain the second line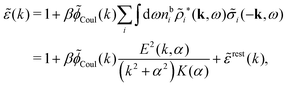 | (144) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) rest is the part of
rest is the part of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) originating from
(k) originating from 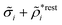 . Since E(k,α)|k=iα is normally nonzero, the functions
. Since E(k,α)|k=iα is normally nonzero, the functions ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*,
ij*, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i* and
i* and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) diverge when k → iα due to k2 + α2 in the denominator. The remaining terms in the expressions stay finite for k = iα.
(k) diverge when k → iα due to k2 + α2 in the denominator. The remaining terms in the expressions stay finite for k = iα.
We now insert eqn (142) and (144) into the last term in eqn (113) and since ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) i*,
i*, ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) j* and
j* and ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) are dominated by the diverging contributions for k values close to iα, it follows that we have when k → iα
(k) are dominated by the diverging contributions for k values close to iα, it follows that we have when k → iα
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* given by the first term on the rhs of eqn (141). This means that provided E(
ij* given by the first term on the rhs of eqn (141). This means that provided E(![[k with combining circumflex]](https://www.rsc.org/images/entities/b_char_006b_0302.gif) ,α) is nonzero, the only poles of the entire rhs of eqn (113) are those that originate from the zeros of
,α) is nonzero, the only poles of the entire rhs of eqn (113) are those that originate from the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) in the denominator.
(k) in the denominator.
Charge-inversion invariant systems, which are treated in Section 4.2, are, however, different. For such systems E(k,α) is identically equal to zero because for each positive contribution on the rhs of eqn (143) there is an equally large negative contribution. Therefore, the pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* at k = iα is not cancelled in
ij* at k = iα is not cancelled in ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij. For other systems it may happen at exceptional points in the system's parameter space that E(k,α)|k=iα fortuitously happens to be equal to zero, which means that the cancellation may not take place at such points. Otherwise the cancellation always occurs and the poles of
ij. For other systems it may happen at exceptional points in the system's parameter space that E(k,α)|k=iα fortuitously happens to be equal to zero, which means that the cancellation may not take place at such points. Otherwise the cancellation always occurs and the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij are given by the zeros of
ij are given by the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k).
(k).
For systems that are close to being charge-inversion invariant, E(k,α) is small but nonzero. Such systems should have properties that are very similar to the corresponding charge-inversion invariant system. For the latter, it is shown in Section 4.2 that the decay parameter values of hij belong to two groups: those that are poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* and those that zeros of
ij* and those that zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k). When the system deviates only slightly from being charge-inversion invariant and all poles of
(k). When the system deviates only slightly from being charge-inversion invariant and all poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij are given by the zeros of
ij are given by the zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k), the former group must have turned into zeros of
(k), the former group must have turned into zeros of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) because the poles of
(k) because the poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* are not poles of
ij* are not poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij. This is indeed the case as we now are going to see.
ij. This is indeed the case as we now are going to see.
When E(k,α) is small but nonzero and ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij* has a pole at k = iα, the function
ij* has a pole at k = iα, the function ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij does not have a pole there, but instead there is, in fact, a pole of
ij does not have a pole there, but instead there is, in fact, a pole of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij close to this k value, that is, there exist a zero of
ij close to this k value, that is, there exist a zero of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) close to k = iα, say, at k = iκν. This can be realized as follows. Since
(k) close to k = iα, say, at k = iκν. This can be realized as follows. Since ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκν) = 0 we obtain from eqn (144)
(iκν) = 0 we obtain from eqn (144)
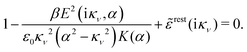 | (145) |
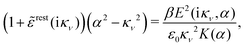 | (146) |
![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) rest(iκν) stays finite there. Likewise, there exist solutions of
rest(iκν) stays finite there. Likewise, there exist solutions of ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (k) = 0 that are connected in the same manner to other poles of
(k) = 0 that are connected in the same manner to other poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*. The remaining solutions κv′ of eqn (146) are not interesting here because in the same limit they go to the solutions of 1 +
ij*. The remaining solutions κv′ of eqn (146) are not interesting here because in the same limit they go to the solutions of 1 + ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) rest(iκν′) = 0, which is the same as
rest(iκν′) = 0, which is the same as ![[small epsilon, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0de.gif) (iκν′) = 0 as seen from eqn (144) with E(k,α) = 0. Thus they belong to the second group mentioned above for charge-inversion invariant systems (these solutions are poles of
(iκν′) = 0 as seen from eqn (144) with E(k,α) = 0. Thus they belong to the second group mentioned above for charge-inversion invariant systems (these solutions are poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) D,AB in eqn (125) and not poles of
D,AB in eqn (125) and not poles of ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*).
ij*).
References
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432 CrossRef CAS PubMed.
- R. M. Espinosa-Marzal, A. Arcifa, A. Rossi and N. D. Spencer, J. Phys. Chem. Lett., 2014, 5, 179 CrossRef CAS PubMed.
- T. Baimpos, B. R. Shrestha, S. Raman and M. Valtiner, Langmuir, 2014, 30, 4322 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157 CrossRef CAS PubMed.
- M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214 RSC.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Faraday Discuss., 2017, 199, 239 RSC.
- N. Hjalmarsson, R. Atkin and M. W. Rutland, Chem. Commun., 2017, 53, 647 RSC.
- A. M. Smith, A. A. Lee and S. Perkin, Phys. Rev. Lett., 2017, 118, 096002 CrossRef PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Phys. Rev. Lett., 2017, 119, 026002 CrossRef PubMed.
- D. G. Hall, Z. Phys. Chem., 1991, 174, 89 CrossRef CAS.
- R. Kjellander, J. Phys. Chem., 1995, 99, 10392 CrossRef CAS.
- R. J. F. Leote de Carvalho and R. Evans, Mol. Phys., 1994, 83, 619 CrossRef.
- J. G. Kirkwood, Chem. Rev., 1936, 19, 275 CrossRef CAS.
- J. G. Kirkwood and J. C. Poirier, J. Phys. Chem., 1954, 58, 591 CrossRef CAS.
- C. W. Outhwaite, Chem. Phys. Lett., 1970, 5, 77 CrossRef CAS.
- C. W. Outhwaite, in Statistical Mechanics: A Specialist Periodical Report, ed. K. Singer, The Chemical Society, London, 1975, vol. 2, p. 188 Search PubMed.
- J. Ulander and R. Kjellander, J. Chem. Phys., 2001, 114, 4893 CrossRef CAS.
- J. Ennis, PhD thesis, Australian National University, 1993.
- J. Ennis, R. Kjellander and D. J. Mitchell, J. Chem. Phys., 1995, 102, 975 CrossRef CAS.
- R. Kjellander and D. J. Mitchell, J. Chem. Phys., 1994, 101, 603 CrossRef CAS.
- D. J. Mitchell and B. W. Ninham, Chem. Phys. Lett., 1978, 53, 397 CrossRef CAS.
- A. M. Smith, P. Maroni, G. Trefalt and M. Borkovec, J. Phys. Chem. B, 2019, 123, 1733 CrossRef CAS PubMed.
- P. Keblinski, J. Eggebrecht, D. Wolf and S. R. Phillpot, J. Chem. Phys., 2000, 113, 282 CrossRef CAS.
- J. Ulander and R. Kjellander, J. Chem. Phys., 1998, 109, 9508 CrossRef CAS.
- G. Stell, J. Stat. Phys., 1995, 78, 197 CrossRef.
- F. Coupette, A. A. Lee and A. Härtel, Phys. Rev. Lett., 2018, 121, 075501 CrossRef CAS PubMed.
- ESI for ref. 27 at http://link.aps.org/supplemental/10.1103/PhysRevLett.121.075501.
- R. Kjellander, J. Chem. Phys., 2018, 148, 193701 CrossRef PubMed.
- R. Kjellander, Phys. Chem. Chem. Phys., 2016, 18, 18985 RSC.
- R. Kjellander, J. Chem. Phys., 2016, 145, 124503 CrossRef PubMed.
- R. Kjellander and D. J. Mitchell, Chem. Phys. Lett., 1992, 200, 76 CrossRef CAS.
- R. Ramirez and R. Kjellander, J. Chem. Phys., 2003, 119, 11380 CrossRef CAS.
- R. Ramirez and R. Kjellander, J. Chem. Phys., 2006, 125, 144110 CrossRef PubMed.
- R. Kjellander and R. Ramirez, J. Phys.: Condens. Matter, 2008, 20, 494209 CrossRef.
- J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic, Amsterdam, 2013 Search PubMed.
- M. Ohba and K. Arakawa, J. Phys. Soc. Jpn., 1981, 50, 743 CrossRef CAS.
- A. Chandra and B. Bagchi, J. Chem. Phys., 1989, 91, 3056 CrossRef.
- P. Attard, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 48, 3604 CrossRef CAS.
Footnotes |
| † Dedicated to the memory of Per Linse, Lund University, Sweden. |
| ‡ As shown in Section 3.2.4, for a binary symmetric electrolyte with ions of equal diameters we have the exact relationship κ2/κD2 = qeff/q [eqn (101)], where qeff is an effective ionic charge and q = q+ = −q−. Using the LPB approximation as a guide for an approximative value of qeff for all ions (i.e., not only for the ion at the origin), we set qeff = qeκd/(1 + κd) and obtain eqn (2); for details see Section 3.2.4. |
| § The general limiting law at high dilution for the decay parameter κ of the leading decay mode is from ref. 21 where zj = qj/qe is the valency of species j and ηj is the stoichiometric coefficient. The term proportional to Λ, which was originally derived in ref. 22, vanishes for symmetric binary electrolytes. Both terms originate solely from the long-range, purely electrostatic correlations, while contributions that depend on other properties of the ions (like their sizes) affect the higher order terms, that here are included in |
| ¶ In the work by Keblinski et al. they use the notation Q(r) and G(r), where Q(r) is proportional to HQQ(r) and the function G(r) − 4nbtot is proportional to HNN(r) [nbtot is the total ion density]. The definitions of HQQ(r) and HNN(r) can be found in Appendix B. |
|| We can, for example, take  where (φ,θ,η) are the Euler angles of the particle or, for a linear molecule, where (φ,θ,η) are the Euler angles of the particle or, for a linear molecule,  since η is redundant in the latter case. since η is redundant in the latter case. |
| ** The formalism has a general validity, but in the presence of nonelectrostatic interactions that decay like a power law (like dispersion interactions) there are terms that are not explicitly included in the asymptotic expressions for large distances obtained in this work; see the comments at the end of Section 4.1. |
| †† In macroscopic electrostatics we have P = ε0χeE in ordinary space, while in the present microscopic case for bulk fluids we have the corresponding relationship in Fourier space. |
| ‡‡ This can be shown by contour integration and residue calculus in complex k-space. |
| §§ This is a consequence of the Stillinger–Lovett second moment condition. |
¶¶ This can be shown by contour integration and residue calculus for ![[small phi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e2.gif) Coul*(k) in complex k-space. Coul*(k) in complex k-space. |
| |||| The higher order terms give singularities in complex Fourier space that are different from simple poles, for instance e−2κr/r2 gives a logarithmic branch point at k = 2iκ. |
| *** At least for low ionic densities, the leading term Yukawa function term in the presence of dispersion interactions is oscillatory with a wavelength that is much larger than the decay length,35 so in practice it appears like monotonic Yukawa functions. |
| ††† A full treatment of the theory that uses and generalizes the approach in Appendix D of ref. 29 will be published in a separate paper. |
| ‡‡‡ The details will be published elsewhere. |
§§§ The factorization is a consequence of a general result for matrices that turn singular at some parameter value because the determinant becomes zero, which in the present case occurs at k = ±iα. In the notation of Appendix D in ref. 29 the matrix H*(k) = {![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) ij*(k,ω1,ω2)} is the solution of the Ornstein–Zernike (OZ) equation (N + NH*N) ★ (N−1 − C*) = 1, where C*(k) = { ij*(k,ω1,ω2)} is the solution of the Ornstein–Zernike (OZ) equation (N + NH*N) ★ (N−1 − C*) = 1, where C*(k) = {![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) ij*(k,ω1,ω2)} is the matrix of the short-range part of the direct correlation function cij* ≡ cij + βuelij, N is the diagonal matrix of the densities nbi and 1 is the unit matrix (note that there is a misprint in ref. 29 for the OZ equation). The inverse matrix (N−1 − C*)−1 = Adj(N−1 − C*)/D*, where Adj denotes the adjugate matrix and D* = Det(N−1 − C*) is the determinant, becomes singular because D* turns zero at k = ±iα. The adjugate matrix can in this situation be factorized at k = ±iα in the manner indicated. These and other matters regarding the direct correlation function approach to the general exact theory will be dealt with in more detail in a forthcoming publication by the author. ij*(k,ω1,ω2)} is the matrix of the short-range part of the direct correlation function cij* ≡ cij + βuelij, N is the diagonal matrix of the densities nbi and 1 is the unit matrix (note that there is a misprint in ref. 29 for the OZ equation). The inverse matrix (N−1 − C*)−1 = Adj(N−1 − C*)/D*, where Adj denotes the adjugate matrix and D* = Det(N−1 − C*) is the determinant, becomes singular because D* turns zero at k = ±iα. The adjugate matrix can in this situation be factorized at k = ±iα in the manner indicated. These and other matters regarding the direct correlation function approach to the general exact theory will be dealt with in more detail in a forthcoming publication by the author. |
| This journal is © The Royal Society of Chemistry 2019 |

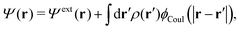
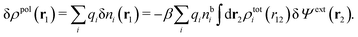
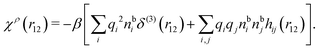
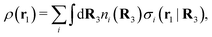
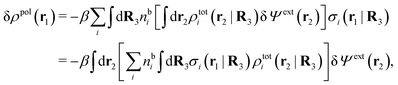
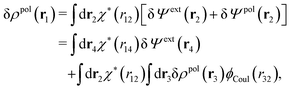
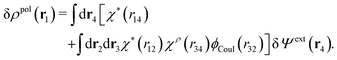
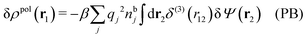
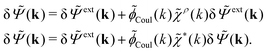
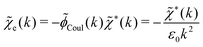
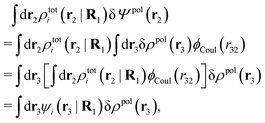
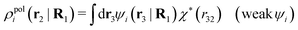
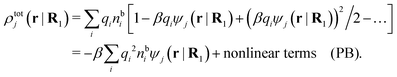
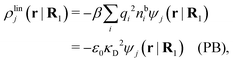
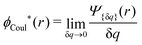
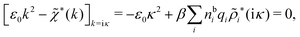
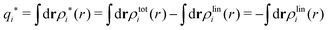
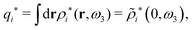
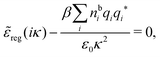

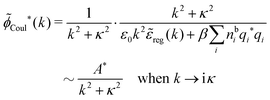
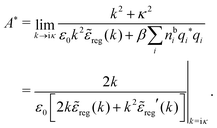
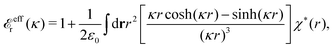
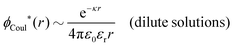
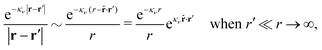
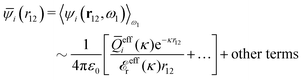
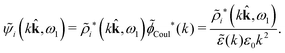
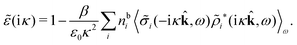
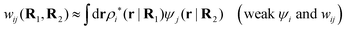
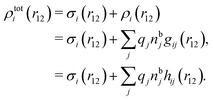
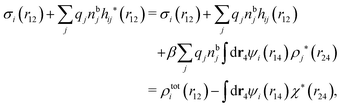
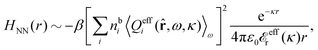
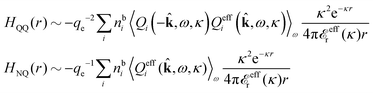
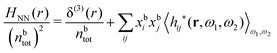
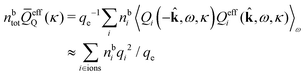
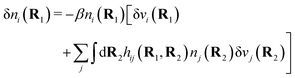
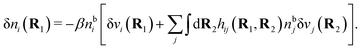
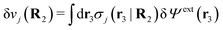
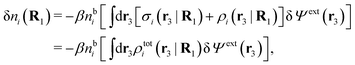
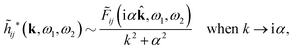
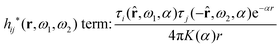
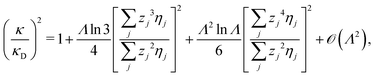
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (
(