Open Access Article
Open Access ArticleUncovering the dynamic precursors to motor-driven contraction of active gels†
José
Alvarado‡
 ab,
Luca
Cipelletti
ab,
Luca
Cipelletti
 *c and
Gijsje H.
Koenderink§
*c and
Gijsje H.
Koenderink§
 *a
*a
aAMOLF, Living Matter Department, 1098 XG Amsterdam, The Netherlands. E-mail: luca.cipelletti@umontpellier.fr; g.h.koenderink@tudelft.nl
bMassachusetts Institute of Technology, Department of Mechanical Engineering, Cambridge, MA 02139, USA
cL2C, Univ. Montpellier, CNRS, Montpellier, France
First published on 22nd October 2019
Abstract
Cells and tissues have the remarkable ability to actively generate the forces required to change their shape. This active mechanical behavior is largely mediated by the actin cytoskeleton, a crosslinked network of actin filaments that is contracted by myosin motors. Experiments and active gel theories have established that the length scale over which gel contraction occurs is governed by a balance between molecular motor activity and crosslink density. By contrast, the dynamics that govern the contractile activity of the cytoskeleton remain poorly understood. Here we investigate the microscopic dynamics of reconstituted actin–myosin networks using simultaneous real-space video microscopy and Fourier-space dynamic light scattering. Light scattering reveals different regimes of microscopic dynamics as a function of sample age. We uncover two dynamical precursors that precede macroscopic gel contraction. One is characterized by a progressive acceleration of stress-induced rearrangements, while the other consists of sudden, heterogeneous rearrangements. Intriguingly, our findings suggest a qualitative analogy between self-driven rupture and collapse of active gels and the delayed rupture of passive gels observed in earlier studies of colloidal gels under external loads.
1. Introduction
Active matter designates a fast-growing research area in soft condensed matter dealing with systems comprised of self-propelled constituents, as opposed to passive materials, for which thermal energy is the only driver of dynamics. Active soft systems are found in living organisms and there is also a growing class of synthetic variants, which are for instance based on self-propelled colloids, molecular motors, or DNA.1 Active gels are a class of active matter systems particularly relevant to biology. Their prototypical example is the cell cytoskeleton: a network of protein filaments that spans the cytoplasm and actively deforms the cell boundaries via pushing and pulling forces.2The major contributor to cell shape changes is the actin cytoskeleton, which generates contractile forces with the help of myosin-II motors.3,4 Myosin-II is a double-headed motor protein that organizes into bipolar filaments, which harness chemical energy derived from ATP hydrolysis to pull pairs of antiparallel actin filaments towards one another.5 Although myosin filaments are only micrometer-sized and exert only pN-level forces, cells spatially integrate the activity of many motors to produce larger contractile forces (∼nN and greater) on cellular length scales.6 The most efficient example of this sort of force integration occurs in striated muscle cells, where contraction occurs on force and length scales that approach the dimensions of the host organism. In this case contraction is mediated by a sarcomeric organization of the actin and myosin filaments into aligned arrays with a regular architecture that promotes efficient force transmission.7 Non-muscle cells lack such an ordered sarcomeric organization. They have a much more dynamic and adaptive actin–myosin cytoskeleton than muscle cells, which allows them to change the length scale over which contractile forces propagate. Myosin motors for instance exert localized pulling forces at the equator of dividing cells8 and in the rear of migrating cells,9 yet they can also generate cell-scale pulling forces to drive cortical polarizing flows in developing oocytes.10 Collectively, cells can even generate contractile forces that drive shape changes of entire tissues in developing embryos and wounded tissues.11
Until now most research on the physical basis of actomyosin contractility has focused on the question of how cells control the length scale on which contraction occurs. Single myosin II motors are non-processive and cannot produce actin filament sliding or contraction.12,13 In cells, they therefore assemble into processive filaments composed of 10–30 tail-to-tail associated myosins.14 These so-called bipolar filaments can slide actin filaments past one another, which can in principle give rise to either a contractile or an extensile force.15,16 Yet, cellular and reconstituted actin–myosin networks are predominantly contractile. Multiple mechanisms have been identified that bias actin networks towards contraction, including actin filament buckling under compressive loading17–20 and motor-driven polarity sorting of actin filaments.21–23 Experiments performed on cells,24,25 cytoplasmic extracts,26,27 and reconstituted actin–myosin gels28–32 furthermore established that the connectivity of the actin network (which depends on actin filament entanglements and actin-binding crosslinkers) tunes the length scale of contraction. Sufficient crosslinking is required to help transmit forces over long distances,32,33 but excess crosslinking can hamper contraction.16,34 Conversely, myosin motors can actively change the network connectivity by driving forced crosslink unbinding and actin filament breakage.19,33,35,36 Altogether, it is now relatively well understood which parameters govern the length scale of contraction. It is known that these length scales interact with other length scales resulting from cell, tissue, and organismal spatial organization, resulting in rich multiscale mechanobiological phenomena.37,38
By contrast, it remains less clear what governs the dynamics of contraction. Several studies have measured the time scale of macroscopic actin–myosin gel contraction, typically by measuring strain or contractile force as a function of time.19,34,39–42 By contrast, quantitative measurements of the microscopic dynamics of contractile networks are relatively scarce. There have been a few microrheology studies that indirectly probed the network dynamics by measuring the fluctuations of embedded probe particles by video microscopy.43–46 Motors were shown to induce non-thermal fluctuations, which evolved with sample age. However, probe particles may potentially locally modify the structure of the gel and they are affected by heterogeneities in the gel structure because their size is comparable to that of the network pores.47–49 Furthermore, microrheology studies were made on networks where macroscopic contraction was prevented by specific biochemical conditions or by pinning to the boundaries. A recent study reported the microscopic dynamics of synthetic active gels, obtained by incorporating self-propelled colloidal particles in a passive network.50 However, this study was restricted to systems with relatively weak activity, such that no insight could be gained on the mechanisms leading to the macroscopic contraction and network rupture that occur in highly contractile actin networks.51,52 Therefore, it currently remains unclear how the microscopic dynamics evolve over time within contractile active gels as they are remodeled over time by motor activity.
Here we address this question by measuring the dynamical behavior of contractile actin–myosin networks with dynamic light scattering (DLS). The main advantage of DLS as compared to microscopy used in previous studies of actin–myosin networks is to decouple the size of the probed sample volume from the resolution with which motion can be detected. In microscopy, the resolution is a fixed fraction of the field of view: to increase the resolution, one has to increase the magnification, thereby decreasing the field of view. In a light scattering experiment, the probed sample volume is set by the size of the illuminating beam, while the length scale over which the dynamics are measured is independently set by choosing the angle at which scattered light is collected. We can thus probe the microscopic dynamics while using a large sample volume, which is important to detect the onset of motor-driven network failure. We use a custom-built setup that allows us to directly correlate the light scattering analysis with the macroscopic contraction dynamics of the gels probed by low-magnification video microscopy. We find that the microscopic dynamics go through several sequential stages as the samples age. The gels initially exhibit simple aging, characterized by a linear relationship between the microscopic relaxation time and the time elapsed since gelation, which is reminiscent of that of glassy and jammed passive soft matter. This is followed by two distinct dynamic precursors of contraction. One precursor manifests itself as apparent rejuvenation, with a slow acceleration of the network-restructuring dynamics before contraction. The other precursor manifests itself as sudden discrete rearrangement events characteristic of heterogeneous dynamics. Simultaneous measurements at several scattering vectors reveal that the dynamics associated to these sudden rearrangements are length-scale independent. Both precursors are measurable long before macroscopic gel contraction occurs, in analogy to the dynamic precursors of macroscopic failure recently unveiled in passive gels subject to a mechanical load.53
2. Results
2.1 Dynamic light scattering of contractile gels
We investigate contractile gels reconstituted from three essential components of the actin cytoskeleton of the cell: purified monomeric actin, myosin motors, and fascin crosslink proteins. This model system was introduced in our earlier work on myosin-driven actin network contraction, where we used time-lapse microscopy to show that the length scale of contraction is set by a balance between the concentrations of the myosin motors that drive contraction and the fascin cross-links that tune network connectivity.33 We initiated contraction by mixing the three proteins in cylindrical cuvettes and warming the system up to room temperature. Upon mixing, actin rapidly polymerizes into a network and the myosin motors contract the gel to a dense cluster in a process that takes many minutes to hours.In order to probe the internal dynamics of the gels during network formation and subsequent contraction, we used dynamic light scattering.54 We illuminated the gels through the side of the cuvette with a laser beam (in vacuo wavelength λ = 532 nm) and detected the scattered light with a charge-coupled device (CCD) placed at an angle θ = 45° (Fig. 1a).55 This angle corresponds to a scattering vector 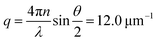 , where n is the refractive index of the solvent. We therefore measured movements of the gel strands on a scale length
, where n is the refractive index of the solvent. We therefore measured movements of the gel strands on a scale length 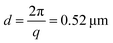 that is comparable to the average mesh size of the actin networks (0.5 μm at an actin concentration of 12 μM56). The detection volume is given by the laser cross-section (1/e2 beam diameter of 1 mm) times the depth of the sample (5 mm). We placed a lens in the light path in order to spatially resolve the scattered light and make a real-space image of the scattering volume47,57 from the top of the sample.
that is comparable to the average mesh size of the actin networks (0.5 μm at an actin concentration of 12 μM56). The detection volume is given by the laser cross-section (1/e2 beam diameter of 1 mm) times the depth of the sample (5 mm). We placed a lens in the light path in order to spatially resolve the scattered light and make a real-space image of the scattering volume47,57 from the top of the sample.
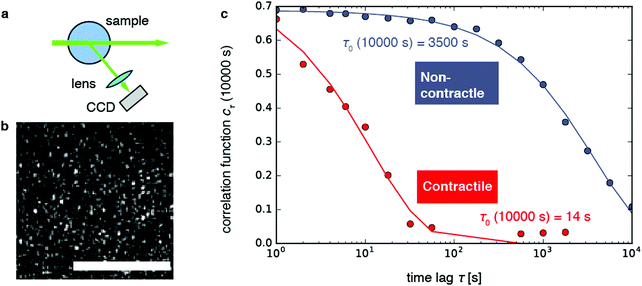 | ||
Fig. 1 Dynamic light scattering measurements on actin gels. (a) Schematic top view of the dynamic light scattering setup. The sample is contained in a cylindrical tube. A laser beam (in vacuo λ = 532 nm) passes through the gel and scattered light is acquired with a CCD camera at a fixed angle of 45° (q = 12.0 μm−1). (b) Crop of a typical speckle pattern recorded by the CCD. Full images contained ca. 500–700 speckles. Scale bar 200 μm. (c) Determination of the relaxation timescale τ0 from the intensity correlation function cτ (here shown at a sample age of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s) as a function of the time lag τ, for a non-contractile sample (grey symbols; sample 1 in Fig. 2) and a contractile sample (red symbols; sample 7 in Fig. 2). Stretched exponential fits (lines) of the data (circles) yield the microscopic relaxation timescale τ0 and stretching exponent. The stretching exponent was comparable for the non-contractile sample (0.72 ± 0.03) and the contractile sample (0.71 ± 0.1) sample, where the error bounds result from the nonlinear fitting algorithm of the data presented in panel c. 000 s) as a function of the time lag τ, for a non-contractile sample (grey symbols; sample 1 in Fig. 2) and a contractile sample (red symbols; sample 7 in Fig. 2). Stretched exponential fits (lines) of the data (circles) yield the microscopic relaxation timescale τ0 and stretching exponent. The stretching exponent was comparable for the non-contractile sample (0.72 ± 0.03) and the contractile sample (0.71 ± 0.1) sample, where the error bounds result from the nonlinear fitting algorithm of the data presented in panel c. | ||
As shown in Fig. 1b, the images appeared as patterns of speckles, with typically ∼600 speckles per image. Each speckle pattern corresponds to a particular microscopic conformation of the sample. If the sample is static, the speckle pattern does not change. By contrast, if the sample is dynamic, the intensity of each speckle fluctuates in time, with a timescale τ0 we will refer to as the relaxation time for gel strand motions. We determined τ0 from time series of speckle images by image correlation. Briefly, we computed the degree of correlation cτ(t) between pairs of images at times t and t + τ, where τ is the time lag (Fig. 1c). We performed this analysis in a reference frame where any mesoscopic drift (e.g. due to contraction) cancels out, by using mixed spatio-temporal correlation functions.47 We fitted the resulting correlation functions cτ(t) to a phenomenological stretched exponential function (lines in Fig. 1c):
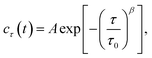 | (1) |
We first examined the relaxation time τ0 for non-contractile samples, which can be obtained with different biochemical conditions (Fig. 2, blue-gray curves). The first non-contractile sample (labeled sample 1 in the figure) is a sample that is passive, because it contains myosin motors and fascin crosslinks but lacks the chemical fuel, adenosine triphosphate (ATP). As shown in Fig. 2, the relaxation time τ0 for this sample monotonically rises with sample age, reaching an apparent steady state value of ∼104 s (2.7 h) after about 4 hours. This long microscopic relaxation time reflects a nearly static gel structure, which is consistent with the formation of a predominantly elastic polymer network. The time scale of 4 h over which the relaxation time evolves is significantly longer than observed in rheological measurements of polymerizing actin networks, which showed that the shear modulus requires ∼1 h to reach a steady-state value.63 However, it is likely that dynamic light scattering is more sensitive to residual rearrangements of the network that are too small-scale to significantly change the macroscopic modulus. Indeed, similar long durations of sample aging have been reported in prior dynamic light scattering studies of passive actin networks containing cross-linkers but no motors.64
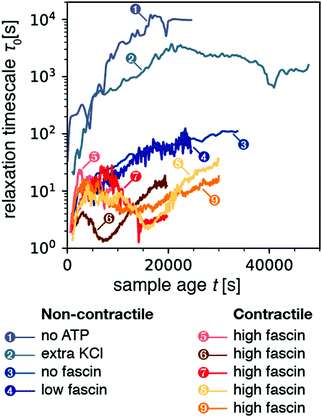 | ||
| Fig. 2 Temporal evolution of the microscopic relaxation time τ0 for all nine samples presented in this study (all with q = 12.0 μm−1). Samples 1–4 correspond to non-contractile samples, where sample 1 is a passive sample (no ATP) while samples 2–4 are active (0.1 mM ATP) but nevertheless non-contractile. Samples 5–9 are active and made contractile by the addition of extra fascin compared to sample 4. The relaxation time was obtained by fitting correlation functions averaged over a time bin of size Δt = 50 s for samples 1–3, and 10 s for samples 4–9. As a result, the data for samples 4–9 appear noisier. The corresponding stretching exponent β from the stretched exponential fit is plotted in Fig. S1 (ESI†). | ||
We next examined three samples that were active, but nevertheless non-contractile (samples 2–4). We first consider sample 2, which contains extra monovalent salt (150 mM KCl instead of the standard concentration of 50 mM). High ionic strengths are known to weaken motor activity because the motors form shorter, less processive filaments65–67 and the binding affinity of the motor heads for actin is weakened.68,69 As shown in Fig. 2, this sample again exhibited a monotonic increase of the relaxation time τ0 over a period of several hours (5.6 h) before reaching an apparent steady-state. However, the value of τ0 in steady-state was now 2000 s, 5-fold lower than for the passive (no-ATP) sample. We suspect that this difference arises because the motors in the presence of ATP and high KCl bind weakly, whereas myosin in the absence of ATP binds strongly in a so-called rigor state. We next examined two non-contractile samples at the standard low-salt conditions (50 mM KCl), where the myosin motors were highly processive, but contraction was prevented by using crosslink (fascin) densities below the connectivity percolation threshold required for macroscopic contraction.33 Both at zero (sample 3) and at low (0.24 μM; sample 4) fascin concentration, the active samples exhibited a monotonic rise of the relaxation time over a period of ∼2.7 hours to a final value τ0 ≈ 102 s. This relaxation time was about a 100-fold lower than for the passive (no ATP) and the active high KCl sample, perhaps due to the higher motor processivity. We conclude that motor activity clearly results in enhanced microscopic dynamics, as evidenced by a decrease in the relaxation timescale τ0 of active samples as compared to that of passive samples.
We now consider contractile samples (red curves in Fig. 2, corresponding to 5 experiments labeled as samples 5–9), which are all prepared with a fascin concentration (0.6 μM) that exceeds the threshold required for macroscopic contraction.33 All five contractile samples exhibited relatively small relaxation timescales in the range τ0 ≈ 1–30 s. The average value of τ0 for the contracting samples was 9.2 ± 2.4 s (computed by averaging τ0 over sample age for each sample, and then averaging over all contractile samples). This value is lower than the average τ0 of 1506 ± 1697 s for the non-contracting samples. Values of relaxation time for non-contracting samples spanned three orders of magnitude, resulting in a large standard deviation which frustrates the T-test (p = 0.2). However, the non-parametric Mann-Whitney U test confirmed that the two populations of time-averaged mean relaxation times between contractile and non-contractile samples were significantly different (p = 0.01). Interestingly, the relaxation time scales we observe for contractile samples are consistent with the time scale of motor-induced active fluctuations observed in microrheology studies, which were in the frequency range of 0.1–10 Hz.43,70 Moreover, in contrast with the noncontractile samples, the contractile samples exhibited a non-monotonic time course of τ0: initially τ0 increased, it reached a peak, decreased, and finally increased again (see Section 2.5).
Finally, we turn our attention to the stretching exponent. Fig. S1 (ESI†) shows the stretching exponent β as a function of sample age t for all nine samples. The non-contracting samples (blue-gray curves) exhibited exponents generally constrained in the range 0.25–1, though we observed peaks that briefly exceeded 1 at late sample ages. Meanwhile the contractile samples (orange-red curves) exhibited values of β that were above one. We computed the mean β for each sample's time-course and averaged across samples to obtain a stretching exponent of 0.67 ± 0.24 for non-contracting samples, and 1.13 ± 0.04 for contractile samples (p = 0.04 by T-test). As mentioned above, values of β > 1 are generally attributed to non-diffusive dynamics associated with internal stress relaxation.60 The higher value of the stretching exponent for the contractile samples as compared to that of the non-contracting gels suggests that larger internal stresses develop in the former, presumably due to the motor activity.
2.2 Dynamic light scattering of contractile gels
In order to study the effect of myosin contractility on the gel relaxation dynamics more closely, we measured light scattering of one of the contractile gels (sample 5) at different scattering angles. To this end, we detected the scattered light with four charge-coupled devices (CCDs) placed at angles θ = 22.5°, 45°, 90°, and 120° (Fig. 3a), which correspond to scattering vectors and corresponding length scales d = 1.0, 0.52, 0.28, and 0.23 μm. As shown in Fig. 3b, the relaxation time τ0 evolves with sample age differently at different wave vectors: it appears to fluctuate around a constant value of 5–15 s for the two larger scattering vectors (green and yellow curves), whereas it exhibits a non-monotonic behavior with two sudden drops at t ≈ 3100 s and t ≈ 7500 s for the two smaller scattering vectors (blue and purple curves). This non-monotonic behavior is in contrast to the nearly monotonic aging seen in Fig. 2 for the non-contractile samples.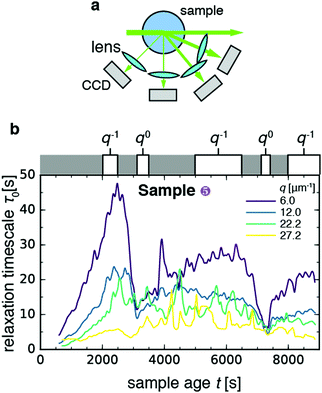 | ||
| Fig. 3 Length scale dependence of the evolution of the microscopic dynamics of contractile sample 5 with sample age. (a) Schematic top view of the dynamic light scattering setup, where scattered light is acquired at four different angles corresponding to scattering vectors q = 6.0, 12.0, 22.2, 27.2 μm−1. (b) Time course of the relaxation time τ0 for the four scattering vectors (see legend). White boxes on top of the graph denote time intervals over which τ0vs. q data were pooled and fitted to a power-law, with an approximate indication of the power-law exponent in each time interval (for details see Fig. S2, ESI†). Bin size Δt = 10 s. | ||
In order to investigate the age-dependent dynamics further, we selected five windows of sample age and performed power-law fits to the q-dependence of the relaxation time (Fig. S2, ESI†), according to the functional form τ0 ∼ qν. The value of the exponent ν can be used to determine whether the network strands move diffusively (ν = −2), ballistically (ν = −1), or with no dependence on the probed length scale (ν = 0). Diffusive dynamics have been observed in passive gels and have been assigned to rapid thermal fluctuations of gel strands.58 Ballistic dynamics have been reported in a wide variety of transiently crosslinked passive gels, including both colloidal gels61 and (bio)polymer gels (see e.g.ref. 64). Ballistic dynamics has been attributed to network remodeling driven by the relaxation of internal stresses, stored in the sample upon gelation.61 Length scale-independent dynamics (ν = 0) have been reported in soft systems with heterogeneous dynamics, such as a coarsening foam,71 and correspond to sudden rearrangement events that fully decorrelate the contribution of photons scattered by the region where the decorrelation event occurs. For the contractile gel, we found that the scaling exponent ν depended on the sample age window over which we measured. During the two drops of τ0, we found q0 scaling indicative of sudden rearrangement events on scales exceeding 1 μm, the largest length scale probed by our experiment. In the intervening time windows, we found ν in the range −0.7 to −1, consistent with the q−1 scaling expected in case of ballistic motion.
A possible explanation for the sudden rearrangement events could be contraction of the entire gel. To test this idea, we plotted the intensity I of speckles in the image plane normalized by the initial average intensity I0. As shown in Fig. S3 (ESI†), the normalized intensity initially fluctuates about a constant value of 1.0–1.4 for all four q-values. Beyond a sample age of ca. 6000 s, the intensity begins to increase towards values of 1.7–2.4. This rise can either be due to densification as a result of macroscopic contraction, or to local remodeling of the gel such that it accommodates more density inhomogeneities at the length scale probed by the scattering experiment. It was shown in earlier high-resolution fluorescence microscopy studies of contractile gels that motors tend to organize actin filaments into dense foci with sizes in the range of 2–20 μm, comprised of a myosin core and actin coat.15,17,33 We note that the increase of the scattering intensity is highest for the lowest q. This indicates the formation of large clusters of material, since these efficiently scatter light at low q. It is therefore indeed likely that contraction occurred, as expected from our prior confocal microscopy of these gels that showed that macroscopic contraction should occur for the myosin and fascin concentrations used.33 However, we cannot be entirely certain because we could not observe the gel in real space during this experiment. In order to determine directly whether and how contraction occurs, we therefore turned back to the light scattering measurements performed at a single scattering angle (samples 6–9 in Fig. 2), since this geometry allowed us to perform simultaneous real-space video imaging.
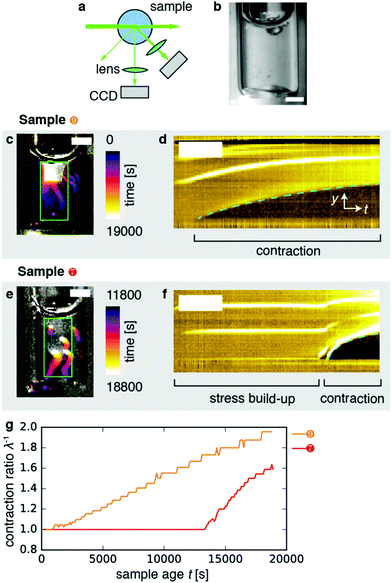
2.3 Macroscopic dynamics probed by real-space video imaging
To perform real-space imaging combined with DLS (Fig. 4a), we combined detection of Fourier-space scattering with a CCD camera positioned at 45° with detection of real-space images with another CCD at 90° (Fig. 4b). Both laser light and white light were used to illuminate the sample. Real-space imaging confirmed that the samples contracted, as exemplified in Fig. 4c showing a time-projection of a movie recorded over a period of 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s for sample 9 (Movie 1, right). The kymograph (y–t projection) representation of the data in Fig. 4d clearly shows that contraction began after an induction time of ∼2000 s from the bottom surface, and proceeded upward. In this case, the gel appeared to be anchored only to its upper interface with air. Samples 6 and 8 similarly contracted shortly after sample preparation (Movie 1; left, and second from right, respectively). By contrast, Fig. 4e depicts the contraction event of sample 7 (cf. Movie 1, second from left). Here, the contraction event exhibited a long induction time of ∼12
000 s for sample 9 (Movie 1, right). The kymograph (y–t projection) representation of the data in Fig. 4d clearly shows that contraction began after an induction time of ∼2000 s from the bottom surface, and proceeded upward. In this case, the gel appeared to be anchored only to its upper interface with air. Samples 6 and 8 similarly contracted shortly after sample preparation (Movie 1; left, and second from right, respectively). By contrast, Fig. 4e depicts the contraction event of sample 7 (cf. Movie 1, second from left). Here, the contraction event exhibited a long induction time of ∼12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s (Fig. 4f). In the moments before the contraction event, the gel appeared macroscopically undeformed. However, stresses had evidently built up across the gel before contraction set in, as evidenced by the rapid deformation that occurred in the initial moments of the contraction event. This particular gel appeared to be anchored both to the top and bottom surfaces, which may potentially account for the long induction time we observed compared to the 3 samples that were anchored only at the top. Note that we do not have experimental control of boundary adhesion or contraction induction time in our experiments.
000 s (Fig. 4f). In the moments before the contraction event, the gel appeared macroscopically undeformed. However, stresses had evidently built up across the gel before contraction set in, as evidenced by the rapid deformation that occurred in the initial moments of the contraction event. This particular gel appeared to be anchored both to the top and bottom surfaces, which may potentially account for the long induction time we observed compared to the 3 samples that were anchored only at the top. Note that we do not have experimental control of boundary adhesion or contraction induction time in our experiments.
In order to quantify the macroscopic deformation of the gels, we computed the contraction ratio 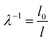 (which is the inverse of the elongation ratio λ), where l is the instantaneous gel length and l0 the initial length, both obtained from the thresholded y–t projections (Fig. 4d and f). As contraction proceeded, the contraction ratio increased from 1 to values close to 2 (Fig. 4g), indicating volume changes of up to ≈8-fold, assuming isotropic contraction. The slope of the contraction ratio vs. time plot gives the contraction rate, which was nearly threefold higher for sample 7 with delayed contraction (17 × 10−5 s−1, red curve) than for sample 9 (6 × 10−5 s−1, orange curve, see additional data in Fig. S4, ESI†). In dimensional units, these rates correspond to velocities in the 0.01 to 0.1 μm s−1 range, depending on the position in the network.
(which is the inverse of the elongation ratio λ), where l is the instantaneous gel length and l0 the initial length, both obtained from the thresholded y–t projections (Fig. 4d and f). As contraction proceeded, the contraction ratio increased from 1 to values close to 2 (Fig. 4g), indicating volume changes of up to ≈8-fold, assuming isotropic contraction. The slope of the contraction ratio vs. time plot gives the contraction rate, which was nearly threefold higher for sample 7 with delayed contraction (17 × 10−5 s−1, red curve) than for sample 9 (6 × 10−5 s−1, orange curve, see additional data in Fig. S4, ESI†). In dimensional units, these rates correspond to velocities in the 0.01 to 0.1 μm s−1 range, depending on the position in the network.
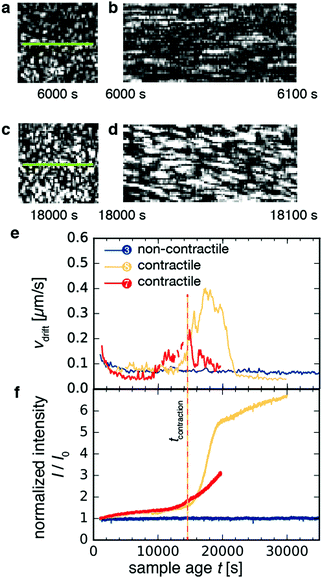
2.4 Microscopic signatures of network contraction in dynamics probed by space-resolved dynamic light scattering
As shown in Fig. 5a–d for sample 8, macroscopic contraction was sometimes accompanied by a systematic drift of the speckles, indicative of drift in the sample parallel to the imaged plane. Using mixed spatio-temporal intensity correlation functions as detailed in ref. 47, we were able to measure the drift velocity vdrift. Fig. 5e shows the time-course of vdrift for three different samples. For non-contractile sample 1, which contained motors and ATP but no crosslink protein (blue curve), we found a flat curve with small fluctuations around an average baseline value of ∼0.05–0.1 μm s−1, which corresponds to spurious drift due to noise measured by the algorithm. By contrast, for the contractile samples 7 and 8 (red and orange curves, respectively), the curves began and ended at the same baseline values as for the non-contractile sample but exhibited peaks with a maximum drift velocity of ∼0.4 μm s−1 for sample 8 and ∼0.2 μm s−1 for sample 7. These velocities are consistent with the 0.01–0.1 μm s−1 range measured from the y–t projections of the video images in Fig. 4. The drift velocity of all contractile samples is shown in Fig. S5a (ESI†).Macroscopic gel contraction was also accompanied by an increase in the average scattering intensity I of the speckles, as shown in Fig. 5f and Fig. S5b (ESI†), where the average intensity is normalized by the initial average intensity I0. For the non-contractile sample (blue curve), I/I0 fluctuated about a value of 1, consistent with the observation that this sample did not contract and hence its structure was essentially unchanging. By contrast, I/I0 increased gradually from 1 to 1.5 over approximately 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s and then turned up to values of 3–7 for both contractile samples (orange and red curves). These values are in reasonable agreement with the ∼8-fold macroscopic volume change estimated from video. This agreement suggests that at the probed length scale, the contribution from macroscopic contraction dominated over any microstructural changes. The initial, slow increase in intensity may be due to coarsening of the network. Defining the time of contraction tcontraction as the sample age when the normalized scattering intensity exceeds 1.5 (vertical dashed line in Fig. 5f), we find that tcontraction coincides with the peaks in drift velocity in Fig. 5e.
000 s and then turned up to values of 3–7 for both contractile samples (orange and red curves). These values are in reasonable agreement with the ∼8-fold macroscopic volume change estimated from video. This agreement suggests that at the probed length scale, the contribution from macroscopic contraction dominated over any microstructural changes. The initial, slow increase in intensity may be due to coarsening of the network. Defining the time of contraction tcontraction as the sample age when the normalized scattering intensity exceeds 1.5 (vertical dashed line in Fig. 5f), we find that tcontraction coincides with the peaks in drift velocity in Fig. 5e.
It is at first sight surprising that the scattering intensity trajectories of sample 7 (red curve) and sample 8 (orange curve) are similar, even though their macroscopic strain trajectories observed by video microscopy are markedly different (cf.Fig. 4e). This discrepancy may be explained by the fact that contraction propagates as a wave, from the bottom of the sample where the gel detaches, toward the top where the gel is anchored. Because we measure scattering only at the top of the sample, the local measurement of scattering intensity only increases once the contraction wave reaches the measurement volume. Therefore, our definition of tcontraction only captures whether the portion of the sample that is illuminated by the laser is contracting.
2.5 The three stages of a contracting gel
Having characterized the macroscopic contraction dynamics of the samples, we can attempt to interpret the non-monotonic changes in the relaxation time of the contractile samples with sample age that we showed in Fig. 3. For simplicity, Fig. 6a displays the time trajectories for two contractile gels (sample 9, orange; sample 7, red) and one non-contractile gels (blue line). Time trajectories for the other 3 contractile samples, which showed similar behavior, are shown in Fig. S6 (ESI†). The contractile samples displayed a non-monotonic time course for τ0 with sample age that can be broken down into at least three distinct stages, which we label as follows (Fig. 6a):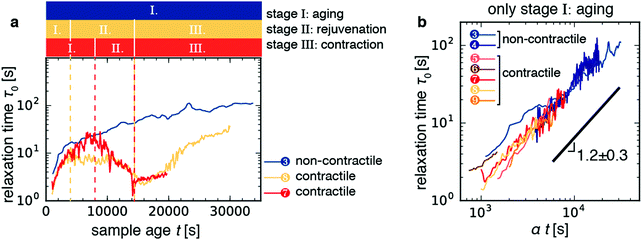 | ||
| Fig. 6 The time evolution of the relaxation time τ0 for active contractile gels can be broken up into three distinct regimes. (a) Time trajectories for the three samples shown in Fig. 5. Colored bars denote the three stages of contractile gel evolution as defined in the main text. Stage I is aging, where τ0 increases with sample age. Stage II is rejuvenation, where τ0 decreases with sample age. Stage III is the contraction stage, where τ0 starts to increase right after contraction begins. The non-contractile gel (sample 3, blue line) does not exhibit rejuvenation nor contraction. (b) Log–log plots of relaxation time τ0 as a function of sample age t during stage I collapse onto a single master curve upon rescaling with a factor α, which varies in the range 0.5–2.0. The black line denotes a power-law with an average best-fit exponent 1.2 ± 0.3. Fits were performed on individual curves and the error bound is given by the standard deviation across the seven samples depicted in panel b. Red-orange lines denote contractile samples; blue lines denote passive and active, but non-contractile, samples (see legend and Table 1). | ||
| Sample | [ATP] (mM) | [KCL] (mM) | [myosin] (nM) | [fascin] (nM) |
|---|---|---|---|---|
| 1 | 0 | 50 | 60 | 600 |
| 2 | 0.1 | 150 | 60 | 600 |
| 3 | 0.1 | 50 | 60 | 0 |
| 4 | 0.1 | 50 | 60 | 240 |
| 5 | 0.1 | 50 | 120 | 600 |
| 6 | 0.1 | 50 | 120 | 600 |
| 7 | 0.1 | 50 | 60 | 600 |
| 8 | 0.1 | 50 | 60 | 600 |
| 9 | 0.1 | 50 | 60 | 600 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s (∼2.8 h) prior (Fig. S6, light orange curve, ESI†). The smooth decrease of τ0 during the rejuvenation stage therefore amounts to a dynamic precursor of macroscopic contraction.
000 s (∼2.8 h) prior (Fig. S6, light orange curve, ESI†). The smooth decrease of τ0 during the rejuvenation stage therefore amounts to a dynamic precursor of macroscopic contraction.
2.6 Contractile gels exhibit discrete stress-driven rearrangements
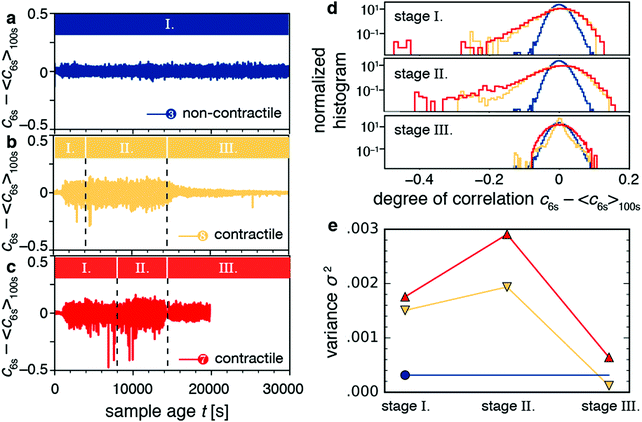
The video data showed that macroscopic contraction only occurred after an induction time, during which stresses apparently built up (Fig. 4e and g). This observation raises the question whether those stored stresses affect the microscopic dynamics. To answer this question, we considered the time dependence of the degree of correlation cτ(t) between speckle images for lag times τ close to the typical relaxation time τ0. In particular, we looked at the fluctuations of the dynamics as quantified by c6s − 〈c6s〉100s, where c6s is the degree of correlation for a lag time τ = 6 s, and 〈·〉100s denotes a temporal average over a 100 s window. We chose the timescale of 6 s to agree roughly with the relaxation time of the contractile samples, and the timescale of 100 s to filter out the long-time evolution of the degree of correlation.For non-contractile samples, we observed fluctuations of the quantity c6s − 〈c6s〉100s around zero, irrespective of sample age, as exemplified in Fig. 7a for sample 3 (an active sample that contains motors but no fascin crosslinkers). We attribute these fluctuations to statistical noise stemming from the finite number of speckles in the CCD images.74Fig. 7b and c show c6s − 〈c6s〉100s for contractile samples 7 and 8, respectively. Apart from fluctuations about zero, these samples exhibited occasional dips that indicate discrete decorrelation events. The dips occurred in stages I (aging stage) and II (rejuvenation), but not in stage III (macroscopic contraction). The decorrelation events lasted only 1–10 s, which is probably why they do not significantly affect τ0.
The decorrelation events can also be quantified by considering the histogram of the fluctuation values (Fig. 7d). The histogram for the non-contractile sample (blue curve) has a Gaussian shape and low variance (σ2 = 0.0003), characteristic of temporally homogeneous dynamics and stemming from the statistical noise discussed above.74 By contrast, the contractile samples (orange and red curves) exhibit non-Gaussian distributions indicating temporally heterogeneous dynamics,74–77 with long tails towards negative values characteristic of decorrelation events and with a high variance (σ2 = 0.0015–0.003). The variance of the distribution is indicative of the dynamic susceptibility χ4,74 which is widely used as an indicator of dynamic heterogeneity in glassy systems.78 The variance has the largest values during stages I (aging) and II (rejuvenation) and lowest values in stage III (contraction). We see the non-Gaussian distributions as well as the large variance for contractile samples for different values of the lag time (Fig. S7a and b, ESI†). We also see the same behaviors for contractile samples 5, 6, and 9 (Fig. S8, ESI†). We computed variances across all samples and compared the two populations of non-contracting and contracting gels. The non-contracting samples had an average variance (multiplied by 106) of 261 ± 85. Meanwhile, the contracting samples had 1363 ± 461 for stage 1, 1928 ± 602 for stage 2, and 466 ± 218 for stage 3. Stages 1 and 2 were not distinguishable (p = 0.18). Stages 1 and 2 were significantly different from stage 3 and from the noncontracting samples (p = 0.005 to 0.014). These results show that stress buildup before the onset of macroscopic contraction is accompanied by discrete stress-driven rearrangements.
3. Discussion
To reveal the microscopic dynamics that emerge from the contractile activity of active cytoskeletal gels, we have performed simultaneous real-space video and Fourier-space light-scattering measurement on reconstituted actin networks driven by myosin motors. We found that the active gels show rich microscopic dynamics that evolve with sample age in three distinct stages.We showed that the samples initially age (stage I), as evidenced by a close-to linear increase of the microscopic relaxation time τ0 with sample age (cf.Fig. 6b). This linear dependence demonstrates that active gels exhibit simple aging, even though there are several concurrent processes that influence stress build-up during the aging stage. We anticipate rapid actin polymerization, which occurs at the filament ends on timescales of the order of 1 min.79 The presence of crosslink proteins such as fascin is expected to slow down depolymerization of the actin network to timescales of 1–10 h.80 As soon as the actin filaments are long enough (μm range), they form topological entanglements, which relax via reptation over several hours.81 In addition there is transient binding of fascin crosslink proteins, with a typical dissociation timescale of 0.1 s.64,82,83 Active samples (both contractile and non-contractile) are expected to exhibit motor-induced sliding of actin filaments, which can relieve macroscopic stresses much faster (within seconds) than reptation.84
On the whole, the relaxation times measured for contractile samples were significantly lower than for non-contractile samples. It remains unclear how to interpret this finding in terms of microscopic processes such as the interplay between elastic constraints posed by the crosslinkers and the load-sensitivity of the myosin motor. Computational modelling of active networks, for instance by agent-based simulations, could provide microscopic insights into this question.16,82,85–87
For contractile samples, the aging regime was followed by a rejuvenation stage (stage II) whereas non-contractile samples simply continued to age. We therefore conclude that rejuvenation in the contractile samples is dominated not simply by myosin motor activity (because some non-contractile samples still had active motors), but to the coupling of myosin motor activity to a well-connected network. How microscopic processes such as motor-induced sliding of actin filaments and transient crosslinking by fascin percolate over increasingly larger length scales to produce macroscopic contraction is still not fully understood.
Our study identifies two distinct relaxation mechanisms that characterize a gel's dynamics in the rejuvenation stage of contracting gels. The first mechanism is a continuous relaxation mechanism, characterized by a gradual decrease of τ0 over prolonged periods of up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s before contraction (cf.Fig. 6a and Fig. S6 ESI,† for t < tcontraction). Qualitatively, this behavior is reminiscent of failure precursors observed in passive colloidal gels submitted to a constant shear stress, which also manifested as enhanced microscopic dynamics before macroscopic failure.53 By contrast, the second relaxation mechanism that occurs during the rejuvenation stage and is superposed on the enhanced dynamics is characterized by sudden decorrelation events. These events, which we observed for all 5 contractile samples, are too short to significantly affect τ0 but they show up in the fluctuations of the correlator, defined as c6s − 〈c6s〉100s, where c6s is the degree of correlation for a lag time τ = 6 s, and 〈·〉100s denotes a temporal average over a 100 s window. This quantity showed occasional strong negative peaks as the samples aged (cf.Fig. 7b–d) and had a non-Gaussian distribution (cf.Fig. 7d and Fig. S7a, ESI†).
000 s before contraction (cf.Fig. 6a and Fig. S6 ESI,† for t < tcontraction). Qualitatively, this behavior is reminiscent of failure precursors observed in passive colloidal gels submitted to a constant shear stress, which also manifested as enhanced microscopic dynamics before macroscopic failure.53 By contrast, the second relaxation mechanism that occurs during the rejuvenation stage and is superposed on the enhanced dynamics is characterized by sudden decorrelation events. These events, which we observed for all 5 contractile samples, are too short to significantly affect τ0 but they show up in the fluctuations of the correlator, defined as c6s − 〈c6s〉100s, where c6s is the degree of correlation for a lag time τ = 6 s, and 〈·〉100s denotes a temporal average over a 100 s window. This quantity showed occasional strong negative peaks as the samples aged (cf.Fig. 7b–d) and had a non-Gaussian distribution (cf.Fig. 7d and Fig. S7a, ESI†).
The continuous and sudden relaxation mechanisms mentioned above reflect dynamic precursors to macroscopic contraction. The sudden relaxation mechanism characterized by heterogeneous dynamics likely results from local depinning of contractile actin network from anchoring surfaces as well as local nucleation and propagation of ruptures within the material, events that we also previously identified in experiments employing fluorescence microscopy33 and that were also seen in computational studies of contractile gels.52,88,89 These rupture events likely gradually weaken the network, eventually triggering macroscopic contraction. Prior studies have investigated dynamic precursors to catastrophic failure events across a broad range of systems, including earthquakes,90 avalanches,91 and gels that fracture under the influence of an external mechanical load.53,92 Our findings strongly suggest that similar dynamic precursors occur during motor-induced contraction of active systems that evolve by internal driving. Previous research73,93,94 highlighted the analogy between the microscopic dynamics of biological networks and glassy systems in the regime where the stresses acting on the network are sufficiently small to prevent macroscopic failure. Our findings suggest that this analogy (at least in a qualitative sense) can be extended to active gels undergoing macroscopic failure.
To probe the length scale dependence of the dynamics, we also measured the microscopic dynamics of a typical contraction event simultaneously at different q-vectors (cf.Fig. 3). We found different q-dependencies of the relaxation time τ0 depending on sample age. We measured a scaling exponent of −1 during the aging stage (stage I, window 2000–2500 s) and the contraction stage (stage III, window 8000–9000 s). This exponent is consistent with prior studies of passive systems, including actin networks cross-linked with fascin64 and fractal gels of polystyrene colloids.60,76 The exponent of −1 in these systems was attributed to slow relaxation of internal stress and glassy dynamics. Also during the contraction stage (stage III), we observed ballistic dynamics (ν = −1), consistent with the dynamics in this regime being dominated by macroscopic deformation. During the rejuvenation stage (stage II), the exponent ν was slightly different (−0.7), perhaps due to the continuous and discrete motor-driven relaxation mechanisms mentioned above. These active effects are likely to decrease the magnitude of the exponent due to a crossover effect between the ν = −1 value of regime I and the ν = 0 value observed during major decorrelation events. Moreover, the sample underwent sudden major decorrelation events (at t = 3100 s and t = 7400 s in Fig. 1) during which the scaling exponent ν was close to zero. An exponent of zero signifies that the dynamics are independent of the length scale that is probed. This behavior can be rationalized as the result of discrete, localized rearrangement events that reconfigure the network structure by displacing gel strands over distances larger than the largest length scale probed by our light scattering experiments (>1 μm). Indeed, light scattered by a rearranged region is completely decorrelated at all probed q vectors. Therefore, the decay rate of the correlation functions is identical for all scattering vectors, being only dictated by the rearrangement rate per unit volume.
Length-scale-independent dynamics are quite rare. They have been reported for a shaving cream foam, where they stem from sudden bubble rearrangements resulting from internal stress that builds up during foam coarsening.71 They have also been observed in passive colloidal gels, where they have been attributed to rearrangement events triggered by internal stress resulting from the rapid, disordered gelation process.76 They have furthermore been found in DNA tetravalent networks, where they have been attributed to fluctuations in local elasticity and connectivity.95 In passive gels, length-scale-independent dynamics are difficult to observe, because individual rearrangement events involve displacements comparable to thermally activated fluctuations of the network at fixed connectivity.76 By contrast, these events are clearly seen in the active gels studied here, showing that the stress build-up generated by the motors cause major bond breaking and network remodeling on length scales that are much larger than those corresponding to the thermal fluctuations at fixed network connectivity.
In this study, we combined simultaneous real- and Fourier-space measurements in order to connect the microscopic observations from Fourier space to the macroscopic contraction state of the gel. However, we were not able to also perform simultaneous real-space microscopic measurements in order to observe how the myosin motors and actin filaments interacted. It would be interesting to make a direct comparison to the mechanisms identified in previous microscopy experiments. However, one difficulty is that the gels presented in this study take longer to contract than initially expected. Several studies have quantified the time for a gel to contract, and found timescales ranging from a few minutes up to an hour.28,33 However, the gels in our study took several hours to contract. The reasons for this difference remain elusive. It is may be the case that large gels (∼200 μL in this study) crosslinked with fascin contract slower than large gels crosslinked with filamin (500 μL28) and smaller gels (∼1 μL) crosslinked with fascin.33 However, the dependence of contraction time on crosslink type or system size remains poorly understood. Again, theoretical and numerical models could provide interesting insights into this question.
It would also be interesting to extend our combined real and Fourier space approach to study motor-driven dynamics within cells or tissues.37,38 The small size of cells and tissues unfortunately prohibits light scattering using the setup described here. An interesting alternative could be differential dynamic microscopy, which derives Fourier-space information analogous to that obtained by light scattering from time-lapse imaging data.96,97
4. Conclusion
We investigated the macroscopic and microscopic dynamics of contractile active gels driven by molecular motor activity. We measured the macroscopic state of the gels with time-lapse video imaging, and simultaneously measured the corresponding microscopic dynamics using space- and time-resolved dynamic light scattering. We uncovered three dynamical properties. First, we found that active gels initially exhibit simple aging (stage I). Second, we found that aging is followed by a self-rejuvenation stage (stage II), characterized by a gradual decrease of the relaxation time τ0. Third, we found an increased occurrence of decorrelation events and hence heterogeneous dynamics. These observations point to two separate stress-relaxation mechanisms: a continuous one involving local motor-driven network remodeling and a discrete one involving sudden displacements spanning length scales greater than 1 μm, the largest length scale probed by our setup. We interpret these stress-relaxation mechanisms as dynamic precursors to motor-driven contraction of active gels. Our findings provide a more detailed understanding of the unusual dynamical properties of active gels driven by molecular motors, and suggest an analogy between the self-induced failure of active, contractile networks and that of passive gels subject to an external load.5. Methods
5.1 Protein purification
Monomeric (G−) actin was purchased from Cytoskeleton Inc. as a lyophilized powder and resuspended in water to final buffer conditions of 5 mM Tris–HCl (pH 8.0), 0.2 mM CaCl2, 0.2 mM ATP, 5% (w/v) sucrose and 1% (w/v) dextran. Actin solutions were stored fresh on ice (0 °C) for up to one week. Myosin II was purified from rabbit psoas skeletal muscle according to a published procedure17 and stored at −20 °C in a high-salt storage buffer (25 mM monopotassium phosphate (pH 6.5), 600 mM potassium chloride, 10 mM ethylenediaminetetraacetic acid, 1 mM dithiothreitol) supplemented with 50% w/w glycerol. Creatine phosphate disodium and creatine kinase were purchased from Roche Diagnostics (Indianapolis, IN, USA), all other chemicals from Sigma Aldrich (St. Louis, MO, USA). Magnesium adenosine triphosphate was prepared as a 100 mM stock solution in 10 mM imidazole (pH 7.4) using equimolar amounts of disodium adenosine triphosphate and magnesium chloride. Recombinant mouse fascin was prepared from T7 pGEX E. coli as described98 using a plasmid kindly provided by Scott Hansen and R. Dyche Mullins (UC, San Francisco). Fascin aliquots were snap-frozen and stored at –80 °C in a buffer (20 mM imidazole (pH 7.4), 150 mM potassium chloride, 1 mM dithiothreitol) supplemented with 10% v/v glycerol.5.2 Dynamic light scattering experiments
All buffer solutions were filtered through 0.22 μm filters to remove dust, which may interfere with light scattering measurements. We furthermore degassed the buffers to minimize the occurrence of bubbles. Nevertheless, some contractile samples still developed bubbles over the course of the experiment. Because bubbles scatter light strongly, they interfere with measurements. Our spatially-resolved light scattering setup (see below) is able to detect the presence of bubbles: bubbles are clearly seen as anomalously bright, uniform regions in the speckle images (Movie 2). We therefore visually inspected all data for bubbles, and excluded samples where bubbles were evident.
CCD data acquisition was performed using a variable delay between images, as described previously.99 In brief, we acquired pairs of images: the delay between two pairs of images varied from 5 ms to 1 s using 1/4-order-of-magnitude steps, scaled logarithmically (e.g. 100 ms, 178 ms, 316 ms, 562 ms, 1 s); the delay between subsequent pairs was fixed at 1 s. We cycled through these logarithmically separated pairs of images continuously throughout the entire experiment.99 The acquisition of all CCDs was triggered simultaneously. The image exposure time was 1 ms. The CCD data were processed to correct for dark background and uneven illumination as described previously.74
The CCD images have a speckled appearance, due to the interference between photons scattered by the sample (see Fig. 1a). With time, the speckle pattern drifted, reflecting the local drift motion of the sample, e.g. due to contraction. Additionally, the intensity of each speckle fluctuated as a result of the relative motion of the gel strands contributing to that speckle. We separately quantified the drift velocity and the drift-subtracted dynamics by a mixed spatio-temporal correlation function:47
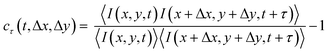 | (2) |
Here, I(x,y,t) is the CCD intensity of a pixel with spatial coordinates (x,y) at time t and 〈⋯〉 denotes an average over a rectangular region of interest (ROI) centered around (x,y). The ROI size was typically 235 × 107 pixels. The correlation function defined in eqn (2) exhibits a peak, whose position yields the drift between times t and t + τ and whose height quantifies the microscopic dynamics in a reference frame co-moving with the local sample drift.47 To simplify the notation, we denote cτ(t,Δx*,Δy*) in the main text simply by cτ(t). For a sample with no drift and stationary dynamics, the t-averaged cτ reduces to the usual intensity correlation function g2(τ) − 1 measured in conventional dynamic light scattering.100
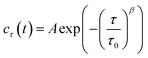 | (3) |
The fit produces three constants: the amplitude A, the stretching exponent β, and the relaxation timescale τ0. Repeating this analysis for different values of the sample age t yielded trajectories τ0(t), which describe the evolution of the microscopic sample dynamics. Performing this analysis for all possible values of t results in a noisy curve. In order to reduce noise, we binned values of cτ(t) into intervals of a certain duration Δt, which we call the bin size, and average within these interval.
5.3 Samples
In this study, we prepared samples with two myosin concentrations. Samples 5–6 had 120 nM myosin, while all other samples had 60 nM. Amongst the contractile samples (5–9), we did not observe a noticeable effect of myosin concentration. However, we did observe that samples 5 and 6 enter the rejuvenation stage more quickly than other samples, as can be seen in Fig. 2. We do not have enough statistics, however, to establish whether the duration of stage I is statistically significantly different for the two populations (samples 5–6 vs. 7–9).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank M. Kuit-Vinkenoog for help with protein purifications, S. Hansen and R.D. Mullins (UCSF, San Francisco, USA) for the fascin plasmid, and T. Divoux for insightful discussions. We gratefully acknowledge financial support from the CNES (LC), a VIDI grant from the Netherlands Organization for Scientific Research (680-47-233) (GHK), and the US Army Research Office under grant number W911NF-14-1-0396 (JA).References
- D. Needleman and Z. Dogic, Nat. Rev. Mater., 2017, 2(9), 17048 CrossRef CAS.
- A. Diz-Muñoz, O. D. Weiner and D. A. Fletcher, Nat. Phys., 2018, 14, 648–652 Search PubMed.
- G. H. Koenderink and E. K. Paluch, Curr. Opin. Cell Biol., 2018, 50, 79–85 CrossRef CAS PubMed.
- M. Murrell, P. W. Oakes, M. Lenz and M. L. Gardel, Nat. Rev. Mol. Cell Biol., 2015, 16, 486–498 CrossRef CAS PubMed.
- A. Houdusse and H. L. Sweeney, Trends Biochem. Sci., 2016, 41, 989–997 CrossRef CAS PubMed.
- P. Roca-Cusachs, V. Conte and X. Trepat, Nat. Cell Biol., 2017, 19, 742–751 CrossRef CAS PubMed.
- M. Gautel and K. Djinovic-Carugo, J. Exp. Biol., 2016, 219, 135–145 CrossRef PubMed.
- F. Spira, S. Cuylen-Haering, S. Mehta, M. Samwer, A. Reversat, A. Verma, R. Oldenbourg, M. Sixt and D. W. Gerlich, eLife, 2017, 6, 983 CrossRef PubMed.
- M. Vicente-Manzanares, J. Zareno, L. Whitmore, C. K. Choi and A. F. Horwitz, J. Cell Biol., 2007, 176, 573–580 CrossRef CAS PubMed.
- M. Mayer, M. Depken, J. S. Bois, F. Jülicher and S. W. Grill, Nature, 2010, 467, 617–621 CrossRef CAS PubMed.
- R. Fernandez-Gonzalez and J. A. Zallen, Mol. Biol. Cell, 2013, 24, 3227–3237 CrossRef CAS PubMed.
- F. Wang, M. Kovács, A. Hu, J. Limouze, E. V. Harvey and J. R. Sellers, J. Biol. Chem., 2003, 278, 27439–27448 CrossRef CAS PubMed.
- M. Kovács, F. Wang, A. Hu, Y. Zhang and J. R. Sellers, J. Biol. Chem., 2003, 278, 38132–38140 CrossRef PubMed.
- X. Liu, N. Billington, S. Shu, S.-H. Yu, G. Piszczek, J. R. Sellers and E. D. Korn, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E6516–E6525 CrossRef CAS PubMed.
- S. Stam, S. L. Freedman, S. Banerjee, K. L. Weirich, A. R. Dinner and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E10037–E10045 CrossRef CAS PubMed.
- J. M. Belmonte, M. Leptin and F. Nedelec, Mol. Syst. Biol., 2017, 13, 941 CrossRef PubMed.
- M. Soares e Silva, M. Depken, B. Stuhrmann, M. Korsten, F. C. Mackintosh and G. H. Koenderink, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 9408–9413 CrossRef PubMed.
- M. Lenz, T. Thoresen, M. Gardel and A. Dinner, Phys. Rev. Lett., 2012, 108, 238107 CrossRef PubMed.
- M. P. Murrell and M. L. Gardel, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 20820–20825 CrossRef CAS PubMed.
- P. Ronceray, C. P. Broedersz and M. Lenz, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 2827–2832 CrossRef CAS PubMed.
- K. Kruse and F. Julicher, Phys. Rev. Lett., 2000, 85, 1778–1781 CrossRef CAS PubMed.
- D. B. Oelz, B. Y. Rubinstein and A. Mogilner, Biophys. J., 2015, 109, 1818–1829 CrossRef CAS PubMed.
- V. Wollrab, R. Thiagarajan, A. Wald, K. Kruse and D. Riveline, Nat. Commun., 2016, 7, 11860 CrossRef CAS PubMed.
- P. Chugh, A. G. Clark, M. B. Smith, D. A. D. Cassani, K. Dierkes, A. Ragab, P. P. Roux, G. Charras, G. Salbreux and E. K. Paluch, Nat. Cell Biol., 2017, 19, 689–697 CrossRef CAS PubMed.
- W. Y. Ding, H. T. Ong, Y. Hara, J. Wongsantichon, Y. Toyama, R. C. Robinson, F. Nedelec and R. Zaidel-Bar, J. Cell Biol., 2017, 216, 1371–1386 CrossRef CAS PubMed.
- M. Malik-Garbi, N. Ierushalmi, S. Jansen, E. Abu-Shah, B. L. Goode, A. Mogilner and K. Keren, Nat. Phys., 2019, 15, 509–516 Search PubMed.
- T. H. Tan, M. Malik-Garbi, E. Abu-Shah, J. Li, A. Sharma, F. C. Mackintosh, K. Keren, C. F. Schmidt and N. Fakhri, Sci. Adv., 2018, 4, eaar2847 Search PubMed.
- L. W. Janson, J. Kolega and D. L. Taylor, J. Cell Biol., 1991, 114, 1005–1015 CrossRef CAS PubMed.
- S. Köhler, V. Schaller and A. R. Bausch, Nat. Mater., 2011, 10, 462–468 CrossRef PubMed.
- Y. Ideses, A. Sonn-Segev, Y. Roichman and A. Bernheim-Groswasser, Soft Matter, 2013, 9, 7127–7137 RSC.
- H. Ennomani, G. Letort, C. Guérin, J.-L. Martiel, W. Cao, F. Nedelec, E. M. De La Cruz, M. Théry and L. Blanchoin, Curr. Biol., 2016, 26, 616–626 CrossRef CAS PubMed.
- Y. Ideses, V. Erukhimovitch, R. Brand, D. Jourdain, J. S. Hernandez, U. R. Gabinet, S. A. Safran, K. Kruse and A. Bernheim-Groswasser, Nat. Commun., 2018, 9, 1–13 CrossRef CAS PubMed.
- J. Alvarado, M. Sheinman, A. Sharma, F. C. MacKintosh and G. Koenderink, Nat. Phys., 2013, 9, 591–597 Search PubMed.
- P. M. Bendix, G. H. Koenderink, D. Cuvelier, Z. Dogic, B. N. Koeleman, W. M. Brieher, C. M. Field, L. Mahadevan and D. A. Weitz, Biophys. J., 2008, 94, 3126–3136 CrossRef CAS PubMed.
- L. Haviv, D. Gillo, F. Backouche and A. Bernheim-Groswasser, J. Mol. Biol., 2008, 375, 325–330 CrossRef CAS PubMed.
- A.-C. Reymann, R. Boujemaa-Paterski, J.-L. Martiel, C. Guerin, W. Cao, H. F. Chin, E. M. De La Cruz, M. Théry and L. Blanchoin, Science, 2012, 336, 1310–1314 CrossRef CAS PubMed.
- M. Mak, T. Kim, M. H. Zaman and R. D. Kamm, ib, 2015, 7, 1093–1108 CAS.
- J. H. Shawky, U. L. Balakrishnan, C. Stuckenholz and L. A. Davidson, Development, 2018, 145, dev161281 CrossRef PubMed.
- H. Wang, A. A. Svoronos, T. Boudou, M. S. Sakar, J. Y. Schell, J. R. Morgan, C. S. Chen and V. B. Shenoy, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20923–20928 CrossRef CAS PubMed.
- P. J. Foster, S. Fürthauer, M. J. Shelley and D. J. Needleman, eLife, 2015, e10837 CrossRef PubMed.
- I. Linsmeier, S. Banerjee, P. W. Oakes, W. Jung, T. Kim and M. P. Murrell, Nat. Commun., 2016, 7, 12615 CrossRef CAS PubMed.
- M. Schuppler, F. C. Keber, M. Kröger and A. R. Bausch, Nat. Commun., 2016, 7, 13120 CrossRef CAS PubMed.
- D. Mizuno, C. Tardin, C. F. Schmidt and F. C. MacKintosh, Science, 2007, 315, 370–373 CrossRef CAS PubMed.
- D. Mizuno, D. A. Head, F. C. MacKintosh and C. F. Schmidt, Macromolecules, 2008, 41, 7194–7202 CrossRef CAS.
- B. Stuhrmann, M. Soares e Silva, M. Depken, F. C. MacKintosh and G. H. Koenderink, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 020901(R) CrossRef PubMed.
- A. Sonn-Segev, A. Bernheim-Groswasser and Y. Roichman, J. Phys.: Condens. Matter, 2017, 29, 163002 CrossRef PubMed.
- L. Cipelletti, G. Brambilla, S. Maccarrone and S. Caroff, Opt. Express, 2013, 21, 22353–22366 CrossRef CAS PubMed.
- J. He and J. Tang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 041902 CrossRef PubMed.
- B. S. Chae and E. M. Furst, Langmuir, 2005, 21, 3084–3089 CrossRef CAS PubMed.
- M. E. Szakasits, W. Zhang and M. J. Solomon, Phys. Rev. Lett., 2017, 119, 058001 CrossRef PubMed.
- M. Sheinman, A. Sharma, J. Alvarado, G. H. Koenderink and F. C. MacKintosh, Phys. Rev. Lett., 2015, 114, 098104 CrossRef CAS PubMed.
- C. F. Lee and G. Pruessner, Phys. Rev. E, 2016, 93, 052414 CrossRef PubMed.
- S. Aime, L. Ramos and L. Cipelletti, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 3587–3592 CrossRef CAS PubMed.
- B. Berne and R. Pecora, Dynamic Light Scattering, 2000.
- D. El Masri, M. Pierno, L. Berthier and L. Cipelletti, J. Phys.: Condens. Matter, 2005, 17, S3543–S3549 CrossRef CAS.
- C. F. Schmidt, M. Baermann, G. Isenberg and E. Sackmann, Macromolecules, 1989, 22, 3638–3649 CrossRef CAS.
- A. Duri, D. Sessoms, V. Trappe and L. Cipelletti, Phys. Rev. Lett., 2009, 102, 085702 CrossRef CAS PubMed.
- A. H. Krall and D. A. Weitz, Phys. Rev. Lett., 1998, 80, 778–781 CrossRef CAS.
- V. P. Privalko, J. Non-Cryst. Solids, 1999, 255, 259–263 CrossRef CAS.
- L. Cipelletti, S. Manley, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 2000, 84, 2275–2278 CrossRef CAS PubMed.
- L. Cipelletti, L. Ramos, S. Manley, E. Pitard, D. A. Weitz, E. E. Pashkovski and M. Johansson, Faraday Discuss., 2003, 123, 237–251 RSC.
- L. Cipelletti and L. Ramos, J. Phys.: Condens. Matter, 2005, 17, R253–R285 CrossRef CAS.
- Y. Tseng, K. M. An and D. Wirtz, J. Biol. Chem., 2002, 277, 18143–18150 CrossRef CAS PubMed.
- O. Lieleg, J. Kayser, G. Brambilla, L. Cipelletti and A. R. Bausch, Nat. Mater., 2011, 10, 236–242 CrossRef CAS PubMed.
- H. Noda and S. Ebashi, Biochim. Biophys. Acta, 1960, 41, 386–392 CrossRef CAS.
- E. Reisler, C. Smith and G. Seegan, J. Mol. Biol., 1980, 143, 129–145 CrossRef CAS PubMed.
- B. Kaminer and A. L. Bell, J. Mol. Biol., 1966, 20, 391–401 CrossRef CAS PubMed.
- B. Brenner, M. Schoenberg, J. M. Chalovich, L. E. Greene and E. Eisenberg, Proc. Natl. Acad. Sci. U. S. A., 1982, 79, 7288–7291 CrossRef CAS PubMed.
- K. Takiguchi, H. Hayashi, E. Kurimoto and S. Higashi-Fujime, J. Biochem., 1990, 107, 671–679 CrossRef CAS PubMed.
- M. Soares e Silva, B. Stuhrmann, T. Betz and G. H. Koenderink, New J. Phys., 2014, 16, 075010 CrossRef.
- D. A. Sessoms, H. Bissig, A. Duri, L. Cipelletti and V. Trappe, Soft Matter, 2010, 6, 3030–3037 RSC.
- E. Vincent, J. Hammann, M. Ocio, J.-P. Bouchaud and L. F. Cugliandolo, in Complex Behavior of Glassy Systems, ed. M. Rubi, Springer Verlag, Berlin, 1997 Search PubMed.
- E. H. Zhou, X. Trepat, C. Y. Park, G. Lenormand, M. N. Oliver, S. M. Mijailovich, C. Hardin, D. A. Weitz, J. P. Butler and J. J. Fredberg, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10632–10637 CrossRef CAS PubMed.
- A. Duri, H. Bissig, V. Trappe and L. Cipelletti, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 051401 CrossRef PubMed.
- L. Cipelletti, H. Bissig, V. Trappe, P. Ballesta and S. Mazoyer, J. Phys.: Condens. Matter, 2002, 15, S257–S262 CrossRef.
- A. Duri and L. Cipelletti, Europhys. Lett., 2006, 76, 972–978 CrossRef CAS.
- M. Bouzid, J. Colombo, L. V. Barbosa and E. Del Gado, Nat. Commun., 2017, 8, 15846 CrossRef CAS PubMed.
- Dynamical Heterogeneities in Glasses, Colloids, and Granular Media, ed. L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti and W. van Saarloos, Oxford University Press, 2011 Search PubMed.
- T. D. Pollard, J. Cell Biol., 1986, 103, 2747–2754 CrossRef CAS PubMed.
- K. M. Schmoller, C. Semmrich and A. R. Bausch, J. Struct. Biol., 2010, 350–357 Search PubMed.
- A. C. Maggs, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1997, 55, 7396–7400 CrossRef CAS.
- T. T. Falzone, M. Lenz, D. R. Kovar and M. L. Gardel, Nat. Commun., 2012, 3, 861 CrossRef PubMed.
- K. M. Schmoller, O. Lieleg and A. R. Bausch, Soft Matter, 2008, 4, 2365–2367 RSC.
- D. Humphrey, C. Duggan, D. Saha, D. Smith and J. Käs, Nature, 2002, 416, 413–416 CrossRef CAS PubMed.
- M. Mak, M. H. Zaman, R. D. Kamm and T. Kim, Nat. Commun., 2016, 7, 10323 CrossRef CAS PubMed.
- S. L. Freedman, G. M. Hocky, S. Banerjee and A. R. Dinner, Soft Matter, 2018, 14, 7740–7747 RSC.
- P. Lang and E. Frey, Nat. Commun., 2018, 9, 494 CrossRef PubMed.
- M. Sheinman, A. Sharma, J. Alvarado, G. H. Koenderink and F. C. MacKintosh, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 012710 CrossRef CAS PubMed.
- Y. Mulla, G. Oliveri, J. T. B. Overvelde and G. H. Koenderink, Phys. Rev. Lett., 2018, 120, 268002 CrossRef PubMed.
- M. Ohnaka, The Physics of Rock Failure and Earthquakes, Cambridge University Press, 2013 Search PubMed.
- I. Reiweger and J. Schweizer, Geophys. Res. Lett., 2010, 37, L24501 CrossRef.
- F. Gobeaux, E. Belamie, G. Mosser, P. Davidson and S. Asnacios, Soft Matter, 2010, 6, 3769–3777 RSC.
- P. Bursac, G. Lenormand, B. Fabry, M. Oliver, D. A. Weitz, V. Viasnoff, J. P. Butler and J. J. Fredberg, Nat. Mater., 2005, 4, 557–561 CrossRef CAS PubMed.
- S. Wang and P. G. Wolynes, J. Chem. Phys., 2013, 138, 12A521 CrossRef PubMed.
- G. Nava, M. Rossi, S. Biffi, F. Sciortino and T. Bellini, Phys. Rev. Lett., 2017, 119, 078002 CrossRef PubMed.
- R. Cerbino and V. Trappe, Phys. Rev. Lett., 2008, 100, 188102 CrossRef PubMed.
- R. Cerbino and P. Cicuta, J. Chem. Phys., 2017, 147, 110901 CrossRef PubMed.
- B. S. Gentry, S. Meulen, P. Noguera, B. Alonso-Latorre, J. Plastino and G. H. Koenderink, Eur. Biophys. J., 2012, 41, 979–990 CrossRef CAS PubMed.
- A. Philippe, S. Aime, V. Roger, R. Jelinek, G. Prévot, L. Berthier and L. Cipelletti, J. Phys.: Condens. Matter, 2016, 28, 075201 CrossRef CAS PubMed.
- B. J. Berne and R. Pecora, Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics, Dover Publications, 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9sm01172b |
| ‡ Current address: University of Texas at Austin, Department of Physics, Austin, TX, 78712, USA. |
| § Current address: Department of Bionanoscience, Kavli Institute of Nanoscience Delft, Delft University of Technology, 2629 HZ Delft, The Netherlands. |
| This journal is © The Royal Society of Chemistry 2019 |