How far does the defect tolerance of lead-halide perovskites range? The example of Bi impurities introducing efficient recombination centers

Abstract

One of the key properties of lead-halide perovskites employed in solar cells is the defect tolerance of the materials, in particular regarding intrinsic point defects, which mainly form shallow traps. Considering that high luminescence yields and photovoltaic performance are obtained by simple solution processing from commercial chemicals, it is commonly anticipated that the defect tolerance – at least to a considerable degree – extends to grain boundaries and extrinsic defects, i.e. impurities, as well. However, the effect of impurities has hardly been investigated. Here, we intentionally introduce small quantities of bismuth (10 ppm to 2%) in solution to be incorporated in the perovskite films based on mixed cation mixed anion compositions. We observe that Bi impurities in the %-regime reduce charge carrier collection efficiency and, more importantly, that the open-circuit voltage decreases systematically with impurity concentration even in the ppm regime. This strong defect intolerance against Bi impurities comes along with reduced electroluminescence yields and charge carrier lifetimes obtained from transient photoluminescence experiments. Calculations based on molecular dynamics and density functional theory predict delocalized (≈0.16 eV) and localized deep (≈0.51 eV) trap states dependent on the structural arrangement of the surrounding atoms. Structural characterization supports the idea of Bi being present as a homogeneously spread point defect, which substitutes the Pb²⁺ by Bi³⁺ as seen from XPS and a reduction of the lattice parameter in XRD. Sensitive measurements of the photocurrent (by FTPS) and surface photovoltage (SPV) confirm the presence of tail states. Photoelectron spectroscopy measurements show evidence of a deep state. These results are consistent with the common idea of shallow traps being responsible for the reduced charge collection efficiency and the decreased fill factor, and deeper traps causing a substantial reduction of the open-circuit voltage. As Bi is only one potential impurity in the precursor salts used in perovskite solar cell fabrication, our findings open-up a research direction focusing on identifying and eliminating impurities that act as recombination centers – a topic that has so far not been fully considered in device optimization studies.

---

Introduction

Perovskite solar cells have progressed in a way that is unprecedented in photovoltaics.^1,2 Within a few years of research, efficiency values comparable to those of other thin film technologies have been obtained. Besides the favorable bandgap of the CH₃NH₃PbI₃ compound,^3–5 high charge carrier extraction efficiencies due to sufficiently high diffusion lengths^6,7 made this development possible. Whereas other materials with similarly suited absorption coefficients and charge carrier mobilities exist such as Cu₂ZnSn(S,Se)₄ kesterites,^8,9 some metal halide perovskites additionally offer exceptionally low non-radiative recombination losses.^10–13 This property allows for a low voltage deficit, whose further reduction is required to approach the maximum theoretical efficiency. This so called Shockley–Queisser limit is characterized by the condition that only radiative recombination prevails as the reciprocal process to absorption.¹⁴ The best state-of-the-art perovskite solar cells (consisting of mixed cation and mixed halide compositions) show a non-radiative voltage deficit of around 120 to 150 meV.^11,12,15,16 These values correspond to luminescence yields in the order of around 1% at open-circuit conditions under solar irradiance. Very recently, non-radiative voltage losses of <100 mV with luminescence yields larger than several percent have been achieved.^17,18

Such low voltage deficit and high luminescence yields are quite astonishing for a thin film of a nano-crystalline material processed from solution and at low temperature. The anticipated defects originating from grain boundaries, crystal imperfections and solvent remnants do apparently not act as effective recombination centers. One reason is that many of the intrinsic point defects form only shallow traps because of the strongly ionic bonds and the antibonding nature of the valence states, as described by density functional theory (DFT) simulations.^19–21 However, deep defects caused e.g. by a dissociation of the methylammonium molecule have also been predicted.²² The role of grain boundaries in recombination is still under lively debate^23–29 and probably depends on which moiety is predominantly terminating the crystallite surface and the respective surface states created. Notably, perovskite films prepared by thermal evaporation show small grains yet deliver high performance.³⁰ Other sources of recombination may also be present. If interfaces to charge transport layers are not perfectly selective to the designated charge carrier, they constitute a source of surface recombination. Therefore, tuning the charge selectivity by employing wide band gap oxides³¹ and organic interlayers³² is essential to maintain the high chemical potential difference, which is photogenerated in the absorber, at the contacts in terms of a high open-circuit voltage (V_OC).

Despite the outstanding achievements, there is still a long way to go towards reaching the radiative efficiency limit considering that still around 99% of recombination in the best devices is non-radiative. One source of such recombination might be recombination centers resulting from impurities introduced during processing or already present in the precursors. The role of these extrinsic defects is almost completely neglected in perovskite solar cell research, because it is anticipated that the defect tolerance^21,33 predicted from several intrinsic defects^19,20,34 extends to extrinsic defects as well. The aim of this work is to question whether this assumption is correct and investigate whether extrinsic defects are the limiting factor of the efficiency of state-of-the-art perovskite solar cells. We, therefore, intentionally introduce and characterize the impact of impurities on device performance by a selected conspicuous deliberate defect.

This approach has not been followed so far except for one study where iron was added.³⁵ Here, we have selected Bi because it is a common byproduct of lead refining and may be an unwanted impurity in many lead salt precursors. We find that, unlike other elements such as Cs, Na, K, Al, Sb, or Co,^36–39 Bi indeed acts as an efficient non-radiative recombination center (as recently found for CH₃NH₃PbBr₃ (ref. 40)) that reduces V_OC even if present in quantities of ppm. The increased recombination is also visible in reduced photo- and electroluminescence yields and charge-carrier lifetimes. For larger quantities of Bi, changes in charge carrier transport properties can be observed. The results of this study show that the metal halide perovskites, even though in general defect tolerant, are not necessarily tolerant against all kind of impurities, even if present in the ppm range.

Experimental methods

Fabrication of perovskite solar cells

Fluorine-doped tin oxide (FTO) glass sheets (Nippon Sheet Glass) were etched with zinc powder and HCl (4 M) to form a detached electrode pattern. Substrates were ultrasonically cleaned by a sequential 15 min 2% Hellmanex water solution, deionized water, ethanol and acetone. Substrates were treated under UV-ozone for 15 min to remove the last traces of organic residues. A 30–50 nm thin compact TiO₂ layer was then deposited on top of the clean pre-heated substrates by spray pyrolysis from a precursor solution of titanium diisopropoxide bis(acetylacetonate) in anhydrous ethanol, using oxygen as the carrier gas on a hot plate set to 450 °C, followed by annealing at 450 °C, for 30 minutes in air. A mesoporous TiO₂ layer was deposited by spin coating for 20 s at 4000 rpm with a ramp of 2000 rpm, using 30 nm particle size paste (Dyesol 30 NR-D) diluted in ethanol to achieve a 200 nm layer thickness (150 mg ml⁻¹). After the spin coating, the substrates were immediately dried at 100 °C for 10 min and then sintered again at 450 °C for 30 min under dry air flow. Li-doping of mesoporous TiO₂ was accomplished by spin coating a 0.1 M solution of lithium bis(trifluoromethanesulfonyl)imide (Li-TFSI) in acetonitrile at 3000 rpm with a ramp of 1000 rpm for 10 s, followed by another sintering step at 450 °C for 30 min. After cooling down to 150 °C, the substrates were immediately transferred to a nitrogen atmosphere glove box for depositing the perovskite films.

The organic monovalent cation salts were purchased from Dyesol; the lead compound from TCI; CsI from abcr GmbH. The perovskite precursor solution contained FAI (1 M), CsI (0.05 M), PbI₂ (1.1 M), MABr (0.2 M) and PbBr₂ (0.22 M) dissolved in anhydrous DMF : DMSO 4 : 1 (v/v) in an argon-filled glovebox. We refer to this mixture as “CsMAFA” throughout the paper. Bi was incorporated by separately preparing Bi(III) iodide (Sigma-Aldrich, 99.99%) solution (0.31 M) in DMF, which was used as the source solution for the 2, 1, 0.5, 0.25, 0.1, 0.01 and 0.001 at% (referred to Pb) samples. The low concentrations were obtained by sequential dilution of the Bi-containing perovskite solutions with Bi-free perovskite solution. The respective perovskite solution was spin-coated in a two-step procedure at 1000 and 6000 rpm for 10 and 20 s, respectively. During the second step, 200 μL of chlorobenzene was poured on the spinning substrate 5 s before the end of the procedure. The substrates were then annealed at 100 °C for 1 h in a dry box.

The hole transport layer was deposited by spin coating (4000 rpm, 30 s) 50 μL of solution prepared by dissolving 72.3 mg (2,2′,7,7′-tetrakis(N,N-di-p-methoxyphenylamine)-9,9-spirobifluorene) (spiro-OMeTAD), 17.5 μL of a stock solution of 520 mg mL⁻¹ bis(trifluoromethylsulphonyl)imide in acetonitrile, and 29 μL of a stock solution of 300 mg mL⁻¹ tris(2-(1H-pyrazol-1-yl)-4-tert-butylpyridine)cobalt(III) bis(trifluoromethylsulphonyl)imide in acetonitrile, and 28.8 μL 4-tert-butylpyridine in 1 mL chlorobenzene.

Finally, the device fabrication was completed by thermally evaporating a 70 nm gold layer as a back contact. All device fabrication was carried out under controlled atmospheric conditions with humidity <2%.

Perovskite solar cell characterization

Solar cell performance was measured using a 450 W xenon light source (Oriel) or a Verasol LED solar simulator. Current–voltage characteristics were obtained by applying an external voltage bias while measuring the current response with a digital source meter (Keithley 2400). The voltage scan rate was 10 mV s⁻¹ if not denoted differently. The cells (with an active area of 0.25 cm²) were masked with a black metal aperture (0.16 cm²).

UV-vis absorption measurements

UV-vis absorption measurements were performed on a PerkinElmer spectrophotometer. The absorbance was approximated from the transmission data of thin films on glass.

Photoluminescence

Photoluminescence was measured using a Fluorolog, Horiba Jobon Yvon, FL-1065. An excitation wavelength of 460 nm was used for all the samples. When comparing non-normalized spectra, all settings such as integration time and wavelength interval were kept constant. The PL decay experiments were performed using the same Fluorolog with a pulsed source at 406 nm (Horiba NanoLED 402-LH; pulse width <200 ps, 11 pJ per pulse, approximately 1 mm² in spot size) at a repetition rate of 50 kHz. The signal was recorded using time correlated single photon counting (TCSPC) by a TBX-04 photomultiplier tube.

Electroluminescence

Electroluminescence was measured by performing a current–voltage sweep using a Biologic SP300 potentiostat and detecting the emitted photon flux on a further channel connected to a photodiode (Hamamatsu S1227-1010BQ) placed in close vicinity of the sample.

Photothermal deflection spectroscopy (PDS) and Fourier transform infrared photocurrent spectroscopy (FTPS)

PDS was measured using an in-house built PDS setup, which is equipped with a halogen lamp. The experimental setup here also allows for the monitoring of the specular transmittance, T_spec and reflectance R_spec. Fluorinert FC-72 solution was used as the inert liquid medium which has a strongly temperature-dependent refractive index of 1.25 at room temperature. It was shown previously that there was no reaction nor detrimental transformation between standard perovskite CH₃NH₃PbI₃ thin-films when immersed in this Fluorinert solution.⁵ PDS absorptance curves were scaled at 3.18 eV with the total absorptance, A, measured with a Perkin-Elmer UV/VIS/NIR Lambda 950 spectrometer using the integrating sphere setup, where A = 1 − (T + R).

FTPS was measured in an in-house built FTPS setup, which consisted of a Thermo Nicolet 8700 FTIR spectrophotometer. To ensure a high absorptance dynamic range, colored-glass filters were employed for a particular spectral range. Measurements on the Bi doped perovskite solar cells were performed in air in a dark room. A current preamplifier, Stanford Research Systems SR570, was used with preamplification of 200 μA V⁻¹ and 20 nA V⁻¹ for the higher (above the band edge) and lower (below the band edge) wavelength ranges, respectively. The measurement results were plotted as a normalized Internal Percentage Conversion Efficiency (IPCE) vs. energy (eV) to compare between the different effects of Bi doping. More details on the FTPS measurement of perovskite layers and solar cells can be found in ref. 5.

Modulated surface photovoltage (SPV) spectroscopy

Modulated (frequency 14 Hz) SPV signals were measured in the fixed parallel plate capacitor arrangement with an insulating mica sheet between the sample surface and a transparent SnO₂:F electrode.⁴¹ Illumination was performed with a halogen lamp, an optical chopper and a quartz prism monochromator (SPM2). An optical filter (cutoff at 800 nm) at the exit of the monochromator was used for suppression of stray light of shorter wavelengths.

UV photoelectron spectroscopy (UPS)

UV photoelectron spectroscopy (UPS) measurements were performed in a custom made ultra high vacuum chamber, using a monochromatic UV-lamp for excitation (VG Scienta, VUV 5000, at 21.22 eV photon energy) and a hemispherical energy analyzer (Specs, Phoibos 100) for the measurement of the ejected photo-electrons.

X-ray photoelectron spectroscopy (XPS)

Determination of the oxidation state of Bi was performed by XPS with a Thermo Scientific K-Alpha + XPS system using an Al Kα micro-focused monochromator with variable spot size (30–400 μm in 5 μm steps).

X-ray diffraction (XRD)

X-ray diffraction (XRD) measurements were performed on mix-cation perovskite films using a Rigaku SmarLab diffractometer with Cu-Kα radiation (λ = 1.54050 Å). For the grazing incidence X-ray diffraction, out-plane incident angle was set at 1°. Lattice parameters were deduced from Pawley refinement using Topas Academic V6.

Density functional theory (DFT) simulations

Calculations were performed on a supercell consisting of 4 × 4 × 4 cubic units, corresponding to 768 atoms for the bulk system and substitutional defects, and 769 for the interstitial case. All calculations were performed within the Perdew–Burke–Ernzerhof (PBE)⁴² generalized gradient approximation (GGA) to the density functional theory (DFT). In principle, one expects a significant spin–orbital coupling (SOC) contribution to the energy of the Kohn–Sham orbitals. However, it is well-known that, due to an error cancellation, GGA is able to reproduce very well the bandgap of lead halide perovskites.⁴³ This allowed us to use the computationally efficient PBE–GGA approach without the very computationally demanding (for samples of this size) SOC. Also van der Waals interactions might have an effect on the properties of the system. However, recent reports have shown that these effects on structural, vibrational and electronic properties of hybrid perovskites are relatively minor.⁴⁴ Thus, we preferred to use the GGA–DFT approach and validate the reliability of the results on specific cases taking as reference the non-local vdW-DF2 functional.⁴⁵ It is worth remarking that this setup is consistent with computational approaches used in the recent literature.⁴⁶

Ultrasoft pseudopotentials were employed to describe interaction between valence electrons and nuclei plus core electrons. Kohn–Sham orbitals were expanded on a plane wave basis set with a cutoff of 40 Ry. Structure optimizations, achieved by combining molecular dynamics and cell and atomic position optimization (see below), were performed with a Γ-point sampling of the Brilluoin zone. Electronic and optical properties are, instead, computed with a 4 × 4 × 4 Monkhorst–Pack k-point sampling.⁴⁷

Calculations have been performed with the Quantum Espresso suite of codes.⁴⁸ Thermodynamic transition energy levels have been computed according to the formula ε(+/0) = E^f(0, E_F = 0) − E^f(+, E_F = 0) = E(0) − E(+) + E_corr, where E^f(0, E_F = 0) and E^f(+, E_F = 0) are the formation energies of the neutral and charged defects at zero Fermi energy (E_F = 0), respectively, E(0) and E(+) are the energies of the neutral and charged defects as computed from the supercell calculations, and E_corr is a correction term accounting for electrostatic interaction between periodic images of charged defects and energy level alignment.⁴⁹ The second equality stems from the fact that the reference states of the neutral and charged defects are the same. Corrections for charged defects and energy levels alignment have been performed following the approach proposed by Freysoldt et al.⁵⁰ using the SXDEFECTALIGN software.⁵¹ It is worth mentioning that transition energy levels include the reorganization energy upon change of the charge state of the defect. If the transition energy level satisfies the condition ε(+/0) ≥ E_CBM it means that the untrapped state, consisting of the empty defect state, Bi_Pb˙, and the electron in the conduction band, is energetically favored. If ε(+/0) < E_CBM but this difference is small, few k_BT, the untrapped state is still thermally accessible. Finally, if ε(+/0) ≪ E_CBM thermal detrapping cannot take place and non-radiative recombination is enhanced.

At room temperature, organic cations of hybrid lead-halide perovskites are orientationally disordered, and this affects the configuration of the 3D PbI₃ framework. To reproduce such a complex system a simple (local) optimization of the atomistic configuration obtained from the 4 × 4 × 4 replication of the cubic unit cell, similar to that adopted in previous works,^46,52 is not sufficient. To cope with this problem, we implemented a multi-step protocol. The initial sample is (i) aged by constant temperature (400 K) and pressure (ambient pressure) ab initio molecular dynamics (MD) for 3 ps and then (ii) (gently) annealed at 300 K. (iii) After 2 ps of thermalization at ambient conditions (iv) the system is further annealed at 100 K. (v) In the last configuration of this step we introduce defects either by replacing a Pb with a Bi atom (Bi_Pb˙) or introducing an interstitial Bi (Bi_i˙). (vi) The systems with and without defects are further annealed down to 10 K and the last configuration is used as starting point for (vii) the final geometry and cell optimization. To check the possible presence of inequivalent defects of the same Bi_Pb˙ nominal kind, we generated 5 different initial configurations by replacing 5 different Pb atoms selected randomly out of the 64 present in the sample. Indeed, as mentioned above, this approach allowed us to identify two kinds of defects, shallow and deep. The interstitial Bi has been inserted in the cell at a random position in the proximity of iodine atoms. To avoid problems with the integration of the dynamics, before proceeding with the annealing step atomic forces are partly relaxed keeping the PbI₃ framework fixed.

Device simulations

A one-dimensional drift-diffusion model was used considering electronic and ionic charge carriers. Continuity equations for electrons, holes, and a positive ionic defect, as well as Poisson's equation, were solved by MATLAB's pdepe solver in space and time domains, using a modified version of the open-source software Driftfusion⁵³ developed by Barnes and Calado in their previous work.⁵⁴ The stack hole transport layer/perovskite layer/electron transport layer was represented by a p–i–n structure. The mobile (positive) ionic defects were confined in the perovskite layer, and charge neutrality was maintained by a homogeneous static negative charge. Besides radiative recombination, SRH recombination was implemented in the bulk of the perovskite layer and its interface regions with the doped transporting layers. Schottky contact boundary conditions were set at the electrodes. Detailed parameters used in the model can be found in Table S3.†

Results

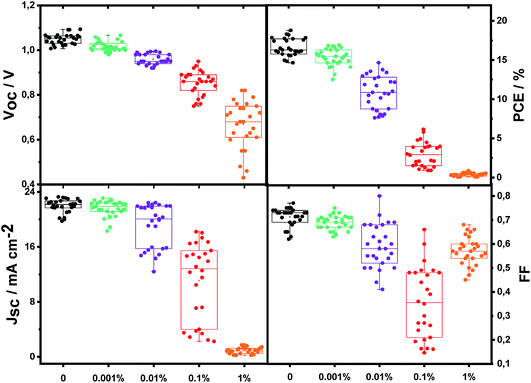
Perovskite solar cells were prepared by employing a 500 nm thick perovskite film of the triple cation composition CsMAFA (for more details on the precursor ratios, see the experimental section), sandwiched in between mesoporous TiO₂ (ca. 200 nm) on FTO and the organic hole-transport layer spiro-MeOTAD.⁵⁵ Bi was introduced by adding bismuth(III) iodide (BiI₃) to the perovskite solution in low quantities (8 μl of 0.3 molar solution to 200 μl of 1.2 molar perovskite solution to get approximately 1 at% of Bi compared to Pb). To reach lower concentrations, the Bi containing perovskite solutions were subsequently diluted with Bi-free perovskite solutions. To confirm that Bi was incorporated into the film as expected, we performed mass spectroscopy (ICP-MS/OES) upon re-dissolving a film nominally containing 1% Bi. The obtained result of (1 ± 0.5)% confirms the nominal concentration.

Fig. 1 shows the solar cell performance parameters as a function of Bi content. Interestingly, even a concentration of 0.001% (i.e. 10 ppm) affects the power-conversion efficiency negatively, which decreases monotonically with increasing amount of Bi; for 1% of Bi the PCE approaches 0. This trend, which is not limited to this specific perovskite composition, but holds for CH₃NH₃PbI₃ as well (Fig. S1†), is reflected in the individual solar cell parameters to different extents. The short circuit current density (J_SC) initially remains rather unaffected, but drops drastically when going from 0.01 to 1%. The fill factor (FF) decreases moderately and is particularly low for the 0.1% sample. The most systematic trend is however found in the V_OC, which decreases continuously without a strong spread upon increasing the Bi concentration. This behavior is strongly indicative of the Bi impurity acting as a recombination center. Before further characterizing recombination at V_OC, we aim to better understand the observed trends in J_SC and FF.

Fig. 1 Characteristic parameters for solar cells containing different concentrations of intentionally added Bi denoted in at% referred to Pb. Even a concentration of 10 ppm results in a decrease of performance.

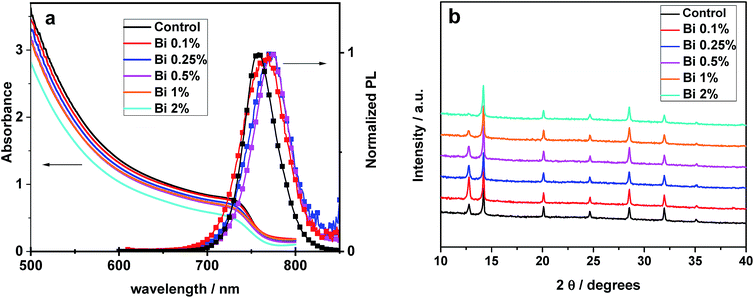
We start with optical and structural characterization, where we show data measured on films with up to 2% Bi concentration (all samples with [Bi] <0.1% are indistinguishable here). The absorption data, plotted in Fig. 2a, show that the absorbance is comparable for all perovskite films with the investigated Bi concentrations. This finding is consistent with a recent report on CH₃NH₃PbBr₃, where it was shown that the bandgap is not modified upon addition of Bi.⁴⁰ Only the absorption onsets seem to be broadened for higher concentrations of Bi, which is consistent with the slight red shift of the PL spectra seen for this series. However, this shift of 15 nm is close to what we commonly observe as sample-to-sample variations (≈±5 nm). The XRD data in Fig. 2b do not indicate that the crystal structure or lattice parameters of the perovskite are considerably modified upon addition of Bi, similar to the recent report on CH₃NH₃PbBr₃.⁴⁰ The Bi-containing perovskite keeps a cubic symmetry and no evidence of the impurity phase (CH₃NH₃)₃Bi₂I₉ was observed. We will proceed with a more detailed analysis of peak positions below.

Fig. 2 Characterization of thin films with different Bi content on glass (a) absorption spectra, which are rather unaffected apart from a slight broadening of the onset. Normalized photoluminescence showing a slight red shift for higher Bi concentrations. (b) XRD data not showing any significant changes in the perovskite structure nor new phases.

Overall, the small changes observed in the optical properties can by no means explain the trends seen in J_SC. The reduced J_SC, in accordance with the reduced FF, indicates instead a reduced charge carrier collection efficiency because of either increased recombination rates or decreased charge carrier transport properties. Before quantifying those parameters, we make use of the knowledge that charge carrier collection efficiency in perovskite solar cells is influenced by preconditioning.^56,57 This behavior results in the well-known hysteresis, when performing a current–voltage (JV)-sweep.^58,59 For instance we have shown previously that the photocurrent of degraded devices could be recovered by a fast JV scan following a positive pre-bias, confirming that the major reason for the low J_SC was a reduced charge carrier collection efficiency, whereas absorption remained unmodified.⁵⁶

Fig. 3 shows JV loops from 1.2 V to −1.5 V and back for different voltage sweep rates (0% Bi device shown in Fig. S2†). All devices exhibit severe hysteresis although the stabilized maximum power output is very close to the maximum power point of the backward scan (Fig. S3†). For devices with 0.001% and 0.01% Bi, J_SC reaches values larger than 20 mA cm⁻² independent of scan rate. However, the 0.1% device shows clear kinks in the JV curve, which reduce the FF substantially. The higher FF of the 1% device is therefore merely due to the kink removal via the much lower photocurrent. One major reason for kinks in the JV curve is charge accumulation due to unfavorable charge extraction properties by the electrodes. In perovskite solar cells, mobile ions tend to screen the electric field.⁵⁶ Hence, photocurrent for slow scan rates is expected to be mainly diffusion driven. In case of moderately low effective mobilities, this constellation can give rise to S-kinks.⁶⁰ If mobilities are sufficiently high, the S-kink vanishes and the FF increases (as here for [Bi] ≤ 0.01%). The S-kink can vanish for very low mobilities as well because only a small fraction of photogenerated charges is collected. This effect could explain the observed trend in the FF.

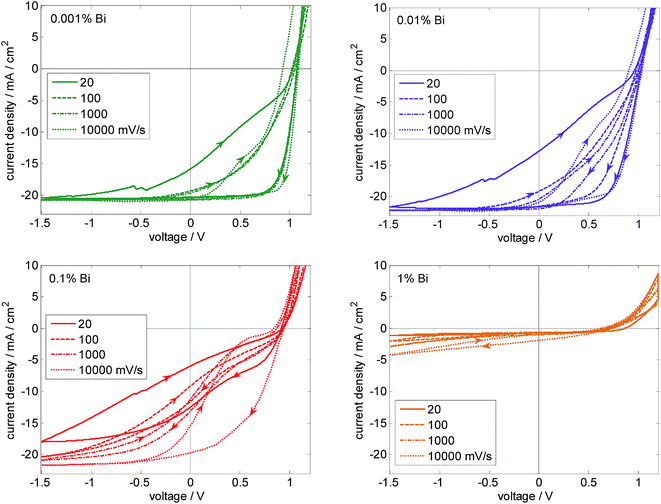Fig. 3 JV hysteresis loops starting from 1.2 V for various voltage sweep rates measured at solar cells with different Bi concentrations. Reduced J_SC and FF upon addition of Bi are mainly due to a strong dependence of charge extraction on the electric field. (The 0% Bi device behaves similarly as the 0.001%, see Fig. S2†).

The reduction of J_SC with increasing Bi content is partially explained by the fact that the photocurrent saturates only at reverse voltages, indicating that high electric fields are required for successful charge extraction. Performing faster scans, almost the full absorbed photon flux can be extracted as electron–hole pairs, resulting in currents larger than 20 mA cm⁻². The faster scans benefit from the persistence of the preconditioning state of forward bias (1.2 V), providing an enhanced electric field for charge carrier extraction. Even for the 1% device, which delivers a J_SC < 1 mA cm⁻² in a slow scan (20 mV s⁻¹), we can reach almost 5 mA cm⁻² at 1.5 V reverse bias for a fast scan (10 000 mV s⁻¹). The slope indicates that even more charge carries could be collected under higher reverse bias. This clearly shows that addition of Bi increases charge carrier loss by recombination, outcompeting the charge extraction which strongly relies on the electric field. The reason could be either enhanced recombination consistent with the trend in V_OC, or reduced charge carrier transport properties, or a combination of both; the latter case is supported by our device simulations (see below and Fig. S20†).

Scanning electron microscopy (SEM) images, shown in Fig. S4,† do not indicate a considerable change of film morphology. Especially for low (<0.25%) Bi concentrations, the average grain dimension remain between 300 and 450 nm. However, grains become smaller and bright features appear for samples with 1 and 2% Bi, indicating accumulation of possibly Bi-rich material on the surface.

To further explore whether charge transport is modified (as already mentioned when discussing the S-shape), we deduce the series resistance from the JV curve in the forward direction. For the data shown in Fig. 3 we obtain 25, 62, 56, and 190 Ohm as values for slow scans for 0.001, 0.01, 0.1, and 1% Bi concentration, respectively. Statistics are shown in Fig. S5.† This indicates that indeed charge carrier transport, either in the perovskite or at the interfaces to the charge transport layers, is negatively affected, in particular in the case of 1% Bi. A considerably larger series resistance for devices with 1% Bi compared to lower concentrations is also observed when extracted from dark JV curves as shown in Table 1. The reason could be connected to the presence of shallow trap states as discussed below.

Table 1 Data of representative devices. For statistics, see Fig. 1. The radiative limit of the open-circuit voltage V_{OC, rad} is obtained from IPCE data (cf.Fig. 6). The predicted V_{OC, calc} is calculated using eqn (1) and the external quantum efficiency of electroluminescence EQE_EL. V_OC is measured without aperture. PL decay times are measured on films (Fig. 4b). A phenomenological series resistance is approximated by a linear fit of the forward dark current between 1.1 and 1.2 V

Bi concentration	V OC, rad/V	EQEEL	V OC, calc/V	V OC/V	PL decay time/μs	R s/Ohm cm^2
a The pronounced tail and a too low electroluminescence yield did not allow the analysis of the data for 1% Bi.
0	1.34	1 × 10^−3	1.16	1.18	2.7	5
0.001%	1.34	1 × 10^−4	1.10	1.11	1.9	15
0.01%	1.34	6 × 10^−6	1.03	1.04	1.1	9
0.1%	1.34	2 × 10^−8	0.88	0.90	0.4	14
1%	—^a	—^a	—^a	0.85	0.1	78

---

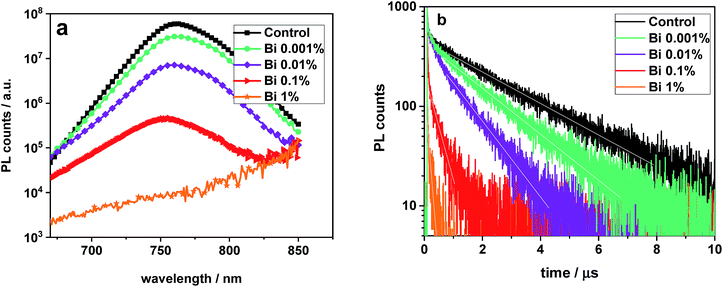
Now we turn the focus on V_OC and recombination. We measured steady-state and transient PL of perovskite films deposited on glass substrates (Fig. 4). Whereas the shapes of the PL spectra remain almost unmodified upon addition of Bi, the overall signal decreases by around four orders of magnitude, indicating a reduced PL yield (consistent with data on CH₃NH₃PbI₃ in ref. 61 and CH₃NH₃PbBr₃ in ref. 40) and enhanced non-radiative recombination in those films. This finding is confirmed by the PL decay experiments, where the long exponential decay time of several μs for a Bi-free perovskite film is reduced to values below 100 ns for a film with 1% Bi. Therefore, Bi is responsible for faster non-radiative recombination in the perovskite films. For simplicity and due to the complexity of the interpretation of PL decay curves,^13,62 time constants are extracted by simply fitting a mono-exponential function in the time range indicated by the white lines. The obtained values are included in Table 1.

Fig. 4 Photoluminescence of perovskite films (a) absolute PL spectra showing that adding Bi reduces the PL yield so substantially that it is hardly detectable for [Bi] = 1%. (b) Transient PL with a reduced decay time for higher Bi concentrations. The white lines are mono-exponential fits and span the time range selected for the fits.

We measured the ideality factor from intensity dependent V_OC data following the approach of ref. 63. Due to light-soaking effects, an unambiguous determination of the ideality factor and assignment to a dominant recombination mechanism was not feasible. Roughly, we deduce values lower than 2 (mostly around 1.6), which reduce towards 1.3 for higher concentrations of Bi. This reduction could indicate a larger majority charge carrier density in tail states as discussed below. From the series resistance analysis, such hypothesized larger charge carrier density does however not seem to translate into a higher conductivity as expected for a doping effect reported for Bi addition to MAPbBr₃ (ref. 64) or CsPbBr₃ (ref. 65) single crystals. Additionally, this phenomenological series resistance might be limited by charge carrier injection.

We proceeded by using electroluminescence (EL) as a complementary measurement technique to quantify the share of radiative recombination expressed by the external quantum efficiency of EL (EQE_EL). As EL is measured on the complete device, V_OC can be predicted according to:¹⁰

V _{OC, rad} is the radiative limit of V_OC, which is obtained using detailed balance and reciprocity between IPCE and EL.¹⁰ The EQE_EL is measured in the dark at a forward current that equals the short-circuit current under illumination with one sun (full sweeps in Fig. S7†). The deduced V_OC values coincide with experimental V_OC data and are included in Table 1, showing a reduction of the EQE_EL by roughly five orders of magnitude with increasing Bi content. Whereas the EL results can be used to quantitatively describe the V_OC, the trends in our PL data match rather qualitatively. This difference is attributed to the fact that EL is measured at conditions similar to V_OC. This is important because the luminescence yield is a function of charge carrier densities and thus of the excitation source in a PL measurement. For transient PL as a non-steady-state measurement at high excitation densities, it is even more challenging to quantify recombination time constants.⁶² Furthermore, EL results contain the effects of contact layers, which might cause surface recombination. Although we do not have indications that surface recombination introduced by the contact materials should depend on the Bi concentration, we cannot exclude that it contributes to the decrease in V_OC to some extent. Within the sensitivity of our detectors in EL and PL, we could not detect the onset of a broad NIR emission peak as reported in ref. 61.

The IPCE onset sensitively measured by FTPS is displayed in Fig. 5a. It shows the typical sharp absorption onset with a narrow Urbach tail (14 meV) at 1.6 eV.^5,66 Interestingly, for higher (>0.1%) concentrations of Bi, additional tail states are observed yielding a characteristic trap energy of 37 meV when fitted by an exponential function. This observation is consistent with the absorption data presented in Fig. 2 and the more sensitive PDS data in Fig. 5b.

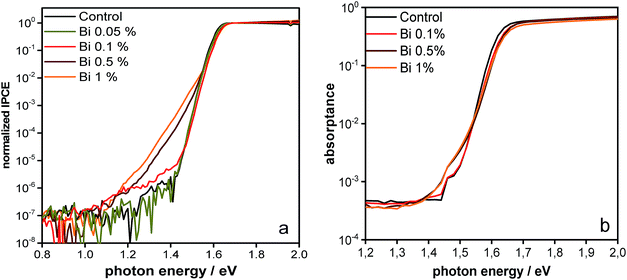Fig. 5 Sensitive optical measurements at the band edge (a) IPCE measured by FTPS and (b) PDS. Both measurements show that larger amounts of Bi introduce optically detectable tail states.

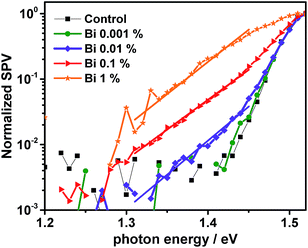
To perform a more sensitive measurement of the tail states, we switch from the current to the voltage response measured as a surface photovoltage⁶⁷ (SPV) on top of perovskite, deposited on FTO. Note that we used a slightly modified perovskite composition with a slightly lower bandgap. However, the effect of Bi on device performance and tail states is the same. The SPV signal arises from spatial charge separation upon photon absorption and does not require charge transfer to the contacts. Performed as a function of energy of the incident light it can be used to measure tail states. The results plotted in Fig. 6 clearly show a more strongly pronounced tail with the addition of Bismuth. Fitting an exponential decay between 1.3 and 1.44 eV (for 0.01 to 1% Bi), we find a characteristic energy of 47 meV, which is approx. 3 times higher than the value of 15 meV for the 0% device. Despite being a voltage response, this value matches the one from the current response (IPCE, Fig. 5) and corresponds to the well-documented Urbach tail in metal-halide perovskites.^5,66 The energy of the additional tail states is independent of Bi concentration, which indicates that Bi within the perovskite leads to a defect with a characteristic energy, whereas the Bi concentration only changes the magnitude of the signal as expected for conventional defects. This result is independent of whether the perovskite is deposited onto TiO₂ or whether doped spiro-MeOTAD is present on the perovskite surface.

Fig. 6 Surface photovoltage (SPV) measurements on samples with Cs_0.1FA_0.9Pb(Br_0.1I_0.9)₃ showing the presence of tail states with higher Bi content. The lines indicate an exponential fit between 1.3 and 1.45 eV, yielding characteristic energies of 47, 47, and 46 meV, for [Bi] = 1, 0.1, and 0.01%, respectively.

It is suspected that these shallow states are mostly responsible for a dispersive charge transport due to trapping and detrapping events resulting in lower effective charge carrier mobilities and, thus, a reduced J_SC and FF. The shallower states are obviously still associated with a transition dipole moment allowing for absorption of photons visible in the IPCE and SPV. Based on the results from EQE_EL, we conclude that the reduction of V_OC is associated with non-radiative transitions, and therefore not detectable in absorption and emission measurements. This non-radiative recombination could result from a low emission yield of these tail states (as we cannot detect emission from them) or additional deep recombination centers, discussed in the subsequent paragraph.

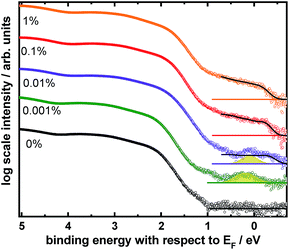
To probe the overall density of occupied states (DOS), we performed UV photoelectron spectroscopy measurements (UPS) on perovskite films deposited onto FTO; the full spectra are presented in Fig. S8 of the ESI.† We find no significant change in the overall shape of the valence band (VB) with addition of Bi, however we observe the appearance of states within the band gap. This is best observable in a log scale representation of the DOS, as presented in Fig. 7. For the lowest investigated Bi concentration, a distinct peak appears approximately 200 meV below the Fermi energy E_F. This feature is still noticeable for the 0.01% sample, however for higher ratios a broad distribution of gap states appears (black line) that cover up that signal. Likely this broad distribution originates from excessive Bi at the surface as observed in XPS that could form continuous (metallic) states. It should be noted that these states appear to stretch significantly beyond E_F (wider than expected from the energy resolution of 120 meV), which is an artefact of the log scale presentation that blows up very low signal intensities as further discussed in the ESI, Fig. S9.†

Fig. 7 UPS measurements of Cs_0.1FA_0.9Pb(Br_0.1I_0.9)₃ films with different Bi concentration (on FTO) showing the valence band region in a semi-logarithmic plot. For intermediate Bi concentrations, a deep defect state (yellow) is observable which is superimposed by a broader density of states extending to the Fermi edge (black) for higher concentrations.

The before mentioned discrete state, marked in yellow for the 0.001% and 0.01% Bi measurements in Fig. 7, is likely originating from a specific Bi related defect state, since it is not present in the 0% sample. Additional inverse photoelectron spectroscopy measurements (see Fig. S8†) show that the conduction band (CB) is located close to E_F as well. Therefore, it can be concluded that this defect is located around 0.3–0.5 eV below the conduction band (Table 2), which is in good agreement with DFT calculations shown below.

Table 2 Energy level values extracted from photoelectron spectroscopy measurements shown in Fig. S8. All values are in eV; onsets of VB and CB are extracted by linear extrapolation and the value indicates the distance from the Fermi energy

[Bi] (%)	Cutoff UPS	VB onset (lin)	CB onset (lin)	Wf	IE	EA
0	17.21	1.79	0.05	4.01	5.8	3.96
0.001	17.27	1.75	0.13	3.95	5.7	3.82
0.01	17.03	1.43	0.31	4.18	5.61	3.87
0.1	16.99	1.49	0.38	4.23	5.72	3.85
1	16.97	1.42	0.33	4.25	5.67	3.92

---

In addition to the occurrence of gap states, we observe a shift of the work function towards higher values upon addition of Bi, whereas IE and EA remain roughly constant (Table 2). While for 0% the CB is in close proximity to E_F, as often observed for Pb based perovskites,^68,69 the difference between CB and E_F increases with increasing Bi content. This could indicate a mild p-type doping by the Bi addition. However, knowing from UPS (as well as theory discussed at the bottom of this article) that gap states appear, we rather assume that newly created unoccupied states close to the CB lead to a pinning of the Fermi energy a few 100 meV below the CB. We tried observing these states in the IPES measurements shown in the ESI (Fig. S8†), however due to the significantly lower signal intensities they are not observable within the noise level of the experiment.

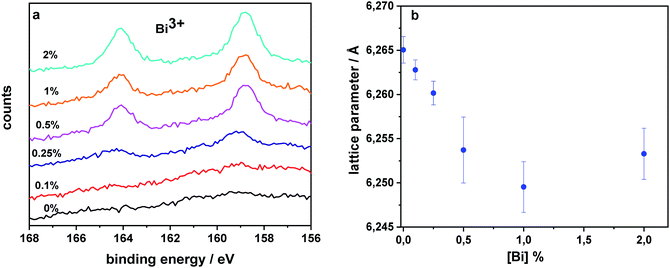
After having analyzed and characterized the device performance and optoelectronic properties, we want to shed light on the structural and chemical effects of Bi in our perovskite films to understand why Bi in such small quantities is so detrimental. For this purpose we characterize films deposited on glass substrates by XPS. We clearly observe the signature of Bi³⁺ independent of concentration (clearly resolved for [Bi] > 0.25%, Fig. 8a). The signal originates from Bi 4f (7/2 peak at 159 eV), suggesting that the only oxidation state is Bi³⁺.⁷⁰ This can be seen as a first indication that instead of forming interstitials, Bi replaces Pb in the perovskite lattice consistent with recent studies on CH₃NH₃Bi_xPb_1−xI₃.^61,71 Quantifying the molar ratio between Bi and Pb for the sample with 1% Bi, we observe an accumulation of Bi on the surface (up to 10% detected). Given that 1% is in the film, as verified by mass spectroscopy, and assuming an XPS probe depth of 10 nm, we conclude that there should be approx. 0.8% Bi in the bulk of the 500 nm thick layer. Carefully analyzing the XRD data (Fig. S10 and S11†), we observe a slight reduction of the lattice parameter (Fig. 8b, Table S1†) deduced using Pawley refinement (TOPAS Academic V6) in cubic symmetry (Pm3̄m).⁷² This decrease is consistent with our expectation since Bi³⁺ (1.03 Å) has a smaller ionic radius than Pb²⁺ (1.19 Å) in an octahedral environment,⁷³ as also found for CsPbBr₃:Bi single crystals.⁶⁵ To probe whether this Bi substitution is homogeneous in the perovskite layer, we measured grazing incidence X-ray diffraction. Comparing diffraction patterns from the surface and the bulk, we deduce the same trend, indicating that Bi substitution occurs also in the bulk of the perovskite layer (Fig. S12†). A reduction of lattice parameters is also predicted by simulation when assuming that Bi substitutes Pb (Bi_Pb˙), as presented in the following section.

Fig. 8 Structural characterization of perovskite films containing Bi (a) XPS spectra showing the characteristic signal for Bi³⁺ which increases for higher Bi content. (b) Lattice parameter deduced from fitting XRD spectra. Incorporation of Bi decreases the lattice parameter.

In order to simplify the theoretical analysis, DFT calculations were performed on CH₃NH₃PbI₃. We remark that our experiments show comparable Bi-related features for CsMAFA and CH₃NH₃PbI₃ perovskite (Fig. S1†). Thus, the simpler CH₃NH₃PbI₃ model allows to identify the fundamental effects of Bi-related defects on the properties of the mixed perovskite. In particular, we considered both substitutional Bi on Pb sites (Bi_Pb˙) and interstitial Bi (Bi_i˙) in a sample consisting of 64 stoichiometric units (768 atoms) in periodic boundary conditions, corresponding to a Bi concentration of ≈1.5% (see section Experimental methods for details). Additional data are available in the ESI, Fig. S13 to S20.†

Previous theoretical studies⁴⁶ have indicated that Bi_Pb˙ is the most stable bismuth defect, which is consistent with the +3 charge of bismuth determined by XPS. In addition, computational results show a consistent ≈0.01 Å shrinking of the lattice parameter for the samples containing Bi_Pb˙, in nice agreement with the ≈0.01 Å reduction deduced from XRD data of samples containing 1–2% of Bi (see Fig. 8b). On the other hand, we verified that Bi_i˙ produces a negligible change of the lattice parameter, and its charge state is inconsistent with XPS data (additional data for Bi_Pb˙ are available in the following and in the ESI†).

CH₃NH₃PbI₃ is a soft material and at room temperature presents an orientationally disordered cation sub-lattice, which also affects the local structure of the PbI₃ 3D framework. This gives rise to a multiplicity of different local environments for Bi_Pb˙, which might have an effect on the features of defect states. To take this into account, we generated a series of different configurations with Bi substituting different Pb sites in a well thermalized CH₃NH₃PbI₃ sample. These initial configurations are then gently annealed. At first sight, the various structural configurations appear rather similar, with Bi well incorporated into the inorganic 3D framework of the perovskite, and no relevant differences in the structure are observed. However, a closer look at the structure surrounding the Bi atom reveals two different types of atomic configurations of the same nominal defect state. In the first type, the Bi atom is at the center of an almost perfect octahedral BiI₆ unit, in which all the I–Bi–I angles α along the axes are almost perfectly flat, α ≥ 175° (see Fig. S13†). In the second configuration, the I–Bi–I angle along a specific axis is sizably smaller (α ≈ 170°).

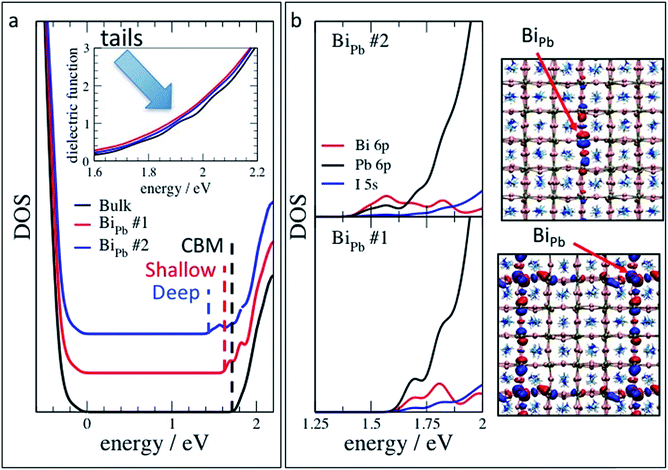
The difference in the local atomistic structure has a pronounced effect on the energetics of defect states. Bi_Pb˙ presents both shallow (E_CBM − ε(+/0) = 0.16 eV, where e(+/0) is the thermodynamic transition energy level and E_CBM is the energy of the conduction band minimum, CBM) and deep (E_CBM − ε(+/0) = 0.51 eV) defect states, corresponding to the less and more distorted atomistic structures, respectively. We remark that here we report for the first time the double nature, i.e. shallow and deep, of substitutional Bi-related defects. We speculate that this novel finding is due the careful procedure for producing the computational samples, which allowed to access defect configurations not achievable by standard total energy minimization procedures.^46,52

The difference in the transition energy levels is related to a difference between the density of states (DOS) of the two configurations: in the neutral charge state, i.e. when the defect has captured an electron, the DOS of the first defect configuration shows two defect peaks almost overlapping with the conduction band minimum (CBM, Fig. 9a), with a small shift to lower energy with respect to the CBM of pure CH₃NH₃PbI₃. This shift is due to hybridisation of Pb 6p and I 5 s with lower energy Bi 6p orbitals. These shallow defect states (Fig. 9b, bottom) are analogous to the partially localized Bi-related conduction band orbital of ref. 52, which consistently with present results, is 0.13 eV below the pristine CBM. The DOS of the second Bi_Pb is characterized by three defects-derived peaks, two at higher energy, empty and almost overlaping with the conduction band, and the third half-filled, and farther in energy from the CBM. This latter orbital is highly localized, more than the lowest energy defect state in the other configuration and reported in the literature,⁵² as confirmed by the dominant contribution of the Bi 6p orbitals to the DOS in the relevant energy range, and by the shape of the electronic density of the defect state (Fig. 9b). An extended explanation of the relation between the atomistic and electronic structure of the defect states, based on the comparison between present and literature results,^34,44,74 is reported in the ESI (Fig. S14–S16†). Interestingly, van der Waals interaction have minor effects on both the thermodynamic transition energy levels, within few tens of meV, and DOS of shallow and deep defects (Fig. S18†). Also cation mixing plays a minor role, both when a second cation, e.g. FA, is near or far from the substitutional bismuth (Fig. S19†).

Fig. 9 Results of theoretical calculations. (a) Density of state of the bulk (black) and two neutral Bi_Pb defect configurations corresponding to shallow (red) and deep (blue) defect states. The zero of the energy axis is set to the valence band maximum (VBM). The lowest (half-filled) energy defect state of the first configuration overlaps with the bulk CBM. On the contrary, the corresponding state of the second configuration is well separated from the conduction band. In the inset it is reported the low energy part of the absorption spectrum, which shows the defect related low energy tails. (b) Contribution of Bi 6p, Pb 6p and I 5s atomic orbitals to the DOS in the energy range of defect states. On the right-hand side of the panel are reported the isosurface of the defect states of minimum energy. Isosurfaces are colored in blue and red according to the sign of the corresponding orbitals to put in evidence their antibonding character.

The fact that Bi_Pb can generate both shallow and deep defect states depicts a scenario coherent with the main experimental findings including the results from FTPS, PDS, and UPS. In fact, 0.16 eV, the transition energy level of the shallow defect state, is ≈6 times the thermal energy available to the system at room temperature. Thus an electron trapped in this orbital has a non-neglibigle probability of getting thermally detrapped and reach the conduction band. The trapping/detrapping process slows down the carrier conduction which negatively affects FF and J_SC. On the contrary, detrapping from the deeper defect configuration requires 0.51 eV, ≈20 times the thermal energy; a carrier stuck in this highly localized state has very little probability to be thermally excited into the conduction band. Instead, it will more easily recombine non-radiatively, thus most likely being responsible for the reduced V_OC. This recombination can be quantitatively described by Shockley–Read–Hall theory. Implemented in drift-diffusion simulations of a p–i–n device, the observed reduction of V_OC requires defects that are at least as deep as 0.3 eV (Fig. S21†). Comparing the simulated current–voltage curves (Fig. S22†) with the hysteresis curves of Fig. 3, this enhanced recombination can also explain the reduction of photocurrent as a function of scan rate. However, the reduced fill factor and enhanced series resistance is better described by an additionally reduced charge carrier mobility.

We also computed the dielectric function of the (positively charged) defect states in the configurations described above. The theoretical results are consistent with experimental spectra. In fact, both defects only contribute with low energy tails to the spectrum of the pristine material (inset of Fig. 9a, cfr. with Fig. 5 and 6). We, thus, infer that the deep unoccupied energy level of Bi_Pb˙ is dark (see also ESI†). In addition, the dielectric function of Bi_i˙ shows no tails (Fig. S20†), which further supports the hypothesis that it is Bi_Pb˙ responsible for the low energy tails defect signature in the experimental spectra.

Conclusions

We have investigated the tolerance of the lead-halide perovskite semiconductor against the presence of intentional defects, introduced by bismuth impurities. We have found that, contrary to many other impurities, the solar cell performance decreases substantially, even for Bi concentrations in the ppm range. This is rationalized by calculations, showing that Bi³⁺ substituting Pb²⁺ introduces both shallow and deep electronic states in the bandgap dependent on the local environment. Such a Bi substitution reduces the angle of the bonds with iodine compared to Pb. This leads to a reduced overlap of the antibonding orbitals forming the conduction band, which in turn lead to states lower in energy. The shallow states explain the reduced photocurrents and fill factors due to lower effective charge carrier mobilities caused by trapping and detrapping events. The deep states are supposed to be responsible for increased defect recombination, reducing the open-circuit voltage and luminescence yields. This study provides evidence that the defect tolerance, often associated with perovskites, does not extend to all kinds of impurities. Certain impurities in the ppm range in the perovskite precursor solutions might be a limiting factor when it comes to reaching the optimum efficiency in state-of-the-art high-performance and high-V_OC perovskite solar cells.

Author contributions

M. Y. and F. E. contributed equally. They prepared devices and films, performed PL, absorption and JV measurements and edited the figures. S. M. performed molecular dynamics simulations and DFT calculations under consultation with A. F. and contributed the respective sections and figure. Z. S. W. performed drift-diffusion simulations. T. C. J. Y. and B. N. performed FTPS and PDS measurements. H. S. and S. O. conducted UPS measurements and analyses. S. S. performed the XRD analysis and T. B. supervised this research. Z. W. performed SEM and XRD measurements. J. D. and T. D. performed SPV measurements together with F. E. and W. T. W. C. supervised ZS.W. JP. CB. lead the structural characterization. W. T. conceptualized the study together with JP. CB. W. T. coordinated it, performed optoelectronic measurements and wrote the paper. All authors contributed to discussions and finalizing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Amita Ummadisingu for performing transient PL measurements. W.T. acknowledges the Swiss National Science Foundation (SNSF) for an Ambizione Energy fellowship. T.C.J.Y acknowledges support from the Marie Skłodowska-Curie Individual Fellowship. S.S. and T.B acknowledge the support from a TOTAL research grant. A.F. acknowledges funds by “Progetti biennali d'Ateneo Finanziati dalla Fondazione di Sardegna annualità 2017” (project no. F71I17000170002), and computing support by CRS4 Computing Center (Loc. Piscina Manna, Pula, Italy). S.M. acknowledges support form CINECA for awarding the access to resource Marconi for the project SEMPRE. Z.W. acknowledges the Swiss State Secretary for Education, Research, and Innovation for an SSSTC scholarship (EQ-CN_03-042018). K.T. acknowledges the German Research Foundation (DFG) for funding through project 382633022 (RECOLPER). S.O. acknowledges support from the DFG for funding through the project MUJUPO (415231147). P.R. acknowledges the German Federal Ministry of Education and Research (BMBF) for funding through the grant HYPER with grant agreement number 03SF0514A.

References

1. J.-P. Correa-Baena, A. Abate, M. Saliba, W. Tress, T. J. Jacobsson, M. Grätzel and A. Hagfeldt, The Rapid Evolution of Highly Efficient Perovskite Solar Cells, Energy Environ. Sci., 2017, 10(3), 710–727,  10.1039/c6ee03397k.
2. J.-P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Promises and Challenges of Perovskite Solar Cells, Science, 2017, 358(6364), 739–744,  DOI:10.1126/science.aam6323.
3. A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, Organometal Halide Perovskites as Visible-Light Sensitizers for Photovoltaic Cells, J. Am. Chem. Soc., 2009, 131(17), 6050–6051,  DOI:10.1021/ja809598r.
4. H.-S. Kim, C.-R. Lee, J.-H. Im, K.-B. Lee, T. Moehl, A. Marchioro, S.-J. Moon, R. Humphry-Baker, J.-H. Yum and J. E. Moser, et al., Lead Iodide Perovskite Sensitized All-Solid-State Submicron Thin Film Mesoscopic Solar Cell with Efficiency Exceeding 9%, Sci. Rep., 2012, 2, 591,  DOI:10.1038/srep00591.
5. S. de Wolf, J. Holovsky, S.-J. Moon, P. Löper, B. Niesen, M. Ledinsky, F. Haug, J. Yum and C. Ballif, Organometallic Halide Perovskites: Sharp Optical Absorption Edge And, J. Phys. Chem. C, 2014, 5, 1035–1139,  DOI:10.1021/jz500279b.
6. G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH₃NH₃PbI₃, Science, 2013, 342(6156), 344–347,  DOI:10.1126/science.1243167.
7. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Electron-Hole Diffusion Lengths Exceeding 1 Micrometer in an Organometal Trihalide Perovskite Absorber, Science, 2013, 342(6156), 341–344,  DOI:10.1126/science.1243982.
8. S. Bourdais, C. Choné, B. Delatouche, A. Jacob, G. Larramona, C. Moisan, A. Lafond, F. Donatini, G. Rey and S. Siebentritt, et al., Is the Cu/Zn Disorder the Main Culprit for the Voltage Deficit in Kesterite Solar Cells?, Adv. Energy Mater., 2016, 6(12), 1502276,  DOI:10.1002/aenm.201502276.
9. X. Liu, Y. Feng, H. Cui, F. Liu, X. Hao, G. Conibeer, D. B. Mitzi and M. Green, The Current Status and Future Prospects of Kesterite Solar Cells: A Brief Review, Progress in Photovoltaics: Research and Applications, 2016, 24(6), 879–898,  DOI:10.1002/pip.2741.
10. W. Tress, N. Marinova, O. Inganäs, M. K. Nazeeruddin, S. M. Zakeeruddin and M. Graetzel, Predicting the Open-Circuit Voltage of CH₃NH₃PbI₃ Perovskite Solar Cells Using Electroluminescence and Photovoltaic Quantum Efficiency Spectra: The Role of Radiative and Non-Radiative Recombination, Adv. Energy Mater., 2015, 5(3), 140812,  DOI:10.1002/aenm.201400812.
11. D. Bi, W. Tress, M. I. Dar, P. Gao, J. Luo, C. Renevier, K. Schenk, A. Abate, F. Giordano and J.-P. C. Baena, et al., Efficient Luminescent Solar Cells Based on Tailored Mixed-Cation Perovskites, Sci. Adv., 2016, 2(1), e1501170,  DOI:10.1126/sciadv.1501170.
12. M. Saliba, T. Matsui, K. Domanski, J.-Y. Seo, A. Ummadisingu, S. M. Zakeeruddin, J.-P. Correa-Baena, W. R. Tress, A. Abate and A. Hagfeldt, et al., Incorporation of Rubidium Cations into Perovskite Solar Cells Improves Photovoltaic Performance, Science, 2016, 354(6309), 206–209,  DOI:10.1126/science.aah5557.
13. W. Tress, Perovskite Solar Cells on the Way to Their Radiative Efficiency Limit – Insights Into a Success Story of High Open-Circuit Voltage and Low Recombination, Adv. Energy Mater., 2017, 7(14), 1602358,  DOI:10.1002/aenm.201602358.
14. W. Shockley and H. J. Queisser, Detailed Balance Limit of Efficiency of P–n Junction Solar Cells, J. Appl. Phys., 1961, 32(3), 510–519,  DOI:10.1063/1.1736034.
15. C. M. Wolff, F. Zu, A. Paulke, L. P. Toro, N. Koch and D. Neher, Reduced Interface-Mediated Recombination for High Open-Circuit Voltages in CH₃NH₃PbI₃ Solar Cells, Adv. Mater., 2017, 29(28), 1700159,  DOI:10.1002/adma.201700159.
16. T. C.-J. Yang, P. Fiala, Q. Jeangros and C. Ballif, High-Bandgap Perovskite Materials for Multijunction Solar Cells, Joule, 2018, 2(8), 1421–1436,  DOI:10.1016/j.joule.2018.05.008.
17. M. M. Tavakoli, W. Tress, J. V. Milić, D. Kubicki, L. Emsley and M. Grätzel, Addition of Adamantylammonium Iodide to Hole Transport Layers Enables Highly Efficient and Electroluminescent Perovskite Solar Cells, Energy Environ. Sci., 2018, 11(11), 3310–3320,  10.1039/c8ee02404a.
18. Z. Liu, L. Krückemeier, B. Krogmeier, B. Klingebiel, J. A. Márquez, S. Levcenko, S. Öz, S. Mathur, U. Rau and T. Unold, et al., Open-Circuit Voltages Exceeding 1.26 V in Planar Methylammonium Lead Iodide Perovskite Solar Cells, ACS Energy Lett., 2019, 4(1), 110–117,  DOI:10.1021/acsenergylett.8b01906.
19. J. Kim, S.-H. Lee, J. H. Lee and K.-H. Hong, The Role of Intrinsic Defects in Methylammonium Lead Iodide Perovskite, J. Phys. Chem. Lett., 2014, 5(8), 1312–1317,  DOI:10.1021/jz500370k.
20. A. Buin, P. Pietsch, J. Xu, O. Voznyy, A. H. Ip, R. Comin and E. H. Sargent, Materials Processing Routes to Trap-Free Halide Perovskites, Nano Lett., 2014, 14(11), 6281–6286,  DOI:10.1021/nl502612m.
21. R. E. Brandt, V. Stevanović, D. S. Ginley and T. Buonassisi, Identifying Defect-Tolerant Semiconductors with High Minority-Carrier Lifetimes: Beyond Hybrid Lead Halide Perovskites, MRS Commun., 2015, 5(02), 265–275,  DOI:10.1557/mrc.2015.26.
22. P. Delugas, A. Filippetti and A. Mattoni, Methylammonium Fragmentation in Amines as Source of Localized Trap Levels and the Healing Role of Cl in Hybrid Lead-Iodide Perovskites, Phys. Rev. B, 2015, 92(4), 045301,  DOI:10.1103/physrevb.92.045301.
23. M. Yang, Y. Zeng, Z. Li, D. H. Kim, C.-S. Jiang, J. van de Lagemaat and K. Zhu, Do Grain Boundaries Dominate Non-Radiative Recombination in CH₃NH₃PbI₃ Perovskite Thin Films?, Phys. Chem. Chem. Phys., 2017, 19(7), 5043–5050,  10.1039/c6cp08770a.
24. J.-P. Correa-Baena, W. Tress, K. Domanski, E. H. Anaraki, S.-H. Turren-Cruz, B. Roose, P. P. Boix, M. Grätzel, M. Saliba and A. Abate, et al., Identifying and Suppressing Interfacial Recombination to Achieve High Open-Circuit Voltage in Perovskite Solar Cells, Energy Environ. Sci., 2017, 10(5), 1207–1212,  10.1039/c7ee00421d.
25. W.-J. Yin, H. Chen, T. Shi, S.-H. Wei and Y. Yan, Origin of High Electronic Quality in Structurally Disordered CH₃NH₃PbI₃ and the Passivation Effect of Cl and O at Grain Boundaries, Adv. Electron. Mater., 2015, 1(6), 1500044,  DOI:10.1002/aelm.201500044.
26. Y. Du, H. Cai, H. Wen, Y. Wu, Z. Li, J. Xu, L. Huang, J. Ni, J. Li and J. Zhang, Revealing the Unfavorable Role of Superfluous CH₃NH₃PbI₃ Grain Boundary Traps in Perovskite Solar Cells on Carrier Collection, RSC Adv., 2016, 6(86), 83264–83272,  10.1039/c6ra15512j.
27. R. Long, J. Liu and O. V. Prezhdo, Unravelling the Effects of Grain Boundary and Chemical Doping on Electron–Hole Recombination in CH₃ NH₃ PbI₃ Perovskite by Time-Domain Atomistic Simulation, J. Am. Chem. Soc., 2016, 138(11), 3884–3890,  DOI:10.1021/jacs.6b00645.
28. J.-W. Lee, S.-H. Bae, N. De Marco, Y.-T. Hsieh, Z. Dai and Y. Yang, The Role of Grain Boundaries in Perovskite Solar Cells, Materials Today Energy, 2018, 7, 149–160,  DOI:10.1016/j.mtener.2017.07.014.
29. R. Brenes, D. Guo, A. Osherov, N. K. Noel, C. Eames, E. M. Hutter, S. K. Pathak, F. Niroui, R. H. Friend and M. S. Islam, et al., Metal Halide Perovskite Polycrystalline Films Exhibiting Properties of Single Crystals, Joule, 2017, 1(1), 155–167,  DOI:10.1016/j.joule.2017.08.006.
30. C. Momblona, L. Gil-Escrig, E. Bandiello, E. M. Hutter, M. Sessolo, K. Lederer, J. Blochwitz-Nimoth and H. J. Bolink, Efficient Vacuum Deposited P–i–n and n–i–p Perovskite Solar Cells Employing Doped Charge Transport Layers, Energy Environ. Sci., 2016, 9(11), 3456–3463,  10.1039/c6ee02100j.
31. Y. Hou, W. Chen, D. Baran, T. Stubhan, N. A. Luechinger, B. Hartmeier, M. Richter, J. Min, S. Chen and C. O. R. Quiroz, et al., Overcoming the Interface Losses in Planar Heterojunction Perovskite-Based Solar Cells, Adv. Mater., 2016, 28(25), 5112–5120,  DOI:10.1002/adma.201504168.
32. K. Tvingstedt, L. Gil-Escrig, C. Momblona, P. Rieder, D. Kiermasch, M. Sessolo, A. Baumann, H. J. Bolink and V. Dyakonov, Removing Leakage and Surface Recombination in Planar Perovskite Solar Cells, ACS Energy Lett., 2017, 2(2), 424–430,  DOI:10.1021/acsenergylett.6b00719.
33. H. Huang, M. I. Bodnarchuk, S. V. Kershaw, M. V. Kovalenko and A. L. Rogach, Lead Halide Perovskite Nanocrystals in the Research Spotlight: Stability and Defect Tolerance, ACS Energy Lett., 2017, 2(9), 2071–2083,  DOI:10.1021/acsenergylett.7b00547.
34. W.-J. Yin, T. Shi and Y. Yan, Unusual Defect Physics in CH₃NH₃PbI₃ Perovskite Solar Cell Absorber, Appl. Phys. Lett., 2014, 104(6), 063903,  DOI:10.1063/1.4864778.
35. J. R. Poindexter, R. L. Z. Hoye, L. Nienhaus, R. C. Kurchin, A. E. Morishige, E. E. Looney, A. Osherov, J.-P. Correa-Baena, B. Lai and V. Bulović, et al., High Tolerance to Iron Contamination in Lead Halide Perovskite Solar Cells, ACS Nano, 2017, 11(7), 7101–7109,  DOI:10.1021/acsnano.7b02734.
36. S. Bag and M. F. Durstock, Large Perovskite Grain Growth in Low-Temperature Solution-Processed Planar p–i–n Solar Cells by Sodium Addition, ACS Appl. Mater. Interfaces, 2016, 8(8), 5053–5057,  DOI:10.1021/acsami.5b11494.
37. J. T.-W. Wang, Z. Wang, S. Pathak, W. Zhang, D. W. deQuilettes, F. Wisnivesky-Rocca-Rivarola, J. Huang, P. K. Nayak, J. B. Patel and H. A. M. Yusof, et al., Efficient Perovskite Solar Cells by Metal Ion Doping, Energy Environ. Sci., 2016, 9(9), 2892–2901,  10.1039/c6ee01969b.
38. M. T. Klug, A. Osherov, A. A. Haghighirad, S. D. Stranks, P. R. Brown, S. Bai, J. T.-W. Wang, X. Dang, V. Bulović and H. J. Snaith, et al., Tailoring Metal Halide Perovskites through Metal Substitution: Influence on Photovoltaic and Material Properties, Energy Environ. Sci., 2017, 10(1), 236–246,  10.1039/c6ee03201j.
39. J. Zhang, M. Shang, P. Wang, X. Huang, J. Xu, Z. Hu, Y. Zhu and L. Han, N-Type Doping and Energy States Tuning in CH₃NH₃Pb₁–XSb2_x/3I₃ Perovskite Solar Cells, ACS Energy Lett., 2016, 1(3), 535–541,  DOI:10.1021/acsenergylett.6b00241.
40. P. K. Nayak, M. Sendner, B. Wenger, Z. Wang, K. Sharma, A. J. Ramadan, R. Lovrinčić, A. Pucci, P. K. Madhu and H. J. Snaith, Impact of Bi₃ + Heterovalent Doping in Organic–Inorganic Metal Halide Perovskite Crystals, J. Am. Chem. Soc., 2018, 140(2), 574–577,  DOI:10.1021/jacs.7b11125.
41. V. Duzhko, V. Y. Timoshenko, F. Koch and T. Dittrich, Photovoltage in Nanocrystalline Porous TiO₂, Phys. Rev. B, 2001, 64(7), 075204,  DOI:10.1103/physrevb.64.075204.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/physrevlett.77.3865.
43. P. Umari, E. Mosconi and F. D. Angelis, Relativistic GW Calculations on CH₃NH₃PbI₃ and CH₃NH₃SnI₃ Perovskites for Solar Cell Applications, Sci. Rep., 2014, 4, 4467,  DOI:10.1038/srep04467.
44. N. Ashari-Astani, S. Meloni, A. H. Salavati, G. Palermo, M. Grätzel and U. Rothlisberger, Computational Characterization of the Dependence of Halide Perovskite Effective Masses on Chemical Composition and Structure, J. Phys. Chem. C, 2017, 121(43), 23886–23895,  DOI:10.1021/acs.jpcc.7b04898.
45. K. Lee, É. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Higher-Accuracy van Der Waals Density Functional, Phys. Rev. B, 2010, 82(8), 081101,  DOI:10.1103/physrevb.82.081101.
46. T. Shi, W.-J. Yin and Y. Yan, Predictions for P-Type CH₃NH₃PbI₃ Perovskites, J. Phys. Chem. C, 2014, 118(44), 25350–25354,  DOI:10.1021/jp508328u.
47. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B, 1976, 13(12), 5188–5192,  DOI:10.1103/physrevb.13.5188.
48. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., QUANTUM ESPRESSO: A Modular and Open-Source Software Project for Quantum Simulations of Materials, J. Phys.: Condens. Matter, 2009, 21(39), 395502,  DOI:10.1088/0953-8984/21/39/395502.
49. C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, First-Principles Calculations for Point Defects in Solids, Rev. Mod. Phys., 2014, 86(1), 253–305,  DOI:10.1103/revmodphys.86.253.
50. C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Fully Ab Initio Finite-Size Corrections for Charged-Defect Supercell Calculations, Phys. Rev. Lett., 2009, 102(1), 016402,  DOI:10.1103/physrevlett.102.016402.
51. Files - SPHInX Add-ons - The SPHInX repository https://sxrepo.mpie.de/projects/sphinx-add-ons/files accessed Feb 3, 2018.
52. E. Mosconi, B. Merabet, D. Meggiolaro, A. Zaoui and F. De Angelis, First-Principles Modeling of Bismuth Doping in the MAPbI3 Perovskite, J. Phys. Chem. C, 2018 DOI:10.1021/acs.jpcc.8b01307.
53. P. R. F. Barnes, P. Calado, Driftfusion, http://https://github.com/barnesgroupICL/Driftfusion.
54. P. Calado, A. M. Telford, D. Bryant, X. Li, J. Nelson, B. C. O'Regan and P. R. F. Barnes, Evidence for Ion Migration in Hybrid Perovskite Solar Cells with Minimal Hysteresis, Nat. Commun., 2016, 7, 13831,  DOI:10.1038/ncomms13831.
55. M. Saliba, T. Matsui, J.-Y. Seo, K. Domanski, J.-P. Correa-Baena, M. K. Nazeeruddin, S. M. Zakeeruddin, W. Tress, A. Abate and A. Hagfeldt, et al., Cesium-Containing Triple Cation Perovskite Solar Cells: Improved Stability, Reproducibility and High Efficiency, Energy Environ. Sci., 2016, 9(6), 1989–1997,  10.1039/c5ee03874j.
56. W. Tress, N. Marinova, T. Moehl, S. M. Zakeeruddin, M. K. Nazeeruddin and M. Grätzel, Understanding the Rate-Dependent J–V Hysteresis, Slow Time Component, and Aging in CH₃NH₃PbI₃ Perovskite Solar Cells: The Role of a Compensated Electric Field, Energy Environ. Sci., 2015, 8(3), 995–1004,  10.1039/c4ee03664f.
57. B. C. O'Regan, P. R. F. Barnes, X. Li, C. Law, E. Palomares and J. M. Marin-Beloqui, Optoelectronic Studies of Methylammonium Lead Iodide Perovskite Solar Cells with Mesoporous TiO₂: Separation of Electronic and Chemical Charge Storage, Understanding Two Recombination Lifetimes, and the Evolution of Band Offsets during J–V Hysteresis, J. Am. Chem. Soc., 2015, 137(15), 5087–5099,  DOI:10.1021/jacs.5b00761.
58. H. J. Snaith, A. Abate, J. M. Ball, G. E. Eperon, T. Leijtens, N. K. Noel, S. D. Stranks, J. T.-W. Wang, K. Wojciechowski and W. Zhang, Anomalous Hysteresis in Perovskite Solar Cells, J. Phys. Chem. Lett., 2014, 5(9), 1511–1515,  DOI:10.1021/jz500113x.
59. E. L. Unger, E. T. Hoke, C. D. Bailie, W. H. Nguyen, A. R. Bowring, T. Heumüller, M. G. Christoforo and M. D. McGehee, Hysteresis and Transient Behavior in Current–Voltage Measurements of Hybrid-Perovskite Absorber Solar Cells, Energy Environ. Sci., 2014, 7(11), 3690–3698,  10.1039/c4ee02465f.
60. W. Tress, K. Leo and M. Riede, Influence of Hole-Transport Layers and Donor Materials on Open-Circuit Voltage and Shape of I–V Curves of Organic Solar Cells, Adv. Funct. Mater., 2011, 21(11), 2140–2149,  DOI:10.1002/adfm.201002669.
61. Y. Zhou, Z.-J. Yong, K.-C. Zhang, B.-M. Liu, Z.-W. Wang, J.-S. Hou, Y.-Z. Fang, Y. Zhou, H.-T. Sun and B. Song, Ultrabroad Photoluminescence and Electroluminescence at New Wavelengths from Doped Organometal Halide Perovskites, J. Phys. Chem. Lett., 2016, 7(14), 2735–2741,  DOI:10.1021/acs.jpclett.6b01147.
62. S. D. Stranks and A. Petrozza, Revisiting Photocarrier Lifetimes in Photovoltaics, Nat. Photonics, 2016, 10(9), 562,  DOI:10.1038/nphoton.2016.164.
63. W. Tress, M. Yavari, K. Domanski, P. Yadav, B. Niesen, J. P. C. Baena, A. Hagfeldt and M. Graetzel, Interpretation and Evolution of Open-Circuit Voltage, Recombination, Ideality Factor and Subgap Defect States during Reversible Light-Soaking and Irreversible Degradation of Perovskite Solar Cells, Energy Environ. Sci., 2018, 11(1), 151–165,  10.1039/c7ee02415k.
64. A. L. Abdelhady, M. I. Saidaminov, B. Murali, V. Adinolfi, O. Voznyy, K. Katsiev, E. Alarousu, R. Comin, I. Dursun and L. Sinatra, et al., Heterovalent Dopant Incorporation for Bandgap and Type Engineering of Perovskite Crystals, J. Phys. Chem. Lett., 2016, 7(2), 295–301,  DOI:10.1021/acs.jpclett.5b02681.
65. X. Miao, T. Qiu, S. Zhang, H. Ma, Y. Hu, F. Bai and Z. Wu, Air-Stable CsPb1–xBixBr₃ (0 ≤ x ≪ 1) Perovskite Crystals: Optoelectronic and Photostriction Properties, J. Mater. Chem. C, 2017, 5(20), 4931–4939,  10.1039/c7tc00417f.
66. W. Tress, Maximum Efficiency and Open-Circuit Voltage of Perovskite Solar Cells, in Organic-Inorganic Halide Perovskite Photovoltaics, ed. N.-G. Park, M. Grätzel and T. Miyasaka, Springer International Publishing, 2016, pp. 53–77,  DOI:10.1007/978-3-319-35114-8_3.
67. L. Kronik and Y. Shapira, Surface Photovoltage Phenomena: Theory, Experiment, and Applications, Surf. Sci. Rep., 1999, 37(1), 1–206,  DOI:10.1016/S0167-5729(99)00002-3.
68. S. Olthof and K. Meerholz, Substrate-Dependent Electronic Structure and Film Formation of MAPbI₃ Perovskites, Sci. Rep., 2017, 7, 40267,  DOI:10.1038/srep40267.
69. S. Prathapani, P. Bhargava and S. Mallick, Electronic Band Structure and Carrier Concentration of Formamidinium–Cesium Mixed Cation Lead Mixed Halide Hybrid Perovskites, Appl. Phys. Lett., 2018, 112(9), 092104,  DOI:10.1063/1.5016829.
70. W. E. Morgan, W. J. Stec and J. R. Van Wazer, Inner-Orbital Binding-Energy Shifts of Antimony and Bismuth Compounds, Inorg. Chem., 1973, 12(4), 953–955,  DOI:10.1021/ic50122a054.
71. P. Dey, V. Khorwal, P. Sen, K. Biswas and T. Maiti, Spectral Studies of Lead-Free Organic-Inorganic Hybrid Solid-State Perovskites CH₃NH₃Bi₂/3I₃ and CH₃NH₃Pb₁/2Bi1/3I₃: Potential Photo Absorbers, ChemistrySelect, 2018, 3(2), 794–800,  DOI:10.1002/slct.201702745.
72. R. W. Cheary and A. Coelho, IUCr, A Fundamental Parameters Approach to X-Ray Line-Profile Fitting, J. Appl. Crystallogr., 1992, 25(2), 109–121,  DOI:10.1107/s0021889891010804.
73. R. D. Shannon, IUCr, Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767,  DOI:10.1107/s0567739476001551.
74. S. Meloni, G. Palermo, N. Ashari-Astani, M. Grätzel and U. Rothlisberger, Valence and Conduction Band Tuning in Halide Perovskites for Solar Cell Applications, J. Mater. Chem. A, 2016, 4(41), 15997–16002,  10.1039/c6ta04949d.

---

Footnotes

† Electronic supplementary information (ESI) available: JV data of CH₃NH₃PbI₃, SEM data, XRD data, UPS data, details to the calculations. See DOI: 10.1039/c9ta01744e

‡ These authors contributed equally.

---