Open Access Article
Open Access ArticleInfluence of composition and structure on the thermal quenching of the 5d–4f emission of Eu2+ doped M–Si–N (M = alkali, alkaline earth, rare earth) nitridosilicates†
Otmar M.
ten Kate
 *a,
J. Ruud
van Ommen
*a,
J. Ruud
van Ommen
 a and
H. T. (Bert)
Hintzen
b
a and
H. T. (Bert)
Hintzen
b
aProduct and Process Engineering, Chemical Engineering, Applied Sciences, Delft University of Technology, Van der Maasweg 9, 2629 HZ Delft, The Netherlands. E-mail: o.m.tenkate@tudelft.nl
bLuminescent Materials Group, Radiation Science and Technology, Applied Sciences, Delft University of Technology, Mekelweg 15, 2629 JB Delft, The Netherlands
First published on 30th April 2019
Abstract
Experimental data from literature on the thermal quenching of the Eu2+ 5d–4f emission in the MxSiyNz (M = alkali, alkaline earth or rare earth) nitridosilicates have been collected and evaluated. No clear correlation was observed between the activation energy for thermal quenching and the Stokes shift, suggesting that non-radiative relaxation via a thermally excited cross-over from the 5d excited state to the 4f ground state is not the main reason for thermal quenching in the nitridosilicates. Based on literature data on rare-earth charge transfer transitions, host-lattice bandgap and Eu2+ 5d–4f emission energy, the energy difference between the Eu2+ 5d level and the bottom of the host-lattice conduction band has been determined. This energy difference correlates fairly well with the quenching temperature, suggesting that thermal ionization of the 5d electron to the conduction band is responsible for the thermal quenching of the Eu2+ 5d–4f emission in the nitridosilicates. The energy difference between the lowest 5d level and the bottom of the conduction band, and consequently the quenching temperature, increases with increasing Si/N ratio of the nitridosilicates. From this, it is concluded that the combined effect of the larger Stokes shift and the raise in energy of the bottom of the host lattice conduction band with increasing Si/N ratio is stronger than the decrease of the centroid shift and crystal field splitting of the Eu2+ 5d level.
1. Introduction
Phosphor-converted white light-emitting diodes (pc-wLEDs) have attracted significant attention in recent years as they are considered an environmental friendly, cost-effective and energy efficient way to generate white light.1–4 The first efficient pc-wLEDs, based on a blue LED chip and the yellow YAG:Ce3+ phosphor, still had a relatively poor colour rendering, as the white light from the LED missed a red component. Alternative approaches have therefore been the main interest of research and development, where a blue or UV LED chip is combined with a combination of (blue) red and green phosphors, leading to white light with a much better colour rendering.An important class of phosphors for these high colour rendering pc-wLEDs, are the Eu2+ doped nitridosilicates.5 These phosphors have the general composition MxSiyNz:Eu2+, where M can be an alkali, alkaline earth or rare-earth metal. Some of these nitridosilicate phosphors can very efficiently convert the UV or blue excitation light into longer wavelengths. Moreover, many of them are chemically stable in air (in particular those with low M/Si ratios) and the wide range of nitridosilicate structures, arising from the variety in Si/N ratios, allows for a large range of emission colours. Examples are blue-emitting SrSi6N8:Eu2+,6 green-emitting LaSi3N5:Eu2+,7 yellow-emitting SrYSi4N7:Eu2+,8 and red-emitting SrSiN2:Eu2+.9 The red-emitting Sr2Si5N8:Eu2+ phosphor has been commercially applied as an LED phosphor. As an extension to the Eu2+ doped nitridosilicates, silicon can be partially substituted by aluminium and nitrogen by oxygen, leading to the even wider class of sialon phosphors. Well-known examples hereof are CaAlSiN3:Eu2+,10 (AE)Si2O2N2:Eu2+ (AE = Ca, Sr, Ba),11 Ca-α-sialon:Eu2+,12,13 and β-sialon:Eu2+.14
A very important property for LED phosphors, affecting the performance of in particular high-power LEDs, is the temperature dependency of the emission intensity. It is well known that with increasing temperature, the luminescence efficiency of the phosphors generally tends to decrease. This is especially a drawback for pc-wLEDs containing multiple phosphors, as it will not only decrease the light output, but will also change the overall colour emitted by the LED. Various strategies have therefore been developed to obtain thermally stable LED phosphors,15 like for the blue-emitting Na3Sc2(PO4)3:Eu2+ phosphor that does not have any decrease of emission intensity up to 200 °C.16 As for the (oxy)-nitride phosphors, the commercially available Sr2Si5N8:Eu2+, β-sialon:Eu2+, CaAlSiN3:Eu2+ and SrSi2O2N2:Eu2+ phosphors show relatively good thermal stability, while for many other phosphors the emission intensity rapidly decreases with temperature.
The decrease of luminescence intensity with temperature can have two principally different reasons:17 (1) by a degradation of the phosphor at higher temperature often caused by a reaction with water or oxygen, or (2) by thermal quenching of the luminescence. The first one is a permanent decrease of the luminescence, even if the phosphor is cooled down again, and depends on the (thermo-)chemical stability of the phosphor; the second one, the thermal quenching, is not permanent as the initial intensity restores when cooling down the phosphor. In this manuscript we will focus on this thermal quenching, with specific attention to the influence of composition and structure.
Various mechanisms have been proposed in literature that can be the origin of the thermal quenching of the Eu2+ 5d–4f emission. The two main ones are: (1) direct radiationless relaxation from the 5d excited state to the 4f ground state via a thermally activated cross-over,18,19 and (2) thermal ionization by excitation of an Eu2+ electron from the 5d level to the conduction band.20 In literature, both these models have been used to explain the differences in thermal quenching behaviour of the Eu2+ 5d–4f emission for the nitridosilicates. Thermal quenching via a thermally activated cross-over was considered by for example Fukuda,21 who concluded that the thermal quenching in various Eu2+ doped Sr-containing sialon phosphors is influenced by the phonon frequency. On the other hand, thermal quenching via thermal ionization to the conduction band was, for example, considered by Tolhurst et al.,22 using X-ray absorption spectroscopy to show that the lowest Eu2+ 5d level is closer to the bottom of the conduction band in SrMg3SiN4:Eu2+ than in Li2Ca2Mg2Si2N6:Eu2+, explaining the stronger thermal quenching for SrMg3SiN4:Eu2+ as compared to Li2Ca2Mg2Si2N6:Eu2+. The thermal quenching of Ce3+ and Eu2+ doped oxide and nitride phosphors has been reviewed recently by Wang et al.,23 discussing various strategies to obtain phosphors with high thermal stability. In addition, Yan24 recently reviewed and explained the causes of the shift of the Eu2+ and Ce3+ emission maxima with temperature for many different phosphors, including various nitridosilicates.
Recently, we have shown that the degree of condensation, expressed by the Si/N ratio, acts as a principle parameter that determines the coordination number of N with Si (NSix), the Si–N and M–N bond lengths and bandgap of the MxSiyNz nitridosilicates,25 as well as the energy of the Eu2+ 4f–5d absorption and 5d–4f emission in the Eu2+ doped nitridosilicates.26 The dependence on the Si/N ratio was explained by considering that with increasing Si/N ratio the coordination number of N with Si increases, which results in more N electrons that participate in the bonding with Si and consequently less N electrons that are available for M–N bonding. This makes the M–N bonds longer and less covalent, while the Si–N bonds become shorter, consequently resulting in a wider bandgap of the nitridosilicates.25 The less covalent and longer Eu–N bonds for higher Si/N ratio also result in an increase of the Eu2+ 4f–5d absorption and 5d–4f emission energy due to a weaker nephelauxetic effect and a smaller crystal field splitting. The Stokes shift becomes larger with increasing Si/N ratio as the local rigidity of the site on which Eu2+ is located, decreases due to the longer Eu–N bonds.26
In this work we will extend this model by studying the effect of the Si/N ratio on the thermal quenching of the Eu2+ 5d–4f emission of the Eu2+ doped nitridosilicates. First, in Section 2, the two main mechanisms are discussed that have been proposed in literature as responsible for the thermal quenching of the Eu2+ 5d–4f emission. In Section 3, we summarize and evaluate data from literature on the thermal quenching of the Eu2+ 5d–4f emission in the nitridosilicates and determine the activation energy for thermal quenching as well as the quenching temperature. In Section 4 we evaluate and discuss the correlation between the quenching temperature and the degree of condensation (Si/N ratio) for the nitridosilicates, and show that this correlation can best be explained with the thermal ionization model.
2. Mechanisms of the thermal quenching of the Eu2+ 5d–4f emission
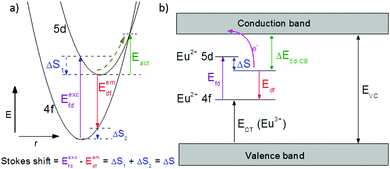
In literature, different mechanisms have been proposed that may be responsible for the decrease of Eu2+ 5d–4f emission intensity with increasing temperature. The main ones are: (1) thermally activated non-radiative relaxation from the Eu2+ 5d excited state to the 4f ground state via the crossing point of the 5d and 4f parabola, and (2) thermal ionization of the Eu2+ 5d electron to the host lattice conduction band. These mechanisms will be briefly discussed in Sections 2.1 and 2.2, respectively. In Section 2.3 other factors will be discussed that may influence the temperature dependency of the emission intensity.2.1 Thermal quenching by direct radiationless relaxation to the ground state
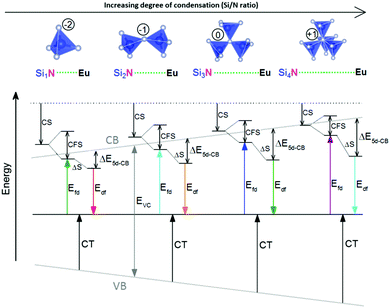
One of the first mechanisms proposed in literature that can be the cause of the thermal quenching of the Eu2+ 5d–4f emission, is the direct relaxation from the 5d excited state to the 4f ground state via a thermally activated cross-over.18,19,27 This mechanism can be described using a quantum mechanical single configurational coordinate (QMSCC) model, illustrated with the configurational coordinate diagram in Fig. 1a. After excitation of an Eu2+ electron from the 4f ground state to the 5d excited states, relaxation to the lowest 5d level will occur. From here 5d–4f emission can take place. According to the Franck–Condon principle these electronic transitions are vertical because the electronic transitions are much faster than any change in positions of the atomic nuclei. As an alternative to 5d–4f emission, the crossing point between the 4f and the 5d parabola may be reached if the thermal energy is higher than the energy difference between the minimum of the 5d parabola and the crossing point with the 4f ground state parabola, resulting in a non-radiative return from the 5d excited state to the 4f ground state and thus thermal quenching of the 5d–4f emission. In this model, the 4f and 5d parabolas can be described with eqn (1) and (2) respectively:28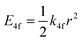 | (1) |
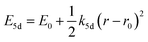 | (2) |
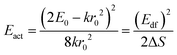 | (3) |
2.2 Thermal quenching by thermal ionization to the host lattice conduction band
Another mechanism considered in literature to be responsible for the quenching of the Eu2+ 5d–4f emission, is the thermal ionization of the Eu2+ 5d electron to the host lattice conduction band,20,29 illustrated in Fig. 1b. If the lowest 5d state is relatively close to the bottom of the conduction band, there is only a small energy barrier to overcome in order to bring the electron from the 5d state into the conduction band. Once this ionization has occurred, the return to the ground state of Eu2+ occurs non-radiatively, hence the Eu2+ 5d–4f emission is quenched. In the case of thermal ionization, the activation energy for thermal quenching will depend on the energy difference between the lowest relaxed (since the relaxation is much faster than the thermal ionization) Eu2+ 5d state and the bottom of the host-lattice conduction band. If the energy difference is large, the energy barrier for thermal quenching will also be large, and vice versa. If the lowest relaxed 5d state is located inside the conduction band, auto-ionization may occur even at low temperature, and the emission will be completely quenched.30The energy difference between the lowest non-relaxed 5d state and the bottom of the host lattice conduction band is, by definition, equal to the bandgap minus the Eu2+ 4f–5d absorption energy and minus the energy between the top of the host lattice valence band and the Eu2+ 4f ground state,20 as illustrated in Fig. 1b. The energy between the top of the valence band and the Eu2+ 4f ground state equals the Eu3+ charge transfer (CT) energy, for the transfer of an electron from a coordinating anion to Eu3+.31 In order to obtain the energy difference ΔE5d-CB between the lowest relaxed 5d state and the bottom of the conduction band, the energy for relaxation needs to be taken into account, which can be approximated by the Stokes shift ΔS (ΔS = Efd − Edf).20 From the above we obtain the following approximate relationship (see also Fig. 1b):
| ΔE5d-CB = EVC − Edf − ECT | (4) |
The energy of the lowest relaxed 5d state is determined by the centroid shift (CS) and crystal field splitting (CFS) of the 5d levels, together with the Stokes shift. CS and CFS both decrease with increasing Eu–X distance (X = anion).32,33 Since most compounds tend to expand with increasing temperature, resulting in larger Eu–X distances, CS and CFS both become smaller with increasing temperature, meaning that the Eu2+ 4f–5d energy increases with temperature. According to the Varshni equation,34 the temperature dependency of the bandgap is given by:
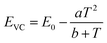 | (5) |
2.3 Other causes of thermal quenching
Besides the intrinsic thermal quenching caused by either thermal ionization from the 5d to the conduction band or by direct relaxation to the ground state via the crossing point of the 4f and 5d parabola, other mechanisms can also cause a decrease of emission intensity with increasing temperature. One of these is temperature dependent energy transfer. Since the probability of energy transfer is likely to increase with increasing temperature, the transfer towards defects on which the Eu2+ 5d–4f emission is quenched, will also increase. Thermally activated concentration quenching is especially significant if the Eu2+ concentration is relatively high, in which case there is a lot of energy transfer between Eu2+ ions. In that case the thermal quenching is strongly dependent on the Eu concentration, as has been observed in for example Sr2Si5N8:Eu2+.35 So in order to identify the intrinsic thermal quenching behaviour, the measurements have to be performed with a low activator concentration. However, concentration dependence may even occur at lower concentrations around 1%. Thermally activated concentration quenching has for example been shown to be responsible for the decrease of luminescence intensity in YAG:1%Ce3+ between room temperature and 600 K, even though the intrinsic quenching temperature in YAG:Ce3+ is well above 600 K.36Another effect, which can decrease the observed emission intensity (external quantum efficiency) without decreasing the internal quantum efficiency of the phosphor, is a temperature dependency of the absorption strength. This may be due to for example a temperature dependency of the oscillator strength, or as a result of a shift of the absorption band maximum as a consequence of a temperature dependency of the centroid shift or the crystal field splitting of the 5d levels due to expansion of the host lattice at higher temperatures. Note that the absorption strength may also increase with increasing temperature, resulting in an increase of the emission intensity.
3. Eu2+ absorption and emission in the nitridosilicates
3.1 Thermal quenching data of the Eu2+ doped nitridosilicate phosphors
Data have been collected from literature on the thermal quenching of the Eu2+ 5d–4f emission of all Eu2+ doped nitridosilicate phosphors with the general composition MxSiyNz:Eu2+ (M = alkali, alkaline earth or rare earth), see Table 1. As the thermal quenching is generally strongly dependent on the Eu2+ concentration with a stronger thermal quenching for higher concentrated samples,37 we have limited ourselves to samples with a low Eu2+ concentration. Structural information, as well as information on the optical properties of the Eu2+ doped nitridosilicate phosphors is reviewed in our previous publications.25,26 For some nitridosilicate phosphors, the thermal quenching of the luminescence has been reported by various authors in multiple different publications. If there are no significant differences between the reported results, we use in this work the thermal quenching from the paper that shows the most detailed information and considers the longest temperature range, as indicated in Table 1. In case there are significant differences (Ba2Si5N8:Eu2+, SrScSi4N7:Eu2+) or in case different, non-comparable temperature ranges were considered (Sr2Si5N8:Eu2+), both results are shown in Table 1. For the interest of the reader, Table 1 also lists all other references in which thermal quenching data have been published. Note that we have included, for the sake of completeness, various Mg and Li containing nitridosilicates, such as SrMg3SiN4:Eu2+ and LiSi2N3:Eu2+, even though one may argue that some of these are not really nitridosilicates, but magneso- or litho-nitridosilicates, as Mg and Li may form MgN4 and LiN4 tetrahedra similar to the SiN4 tetrahedra and can thus be considered part of the framework.| Host lattice | Temp. range (K) | Thermal quenching category | Ref. used for evaluation | Other ref. |
|---|---|---|---|---|
*![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Thermal quenching is already severe at the lowest recorded temperature (i.e. room temperature).a Emission intensity of Ca2Si5N8:Eu as a function of temperature has also been reported for the low temperature range (10–300 K) by Wei et al.47 However, only for a very high Eu concentration (Ca1.9Eu0.1Si5N8). Thermal quenching is already severe at the lowest recorded temperature (i.e. room temperature).a Emission intensity of Ca2Si5N8:Eu as a function of temperature has also been reported for the low temperature range (10–300 K) by Wei et al.47 However, only for a very high Eu concentration (Ca1.9Eu0.1Si5N8). |
||||
| α-Si3N4 | 298–573 | 2 | 38 | — |
| LiSi2N3* | 298–473 | 1 | 39 | 40 |
| CaSiN2* | 293–573 | 3 | 41 | — |
| Ca16Si17N34 | 298–523 | 3 | 42 | — |
| Ca2Si5N8 | 295–573a | 3 | 43 | 44–47 |
| SrSiN2 | 298–473 | 1 | 48 | — |
| Sr2Si5N8 | 298–573 | 1 | 43 | 44, 45 and 49–57 |
| –Sr2Si5N8 | 5–433 | 1 | 58 | |
| SrSi6N8 | 298–573 | 1 | 6 | — |
| Ba2Si5N8 | 298–573 | 1 | 44 | 43–45 and 59 |
| –Ba2Si5N8 | 4–280 | 1 | 60 | — |
| –Ba2Si5N8 | 80–500 | 4 | 61 | — |
| BaSi7N10 | 80–480 | 1 | 62 | 63 and 64 |
| BaSi6N8 | 298–573 | 3 | 65 | — |
| Sr8Mg7Si9N22* | 298–523 | 1 | 66 | — |
| SrMg3SiN4 | 4–310 | 3 | 67 | 68 |
| BaMg3SiN4 | 4–600 | 3 | 69 | — |
| Li4Ca3Si2N6 | 293–523 | 1 | 70 | — |
| Li2CaSi2N4* | 298–423 | 1 | 71 | — |
| Li2SrSi2N4* | 298–473 | 1 | 72 | — |
| Li2Ca2Mg2Si2N6 | 303–563 | 1 | 22 | — |
| SrScSi4N7 | 293–453 | 1 | 73 | — |
| SrScSi4N7 | 298–423 | 1 | 74 | — |
| CaYSi4N7* | 293–443 | 2 | 75 | — |
| SrYSi4N7 | 298–523 | 3 | 76 | 73 and 75 |
| BaYSi4N7* | 298–443 | 1 | 75 | — |
| La2.23Ca1.155Si6N11 | 4–300 | 3 | 77 | — |
If the thermal quenching of the Eu2+ 5d–4f emission occurs via one dominating thermally activated process, the temperature dependent internal quantum efficiency can be described by the equation:20
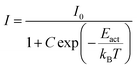 | (6) |
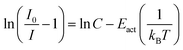 | (7) |
When considering an ln(I0/I − 1) versus (1/kBT) plot of the temperature dependent emission intensity data of the Eu2+ doped nitridosilicates, four different categories can be distinguished based on the shape of the curve, as illustrated in Fig. 2.
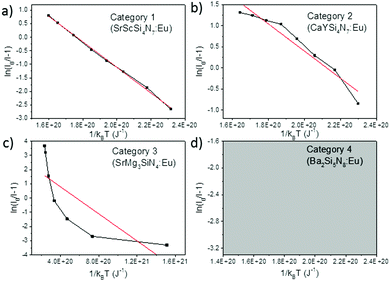 | ||
| Fig. 2 Examples of the four different categories of thermal quenching on an ln(I0/I − 1) versus (1/kBT) plot: category 1 (linear), category 2 (downward slope with an increasing gradient), category 3 (downward slope with a decreasing gradient), and category 4 (emission intensity initially increases with increasing temperature, which cannot be displayed on an ln(I0/I − 1) vs. (1/kBT) plot). The black lines represent the measured data, the red lines represent the fits with eqn (7). | ||
• Category 1: the data (Fig. 2a) are on a straight line, of which the slope is equal to −Eact and the intersect with the y-axis is equal to ln(C), suggesting that the thermal quenching can be well described by eqn (6).
• Category 2: the data (Fig. 2b) are on a downward slope with an increasing gradient, i.e. the slope is less steep at higher temperature (small 1/kBT) than at lower temperature (large 1/kBT).
• Category 3: the data (Fig. 2c) are on a downward slope with a decreasing gradient, i.e. the slope is steeper at higher temperature (small 1/kBT) than at lower temperature (large 1/kBT).
• Category 4: the emission intensity initially increases with increasing temperature, giving I0 < I, which cannot be displayed on an ln(I0/I − 1) vs. (1/kBT) plot (Fig. 2d).
As listed in Table 1, the thermal quenching behaviour of LiSi2N3:Eu2+, SrSiN2:Eu2+, Sr2Si5N8:Eu2+, SrSi6N8:Eu2+, BaSi7N10:Eu2+, Sr8Mg7Si9N22:Eu2+, Li2CaSi2N4:Eu2+, Li4Ca3Si2N6:Eu2+, SrScSi4N7:Eu2+ and BaYSi4N7:Eu2+ belong to category 1 as the data fall (almost) on a straight line on an ln(I0/I − 1) versus (1/kBT) plot, while in Li2Ca2Mg2Si2N6:Eu2+ and Li2SrSi2N4:Eu2+ the data fluctuate around a straight line. For CaYSi4N7:Eu2+ and α-Si3N4:Eu2+ there is an increasing gradient with increasing (1/T) (category 2), while for CaSiN2:Eu2+, Ca16Si17N34:Eu2+, Ca2Si5N8:Eu2+, BaSi6N8:Eu2+, SrMg3SiN4:Eu2+, BaMg3SiN4:Eu2+, SrYSi4N7:Eu2+ and La2.23Ca1.155Si6N11:Eu2+ there is a decreasing gradient with increasing (1/T) (category 3). In the low temperature range (80–300 K) for Ba2Si5N8:Eu2+ the integrated emission intensity initially increases with increasing temperature according to Wang et al.61 (category 4). In contrast, Piao et al.60 report a slow gradual decrease of integrated emission intensity with increasing temperature between 4 K and 280 K. For all authors, above 300 K the emission intensity decreases with increasing temperature, following approximately a linear trend on an ln(I0/I − 1) vs. (1/kBT) plot (i.e. category 1). A more detailed analysis of the thermal quenching of Ba2Si5N8:Eu2+ can be found in the ESI† (Section S1.4).
3.2 Activation energy and quenching temperature
In the ESI† (Section S1) the thermal quenching of all the nitridosilicates is analysed in more detail, with regard to the four different thermal quenching categories discussed above, and the activation energy has been determined. The main conclusions from this analysis are summarized in this section.For the nitridosilicates belonging to category 2 or 3, for which there is a deviation from a straight line on an ln(I0/I − 1) vs. (1/kBT) plot (Fig. 2b and c), various causes have been considered that may explain the deviation from the linear behaviour. These possible causes are: (1) a temperature dependency of the activation energy, (2) a temperature dependency of the absorption strength, (3) the presence of Eu2+ in different crystallographic environments with different thermal quenching behaviour, (4) temperature dependent energy transfer, and (5) the presence of secondary (anomalous) emission. In order to determine whether these possible causes can reasonably explain the observed deviations from the linear behaviour, we have made adaptations to eqn (6) and checked whether the thermal quenching data can be well described with these adapted equations (see ESI†). From our analysis, we can conclude that the deviations from the non-linear behaviour observed for the two compounds of category 2 (α-Si3N4:Eu2+ and CaYSi4N7:Eu2+) are attributed to disorder in these structures, which gives rise to Eu2+ ions in many slightly different crystallographic environments. Of the compounds of category 3, the non-linear quenching in BaMg3SiN4:Eu2+, and possibly also SrMg3SiN4:Eu2+, is caused by the presence of trapped-exciton emission. The non-linear behaviour for Ca2Si5N8:Eu2+, Ca16Si17N34:Eu2+ and La2.23Ca1.155Si6N11:Eu2+, which also belong to category 3, is likely due to the presence of Eu2+ at different crystallographic sites.
As for the nitridosilicates of thermal quenching category 1, i.e. the emission intensity data approximately follow a linear trend on an ln(I0/I − 1) vs. (1/kBT) plot (Fig. 2a), it is noted that the value of C obtained from either fitting with eqn (6) or (7), shows large differences among the various nitridosilicates. For Li2Ca2Mg2Si2N6:Eu2+, Li4Ca3Si2N6:Eu2+ and BaYSi4N7:Eu2+ the value of C is relatively large (>104). However, for the other compounds, C is much smaller and ranges between 1 and 104. C is equal to the ratio of the attempt rate for thermal quenching and the radiative decay rate of the 5d–4f emission of Eu2+. The first one is typically in the order of 1013 s−1,20 while the latter one is in the order of 106 s−1,20 giving a value of C of about 107. Although these rates will vary among the different hosts, it seems not realistic that C can be more than a factor 1000 smaller, i.e. smaller than 104. It was found that a temperature dependency of the absorption strength or temperature dependency of the activation energy cannot explain the unrealistically low value of C. Thermally activated concentration quenching can however not be excluded as the cause for the low value of C and is suggested to even be the main reason for the thermal quenching observed in BaSi7N10:Eu2+. For Sr2Si5N8:Eu2+, and possibly also Li2CaSi2N4:Eu2+, Li2SrSi2N4:Eu2+ and Sr8Mg7Si9N22:Eu2+ the presence of Eu2+ on different crystallographic sites, in combination with a temperature dependent energy transfer between these sites, can be assigned as the cause of the low observed value of C.
The activation energies for the intrinsic quenching of the Eu2+ 5d–4f emission in the nitridosilicates, as obtained from the analysis in the ESI,† are listed in Table 2. The activation energy for thermal quenching is generally below 0.5 eV. However, if the activation energy for thermal quenching is calculated with eqn (3), which is based on the model that thermal quenching occurs by direct relaxation from the 5d excited state to the 4f ground state via a thermally activated cross-over, a significantly higher activation energy is obtained (typically around 6 eV), see ESI,† Fig. S1b. In addition, there is no clear correlation between the activation energy and the Stokes shift. This indicates that the thermally activated cross-over model cannot be the main cause of thermal quenching in the nitridosilicates.
| Compound | E act (eV) | T 50% (K) |
|---|---|---|
| α-Si3N4 | ? | >600 |
| LiSi2N3 | >0.23 | ∼420 |
| CaSiN2 | ? | ∼390 |
| Ca16Si17N34 | ? | 500 |
| Ca2Si5N8 | ? | 460 |
| SrSiN2 | >0.22 | 450 |
| Sr2Si5N8 (site 1) | 0.42 | 600 |
| Sr2Si5N8 (site 2) | 0.34 | 450 |
| SrSi6N8 | >0.25 | 440 |
| Ba2Si5N8 | ? | 530 |
| BaSi7N10 | ? | >600 |
| BaSi6N8 | ? | 510 |
| Sr8Mg7Si9N22 | >0.09 | ∼170 |
| SrMg3SiN4 | 0.28 | 240 |
| BaMg3SiN4 | 0.46 | 400 |
| Li4Ca3Si2N6 | 0.44 | 460 |
| Li2CaSi2N4 | >0.17 | ∼200 |
| Li2SrSi2N4 | >0.12 | ∼290 |
| Li2Ca2Mg2Si2N6 | 0.45 | 420 |
| SrScSi4N7 | >0.22 | 380 |
| CaYSi4N7 | ? | <300 |
| SrYSi4N7 | ? | 460 |
| BaYSi4N7 | 0.31 | ∼370 |
| La2.23Ca1.155Si6N11 | ? | 260 |
The quenching temperature (T50%) of the Eu2+ 5d–4f emission, i.e. the temperature at which half of the emission is quenched, has been determined for the nitridosilicates from literature data (see ESI†) and is shown in Table 2. Following eqn (6), T50% can also be calculated from Eact and C:
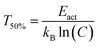 | (8) |
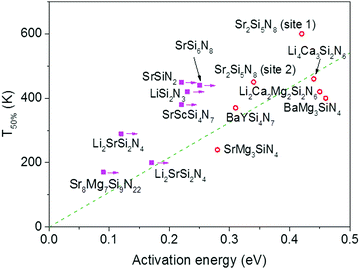 | ||
| Fig. 3 Temperature at which 50% of the Eu2+ 5d–4f emission is quenched (T50%) versus the activation energy for thermal quenching (Eact) for the Eu2+ doped nitridosilicates. A compound is given a magenta solid square if the activation energy represents a minimum value. Other compounds are given a red open circle. See ESI† for more details. The dashed green line is a linear fit of the red data points through the origin with the equation T50% (K) = 1082 × Eact (eV). | ||
4. Cause of the thermal quenching and its dependence on the nitridosilicate composition
4.1 Composition dependence of the thermal quenching
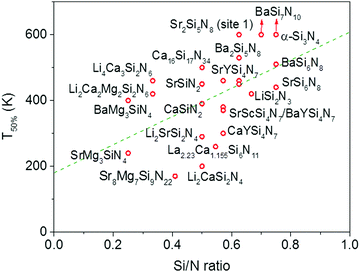
In Fig. 4 the quenching temperature (T50%) is given as a function of the Si/N ratio. With increasing degree of condensation (Si/N ratio) the quenching temperature tends to increase. For example, SrMg3SiN4:Eu2+ with low Si/N ratio of 0.25 has a T50% of about 200 K, while α-Si3N4:Eu2+ with high Si/N ratio of 0.75 has a T50% above 600 K. The scattering is however large and T50% of LiSi2N3:Eu2+ with relatively high Si/N ratio of 0.67 is about the same as T50% of BaMg3SiN4:Eu2+ (about 400 K) with relatively low Si/N ratio of 0.25. In the next sections we will discuss what the mechanism is of the thermal quenching in the nitridosilicates and why there seems to be a correlation between the Si/N ratio and quenching temperature.4.2 Thermal quenching by thermal ionization to the conduction band
If thermal ionization of the Eu2+ 5d electron to the host lattice conduction band is responsible for the thermal quenching of the Eu2+ 5d–4f emission in the nitridosilicates, one would expect a relation between the quenching temperature or activation energy at one side, and the energy difference between the lowest Eu2+ 5d level and the bottom of the host lattice conduction band (ΔE5d-CB) at the other side. Following eqn (4) in Section 2.2, ΔE5d-CB can be approximated from the bandgap (EVC), the Eu2+ 5d–4f emission energy (Edf) and the Eu3+ charge transfer energy (ECT). The bandgap and the emission energy have been measured for many nitridosilicates, but unfortunately the energy of the Eu3+ CT transition cannot be measured directly for most nitridosilicates. It namely requires the presence of Eu3+, while in most nitridosilicates Eu is only present in the divalent state, with the notable exception of Li2SiN2:Eu3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 78 and (Eu2+)(Eu3+)SiN3.79 Fortunately, the Eu3+ CT transition in a specific nitridosilicate host lattice can be estimated based on the experimentally observed CT transitions of Sm3+ and Yb3+ in the same nitridosilicate host lattice. The CT energy of a Ln3+ (Ln = lanthanide) ion is namely equal to the energy difference between the top of the host lattice valence band and the 4f ground state of the corresponding divalent Ln2+ ion,80 while the energy differences between the different lanthanides does not change between compounds. The Eu3+ CT energy can therefore be calculated from the CT transitions of Sm3+ or Yb3+, using the fixed energy differences between the 4f ground states of Eu2+, Sm2+ and Yb2+: for every compound the Sm3+ CT is 1.25 eV higher in energy than the Eu3+ CT in the same compound, and the Yb3+ CT is 0.43 eV higher in energy than the Eu3+ CT in the same compound.81 Using these CT transitions, ΔE5d-CB can then be calculated based on eqn (4). The results are presented in Table 3.
78 and (Eu2+)(Eu3+)SiN3.79 Fortunately, the Eu3+ CT transition in a specific nitridosilicate host lattice can be estimated based on the experimentally observed CT transitions of Sm3+ and Yb3+ in the same nitridosilicate host lattice. The CT energy of a Ln3+ (Ln = lanthanide) ion is namely equal to the energy difference between the top of the host lattice valence band and the 4f ground state of the corresponding divalent Ln2+ ion,80 while the energy differences between the different lanthanides does not change between compounds. The Eu3+ CT energy can therefore be calculated from the CT transitions of Sm3+ or Yb3+, using the fixed energy differences between the 4f ground states of Eu2+, Sm2+ and Yb2+: for every compound the Sm3+ CT is 1.25 eV higher in energy than the Eu3+ CT in the same compound, and the Yb3+ CT is 0.43 eV higher in energy than the Eu3+ CT in the same compound.81 Using these CT transitions, ΔE5d-CB can then be calculated based on eqn (4). The results are presented in Table 3.
| Host lattice | Experimental CT (eV) | Ref. | Derived CT of Eu3+ (eV) | ΔE5d-CB (eV) |
|---|---|---|---|---|
| a ΔE5d-CB of Li2SiN2 cannot be calculated since Edf is unknown. | ||||
| Li2SiN2 | 3.47 (Eu3+) | 78 | 3.47 | |
| Ca2Si5N8 | 4.1 (Sm3+), 3.3 (Yb3+) | 82 | 2.87 | 0.43 |
| LaSi3N5 | 3.1 (Yb3+) | 83 | 2.67 | 0.03 |
| Sr2Si5N8 (site 1) | 3.6 (Sm3+) | 82 | 2.35 | 0.85 |
| SrMg3SiN4 | 3.54 (Sm3+) | 68 | 2.29 | −0.19 |
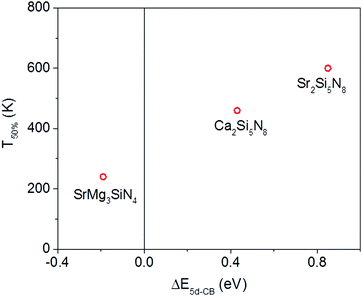
Of the five compounds listed in Table 3, there are three compounds (SrMg3SiN4:Eu2+, Ca2Si5N8:Eu2+ and Sr2Si5N8:Eu2+) of which we also know the quenching temperature of the Eu2+ 5d–4f emission. For these three compounds the calculated ΔE5d-CB has been plotted versus the quenching temperature (Fig. 5). As can be clearly seen, a linear relationship is observed between ΔE5d-CB and the quenching temperature, as expected from eqn (8), supporting that the thermal quenching is caused by thermal activation of the Eu2+ 5d electron to the host lattice conduction band.
Unfortunately, the amount of nitridosilicates for which the CT energy of Eu3+ can be directly calculated from experimental data is very limited. However, we can make an estimation of the CT energy of Eu3+ for the other nitridosilicates, considering that the CT energy is determined by: (1) the distance of Eu to the neighbouring anions and (2) the nature (i.e. the electronegativity) of the anions involved. The Eu–N distance is determined by the size of the cation M (M = Li, Ca, Sr, Ba, La) for which Eu is substituted and can therefore be approximated by the average distance (RM–N) of the metal M towards the coordinating N anions, which can be obtained from crystallographic data (Table 4). Since all neighbouring anions are N3− anions, their electronegativity will only vary because of differences in the N by Si coordination number. As explained in our previous work,25 the N by Si coordination number is directly proportional to the Si/N ratio (κ). Therefore, in order to estimate the Eu3+ CT energy of other nitridosilicates, we need to know how the CT energy depends on the average M–N distance and how it depends on the Si/N ratio. Since Ca2Si5N8 and Sr2Si5N8 have the same Si/N ratio, the CT energy should mainly depend on the average M–N distance. Using their CT energy (Table 3) and average RM–N (Table 4), the following relation is obtained:
| ECT(Eu3+) (eV) = 9.3 − 2.4RM–N (Å) if κ = 0.625 | (9) |
| ECT(Eu3+) (eV) = 2.1 + 0.8κ if RM–N = 2.802 Å | (10) |
| Compound | R M–N (Å) | κ | Eu3+ CT (eV) | ΔE5d-CB (eV) |
|---|---|---|---|---|
| a ΔE5d-CB of Eu2+ in Li2SiN2 cannot be determined as no Eu2+ 5d–4f emission has been reported for Li2SiN2; the Eu3+ CT value for Li2SiN2 was reported in literature. b Eu3+ CT value was derived obtained from Yb3+ or Sm3+ CT reported in literature. Other CT values have been obtained by calculation (eqn (11)). | ||||
| Li2SiN2 | 2.160 | 0.5 | 3.47a | |
| LiSi2N3 | 2.263 | 0.667 | 3.9 | 0.7 |
| CaSiN2 | 2.583 | 0.5 | 2.6 | −0.3 |
| Ca16Si17N34 | 2.579 | 0.5 | 3.0 | −0.3 |
| Ca2Si5N8 | 2.681 | 0.625 | 2.87b | 0.4 |
| SrSiN2 | 2.859 | 0.5 | 2.3 | 0.8 |
| Sr2Si5N8 (site 1) | 2.928 | 0.625 | 2.35b | 0.9 |
| Sr2Si5N8 (site 2) | 2.866 | 0.625 | 2.35b | 0.7 |
| SrSi6N8 | 3.028 | 0.75 | 2.1 | −1.2 |
| Ba2Si5N8 | 2.982 | 0.625 | 2.2 | 0.8 |
| BaSi7N10 | 3.287 | 0.7 | 1.5 | 1.7 |
| Sr8Mg7Si9N22 | 2.864 | 0.409 | 2.3 | −0.2 |
| SrMg3SiN4 | 2.802 | 0.25 | 2.29b | −0.2 |
| BaMg3SiN4 | 2.953 | 0.25 | 1.9 | 0.3 |
| Li4Ca3Si2N6 | 2.706 | 0.333 | 2.6 | −0.2 |
| Li2CaSi2N4 | 2.528 | 0.5 | 3.1 | −0.2 |
| Li2SrSi2N4 | 2.722 | 0.5 | 2.7 | 0.1 |
| Li2Ca2Mg2Si2N6 | 2.588 | 0.333 | 2.9 | 0.0 |
| SrYSi4N7 | 3.012 | 0.571 | 2.0 | 0.9 |
| BaYSi4N7 | 3.014 | 0.571 | 2.0 | 0.8 |
| La2.23Ca1.155Si6N11 | 2.642 | 0.545 | 2.9 | −0.4 |
By combining eqn (9) and (10) the following relation is obtained for the Eu3+ CT energy in the nitridosilicates:
| ECT(Eu3+) (eV) = 8.8 − 2.4RM–N (Å) + 0.8κ | (11) |
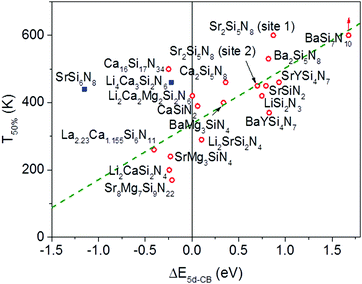
In Fig. 6 the temperature at which 50% of the luminescence is quenched (T50%) is plotted versus ΔE5d-CB for all Eu2+ doped nitridosilicate phosphors of Table 3. From the graph, as expected, an increase of the quenching temperature can be observed with increasing energy difference between the lowest Eu2+ 5d state and the bottom of the host lattice conduction band. Most of the data points follow the trend line. This again supports that the thermal ionization of the 5d electron to the conduction band is responsible for the thermal quenching in these nitridosilicates.
For SrSi6N8:Eu2+ the T50% is much higher than expected based on the calculated ΔE5d-CB. The calculated ΔE5d-CB is less than −1 eV, i.e. the lowest Eu2+ 5d level is positioned inside the host lattice conduction band. As a result all Eu2+ 5d–4f emission should actually be quenched for SrSi6N8:Eu2+, even at 4 K, which obviously is not the case. Note that SrSi6N8, in which the uncommon direct Si–Si bond is present,86 tends to deviate more often from the trends of the other nitridosilicates, having for example a smaller than expected Stokes shift for the Eu2+ emission,26 and a smaller than expected bandgap than one would expect based on its Si/N ratio.25 The low energy of the host lattice transition in SrSi6N8 has been attributed to the Si–Si bond, which forms an empty σ* state below the bottom of the conduction band.87 For this reason SrSi6N8:Eu2+ has been excluded from the fit in Fig. 6. Li4Ca3Si2N6:Eu2+ has also been excluded, because of the uncertainties in its excitation and emission spectra: the reported data suggest an extraordinary large Stokes shift of 1.76 eV,70 which is considered very unlikely,26 and it is more likely that the reported 5d bands have a different origin. Also for Ca16Si17N34:Eu2+, La2.23Ca1.155Si6N11:Eu2+, Sr8Mg7Si9N22:Eu2+, Li2CaSi2N4:Eu2+ and SrMg3SiN4:Eu2+ a (small) negative value for ΔE5d-CB has been obtained. For the latter four this is within expectation when taking into account the standard deviation, considering the fast thermal quenching of the Eu2+ emission in these compounds. For Ca16Si17N34:Eu2+ ΔE5d-CB seems to be too low given its relatively high quenching temperature. It might be that this deviation is related to the presence of Eu2+ in three different crystallographic environments in Ca16Si17N34, which was not taken into account due to a lack of information about the difference in quenching behaviour for Eu2+ in these different crystallographic environments.
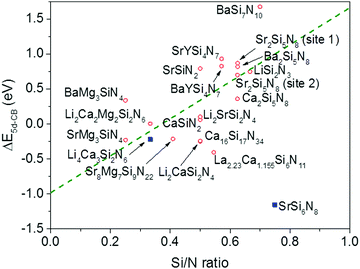
4.3 Relation between the nitridosilicate composition and ΔE5d-CB
From Fig. 7 one can see that there is a correlation between the degree of condensation (Si/N ratio) and ΔE5d-CB. ΔE5d-CB tends to be small for compounds with a low Si/N ratio, such as SrMg3SiN4:Eu2+, and large for compounds with a high Si/N ratio, like BaSi7N10:Eu2+. SrSi6N8:Eu2+, which is the only structure in which direct Si–Si bonds are present, is the only compound that strongly deviates from the trend. Note that the increase of ΔE5d-CB with increasing Si/N ratio is in agreement with the earlier observations that T50% tends to increase with Si/N ratio (Fig. 4) and that T50% also increases with increasing ΔE5d-CB (Fig. 6).The increase of ΔE5d-CB with increasing degree of condensation is in line with our conclusions in previous work,25,26 in which we explained how the degree of condensation, expressed by the Si/N ratio, acts as a principle parameter that influences the structural parameters (such as bond lengths) and bandgap of the nitridosilicate lattices,25 as well as how the degree of condensation influences 5d energy levels of the Eu2+ doped nitridosilicate phosphors.26 This is illustrated in Fig. 8. With increasing Si/N ratio the N by Si coordination number increases, which results in more N electrons that participate in the bonding with Si and consequently less N electrons that are available for M–N bonding. This reduces the covalency of the M–N bonds, making them longer, while the Si–N bonds become shorter. As a consequence of the lower effective charge of N, the top of the valence band, which mainly consists of N orbitals, tends to move downward with increasing Si/N ratio, increasing the CT energy, while the bottom of the conduction band moves upward due to the decrease of the Si–N bond lengths, resulting in an overall widening of the bandgap. The lower covalency of the Eu–N bonds with increasing Si/N ratio also weakens the nephelauxetic effect, reducing the centroid shift of the Eu2+ 5d levels, while the crystal field splitting of the 5d levels also becomes smaller because the Eu–N bonds become longer and the effective negative charge on N lower. The weakening of both the nephelauxetic and crystal field splitting effects result in an increase of the lowest Eu2+ 4f–5d absorption energy, while the Stokes shift becomes larger as the local rigidity of the Eu2+ sites decreases due to the longer Eu–N bonds. The consequence is that the energy difference between the relaxed 5d state and the bottom of the conduction band (ΔE5d-CB) will become larger with increasing Si/N ratio due to raise of the bottom of the conduction band and the increase of the Stokes shift, but that at the same time ΔE5d-CB will be a bit reduced due to the decrease of the 5d redshift (which includes the nephelauxetic effect and crystal field splitting). Based on Fig. 7, that shows an increase of ΔE5d-CB with increasing Si/N ratio, we can now conclude that the raise of the conduction band and increase of the Stokes shift with increasing Si/N ratio is more than compensating the reduction of the redshift. Note that we can draw this conclusion also in another way: the bandgap increases with about 4.1 eV/κ,25 the CT increases with about 0.8 eV/κ (eqn (11)), and Edf increases with about 1.3 eV/κ,26 therefore ΔE5d-CB should increase with about 2 eV/κ, where κ is the Si/N ratio.
One additional issue to consider is that, in the thermal ionization to the conduction band model, the positions of the relaxed 5d level and the bottom of the conduction band are to some extent temperature dependent. With increasing temperature, as a consequence of the expansion of the lattice, a decrease of the bandgap is expected as there will be less overlap between the bonding orbitals in the valence band and the anti-bonding orbitals in the conduction band due to the longer atomic distances (Varshni equation, eqn (5)). In addition, the lowest 5d level is expected to go slightly upward in energy due to a smaller crystal field splitting as a result of the thermal expansion. Both effects are in the same direction and reinforce each other. Therefore, if one assumes that the position of the Eu2+ 4f ground state remains the same and that the Stokes shift does not increase (which is supported by experimental data), ΔE5d-CB is expected to decrease in energy with increasing temperature as the bottom of the conduction band moves downward and the lowest 5d level moves upward. Hence, the thermal quenching will be stronger at higher temperature as ΔE5d-CB (i.e. Eact) decreases, compared to what the thermal quenching would be if ΔE5d-CB would remain constant. Note that eqn (6) or (7), which assume Eact to be constant, cannot describe any temperature dependency of ΔE5d-CB, consequently resulting in an error of the fitting parameters when these equations are used.
5. Conclusions and outlook
Thermal quenching of the Eu2+ 5d–4f emission in the nitridosilicates have been collected from literature and have been evaluated and analysed with regard to structure and composition of the nitridosilicates. According to the presented relationships, the main cause of thermal quenching of the Eu2+ 5d–4f emission in the nitridosilicates is the thermal ionization of the Eu2+ 5d electron to the host lattice conduction band, as is supported by the increase of quenching temperature (T50%) with increasing energy difference between the relaxed 5d state and the bottom of the conduction band (ΔE5d-CB). In addition, ΔE5d-CB tends to increase with increasing degree of condensation (Si/N ratio) because the combined effect of the raise of the conduction band and increase of the Stokes shift with increasing degree of condensation is stronger than the decrease of redshift of the 5d levels. The weaker thermal quenching with increasing degree of condensation can thus be understood based on the interpretation described above and cannot be attributed to a more rigid structure, as is often done in literature using the configurational coordinate model.Besides the intrinsic quenching of the emission due to thermal ionization, other effects seem to further reduce the emission intensity with increasing temperature in many nitridosilicates. These effects include quenching at defects by energy transfer, which becomes stronger at higher Eu2+ concentrations, and the quenching of anomalous emission.
It was found that for many compounds, even though the thermal quenching of the Eu2+ emission could be well fitted with an Arrhenius type of equation (eqn (6) or (7)), the obtained value of C, representing the ratio of the attempt rate for thermal quenching over the radiative decay rate of the 5d–4f emission, is unrealistically low. This raises the question whether one can trust the obtained value for the activation energy. In literature however, this low value of C is usually neither discussed nor reported. Future research should therefore focus on obtaining a better understanding of the cause of the low value of C and whether the Arrhenius type of equation is actually a good description of the full thermal quenching behaviour in these compounds.
Although this work was focussed on the quenching of the Eu2+ 5d–4f emission in the nitridosilicates, it is believed that the conclusions are more general and would also apply for the thermal quenching of the 5d–4f emission of other lanthanides such as Ce3+ or Yb2+. In addition, other host lattices that consist of cross-linked TX4 tetrahedra (T = cation, X = anion) with M cations in between, such as oxo-silicates, phosphates and aluminates, are expected to show similar relationships.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has received funding from the Netherlands Organisation for Scientific Research (NWO) as part of the Joint Research Project on Advanced Materials with the National Natural Science Foundation of China (NSFC). We acknowledge the valuable input given by Prof. Dr Pieter Dorenbos during the preparation of this manuscript.Notes and references
- G. Li, Y. Tian, Y. Zhao and J. Lin, Chem. Soc. Rev., 2015, 44, 8688–8713 RSC.
- Z. Xia, Z. Xu, M. Chen and Q. Liu, Dalton Trans., 2016, 45, 11214–11232 RSC.
- J. Meyer and F. Tappe, Adv. Opt. Mater., 2015, 3, 424–430 CrossRef CAS.
- N. C. George, K. A. Denault and R. Seshadri, Annu. Rev. Mater. Res., 2013, 43, 481–501 CrossRef CAS.
- L. Wang, R.-J. Xie, T. Suehiro, T. Takeda and N. Hirosaki, Chem. Rev., 2018, 118, 1951–2009 CrossRef CAS PubMed.
- K. Shioi, N. Hirosaki, R. J. Xie, T. Takeda and Y. Q. Li, J. Mater. Sci., 2008, 43, 5659–5661 CrossRef CAS.
- K. Uheda, H. Takizawa, T. Endo, H. Yamane, M. Shimada, C. M. Wang and M. Mitomo, J. Lumin., 2000, 87–89, 967–969 CrossRef CAS.
- Y. Q. Li, C. M. Fang, G. de With and H. T. Hintzen, J. Solid State Chem., 2004, 177, 4687–4694 CrossRef CAS.
- C. J. Duan, X. J. Wang, W. M. Otten, A. C. A. Delsing, J. T. Zhao and H. T. Hintzen, Chem. Mater., 2008, 20, 1597–1605 CrossRef CAS.
- K. Uheda, N. Hirosaki, Y. Yamamoto, A. Naito, T. Nakajima and H. Yamamoto, Electrochem. Solid-State Lett., 2006, 9, H22–H25 CrossRef CAS.
- Y. Q. Li, A. C. A. Delsing, G. de With and H. T. Hintzen, Chem. Mater., 2005, 17, 3242–3248 CrossRef CAS.
- J. W. H. van Krevel, J. W. T. van Rutten, H. Mandal, H. T. Hintzen and R. Metselaar, J. Solid State Chem., 2002, 165, 19–24 CrossRef CAS.
- R. J. Xie, M. Mitomo, K. Uheda, F. F. Xu and Y. Akimune, J. Am. Ceram. Soc., 2002, 85, 1229–1234 CrossRef CAS.
- N. Hirosaki, R. J. Xie, K. Kimoto, T. Sekiguchi, Y. Yamamoto, T. Suehiro and M. Mitomo, Appl. Phys. Lett., 2005, 86, 211905 CrossRef.
- J. Qiao, J. Zhao, Q. Liu and Z. Xia, J. Rare Earths, 2019 DOI:10.1016/j.jre.2018.11.001.
- Y. H. Kim, P. Arunkumar, B. Y. Kim, S. Unithrattil, E. Kim, S.-H. Moon, J. Y. Hyun, K. H. Kim, D. Lee and J.-S. Lee, Nat. Mater., 2017, 16, 543 CrossRef CAS PubMed.
- C. W. Yeh, W. T. Chen, R. S. Liu, S. F. Hu, H. S. Sheu, J. M. Chen and H. T. Hintzen, J. Am. Chem. Soc., 2012, 134, 14108–14117 CrossRef CAS PubMed.
- C. Struck and W. Fonger, J. Lumin., 1975, 10, 1–30 CrossRef CAS.
- K. Bleijenberg and G. Blasse, J. Solid State Chem., 1979, 28, 303–307 CrossRef CAS.
- P. Dorenbos, J. Phys.: Condens. Matter, 2005, 17, 8103–8111 CrossRef CAS.
- Y. Fukuda, ECS J. Solid State Sci. Technol., 2017, 6, R69–R74 CrossRef CAS.
- T. M. Tolhurst, P. Strobel, P. J. Schmidt, W. Schnick and A. Moewes, Chem. Mater., 2017, 29, 7976–7983 CrossRef CAS.
- Y. Wang, J. Ding, Y. Wang, X. Zhou, Y. Cao, B. Ma, J. Li, X. Wang, T. Seto and Z. Zhao, J. Mater. Chem. C, 2019, 7, 1792–1820 RSC.
- S. Yan, Opt. Mater., 2018, 79, 172–185 CrossRef CAS.
- O. M. ten Kate, Z. Zhang and H. T. Hintzen, J. Mater. Chem. C, 2017, 5, 11504–11514 RSC.
- O. M. ten Kate, Z. Zhang, J. R. van Ommen and H. T. Hintzen, J. Mater. Chem. C, 2018, 6, 5671–5683 RSC.
- G. Blasse, Mater. Chem. Phys., 1987, 16, 201–236 CrossRef CAS.
- A. Alias, Y. Yaacob, Z. Zabidi, S. Alshurdin and N. Aini, J. Fundam. Appl. Sci., 2017, 9, 568 CrossRef CAS.
- M. Ando and Y. A. Ono, J. Cryst. Growth, 1992, 117, 969–974 CrossRef CAS.
- E. Van der Kolk, J. De Haas, A. Bos, C. Van Eijk and P. Dorenbos, J. Appl. Phys., 2007, 101, 083703 CrossRef.
- P. Dorenbos, J. Phys.: Condens. Matter., 2003, 15, 8417–8434 CrossRef CAS.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15640–15649 CrossRef CAS.
- P. Dorenbos, J. Alloys Compd., 2002, 341, 156–159 CrossRef CAS.
- Y. P. Varshni, Physica, 1967, 34, 149–154 CrossRef CAS.
- Y. Q. Li, J. E. J. van Steen, J. W. H. van Krevel, G. Botty, A. C. A. Delsing, F. J. DiSalvo, G. de With and H. T. Hintzen, J. Alloys Compd., 2006, 417, 273–279 CrossRef CAS.
- V. Bachmann, C. Ronda and A. Meijerink, Chem. Mater., 2009, 21, 2077–2084 CrossRef CAS.
- Y. Q. Li and H. Hintzen, J. Light Visual Environ., 2008, 32, 129–134 CrossRef CAS.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takeda and M. Mitomo, J. Lumin., 2010, 130, 1147–1153 CrossRef CAS.
- Q. S. Wu, Y. Y. Li, X. C. Wang, Z. Y. Zhao, C. Wang, H. Li, A. J. Mao and Y. H. Wang, RSC Adv., 2014, 4, 39030–39036 RSC.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takeka and M. Mitomo, J. Solid State Chem., 2009, 182, 301–311 CrossRef CAS.
- Y. Q. Li, N. Hirosaki, R. J. Xie, T. Takada, Y. Yamamoto, M. Mitomo and K. Shioi, Int. J. Appl. Ceram. Technol., 2010, 7, 787–802 CrossRef CAS.
- H. Chen, J. Ding, X. Ding, X. Wang, Y. Cao, Z. Zhao and Y. Wang, Inorg. Chem., 2017, 56, 10904–10913 CrossRef CAS PubMed.
- W. T. Chen, H. S. Sheu, R. S. Liu and J. P. Attfield, J. Am. Chem. Soc., 2012, 134, 8022–8025 CrossRef CAS PubMed.
- H. L. Li, R. J. Xie, N. Hirosaki, T. Takeda and G. H. Zhou, Int. J. Appl. Ceram. Technol., 2009, 6, 459–464 CrossRef CAS.
- Y. Q. Li, G. De With and H. T. Hintzen, J. Solid State Chem., 2008, 181, 515–524 CrossRef CAS.
- C. Wang, Z. Y. Zhao, X. C. Wang, Y. Y. Li, Q. S. Wu and Y. H. Wang, RSC Adv., 2014, 4, 55388–55393 RSC.
- X. D. Wei, L. Y. Cai, F. C. Lu, X. L. Chen, X. Y. Chen and Q. L. Liu, Chin. Phys. B, 2009, 18, 3555–3562 CrossRef CAS.
- L. Chen, R. H. Liu, W. D. Zhuang, Y. H. Liu, Y. S. Hu, X. L. Ma and B. Hu, J. Rare Earths, 2016, 34, 30–35 CrossRef CAS.
- R. J. Xie, N. Hirosaki, N. Kimura, K. Sakuma and M. Mitomo, Appl. Phys. Lett., 2007, 90, 191101 CrossRef.
- L. Chen, R. H. Liu, W. D. Zhuang, Y. H. Liu, Y. S. Hu, X. F. Zhou, W. Gao and X. L. Ma, CrystEngComm, 2015, 17, 3687–3694 RSC.
- Y. Liu, L. Chen, X. Zhou, R. Liu and W. Zhuang, J. Solid State Chem., 2017, 246, 145–149 CrossRef CAS.
- C. C. Lin, Y.-T. Tsai, H. E. Johnston, M.-H. Fang, F. Yu, W. Zhou, P. S. Whitfield, Y. Li, J. Wang and R.-S. Liu, J. Am. Chem. Soc., 2017, 139, 11766–11770 CrossRef CAS PubMed.
- H. Yuan, Z. Huang, F. Chen, Q. Shen and L. Zhang, J. Alloys Compd., 2017, 720, 521–528 CrossRef CAS.
- V. D. Luong, W. T. Zhang and H. R. Lee, Adv. Mater. Res., 2011, 233–235, 2705–2709 CAS.
- T. Wang, P. Zheng, X. L. Liu, H. F. Chen, L. Bian and Q. L. Liu, J. Lumin., 2014, 147, 173–178 CrossRef CAS.
- C. Wang, S. Y. Xin, X. C. Wang, G. Zhu, Q. S. Wu and Y. H. Wang, New J. Chem., 2015, 39, 6958–6964 RSC.
- X. Q. Piao, K. Machida, T. Horikawa and B. G. Yun, J. Lumin., 2010, 130, 8–12 CrossRef CAS.
- X. Q. Piao, T. Horikawa, H. Hanzawa and K. Machida, Appl. Phys. Lett., 2006, 88, 161908 CrossRef.
- J. M. Song, J. S. Park and S. Nahm, Ceram. Int., 2013, 39, 2845–2850 CrossRef CAS.
- X. Piao, K. I. Machida, T. Horikawa and H. Hanzawa, Appl. Phys. Lett., 2007, 91, 041908 CrossRef.
- J. Wang, H. Zhang, Y. Liu, H. Dong, B. Lei, M. Zheng, Y. Xiao, M. Peng and J. Wang, J. Mater. Chem. C, 2015, 3, 9572–9579 RSC.
- J. L. Qin, H. R. Zhang, B. F. Lei, H. W. Dong, Y. L. Liu, J. X. Meng, M. T. Zheng and Y. Xiao, J. Lumin., 2014, 152, 230–233 CrossRef CAS.
- H. L. Li, R. J. Xie, G. H. Zhou, N. Hirosaki and Z. O. Sun, J. Electrochem. Soc., 2010, 157, J251–J255 CrossRef CAS.
- G. Anoop, D. W. Lee, D. W. Suh, S. L. Wu, K. M. Ok and J. S. Yoo, J. Mater. Chem. C, 2013, 1, 4705–4712 RSC.
- K. Ueda, H. Yamane, T. Nagura and T. Miyazaki, Japanese Pat., JP2015-196717, 2015 Search PubMed.
- C. Li, H. W. Zheng, H. W. Wei, J. Su, F. H. Liao, Z. Y. Zhang, L. Xu, Z. P. Yang, X. M. Wang and H. Jiao, Chem. Commun., 2018, 54, 11598–11601 RSC.
- T. M. Tolhurst, S. Schmiechen, P. Pust, P. J. Schmidt, W. Schnick and A. Moewes, Adv. Opt. Mater., 2016, 4, 584–591 CrossRef CAS.
- D. Cui, Z. Song, Z. Xia and Q. Liu, Inorg. Chem., 2017, 56, 11837–11844 CrossRef CAS.
- S. Schmiechen, P. Strobel, C. Hecht, T. Reith, M. Siegert, P. J. Schmidt, P. Huppertz, D. Wiechert and W. Schnick, Chem. Mater., 2015, 27, 1780–1785 CrossRef CAS.
- Q. Wu, J. Ding, Y. Li, X. Wang and Y. Wang, J. Lumin., 2017, 186, 144–151 CrossRef CAS.
- Q. Wu and J. Zhou, Dyes Pigm., 2019, 161, 324–330 CrossRef CAS.
- Q. Wu, Y. Li, C. Wang and J. Luo, J. Lumin., 2018, 201, 485–492 CrossRef CAS.
- T. Horikawa, M. Fujitani, H. Hanzawa and K.-I. Machida, ECS J. Solid State Sci. Technol., 2012, 1, R113–R118 CrossRef CAS.
- D. Porob, N. Karkada, N. P. Kumar and A. Setlur, ECS Trans., 2012, 41, 27–38 CAS.
- T. Kurushima, G. Gundiah, Y. Shimomura, M. Mikami, N. Kijima and A. K. Cheetham, J. Electrochem. Soc., 2010, 157, J64–J68 CrossRef CAS.
- X. C. Wang, T. Seto, Z. Y. Zhao, Y. Y. Li, Q. S. Wu, H. Li and Y. H. Wang, J. Mater. Chem. C, 2014, 2, 4476–4481 RSC.
- C. Maak, D. Durach, C. Martiny, P. J. Schmidt and W. Schnick, Chem. Mater., 2018, 30, 3552–3558 CrossRef CAS.
- J. Y. Ding, Y. Y. Li, Q. S. Wu, Q. Long, C. Wang and Y. H. Wang, J. Mater. Chem. C, 2015, 3, 8542–8549 RSC.
- M. Zeuner, S. Pagano, P. Matthes, D. Bichler, D. Johrendt, T. Harmening, R. Pöttgen and W. Schnick, J. Am. Chem. Soc., 2009, 131, 11242–11248 CrossRef CAS PubMed.
- P. Dorenbos, J. Alloys Compd., 2009, 488, 568–573 CrossRef CAS.
- P. Dorenbos, ECS J. Solid State Sci. Technol., 2013, 2, R3001 CrossRef CAS.
- O. M. ten Kate, Z. Zhang, P. Dorenbos, H. T. Hintzen and E. van der Kolk, J. Solid State Chem., 2013, 197, 209–217 CrossRef CAS.
- O. M. ten Kate, H. T. Hintzen, P. Dorenbos and E. van der Kolk, J. Mater. Chem., 2011, 21, 18289–18294 RSC.
- H. Hoefdraad, J. Solid State Chem., 1975, 15, 175–177 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2005, 111, 89–104 CrossRef CAS.
- F. Stadler, O. Oeckler, J. Senker, H. A. Höppe, P. Kroll and W. Schnick, Angew. Chem., Int. Ed., 2005, 44, 567–570 CrossRef CAS.
- Z. Huang, F. Chen, J. Zhang, Q. Shen and L. Zhang, RSC Adv., 2017, 7, 8779–8785 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9tc01445d |
| This journal is © The Royal Society of Chemistry 2019 |