Ferromagnetic Ising chains in frustrated LnODCO₃: the influence of magnetic structure in magnetocaloric frameworks

Abstract

Probing the magnetic interactions in functional magnetic materials can reveal detailed insight into how to optimise the properties they possess while providing key understanding of the exotic phenomena they may host. This study probes the short and long range magnetic order in the LnODCO₃ (where Ln = Tb, Dy, Ho, and Er) framework magnetocalorics using variable-temperature neutron scattering measurements. Reverse Monte Carlo analysis of neutron scattering data shows that TbODCO₃, DyODCO₃ and HoODCO₃ develop short range Ising-like magnetic order between 1.5 and 20 K, consistent with dominant ferromagnetic correlations within chains along the b-axis. Through magnetic susceptibility measurements we identify that long range magnetic order develops in TbODCO₃ and HoODCO₃ at ∼1.2 and ∼0.9 K, respectively. Neutron diffraction measurements were conducted on HoODCO₃ revealing incommensurate magnetic order develops between 1.2 and 0.9 K, before a commensurate magnetic phases emerges at 0.8 K with long-range ferromagnetic order in the chains. The results suggest Ising-like ferromagnetic chains associated with frustration are responsible for the improved magnetocaloric properties, of some members in this family, at higher temperatures and low applied fields.

---

Introduction

Many areas of fundamental and applied science, including spintronics, quantum computing, and medicine require cooling to sub-20 K temperatures.^1,2 Traditionally cooling to T < 20 K is dominated by liquid helium vapor compression or dilution refrigeration. However helium, a by-product obtained from natural gas extraction, is a non-renewable resource and is becoming increasing scarce and expensive.³ Developing new methods for cooling to below 20 K, through renewable and energy efficient means is therefore essential for developing technology. Solid state caloric refrigerants are one efficient alternative for such applications;⁴ recent advances have been made in developing magnetocalorics with good performance at low temperatures under fields that can be generated using permanent magnets, required for energy efficient and practical magnetocaloric devices.^5–9 In recent years work on magnetocaloric materials has extended from purely ionic systems to those containing molecular building blocks and this appears a very promising route forward for developing improved materials.^10–12

The paramagnetic magnetocaloric effect (MCE) is an entropically driven cooling process that occurs when paramagnets are in a cycled magnetic field.¹³ The MCE was first observed in 1917,¹⁴ and exploited in dilute paramagnetic salts in 1933 to reach sub millikelvin temperatures.¹⁵ It has now been studied extensively for the last century, and measured in a multitude of compounds.⁴ Applying a magnetic field to a paramagnetic sample aligns the disordered spins with the applied field. The magnetisation of the sample leads to a significant decrease in entropy, inducing an adiabatic increase in temperature. Removal of the excess heat and decreasing the field leads to an entropically driven cooling process, which become useful in an adiabatic demagnetisation refrigerator.

Gadolinium containing materials such as Gd₃Ga₅O₁₂ (GGG), are often utilised in magnetocalorics for their high magnetic entropy resulting from their half-filled f-orbitals combined with lack of spin–orbit coupling. The magnetocaloric entropy change, −ΔS_m, scales with the number of unpaired spins in a paramagnet, making high entropy changes with applied magnetic fields possible in compounds with a large number of unpaired electrons. The Heisenberg-like spins of Gd can point in any direction and thus applying fields to a powder sample can align the spins fully, producing large change in entropy from a paramagnetic to ferromagnetic state. In contrast, when spins are confined to an easy axis, as in the Ising model,¹⁶ an applied field perpendicular to the easy axis will incur no change in magnetisation. Thus Ising anisotropy prevents full magnetisation with field in bulk powders, which is detrimental to the magnetocaloric effect. Recently, however, literature has shown that materials containing cations with strong Ising anisotropy improves the magnetocaloric effect in powders under the low applied magnetic fields that can be generated using a permanent magnet (<2 T).^5,7,17 This surprising result is an outcome of the greater ease of magnetisation of these materials under low applied fields, but the microscopic cause of this remains unknown. Uncovering how magnetic interactions in such compounds are best optimised to improve magnetocaloric performance requires an understanding of these materials at the microscopic level, which is most readily achieved using neutron scattering rather than indirect bulk property measurements.

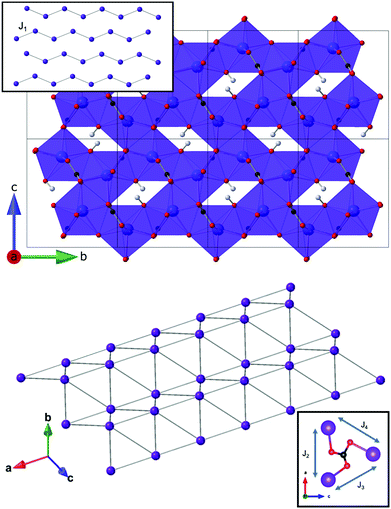
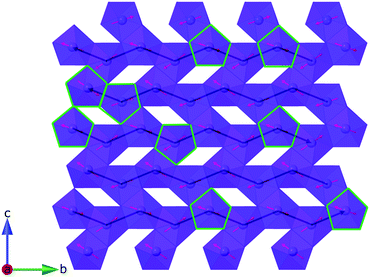
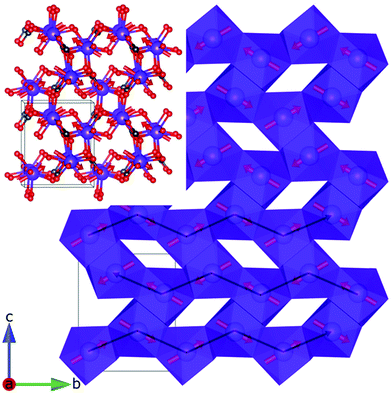
The orthorhombic LnOHCO₃ (Ln = Tb, Dy, Ho and Er) frameworks, which adopt P2₁2₁2₁ symmetry, are isostructural with a lattice structure that combines the elements required for ferromagnetic chains and frustrated magnetism, with nearest neighbour chains along the b-axis and a triangular-like lattice in ac plane (Fig. 1).⁷ Ln³⁺ ions in the ac plane are arranged into buckled triangular lattices with the nearest neighbour, in this plane, coupled through an oxygen atom of the carbonate ligand, along the a-axis. As we have reported in our previous work⁷ amongst these materials the Tb, Dy and Ho, frameworks provide optimised −ΔS_m above 4 K and for applied magnetic field changes of less than 2 T of up to 30.99 J kg⁻¹ K⁻¹ or 186.15 mJ cm⁻³ K⁻¹, at the expense of decreasing performance below this temperature. This offers the prospect of using these materials as magnetocalorics for the wider range of applications that need cooling to near 4 K. The performance of TbOHCO₃ and DyOHCO₃ compounds are particularly impressive. These feature higher −ΔS_m for applied fields achievable using a permanent magnet (less that 2 T)⁷ up to nearly 10 K, than the maximum of the canonical magnetocaloric material Gd₃Ga₅O₁₂ under analogous fields, which occurs at 1.2 K.¹⁸ In comparison the MCE of GdOHCO₃, which is isostructural to the other LnOHCO₃ frameworks, and ErOHCO₃ increase with decreasing temperature, down to 2 K but perform less well in low applied fields.

Fig. 1 (top) Crystal structure of the orthorhombic LnOHCO₃ frameworks. Ln³⁺ coordination environments are shown as purple polyhedra, carbon, oxygen and hydrogen are shown in black, red and white respectively, with only Ln³⁺ nearest neighbour (J₁) chains shown in inset, along the 100 direction. (bottom) The interactions between Ln³⁺ with a distance of 4.0–5.0 Å, shown arranged into layers of triangular motifs, off the [111] direction, with the couplings of the triangles through the carbonate anion.

It is notable that the magnetisation behaviour of the Tb, Dy, Ho and Er members of the LnOHCO₃ are consistent with these cations having Ising spins despite the very different performance of ErOHCO₃ compared to other members of the series. Clearly, therefore while Ising-like interactions may play a role in optimising the performance of such materials it is not sufficient on its own. This is perhaps unsurprising given magnetic frustration arising from competing antiferromagnetic couplings, in which all magnetic interactions in a material are unable to be optimised simultaneously, is well known to play a key role in the properties of magnetocaloric oxides, including Gd₃Ga₅O₁₂ itself.^19–21 Similarly recent neutron scattering studies of Tb(HCO₂)₃ and Ho(HCO₂)₃ suggests that their magnetocaloric properties, also optimised for use above 4 K in less than 2 T applied fields, are linked to the presence of 1D ferromagnetic chains packed in a frustrated antiferromagnetic triangular lattice.^17,22,23 A subsequent study finds ferromagnetic chains improve magnetocaloric performance, over a similar temperature range, also in oxide materials.²⁴ This emphasises the case for using neutron diffraction to understand the way in which the atomic-level magnetic interactions in these materials influence their macroscopic properties. The utility of neutron diffraction for probing magnetic interactions is well known²⁵ but it has been highlighted recently for materials containing molecular building blocks.^26–28

To establish a clear understanding of how the microscopic interactions of LnOHCO₃ affect their magnetocaloric entropy change we have studied these compounds using neutron diffraction. We have established both the local magnetic correlations in these materials in their short ranged ordered phases, in which they exhibit their magnetocaloric properties, and in the case of HoOHCO₃ the long range ordered magnetic states they exhibit at low temperatures. Those compounds with magnetocaloric properties optimised for use above 4 K in low applied magnetic fields all exhibit clear magnetic diffuse scattering. The diffuse arises from a lattice featuring competing antiferromagnetic couplings in the ac plane, and ferromagnetic Ising chains along the b axis. The ferromagnetic chains are non-collinear with spins preferring to orient close to the b-axis, but canted into the ac plane. The long range incommensurate and commensurate magnetic structures of HoOHCO₃ exhibited below 1.2 K and 0.8 K, respectively, also feature ferromagnetic chains that are coupled together antiferromagnetically. This highlights that ferromagnetic units coupled antiferromagnetically to each other in a frustrated lattice can be lead to optimised magnetocaloric performance under more moderate conditions.

Experimental methods

Samples of LnOHCO₃ and analogous LnODCO₃, used for neutron diffraction experiments, were synthesised via a hydrothermal method, by reacting Ln(NO₃)₃·6H₂O (99.9%, Sigma-Aldrich, 1 mmol) and Na₂CO₃ (99.5%, Sigma-Aldrich, 1 mmol) in water (10 mL). The mixture was sealed in a Teflon-lined (23 mL) Parr-Bomb autoclave and heated at 170 °C for 72 h, followed by cooling to room temperature at a rate of 3 °C h⁻¹. The samples were isolated by vacuum filtration, washed with water, and dried in a desiccator. 2 g deuterated samples were produced with D₂O (99.9%) under an N₂ atmosphere in multiple batches. It is necessary to deuterate neutron samples to minimise the background caused by the incoherent scattering of hydrogen. We expect the deuteration of the framework for neutron studies will have an insignificant affect on the magnetic exchange correlations.

Magnetic susceptibility measurements of the polycrystalline samples were carried out between 400 mK and 100 K, using a Quantum Design MPMS SQUID magnetometer in a 1000 Oe DC magnetic field. These were measured inside a ³He inset, which was used to cool below 1.8 K.

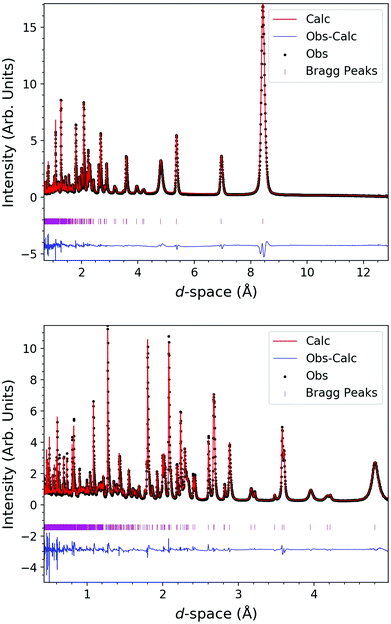
Powder neutron diffraction measurements were carried out on the high-resolution time-of-flight (TOF) WISH diffractometer at the ISIS neutron source, Rutherford Appleton Laboratory.²⁹ LnODCO₃ measurements were carried out between 1.5 K to 100 K, with the samples loaded into 8 mm vanadium cans and cooled using a standard Oxford Instruments cryostat. Low temperature measurements of HoODCO₃ were carried out between 0.28 K to 1.95 K, with the sample loaded in an 8 mm copper can and cooled in a ³He Heliox sorption refrigerator. Strong absorption was noted in DyODCO₃ and absorption corrections were applied to the raw data before fitting. A packing density of ∼30% was used as a basis for absorption corrections, before parameters were optimised so the backgrounds approached linearity with comparable intensities across the different detector banks. Absorption was negligible in TbODCO₃ and HoODCO₃ and so absorption corrections were only applied during Rietveld refinements. Rietveld refinements were performed in FULLPROF,³⁰ with aluminium and copper sample environment peaks fitted using the Le Bail method. A linear interpolation of points were used to fit the background and a convolution of back-to-back exponentials with a pseudo-Voight TOF function was used to fit the diffraction peak shapes. The full width half-maximums of the finite correlation length magnetic peaks were fitted with an anisotropic broadening model.³¹

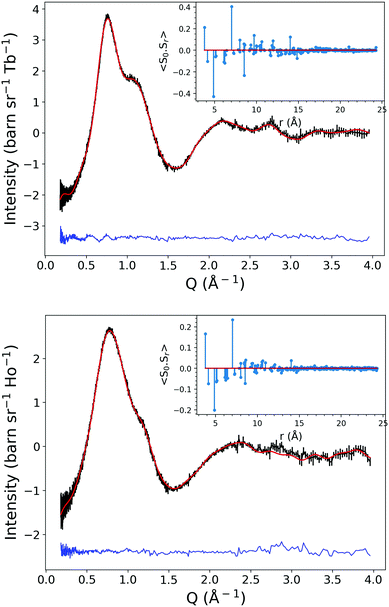
Diffuse neutron patterns were fitted with the reverse Monte Carlo (RMC) program – SPINVERT,³² using a supercell of 49 × 49 × 51 ų or 10 × 7 × 6 unit cells consisting of 1680 unique spins. To isolate the total magnetic contribution to the neutron-scattering data, data collected at a high temperature T_high were subtracted from the low-temperature data of interest, where T_high = 20 K. Banks were merged and binned over a Q range of 0.2 to 4.0 Å⁻¹ to improve statistics. The data were placed on an absolute intensity scale (barn sr⁻¹ Ln⁻¹) by normalisation to the calculated nuclear Bragg profile at T_high.

Results and discussion

Physical property measurements

It has previously been reported that the LnOHCO₃ frameworks do not show any indication of long range order down to 2 K, and follow Curie–Weiss behaviour, with Weiss temperatures of −5.04 K, −0.84 K, −3.83 K and −7.47 K, for Tb, Dy, Ho and Er.⁷ Magnetic susceptibility measurements below 2 K of TbOHCO₃ and HoOHCO₃ show features indicative of the formation of long range order (Fig. 2) at ∼1.2 K and ∼0.8 K, respectively. The observed divergence of the zero field-cooled (ZFC) and field-cooled (FC) susceptibility suggest a weak ferromagnetic nature to this order, which we ascribe to a small degree of spin canting of long-range ordered antiferromagnets in applied fields. As discussed below there is no indication of a net ferromagnetic moment in the ordered magnetic structure of HoOHCO₃, in zero field, as determined by neutron diffraction.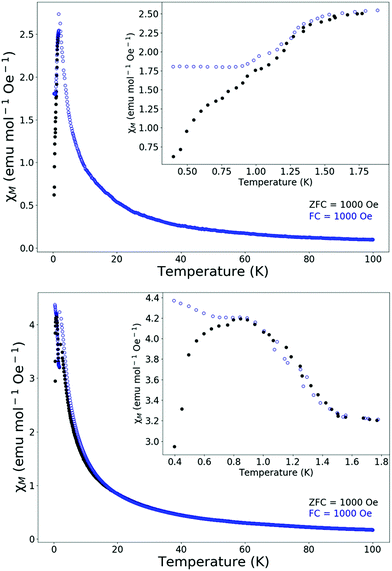

Fig. 2 Magnetic susceptibility of (top) TbOHCO₃ and (bottom) HoOHCO₃ in 1000 Oe field below 100 K, close up below 1.8 K in inset.

Short range order in LnODCO₃

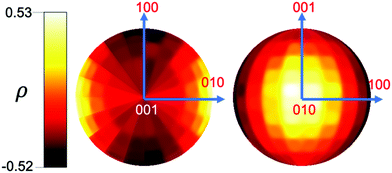
Neutron diffraction measurements in zero-field of the LnODCO₃ frameworks indicated that of the samples measured, TbODCO₃, DyODCO₃ and HoODCO₃ showed significant magnetic diffuse scattering below 20 K, indicative of short range order. Refinements down to the base temperature of T_base = 1.5 K, revealed typical reduction in the unit cell volume upon cooling (see Fig. S1–S4, ESI†). Refined models of the nuclear structures at 1.5 K of TbODCO₃, DyODCO₃ and HoODCO₃ yield J₁ distances of 3.799(3), 3.778(5) and 3.762(5) Å, J₂ distances of 4.851(9), 4.843(9) and 4.802(12) Å; J₃ distances of 5.077(5), 5.048(6) and 5.101(7) Å; and J₄ distances of 5.162(5), 5.183(6) and 5.115(7) Å, respectively. The emergence of short range correlations in only these materials is an important result, as these materials show magnetocaloric properties maximised for use above 4 K for low applied magnetic field changes.⁷ Only ErODCO₃, whose magnetocaloric properties gradually increases on cooling down to 2 K and resembles GdOHCO₃ but with overall poorer performance, did not show any sign of magnetic diffuse scattering, indicating a lack of significant magnetic correlations. It was noted that the strength of magnetic diffuse scattering observed at 1.5 K decreased significantly from TbODCO₃ to HoODCO₃ to DyODCO₃, indicating a decrease in the strength of the magnetic correlations giving rise to this, but does not correlate with bond distances. The observed diffuse magnetic scattering of TbODCO₃, DyODCO₃ and HoODCO₃ were well fitted by the RMC method, with stereographic projections of refined Heisenberg-like moments, which have unconstrained spin orientations, showing the spin preferentially aligned close to the b-axis (Fig. 3).

Fig. 3 Stereographic projections of the spin orientations averaged over 100 RMC Heisenberg-like fits to diffuse neutron scattering data from TbODCO₃ at 1.5 K. The relative spin density, ρ(θ,ϕ), is defined as ρ(θ,ϕ) = ln . Bright spots indicate areas of high spin density.

Attempts were therefore made to fit the diffuse scattering data with Ising spins constrained to point only along the b-axis. These refinements produced poor fits to the data and so Ising moment directions were manually modified and repeatedly tested until an optimal fit was achieved for TbODCO₃ at 1.5 K, because this data provided the best signal to noise ratio. The best fit was found to occur using a model in which the orientations of the Ising spins were allowed to orient towards four independent easy axes, primarily along the b-axis but canted into the ac plane. This four-site Ising model indicates the easy axes are oriented in the direction of the nearest chain neighbour with the unit vectors of these moments corresponding to [±0.33, 1, ±0.66]. These spin orientation produced excellent fits to the data for TbODCO₃ at all temperatures (see Fig. 4 for fit and Fig. 5 for resulting structure), although of slightly lower quality than the Heisenberg refinement (χ² = ∼130 and ∼150 at 1.5 K for typical Heisenberg and Ising models respectively); the marginal improvement of the Heisenberg model is inevitable due to its higher degrees of freedom.

Fig. 4 Reverse Monte Carlo fits to magnetic diffuse for (top) TbODCO₃ and (bottom) HoODCO₃. Data points in black, fit in red and the difference in blue, using an Ising model at 1.5 K. Spin correlations as produced from SPINVERT are shown in the inset. Spin correlations are similar for both materials.

Fig. 5 Spin orientations in the short range ordered phase of TbODCO₃, along 100 direction. Tb³⁺ coordination environment shown as purple polyhedral, magnetic vectors shown as red arrows, and nearest neighbour chains highlighted with black lines. Spins disordered from the average ferromagnetic chain direction are highlighted in green.

Since the HoODCO₃ data is qualitatively similar and Heisenberg refinements yield similar spin orientations, the same Ising model was also used to fit the HoODCO₃ data, producing equally good fits (χ² = ∼120 and ∼170 at 1.5 K). Fitting the same model to the DyODCO₃ data, however, did not produce suitable fits and, despite refinement of the spin orientation for the DyODCO₃, no quality fits were obtained for an Ising model (χ² = ∼112 for Heisenberg compared to ∼450 for Ising at 1.5 K, see Fig. S5 and S6†). We expect that the significantly poorer fit for DyODCO₃ using Ising-like spins is as a result of the combination of the failure to fully correct the high level of absorption caused by the presence of Dy and the large degree of incoherent scattering caused by this element, combined with the weaker diffuse scattering observed. The strong similarly of the diffuse scattering features of the three samples, and previous inference of Ising-like dimensionality based on magnetisation of these materials,⁷ leads us to suggest all three compounds have Ising-like spins.

Spin correlations 〈S₀·S_r〉, averaged over 100 RMC refinements show that the dominant spin correlations in all these materials are qualitatively very similar, in both Heisenberg and Ising refinement models. Significant ferromagnetic correlations are clearly noted along the chain direction out to distances of about 15 Å at low temperatures with significant nearest neighbour antiferromagnetic correlations between chains packed into a distorted triangular lattice (see Fig. 6). The strongest ferromagnetic correlations at 3.79 and 7.01 Å correspond to the first and second nearest neighbours in the chain, coupled through oxygen and O–C–O bridges from the hydroxy and carbonate groups. The strongest antiferromagnetic correlations at 4.85 and 8.52 Å correspond to the neighbouring atoms within the triangles along the a-axis, coupled by a O–C–O bridge of the carbonate group, and an analogous interaction between cations along the a-axis but with one atom displaced along the chain.

Fig. 6 Chain correlation lengths with respect to temperature for (top) TbODCO₃ and (bottom) HoODCO₃. The solid blue line shows the fit. Spin correlations in the b-axis only at 1.5 K shown in the inset. The black points indicate the correlations within the chains.

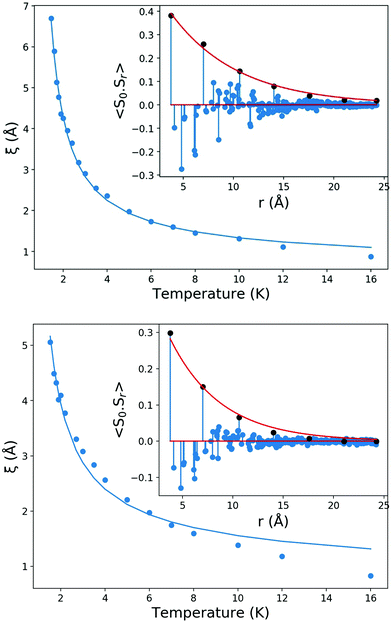
We have extracted intrachain correlation lengths with the function – 〈S₀·S_r〉 = A exp(−r/ε), where A is the Ising-like anisotropy, r is the correlation distance and ε is the correlation length, from the Ising fits to the data. Due to the non-linear alignment of spins along the buckled chain direction, it is necessary to only consider the correlations of the components of the magnetic moment along the b-axis when extracting the ferromagnetic correlation length. This is required because otherwise the non-collinear nature of the spins lead to next nearest neighbour in the chain, whose spins are collinear, having higher correlations than the nearest neighbour. Considering only the component of the magnetic moment along the b-axis allows us to decouple the Ising-like interactions in these materials, which would be expected to arise due to the strong single-ion of lanthanides, from the magnetic interactions between neighbouring lanthanide cations. This yields a correlation length of 6.69(11), 1.49(4) and 5.06(2) Å for TbODCO₃, DyODCO₃ and HoODCO₃, respectively, at 1.5 K, consistent with the overall weaker interactions in DyOHCO₃ and the weaker diffuse scattering observed. The values of A determined for TbODCO₃, DyODCO₃ and HoODCO₃ are 0.689(9), 0.514(5), and 0.596(13) at 1.5 K (cf. to the value of 1 that would be expected for the ideal Ising system), suggesting some deviation from a purely Ising model.

As the temperature was raised and the correlations became significantly weaker, the best fit to data was found with un-physical A values; for this reason A was fixed to the values determined for the lowest temperature fit for all temperatures. Temperature evolution of the ferromagnetic intrachain correlation length ε follows the expression for an independent ferromagnetic Ising chain 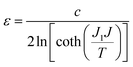(Fig. 6 and Fig. S7, ESI†).^33,34 In this expression J₁ is nearest neighbour exchange interaction from the Ising Hamiltonian. At higher temperatures the correlation length evolution diverges from the fit indicating the limitation of the approach, but this only occurs above 12 K and 8 K for TbODCO₃ and HoODCO₃, respectively, at which point magnetic correlations are very short. The fit to the correlation length yields values for J₁ of TbODCO₃, DyODCO₃ and HoODCO₃ of 1.11, 0.1, 0.76 K – consistent with the strength of the magnetic interactions following the trend TbODCO₃ > HoODCO₃ ≫ DyODCO₃. The energies determined for the J₁ interactions in TbODCO₃ and HoODCO₃ are very close to the ordering temperatures shown in magnetic susceptibility measurements, reflecting the Ising chain-like behaviour.

We expect the short-range magnetic correlations in these materials are key to the highly efficient magnetocaloric effect of these materials above 4 K under modest applied magnetic fields. As previously suggested for Tb(HCO₂)₃ and Ho(HCO₂)₃ the ferromagnetic Ising chains allow for high entropy changes in small applied magnetic fields as ferromagnetic units are more readily aligned with the applied magnetic field.^17,23 The competing weaker antiferromagnetic interchain interactions help to suppress long-range order, required for paramagnetic magnetocalorics, but are weak enough to require only small fields to be overcome to lead to a ferromagnetic field-induced state. This dominant ferromagnetic intrachain coupling allows the moments to be more easily aligned with the applied field. In the magnetocaloric studies of these materials,⁷ the materials that show this structured diffuse scattering, and this exotic magnetic order are the materials that have optimised performance in low applied magnetic fields above 4 K.

The precise extent to which these three systems resemble ideal Ising system may be somewhat different, which likely affects how these materials respond to applied magnetic fields. Given the powder averaging this data suffers from, it is possible there may be other solutions that provide suitable fits to the diffuse scattering data, or there are some deviations in the precise spin orientations that have been overlooked. However, the data are consistent with a four site Ising model, and the later discussed long range order, so this is likely an optimal model. The Ising-like nature of the spins of these materials would be ideally confirmed by measuring the inelastic neutron spectra of these materials, where a spin gap is expected to be present. Such measurements, which go well beyond the scope of this work whose focus is on analysing the magnetic correlations in these materials, would also more clearly identify the strength of the Ising-like interactions. This may be important as the magnetisation measurements previously reported for TbODCO₃ and DyODCO₃ indicate magnetisation is somewhat higher than that expected for Ising powder averaged samples, but far lower than a Heisenberg magnetisation curve.⁷ This suggests that these compounds are mostly but not entirely Ising, which combined with the large magnetic moments in these systems allows for large changes in magnetisation in applied fields, greater than that of a purely Ising material; this is thus beneficial to the MCE in these samples. This, along with the greater overall magnetic moment of DyOHCO₃ may explain why it exhibits a greater magnetic entropy change despite its weaker magnetic interactions.

Antiferromagnetic order in HoODCO₃

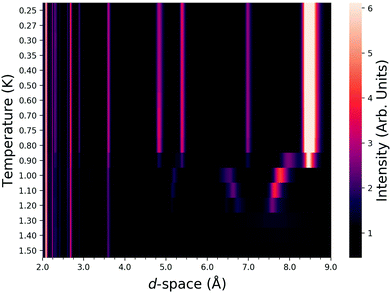
To probe the nature of the magnetic transitions observed via low temperature magnetic susceptibility measurements of these compounds we continued these studies on HoODCO₃, below 1.5 K. Upon cooling the sample further, the magnetic diffuse scattering shifts and sharpens into Bragg peaks ascribable to the development of long range order (Fig. 7). The broadening of these Bragg peaks is an indication of the finite correlation length in this material, varying from ∼419 to ∼1520 Å, between 1.2 and 0.9 K. These broad Bragg features sharpen with decreasing temperature, and indicate a growing correlation length. Between 1.2 and 0.9 K, these magnetic reflections can be indexed with a k-vector – [α,0,0], summarised in Table 1, corresponding to the Σ symmetry line of the first Brillouin zone (BZ).

Table 1 Summary of k-vectors and moments of the incommensurate phase of HoODCO₃

Temperature (K)	α	Moment (μB)
1.0	0.24811(12)	7.68(04)
1.1	0.27259(8)	6.54(04)
1.2	0.28421(13)	4.20(05)

---

Rietveld refinements of the data with this k-vector produced an excellent fit to the data (Fig. 8). The broadening of the peaks associated with finite correlations length, was modelled with an anisotropic broadening model and accounted for the peak broadening sufficiently well to model the peak intensities. This magnetic phase can be described by a longitudinal amplitude modulated spin-density wave propagating along the a-axis.

Fig. 7 Contour plot of HoODCO₃ diffraction patterns with respect to temperature, between 0.25 and 1.5 K, showing the movement of the magnetic peaks with temperature and thus a changing propagation vector.

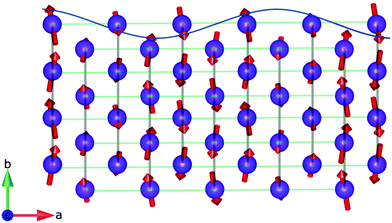
The moments in HoODCO₃ are oriented primarily along the b-axis, canted into the ac plane (see Fig. 9), with the unit vector [±0.28, 1.06, ±0.66] consistent with the RMC refinements. In insulating materials, such as LnODCO₃, the total magnetic moment on each is expected to remain constant so the modulated moments reflect an average structure interpretation of a structure in which some of the magnetic moments remains disordered. The observation of such a state, therefore, is support for magnetic frustration between adjacent chains caused by Ising-like spins on a distorted triangular lattice. In particular the magnetic modulation is observed along the same axis in which there are ferromagnetic coupling between chains in the incommensurate structure despite the antiferromagnetic correlations observed in the short range ordered phase, reflecting the comprise needed to achieve long-range magnetic order.

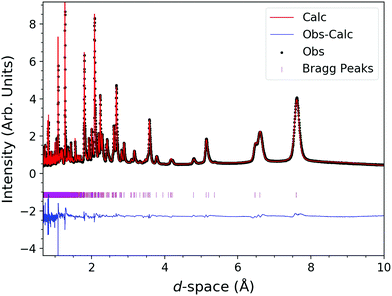Fig. 8 Rietveld fits to neutron diffraction pattern of HoODCO₃ at 1.1 K, from the 90° bank of WISH, along with the fitting statistics R_p = 6.72% and R_wp = 4.20%.

Cooling further, at 0.9 K there is some magnetic phase separation, with the model producing the best fit to our data consisting of two magnetic phases, an incommensurate and a k = 0 phase. At 0.8 K and below only the commensurate magnetic order exists. Using the Bilbao Server³⁵ and Rietveld refinement we have determined the data agrees with the P2₁2₁2₁ magnetic space group, with the lattice parameters a = 4.80206(15) Å, b = 6.95563(20) Å, c = 8.42543(27) Å at 0.25 K (see Fig. 10 for quality of the fit and Tables S1 and S2 (ESI†) for model information). Since the k-vector is a special point of the Brillouin zone the phase of the system is fixed to a solution, that produces symmetry equivalent magnetic moments, with a single independent magnetic site, and a moment of 7.63(6) μ_B at 0.25 K. The P2₁2₁2₁ magnetic space group does not allow any ferromagnetic component, while magnetic susceptibility suggests a ferromagnetic component in applied fields indicating this symmetry is likely lowered further. The weak ferromagnetic order that leads to this, however, is evidently too subtle to be observed in the neutron diffraction patterns. Fig. 11 shows the moments oriented in the direction of the nearest neighbour along the face-sharing polyhedral, in the direction of the chain. Magnetic coupling along the chains remains ferromagnetic, with spins canted into the ab plane caused by the strong Ising-like single ion anisotropy, with antiferromagnetic coupling of chains along the c-axis but ferromagnetic correlation of spins along the a-axis.

Fig. 9 Magnetic structure of the incommensurate magnetic phase of HoODCO₃ at 1.1 K, along 100 direction. Moments are aligned primarily along the b-axis, and canted into the c-axis. The amplitude modulated spin-wave propagates along the incommensurate a-axis. Only magnetic atoms are included for clarity. Black lines indicate the ferromagnetic chains, the green lines indicate magnetic moments with the same fractional coordinates in translated unit cells. Sine wave indicates the propagation of the amplitude modulated magnetic moments.

Fig. 10 Rietveld fits to neutron diffraction patterns of HoODCO₃ at 0.25 K, in the k = 0 phase, from the 90° bank (top) and the high resolution 153° (bottom) of WISH along with the fitting statistics R_p = 7.06%, R_wp = 6.00% and R_p = 7.84%, R_wp = 4.74%.

Fig. 11 Magnetic structure of the k = 0 ordered magnetic phase of HoODCO₃ at 0.25 K, shown along [100] direction. This highlights ferromagnetic intrachain coupling along the b-axis, and antiferromagnetic interchain coupling along the c-axis. Ho coordination environment shown as purple polyhedra, and magnetic vector orientations shown as red arrows. Nearest neighbour intrachain correlations have been highlighted with black arrows in the direction of the ferromagnetic chain vector. The inset shows the ball and stick model off the [100] direction, carbon and oxygen are shown in black and red respectively. Deuterium has been omitted for clarity. Nuclear and magnetic unit cells are shown as black boxes.

In the commensurate magnetic structure the spins remain oriented in the same direction as in the incommensurate phase, but are now all spins exhibit the same degree of magnetic order. In this ordered phase the magnetic Bragg peaks are sharper than in the incommensurate phase but still much broader than instrumental resolution, and we observed no reduction in the width of the magnetic peaks upon further cooling, indicating the magnetic domain size remains unchanged. Therefore, even in this commensurate long range ordered state the magnetic domains remain relatively small, with an average correlation length of ∼1580 Å. The correlation length along the a-axis is even shorter, as indicated by the most significant broadening of the (100) reflection. Extracting the correlation length from the anisotropic broadening, reveals a correlation length of ∼438 Å along this direction. We attribute this anisotropic peak broadening to underlying frustration since in this commensurately ordered phase the moment along the a-axis are aligned ferromagnetically with respect to each other while in the short range ordered phases we observe significant antiferromagnetic correlations in this direction. The ordered magnetic moment observed at 0.25 K is still significantly lower than the 10 μ_B expected from a fully ordered Ho³⁺ moment, observed through neutron diffraction (see Fig. S8 (ESI†) for the magnetic moment evolution); indicative of the retention of significant disorder within the system.

It should be noted that the model of the magnetic interactions of the short range ordered phase is broadly consistent with the order seen in the commensurate and incommensurate phases of HoODCO₃. The ferromagnetic intrachain correlations remain present in the ordered phases, while the Ising-like character are reflected by the non-collinear ordered magnetic structures. Clear evidence of magnetic frustration is presented by both the nature of the incommensurately modulated phase and the reduced magnetic domain size and ordered moment. Given the similar short range order and susceptibility data we expect that TbODCO₃, will also undergo a transition to a similar longer range ordered state, which could be confirmed using neutron diffraction. Further exploration of the magnetic frustrations within these frameworks with inelastic neutron scattering would enable the magnetic interactions to be probed directly. Direct observation of the magnetocaloric effect in these materials, through neutron diffraction in applied fields would also provide great detail about the mechanism of the magnetocaloric effect.

Conclusions

This work reports the low temperature magnetic susceptibility and magnetic order of LnODCO₃ frameworks. We show that that the promising magnetocaloric phases develop significant magnetic correlations below 20 K. In the short range ordered phase these systems show features consistent with a ferromagnetic Ising chains with frustrated antiferromagnetic interchain packing and non-collinear magnetic moments. At 1.2 K, HoODCO₃ undergoes a transition to an incommensurate magnetic state, with the k-vector [α,0,0], characterised by a spin-density wave in the same direction. Upon further cooling HoODCO₃ transitions to a k = 0 commensurate magnetic state with similar spin orientation and magnetic order to the incommensurate ordered state, with a finite correlation length of ∼438 Å along the a-axis, which may arise from the magnetic frustration in this material. We attribute these correlations to the efficient magnetocaloric effect observed in these materials. We propose that frustration and ferromagnetic chains present in these materials, which persist in the paramagnetic phase, as short range order, are responsible for the excellent magnetocaloric properties in these materials and are a recipe for enhanced refrigeration materials. Additionally the search for ferromagnetic chain compounds may be aided by searching for efficient magnetocaloric materials, as seen in the LnODCO₃ and Ln(DCO₂)₃ frameworks.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

RJCD would like to thank J. A. M. Paddison for his continued support and in-depth discussions of reverse Monte-Carlo analysis using SPINVERT and the University of Kent's for financial support through the provision of a Vice-Chancellors scholarship. We would also like to thank the Science and Technologies Facilities Council for access to the ISIS facility at Harwell and the Leverhulme Trust through funding via RPG-2018-268.

References

1. S. D. Bader and S. S. P. Parkin, Annu. Rev. Condens. Matter Phys., 2010, 1, 71–88.
2. T. D. Ladd, F. Jelezko, R. Laflamme, Y. Nakamura, C. Monroe and J. L. O’Brien, Nature, 2010, 464, 45–53.
3. A. Cho, Science, 2009, 326, 778–779.
4. J. Lyubina, J. Phys. D: Appl. Phys., 2017, 50, 053002.
5. P. Mukherjee and S. E. Dutton, Adv. Funct. Mater., 2017, 27, 1701950.
6. P. Mukherjee, E. Suard and S. E. Dutton, J. Phys.: Condens. Matter, 2017, 29, 405807.
7. R. J. C. Dixey and P. J. Saines, Inorg. Chem., 2018, 57, 12543–12551.
8. G. Lorusso, J. W. Sharples, E. Palacios, O. Roubeau, E. K. Brechin, R. Sessoli, A. Rossin, F. Tuna, E. J. L. McInnes, D. Collison and M. Evangelisti, Adv. Mater., 2013, 25, 4653–4656.
9. E. Palacios, J. A. Rodríguez-Velamazán, M. Evangelisti, G. J. McIntyre, G. Lorusso, D. Visser, L. J. De Jongh and L. A. Boatner, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 214423.
10. Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Chem. Soc. Rev., 2014, 43, 1462–1475.
11. J. L. Liu, Y. C. Chen and M. L. Tong, Chem. Rec., 2016, 16, 825–834.
12. J. L. Liu, Y. C. Chen, F. S. Guo and M. L. Tong, Coord. Chem. Rev., 2014, 281, 26–49.
13. A. Smith, Eur. Phys. J. H, 2013, 38, 507–517.
14. P. Weiss and A. Piccard, J. Phys. Theor. Appl., 1917, 7, 103–109.
15. W. F. Giauque and D. P. MacDougall, Phys. Rev., 1933, 43, 768.
16. E. Ising, Z. Phys., 1925, 31, 253–258.
17. P. J. Saines, J. A. M. Paddison, P. M. M. Thygesen and M. G. Tucker, Mater. Horiz., 2015, 2, 528–535.
18. Y.-C. Chen, L. Qin, Z.-S. Meng, D.-F. Yang, C. Wu, Z. Fu, Y.-Z. Zheng, J.-L. Liu, R. Tarasenko, M. Orendáč, J. Prokleška, V. Sechovský and M.-L. Tong, J. Mater. Chem. A, 2014, 2, 9851–9858.
19. J. A. M. Paddison, H. Jacobsen, O. A. Petrenko, M. T. Fernández-Díaz, P. P. Deen and A. L. Goodwin, Science, 2015, 350, 179–181.
20. P. Schiffer, A. P. Ramirez, D. A. Huse, P. L. Gammel, U. Yaron, D. J. Bishop and A. J. Valentino, Phys. Rev. Lett., 1995, 74, 2379–2382.
21. O. A. Petrenko, C. Ritter, M. Yethiraj and D. M. K. Paul, Phys. B, 1997, 241–243, 727–729.
22. D. R. Harcombe, P. G. Welch, P. Manuel, P. J. Saines and A. L. Goodwin, Phys. Rev. B, 2016, 94, 174429.
23. R. J. C. Dixey, F. Orlandi, P. Manuel and S. E. Dutton, Philos. Trans. R. Soc., A, 2019, 377, 20190007.
24. R. Li, P. Manuel, F. Orlandi and C. Greaves, J. Mater. Chem. A, 2018, 6, 21149–21155.
25. B. T. M. Willis and C. J. Carlile, Experimental neutron scattering, Oxford University Press, 2009.
26. P. J. Saines and N. C. Bristowe, Dalton Trans., 2018, 47, 13257–13280.
27. Z. L. Xue, A. J. Ramirez-Cuesta, C. M. Brown, S. Calder, H. Cao, B. C. Chakoumakos, L. L. Daemen, A. Huq, A. I. Kolesnikov, E. Mamontov, A. A. Podlesnyak and X. Wang, Eur. J. Inorg. Chem., 2019, 1065–1089.
28. P. Day, Inorg. Chim. Acta, 2008, 361, 3365–3370.
29. L. C. Chapon, P. Manuel, P. G. Radaelli, C. Benson, L. Perrott, S. Ansell, N. J. Rhodes, D. Raspino, D. Duxbury, E. Spill and J. Norris, J. Neutron Res., 2011, 22, 22–25.
30. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
31. J. Rodriguez-Carvajal, M. T. Fernandez-Diaz and J. L. Martinez, J. Phys.: Condens. Matter, 1991, 3, 3215–3234.
32. J. A. M. Paddison, J. Ross Stewart and A. L. Goodwin, J. Phys.: Condens. Matter, 2013, 25, 454220.
33. J. Rodney, F. R. S. Baxter, H. B. Jovanovich and P. L. S. Diego, Exactly Solved Models in Statistical Mechanics, Academic Press, New York, Berkeley, Boston, Sydney, Tokyo, Toronto, 1982.
34. J. A. M. Paddison, S. Agrestini, M. R. Lees, C. L. Fleck, P. P. Deen, A. L. Goodwin, J. R. Stewart and O. A. Petrenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 014411.
35. J. M. Perez-Mato, S. V. Gallego, E. S. Tasci, L. Elcoro, G. de la Flor and M. I. Aroyo, Annu. Rev. Mater. Res., 2015, 45, 217–248.

---

Footnote

† Electronic supplementary information (ESI) available: Tables and figures of crystallographic details and local magnetic structure refinements. See DOI: 10.1039/c9tc04980k

---