Ultrafast X-ray photoelectron diffraction in triatomic molecules by circularly polarized attosecond light pulses
Received
21st September 2019
, Accepted 28th November 2019
First published on 4th December 2019
Abstract
We theoretically study ultrafast photoelectron diffraction in triatomic molecules with cyclic geometry by ultrafast circular soft X-ray attosecond pulses. Molecular frame photoelectron distributions show complex diffraction patterns, arising from molecular multiple center interference and circular charge migration. It is found that photoelectron diffraction patterns depend on the initial electronic state, encoding the information of molecular orbital symmetries. In a resonant coherent electron excitation process, time-resolved photoelectron diffraction patterns enables us to reconstruct the charge migration with highly spatiotemporal resolutions. We simulate and analyze the results from ab initio calculations of the single electron triangular hydrogen molecular ion H32+ which is used as a benchmark molecular system in combination with an ultrafast multi-center and multi-state photoionization model. This approach presents a general scheme which can be applied to explore circular charge migration from electron orbits and attosecond coherent electron dynamics in polyatomic systems by circular ultrafast laser pulses.
1 Introduction
Imaging and manipulating nuclear and electronic dynamics on their natural time and spatial scales by ultrafast laser pulses is a fundamental issue in photophysics and photochemsitry.1–6 The developments of ultrashort laser technology7,8 have led to photoimaging techniques such as Coulomb explosion9,10 for nuclear motion on femtosecond (1 fs = 10−15 s) time scale to laser-induced electron diffraction (LIED)11–14 for coupled electron-nuclear motion on the attosecond (1 as = 10−18 s) time scale. Now the shortest 43 as pulses are available for new ultrafast optical imaging.15 Illuminating molecules from within with ultrafast lasers will allow one to rely on electron interference and diffraction where structural information is encoded in interference patterns that result from the intrinsic wave nature of the electron and its laser-assisted scattering.16 Photoelectron diffraction therefore has been shown to be a promising candidate for studies of molecular structural dynamics.17–23 Such phenomena in diatomic molecules were predicted earlier by Cohen and Fano24 in linear polarization perturbative single photon ionization. Based on multiple-scattering X-ray photoelectron diffraction, one can measure molecular geometry structure.21 Effects of nuclear motion in molecular photoionization have also been investigated.25 Most recently, ultrafast X-ray photoelectron diffraction from diatomic molecules undergoing photodissociation has also been studied for tracking dissociation and elimination processes in chemical reactions.26 It has been shown that the LIED technique can be used to monitor geometric and orbital structures of a triatomic molecule with a resolution of a fraction of an Ångström.27,28 However, most of the work has been focused on linear molecular systems and single electronic state processes.
In a resonant excitation process, the pulse induces nonstationarity of electronic states in the molecule.29 The corresponding coherent population in multiple electronic states leads to charge migration in molecules on the attosecond time scale.30–44 The process can be used for selective laser excitation in molecules, leading to the concept of charge-directed chemistry.45,46 Therefore, steering charge migration by ultrafast laser pulses offers a new approach to controlling chemical reactions. The charge migration is related to a strong coupling between electronic states in the molecule which can enhance ionization47 and induce transient localization of electron wave packets,48,49 thus allowing to control photoelectron emission spectra50 and high-order harmonic spectra.51 It has also been shown that quantum control of electron flux during intramolecular charge migration is possible by designing ultrafast laser pulses that prepare the system in selective electronic states,42,52 giving rise to ultrafast molecular magnetism53–55 for new quantum devices.56 Experiments have for the first time measured attosecond charge migration with linearly polarized high harmonic spectroscopy in ionized iodoacetylene via attosecond electron recollision processes.57 The developments of attosecond laser pulses enable us therefore to obtain insights into electron dynamics by time-resolved photoelectron spectroscopy on the attosecond time scale and sub-nanometer dimension.58–61 We have therefore proposed that one can monitor coherent excitation and attosecond charge migration in time-dependent photoelectron diffraction in molecular photoelectron distributions which encode information on the symmetry of electron orbitals and molecular bonding62–64 by a model which describes the electron coherent excitation between two electronic states in the diatomic H2+. In polyatomic molecules, effects of multiple center interference and electronic degeneracy make time-resolved photoelectron diffraction more complex. One thus requires modelling exact photoelectron diffraction patterns to explore coherent electron excitation in complex molecular systems.
In this paper, we demonstrate attosecond photoelectron diffraction patterns in triatomic molecular systems with cyclic geometry by a circularly polarized attosecond soft X-ray pulse. We first present photoelectron diffraction patterns from different initial electronic states, which are shown to be dependent on the molecular geometry and orbital symmetry. The ionization process from degenerate electronic states is also presented where electronic state interference effects have been shown to be important in molecular photoionization.65,66 For a coherent superposition state in a resonant excitation process created by a pump pulse, we use a time-delayed circularly polarized soft X-ray probe pulse to produce photoelectron distributions. Results show that photoelectron diffraction patterns are dependent on the time delay between the pump–probe pulses, inferring the coherent intramolecular electron dynamics. A cyclic triatomic single electron molecular ion H32+ is adopted as a benchmark molecular system model. The trihydrogen cations, as well as their isotopes, due to the unique equilateral triangular geometry, provide a fundamental original system for the theoretical development of the nonperturbative response of nonlinear polyatomic molecules to intense laser pulses.67–72 Simulation results are obtained by solving the time-dependent Schrödinger equation (TDSE). The molecular internuclear distance is always fixed during excitation and ionization processes. We analyze the photoelectron distributions by multi-center and multi-state diffraction models derived from ultrafast photoionization models.11 Moreover, the molecular rotational and vibrational motions on picosecond (1 ps = 10−12 s) and femtosecond time scales are ignored because these effects are much slower than the laser-molecule interaction that occurs within the attosecond time scale. We use a circularly polarized probe laser pulse with equal field amplitude in each orthogonal direction, which does not influence the symmetry of photoionization. Such ultrafast attosecond circularly polarized X-ray pulses have been generated by current laser techniques from circularly polarized high harmonics.73–75
The paper is arranged as follows: in Section 2, we briefly describe the numerical and computational methods. Section 3 presents numerical results for photoelectron diffraction obtained by time-dependent quantum electron wave-packet calculations from the corresponding TDSE for oriented H32+. A theoretical analysis based on ultrafast multi-center and multi-state photoionization models is also derived. Finally, we summarize our findings in Section 4 (throughout this paper, atomic units, a.u., are used unless otherwise noted).
2 Computational and numerical methods
The excitation and ionization dynamics of the molecular ion H32+ can be exactly described by numerically solving the three-dimensional (3D) TDSE, thus allowing to describe ultrafast electron dynamics in molecular reaction processes.76 For the molecular ion H32+ oriented in the (x,y) plane, Fig. 1, the corresponding TDSE with a static nuclei frame described in cylindrical coordinates (ρ, θ, z) with (x = ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, y = ρ
θ, y = ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) as the molecular plane is written as,
θ) as the molecular plane is written as,| |  | (1) |
The kinetic energy operator is| |  | (2) |
The molecular electron Coulomb potential is given by,| |  | (3) |
The nuclear coordinates Nix and Niy are fixed by the relations N1x = 0, N2x = −R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Θ/2), N3x = +R
sin(Θ/2), N3x = +R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Θ/2), N1y = (2/3)R
sin(Θ/2), N1y = (2/3)R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Θ/2), N2y = −(1/3)R
cos(Θ/2), N2y = −(1/3)R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Θ/2), N3y = −(1/3)R
cos(Θ/2), N3y = −(1/3)R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Θ/2), R being the distance between two protons and the bond angle Θ = 60°, see Fig. 1(a). A soft parameter β = 0.35 is used to remove the Coulomb singularity and produce accurately the electronic state potential energies of H32+.77 The field-molecule interaction VL(r,t) = r·E(t) is treated in the length gauge and dipole approximation, since by exact solutions of the TDSE, numerical results are gauge invariant.78 The laser fields E(t) = Epu(t) + Epr(t) always propagate along the z axis, perpendicular to R and the molecular (x,y) plane. The forms, for the circularly polarized pump pulse Epu(t) are defined as
cos(Θ/2), R being the distance between two protons and the bond angle Θ = 60°, see Fig. 1(a). A soft parameter β = 0.35 is used to remove the Coulomb singularity and produce accurately the electronic state potential energies of H32+.77 The field-molecule interaction VL(r,t) = r·E(t) is treated in the length gauge and dipole approximation, since by exact solutions of the TDSE, numerical results are gauge invariant.78 The laser fields E(t) = Epu(t) + Epr(t) always propagate along the z axis, perpendicular to R and the molecular (x,y) plane. The forms, for the circularly polarized pump pulse Epu(t) are defined as| | 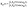 | (4) |
and for the circularly polarized probe pulse Epr(t − Δτ),| |  | (5) |
êx/y is the laser field polarization vector. ωpu and ωpr are frequencies of the pump and probe pulses. A temporal slowly varying envelope f(t) = sin2(πt/Tpu/pr) is used with duration Tpu/pr = nτpu/pr, where τpu/pr = 2π/ωpu/pr, one optical cycle of pump/probe pulses. Multiple optical cycle duration Tpu/pr ensures the field area  to eliminate effects of static fields and carrier envelope phases of pulses. The time delay Δτ = tpr0 − tpu0 defines the time interval between the peak times tpu0 and tpr0 of the pump Epu(t) and probe Epr(t) pulses.
to eliminate effects of static fields and carrier envelope phases of pulses. The time delay Δτ = tpr0 − tpu0 defines the time interval between the peak times tpu0 and tpr0 of the pump Epu(t) and probe Epr(t) pulses.
 |
| | Fig. 1 (a) Molecular geometry of the cyclic triangular molecular ion H32+ oriented in the (x,y) plane. si denotes the s orbital of the atomic H on proton i, where i = 1, 2, and 3. Rij = Rj − Ri presents the molecular internuclear distance and Θ = 60° is the bond angle between two molecular bonds. (b) Illustration of the molecular photoionization process in H32+ by an attosecond soft X-ray probe pulse initiated from the three electronic states, ψie, ie = A′, E+, or E−, in eqn (10)–(12), where the E+ and E− states are degenerate, and ψco, a superposition state in eqn (16) created by a circularly polarized resonant pump pulse. (c) The density distributions of the three electronic states, and arbitrary units are used. | |
We numerically solve the 3D TDSE of H32+ in eqn (1) by using a five-point finite difference method and fast Fourier transform technique combined with high-order split-operator methods.79,80 The time step is fixed at Δt = 0.01 a.u. = 0.24 as and the spatial discretization is Δρ = Δz = 0.25 a.u. (1 a.u. = 1 a0, Bohr radius) for radial grid sizes 0 ≤ ρ ≤ 128 a.u. and |z| ≤ 64 a.u., and angle grid size Δθ = 0.01 radian. The grid sizes exceed largely the maximum field induced electron displacements αd = E0/ωpu/pr2. To prevent unphysical effects due to the reflection of the ionized wave packet from the boundary, a mask function with the form cos1/8[π(ρ − ρa)/2ρabs] is used at ρabs = ρmax − ρa = 24 a.u. with ρmax = 128 a.u.
Molecular frame photoelectron distributions are calculated by a Fourier transform of the 3D time dependent electronic wavefunction ψ(ρ,θ,z,t) which exactly describe the electron dynamics in the continuum:81
| |  | (6) |
where
tp is the time after the pulse turn off and
ρf = 100 a.u. is an asymptotic point before the wavepacket is absorbed.
E is the kinetic energy of an ionized electron with wave vector
k =
p = 2π/
λe,
p = (
px2 +
py2)
1/2 is the momentum of a photoelectron of wavelength
λe. Since the ionization occurs in the laser polarization (
x,
y) molecular plane, we define
θ as the angle between the electron momentum
p and the
x polarization axis. With the transformation
px =
p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ and
py =
p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
sin
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ, we then obtain the two-dimensional (2D) momentum distributions of photoelectrons from
eqn (6). Photoelectron angular distributions at photoelectron kinetic energy
Ee are obtained by integrating over the one photon energy, where the spectra width of the probe pulse Δ
ω ≈
ωpr/3,
| |  | (7) |
where
Ee =
p2/2 =
ωpr −
Ip, corresponding to the main one photon
ωpr frequency of absorption with the orbital ionization potential
Ip. In this work, the wavelength of photoelectron
λe <
R leads to photoelectron diffraction effects
11 in photoelectron distributions obtained from
eqn (7).
3 Results and discussions
The purpose of the present work is to study ultrafast photoelectron diffraction patterns in molecular photoionization by circularly polarized attosecond X-ray pulses. The result provides a way to monitor molecular structure and orbital symmetry and coherent electron dynamics. We adopt the triangular molecular ion as a benchmark system to illustrate the photoelectron imaging process. The single electron molecular ion H32+ system can be considered as the fundamental element of triatomic molecular systems. The molecule is excited and ionized by high-frequency pump and probe pulses. Such high-frequency pulse can not lead to tunnelling ionization and electron recollision. The ponderomotive energy Up = E02/4ωpu/pr2 is weak and the Keldysh parameter  .7 Therefore, the modification of the ionization potential by laser-induced Stark shifts can be ignored. The dipole approximation, in which the spatial dependence and magnetic component of the external field are neglected, remains valid. Moreover, the non-adiabatic coupling effects due to electron-nuclear combined dynamics in triatomic molecules68 are also ignored in the ultrafast photoionization processes.
.7 Therefore, the modification of the ionization potential by laser-induced Stark shifts can be ignored. The dipole approximation, in which the spatial dependence and magnetic component of the external field are neglected, remains valid. Moreover, the non-adiabatic coupling effects due to electron-nuclear combined dynamics in triatomic molecules68 are also ignored in the ultrafast photoionization processes.
3.1 Electronic state symmetry dependent photoelectron diffraction
Photoelectron diffraction has been shown to be determined by the initial molecular symmetry, thus providing a tool for imaging of molecular orbitals.11,27,28 We first compare the photoelectron diffraction patterns with different molecular orbital symmetries in the equilateral triangular molecular ion H32+, as illustrated in Fig. 1(b). The three lowest electronic states of H32+, A′, E+, and E−, are used respectively as the initial state. The excited electronic states E+ and E−, are degenerate with E-symmetry. The complex wavefunctions can be expressed in terms of two real ones,| |  | (8) |
and| |  | (9) |
corresponding to angular momentum m = ±1 around the z axis.53 The two orthogonal real components ψ(1)E and ψ(2)E are obtained numerically from imaginary time propagation of the field-free Hamiltonian eqn (1). In Fig. 1(c) we also display the corresponding electron density distributions |ψie(x,y)|2, ie = A′, E+, or E−, of the three electronic states. The corresponding ionization potentials are respectively Ip(A′) = 1.08 a.u. (29.38 eV) and Ip(E+) = Ip(E−) = 0.92 a.u. (25.02 eV) for the molecular internuclear distance R = 4 a.u. and the bond angle Θ = 60°.
Fig. 2 shows photoelectron momentum distributions of the three electronic states, (a) A′, (b) E+, and (c) E−, of H32+ by the single circularly polarized attosecond soft X-ray probe pulse Epr(t), eqn (5). The molecular ion H32+ with internuclear distance R = 4 a.u. is oriented in the (x,y) plane, Fig. 1. The circularly polarized attosecond probe pulse with its field vector in the (x,y) plane propagates along the z axis. The pulse wavelength λpr = 5 nm (ωpr = 9.11 a.u.), duration Tpr = 10τpr = 165.4 as, corresponding to 83 as full width at half maximum (FWHM), and intensities I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.) are used. Inserts (white lines) are the corresponding photoelectron angular distributions calculated from eqn (7). From Fig. 2 we see that photoelctron momentum distributions exhibit ring structure at momentum  a.u. With such high frequency X-ray pulse, the wavelength of the photoelectron is λe = 2π/p = 1.57 a.u., less than the molecular internuclear distance R. As a result, diffraction of the photoelectron occurs11 where multiple angular nodes are produced in photoelectron distributions. Of note is that the geometries of the photoelectron distributions are different for various electronic states, i.e., the photoelectron diffraction patterns depend on the orbital symmetry of the initial electronic state. One further finds that for the two degenerate excited electronic states, E+, and E−, photoelectron momentum and angular distributions are mirror image with respect to the molecule center, as shown in Fig. 2(b) and (c), since the angular momentum of each is m = +1 and −1, i.e., reflection images of each current.
a.u. With such high frequency X-ray pulse, the wavelength of the photoelectron is λe = 2π/p = 1.57 a.u., less than the molecular internuclear distance R. As a result, diffraction of the photoelectron occurs11 where multiple angular nodes are produced in photoelectron distributions. Of note is that the geometries of the photoelectron distributions are different for various electronic states, i.e., the photoelectron diffraction patterns depend on the orbital symmetry of the initial electronic state. One further finds that for the two degenerate excited electronic states, E+, and E−, photoelectron momentum and angular distributions are mirror image with respect to the molecule center, as shown in Fig. 2(b) and (c), since the angular momentum of each is m = +1 and −1, i.e., reflection images of each current.
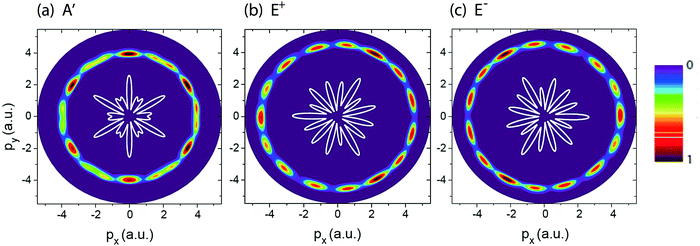 |
| | Fig. 2 Photoelectron momentum (px,py) distributions of different H32+ initial electronic states, (a) A′, (b) E+, and (c) E−, (Fig. 1) by the circularly polarized attosecond soft X-ray probe pulse Epr(t). The corresponding electron momentum is about p = 4.0 a.u. The molecular ion H32+ with internuclear distance R = 4 a.u. is oriented in the (x,y) plane. The probe pulses are polarized in the (x,y) plane, propagating along the z axis. The probe pulse wavelength λpr = 5 nm (ωpr = 9.11 a.u.), duration Tpr = 10τpr = 165.4 as (83 as FWHM), and intensities I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.) are used. Inserts (white lines) are the corresponding photoelectron angular distributions. Arbitrary units are used. | |
We describe the ultrafast photoelectron distributions of H32+ by deriving the delta function photoionization model which has been used successfully in ultrafast H2+ ionization processes.11 For the molecule H32+, each H atom has a 1s orbital. According to molecular orbital theory, the electronic states are linear combinations of the three 1s orbitals. The molecular wavefunctions of the bound atomic configurations are given by82
| |  | (10) |
for the
A′ state,
| |  | (11) |
for the
E+ state, and
| |  | (12) |
for the
E− state, where
ε = e
i2π/3.
ψs1,
ψs2, and
ψs3 denote the wavefunctions of the 1s atomic orbital on protons 1, 2, and 3. The
E+ and
E− states are doubly-degenerate with the same eigenenergies and are reflection of each other
ψE+ =
ψE−*. According to the ultrafast photoionization model
11,83 derived in Appendix B, photoelectron distributions are dependent on the orbital symmetry of the initial state. In this work, the pulse field strength
E0 can be ignored to describe the effect on the photoelectron dynamics in high-frequency photoionization since the chosen intensities (
I0 = 2.75 × 10
13 W cm
−2 and
E0 = 2.84 × 10
−2 a.u.) in the simulations produce negligible ponderomotive energies
Up ≪
Ip and
E0 ≪
p. The transition amplitude for the ground
A′ electronic state in
eqn (31) can be simply expressed as
| |  | (13) |
where
ϑp defines the angle between the photoelectron momentum
p and the
x axis. Similarly, for the two degenerate excited
E+ and
E− electronic state, the corresponding photoelectron distributions are,
| | 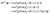 | (14) |
and
| | 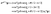 | (15) |
From eqn (13)–(15) one notes that in the nonlinear ultrafast three center photoionization model, the interference is simply the sum of the contributions from all centers. The ionized electron wave packets from different centers will interfere with each other. For the triatomic molecular system, the initial orbitals are separated by R. The terms of sine and cosine triangle functions present the interference effects of the three outgoing electron wave packets emanating from the three nuclear centers.
In Fig. 3 (left column) we show results of molecular photoelectron momentum (px,py) distributions obtained from eqn (13)–(15) for the three lowest electronic states with the photoelectron momentum ranging from 0 to 7.5 a.u. The molecular internuclear distance is set as R = 4 a.u. It is found that for the three electronic states, A′, E+, and E−, a set of alternating bright and dark interference fingers with points are obtained in Fig. 3. We also plot the molecular photoelectron angular distributions at a certain momentum p = 4 a.u., corresponding to the ionization by a λ = 5 nm X-ray pulse, right column in Fig. 3. From Fig. 3 we see that the predictions are in good agreement with the simulation in Fig. 2. The mirror images of photoelectron distributions for the degenerate excited E+ and E− electronic states satisfy ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+)(p,ϑp) =
(E+)(p,ϑp) = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E−)(p,ϑp ± π). Multiple angular nodes with different amplitudes are produced, arising from the multiple center interference of photoelectron. The different diffraction patterns illustrate the various symmetries of the initial electronic state, thus allowing for imaging of molecular orbitals.
(E−)(p,ϑp ± π). Multiple angular nodes with different amplitudes are produced, arising from the multiple center interference of photoelectron. The different diffraction patterns illustrate the various symmetries of the initial electronic state, thus allowing for imaging of molecular orbitals.
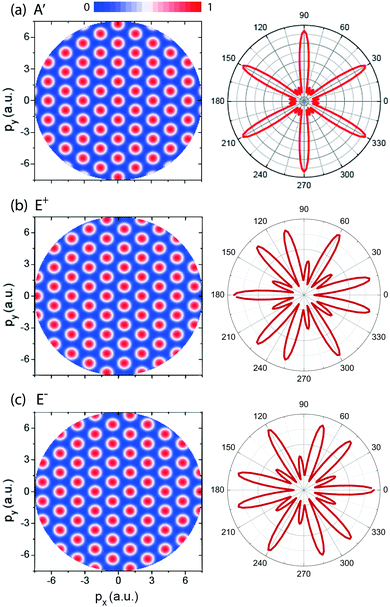 |
| | Fig. 3 (left column) Photoelectron momentum (px,py) distributions of the H32+ three electron states, (a) A′, (b) E+, and (c) E−, predicted in eqn (13)–(15). The photoelectron momentum ranges from 0 to 7.5 a.u. The molecular ion with intercnulear distance R = 4 a.u. is oriented in the (x,y) plane. (right column) Photoelectron angular distribution at a certain momentum p = 4 a.u., corresponding the photoelectron wavelength λe = 1.57 a.u. obtained by a 5 nm photon absorption. Arbitrary units are used. | |
3.2 Time-resolved photoelectron diffraction in molecular coherent resonant excitation
We next consider the photoelectron diffraction in a coherent resonant excitation process. In the molecule H32+, a resonant excitation from the ground A′ electronic state, ψA′ with the eigenenergy EA′, to the two degenerate electronic excited E+ and E− states, ψE+ and ψE−, with the eigenenergies EE+ = EE− can be triggered by a frequency ωpu = EE+/E− − EA′ pump laser pulse. A coherent superposition of the three electronic states created by the ωpu pump pulse, ψco(r,t) in eqn (36) can be obtained due to a strong charge-resonance excitation,29 as shown in Fig. 1(b). The corresponding ionization potentials of the three electronic states are respectively, Ip(A′) = 1.69 a.u., and Ip(E+) = Ip(E−) = 1.08 a.u. at R = 2 a.u. We choose a smaller internuclear distance R, in order to produce larger energy difference between the ground electronic and the two degenerate excited states. As a result, a shorter wavelength resonant pump pulse can be used, thus giving rise to better energy and angular momentum resolutions.
Fig. 4 displays numerical results of electron density distributions ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (x,y) of the superposition state created by the λpu = 75 nm (ωpu = 0.608 a.u.) pump pulse in eqn (4) as a function of time t, where
(x,y) of the superposition state created by the λpu = 75 nm (ωpu = 0.608 a.u.) pump pulse in eqn (4) as a function of time t, where  in eqn (1). We use a left handed circularly polarized XUV pulse to excite the molecular ion H32+. The pulse intensity and duration are chosen as I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.), Tpu = 10τpu = 2.48 fs (1.24 fs FWHM). Fig. 5 displays the evolution of the probabilities of the two ground A′ and excited E+ electronic states, |ci(t)|2, where cie(t) = 〈ψie(r)|ψ(r,t)〉 and ie denotes the A′, E+, or E− electronic state, with time t. By this pump pulse, a resonant excitation between the ground A′ and excited E+ states occurs. After the pump pulse t > 10τpu, the occupation coefficients are nearly constant. As displayed in Fig. 5, the occupation in the excited E+ state is |cE+(t)|2 = 0.5. The population remaining in the ground A′ state is |cA′(t)|2 = 0.42. Of note is that during the excitation processes, the molecule is also excited E+ to higher excited state and ionized to the continuum after absorptions of one and two ωpu from the excited state. As a result, the total population in the three electronic state is less than 1, i.e., |cA′(t)|2 + |cE+(t)|2 < 1.
in eqn (1). We use a left handed circularly polarized XUV pulse to excite the molecular ion H32+. The pulse intensity and duration are chosen as I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.), Tpu = 10τpu = 2.48 fs (1.24 fs FWHM). Fig. 5 displays the evolution of the probabilities of the two ground A′ and excited E+ electronic states, |ci(t)|2, where cie(t) = 〈ψie(r)|ψ(r,t)〉 and ie denotes the A′, E+, or E− electronic state, with time t. By this pump pulse, a resonant excitation between the ground A′ and excited E+ states occurs. After the pump pulse t > 10τpu, the occupation coefficients are nearly constant. As displayed in Fig. 5, the occupation in the excited E+ state is |cE+(t)|2 = 0.5. The population remaining in the ground A′ state is |cA′(t)|2 = 0.42. Of note is that during the excitation processes, the molecule is also excited E+ to higher excited state and ionized to the continuum after absorptions of one and two ωpu from the excited state. As a result, the total population in the three electronic state is less than 1, i.e., |cA′(t)|2 + |cE+(t)|2 < 1.
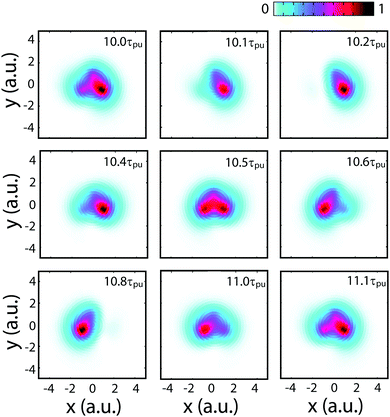 |
| | Fig. 4 Evolution of the coherent electronic wave packets with time in the molecular ion H32+ oriented in the (x,y) plane excited by a λpu = 75 nm (ωpu = 0.608 a.u.) circularly polarized laser pulse with its field vector polarized in the (x,y) plane, eqn (4). The molecular internuclear distance is R = 2 a.u. The pulse intensity I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.) and duration Tpu = 10τpu = 2.48 fs (1.24 fs FWHM). Arbitrary units are used. | |
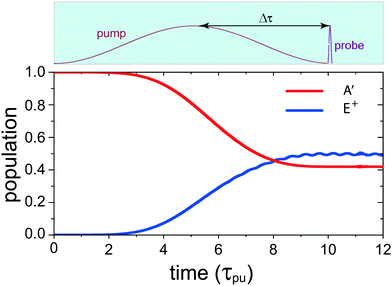 |
| | Fig. 5 Time-dependent occupations in the ground A′ and the excited E+ electronic states in H32+ excited by a λpu = 75 nm (ωpu = 0.608 a.u.) circularly polarized pump laser pulse with its field vector polarized in the (x,y) plane. The molecule is oriented in the (x,y) plane and its internuclear distance is R = 2 a.u. The pulse intensity I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.) and duration Tpu = 10τpu = 2.48 fs (1.24 fs FWHM). Insert (top): the pump–probe scheme for time-resolved photoelectron imaging. Δτ denotes the time delay between the pump and probe pulses for monitoring coherent excitation processes. The used time delay is about 1.2–1.5 fs. | |
From Fig. 4 one sees that the electron density distribution ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (x,y,t) shows an asymmetric structure in molecules which is dependent on the time t. The coherent electron wave packet moves periodically among the three nuclear centers. At time t = 10.2τpu, a strong electron localization is obtained and the coherent electronic wave packet mainly lies on proton 3. Increasing t leads to a variation of the electron distribution. The electron moves to proton 2 through proton 1. At time t = 10.8τpu, the electron is mainly localized on proton 2. As the time t increases further, the electron moves back to proton 1, and then proton 3. The period of the oscillation is approximately τ(0) = τpu = 248 as, one cycle of the circular pump pulse at 75 nm.
(x,y,t) shows an asymmetric structure in molecules which is dependent on the time t. The coherent electron wave packet moves periodically among the three nuclear centers. At time t = 10.2τpu, a strong electron localization is obtained and the coherent electronic wave packet mainly lies on proton 3. Increasing t leads to a variation of the electron distribution. The electron moves to proton 2 through proton 1. At time t = 10.8τpu, the electron is mainly localized on proton 2. As the time t increases further, the electron moves back to proton 1, and then proton 3. The period of the oscillation is approximately τ(0) = τpu = 248 as, one cycle of the circular pump pulse at 75 nm.
The evolution of the superposition state with time t in Fig. 4 arises from the coherent electron wave packet interference between the two A′ and E+ electronic states. As shown in Appendix C, the distributions of the coherent electronic states are time-dependent after the pulse excitation. The coherent superposition between the ground A′ state and the excited E+ state, is given by
| |  | (16) |
As shown in
eqn (37), the time-dependent coherent electron density distributions come from the
A′–
E+ state interference,
i.e.,
| | ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) intco(r,t) ∼ |cA′(t)cE+(t)‖ψA′(r)ψE+(r)|cos(ΔEt), intco(r,t) ∼ |cA′(t)cE+(t)‖ψA′(r)ψE+(r)|cos(ΔEt), | (17) |
where Δ
E is the energy difference between the excited
E+ states and the ground
A′ electronic states, Δ
E =
EE+ +
EA′.
Eqn (17) shows that the electron density distributions oscillate periodically with
τ(0) = 2π/Δ
E = 10.37 a.u. = 248 as. From
eqn (17) one also sees that the electron density probability
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif)
(
r,
t) will evolve among protons 1 ← 2 ← 3,
i.e., rotating around the molecular center with an anti-clockwise direction, corresponding to a left handed current, the helicity of the pump pulse. Comparing with
Fig. 4 and
eqn (17) shows that the numerical simulations are in good agreement with the theoretical predictions. At Δ
Et =
nπ, where
n is an integer, the superposition term cos(Δ
Et) = ±1 gives rise the maximum asymmetry of electron density distributions, whereas at Δ
Et = (
n + 1/2)π,
i.e., cos(Δ
Et) = 0 and
t = (
n + 1/2)
τpu, symmetric electron distribution are produced, as illustrated in
Fig. 4. The evolution of the electron density distribution therefore corresponds to the dependence of the attosecond electron coherence and resulting currents on the time
t in charge migration.
The corresponding time resolved photoelectron distribution can be derived based on a δ-function model11 for the ultrafast multi-center photoionization process in Appendix C which is given by, [eqn (39)],
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) intco(p,t) ∼ intco(p,t) ∼ ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int12 + int12 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int23 + int23 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int13, int13, | (18) |
where
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int12 = {cos[pR int12 = {cos[pR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑp − Θ) + π/3] + 1/2} × cos(ΔEt − π/3)ψs2(p), cos(ϑp − Θ) + π/3] + 1/2} × cos(ΔEt − π/3)ψs2(p), | (19) |
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int23 = {cos[pR int23 = {cos[pR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑp) − π/3] + 1/2}cos(ΔEt)ψs2(p), cos(ϑp) − π/3] + 1/2}cos(ΔEt)ψs2(p), | (20) |
and
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int13 = {cos[pR int13 = {cos[pR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑp + Θ) − π/3] + 1/2} × cos(ΔEt + π/3)ψs2(p), cos(ϑp + Θ) − π/3] + 1/2} × cos(ΔEt + π/3)ψs2(p), | (21) |
where 1, 2, and 3 are the three protons in
Fig. 1(a). In
eqn (18) the superposition term
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) co
co(
p,
θ,
t) ∼ cos(Δ
Et) leads to the evolution of the photoelectron distributions with the time
t. The photoelectron distributions encode the information on the time dependent electron motion in molecules, which is much faster than nuclear motion.
Fig. 6 illustrates photoelectron angular distributions obtained from the photoionization model, theoretically predicted in
eqn (18), at two different moments (a)
t = 0 and (b) π/Δ
E,
i.e., Δ
Et = 0 and π. The proton internuclear distance is
R = 2 a.u. and the photoelectron momentum
p = 4.0 a.u., corresponding to a 5 nm photon soft X-ray photon absorption. The time resolved photoelectron angular distributions show asymmetric structure and mirror image, indicating the coherent coupling between the ground
A′ and the excited
E+ electronic states.
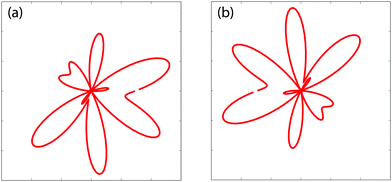 |
| | Fig. 6 Time-resolved photoelectron diffraction patterns (angular distributions) obtained from ultrafast photoionization models for a coherent electronic state predicted in eqn (18) at moments (a) t = 0 and (b) π/ΔE = 124 as (ΔE = 0.608 a.u.). The photoelectron momentum p = 4.0 a.u. and the molecular internuclear distance R = 2 a.u., cf., Fig. 7. | |
Fig. 7 displays the time-resolved molecular photoelectron distributions from 3D TDSE simulations produced by a left handed circularly polarized λpr = 5 nm (τpr = 16.5 as) attosecond probe pulse. The molecule H32+ is first excited by a circularly polarized λpu = 75 nm pump pulse. The time delays between the pump and probe pulses vary from Δτ = 5.0τpu to 6.0τpu with a time interval 0.25τpu (τpu = 248 as), i.e., the ionization time of the excited molecule by the probe pulse ranges from t = 10τpu to 11τpu. The other laser parameters are always fixed at pulse intensities I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.) and durations Tpu = 10τpu = 2.48 fs (1.24 fs FWHM) and Tpr = 10τpr = 165.4 as (83 as FWHM). With such 5 nm X-ray pulse, the extremely short duration on attosecond time scale can be utilized to resolve the coherent electron motion with the period since Tpr(FWHM) ≈ τ(0)/3. It should be noted that the pump pulse can also ionize the molecular ion H32+. The corresponding photoelectron energy is nωpu − Ip, much less than that of the X-ray ωpr photon absorption due to ωpr/ωpu = 15. Therefore we only focus on probing photoelectron distributions produced by the soft X-ray puls, i.e., the photoionization yields around the momentum p = 4.0 a.u., where  corresponding to one ωpr photon absorption to the continuum.
corresponding to one ωpr photon absorption to the continuum.
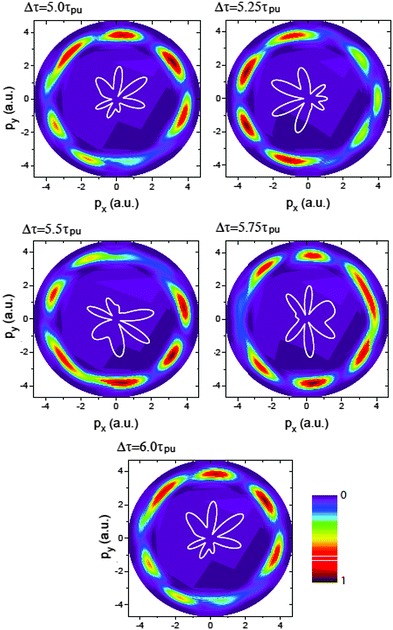 |
| | Fig. 7 Photoelectron momentum (px,py) distributions at different time delays Δτ between the pump Epu(t) and probe Epr(t − Δτ) pulses. The molecular ion H32+ with internuclear distance R = 2 a.u. is oriented in the (x,y) plane. The pump and probe pulses are polarized in the (x,y) plane, propagating along the z axis. The pulse wavelengths λpu = 75 nm (ωpu = 0.608 a.u.) and λpr = 5 nm (ωpr = 9.11 a.u.), duration Tpu = 10τpu = 2.48 fs (1.24 fs FWHM) and Tpr = 10τpr = 165.4 as (83 as FWHM), and intensities I0 = 2.75 × 1013 W cm−2 (E0 = 2.8 × 10−2 a.u.) are used. Inserts (white lines) are the corresponding photoelectron angular distributions. Arbitrary units are used. | |
From Fig. 7 one sees that similar results of X-ray photoelectron distributions with multiple angular nodes are obtained. With such λpr = 5 nm (ωpr = 9.11 a.u.) soft X-ray probe pulse, the photoelectron momentum and wavelength are p = 4.0 a.u. and λe = 2π/p = 1.57 a.u. less than the molecular internuclear distance R = 2 a.u. As a result, diffraction effects with multiple angular nodes appear in photoelectron distributions. It is, however, found that for these time-delayed cases, the photoelectron distributions show significant asymmetry with respect to the molecular center. Varying the time delay Δτ leads to a rotation of the photoelectron momentum and angular distributions in an anti-clockwise direction. The period of the rotation is τpu = 2π/ΔE = τ(0). The periodical rotation feature of the asymmetric photoelectron distributions indicates the electronic coherent excitation by the pump pulses in Fig. 4. One sees that due to the transformer of the electron between the protons, asymmetric distributions of the coherent superposition state evolve with the time t. The density distributions evolve with a period of τ(0) = 2π/ΔE = τpu. Consequently, altering the time-delay gives rise to a rotation of photoelectron diffraction patterns. The numerical results in Fig. 7 are in consonance with the predictions of photoelectron diffraction in coherent electron excitation processes in eqn (18) and Fig. 6, illustrating the evolution of the electron wave packets with time in molecules. Therefore the time-resolved photoelectron diffraction in Fig. 7 and eqn (18) allows us to explore the coherent electron dynamics of molecular attosecond circular charge migration.
Similar results of time-resolved coherent electron dynamics and photoelectron diffraction can also be obtained by a right-handed circularly polarized pump pulse. A resonant excitation between the ground A′ and E− electronic states is triggered, thus leading to a superposition state ψco(r,t) which reads as
| |  | (22) |
The corresponding electron density distributions and photoelectron momentum distributions evolve with time as well, as predicted in
eqn (37) and (40). Comparing to the previous left handed case in
Fig. 4 and 7, a phase difference of ±π occurs in right-handed cases, due to the photoelectron mirror images of the degenerate
E+ and
E− electronic states in
Fig. 2 and
eqn (14) and (15).
Of note is that in the present work, we only consider a single electron molecular model. It has also been shown that in the diatomic H2 at large internuclear distances where entanglement of atomic configurations, corresponding to the Heitler–London wave functions, photoelectron diffraction patterns can also be influenced due to the effect of the electron–electron correlation, as reported previously.84 The photoelectron angular distributions exhibit signature of electron correlation. Therefore, for multiple electron molecular systems, electron entanglement via exchange due to spin strongly may influence photoionization emission in circular polarization. Moreover, to clearly observe photoelectron diffraction patterns in triatomic molecular systems, perfect alignments are required. As derived analytically in Appendixes, photoelectron angular distributions are functions of the molecular internuclear distance and the angle between the molecular axis and the photoelectron momentum direction. Current laser technology allows for orienting such molecules using coherently prepared rotational wave packets.85
4 Conclusions
In the present work, we study molecular photoelectron diffraction by circularly polarized X-ray laser pulses. Simulations are performed on the oriented molecular ion H32+ by numerically solving TDSEs. We first present the photoionization by a circular X-ray pulse for stationary electronic states. Photoelectron distributions exhibit diffraction patterns with multiple angular nodes, which are determined by the initial electronic state symmetry. We also present the photoionization in a charge migration process. The molecule is excited by a UV pulse, creating a coherent superposition of the ground and degenerate excited electronic states of different helicities, E+ or E−. Subsequently, a time-delayed circularly polarized soft X-ray attosecond probe pulse is used to ionize the excited molecule. X-ray photoelectron diffraction distributions display asymmetric structure, which is shown to be sensitive to the time delay between the pump and probe pulses.
We present ultrafast multiple center and multiple electronic state molecular photoionization models to describe the photoelectron diffraction patterns. Theoretical analysis confirms these numerical simulations from TDSEs. Molecular orbital and coherent state symmetries determine the diffraction fringes in photoelectron distributions. In a coherent excitation process, the time-resolved asymmetric photoelectron diffraction patterns result from the evolution of the coherent electronic wave packets in the molecule. The time-dependent probing photoelectron diffraction illustrates the electron coherence, thus allowing to explore time-dependent charge migration in molecular reaction processes. Relating to new experiments in attosecond photoionization of molecules,86 our results pave a way to image molecular orbital and monitor intramolecular coherent electron dynamics by photoelectron diffraction which can be extended to more complex systems and laser control of chemical reactions.87–90
Conflicts of interest
There are no conflicts to declare.
Appendix
A Circularly polarized δ-function field pulses
The Dirac δ-function is expressed as| |  | (23) |
For a circularly polarized laser field with its polarization vector in the (x,y) plane, the form can be defined as E(t) = E[![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) ± ŷ
cos(ωt) ± ŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt)], where the sign ± presents left/right handed helicity. From eqn (23), one obtains the following relations by integrating over all ω,
sin(ωt)], where the sign ± presents left/right handed helicity. From eqn (23), one obtains the following relations by integrating over all ω,| |  | (24) |
and| |  | (25) |
Consequently, the δ-function circularly polarized laser pulse is| | E(t) = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) Eδ(t)/2π, Eδ(t)/2π, | (26) |
for both left and right handed helicities, similar to a linear process.
B Ultrafast photoelectron diffraction models of triatomic molecular systems
For an impulsive field model, the wavefunction in momentum space right after the pulse E(t) = Eδ(t = 0) is given by91where ψ0(p) is the wavefunction of the initial electronic state in momentum p space. Transforming the wavefunction ψ(p,0+) to coordinate space, we then obtain| | | ψ(r,0+) = exp(−iE·r)ψ0(r). | (28) |
The transition amplitude to the continuum then can be obtained by a Fourier transform of the function ψ(r,0+),| |  | (29) |
For the ground A′ electronic state of H32+ at internuclear distance R, the corresponding wavefunction is
| |  | (30) |
In
eqn (30) the electron wavefunction
ψA′(
r) is a linear combinations of hydrogenic 1s orbital located at positions
Ri,
i = 1, 2, 3. Setting the molecular orbital
ψ0(
r) =
ψA′(
r), one then obtains the transition amplitude
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif)
(
p),
i.e., the momentum distribution of photoelectron in
eqn (29) which can be written as
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′)(p) = [cos2(P·R12/2) + cos2(P·R23/2) + cos2(P·R13/2)]ψs2(P), (A′)(p) = [cos2(P·R12/2) + cos2(P·R23/2) + cos2(P·R13/2)]ψs2(P), | (31) |
where the vector
P =
p +
E and
Rij =
Rj −
Ri,
i,
j = 1, 2, 3 and
Ri,j =
R, the molecular internuclear distance, as illustrated in
Fig. 1(a). The wavefunctions of the two degenerate excited states are given by
| |  | (32) |
for the
E+ electronic state, and
| |  | (33) |
for the
E− electronic state. Of note is that
ψE+(
r) =
ψE−*(
r). Then the corresponding photoelectron distributions in
eqn (29) are given by
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+)(p) = [cos2(P·R12/2 + π/3) + cos2(P·R23/2 + 2π/3) + cos2(P·R13/2 + π/3)]ψs2(P), (E+)(p) = [cos2(P·R12/2 + π/3) + cos2(P·R23/2 + 2π/3) + cos2(P·R13/2 + π/3)]ψs2(P), | (34) |
and
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E−)(p) = [cos2(P·R12/2 − π/3) + cos2(P·R23/2 − 2π/3) + cos2(P·R13/2 − π/3)]ψs2(P), (E−)(p) = [cos2(P·R12/2 − π/3) + cos2(P·R23/2 − 2π/3) + cos2(P·R13/2 − π/3)]ψs2(P), | (35) |
From
eqn (31)–(35) one sees that, in the ultrafast photoionization model, the effect of the delta-function pulse is to shift the total photoelectron distributions by the amount of the field vector
E. The phase of
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+)
(E+)(
p) =
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E−)
(E−)(−
p),
i.e., opposite helicity. This corresponds to opposite current helicity since the current is
j(
r,
t) =
ψ(
r,
t)∇
ψ*(
r,
t) −
ψ*(
r,
t)∇
ψ(
r,
t) = −[
ψ*(
r,
t)∇
ψ(
r,
t) −
ψ(
r,
t)∇
ψ*(
r,
t)] with
ψE+(
r) =
ψE−*(
r).
C Time-resolved photoelectron diffraction patterns
We next consider the case for a photoionization process from a time-dependent coherent superposition state ψ0 = ψco of the three electronic states. A resonant excitation between the A′ and E+ (or E−) can be obtained by a circularly polarized pump pulse. The corresponding electronic wavefunction reads as| |  | (36) |
where cie(t), ie = A′, E+ or E−, is the occupation coefficients of the ie electronic state, and Eie is the eigenenergy of the ie electronic state. Then the corresponding time-dependent coherent electron density distributions are described by| | 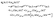 | (37) |
with ℜ being the real part. ΔE = EE+ − EA′ = EE− − EA′ is the energy difference between the excited E+/E− state and the ground A′ electronic states. From eqn (37) one sees that the total coherent electron dynamics are composed of three components, two electronic state densities, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) A′(r,t) and
A′(r,t) and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (E+/E−)(r,t), and their interfering superposition terms
(E+/E−)(r,t), and their interfering superposition terms ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (A′,E+/E−)(r,t). In general, the population probabilities |cie(t)|2 are constant after pump pulses. Therefore, the state densities
(A′,E+/E−)(r,t). In general, the population probabilities |cie(t)|2 are constant after pump pulses. Therefore, the state densities ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (A′)(r,t) and
(A′)(r,t) and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (E+/E−)(r,t) do not depend on the time. The interference term between electronic states,
(E+/E−)(r,t) do not depend on the time. The interference term between electronic states, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (A′,E+/E−)(r,t) is shown to be dependent on the time t with oscillation period τ(0) = 2π/ΔE. The evolution of the superposition terms describes the attosecond electron coherence.
(A′,E+/E−)(r,t) is shown to be dependent on the time t with oscillation period τ(0) = 2π/ΔE. The evolution of the superposition terms describes the attosecond electron coherence.
According to the ultrafast photoionization model, the instantaneous transition amplitude in eqn (29) can be written as
| | ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) co(p,t) = |cA′(t)|2 co(p,t) = |cA′(t)|2![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′)(p) + |cE+/E−(t)|2 (A′)(p) + |cE+/E−(t)|2![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+/E−)(p) + |cA′(t)cE+/E−(t)| (E+/E−)(p) + |cA′(t)cE+/E−(t)|![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′,E+/E−)(p,t) (A′,E+/E−)(p,t) | (38) |
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (ie)
(ie)(
p) is the distribution for the
ie single electronic state, in
eqn (31), (34), and (35). Their interference terms are given by
| | 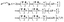 | (39) |
between the
A′ and
E+ states, and
| | 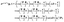 | (40) |
between the
A′ and
E− states. It is also found that the interference terms
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′,E+)
(A′,E+)(
p,t) and
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′,E−)
(A′,E−)(
p,t) are also time dependent with an oscillation period
τ(0) = 2π/Δ
Eij, the same as in
eqn (37). The time-dependent photoelectron distribution
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) co
co(
p,
t) in
eqn (38) describe the coherent excitation between the electronic states.
Acknowledgements
This work is in part supported by the National Natural Science Foundation of China (Grants No. 11974007) and the Natural Sciences and Engineering Research Council of Canada (NSERC), Fonds de Recherche du Québec-Nature et Technologies (FRQNT). The authors also thank Compute Canada for access to massively parallel computer clusters.
Notes and references
- A. H. Zewail, J. Phys. Chem. A, 2000, 104, 5660–5694 CrossRef CAS
 .
.
- W. Becker, X. Liu, P. J. Ho and J. H. Eberly, Rev. Mod. Phys., 2012, 84, 1011–1043 CrossRef CAS
 .
.
- T. Bredtmann, D. J. Diestler, S. D. Li, J. Manz, J. F. Pérez-Torres, W. J. Tian, Y. B. Wu, Y. Yang and H. J. Zhai, Phys. Chem. Chem. Phys., 2015, 17, 29421–29464 RSC
 .
.
- P. Baum and F. Krausz, Chem. Phys. Lett., 2017, 683, 57–61 CrossRef CAS
 .
.
- S. Beaulieu, A. Comby, D. Descamps, B. Fabre, G. A. Garcia, R. Géneaux, A. G. Harvey, F. Légaré, Z. Masin, L. Nahon, A. F. Ordonez, S. Petit, B. Pons, Y. Mairesse, O. Smirnova and V. Blanchet, Nat. Phys., 2018, 14, 484 Search PubMed
 .
.
- C. C. Shu, K. J. Yuan, D. Dong, I. Petersen and A. D. Bandrauk, J. Phys. Chem. Lett., 2017, 8, 1 Search PubMed
 .
.
- F. Krausz and M. Ivanov, Rev. Mod. Phys., 2009, 81, 163 CrossRef
 .
.
- Z. Chang, P. B. Corkum and S. R. Leone, J. Opt. Soc. Am. B, 2016, 33, 1081–1097 CrossRef CAS
 .
.
- S. Chelkowski, P. B. Corkum and A. D. Bandrauk, Phys. Rev. Lett., 1999, 82, 3416–3419 CrossRef CAS
 .
.
- C. Beylerian and C. Cornaggia, J. Phys. B: At., Mol. Opt. Phys., 2004, 37, L259–L265 CrossRef CAS
 .
.
- T. Zuo, A. D. Bandrauk and P. B. Corkum, Chem. Phys. Lett., 1996, 259, 313–320 CrossRef CAS
 .
.
- M. Meckel, D. Comtois, D. Zeidler, A. Staudte, D. Pavičić, H. C. Bandulet, H. Pépin, J. C. Kieffer, R. Dörner, D. M. Villeneuve and P. B. Corkum, Science, 2008, 320, 1478–1482 CrossRef CAS PubMed
 .
.
- C. I. Blaga, J. Xu, A. D. DiChiara, E. Sistrunk, K. Zhang, P. Agostini, T. A. Miller, L. F. DiMauro and C. D. Lin, Nature, 2012, 483, 194–197 CrossRef CAS PubMed
 .
.
- K. Amini, M. Sclafani, T. Steinle, A.-T. Le, A. Sanchez, C. Müller, J. Steinmetzer, L. Yue, J. R. Martnez Saavedra, M. Hemmer, M. Lewenstein, R. Moshammer, T. Pfeifer, M. G. Pullen, J. Ullrich, B. Wolter, R. Moszynski, F. J. Garca de Abajo, C. D. Lin, S. Gräfe and J. Biegert, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8173–8177 CrossRef CAS PubMed
 .
.
- T. Gaumnitz, A. Jain, Y. Pertot, M. Huppert, I. Jordan, F. Ardana-Lamas and H. J. Wörner, Opt. Express, 2017, 25, 27506–27518 CrossRef CAS PubMed
 .
.
- M. J. J. Vrakking, Phys. Chem. Chem. Phys., 2014, 16, 2775–2789 RSC
 .
.
- M. G. Pullen, B. Wolter, A.-T. Le, M. Baudisch, M. Hemmer, A. Senftleben, C. D. Schröter, J. Ullrich, R. Moshammer, C. D. Lin and J. Biegert, Nat. Commun., 2015, 6, 7262 CrossRef CAS PubMed
 .
.
- Y. Ito, C. Wang, A. T. Le, M. Okunishi, D. Ding, C. D. Lin and K. Ueda, Struct. Dyn., 2016, 3, 034303 CrossRef PubMed
 .
.
- T. T. Nguyen-Dang, M. Peters, J. Viau-Trudel, E. Couture-Bienvenue, R. Puthumpally-Joseph, E. Charron and O. Atabek, Mol. Phys., 2017, 115, 1934–1943 CrossRef CAS
 .
.
- M. Peters, T. T. Nguyen-Dang, C. Cornaggia, S. Saugout, E. Charron, A. Keller and O. Atabek, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 051403(R) CrossRef
 .
.
- M. Kazama, T. Fujikawa, N. Kishimoto, T. Mizuno, J. Adachi and A. Yagishita, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 87, 063417 CrossRef
 .
.
- H. C. Shao and A. F. Starace, Phys. Rev. A: At., Mol., Opt. Phys., 2016, 94, 030702 CrossRef
 .
.
- D.-D. T. Vu, N.-L. T. Phan, V.-H. Hoang and V.-H. Le, J. Phys. B: At., Mol. Opt. Phys., 2017, 50, 245101 CrossRef
 .
.
- H. D. Cohen and U. Fano, Phys. Rev., 1966, 150, 30–33 CrossRef CAS
 .
.
- A. Palacios, A. González-Castrillo and F. Martín, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3973–3978 CrossRef CAS PubMed
 .
.
- S. Tsuru, T. Fujikawa, M. Stener, P. Decleva and A. Yagishita, J. Chem. Phys., 2018, 148, 124101 CrossRef PubMed
 .
.
- M. Peters, T. T. Nguyen-Dang, E. Charron, A. Keller and O. Atabek, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 053417 CrossRef
 .
.
- R. Puthumpally-Joseph, J. Viau-Trudel, M. Peters, T. T. Nguyen-Dang, O. Atabek and E. Charron, Mol. Phys., 2017, 115, 1889 CrossRef CAS
 .
.
- R. S. Mulliken, Phys. Rev., 1937, 51, 310–332 CrossRef CAS
 .
.
- R. Weinkauf, P. Schanen, S. Yang, D. Soukara and E. W. Schlag, J. Chem. Phys., 1995, 99, 11255–11265 CrossRef CAS
 .
.
- L. S. Cederbaum and J. Zobeley, Chem. Phys. Lett., 1999, 307, 205–210 CrossRef CAS
 .
.
- I. Barth and J. Manz, Angew. Chem., Int. Ed., 2006, 45, 2962–2965 CrossRef CAS PubMed
 .
.
- F. Remacle and R. D. Levine, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 6793–6798 CrossRef CAS PubMed
 .
.
- W. Li, A. A. Jaron-Becker, C. W. Hogle, V. Sharma, X. Zhou, A. Becker, H. C. Kapteyn and M. M. Murnane, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20219–20222 CrossRef CAS PubMed
 .
.
- H. Mineo, M. Yamaki, Y. Teranishi, M. Hayashi, S. H. Lin and Y. Fujimura, J. Am. Chem. Soc., 2012, 134, 14279–14282 CrossRef CAS PubMed
 .
.
- B. Mignolet, R. D. Levine and F. Remacle, J. Phys. B: At., Mol. Opt. Phys., 2014, 47, 124011 CrossRef
 .
.
- V. Despré, A. Marciniak, V. Loriot, M. C. E. Galbraith, A. Rouzée, M. J. J. Vrakking, F. Lépine and A. I. Kuleff, J. Phys. Chem. Lett., 2015, 6, 426–431 CrossRef
 .
.
- G. Hermann, C. Liu, J. Manz, B. Paulus, J. F. Pérez-Torres, V. Pohl and J. C. Tremblay, J. Phys. Chem. A, 2016, 120, 5360–5369 CrossRef CAS
 .
.
- K.-J. Yuan and A. D. Bandrauk, J. Chem. Phys., 2016, 145, 194304 CrossRef
 .
.
- H. C. Shao and A. F. Starace, Phys. Rev. Lett., 2010, 105, 263201 CrossRef PubMed
 .
.
- H. C. Shao and A. F. Starace, Phys. Rev. A, 2018, 97, 022702 CrossRef CAS
 .
.
- D. Jia, J. Manz, B. Paulus, V. Pohl, J. C. Tremblay and Y. Yang, Chem. Phys., 2017, 482, 146–159 CrossRef CAS
 .
.
- G. Hermann, C. Liu, J. Manz, B. Paulus, V. Pohl and J. C. Tremblay, Chem. Phys. Lett., 2017, 683, 553–558 CrossRef CAS
 .
.
- D. J. Diestler, G. Hermann and J. Manz, J. Phys. Chem. A, 2017, 121, 5332–5340 CrossRef CAS
 .
.
- R. Weinkauf, P. Schanen, A. Metsala, E. Schlag, M. Bürgle and H. Kessler, J. Phys. Chem. A, 1996, 100, 18567–18585 CrossRef CAS
 .
.
- R. Weinkauf, E. W. Schlag, T. J. Martinez and R. D. Levine, J. Phys. Chem. A, 1997, 101, 7702–7710 CrossRef CAS
 .
.
- M. R. Miller, Y. Xia, A. Becker and A. Jaron-Becker, Optica, 2016, 3, 259–269 CrossRef CAS
 .
.
- B. Mignolet, R. D. Levine and F. Remacle, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 021403 CrossRef
 .
.
- B. Mignolet, R. D. Levine and F. Remacle, J. Phys. Chem. A, 2014, 118, 6721–6729 CrossRef CAS PubMed
 .
.
- A. D. Bandrauk, S. Chelkowski, P. B. Corkum, J. Manz and G. L. Yudin, J. Phys. B: At., Mol. Opt. Phys., 2009, 42, 134001 CrossRef
 .
.
- T. Bredtmann, S. Chelkowski and A. D. Bandrauk, J. Phys. Chem. A, 2012, 116, 11398–11405 CrossRef CAS PubMed
 .
.
- H. Mineo, S. H. Lin and Y. Fujimura, J. Chem. Phys., 2013, 138, 074304 CrossRef CAS PubMed
 .
.
- I. Barth, J. Manz, Y. Shigeta and K. Yagi, J. Am. Chem. Soc., 2006, 128, 7043–7047 CrossRef CAS PubMed
 .
.
- K. J. Yuan and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2013, 88, 013417 CrossRef
 .
.
- K. J. Yuan, J. Guo and A. D. Bandrauk, Phys. Rev. A, 2018, 98, 043410 CrossRef CAS
 .
.
- E. Räsänen, A. Castro, J. Werrschnik, A. Rubio and E. K. U. Gross, Phys. Rev. Lett., 2007, 98, 157404 CrossRef PubMed
 .
.
- P. M. Kraus, B. Mignolet, D. Baykusheva, A. Rupenyan, L. Horný, E. F. Penka, G. Grassi, O. I. Tolstikhin, J. Schneider, F. Jensen, L. B. Madsen, A. D. Bandrauk, F. Remacle and H. J. Wörner, Science, 2015, 350, 790–795 CrossRef CAS PubMed
 .
.
- P. Hockett, C. Z. Bisgaard, O. J. Clarkin and A. Stolow, Nat. Phys., 2011, 7, 612–615 Search PubMed
 .
.
- T. Okino, Y. Furukawa, Y. Nabekawa, S. Miyabe, A. Amani Eilanlou, E. Takahashi, K. Yamanouchi and K. Midorikawa, Sci. Adv., 2015, 1, e1500356 Search PubMed
 .
.
- F. Lépine, M. Y. Ivanov and M. J. J. Vrakking, Nat. Photonics, 2014, 8, 195–204 CrossRef
 .
.
- K. Ramasesha, S. R. Leone and D. M. Neumark, Annu. Rev. Phys. Chem., 2016, 67, 41–63 CrossRef CAS
 .
.
- K. J. Yuan and A. D. Bandrauk, Phys. Chem. Chem. Phys., 2017, 19, 25846–25852 RSC
 .
.
- K. J. Yuan and A. D. Bandrauk, J. Phys. Chem. A, 2018, 122, 2241–2249 CrossRef CAS PubMed
 .
.
- K. J. Yuan and A. D. Bandrauk, J. Phys. Chem. A, 2019, 123, 1328–1336 CrossRef CAS PubMed
 .
.
- W. Hu, Y. Liu, S. Luo, X. Li, J. Yu, X. Li, Z. Sun, K.-J. Yuan, A. D. Bandrauk and D. Ding, Phys. Rev. A, 2019, 99, 011402 CrossRef CAS
 .
.
- Y. Liu, W. Hu, S. Luo, K.-J. Yuan, Z. Sun, A. D. Bandrauk and D. Ding, Phys. Rev. A, 2019, 100, 023404 CrossRef CAS
 .
.
- J. McKenna, A. M. Sayler, B. Gaire, N. G. Johnson, K. D. Carnes, B. D. Esry and I. Ben-Itzhak, Phys. Rev. Lett., 2009, 103, 103004 CrossRef CAS
 .
.
- B. Mukherjee, D. Mukhopadhyay, S. Adhikari and M. Baer, Mol. Phys., 2018, 116, 2435 CrossRef CAS
 .
.
- S. Ghosh, S. Mukherjee, B. Mukherjee, S. Mandal, R. Sharma, P. Chaudhury and S. Adhikari, J. Chem. Phys., 2017, 147, 074105 CrossRef PubMed
 .
.
- C. Lefebvre, H. Z. Lu, S. Chelkowski and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2014, 89, 023403 CrossRef
 .
.
- K. J. Yuan, H. Lu and A. D. Bandrauk, ChemPhysChem, 2013, 14, 1496–1501 CrossRef CAS
 .
.
- M. Paul, L. Yue and S. Gräfe, Phys. Rev. Lett., 2018, 120, 233202 CrossRef CAS
 .
.
- X. Xie, A. Scrinzi, M. Wickenhauser, A. Baltuška, I. Barth and M. Kitzler, Phys. Rev. Lett., 2008, 101, 033901 CrossRef
 .
.
- K.-J. Yuan and A. D. Bandrauk, Phys. Rev. Lett., 2013, 110, 023003 CrossRef
 .
.
- P.-C. Huang, C. Hernandez-Garcia, J.-T. Huang, P.-Y. Huang, C.-H. Lu, L. Rego, D. D. Hickstein, J. L. Ellis, A. Jaron-Becker, A. Becker, S.-D. Yang, C. G. Durfee, L. Plaja, H. C. Kapteyn, M. M. Murnane, A. H. Kung and M.-C. Chen, Nat. Photonics, 2018, 12, 349–354 CrossRef CAS
 .
.
- K. J. Yuan, H. Lu and A. D. Bandrauk, Struct. Chem., 2017, 28, 1297–1309 CrossRef CAS
 .
.
- D. S. Tchitchekova, H. Lu, S. Chelkowski and A. D. Bandrauk, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 065601 CrossRef
 .
.
- A. D. Bandrauk, F. Fillion-Gourdeau and E. Lorin, J. Phys. B: At., Mol. Opt. Phys., 2013, 46, 153001 CrossRef
 .
.
- A. D. Bandrauk and H. Shen, J. Chem. Phys., 1993, 99, 1185–1193 CrossRef CAS
 .
.
- A. D. Bandrauk and H. Lu, J. Theor. Comput. Chem., 2013, 12, 1340001 CrossRef
 .
.
- K. J. Yuan, H. Z. Lu and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2011, 83, 043418 CrossRef
 .
.
-
G. C. Schatz and M. A. Ratner, Quantum Mechanics in Chemistry, Dover Publications Inc., New York, 2002 Search PubMed
 .
.
- K. J. Yuan and A. D. Bandrauk, Struct. Dyn., 2015, 2, 014101 CrossRef PubMed
 .
.
- K.-J. Yuan, H. Lu and A. D. Bandrauk, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 061403 CrossRef
 .
.
- K. F. Lee, D. M. Villeneuve, P. B. Corkum, A. Stolow and J. G. Underwood, Phys. Rev. Lett., 2006, 97, 173001 CrossRef PubMed
 .
.
- M. Huppert, I. Jordan, D. Baykusheva, A. von Conta and H. J. Wörner, Phys. Rev. Lett., 2016, 117, 093001 CrossRef PubMed
 .
.
- M. F. Kling and M. J. Vrakking, Annu. Rev. Phys. Chem., 2008, 59, 463–492 CrossRef CAS PubMed
 .
.
- S. Beaulieu, A. Comby, A. Clergerie, J. Caillat, D. Descamps, N. Dudovich, B. Fabre, R. Géneaux, F. Légaré, S. Petit, B. Pons, G. Porat, T. Ruchon, R. Taeb, V. Blanchet and Y. Mairesse, Science, 2017, 358, 1288–1294 CrossRef CAS PubMed
 .
.
- K. Wilma, C.-C. Shu, U. Scherf and R. Hildner, New J. Phys., 2019, 21, 045001 CrossRef
 .
.
- L. Gallmann, I. Jordan, H. J. Wörner, L. Castiglioni, M. Hengsberger, J. Osterwalder, C. A. Arrell, M. Chergui, E. Liberatore, U. Rothlisberger and U. Keller, Struct. Dyn., 2017, 4, 061502 CrossRef CAS PubMed
 .
.
- M. D. Girardeau, K. G. Kim and C. C. Widmayer, Phys. Rev. A: At., Mol., Opt. Phys., 1992, 46, 5932–5937 CrossRef CAS PubMed
 .
.
|
| This journal is © the Owner Societies 2020 |
Click here to see how this site uses Cookies. View our privacy policy here.  *ab and
André D.
Bandrauk
*b
*ab and
André D.
Bandrauk
*b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, y = ρ
θ, y = ρ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) as the molecular plane is written as,
θ) as the molecular plane is written as,


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Θ/2), N3x = +R
sin(Θ/2), N3x = +R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(Θ/2), N1y = (2/3)R
sin(Θ/2), N1y = (2/3)R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Θ/2), N2y = −(1/3)R
cos(Θ/2), N2y = −(1/3)R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Θ/2), N3y = −(1/3)R
cos(Θ/2), N3y = −(1/3)R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(Θ/2), R being the distance between two protons and the bond angle Θ = 60°, see Fig. 1(a). A soft parameter β = 0.35 is used to remove the Coulomb singularity and produce accurately the electronic state potential energies of H32+.77 The field-molecule interaction VL(r,t) = r·E(t) is treated in the length gauge and dipole approximation, since by exact solutions of the TDSE, numerical results are gauge invariant.78 The laser fields E(t) = Epu(t) + Epr(t) always propagate along the z axis, perpendicular to R and the molecular (x,y) plane. The forms, for the circularly polarized pump pulse Epu(t) are defined as
cos(Θ/2), R being the distance between two protons and the bond angle Θ = 60°, see Fig. 1(a). A soft parameter β = 0.35 is used to remove the Coulomb singularity and produce accurately the electronic state potential energies of H32+.77 The field-molecule interaction VL(r,t) = r·E(t) is treated in the length gauge and dipole approximation, since by exact solutions of the TDSE, numerical results are gauge invariant.78 The laser fields E(t) = Epu(t) + Epr(t) always propagate along the z axis, perpendicular to R and the molecular (x,y) plane. The forms, for the circularly polarized pump pulse Epu(t) are defined as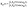

 to eliminate effects of static fields and carrier envelope phases of pulses. The time delay Δτ = tpr0 − tpu0 defines the time interval between the peak times tpu0 and tpr0 of the pump Epu(t) and probe Epr(t) pulses.
to eliminate effects of static fields and carrier envelope phases of pulses. The time delay Δτ = tpr0 − tpu0 defines the time interval between the peak times tpu0 and tpr0 of the pump Epu(t) and probe Epr(t) pulses.

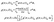
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and py = p
θ and py = p![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, we then obtain the two-dimensional (2D) momentum distributions of photoelectrons from eqn (6). Photoelectron angular distributions at photoelectron kinetic energy Ee are obtained by integrating over the one photon energy, where the spectra width of the probe pulse Δω ≈ ωpr/3,
θ, we then obtain the two-dimensional (2D) momentum distributions of photoelectrons from eqn (6). Photoelectron angular distributions at photoelectron kinetic energy Ee are obtained by integrating over the one photon energy, where the spectra width of the probe pulse Δω ≈ ωpr/3,
 .7 Therefore, the modification of the ionization potential by laser-induced Stark shifts can be ignored. The dipole approximation, in which the spatial dependence and magnetic component of the external field are neglected, remains valid. Moreover, the non-adiabatic coupling effects due to electron-nuclear combined dynamics in triatomic molecules68 are also ignored in the ultrafast photoionization processes.
.7 Therefore, the modification of the ionization potential by laser-induced Stark shifts can be ignored. The dipole approximation, in which the spatial dependence and magnetic component of the external field are neglected, remains valid. Moreover, the non-adiabatic coupling effects due to electron-nuclear combined dynamics in triatomic molecules68 are also ignored in the ultrafast photoionization processes.


 a.u. With such high frequency X-ray pulse, the wavelength of the photoelectron is λe = 2π/p = 1.57 a.u., less than the molecular internuclear distance R. As a result, diffraction of the photoelectron occurs11 where multiple angular nodes are produced in photoelectron distributions. Of note is that the geometries of the photoelectron distributions are different for various electronic states, i.e., the photoelectron diffraction patterns depend on the orbital symmetry of the initial electronic state. One further finds that for the two degenerate excited electronic states, E+, and E−, photoelectron momentum and angular distributions are mirror image with respect to the molecule center, as shown in Fig. 2(b) and (c), since the angular momentum of each is m = +1 and −1, i.e., reflection images of each current.
a.u. With such high frequency X-ray pulse, the wavelength of the photoelectron is λe = 2π/p = 1.57 a.u., less than the molecular internuclear distance R. As a result, diffraction of the photoelectron occurs11 where multiple angular nodes are produced in photoelectron distributions. Of note is that the geometries of the photoelectron distributions are different for various electronic states, i.e., the photoelectron diffraction patterns depend on the orbital symmetry of the initial electronic state. One further finds that for the two degenerate excited electronic states, E+, and E−, photoelectron momentum and angular distributions are mirror image with respect to the molecule center, as shown in Fig. 2(b) and (c), since the angular momentum of each is m = +1 and −1, i.e., reflection images of each current.




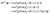
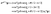
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+)(p,ϑp) =
(E+)(p,ϑp) = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E−)(p,ϑp ± π). Multiple angular nodes with different amplitudes are produced, arising from the multiple center interference of photoelectron. The different diffraction patterns illustrate the various symmetries of the initial electronic state, thus allowing for imaging of molecular orbitals.
(E−)(p,ϑp ± π). Multiple angular nodes with different amplitudes are produced, arising from the multiple center interference of photoelectron. The different diffraction patterns illustrate the various symmetries of the initial electronic state, thus allowing for imaging of molecular orbitals.
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (x,y) of the superposition state created by the λpu = 75 nm (ωpu = 0.608 a.u.) pump pulse in eqn (4) as a function of time t, where
(x,y) of the superposition state created by the λpu = 75 nm (ωpu = 0.608 a.u.) pump pulse in eqn (4) as a function of time t, where  in eqn (1). We use a left handed circularly polarized XUV pulse to excite the molecular ion H32+. The pulse intensity and duration are chosen as I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.), Tpu = 10τpu = 2.48 fs (1.24 fs FWHM). Fig. 5 displays the evolution of the probabilities of the two ground A′ and excited E+ electronic states, |ci(t)|2, where cie(t) = 〈ψie(r)|ψ(r,t)〉 and ie denotes the A′, E+, or E− electronic state, with time t. By this pump pulse, a resonant excitation between the ground A′ and excited E+ states occurs. After the pump pulse t > 10τpu, the occupation coefficients are nearly constant. As displayed in Fig. 5, the occupation in the excited E+ state is |cE+(t)|2 = 0.5. The population remaining in the ground A′ state is |cA′(t)|2 = 0.42. Of note is that during the excitation processes, the molecule is also excited E+ to higher excited state and ionized to the continuum after absorptions of one and two ωpu from the excited state. As a result, the total population in the three electronic state is less than 1, i.e., |cA′(t)|2 + |cE+(t)|2 < 1.
in eqn (1). We use a left handed circularly polarized XUV pulse to excite the molecular ion H32+. The pulse intensity and duration are chosen as I0 = 2.75 × 1013 W cm−2 (E0 = 2.84 × 10−2 a.u.), Tpu = 10τpu = 2.48 fs (1.24 fs FWHM). Fig. 5 displays the evolution of the probabilities of the two ground A′ and excited E+ electronic states, |ci(t)|2, where cie(t) = 〈ψie(r)|ψ(r,t)〉 and ie denotes the A′, E+, or E− electronic state, with time t. By this pump pulse, a resonant excitation between the ground A′ and excited E+ states occurs. After the pump pulse t > 10τpu, the occupation coefficients are nearly constant. As displayed in Fig. 5, the occupation in the excited E+ state is |cE+(t)|2 = 0.5. The population remaining in the ground A′ state is |cA′(t)|2 = 0.42. Of note is that during the excitation processes, the molecule is also excited E+ to higher excited state and ionized to the continuum after absorptions of one and two ωpu from the excited state. As a result, the total population in the three electronic state is less than 1, i.e., |cA′(t)|2 + |cE+(t)|2 < 1.
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (x,y,t) shows an asymmetric structure in molecules which is dependent on the time t. The coherent electron wave packet moves periodically among the three nuclear centers. At time t = 10.2τpu, a strong electron localization is obtained and the coherent electronic wave packet mainly lies on proton 3. Increasing t leads to a variation of the electron distribution. The electron moves to proton 2 through proton 1. At time t = 10.8τpu, the electron is mainly localized on proton 2. As the time t increases further, the electron moves back to proton 1, and then proton 3. The period of the oscillation is approximately τ(0) = τpu = 248 as, one cycle of the circular pump pulse at 75 nm.
(x,y,t) shows an asymmetric structure in molecules which is dependent on the time t. The coherent electron wave packet moves periodically among the three nuclear centers. At time t = 10.2τpu, a strong electron localization is obtained and the coherent electronic wave packet mainly lies on proton 3. Increasing t leads to a variation of the electron distribution. The electron moves to proton 2 through proton 1. At time t = 10.8τpu, the electron is mainly localized on proton 2. As the time t increases further, the electron moves back to proton 1, and then proton 3. The period of the oscillation is approximately τ(0) = τpu = 248 as, one cycle of the circular pump pulse at 75 nm.
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) intco(r,t) ∼ |cA′(t)cE+(t)‖ψA′(r)ψE+(r)|cos(ΔEt),
intco(r,t) ∼ |cA′(t)cE+(t)‖ψA′(r)ψE+(r)|cos(ΔEt),![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (r,t) will evolve among protons 1 ← 2 ← 3, i.e., rotating around the molecular center with an anti-clockwise direction, corresponding to a left handed current, the helicity of the pump pulse. Comparing with Fig. 4 and eqn (17) shows that the numerical simulations are in good agreement with the theoretical predictions. At ΔEt = nπ, where n is an integer, the superposition term cos(ΔEt) = ±1 gives rise the maximum asymmetry of electron density distributions, whereas at ΔEt = (n + 1/2)π, i.e., cos(ΔEt) = 0 and t = (n + 1/2)τpu, symmetric electron distribution are produced, as illustrated in Fig. 4. The evolution of the electron density distribution therefore corresponds to the dependence of the attosecond electron coherence and resulting currents on the time t in charge migration.
(r,t) will evolve among protons 1 ← 2 ← 3, i.e., rotating around the molecular center with an anti-clockwise direction, corresponding to a left handed current, the helicity of the pump pulse. Comparing with Fig. 4 and eqn (17) shows that the numerical simulations are in good agreement with the theoretical predictions. At ΔEt = nπ, where n is an integer, the superposition term cos(ΔEt) = ±1 gives rise the maximum asymmetry of electron density distributions, whereas at ΔEt = (n + 1/2)π, i.e., cos(ΔEt) = 0 and t = (n + 1/2)τpu, symmetric electron distribution are produced, as illustrated in Fig. 4. The evolution of the electron density distribution therefore corresponds to the dependence of the attosecond electron coherence and resulting currents on the time t in charge migration.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) intco(p,t) ∼
intco(p,t) ∼ ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int12 +
int12 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int23 +
int23 + ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int13,
int13,![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int12 = {cos[pR
int12 = {cos[pR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑp − Θ) + π/3] + 1/2} × cos(ΔEt − π/3)ψs2(p),
cos(ϑp − Θ) + π/3] + 1/2} × cos(ΔEt − π/3)ψs2(p),![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int23 = {cos[pR
int23 = {cos[pR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑp) − π/3] + 1/2}cos(ΔEt)ψs2(p),
cos(ϑp) − π/3] + 1/2}cos(ΔEt)ψs2(p),![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) int13 = {cos[pR
int13 = {cos[pR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ϑp + Θ) − π/3] + 1/2} × cos(ΔEt + π/3)ψs2(p),
cos(ϑp + Θ) − π/3] + 1/2} × cos(ΔEt + π/3)ψs2(p),![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) co(p,θ,t) ∼ cos(ΔEt) leads to the evolution of the photoelectron distributions with the time t. The photoelectron distributions encode the information on the time dependent electron motion in molecules, which is much faster than nuclear motion. Fig. 6 illustrates photoelectron angular distributions obtained from the photoionization model, theoretically predicted in eqn (18), at two different moments (a) t = 0 and (b) π/ΔE, i.e., ΔEt = 0 and π. The proton internuclear distance is R = 2 a.u. and the photoelectron momentum p = 4.0 a.u., corresponding to a 5 nm photon soft X-ray photon absorption. The time resolved photoelectron angular distributions show asymmetric structure and mirror image, indicating the coherent coupling between the ground A′ and the excited E+ electronic states.
co(p,θ,t) ∼ cos(ΔEt) leads to the evolution of the photoelectron distributions with the time t. The photoelectron distributions encode the information on the time dependent electron motion in molecules, which is much faster than nuclear motion. Fig. 6 illustrates photoelectron angular distributions obtained from the photoionization model, theoretically predicted in eqn (18), at two different moments (a) t = 0 and (b) π/ΔE, i.e., ΔEt = 0 and π. The proton internuclear distance is R = 2 a.u. and the photoelectron momentum p = 4.0 a.u., corresponding to a 5 nm photon soft X-ray photon absorption. The time resolved photoelectron angular distributions show asymmetric structure and mirror image, indicating the coherent coupling between the ground A′ and the excited E+ electronic states.

 corresponding to one ωpr photon absorption to the continuum.
corresponding to one ωpr photon absorption to the continuum.

![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif)
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ωt) ± ŷ
cos(ωt) ± ŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ωt)], where the sign ± presents left/right handed helicity. From eqn (23), one obtains the following relations by integrating over all ω,
sin(ωt)], where the sign ± presents left/right handed helicity. From eqn (23), one obtains the following relations by integrating over all ω,

![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) Eδ(t)/2π,
Eδ(t)/2π,

![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (p), i.e., the momentum distribution of photoelectron in eqn (29) which can be written as
(p), i.e., the momentum distribution of photoelectron in eqn (29) which can be written as![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′)(p) = [cos2(P·R12/2) + cos2(P·R23/2) + cos2(P·R13/2)]ψs2(P),
(A′)(p) = [cos2(P·R12/2) + cos2(P·R23/2) + cos2(P·R13/2)]ψs2(P),

![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+)(p) = [cos2(P·R12/2 + π/3) + cos2(P·R23/2 + 2π/3) + cos2(P·R13/2 + π/3)]ψs2(P),
(E+)(p) = [cos2(P·R12/2 + π/3) + cos2(P·R23/2 + 2π/3) + cos2(P·R13/2 + π/3)]ψs2(P),![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E−)(p) = [cos2(P·R12/2 − π/3) + cos2(P·R23/2 − 2π/3) + cos2(P·R13/2 − π/3)]ψs2(P),
(E−)(p) = [cos2(P·R12/2 − π/3) + cos2(P·R23/2 − 2π/3) + cos2(P·R13/2 − π/3)]ψs2(P),![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+)(p) =
(E+)(p) = ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E−)(−p), i.e., opposite helicity. This corresponds to opposite current helicity since the current is j(r,t) = ψ(r,t)∇ψ*(r,t) − ψ*(r,t)∇ψ(r,t) = −[ψ*(r,t)∇ψ(r,t) − ψ(r,t)∇ψ*(r,t)] with ψE+(r) = ψE−*(r).
(E−)(−p), i.e., opposite helicity. This corresponds to opposite current helicity since the current is j(r,t) = ψ(r,t)∇ψ*(r,t) − ψ*(r,t)∇ψ(r,t) = −[ψ*(r,t)∇ψ(r,t) − ψ(r,t)∇ψ*(r,t)] with ψE+(r) = ψE−*(r).

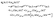
![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) A′(r,t) and
A′(r,t) and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (E+/E−)(r,t), and their interfering superposition terms
(E+/E−)(r,t), and their interfering superposition terms ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (A′,E+/E−)(r,t). In general, the population probabilities |cie(t)|2 are constant after pump pulses. Therefore, the state densities
(A′,E+/E−)(r,t). In general, the population probabilities |cie(t)|2 are constant after pump pulses. Therefore, the state densities ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (A′)(r,t) and
(A′)(r,t) and ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (E+/E−)(r,t) do not depend on the time. The interference term between electronic states,
(E+/E−)(r,t) do not depend on the time. The interference term between electronic states, ![[scr D, script letter D]](https://www.rsc.org/images/entities/char_e523.gif) (A′,E+/E−)(r,t) is shown to be dependent on the time t with oscillation period τ(0) = 2π/ΔE. The evolution of the superposition terms describes the attosecond electron coherence.
(A′,E+/E−)(r,t) is shown to be dependent on the time t with oscillation period τ(0) = 2π/ΔE. The evolution of the superposition terms describes the attosecond electron coherence.
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) co(p,t) = |cA′(t)|2
co(p,t) = |cA′(t)|2![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′)(p) + |cE+/E−(t)|2
(A′)(p) + |cE+/E−(t)|2![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (E+/E−)(p) + |cA′(t)cE+/E−(t)|
(E+/E−)(p) + |cA′(t)cE+/E−(t)|![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′,E+/E−)(p,t)
(A′,E+/E−)(p,t)![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (ie)(p) is the distribution for the ie single electronic state, in eqn (31), (34), and (35). Their interference terms are given by
(ie)(p) is the distribution for the ie single electronic state, in eqn (31), (34), and (35). Their interference terms are given by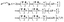
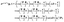
![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′,E+)(p,t) and
(A′,E+)(p,t) and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) (A′,E−)(p,t) are also time dependent with an oscillation period τ(0) = 2π/ΔEij, the same as in eqn (37). The time-dependent photoelectron distribution
(A′,E−)(p,t) are also time dependent with an oscillation period τ(0) = 2π/ΔEij, the same as in eqn (37). The time-dependent photoelectron distribution ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) co(p,t) in eqn (38) describe the coherent excitation between the electronic states.
co(p,t) in eqn (38) describe the coherent excitation between the electronic states.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.


