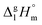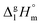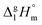Dissecting intermolecular interactions in the condensed phase of ibuprofen and related compounds: the specific role and quantification of hydrogen bonding and dispersion forces†
V. N.
Emel’yanenko
 a,
P.
Stange
a,
P.
Stange
 a,
J.
Feder-Kubis
a,
J.
Feder-Kubis
 b,
S. P.
Verevkin
b,
S. P.
Verevkin
 *ac and
R.
Ludwig
*ac and
R.
Ludwig
 *acd
*acd
aUniversität Rostock, Institut für Chemie, Abteilung für Physikalische Chemie, Dr.-Lorenz-Weg 2, 18059, Rostock, Germany. E-mail: sergey.verevkin@uni-rostock.de; ralf.ludwig@uni-rostock.de
bFaculty of Chemistry, Wroclaw University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland
cDepartment LL&M, University of Rostock, Albert-Einstein-Str. 25, 18059, Rostock, Germany
dLeibniz-Institut für Katalyse an der Universität Rostock e.V., Albert-Einstein-Str. 29a, 18059 Rostock, Germany
First published on 3rd January 2020
Abstract
Ibuprofen is a well-established non-steroidal anti-inflammatory drug, inhibiting the prostaglandin-endoperoxide synthase. One of the key features defining the ibuprofen structure is the doubly intermolecular O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond in cyclic dimers as know from carboxylic acids and confirmed by X-ray analysis. Until now, there was neither information about the vaporization enthalpy of ibuprofen nor about how this thermal property is determined by the subtle balance between different types of intermolecular interaction. In this study we derive the vaporization enthalpy of ibuprofen from thermochemical experiments to be
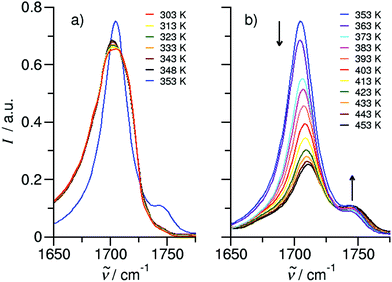
C hydrogen bond in cyclic dimers as know from carboxylic acids and confirmed by X-ray analysis. Until now, there was neither information about the vaporization enthalpy of ibuprofen nor about how this thermal property is determined by the subtle balance between different types of intermolecular interaction. In this study we derive the vaporization enthalpy of ibuprofen from thermochemical experiments to be 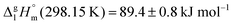 . We dissected the hydrogen bond energy, EHB = 45.0 kJ mol−1, exclusively from measured vaporization enthalpies of related aliphatic carboxylic acids, their homomorph methyl esters and alkyl acetates, respectively. This contribution from hydrogen bonding could be confirmed almost quantitatively from quantum chemical calculations of ibuprofen clusters, which also suggest dispersion interaction of similar order (Edisp = 47 kJ mol−1). Following the full analysis of the gas–vapor transition enthalpy, we studied the changing structural components from the solid to the liquid phase of ibuprofen by means of Attenuated Total Reflection Infrared (ATR-IR) spectroscopy. The cyclic dimers as observed in the X-ray patterns are essentially preserved in the liquid state just above the melting point. However, with increasing temperature the doubly hydrogen-bonded cyclic dimers are replaced by singly hydrogen-bonded linear dimers in the liquid ibuprofen. The transfer enthalpy from the temperature-dependent equilibria of both dimers as obtained from the IR intensity ratios of the vibrational bands quantifies for the first time the energy of the released, single hydrogen bond to be EHB = 21.0 kJ mol−1. Overall, we show that a combination of thermodynamics, infrared spectroscopy and quantum chemistry provides quantification and detailed understanding of structure and molecular interaction in ibuprofen and related compounds.
. We dissected the hydrogen bond energy, EHB = 45.0 kJ mol−1, exclusively from measured vaporization enthalpies of related aliphatic carboxylic acids, their homomorph methyl esters and alkyl acetates, respectively. This contribution from hydrogen bonding could be confirmed almost quantitatively from quantum chemical calculations of ibuprofen clusters, which also suggest dispersion interaction of similar order (Edisp = 47 kJ mol−1). Following the full analysis of the gas–vapor transition enthalpy, we studied the changing structural components from the solid to the liquid phase of ibuprofen by means of Attenuated Total Reflection Infrared (ATR-IR) spectroscopy. The cyclic dimers as observed in the X-ray patterns are essentially preserved in the liquid state just above the melting point. However, with increasing temperature the doubly hydrogen-bonded cyclic dimers are replaced by singly hydrogen-bonded linear dimers in the liquid ibuprofen. The transfer enthalpy from the temperature-dependent equilibria of both dimers as obtained from the IR intensity ratios of the vibrational bands quantifies for the first time the energy of the released, single hydrogen bond to be EHB = 21.0 kJ mol−1. Overall, we show that a combination of thermodynamics, infrared spectroscopy and quantum chemistry provides quantification and detailed understanding of structure and molecular interaction in ibuprofen and related compounds.
1. Introduction
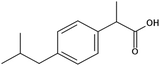
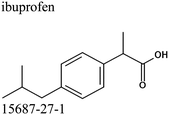
Ibuprofen (IBP), (RS)-2-[4-(2-methylpropyl)phenyl]propanoic acid, is a well-established non-steroidal anti-inflammatory drug (NSAID). Ibuprofen is one of the representatives of profen drugs, among which ketoprofen, flurbiprofen and ibuprofen mainly used to treat pain, fever, and inflammation all over the world.1,2 As previously reported by various scientific groups, the therapeutic effects of profens are nearly entirely attributed to their S-enantiomers.2–4 Nevertheless, those drugs are usually sold as racemic mixtures because the production of a single isomer and enantiomeric purification processes are difficult and rather expensive.1 Therefore, it seems highly justified to study both the intermolecular interactions and physicochemical properties of profens and to conduct detailed studies of their biological activity. Regarding IBP, it is generally recognized that the (+)-IBP enantiomer inhibits prostaglandin synthetase, which is related to IBP's analgesic, antipyretic, and anti-inflammatory activities.1 However, although the (+)-IBP enantiomer is presumed to be the only pharmacologically active molecule, it has been shown that the relative pharmacological potencies of the (+)-IBP and (−)-IBP enantiomers, as well as that of the (±)-IBP are quite similar.1Explicit structures of both (+)-IBP and (±)-IBP crystals are known from diffraction methods such as X-ray5–7 and pulsed neutron diffraction.8–10 The general structure of the racemic ibuprofen is given in Scheme 1. The (+)-IBP enantiomer as well as the (±)-IBP racemate are characterized by the formation of cyclic dimers through hydrogen bonding of their carboxylic groups. This structural motif including two equivalent O–H⋯O hydrogen bonds between each molecule's functional COOH groups is well-known for the gas phase and partially for the crystalline structures of carboxylic acids (see Scheme 2).11–36
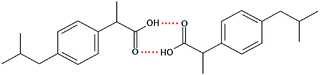 | ||
| Scheme 2 Structure of the cyclic dimer of ibuprofen with two equivalent O–H⋯O hydrogen bonds between each molecule's functional COOH group. | ||
Additionally, experimental thermochemical data on the melting and the sublimation process of the (+)-IBP enantiomer and the (±)-IBP racemate are available.5,37–40 The sublimation enthalpies of (+)-IBP and (±)-IBP were determined to be ΔHsub = 107.4 kJ mol−1 and ΔHsub = 115.8 kJ mol−1, respectively.5 Using different force fields for comparative analysis of the crystal lattice energies resulted in 29.7% and 32.3% hydrogen bonding relative to the overall interaction energies.5 However, the measured data and the analysis of non-covalent forces for ibuprofen were heavily error-prone. Moreover, no detailed interpretation for the structural motifs and the subtle balance of intermolecular forces such as hydrogen bonding and dispersion interaction is given for the condensed phase. So far, no enthalpy of vaporization has been measured which provides important information about the liquid phase of ibuprofen above the relatively low melting point of 349 K for the (±)-IBP racemate.40
It is the purpose of this work to derive the vaporization enthalpy of ibuprofen (here the (±)-IBP racemate) from vapor pressure measurements applying the transpiration method.41–43 The vaporization enthalpies known from the literature of carboxylic acids, their homomorph methyl esters and related alkyl acetates should allow dissecting the hydrogen bonding contributions from the overall interaction energies purely by experimental methods. We support this thermochemical analysis by quantum chemical calculations on molecular clusters. Here, the goal is reproducing the measured vaporization enthalpy and analyzing the overall interaction energies in terms hydrogen bonding and dispersion interaction as both present in ibuprofen. With this approach we address to which extend these two types of non-covalent interactions contribute to the stability and the physical properties of ibuprofen. We also apply Attenuated Total Refection Infrared (ATR-IR) spectroscopy for gaining information about structural changes in ibuprofen upon melting. Moreover, the temperature-dependent infrared spectra of liquid ibuprofen should indicate whether the cyclic dimers of the solid state survive or whether other hydrogen-bonded or non-hydrogen-bonded species replace them. We hope to obtain transition enthalpies between the different species related to the hydrogen bond strength present in ibuprofen. Overall, our combined approach of thermodynamic measurements, quantum chemical calculations and ATR-IR spectroscopy should provide detailed information about structure and interaction in ibuprofen, particularly in its liquid state.
2. Materials and methods
2.1. Materials
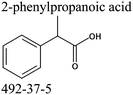
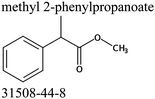
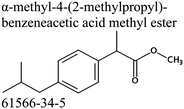
Commercially available samples of the (+)-IBP and the (±)-IBP racemate, α-methyl-4-(2-methylpropyl)-benzeneacetic acid methyl ester, and 2-phenylpropanoic acid with the purity of 0.98–0.99 mass fraction (according to the specification) were used for the vapor pressure measurements. Samples were additionally purified by the fractional sublimation in a vacuum. No impurities (greater than 0.0002 mass fraction) could be detected in samples used for the thermochemical measurements. The degree of purity was determined using a GC equipped with a FID. A capillary column HP-5 was used with a column length of 30 m, an inside diameter of 0.32 mm, and a film thickness of 0.25 μm. For the infrared spectroscopy, the sample (RS)-2-[4-(2-methylpropyl)phenyl]propanoic acid (Ibuprofen, 99%) was purchased from Alfa Aesar and used without further purification. Provenance, purity, methods of purification and analysis of chemicals used in this work are given in Table S1 (ESI†).2.2. Transpiration method: vapor pressure measurements
Vapor pressures of the (+)-IBP enantiomer and the (±)-IBP racemate were measured using the transpiration method.41–43 Surface of the small glass beads was covered with the sufficient amount of the sample by evaporation of solvent from the saturated solution. About 30 g of beads were placed in the saturator. A well-defined nitrogen stream was passed through the saturator at a constant temperature (±0.1 K). The range of flow-rates was localized in preliminary experiments in order to achieve saturation of the gas stream. The transported material was collected in a cold trap for a certain time. The amount of condensed sample was determined by GC analysis using the n-alkanes as an external standard. The absolute vapor pressure psat at each temperature of experiment Ti was calculated from the amount of the product, collected within a definite period. Assuming validity of Dalton's law, applied to the nitrogen stream saturated with the substance, values of psat were calculated with eqn (1):| psat = mi·R·Ta/V·Mi; V = VN2 + Vi; (VN2 ≫ Vi) | (1) |
The temperature dependence of vapor pressure psat measured in this work by transpiration was approximated with the following equation:1
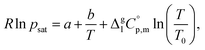 | (2) |
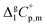 is the difference of the molar heat capacities of the gas and the liquid phases respectively, a and b are adjustable parameters and T0 appearing in eqn (2) is an arbitrarily chosen reference temperature (which has been chosen to be T0 = 298.15 K) and R is the molar gas constant.
is the difference of the molar heat capacities of the gas and the liquid phases respectively, a and b are adjustable parameters and T0 appearing in eqn (2) is an arbitrarily chosen reference temperature (which has been chosen to be T0 = 298.15 K) and R is the molar gas constant.
The standard molar enthalpies of vaporization 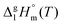 at different temperatures, T, were derived from the vapor temperature dependences using the following equation:
at different temperatures, T, were derived from the vapor temperature dependences using the following equation:
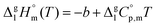 | (4) |
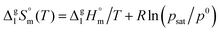 | (5) |
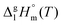 and
and 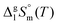 are collected in Table S2 (ESI†). Procedure for calculation of the combined uncertainties of the vaporization enthalpies includes uncertainties in vapor pressure, uncertainties from the transpiration experimental conditions, and uncertainties in the temperature adjustment to T = 298.15 K as described elsewhere.41–43 The values of
are collected in Table S2 (ESI†). Procedure for calculation of the combined uncertainties of the vaporization enthalpies includes uncertainties in vapor pressure, uncertainties from the transpiration experimental conditions, and uncertainties in the temperature adjustment to T = 298.15 K as described elsewhere.41–43 The values of 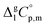 used for the data treatment of vapor pressures in eqn (2) were derived according to procedure developed by Chickos and Acree46,47 and they are given in Table S3 (ESI†).
used for the data treatment of vapor pressures in eqn (2) were derived according to procedure developed by Chickos and Acree46,47 and they are given in Table S3 (ESI†).
2.3. Attenuated total reflection infrared (ATR-IR) spectroscopy
Infrared spectra of Ibuprofen were recorded from 20 to 180 °C in steps of 10 °C on a BRUKER VECTOR 22 FT-IR spectrometer with a Globar® IR source, KBr beamsplitter and a DTGS detector. The FT-IR spectrometer was equipped with a MKII Golden Gate™ single reflection ATR system and a Golden Gate™ heated diamond crystal 45° ATR top plate with a 3000 Series™ High Stability Temperate Controller and a Golden Gate™ Reactive Sample Anvil from SPECAC.The spectra were recorded with the OPUS 6.5 spectroscopy software from BRUKER in the spectral range between 5000 to 500 cm−1 with a resolution of 2 cm−1 and 128 scans. The aperture setting was 3 mm and the scanner velocity was 10 kHz. The Mertz phase correction and Blackman–Harris (3-Term) apodisation function were employed. Atmospheric compensation and baseline correction were performed with the OPUS 6.5 spectroscopy software.
The IR spectra were deconvoluted separately into a number of Voigt-profiles (convolution of Lorentzian and Gaussian functions) following the Levenberg–Marquardt procedure. The Voigt profiles have four parameters: maximum intensity, frequency, half-width of the Lorentzian, and half-width of the Gaussian. The software used for spectral deconvolution was developed by Dr Henning Schröder from the Institute of Mathematics at the University of Rostock and is intended for the use with the MATLAB® software package by MathWorks®.
2.4. Density functional theory (DFT) calculations including dispersion correction
We calculated ibuprofen clusters including up to twelve molecules (n = 12) at the B3LYP/6-31G* level of theory.48 The widely popular hybrid density functional B3LYP is known to lack a proper description of dispersion.49–55 Thus, we re-optimized all clusters at the B3LYP-D3/6-31G* level of theory considering additional dispersion interaction as provided by Grimme's D3 method.56–58 For calculating all clusters (including frequencies) at the same level of theory, we had to use the small 6-31G* basis set. It includes polarization functions and has been shown to be suitable for calculating hydrogen-bonded clusters.59–63To ensure that the optimized structures correspond to true minima on the potential energy hypersurface, we performed frequency calculations, which yield no imaginary frequencies. The clusters with even numbers of molecules (n = 2, 4, 6, 8, 10, 12) consist exclusively of cyclic dimers showing the typical double hydrogen bonds as well-known in carboxylic acids. The clusters with odd numbers of molecules includes one molecule, which is not involved in such a stable configuration. This is why the binding energies per monomer for clusters n = 3, 5, 7, 9, 11 are slightly lower compared to those for the other clusters. Overall, the clusters were constructed from multiples of cyclic dimers.64–68
3. Results and discussion
a. Vaporization enthalpies of ibuprofen and related compounds
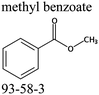
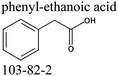
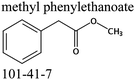
We measured the temperature-dependent vapor pressures of ibuprofen and its homomorph α-methyl-4-(2-methylpropyl)-benzeneacetic acid methyl ester (see Table 1) by using the transpiration method. Additionally, we measured the vapor pressures of 2-phenylpropanoic acid for completing the list of aromatic monocarboxylic acids and their homomorph methyl esters (see ESI†) required for thermochemical analysis. The derived enthalpies of vaporization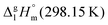 of the aromatic monocarboxylic acids and their homomorph methyl esters at T = 298.15 K (in kJ mol−1) are given in Table 1 along with the literature data for the related acids and esters.69–73 The experimental vaporization enthalpy is 89.4 ± 0.8 kJ mol−1 for ibuprofen and 69.5 ± 0.3 kJ mol−1 for its homomorph α-methyl-4-(2-methylpropyl)benzenacetic acid methyl ester. The difference
of the aromatic monocarboxylic acids and their homomorph methyl esters at T = 298.15 K (in kJ mol−1) are given in Table 1 along with the literature data for the related acids and esters.69–73 The experimental vaporization enthalpy is 89.4 ± 0.8 kJ mol−1 for ibuprofen and 69.5 ± 0.3 kJ mol−1 for its homomorph α-methyl-4-(2-methylpropyl)benzenacetic acid methyl ester. The difference 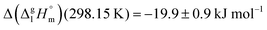 between ibuprofen and homomorph is obviously related to the formation of hydrogen bonding in ibuprofen, which is prevented in the ester by substituting the hydroxy group by a methyl group. This
between ibuprofen and homomorph is obviously related to the formation of hydrogen bonding in ibuprofen, which is prevented in the ester by substituting the hydroxy group by a methyl group. This 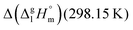 values are similar to those for the three other pairs of acids and esters as given in Table 1. For demonstrating that these differences in enthalpies of vaporization are reasonable, we show the experimental values
values are similar to those for the three other pairs of acids and esters as given in Table 1. For demonstrating that these differences in enthalpies of vaporization are reasonable, we show the experimental values 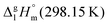 for a large set of aliphatic monocarboxylic acids and their homomorph methyl alkanoates in Table 2. Also here, the
for a large set of aliphatic monocarboxylic acids and their homomorph methyl alkanoates in Table 2. Also here, the 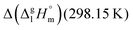 values range between 18 and 23 kJ mol−1, slightly increasing with the growing alkyl chain length. The differences of enthalpies of vaporization for the aliphatic acids (−18.0 ± 0.5 kJ mol−1) and ibuprofene (−20.3 ± 1.5 kJ mol−1) relative to their esters are illustrated in Fig. 1. They will be used for developing the intermolecular HB-strength in aliphatic acids and ibuprofen in terms of the
values range between 18 and 23 kJ mol−1, slightly increasing with the growing alkyl chain length. The differences of enthalpies of vaporization for the aliphatic acids (−18.0 ± 0.5 kJ mol−1) and ibuprofene (−20.3 ± 1.5 kJ mol−1) relative to their esters are illustrated in Fig. 1. They will be used for developing the intermolecular HB-strength in aliphatic acids and ibuprofen in terms of the 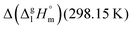 .
.
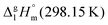 of the aromatic monocarboxylic acids and their homomorph methyl esters at T = 298.15 K (in kJ mol−1)69–73
of the aromatic monocarboxylic acids and their homomorph methyl esters at T = 298.15 K (in kJ mol−1)69–73
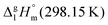 of the aliphatic monocarboxylic acids and their homomo1
of the aliphatic monocarboxylic acids and their homomo1
| Acid | 44 | Ester | 45 | Δ |
|---|---|---|---|---|
| Metanoic acid | 46.3 ± 0.5 | Methyl methanoate | 27.9 ± 0.2 | −18.4 ± 0.5 |
| Ethanoic acid | 50.3 ± 0.5 | Methyl ethanoate | 32.3 ± 0.2 | −18.0 ± 0.5 |
| Propanoic acid | 54.4 ± 0.5 | Methyl propanoate | 35.8 ± 0.3 | −18.6 ± 0.6 |
| Butanoic acid | 58.2 ± 0.3 | Methyl butanoate | 39.3 ± 0.3 | −18.9 ± 0.4 |
| Pentanoic acid | 63.0 ± 0.5 | Methyl pentanoate | 43.1 ± 0.3 | −19.9 ± 0.6 |
| Hexanoic acid | 69.2 ± 0.9 | Methyl hexanoate | 48.0 ± 0.5 | −21.2 ± 1.0 |
| Heptanoic acid | 72.9 ± 0.8 | Methyl heptanoate | 51.6 ± 0.5 | −21.3 ± 0.9 |
| Octanoic acid | 81.0 ± 0.6 | Methyl octanoate | 57.3 ± 0.5 | −23.7 ± 0.8 |
| Nonanoic acid | 82.4 ± 0.4 | Methyl nonanoate | 62.0 ± 0.5 | −20.4 ± 0.6 |
| Decanoic acid | 89.4 ± 2.4 | Methyl decanoate | 66.3 ± 0.5 | −23.1 ± 2.5 |
| Tridecanoic acid | 103.3 ± 2.7 | Methyl tridecanoate | 81.3 ± 0.8 | −22.0 ± 8.8 |
| Pentadecanoic acid | 112.8 ± 4.6 | Methyl pentadecanoate | 91.6 ± 0.9 | −21.2 ± 4.7 |
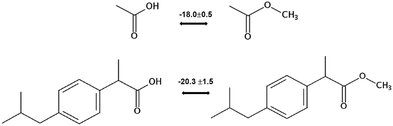 | ||
| Fig. 1 Development of the intermolecular hydrogen bonding energy in aliphatic carboxylic acids and ibuprofen according to the homomorph model. | ||
b. Hydrogen bonding derived from vaporization enthalpies
However, before doing so, we have to correct the HB-strength for the presence of the methyl group in the esters taken for comparison. Indeed, the CH3-group is contributing to the vaporization enthalpy of esters and this contribution should be evaluated and excluded by assessment of the HB-strength. For evaluation of the CH3-group contribution, we plotted experimental enthalpies of vaporization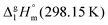 of alkyl acetates versus the number of carbon atoms, NC, present in the sidechains of these compounds. In Fig. 2 we observe a nice slope decreasing about 4.3 kJ mol−1 with each removed methylene group. This behavior is well-known for n-alkanes, n-alcohols or even for ionic liquids with cations bearing alkyl chain groups.69–83 However, the desired value here is given by the intercept. At NC = 0 only the contribution for the CH3 group present in the alkyl acetates remains. This value of about 27 kJ mol−1 can be now used for correcting the intermolecular HB-strength in aliphatic acids due to the redundant methyl contribution. This procedure finally allows us to determine the HB energies present in the aliphatic carboxylic acids and ibuprofen, respectively. The approach to evaluate the CH3-group correction is illustrated in Fig. 3. The total HB energy results from the difference of the enthalpies of vaporization of aliphatic carboxylic acids and their esters (−18 kJ mol−1) corrected for the redundant CH3 contribution (−27 kJ mol−1). The HB energy in the doubly hydrogen-bonded aliphatic carboxylic acids sums up to a total of 45 kJ mol−1, which is twice as high as the HB energies in water and alcohols.59–64
of alkyl acetates versus the number of carbon atoms, NC, present in the sidechains of these compounds. In Fig. 2 we observe a nice slope decreasing about 4.3 kJ mol−1 with each removed methylene group. This behavior is well-known for n-alkanes, n-alcohols or even for ionic liquids with cations bearing alkyl chain groups.69–83 However, the desired value here is given by the intercept. At NC = 0 only the contribution for the CH3 group present in the alkyl acetates remains. This value of about 27 kJ mol−1 can be now used for correcting the intermolecular HB-strength in aliphatic acids due to the redundant methyl contribution. This procedure finally allows us to determine the HB energies present in the aliphatic carboxylic acids and ibuprofen, respectively. The approach to evaluate the CH3-group correction is illustrated in Fig. 3. The total HB energy results from the difference of the enthalpies of vaporization of aliphatic carboxylic acids and their esters (−18 kJ mol−1) corrected for the redundant CH3 contribution (−27 kJ mol−1). The HB energy in the doubly hydrogen-bonded aliphatic carboxylic acids sums up to a total of 45 kJ mol−1, which is twice as high as the HB energies in water and alcohols.59–64
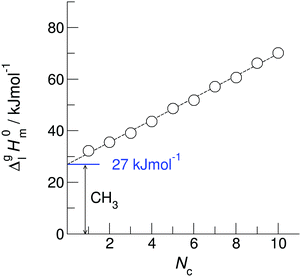 | ||
Fig. 2 Measured vaporization enthalpies, 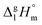 , of alkyl acetates plotted versus the total number of carbon atoms (NC) in the side chains. The intercept of about 27 kJ mol−1 at NC = 0 gives the contribution of the CH3 group and allows the correction of the intermolecular HB energy in aliphatic carboxylic acids. The experimental data are taken from Table 2. , of alkyl acetates plotted versus the total number of carbon atoms (NC) in the side chains. The intercept of about 27 kJ mol−1 at NC = 0 gives the contribution of the CH3 group and allows the correction of the intermolecular HB energy in aliphatic carboxylic acids. The experimental data are taken from Table 2. | ||
c. Dissecting hydrogen bonding and dispersion forces from vaporization enthalpies by means of electronic structure calculations
For dissecting the vaporization enthalpy of ibuprofen into contributions from hydrogen bonding and dispersion interaction, we calculated clusters n including up to twelve molecules (n = 12) at the B3LYP/6-31G* level of theory.48 The clusters with even numbers of molecules consist exclusively of cyclic dimers showing the typical double hydrogen bonds in carboxylic acids. The clusters with odd numbers of molecules include one molecule which is not involved in stable cyclic dimers. Thus the binding energies for n = 3, 5, 7, 9, 11 are slightly lower compared to those for the other clusters comprised of cyclic dimers only. In Fig. 4 we show that with increasing cluster size the binding energies ΔE converge to 45 kJ mol−1. Both values are only half of the experimental vaporization enthalpies of ibuprofen of about 89.4 ± 0.8 kJ mol−1, but almost perfectly agree with the dissected HB energy at the level of 45 kJ mol−1. It seems that the larger clusters describe the amount of hydrogen bonding present in liquid ibuprofen. We could show earlier that such a cluster size is sufficient to mimic liquid phase properties.59–64 The agreement between experimental and calculated HB energies also suggests that liquid ibuprofen mainly consists of cyclic dimers as observed solely in the solid material. It is well-known, that DFT methods fail to describe dispersion interaction properly. Thus, we re-optimized the ibuprofen clusters by using Grimme's D3 dispersion correction.56–58 A comparison of the DFT and DFT-D3 energies provides a lower bound estimate of the stabilization due to dispersion ΔΔEdisp = ΔE(B3LYP-D3) − ΔE(B3LYP). The ΔΔEdisp correction is not exactly equal to the dispersion stabilization as the correction depends on the repulsiveness of the functional employed, but it provides an excellent estimate of the magnitude of this interaction.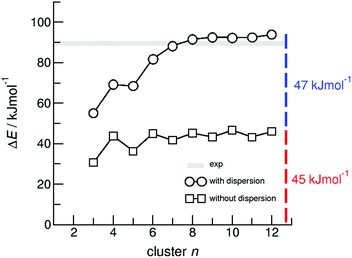 | ||
| Fig. 4 B3LYP/6-31G* (squares) and B3LYP-D3/6-31G* (circles) calculated binding energies ΔE per molecule of ibuprofen clusters n = 3–12. | ||
In Fig. 4 we show that the “odd/even effect” disappears for larger clusters, suggesting that the differences in hydrogen bonding are compensated by taking dispersion interaction into account. However, the main result is that the binding energies for the larger clusters (n > 8) now perfectly describe the experimental enthalpies of vaporization. The calculated ΔE values of about 92 kJ mol−1 lie slightly above the experimental values of 89.4 ± 0.8 kJ mol−1. Obviously, the measured enthalpies of vaporization are reasonably described by the calculated interaction energies present in larger clusters. Moreover, we can dissect the binding energies into hydrogen bonding and dispersion interaction, both being of equal magnitude with 45 kJ mol−1 and 47 kJ mol−1, respectively. In particular, the HB energies are in almost perfect agreement with the experimentally derived value of about 45 kJ mol−1, suggesting that the experimental approach for dissecting the HB energy seems to be appropriate, too. The HB contribution in the order of 50% of the overall interaction energy as calculated here, is substantially higher than the HB contribution calculated for the crystal lattice from force fields estimated to be about 30%.5
It seems to be surprising that for the strongly hydrogen-bonded carboxylic acids (more than twice strong as the HB bonds in water or alcohols due to the cyclic dimers), dispersion interaction plays such an important role and definitely has to be considered for describing thermodynamic properties.
At this point we understand the liquid/gas phase transition for ibuprofen on the basis of hydrogen bonding and dispersion forces. However, we still do not know exactly the cluster distribution in the liquid phase of ibuprofen. Does the liquid ibuprofen solely consist of doubly hydrogen-bonded pairs or does it include also singly hydrogen bonded species particularly at higher temperature towards the boiling point? What about the HB strength of the singly bonded molecules? Is it comparable to those known for molecular liquids, such as water or alcohols? These questions will be properly addressed in the following section by applying Attenuated Total Reflection Infrared spectroscopy (ATR-IR).
d. The liquid structure of ibuprofen by means of infrared (IR) spectroscopy
We measured the ATR-IR spectra of ibuprofen in the temperature range between 303 K and 453 K. Hereby, we mainly focus on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching vibrational bands which are usually observed between 1600 cm−1 and 1800 cm−1. The solid state spectra are shown for temperatures from 303 K to 348 K (Fig. 5a). The X-ray diffraction pattern of solid ibuprofen clearly showed only the existence of cyclic dimers which are characterized by two strong hydrogen bonds that form between the hydroxy H-bond donor position and the carbonyl H-bond acceptor position of the carboxyl functional groups of either molecule.5–7 This binding motif is reflected in the solid state ATR-IR spectra showing symmetric and asymmetric C
O stretching vibrational bands which are usually observed between 1600 cm−1 and 1800 cm−1. The solid state spectra are shown for temperatures from 303 K to 348 K (Fig. 5a). The X-ray diffraction pattern of solid ibuprofen clearly showed only the existence of cyclic dimers which are characterized by two strong hydrogen bonds that form between the hydroxy H-bond donor position and the carbonyl H-bond acceptor position of the carboxyl functional groups of either molecule.5–7 This binding motif is reflected in the solid state ATR-IR spectra showing symmetric and asymmetric C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch vibrational bands separated by about 50 cm−1 in the calculated cyclic dimer. Due to the significantly larger transition dipole moment, most of the intensity is focused in the asymmetric C
O stretch vibrational bands separated by about 50 cm−1 in the calculated cyclic dimer. Due to the significantly larger transition dipole moment, most of the intensity is focused in the asymmetric C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching band. Above the melting point of 349 K, we recorded the IR spectra of the liquid ibuprofen for temperatures between 353 K and 453 K (Fig. 5b). We clearly observe that the most intense band at 1705 cm−1 assigned to the asymmetric stretch of the C
O stretching band. Above the melting point of 349 K, we recorded the IR spectra of the liquid ibuprofen for temperatures between 353 K and 453 K (Fig. 5b). We clearly observe that the most intense band at 1705 cm−1 assigned to the asymmetric stretch of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond within the cyclic dimer (here I4) is decreasing with increasing temperature to the benefit of a new vibrational band occurring at 1746 cm−1. This vibrational frequency is referred to an almost freely vibrating C
O bond within the cyclic dimer (here I4) is decreasing with increasing temperature to the benefit of a new vibrational band occurring at 1746 cm−1. This vibrational frequency is referred to an almost freely vibrating C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Obviously, increasing temperature breaks at least one of the hydrogen bonds of the cyclic dimers. For better understanding of the temperature behavior in the liquid phase, we deconvoluted the IR spectra simultaneously with temperature. We used five vibrational bands for describing the measured spectra for all temperatures. The vibrational bands I1 and I2 with maxima at 1612 cm−1 and 1640 cm−1 were needed for fitting the overall spectra but not further considered here, because they are not directly related to the C
O bond. Obviously, increasing temperature breaks at least one of the hydrogen bonds of the cyclic dimers. For better understanding of the temperature behavior in the liquid phase, we deconvoluted the IR spectra simultaneously with temperature. We used five vibrational bands for describing the measured spectra for all temperatures. The vibrational bands I1 and I2 with maxima at 1612 cm−1 and 1640 cm−1 were needed for fitting the overall spectra but not further considered here, because they are not directly related to the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretches. The deconvoluted spectra in the C
O stretches. The deconvoluted spectra in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region is shown in Fig. 6 for temperatures 363 K, 393 K, 423 K and 453 K, respectively. We observed that the bands I3 and I4 decrease to the benefit of band I5. Thus, the temperature-dependent behavior describes the transition between the doubly H-bonded cyclic dimers and the singly H-bonded linear dimers which exhibits one free C
O stretching region is shown in Fig. 6 for temperatures 363 K, 393 K, 423 K and 453 K, respectively. We observed that the bands I3 and I4 decrease to the benefit of band I5. Thus, the temperature-dependent behavior describes the transition between the doubly H-bonded cyclic dimers and the singly H-bonded linear dimers which exhibits one free C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. We calculated the equilibrium constants K for both species from the ratios of the IR intensities I4 and I5. In Fig. 7a we show the resulting linear plot of ln(K) versus 1000/T indicating van 't Hoff behavior. From the slope we derive the transition enthalpy ΔHtrans = −21.2 kJ mol−1, which is released by breaking one of the hydrogen bonds in the cyclic dimers. This value is thus in the order of a typical H-bond energy. For completeness we also show the temperature behavior of the equilibrium constants K = (I3 + I4)/I5, wherein the vibrational band I3 (also related to the cyclic dimers) with minor intensity is taken into account as well (Fig. 7b). At a first glance it seems to be surprising that the release of one hydrogen bond from the cyclic dimer (ΔE = 21 kJ mol−1) should result in a remaining stronger hydrogen bond of the linear dimer (ΔE = (45 − 21) kJ mol−1 = 24 kJ mol−1). The reason is illustrated by the B3LYP-D3 calculated cyclic and linear dimers shown in Fig. 8. In the cyclic dimer, the two hydrogen bonds
O bond. We calculated the equilibrium constants K for both species from the ratios of the IR intensities I4 and I5. In Fig. 7a we show the resulting linear plot of ln(K) versus 1000/T indicating van 't Hoff behavior. From the slope we derive the transition enthalpy ΔHtrans = −21.2 kJ mol−1, which is released by breaking one of the hydrogen bonds in the cyclic dimers. This value is thus in the order of a typical H-bond energy. For completeness we also show the temperature behavior of the equilibrium constants K = (I3 + I4)/I5, wherein the vibrational band I3 (also related to the cyclic dimers) with minor intensity is taken into account as well (Fig. 7b). At a first glance it seems to be surprising that the release of one hydrogen bond from the cyclic dimer (ΔE = 21 kJ mol−1) should result in a remaining stronger hydrogen bond of the linear dimer (ΔE = (45 − 21) kJ mol−1 = 24 kJ mol−1). The reason is illustrated by the B3LYP-D3 calculated cyclic and linear dimers shown in Fig. 8. In the cyclic dimer, the two hydrogen bonds ![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ⋯OC are not cooperative, whereas in the linear dimer, one OH group is hydrogen bonded as proton acceptor to the other OH group and as proton donor to a carbonyl oxygen (OH⋯
⋯OC are not cooperative, whereas in the linear dimer, one OH group is hydrogen bonded as proton acceptor to the other OH group and as proton donor to a carbonyl oxygen (OH⋯![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif)
![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ⋯OC), resulting in somewhat stronger hydrogen bonding. The calculated energy difference between the cyclic and the linear dimer is 17.8 kJ mol−1, close to the 21.2 kJ mol−1 due to the loss of one hydrogen bond as obtained from the van 't Hoff plot in Fig. 7.
⋯OC), resulting in somewhat stronger hydrogen bonding. The calculated energy difference between the cyclic and the linear dimer is 17.8 kJ mol−1, close to the 21.2 kJ mol−1 due to the loss of one hydrogen bond as obtained from the van 't Hoff plot in Fig. 7.
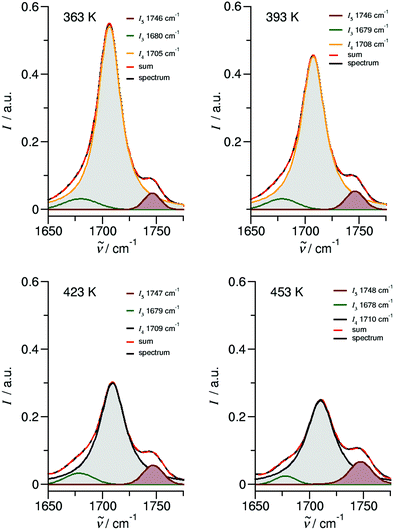 | ||
Fig. 6 Deconvoluted ATR-IR spectra of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region for ibuprofen in the liquid state at temperatures 363 K, 393 K, 423 K and 453 K, respectively. O stretching region for ibuprofen in the liquid state at temperatures 363 K, 393 K, 423 K and 453 K, respectively. | ||
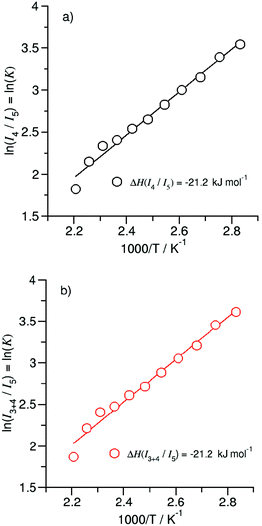 | ||
| Fig. 7 Plots of the natural logarithm of the ratios (a) I4/I5 and (b) I3+4/I5versus inverse temperature taken from the deconvoluted spectra in Fig. 6 between 363 K and 453 K. The solid lines represent linear fits (R2 ≥ 0.98) with slopes indicating the transfer enthalpies. | ||
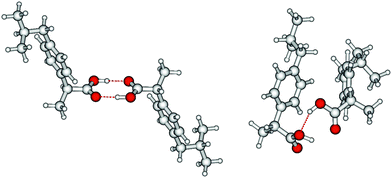 | ||
Fig. 8 B3LYP-D3 calculated ibuprofen cyclic (left) and linear dimer (right). In the cyclic dimer, the two hydrogen bonds ![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ⋯OC are not cooperative, whereas in the linear dimer, one OH group is hydrogen-bonded as proton acceptor to the other OH group and as proton donor to a carbonyl oxygen (OH⋯ ⋯OC are not cooperative, whereas in the linear dimer, one OH group is hydrogen-bonded as proton acceptor to the other OH group and as proton donor to a carbonyl oxygen (OH⋯![[O with combining low line]](https://www.rsc.org/images/entities/char_004f_0332.gif) ![[H with combining low line]](https://www.rsc.org/images/entities/char_0048_0332.gif) ⋯OC), resulting in somewhat stronger hydrogen bonding. The calculated energy difference between the cyclic and the linear dimer is 17.8 kJ mol−1, close to the 21.2 kJ mol−1 due to the loss of one hydrogen bond obtained from the van ‘t Hoff plots in Fig. 7. ⋯OC), resulting in somewhat stronger hydrogen bonding. The calculated energy difference between the cyclic and the linear dimer is 17.8 kJ mol−1, close to the 21.2 kJ mol−1 due to the loss of one hydrogen bond obtained from the van ‘t Hoff plots in Fig. 7. | ||
Overall, the temperature-dependent ATR-IR experiments in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretching region provide valuable information about the hydrogen-bonded structures present in solid and liquid ibuprofen. Moreover, the formation of linear dimers at the expense of cyclic dimers with increasing temperature in the liquid phase yields the energy of the released hydrogen bond.
O stretching region provide valuable information about the hydrogen-bonded structures present in solid and liquid ibuprofen. Moreover, the formation of linear dimers at the expense of cyclic dimers with increasing temperature in the liquid phase yields the energy of the released hydrogen bond.
4. Conclusion
Herein we determined the enthalpy of vaporization of ibuprofen from vapor pressure measurements to be 89 kJ mol−1. The hydrogen bond energy within the cyclic dimers of about 45 kJ mol−1 could be derived exclusively from the experimental data of ibuprofen and related aromatic carboxylic acids, homomorph methyl esters and alkyl acetates. It could be confirmed by DFT calculations on clusters including up to twelve molecules that the enthalpies of vaporization of ibuprofen consists of almost equal contributions from hydrogen bonding and dispersion interaction. ATR-IR spectra of the solid and liquid ibuprofen suggested that the dominating doubly hydrogen-bonded cyclic dimers are partially replaced by singly hydrogen-bonded linear dimers with increasing temperature. Vibrational bands in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O stretch region could be clearly assigned to either one of the species and allowed calculating temperature-dependent equilibrium constants. From the van’t Hoff plots we determined the transition enthalpy and could thus calculated the energy of the released hydrogen bond to be 21 kJ mol−1. Our combined approach including thermodynamic methods, IR spectroscopy and DFT calculations allowed comprehensive understanding of structure and molecular interaction in ibuprofen and related compounds.
O stretch region could be clearly assigned to either one of the species and allowed calculating temperature-dependent equilibrium constants. From the van’t Hoff plots we determined the transition enthalpy and could thus calculated the energy of the released hydrogen bond to be 21 kJ mol−1. Our combined approach including thermodynamic methods, IR spectroscopy and DFT calculations allowed comprehensive understanding of structure and molecular interaction in ibuprofen and related compounds.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the German Science Foundation (DFG) in frame of the priority program SPP 1807 “Control of London Dispersion Interactions in Molecular Chemistry” VE 265/9-2 (for S. P. Verevkin) and LU506/12-2 (for R. Ludwig). J. Feder-Kubis is grateful for the financial support given from the Polish Ministry of Science and Higher Education by subvention activity for the Faculty of Chemistry of Wrocław University of Science and Technology.References
- X. Yuan, X. Li, P. Guo, Z. Xiong and L. Zhao, Anal. Methods, 2018, 10, 4404–4413 RSC.
- C. Caballo, M. D. Sicilia and S. Rubio, Talanta, 2015, 134, 325–332 CrossRef CAS PubMed.
- S. S. Adams, P. Bresloff and C. G. Mason, J. Pharm. Pharmacol., 1976, 28, 256–257 CrossRef CAS PubMed.
- N. H. Hashim and S. J. Khan, J. Chromatogr. A, 2011, 1218, 4746–4754 CrossRef CAS PubMed.
- G. L. Perlovich, S. V. Kurkov, L. F. Hansen and A. Bauer-Brandl, J. Pharm. Sci., 2004, 93, 654–666 CrossRef CAS PubMed.
- A. A. Freer, J. M. Bunyan, N. Shankland and D. B. Sheen, Acta Crystallogr., Sect. B: Struct. Sci., 1993, 49, 1378–1380 Search PubMed.
- J. F. McConnell, Cryst. Struct. Commun., 1974, 3, 73–75 CAS.
- C. P. Brock, W. B. Schweizer and J. D. Dunitz, J. Am. Chem. Soc., 1991, 113, 9811–9820 CrossRef CAS.
- N. Shankland, A. J. Florence, P. J. Cox, D. B. Sheen, S. W. Love, N. S. Stewart and C. C. Wilson, Chem. Commun., 1996, 855–856 RSC.
- N. Shankland, C. C. Wilson, A. J. Florence and P. J. Cox, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1997, 53, 951–954 CrossRef.
- N. Brinkmann, G. Tschumper, G. Yan and H. F. Schaefer, J. Phys. Chem. A, 2003, 107, 10208–10216 CrossRef CAS.
- L. Turi, J. Phys. Chem., 1996, 100, 11285–11291 CrossRef CAS.
- W. Qian and S. Krimm, J. Phys. Chem. A, 2001, 105, 5046–5053 CrossRef CAS.
- M. Gantenberg, M. Halupka and W. Sander, Chem. – Eur. J., 2000, 6, 1865–1869 CrossRef CAS.
- W. Sander and M. Gantenberg, Spectrochim. Acta, Part A, 2005, 62, 902–909 CrossRef PubMed.
- F. Madeja, M. Havenith, K. Nauta, R. E. Miller, J. Chocholoušová and P. Hobza, J. Chem. Phys., 2004, 120, 10554–10560 CrossRef CAS PubMed.
- C. Emmeluth and M. A. Suhm, Phys. Chem. Chem. Phys., 2003, 5, 3094–3099 RSC.
- S. Bratož, D. Hadži and N. Sheppard, Spectrochim. Acta, 1956, 8, 249–261 CrossRef.
- S. Bratož and D. Hadži, J. Chem. Phys., 1957, 27, 991 CrossRef.
- A. Witkowski and M. J. Wójcik, Chem. Phys., 1973, 1, 9–16 CrossRef CAS.
- M. J. Wójcik, Mol. Phys., 1978, 36, 1757–1767 CrossRef.
- Y. Maréchal, J. Chem. Phys., 1987, 87, 6344–6353 CrossRef.
- D. Chamma and O. Henri-Rousseau, Chem. Phys., 1999, 248, 91–104 CrossRef CAS.
- G. M. Florio, T. S. Zwier, E. M. Myshakin, K. D. Jordan and E. L. Sibert III, J. Chem. Phys., 2003, 118, 1735–1746 CrossRef CAS.
- J. Dreyer, J. Chem. Phys., 2005, 122, 184306 CrossRef PubMed.
- P. Blaise, M. J. Wójcik and O. Henri-Rousseau, J. Chem. Phys., 2005, 122, 064306 CrossRef PubMed.
- F. Ito and T. Nakanaga, Chem. Phys., 2002, 277, 163–169 CrossRef CAS.
- G. M. Florio, E. L. Sibert III and T. S. Zwier, Faraday Discuss., 2001, 118, 315–330 RSC.
- C. K. Nandi, N. K. Hazra and T. Chakraborty, J. Chem. Phys., 2005, 123, 124310 CrossRef PubMed.
- C. Emmeluth, M. A. Suhm and D. Luckhaus, J. Chem. Phys., 2003, 118, 2242–2255 CrossRef CAS.
- M. Lim and R. M. Hochstrasser, J. Chem. Phys., 2001, 115, 7629–7643 CrossRef CAS.
- G. Seifert, T. Patzlaff and H. Graener, J. Mol. Liq., 2003, 102, 227–240 CrossRef CAS.
- K. Heyne, N. Huse, J. Dreyer, E. T. J. Nibbering, T. Elsaesser and S. Mukamel, J. Chem. Phys., 2004, 121, 902–913 CrossRef CAS PubMed.
- N. Huse, B. D. Brunder, M. L. Cowan, J. Dreyer, E. T. J. Nibbering, R. J. D. Miller and T. Elsaesser, Phys. Rev. Lett., 2005, 95, 147402 CrossRef CAS PubMed.
- H. Sauren, A. Winkler and P. Hess, Chem. Phys. Lett., 1995, 239, 313–319 CrossRef CAS.
- K. Marushkevich, L. Khriachtchev, J. Lundell and M. Räsänen, J. Am. Chem. Soc., 2006, 128, 12060–12061 CrossRef CAS PubMed.
- Z. J. Li, W. H. Ojala and D. J. W. Grant, J. Pharm. Sci., 2001, 90, 1523–1539 CrossRef CAS PubMed.
- K. D. Ertl, R. A. Heasly, C. Koegel, A. Chakrabarti and J. T. Carstensen, J. Pharm. Sci., 1990, 79, 552 CrossRef PubMed.
- P. Mura, G. P. Bettinetti, A. Mandetioli, M. T. Faucci, G. Bramanti and M. Sorrenti, Int. J. Pharm., 1998, 166, 189–203 CrossRef CAS.
- A. J. Romero and C. T. Rhodes, J. Pharm. Pharmacol., 1993, 45, 258–262 CrossRef CAS PubMed.
- S. P. Verevkin and V. N. Emel’yanenko, Fluid Phase Equilib., 2008, 266, 64–75 CrossRef CAS.
- S. P. Verevkin, A. Y. Sazonova, V. N. Emel’yanenko, D. H. Zaitsau, M. A. Varfolomeev, B. N. Solomonov and K. V. Zherikova, J. Chem. Eng. Data, 2015, 60, 89–103 CrossRef CAS.
- V. N. Emel’yanenko and S. P. Verevkin, J. Chem. Thermodyn., 2015, 85, 111–119 CrossRef.
- S. P. Verevkin, J. Chem. Eng. Data, 2000, 45, 953–960 CrossRef CAS.
- G. Pilcher, in The Chemistry of Acid Derivatives, ed. S. Patai, Wiley, New York, 1992, ch. 2, vol. 2 Search PubMed.
- J. S. Chickos, S. Hosseini, D. G. Hesse and J. F. Liebman, Struct. Chem., 1993, 4, 271–278 CrossRef CAS.
- J. S. Chickos and W. E. Acree, J. Phys. Chem. Ref. Data, 2003, 32, 519–878 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision A.02, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- P. Hobza, J. Šponer and T. Reschel, J. Comput. Chem., 1995, 16, 1315–1325 CrossRef CAS.
- S. Kristyan and P. Pulay, Chem. Phys. Lett., 1994, 220, 175–180 CrossRef.
- E. J. Meijer and M. Sprik, J. Chem. Phys., 1996, 105, 8684 CrossRef CAS.
- C. Tuma, A. D. Boese and N. C. Handy, Chem. Phys., 1999, 1, 3939 CAS.
- A. K. Rappe and E. R. Bernstein, J. Phys. Chem. A, 2000, 104, 6117 CrossRef CAS.
- G. A. Jones, M. N. Paddon-Row, M. S. Sherburn and C. I. Turner, Org. Lett., 2002, 4, 3789–3792 CrossRef CAS PubMed.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, 2001 Search PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Ehrlich, J. Moellmann, W. Reckien, T. Bredow and S. Grimme, Chem. Phys. Chem., 2011, 12, 3414–3420 CrossRef CAS PubMed.
- S. Grimme and A. Jansen, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- R. Ludwig, F. Weinhold and T. Farrar, Mol. Phys., 1999, 97, 465–477 CrossRef CAS.
- R. Ludwig, F. Weinhold and T. Farrar, Mol. Phys., 1999, 97, 479–486 CrossRef CAS.
- R. Ludwig, Phys. Chem. Chem. Phys., 2002, 4, 5481–5487 RSC.
- K. M. Murdoch, T. D. Ferris, J. C. Wright and T. C. Farrar, J. Chem. Phys., 2002, 116, 5717 CrossRef CAS.
- R. Ludwig, Chem. Phys. Chem., 2005, 6, 1369–1375 CrossRef CAS PubMed.
- R. Ludwig, Chem. Phys. Chem., 2000, 1, 53–56 CrossRef CAS PubMed.
- R. Ludwig and F. Weinhold, J. Chem. Phys., 1999, 110, 508–515 CrossRef CAS.
- R. Ludwig, Phys. Chem. Chem. Phys., 2008, 10, 4333–4339 RSC.
- R. Ludwig, J. Mol. Liq., 2000, 84, 65–75 CrossRef CAS.
- A. Knorr, P. Stange, K. Fumino, F. Weinhold and R. Ludwig, ChemPhysChem, 2016, 17, 458–462 CrossRef CAS PubMed.
- S. P. Verevkin, D. H. Zaitsau, V. N. Emel’yanenko, E. N. Stepurko and K. V. Zherikova, Thermochim. Acta, 2015, 622, 18–30 CrossRef CAS.
- K. Kusano and I. Wadso, Bull. Chem. Soc. Jpn., 1971, 44, 1705–1717 CrossRef CAS.
- M. V. Roux, M. Temprado, R. Notario, S. P. Verevkin, V. N. Emel'yanenko, D. E. Demasters and J. F. Liebman, Mol. Phys., 2004, 102, 1909–1917 CrossRef CAS.
- M. Hoskovec, D. Grygarova, J. Cvacka, L. Streinz, J. Zima, S. P. Verevkin and B. Koutek, J. Chromatogr. A, 2005, 1083, 161–172 CrossRef CAS PubMed.
- S. P. Verevkin, Thermochim. Acta, 1999, 332, 27–32 CrossRef CAS.
- J. S. Chickos and W. E. Acree Jr, J. Phys. Chem. Ref. Data, 2003, 32, 519–878 CrossRef CAS.
- D. Matulis, Biophys. Chem., 2001, 93, 67–82 CrossRef CAS PubMed.
- D. Kulikov, S. P. Verevkin and A. Heintz, Fluid Phase Equilib., 2001, 192, 187–207 CrossRef CAS.
- J. B. Pedley, Thermochemical Data and Structures of Organic Compounds, TRC Data Series, Texas, 1994, vol. 1 Search PubMed.
- V. N. Emel’yanenko, G. Boeck, S. P. Verevkin and R. Ludwig, Chem. – Eur. J., 2014, 20, 11640–11645 CrossRef PubMed.
- K. Fumino, A. Wulf, S. P. Verevkin, A. Heintz and R. Ludwig, Chem. Phys. Chem., 2010, 11, 1623–1626 CrossRef CAS PubMed.
- D. H. Zaitsau, V. N. Emel'yanenko, P. Stange, C. Schick, S. P. Verevkin and R. Ludwig, Angew. Chem., Int. Ed., 2016, 55, 11682–11686 CrossRef CAS PubMed.
- D. H. Zaitsau, V. N. Emel'yanenko, P. Stange, C. Schick, S. P. Verevkin and R. Ludwig, Angew. Chem., 2016, 128, 11856–11860 CrossRef.
- D. H. Zaitsau, V. N. Emel’yanenko, P. Stange, S. P. Verevkin and R. Ludwig, Angew. Chem., Int. Ed., 2019, 58, 8589–8592 CrossRef CAS PubMed.
- D. H. Zaitsau, V. N. Emel’yanenko, P. Stange, S. P. Verevkin and R. Ludwig, Angew. Chem., 2019, 131, 8679–8683 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cp06641a |
| This journal is © the Owner Societies 2020 |