Open Access Article
Open Access ArticleIncluding dispersion in density functional theory for adsorption on flat oxide surfaces, in metal–organic frameworks and in acidic zeolites†
Florian R.
Rehak‡
 ,
GiovanniMaria
Piccini§
,
GiovanniMaria
Piccini§
 ,
Maristella
Alessio¶
,
Maristella
Alessio¶
 and
Joachim
Sauer
and
Joachim
Sauer
 *
*
Institut für Chemie, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. E-mail: js@chemie.hu-berlin.de
First published on 30th March 2020
Abstract
We examine the performance of nine commonly used methods for including dispersion interactions in density functional theory (DFT): three different parametrizations of damped 1/Rn terms (n = 6, 8, …) added to the DFT energy (Grimme's D2 and D3 parameterizations as well as that of Tkatchenko and Scheffler), three different implementations of the many-body dispersion approach (MBD, MBD/HI and MBD/FI), the density-dependent energy correction, called dDsC, and two “first generation” van der Waals density functionals, revPBE-vdW and optB86b-vdW. As test set we use eight molecule–surface systems for which agreement has been reached between experiment and hybrid QM:QM calculations within chemical accuracy limits (±4.2 kJ mol−1). It includes adsorption of carbon monoxide and dioxide in the Mg2(2,5-dioxido-1,4-benzenedicarboxylate) metal–organic framework (Mg-MOF-74, CPO-27-Mg), adsorption of carbon monoxide as well as of monolayers of methane and ethane on the MgO(001) surface, as well as adsorption of methane, ethane and propane in H-chabazite (H-CHA). D2 with Ne parameters for Mg2+, D2(Ne), MBD/HI and MBD/FI perform best. With the PBE functional, the mean unsigned errors are 6.1, 5.6 and 5.4 kJ mol−1, respectively.
1. Introduction
Dispersion forces as part of van der Waals (vdW) forces are ubiquitous in molecule–surface interactions, see, e.g., ref. 1–3, but the workhorse of present day quantum chemistry, density functional theory (DFT), has problems in describing them.4–7 This was first noted by Kristyán and Pulay.8 Before the advent of DFT in chemistry, the quantum chemical ab initio treatment of intermolecular interactions was based on Hartree–Fock calculations with dispersion described by a damped multipole expansion with 1/R6, 1/R8, 1/R10, … terms.9 The damping accounts for charge penetration effects. This approach was applied also to small model systems relevant for adsorption on flat surfaces and in zeolites.10,11 For example, for the interaction of water molecules with transition metal atoms the conclusion was reached that “a substantial share … is due to intersystem correlation effects (dispersion).”11In 2001, Scoles and co-workers extended the SCF (self-consistent field) + damped multipole expansion to Kohn–Sham DFT12 and defined the damping functions such that double counting of dispersion in the range of overlapping densities is avoided. Soon after, Grimme seized this idea and suggested to add a damped 1/R6 term,
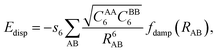 | (1) |
For a key problem in acid zeolite reactivity, protonation of isobutene to tert-butyl cation or surface alkoxides, Tuma and Sauer4 had calculated the difference between reaction energies obtained with MP2 (second order Møller–Plesset perturbation theory), a wave function electron correlation method which accounts for dispersion, and those obtained with DFT using the PBE (Perdew–Burke–Ernzerhof)14 functional. For a series of zeolite cluster models of increasing size they showed that this difference can be fit with the same expression as used by Grimme, eqn (1), plus an additive constant. The latter was needed because the dispersion term does not correct for all shortcomings of the exchange–correlation functional such as the self-interaction correction error.15,16 Kerber et al.15 also found that fitting parameters for specific systems as Tuma and Sauer did, has no advantage compared to the use of Grimme's D2 parametrization.
For applications with periodic boundary conditions an Ewald-type summation of the 1/R6 term was implemented in the VASP code,15 and a series of PBE-D2 calculations were performed for adsorption and reactions of small molecules in zeolites, as well as for adsorption in metal–organic frameworks (MOFs) and on the flat MgO(001) surface. In these calculations PBE-D2 served as low-level method within a hybrid high-level – low-level quantum approach.17 As high-level description, MP2 calculations were performed on a cluster model for the adsorption site. In addition, to check if MP2 is accurate enough, coupled cluster (CC) corrections with single, double and perturbatively treated triple substitutions, CCSD(T), were calculated for models of the reaction site that are sufficiently small to make the CCSD(T) calculations feasible. This multilevel hybrid MP2:DFT-D+ΔCC method has been shown to yield chemical accuracy for a set of twelve molecule–surface interaction systems for which reliable experimental data are available.17 This data set provides a unique opportunity for testing some of the various proposals to take dispersion into account with respect to their performance for molecule–surface interactions.6
Here, we examine the performance of commonly used methods such as Grimme's D213 and D318 parameterizations, the Tkatchenko and Scheffler (TS) parametrization,19 many-body dispersion (MBD) approaches in different implementations,20–23 the density-dependent energy correction, called dDsC,24,25 and also two “first generation” vdW density functionals (vdW-DFs),26 vdW-revPBE and vdW-optB86b. Performing best is PBE-MBD/FI, closely followed by PBE-D2. The mean unsigned errors are about 5 to 6 kJ mol−1.
2. Methods used
The simplest way of including dispersion in DFT is adding a damped multipole expansion term, Edisp, to the DFT energy, EDFT,| Etotal = EDFT + Edisp. | (2) |
In the D2 scheme, Edisp is given by eqn (1) with read-to-use parameters specified in ref. 13. It is possible to define specific CAA6 parameters to include effects of the chemical environment as Tosoni and Sauer did for Mg2+ ions in MgO.27 Since Mg2+ ions miss the electrons in the 3s shell, C6 parameters derived from the atom13 may not be the best choice for Mg2+ ions. It turns out that parameters derived for Mg2+ ions following the D2 protocol are – not unexpectedly – very close to the parameters of the isoelectronic Ne atom.27 To avoid additional parameters Tosoni and Sauer recommended use of Ne parameters for Mg2+. We refer to these results as D2(Ne) and this approach is one possible way to account for the ionic character of MgO.
In the D3 method Edisp includes also a three-body term, E(3),
| Edisp = E(2) + E(3), | (3) |
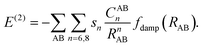 | (4) |
Since the 1/R8 term is more short-ranged, adjustment to different functionals is done by s8 whereas s6 is set to unity. In addition, the CABn coefficients are coordination number dependent to account for different chemical environments. E(3) consist of a damped Axilrod–Teller–Muto term28 derived from third-order perturbation theory for three atoms. The TS scheme also employs eqn (1), but the CAA6 coefficients are combined by another combination rule based on rescaled coefficients that depend on the ratio of free and effective volumes of the atom.
Subsequently, TS introduced self-consistent screening (SCS)29,30 of atomic polarizabilities to account for the electric field of surrounding atoms. Adding many-body interactions with the coupled fluctuating dipole model,31 the many-body dispersion (MBD) scheme was derived.30 To avoid double counting of interactions by SCS and MBD, range separation was introduced. This method was named MBD@rsSCS.20 For brevity, this method is termed MBD in the following. Within MBD, the dispersion contribution is written as
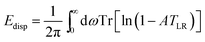 | (5) |
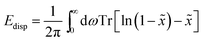 | (6) |
![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) are the remapped eigenvalues of the Hermitian matrix
are the remapped eigenvalues of the Hermitian matrix 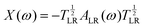 . Due to the reciprocal space implementation23 of MBD and its variants, higher k-point sampling is required as one would need for the other methods.
. Due to the reciprocal space implementation23 of MBD and its variants, higher k-point sampling is required as one would need for the other methods.
Steinmann and Corminboeuf introduced a new density-dependent dispersion correction, named dDsC,24,25 which was shown to provide balanced treatment of both intra- and intermolecular interactions, see, for examples, benchmark studies in ref. 24 and 25. The dispersion coefficients are computed on the basis of an approximation to Becke and Johnson's exchange-hole-dipole moment formalism,35 and rely on a classical Hirshfeld partitioning of the electron density among atomic centers. An extended Tang and Toennies damping function36 is applied, in which the damping parameter depends on the atomic (overlap) populations. The dDsC implementation by Steinmann in the VASP code is not self-consistent.37 Sautet and co-workers applied the dDsC dispersion correction to selected surface problems, e.g. adsorption of small alkanes on the Pt(111) surface,38 and most recently dehydrogenation reactivity of Pt clusters supported on γ-Al2O3.39
We consider also the first generation of vdW density functionals, including revPBE14,40 and optB86b41 as density functional approximation. This approach splits the correlation energy into two terms. The first accounts for the short-ranged dispersion and is described in the original approach by the local density approximation. The second term describes long-range dispersion as
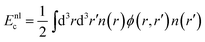 | (7) |
3. Systems studied
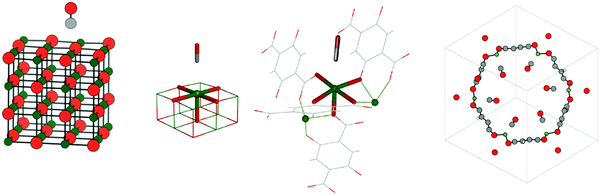
The list of studied systems includes adsorption of carbon monoxide,43 as well as of monolayers of methane and ethane at the MgO(001) surface,43 adsorption of carbon monoxide44 and dioxide45 in a MOF with the composition Mg2(dobdc) (dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate), and adsorption of methane, ethane, and propane in H-chabazite46 (H-CHA). A four layer MgO slab with a 4 × 4 surface cell is adopted for CO, CH4, and C2H6 on the MgO(001) surface. Fig. 1 shows the adsorption structure of CO on MgO(001).For CO and CO2 on Mg2+ sites in Mg2(dobdc), high coverage was assumed resulting in six adsorbed molecules per unit cell (θ = 1.0), as shown for CO in Fig. 1. In Mg2(dobdc), Mg2+ is five-fold coordinated as at the MgO(001) surface. Fig. 1 shows CO attached to five-fold coordinated Mg2+ ions on the MgO(001) surface (center left) and in Mg2(dobdc) (center right).
For CH4, C2H6, and C3H8 in H-CHA, adsorption occurs preferentially at Brønsted acid sites (Si-OH-Al),47,48 as illustrated in Fig. 2 for adsorption of methane in H-CHA.46 The H-CHA model with an Al/Si ratio of 1/11 was obtained by doubling the triclinic unit cell along the lattice vector a.46 An adsorption coverage of θ = 0.5 was assumed.
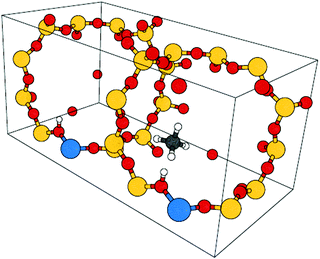 | ||
| Fig. 2 Unit cell for CH4 in H-CHA. The Al/Si ratio is 1/11. Color code: Al – blue, O – red, Si – yellow, C – grey, H – white. | ||
4. Computational details
The DFT-D calculations using D2,13 D3 with zero damping,18 and TS,19 as well as the vdW-DF26 calculations were carried out with the Vienna ab initio Simulation Package (VASP, Version 5.3.5).49–51 For MBD,20,23 MBD/HI,20,21,23 and dDsC24,25 VASP Version 5.4.1 was used. Furthermore, an additional patch, provided by the developers, was installed to use the fractional ion scheme (MBD/FI).22 Throughout the different VASP versions convergence of electronic adsorption energies within 0.1 kJ mol−1 for the different dispersion corrected DFT approaches were found. If not stated differently, an energy cutoff of 600 eV and standard projector augmented-wave method52 (PAW) potentials were applied for all calculations.CO, CO2/Mg2(dobdc)
For Mg2(dobdc) the primitive unit cell (a = b = c = 15.22225 Å; α = β = γ = 117.76°) was adopted and the calculations were performed at the Γ-point only, except for the MBD approaches which used a 4 × 4 × 4 k-point grid. For Mg2+ the 2p shell has been considered as valence state (Mg_pv).51 First, the cell shape, the cell volume, and the atomic positions of the empty MOF and of the MOF loaded with adsorbed CO and CO2 were optimized at 800 eV cutoff. This was followed by relaxation of atomic positions at 600 eV keeping the cell shape and cell volume fixed. The same cutoff (600 eV) was used for the calculations of CO and CO2 in the gas phase (Γ-point only). The molecules were put in the middle of a 20 Å box. Adsorption energies were obtained from these 600 eV cutoff results. All structures were considered as relaxed when the gradients were smaller than −0.01 eV Å−1 for PBE,14 revPBE,40 optB86b41 (conjugated gradient algorithm) and smaller than −0.05 eV Å−1 for B3LYP (Newton–Raphson algorithm). Additionally, the “scaling constant” was set to POTIM = 0.3 for B3LYP.53 An energy convergence threshold of 10−8 eV per cell was chosen for PBE, revPBE, optB86b and 10−5 eV per cell for B3LYP.CO, CH4, C2H5/MgO(001)
A four-layer 4 × 4 slab with two frozen bottom layers was chosen to simulate MgO(001). For Mg, the 2p shell has been included in the valence state (Mg_pv).51 The ion position optimizations were carried out in an orthorhombic cell (a = b = 8.48 Å; c = 25.0 Å). The same cell was used to simulate the CO molecule in gas phase with Γ-point only. For adsorption on the MgO(001) surface, a coverage θ = 0.125 was assumed. The k-point sampling was 2 × 2 × 1, whereas for MBD and its variants 8 × 8 × 1 k-point sampling was applied. To simulate methane and ethane in the gas phase one molecule was placed in the middle of a 15 Å box with Γ-point only. Adsorption of CH4 and C2H6 was simulated with four molecules per unit cell (θ = 1.0). For structure optimizations with PBE, revPBE and optB86b the gradient threshold was −0.01 eV Å−1 for the conjugated gradient algorithm, and the SCF criterion was 10−5 eV per cell. For B3LYP, the gradient threshold was −0.05 eV Å−1 with the Newton–Raphson algorithm and the SCF criterion was 10−4 eV per cell.Alkanes/H-CHA
For all calculations on H-CHA (Al/Si ratio of 1/11), both empty and loaded with alkanes, atomic positions, cell shape and cell volume were relaxed. A 15 Å box cell was chosen to simulate the gas phase molecules. The calculations were performed at the Γ-point, except for the different MBD approaches which used 4 × 4 × 4 k-points. The structure optimizations with PBE, revPBE, and optB86b used the conjugated gradient algorithm, whereas for B3LYP the Newton–Raphson algorithm was chosen. The structures were considered as relaxed when the forces were smaller than −0.01 eV Å−1. For the isolated alkanes the threshold was −0.002 eV Å−1. For SCF calculations with PBE, revPBE and optB86b the energy convergence criteria were set to 10−8 eV per cell, for B3LYP to 10−5 eV per cell.5. Results
For N molecules, the electronic adsorption energy per molecule, ΔE, was calculated as difference between the electronic energy of the adsorbate structure, EM,S, and the sum of the energies of the clean structure, ES, and N molecules in the gas phase, EM,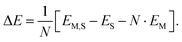 | (8) |
Eqn (8) defines the adsorption energy as difference between the bottoms of the respective potential wells. In contrast, experiments yield the enthalpy of adsorption, ΔHexpT, at a given temperature which differs from ΔEref by the volume work pV = RT, thermal energy contributions, ΔET, and the zero-point vibrational energy, ΔEZPV. The latter are mostly unknown from experiment, but can be estimated using structures and vibrational wavenumbers obtained by DFT-D calculations. This allows defining an “experimentally derived” reference energy:17,46
| ΔEref = ΔHexpT + RT − ΔET(DFT-D) − ΔEZPV(DFT-D). | (9) |
For the eight systems considered here, Table 1 shows the ΔHT and ΔEref values as well as the results of hybrid QM:QM calculations, all taken from ref. 17.
| System | ΔHTa | ΔErefb | ΔE | ΔE | ΔE |
|---|---|---|---|---|---|
| Exp. | Exp. Ref. | QM:QM | PBE-D2(Ne) | PBE-MBD/FI | |
| a See eqn (9); see ref. 17 for original references. b Hybrid MP2:PBE-D2+ΔCC energies.17 c Metal–organic framework also known as Mg-MOF-74 or CPO-27-Mg (dobdc4− = 2,5-dioxido-1,4-benzenedicarboxylate), loading 1:1: one molecule on each Mg2+ ion. d Numbers are different from Table 1 in ref. 17 because for the 1:1 loading lateral interaction energies of −2.8 kJ mol−1 are included, see Table 3 of ref. 45. | |||||
| CO/Mg2(dobdc)c | −39.8 ± 1.0 | −43.8 ± 1.0 | −43.3 ± 1.4 | −41.3 | −44.3 |
| CO2/Mg2(dobdc)c | (−46.3)d | −49.0d | −51.6d | −41.5 | −45.7 |
| CO/MgO(001) | −16.5 | −20.6 ± 2.4 | −21.2 ± 0.5 | −22.1 | −31.4 |
| CH4/MgO(001) | −12.2 | −15.0 ± 0.6 | −14.0 ± 1.0 | −14.7 | −17.2 |
| C2H6/MgO(001) | −22.1 | −24.4 ± 0.6 | −23.3 ± 0.6 | −23.7 | −30.1 |
| CH4/H-CHA | −17.0 | −27.2 | −25.3 | −35.6 | −30.0 |
| C2H6/H-CHA | −27.5 | −33.5 | −36.2 | −46.8 | −41.7 |
| C3H8/H-CHA | −37.6 | −43.8 | −46.7 | −58.7 | −53.6 |
Fig. 3 shows the computed adsorption energies calculated with PBE and different methods of including dispersion and compares them with the experimentally derived reference energies and the results of hybrid QM:QM calculations. For the numbers see ESI,† Tables S1, S3, and S5, which include also results for B3LYP. For the two best performing methods, PBE-D2(Ne) and PBE-MBD/FI the energies are also listed in Table 1.
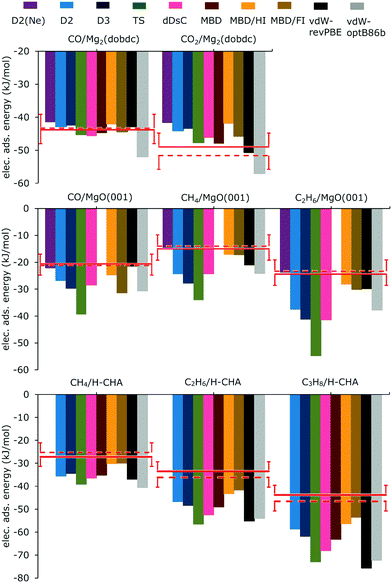 | ||
| Fig. 3 Electronic adsorption energies (kJ mol−1) of molecules interacting with sites in Mg2(dobdc) (top), on MgO(001) (middle), and in H-CHA (bottom) calculated with PBE and various methods taking dispersion into account. Comparison is made with experimentally derived reference energies, eqn (9) (red line) and QM:QM results (broken red line). Error bars indicate the chemical accuracy range (±4.2 kJ mol−1). | ||
CO, CO2/Mg2(dobdc)
The calculations were carried out for high loading, i.e. six CO or CO2 per unit cell, as shown for CO in Fig. 1. D2(Ne) parameters which had been suggested for Mg2+ ions at the MgO(001) surface were also applied to Mg2+ in Mg2(dobdc). For CO in Mg2(dobdc) the heat of adsorption has been derived from the experimental Gibbs free energy of adsorption and an entropy term calculated for a PBE-D2(Ne) potential energy surface including anharmonicities, see ref. 19 and ESI† for more details. Except for B3LYP-D2(Ne) and vdW-optB86b, the deviations from experiment are between −2 and +3 kJ mol−1, see ESI,† Table S1 and Fig. 3. MBD/FI shows the smallest deviation from ΔEref. For the same dispersion correction method deviations are nearly twice as large with B3LYP as with PBE (ESI,† Table S1). PBE-D2 and PBE-D3 results show no significant differences, whereas PBE-D2(Ne) deviates more from the reference value (2.5 kJ mol−1).For CO2 adsorption, in contrast to CO adsorption, with the same dispersion correction method, dispersion corrected B3LYP deviates less than PBE (Table S1, ESI†). The smallest deviation is found for B3LYP-D3 followed by PBE-MBD and PBE-TS. With PBE, D2 and D3 perform similarly, but D2(Ne) deviates more from the reference energy than D2 or D3. PBE-MBD/FI is worse than PBE-MBD and MBD/HI performs even worse.
CO/MgO(001)
Only B3LYP-D2 and B3LYP-D2(Ne), PBE-D2(Ne) and PBE-MBD/HI as well as vdW-revPBE deviate from ΔEref less than 4.2 kJ mol−1 (Fig. 3 and ESI,† Table S3). For the same dispersion method B3LYP results are closer to the reference energy than PBE ones with the exception of D2(Ne). Using PBE-D2(Ne) instead of the original D2 parametrization diminishes the deviation from −6.2 to −1.5 kJ mol−1, which is remarkable given the reference value of −20.6 kJ mol−1. In contrast, passing from D2 to D3 and TS increases the deviation to −9.1 and −18.8 kJ mol−1, respectively, resulting in almost twice the adsorption energy for PBE-TS. The MBD approach suffers from numerical instabilities22 when highly polarizable atoms are packed close together, which is the case for MgO. Therefore it was not possible to perform MBD calculations for any adsorbate on MgO(001). For MBD/HI and MBD/FI the numerical instabilities are not present, and the calculated adsorption energies deviate from the reference value by just −4.1 kJ mol−1 and (rather surprisingly) −10.8 kJ mol−1, respectively. With −7.9 kJ mol−1 the deviation for dDsC is in between.The deviations for CO/Mg(001) are much larger than the ones obtained for CO/Mg2(dobdc). Fig. 1 shows that CO/MgO(001) and CO/Mg2(dobdc) share the five-fold coordinated Mg2+ surface ions as adsorption sites, but in the latter structure there are additional interactions between CO and the benzene rings of the dobdc4− linkers which increase the binding energy from 21 to 43 kJ mol−1, see hybrid QM:QM results in Table 2. For CO/MgO(001), Ugliengo and Damin54 have shown that dispersion is about one half of the total binding energy at large distances, the other half is electrostatics. Table 2 further shows that the share of the correlation energy is different for the two systems. For CO/MgO(001) it is almost 100% whereas for CO/Mg2(dobdc) it is around 80% only. This indicates that dispersion may play a different role in the two systems and explains that different DFT-D methods perform differently. For those listed in Table 2, the share of dispersion on the total adsorption energy varies little for CO/Mg2(dobdc), between 39 and 47%, but for CO/MgO(001) the variation is much larger, between 31 and 63%.
| MgO(001)a | Mg2(dobdc)b | Difference | ||||
|---|---|---|---|---|---|---|
| QM:QM | Correl. | QM:QM | Correl. | QM:QM | Correl. | |
| a Ref. 43 hybrid QM:QM results, R(C⋯Mg2+) = 251 pm. b Ref. 55 neutron powder diffraction, R(C⋯Mg2+) = 241 pm. c Ref. 44. d Modified D2 parameters, ref. 56. | ||||||
| QM:QM | 21.2a | 20.5a | 43.3c | 35.0c | 22.1 | 14.5 |
| DFT-Da | D//DFT-D | DFT-D | D//DFT-D | DFT-D | D//DFT-D | |
| PBE-D2(Ne) | 22.1 | 6.8 | 41.3 | 16.0 | 19.2 | 9.2 |
| PBE-dDsC | 28.5 | 13.8 | 45.7 | 20.7 | 17.2 | 6.9 |
| PBE-MBD/FI | 31.4 | 17.0 | 44.3 | 19.4 | 12.9 | 2.4 |
| B3LYP-D*d | 16 | 10 | 34 | 16 | 18 | 6 |
CH4 and C2H6/MgO(001)
For the methane and ethane monolayers on MgO(001), with both B3LYP and PBE, the D2(Ne) results are closest to the reference energy (ESI,† Table S3), D3 and TS perform worse than D2 and D2(Ne), and for PBE the MBD/HI and MBD/FI deviations are much smaller than the dDsC deviations.Alkanes/H-chabazite
The experimental value for the adsorption of propane is assigned to an adsorption via primary carbon, C(1°), only, adsorption via secondary carbon is entropically disfavoured.46 Results for adsorption via the secondary carbon can be found in Table S6 (ESI†).For adsorption of methane in H-CHA, compared to the experimentally derived reference values, only the PBE-MBD/HI and PBE-MBD/FI results are within chemical accuracy limits of 4.2 kJ mol−1, see Fig. 3. With increasing chain length, the deviations increase. Among the different MBD approaches the iterative Hirshfeld partitioning (MBD/HI) improves the results. For methane, ethane and propane, the deviations diminish from −8.0, −15.6, and −19.4 kJ mol−1, respectively, for MBD to −3.0, −9.8, and −12.6 kJ mol−1, respectively (Table S5, ESI†). Introducing the fractional ion scheme (MBD/FI) diminishes the deviations further to −2.8, −8.2, and −9.8 kJ mol−1, respectively. Taking the simplicity of the method into account it is surprising that D2 yields nearly the same or even smaller deviations than D3, dDsC or MBD, as shown in Fig. 3. For PBE-D2 and vdW-revPBE, we reproduce the adsorption energies obtained by Göltl et al.,57 whereas our PBE-TS results are somewhat different, probably due to different calculation settings. Adding dispersion to a hybrid functional like B3LYP, the deviations from the reference are larger for D3 than for D2 (ESI,† Table S5), but smaller for B3LYP-TS than for B3LYP-D2.
The deviations from the reference energy increase with increasing carbon number, indicating the difficulties of accounting properly for dispersion interactions with increasing chain length. For the methane and ethane monolayers on the Mg(001) surface a similar trend is observed, see ESI,† Table S3. The deviations per carbon atoms (Table S5, ESI†) are −3.4 ± 0.7 and −4.0 ± 1.0 kJ mol−1 for MBD/FI and MBD/HI, respectively, whereas for D2 they diminish from −8.4 to −6.7 and −5.0 kJ mol−1 for CH4, C2H6, and C3H8, respectively, indicating a more “healthy” size dependence of D2, at least for alkanes.
6. Discussion
It is already known that some functionals yield reasonable adsorption energies at the expense of unrealistic molecule–surface distances. An example is the overestimation of intermolecular distances by vdW-revPBE58 which we also find for adsorption of alkanes on Mg2+ sites of MgO(001) (35 to 36 pm, see ESI,† Table S4) and on the proton sites of H-CHA (32 to 45 pm, ESI,† Table S6). For these systems PBE-D2 underestimates the distances by 8 to 14 pm. For methane and ethane on Mg(001) the underestimation is diminished from 13 and 14 pm, respectively, to 4 and 1 pm, respectively, when Ne parameters on Mg2+ are used (PBE-D2(Ne)).For CO/Mg(001) all methods based on PBE underestimate the C⋯Mg2+ distance by 11 to 13 pm (ESI,† Table S4) with respect to the hybrid MP2:PBE-D2 reference value (251 pm), whereas for CO/Mg2(dobdc) they all overestimate it by 3 to 6 pm (ESI,† Table S2) with respect to the neutron powder diffraction result (241 pm).55
Table 3 shows the mean unsigned error (MUE), mean signed error (MSE), the absolute maximum deviation (|MAX|), and the system for which |MAX| occurs. MBD is not included in Table 3 since the results for CO, methane and ethane on the MgO(001) surface are not available as described above.
| MUE | MSE | |MAX| | System | ||
|---|---|---|---|---|---|
| B3LYP | D2(Ne) | 8.1 | −0.2 | 21.7 | C3H8/H-CHA |
| D2 | 9.4 | −8.7 | 21.7 | C3H8/H-CHA | |
| D3 | 13.2 | −12.6 | 26.4 | C3H8/H-CHA | |
| TS | 13.8 | −13.1 | 29.1 | C2H6/MgO(001) | |
| PBE | D2(Ne) | 6.1 | −3.4 | 14.9 | C3H8/H-CHA |
| D2 | 8.9 | −7.4 | 14.9 | C3H8/H-CHA | |
| D3 | 10.8 | −9.0 | 18.1 | C3H8/H-CHA | |
| TS | 16.9 | −16.6 | 30.4 | C2H6/MgO(001) | |
| dDsC | 11.4 | −10.7 | 24.3 | C3H8/H-CHA | |
| MBD/HI | 5.6 | −3.3 | 12.6 | C3H8/H-CHA | |
| MBD/FI | 5.4 | −4.6 | 10.8 | CO/MgO(001) | |
| revPBE | vdW | 9.8 | −9.6 | 31.9 | C3H8/H-CHA |
| optB86b | vdW | 13.9 | −13.9 | 28.5 | C3H8/H-CHA |
The MUEs for the PBE calculations show that D3 and TS are not an improvement compared to D2, while the use of Ne parameters for Mg2+, D2(Ne), is. Note that the D2(Ne) set does not differ from the D2 set for small alkanes in H-CHA since Mg2+ ions are not present in these systems. On average vdW-revPBE is about the same as D2, whereas vdW-optB86b is worse, even worse than PBE-D3.
The similarity of the MUEs and the absolute MSE values indicates that the deviations are largely systematic. D2, D3, TS and dDsC all predict too much binding, the overbinding increases from D2 to D3, dDsC and TS, see Table 3.
Most methods have their |MAX| for the largest alkane studied, i.e., for propane in H-CHA and for ethane on MgO(001). Only MBD/FI has a |MAX| for CO on MgO(001) with 10.8 kJ mol−1. Additionally, MBD/FI has the lowest deviation for propane in H-CHA with −9.8 kJ mol−1, see Fig. 3. Since the binding of small alkanes on MgO(001) surface and at the bridging OH group of H-CHA is dominated by dispersion which scales with the number of carbon atoms, the deviation per carbon atom Δ/nc was also calculated for each method (see ESI,† Tables S3 and S5). Table S7 (ESI†) shows the corresponding MUE, MSE and |MAX| values. Per C atom, the methods have their |MAX| changed from propane in H-CHA to methane either in H-CHA or on MgO(001). From Table S7 (ESI†), similar conclusions are reached as from Table 3, with MUEs of 3.7, 3.7 and 4.0 kJ mol−1 for PBE-MBD/HI, MBD/FI, D2(Ne), respectively.
Considering the deviations per molecule (Table 3), the best performing methods, D2(Ne), MBD/HI and MBD/FI, approach chemical accuracy on average. For D2(Ne), the MUEs are 8.1 and 6.1 kJ mol−1 with B3LYP and PBE, respectively, and for MBD/HI and MBD/FI with PBE, 5.6 and 5.4 kJ mol−1, respectively.
However, the maximum errors are still 21.7 and 14.9 kJ mol−1 for D2(Ne) with B3LYP and PBE, respectively, and 12.6 and 10.8 kJ mol−1 for MBD/HI and MBD/FI with PBE, respectively.
There is some uncertainty in the reference energies due to experimental error bars and estimates of ΔEZPV and ΔET in eqn (9). The differences between the experimentally derived adsorption energies, ΔEref and the hybrid QM:QM results in Table 1 range from −2.9 to +2.9 kJ mol−1 which reflects the experimental error and the estimated uncertainty of the hybrid QM:QM results, e.g. for CO/MgO(001) ΔEref is −20.6 ± 2.4 kJ mol−1 and ΔEQM:QM is −21.2 ± 0.5 kJ mol−1 yielding 0.6 ± 2.9 kJ mol−1 for the difference (Table 1). However, on average the effect is smaller. If the ΔEQM:QM values are used as reference instead of the ΔEref values the MSEs and MUEs change only marginally, see ESI,† Table S8. The MSEs all get 0.5 kJ mol−1 less negative, i.e. become smaller in absolute terms, whereas the MUEs change from 8.1 to 7.7 kJ mol−1 and from 6.1 to 5.9 kJ mol−1 for D2(Ne) with B3LYP and PBE, respectively, and remain constant for MBD/HI and MBD/FI for PBE. The only noticeable changes are on the maximum absolute deviations which decrease to 18.8 and 12.0 kJ mol−1 for D2(Ne) with B3LYP and PBE, respectively, and to 9.9 and 10.2 kJ mol−1 for PBE with MBD/HI and MBD/FI, respectively.
That chemical accuracy is not reached in DFT by just taking dispersion into account is not really surprising. There are other sources of error as the self-interaction correction (SIC) error which is particularly severe for generalized gradient type functionals such as PBE. It gives undue stability to more polar structures and is also the cause of systematically underestimated barriers. For example, for the methylation of ethene, propene, and t-butene-2 in zeolite H-MFI, without any dispersion included, PBE yields (apparent) barriers that are 16, 36 and 57 kJ mol−1, respectively, too high,16 whereas after the D2 term is added, the barriers are systematically too low by 12 to 21 kJ mol−1.17
For 17 elementary steps of the methanol-to-olefins process, PBE-D3 was found to underestimate energy barriers by 42 kJ mol−1, whereas with the hybrid functionals B3LYP-D3 and PBE0-D3 the underestimation is reduced to 27 and 17 kJ mol−1, respectively,42,59 in agreement with a reduced SIC for hybrid functionals. For 38 molecular hydrogen atom transfer reactions Zhao and Truhlar had reported systematic underestimation of energy barriers by PBE and B3LYP with 39 and 17 kJ mol−1, respectively.60
For adsorption of 13 molecules on a different type of surface for which experimental data are known, the Pt(111) metal surface, Sautet and co-workers38 found MUEs as large as 42 and 44 kJ mol−1 for plain PBE and the vdW-optB86b. With vdW-BEEF the MUE is reduced to 32 kJ mol−1 only, but with the best performing PBE-dDsC and the vdW-DF optPBE methods it is still 23 and 20 kJ mol−1, respectively – far outside the chemical accuracy range.
7. Conclusions
For the eight cases of adsorption on flat oxide surfaces and in nanopores of MOFs and zeolites studied here – for other systems findings may be different – D3 or TS are not an improvement compared to D2, neither with PBE nor with B3LYP, but D2(Ne) that uses the parameters of Ne for the isoelectronic Mg2+ ion in oxides is an improvement. The MUEs for D2(Ne) are about 8 and 6 kJ mol−1 with B3LYP and PBE, respectively, whereas for D2 they are about 9 kJ mol−1 with both PBE and B3LYP.With PBE additional methods of including dispersion have been examined. Neither dDsC nor the van der Waals functionals vdW-revPBE or vdW-optB86b are an improvement compared to D2. With the many-body approaches MBD/HI and MBD/FI a slightly better accuracy for the adsorption energies is achieved than with D2 or D2(Ne). With MUEs of 5 to 6 kJ mol−1, and maximum errors of 10 to 13 kJ mol−1, the MBD/HI and MBD/FI many body approaches are getting close to chemical accuracy (4.2 kJ mol−1).
We are well aware of the fact that we look at a very limited set of molecule–surface interactions for our comparison. D2 has more serious problems for the interaction of molecules with metal surfaces, but recent tests have shown that the best performing methods for such systems, vdW-optB86b and PBE-dDsC yield MUEs of 20 and 23 kJ mol−1, respectively,38 even larger than we find here (14 and 11 kJ mol−1, respectively).
For our DFT studies on ionic crystals, MOFs and zeolites we see little motivation to pass from D2 to more sophisticated schemes of including dispersion, in particular not when it is used as low level QM method in a hybrid QM:QM scheme that uses wave function correlation methods (MP2, CCSD(T)) for local improvements at the reaction site. The future use of MBD/FI as low level method could have the advantage that PBE-MBD/FI optimized structures are better starting points for structure optimizations at the hybrid QM:QM level.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work has been supported by German Science Foundation (DFG) within a Reinhart Koselleck grant to J. S. and by the “Fonds der Chemischen Industrie”. M. A. has been a member of the International Max-Planck Research School “Complex Surfaces in Materials Science”.References
- J. Sauer, P. Ugliengo, E. Garrone and V. Saunders, Chem. Rev., 1994, 94, 2095–2160 CrossRef CAS.
- J. Carrasco, J. Klimeš and A. Michaelides, J. Chem. Phys., 2013, 138, 024708 CrossRef PubMed.
- C. T. Campbell, Acc. Chem. Res., 2019, 52, 984–993 CrossRef CAS.
- C. Tuma and J. Sauer, Phys. Chem. Chem. Phys., 2006, 8, 3955–3965 RSC.
- J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901 CrossRef PubMed.
- S. Grimme, A. Hansen, J. G. Brandenburg and C. Bannwarth, Chem. Rev., 2016, 116, 5105–5154 CrossRef CAS PubMed.
- W. Liu, A. Tkatchenko and M. Scheffler, Acc. Chem. Res., 2014, 47, 3369–3377 CrossRef CAS.
- S. Kristyán and P. Pulay, Chem. Phys. Lett., 1994, 229, 175–180 CrossRef.
- R. Ahlrichs, R. Penco and G. Scoles, Chem. Phys., 1977, 19, 119–130 CrossRef CAS.
- J. Sauer and R. Zahradník, Int. J. Quantum Chem., 1984, 26, 793–822 CrossRef CAS.
- J. Sauer, H. Haberlandt and G. Pacchioni, J. Phys. Chem., 1986, 90, 3051–3052 CrossRef CAS.
- X. Wu, M. Vargas, S. Nayak, V. Lotrich and G. Scoles, J. Chem. Phys., 2001, 115, 8748–8757 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396 CrossRef CAS.
- T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097 CrossRef CAS PubMed.
- S. Svelle, C. Tuma, X. Rozanska, T. Kerber and J. Sauer, J. Am. Chem. Soc., 2008, 131, 816–825 CrossRef PubMed.
- J. Sauer, Acc. Chem. Res., 2019, 52, 3502–3510 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- A. Ambrosetti, A. M. Reilly, R. A. DiStasio and A. Tkatchenko, J. Chem. Phys., 2014, 140, 18A508 CrossRef PubMed.
- T. Bučko, S. Lebègue, J. Hafner and J. G. Ángyán, J. Chem. Theory Comput., 2013, 9, 4293–4299 CrossRef PubMed.
- T. Gould, S. Lebègue, J. G. Ángyán and T. Bučko, J. Chem. Theory Comput., 2016, 12, 5920–5930 CrossRef CAS PubMed.
- B. Tomáš, L. Sébastien, G. Tim and G. Á. János, J. Phys.: Condens. Matter, 2016, 28, 045201 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2011, 134, 044117 CrossRef PubMed.
- S. N. Steinmann and C. Corminboeuf, J. Chem. Theory Comput., 2011, 7, 3567–3577 CrossRef CAS PubMed.
- M. Dion, H. Rydberg, E. Schroder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- S. Tosoni and J. Sauer, Phys. Chem. Chem. Phys., 2010, 12, 14330–14340 RSC.
- B. M. Axilrod and E. Teller, J. Chem. Phys., 1943, 11, 299–300 CrossRef CAS.
- T. Bučko, S. Lebègue, J. Hafner and J. G. Ángyán, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 064110 CrossRef.
- A. Tkatchenko, R. A. DiStasio, R. Car and M. Scheffler, Phys. Rev. Lett., 2012, 108, 236402 CrossRef PubMed.
- M. W. Cole, D. Velegol, H.-Y. Kim and A. A. Lucas, Mol. Simul., 2009, 35, 849–866 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef.
- T. Bučko, S. Lebègue, J. G. Ángyán and J. Hafner, J. Chem. Phys., 2014, 141, 034114 CrossRef PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2006, 124, 014104 CrossRef PubMed.
- K. Tang and J. P. Toennies, J. Chem. Phys., 1984, 80, 3726–3741 CrossRef CAS.
- É. Brémond, N. Golubev, S. N. Steinmann and C. Corminboeuf, J. Chem. Phys., 2014, 140, 18A516 CrossRef PubMed.
- S. Gautier, S. N. Steinmann, C. Michel, P. Fleurat-Lessard and P. Sautet, Phys. Chem. Chem. Phys., 2015, 17, 28921–28930 RSC.
- W. Zhao, C. Chizallet, P. Sautet and P. Raybaud, J. Catal., 2019, 370, 118–129 CrossRef CAS.
- Y. Zhang and W. Yang, Phys. Rev. Lett., 1998, 80, 890 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- I. Hamada, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103 CrossRef.
- M. Alessio, D. Usvyat and J. Sauer, J. Chem. Theory Comput., 2018, 15, 1329–1344 CrossRef PubMed.
- A. Kundu, G. Piccini, K. Sillar and J. Sauer, J. Am. Chem. Soc., 2016, 138, 14047–14056 CrossRef CAS PubMed.
- K. Sillar, A. Kundu and J. Sauer, J. Phys. Chem. C, 2017, 121, 12789–12799 CrossRef CAS.
- G. Piccini, M. Alessio, J. Sauer, Y. Zhi, Y. Liu, R. Kolvenbach, A. Jentys and J. A. Lercher, J. Phys. Chem. C, 2015, 119, 6128–6137 CrossRef CAS.
- W. Mortier, J. Sauer, J. Lercher and H. Noller, J. Phys. Chem., 1984, 88, 905–912 CrossRef CAS.
- W. O. Haag, R. M. Lago and P. B. Weisz, Nature, 1984, 309, 589 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. Ugliengo and A. Damin, Chem. Phys. Lett., 2002, 366, 683–690 CrossRef CAS.
- E. D. Bloch, M. R. Hudson, J. A. Mason, S. Chavan, V. Crocellà, J. D. Howe, K. Lee, A. L. Dzubak, W. L. Queen and J. M. Zadrozny, J. Am. Chem. Soc., 2014, 136, 10752–10761 CrossRef CAS PubMed.
- L. Valenzano, B. Civalleri, K. Sillar and J. Sauer, J. Phys. Chem. C, 2011, 115, 21777–21784 CrossRef CAS.
- F. Göltl, A. Grüneis, T. Bučko and J. Hafner, J. Chem. Phys., 2012, 137, 114111 CrossRef PubMed.
- A. Puzder, M. Dion and D. C. Langreth, J. Chem. Phys., 2006, 124, 164105 CrossRef PubMed.
- T. J. Goncalves, P. N. Plessow and F. Studt, ChemCatChem, 2019, 11, 4368–4376 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp00394h |
| ‡ Present address: Institute of Physical Chemistry – Theoretical Chemistry Group, Karlsruhe Institute of Technology (KIT), Fritz-Haber-Weg 2, 76131 Karlsruhe, Germany. |
| § Present address: Department of Chemistry and Applied Bioscience, ETH Zürich, c/o USI Campus, Via Giuseppe Buffi 13, CH-6900 Lugano, Switzerland. |
| ¶ Present address: Department of Chemistry, University of Southern California, Los Angeles, California 90089-0482, USA. |
| This journal is © the Owner Societies 2020 |