Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Microfluidic out-of-equilibrium control of molecular nanotubes†
Björn
Kriete
,
Carolien J.
Feenstra
and
Maxim S.
Pshenichnikov
*
Zernike Institute for Advanced Materials, University of Groningen, Nijenborgh 4, 9747AG Groningen, The Netherlands. E-mail: m.s.pchenitchnikov@rug.nl
First published on 21st April 2020
Abstract
The bottom-up fabrication of functional nanosystems for light-harvesting applications and excitonic devices often relies on molecular self-assembly. Gaining access to the intermediate species involved in self-assembly would provide valuable insights into the pathways via which the final architecture has evolved, yet difficult to achieve due to their intrinsically short-lived nature. Here, we employ a lab-on-a-chip approach as a means to obtain in situ control of the structural complexity of an artificial light-harvesting complex: molecular double-walled nanotubes. Rapid and stable dissolution of the outer wall was realized via microfluidic mixing thereby rendering the thermodynamically unstable inner tubes accessible to spectroscopy. By measurement of the linear dichroism and time-resolved photoluminescence of both double-walled nanotubes and isolated inner tubes we show that the optical (excitonic) properties of the inner tube are remarkably robust to such drastic perturbation of the system's supramolecular structure as removal of the outer wall. The developed platform is readily extendable to a broad range of practical applications such as e.g. self-assembling systems and molecular photonics devices.
Introduction
Molecular self-assembly has become a key tool for the fabrication of functional nanomaterials and supramolecular structures for efficient transport of excitation energy.1–5 In order to understand, utilize and ultimately optimize their functional properties for light-harvesting applications, controlled modifications of the supramolecular structure are of vital importance. Traditionally, building blocks are ‘programmed’ such that they autonomously assemble into the desired structures that are held together by non-covalent forces such as van-der-Waals forces, hydrogen and halogen bonding, and π-stacking.6–8 The quest to make controlled changes of the self-assembly process, hence, typically targets the structure of individual building blocks in order to engineer the balance of the intermolecular interactions and thereby alter the equilibrium state of the final assembly.9,10In this context, amphiphilically driven self-assembly is of special interest, as changing the relative strength and size of the hydrophobic/hydrophilic moieties allows fine-tuning the final supramolecular structure towards micelles, bilayer sheets or nanofibers.11–13 A notable example of one of such systems is a class of amphiphilic cyanine derivatives that are known to self-assemble in aqueous solution into highly homogenous, double-walled nanotubes with outer and inner diameters of ∼13 nm and ∼7 nm, respectively, and lengths on the order of several μm's.9 These systems comprise a large number of strongly coupled chromophores leading to the formation of delocalized excited stated (Frenkel excitons), which is considered promising for quasi-one-dimensional excitonic wires.14–16 The interest in such systems is further propelled by their structural resemblance of natural light-harvesting antenna complexes such as the chlorosomes of green sulfur bacteria.17–19
While the final, thermodynamically stable outcome of the self-assembly can be modified via molecular engineering of the initial building blocks and is readily accessible via a number of characterization techniques, the intermediate stages are much harder to target due to their short-lived nature as out-of-equilibrium species. Nevertheless, understanding these transient stages of the self-assembly process would not only provide great insight into how to steer the process into a certain (otherwise inaccessible) direction, but also shed light on the functional properties of intermediate species as simplified components of the more complex final assembly. One strategy that has successfully been used to gain access to out-of-equilibrium species of a self-assembly system relies on microfluidics.20,21 For instance, it has been used for real time monitoring22–24 and control25,26 of chemical reactions, following mixing reactions,27,28 steer molecular self-assembly29,30 and study (out-of-equilibrium) reactions in biological systems.31–33
In this paper, we use a lab-on-a-chip approach as a means to achieve out-of-equilibrium control over the structural hierarchy of an artificial light-harvesting complex: double-walled molecular nanotubes. Structural simplification of such nanotubes has previously been demonstrated in bulk solution by dissolving the outer tube via flash-dilution thereby exposing the bare inner tube for linear absorption spectroscopy.34,35 However, a rapid partial recovery of the original double-walled structure (within ∼60 s) leaves no time for more advanced and therefore informative spectroscopies. Here, we successfully transfer the flash-dilution technique to a microfluidic platform to achieve stable and continuous removal of the outer layer of the supramolecular assembly. Linear dichroism and time-resolved photoluminescence (PL) experiments demonstrated that the inner nanotube alone retains its excitonic functionality despite such drastic modifications of the supramolecular structure.
Experimental
Materials and sample preparation
The dye 3,3′-bis(2-sulfopropyl)-5,5′,6,6-tetrachloro-1,1′-dioctylbenzimidacarbocyanine (C8S3, M = 903 g mol−1) was purchased from FEW Chemicals GmbH (Wolfen, Germany) and used as received. C8S3 nanotubes were prepared via the alcoholic route.9 The molecules were first dissolved in pure methanol (MeOH, Biosolve) to form 2.32 mM stock solutions. Addition of Milli-Q water to the methanolic stock solution (1 ml![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.26 ml) induced aggregation of molecules into double-walled nanotubes. The resulting solution was gently shaken and stored in the dark at room temperature. After a variable timespan between 12 and 24 hours the nanotube solution was further diluted by addition of 1 ml of Milli-Q water rendering a final dye concentration in the nanotube solution of 0.267 mM and MeOH content of 9 wt% (11 vol%). Sample solutions were used within three days for experiments to minimize the thermodynamically induced formation of thicker bundles; see e.g.ref. 35 for more details.
0.26 ml) induced aggregation of molecules into double-walled nanotubes. The resulting solution was gently shaken and stored in the dark at room temperature. After a variable timespan between 12 and 24 hours the nanotube solution was further diluted by addition of 1 ml of Milli-Q water rendering a final dye concentration in the nanotube solution of 0.267 mM and MeOH content of 9 wt% (11 vol%). Sample solutions were used within three days for experiments to minimize the thermodynamically induced formation of thicker bundles; see e.g.ref. 35 for more details.
Steady-state absorption and photoluminescence (PL)
Steady-state UV-Vis absorption and PL spectra were measured in 1 mm and 10 mm quartz cuvettes (Starna GmbH, Germany) using a PerkinElmer Lambda 900 UV/VIS/NIR spectrometer and a PerkinElmer LS50B Luminescence spectrometer (spectral resolution ∼75 cm−1), respectively. For recording the PL spectra, the sample was excited at λexc = 561 nm. Prior to absorption (PL) measurements, sample solutions were diluted with Milli-Q water by factor ∼3.5 (∼400). The latter rendered a maximum optical density of the sample of 0.1–0.2.Microfluidic flash-dilution
Microfluidic flash-dilution was realized by mixing neat nanotube sample solution with a mixture of H2O and methanol (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume) in a commercially available tear-drop micromixer (micronit, The Netherlands; manufactured from borosilicate glass) at a flowrate ratio of 5
1 by volume) in a commercially available tear-drop micromixer (micronit, The Netherlands; manufactured from borosilicate glass) at a flowrate ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7. This micromixer is specifically designed for efficient mixing of two reagents at low Reynolds numbers (Re ≈ 1) by folding the flow upon itself multiple times.36 The parent reagents were supplied by two syringe pumps (New Era, model NE-300), which continuously pumped the solutions through the microfluidic channel (thickness 150 μm, width 200 μm). In a typical experiment with a total flowrate of 600 μl h−1 the mixing time was estimated as ∼12 s assuming a uniform flow-speed profile across the entire cross-section of the microfluidic channel. This specific flowrate was chosen as a compromise between sample refresh rate for spectroscopic experiments (to avoid unwanted effects such as photobleaching) and sample consumption that limits the maximum duration of experiments (up to ∼30 hours under these settings).
7. This micromixer is specifically designed for efficient mixing of two reagents at low Reynolds numbers (Re ≈ 1) by folding the flow upon itself multiple times.36 The parent reagents were supplied by two syringe pumps (New Era, model NE-300), which continuously pumped the solutions through the microfluidic channel (thickness 150 μm, width 200 μm). In a typical experiment with a total flowrate of 600 μl h−1 the mixing time was estimated as ∼12 s assuming a uniform flow-speed profile across the entire cross-section of the microfluidic channel. This specific flowrate was chosen as a compromise between sample refresh rate for spectroscopic experiments (to avoid unwanted effects such as photobleaching) and sample consumption that limits the maximum duration of experiments (up to ∼30 hours under these settings).
For spectroscopic measurements (linear dichroism and time-resolved PL) the (flash-diluted) sample solution was relayed to a second, thin-bottom flowcell (micronit, The Netherlands; borosilicate glass) with a channel thickness of 50 μm and a channel width of 500 μm connected by ∼15 cm of tubing (Teflon, channel diameter 250 μm). This flowcell allowed conducting spectroscopic experiments in transmission, as e.g. linear dichroism (vide infra) which was not possible in the micromixer because of the curved channel profile. Both the micromixer and the flowcell were used as received from the manufacturer without any additional surface treatment. Blockage of the channel or surface sticking of the sample were not observed, as these would have immediately been reflected in the gradual increase or decrease of the optical density of the sample.
For the measurements on the double-walled nanotubes, the diluting agent was replaced by Milli-Q water, operated at the same flow rate as in flash-dilution experiments. Under these conditions the maximum optical density of the sample solution was between 0.1 and 0.2 to avoid PL reabsorption.
Results and discussion
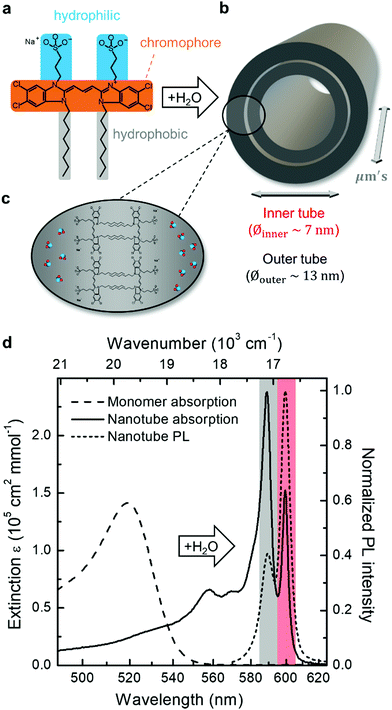
The formation of double-walled nanotubes from dissolved C8S3 molecules (Fig. 1a–c) is evident from formation of several narrow excitonic peaks in the absorption spectrum and a strong spectral red-shift (∼75 nm, 2400 cm−1) relative to the monomer spectrum (Fig. 1d) due to strong intermolecular couplings. The most distinct peaks at ∼590 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 cm−1) and ∼600 nm (16
950 cm−1) and ∼600 nm (16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 cm−1) are associated with absorption of the outer and inner tube of the double-walled assembly, respectively.10,34 The spectral separation of these peaks provides a straightforward way of identifying changes to either tube, which has been utilized in previous spectro-chemical studies as well as bulk flash-dilution experiments by quenching the spectral response from the outer tube.34,35,37,38 The band of higher-lying transitions between ∼550 nm and ∼580 nm has a mixed character with overlapping contributions from both inner and outer tubes.34,37
670 cm−1) are associated with absorption of the outer and inner tube of the double-walled assembly, respectively.10,34 The spectral separation of these peaks provides a straightforward way of identifying changes to either tube, which has been utilized in previous spectro-chemical studies as well as bulk flash-dilution experiments by quenching the spectral response from the outer tube.34,35,37,38 The band of higher-lying transitions between ∼550 nm and ∼580 nm has a mixed character with overlapping contributions from both inner and outer tubes.34,37
The same peak assignment also holds for the PL spectrum (Fig. 1, short dashed line), where the reversed peak ratio (i.e., Iinner > Iouter) is a consequence of the equilibration of the exciton populations between both tubes on a sub-ps timescale prior to PL.39–41 The higher-frequency transitions are not observed in PL as they quickly (within ∼100 fs) relax to the two lowest-energy states.
Dissolution of the outer tube of double-walled nanotubes is achieved in a tear-drop micromixer (Fig. 2a) via mixing of the two parent reactants, i.e., a H2O/MeOH diluting agent (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 by volume), and nanotube sample solution. Efficient intermixing of the two reactants in the mixing zone of the micromixer is evident from the wide-field PL images superimposed with bright-field microscope images of the microfluidic channel. Here the laminar flow regime (Fig. 2b, top) and mixed phase (Fig. 2b, bottom) can clearly be distinguished. This rapid mixing induces flash-dilution during which the outer layer is dissolved from the double-walled nanotubes.34,35 Note that the PL signal after flash-dilution does not contain any contribution from dissolved C8S3 monomers, because their absorption is not in resonance with the excitation wavelength (λexc = 561 nm); see ESI,† Section S3 for results using a different excitation wavelength.
1 by volume), and nanotube sample solution. Efficient intermixing of the two reactants in the mixing zone of the micromixer is evident from the wide-field PL images superimposed with bright-field microscope images of the microfluidic channel. Here the laminar flow regime (Fig. 2b, top) and mixed phase (Fig. 2b, bottom) can clearly be distinguished. This rapid mixing induces flash-dilution during which the outer layer is dissolved from the double-walled nanotubes.34,35 Note that the PL signal after flash-dilution does not contain any contribution from dissolved C8S3 monomers, because their absorption is not in resonance with the excitation wavelength (λexc = 561 nm); see ESI,† Section S3 for results using a different excitation wavelength.
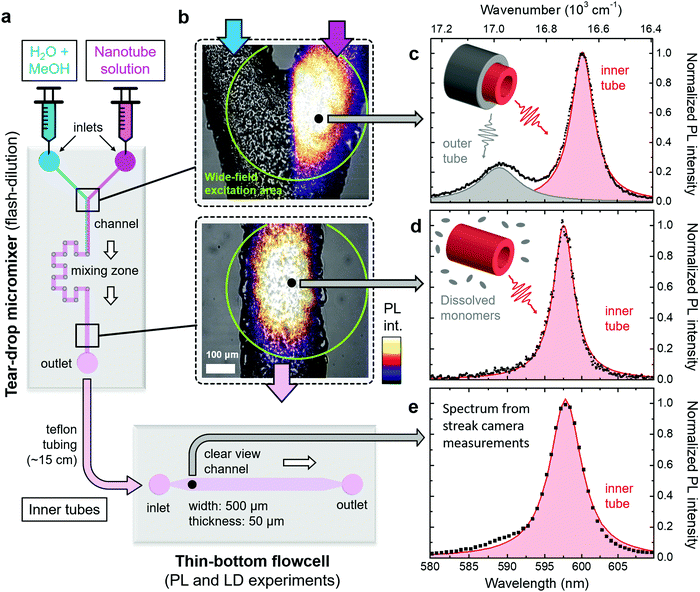 | ||
| Fig. 2 Overview of microfluidic setup. (a) Schematic of the micromixer and flowcell used in this study. The flow direction of the sample is indicated by the white arrows. (b) Microscope images of two sections of the micromixer marked in panel (a). The upper and lower panels show the Y-junction before and the microfluidic channel behind the mixing zone, respectively. The bright-field microscope images (in black and white) are superimposed with wide-field excitation PL images following excitation at λexc = 561 nm; ESI,† Section S6. The wide-field excitation area is indicated by green circles in both panels. The bottom panel corresponds to a mixing time of ∼12 s. (c)–(e) Steady-state PL spectra (black dots) of double-walled nanotubes (top) and isolated inner tubes (center and bottom) following tightly focused excitation at λexc = 561 nm at the spots indicated in panel (b). The PL spectrum in panel (e) was obtained from streak camera measurements (spectral resolution 85 cm−1). The shaded peaks (red: inner tube; gray: outer tube) are obtained by fitting the PL spectra to a sum of two (black line) and a single Lorentzian lineshape(s) in the case of double-walled nanotubes and isolated inner tubes, respectively. Insets: Schematics of double and single-walled nanotubes, which illustrate the origin of the observed peaks in the PL spectra. | ||
After flash-dilution, the isolated inner tubes are in a thermodynamically unfavourable configuration, since the hydrophobic side-group are now directly exposed to the H2O/MeOH environment. This out-of-equilibrium configuration leads to a quick partial recovery of the outer tube on a timescale of tens of seconds via re-attachment of the dissolved monomers to the exterior of the isolated inner tubes. This process continues until a new equilibrium between monomers and nanotubes is established that is dictated by the solvent composition after flash-dilution (ESI,† Section S4). The longer-time (tens of minutes later) consequences of this process can be monitored using absorption spectroscopy (ESI,† Section S4) or cryo-TEM imaging (ESI,† Section S5). To the best of our knowledge, this re-assembly of the outer layer can neither be restricted nor halted. However, by using the microfluidics platform, it is possible to spatially separate the regions where the isolated inner tubes are continuously being produced, from the region where the outer layer starts to recover. This approach, thus, enables spectroscopy on the clean isolated inner tubes for which the attainable experimental time (i.e., supply time of isolated inner tubes) is only limited by the amount of sample solutions (up to ∼30 hours in practice). This way, microfluidic flash-dilution can also be interfaced with other, more advanced and often time-consuming types of spectroscopy, e.g., 2D spectroscopy.28,42
In order to verify the successful dissolution of the outer tube upon microfluidic flash-dilution we use the spectral band assignment in the steady-state nanotube PL spectra (Fig. 2c–e). These PL spectra prove that the high energy band (∼590 nm, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 cm−1) corresponding to the outer tube is almost completely eliminated after microfluidic mixing, while the spectral signature of the inner tubes (∼600 nm, 16
950 cm−1) corresponding to the outer tube is almost completely eliminated after microfluidic mixing, while the spectral signature of the inner tubes (∼600 nm, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 cm−1) is preserved. The similarity of the PL spectra at the exit of the micromixer and in the thin-bottom flowcell (given lower spectral resolution in the latter case) proves negligible recovery of the outer layer in the relaying tubing. The weak shoulder on the blue flank (around ∼590 nm) of the inner tube PL spectrum (Fig. 2d and e) is due to a small number of residual undissolved parts of the outer nanotube layer.
670 cm−1) is preserved. The similarity of the PL spectra at the exit of the micromixer and in the thin-bottom flowcell (given lower spectral resolution in the latter case) proves negligible recovery of the outer layer in the relaying tubing. The weak shoulder on the blue flank (around ∼590 nm) of the inner tube PL spectrum (Fig. 2d and e) is due to a small number of residual undissolved parts of the outer nanotube layer.
Upon flash-dilution the PL peak of isolated inner tubes undergoes a small spectral blue-shift of about 50 cm−1 relative to the case of double-walled nanotubes. Such behaviour has also previously been reported for conventional ‘bulk’ flash-dilution experiments.34,35,42 We hypothesize that the sudden dissolution of the outer tube may lead to slight decrease of the inner tube radius and, consequently shift its absorption/PL spectrum. Substantial shortening of the nanotubes (down to sub-100 nm length, where the nanoconfinment effects are expected to occur43) can be excluded as the reason for this blue-shift, because no short fragments were found in PL microscopy images recorded directly after flash-dilution (ESI,† Section S6).
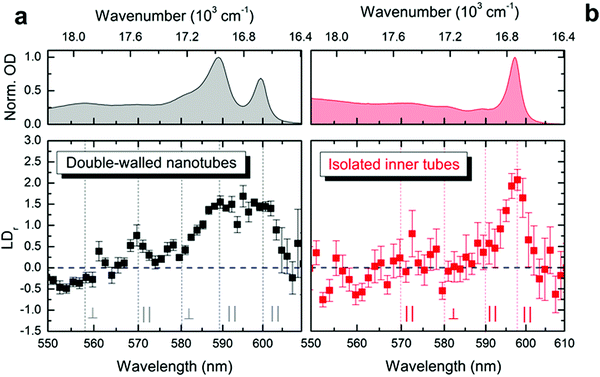
The exciton transition dipole moments associated with different peaks in the nanotubes’ absorption spectrum (Fig. 1d) have different alignment along the nanotube.10,34,37 This leads to linear dichroism in absorption (providing the nanotubes are aligned along a certain direction) which can be used as an indication for retaining the exciton properties upon flash-dilution. The nanotubes tend to flow-align in a microfluidics channel owing to their large aspect ratio (μm length versus ∼13 nm diameter); similar alignment effects have previously been observed for other systems.44–47 The reduced linear dichroism (LDr) spectra (Fig. 3) were obtained by recording the absorption spectra with light polarized parallel and perpendicular to the flow direction in the microfluidic channel; a detailed description of the experimental apparatus and data processing protocol is given in the ESI,† Section S1. The alignment of double-walled nanotubes along the flow is evident from the pronounced positive amplitude peaks in the LDr spectrum at the spectral positions of the outer (at ∼590 nm, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 cm−1) and inner tube (at ∼600 nm, 16
950 cm−1) and inner tube (at ∼600 nm, 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 670 cm−1) absorption peaks (Fig. 3a). This proves that the nanotubes efficiently flow-align despite the lower flow speeds reached in microfluidics as compared to conventional flow cuvettes.37 These data also reveal the mixed polarization character (i.e., both parallel and perpendicular) of the absorption peaks towards shorter wavelengths between 550 nm and 580 nm; both shape and amplitude of the measured LDr spectra agree remarkably well with previous findings.37
670 cm−1) absorption peaks (Fig. 3a). This proves that the nanotubes efficiently flow-align despite the lower flow speeds reached in microfluidics as compared to conventional flow cuvettes.37 These data also reveal the mixed polarization character (i.e., both parallel and perpendicular) of the absorption peaks towards shorter wavelengths between 550 nm and 580 nm; both shape and amplitude of the measured LDr spectra agree remarkably well with previous findings.37
After flash-dilution the maximal LDr amplitude (of ∼2.1 ± 0.2; mean ± standard error) of the inner tube transition is retained (Fig. 3b), which shows that the excitonic character of the main absorption peak is preserved even upon complete removal of the outer tube. Strong alignment of the flash-diluted nanotubes along the flow direction also indicates that the nanotubes are not substantially shortened during flash-dilution. Unlike for double-walled nanotubes, any low amplitude LDr peaks occurring at shorter wavelengths cannot be distinguished given the signal-to-noise ratio of the data, which is limited by the low molar concentration of nanotubes after flash-dilution and the channel thickness of only 50 μm.
Next, we study the exciton dynamics of double-walled nanotubes and isolated inner tubes. Hereby, we utilize the fact that under intense laser excitation excitons start to mutually interact leading to exciton–exciton annihilation (EEA).48,49 The probability that two excitons are able to meet and consequently annihilate depends on the exciton density (i.e., the number of excitons per number of molecules; ESI,† Section S7) as well as the excitonic properties of the system, such as exciton delocalization and exciton diffusion. EEA then opens a new non-radiative (and intensity dependent) decay channel for excitons,50–52 which leads to acceleration of the observed PL dynamics. In multi-chromophoric systems excitons are collectively shared by many molecules so that it can be experimentally challenging to reach sufficiently low exciton densities to isolate the true response of single excitons, while avoiding EEA. In this regard, time-resolved PL offers unprecedented sensitivity down to extremely low exciton densities (as low as 1 exciton per ∼106 chromophores).
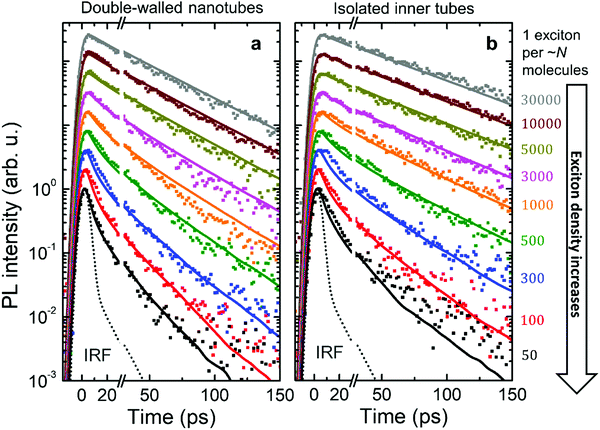
Fig. 4 shows the PL transients obtained by spectrally integrating the PL decay maps between 588–603 nm for double-walled nanotubes and 598–603 nm for isolated inner tubes (a schematic of the experimental setup and a few representative PL decay maps are shown in the ESI,† Sections S2 and S8, respectively). In the case of double-walled nanotubes, the PL transients of the inner and outer layer are identical, except for their different amplitudes, which is why only one set of PL transients is shown for both inner and outer tube. This observation is further corroborated by the fact that no spectral relaxation of the PL mean frequency is observed (ESI,† Section S8) at any excitation intensity. Had spectral relaxation on the timescale of PL been the case (due to e.g. ‘slow’ exciton transfer between the two tubes), the mean frequency would have dynamically shifted.53–55
At low exciton densities the PL of double-walled nanotubes (Fig. 4a) and isolated inner tubes (Fig. 4b) decays mono-exponentially with time constants of 43 ± 1 ps and 58 ± 1 ps, respectively. These time constants are independent of the excitation intensity, because the large average distance between the excitons – 1 exciton per ∼10 μm of nanotube length (containing 106 molecules) at the lowest intensity – prevents EEA. The observed increase of the lifetime of isolated inner tubes agrees well with previous spectro-chemical studies on nanotubes embedded in a sugar matrix,38 where the spectral response of the outer layer was quenched via oxidation with silver nitrate. We hypothesize that the presence of the outer layer may open an additional non-radiative decay channel for excitons and, thus, lead to a reduced PL lifetime in the case of double-walled nanotubes.
At high exciton densities, the PL transients of double-walled nanotubes and isolated inner tubes become increasingly multi-exponential, which is a typical fingerprint of EEA.48,52 After a rapid initial decay of the PL signal due to prominent EEA, the dynamics slow down as the surviving excitons become sparser and hence less likely to meet and annihilate. We will use these two time intervals to quantify the PL dynamics separately. In the first interval (up to 30 ps), we extract the PL lifetimes of double-walled nanotubes as well as isolated inner tubes by fitting the transients to a convolution of an exponential decay and a Gaussian apparatus function (as an approximation of the IRF; Fig. 4). In the second interval (30–150 ps), the tails of the PL transients are fitted to an exponential decay F(t) = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−t/τ). In both cases, the PL decay rate is determined as the inverse lifetime τ−1, normalized to the intrinsic (non-)radiative decay rate and plotted as a function of exciton density (Fig. 5a and b).
exp(−t/τ). In both cases, the PL decay rate is determined as the inverse lifetime τ−1, normalized to the intrinsic (non-)radiative decay rate and plotted as a function of exciton density (Fig. 5a and b).
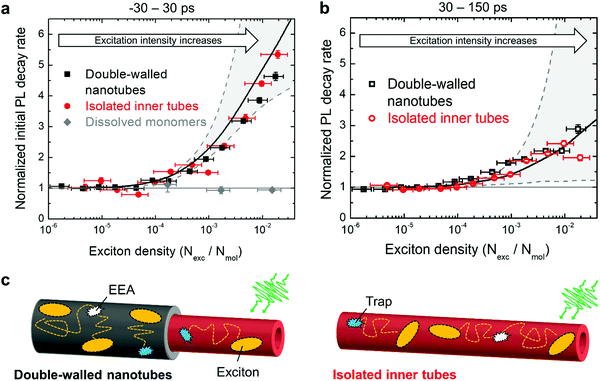 | ||
| Fig. 5 Acceleration of PL dynamics. (a) and (b) experimental PL decay rates of double-walled nanotubes (black dots), isolated inner tube (red dots) and dissolved monomers (gray dots; ESI,† Section S9) as a function of exciton density in the first interval (−30 → 30 ps) and in the second interval (30 → 150 ps), respectively. The decay rates are normalized to the intrinsic (non-)radiative decay rate. The vertical error bars refer to the standard deviation of the respective fit. The horizontal error bars for the exciton density are obtained from propagation of uncertainty of all input parameters (ESI,† Section S7). Solid and dashed lines in panels (a) and (b) are derived from Monte-Carlo simulations. The solid black lines originate from the Monte-Carlo simulated transients (solid lines in Fig. 4). The dashed gray lines refer to the lower and upper limits of the acceleration of the PL decay (see main text for explanation); the region between these limits is shaded in gray for illustration. (c) Schematic representation of diffusion-assisted EEA on double-walled nanotubes (left) and isolated inner tubes (right). Excitons are depicted as yellow ellipses. Exciton diffusion (dotted paths) allows excitons to meet and annihilate (white symbols) or encounter a non-radiative trap state (blue symbols), both immediately quench the exciton. | ||
In the first time interval, PL of both double-walled nanotubes and isolated inner tubes feature a steep increase of the PL decay rate for exciton densities exceeding 1 exciton per ∼104 molecules (Fig. 5a), which corresponds to 1 exciton per ∼100 nm of the nanotube length. This value marks the onset of EEA, which refers to the critical exciton density at which excitons are able to undergo diffusion-assisted EEA. Below that threshold excitons are statistically spaced too far apart so that they hardly meet during their lifetime.
A similar behaviour is observed in the second interval, but with a shallower acceleration of the PL dynamics (Fig. 5b). Conceptually, this agrees with the previous assignment that the initial interval is dominated by EEA, while the second interval is less affected due to an already depleted exciton population. Note that the occurrence of EEA faster than the temporal resolution of the streak camera (∼7 ps) is manifested in a sub-linear scaling behaviour of the initial PL amplitude (ESI,† Section S8).
Comparison of the intensity-dependent acceleration of PL of double-walled nanotubes and isolated inner tubes reveals that independently of the chosen spectroscopic observable (PL decay rate and amplitude) the response of both systems is virtually identical at all exciton densities. This implies that the excitonic properties of the inner tube are robust towards stripping the outer layer and, hence, long-range exciton transport as a crucial factor for the occurrence of EEA, is not compromised (Fig. 5c). If the exciton transport had been compromised by complete dissolution of the nanotubes into diluted non-interacting molecules, no exciton density dependence would have been observed (Fig. 5a, gray dots).
To model the observed PL dynamics, we use Monte-Carlo (MC) simulations of the exciton populations; an elaborate description of the MC simulations including a complete overview of the model and parameters has been published elsewhere.42 In essence, at time zero (marked by the arrival of the laser pulse at the sample) excitons are planted on a molecular grid representing the inner and (in the case of double-walled nanotubes) outer tube. The number of planted excitons is set in accordance with the experimental exciton density. Thereafter, excitons perform a random walk on the molecular grid during which they can hop between the inner and outer tube at a given transfer rate, decay (non-)radiatively according to their lifetime or undergo EEA once two excitons approach closer than a critical distance (the annihilation radius). The PL intensity at a given time in the simulation is evaluated as the number of remaining excitons. For comparison with experiment the PL transients are convoluted with a Gaussian apparatus function (FWHM ≈ 7 ps). The PL decay rates are obtained by applying the same fitting protocol as for the experimental data to the thus obtained transients.
Under these settings, MC simulations satisfactorily reproduce the initial (fast) PL dynamics (Fig. 5a, lower dashed line), but totally fail to capture the PL tails at high excitation densities (Fig. 5b, lower dashed line; and ESI,† Section S10). The reason for this is that towards the end of the first time interval (i.e., around ∼30 ps) the exciton density is already too depleted for further EEA, as most of the excitons have either decayed naturally or annihilated. Therefore, we are forced to conclude that the acceleration of the PL tail is unlikely caused by EEA. We also eliminated experimentally two other foreseeable reasons for such acceleration: accumulated photobleaching (ESI,† Section S11) and temperature dependence of the non-radiative decay (ESI,† Section S12).
As a possible scenario to explain the intensity dependent acceleration of the PL tails, we explore the formation of light-induced non-radiative trap states (or simply traps). Traps such as chemical impurities or morphological dislocations are known to act as quenching sites for excitons (as schematically depicted in Fig. 5c) and, thus, have profound impact on the exciton lifetime.56–60 For instance, it has been shown in a recent study61 that light exposure of the double-walled nanotubes embedded in a sugar matrix leads to reversible changes of their optical properties. Here, we include such possibility by allowing molecular grid sites to be converted into traps with probability P upon the decay (either naturally or due to EEA) of an exciton on that site, which thereafter is labelled as a trap until the end of the simulation run. Diffusion of another exciton onto a trap then causes the immediate death of that exciton. In the MC simulations, the probability P evolves according to:
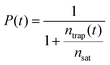 | (1) |
At low trap density, ntrap(t) ≪ nsat so that the probability to convert the site into the trap is unity, P(t) = 1. At high trap density (ntrap(t) ≫ nsat) the probability reduces to naught. Therefore, the saturation trap density implies a finite number of the molecular sites which can be converted into traps (‘weak links’). The trap formation is reversible in the sense that they fully recover before arrival of the next excitation laser pulse (after ∼12 ns), as otherwise accumulation effects would have been observed, which is not the case (ESI,† Sections S11 and S12). The photochemical mechanism behind the light-induced trap formation might be, for instance, photo-isomerization of the chromophore via a conical intersection.62–64
In our simulations nsat was the only fitting parameter; all other parameters (hopping rate, annihilation radius, etc.) were fixed according to ref. 42. The resulting transients from MC simulations are shown in Fig. 4 superimposed with the experimental data. Setting nsat = 10−4 yielded the most satisfactory global fit of all PL transients (Fig. 4) and PL decay rates (Fig. 5a and b) of both isolated inner tubes and double-walled nanotubes despite the simplicity of the model. This value of nsat implies that conversion of only one C8S3 molecule out of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 into a trap leads to substantial PL quenching, which is consistent with high exciton mobilities.14,15,42 Note that neglecting the saturation of the trap density does not lead to a satisfactory description of the experimental data (upper dashed lines in Fig. 5a and b, and ESI,† Section S10). Nevertheless, the origin of the saturation behaviour of the number of available light-induced traps still remains debatable.
000 into a trap leads to substantial PL quenching, which is consistent with high exciton mobilities.14,15,42 Note that neglecting the saturation of the trap density does not lead to a satisfactory description of the experimental data (upper dashed lines in Fig. 5a and b, and ESI,† Section S10). Nevertheless, the origin of the saturation behaviour of the number of available light-induced traps still remains debatable.
Conclusions
In conclusion, we have successfully transferred flash-dilution technique into a microfluidic platform to achieve real-time control over the supramolacular complexity of double-walled molecular nanotubes. By combining microfluidics with optical measurements, we have shown that isolated inner tubes retain their optical (excitonic) properties upon aggressive flash-dilution of the outer wall. In other words, excitonic properties of the inner nanotube are remarkably robust against perturbations of the supramolecular structure such as removal of the adjacent nanotube layer and exposure of the inner layer to the surrounding. Such excitonic robustness has previously been reported upon bundling of several nanotubes into complex superstructures, so-called bundles.35 Here, we have demonstrated similar excitonic robustness for the opposite direction: single-walled nanotubes as a simplified component of the more complex double-walled system.Our findings underpin the versatility of the microfluidic approach to manipulate a nanoscale system via controlled reduction of the complexity of its hierarchical supramolecular structure. Working in tandem with ultrafast spectroscopy, this approach opens up unprecedented opportunities to study exciton dynamics in complex self-assembling molecular systems.
Author contributions
B. K. and M. S. P. have devised the project and designed the microfluidic experiments. The samples were prepared by B. K. and C. F. C. F. conducted the linear dichroism experiments and analyzed the data; the analysis was supervised by B. K. B. K. performed all other experiments, analyzed the experimental data and performed Monte-Carlo simulations under supervision of M. S. P. B. K. and M. S. P. co-wrote the manuscript with a contribution from C. F.Conflicts of interest
The authors declare no competing financial interests.Acknowledgements
B. K. and M. S. P. gratefully acknowledge numerous discussions with A. S. Bondarenko, T. L. C. Jansen, and J. Knoester. F. de Haan is greatly acknowledged for writing the code for Monte-Carlo simulations as well as general laboratory assistance. We also thank V. V. Krasnikov for his help with designing, building and characterizing the microscopy setup. B. K. and M. S. P. acknowledge funding by the Dieptestrategie Programme of the Zernike Institute for Advanced Materials (University of Groningen, The Netherlands).References
- T. Aida, E. W. Meijer and S. I. Stupp, Science, 2012, 335, 813–817 CrossRef CAS PubMed.
- S. Seki, A. Saeki, T. Sakurai and D. Sakamaki, Phys. Chem. Chem. Phys., 2014, 16, 11093–11113 RSC.
- J.-L. Brédas, E. H. Sargent and G. D. Scholes, Nat. Mater., 2017, 16, 35–44 CrossRef PubMed.
- M. R. Wasielewski, Acc. Chem. Res., 2009, 42, 1910–1921 CrossRef CAS PubMed.
- A. T. Haedler, K. Kreger, A. Issac, B. Wittmann, M. Kivala, N. Hammer, J. Köhler, H. W. Schmidt and R. Hildner, Nature, 2015, 523, 196–199 CrossRef CAS PubMed.
- F. J. M. Hoeben, P. Pascal Jonkheijm, E. W. Meijer and A. P. H. J. Schenning, Chem. Rev., 2005, 105, 1491–1546 CrossRef CAS PubMed.
- A. Priimagi, G. Cavallo, A. Forni, M. Gorynsztejn-Leben, M. Kaivola, P. Metrangolo, R. Milani, A. Shishido, T. Pilati, G. Resnati and G. Terraneo, Adv. Funct. Mater., 2012, 22, 2572–2579 CrossRef CAS.
- F. Würthner, Acc. Chem. Res., 2016, 49, 868–876 CrossRef PubMed.
- H. von Berlepsch, S. Kirstein, R. Hania, A. Pugžlys and C. Böttcher, J. Phys. Chem. B, 2007, 111, 1701–1711 CrossRef CAS PubMed.
- B. Kriete, A. S. Bondarenko, V. R. Jumde, L. E. Franken, A. J. Minnaard, T. L. C. Jansen, J. Knoester and M. S. Pshenichnikov, J. Phys. Chem. Lett., 2017, 8, 2895–2901 CrossRef CAS PubMed.
- J. D. Hartgerink, E. Beniash and S. I. Stupp, Science, 2001, 294, 1684–1688 CrossRef CAS PubMed.
- C. Wang, Z. Wang and X. Zhang, Acc. Chem. Res., 2012, 45, 608–618 CrossRef CAS PubMed.
- M. Ramanathan, L. K. Shrestha, T. Mori, Q. Ji, J. P. Hill and K. Ariga, Phys. Chem. Chem. Phys., 2013, 15, 10580–10611 RSC.
- K. A. Clark, E. L. Krueger and D. A. Vanden Bout, J. Phys. Chem. Lett., 2014, 5, 2274–2282 CrossRef CAS PubMed.
- J. R. Caram, S. Doria, D. M. Eisele, F. S. Freyria, T. S. Sinclair, P. Rebentrost, S. Lloyd and M. G. Bawendi, Nano Lett., 2016, 16, 6808–6815 CrossRef CAS PubMed.
- F. S. Freyria, J. M. Cordero, J. R. Caram, S. Doria, A. Dodin, Y. Chen, A. P. Willard and M. G. Bawendi, Nano Lett., 2017, 17, 7665–7674 CrossRef CAS PubMed.
- J. Dostál, T. Mančal, R. Augulis, F. Vácha, J. Pšenčík and D. Zigmantas, J. Am. Chem. Soc., 2012, 134, 11611–11617 CrossRef PubMed.
- G. S. Orf and R. E. Blankenship, Photosynth. Res., 2013, 116, 315–331 CrossRef CAS PubMed.
- L. M. Günther, M. Jendrny, E. A. Bloemsma, M. Tank, G. T. Oostergetel, D. A. Bryant, J. Knoester and J. Köhler, J. Phys. Chem. B, 2016, 120, 5367–5376 CrossRef PubMed.
- G. M. Whitesides, Nature, 2006, 442, 368–373 CrossRef CAS PubMed.
- S. Sevim, A. Sorrenti, C. Franco, S. Furukawa, S. Pané, A. J. Demello and J. Puigmartí-Luis, Chem. Soc. Rev., 2018, 47, 3788–3803 RSC.
- M. Bonn, H. J. Bakker, G. Rago, F. Pouzy, J. R. Siekierzycka, A. M. Brouwer and D. Bonn, J. Am. Chem. Soc., 2009, 131, 17070–17071 CrossRef CAS PubMed.
- K. L. A. Chan, X. Niu, A. J. de Mello and S. G. Kazarian, Lab Chip, 2010, 10, 2170–2174 RSC.
- K. L. A. Chan and S. G. Kazarian, Anal. Chem., 2012, 84, 4052–4056 CrossRef CAS PubMed.
- H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 7336–7356 CrossRef CAS PubMed.
- A. J. DeMello, Nature, 2006, 442, 394–402 CrossRef CAS PubMed.
- R. K. P. Benninger, O. Hofmann, J. McGinty, J. Requejo-Isidro, I. Munro, M. A. A. Neil, A. J. deMello and P. M. W. French, Opt. Express, 2005, 13, 6275 CrossRef CAS PubMed.
- K. M. Tracy, M. V. Barich, C. L. Carver, B. M. Luther and A. T. Krummel, J. Phys. Chem. Lett., 2016, 7, 4865–4870 CrossRef CAS PubMed.
- Z. A. Arnon, A. Vitalis, A. Levin, T. C. T. Michaels, A. Caflisch, T. P. J. Knowles, L. Adler-Abramovich and E. Gazit, Nat. Commun., 2016, 7, 13190 CrossRef CAS PubMed.
- A. Sorrenti, R. Rodriguez-Trujillo, D. B. Amabilino and J. Puigmartí-Luis, J. Am. Chem. Soc., 2016, 138, 6920–6923 CrossRef CAS PubMed.
- D. J. Beebe, G. A. Mensing and G. M. Walker, Annu. Rev. Biomed. Eng., 2002, 4, 261–286 CrossRef CAS PubMed.
- S. Maillot, A. Carvalho, J.-P. Vola, C. Boudier, Y. Mély, S. Haacke and J. Léonard, Lab Chip, 2014, 14, 1767–1774 RSC.
- A. Chauvet, T. Tibiletti, S. Caffarri and M. Chergui, Rev. Sci. Instrum., 2014, 85, 103118 CrossRef PubMed.
- D. M. Eisele, C. W. Cone, E. A. Bloemsma, S. M. Vlaming, C. G. F. van der Kwaak, R. J. Silbey, M. G. Bawendi, J. Knoester, J. P. Rabe and D. A. Vanden Bout, Nat. Chem., 2012, 4, 655–662 CrossRef CAS PubMed.
- D. M. Eisele, D. H. Arias, X. Fu, E. A. Bloemsma, C. P. Steiner, R. A. Jensen, P. Rebentrost, H. Eisele, A. Tokmakoff, S. Lloyd, K. A. Nelson, D. Nicastro, J. Knoester and M. G. Bawendi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, E3367–E3375 CrossRef CAS PubMed.
- V. Viktorov and M. Nimafar, J. Micromech. Microeng., 2013, 23, 55023 CrossRef.
- K. A. Clark, C. W. Cone and D. A. Vanden Bout, J. Phys. Chem. C, 2013, 117, 26473–26481 CrossRef CAS.
- R. Pandya, R. Chen, A. Cheminal, T. H. Thomas, A. Thampi, A. Tanoh, J. M. Richter, R. Shivanna, F. Deschler, C. Schnedermann and A. Rao, J. Phys. Chem. Lett., 2018, 9, 5604–5611 CrossRef CAS PubMed.
- A. Pugžlys, R. Augulis, P. H. M. Van Loosdrecht, C. Didraga, V. A. Malyshev and J. Knoester, J. Phys. Chem. B, 2006, 110, 20268–20276 CrossRef PubMed.
- R. Augulis, A. Pugzlys and P. H. M. van Loosdrecht, Phys. Status Solidi, 2006, 3, 3400–3403 CrossRef CAS.
- K. A. Clark, E. L. Krueger and D. A. Vanden Bout, J. Phys. Chem. C, 2014, 118, 24325–24334 CrossRef CAS.
- B. Kriete, J. Lüttig, T. Kunsel, P. Malý, T. L. C. Jansen, J. Knoester, T. Brixner and M. S. Pshenichnikov, Nat. Commun., 2019, 10, 4615 CrossRef PubMed.
- A. Bondarenko, PhD thesis, University of Groningen, 2019.
- N. F. Bouxsein, L. S. Hirst, Y. Li, C. R. Safinya, Z. A. Samah, N. C. MacDonald and R. Pynn, Appl. Phys. Lett., 2004, 85, 5775–5777 CrossRef CAS.
- M. Yamauchi, K. Mawatari, A. Hibara, M. Tokeshi and T. Kitamori, Anal. Chem., 2006, 78, 2646–2650 CrossRef CAS PubMed.
- K. J. Humphry, P. M. Kulkarni, D. A. Weitz, J. F. Morris and H. A. Stone, Phys. Fluids, 2010, 22, 081703 CrossRef.
- M. Trebbin, D. Steinhauser, J. Perlich, A. Buffet, S. V. Roth, W. Zimmermann, J. Thiele and S. Förster, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6706–6711 CrossRef CAS PubMed.
- E. Engel, K. Leo and M. Hoffmann, Chem. Phys., 2006, 325, 170–177 CrossRef CAS.
- J. Dostál, F. Fennel, F. Koch, S. Herbst, F. Würthner and T. Brixner, Nat. Commun., 2018, 9, 2466 CrossRef PubMed.
- A. Suna, Phys. Rev. B: Condens. Matter Mater. Phys., 1970, 1, 1716–1739 CrossRef.
- I. G. Scheblykin, O. P. Varnavsky, M. M. Bataiev, O. Sliusarenko, M. Van der Auweraer and A. G. Vitukhnovsky, Chem. Phys. Lett., 1998, 298, 341–350 CrossRef CAS.
- L. Valkunas, Y.-Z. Ma and G. R. Fleming, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 115432 CrossRef.
- M. G. Bawendi, P. J. Carroll, W. L. Wilson and L. E. Brus, J. Chem. Phys., 1992, 96, 946–954 CrossRef.
- S. A. Crooker, J. A. Hollingsworth, S. Tretiak and V. I. Klimov, Phys. Rev. Lett., 2002, 89, 186802 CrossRef CAS PubMed.
- J. Conyard, K. Addison, I. A. Heisler, A. Cnossen, W. R. Browne, B. L. Feringa and S. R. Meech, Nat. Chem., 2012, 4, 547–551 CrossRef CAS PubMed.
- H. Marciniak, M. Fiebig, M. Huth, S. Schiefer, B. Nickel, F. Selmaier and S. Lochbrunner, Phys. Rev. Lett., 2007, 99, 176402 CrossRef CAS PubMed.
- Y. Wan, A. Stradomska, S. Fong, Z. Guo, R. D. Schaller, G. P. Wiederrecht, J. Knoester and L. Huang, J. Phys. Chem. C, 2014, 118, 24854–24865 CrossRef CAS.
- A. V. Malyshev, V. A. Malyshev and F. Domínguez-Adame, J. Phys. Chem. B, 2003, 107, 4418–4425 CrossRef CAS.
- O. V. Mikhnenko, M. Kuik, J. Lin, N. van der Kaap, T.-Q. Nguyen and P. W. M. Blom, Adv. Mater., 2014, 26, 1912–1917 CrossRef CAS PubMed.
- G. M. Akselrod, P. B. Deotare, N. J. Thompson, J. Lee, W. A. Tisdale, M. A. Baldo, V. M. Menon and V. Bulovic, Nat. Commun., 2014, 5, 3646 CrossRef CAS PubMed.
- S. Doria, T. S. Sinclair, N. D. Klein, D. I. G. Bennett, C. Chuang, F. S. Freyria, C. P. Steiner, P. Foggi, K. A. Nelson, J. Cao, A. Aspuru-Guzik, S. Lloyd, J. R. Caram and M. G. Bawendi, ACS Nano, 2018, 12, 4556–4564 CrossRef CAS PubMed.
- B. D. Rose, L. E. Shoer, M. R. Wasielewski and M. M. Haley, Chem. Phys. Lett., 2014, 616–617, 137–141 CrossRef CAS.
- A. Prlj, N. Došlić and C. Corminboeuf, Phys. Chem. Chem. Phys., 2016, 18, 11606–11609 RSC.
- J. Shi, L. E. Aguilar Suarez, S.-J. Yoon, S. Varghese, C. Serpa, S. Y. Park, L. Lüer, D. Roca-Sanjuán, B. Milián-Medina and J. Gierschner, J. Phys. Chem. C, 2017, 121, 23166–23183 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp01734e |
| This journal is © the Owner Societies 2020 |