Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Sodium cationization can disrupt the intramolecular hydrogen bond that mediates the sunscreen activity of oxybenzone†
Jacob A.
Berenbeim
 a,
Natalie G. K.
Wong
a,
Natalie G. K.
Wong
 a,
Martin C. R.
Cockett
a,
Giel
Berden
a,
Martin C. R.
Cockett
a,
Giel
Berden
 b,
Jos
Oomens
b,
Jos
Oomens
 b,
Anouk M.
Rijs
b,
Anouk M.
Rijs
 b and
Caroline E. H.
Dessent
b and
Caroline E. H.
Dessent
 *a
*a
aDepartment of Chemistry, University of York, Heslington, York YO10 5DD, UK. E-mail: caroline.dessent@york.ac.uk
bRadboud University, Institute for Molecules and Materials, FELIX Laboratory, Toernooiveld 7, Nijmegen, The Netherlands
First published on 12th August 2020
Abstract
A key decay pathway by which organic sunscreen molecules dissipate harmful UV energy involves excited-state hydrogen atom transfer between proximal enol and keto functional groups. Structural modifications of this molecular architecture have the potential to block ultrafast decay processes, and hence promote direct excited-state molecular dissociation, profoundly affecting the efficiency of an organic sunscreen. Herein, we investigate the binding of alkali metal cations to a prototype organic sunscreen molecule, oxybenzone, using IR characterization. Mass-selective IR action spectroscopy was conducted at the free electron laser for infrared experiments, FELIX (600–1800 cm−1), on complexes of Na+, K+ and Rb+ bound to oxybenzone. The IR spectra reveal that K+ and Rb+ adopt binding positions away from the key OH intermolecular hydrogen bond, while the smaller Na+ cation binds directly between the keto and enol oxygens, thus breaking the intramolecular hydrogen bond. UV laser photodissociation spectroscopy was also performed on the series of complexes, with the Na+ complex displaying a distinctive electronic spectrum compared to those of K+ and Rb+, in line with the IR spectroscopy results. TD-DFT calculations reveal that the origin of the changes in the electronic spectra can be linked to rupture of the intramolecular bond in the sodium cationized complex. The implications of our results for the performance of sunscreens in mixtures and environments with high concentrations of metal cations are discussed.
1 Introduction
Skin exposure to excess ultraviolet radiation has the potential to trigger skin cancers, with commercial sunscreens having thus been widely used to filter light at the skin's surface. For any molecule employed as a UV filter, its ability to act as a photoprotector relies primarily on a capacity to absorb light strongly across the UVA and UVB. However, it is also crucial that the initial electronic excitation is rapidly converted to vibrational energy in high quantum yield, with the vibrational energy subsequently being dissipated into the local environment as benign heat.1,2 This process is facilitated by conical intersections (CI) between the excited and ground state surfaces, which convey photostability by allowing rapid channelling of the excited-state population back to the electronic ground-state.One of the key processes by which organic sunscreen molecules access conical intersections involve an H-atom donor (e.g., hydroxyl group) and acceptor (e.g., carbonyl) which are aligned to facilitate ultrafast intramolecular hydrogen transfer. These electron-driven excited state H atom transfer processes have been identified as key relaxation pathways for photostable biomolecules as well as sunscreens.2,3 Oxybenzone (OB: Scheme 1) provides a classic example of a system that uses this mechanism to dissipate UV energy. Karsili et al. have performed ab initio calculations of oxybenzone's excited states to better understand its non-radiative relaxation pathways.4 They found that internal conversion occurs on an ultrafast timescale via a barrierless electron-driven H atom transfer pathway from the S1 state to a conical intersection with the S0 ground-state. Transient pump–probe spectroscopy performed by Baker et al. supports a more complicated relaxation mechanism, where H-atom transfer corresponds to a S1 ← S2 CI and internal conversion from S0 ← S1 is accessed via C2–C3 twisting.5,6 Surface-hopping dynamics performed by Li et al. have since supported this latter model.7 From these studies, it is clear that H-atom transfer is critical to the non-radiative relaxation of oxybenzone.
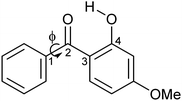 | ||
| Scheme 1 Schematic diagram of oxybenzone (OB). The figure illustrates the dihedral angle ϕ, which is defined as the minimum angle between Cortho–C1–C2–O2. | ||
While excited-state H-atom transfer between a suitably aligned donor and acceptor group offers a facile route to ultrafast UV decay, structural modifications of the molecular geometry needed to access the relevant CI can occur through interactions of the molecule with its local environment. Recent work from our group has demonstrated how pH can impact at the molecular level on the function of an organic sunscreen.8–10 Upon protonation, both oxybenzone and avobenzone were observed to photodissociate directly from the excited state surface, i.e., undergo non-statistical dissociation, which is an undesirable photodegradation process. A similar effect was also observed for oxybenzone and 2-phenylbenzimidazole-5-sulfonic acid upon deprotonation. These experiments were conducted in the gas-phase, with mass selection being used to unambiguously isolate and characterize the different protonation states.
In this work, we investigate the binding of alkali metal cations to OB to probe its potential to affect sunscreen function. We use gas-phase IR photodissociation spectroscopy (600–1800 cm−1) of mass-selected molecular complexes, M+·OB, where M+ = Na+, K+ and Rb+, supported by ab initio calculations to probe directly the binding motifs of this series of alkali–metal cations to oxybenzone. In particular, we seek to understand whether the alkali metal cations can disrupt the key OB intramolecular bond that facilities its UV filtering property. In addition, we obtain the gas-phase electronic spectra to probe the extent to which alkali metal binding perturbs the OB absorption spectrum. We note that a number of previous studies have been conducted to characterize the structures of isolated complexes of alkali metal cations bound to aromatic and carbonyl-containing molecules, using both IR and UV laser spectroscopy.11–20
The interaction of an organic sunscreen such as OB with alkali metal cations is of practical interest since sunscreen mixtures include such counterions (e.g., coupled to pH buffer anions),21 but also since they are commonly encountered in the environments where sunscreens are intensively used, including oceans and swimming pools, as well as on human skin.22,23
2 Methods
2.1 UV photodepletion spectroscopy
Gas-phase UV photodissociation experiments were conducted in an AmaZon SL dual funnel electrospray ionization quadrupole ion trap (ESI-QIT) mass spectrometer (Bruker Daltonics Inc., Billerica, MA, USA), modified for LIMS.10,24,25 Solutions of OB (1 × 10−5 mol dm−3) and M+ (1 × 10−5 mol dm−3) in ethanol were electrosprayed using typical instrumental parameters (nebulizing gas pressure of 10.0 psi, injection rate of 0.33 mL h−1, drying gas flow rate of 8.0 L min−1), and run in at capillary temperatures of 100 °C. Oxybenzone (OB) was purchased from Alfa Aesar (Ward Hill, MA, USA) and HPLC-grade ethanol from Fisher Scientific, Inc. (Pittsburgh, PA, USA).UV-Vis photons were produced by a 10 Hz Nd:YAG (Surelite™, Amplitude Laser Group, San Jose, CA, USA) pumped OPO (Horizon™, Amplitude Laser Group) laser, giving ∼1.0 mJ across the range 400–250 nm (3.10–5.0 eV). A 2 nm laser step size was used to record the photodepletion and photofragment spectra of the M+·OB parent ion. To check for single-photon conditions, the laser power dependence on signal was determined, as described previously.8,10
Photofragmentation experiments were conducted with an ion accumulation time of 20 ms and a fragmentation time of 100 ms, thereby ensuring that each mass-selected ion packet interacted with one laser pulse, minimizing the likelihood of multiphoton events. When fluorescence is negligible,26 the UV excited gaseous ion will fragment upon excited-state relaxation, yielding an action absorption spectrum by photodepletion (PD).25,27,28 PD was measured as a function of the scanned wavelength, with the photofragment production (PF) also recorded simultaneously at each wavelength, both of which according to:
 | (1) |
 | (2) |
2.2 IRMPD spectroscopy
IR experiments were performed in a modified commercial quadrupole ion-trap mass spectrometer (Bruker, AmaZon Speed ETD).29,30 Ions were generated in an Apollo ESI source. Solutions of OB (1 × 10−6 mol dm−3) and M+ (1 × 10−6 mol dm−3) in methanol were introduced at 180 μL h−1 flow rates, electrosprayed and transferred into the trap. The ions of interest were mass-selected and fragmented by IRMPD. IR spectra in the 700–1800 cm−1 region were recorded using the FELIX infrared free electron laser.31 FELIX was set to produce IR radiation in the form of 8–10 μs macropulses of 80–120 mJ per pulse at a 10 Hz repetition rate and with a bandwidth of ∼0.4% of the centre frequency. The mass-selected ions were irradiated with one macropulse. Resonant absorption of IR radiation leads to an increase of the internal energy of an ion mediated by intramolecular vibrational redistribution (IVR), which eventually leads to unimolecular dissociation.32 After irradiation, a mass spectrum of the resulting ions in the trap is recorded. At each IR frequency point, six mass spectra were averaged. The dissociation was calculated from the mass spectra by relating the precursor ion and fragment ion intensities (eqn (3)) and plotted as a function of IR frequency.33 | (3) |
The IRMPD intensity was linearly corrected for frequency-dependent laser pulse energy. Spectra were also recorded at two levels of laser-pulse energy attenuation (factors of 2.00 and 3.16) to prevent excessive depletion of the precursor ions (saturation) and minimize formation of low m/z fragment ions which may be undetected in the ion trap and which would result in underestimated IRMPD intensities.33
2.3 Computational chemistry
Conformational molecular dynamics searches implemented by Schrodinger's MacroModel were conducted with mixed Monte Carlo torsional and low-mode sampling to generate possible conformers which were rapidly energy gradient minimized with the OPLS3e force field.34 Unique structures (RMSD 0.4 Å, <100 kJ mol−1) were then energy minimized at the B3LYP/cc-pVTZ level, and frequency calculations performed.35 For K+ and Rb+, the Stuttgard–Dresden–Bonn RLC ECP and valence basis sets were used.36 All quantum mechanical calculations were performed using density functional theory (DFT) in Gaussian 09.37 Frequency spectra have been scaled by 0.98 and convolved with a Lorrentzian of FWHM 25 cm−1. TD-DFT spectra (M06-2X)38 were convolved with a Gaussian of FWHM 0.5 eV. A polarizable continuum model using the integral equation formalism was used to calculate the relative energies of conformers upon solvation.2.4 Spectral matching
The fit between the experimental IRMPD spectra and spectra generated by DFT calculations was assessed by comparing the cosine similarity of the lowest-energy structures. This similarity measure has been shown to be a successful tool for evaluating molecular-based systematic relationships,39–41 including IRMPD spectral fits.42 Fit similarity is assessed as the cosine of the angle θ between two spectral vectors A and B, which is calculated as the dot product of these vectors divided by the product of their Euclidian norms, according to: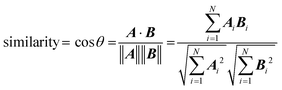 | (4) |
The most analogous spectral vectors will have the smallest angle between them and a similarity value that approaches unity.
3 Results and discussion
3.1 Quantum chemical calculations of M+·OB
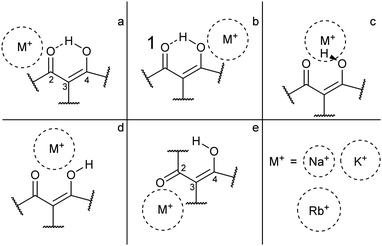
For each of the M+·OB complexes studied here a semi-rigorous MD/QM conformational search was performed to provide starting structures for the subsequent quantum-chemical calculations. Scheme 2 illustrates the coordination motifs of the cations to the OB molecule that were observed in the MD/QM searches. They differ from one another in the monodentate (a and b) or bidentate (c and d) coordination, in the identity of the coordinating nucleophile (a and d), or in the conformation of the OB ligand (e).Table 1 displays the computational results for the M+·OB complexes. No upper limit was chosen to define the “low-energy” window for the simulations, rather, all isomers found were included up to the point where structures corresponding to at least one of each of the coordination motifs (a–e) were represented. Two significant trends emerge from the calculations:
| M+·OB | Gas-phase | Ethanol | n-Hexane | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rel. Ea (kJ mol−1) | % Pop.b | Coord. isomer | Dihedral ϕ | Rel. Ea (kJ mol−1) | % Pop.b | Coord. isomer | Dihedral ϕ | Rel. Ea (kJ mol−1) | % Pop.b | Coord. isomer | Dihedral ϕ | |
| a Rel. E is the electronic energy relative to the lowest energy isomer. b T = 375 K was chosen here; however, trapped ions thermalize with a helium backing gas during accumulation and isolation steps in the quadrupole ion trap (QIT) and estimations of effective ion temperatures within a QIT are ∼310 ± 20 K.46 c The abbreviations for OB are as follows: intramolecular hydrogen bonded (I), twisted (II), and non-intramolecular hydrogen bonded (III). See ESI for schematics of the OB structures. | ||||||||||||
| Na+·OB | 0.0 | 72 | d | 28 | 0.0 | 73 | a | 47 | 0.0 | 38 | d | 31 |
| 4.4 | 17 | d2 | 27 | 4.8 | 16 | a2 | 46 | 0.5 | 33 | a | 49 | |
| 6.6 | 9 | a | 56 | 6.0 | 11 | b | 42 | 2.3 | 18 | a2 | 53 | |
| 11.5 | 2 | a2 | 55 | 18.6 | 0 | b2 | 41 | 4.3 | 10 | d | 30 | |
| 27.2 | 0 | b | 37 | 19.3 | 0 | b3 | 42 | 10.9 | 1 | b | 38 | |
| 29.5 | 0 | c | 39 | 21.2 | 0 | b4 | 42 | 20.0 | 0 | c | 41 | |
| 36.3 | 0 | e | 49 | 22.3 | 0 | d | 30 | 24.3 | 0 | e | 42 | |
| 22.5 | 0 | d2 | 32 | |||||||||
| 28.8 | 0 | e | 26 | |||||||||
| K+·OB | 0.0 | 79 | a | 56 | 0.0 | 44 | a | 46 | 0.0 | 52 | a | 51 |
| 6.8 | 9 | d | 28 | 2.2 | 22 | a2 | 46 | 0.8 | 40 | a2 | 50 | |
| 9.3 | 4 | b | 38 | 2.4 | 20 | a3 | 45 | 6.7 | 6 | b | 39 | |
| 10.4 | 3 | c | 31 | 4.3 | 11 | b | 42 | 12.3 | 1 | c | 35 | |
| 11.0 | 2 | c2 | 33 | 10.1 | 2 | b2 | 42 | 15.2 | 0 | d | 28 | |
| 11.1 | 2 | d2 | 28 | 11.0 | 1 | b3 | 43 | 18.2 | 0 | d2 | 28 | |
| 23.3 | 0 | e | 44 | 26.8 | 0 | d | 30 | 24.1 | 0 | e | 42 | |
| 27.3 | 0 | d2 | 30 | |||||||||
| 29.0 | 0 | e | 38 | |||||||||
| Rb+·OB | 0.0 | 75 | a | 54 | 0.0 | 53 | a | 46 | 0.0 | 35 | a | 52 |
| 4.1 | 20 | a2 | 55 | 2.2 | 26 | a2 | 45 | 1.3 | 23 | a2 | 50 | |
| 11.7 | 2 | b | 38 | 3.9 | 15 | b | 42 | 1.3 | 23 | a3 | 50 | |
| 13.1 | 1 | c | 34 | 9.4 | 3 | b2 | 42 | 2.5 | 16 | a4 | 52 | |
| 13.2 | 1 | c2 | 36 | 10.5 | 2 | b3 | 42 | 7.5 | 3 | b | 39 | |
| 14.0 | 1 | d | 28 | 10.8 | 2 | b4 | 43 | 12.6 | 1 | c | 36 | |
| 18.1 | 0 | d2 | 28 | 27.3 | 0 | d | 30 | 19.7 | 0 | d | 29 | |
| 27.4 | 0 | e | 44 | 27.9 | 0 | d2 | 30 | 22.3 | 0 | d | 30 | |
| 28.7 | 0 | e | 38 | 26.3 | 0 | e | 43 | |||||
| OBc | 0.0 | 100 | I | 40 | 0.0 | 100 | I | 43 | 0.0 | 100 | I | 42 |
| 31.9 | 0 | II | 34 | 28.4 | 0 | II | 35 | 30.5 | 0 | II | 35 | |
| 45.3 | 0 | III | 22 | 33.1 | 0 | III | 27 | 41.1 | 0 | III | 25 | |
(i) The gas-phase ion population is expected to exist primarily in complexes which display the bidentate coordination motif (d) for the Na+ complexes. For the larger alkali metals (K+ and Rb+) isomers that display the coordination motif (a) dominate; the intramolecular H-bond interaction apparently outcompetes the weaker metal–oxygen interaction for these larger ions.
(ii) In ethanol, >79% of the M+·OB complexes are predicted to adopt structures where the ion coordinates by motif (a).
(iii) In n-hexane, >90% of the K+ and Rb+ complexes are predicted to adopt structures where the ion coordinates by motif (a), however, for Na+ complexes these (a) motif structures only account for 51%. The bidentate coordination motif (d) accounts for 48% of the remaining Na+ complex structures when modeling non-polar aprotic conditions.
For the present investigation, it is notable that Na+ coordination favors structures that display motif (d) binding while larger cations do not. This can be interpreted a combination of factors: Na+ is small enough to coordinate between the two OB oxygen atoms, whereas the other cations are too large to adopt this bidentate position. Alternatively, larger-radius metal cations are well recognized to preferentially adopt non-covalent π-cation structures13,43–45 leading to a preference for above-ring binding motifs. In the M+·OB complexes, we observe the ϕ dihedral angle opening to support this non-covalent interaction between the larger alkali metal cations and benzene ring in the (a) structures.
For the larger radius ions, the (c) motif isomers were found to lie lower in energy than the (d) motif isomers, while both lie significantly higher than the lowest-energy (a) motif isomers. In short, the larger-radius ions do not break the intramolecular H-bond. The (c) motif structures have the alkali metal ion chelated between the two adjacent oxygen atoms, but alongside the interstitial proton. No (c) motif structures were found for any of the complexes in ethanol.
For structures displaying motif (a) and (b) binding, the intramolecular hydrogen bond remains intact, and shares a symmetry plane with the C2, C3, and C4 carbon atoms. Inspection of the benzoyl dihedral angle ϕ (Scheme 1) values listed in Table 1 show the increased angle required to stabilize the alkali ion in (a) motifs, compared to (b–d) motifs. In the (a) motifs, the alkali ions appear to be cradled between the OB carbonyl and benzene functional groups. There is no clear trend for the dihedral angles of the (e) motifs as a function of metal ion size, an effect that can be attributed to the metal ion coordination position in these structures having more degrees of freedom compared to other binding motifs. This is due to the breaking of the intramolecular hydrogen-bond and rotation of the C3 carbon.
For cases where we found multiple M+·OB isomers corresponding to a particular structural motif, only the lowest energy isomer (Table 1) was used for generating the calculated IR and UV spectra. This assumes that differences within a given motif class, such as dihedral angle ϕ or O-methyl rotational, will have negligible impact on the calculated spectra. This is a reasonable assumption at the spectral resolution of our experiment.
Table 1 also includes results for bare OB, which displays an intramolecular hydrogen-bonding structure (I),47 and has a dihedral angle of 40° in the gas-phase. The corresponding isomer without an intramolecular hydrogen bond (II) lies 45.3 kJ mol−1 higher in energy with a dihedral angle of 22°. A third gaseous conformation, the twisted (III) isomer, lies 31.9 or 40.0 kJ mol−1 higher in energy than the (I) form, depending on whether the OH bond points toward or away from the neighboring benzene ring, respectively, and has a dihedral angle of 33° or 24°, respectively.
We next turn to presenting the IRMPD spectra of the M+·OB complexes, to directly probe the binding sites of the various cations to OB.
3.2 IRMPD spectroscopy of the M + ·OB complexes
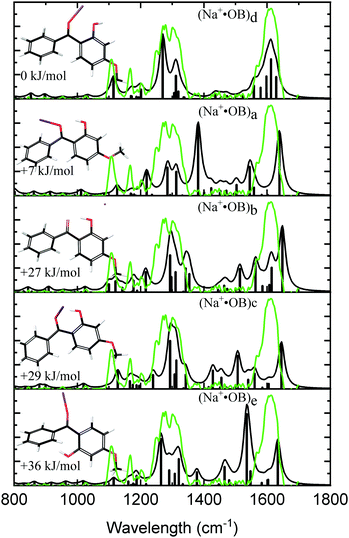
Fig. 1 displays the experimental IRMPD spectrum of Na+·OB, along with the calculated IR spectra of the (a–e) isomers. The experimental spectrum shows two strong sets of peaks at 1289 and 1610 cm−1, along with three lower-intensity bands at 1108, 1166, and 1202 cm−1. The calculated spectrum of the Na+·OB (d) isomer best reproduces the experimental spectrum, exhibiting these same features, where the dominant doublet feature associated with the 1289 cm−1 band corresponds to an OH-bend, and a coupled symmetric ortho-CO and para-CO bond stretch, respectively, while the 1610 cm−1 vibration corresponds to a C2-carbonyl stretch. (Section S3, ESI†). Of the remaining calculated spectra, isomer (b) somewhat duplicates the experimental IR spectrum in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O region around 1600 cm−1. However, the calculated IR spectrum of isomer (b), as well as those of isomers (a, c, and e) provide a poorer visual match to the three minor bands; the calculated spectra for these isomers display features across the 1360–1540 cm−1 region which are not well matched by experiment. We note that the Boltzmann calculation (Table 1) predicted that (a) motif structures would be present at 11% of the experimental ion ensemble. The experimental IRMPD spectrum does display a partially resolved feature to the low energy side of the strong 1289 cm−1 doublet, which could be associated with such structures (e.g., if the predicted 1250 cm−1 vibration is blue shifted). Higher-resolution IR spectra would be valuable to further confirm this.
O region around 1600 cm−1. However, the calculated IR spectrum of isomer (b), as well as those of isomers (a, c, and e) provide a poorer visual match to the three minor bands; the calculated spectra for these isomers display features across the 1360–1540 cm−1 region which are not well matched by experiment. We note that the Boltzmann calculation (Table 1) predicted that (a) motif structures would be present at 11% of the experimental ion ensemble. The experimental IRMPD spectrum does display a partially resolved feature to the low energy side of the strong 1289 cm−1 doublet, which could be associated with such structures (e.g., if the predicted 1250 cm−1 vibration is blue shifted). Higher-resolution IR spectra would be valuable to further confirm this.
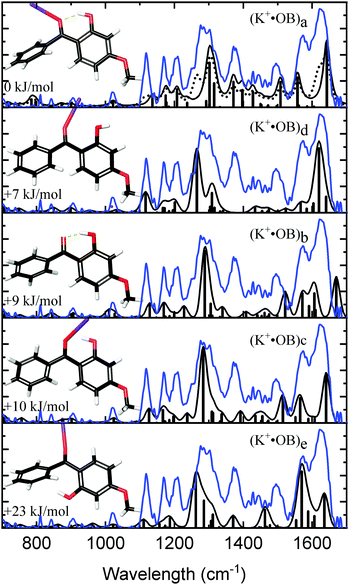
Fig. 2 compares the experimental IRMPD spectrum with the calculated spectra for K+·OB. The experimental spectrum displays three strong sets of bands at 1282, 1375, and 1600 cm−1, along with three minor bands at 1117, 1167, and 1207 cm−1. The calculated spectra for isomers (a, d, c, and e) all show reasonable agreement with the dominant features at 1600 cm−1, although the spectrum for isomer (e) compares poorly in the region between the 1360–1540 cm−1 and the second dominant band at 1282 cm−1. In general, the calculated spectrum for the (a) isomer of K+·OB reproduces the majority of the observed features in the experimental spectrum well. Given that the Boltzman population (Table 1) predicts that this isomer should dominate the ion ensemble, we primarily assign the experimental spectrum to (a) motif structures. However, the intensities of the two major sets of bands in the calculated spectrum for isomer (a) are not a good match to the IRMPD. The calculated spectra of both the (c) and (d) isomers of K+·OB exhibit these “missing” features. It is notable in this context that our Boltzman population analysis (Table 1) predict that the experimental ion ensemble should include some (d) isomer. A composite calculated spectrum using a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 mixture of the (a
40 mixture of the (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d) isomers of K+·OB is included in Fig. 2 (dotted top trace), and matches the experimental IRMPD spectrum well. The calculations predict that the 1282 cm−1 vibration corresponds to a coupled antisymmetric OH-bending and para-CO stretching motion, the 1375 cm−1 feature a coupled symmetric OH-bending and ortho-CO stretching motion, and that the strong doublet at 1600 cm−1 is a mixed C2-carbonyl stretch and OH-bend, and an OH-bend. (We note that the calculated IR spectra corresponding to individual isomers (a, b, c, e) provide a poor match the three minor features, since all predict modes across the 1365–1500 cm−1 region which are absent from the experimental spectrum.)
d) isomers of K+·OB is included in Fig. 2 (dotted top trace), and matches the experimental IRMPD spectrum well. The calculations predict that the 1282 cm−1 vibration corresponds to a coupled antisymmetric OH-bending and para-CO stretching motion, the 1375 cm−1 feature a coupled symmetric OH-bending and ortho-CO stretching motion, and that the strong doublet at 1600 cm−1 is a mixed C2-carbonyl stretch and OH-bend, and an OH-bend. (We note that the calculated IR spectra corresponding to individual isomers (a, b, c, e) provide a poor match the three minor features, since all predict modes across the 1365–1500 cm−1 region which are absent from the experimental spectrum.)
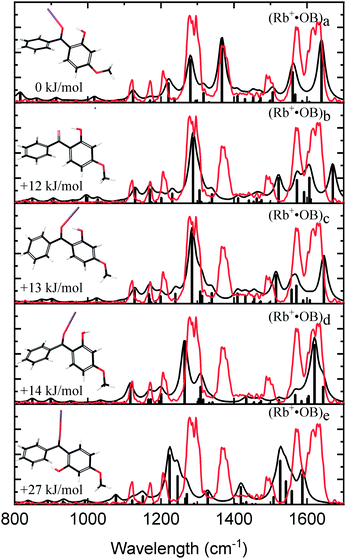
Fig. 3 compares the experimental IRMPD spectrum with the calculated spectra for the calculated Rb+·OB isomers. The experimental spectrum has four strong bands at 1275, 1368, 1569, and 1626 cm−1, and bands with minor intensity at 1122, 1170, 1205, and 1488 cm−1. The calculated spectrum for the (a) isomer displays an excellent match to these experimental features. The calculated 1275 cm−1 mode for isomer (a) is described best as a coupled asymmetric OH-bend and para-CO stretch motion, with the vibration at 1368 cm−1 being a coupled symmetric OH-bend and ortho-CO stretch motion. The vibration at 1569 cm−1 is a mixture of C2-carbonyl stretch, OH-bend, and ortho-CO stretching motions; and the 1626 cm−1 vibration is a mixture of asymmetric OH-bend and para-CO stretch vibrations. The calculated IR spectra for the remaining (b–e) isomers fail to match the experimental 1368 and 1488 cm−1 features, leading to a clear assignment that the Rb+·OB experimental ions correspond to isomer (a).
3.3 Spectral matching between IRMPD and theory
To confirm the qualitative assignment of the experimental M+·OB IRMPD spectra presented in the last section, spectral matching was performed.42Table 2 lists the spectral matching scores obtained. Further details of how the matching scores were obtained are available in Section S5 of the ESI.† The Na+·OB IRMPD spectra were found to be best matched by the computed spectrum for the (d) isomer, while the K+·OB and Rb+·OB spectra matched best to the respective (a) motif structures. For K+·OB, using a 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 (a
40 (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d) isomer composite improves the spectral matching score to 0.92, compared to 0.85 for just isomer (a). This supports our qualitative arguments above that the K+·OB experimental ion population derives from a mixture of isomers.
d) isomer composite improves the spectral matching score to 0.92, compared to 0.85 for just isomer (a). This supports our qualitative arguments above that the K+·OB experimental ion population derives from a mixture of isomers.
| Motif | Matching score | ||
|---|---|---|---|
| Na+·OB | K+·OB | Rb+·OB | |
a For K+·OB a (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) mixture of (a 50) mixture of (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c) and (50 c) and (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50) mixture of (a 50) mixture of (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d) were determined by maximizing the similarity quotient. See Section S5 in the ESI for more details. d) were determined by maximizing the similarity quotient. See Section S5 in the ESI for more details.
|
|||
| a | 0.528 | 0.852 | 0.835 |
| b | 0.727 | 0.709 | 0.775 |
| c | 0.667 | 0.812 | 0.782 |
| d | 0.952 | 0.812 | 0.777 |
| e | 0.649 | 0.824 | 0.433 |
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ca ca |
— | 0.876 | — |
a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) da da |
— | 0.938 | — |
3.4 Gas-phase UV absorption spectroscopy of the M+·OB complexes
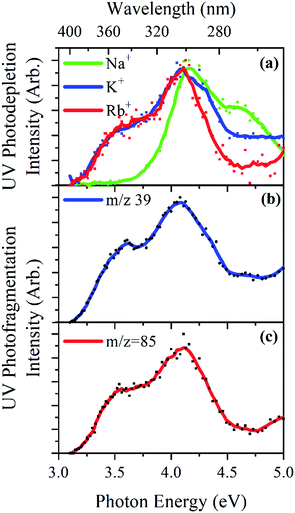
Fig. 4a displays the gas-phase UV absorption spectra of the M+·OB complexes recorded by photodepletion over the range 3.1–5.0 eV. The K+·OB and Rb+·OB spectra are similar with both species exhibiting broad UVA/UVB absorption that seem to correspond to two absorption bands which peak at λmax wavelengths of 3.5 and 4.1 eV, for both complexes. The band with λmax centered at 4.1 eV is broader for K+·OB than for Rb+·OB, and displays a rather high, flat region of absorbance above 4.5 eV, while the Rb+·OB spectral intensity drops over that region. It is notable that the K+·OB and Rb+·OB spectra have a similar absorption profile to protonated OB, [OB + H]+.9In contrast, the absorption spectrum of Na+·OB differs significantly from those of K+·OB and Rb+·OB, with the UVA band with λmax = 3.5 eV which is present for K+·OB and Rb+·OB being entirely absent for Na+·OB. Instead, the complex displays a UVB band with λmax = 4.2 eV, and a higher-energy band which peaks with λmax = 4.6 eV.
The UV photofragmentation spectra of K+·OB and Rb+·OB are shown in Fig. 4b and c, respectively. K+·OB and Rb+·OB photofragment only into their respective alkali ions. These photofragmentation spectra closely mirror the photodepletion spectra, indicating that no additional low-mass photofragments are being produced following photoexcitation. (No photofragments were recorded for Na+·OB. This behavior is in line with that of the other complexes since Na+ has a mass that falls below the cutoff of our ion trap.) The production of the M+ cations as the sole photofragments reflects the weaker cation–OB binding energy, compared to the OB covalent bonds, and is typical of the photofragmentation of metal cation–molecule complexes.15,16,48–50
The distinctive profile of the Na+·OB gaseous absorption spectrum compared to that of K+·OB and Rb+·OB is again consistent with the sodium cation binding to OB in a unique manner.
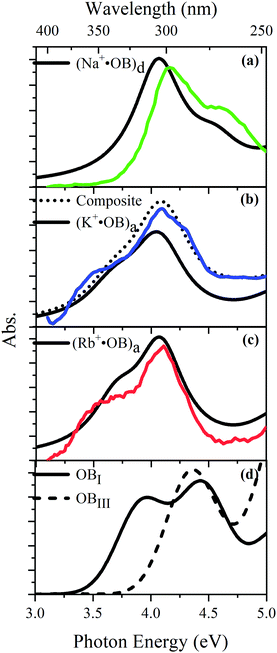
TD-DFT calculations for each of the lowest-energy geometries were used to generate computed electronic spectra for comparison to the experimental spectra. Fig. 5 overlays the experimental UV absorption spectra with the respective TD-DFT spectra. Calculated spectra are also shown for isomers of neutral OB. Fig. 5a shows that the calculated spectrum for the (d) isomer of Na+·OB exhibits bands with λmax at 4.1 and 4.6 eV, in good agreement with the experimental spectrum. Similarly, the calculated TD-DFT spectra for the predicted (a) isomers of K+·OB and Rb+·OB (Fig. 5b and c) agree reasonably well with the experimental spectra, displaying bands with λmax at 4.0 and 4.4 eV, and at 3.7 and 4.2 eV, respectfully. Using a 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 (a
30 (a![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d) isomer mixture for K+·OB, again produces a better match to the experimental spectrum. The (I) and (III) isomers of neutral OB have very distinctive spectral profiles. While the calculated spectrum of isomer (I) displays bands with λmax at 3.9 and 4.4 eV, the calculated spectrum of isomer (III) displays a band with λmax at 4.4 eV, and a rising absorption towards higher energy. There is a good resemblance between the calculated OB isomer (I) and M+·OB (a) motif calculated spectra, all of which contain an intact intramolecular hydrogen bond. For the systems without an intramolecular hydrogen bond, OB isomer (III) and isomer (d) of Na+·OB, the calculated spectra are again similar, with the first prominent electronic band lying at significantly higher energy than for the systems where the hydrogen bond is intact.
d) isomer mixture for K+·OB, again produces a better match to the experimental spectrum. The (I) and (III) isomers of neutral OB have very distinctive spectral profiles. While the calculated spectrum of isomer (I) displays bands with λmax at 3.9 and 4.4 eV, the calculated spectrum of isomer (III) displays a band with λmax at 4.4 eV, and a rising absorption towards higher energy. There is a good resemblance between the calculated OB isomer (I) and M+·OB (a) motif calculated spectra, all of which contain an intact intramolecular hydrogen bond. For the systems without an intramolecular hydrogen bond, OB isomer (III) and isomer (d) of Na+·OB, the calculated spectra are again similar, with the first prominent electronic band lying at significantly higher energy than for the systems where the hydrogen bond is intact.
4 Further discussions
4.1 Natural transition orbital analysis of M+·OB coordinate effects
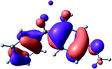
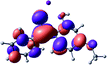
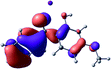
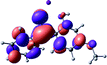
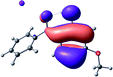
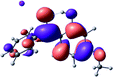
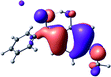
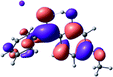
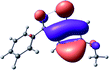
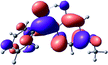
To provide insight into the differences between the TD-DFT results for the (a) and (d) motif structures, Table 3 lists the natural transition orbitals (NTOs) of the most intense electronic excitations (both ππ*) of the Na+·OB and K+·OB complexes. Results for bare OB are also included for comparison. We note that the NTOs shown account for ≥90% of the total transition densities. Based on the calculated NTOs, there is no involvement of orbital density from the alkali ions in any of the complexes studied. Further details are available in the ESI.† (S2 and S5 having nearly identical oscillator strengths for the (d) isomers of Na+·OB and K+·OB, with S1 and S3 having nearly identical oscillator strengths for the (a) isomers of K+·OB and Rb+·OB, as well as identical NTO densities. The NTOs of the (d) isomer of K+·OB are not shown, but are highly similar to those presented for Na+·OB.)Qualitatively, the NTOs of the (d) isomers of Na+·OB and K+·OB are fully delocalized for the occupied and unoccupied states whereas the NTOs of the (a) isomers of K+·OB and Rb+·OB are semi-delocalized (across all but the C1 benzene moiety) for the ground-state orbitals, but then fully delocalized upon excitation. The NTOs for OB (I) closely resemble those shown for (a) isomer of K+·OB, though the ππ* state ordering is different. The dramatic differences between the NTOs associated with the (a) and (d) motifs highlight the impact of the intramolecular hydrogen bond on the molecular electron density, and hence provides insight into why Na+ coordination to OB perturbs its absorption profile so strongly.
4.2 Implications of M+·OB cationization
The comparisons between computed and experimental spectra described above demonstrate that, under the gas-phase experimental conditions employed in this work, Na+ disruptively coordinates to OB by breaking the intramolecular hydrogen bond. This geometric structural change leads directly to a substantial change in the electronic spectrum of the OB chromophore.No neutral gaseous UV absorption spectrum of OB has been recorded to date, but the K+ and Rb+ OB complexes display experimental UV absorption spectra that are largely consistent with a calculated neutral OB absorption spectrum, since these ions only weakly perturb the organic chromophore and leave the key section of the intramolecular hydrogen-bond intact. While the dihedral angles in Table 1 show a greater change relative to bare OB when K+ and Rb+ coordinate rather than Na+, the NTO analysis highlights that this particular geometric change does not significantly affect the electronic structure of OB. This effect can be traced to the local molecular structure not being involved with the bright transitions (S1 and S3 for K+ and Rb+ cationated OB) which dominate the UVA/UVB region. The NTOs shown for isomer (I) of OB match those shown for K+ and Rb+ coordinated ions. Coordination of OB with K+ and Rb+ produces a charged complex, and can thus be considered to facilitate the experiment measurement of the neutral OB electronic spectrum via ion action spectroscopy. Such behavior has previously been labelled “charge tagging”.51,52 Interestingly, the microhydration of OB in a molecular beam was very recently probed with microwave spectroscopy, revealing that a single water molecule did not break the intramolecular hydrogen bond, but lead to cluster structures which were similar to the (a) and (b) motif cluster structures studied here.53
A dramatic change in the electronic character of OB occurs as a result of the breaking of the intramolecular hydrogen bond. The Na+·OB (d) isomer displays significantly different electronic transitions and associated electron density distributions compared to neutral OB (Table 3). The strength of the S2 and S3 transitions present in the bare neutral are therefore lost upon Na+ cationization.
The implications of the Na+ cationization of OB binding in a manner that ruptures the intramolecular bond seems likely to extend beyond its impact on the profile of the absorption spectra. Commercial sunscreen mixtures typically provide a non-polar medium, with high oil concentration, and such an environment would likely favor coordination geometries where Na+ breaks the intramolecular hydrogen bond. This could be particularly relevant under environmental conditions where local Na+ concentrations are high, such as in swimming pools in and the ocean. Moreover, if the OB intramolecular hydrogen bond is broken, the predominant non-radiative excited-state mechanism discussed by Karsili et al.4 would not exist. This issue is of key importance for the range of sunscreen molecules where ultrafast excited-state decay is mediated by excited state H atom transfer (e.g., dioxybenzone and octyl salicylate), since in the absence of ultrafast decay, the excited state system can undergo irreversible photodegradation.54,55 Even if the quantum yield for photodegradation is low, over time this will lead to a substantial reduction in sunscreen activity due to the non-equilibrium syphoning of the cationized, disrupted H-bond structures, into the degradant products.
5 Conclusions
In this work the gas-phase UV laser photodissociation absorption spectra of the M+·OB (M+ = Na+, K+, Rb+) complexes were measured for the first time. The electronic spectrum associated with the Na+·OB complex is strikingly different from those of K+·OB and Rb+·OB. Mass-selective IRMPD spectroscopy and computational chemistry was used to show that the cation-dependent UV spectra can be traced to the Na+ ion breaking the intramolecular H-bond in OB, and occupying the position originally taken by the H atom. This is an important result with respect to the UV filtering property of OB, since the resulting perturbed OB geometry blocks the known non-radiative relaxation mechanism which relies on excited state electron-driven H atom transfer.OB is a widely used organic sunscreen that has been highly regarded due its photostability.56–59 However, given that many organic sunscreens (e.g., dioxybenzone and octyl salicylate) rely on similar intramolecular hydrogen bonding for non-radiative relaxation efficacy, we suggest that close coordination to Na+ may jeopardize the intrinsic photostability of these molecules. Time-dependent studies of sunscreen molecules which rely on intramolecular hydrogen bonds for their action are now desirable in the presence of sodium cations to explore the extent to which photostability is impacted by high counterion concentrations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded through the Leverhulme Trust Research Project Grant RPG-2017-147. We thank the University of York and the Department of Chemistry for provision of funds for the OPO laser system, and the University of York High Performance Computing service, Viking, and the Research Computing team, for the provision of computational resources. We gratefully acknowledge the Nederlandse Organisatie voor Wetenschappelijk Onderzoek (NWO) for the support of the FELIX Laboratory. The research leading to this result has been supported by the project CALIPSOplus under the Grant Agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020.Notes and references
- E. L. Holt and V. G. Stavros, Int. Rev. Phys. Chem., 2019, 38, 243–285 Search PubMed.
- L. A. Baker, B. Marchetti, T. N. V. Karsili, V. G. Stavros and M. N. R. Ashfold, Chem. Soc. Rev., 2017, 46, 3770–3791 RSC.
- J. Zhao, S. Ji, Y. Chen, H. Guo and P. Yang, Phys. Chem. Chem. Phys., 2012, 14, 8803–8817 RSC.
- T. N. Karsili, B. Marchetti, M. N. Ashfold and W. Domcke, J. Phys. Chem. A, 2014, 118, 11999–12010 CrossRef CAS PubMed.
- L. A. Baker, M. D. Horbury, S. E. Greenough, P. M. Coulter, T. N. Karsili, G. M. Roberts, A. J. Orr-Ewing, M. N. Ashfold and V. G. Stavros, J. Phys. Chem. Lett., 2015, 6, 1363–1368 CrossRef CAS PubMed.
- L. A. Baker, M. D. Horbury, S. E. Greenough, M. N. Ashfold and V. G. Stavros, Photochem. Photobiol. Sci., 2015, 14, 1814–1820 RSC.
- C. X. Li, W. W. Guo, B. B. Xie and G. Cui, J. Chem. Phys., 2016, 145, 074308 CrossRef PubMed.
- N. G. K. Wong, J. A. Berenbeim and C. E. H. Dessent, ChemPhotoChem, 2019, 3, 1231–1237 CrossRef CAS.
- N. G. K. Wong, J. A. Berenbeim, M. Hawkridge, E. Matthews and C. E. H. Dessent, Phys. Chem. Chem. Phys., 2019, 21, 14311–14321 RSC.
- J. A. Berenbeim, N. G. K. Wong, M. C. R. Cockett, G. Berden, J. Oomens, A. M. Rijs and C. E. H. Dessent, J. Phys. Chem. A, 2020, 124, 2919–2930 CrossRef CAS PubMed.
- P. Nieto, A. Gunther, G. Berden, J. Oomens and O. Dopfer, J. Phys. Chem. A, 2016, 120, 8297–8308 CrossRef CAS PubMed.
- N. R. Walker, R. S. Walters and M. A. Duncan, New J. Chem., 2005, 29, 1495–1503 RSC.
- O. M. Cabarcos, C. J. Weinheimer and J. M. Lisy, J. Chem. Phys., 1999, 110, 8429–8435 CrossRef CAS.
- J. Oomens, N. C. Polfer, G. Berden and J. R. Eyler, Eur. J. Mass Spectrom., 2019, 25, 86–96 CrossRef CAS PubMed.
- N. C. Polfer, J. Oomens and R. C. Dunbar, ChemPhysChem, 2008, 9, 579–589 CrossRef CAS PubMed.
- N. C. Polfer, J. Oomens and R. C. Dunbar, Phys. Chem. Chem. Phys., 2006, 8, 2744–2751 RSC.
- P. B. Armentrout, M. T. Rodgers, J. Oomens and J. D. Steill, J. Phys. Chem. A, 2008, 112, 2248–2257 CrossRef CAS PubMed.
- D. R. Carl, T. E. Cooper, J. Oomens, J. D. Steill and P. B. Armentrout, Phys. Chem. Chem. Phys., 2010, 12, 3384–3398 RSC.
- M. A. Duncan, Int. J. Mass Spectrom., 2000, 200, 545–569 CrossRef CAS.
- R. Z. Li, S. H. M. Deng, G. L. Hou, M. Valiev and X. B. Wang, Phys. Chem. Chem. Phys., 2018, 20, 29051–29060 RSC.
- U. Osterwalder, M. Sohn and B. Herzog, Photodermatol., Photoimmunol. Photomed., 2014, 30, 62–80 CrossRef PubMed.
- L. H. Hofmeister, S. Perisic and J. Titze, Pflug. Arch., 2015, 467, 551–558 CrossRef CAS PubMed.
- S. B. Heymsfield, M. Waki, J. Kehayias, S. Lichtman, F. A. Dilmanian, Y. Kamen, J. Wang and R. N. Pierson, Jr., Am. J. Physiol., 1991, 261, E190–E198 CAS.
- E. Matthews and C. E. H. Dessent, Phys. Chem. Chem. Phys., 2017, 19, 17434–17440 RSC.
- E. Matthews, A. Sen, N. Yoshikawa, E. Bergstrom and C. E. Dessent, Phys. Chem. Chem. Phys., 2016, 18, 15143–15152 RSC.
- S. M. Wellman and R. A. Jockusch, J. Phys. Chem. A, 2015, 119, 6333–6338 CrossRef CAS PubMed.
- A. Sen, T. F. Luxford, N. Yoshikawa and C. E. Dessent, Phys. Chem. Chem. Phys., 2014, 16, 15490–15500 RSC.
- R. Antoine and P. Dugourd, Phys. Chem. Chem. Phys., 2011, 13, 16494–16509 RSC.
- R. E. van Outersterp, J. Martens, G. Berden, J. D. Steill, J. Oomens and A. M. Rijs, Phys. Chem. Chem. Phys., 2018, 20, 28319–28330 RSC.
- J. Martens, G. Berden, C. R. Gebhardt and J. Oomens, Rev. Sci. Instrum., 2016, 87, 103108 CrossRef PubMed.
- D. Oepts, A. F. G. van der Meer and P. W. van Amersfoort, Infrared Phys. Technol., 1995, 36, 297–308 CrossRef CAS.
- A. M. Rijs and J. Oomens, Top. Curr. Chem., 2015, 364, 1–42 CrossRef CAS PubMed.
- G. Berden, M. Derksen, K. J. Houthuijs, J. Martens and J. Oomens, Int. J. Mass Spectrom., 2019, 443, 1–8 CrossRef CAS.
- Schrödinger, 2019.
- A. F. Rodrigues-Oliveira, F. W. M. Ribeiro, G. Cervi and T. C. Correra, ACS Omega, 2018, 3, 9075–9085 CrossRef CAS PubMed.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- P. Verma and D. G. Truhlar, Trends Chem., 2020, 2, 302–318 CrossRef.
- W. Fu and W. S. Hopkins, J. Phys. Chem. A, 2018, 122, 167–171 CrossRef CAS PubMed.
- Y. Nagai, W. Y. Sohn and K. Katayama, Analyst, 2019, 144, 5986–5995 RSC.
- K. X. Wan, I. Vidavsky and M. L. Gross, J. Am. Soc. Mass Spectrom., 2002, 13, 85–88 CrossRef CAS PubMed.
- L. J. M. Kempkes, J. Martens, G. Berden, K. J. Houthuijs and J. Oomens, Faraday Discuss., 2019, 217, 434–452 RSC.
- D. A. Dougherty, Science, 1996, 271, 163–168 CrossRef CAS PubMed.
- K. S. Kim, P. Tarakeshwar and J. Y. Lee, Chem. Rev., 2000, 100, 4145–4186 CrossRef CAS PubMed.
- O. M. Cabarcos, C. J. Weinheimer and J. M. Lisy, J. Chem. Phys., 1998, 108, 5151–5154 CrossRef CAS.
- S. Gronert, J. Am. Soc. Mass Spectrom, 1998, 9, 845–848 CrossRef CAS.
- The intramolecular hydrogen bonded structure is sometimes refered to as “chelated” and the non hydrogen bonded as “non-chelated” in the oxybenzone literature. We’ve chosen to forgo this termonology to preempt any confusion the term might have with the metal ligand community.
- Y. Xie and C. B. Lebrilla, Anal. Chem., 2003, 75, 1590–1598 CrossRef CAS PubMed.
- K. Rajabi, E. A. Gillis and T. D. Fridgen, J. Phys. Chem. A, 2010, 114, 3449–3456 CrossRef CAS PubMed.
- A. Gunther, P. Nieto, G. Berden, J. Oomens and O. Dopfer, Phys. Chem. Chem. Phys., 2014, 16, 14161–14171 RSC.
- B. F. Milne, Y. Toker, A. Rubio and S. B. Nielsen, Angew. Chem., 2015, 127, 2198–2201 CrossRef.
- M. H. Stockett, L. Musbat, C. Kjaer, J. Houmoller, Y. Toker, A. Rubio, B. F. Milne and S. Brondsted Nielsen, Phys. Chem. Chem. Phys., 2015, 17, 25793–25798 RSC.
- S. R. Domingos and M. Schnell, J. Phys. Chem. Lett., 2018, 9, 4963–4968 CrossRef CAS PubMed.
- R. Kumasaka, A. Kikuchi and M. Yagi, Photochem. Photobiol., 2014, 90, 727–733 CAS.
- M. T. Ignasiak, C. Houee-Levin, G. Kciuk, B. Marciniak and T. Pedzinski, ChemPhysChem, 2015, 16, 628–633 CrossRef CAS PubMed.
- S. Forestier, J. Am. Acad. Dermatol., 2008, 58, S133–S138 CrossRef PubMed.
- A. R. Abid, B. Marciniak, T. Pędziński and M. Shahid, J. Photochem. Photobiol., A, 2017, 332, 241–250 CrossRef CAS.
- Y.-S. Liu, G.-G. Ying, A. Shareef and R. S. Kookana, Environ. Chem., 2011, 8, 174–181 CrossRef CAS.
- N. Tarras-Wahlberg, G. Stenhagen, O. Larko, A. Rosen, A. M. Wennberg and O. Wennerstrom, J. Invest. Dermatol., 1999, 113, 547–553 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp03152f |
| This journal is © the Owner Societies 2020 |