Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The nanomechanics of individual proteins
Marc
Mora
 ab,
Andrew
Stannard
ab,
Andrew
Stannard
 ab and
Sergi
Garcia-Manyes
ab and
Sergi
Garcia-Manyes
 *ab
*ab
aDepartment of Physics and Randall Centre for Cell and Molecular Biophysics, King's College London, WC2R 2LS, London, UK. E-mail: sergi.garcia-manyes@kcl.ac.uk
bThe Francis Crick Institute, 1 Midland Road, London NW1 1AT, UK
First published on 15th September 2020
Abstract
Mechanical forces regulate a large variety of cellular functionalities, encompassing e.g. motility, differentiation and muscle contractility. To adapt to the dynamic change in mechanical stress, the constitutive individual proteins need to reversibly stretch and recoil over long periods of time. Yet, the molecular mechanisms controlling the mechanical unfolding and refolding of proteins cannot be accessed by protein folding biochemistry experiments conducted in the bulk, because they cannot typically apply forces to individual proteins. The advent of single-molecule nanomechanical techniques, often combined with bespoke protein engineering strategies, has enabled monitoring the conformational dynamics of proteins under force with unprecedented length-, time- and force-resolution. This review focuses on the fundamental operational principles of the main single-molecule nanomechanical techniques, placing particular emphasis on the most common analytical approaches used to extract information directly from the experiments. The breadth of enabling applications highlights the most exciting and promising outputs from the nanomechanics field to date.
Key learning points1. Mechanical unfolding of proteins is a localized process that results from the disrupting of just a few key hydrogen bonds that bear mechanical stress – the so-called mechanical clamp.2. The anisotropic nature of mechanical force propagation across the protein backbone implies that proteins equilibrate along a completely different set of reaction coordinates than in classical biochemistry protein folding experiments conducted in the bulk. 3. Single-molecule nanomechanical experiments, and namely those conducted with the atomic force microscope (in the high-force regime) and optical and magnetic tweezers (in the low-force regime), capture the conformational dynamics of single proteins under force. 4. The force-extension operational mode enables easy characterization of the mechanical stability of proteins, whereas force-clamp experiments allow more reliable reconstruction of the 1D (un)folding energy landscape by measuring the kinetics of the (un)folding reaction. 5. Single-molecule nanomechanical experiments enable a variety of applications that, collectively, are building up a new portfolio of protein biochemistry under force. |
Introduction
From the fast flapping wings of a hummingbird in flight, to the slithering of a snake or the bending response of sunflower plants to track light, molecular biomechanics are at play. Mechanical forces also control a variety of functionalities relevant to human physiology.1 The continuous stretching and relaxing of a beating heart or the cyclic distension and contraction of the lungs during respiration require tissues to elastically accommodate to the dynamic changes imposed by rapidly fluctuating mechanical stress. At the cellular level, a number of crucial functionalities, including differentiation, proliferation, or motility have proved to be finely regulated by mechanical perturbations.2 All these macroscopic mechanically-regulated functionalites underpin a myriad of microscopic mechanisms—ultimately reaching individual proteins and their constituent chemical bonds—that need to continuously break and reform upon the application mechanical stimuli. Unfortunately, and despite a wealth of impressive progress, classical biochemistry techniques using chemicals (e.g. GuHCL or urea) or temperature as denaturant agents cannot provide useful information in this context, simply because they are unable to apply forces to the studied proteins. To circumvent this limitation, the development of a number of single molecule nanomechanical techniques has enabled the investigation of the molecular mechanisms by which proteins (whether exposed to in vivo physiological forces or not) unfold and refold under force. Collectively, these experiments have created a prolific and exciting field of research that have established mechanical force as an orthogonal way to study protein folding from a complementary and completely new vista to the classical biochemistry-led approach. While this technical review aims to provide the reader with a first snapshot of the state-of-the-art of the protein nanomechanics field, it is particularly devoted to illustrate the basic principles of operation and the most fundamental and practical approaches used to extract information from the individual unfolding and refolding trajectories obtained in the laboratory, mostly using the single-molecule force-spectroscopy mode of the atomic force microscope (AFM), and complemented by the magnetic tweezers (MT) technique. A final, general description of the most outstanding enabling applications might help the reader obtain a global overview of the level of (single-bond) detail that can be extracted today from this compelling experimental approach.Tensile force as an orthogonal way to trigger protein unfolding
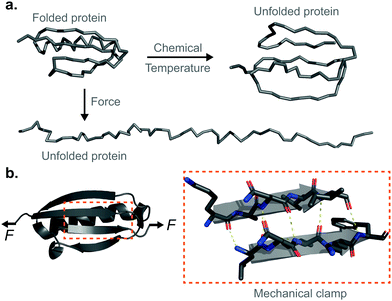
Proteins are fundamental biomolecules constructed by the covalent polymerisation of individual amino acids. They are involved in most cellular processes, either functioning individually or comprising parts of complex supramolecular machineries. Their functionality is ultimately dependent on their structure; to perform optimally, proteins are generally required to fold into their well-defined—native—conformations, as dictated by the fine interplay of non-covalent interactions (e.g. hydrophobic, hydrogen bonding, electrostatic, van der Waals) and covalent bonds (e.g. disulfide, isopeptide) between the composing amino acids. Anfinsen led the fundamental discovery that protein folding is a reversible process; upon quenching the denaturing agent (either temperature or the chemical environment of the solution) the unfolded protein is usually able to return back into its natively-folded conformation. Mechanical force is not an exception—once a protein is mechanically unfolded, removing the stretching force typically results in the protein refolding back into its folded conformation, recovering the mechanical stability of the protein's native state. Despite this general analogy, when mechanical force is used as a ‘denaturant’, proteins equilibrate through a completely different set of reaction coordinates upon unfolding/refolding compared to those sampled by biochemical technqiues, rendering the unfolding and refolding processes fundamentally different, and hence making them difficult to conceptually compare or assimilate (Fig. 1a). The fundamental differences between the protein folding in vitro studies conducted with the classical biochemistry-based bulk techniques and those using nanomechanical techniques stem from the inherent way the experiments are conducted; (1) being of a vectorial nature, the applied force distributes non-isotropically across the protein backbone, implying that not all residues are exposed in the same way to the denaturing force. By contrast, when e.g. the temperature of a protein solution is increased, all of the amino acids are equally affected by this global perturbation. (2) Contrary to bulk denaturation methods, where all amino acids contribute to the overall energy underpinning the unfolding process, mechanical denaturation is a localised process depending on only the non-covalent bonds established between few residues, which form the force-bearing motif3—the mechanical clamp. In general, the mechanical clamp (which is often associated with the position of the transition state in the 1D energy landscape) is composed by a set of key hydrogen-bonds (usually ∼3–5 hydrogen bonds) between secondary structural elements that resist extension in the vectoral direction of the applied force (Fig. 1b). Once the mechanical clamp is disrupted, the protein unfolding process is typically ‘downhill’, leading to the complete unfolding without further mechanical resistance. Hence, knowledge of the tertiary structure is crucial to predicting and interpreting the behaviour of proteins under force. As a rule of thumb, β-structured proteins such as the immunoglobulin domains of titin,4 requiring ∼200 pN to unfold, exhibit greater mechanical stability than α-structured proteins—for example, spectrin repeats5 require forces as low as ∼25 pN. At the lower end of the spectrum, unstructured proteins display almost no mechanical resistance. However, structural considerations are not enough; in addition to understanding the precise topology of the mechanical clamp, the directionality of the applied force—and therefore the precise mechanism by which the mechanical clamp is disrupted (in general, shearing two neighboring β-strands requires a higher force than simply unzipping or peeling them)—plays an important role in establishing the resistance of the protein to unfolding.6 In fact, the important empirical observation that the protein pulling direction dramatically changes the mechanical stability of proteins7 is in sharp contrast with the isotropic behaviour of classical protein folding experiments. (3) Arguably the most conspicuous difference between the mechanical and biochemical denaturation methods are the conformations sampled in each distinct set of experiments. For example, in classical bulk techniques, unfolding leads to a protein conformation that, for an e.g. ∼100-residue globular protein, exhibits an average radius of gyration that is only ca. ∼2 nm larger than that of the natively-folded state.8 By contrast, mechanical unfolding of this exemplar protein would result in the end-to-end distance—extension—between the N- and C-termini increasing from the few nanometres described by the crystal structure of the natively-folded state to tens of nanometres of the resulting unfolded, mechanically-extended conformation. Thus, while the ‘unfolded’ state nomenclature applies to both methodologies, they describe radically different protein conformations, which underlie the different regions of the protein's folding energy landscape sampled by the distinct experimental methods.9 (4) Given all the above considerations, it follows that the data emerging from both protein folding experiments (namely, the biochemical perturbations or changes in temperature conducted in the bulk, or the single protein experiments under force) are different and should not be directly compared. In particular, the thermodynamic stability of the protein does not need to correlate with its mechanical stability—a kinetic (and not thermodynamic) quantity. In that sense, it is completely possible to encounter a protein with high thermodynamic stability (exhibiting a high melting temperature) that exhibits a low mechanical stability (requiring low forces to unfold). For example, the c1C domain of the cohesin I multidomain protein exhibits an unfolding force of ∼425 pN and a melting temperature of ∼74 °C, whereas another domain of the same protein (the c2A) displays a lower unfolding force (∼214 pN) and a higher melting temperature (∼87 °C).10 As a consequence, mechanical unfolding of a long polyprotein chain composed of different proteins with distinct mechanical stabilities follows a hierarchy in their mechanical—and not thermodynamic—stabilities, implying that mechanically weak proteins unfold first, followed by the mechanical unfolding of the mechanically resilient proteins of the polyprotein chain.11Single-protein force spectroscopy techniques
The nanomechanical characterisation of proteins has only been made possible thanks to the advent of single-molecule force spectroscopy techniques coupled with advances in protein expression and purification methods. Given the wide range of mechanical resistance exhibited across proteins (∼10 pN – 2 nN), a single technique alone cannot be used for all characterisations. The three most commonly-used instruments for single-molecule force spectroscopy (SMFS) studies12—atomic force microscopes (AFMs), magnetic tweezers (MT), and optical tweezers (OT)—are all capable of probing protein conformational changes at the single-molecule level with different force-, temporal-, and spatial-resolutions. Two main operational modes are typically used by the 3 techniques; (a) ‘force-extension’ and ‘constant velocity’ are the terms frequently used to describe the operational mode where force is monitored as extension is increased at a steady rate; a mode commonly used with AFM and OT that does not require electronic feedback. (b) ‘Force-clamp’ or ‘constant force’ refer to the operational mode where the protein extension is monitored over time as force is held constant. This requires force feedback in AFM, but not in MT (due to the insignificant variation in magnetic field experienced by the magnetic bead when the tethered protein folds/unfolds). OT can work under ‘active’ or ‘passive’ clamp conditions, depending on whether an external feedback mechanism is applied. Finally, (c) ‘force-ramp’ refers to the mode where extension is monitored as force is increased at a steady rate; this requires force feedback in AFM and OT, and subtly, but significantly, differs from force-extension due to the nonlinear elasticity of proteins.We next discuss how force and extension are controlled and monitored across SMFS experiments, including how proteins of interest are tethered to the respective pulling devices in these different techniques, before briefly discussing the necessary molecular biology steps to engineer the required protein constructs amenable to these single molecule experiments.
SMFS using an atomic force microscope
The atomic force microscope (AFM), originally designed for the topographic imaging of non-conducting surfaces with sub-nanometre resolution, is now also widely-used for the nanomechanical characterisation of molecules. The usual set-up of an AFM used for SMFS studies consists of a piezoelectric actuator, which the sample substrate is affixed to, and a flexible cantilever with a sharp tip at the free end (Fig. 2). A laser is reflected off the rear side of the cantilever into a photodetector (usually four-quadrant, although two quadrants suffice for SMFS). The sample used in such experiments is a substrate coated with a solution containing the engineered protein construct; one terminus of these constructs is tethered to the substrate, often with chemical specificity. Several surface-tethering strategies are reported in the literature; an extremely common example is the physisorption of proteins on freshly evaporated gold substrates; the attachment can be improved through the presence of a cys-tag at one terminus to form covalent gold–sulfhydryl (Au–SH) bonds. Other tethering strategies include the use of receptor–ligand interactions (mainly antibodies) such as avidin/biotin, streptavidin/biotin, cohesin/dockerin and antidioxigen/dioxigen, as well as different surface chemistry coatings (mica and hexahistidine-Ni-NTA chemistry). More recently, the use of HaloTag and SpyTag/catcher chemistry has been described to provide covalent attachment, both to the substrate and to the cantilever tip.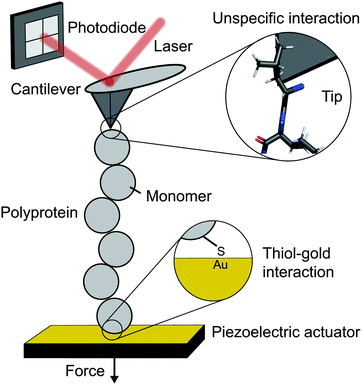 | ||
| Fig. 2 Schematic diagram showing the key elements in a single molecule experiment using an atomic force microscope (AFM). | ||
The experimental control is achieved by the movement of the piezoelectric actuator. As the actuator is retracted (away from the cantilever), tensile force is generated in the tethered protein, which in turn deflects the cantilever until the protein's tensile force and cantilever's restoring force balance. This force is simply given by Hooke's Law – the physical deflection of the cantilever multiplied by the cantilever spring constant, kc, (independently measured through thermal tuning). The cantilever deflection is measured through the change in the photodetector signal; when the cantilever deflects, the reflected laser strikes the photodetector in a different position resulting in a voltage change. The optical lever sensitivity (dependent on the precise position the laser strikes the cantilever) is calibrated in advance of measurements to convert this voltage change into the physical deflection (which is then converted to force).
The simplest operational mode of SMFS with an AFM is force-extension; while the actuator is retracted at a constant velocity, v, the force, F, is measured as a function of protein extension, x (the actuator displacement minus the cantilever deflection). When operating in force-clamp mode, the protein is held at a constant force over time, t. When the protein unfolds, increasing its contour length, the force will momentarily drop. Active electronic feedback in the form of a proportional-integral-derivative loop is employed to retract the actuator the necessary amount to re-establish the desired set-point force.
The spatial range and resolution of these experiments are dictated by the piezoelectric actuator; sub-nm resolution with ∼1 μm range is typical. Force resolution depends on the cantilever spring constant, smaller values give higher resolution (kc ∼ 10 pN nm−1 is typical); inherent noise sets a ∼10 pN lower limit of force sensitivity. Temporal resolution (bandwidth) is dictated by cantilever response rate (resonant frequency) and, where relevant, the speed of feedback electronics. Recent work on home-made modified cantilevers have achieved a temporal resolution of 2 μs.
SMFS using magnetic tweezers
Until the last decade, magnetic tweezers were primarily restricted to studying the stretching and twisting of nucleic-acid-based biopolymers. The development of new anchoring strategies, however, has extended their use to study protein (un)folding under low force conditions with exceptional stability over long time periods (up to weeks).13 The usual MT set-up used for protein SMFS studies consists of a fluid cell situated on a piezoelectrically-controlled high-magnification objective of an inverted microscope, with moveable magnets, permanent or electromagnets, positioned above the cell (Fig. 3).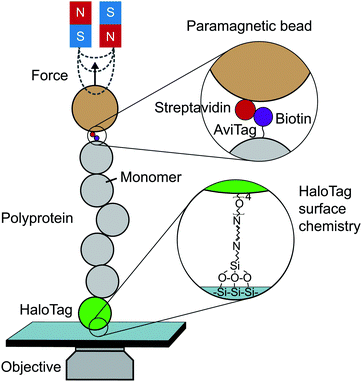 | ||
| Fig. 3 Schematic diagram showing the key elements required to perform a single-molecule magnetic tweezers (MT) experiment. | ||
The fluid cell contains a solution of engineered protein constructs and paramagnetic beads (polystyrene microspheres embedded with superparamagnetic nanoparticles). The lower surface of the cell is a functionalised glass substrate to which one terminus of the protein constructs specifically tether to. Several substrate-construct binding strategies, including HaloTag, SpyTag, and NHS-maleimide crosslinkers, have been implemented in protein SMFS experiments. The other terminus specifically tethers to paramagnetic beads; a common strategy is streptavidin–biotin binding between streptavidin-coated beads and biotinylated AviTag-terminating constructs (although SpyTag binding has also been used for construct-bead interactions).
Tensile force is applied via the magnetic force acting on the paramagnetic bead, the magnitude and direction of which is dictated the magnetic field. The field shape is determined by the geometrical configuration of the permanent (or electro-) magnets used; the field the bead experiences is modulated by changing the magnet position (or current). The magnetic force is the product of the bead magnetic moment (induced by the field) and the magnetic field gradient it experiences, forces of up to ∼100 pN can be applied to manipulate paramagnetic beads ranging from 0.5 to 5 μm in diameter. Complete knowledge of the field shape and the bead magnetisation curve allows one to calculate force as a function of magnet position. Force calibration is, however, typically achieved empirically via measurement of lateral fluctuations for long (∼10 μm) constructs or by relating protein unfolding extensions to polymer elasticity models for short (∼100 nm) constructs – such as proteins. Typically, the magnetic force is a very-slowly-varying nonlinear function of magnet-bead separation, from ∼100 pN at closest approach to ∼1 pN at ∼5 mm separation. As such, any protein un/folding events (i.e. ∼10 nm changes in magnet-bead separation) during an experiment will insignificantly change the force experienced by the bead, and so with magnet position fixed, experiments operate in passive force-clamp conditions.
MT experiments are performed on an optical microscope to image tethered beads and calculate changes in their vertical positions, which correspond to the changes in the extension of their tethering proteins under force. 2D Fourier transforms of the bead images are taken and compared to libraries of calibration measurements (a z-stack of images aquired for a bead in the absence of magnetic field) to determine vertical position. The temporal resolution is determined by (1) the temporal resolution as dictated by the frame rate of the CCD camera (∼1 ms), and (2) the rate at which force can be changed by moving the mechanical stage adjusting the magnets position. Improving both sources has led a recent electromagnetic tweezer set-up to achieve a temporal resolution as low as 0.1 μs. Experimental drift is removed by subtracting at each time point the vertical position of a (non-magnetic) reference bead firmly attached to the substrate. Thus, in MT force-clamp experiments, the force F is set to the desired (by definition, constant) value and protein extension (i.e. magnetic bead position) is measured over time.
SMFS using optical tweezers
An optical trap is obtained by focussing a laser beam through a high numerical aperture objective, capable of holding dielectric particles at its centre. The magnitude of the restoring force is linearly proportional to the laser intensity for small displacements from the trap centre (up to ∼150 nm).By tethering an individual biomolecule between a trapped bead and a pipette-fixed bead, or between two laser-trapped beads (dumbbell assay, Fig. 4), optical traps have been used to measure with high accuracy the force required to unfold individual nucleic acids and proteins. In the case of proteins, this experimental assay requires that the protein under study is bracketed between two DNA handles that are typically attached to beads using one of several molecular strategies. Commonly, to tether DNA handles to dielectric beads, biotin–dioxygen and biotin/avidin–streptavidin chemistry is used, whereas to attach the DNA handles with the molecule of interest, cysteine crosslinker, ssrA tag, OligoCoA/biotin, HaloTag, ybbRtag and SpyTag-Catcher are employed. The requirement of DNA molecular handles poses an intrinsic limitation to the protein unfolding experiments, since at ∼65 pN the well-characterised B–S transition in DNA occurs, placing an upper limit to the mechanical stability of the proteins that are amenable to study using the OT technique. While mostly used to investigating the folding energy landscape of DNA and RNA, very elegant works on individual proteins have emerged with OT, with applied forces ranging from ∼0.1 to ∼65 pN with subnanometer precision and millisecond temporal resolution. OT experiments can be perfomed in either constant velocity or constant force modes. However, as opposed as AFM and MT, OT can apply constant force both actively (with the use of feedback electronics) and passively (by working in the anharmonic region of the trapping potential).
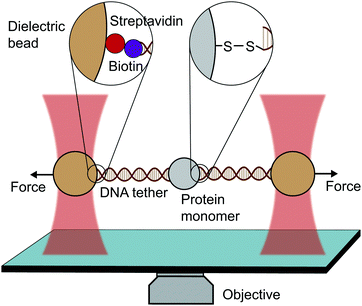 | ||
| Fig. 4 Diagram representing a single-molecule experiment on a monomeric protein using optical tweezers (OT). | ||
In conclusion, the different SMFS techniques have their inherent advantages and limitations, but combined, they are a powerful suite of advanced tools enabling the investigation of a wide spectrum of proteins with distinct mechanical stabilities. From a practical viewpoint, the AFM is more suitable for studying mechanically resistant proteins, whereas the MT and the OT are a better fit for analysing mechanically labile proteins.
Polyprotein engineering provides unmistakable molecular fingerprints
With some exceptions, OT nanomechanical studies on proteins have typically employed individual monomers. By contrast, AFM (and most recently, MT) typically rely on the use of polyproteins, which are long protein chains containing identical repeats of the same protein monomer of interest (homopolyproteins), or protein chimeras (heteropolyproteins) typically containing the protein of interest bracketed between a few domains of another protein marker, the mechanical stability of which has been widely studied, or constructs alternating between marker proteins and the protein of interest. In either case, the use of polyproteins emerged as a molecular strategy to overcome the challenge in earlier AFM studies (and current ones that are plaguing the field) using short protein monomers, where the unavoidable spurious interaction between the substrate and the cantilever tip would often mask the unfolding signal. The use of polyproteins, exhibiting a regular unfolding pattern, provided the single molecule field with a high-quality standard practice that ensures the use of reliable and unmistakable internal molecular fingerprints. The molecular engineering of such long polyproteins is in general rather straightforward through the concatenated ligation of cDNA.14 Once engineered, the resulting plasmids are transformed into bacteria (normally E. coli), which promote expression of the protein construct. Following expression and lysis, proteins are purified through a resin Talon column prior to conventional size-exclusion chromatography. Other methods used in the literature to successfully obtain polyproteins include the use of bis-maleimide crosslinkers and disulfide bond formation by polymerizing protein monomers with two engineered cysteine residues,15 however, by using these methods the length of the resulting polyprotein cannot be controlled. More recently, a new enzymatic approach using the combination of a strict protein ligase OaAEP1 and a protease TEV to polymerize protein monomers was successfully developed.16An important observation that broadly validates the use of polyproteins is that each of the individual domains behaves independently, i.e. its mechanical unfolding/refolding properties are not compromised by them being part of the long polyprotein chain. In what follows, we focus on the description of the main operational modes and the most important findings enabled by two complementary techniques that have been successfully applied to protein nanomechanics and that complement each other by covering different regions of the measurable force spectrum; while the most established AFM technique excels at interrogating the mechanical stability of proteins with relatively large mechanical stability, the comparatively novel MT technique applied to proteins provides invaluable information on the nanomechanical properties of proteins in the low force regime.
Protein unfolding with force
We start by discussing in detail the two main modes of operation of the single molecule techniques, putting special emphasis on how the data are extracted from the individual unfolding and refolding trajectories obtained in the laboratory, and how this data is then analysed. Although the basic operational principles stay the same for OT, we will mainly focus the experimental description to those conducted with AFM and MT.Operational modes
(a) Force extension (or constant-velocity) mode
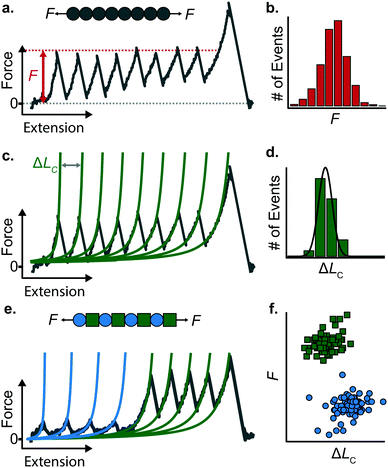
When a surface-tethered polyprotein composed of identical domains of the same protein (homopolyprotein) is picked up by the cantilever tip and extended at a constant velocity v, the tensile force experienced by the protein increases in a nonlinear fashion. When the force has increased sufficiently, one domain—irrespective of its position in the construct—unfolds due its mechanical clamp being ruptured. This liberates amino acids trapped behind the clamp, incrementing the contour length by ΔLC, resulting in a momentary drop in tensile force. This process is repeated until all domains are unfolded, producing a characteristic saw-tooth pattern of force against extension, F(x) (Fig. 5a). Eventually one of the tethering points of the protein fails; this final peak in the unfolding trajectory corresponds to the detachment of the protein either from the surface or from the cantilever tip, and is hence not considered in the analysis. Two relevant experimental read-outs can be extracted from these saw-tooth unfolding trajectories; each unfolding event can be characterised by (i) an unfolding force F and (ii) a contour length increment ΔLC; the former can be read directly from the data, the latter needs more analysis.(i) The unfolding force F provides a measure of the mechanical stability of the domain. Mechanically unfolding of a protein is a stochastic (thermally-activated) process and as such there will be a distribution of F values, which can be characterised by an average 〈F〉, or most-probable Fmp, value (Fig. 5b). These values have a dependency on velocity, so characteristic unfolding forces should only be compared between two proteins if they were extended at the same pulling speed. A large number of proteins have been characterized using this constant velocity approach, displaying a large spread in their mechanical stabilities that roughly spans from ∼20 pN all the way up to 2–3 nN; to illustrate this breadth of forces, measured (at comparable pulling velocities) in three different examples from the literature, we start with the seminal work in the late 1990's that first reported the characteristic saw-tooth unfolding pattern of a naturally-occurring polyprotein—titin—composed of many immunoglobulin domains, which required ∼200 pN to unfold.4 At the upper end of the force spectrum, it was recently shown that the SdrG:Fgβ complex (between the SD-repeat protein G from Staphylococcus epidermidis and the β chain of human fibrinogen) ruptures at ∼2.3 nN.17 By contrast, the mechanosensitive rod protein talin, exhibiting an α-helix topology, unfolds at forces as low as ∼25 pN,18 at the lower force resolution limit for AFM SMFS.
(ii) The change in extension between two consecutive unfolding events (i.e. between two consecutive peaks) in an unfolding trajectory relates to the number of amino acids liberated upon unfolding. In order to determine ΔLC from experimental unfolding trajectories, models of polymer elasticity must be employed, of which several exist, but here we focus on the worm-like chain (WLC) model due to its common use in the field.
Polymer elasticity models describe the behaviour of semi-flexible polymers when experiencing tensile forces. These models assume that in the absence of force, polymers remain in random, collapsed conformations. When force is applied, the number of possible conformations is increasingly reduced, resulting in an entropic opposition to elongation. For the WLC model, this restoring force as a function of the extension can be approximated by
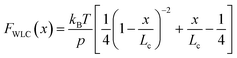 | (1) |
To find the contour length increment of an unfolding event of interest, two fits of FWLC(x) are applied to data keeping the contour length as a free parameter. First, data acquired between the previous unfolding event (if there was one) and the event of interest are fitted to find LC. Second, data acquired between the event of interest and the next unfolding event (or the final detachment event) is fitted to find LC + ΔLC. Thus, the difference between the contour lengths found in the consecutive two fits gives the contour length increment. This analysis is performed for each unfolding event in a given force-extension measurement (Fig. 5c); analysing repeated measurements generates a distribution of contour length increments from which an average can be found (Fig. 5d). The experimentally measured value of ΔLC can provide an educated guess on the location of the protein's mechanical clamp if the crystal structure is available. The predicted value of the ΔLC can be estimated by using the following relationship:
| ΔLC = #aa·(L/aa) − LF | (2) |
Stretching a heteropolyprotein (whereby the protein of interest is typically intercalated between two protein marker domains with well-characterised mechanical properties) under constant velocity conditions results in a saw-tooth pattern consisting of two populations of unfolding events (Fig. 5e), each of which being characterised by an unfolding force F and contour length increment ΔLC. With an appropriate choice of the marker protein, the two populations can be easily singled out using a F − ΔLC scatterplot (Fig. 5f).
The use of heteropolyproteins has been also very useful when it comes to investigating the unknown mechanical properties of a protein of interest in its monomeric form. In this case, the common strategy consists in flanking a protein within multiple marker proteins. For example, Dietz and Rief studied the mechanical unfolding of green fluorescent protein (GFP) when it was flanked either side by 4 titin domains,19 revealing that GFP exhibits a characteristic 〈F〉 = 104 pN and ΔLC = 76.6 nm when it is pulled from the direction of its N and C termini at 300 nm s−1. Since proteins unfold following a hierarchy in their mechanical stabilities, a potential problem in characterising the protein monomers with lower mechanical stability than the markers (i.e. it unfolds first), is the possible undesired, non-specific interactions between the cantilever and the surface, which could mask or introduce uncertainty in the measurements. To circumvent this problem, either a strict choice of clean trajectories for further analysis (thus increasing the experimental effort) or the design of proteins within a specifically-designed vector that separates the protein of interest from the surface upon unfolding are required.
While most proteins unfold in a two-state fashion (i.e. displaying just one unfolding peak characterised by a unique associated ΔLC value), some others exhibit mechanical intermediate states that are hallmarked by additional peaks in individual unfolding trajectories (and hence showing an associated shorter ΔLC than the total extension of the protein). For example, the Li lab showed that T4 lysozyme unfolds through multiple pathways displaying different mechanical intermediates,20 a phenomena generally described as ‘kinetic partitioning’.
Besides being an easy tool aimed at the fast characterization of the mechanical properties of a protein, the force-extension mode was also used in early days to investigate the kinetic parameters defining the mechanical energy landscape of a protein. Due to the nature of the technique, single-molecule experiments only have access to the 1D projection of the—multidimensional and complex—(un)folding energy landscape. The shape of this landscape is dominated by the enthalpic interactions (that keep the protein folded and mechanically rigid) at small extensions and the entropic elasticity at large extensions. It follows that, in the absence of external force, the folded structure is the only energy minimum of the system. This minimum can be characterised by its height and width—the activation energy, ΔE, and the distance to the transition state, Δx, respectively. The application of external tensile force adds a new term, −Fx, to the energetic profile of the system. The incorporation of this term, representing the work done by the external force, ‘tilts’ the energy landscape towards extended conformations and reduces the energy barrier to ΔE − FΔx. Notably, the application of force will also lead to the establishment of a second energy minima (corresponding to an unfolded state) at an extension dictated by the balance between the applied force and the entropic restoring force generated by the protein (that can be predicted with the WLC model).
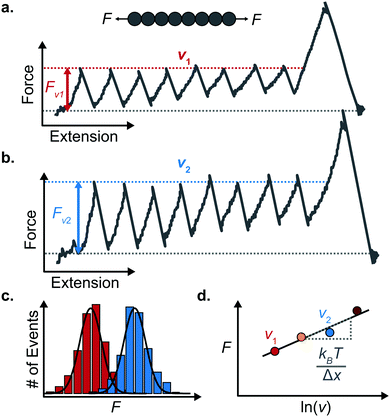
An important observation using the force-extension mode is that traversing the unfolding energy landscape at higher velocities gives rise to higher unfolding forces (Fig. 6a–c). This can be intuitively understood from considering the time it takes to stochastically surmount the free energy barrier to unfold. While force acts to reduce the barrier height, a higher velocity means less sampling time (thus less probability) of surmounting the energy barrier at any given force. Assuming that a protein unfolds in a two-state manner, and that Δx is invariant with the applied force, the dependency of the most probable unfolding force with the loading rate (r) is given by the model developed by Evans and Ritchie:
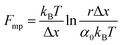 | (3) |
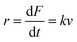 | (4) |
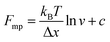 | (5) |
The MC method simulates force-extension traces at different pulling speeds by taking into account the force that the protein experiences at different extensions (by using the relationship given by WLC model) and the probability of protein unfolding in order to generate unfolding force distributions at the different pulling speeds used in the experiment. Through trial and error, Δx and α0 are optimised to best match the experimental unfolding force distributions over the same span of experimental pulling velocities. Alternatively, a graphical approach of measuring the loading rate at the moment of unfolding can be used. Here, each unfolding event (i.e. each rupture peak) is characterised by both an unfolding force F and a loading rate r (where the latter is determined by the effective stiffness and the pulling velocity, as per eqn (4)). At a given pulling speed, many individual unfolding events are recorded, and the unfolding force and the loading rate can be determined. By repeating this process for different pulling speeds, the resulting plot of F against ln(r) allows the kinetic parameters to be found. Milles et al.,17 for example, used this method of data analysis to show that the extreme mechanostabiliity of the SdrG:Fgβ complex corresponds to small values of both Δx = 0.047 nm and α0 = 1.0 × 10−9 s−1.
While the Evans–Ritchie model is useful to approximate kinetic information from force-extension data, the assumption that there is a linear dependency between F and ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v has been shown, in some cases, to be an oversimplification, as the linear dependency deviates at high and low pulling speeds—due to the dependency of Δx with force (in addition to nonlinear protein elasticity, as already discussed). In an effort to better reproduce the experimental complexity of the protein unfolding process when pulled at a constant velocity, the Dudko–Hummer–Szabo model21 was developed to take into account the dependence of the transition state with the applied force:
v has been shown, in some cases, to be an oversimplification, as the linear dependency deviates at high and low pulling speeds—due to the dependency of Δx with force (in addition to nonlinear protein elasticity, as already discussed). In an effort to better reproduce the experimental complexity of the protein unfolding process when pulled at a constant velocity, the Dudko–Hummer–Szabo model21 was developed to take into account the dependence of the transition state with the applied force:
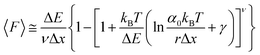 | (6) |
![[7 with combining tilde]](https://www.rsc.org/images/entities/char_0037_0303.gif) is the Euler–Mascheroni constant and v is a parameter describing different shapes that the energy landscape can adopt, with v = 1/2, 2/3 and 1 corresponding to cusped, linear-cubic and linear landscapes, respectively. A key aspect of this model is that it enables extraction of the activation energy, ΔE. Returning to the recent study by Miles et al. of the SdrG:Fgβ complex, using this model gives ΔE = 78 kBT (and Δx = 0.12 nm and α0 = 6.1 × 10−22 s−1) for a cusped landscape and ΔE = 66 kBT (and Δx = 0.093 nm and α0 = 7.7 × 10−18 s−1) for a linear-cubic landscape.
is the Euler–Mascheroni constant and v is a parameter describing different shapes that the energy landscape can adopt, with v = 1/2, 2/3 and 1 corresponding to cusped, linear-cubic and linear landscapes, respectively. A key aspect of this model is that it enables extraction of the activation energy, ΔE. Returning to the recent study by Miles et al. of the SdrG:Fgβ complex, using this model gives ΔE = 78 kBT (and Δx = 0.12 nm and α0 = 6.1 × 10−22 s−1) for a cusped landscape and ΔE = 66 kBT (and Δx = 0.093 nm and α0 = 7.7 × 10−18 s−1) for a linear-cubic landscape.
These different approaches employed to determine the kinetic parameters from force-extension measurements have their own advantages and disadvantages. However, the main limitation stems from changes in protein stiffness while the molecule is pulled at a constant velocity. Such a drawback can be overcome by applying a constant force to the protein.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v. (v) By fitting the Evans–Ritchie model (eqn (3)) and with the help of MC simulations or by using the graphical mehod, the α0 and Δx values can be obtained.
v. (v) By fitting the Evans–Ritchie model (eqn (3)) and with the help of MC simulations or by using the graphical mehod, the α0 and Δx values can be obtained.
(b) Force clamp
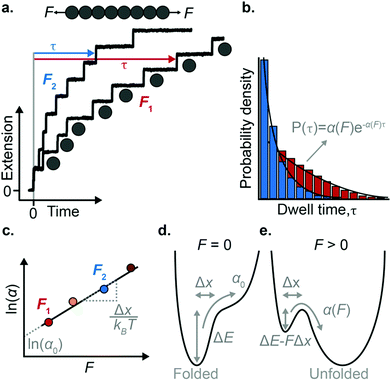
The force-clamp mode of nanomechanical experiments involves applying a constant force during the timecourse of a single molecule measurement. This technical achievement greatly simplifies the extraction of the fundamental parameters defining the (un)folding energy landscape. Under force-clamp conditions, mechanical unfolding of a homopolyprotein results in a staircase-like unfolding trajectory, where each individual step corresponds to the unfolding of an individual domain within the polyprotein chain. Each unfolding event has an associated dwell/survival time τ—the time between force application and unfolding (Fig. 7a). After measuring many unfolding events at a constant force, a probability density distribution of dwell times can be created (Fig. 7b), from which the force-dependent unfolding rate α(F) can be found.According to the Bell model, the probability density function of dwell times is given by f(τ) = α(F)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−α(F)τ), such that the average dwell time is
exp(−α(F)τ), such that the average dwell time is 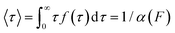 , and hence the force-dependent unfolding rate is simply the inverse of the average dwell time α(F) = 1/〈τ〉 (this argument assumes that each unfolding event is a two-state process, this is not always the case, however, and more complicated models can be needed to better capture the dynamics of unfolding transition). In one of the first applications of force-clamp measurements using an AFM, Schlierf et al. found α(100 pN) = 0.36 s−1, α(120 pN) = 1.9 s−1, and α(140 pN) = 7.7 s−1 for the model protein ubiquitin.22
, and hence the force-dependent unfolding rate is simply the inverse of the average dwell time α(F) = 1/〈τ〉 (this argument assumes that each unfolding event is a two-state process, this is not always the case, however, and more complicated models can be needed to better capture the dynamics of unfolding transition). In one of the first applications of force-clamp measurements using an AFM, Schlierf et al. found α(100 pN) = 0.36 s−1, α(120 pN) = 1.9 s−1, and α(140 pN) = 7.7 s−1 for the model protein ubiquitin.22
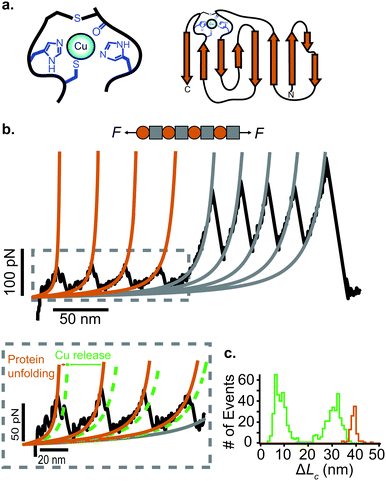
Once the unfolding rate at each individual force is established, one can have access to the underlying parameters defining the unfolding energy landscape of the protein under force. Different models on how to interpret the force-dependent unfolding rate of a protein have been developed, recapitulating different shapes of the underlying free-energy landscape.23 The Bell model is the simplest, describing the exponential relationship between the external applied force and the lifetime of bonds. In the absence of external force, the spontaneous rate of protein unfolding, α0, can be given by an Arrhenius model:
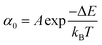 | (7) |
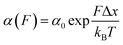 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α against F will yield a gradient of Δx/kBT and intercept of ln
α against F will yield a gradient of Δx/kBT and intercept of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α0 (Fig. 7c–e). Returning to the early work of Schlierf et al.,22 analysis of the force-dependent unfolding rates of ubiquitin using this model revealed Δx = 0.17 nm and α0 = 0.015 s−1. With α0 determined, rearranging the Arrhenius expression to ΔE = kBT
α0 (Fig. 7c–e). Returning to the early work of Schlierf et al.,22 analysis of the force-dependent unfolding rates of ubiquitin using this model revealed Δx = 0.17 nm and α0 = 0.015 s−1. With α0 determined, rearranging the Arrhenius expression to ΔE = kBT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(A/α0) allows the height of the free energy barrier to be determined, provided that A is known. In the case of ubiquitin, A ∼ 4 × 109 s−1 was experimentally determined through investigation of the temperature dependence of mechanical unfolding at a constant force,24 yielding ΔE = 71 kJ mol−1.
ln(A/α0) allows the height of the free energy barrier to be determined, provided that A is known. In the case of ubiquitin, A ∼ 4 × 109 s−1 was experimentally determined through investigation of the temperature dependence of mechanical unfolding at a constant force,24 yielding ΔE = 71 kJ mol−1.
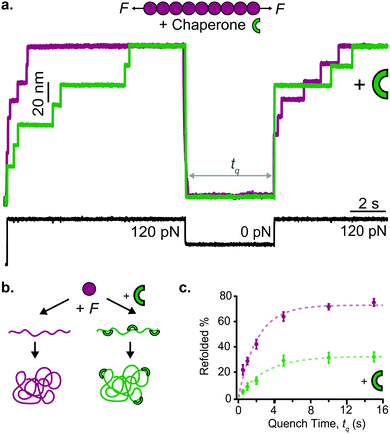
The previously-discussed Dudko–Hummer–Szabo model21 is directly applicable to data acquired in force-clamp experiments, permitting elucidation of α0 and Δx – in addition to ΔE – from force-dependent unfolding rates using
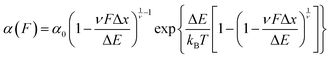 | (9) |
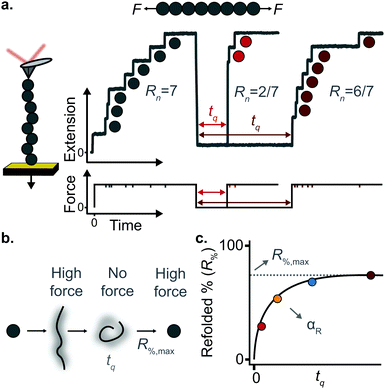
(c) Protein folding using a force-quench approach
A key requirement of tissue exposed to mechanical force in vivo is that, when force is withdrawn, it reversibly returns to its initial, pre-loaded condition. This behaviour necessitates that the folding of any underlying mechanically-unfolded proteins is reversible over multiple stretch/relaxation cycles. From the nanomechanical perspective, reversibility implies that a protein recovers the mechanical stability of the native state upon force removal.Single-molecule force spectroscopy techniques are capable of probing the reversibility of the unfolding process by removing the pulling force before re-stretching the protein back again. While earlier experiments using force-extension demonstrated the feasibility of the mechanical folding approach, the force-clamp method is ideally suited to this task thanks to its unbeatable control of the force and of the protein–surface distance. In the so-called force-quench approach, a polyprotein is first mechanically unfolded at a high constant force, resulting in the protein step-wise extension over time. Then, the force is quenched to a lower value (or altogether withdrawn) for a quenching time tq. During this period of time (quench pulse), the unfolded and stretched polypeptide collapses and subsequently refolds by successfully reforming of the native contact network which defines the natively-folded state. To probe the efficiency of the native-fold recovery, the high constant force is reapplied (probe pulse) (Fig. 8a and b). The fraction of domains which recover their mechanical stability during the force quench (in these experiments the recovery of mechanical stability is the unambiguous fingerprint of successful refolding) yields the refolding efficiency, R%, which varies with the quench time (Fig. 8c).
To measure the refolding kinetics, the refolding efficiency is measured for a range of quench times. Plotting the refolding efficiency against tq has typically the form:
| R%(tq) = R%,max(1 − exp[−αRtq]) | (10) |
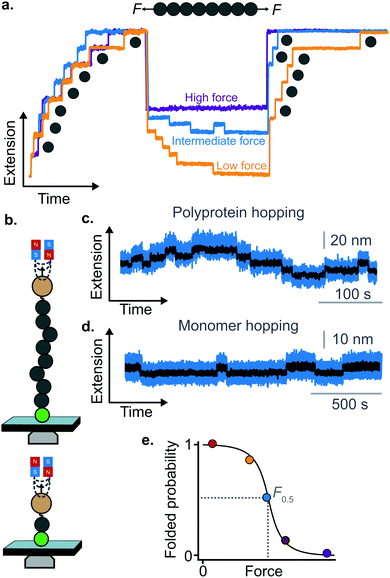
A rather intuitive finding from the force-quench experiments is that proteins need to collapse before recovering their mechanical stability. Triggering protein collapse requires withdrawing the force after mechanical unfolding, or quenching it to a very low value of only a few pN. These early force quench experiments were conducted with the AFM, whereby the intrinsic stiffness of the cantilever sets the instrumental capability below e.g. ∼15 pN to be challenging, hence precluding observation of the processes occurring at low forces, during the last stages of folding. In fact, the force-quench AFM experiments cannot capture the protein length evolution over time at low forces, and use instead the mechanical stability of proteins in the probe pulse as their structural fingerprint.25 To circumvent this limitation, optical and magnetic tweezers, due to their suitability to low-force experimentation, can be used to directly capture the final folding transitions. In this approach, a (poly)protein is first unfolded at high force (typically ∼30–50 pN), the force is subsequently quenched to a much lower value (typically ∼2–15 pN). While the protein is held at low force, distinct step-wise decreases in extension (steps down) can be observed,13 hallmarking individual domains transitioning from unfolded to collapsed/folded conformations (Fig. 9a). This observation has unambiguously demonstrated that proteins can refold against mechanical load, with potentially important consequences for e.g. muscle biology.
The observation that proteins can still refold even if a stretching force is applied necessarily entails that there will be a force value where the rates of unfolding and folding may be approximately equal. In such a situation, ‘hopping’ behaviour can be observed, with step-wise increases and decreases in extension occurring at physiologically-relevant low forces (Fig. 9b–d). Such a hopping behaviour was observed in the folding of monomeric RNase H using OT, showing a marked mechanical intermediate conformation during the folding pathway.27 Similarly, by using MT the Ig27 module from titin was found to hop at forces ranging between 4–8 pN, and a similar behaviour was observed in talin at forces ranging from 5 pN to 10 pN.26
In all these cases, the folded probability varies in a smooth-step, sigmoidal-like, fashion (Fig. 9e), and is notably very sensitive to the applied force (i.e. a change of 2–3 pN) can completely shift the unfolded population to become completely folded, or vice versa.
Regulating protein nanomechanics through varied chemical strategies
In the cellular environment proteins are exposed to a myriad of fluctuating physicochemical conditions that have knock on effects on their stability and, ultimately, on their function. Classical in vitro experiments have strived to elucidate how each independent biochemical/physicochemical property (pH, ionic strength, temperature, ligand binding, mutations, post-translational modifications, etc.) modifies the protein folding energy landscape. However, given the fundamental disparity between biochemical and mechanical protein folding experiments, the results obtained using bulk techniques cannot be generally translated into the nanomechanical experiments. In particular, during the last years, new efforts have focused on unravelling how different chemical modifications affect the mechanical stability of proteins, directly impacting their individual unfolding and refolding pathways. The most successful strategies have uncovered the rational introduction of point mutations, protein–protein interactions, metal binding or post-translational modifications. In what follows we provide a qualitative perspective on the different applications of single molecule force-spectroscopy techniques, with a specific emphasis on reviewing the different chemical tactics used by proteins to regulate their nanomechanical properties.Point mutations as localised modulators of protein mechanics
One of the first strategies found to modulate the nanomechanical properties of proteins is via the introduction of point mutations in the amino acid sequence. In contrast to bulk classical biochemistry techniques, where each mutation has an impact on the overall thermodynamic stability of a protein, the influence of point mutations on a protein's mechanical stability is largely dependent on the precise location of the substitution in the protein structure i.e. whether it disrupts specific non-covalent interactions in the vicinity of the mechanical clamp.For example, various point mutations introduced in the mechanical clamp region of titin domain Ig27 demonstrated both decreases and increases in mechanical stability as compared to the wild-type form,28 as determined by changes in the average unfolding force from force-extension measurements. Specifically, while three mutations (V11P, V13P, and V15P) lowered the unfolding force by varying degrees, the Y9P mutation (which in fact entails a reduction in the thermal stability) significantly raised the average unfolding force. By contast, a point mutation away from the mechanical clamp of the same Ig27 domain (C47A)—which exhibits an expected decrease in thermal stability—does not have any effect on the mechanical stability of the protein.
Metal binding and the creation of new mechanical barriers
Approximately half of all known proteins contain at least one metal centre. In these proteins, metal coordination often occurs through the presence of multiple organometallic bonds, which keep the metal ‘trapped’ in a stable position within the three-dimensional protein structure. If the chemical bonds defining the metal centre rupture upon force application (i.e., if the metal centre is in the path of the force propagation), they create an additional barrier to protein unfolding, mid-way along the unfolding pathway. Such binding interactions can be directly identified by the appearance of additional (intermediate) unfolding peaks in force-extension measurements. The force value required to disrupt the metal centre is a read-out of the mechanical stability of the organometallic bond, with the associated contour length increment unambiguously indicating the position of the metal centre within the protein structure.In a series of experiments pioneered by the Hongbin Li lab using single molecule force-spectroscopy AFM,29 the forces required to break the native Fe–S bond in rubredoxin, and Ni–N binding in artificial histidines present on a protein G scaffold, were measured. Follow-up experiments unravelled the mechanical properties of Cu–S bonds in azurin and plastocyanin (Fig. 10), the Zn–S bonds that determine the mechanical stability of zinc finger domains and the Au–S bonds in the gold specific binding (GolB) protein. Collectively, nanomechanical studies on metalloproteins have concluded that the mechanical stability of individual organometallic bonds is surprisingly lower than expected (occurring at ∼30–200 pN for typical force-extension conditions) given the covalent nature of the coordination bonds. From the refolding perspective, a seminal paper from the Rief lab demonstrated the Ca2+ modulation of the mechanical folding of calmodulin,30 and Fe2+ was shown to remain bound to rubredoxin after mechanical unfolding, thus facilitating the reformation of the organometallic centre after force relaxation.31
 | ||
| Fig. 10 (a) Schematic structure of the metalloprotein azurin, highlighting the copper coordination site. (b) Stretching a heteropolyprotein containing azurin (orange) and a marker protein (grey) at a constant velocity (400 nm s−1) results in an unfolding trajectory, where the unfolding of azurin occurs first at ∼55 pN, followed by the unfolding of the marker protein at higher forces. Inset: After the main azurin unfolding peak (orange WLC fits) an additional intermediate peak (green WLC fits) can be observed, reminiscent of the mechanical disruption of the copper coordination site. (c) The contour length increment analysis shows that complete unfolding of azurin entails ΔLC ∼ 38 nm. The mechanical intermediate is placed ∼10 nm after the main unfolding event. The rupture of the metal centre represents a further increment of extension of ∼30 nm, (reproduced from ref. 55 with permission from Springer Nature, copyright 2015). | ||
Protein–ligand interactions as key unexpected regulators of protein nanomechanics
Protein–protein interaction (ligand binding) is a well-known strategy to modify the thermodynamic stability of the binding partners, and its occurrence is widespread in nature. A substantial body of literature has now demonstrated that protein binding can also modify (often enhancing) the mechanical stability of proteins. Changes in mechanical stability due to ligand binding can be simply measured by comparing the average unfolding force in force-extension measurements on the protein of interest with and without the ligand in solution. Typically, two scenarios have been observed; in the first one, protein (ligand) binding endows with mechanical stability a protein that was otherwise mechanically labile and devoid (within resolution) of mechanical stability. Alternatively, ligand binding can increase the stability of a protein with an already significant mechanical resistance.The former case is well exemplified by the first single-molecule force spectroscopy study on dihydrofolate reductase (DHFR),32 the apo-form of which behaves like an entropic spring. Upon binding to a variety of ligands—methotrexate, nicotinamide adenine dihydrogen phosphate, or dihydrofolate—DFHR converts into a shock absorber, exhibiting well-marked force peaks (∼90 pN) in the force-extension measurements. Similarly, the binding of short nucleic acid sequences has been shown to provide mechanical stability (∼40 pN unfolding force) to the RRM1 domain of TDP-43.33 As a key example of the second case, the mechanical stability of NuG2 (a mutant of the B1 IgG binding domain of protein G), which exhibits an unfolding force of ∼105 pN, is increased up to ∼210 pN after binding of the Fc fragment of human IgG.34
Not all protein–ligand interactions occur when the protein is in its natively-folded conformation. In some instances, binding only occurs when buried amino acids (i.e. those not solvent accessible when the protein is folded) become solvent exposed upon protein unfolding. Force-clamp experiments allow proteins to be held for varying periods of time in their mechanically extended, low-entropy conformations, revealing previously cryptic residues to the solvent. Exciting research has started to elucidate the mechanisms by which ligands can regulate protein folding when interacting with previously buried amino acids that suddenly become exposed to the solution upon mechanical unfolding.
Early work from the Tans lab reported, using OT, how the folding properties of maltose binding protein (MBP) were affected by the binding with the SecB chaperone,35 revealing that SecB could only bind to extended or molten globule-like states of the MBP, compromising effective refolding. Analogous, follow-up experiments on the same MBP substrate showed that while the trigger factor chaperone binds to folded structures and stimulates native folding,36 the Hsp70 (DnaK) system can suppress aggregation by binding partially folded structures as well as unfolded protein chains.37 Similarly, using AFM it was demonstrated that, when working independently, DnaJ (Hsp40) and DnaK (Hsp70) work as holdases, blocking refolding by binding to distinct substrate conformations. Whereas DnaK binds to molten globule–like forms, DnaJ recognizes a cryptic sequence in the extended state in an unanticipated force-dependent manner (Fig. 11). By contrast, the synergetic coupling of the Hsp70 system exhibits a marked foldase behavior.38 In a conceptually similar approach, when membrane proteins were used as substrates, it was demonstrated that YidC,39 a transmembrane chaperone and insertase, stabilises the unfolded state of LacY, avoiding misfolding.
 | ||
| Fig. 11 (a) The capability of ubiquitin (purple) to mechanically refold is significantly reduced when the Hsp40 DnaJ chaperone (green) is present in the solution, as less refolding steps can be observed in the probe force pulse when comparing refolding with (green trace) and without (purple trace) the chaperone present in solution. (b) Schematic representation of the DnaJ binding mechanism, whereby the chaperone only recognises the mechanically unfolded and stretched ubiquitin. (c) The kinetic analysis of ubiquitin refolding shows that the presence of DnaJ reduces refolding by almost 50%, (reproduced from ref. 38 with permission from AAAS, copyright 2018). | ||
Protein–protein interactions in previously cryptic sites seem to be an emerging theme in mechanotransduction. For example, del Rio et al. discovered that vinculin can only bind to talin after mechanical unfolding,40 a discovery that was later on extended to the α-catenin–vinculin system.41 Finally, the ribosome itself can work as an effective chaperone, effectively promoting successful co-translational folding.42
Isopeptide and disulfide covalent bonds: molecular staples that prevent mechanical unfolding
Whether featuring mechanical intermediates or unfolding in a classical all-or-none fashion, mechanical force triggers proteins to unfold and ultimately reach highly extended conformations. Nature has devised chemical strategies to help proteins maintain their folded conformations. The most conspicuous example is the presence of covalent isopeptide bonds inside the protein structure—formed between the carbonyl group (–COOH) of one residue and the amino group (–NH2) of a nearby one. If placed close to the protein termini, as it is the case of Spy0128 (the major pilin of Streptococcus pyogenes), the isopeptide bond locks the protein into a rigid, native and inextensible conformation.43Conceptually similar to isopeptide bonds are disulfide bonds (formed between two cysteines), of wide presence in nature (around 20% of entries in the Protein Data Bank contain at least one disulfide bridge). From a mechanical perspective, disulfide bridges are covalent rigid bonds that shortcut protein extensibility and cannot be ruptured in SMFS experiments by force alone. Hence, in force-extension measurements, protein domains containing disulfide bridges will exhibit a reduction in the contour length increment, as reported, for example, in different mutants of Ig27 containing artificial disulfide bonds in different positions within the structure.44 However, and in sharp contrast with isopeptide bonds, disulfide bonds are chemically reactive, directly modulating protein extensibility upon chemical reduction. One of the conditions for their reactivity is that they need to be exposed to the attack of a nucleophilic molecule capable of catalysing the thiol-disulfide exchange reaction. However, disulfide bridges are often buried within the 3D structure of a protein, and hence typically unreactive due to their solvent inaccessibility. Upon the application of force, however, protein unfolding exposes previously cryptic disulfide bonds to solution, facilitating their reactivity with nucleophiles in solution. A crucial discovery from these experiments is that the reduction of the disulfide bonds by a solution nucleophile is force-accelerated. Using force-clamp spectroscopy AFM at relatively high forces, these experiments allowed reconstruction of the free energy surface governing a force-induced chemical reaction at the single bond level, and demonstrated that the disulfide bond reduction is (about an order of magnitude) less sensitive to force (Δx ∼ 0.3 Å) than protein unfolding (Δx ∼ 0.2 nm).45 Notably, an important finding in these mechanochemistry experiments is that mechanical force can by-pass thermodynamical restrictions, implying that it can catalyse chemical reactions that would be otherwise unfavored from the classical thermodynamic perspective.46
Applying the force-quench protocol to the resulting mechanical unfolded and chemically reduced proteins allows monitoring oxidative folding—the mechanism by which mechanical folding encompasses the reformation of the original, natively-formed disulfide bonds (Fig. 12). These oxidative folding experiments can be enzymatic or non-enzymatic in origin, according to whether the active moiety facilitating disulfide reformation is a small nucleophile (often the mixed-disulfide post-translational modification resulting from the disulfide rupture)47 or an active chaperone oxidoreductase such as the protein disulfide isomerase (PDI) enzyme,48 which acts as a placeholder that guides the formation of disulfide bridges at late stages of the folding process.
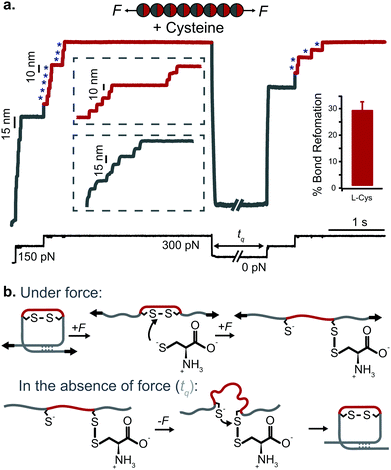 | ||
| Fig. 12 (a) L-Cysteine mediates the reversible reformation of protein disulfide bonds. The application of an initial ‘low’ (150 pN) force-pulse to a polyprotein containing an engineered disulfide bridge (I27E24C–K55C)8 results in the unfolding of each domain up to the rigid covalent bond (inset: grey steps of ∼15 nm), which becomes solvent exposed. Then, the presence of a nucleophile such L-cysteine together with a higher force pulse (300 pN) is able to reduce the disulfide bond through an SN2 nucleophilic attack, marked by the extension of the amino acids that were trapped behind the disulfide (inset: red steps of ∼10 nm). Quenching the pulling force for 8 s triggers the protein to collapse and fold. The subsequent test pulse probes the folding status of the protein. The reapplication of the same low-high force pulse sequence results in the subsequent unfolding and re-rupture of the previously reformed disulfide bond. Combining a number of proteins allows measurement of the efficiency of disulfide reformation (∼30%). (b) Schematics of the different chemical reactions occurring with and without force, (reproduced from ref. 47 with permission from Springer Nature, copyright 2017). | ||
State-of-the-art applications, new directions and final conclusions
The ability to ‘grab’ individual proteins and measure their reactivity with force has opened a new view of inquiry in the protein field, providing an alternative and complementary perspective to the classical biochemistry protein (un)folding bulk experiments. The field has attracted interest from life and physical scientists alike; earlier experiments developed methods and analytical approaches (including the development of protein engineering methods and steered molecular dynamics simulations) to establish a reliable ‘standard’ to mechanically characterise of a number of proteins (regardless of whether they play a mechanical role in vivo or simply as folding ‘models’). Later on, physicists became interested in developing statistical mechanics tools and analytical methods to reconstruct the energy landscape of proteins under force by analysing a statistically-relevant number of individual unfolding and folding trajectories.23 In parallel, a continuous push for the development of new technology to systematically achieve better time-, length- and force-resolution has now provided the field with different complementary techniques that are ideally suited to characterise a given protein according to its specific mechanical stability. Particularly timely is the new applicability of magnetic tweezers, which are capable of probing the low force regime while cyclically pulling on the very same individual protein over extended time-scales of hours, and even days.13Besides access to the most fundamental knowledge collectively allowed by these techniques, recent studies have employed the knowledge obtained from single-molecule experiments to explore biologically relevant open questions. For example, recent experiments on membrane proteins have revealed previously hidden states using high resolution AFM cantilevers;49 similarly, novel magnetic tweezers experiments on membrane proteins using standing bicelles have revealed the individual folding pathways and directionality of two distinct membrane proteins, occurring one α-helix at a time.50 A key, striking finding in the field, enabled by the combined use of OT and polyproteins, was the discovery that proteins need to mechanically unfold to go through the ClpX proteasomal machinery.51 Along similar lines, using a combination of OT and fluorescence particle-tracking, it was very recently discovered that the ClpB disaggregase translocates protein loops at forces in excess of ∼50 pN.52 From an in vivo perspective, single-molecule experiments have helped calibrate the design of FRET sensors, which, despite their limitations, provide an enticing way to quantify mechanical forces inside cells.53 Finally, the use of single-molecule experiments has provided a benchmark to discover that the protein import rate to the cell nucleus is regulated by the mechanical stability of the translocating protein cargos.54
To conclude, the parallel progress in instrument development, the application of novel analytical tools and the widening of the range of applications (which parallels the increasing evidences of the number of cellular functionalities revealed to be mechanosensitive), the field of protein nanomechanics is thriving. Having reached technical maturity, and teamed with a large list of scrutinised proteins, we are now in the position of addressing key open questions in our fundamental understanding of the nanomechanics of individual proteins. This includes, but is not limited to, using model proteins to delve deeper into our knowledge on the key regulators and mechanisms governing mechanical protein folding, and elucidating the complex relationship between force and function for proteins that are physiologically exposed to mechanical forces, of common occurrence in nature.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Amy Beedle for critical reading of the manuscript. MM was funded by a Fight for Sight studentship (1562/1563). The work is supported by the European Commission (FET Proactive 731957), EPSRC Fellowship K00641X/1, EPSRC Strategic Equipment Grant EP/M022536/1, Leverhulme Trust Research Leadership Award RL-2016-015, Wellcome Trust Investigator Award 212218/Z/18/Z and Royal Society Wolfson Fellowship RSWF/R3/183006, all to S. G.-M.References
- Y. Javadi, J. M. Fernandez and R. Perez-Jimenez, Physiology, 2013, 28, 9–17 CrossRef CAS.
- V. Vogel and M. Sheetz, Nat. Rev. Mol. Cell Biol., 2006, 7, 265–275 CrossRef CAS.
- H. Lu and K. Schulten, Biophys. J., 2000, 79, 51–65 CrossRef CAS.
- M. Rief, M. Gautel, F. Oesterhelt, J. M. Fernandez and H. E. Gaub, Science, 1997, 276, 1109–1112 CrossRef CAS.
- M. Rief, J. Pascual, M. Saraste and H. E. Gaub, J. Mol. Biol., 1999, 286, 553–561 CrossRef CAS.
- D. K. West, D. J. Brockwell, P. D. Olmsted, S. E. Radford and E. Paci, Biophys. J., 2006, 90, 287–297 CrossRef CAS.
- D. J. Brockwell, E. Paci, R. C. Zinober, G. S. Beddard, P. D. Olmsted, D. A. Smith, R. N. Perham and S. E. Radford, Nat. Struct. Biol., 2003, 10, 731–737 CrossRef CAS.
- J. E. Kohn, I. S. Millett, J. Jacob, B. Zagrovic, T. M. Dillon, N. Cingel, R. S. Dothager, S. Seifert, P. Thiyagarajan, T. R. Sosnick, M. Z. Hasan, V. S. Pande, I. Ruczinski, S. Doniach and K. W. Plaxco, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 12491–12496 CrossRef CAS.
- G. Stirnemann, S. G. Kang, R. Zhou and B. J. Berne, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 3413–3418 CrossRef CAS.
- A. Valbuena, J. Oroz, R. Hervas, A. M. Vera, D. Rodriguez, M. Menendez, J. I. Sulkowska, M. Cieplak and M. Carrion-Vazquez, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13791–13796 CrossRef CAS.
- H. Li, A. F. Oberhauser, S. B. Fowler, J. Clarke and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 6527–6531 CrossRef CAS.
- K. C. Neuman and A. Nagy, Nat. Methods, 2008, 5, 491–505 CrossRef CAS.
- I. Popa, J. A. Rivas-Pardo, E. C. Eckels, D. J. Echelman, C. L. Badilla, J. Valle-Orero and J. M. Fernandez, J. Am. Chem. Soc., 2016, 138, 10546–10553 CrossRef CAS.
- M. Carrion-Vazquez, A. F. Oberhauser, T. E. Fisher, P. E. Marszalek, H. Li and J. M. Fernandez, Prog. Biophys. Mol. Biol., 2000, 74, 63–91 CrossRef CAS.
- H. Dietz, M. Bertz, M. Schlierf, F. Berkemeier, T. Bornschlogl, J. P. Junker and M. Rief, Nat. Protoc., 2006, 1, 80–84 CrossRef CAS.
- Y. Deng, T. Wu, M. Wang, S. Shi, G. Yuan, X. Li, H. Chong, B. Wu and P. Zheng, Nat. Commun., 2019, 10, 2775 CrossRef.
- L. F. Milles, K. Schulten, H. E. Gaub and R. C. Bernardi, Science, 2018, 359, 1527–1532 CrossRef CAS.
- A. W. M. Haining, M. von Essen, S. J. Attwood, V. P. Hytonen and A. D. Hernandez, ACS Nano, 2016, 10, 6648–6658 CrossRef CAS.
- H. Dietz and M. Rief, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 16192–16197 CrossRef CAS.
- Q. Peng and H. Li, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 1885–1890 CrossRef CAS.
- O. K. Dudko, G. Hummer and A. Szabo, Phys. Rev. Lett., 2006, 96, 108101 CrossRef.
- M. Schlierf, H. B. Li and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 7299–7304 CrossRef CAS.
- M. T. Woodside and S. M. Block, Annu. Rev. Biophys., 2014, 43, 19–39 CrossRef CAS.
- I. Popa, J. M. Fernandez and S. Garcia-Manyes, J. Biol. Chem., 2011, 286, 31072–31079 CrossRef CAS.
- S. Garcia-Manyes, L. Dougan, C. L. Badilla, J. Brujic and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10534–10539 CrossRef CAS.
- R. Tapia-Rojo, E. C. Eckels and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 7873–7878 CrossRef CAS.
- C. Cecconi, E. A. Shank, C. Bustamante and S. Marqusee, Science, 2005, 309, 2057–2060 CrossRef CAS.
- H. B. Li, M. Carrion-Vazquez, A. F. Oberhauser, P. E. Marszalek and J. M. Fernandez, Nat. Struct. Biol., 2000, 7, 1117–1120 CrossRef CAS.
- H. Li and P. Zheng, Curr. Opin. Chem. Biol., 2018, 43, 58–67 CrossRef CAS.
- J. Stigler and M. Rief, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 17814–17819 CrossRef CAS.
- P. Zheng, Y. Wang and H. Li, Angew. Chem., Int. Ed., 2014, 53, 14060–14063 CrossRef CAS.
- R. K. Ainavarapu, L. Li, C. L. Badilla and J. M. Fernandez, Biophys. J., 2005, 88, 168a Search PubMed.
- Y. J. Wang, P. Rico-Lastres, A. Lezamiz, M. Mora, C. Solsona, G. Stirnemann and S. Garcia-Manyes, J. Phys. Chem. Lett., 2018, 9, 3800–3807 CrossRef CAS.
- Y. Cao, M. M. Balamurali, D. Sharma and H. Li, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 15677–15681 CrossRef CAS.
- P. Bechtluft, R. G. van Leeuwen, M. Tyreman, D. Tomkiewicz, N. Nouwen, H. L. Tepper, A. J. Driessen and S. J. Tans, Science, 2007, 318, 1458–1461 CrossRef CAS.
- A. Mashaghi, G. Kramer, P. Bechtluft, B. Zachmann-Brand, A. J. Driessen, B. Bukau and S. J. Tans, Nature, 2013, 500, 98–101 CrossRef CAS.
- A. Mashaghi, S. Bezrukavnikov, D. P. Minde, A. S. Wentink, R. Kityk, B. Zachmann-Brand, M. P. Mayer, G. Kramer, B. Bukau and S. J. Tans, Nature, 2016, 539, 448–451 CrossRef CAS.
- J. Perales-Calvo, D. Giganti, G. Stirnemann and S. Garcia-Manyes, Sci. Adv., 2018, 4, eaaq0243 CrossRef.
- T. Serdiuk, D. Balasubramaniam, J. Sugihara, S. A. Mari, H. R. Kaback and D. J. Muller, Nat. Chem. Biol., 2016, 12, 911–917 CrossRef CAS.
- A. del Rio, R. Perez-Jimenez, R. Liu, P. Roca-Cusachs, J. M. Fernandez and M. P. Sheetz, Science, 2009, 323, 638–641 CrossRef CAS.
- M. Yao, W. Qiu, R. Liu, A. K. Efremov, P. Cong, R. Seddiki, M. Payre, C. T. Lim, B. Ladoux, R. M. Mege and J. Yan, Nat. Commun., 2014, 5, 4525 CrossRef CAS.
- D. H. Goldman, C. M. Kaiser, A. Milin, M. Righini, I. Tinoco, Jr. and C. Bustamante, Science, 2015, 348, 457–460 CrossRef CAS.
- J. Alegre-Cebollada, C. L. Badilla and J. M. Fernandez, J. Biol. Chem., 2010, 285, 11235–11242 CrossRef CAS.
- R. K. Ainavarapu, J. Brujic, H. H. Huang, A. P. Wiita, H. Lu, L. W. Li, K. A. Walther, M. Carrion-Vazquez, H. B. Li and J. M. Fernandez, Biophys. J., 2007, 92, 225–233 CrossRef.
- J. Liang and J. M. Fernandez, ACS Nano, 2009, 3, 1628–1645 CrossRef CAS.
- A. E. M. Beedle, M. Mora, C. T. Davis, A. P. Snijders, G. Stirnemann and S. Garcia-Manyes, Nat. Commun., 2018, 9, 3155 CrossRef.
- A. E. M. Beedle, M. Mora, S. Lynham, G. Stirnemann and S. Garcia-Manyes, Nat. Commun., 2017, 8, 15658 CrossRef CAS.
- P. Kosuri, J. Alegre-Cebollada, J. Feng, A. Kaplan, A. Ingles-Prieto, C. L. Badilla, B. R. Stockwell, J. M. Sanchez-Ruiz, A. Holmgren and J. M. Fernandez, Cell, 2012, 151, 794–806 CrossRef CAS.
- H. Yu, M. G. Siewny, D. T. Edwards, A. W. Sanders and T. T. Perkins, Science, 2017, 355, 945–950 CrossRef CAS.
- H. K. Choi, D. Min, H. Kang, M. J. Shon, S. H. Rah, H. C. Kim, H. Jeong, H. J. Choi, J. U. Bowie and T. Y. Yoon, Science, 2019, 366, 1150–1156 CrossRef CAS.
- H. C. Kotamarthi, R. T. Sauer and T. A. Baker, Cell Rep., 2020, 30, 2644–2654 CrossRef , e2643.
- M. J. Avellaneda, K. B. Franke, V. Sunderlikova, B. Bukau, A. Mogk and S. J. Tans, Nature, 2020, 578, 317–320 CrossRef CAS.
- P. Ringer, A. Weissl, A. L. Cost, A. Freikamp, B. Sabass, A. Mehlich, M. Tramier, M. Rief and C. Grashoff, Nat. Methods, 2017, 14, 1090–1096 CrossRef CAS.
- E. Infante, A. Stannard, S. J. Board, P. Rico-Lastres, E. Rostkova, A. E. M. Beedle, A. Lezamiz, Y. J. Wang, S. Gulaidi Breen, F. Panagaki, V. Sundar Rajan, C. Shanahan, P. Roca-Cusachs and S. Garcia-Manyes, Nat. Phys., 2019, 15, 973–981 Search PubMed.
- A. E. M. Beedle, A. Lezamiz, G. Stirnemann and S. Garcia-Manyes, Nat. Commun., 2015, 6, 7894 Search PubMed.
| This journal is © The Royal Society of Chemistry 2020 |