The origin of different driving forces between O–H/N–H functional groups in metal ligand cooperation: mechanistic insight into Mn(I) catalysed transfer hydrogenation

Abstract

Metal–ligand cooperation catalysis is currently the prevailing strategy in the field of homogeneous catalyst research, and is widely used in direct catalytic hydrogenation and transfer hydrogenation reactions. Herein, a density functional theory (DFT) study is conducted to clarify the origin of the different activities of Mn(I) bifunctional catalysts bearing similar Lewis base functional ligands, and amine and hydroxyl groups. The results indicate that a Mn(I) catalyst with an OH group as a bifunctional group requires a higher activation free energy barrier relative to the catalyst with amine as an active ligand, which is in line with the experimental observations. By comparing the electronic structures of the key intermediates in the two catalytic systems, it is found that the Mn–O complex catalyst is thermodynamically unstable and may lead to irreversible decomposition, which accounts for its lower catalytic activity. Moreover, the inductive effect between the OH group and the metal hydride increases unfavorable orbital interactions in the Mn–O system. Consequently, the generation of a metal hydride intermediate becomes a thermodynamically uphill process, further leading to a lack in driving force for the dehydrogenation of ⁱPrOH. Further investigation suggests that the driving force of the catalyst can be tuned by changing the different oxidation states of the metal centers, revealing a crucial role for the metal center in M–L bond cooperation mode in MLC catalysis. This study highlights that although the hydroxyl and amine groups are both Lewis base functional ligands, subtle differences in the electronic effects of ligand have a significant impact on the activities of the metal–ligand cooperation (MLC) catalysts.

---

1. Introduction

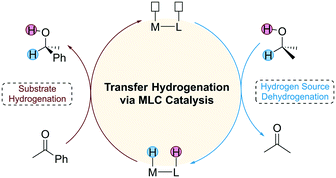
Catalytic hydrogenation has important applications in the fields of pharmaceutical and organic synthesis. Depending on the different types of hydrogen source used, the catalytic hydrogenation reaction can be classified into direct hydrogenation and transfer hydrogenation (TH). Direct hydrogenation uses pressurized flammable H₂ as a hydrogen source, which requires harsh experimental conditions. In contrast, TH employs small organic molecules such as alcohols and formic acid as a hydrogen source, which provides an alternative route for environmentally benign hydrogenation.¹ Since many hydrogen sources are polar molecules, an important strategy used in the design of TH catalysts is to introduce a Lewis base (LB) active site on the ligand of the catalyst that cooperates with the Lewis acid (LA) metal centre to achieve high catalytic activity. This unique catalytic strategy is also known as metal–ligand cooperation (MLC) catalysis, and the catalysts that follow this mechanism are often referred to as bifunctional catalysts.² The mechanism of TH mediated by a bifunctional catalyst consists of two stages (Fig. 1). The first stage is the dehydrogenation of the hydrogen source and the second stage is the hydrogenation of the substrate. The two stages of the reaction are independent of each other, requiring an appropriate driving force to connect them.

Fig. 1 The general mechanism of transfer hydrogenation using MLC catalysts.

The history of bifunctional catalysts can be traced back to the BINAP (bis(diphenylphosphino))/diamine-Ru catalytic system synthesized by Noyori et al., which represents a milestone in the development of homogenous transition metal catalysts.³ For a long period of time after this catalyst, the active metal centre of bifunctional catalysts was limited to noble metals such as Ru,⁴ Rh,⁵ Ir (ref. 6) and Os.⁷ Although these have good catalytic activity and thermodynamic stability, their high toxicity and cost restrict the large-scale industrial application of such catalysts. In the past five years, replacing non-precious metals with the earth-abundant elements such as Mn, Fe, Co and Ni as the metal centre has become an important trend.⁸ A representative catalyst is the Fe(II) TH catalyst developed by Morris et al.⁹ This catalyst has undergone three generations of research and development,¹⁰ the structure of the catalyst has been rationally optimized and to date it is the most efficient Fe catalyst for asymmetric hydrogenation reactions.¹¹ Hanson et al. developed a Co(II)-pincer catalyst for the TH of ketones, aldehydes, and imines under mild conditions.^12,13 Interestingly, MLC is not involved during the catalytic cycle, which underscores the mechanistic diversity of first row transition metal catalysts. Along with these mentioned experimental achievements, theoretical studies based on density functional theory (DFT) calculations also offer important insights on the mechanistic details of the MLC process.^14–31

Later, manganese attracted great research interest as it ranks third among all of the earth-abundant transition metals. In 2016, Beller et al. reported the first manganese TH catalyst using easily synthesized aminopyridine as the chelating ligand.³² Leitner et al. prepared a Mn(I) complex using aminotriazole as the ligand.³³ Through a comparative study on a series of catalysts, an outer-sphere MLC mechanism was proposed. Using a benzimidazole aniline ligand, a new type of bifunctional catalyst was developed by Kundu et al. The catalyst can effectively catalyse the hydrogenation of ketones and imines with excellent chemo-selectivity.³⁴ With the aid of DFT calculations, they also proposed a concerted outer-sphere MLC mechanism. Based on a simple bipyridine ligand substituted with a hydroxyl group as an active site, Khusnutdinova et al. developed a Mn(I) catalytic system that is effective for ketones, aldehydes, imines and N-heterocycles.³⁵ The DFT calculated results suggest a monohydride mechanism via outer-sphere MLC, which was further confirmed via a deuterium labelling experiment.

Recently, Sortais et al. developed a simple transfer hydrogenation catalytic system based on manganese and an inexpensive phosphorus-free bidentate ligand (2-(aminomethyl)pyridine).³⁶ Efficient TH can be achieved at room temperature with low catalyst loading. Interestingly, two catalysts bearing similar LB functional groups (OH and NH₂) as the functional ligands show completely different activity (Fig. 2). The conversion of the catalyst (Cat. A) with the NH₂ functional group is 97%, which exhibits excellent activity. On the other hand, the conversion of the catalyst (Cat. B) with the OH group is only 6%, showing very low activity. This unexpected experimental observation raises several questions: why do two structurally similar LB-bifunctional catalysts exhibit such large differences in catalytic activity? What does this abnormal experimental phenomenon imply? Is there any possibility that other reaction mechanisms exist beyond the traditional MLC process? Herein, using DFT calculations, all of the possible reaction pathways in the two catalytic systems are explored to shed light on these questions, which should provide useful theoretical insights for future MLC catalyst design.

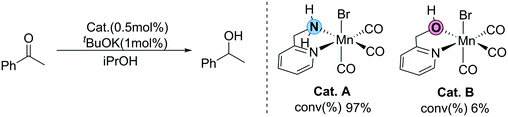Fig. 2 Different activities of N–H and O–H functional groups in the Mn(I) catalyst developed by Sortais et al.

2. Computational details

All DFT calculations were performed using the Gaussian 16 A.03 program.³⁷ Different functionals were compared (please see ESI,† Table S1), and eventually we chose the M06-L functional³⁸ in this study considering computational expense and accuracy, as it has been successfully applied in many relevant theoretical studies.^14,18,25 Geometry optimizations were carried out at the M06-L/def2-SVP³⁹ level of theory. All of the optimized structures were further verified to be stationary points as local minima (showing no imaginary frequencies) or transition states (showing one imaginary frequencies) via vibrational frequency analyses at the same level of theory. Intrinsic reaction coordinate (IRC) calculations were employed to confirm the connection between the two corresponding minima for every transition state. With M06-L/def2-SVP geometries, the energy results were further refined by calculating the single-point energy at the M06-L/def2-TZVP level. The solvation effect of ⁱPrOH was simulated using the SMD continuum solvent model.⁴⁰ The 3D optimized structural figures in this paper were displayed using the CYLview visualization program.⁴¹ Additional computational information and the Cartesian coordinates of the optimized structures are given in the ESI.†

3. Results

Pre-activation of the catalyst in the Mn–N catalytic system

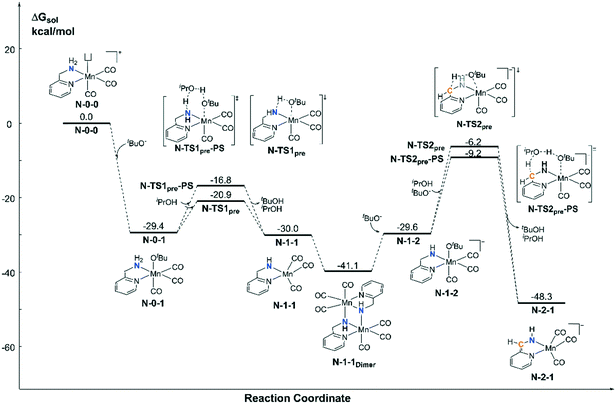
For the pre-catalyst activation process, the amino group is normally deprotonated by the base ^tBuOK in the classical MLC catalytic system.⁴² With the addition of an excess of strong base into the system, the CH₂ group on the ortho-position of the pyridine ligand can further undergo a dearomatization process to provide an extra active bifunctional site, which was observed in a former study carried out by Milstein et al. Since two equivalents of ^tBuOK was added into Sortais's Mn(I) system, the possibility of two active sites was probed via DFT calculations (Fig. 3). The activation process begins with a ligand exchange reaction, where one equivalent of ^tBuO⁻ coordinates to the Mn(I) centre and snatches a proton from the amino group via either a 4-member ring transition state N-TS1_pre or 6-member ring proton shuttle transition state N-TS1_pre-PS. The calculation results show that the proton-shuttle type transition state N-TS1_pre is slightly favoured and the activation energy of the first deprotonation reaction (N-0-1 → N-TS1_pre) is 8.5 kcal mol⁻¹. It is worth noting that after the deprotonation of the catalyst, the coordination structure changes from an octahedral structure (N-0-1) to a trigonal-bipyramidal structure (N-1-1), which form a dimeric manganese complex N-1-1_Dimer. Subsequent deprotonation of the CH₂ moiety requires a higher energy barrier (N-1-1_Dimer → N-TS2_pre-PS: ΔG^≠ = 31.9 kcal mol⁻¹). The entire deprotonation process is an exothermic reaction (ΔG = −48.3 kcal mol⁻¹). Although the double deprotonated species N-2-1 is more thermodynamically favourable, the mono-deprotonated species N-1-1 may proceed via a TH reaction with a lower activation free energy. Therefore, it is necessary to discuss the possibility of the mono-deprotonated species N-1-1 as the active species in the first place.

Fig. 3 Free energy profile of the deprotonation process catalysed by ^tBuOK in the Mn–N system.

Catalytic cycle promoted by the mono-deprotonated species N-1-1 in the Mn–N catalytic system

Both the single deprotonated intermediate N-1-1 and the double deprotonated intermediate N-2-1 are capable of catalysing the TH reaction. We first investigated the activity of the mono-deprotonated species N-1-1 as the active species (Fig. 4). The TH reaction mainly involves two stages, hydrogen source dehydrogenation and substrate hydrogenation. The calculation results suggest a stepwise bifunctional hydrogen transfer mechanism, in which the proton of ⁱPrOH transfers to the NH group initially and there is subsequent hydride transfer to the Mn(I) centre. The hydrogen source ⁱPrOH coordinates to the Mn(I) centre and cleaves the O–H bond via either the four-member ring transition state N-1-TS1_I or the proton-shuttle six-member ring transition state N-1-TS1_I-PS. The calculation results show that the activation free energy barrier of the proton transfer process viaN-1-TS1_I is only 7.1 kcal mol⁻¹. The Mn-alkoxide complex N-1-2_I quickly isomerizes to the ionic adduct complex N-1-2, which undergoes a hydride transfer step through N-1-TS2, where the free activation energy barrier is 13.1 kcal mol⁻¹ (N-1-2_I → N-1-TS2). The ⁱPrOH dehydrogenation process furnishes the Mn(I) hydride complex N-1-3 as the intermediate, which is responsible for the hydrogenation of the acetophenone reaction. In the subsequent substrate hydrogenation process, the free activation energy barrier of the hydride transfer process (N-1-3 → N-1-TS3) is 14.3 kcal mol⁻¹. The activation free energy of the rate-determining step is 23.9 kcal mol⁻¹ (N-1-1_dimer → N-1-TS2), which is much lower compared with the further deprotonation reaction to proceed via an aromatization/dearomatization mechanism viaN-TS2_pre-PS (N-1-1_Dimer → N-TS2_pre-PS: ΔG^≠ = 31.9 kcal mol⁻¹) (please see Fig. 3). Therefore, the TH process is promoted by the mono-deprotonated species N-1-1 and the possibility of a (de)aromatization mechanism via further deprotonation can be disregarded. This is consistent with experimental observations that a mono-deprotonated species can form a dimeric complex as a resting state and is still effective for TH after dissociation without adding any extra base.³⁶ After the proton transfer process, the catalyst is regenerated and the catalytic cycle restarts. The overall reaction free energy of the transfer hydrogenation reaction is 0.025 kcal mol⁻¹, which becomes 0.0 kcal mol⁻¹ in the free energy profile due to rounding down of this figure. The outer-sphere proton transfer mechanism can be ruled out due to its higher energy barrier compared with that of the inner sphere mechanism (please see Fig. S1 in the ESI†). Important optimized structures are depicted in Fig. 5.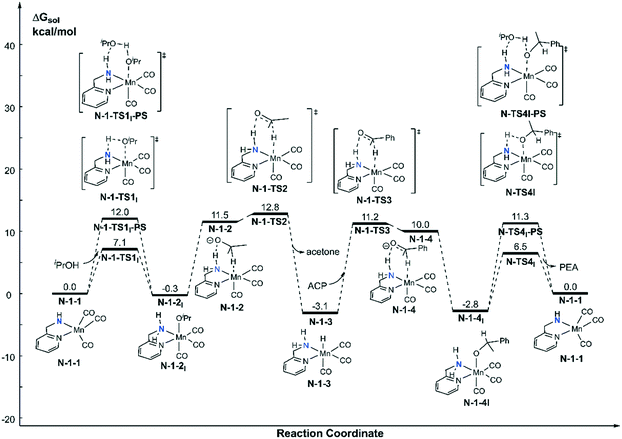

Fig. 4 Free energy profile of transfer hydrogenation with the mono-deprotonated active species in the Mn–N catalytic system. ACP = acetophenone. PEA = phenethyl alcohol.

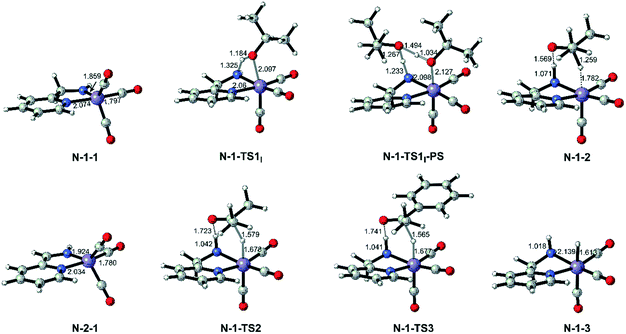Fig. 5 Optimized important intermediates and transition states in Mn–N catalytic system. Bond lengths are in Å.

Pre-activation of the catalyst in the Mn–O catalytic system

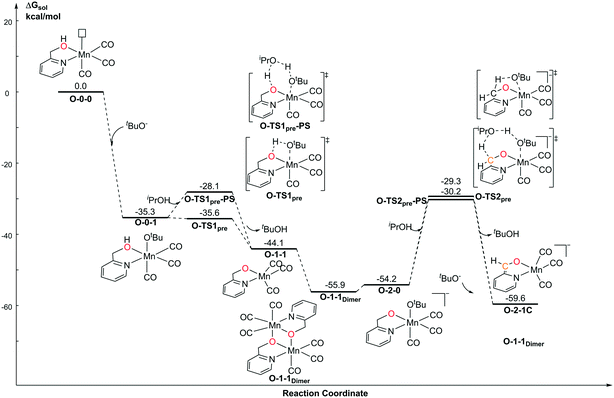
For the Mn–O catalytic system, the first step of the protonation process is the barrierless process (Fig. 6). The free activation energy of O-TS1_pre is 0.3 kcal mol⁻¹ lower than that of O-0-1. Since the transition state is located on the electronic potential energy surface, the electronic energy of the transition state O-TS1_pre is still higher than that of O-0-1 (ΔG^≠ = 1.3 kcal mol⁻¹). The free energy of O-TS1_pre becomes slightly lower than that of the reactant O-0-1 after thermo correction. The deprotonation of CH₂ in the pyridine ligand position requires a higher energy barrier (O-1-1_dimer → O-TS2_pre: 25.7 kcal mol⁻¹) due to the loss of the aromaticity of pyridine, which is also observed in the pre-catalyst activation in the Mn–N catalytic system. The proton-shuttle type transition state, O-TS1_pre-PS is 7.5 kcal mol⁻¹ higher than O-TS1_pre. However, O-TS2_pre-PS is 0.9 kcal mol⁻¹ higher than O-TS2_pre. These results indicate that a proton shuttle type transition state can decrease the free activation energy by lowering the ring strain when the steric repulsion is not significant. When the deprotonation site is close, the steric repulsion and the entropy effect both increase. Therefore, the stabilization effect of the proton shuttle transition state is offset.

Fig. 6 Free energy profile of the deprotonation process by ^tBuOK of the Mn–O catalytic system.

Catalytic cycle promoted by a mono-deprotonated species in the Mn–O catalytic system

With respect to the TH (transfer hydrogenation) reaction, the mono-deprotonated species O-1-1 proceeds via the dehydrogenation process in a concerted bifunctional hydrogen transfer manner (Fig. 7), in which both the hydride and the proton transfer from the complex simultaneously. The free activation energy barrier of O-TS1-PS is 22.0 kcal mol⁻¹. On contrast to the Mn–N system, the dehydrogenation of ⁱPrOH exhibits an endothermic thermodynamic reaction and the free energy of the intermediate O-1-2 is 11.1 kcal mol⁻¹. The subsequent TH process also proceeds in a concerted manner (O-1-TS2), with an activation free energy barrier of 11.6 kcal mol⁻¹. Therefore, the overall barrier is 34.5 kcal mol⁻¹ (O-1-1_dimer → O-1-TS2) when measuring from the Mn dimeric complex (please see Fig. 6).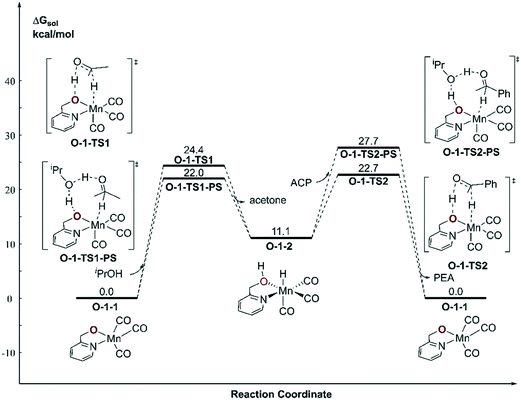

Fig. 7 Free energy profile of transfer hydrogenation with the mono-deprotonated active species in the Mn–O catalytic system. ACP = acetophenone. PEA = phenethyl alcohol.

Since the further deprotonation on CH₂ group with the aid of ^tBuOK (O-1-1_dimer → O-TS2_pre) requires 25.7 kcal mol⁻¹ in free activation energy, which is much lower than the free activation energy barrier (O-1-2 → O-1-1 → O-1-TS2: ΔG^≠ = 32.8 kcal mol⁻¹) in the mono-deprotonated species catalysed pathway, the TH reaction should be catalysed by the double deprotonated complex O-2-1C. The TH process can either occur at the coordinated oxide (O-site) or the C=C bond (C-site) after the deprotonation. The calculated results suggest a concerted bifunctional hydrogen transfer mechanism with a free activation energy of 39.8 kcal mol⁻¹ for the O-site (please see Fig. S2 in the ESI†), which can be ruled out. The free activation energy of the stepwise outer-sphere bifunctional hydrogen transfer mechanism via the C-site is 24.3 kcal mol⁻¹ (Fig. 8, O-2-1C → O-2-TS1C-PS) and the inner-sphere proton transfer mechanism is slightly higher in free energy (ΔG^≠ = 29.1 kcal mol⁻¹, please see Fig. S3 in the ESI†). The DFT calculated free energy profile along with the reaction pathway is depicted in Fig. 8. The results suggest that the overall free energy barrier is 24.3 kcal mol⁻¹. Important optimized structures are depicted in Fig. 9.

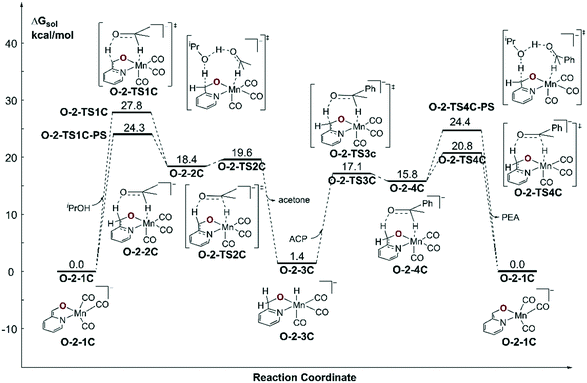Fig. 8 Free energy profile of transfer hydrogenation with the double-deprotonated active species in the Mn–O catalytic system. ACP = acetophenone. PEA = phenethyl alcohol.

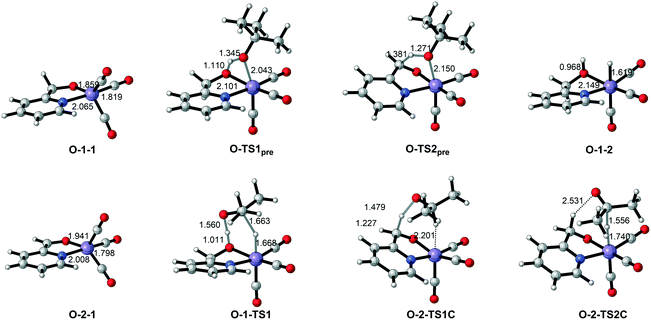Fig. 9 Important optimized intermediates and transition states in Mn–O catalytic system. Bond lengths are in Ångstroms.

In summary, our calculation results suggest that the Mn–N system is catalysed via the mono-deprotonated species N-1-1. The activation energy barrier of the Mn–N system is 23.9 kcal mol⁻¹. The Mn–O system is catalysed via the double-deprotonated species O-2-1C and the activation energy barrier of the aromatization/dearomatization mechanism is 24.3 kcal mol⁻¹. Therefore, the calculated result is consistent with the experimentally observed conversion that the Mn–N system exhibits better activity. Although the result is consistent with the experimental observation, the difference in the activation free energy is not significant, which implies that the observed activity difference is influenced by other factors. Another noticeable difference reflected in the DFT calculated results is the free energy change of the ⁱPrOH dehydrogenation process. The generation of metal hydride catalysed by the mono-deprotonated species in Mn–O system is an endothermic reaction (O-1-1 → O-1-2: ΔG = 11.1 kcal mol⁻¹), which is obviously different compared to the Mn–N system (N-1-1 → N-1-3: ΔG = −3.1 kcal mol⁻¹) and further suggests the Mn–O catalytic system lacks driving force after pre-activation. The next discussion section will illuminate the origin of the different activities of the two catalytic systems.

4. Discussion

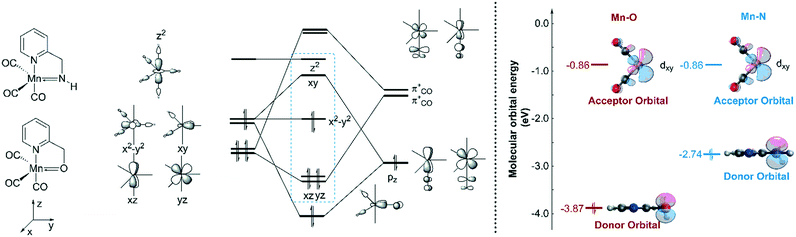
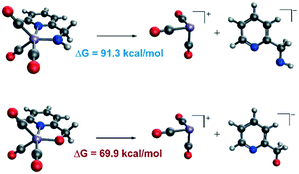
In order to explain the difference in the catalytic activities of the two catalytic systems, a noticeable feature of the catalytic systems is the significant change in the coordination geometries during pre-activation and the catalytic cycle. Such dramatic changes in coordination geometry are rarely seen in traditionally bifunctional catalysts. During the pre-activation period, the complex becomes a 5-coordinated 16e system after the deprotonation of the NH₂ group and the increased trans-effect of the amide moiety forces the CO ligand to isomerize. During the isomerization, the electronic structure of the NH group changes from sp³ to sp². The p orbital with a pair of electrons interacts with the non-bonding d_xy orbital to form a d–p π bond (Fig. 10). Thus, the complex is restored to a relatively stable 18e electronic structure. Further confirmation of the electronic structure (Fig. 10) suggests that the energy level of the frontier molecular orbital energy between the metal centre and the pyridine ligand is closer in the Mn–N complex than in the Mn–O complex, indicating that the d–p π bond is stronger compared to the Mn–O complex, which may further lead to irreversible decomposition. The reaction free energy changes of the decomposition of the Mn(I) complexes were investigated (Fig. 11). For the Mn–N system, the free energy of the dissociation of the pyridine ligand is 91.3 kcal mol⁻¹. However, the free energy of the dissociation of the pyridine ligand is 69.9 kcal mol⁻¹ in the Mn–O system. Moreover, the reaction free energy of the dissociation of the O-arm in the Mn–O system is 14.0 kcal mol⁻¹ and the dissociation of the N-arm in the Mn–N system is 21.9 kcal mol⁻¹, which indicates that the ligand more easily dissociates, leading to decomposition and the occurrence of side reactions (please see page S4 in the ESI†). Although the dissociation of the pyridine is a highly uphill process, these results indicate that the Mn–N complex is more thermodynamically stable than the Mn–O catalyst, which accounts for its higher catalytic activity.

Fig. 10 Qualitative molecular orbitals of the trigonal bipyramidal O-1-1 and N-1-1.

Fig. 11 The free energy changes of the ^tBuO- coordination process.

On the other hand, the DFT calculated potential free energy surface suggests that the ⁱPrOH dehydrogenation reaction in Mn–O is an endothermic reaction, which is opposite to the Mn–N system's exothermic character. Therefore, the hydride complex should be crucial to illuminate such difference. By analysing the geometry of the metal hydride complex N-1-3 and O-1-2, it was found that the metal hydride bond and the O–H bond are almost parallel and the ∠Mn–O–H bond angle is 97.5° in the Mn–O system, which is much smaller than the ∠Mn–N–H bond angle (107.1°) in the Mn–N system (Fig. 12). The reason for the difference in bond angle is due to the difference in electronegativity between the oxygen and nitrogen atoms. As the oxygen atom possesses higher electronegativity, the hydrogen atom in the OH group possesses more positive charge than the hydrogen atom of the NH group. The Mulliken charges of the hydrogen atoms of the N–H and O–H functional groups are +0.172 and +0.228, respectively. The NPA (natural population analysis) charges of the hydrogen atoms of the N–H and O–H functional groups are +0.411 and +0.507, respectively. The inductive effect from the metal hydride causes the hydrogen atom of the OH group to be closer to the metal hydride and even transform the O–H group parallel to the metal hydride bond. When the OH group is parallel to the metal hydride bond, the bonding orbital of the O–H σ-bond and the metal centre non-bonding d_yz orbital repel each other, causing the d_xy orbital to become anti-bonding in character. Therefore, the formation of a metal hydride complex in Mn–O is thermodynamically unfavourable.

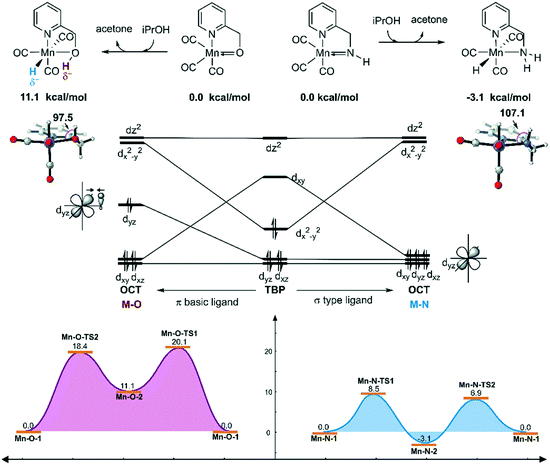Fig. 12 Qualitative molecular orbitals of the metal hydride complexes in the Mn–N and Mn–O systems. The relative free energies are given in kcal mol⁻¹. OCT = octahedral. TBP = trigonal bipyramidal.

The unstable orbital interaction results in a lack of driving force in the dehydrogenation of ⁱPrOH in the catalytic cycle of the Mn–O catalytic system and results in low experimental conversion. Therefore, the OH ligand can be regarded as a π basic ligand instead of a σ-type ligand, while the NH₂ group in the Mn–N system maintains the characteristics of a σ-type ligand, in that it is relatively robust and stable. During the dehydrogenation process, the complex changes from trigonal-bipyramidal to octahedral geometry. The molecular orbital reforms and the complex can achieve the maximum ligand field stabilization energy. Therefore, the generation of the hydride complex N-1-3 is an exothermic process. The hydride complex is capable of promoting the hydrogenation reaction via an approachable free energy barrier.

Based on the above analysis and understanding, if the inductive effect caused by the metal hydride can be reduced and the OH group can be restored to the σ-ligand type, the unfavourable d–σ orbital interaction of the metal and the ligand will be weakened. The hydroxyl group is still a possible candidate for bifunctional catalysis. The simplest way to decrease the negativity of the metal hydride is to increase the oxidation state of the metal centre. Therefore, we replaced the Mn(I) centre in the previous two systems with an Fe^II centre using the same ligand and evaluated their catalytic activities computationally (Fig. 13). The DFT calculation results suggest that both catalysts promote TH via concerted bifunctional hydrogen transfer. The dehydrogenation process of the Fe–O system is exothermic in free energy (Fe–O-1 → Fe–O-2: −5.4 kcal mol⁻¹) and the free activation energy barrier of the whole catalytic process is only 15.4 kcal mol⁻¹ (Fe–O-2 → Fe–O-TS2). In terms of the analysis of the key Fe(II)-hydride complex, it was found that the ∠Fe–O–H bond angle is restored to about 110.0° and the OH group is coordinated to the Fe centre as a σ-bond, which indicates that the unfavourable interaction is avoided. However, the driving force in the Fe–N system is so strong that it even causes a thermodynamic sink to be generated in the catalytic cycle, which makes the subsequent catalysis difficult to carry out, affecting the catalytic activity.

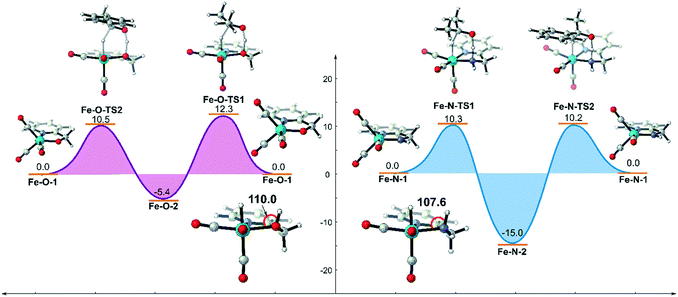Fig. 13 Free energy profile of transfer hydrogenation mediated by Fe(II) catalysts bearing the same ligands. The relative free energies are given in kcal mol⁻¹.

In order to provide general guidelines for future MLC catalyst design, the free energy changes of am ⁱPrOH dehydrogenation reaction catalysed by a series of catalysts based on d⁶ metal centres were measured (Fig. 14). The calculation results show that the dehydrogenation process is endothermic for the Group 6 transition metals. The ∠Mn–X–H bond angle increases with an increase in the oxidation state. However, the length of the M–H bond decreases along with an increase in the oxidation state (please see the ESI,† page S11). The origin of such phenomenon is due to the low oxidation state of metal centres, which increases the electronegativity of the hydride, thereby enhancing the unfavourable interaction between the hydride and functional ligand. For the group 7 metals, there is a significant difference in the thermodynamic tendency of the amine and hydroxyl ligands. The free energy change of the catalyst bearing the hydroxyl group as a functional ligand remains endothermic and the free energy change of the catalyst bearing the amine functional ligand becomes slightly thermodynamically favourable. As the oxidation state of the metal centre gradually increase and the unfavourable orbital interaction is further reduced, the driving force of the dehydrogenation is improved. The DFT results suggest that a group 7 metal centre is suitable for a catalyst with an amine as the active ligand and that a group 8 metal is appropriate for a catalyst with a hydroxyl group as the active ligand with reasonable driving force compared to that of a group 9 metal, which exhibits strong exothermic character that hinders the further catalytic process. Previous studies have indicates that the driving force of the catalyst following (de)aromatization in MLC mode is mostly governed by the functional ligand. In contrast, these results show that the driving force of the catalyst which operates via an M–L bond mode more often relies on the character of the transition metal centre.²¹ As many catalytic reactions consist of multiple stages, this strong driving force could be beneficial and problematic at the same time. These predicted results need to be verified by experiments.

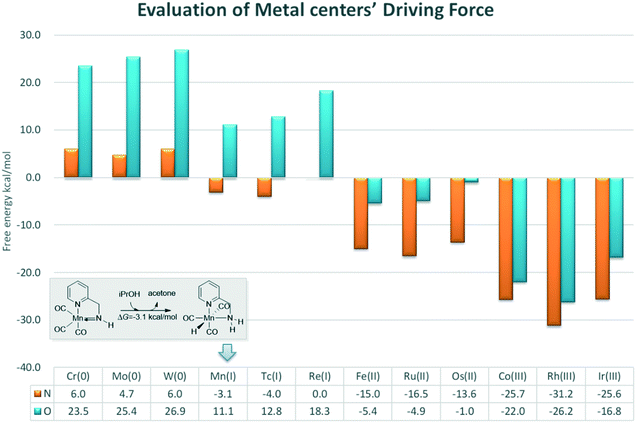Fig. 14 Free energy changes of the dehydrogenation reactions of ⁱPrOH catalysed by different metal centre catalysts. The relative free energies are given in kcal mol⁻¹.

5. Conclusions

In summary, we have presented a detailed theoretical study on TH catalysed by two Mn(I) Lewis base MLC catalysts. The calculated results suggest that the Mn–N catalyst system prefers a classical bifunctional hydrogen transfer mechanism via an accessible activation free energy barrier (N-1-1_dimer → N-1-TS2: 23.9 kcal mol⁻¹), while the Mn–O catalytic system requires further deprotonation and prefers to proceed via an aromatization/dearomatization mechanism with a relatively higher activation energy barrier (O-2-1C → O-2-TS1C-PS: 24.3 kcal mol⁻¹), which is in line with the experimentally observed differences in catalytic activity. By analysing the changes in the detailed electronic structures and coordination geometries of the two catalysts, the origin of the different activities can be attributed to two aspects:

(1) The Mn–O complex catalyst is thermodynamically unstable compared with the Mn–N complex and this may lead to irreversible decomposition, which is the origin of its lower catalytic activity.

(2) The inductive effect between the metal hydride and hydroxyl group leads to an unfavourable orbital interaction and a lack of driving force to generate the metal hydride complex for the Mn–O system.

Further evaluation of the catalysts based on different transition metal centres indicates that the driving force of the catalysts that follow the M–L bond MLC mode is mainly governed by the metal centre, which is an intriguing contrast to the ligand-driven (de)aromatization MLC mode. This study reveals the subtle relationship between the stability and activity of the transition metal complex catalyst in MLC catalysis, which should be informative for future catalyst design.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the NSFC (21803014, 21973113, 21573292, 21673301, 21773312), the Guangdong Natural Science Funds for Distinguished Young Scholars (No. 2015A030306027), the Tip-top Youth Talents of Guangdong special support program (No. 20153100042090537), the Natural Science Foundation of Guangxi (No. 2018GXNSFBA138041) and the Fundamental Research Funds for the Central Universities.

References

1. D. Wang and D. Astruc, Chem. Rev., 2015, 115, 6621–6686.
2. J. R. Khusnutdinova and D. Milstein, Angew. Chem., Int. Ed., 2015, 54, 12236–12273.
3. R. Noyori and S. Hashiguchi, Acc. Chem. Res., 1997, 30, 97–102.
4. S. E. Clapham, A. Hadzovic and R. H. Morris, Coord. Chem. Rev., 2004, 248, 2201–2237.
5. M. Feller, Y. Diskin-Posner, L. J. W. Shimon, E. Ben-Ari and D. Milstein, Organometallics, 2012, 31, 4083–4101.
6. M. Feller, U. Gellrich, A. Anaby, Y. Diskin-Posner and D. Milstein, J. Am. Chem. Soc., 2016, 138, 6445–6454.
7. E. Ben-Ari, G. Leitus, L. J. W. Shimon and D. Milstein, J. Am. Chem. Soc., 2006, 128, 15390–15391.
8. K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Chem. Rev., 2019, 119, 2453–2523.
9. R. H. Morris, Acc. Chem. Res., 2015, 48, 1494–1502.
10. P. E. Sues, K. Z. Demmans and R. H. Morris, Dalton Trans., 2014, 43, 7650–7667.
11. W. W. Zuo, A. J. Lough, Y. F. Li and R. H. Morris, Science, 2013, 342, 1080–1083.
12. G. Q. Zhang, K. V. Vasudevan, B. L. Scott and S. K. Hanson, J. Am. Chem. Soc., 2013, 135, 8668–8681.
13. G. Zhang and S. K. Hanson, Chem. Commun., 2013, 49, 10151–10153.
14. C. Hou, Y. W. Li, C. Y. Zhao and Z. F. Ke, Catal. Sci. Technol., 2019, 9, 125–135.
15. Z. Wei, A. de Aguirre, K. Junge, M. Beller and H. Jiao, Catal. Sci. Technol., 2018, 8, 3649–3665.
16. C. Liu, R. van Putten, P. O. Kulyaev, G. A. Filonenko and E. A. Pidko, J. Catal., 2018, 363, 136–143.
17. P. A. Dub and J. C. Gordon, Nat. Rev. Chem., 2018, 2, 396–408.
18. C. Hou, J. X. Jiang, Y. W. Li, C. Y. Zhao and Z. F. Ke, ACS Catal., 2017, 7, 786–795.
19. P. A. Dub, B. L. Scott and J. C. Gordon, J. Am. Chem. Soc., 2017, 139, 1245–1260.
20. P. A. Dub and J. C. Gordon, ACS Catal., 2017, 7, 6635–6655.
21. C. Hou, Z. H. Zhang, C. Y. Zhao and Z. F. Ke, Inorg. Chem., 2016, 55, 6539–6551.
22. X. Y. Chen and X. Z. Yang, Chem. Rec., 2016, 16, 2364–2378.
23. X. Z. Yang, Chem. Commun., 2015, 51, 13098–13101.
24. Y. Y. Jing, X. Y. Chen and X. Z. Yang, Organometallics, 2015, 34, 5716–5722.
25. C. Hou, J. X. Jiang, Y. W. Li, Z. H. Zhang, C. Y. Zhao and Z. F. Ke, Dalton Trans., 2015, 44, 16573–16585.
26. S. Qu, Y. Dang, C. Song, M. Wen, K.-W. Huang and Z.-X. Wang, J. Am. Chem. Soc., 2014, 136, 4974–4991.
27. H. X. Li and M. B. Hall, J. Am. Chem. Soc., 2014, 136, 383–395.
28. C. Hou, J. X. Jiang, S. D. Zhang, G. Wang, Z. H. Zhang, Z. F. Ke and C. Y. Zhao, ACS Catal., 2014, 4, 2990–2997.
29. T. Chen, H. Li, S. Qu, B. Zheng, L. He, Z. Lai, Z.-X. Wang and K.-W. Huang, Organometallics, 2014, 33, 4152–4155.
30. X. Z. Yang, ACS Catal., 2011, 1, 849–854.
31. H. Li, X. Wang, F. Huang, G. Lu, J. Jiang and Z.-X. Wang, Organometallics, 2011, 30, 5233–5247.
32. M. Perez, S. Elangovan, A. Spannenberg, K. Junge and M. Beller, ChemSusChem, 2016, 10, 83–86.
33. O. Martínez-Ferraté, C. Werlé, G. Franciò and W. Leitner, ChemCatChem, 2018, 10, 4514–4518.
34. K. Ganguli, S. Shee, D. Panja and S. Kundu, Dalton Trans., 2019, 21, 7358–7366.
35. A. Dubey, S. M. W. Rahaman, R. R. Fayzullin and J. R. Khusnutdinova, ChemCatChem, 2019, 11, 3844–3852.
36. A. Bruneau-Voisine, D. Wang, V. Dorcet, T. Roisnel, C. Darcel and J.-B. Sortais, Org. Lett., 2017, 19, 3656–3659.
37. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, Inc., Wallingford CT, 2016.
38. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
39. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
40. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
41. C. Y. Legault, CYLview, 1.0b, Université de Sherbrooke, 2009, Online at http://www.cylview.org.
42. D. E. Prokopchuk and R. H. Morris, Organometallics, 2012, 31, 7375–7385.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9cy02112d

---