Mechanism of CO₂ conversion to methanol over Cu(110) and Cu(100) surfaces

Abstract

Density functional methods are applied to explore the reaction mechanism for CO₂ hydrogenation to methanol over low-index Cu surfaces, namely Cu(110) and Cu(100). A detailed reaction network is obtained, examining several different possible mechanistic routes, including methanol formation via formate and hydrocarboxyl bound intermediates, the role of formaldehyde and formic acid as stable intermediary reaction products, as well as exploring the possibility of CO₂ dissociation and subsequent hydrogenation of the resultant CO. We find that, in contrast to the dominant Cu(111) facet, the Cu(110) and Cu(100) surfaces facilitate a moderate extent of CO₂ activation, which results in lower activation barriers for initial elementary processes involving CO₂ hydrogenation and dissociation, opening up reaction pathways considered unfeasible for Cu(111). Consequently, a wider variety of potential mechanistic routes to achieve methanol synthesis is observed and compared to Cu(111), illustrating the essential role of the Cu surface structure in catalytic activity, and providing insights into the mechanism of CO₂ hydrogenation over Cu-based catalysts. In providing a thorough and detailed exploration of all of the possible mechanistic pathways for CO₂ conversion to methanol, the present work represents a reference point for future studies investigating systems representative of the industrial Cu/ZnO catalyst, enabling a clear identification of the limitations of unsupported Cu catalysts, and thus allowing a more complete understanding of the role of the support material.

---

Introduction

Use of fossil fuels such as coal, oil, and gas, has long been established as a major cause of pollution and global warming, as it results in large quantities of CO₂ and other pollutant gases being released into the atmosphere. As such, new technologies that aim to utilise atmospheric CO₂ in order to reduce its environmental impact are essential in the transition from dependence on fossil fuels towards sustainable alternatives. One such avenue relies on the production of methanol (CH₃OH) from CO₂ derived from waste emissions and from atmospheric sources, and sustainably generated hydrogen (H₂) obtained from efficient water splitting processes, powered by photocatalysis or electricity produced from renewable sources. As well as itself being a valuable industrial product, CH₃OH derived from atmospheric CO₂ could serve as a renewable, carbon neutral fuel source, essentially mirroring nature's photosynthetic carbon cycle.¹ Moreover, as a highly energy dense combustible fuel, CH₃OH can also be used to generate electricity via the direct methanol fuel cell² which could ultimately replace the internal combustion engine. As such, catalytic methods for methanol synthesis are at the forefront in efforts to utilise waste CO₂.

Copper-based catalysts are the most widely used systems for the industrial conversion of CO₂ to methanol, with the Cu/ZnO/Al₂O₃ catalyst being particularly widely used, having been in use since 1966, primarily for the catalytic conversion of syngas to methanol, when a new co-precipitation technique enabled the production of a highly efficient catalyst, considerably more so than earlier ZnO/Al₂O₃ catalysts, whilst also avoiding the rapidly sintering observed in earlier attempts to produce Cu-containing catalysts.³ In addition to the Cu/ZnO/Al₂O₃ catalyst being used for syngas conversion to methanol, the catalyst can also be used for CO₂ hydrogenation. Indeed, previous experimental studies strongly suggest that CO₂ is the key reactant for methanol production from syngas.³ However, despite this widespread use, much remains to be understood regarding the precise role of the components of the industrial catalyst, and how these roles manifest themselves in terms of the catalyst surface structure and the mechanism by which methanol conversion takes place. Initial hypotheses proposed a “synergistic” argument that supposed the existence of a property unique to the Cu/ZnO system that accounted for the considerably improved activity compared to its constituent components, as shown by extensive studies comparing catalytic activity against composition, and thus identifying an optimal Cu : ZnO ratio.^4,5 On the other hand, there is experimental evidence suggesting that maximising Cu surface area is the primary role of the support; indeed, such studies revealed a linear relationship between activity and Cu surface area for a wide range of different support materials,⁶ with Cu/SiO₂ being observed to be the most active catalyst, but also suffering from rapid sintering, preventing its adoption as an industrial catalyst, and the low activity of unsupported Cu being attributed to a low surface area to mass ratio, compared to the supported catalysts. Evidently, there is much that remains unclear regarding the origin of the remarkable activity exhibited by Cu/ZnO catalysts.

Previous computational studies^7,8 examining unsupported Cu as a catalyst for CO₂ hydrogenation to methanol have focused on the Cu(111) facet, as it is the most stable low-index surface and is the dominant surface for polycrystalline copper, as predicted from the surface energies for the low-index Cu surfaces via the Wulff method.^9–11 Other higher index facets, resembling stepped defective pristine low-index surfaces and edge regions of polycrystalline nanoparticles, have also been the subject of similarly detailed experimental and computational studies, such as the Cu(211)^12–14 and Cu(321) facets.¹⁵ Clearly, the high activity of such Cu surface morphologies reported in such studies provides valuable insights for understanding the experimentally observed activity of Cu, and indeed one might expect intuitively that such surfaces, featuring low coordinated Cu atoms, would be highly active. However, in polycrystalline Cu samples such surface structures are likely to account only for a very small fraction of total Cu surface area, being more reflective of Cu particle edges than surface planes which consist mostly of the low index Cu(111), Cu(100), and Cu(110) facets. Compared to Cu(111) and the previously mentioned higher index surfaces, considerably less attention has been devoted to the other low-index facets, namely Cu(110), and Cu(100); computational studies investigate the related forward and reverse water–gas shift reactions,¹⁶ but are not reported for the methanol synthesis reaction. The Cu(110) and Cu(100) facets are only slightly less stable than Cu(111) and form the remainder of the surface of the Wulff nanoparticle. Hence, it is of great interest to explore the reaction mechanism for methanol synthesis over the Cu(110) and Cu(100) surfaces, in order to assess more completely the role of Cu as a catalyst for this particular reaction. Previous experimental studies reveal that the Cu(100) and Cu(110) surfaces have significant activity towards methanol synthesis, and more so than the most stable Cu(111) facet, reflecting structure sensitivity of this catalytic process,^17–20 and warranting a detailed mechanistic overview, which is moreover necessary for a comprehensive overview of the role of copper in this key reaction. Moreover, the insights obtained will pave the way for a greater understanding of the precise role of the ZnO support in the industrially relevant catalyst by understanding more fully the strengths and limitations of the unsupported Cu-only catalyst, investigating the extent to which Cu(110) and Cu(100) facets might be expected to contribute to methanol synthesis activity and exploring the overall reaction mechanism over these surfaces. In this study, 25 distinct elementary processes potentially involved in methanol synthesis over Cu(110) and Cu(100) are explored for each surface from a computational perspective, investigating CO₂ activation, dissociation, and hydrogenation of both CO and CO₂via a range of intermediate species. The results reveal that, unlike the dominant Cu(111) facet, Cu(110) and Cu(100) surfaces are capable of activating CO₂ sufficiently so to reduce considerably activation barriers for CO₂ hydrogenation and dissociation processes, compared to that calculated for Cu(111) by previous studies.^7,8 Consequently, a greater variety of possible reaction mechanisms are relevant for CO₂ hydrogenation over these low index surfaces. The calculations presented in this article shed light on possible means by which supported Cu catalysts may improve upon Cu-only catalysts by identifying elementary processes which provide a common bottleneck to CO₂ hydrogenation for all low index Cu facets. The detailed investigation of several different possible reaction pathways for methanol synthesis presented in this study furthermore provides a foundation for future studies investigating other catalysts for methanol synthesis beyond the Cu-based catalysts which are the focus of our investigation. The complete mechanistic analysis presented here not only illuminates the mechanism for the experimentally reported CO₂ conversion to methanol over unsupported Cu catalyst surfaces,^17–20 but will additionally serve as a valuable reference study for future investigations concerning other, related catalysts, for the same process, enabling a clear identification of the limitations of unsupported Cu catalysts, and allowing deeper insights into the behaviour of complex multi-component catalyst, and the specific roles of individual component materials.

Computational details

All calculations were performed using plane-wave density functional theory (DFT) as implemented in the VASP code (version 5.4.4).^21–24 Slab models for the Cu(110) and Cu(100) facets were constructed consisting of six Cu layers separated by 18 Å of vacuum, ensuring sufficient slab separation to avoid any interaction between surfaces in adjacent periodic images. The top four layers of the slab were allowed to relax, whilst the bottom two were fixed at their bulk lattice positions. Whilst previous computational works examining low-index Cu surfaces used smaller Cu slab models consisting of fewer Cu layers,^7,8 it has been noted that greater slab thicknesses might be required to obtain properly converged surface energies,²⁵ and it has been observed that for the minority Cu low-index surfaces, the calculated surface energy is more sensitive to the slab thickness than for the most stable Cu(111) facet. Hence, the 6-layer slab model employed in this study ensures that any such problems are avoided. A dipole correction was applied to the vacuum to eliminate any spurious electrostatic interaction originating from the asymmetric relaxation of the slab. For the purposes of modelling adsorption and reaction processes, for the Cu(110) surface model a p(3 × 3) supercell was used, whilst for the Cu(100) surface model a p(2 × 2) supercell was used, resulting in two slabs of comparable size (54 and 48 Cu atoms, respectively), and allowing for sufficient separation between adsorbates in adjacent periodic images. A Monkhorst–Pack k-point sampling scheme was used,²⁶ with k-point meshes of (3 × 2 × 1) and (4 × 4 × 1) used for the Cu(110) and Cu(100) surface supercells, respectively, commensurate with the cell dimensions. Inner electrons were replaced by projector-augmented waves (PAW),^27,28 and the valence states were expanded in plane-waves with a cut-off energy of 450 eV. The PBE exchange correlation functional was used throughout,²⁹ with a dispersion correction applied using the D2 scheme devised by Grimme,³⁰ in order to account for the weak van der Waals interactions that are key to determining the physisorption behaviour of species relevant to methanol synthesis, such as CO₂. Additionally, no corrections were made to account for vibrational zero-point energies, since it is expected that any such contribution would be negligible relative to the calculated electronic energy, since in surface catalysis adsorption removes many of the degrees of freedom associated with reactions in vacuum.

In order to investigate the elementary reaction processes taking place on the Cu(110) and Cu(100) surfaces during CO₂ conversion, optimised geometries were obtained for all adsorbed reactants, products, and intermediates, with atomic forces converged to within 0.01 eV Å⁻¹. In each case, electronic wavefunctions were converged such that the total energy was converged to within 10⁻⁵ eV. Transition states were identified using the climbing image nudged elastic bands (CI-NEB) method,³¹ with vibrational analysis confirming that a saddle point had indeed been located. For transition states not converged using the CI-NEB method, the improved dimer method (IDM)^32,33 was applied to refine transition states with atomic forces converged to within 0.03 eV Å⁻¹.

Results

CO₂ adsorption and activation

For each of the three low-index Cu surface, Cu(111), Cu(110), and Cu(100), CO₂ adsorption was explored, with the results collected in Table 1. In all cases, CO₂ adsorption was modestly exothermic, with calculated adsorption energies being in the range of 0.14 eV to 0.39 eV, consistent with CO₂ physisorption. The calculated CO₂ adsorbate geometries reveal no significant changes compared to gas phase CO₂, further supporting the presence of a physisorbed CO₂ species.

Table 1 Calculated CO₂ physisorption energy (i.e. E_ads. = ΔE for the process CO₂(g) → CO₂*), Cu–C distance (d_(Cu–C)), C–O distance (d_(Cu–O)), and O–C–O angle (∠ (O–C–O)/°) for all three low-index Cu surfaces

Cu facet	E ads./eV	d (Cu–C)/Å	d (C–O)/Å	∠ (O–C–O)/°
(111)	−0.353	3.41	1.18	179.45
(110)	−0.148	3.49	1.18	179.40
(100)	−0.391	3.43	1.18	179.20

---

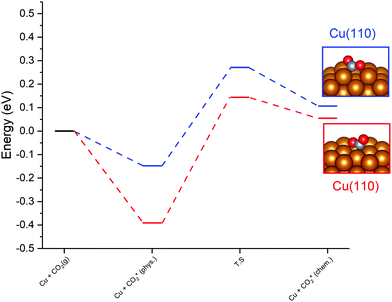
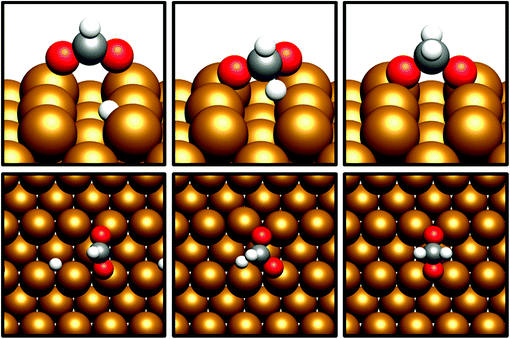
For the Cu(110) and Cu(100) facets, however, a second mode of CO₂ adsorption was identified, featuring a significant distortion of the CO₂ O–C–O angle (∠ (O–C–O) < 130°), implying a considerable weakening of the C=O bond and a degree of chemisorption behaviour with some electron transfer into the CO₂ antibonding orbitals. For the Cu(111) facet, on the other hand, no such adsorption mode was identified. For both the Cu(110) and Cu(100) surfaces, a local minimum structure was identified, lying at a higher energy than the physisorbed species, but being only slightly unstable relative to gas phase CO₂, by approximately 0.1 eV. The calculated energetics for the transition of physisorbed to chemisorbed CO₂, along with calculated geometric data for the latter, are summarised in Table 2. For both the (110) and (100) surfaces, the chemisorbed CO₂ molecule was found in a highly coordinated hollow surface site (see Fig. 1 for graphical depiction). In both cases, a distinct transition state was identified for the conversion of the physisorbed CO₂ species to its chemisorbed counterpart, with activation energies of 0.42 eV and 0.54 eV being determined for the Cu(110) and Cu(100) surfaces, respectively, with a considerable reduction of approximately 1.5 Å in the Cu–C distance occurring during this transition, and an accompanying lengthening of the C–O bonds. Fig. 1 graphically summarises the relative energies associated with gas phase CO₂, the physisorbed and chemisorbed CO₂ species, and the transition state linking the two modes of adsorption.

Fig. 1 Graphical summary of relative energies for gas phase CO₂, physisorbed and chemisorbed CO₂, and the transition state for conversion between the two modes of adsorption. Images depicting the chemisorbed CO₂ geometries are also presented for both the Cu(110) and Cu(100) facets.

Table 2 Calculated energy difference between the physisorbed and chemisorbed CO₂ species (ΔE), with corresponding activation energy (E_a), imaginary vibrational frequency corresponding to the unstable mode (ν), along with the Cu–C distance (d_(Cu–C)), C–O distances (d_(C–O)), and O–C–O angle (∠ (O–C–O))

Process no.	Cu facet	ΔE/eV	E a/eV	v/cm^−1	d (Cu–C)/Å	d (C–O)/Å	∠ (O–C–O)/°
1	(110)	0.254	0.419	190.97	1.998	1.27, 1.27	127.53
1	(100)	0.446	0.535	181.67	2.141	1.22, 1.33	128.45

---

Bader charge analysis was also performed to determine the extent to which the observed CO₂ distortion is accompanied by charge transfer which might indicate the extent of activation. For both Cu(110) and Cu(100), a moderate degree of charge transfer was discovered for the bent chemisorbed CO₂ species, with the respective excess Bader charges calculated as β = 0.77 and β = 0.76, compared to β = 0.07 and β = 0.06 for the physisorbed species. Hence, an increase in charge localisation of 0.70e⁻ is evident as a result of the transition from the physisorbed to the chemisorbed CO₂; in both cases the charge accumulation on CO₂ was primarily localised on the C atom. For both Cu(110) and Cu(100), this charge accumulation on C was accompanied by slight oxidation of the Cu atoms coordinated with the activated CO₂ species. Hence, charge transfer from the Cu surface to the adsorbate is demonstrated, in agreement with the proposal that electron transfer from the Cu surface to the CO₂ antibonding orbitals is responsible for the resulting changes in CO₂ adsorption geometry. Clearly, the chemisorbed bent CO₂ species is activated by both of these low-index Cu facets, and can be assumed to promote subsequent reaction processes such as hydrogenation or dissociation to CO and O, which are explored later in this study.

The limited activation of CO₂ over Cu(111) compared to other low-index surfaces has been documented in past experimental^17,34 and computational^35,36 studies, with both Yoshihara et al.¹⁷ and Wang et al.³⁵ proposing that CO₂ activation over low-index Cu surfaces follows the order Cu(110) > Cu(100) > Cu(111). This conclusion is consistent with the results obtained in this study, with no activation of CO₂ detected for Cu(111), and a more kinetically accessible activated CO₂ for Cu(110) compared to Cu(100). Whilst Wang et al. explored both periodic and cluster models to represent the Cu surfaces, it was found that the lack of inclusion of weak dispersion forces in their periodic approach (as the method devised by Grimme applied in the present work was not developed until two years after the publication of Wang et al.) limited the utility of the periodic slab model, as such interactions are key to modelling CO₂ physisorption. However, the present work combines a periodic slab model (which more accurately represents the extended natures of real Cu surfaces than a cluster model) with a dispersion correction and arrives a largely similar conclusion in terms of the ordering of each of the Cu surfaces according to the extent to which they facilitate CO₂ activation, corroborating the earlier computational results. Interestingly, previous computational studies investigating Cu(111) facets of an octahedral nanocluster, rather than a periodic surface, did identify a stable chemisorbed CO₂ species, albeit with a more limited electron transfer of ∼0.4, as determined from Bader charge analysis.³⁷ The enhanced CO₂ adsorption and activation over such nanocluster facets can be attributed to the changes in electronic structure of metal atoms at nanoparticle edges, hence such behaviour is not observed for periodic Cu(111) surfaces or larger nanoparticle facets, reflecting the highly surface-sensitive nature of CO₂ adsorption and activation on Cu facets. The results reported in the present study suggest a greater degree of activation than that reported by Wang et al. for the Cu(110) and Cu(100) facets, with a considerably greater deviation from the linear geometry of free CO₂. Additionally, the Bader charge analysis confirms a modest degree of activation compared to previous computational studies exploring transition metal carbides which are known to be highly activating towards CO₂;³⁸ for physisorbed CO₂, comparably small Bader charges were calculated for both the low-index Cu facets investigated in this study (β = 0.07 and β = 0.06, for Cu(110) and Cu(100), respectively), and metal carbides such as TiC, VC, ZrC and NbC (β = 0.06, β = 0.06, β = 0.12 and β = 0.07 for the facets of TiC, VC, ZrC and NbC, respectively, which exhibit the greatest extent of electron transfer to the physisorbed state³⁸). However, for the chemisorbed species, the extent of charge transfer from the Cu substrate was considerably less than that calculated previously for the metal carbides, with the most activating carbide surfaces exhibiting Bader charge accumulation of β = 1.79, β = 1.12, β = 1.84 and β = 1.19 for TiC, VC, ZrC and NbC respectively, compared to only 0.7e⁻ for both Cu(110) and Cu(100). For each of these metal carbides, the activated chemisorbed species is more stable than the physisorbed state; in particular, it is notable that the extent of electron transfer, as illustrated by the Bader charge analysis is strongly correlated with the stability of the chemisorbed state (E_ads. = −3.05 eV, E_ads. = −1.93 eV, E_ads. = −3.32 eV and E_ads. = −1.98 eV for TiC, VC, ZrC and NbC, respectively). In contrast with the metal carbides and in accordance with the observed trend correlating the extent of Bader charge accumulation on CO₂ and the stability of the chemisorbed state, for the low-index Cu surfaces investigated in the present work, the chemisorbed state is slightly energetically unstable with respect to gas phase CO₂, (as noted in Table 2) and thus expected to be a comparatively short-lived surface species before either undergoing subsequent reactive processes or reverting to the more stable physisorbed state. One can expect that CO₂ desorption will more readily take place than any subsequent reaction process, given that it would appear to be kinetically unhindered, hence one might conclude that no further reaction, and indeed formation of methanol, would take place. However, it must be considered that the adsorption, activation, and desorption, of CO₂, are essentially reversible processes, whereas it is likely that subsequent reaction processes, such as hydrogenation to formate or hydrocarboxyl will be considerably more exothermic, and thus irreversible (indeed this is reported in the present work). Hence, whilst CO₂ adsorption may predominate, we cannot exclude at least partial, irreversible, consumption of CO₂ to form hydrogenated intermediates, and ultimately methanol. Moreover, one the central aims of this study is to explore all mechanistic routes, hence it is essential to study subsequent reaction processes. Our results imply a significant degree of CO₂ activation over low-index Cu surfaces, enabling the formation of a distinct local minimum adsorption geometry for Cu(110) and Cu(100), which may still enable CO₂ to undergo hydrogenation to yield methanol. Indeed, even if the activated CO₂ species are relatively short lived, and do not accumulate in appreciable quantity on the catalyst surface, this does not preclude such a species participating in subsequent elementary reaction processes as an intermediate between the more stable physisorbed CO₂ species and the products of these processes (i.e. CO₂ dissociation, or hydrogenation processes when H₂ is present).

Consideration must also be given to previous experimental Raman, IR and HREELS studies, which suggest that Cu surface structure and annealing effects have a significant impact on whether the bent, activated CO₂ species is observed, with such species being reported for rough Cu surface, but not for smooth annealed surfaces,^39–41 while the results obtained in the present work only consider the pristine low-index Cu facets. However, rough surfaces will include a variety of facets and the observed activation of CO₂ on such surfaces can be attributed to the two low index components.

Overall, there is considerable experimental evidence suggesting the possibility of an activated CO₂ species being present on Cu surfaces, in agreement with the computational results presented here.^{17,34,39–41} Indeed, previous surface enhanced Raman spectroscopy (SERS) studies suggest the coexistence of both activated and non-activated CO₂ species,³⁹ reflecting the relatively close adsorption energies and low activation barriers to formation of the activated species calculated in the present work. As such, the remainder of this study will focus on only the Cu(110) and Cu(100) surfaces, which do exhibit the activated CO₂ species, for subsequent dissociation and hydrogenation processes which are important for methanol synthesis.

H₂ adsorption and dissociation

Given that CO₂ activation appears to be exhibited by the Cu(110) and Cu(100) surfaces, the next prerequisite for CO₂ hydrogenation is the dissociative adsorption of H₂. Cu catalysts have long been known to be highly active towards H₂ dissociation, which is consistent with the calculations performed in this study.^42–45 The results in Table 3 show that for both Cu(110) and Cu(100), non-dissociative H₂ physisorption was calculated to be very mildly exothermic, at −0.11 eV and −0.08 eV for Cu(110) and Cu(100), respectively. The most stable adsorption site for the H₂ molecule is atop a Cu surface atom (Fig. 2), but other sites, namely bridging (short and long bridge sites for Cu(110)) and hollow adsorption sites, are close in energy. For both surfaces, the dissociated state was determined to have a lower energy with respect to the weakly physisorbed state, with adsorption energies of −0.32 eV for Cu(110) and −0.28 eV for Cu(100); in both cases, it can be seen that H₂ dissociation is exothermic with respect to the physisorbed state by around 0.2 eV, consistent with the well-established role of Cu in facilitating H₂ dissociation. For Cu(100), adsorbed H atoms had lower energies on surface hollow sites affording a highly coordinated adsorption environment, whereas for Cu(110), H atoms adsorbed at the short bridge sites were found to be most stable. Activation barriers were calculated for dissociation of physisorbed H₂, with E_a calculated at 0.28 eV for Cu(110) and 0.52 eV for Cu(100), indicating that such a process is indeed energetically feasible. It is notable that the ease with which we expect H₂ dissociation to occur correlates to high local hydrogen availability, facilitating CO₂ hydrogenation. Previous computational studies investigating H₂ dissociation as part of a study exploring the Cu(111) facet as a catalyst for CO₂ hydrogenation to methanol did not consider H₂ physisorption and the associated barrier for dissociation.⁸ However, it has been demonstrated that the inclusion of weak dispersion forces in simulations plays a key role in determining H₂ physisorption behaviour;⁴⁶ hence the inclusions of such a correction in the calculations in the present study is consistent with the observation of a weakly physisorbed H₂ molecule preceding dissociation, accompanied by a modest activation barrier. Whilst the activation barrier for H₂ dissociation may be greater than that for H₂ desorption, it is clear from the calculated barriers for H₂ dissociation that this process is energetically feasible, with a low barrier calculated for Cu(110) and a moderate barrier for Cu(100). Coupled with the exothermic H₂ dissociation energy, it can be concluded that this overall process is under thermodynamic control, and that atomic H arising from H₂ dissociation is likely to be present on the Cu surface, in line with the well-reported experimental observation of this process.^42–45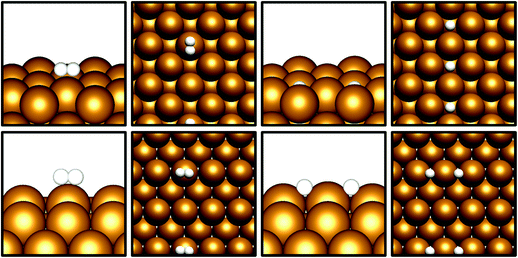

Fig. 2 Graphical depiction from side and top view of physisorbed (left) and dissociated (right) H₂, for Cu(100) (top) and Cu(110) (bottom).

Table 3 Calculated adsorption energy for physisorbed H₂, along with energy differences for dissociation to 2H*, corresponding activation energies for dissociation and the associated imaginary vibrational frequency corresponding to the unstable mode

Process no.	Cu facet	E ads. (phys.)/eV	ΔEdiss./eV	E a/eV	v/cm^−1
2	(110)	−0.113	−0.210	0.284	811.542
2	(100)	−0.083	−0.197	0.517	1239.385

---

Pathways for CO₂ conversion to methanol

Methanol synthesis from CO₂ could take place via a variety of possible reaction pathways with a range of possible intermediates; the process necessarily involves the formation of three C–H bonds and one O–H bond, as well as the cleavage of one of the CO₂ C–O bonds. However, there several different reaction pathways depending on the order in which these processes occur, giving rise to different intermediate species; the pathway featuring the most kinetically accessible and most stable intermediates will therefore be the most favourable. As such, this study considers several different approaches, involving direct hydrogenation of CO₂* to either HCOO* or COOH*, as well as processes derived from CO₂* dissociation and subsequent hydrogenation of the resulting CO*. Intermediate species considered include HCOOH*, H₂CO*, H₂COO*, H₂COOH*, CH₂OH*, and CH₃O*, the latter two being the penultimate adsorbed species before methanol formation. The relation between these intermediates and the reaction processes linking them is summarised in Fig. 3. The subsequent sections will address each reaction process sequentially, before we finally consider H₂O formation which is a by-product of methanol synthesis from CO₂.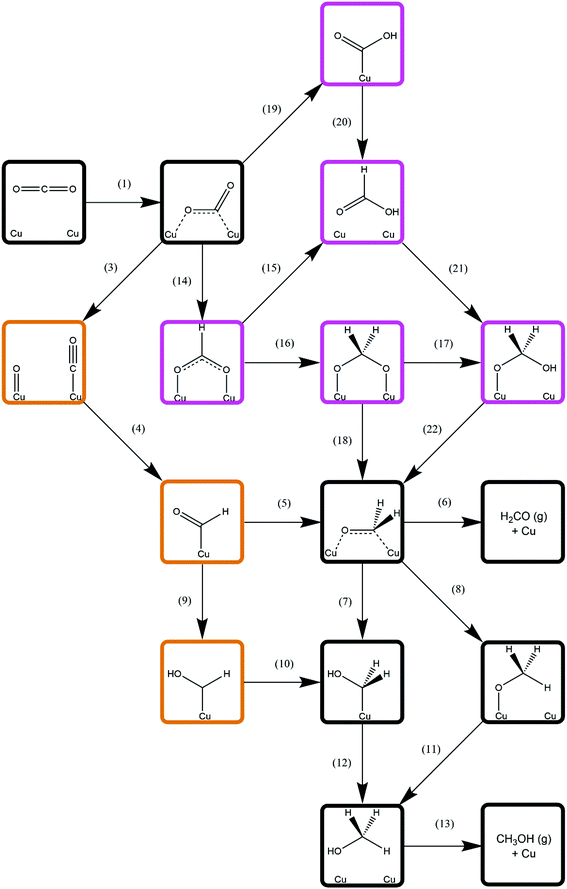

Fig. 3 Simplified schematic depicting possible reaction pathways for methanol synthesis from CO₂. For clarity, only processes involving C-containing species are show; H₂ dissociation (process 2, Table 3) and elementary reaction processes involving H₂O formation (processes 23–25, Table 9) are omitted and are common to all possible reaction pathways. Intermediates associated exclusively with CO₂ hydrogenation are highlighted in purple; those associated exclusively with CO hydrogenation are highlighted in orange; and intermediates common to both pathways are indicated by black borders. Numbers adjacent to arrows representing elementary processes correspond to the process number labels for each unique process as listed in the results tables.

CO₂ dissociation to CO + O

We explore first the pathway involving CO₂ dissociation, and indeed, past studies identified the presence of an activated CO₂ species as a precursor to CO₂ dissociation.^39,47 Furthermore, a series of experimental studies utilising low-energy electron diffraction (LEED), Auger electron spectroscopy (AES) and ellipsometry techniques report CO oxidation to CO₂ by pre-adsorbed surface oxygen (i.e. the reverse of CO₂ dissociation) for all three low-index Cu surfaces.^34,48–50 However, the absence of an activated, bent CO₂ species for Cu(111) makes the reverse dissociation process unlikely for this surface, (which indeed is found to be the case from experimental^34,51 and computational⁵² studies), but, owing to its formation on Cu(110) and Cu(100), CO₂ dissociation to CO on these facets is clearly feasible. This notion is further corroborated by previous computational studies which provide evidence for the involvement of a bent CO₂ intermediate in CO oxidation over Cu(110).³⁶ Additionally, previous computational electrocatalysis studies exploring Cu(100) electrodes suggest that CO is a possible intermediate in not only methanol synthesis, but also the formation of higher alcohols and hydrocarbons.^53,54 Whilst a detailed investigation of the formation of these products lies beyond the scope of the present work, the previous results nonetheless indicate that CO hydrogenation, and by extension CO₂ dissociation, is worthy of investigation. Our calculated results for CO₂ dissociation are tabulated in Table 4. For both cases, accessible transitions states were identified, with activation barriers of 0.79 eV and 0.71 eV calculated for Cu(110) and Cu(100), respectively. Whilst CO₂ dissociation over Cu(100) was found to be very slightly exothermic (−0.08 eV), the corresponding process for Cu(110) was determined to be endothermic by 0.52 eV.

Table 4 Reaction and activation energies for CO₂ dissociation with corresponding imaginary frequency for the unstable mode

Process no.	Cu facet	ΔE/eV	E a/eV	v/cm^−1	d (C–O) (TS)/Å
3	(110)	0.520	0.792	182.416	2.032
3	(100)	−0.083	0.711	319.611	1.943

---

Clearly, the calculated activation barriers for CO₂ dissociation make this possibility distinctly feasible. In particular, there is good agreement with experimental TPD studies conducted on Cu(100) which confirm that CO₂ dissociation readily occurs.⁵⁵ For the Cu(110) facet, the experimental perspective is less clear, with contradictory reports regarding the presence of adsorbed O originating from CO₂ dissociation.⁵¹ Nonetheless, the calculated dissociation energies reproduce the relative order of the activities of these two Cu surfaces, with the Cu(100) facet being more active for CO₂ dissociation than the Cu(110) surface. The calculated activation barriers agree well with previous computational studies,¹⁶ which identify both Cu(100) and Cu(110) as being active for CO₂ dissociation, although the calculated activation barriers were determined to be lower in this study, more so for Cu(100). An important consideration is the overall thermodynamic driving force for CO₂ dissociation; whilst not detecting any significant CO₂ dissociation under UHV conditions over Cu(110), Nakamura et al.⁵¹ identify the thermodynamic driving force for this process as being strongly determined by the loss of translational and rotational entropy resulting from CO₂ dissociative adsorption. However, it must be considered that under hydrogenation conditions, this effect may be mitigated by subsequent hydrogenation of CO to methanol and adsorbed O to water, which may then be desorbed to the gas phase. As such, the energetic barrier to CO₂ dissociation is probably the more important factor, as at least according to the computational results derived in this study, such a process could quite feasibly form part of the overall reaction pathway for CH₃OH formation over Cu(100) and Cu(110). Hence, in the following sections, possible hydrogenation pathways for methanol synthesis from both CO and CO₂ will be considered.

CO hydrogenation to methanol

Having established the possibility of CO₂ dissociation leading to the presence of CO on Cu(110) and Cu(100) surfaces, along with the feasibility of H₂ dissociation to yield H*, hydrogenation of CO to yield methanol is now considered, with the calculated results being presented in Tables 5 and 6 for Cu(110) and Cu(100), respectively. Hydrogenation can take place at either O or C; the former process was investigated briefly and was found to be unfeasible, with high activation barriers of 1.66 eV for Cu(110) and 1.92 eV for Cu(100). As such, this process and subsequent hydrogenation of the resulting COH* intermediate was not considered as a possible mechanistic pathway for methanol synthesis. The latter process, with hydrogenation taking place at C, was, however, found to have much lower activation barriers for both of the Cu surfaces investigated. The first hydrogenation step yields a formyl HCO* species (process 4, Tables 5 and 6); the calculated activation energies were comparable with values of 1.08 eV (process 4, Table 5) and 1.11 eV (process 4, Table 6) obtained, along with endothermic reaction energies of 0.66 (process 4, Table 5) and 0.74 (process 4, Table 6), for Cu(110) and Cu(100), respectively.

Table 5 Calculated reaction energies and activation energies, with corresponding imaginary frequencies for the unstable modes, for the elementary reaction processes involved in CO hydrogenation over Cu(110)

Process no.	Elementary process	ΔE/eV	E a/eV	v/cm^−1
HCO* formation
4	CO* + H* → HCO*	+0.660	1.076	1044.590
H 2 CO formation, desorption and hydrogenation
5	HCO* + H* → H2CO*	−0.597	0.109	644.746
6	H2CO* → H2CO(g)	+0.986	—	—
7	H2CO* + H* → CH2OH*	+0.087	0.963	927.927
8	H2CO* + H* → CH3O*	−0.622	0.388	328.280
HCOH formation and hydrogenation
9	HCO* + H* → HCOH*	−0.095	0.496	1164.784
10	HCOH* + H* → CH2OH*	−0.339	0.284	818.827
CH 3 OH formation and desorption
11	CH3O* + H* → CH3OH*	−0.004	0.960	926.043
12	CH2OH* + H* → CH3OH*	−0.705	0.604	610.080
13	CH3OH* → CH3OH(g)	+0.771	—	—

---

Table 6 Calculated reaction energies and activation energies, with corresponding imaginary frequencies for the unstable modes, for the elementary reaction processes involved in CO hydrogenation over Cu(100)

Process no.	Elementary process	ΔE/eV	E a/eV	v/cm^−1
HCO* formation
4	CO* + H* → HCO*	+0.737	1.116	959.849
H 2 CO formation, desorption and hydrogenation
5	HCO* + H* → H2CO*	−0.537	0.327	689.409
6	H2CO* → H2CO(g)	+0.770	—	λ
7	H2CO* + H* → CH2OH*	−0.258	0.649	985.000
8	H2CO* + H* → CH3O*	−0.905	0.046	311.795
HCOH formation and hydrogenation
9	HCO* + H* → HCOH*	+0.067	0.673	1159.938
10	HCOH* + H* → CH2OH*	−0.422	0.245	642.437
CH 3 OH formation and desorption
11	CH3O* + H* → CH3OH*	−0.148	0.698	1029.907
12	CH2OH* + H* → CH3OH*	−0.829	0.597	586.857
13	CH3OH* → CH3OH(g)	+0.613	—	—

---

At this point, there are two distinct possibilities for subsequent hydrogenation, which may either take place at C, yielding formaldehyde H₂CO* (process 5, Tables 5 and 6), or at O, yielding a hydroxyformyl HCOH* intermediate (process 9, Tables 5 and 6). For both the Cu(110) and Cu(100), the formaldehyde option has a lower activation energy with values of 0.11 eV (process 5, Table 5) and 0.33 eV (process 5, Table 6), and exothermic corresponding reaction energies of −0.60 eV (process 5, Table 5) and −0.54 (process 5, Table 6). Whilst the activation barriers for HCOH* formation are higher at 0.50 eV (process 9, Table 5) and 0.67 eV (process 9, Table 6) for Cu(110) and Cu(100) respectively, they are low enough for the competing HCOH* intermediate to be kinetically accessible, and in both cases the reaction energies are small, with an exothermic −0.10 eV being calculated for Cu(110) and a slightly endothermic 0.07 eV calculated for Cu(100).

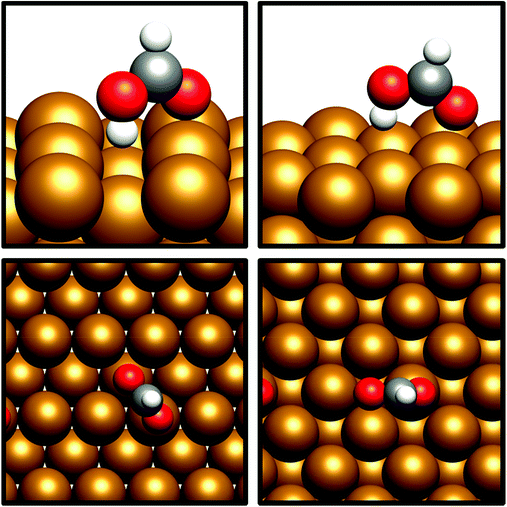
The desorption energy for formaldehyde was also calculated to determine how strongly the species is bound to the catalyst surfaces, and therefore whether it is sufficiently stable and long-lived to participate in subsequently elementary processes. The desorption energy was calculated to be endothermic by 0.99 eV for Cu(110) (process 6, Table 5) and 0.77 eV for Cu(100) (process 6, Table 6), indicating that formaldehyde is strongly bound to the catalyst surface in both cases. It is notable that the adsorption geometry for formaldehyde on both Cu facets considered shows considerable distortion from the usual planar geometry exhibited by the gas-phase molecule, indicating a strong degree of chemical binding to the surface rather than mere physisorption, and perhaps activating formaldehyde towards further hydrogenation to the CH₂OH* and CH₃O* intermediates which are precursors species for methanol (Fig. 4). Indeed, Bader charge analysis confirms a similar extent of electron transfer from the surface to formaldehyde as for CO₂; the Cu(110) surface appears to be slightly more activating with a calculated Bader charge accumulation of β = 0.7, compared to β = 0.67 for Cu(100), relative to gas-phase formaldehyde. Evidently, formaldehyde is a viable intermediate species for methanol formation which can be expected to participate in further elementary reaction processes, rather than simply being desorbed to the gas phase.

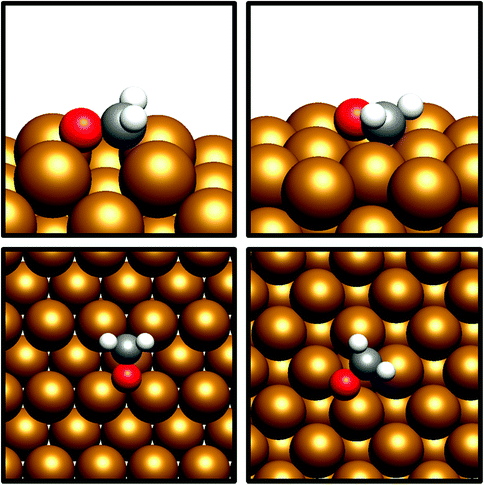Fig. 4 Graphical depiction of optimised formaldehyde adsorption geometry for Cu(100) (top) and Cu(110) (bottom), as seen from the side (left) and from the top (right).

For formaldehyde conversion to methanol, the reaction may either proceed through a methoxy CH₃O* intermediate, or a hydroxylmethylene CH₂OH* intermediate, depending on whether the following hydrogenation process takes place at C or O. For both Cu(110) and Cu(100), the more kinetically feasible pathway involves CH₃O* formation, with activation barriers of 0.39 eV and 0.05 eV and with corresponding reaction energies of −0.62 eV and −0.91 eV for the Cu(110) and Cu(100) surfaces respectively (process 8, Tables 5 and 6). The competing CH₂OH* pathway, whilst still not excessively energetically unfeasible, gave considerably higher activation barriers of 0.96 eV and 0.65 eV (in both cases ∼0.6 eV greater than the corresponding activation energies for the CH₃O* pathway) for the Cu(110) and Cu(100) surfaces, respectively. A similar shift is also seen for the reaction energies, with the calculated values being +0.09 eV and −0.25 eV for Cu(110) and Cu(100) (process 7, Tables 5 and 6). Hence, our calculations suggest that formaldehyde is a likely intermediate in methanol formation from CO, given its strong adsorption to both the (110) and (100) Cu surfaces and the relative ease by which formaldehyde undergoes further hydrogenation to yield CH₃O*.

Hydrogenation of the HCOH* intermediate at C can also result in the formation of the CH₂OH* intermediate, hence both the formaldehyde and HCOH* pathways can converge on this intermediate species. The energetics of HCOH* hydrogenation to CH₂OH* are comparable for both the Cu(110) and Cu(100) surfaces, with respective activation energies of 0.28 eV and 0.25 eV, with corresponding reaction energies of −0.34 eV and −0.42 eV (process 10, Tables 5 and 6). It is notable that whilst the energetics for HCOH* formation are unfavourable compared to H₂CO formation, subsequent formation of the CH₂OH* intermediate is more energetically accessible from HCOH* than H₂CO. Indeed, starting from HCO* hydrogenation and arriving at CH₂OH*, the most energetically demanding step requires only 0.50 eV/0.67 eV for the HCOH* pathway, compared to 0.96 eV/0.65 eV for the H₂CO pathway, for Cu(110)/Cu(100). Hence, at least for Cu(110), the HCOH* intermediate affords the most energetically accessible route to the CH₂OH* intermediate, although the pathway involving formaldehyde and then methoxy before methanol formation is overall the lowest energy route.

We should note, however, that the CH₂OH* intermediate, originating from either HCOH* or H₂CO, must compete with the CH₃O* intermediate, which can only originate from formaldehyde hydrogenation. For Cu(110), a moderately low activation barrier of 0.39 eV was calculated for formation of the latter species (process 8, Table 5), while a very low value of 0.05 eV is obtained for Cu(100) (process 8, Table 6), and the respective calculated reaction energies were determined to be exothermic for both Cu surfaces at −0.62 eV and −0.91 eV (process 8, Tables 5 and 6). Hence, we find that CH₃O* formation is more energetically accessible than the isomeric CH₂OH* intermediate, although for the Cu(110) surface, the highest energy barrier for CH₂OH* formation from HCO* is comparable to the corresponding step for CH₃O* formation (0.50 eV vs. 0.39 eV), whereas the differences for the Cu(100) surface are greater (0.65 eV vs. 0.33 eV).

Methanol formation may ultimately take place by the hydrogenation of either CH₂OH* at C, or by CH₃O* at O. For both Cu(110) and Cu(100), methanol formation from CH₂OH* is less energetically hindered, with activation barriers calculated at 0.60 eV for both surfaces, and both processes are moderately exothermic with values of −0.71 eV and −0.82 eV calculated for Cu(110) and Cu(100) respectively (process 12, Tables 5 and 6). For methanol formation from CH₃O*, the activation barrier is considerably higher for Cu(110) at 0.96 eV, compared to 0.70 eV for Cu(100), and both processes were determined to be only very slightly exothermic, with a reaction energy of <−0.01 eV for the Cu(110) surface and −0.15 eV for Cu(100) (process 11, Tables 5 and 6).

It is clear that for both Cu(110) and Cu(100) surfaces, there is competition between two pairs of intermediates, HCOH* and H₂CO, and CH₂OH* and CH₃O*, which represent two different degrees of hydrogenation, and for both surfaces the overall most energy-demanding elementary process is the primary hydrogenation of CO to HCO, which precedes these competing processes, with activation barriers calculated at slightly greater than 1 eV. Given that all subsequent activation barriers are lower, it is reasonable to speculate that if this kinetic barrier can be overcome, then so should all subsequent, lower, barriers, and we might expect the reaction to proceed through a combination of several intermediate species.

Tables 5 and 6 give details of all of the elementary processes concerned with CO hydrogenation to methanol over Cu(110) and Cu(100), respectively. In both cases, the most energetically demanding processes are HCO* formation and subsequent hydrogenation at O to obtain the O–H bond present in the final product. For Cu(110), the activation barrier for hydrogenation of methoxy to methanol is slightly lower than for HCO* hydrogenation, whilst the inverse is true for Cu(100). We also note that the calculated activation barriers suggest a higher activity for CO hydrogenation over Cu(100) compared to Cu(110) for all elementary processes except for the initial hydrogenation of CO to HCO*, which in both cases is identified as the most energy-demanding step.

It is interesting that whilst for both Cu(110) and Cu(100), formaldehyde formation is more energetically favoured over HCOH* formation, the subsequent hydrogenation processes are invariably more energetically accessible for HCOH* than for formaldehyde. For Cu(110), formaldehyde is energetically favoured with an activation barrier of 0.11 eV (process 5, Table 5), compared to 0.50 eV for HCOH* (process 9, Table 5), yet the barriers for HCOH* hydrogenation to CH₂OH* and then methanol are only 0.28 eV and 0.60 eV respectively (processes 10 and 12, Table 5). On the other hand, the most energetically accessible route for methanol formation via formaldehyde proceeds through CH₃O* hydrogenation with a much higher activation barrier of 0.96. For Cu(100), this behaviour is similar but more subtle, with formaldehyde again being more energetically favoured over HCOH*, but at the cost of subsequent hydrogenation processes being more energetically hindered than those for HCOH*. These results suggest, therefore, that both HCOH* and formaldehyde could participate in methanol synthesis from CO hydrogenation.

As mentioned earlier, the strong calculated adsorption energy for H₂CO is also notable on both surfaces. H₂CO was calculated to bind more strongly to the catalyst surface than the product CH₃OH (0.99 eV vs. 0.77 eV for Cu(110), 0.77 eV vs. 0.61 eV for Cu(100)), and furthermore, the binding energy was calculated to be greater than the activation energies determined for subsequent reaction processes leading to methanol formation. These results imply that the subsequent reaction of formaldehyde to undergo more extensive hydrogenation is kinetically favoured over formaldehyde desorption, indicating that formaldehyde is not a major by-product of CO hydrogenation.

CO₂ hydrogenation – formate vs. hydrocarboxyl

Having already considered methanol formation via intermediate CO hydrogenation, the discussion now focuses on direct hydrogenation of CO₂. There are two possible potential intermediates arising from this process: either hydrogenation takes place at the CO₂ C atom, yielding a formate HCOO* intermediate (process 14, Tables 7 and 8), or at O, resulting in the formation of the hydrocarboxyl species COOH* (process 19, Tables 7 and 8). For both the Cu(110) and Cu(100) surfaces, formation of the HCOO* was kinetically preferred, with respective activation energies calculated at 0.25 eV and 0.40 eV, and corresponding reaction energies of −0.98 eV and −1.17 eV (process 14, Tables 7 and 8). In both cases, the most stable HCOO* coordination geometry was determined to consist of a bidentate orientation with both oxygen atoms positioned on top of surface Cu atoms (Fig. 5 and 6), although alternative diagonal on-top orientations and also those featuring the bidentate HCOO* intermediate adsorbed with both O atoms located between two surface Cu atoms were found to be only marginally less stable. Bidentate HCOO* formation involves CO₂ hydrogenation, yielding initially a monodentate HCOO* adsorption geometry immediately following the transition state, which, by an essentially barrierless rotation, forms the bidentate species.

Fig. 5 Graphical depiction of hydrogenation of activated CO₂ to formate over Cu(110). The left panel shows the initial state geometry, the middle panel shows the monodentate species arising from C–H bond formation, and the right panel shows the most stable bidentate HCOO* geometry. A side view is presented in the top half of each panel, whist the bottom half shows a view from above the Cu(110) slab.

Fig. 6 Graphical depiction of hydrogenation of activated CO₂ to formate over Cu(100). The left panel shows the initial state geometry, the middle panel shows the monodentate species arising from C–H bond formation, and the right panel shows the most stable bidentate HCOO* geometry. A side view is presented in the top half of each panel, whist the bottom half shows a view from above the Cu(100) slab.

Table 7 Calculated reaction energies and activation energies, with corresponding imaginary frequencies for the unstable modes, for the elementary reaction processes involved in CO₂ hydrogenation over Cu(110). The processes which form the reaction pathway for which the highest single activation barrier is minimised compared to competing pathways are italicised, whilst the most energy-demanding process is this pathway is also underlined. LB and SB refer to the “long bridge” and “short bridge” adsorption sites, respectively

Process no.	Elementary process	ΔE/eV	E a/eV	v/cm^−1
HCOO*
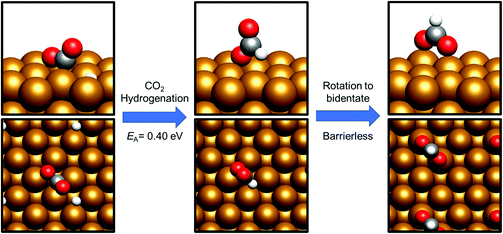
14	CO 2 * + H* → HCOO*	−0.978	0.246	702.298
15	HCOO* + H* → HCOOH*	+0.349	0.938	1061.697
16a	HCOO* + H* → H2COO* (LB)	+0.230	1.056	877.380
17a	H2COO* + H* → OCH2OH* (LB)	+0.196	1.348	1146.997
18a	H2COO* → H2CO* + O* (LB)	+1.205	1.662	151.468
16b	HCOO* + H* → H2COO* (SB)	+0.668	1.789	822.753
17b	H2COO* + H* → OCH2OH* (SB)	−0.286	0.623	1041.733
COOH*
19	CO2* + H* → COOH*	−0.408	0.986	1261.956
20	COOH* + H* → HCOOH*	−0.387	0.517	709.148
21	HCOOH* → HCOOH(g)	+0.816	—	—
HCOOH* hydrogenation
22	HCOOH* + H* → OCH2OH*	−0.194	0.844	606.191
OCH 2 OH* dissociation, H 2 CO desorption and hydrogenation
23	OCH 2 OH* → H2CO* + OH*	+0.037	0.899	136.674
6	H2CO* → H2CO(g)	+0.986	—	—
7	H2CO* + H* → CH2OH*	+0.087	0.963	927.927
8	H 2 CO* + H* → CH3O*	−0.622	0.388	328.280
11	CH 3 O* + H* → CH3OH*	−0.004	0.960	926.043
12	CH2OH* + H* → CH3OH*	−0.705	0.604	610.080
13	CH 3 OH* → CH3OH(g)	+0.771	—	—

---

Table 8 Calculated reaction energies and activation energies, with corresponding imaginary frequencies for the unstable modes, for the elementary reaction processes involved in CO₂ hydrogenation over Cu(100). The processes which form the reaction pathway for which the highest single activation barrier is minimised compared to competing pathways are italicised, whilst the most energy-demanding process is this pathway is also underlined

Process no.	Elementary process	ΔE/eV	E a/eV	v/cm^−1
HCOO*
14	CO2* + H* → HCOO*	−1.174	0.403	565.798
15	HCOO* + H* → HCOOH*	+0.437	0.925	634.635
16	HCOO* + H* → H2COO*	+0.272	1.163	868.135
17	H2COO* + H* → OCH2OH*	−0.113	0.788	1185.234
18	H2COO* → H2CO* + O*	+1.111	1.172	195.307
COOH*
19	CO 2 * + H* → COOH*	−0.160	0.941	1395.513
20	COOH* + H* → HCOOH*	−0.392	1.109	972.935
21	HCOOH* → HCOOH(g)	+0.554	—	—
HCOOH* hydrogenation
22	HCOOH* + H* → OCH2OH*	−0.029	0.813	729.629
OCH 2 OH* dissociation, H 2 CO desorption and hydrogenation
23	OCH 2 OH* → H2CO* + OH*	+0.337	0.826	160.058
6	H2CO* → H2CO(g)	+0.770	—	—
7	H 2 CO* + H* → CH2OH*	−0.258	0.649	985.000
8	H2CO* + H* → CH3O*	−0.905	0.046	311.795
11	CH3O* + H* → CH3OH*	−0.148	0.698	1029.907
12	CH 2 OH* + H* → CH3OH*	−0.829	0.597	586.857
13	CH 3 OH* → CH3OH(g)	+0.613	—	—

---

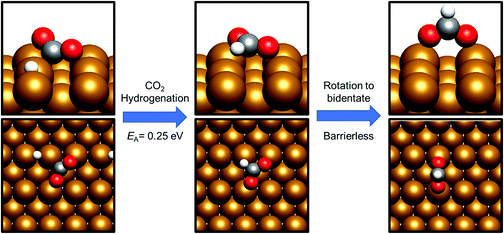
By contrast, COOH* formation involved higher activation barriers for hydrogenation, with E_a being calculated at 0.99 eV and 0.94 eV for Cu(110) and Cu(100) respectively, with the corresponding reaction energies obtained being −0.41 eV and −0.16 eV (process 19, Tables 7 and 8). Hence, the calculated activation barriers suggest that initial CO₂ hydrogenation preferentially takes place at C, with low activation barriers associated with HCOO* formation for both Cu(110) and Cu(100).

HCOO* hydrogenation

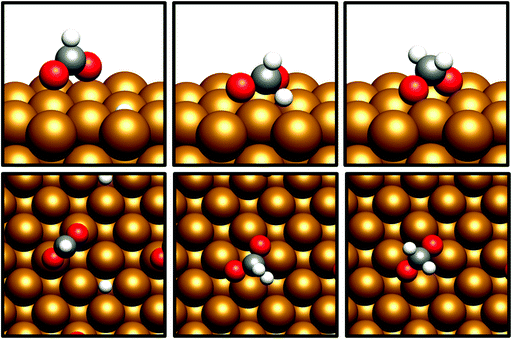
HCOO* can undergo subsequent hydrogenation to form either dioxymethylene, H₂COO*, or formic acid, depending on whether hydrogenation takes place at C or O. HCOO* dissociation to HCO* and O* was briefly considered to test whether this process could offer a potential route to the HCO* intermediate identified in the preceding section; however, the process was found to be highly endothermic, with the elementary process HCOO* → HCO* + O* resulting in an energy change of >+1.5 eV for both Cu(110) and Cu(100). Clearly, any kinetic barrier associated must be greater than or equal to this energy change, rendering any such process kinetically and thermodynamically irrelevant. Of the two possible hydrogenation pathways, HCOOH formation has a slightly lower activation energy, although in both cases activation energies are moderately high: for H₂COO* formation, the respective activation barriers for Cu(110) and Cu(100) are 1.06 eV and 1.16 eV, with corresponding endothermic reaction energies of +0.23 eV and +0.27 eV (process 16a, Table 7, and process 16, Table 8). On the other hand, the activation energies for HCOOH formation from HCOO* were slightly lower, at 0.94 eV and 0.93 eV for Cu(110) and Cu(100), respectively. In both cases, the process is mildly endothermic, with calculated energy changes of +0.35 eV and +0.27 eV for Cu(110) and Cu(100), respectively (process 15, Tables 7 and 8). HCOOH desorption is endothermic with respect to the gas phase, calculated at +0.55 eV for Cu(110) and +0.82 eV for Cu(100) (process 21, Tables 7 and 8), with the optimised adsorption geometry featuring HCOOH adsorbed with the carbonyl O atom atop a surface Cu site (Fig. 7).

Fig. 7 Surface models depicting HCOOH adsorption geometry over Cu(110) (left) and Cu(100) (right). A side view is shown in the top two panel quadrants whilst a view from above the Cu slab is presented in the bottom two panel quadrants.

For H₂COO*, an adsorption geometry consisting of both O atoms bridging two surface Cu atoms is of lower energy, in contrast to the on-top bidentate geometry on HCOO*; the lowest activation barrier for HCOO* hydrogenation was obtained where the adsorbate O coordination shifted during the hydrogenation process to reflect to difference in the preferred environment for the initial and final state (Fig. 8 and 9).

Fig. 8 Graphic depicting shift from O coordination from on-top to bridging Cu sites during hydrogenation from HCOO* to H₂COO* over Cu(110). The initial (left), transition state (middle) and final (right) geometries are depicted from the side (top) and from above (bottom). The “long bridge” adsorption geometry is shown as this is the most stable final state and yields the lowest activation barrier for H₂COO* formation.

Fig. 9 Graphic depicting shift from O coordination from on-top to bridging Cu sites during hydrogenation from HCOO* to H₂COO* over Cu(100). The initial (left), transition state (middle) and final (right) geometries are depicted from the side (top) and from above (bottom).

The behaviour is a little more complex for the Cu(110) surface, as two distinct perpendicular bidentate bridging sites are present, referred to as the short and long bridge sites. The longer bridge site is better able to accommodate both the H₂COO* intermediate (by 0.39 eV), so whilst there is little difference between the stability of the HCOO* intermediate on the short and long bridge sites, H₂COO* formation is only feasible at the long bridge site, with the calculated activation barrier for HCOO* formation at the short bridge site being much too high at 1.79 eV (process 16b, Table 7) to be relevant.

Further hydrogenation of H₂COO* was also investigated, to form the hydroxyoxomethylene species, OCH₂OH*, which for the Cu(110) surface, was found to have a high activation energy of 1.35eV for H₂COO* in the more stable long bridge adsorption site and a reaction energy of +0.20 eV(process 17a, Table 7). However, for the less stable short bridge H₂COO* adsorption geometry, a much lower activation energy of 0.62 eV was determined, with a corresponding reaction energy of −0.29 (process 17b, Table 7). This difference between the two different modes of H₂COO* adsorption is probably attributable to the inherently greater stability of the long bridge site making the H₂COO* intermediate at this site resistant to further hydrogenation. Hence, it would appear that formation of the OCH₂OH* intermediate from HCOO* on the Cu(110) surface is kinetically challenging, given that for the short bridge adsorption mode, the first hydrogenation step is unfeasible, whilst for the long bridge site the second hydrogenation poses a potentially insurmountable barrier. For the Cu(100) surface, on the other hand, hydrogenation of H₂COO* is kinetically feasible, with an activation barrier of 0.79 eV and reaction energy of −0.11 eV (process 17, Table 8). In contrast to the Cu(110) surface, HCOO* hydrogenation over Cu(100) presents a kinetically accessible reaction pathway to obtain the OCH₂OH* intermediate.

Dissociation of the H₂COO* species was also considered as a potential means to obtain H₂CO, which has already been demonstrated to be a potential intermediate for methanol synthesis earlier in our discussion of the discussion on CO hydrogenation. For Cu(110), the calculated activation barrier E_a for dissociation of H₂COO* at the most stable long bridge site was much too large, at 1.66 eV, with a corresponding ΔE of +1.20 eV (process 18a, Table 7). For Cu(100), the calculated activation energy is much smaller, but still potentially limiting at 1.17 eV, with a reaction energy of +1.10 eV (process 18, Table 8). For both surfaces, the strongly endothermic H₂COO* dissociation energies reflect the stability of the H₂COO* intermediate, particularly over Cu(110) as do the calculated activation barriers for hydrogenation processes, with only H₂COO* hydrogenation over Cu(100) having a moderately low activation barrier compared to other less energetically feasible processes.

It is clear that for these elementary processes, the Cu(100) surface is considerably more active. It is likely that the difference in surface structure, in particular the packing and arrangement of surface Cu atoms, is responsible for this behaviour, with the H₂COO* intermediate being too strongly bound on the Cu(110) surface due to the dimensions of the long bridge site being commensurate with that of the adsorbate. Hence, the intermediate is not especially active towards further hydrogenation when bound to Cu(110) in this manner.

COOH* hydrogenation

It is also possible to form HCOOH via the COOH* intermediate by hydrogenation taking place at C, with HCOOH being a common intermediate in both the formate and hydrocarboxyl reaction pathways. For Cu(110), the process is highly favourable, with only a moderate activation energy of 0.52 eV and an exothermic reaction energy of −0.39 eV (process 20, Table 7). The same process on Cu(100) is considerably less kinetically favoured, with an activation energy of 1.11 eV and reaction energy of −0.39 eV (process 20, Table 8).

HCOOH hydrogenation

HCOOH has been identified as a possible product of both the formate and hydrocarboxyl pathways, and as mentioned earlier, desorption of HCOOH to the gas phase is moderately endothermic (+0.55 eV and +0.82 eV for Cu(110) and Cu(100), respectively, process 21, Tables 7 and 8). Hence, it is of interest to consider its subsequent hydrogenation to the OCH₂OH* intermediate, which was also examined as a product of H₂COO* hydrogenation in the formate pathway. The energetics of this process were found to be similar for both of the Cu surfaces, with moderate activation energies of 0.84 eV and 0.81 eV for the Cu(110) and Cu(100) surfaces, respectively. Both processes were modestly exothermic, with respective ΔE of −0.19 eV and −0.03 eV (process 22, Tables 7 and 8). Hence, it is clear that the HCOOH intermediate provides a more kinetically accessible route to OCH₂OH* compared to the alternative H₂COO* hydrogenation which was only determined to be feasible for Cu(100).

OCH₂OH* dissociation

The OCH₂OH* intermediate is fully saturated and cannot accommodate any further hydrogenation. Cleavage of a C–O bond, necessary for obtaining the product methanol, was found to be unrealistic for intermediates arising from CO₂ hydrogenation such as HCOO* and H₂COO*. Hence, OCH₂OH dissociation is the only remaining option for the requisite C–O bond cleavage, except of course via CO₂ dissociation as discussed previously. There are two possible outcomes for OCH₂OH* dissociation:

OCH₂OH* → CH₂OH* + O*

OCH₂OH* → H₂CO + OH*

The first process yields the CH₂OH* intermediate which has been shown in this study to react readily with co-adsorbed H* to generate the product methanol. However, for both Cu(110) and Cu(100), the dissociation was determined to have a high activation barrier of ∼2 eV, which is far too large for this process to be considered as a viable means to generate the CH₂OH* intermediate. The alternative process, yielding formaldehyde, however, was found to be much more kinetically feasible and well within the bounds of accessibility, with comparable activation energies of 0.89 eV and 0.83 eV for the Cu(110) and Cu(100) facets, respectively. For both surfaces, the dissociation process was endothermic, with corresponding reaction energies of 0.04 eV and 0.34 eV (process 23, Tables 7 and 8). The product, formaldehyde, has already been identified in this study as an intermediate species for CO hydrogenation to methanol, and the different formaldehyde hydrogenation pathways have already been calculated. Hence H₂CO originating from OCH₂OH* dissociation during CO₂ hydrogenation will undergo these elementary processes in much the same way.

As already discussed, since all other possibilities for C–O bond cleavage during CO₂ hydrogenation to methanol (i.e. excluding dissociation of CO₂ itself) can be ruled out as kinetically unfeasible on both Cu(110) and Cu(100) surfaces, we may deduce that OCH₂OH* is a key intermediate common to both the HCOO* and COOH* reaction pathways. Furthermore, that the only calculated feasible dissociation process for OCH₂OH* yields formaldehyde also necessitates H₂CO as an essential intermediate. However, the processes leading to the OCH₂OH* intermediate vary between the two Cu facets in question.

Reviewing the calculated values summarised in Tables 7 and 8, it can be seen that that the reaction pathway for which the most highly activated elementary processes is minimised is the formate pathway for Cu(110), and the hydrocarboxyl pathway for Cu(100), although in both cases, the most energy-demanding step for the lowest energy route is only slightly less energetically costly than that of the competing pathway. For Cu(100), the most energetically demanding step via the COOH* route is only 0.054 eV more accessible than that for the competing HCOO* pathway. For Cu(110), a similarly small difference is also observed, with the process with the higher activation energy, formate hydrogenation to formic acid, having a barrier which is only 0.048 eV higher that of than CO₂ hydrogenation to COOH*. Hence, it is reasonable to expect both intermediates to be present and participating in methanol formation for both Cu(110) and Cu(100) surfaces.

H₂O formation

The stoichiometry of the product methanol necessitates that CO₂ hydrogenation yields water as a byproduct. Methanol formation via CO₂ dissociation results in surface O* which may be converted to OH* and then finally to water; for direct CO₂ hydrogenation, the calculations suggest that OH* arising from OCH₂OH* dissociation is the main route by which water formation takes place. Hence, for both Cu(110) and Cu(100), the energetics for O* and OH* hydrogenation have been considered, with the results presented in Table 9.

Table 9 Calculated reaction energies and activation energies, with corresponding imaginary frequencies for the unstable modes, for the elementary reaction processes involved in H₂O formation over Cu(110) and Cu(100)

Process no.	Elementary process	ΔE	E a/eV	v/cm^−1
(110)
24	O* + H* → OH*	−0.951	0.632	1051.683
25	OH* + H* → H2O*	+0.052	0.770	1215.664
26	H2O* → H2O	+0.143	—	—
(100)
24	O* + H* → OH*	−1.147	0.486	784.975
25	OH* + H* → H2O*	+0.022	0.757	403.908
26	H2O* → H2O	+0.438	—	—

---

For both Cu(110) and Cu(100), O* hydrogenation is strongly exothermic, with respective reaction energies of −0.95 eV and −1.15 eV; the corresponding activation energies are modest at 0.63 eV and 0.49 eV (process 24, Table 9). Hydrogenation of OH* to yield water has slightly higher calculated activation barriers of 0.77 eV and 0.76 eV for Cu(110) and Cu(100), respectively. For both surfaces, the elementary process for H₂O formation from OH was found to be almost thermoneutral, with negligibly endothermic energy changes of 0.05 eV and 0.02 eV (process 25, Table 9). The product H₂O was found to be only fairly weakly adsorbed on both the Cu(110) and Cu(100) surfaces, hence it can be assumed to desorb readily to the gas phase, with desorption being endothermic by 0.14 eV over Cu(110), compared to 0.44 eV for Cu(100) (process 26, Table 9). Hence, water formation over both of the low index Cu surfaces considered will occur readily and the resultant water can be expected to desorb to the gas phase, facing competitive adsorption against both reactants CO₂* and H*, as well as molecular intermediates such as H₂CO and HCOOH, generated throughout the overall methanol synthesis reaction. As water is more weakly adsorbed on Cu(110) and Cu(100), competitive adsorption against the reactants and intermediates means that water formation and desorption can be considered as essentially irreversible.

Discussion

The calculations presented here show that a variety of different reaction pathways (summarised in Fig. 3) are potentially feasible for methanol formation over Cu(110) and Cu(100). Comparing the CO and CO₂ reaction pathways, in both cases the activation barriers for CO₂ dissociation were calculated to be somewhat higher than the most energy-demanding elementary processes for the CO₂ pathways with the lowest activation energies, but not significantly so, with the CO₂ dissociation barrier over Cu(110) being only 0.138 eV greater than the barrier for formate hydrogenation to formic acid; the discrepancy is even smaller for Cu(100) where hydrocarboxyl hydrogenation to formic acid is negligibly smaller than that of CO₂ dissociation (0.007 eV). Hence, we might expect not only that methanol synthesis takes place via the formate and hydrocarboxyl intermediates identified for CO₂ hydrogenation, but also via the CO mediated reaction pathway. Of all the intermediates explored, formaldehyde is the only common intermediate to all of the reaction pathways explored for both CO and CO₂ hydrogenation. HCOOH is also identified as playing a key role for CO₂ hydrogenation, featuring in the least kinetically demanding pathways for methanol synthesis via both HCOO* and COOH*, and for both of the Cu surfaces investigated. The reaction energy profile diagrams presented in Fig. 10 and 11 show the interrelation between the various possible reaction pathways. Indeed, for both Cu(110) and Cu(100), the pathways corresponding to CO hydrogenation are overall more energy demanding; however the most energy demanding individual processes for all possible pathways are comparable, further suggesting that several different pathways may be involved in the overall reaction.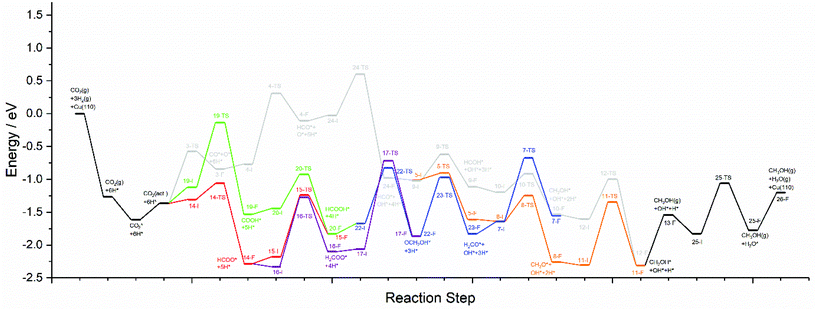

Fig. 10 Reaction energy profile plots for CO₂ hydrogenation to methanol over Cu(110). The various different reaction pathways are presented together to illustrate their interrelation. The processes indicated in black are common to all pathways. The processes indicated in grey correspond to CO₂ dissociation and subsequent hydrogenation to HCO*, then HCOH*, then CH₂OH*, and finally the product CH₃OH*. The processes indicated in orange branch off from the grey pathway and correspond to HCO* hydrogenation to H₂CO*, then CH₃O*, and finally to the product CH₃OH*. The green and red pathways correspond to CO₂ hydrogenation to COOH* and HCOO*, converging at HCOOH* formation, subsequent hydrogenation of which to OCH₂OH* being indicated by the blue pathway. The blue and orange pathways converge since H₂CO* hydrogenation is common to both. Similarly, the blue and grey pathways converge since CH₂OH* is a common intermediate to both. The purple pathway illustrates the alternative HCOO* hydrogenation to H₂COO*, and its subsequent hydrogenation to OCH₂OH*, hence the purple pathway converges with the blue pathway. All energetic minima and transition state are labelled with a number corresponding to the elementary processes detailed in Tables 4–9, with initial state, transition state and final state structure energies being indicated with the letters I, TS, and F, respectively.

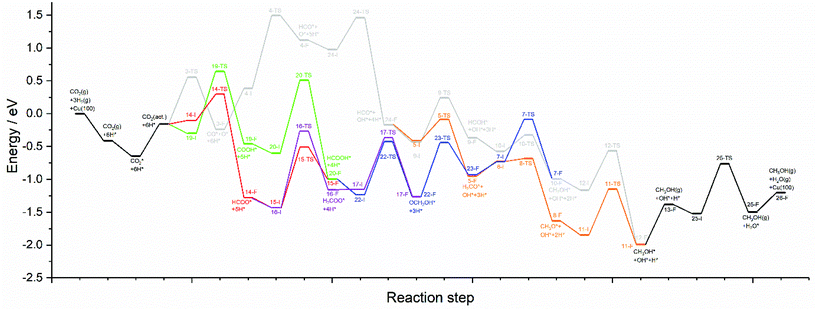Fig. 11 Reaction energy profile plots for CO₂ hydrogenation to methanol over Cu(100). The various different reaction pathways are presented together to illustrate their interrelation. The processes indicated in black are common to all pathways. The processes indicated in grey correspond to CO₂ dissociation and subsequent hydrogenation to HCO*, then HCOH*, then CH₂OH*, and finally the product CH₃OH*. The processes indicated in orange branch off from the grey pathway and correspond to HCO* hydrogenation to H₂CO*, then CH₃O*, and finally to the product CH₃OH*. The green and red pathways correspond to CO₂ hydrogenation to COOH* and HCOO*, converging at HCOOH* formation, subsequent hydrogenation of which to OCH₂OH* being indicated by the blue pathway. The blue and orange pathways converge since H₂CO* hydrogenation is common to both. Similarly, the blue and grey pathways converge since CH₂OH* is a common intermediate to both. The purple pathway illustrates the alternative HCOO* hydrogenation to H₂COO*, and its subsequent hydrogenation to OCH₂OH*, hence the purple pathway converges with the blue pathway. All energetic minima and transition state are labelled with a number corresponding to the elementary processes detailed in Tables 4–9, with initial state, transition state and final state structure energies being indicated with the letters I, TS, and F, respectively.

Although there are comparatively few previous computational studies exploring a detailed reaction network for methanol synthesis over Cu(110) and Cu(100), the previous theoretical studies focusing on the most stable Cu(111) facet can serve as a useful comparison to assess the activity of the remaining low-index surfaces explored in the present work, and to compare possible reaction pathways.^7,8,56 The intermediates identified by Grabow et al.⁸ correspond to those identified in this study as being central to the CO₂ hydrogenation mechanism, namely HCOO*, COOH*, HCOOH, H₂CO and OCH₂OH, and the preference for formic acid formation over dioxomethylene in the HCOO* pathway was also observed for Cu(110) and Cu(100), showing similarities to the activity of the Cu(111) surface.

A key difference between the results presented in this study, and that of Grabow et al., concerns CO₂ dissociation to CO. Grabow et al. reported a very high activation barrier for CO₂ dissociation over Cu(111), calculated to be 1.77 eV, thus making the possibility of CO and intermediates arising from its hydrogenation irrelevant for methanol synthesis. On the other hand, in the present work, it was found that CO₂ dissociation is considerably less activated over Cu(110) and Cu(100), with an activation barrier of ∼1.1 eV for both of the minority facets, although it must be noted that this activation barrier is still slightly higher than any of those for the direct CO₂ hydrogenation pathways. As discussed above, this finding is consistent with experimental evidence which suggests that Cu(111) is not especially active towards CO₂ adsorption and that CO₂ activation readily takes place over Cu(110) and Cu(100), along with the finding in the present work that no CO₂ activation was observed over Cu(111), in contrast to the other low-index surfaces. On the other hand, computational studies conducted by Zhao et al.⁷ appear to report a bent activated CO₂ species over Cu(111) (∠ (O–C–O) = 127.6°) comparable to those identified in this study over Cu(110) and Cu(100), although no appreciable discussion is devoted to the role of this species in the earlier study, which to suggested an Eley–Rideal type mechanism for CO₂ hydrogenation invoking direct reaction of gas-phase CO₂ with adsorbed H*, without exploring CO₂ dissociation. However, both the works of Grabow and Zhao examine some of the same processes on Cu(111) as those associated with CO hydrogenation over Cu(110) and Cu(100) in the present study; Grabow et al. report that the activation barrier and reaction energy for CO* hydrogenation to HCO* over Cu(111) is comparable to that determined here for the remaining low index surfaces, i.e. moderately highly activated and considerably endothermic (E_a ∼1 eV, ΔE = 0.7 ± 0.1 eV). Both of these previous DFT studies suggest that HCOH* formation is considerably more kinetically demanding over Cu(111) compared to the activation barriers determined in this study for Cu(110) and Cu(100), although for HCOH* hydrogenation to H₂CO* and H₂COH* would appear to be facile on all three surfaces, i.e. for Cu(111) as reported by Zhao and Grabow, as well for Cu(110) and Cu(100) as reported in the present work. A similar agreement is seen for H₂CO* hydrogenation to CH₃O* and CH₂OH*, with both processes being kinetically feasible over all three surfaces, with CH₃O* formation having a lower activation barrier and being more exothermic. Further agreement between all three low index facets is observed with regards to methanol formation, with CH₂OH* hydrogenation being less kinetically demanding and more exothermic than the corresponding process for CH₃O*. Hence, it appears that the overall hydrogenation activity does have similarities for all three surfaces, except for the crucial initial CO₂ dissociation and CO* hydrogenation processes, for which Cu(110) and Cu(100) would appear to perform considerably better than the dominant Cu(111) surface. The fact that only the early hydrogenation processes were found to be less activated over Cu(110) and Cu(100) can also be strongly connected to the observed activation of CO₂ over these surface reported in the present work that was absent for Cu(111). Consequently, we suggest a methanol synthesis pathway utilising CO and its subsequent hydrogenation products as intermediates, given that polycrystalline Cu catalysts can be expected to exhibit surface environments resembling all three of the low index facets.

Comparing CO₂ hydrogenation processes, it is also interesting to note that, compared to reports in previous computational works on Cu(111), the calculated kinetic barriers for CO₂ hydrogenation over Cu(110) and Cu(100) reveal the minority low index surfaces to be considerably more active towards CO₂ hydrogenation, both to COOH* and HCOO*; whilst HCOO* formation was reported by both Grabow and Zhao as being both kinetically and thermodynamically feasible over Cu(111), the calculations performed in this study reveal lower activation barriers and more exothermic reaction energies for both Cu(110) and Cu(100). The superior activity of the two minority low index facets towards COOH* formation is even more pronounced; Zhao et al. report this process to be mildly endothermic with a high activation barrier of 1.27 eV, whilst Grabow et al. consider the process to be wholly unfeasible, given that the reverse process (COOH* + * → CO₂* + H*) was reported to be highly activated (E_a = 1.23 eV) and highly exothermic (ΔE = 0.55 eV), making CO₂* hydrogenation to COOH* not kinetically feasible. By contrast, the calculated energetics for Cu(110) and Cu(100) presented in the present work suggest that COOH* formation is only moderately activated, with E_a < 1 eV for both surfaces, and in both cases the process is modestly exothermic. Once again, we find the pattern of initial reaction processes involving CO₂ – in this case hydrogenation rather than dissociation having lower barriers over Cu(110) and Cu(100), compared to the more dominant Cu(111) surface.

For COOH* hydrogenation to formic acid, the behaviour exhibited between the three surfaces is more varied, with the process being kinetically facile over Cu(110) (E_a = 0.52 eV), moderately activated over Cu(111) (E_a = 0.76 ± 0.03 eV) according to Grabow and Zhao, and considerably more so over Cu(100) (E_a = 1.11 eV). Subsequent hydrogenation of HCOOH* to OCH₂OH* was found to be only slightly less activated for Cu(110) and Cu(100) (E_a ∼0.82 eV) compared to Cu(111) (E_a = 0.97 ± 0.07 eV), and mildly exothermic for all three facets. Once again we find the pattern of initial elementary processes involving CO₂ having lower energy barriers over Cu(110) and Cu(100), than Cu(111), but with similar behaviour observed between the three surfaces for subsequent elementary processes such as hydrogenation of intermediates like COOH*. This finding further supports the notion that the CO₂ activation reported for the Cu(110) and Cu(100) is responsible for the main differences in activity compared to the non-CO₂-activating Cu(111) facet.

Turning now to subsequent reactions for HCOO*, there is broad agreement between the previous studies on Cu(111) and the present work on the low-index surface that HCOO* dissociation to yield formyl is not possible, owing to the process on all surfaces being highly endothermic and as such much too kinetically unfeasible to be considered as a possible mechanism for C–O bond cleavage. We find the energetics of HCOO* hydrogenation to yield methanol to be similar for all three surfaces, with Grabow and Zhao agreeing that the process is moderately activated and modestly endothermic (E_a = 0.86 ± 0.05 eV, ΔE ∼0.2 eV) over Cu(111), comparable to the energetics reported for both Cu(110) and Cu(100) in this study (E_a ∼0.93 eV, ΔE = 0.4 ± 0.05 eV). For all three surfaces, this process is considerably more favourable than the competing hydrogenation to yield H₂COO, with the two previous Cu(111) studies reporting activation barriers of at least 1.2 eV; lower activation barriers were obtained for Cu(110) and Cu(100) (E_a ∼1 eV), but nonetheless higher than for HCOOH* formation. On the other hand, whilst subsequent dissociation of H₂COO* to H₂CO* and O*, as well as further hydrogenation to yield OCH₂OH*, were reported to be feasible over Cu(111) in the previous computational studies, for Cu(110) and Cu(100) the present work found the former to be much more highly activated. This behaviour is particularly pronounced for Cu(110), although for all three Cu surfaces the high kinetic barrier is probably associated with the process being highly endothermic in the first place, with calculated activation barriers being only slightly greater than the endothermic overall energy change associated with the process. Whilst we found the latter hydrogenation step to OCH₂OH* to be potentially feasible over Cu(100), with comparable energetics to that reported for Cu(111) by Grabow and Zhao, for Cu(110) H₂COO* hydrogenation is improbable owing to the high activation barrier of nearly 1.7 eV; this result can possibly be attributed to the high relative stability of the H₂COO* adsorbate on Cu(110), which is responsible for both its comparative ease of formation compared to the same process taking place over Cu(111) and Cu(100), and its relative resistance to undergoing subsequent reaction processes. In any case, we find that for all three surfaces, methanol synthesis via HCOO* preferentially takes place via HCOOH* rather than H₂COO*, although the exact limiting processes that makes H₂COO* less favourable vary between the surfaces. This finding further reflects the notion that differences between activity of the three surfaces is largely connected to the process of CO₂ activation, and that subsequent reaction processes involving intermediate species are largely similar for all of the Cu low-index facets.

For Cu(111), the previous computational studies suggest that whilst formation of the key formaldehyde intermediate is kinetically possible via either H₂COO* or OCH₂OH* dissociation (with the reaction pathway to the latter intermediate being overall lower in energy), the reverse process is essentially spontaneous, given that the activation barriers were determined to be almost equal to the endothermicity of the process. Whilst H₂COO* dissociation was found to be similarly kinetically hindered, and almost spontaneous in the reverse, for Cu(110) and Cu(100), OCH₂OH* dissociation, on the other hand, was determined to be a moderately activated and mildly endothermic (E_a ∼0.86, ΔE = +0.04 eV and +0.34 eV for Cu(110) and Cu(100), respectively), thus not suffering from the issue of the reverse process occurring spontaneously as was found to be the case for Cu(111). These results, in addition to the improvement in CO₂ activation observed for Cu(110) and Cu(100), suggest superior activity of these surfaces compared to the dominant Cu(111) surface.

As can be seen from the review and comparison of the reaction network for the three surfaces, many of the most important differences between the Cu(110) and Cu(100) facets, and the Cu(111) surface, lie in the initial elementary processes involving CO₂, rather than subsequent processes taking place later in the reaction pathway, which appear to be more similar between the three Cu surfaces. This observation provides strong evidence for the observed activation of CO₂ for Cu(110) and Cu(100), but not Cu(111), being key to the improved activity of the former surfaces. It is of interest to consider the implications of this with respect to the role of the ZnO support in facilitating methanol synthesis in the industrially ubiquitous Cu/ZnO catalyst. Whilst the extent of activation of CO₂ by Cu(110) and Cu(100) is modest, if the Bader charge analyses presented here and in previous works³⁸ is to be used as a measure of activation, the calculated reaction energetics suggest considerable improvement in activity towards CO₂ hydrogenation and dissociation compared to the non-activating Cu(111). Hence, whilst the ZnO support may potentially play a role in CO₂ activation, Cu is likely to be involved, given that the present work shows that non-dominant low-index Cu facets can facilitate CO₂ activation, and we would expect Cu coordination environments resembling those of the Cu(110) and Cu(100) facets to be present on Cu/ZnO catalysts. The presence of surface environments resembling the Cu(110) and Cu(100) facets may be linked to the role of the ZnO support in hindering sintering and allowing these higher energy surfaces to be expressed. However, as this work demonstrates, CO₂ hydrogenation over Cu(110) and Cu(100) suffers from many of the same energetic bottlenecks at the Cu(111) surface for many subsequent elementary processes concerning formate hydrogenation. Indeed, recently experimental work⁵⁷ suggests that interfacial Cu/ZnO sites could be key to facilitating formate activation, which would represent an avenue for improved catalytic activation that has not been observed for unsupported Cu catalysts.

Conclusions

The calculations presented in this work show that CO₂ activation takes place over Cu(110) and Cu(100) surfaces and that these Cu facets show improved catalytic behaviour for CO₂ dissociation and hydrogenation processes, compared to the more extensively studied dominant Cu(111) facet. Methanol synthesis via CO hydrogenation is not realistic for the Cu(111) surface due to the negligible extent of CO₂ dissociation, whilst for Cu(110) and Cu(100) it remains a distinct possibility. Furthermore, methanol synthesis via both HCOO* and COOH* as intermediates, rather than just HCOO*, is shown to be possible over Cu(110) and Cu(100) owing to the significantly lower barrier to this initial hydrogenation process compared to Cu(111). Overall, the non-dominant Cu surfaces appear to offer considerably more flexibility in terms of possible reaction pathways to obtain the product methanol.

Our analysis provides valuable insights into the importance of Cu surface structure and morphology in understanding fully the nature of Cu-based catalysts for methanol synthesis. It is intended that, based on the calculated activation barriers presented in the current work, future studies will further investigate the mechanism for methanol synthesis and the relative importance of the identified intermediates through microkinetic modelling studies. The data presented in this systematic study of the low-index surfaces of the unsupported copper catalyst will form the basis of future microkinetic work examining the improvement in rate-constants that can be expected in the next generation of industrially relevant supported catalysts. Moreover, this work will not only provide a basis for further investigation of low index Cu catalyst surfaces, but will inform future works exploring supported Cu catalysts and as such assist in furthering progress towards developing a more complete understanding of widely used industrial catalysts. More generally, our study has allowed a detailed exploration of the various mechanistic possibilities in the widely studied CO₂ hydrogenation reaction. It is intended that the key elementary processes identified from our complete mechanistic analysis will facilitate future investigations into more complex multi-component catalyst systems that are representative of industrial catalysts, revealing new insights into the role of support materials and other components of such catalysts.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors acknowledge the GCRF START project (ST/R002754/1) for funding support. Additionally, the authors acknowledge the support of the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via Welsh Government, Science and Technology Facilities Council Scientific Computing Department's SCARF cluster, and the UK National Supercomputing Service ARCHER (accessed via membership of the Materials Chemistry Consortium which is funded by Engineering and Physical Sciences Research Council (EP/L000202)), for the provision of computational resources. The UK Catalysis Hub is thanked for resources and support provided via membership of the UK Catalysis Hub Consortium and funded by EPSRC (Grants EP/R026815/1).

References

1. G. A. Olah, A. Goeppert and G. K. S. Prakash, J. Org. Chem., 2009, 74, 487–498.
2. M. P. Hogarth and G. A. Hards, Platinum Met. Rev., 1996, 40, 150–159.
3. K. C. Waugh, Catal. Lett., 2012, 142, 1153–1166.
4. J. B. Bulko, R. G. Herman, K. Klier and G. W. Simmons, J. Phys. Chem., 1979, 83, 3118–3122.
5. K. Klier, Appl. Surf. Sci., 1984, 19, 267–297.
6. M. Kurtz, N. Bauer, C. Büscher, H. Wilmer, O. Hinrichsen, R. Becker, S. Rabe, K. Merz, M. Driess, R. A. Fischer and M. Muhler, Catal. Lett., 2004, 92, 49–52.
7. Y. F. Zhao, Y. Yang, C. Mims, C. H. F. Peden, J. Li and D. Mei, J. Catal., 2011, 281, 199–211.
8. L. C. Grabow and M. Mavrikakis, ACS Catal., 2011, 1, 365–384.
9. G. Wulff, Z. Kristallogr. – Cryst. Mater., 1901, 449–530.
10. G. D. Barmparis, Z. Lodziana, N. Lopez and I. N. Remediakis, Beilstein J. Nanotechnol., 2015, 6, 361–368.
11. R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 160080.
12. M. Behrens, F. Studt, I. Kasatkin, S. Kuhl, M. Havecker, F. Abild-Pedersen, S. Zander, F. Girgsdies, P. Kurr, B.-L. Kniep, M. Tovar, R. W. Fischer, J. K. Norskov and R. Schlogl, Science, 2012, 336, 893–897.
13. F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111.
14. F. Studt, M. Behrens and F. Abild-Pedersen, Catal. Lett., 2014, 144, 1973–1977.
15. J. L. C. Fajín, M. N. D. S. Cordeiro, F. Illas and J. R. B. Gomes, J. Catal., 2009, 268, 131–141.
16. G. C. Wang and J. Nakamura, J. Phys. Chem. Lett., 2010, 1, 3053–3057.
17. J. Yoshihara and C. T. Campbell, J. Catal., 1996, 161, 776–782.
18. P. B. Rasmussen, M. Kazuta and I. Chorkendorff, Surf. Sci., 1994, 318, 267–280.
19. P. B. Rasmussen, P. M. Holmblad, T. Askgaard, C. V. Ovesen, P. Stoltze, J. K. Nørskov and I. Chorkendorff, Catal. Lett., 1994, 26, 373–381.
20. J. Nerlov and I. Chorkendorff, J. Catal., 1999, 181, 271–279.
21. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
22. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269.
23. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 169.
24. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
25. W. Sun and G. Ceder, Surf. Sci., 2013, 617, 53–59.
26. H. Monkhorst and J. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
27. G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
28. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
31. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978.
32. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022.
33. A. Heyden, A. T. Bell and F. J. Keil, J. Chem. Phys., 2005, 123, 224101.
34. F. H. P. M. Habraken, E. P. Kieffer and G. A. Bootsma, Surf. Sci., 1979, 83, 45–59.
35. G. C. Wang, L. Jiang, Y. Morikawa, J. Nakamura, Z. S. Cai, Y. M. Pan and X. Z. Zhao, Surf. Sci., 2004, 570, 205–217.
36. S. Y. Liem and J. H. R. Clarke, J. Chem. Phys., 2004, 121, 4339–4345.
37. K. S. Rawat, A. Mahata and B. Pathak, J. Catal., 2017, 349, 118–127.
38. M. G. Quesne, A. Roldan, N. H. De Leeuw and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2019, 21, 10750–10760.
39. W. Akemann and A. Otto, Surf. Sci., 1992, 272, 211–219.
40. W. Akemann and A. Otto, Surf. Sci., 1993, 287–288, 104–109.
41. K. H. Ernst, D. Schlatterbeck and K. Christmann, Phys. Chem. Chem. Phys., 1999, 1, 4105–4112.
42. G. Anger, A. Winkler and K. D. Rendulic, Surf. Sci., 1989, 220, 1–17.
43. G. Wiesenekker, G. J. Kroes, E. J. Baerends and R. C. Mowrey, J. Chem. Phys., 1995, 102, 3873–3883.
44. S. Kumar and B. Jackson, J. Chem. Phys., 1994, 100, 5956–5964.
45. J. A. White and D. M. Bird, Chem. Phys. Lett., 1993, 213, 422–426.
46. L. Álvarez-Falcón, F. Viñes, A. Notario-Estévez and F. Illas, Surf. Sci., 2016, 646, 221–229.
47. H. J. Freund and R. P. Messmer, Surf. Sci., 1986, 172, 1–30.
48. F. H. P. M. Habraken, G. A. Bootsma, P. Hofmann, S. Hachicha and A. M. Bradshaw, Surf. Sci., 1979, 88, 285–298.
49. F. H. P. M. Habraken and G. A. Bootsma, Surf. Sci., 1979, 87, 333–347.
50. F. H. P. M. Habraken, C. M. A. M. Mesters and G. A. Bootsma, Surf. Sci., 1980, 97, 264–282.
51. J. Nakamura, J. A. Rodriguez and C. T. Campbell, J. Phys.: Condens. Matter, 1989, 1, SB149–SB160.
52. F. Muttaqien, Y. Hamamoto, I. Hamada, K. Inagaki, Y. Shiozawa, K. Mukai, T. Koitaya, S. Yoshimoto, J. Yoshinobu and Y. Morikawa, J. Chem. Phys., 2017, 147, 094702.
53. W. Luo, X. Nie, M. J. Janik and A. Asthagiri, ACS Catal., 2016, 6, 219–229.
54. K. J. P. Schouten, Z. Qin, E. P. Gallent and M. T. M. Koper, J. Am. Chem. Soc., 2012, 134, 9864–9867.
55. P. B. Rasmussen, P. A. Taylor and I. Chorkendorff, Surf. Sci., 1992, 269–270, 352–359.
56. Y. Yang, C. A. Mims, D. H. Mei, C. H. F. Peden and C. T. Campbell, J. Catal., 2013, 298, 10–17.
57. B. Xie, R. J. Wong, T. H. Tan, M. Higham, E. K. Gibson, D. Decarolis, J. Callison, K. F. Aguey- Zinsou, M. Bowker, C. R. A. Catlow, J. Scott and R. Amal, Nat. Commun., 2020, 11, 1615.

---