Revealing the origin of voltage loss in mixed-halide perovskite solar cells†
Suhas
Mahesh
 a,
James M.
Ball
a,
Robert D. J.
Oliver
a,
James M.
Ball
a,
Robert D. J.
Oliver
 a,
David P.
McMeekin
b,
Pabitra K.
Nayak
a,
David P.
McMeekin
b,
Pabitra K.
Nayak
 *a,
Michael B.
Johnston
*a,
Michael B.
Johnston
 a and
Henry J.
Snaith
a and
Henry J.
Snaith
 *a
*a
aClarendon Laboratory, University of Oxford, Parks Road, Oxford OX1 3PU, UK. E-mail: pabitra.nayak@physics.ox.ac.uk; henry.snaith@physics.ox.ac.uk
bDepartment of Chemical Engineering, Monash University, Clayton, Victoria 3800, UK
First published on 26th November 2019
Abstract
The tunable bandgap of metal-halide perovskites has opened up the possibility of tandem solar cells with over 30% efficiency. Iodide–bromide (I–Br) mixed-halide perovskites are crucial to achieve the optimum bandgap for such tandems. However, when the Br content is increased to widen the bandgap, cells fail to deliver the expected increase in open-circuit voltage (VOC). This loss in VOC has been attributed to photo-induced halide segregation. Here, we combine Fourier transform photocurrent spectroscopy (FTPS) with detailed balance calculations to quantify the voltage loss resulting from halide segregation, thus providing a means to quantify the impact of the low bandgap iodide-rich phases on performance. Our results indicate that, contrary to popular belief, halide segregation is not the dominant VOC loss mechanism in Br-rich wide bandgap cells. Rather, the loss is dominated by the relatively low initial radiative efficiency of the cells, which arises from both imperfections within the absorber layer, and at the perovskite/charge extraction layer heterojunctions. We thus identify that focussing on maximising the initial radiative efficiency of the mixed-halide films and devices is more important than attempting to suppress halide segregation. Our results suggest that a VOC of up to 1.33 V is within reach for a 1.77 eV bandgap perovskite, even if halide segregation cannot be suppressed.
Broader contextFuelled by plummeting prices, global installed photovoltaic (PV) capacity has now grown to over 500 GW. As PV grows to terawatt dimensions, solar cell efficiency will become the crucial determinant of price and capacity. Perovskite solar cells, with their tunable bandgaps, hold the promise of tandem cells that are 30% more efficient than traditional single-junction cells. One of the biggest challenges in the way of such tandem cells is the poor open-circuit voltage (VOC) of wide-bandgap mixed-halide perovskite cells. The loss in the VOC has been attributed to halide segregation – the reversible formation of a low-bandgap phase in the perovskite under illumination. Unfortunately, the cause of halide segregation is still not well understood. Traditionally, techniques like photoluminescence (PL) and X-ray diffraction (XRD) have been used to study the phenomenon. However, they cannot inform us about the impact of halide-segregation on the performance of a solar cell. Here, we quantify the open-circuit voltage loss due to halide-segregation, fully distinguishing it from other loss mechanisms also at work. We also model the impact of halide segregation to predict the voltage losses expected at different compositions. Our work suggests that, contrary to general perception, improving the initial radiative efficiency of cells is more important for improving voltages than suppressing halide-segregation. |
The power conversion efficiency (PCE) of perovskite solar cells has improved at a phenomenal pace since initial reports of 10%1 in 2012, now reaching a certified 25.2% in 2019.2 Their sharp-absorption onsets, apparent defect tolerance, and high radiative efficiencies make them ideal candidates for photovoltaic3 and light-emitting diode (LED) applications.4 There is now considerable effort to integrate perovskites into multi-junction solar cells to surpass single-junction efficiency limitations.5–7 Perovskite-on-silicon,8–10 perovskite–perovskite11–15 and perovskite–CIGS16–18 tandem cells have already been demonstrated. Oxford PV's report of a 28% efficient perovskite-on-silicon tandem cell further bolsters the expectation that future efficiency records are likely to be dominated by multi-junction cells.19 Perovskites are particularly attractive materials for making multi-junction solar cells because their bandgap can be tuned across the visible spectrum simply by ionic substitution and mixing over a wide stoichiometric range. For ABX3 perovskites, with the selection of A = Cs, methylammonium (MA+) or formamidinium (FA+), B = Sn2+ or Pb2+, and X = I−, Br− or Cl−, the bandgap can be tuned from ∼1.24 eV to 3.5 eV.6 Mixed-halide I–Br perovskites, APb(IxBr1−x)3, have bandgaps between 1.48–2.35 eV, making them ideal for tandem and triple junction applications. However, the same ion-interchangeability that facilitates such convenient bandgap tuning also gives rise to a host of problems due to ionic diffusion. Notably, under illumination, “halide segregation” occurs in APb(IxBr1−x)3 films, leading to the formation of iodide-rich phases which have lower bandgaps than the surrounding unsegregated material.20 This was first observed through photoluminescence (PL) spectra in mixed-halide films, where a lower energy emission was correlated with the formation of iodide-rich domains. Much work has since followed up on this phenomenon in an attempt to understand the mechanism.21–26 Notably, some studies have shown that enhanced crystallinity in the perovskite film can lead to greatly reduced severity of the halide segregation.27–29
The most efficient single junction perovskite solar cells reported to-date have bandgaps which range from 1.53 to 1.62 eV, and are generally composed of iodide-rich mixed-cation lead mixed-halide perovskites. These cells only have a loss in VOC of ∼60 mV from the theoretical limit30 (herein, we will refer to these “benchmark” perovskite cells as the ∼1.6 eV gap cells). In contrast, the best mixed-halide devices with a high bromide content of 40% and above, show many hundreds of mV of loss in VOC from the theoretical limit. The open-circuit voltage (VOC) has been observed to “plateau” at about 1.2 V, (or even decrease) with the addition of Br to the APb(I1−xBrx)3 perovskite, once the bromide content exceeds around 20%.31 The prevailing notion in the scientific community is that the emergence of the low energy PL peak in mixed-halide perovskite films corresponds to a limitation upon the open-circuit voltage; the open-circuit voltage will be “pinned” by the low bandgap iodide-rich impurity phases. However, intuition aside, there is yet no quantitative analysis of how halide segregation influences open-circuit voltage. Notably, the wide bandgap cell contributes the majority of the power output of a tandem cell. Thus, both scientifically and commercially, it is important to able to quantify the loss occurring due to halide-segregation.
The plethora of parameters that halide segregation depends on greatly confounds efforts to understand and suppress it. Even studies that have succeeded in suppressing the PL shift show significant VOC loss from the theoretical limit, when benchmarked against ∼1.6 eV cells.32 Photoluminescence has generally been the tool of choice to probe halide segregation. While photoluminescence can detect the presence of low-bandgap phases, it is an insensitive measure of their size and composition. Some have used X-ray diffraction, but this is not quantitatively reliable due to its strong sensitivity to texture.23 Methods that can quantitatively characterize the segregated phase(s) and associated performance losses are highly desirable. In addition, we lack a way to quantify the variation in open-circuit voltage expected as a function of degree of halide segregation, and other fundamental properties such as radiative efficiency.
In this study, we use Fourier-transform photocurrent spectroscopy (FTPS) to reveal the evolution of iodide-rich impurity phase absorption in mixed-halide perovskite solar cell undergoing phase segregation under a simulated AM1.5G illumination. Reports so far have treated halide segregation as a simple two-phase phenomenon. Contrary to general belief, we find that the formation of a distribution of minority phases is also accompanied by significant bandgap broadening in the “majority” phase. We couple the measured FTPS spectra with detailed balance calculations33 to estimate the voltage penalty due to evolution of the sub bandgap absorption tail. This allows us to isolate the voltage penalty due to halide-segregation, ignoring losses from other mechanisms. We also identify that the broadening of the majority phase absorption edge, which is distinct from the minority phase, should have a significant impact upon the VOC. Following the same approach, we present a thermodynamic model that estimates VOC losses for various bandgaps and severities of segregation. By comparing the time evolution of the calculated halide segregation induced VOC loss with the measured time evolution of the open-circuit voltage of the cell, we conclude that the open-circuit voltage losses in bromide-rich high-bandgap cells are not dominated by halide segregation. Large trap densities, which mediate non-radiative Shockley–Read–Hall (SRH) recombination, are the dominant loss channel, and are already present before halide segregation commences. Therefore, significant improvements in VOC are within reach by improving absorber radiative efficiency and quality of the perovskite-charge transport layer heterojunctions, even if halide segregation remains unsuppressed.
What determines the open-circuit voltage of a solar cell?
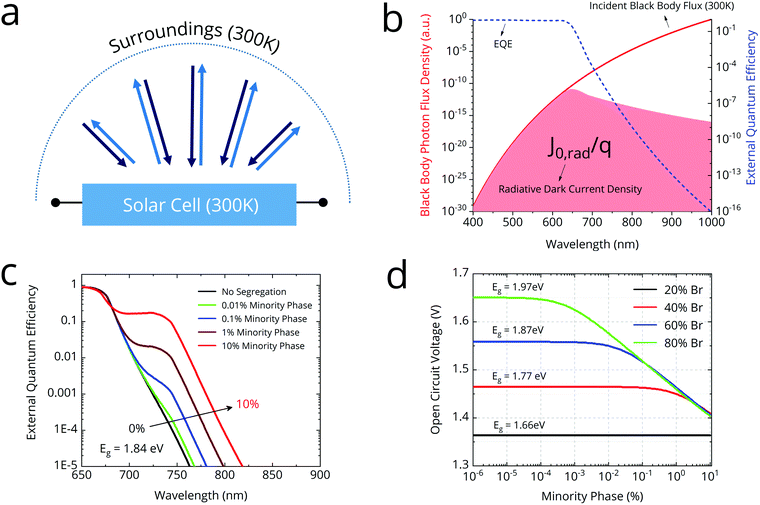
We begin by summarizing the factors that influence the open-circuit voltage of a solar cell, and illustrate how we would expect the open-circuit voltage to evolve with the emergence of lower bandgap impurity phases. The open-circuit voltage of an ideal solar cell is expressed by the well-known relation:34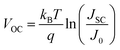 | (1) |
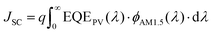 | (2) |
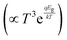 .35
.35
In a real cell which includes non-radiative recombination, the recombination current J0 is the sum of the radiative and the non-radiative recombination currents. The radiative recombination current can be calculated by using the principle of detailed balance: in equilibrium, the absorbed photon current must equal the emitted photon current. Thus, we can calculate the radiative recombination current through the overlap integral between the blackbody flux and the EQEPV of the photoactive material. Thus, J0,rad, which is equal to the emitted photon current can be written as:
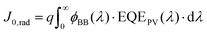 | (3) |
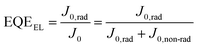 | (4) |
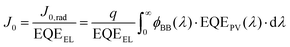 | (5) |
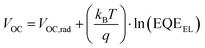 | (6) |
It is worth noting that because the black-body photon flux increases exponentially towards lower energies, tail state absorption makes the largest contribution to J0. In fact, the magnitude of J0 is almost exclusively dictated by the position of the absorption tail. Thus, even small increases in tail-state absorption can increase J0 by orders of magnitude, lowering VOC (cf.eqn (1)). These tail states could even be so small as to be virtually invisible to conventional UV-vis absorption spectroscopy or EQEPV measurements. Consequently, their impact on JSC would be negligible. However, their impact on the VOC would be significant. This fact is central to the understanding of how the presence of low-bandgap phases affects VOC.
The presence of a low-bandgap minority phase in the perovskite film can be expected to show up as a “bump” in the sub-bandgap absorptance. The magnitude of the absorption feature would be determined by the fraction of the film converted to the minority phase. As we have explained above, even a small below bandgap absorption feature would be sufficient to increase J0 significantly. If the feature is sufficiently large, J0 (and hence VOC) would be completely determined by the minority phase, independent of the bandgap of the majority phase. This is the thermodynamic reasoning behind the “pinning” of open-circuit voltage in cells exhibiting halide segregation.
We used a generalized transfer matrix37 based optical model and detailed balance calculations to model the impact of halide segregation on VOC in the radiative limit. The model serves to reveal the susceptibility of different compositions to VOC losses upon halide segregation. We fixed the minority phase bandgap at 1.66 eV, consistent with reports of minority phase composition being 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 Br
80 Br![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I, regardless of majority phase bandgap.38 We modelled the complex refractive index of the perovskite as a Bruggeman effective medium39 of the minority and majority phases. We then used the generalized transfer matrix method to calculate the cell EQEPV in an ITO/SnO2/perovskite/spiro-OMeTAD/gold stack. Our modelled EQEPV curves show a “bump” in the sub-gap absorption whose magnitude increases with fraction of minority phase (Fig. 1c). We then employed detailed balance calculations to estimate the VOC in the radiative limit as a function of percentage of minority phase in the film (Fig. 1d).
I, regardless of majority phase bandgap.38 We modelled the complex refractive index of the perovskite as a Bruggeman effective medium39 of the minority and majority phases. We then used the generalized transfer matrix method to calculate the cell EQEPV in an ITO/SnO2/perovskite/spiro-OMeTAD/gold stack. Our modelled EQEPV curves show a “bump” in the sub-gap absorption whose magnitude increases with fraction of minority phase (Fig. 1c). We then employed detailed balance calculations to estimate the VOC in the radiative limit as a function of percentage of minority phase in the film (Fig. 1d).
Our model reveals that VOC drops off logarithmically once the minority phase fraction exceeds a certain threshold. This threshold is smaller for larger bromide concentrations. For instance, an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 Br
20 Br![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I film with 0.01% minority phase, incurs a voltage penalty of 76 mV. However, a 40
I film with 0.01% minority phase, incurs a voltage penalty of 76 mV. However, a 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60 Br
60 Br![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I film will shows almost no VOC loss at the same minority phase percentage. At higher minority phase concentrations (>1%), the VOC is similar (“pinned”) for all majority phase compositions, but notably still around 70 mV larger than the VOC generated from a 100% minority phase composition cell.
I film will shows almost no VOC loss at the same minority phase percentage. At higher minority phase concentrations (>1%), the VOC is similar (“pinned”) for all majority phase compositions, but notably still around 70 mV larger than the VOC generated from a 100% minority phase composition cell.
Results and discussion
Photo-induced sub-bandgap states
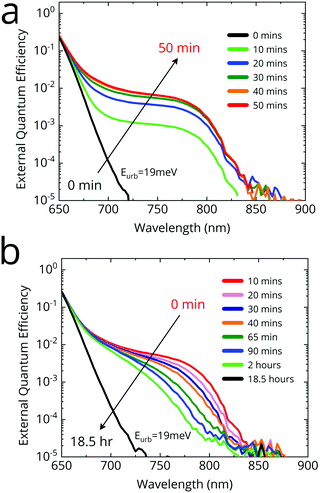
We used Fourier transform photocurrent spectroscopy (FTPS) to study the effect of simulated sunlight on the external quantum efficiency of an FA0.83MA0.17Pb(I0.4Br0.6)3 solar cell deposited via the anti-solvent quenching method. In Fig. 2a we show the time-evolution of the external quantum efficiency (EQEPV) spectrum of an FA0.83MA0.17Pb(I0.4Br0.6)3 device under simulated AM1.5 illumination. We use simulated AM1.5 illumination as phase segregation has been shown to be sensitive to illumination spectrum and intensity.40 We held the cells at open-circuit at all times. After 10 minutes of light soaking, we observe a new shoulder at ∼780 nm (1.59 eV) in the sub-bandgap region of the EQEPV spectrum, consistent with the photo-induced formation of iodide-rich impurity phases. We observe this feature to grow, and eventually saturate at about 1% quantum efficiency after 40 minutes. At saturation, the absorption edge of the feature is approximately 800 nm (1.55 eV), as determined from the EQEPV inflection point. We identify this feature as absorption from the iodide-rich regions formed upon illumination (we note that the A site composition is FA-rich, and hence lower bandgap than MAPbX3 perovskites41). We shall henceforth refer to the iodide-rich regions as the minority phase, and the phase in which the minority phase is embedded as the majority phase. The appearance of the minority phase causes virtually no change in the bandgap of the majority phase, and is hence virtually invisible to conventional UV-vis absorption spectroscopy. Consequently, the photo-induced carrier generation rate in the cell is unaffected. Upon being kept in dark, we observe the feature to relax back towards the original starting point, albeit much more slowly over more than 18 hours (Fig. 2b). Incidentally, upon halide “de-segregation”, the minority phase appears to progressively become less rich in iodide. This is in contrast to segregation, where the heavily iodide-rich phase rapidly forms first. We interpret this to imply that halide segregation proceeds by first nucleating the lowest-bandgap phase, followed by the growth of this phase. In contrast, during desegregation, the iodide-rich phase absorption gradually blue shifts, while also reducing in intensity. This suggests that the mechanism of desegregation is likely to be entropic mixing, which causes the minority phase to be slowly enriched with bromide, consistent with disappearance of the most iodide-rich phases first.Bandgap distribution in a halide segregated absorber
Studies so far treat halide segregation as a simple two phase phenomenon.38,40,42,43 A minority phase of a single composition (often 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 80 Br
80 Br![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I) is assumed to have formed, which is the source of the low-energy photoluminescence peak. In practice, such a clear-cut phase separation is unlikely. A continuum in iodide concentration, or at least multiple phases are more probable. Our FTPS measurements (Fig. 3) confirm this hypothesis. The absorption edge of the pristine cell has an Urbach energy of 19 meV. As the film segregates, we estimate the Urbach energy of the majority phase to increase, reaching 40 meV after 50 minutes of light soaking. This points to considerable compositional inhomogeneity in the majority phase due to segregation. Serious VOC losses are expected when the Urbach energy exceeds kBT.44 This loss mechanism in halide segregated films has hitherto escaped attention. However, the most significant losses do arise from the iodide-rich minority phase. The appearance of a nearly flat shoulder between 725–800 nm indicates that the minority phase is comprised of material with a narrow bandgap range centered on 1.55 eV. The Urbach energy of the tail is 19 meV—similar to that of the unsegregated film, but notably slightly larger than the ∼15 meV expected for FA0.83MA0.17PbI3.
I) is assumed to have formed, which is the source of the low-energy photoluminescence peak. In practice, such a clear-cut phase separation is unlikely. A continuum in iodide concentration, or at least multiple phases are more probable. Our FTPS measurements (Fig. 3) confirm this hypothesis. The absorption edge of the pristine cell has an Urbach energy of 19 meV. As the film segregates, we estimate the Urbach energy of the majority phase to increase, reaching 40 meV after 50 minutes of light soaking. This points to considerable compositional inhomogeneity in the majority phase due to segregation. Serious VOC losses are expected when the Urbach energy exceeds kBT.44 This loss mechanism in halide segregated films has hitherto escaped attention. However, the most significant losses do arise from the iodide-rich minority phase. The appearance of a nearly flat shoulder between 725–800 nm indicates that the minority phase is comprised of material with a narrow bandgap range centered on 1.55 eV. The Urbach energy of the tail is 19 meV—similar to that of the unsegregated film, but notably slightly larger than the ∼15 meV expected for FA0.83MA0.17PbI3.
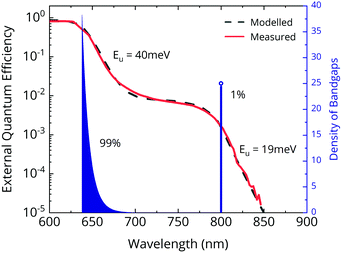 | ||
| Fig. 3 Modelled halide segregated EQEPV (dotted green) and the distribution of bandgaps in perovskite (blue) at saturated halide segregation. | ||
We model the halide segregated EQEPV (Fig. 2a; red curve at 50 min) using the generalized transfer matrix method45 and effective medium approximation, and use it to extract the distribution of bandgaps in the material. We find that the majority phase exhibits an exponential distribution of bandgaps, decaying from a peak at 640 nm. The minority phase has a single bandgap at 800 nm. Through our model, we estimate that the minority phase occupies about 1% by volume of the film (assuming the optical density scales with thickness). This is in agreement with previous estimation at 1% by Hoke et al.38 The extent of segregation can also be roughly estimated from the EQEPV, by observing the magnitude of the minority phase absorption, which is also ∼1%. This follows from Lambert's law, since EQEPV scales linearly with absorptance at low-absorptance (≪1).
Open-circuit voltage penalty due to halide segregation
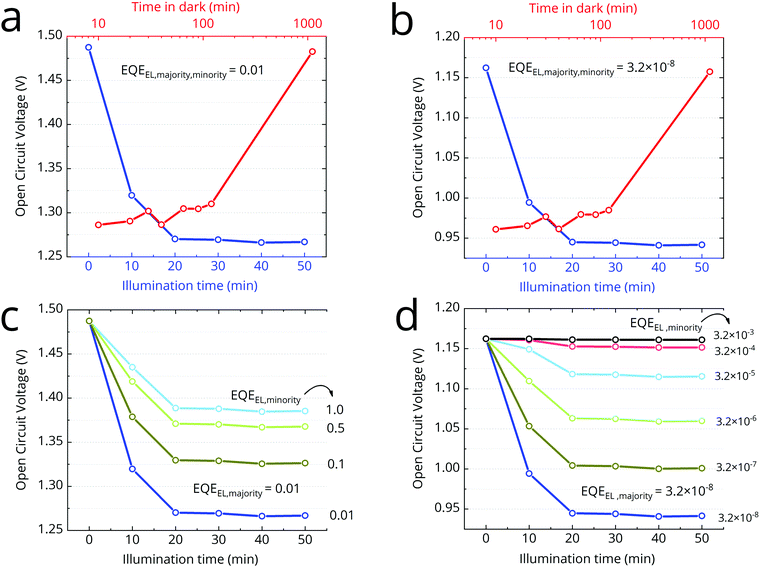
In the context of solar cells, the severity of halide-segregation is best characterized by the accompanying VOC loss. Here, we perform detailed balance calculations on the presented FTPS data to determine the expected loss in VOC arising from halide-segregation. This calculated loss can be used as a measure of the severity of halide-segregation in a cell. We perform the previously described detailed balance calculations (eqn (1), (2) and (5)) on the measured time dependent EQEPV spectra (Fig. 2a and b) to get the expected time dependence of the open-circuit voltage (Fig. 4). In the first instance, we assume that both the majority and minority phase have the same time-invariant radiative efficiency, EQEEL (expressed as a fraction of unity, where EQEEL = 1 is 100%). The magnitude of the voltage loss arising from halide segregation is not dependent on the choice of EQEEL, as long it does not vary with time. So its precise value is not relevant. Later, we also discuss the case of the two phases having different EQEEL.The best perovskite cells (with a bandgap of ∼1.6 eV) today typically have an EQEEL ∼ 0.01.46 We set EQEEL = 0.01 for both the minority and majority phases and calculate the time evolution of VOC (Fig. 4b). We calculate VOC = 1.49 eV from the pristine cell. As segregation proceeds in time, we calculate that the VOC should drop very rapidly in the beginning, losing 170 mV in 10 minutes, despite sub-bandgap EQEPV being just ∼0.1%. After 20 minutes, we estimate the VOC to have dropped by 220 mV and hit 1.27 V. After 20 minutes, we determine that the VOC is stable at 1.27 V, despite an increasing sub-bandgap absorption. Thus, we estimate that the total VOC loss at saturated segregation to be 220 mV. This loss is independent of the EQEEL chosen, provided it does not change during time under illumination. Setting EQEEL = 3.2 × 10−8 predicts a more realistic VOC = 1.16 V from pristine cell (eqn (5)). The calculated VOC loss due to segregation, however, remains the same at 220 mV (Fig. 4b).
Impact of enhanced EQEEL of minority phase
Since the carrier diffusion length in these materials is relatively long, the charge carriers will explore a large volume of film under open-circuit conditions, when they are not being extracted. Therefore, they are likely to find the low bandgap minority phase regions, and will become localized within these regions due to energetic confinement. In a real cell, the minority phase occupies a small fraction of the total film volume. Since the emission from a halide-segregated film is predominantly via this lower energy phase, we know that there is a predominant accumulation of charge carriers in this region. This accumulation of carriers within the low bandgap regions of mixed phase perovskites, is often referred to as charge-funneling.47 The average carrier concentration within the minority phases, will therefore be much higher than in the majority phase regions (and non-segregated film). For a 1% segregated film, this may therefore result in a 100 fold increase in charge-carrier density within the low bandgap phase (in comparison to the charge density in the unsegregated majority phase). This increased charge density will promote radiative recombination, due to bimolecular radiative recombination competing more strongly with monomolecular non-radiative recombination. Trap filling from the local increase in carrier density will also serve to increase the radiative efficiency.48 This therefore suggests that we would expect an increased EQEEL from the minority phase. We note that a narrower bandgap 3D minority phase inclusion in a wider bandgap 2D majority phase matrix, is the strategy adopted for the best perovskite light emitting diodes.47 In our case here, the increase in radiative efficiency of the iodide-rich minority phase, would cause the drop in VOC to be less dramatic. Thus we expect that the 220 mV loss we estimate from the EQEPV measurements, is an upper-bound for the VOC loss. We also calculate the VOC (Fig. 4c) by varying the EQEEL of the minority phase, while keeping the majority phase EQEEL fixed at 0.01. We find that every ten-fold increase in the radiative efficiency of the minority phase, the VOC loss due to halide segregation reduces by ∼55 meV.If we set the majority phase EQEEL at a realistic 3.2 × 10−8, we can vary minority phase EQEEL by many more orders of magnitude (Fig. 4d). When we choose the radiative recombination of the minority phase to be 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 times higher than the majority phase, then we estimate no VOC loss following halide segregation. In this case, the recombination rate in the absorber would be controlled by fast non-radiative recombination in the majority phase, and the formation of a low-bandgap phase would only cause a negligible increase in the net recombination rate.
000 times higher than the majority phase, then we estimate no VOC loss following halide segregation. In this case, the recombination rate in the absorber would be controlled by fast non-radiative recombination in the majority phase, and the formation of a low-bandgap phase would only cause a negligible increase in the net recombination rate.
In order to understand the impact of the enhanced EQEEL that we just described, we measure the time evolution of the open-circuit voltage of a pristine FA0.83MA0.17Pb(I0.4Br0.6)3 cell (bandgap 1.94 eV) under simulated AM1.5 conditions (Fig. 5). We observe the voltage to drop quickly initially and then stabilize with a VOC loss of around 120 mV after 20 minutes. This is consistent with the behavior predicted by our EQEPV measurements (Fig. 4). We model the curve using the approach previously presented (Fig. 5), and vary the EQEEL of the majority and minority phase until we achieve a similar trend. We find consistency if we set the EQEEL of the majority phase to 3.2 × 10−8, and the EQEEL of the minority phase to 6.2 × 10−7. This suggests a 19-fold enhanced EQEEL in the minority phase, as compared to the majority phase, which seems to be perfectly reasonable.
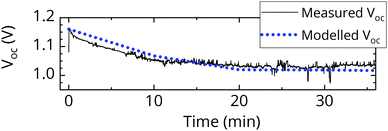 | ||
| Fig. 5 Measured time evolution of the VOC of a halide segregating cell (black). The modelled VOC (dotted blue) allows us to extract EQEEL,majority = 3.2 × 10−8 and EQEEL,minority = 6.2 × 10−7. | ||
Halide segregation in FACs based perovskite cells
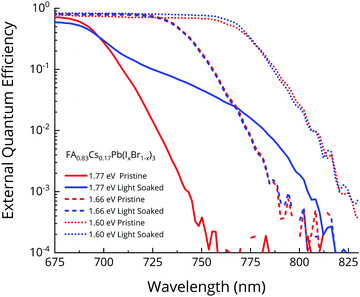
In order to quantify the VOC penalty from halide segregation, in the preceding sections we presented studies on a perovskite composition (FAMA based) and bandgap (1.94 eV) that rapidly underwent halide segregation, in order to exemplify our theoretical assessment. However, in order to exemplify more state-of-the-art wide bandgap compositions, we now present results for the FA0.83Cs0.17Pb(IxBr1−x)3 family. We fabricated FA0.83Cs0.17Pb(IxBr1−x)3 based p–i–n devices of three different bandgaps: 1.77 eV (40% Br, suitable for perovskite–perovskite tandems49), 1.66 eV (23% Br, ideal for perovskite–silicon tandems49), and 1.60 eV (10% Br, best bandgap for single-junction performance in our lab). We light soaked the devices for two hours under 1 sun simulated AM1.5 illumination, till the absorption tail was seen to evolve no more, and show the measured FTPS-EQEPV spectra for the pristine and light-soaked devices in Fig. 6. We provide the VOC for the same devices, tracked simultaneously as the FTPS measurement, in the ESI† (Fig. S1).The 1.66 eV and 1.60 eV absorbers show negligible changes in the absorption tail, indicating that the low bandgap phase segregated fraction is less than our resolution limit of 10−4. As our modelling (Fig. 1d) has indicated, this will be accompanied by negligible VOC loss. Furthermore, the Urbach energy, which is a measure of electronic disorder, is just 15 meV before and after segregation, suggesting that no segregation has occurred. The 1.77 eV bandgap absorber (40% Br), on the other hand, undergoes halide-segregation, evolving a sub bandgap absorption feature. The formed absorption shoulder is also quite broad, suggesting that there is no single prominent composition, but only a mixture of phases. A detailed balance calculation on the EQEPV of this 1.77 eV cell, presented in Fig. 6, reveals a 97 mV VOC penalty due to halide-segregation, assuming no change in the radiative efficiency EQEEL during segregation. As we have already explained, we expect that the actual VOC loss will be less than 97 mV, owing to increased radiative efficiency of the iodide-rich phase. Indeed, the VOC measurement done simultaneously with the FTPS-EQEPV reveals that the loss is only 75 mV, since the VOC drops from 1.105 V to 1.030 V.
The key factor limiting the VOC of wide band gap mixed-halide perovskite cells
In the preceding sections, we combined sensitive EQEPV measurements with detailed balance calculations to quantify the VOC penalty due to halide segregation in FAMA and FACs based mixed-halide perovskite cells. In this section, we quantitatively compare the segregation-loss to the non-radiative VOC loss.In our FAMA based 1.94 eV bandgap cell, we calculated the expected VOC to be 1.61 V in the radiative limit. Our cell shows a VOC, prior to halide segregation, of 1.16 V, suggesting an initial EQEEL ∼ 10−8 (from eqn (6)). The situation is similar in our FACs based 1.77 eV bandgap device, which in the radiative limit would deliver a 1.49 V VOC. However, the device exhibits a VOC, prior to halide segregation of 1.105 V, suggesting an initial EQEEL ∼ 10−6. The non-radiative VOC loss in this instance (385 mV) is over five times the segregation loss (75 mV). Clearly, the VOC loss due to non-radiative recombination is much more overwhelming than the loss from segregation. In comparison, the best perovskite cells (∼1.6 eV) have non-radiative losses of approximately 60 mV.50 If this is achieved for 1.94 and 1.77 eV bandgap cells, they would deliver a VOC of 1.54 and 1.43 V respectively, prior to halide segregation. Hence, even if halide segregation occurred, and induced a voltage penalty to the same extent that we have measured here, we would still reach open-circuit voltages of 1.42 V and 1.33 V for the 1.94 eV and 1.77 eV bandgap cells respectively.
Therefore, the performance of mixed-halide perovskites is predominantly limited by trap-assisted non-radiative recombination and not halide-segregation. The problem in mixed-halide perovskites seems to be two-fold: (a) non-radiative recombination within the perovskite absorber and (b) interfacial non-radiative recombination at the perovskite/charge extraction layer heterojunctions. In our 1.77 eV bandgap FACs based devices, the Urbach energy, which represents electronic disorder in the continuum of states, is low at only 15 meV. This indicates that the poor quality does not arise from electronic disorder in the bands. We measure a PLQE of approximately 0.3% for the isolated perovskite film on glass. In comparison, the PLQE of the best metal halide perovskite films (∼1.6 eV bandgap) is over 10%. Therefore, efforts are required to minimise the defects responsible for non-radiative recombination in these wider band gap mixed-halide perovskites. A further significant loss occurs due to the poor electronic quality of the perovskite/charge-transport-layer heterojunctions. Considering the difference between the inferred EQEEL (10−6) and the PLQE of the isolated perovskite film (10−3), we infer that the contact materials quench the PLQE by three orders of magnitude. From this perspective, the electron-transport layer Phenyl-C61-butyric acid methyl ester (PCBM) is particularly deleterious, since it significantly quenches the PLQE of our 1.77 eV gap perovskite films to below our detector limit (0.01%). By considering these absolute radiative efficiency values, we can estimate that the non-radiative losses from within the 1.77 eV gap perovskite absorber are responsible for ∼180 mV loss in VOC, and the integration into the device induces a further ∼180 mV loss, with the latter primarily governed by the charge extraction layer/perovskite heterojunctions.
Thus, as a first priority, improved transport layers have to be identified by a systematic study of PL quenching, using the approach demonstrated by M. Stolterfoht et al.51 The development of new transport layers with new doping strategies to enable better band alignment, is also essential. Efforts to optimise the crystallisation and passivation of defects are also needed to eventually bring the PLQE of wide bandgap films on par with the best 1.6 eV bandgap films (∼10%).
As a final note, halide segregation has itself been found to correlate positively with the fraction of non-radiative recombination in the film.26 In addition, halide segregation has been shown to be highly suppressed in perovskite films with lower trap densities.26,52,53 We may therefore postulate that it is the accumulated trapped charge which offers the electrostatic driving force for halide-segregation. We therefore expect that the route to maximise the radiative efficiency via reducing the trap density in the mixed-halide perovskites will not only maximise the initial VOC, but will also likely overcome halide segregation itself.
Conclusions
In conclusion, we have quantified the impact of halide-segregation upon the open-circuit voltage (VOC) of mixed-halide perovskite solar cells, using Fourier-transform photocurrent spectroscopy (FTPS) measurements coupled with detailed balance calculations. Our results reveal that the VOC loss from non-radiative recombination (∼400 mV) is four to five times the loss from halide-segregation (∼100 mV) in both FAMA (1.94 eV) and FACs (1.77 eV) based solar cells. These results represent the first quantitative evaluation of the contribution of halide-segregation towards the poor performance of mixed-halide perovskite cells. We suggest that currently, the performance of mixed-halide cells is limited by poor electronic quality of the perovskite cell which results in a low radiative efficiency, and not by halide segregation. The cause of this low radiative efficiency is twofold: (a) perovskite absorber with a high degree of trap assisted non-radiative recombination and (b) poor electronic quality of perovskite/charge-transport-layer heterojunctions, leading to “heterojunction-induced” non-radiative losses.To reach higher open-circuit voltages, improving the radiative efficiencies of mixed-halide perovskite films, and developing more efficient perovskite/charge extraction layer interfaces should be viewed as a matter of priority. With such improved materials processing, we suggest that a VOC of up to 1.33 V is within reach for a 1.77 eV perovskite, even if halide segregation remains unsuppressed. Our work clearly highlights that the means to solve the voltage deficit issue in wide band gap mixed-halide cells, is to focus on reducing the initial defect density, and to neglect halide segregation as an issue, until improved radiative efficiency has been achieved. We also suggest that future studies on mixed-halide perovskites should include sensitive EQEPV measurements coupled with detailed balance calculations to clearly differentiate VOC loss due to halide-segregation and non-radiative recombination.
Author contributions
S. M. analysed the data and performed all the calculations. D. P. M. and R. D. J. O. fabricated the perovskite cells. S. M., J. M. B. and R. D. J. O. performed the FTPS measurements and measured the JV curves for the solar cells. M. B. J. supervised the FTPS measurements and discussed the results, which were measured by S. M., J. M. B. and R. D. J. O. P. K. N. contributed with discussion and feedback for the data analysis and calculations. S. M. and H. J. S. wrote the manuscript. All authors discussed the results and reviewed the manuscript. P. K. N. and H. J. S. guided and supervised the overall project.Conflicts of interest
H. J. S. is cofounder and CSO of Oxford PV Ltd, a company that is commercializing perovskite PV technologies.Acknowledgements
S. M. acknowledges funding from the Rhodes Trust via a Rhodes scholarship (India & Worcester 2016). We thank Zhiping Wang for contributing perovskite solar cell devices towards our study. R. D. J. O. gratefully thanks the Penrose Scholarship for funding. This work was supported by the UK Engineering and Physical Sciences Research Council (EPSRC) grants EP/P006329/1 and EP/S004947/1. The research leading to these results has also received funding from the European Union's Horizon 2020 Research and Innovation Programme under grant agreement no. 763977 of the PerTPV project.Notes and references
- M. M. Lee, J. Teuscher, T. Miyasaka, T. N. Murakami and H. J. Snaith, Science, 2012, 338, 643–647 CrossRef CAS PubMed.
- Best Research-Cell Efficiency Chart, https://www.nrel.gov/pv/cell-efficiency.html, accessed 18 April 2019.
- A. K. Jena, A. Kulkarni and T. Miyasaka, Chem. Rev., 2019, 119, 3036–3103 CrossRef CAS PubMed.
- S.-R. Bae, Q. Van Le and S.-Y. Kim, Ceramist, 2019, 21, 24–43 CrossRef.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- G. E. Eperon, M. T. Hörantner and H. J. Snaith, Nat. Rev. Chem., 2017, 1, 95 CrossRef CAS.
- T. Leijtens, K. A. Bush, R. Prasanna and M. D. McGehee, Nat. Energy, 2018, 3, 828–838 CrossRef CAS.
- F. Sahli, J. Werner, B. A. Kamino, M. Bräuninger, R. Monnard, B. Paviet-Salomon, L. Barraud, L. Ding, J. J. Diaz Leon, D. Sacchetto, G. Cattaneo, M. Despeisse, M. Boccard, S. Nicolay, Q. Jeangros, B. Niesen and C. Ballif, Nat. Mater., 2018, 17, 820–826 CrossRef CAS PubMed.
- K. A. Bush, A. F. Palmstrom, Z. J. Yu, M. Boccard, R. Cheacharoen, J. P. Mailoa, D. P. McMeekin, R. L. Z. Hoye, C. D. Bailie, T. Leijtens, I. M. Peters, M. C. Minichetti, N. Rolston, R. Prasanna, S. Sofia, D. Harwood, W. Ma, F. Moghadam, H. J. Snaith, T. Buonassisi, Z. C. Holman, S. F. Bent and M. D. McGehee, Nat. Energy, 2017, 2, 17009 CrossRef CAS.
- L. Mazzarella, Y. H. Lin, S. Kirner, A. B. Morales-Vilches, L. Korte, S. Albrecht, E. Crossland, B. Stannowski, C. Case, H. J. Snaith and R. Schlatmann, Adv. Energy Mater., 2019, 9, 1–9 Search PubMed.
- G. E. Eperon, et al. , Science, 2016, 354, 861–865 CrossRef CAS PubMed.
- D. Zhao, C. Chen, C. Wang, M. M. Junda, Z. Song, C. R. Grice, Y. Yu, C. Li, B. Subedi, N. J. Podraza, X. Zhao, G. Fang, R. G. Xiong, K. Zhu and Y. Yan, Nat. Energy, 2018, 3, 1093–1100 CrossRef CAS.
- A. Rajagopal, Z. Yang, S. B. Jo, I. L. Braly, P.-W. Liang, H. W. Hillhouse and A. K. Y. Jen, Adv. Mater., 2017, 29, 1702140 CrossRef PubMed.
- D. P. McMeekin, S. Mahesh, N. K. Noel, M. T. Klug, J. Lim, J. H. Warby, J. M. Ball, L. M. Herz, M. B. Johnston and H. J. Snaith, Joule, 2019, 3, 387–401 CrossRef CAS.
- J. Tong, Z. Song, D. H. Kim, X. Chen, C. Chen, A. F. Palmstrom, P. F. Ndione, M. O. Reese, S. P. Dunfield, O. G. Reid, J. Liu, F. Zhang, S. P. Harvey, Z. Li, S. T. Christensen, G. Teeter, D. Zhao, M. M. Al-Jassim, M. F. A. M. van Hest, M. C. Beard, S. E. Shaheen, J. J. Berry, Y. Yan and K. Zhu, Science, 2019, 364, 475–479 CrossRef CAS PubMed.
- T. Todorov, T. Gershon, O. Gunawan, Y. S. Lee, C. Sturdevant, L.-Y. Chang and S. Guha, Adv. Energy Mater., 2015, 5, 1500799 CrossRef.
- Q. Han, Y.-T. Hsieh, L. Meng, J.-L. Wu, P. Sun, E.-P. Yao, S.-Y. Chang, S.-H. Bae, T. Kato, V. Bermudez and Y. Yang, Science, 2018, 361, 904–908 CrossRef CAS PubMed.
- F. Fu, T. Feurer, T. P. Weiss, S. Pisoni, E. Avancini, C. Andres, S. Buecheler and A. N. Tiwari, Nat. Energy, 2017, 2, 16190 CrossRef CAS.
- Oxford PV perovskite solar cell achieves 28% efficiency, https://www.oxfordpv.com/news/oxford-pv-perovskite-solar-cell-achieves-28-efficiency, accessed 18 April 2019.
- E. T. Hoke, D. J. Slotcavage, E. R. Dohner, A. R. Bowring, H. I. Karunadasa and M. D. McGehee, Chem. Sci., 2015, 6, 613–617 RSC.
- D. J. Slotcavage, H. I. Karunadasa and M. D. McGehee, ACS Energy Lett., 2016, 1, 1199–1205 CrossRef CAS.
- C. G. Bischak, C. L. Hetherington, H. Wu, S. Aloni, D. F. Ogletree, D. T. Limmer and N. S. Ginsberg, Nano Lett., 2017, 17, 1028–1033 CrossRef CAS PubMed.
- M. C. Brennan, S. Draguta, P. V. Kamat and M. Kuno, ACS Energy Lett., 2018, 3, 204–213 CrossRef CAS.
- G. F. Samu, C. Janáky and P. V. Kamat, ACS Energy Lett., 2017, 2, 1860–1861 CrossRef CAS.
- S. J. Yoon, M. Kuno and P. V. Kamat, ACS Energy Lett., 2017, 2, 1507–1514 CrossRef CAS.
- A. J. Knight, A. D. Wright, J. B. Patel, D. P. McMeekin, H. J. Snaith, M. B. Johnston and L. M. Herz, ACS Energy Lett., 2019, 4, 75–84 CrossRef CAS.
- W. Rehman, D. P. McMeekin, J. B. Patel, R. L. Milot, M. B. Johnston, H. J. Snaith and L. M. Herz, Energy Environ. Sci., 2017, 10, 361–369 RSC.
- M. Hu, C. Bi, Y. Yuan, Y. Bai and J. Huang, Adv. Sci., 2016, 3, 1500301 CrossRef PubMed.
- Y. Zhou, Y.-H. Jia, H.-H. Fang, M. A. Loi, F.-Y. Xie, L. Gong, M.-C. Qin, X.-H. Lu, C.-P. Wong and N. Zhao, Adv. Funct. Mater., 2018, 28, 1803130 CrossRef.
- Z. Liu, L. Krückemeier, B. Krogmeier, B. Klingebiel, J. A. Márquez, S. Levcenko, S. Öz, S. Mathur, U. Rau, T. Unold and T. Kirchartz, ACS Energy Lett., 2019, 4, 110–117 CrossRef CAS.
- T. C.-J. Yang, P. Fiala, Q. Jeangros and C. Ballif, Joule, 2018, 2, 1421–1436 CrossRef CAS.
- M. Abdi-Jalebi, Z. Andaji-Garmaroudi, S. Cacovich, C. Stavrakas, B. Philippe, J. M. Richter, M. Alsari, E. P. Booker, E. M. Hutter, A. J. Pearson, S. Lilliu, T. J. Savenije, H. Rensmo, G. Divitini, C. Ducati, R. H. Friend and S. D. Stranks, Nature, 2018, 555, 497–501 CrossRef CAS PubMed.
- T. Kirchartz and U. Rau, Phys. Status Solidi A, 2008, 205, 2737–2751 CrossRef CAS.
- S. M. Sze and K. K. Ng, Physics of Semiconductor Devices, Springer International Publishing, Cham, 2014 Search PubMed.
- E. Radziemska, Int. J. Energy Res., 2006, 30, 127–134 CrossRef.
- U. Rau, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 1–8 CrossRef.
- C. C. Katsidis and D. I. Siapkas, Appl. Opt., 2002, 41, 3978 CrossRef PubMed.
- E. T. Hoke, D. J. Slotcavage, E. R. Dohner, A. R. Bowring, H. I. Karunadasa and M. D. McGehee, Chem. Sci., 2015, 6, 613–617 RSC.
- G. A. Niklasson, C. G. Granqvist and O. Hunderi, Appl. Opt., 2008, 20, 26 CrossRef PubMed.
- D. J. Slotcavage, H. I. Karunadasa and M. D. McGehee, ACS Energy Lett., 2016, 1, 1199–1205 CrossRef CAS.
- G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988 RSC.
- S. J. Yoon, S. Draguta, J. S. Manser, O. Sharia, W. F. Schneider, M. Kuno and P. V. Kamat, ACS Energy Lett., 2016, 1, 290–296 CrossRef CAS.
- A. J. Barker, A. Sadhanala, F. Deschler, M. Gandini, S. P. Senanayak, P. M. Pearce, E. Mosconi, A. J. Pearson, Y. Wu, A. R. Srimath Kandada, T. Leijtens, F. De Angelis, S. E. Dutton, A. Petrozza and R. H. Friend, ACS Energy Lett., 2017, 2, 1416–1424 CrossRef CAS.
- J. Jean, T. S. Mahony, D. Bozyigit, M. Sponseller, J. Holovský, M. G. Bawendi and V. Bulović, ACS Energy Lett., 2017, 2, 2616–2624 CrossRef CAS.
- E. Centurioni, Appl. Opt., 2005, 44, 7532 CrossRef PubMed.
- P. K. Nayak, S. Mahesh, H. J. Snaith and D. Cahen, Nat. Rev. Mater., 2019, 4, 269–285 CrossRef CAS.
- M. Yuan, L. N. Quan, R. Comin, G. Walters, R. Sabatini, O. Voznyy, S. Hoogland, Y. Zhao, E. M. Beauregard, P. Kanjanaboos, Z. Lu, D. H. Kim and E. H. Sargent, Nat. Nanotechnol., 2016, 11, 872–877 CrossRef CAS PubMed.
- F. Deschler, M. Price, S. Pathak, L. E. Klintberg, D. D. Jarausch, R. Higler, S. Hüttner, T. Leijtens, S. D. Stranks, H. J. Snaith, M. Atatüre, R. T. Phillips and R. H. Friend, J. Phys. Chem. Lett., 2014, 5, 1421–1426 CrossRef CAS PubMed.
- M. T. Hörantner, T. Leijtens, M. E. Ziffer, G. E. Eperon, M. G. Christoforo, M. D. McGehee and H. J. Snaith, ACS Energy Lett., 2017, 2, 2506–2513 CrossRef.
- Q. Jiang, Y. Zhao, X. Zhang, X. Yang, Y. Chen, Z. Chu, Q. Ye, X. Li, Z. Yin and J. You, Nat. Photonics, 2019, 13, 460–466 CrossRef CAS.
- M. Stolterfoht, C. M. Wolff, J. A. Márquez, S. Zhang, C. J. Hages, D. Rothhardt, S. Albrecht, P. L. Burn, P. Meredith, T. Unold and D. Neher, Nat. Energy, 2018, 3, 847–854 CrossRef CAS.
- D. P. McMeekin, Z. Wang, W. Rehman, F. Pulvirenti, J. B. Patel, N. K. Noel, M. B. Johnston, S. R. Marder, L. M. Herz and H. J. Snaith, Adv. Mater., 2017, 29, 1607039 CrossRef PubMed.
- D. P. McMeekin, G. Sadoughi, W. Rehman, G. E. Eperon, M. Saliba, M. T. Horantner, A. Haghighirad, N. Sakai, L. Korte, B. Rech, M. B. Johnston, L. M. Herz and H. J. Snaith, Science, 2016, 351, 151–155 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ee02162k |
| This journal is © The Royal Society of Chemistry 2020 |